- 1School of Environmental and Materials Engineering, Yantai University, Yantai, China
- 2Department of Earth Sciences, University of Cambridge, Cambridge, United Kingdom
The possibility to use ferroelastic materials as components of neuromorphic devices is discussed. They can be used as local memristors with the advantage that ionic transport is constraint to twin boundaries where ionic diffusion is much faster than in the bulk and does not leak into adjacent domains. It is shown that nano-scale ferroelastic memristors can contain a multitude of domain walls. These domain walls interact by strain fields where the interactions near surfaces are fundamentally different from bulk materials. We show that surface relaxations (∼image forces) are curtailed to short range dipolar interactions which decay as 1/d2 where d is the distance between domain walls. In bigger samples such interactions are long ranging with 1/d. The cross-over regime is typically in the range of some 200–1500 nm using a simple spring interaction model.
Introduction
In contrast to ferroelectric domain walls, ferroelastic domain walls (mostly twin walls) have the advantage that their ‘emerging properties’ are localized within domain walls while the adjacent domains play no role. This remarkable property (Salje, 2010) stems from the local symmetry breaking inside the domain wall but not in the domains. Typical emerging properties are the development of polarity in non-polar materials (Van Aert et al., 2012), high conductivity (Aird and Salje, 1998), photovoltaics (Bhatnagar et al., 2013) and atomic-scale transistors (Chai et al., 2020). Several of these properties exist also in ferroelectric domain walls, both show enhanced conductivity compared to that of the domains (Seidel et al., 2009; Catalan et al., 2012; Meier and Selbach, 2022), and their density and topological complexity can be modulated by the choice of the substrate and the system dimensions (Venkatesan et al., 2007; Nesterov et al., 2013; Feigl et al., 2014), e.g., the film thickness. The non-trivial electronic and transport properties have been demonstrated to be suitable for new applications of domain wall nanoelectronics (Catalan et al., 2012; Meier and Selbach, 2022). Both ferroelectric and ferroelastic domain walls have been proposed as memristor materials (Maksymovych et al., 2011; Kim et al., 2012; Ma et al., 2020; Salje, 2021a; Liu et al., 2023), and as key elements of neuromorphic devices (Indiveri et al., 2013; Christensen et al., 2022). The topology of these wall-related networks was described in (Cipollini et al., 2024) for ferroelectric domain boundaries, although the ferroelasticity of domain walls in materials like BiFeO3 (Kubel and Schmid, 1990; Balke et al., 2009) was ignored in (Cipollini et al., 2024). It was speculated in (Bose et al., 2017) that wiring together memristor devices enables the realization of cross-bar arrays for vector-matrix multiplications. Self-assembled memristor networks of nano-objects, such as nanoparticle self-assembled networks (Bose et al., 2017; Mambretti et al., 2022) or nanowire networks (Cultrera et al., 2021; Hochstetter et al., 2021; Milano et al., 2022), were identified as potential candidates for neuromorphic devices (Lu and Salje, 2024). Ferroelastic twin walls relate to the interface between two domains and not necessarily to any an epitaxial strain imposed by the substrate. The movement of ferroelastic twin walls can be extremely swift and can be initiated by electric fields (Casals et al., 2019). The rearrangement of twin walls often occurs during avalanche processes (Harrison and Salje, 2010). The typical time scale for avalanche movements is some femtoseconds and even an extended kink inside a twin walls can assume a speed faster than the highest speed of sound in the material under consideration (Salje et al., 2017). This very high speed of the wall movement is very difficult to measure experimentally. Examples are avalanche process where events which last below a microsecond are commonly observed (Ding et al., 2012; Chen et al., 2022; Chen et al., 2023). The scale invariance of the process implies that the true local process is orders of magnitude faster but, alas, we are limited in their observation by our limited electronic and piezo-electric detector capabilities. Alternatively, local “swinging”’ of ferroelastic domain walls can be observed in resonance ultrasonic spectroscopy (RUS) and Resonant Piezoelectric Spectroscopy (RPS) (Carpenter, 2015) where the upper frequency is again some 10 MHz. It appears that a big technological advance would be needed to extend the frequency range of avalanches detection and RUS to the GHz regime and above. Such facilities would be most useful for the investigation of the memory capacity and the memristor functionality is a wide range of materials. The driving force for devices is often the external strain exerted from the counter electrode in a memristor (Salje, 2012). Under appropriate boundary conditions, twin boundaries form complex, self-assembled neuromorphic networks where the coupling between twin walls is a key element in the neuromorphic performance (Pastor-Satorras and Vespignani, 2001; Strogatz, 2001; Moreno et al., 2004; Ghavasieh and De Domenico, 2023). In this paper we describe how sample sizes, surfaces, and defects interplay to determine how twin walls interact and how they form the common ferroelastic tangles (Viehland and Salje, 2014; Salje et al., 2016a). Typical ferroelastic materials which may be explored further for neuromorphic computation include WO3 (Aird and Salje, 2000; Kim et al., 2010), CaTiO3 (Lee et al., 2006) and Pb3(PO4)2 (Salje et al., 1993; Wruck et al., 1994).
Theoretical model
Ferroelastic domains, domain walls and the topological atomic kinks inside the walls are described by a Landau-type double-well potential on the interatomic interactions, as schematically shown in Figure 1. Our simulations are based on a two-dimensional toy model with two base atoms carrying negative charges (red atoms) and positive charges (yellow atoms). The total interactions can be divided into two main parts, i. e., short range pairwise interactions and long range Columbic interactions. The potential forms for the short range interactions are summarized in Table 1.
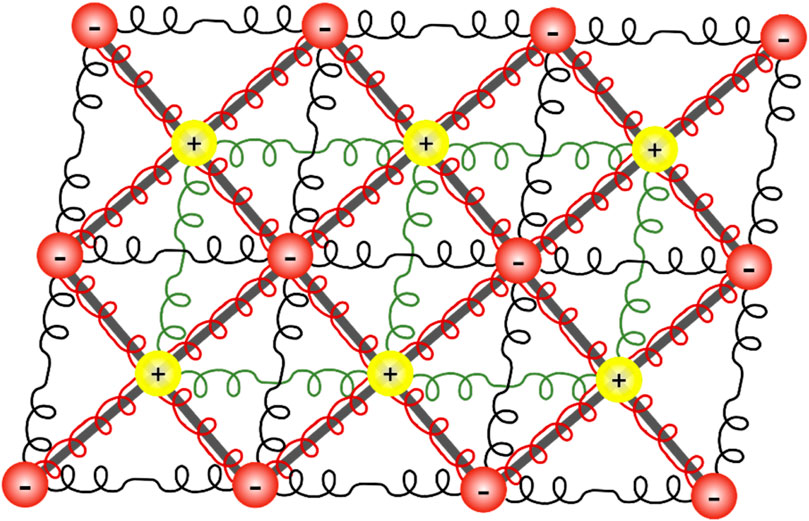
Figure 1. Interatomic potential for a generic ferroelastic model. The model consists of one anion and one cation, carrying elementary charge of 1.602 × 10−19C. Short-range inter-atomic interactions and long-range Coulombic interactions are considered in this ionic spring model.
Where r is the distance between atoms. The first- and third-nearest interactions are related to the elastic interactions and constitute the elastic background in ferroelastic materials. The second-nearest interaction has two minima which are symmetric with respect to
Results
Wall-wall interactions
In most high-density domain patterns, the interaction between domain boundaries stems from junctions between intersecting boundaries (Salje and Ishibashi, 1996; Salje, 2012; Lu et al., 2019a). The resultant domain patterns are highly complex with the intersection of horizontal and vertical domain walls. Many studies focus on the question how this structural complexity influences the switching process (Casals et al., 2021). Here we discuss the case of much milder interactions when such junctions are absent. The relevant inter-wall interaction is first described in a defect free system when the total energy depends on the system size because the main interaction mechanism is the volume strain and not the local shear strain (Lu et al., 2019c). In the case of noninteracting walls the energy is a simple superposition of the wall and the bulk energy. Interactions can still exist in case of electronic interactions. However, such interactions are restricted to lengths scales of the wall thickness and are not relevant in this context (Lajzerowicz and Levanyuk, 1994; Nataf et al., 2020). In simulations using our potentials, the averaged bulk potential energy is −27.41 meV per atom. The averaged excess energy of two polar walls with respect to the bulk is 1.86 meV per atom, which corresponds to a wall energy of 1.19 × 10−9 mJ/m in our two-dimensional structure. Expanding into three dimensions, this value is close to wall energies estimated in three-dimensional structures, which is approximately 20 mJ/m2 (Salje et al., 2005; Barone et al., 2014; Viehland and Salje, 2014). The equivalent potential energy for the bulk and nonpolar walls (when the charges in then model are set to zero) is 10.95 meV and the excess energy of two nonpolar walls is 1.87 meV per atom. The effect of the two walls in this rather dense wall configuration is hence some 10%–20% of the total energy and is large enough to trigger pattern formation of the domain walls. In the nonpolar case, the resulting potential energy is independent of the interwall distance beside for very small distances when the local strain fields overlap (Figure 2A). This is different from the polar system where we find an energy minimum near 25 lattice units which corresponds to approximately 125 nm in a typical perovskite structure. For larger distances we find a weak attractive dipole-dipole interaction (Figure 2B).
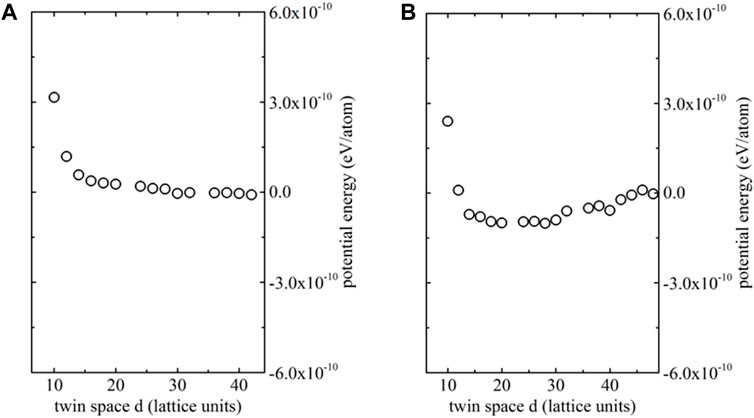
Figure 2. Potential energy of a system with two non-polar domain walls (A) and polar domain walls (B). While the non-polar domain walls repel each other at very short distances, there is no stable wall-wall distance. In the case of polar domain walls this stability point is some 25 lattice units and the stability energy is some 10−10 eV/atom. The increase at small distances is due to the overlap of the strain fields near the walls.
The field dependence of the pair interaction is shown in Figure 3. These results show that purely elastic interactions lead to repulsion over very small distances while the additional dipole moments in domain walls lead to much longer-range interactions and a shallow energy minimum which is the origin of an “intrinsically” stable interwall distance. The dipoles can be swayed by electric fields perpendicular to the walls so that the wall-wall interaction can be modified by electric fields.
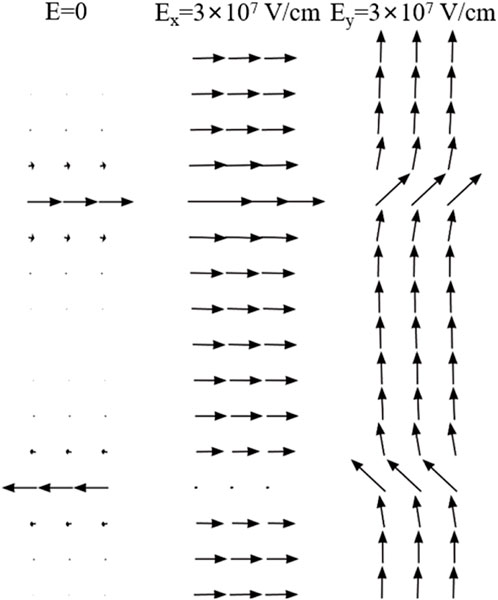
Figure 3. The dipole configurations of wall under fields in the (Nesterov et al., 2013) and [01] directions. The unit length is defined as the repetition length in the bulk with no twin boundaries. The field-free state shows a slightly reduced lattice unit because of the wall-wall interaction. Fields also led to electro-strictive expansion (Ex) and contraction (Ey).
The wall-wall interactions are best seen in the strain fields of needle domains where the thickness of the needle is small. The strain fields are very complex near the needle tips, each bulging of the strain field in Figure 4 is generated by the kink in the needle domain. These additional strain fields give us the inspiration for an even stronger wall-wall interaction, namely, that generated by kinks in domain walls.
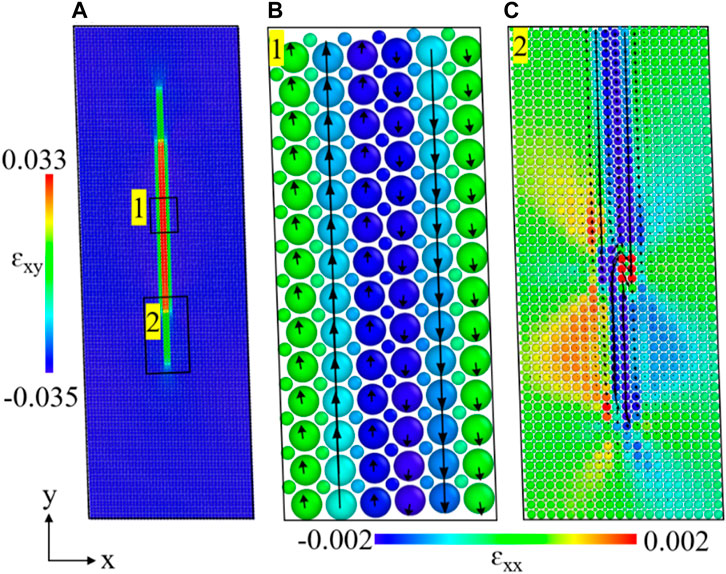
Figure 4. The variation of potential energy as the function of the position of inner domain wall, while the positions of two outer domain walls are kept the same. (A) Double needle with two tips in a system under periodic boundary conditions. (B,C) Atomic images with dipole vectors for site 1 and 2, respectively. The colors are coded by the atomic-level shear strain εxy. The red and blue regions represent two domains, and the green layer represents the domain wall.
The combinations of elastic and columbic forces of polar domain walls were theoretically impact the formations of ferroelastic topological patterns, such as needle domains and comb domain structures when the interwall distances are sufficiently small. We now explore the origin of the equidistant configuration by keeping two outer domain walls at a constant distance while a third inner domain wall is allowed to move sideways. We choose d = 30 lattice units (Figure 5) for the two outer walls. We find an energy minimum for the third wall exactly in the middle. The energy difference between the middle position and the slightly shifted position (position 2 and 3) is very small. We find energy shifts in the order of magnitude of 0.001 meV/atom. This small energy explains why sideways movements are hard to observe experimentally when the walls are widely spaced: The energy gain is very small compared with common pinning energies of domain walls.
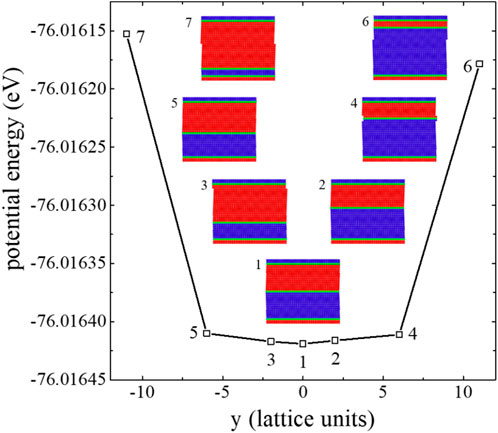
Figure 5. The variation of potential energy as the function of the position of inner domain wall, while the positions of two outer domain walls are kept the same. The distance between two outer walls are 30 lattice units. The system has the lowest energy when the inner domain wall is right in the middle. The colours of atomic images are coded according to the atomic-level shear strain εxy. The red and blue regions represent two domains, and the green layer represents the domain wall.
The role of topological kinks inside twin walls
It was first proposed in 2017 that wall bending may induce kinks in domain walls (Salje et al., 2017). These kinks residing inside domain walls and are not necessarily static but accelerate beyond the speed of sound under even modest external shear stress. The same kinks were subsequently found to be at the core of domain switching in metals (Yang et al., 2020; Yang et al., 2021) and during interactions with wall junctions which determine much of the mechanical properties of ferroelastic materials (He et al., 2019). Very high kink concentrations exist also in domain walls in uniaxial ferroelectrics like LiNbO3 (Gonnissen et al., 2016). The twin wall has often mirror symmetry (the so-called w walls, (Salje, 2012)). The mirror symmetry is broken by kinks and local stress fields and leads to significant strains emanating from the kinks. It is the purpose of this paper to characterize the strain fields and to show that strain-mediated interactions between kinks is a likely source for the interaction between parallel domain walls (Everhardt et al., 2019; Selke, 1988; Roitburd, 1976; Luk’yanchuk et al., 2009). A step forwards was achieved in 2000 when Pertsev et al. (Pertsev et al., 2000) calculated equilibrium shapes of curved ferroelastic domain walls in crystals. Smooth kinks in walls were investigated using their dislocation-disclination model on the basis that the domain walls are infinitely narrow. They found that elastic monopoles (the interaction energy decay as 1/d, where d is the kink-kink distance) exist in the bend regions in large samples.
Figure 6 shows the typical atomic kink structures residing inside the horizontal ferroelastic domain walls.
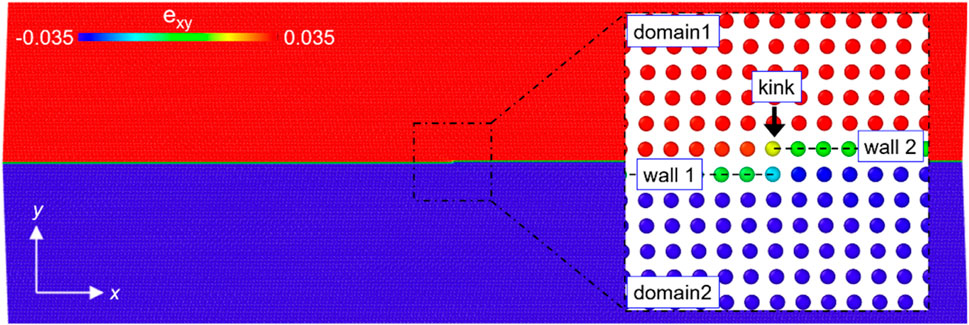
Figure 6. Atomic image of a static kink residing inside a horizontal ferroelastic domain wall. The colours are coded by the atomic shear strain (exy). Green atoms in the inset (indicated by dashed lines) represent the domain walls with a kink.
The kinks have two effects on the crystal structure. The first is that they generate large strain fields near the kink position. The second is that they curve the sample if this bending is not impeded by external forces, like a substrate underneath the sample. Both features give rise to interactions when two kinks are in either the same twin wall or in two parallel twin walls (Figure 7).
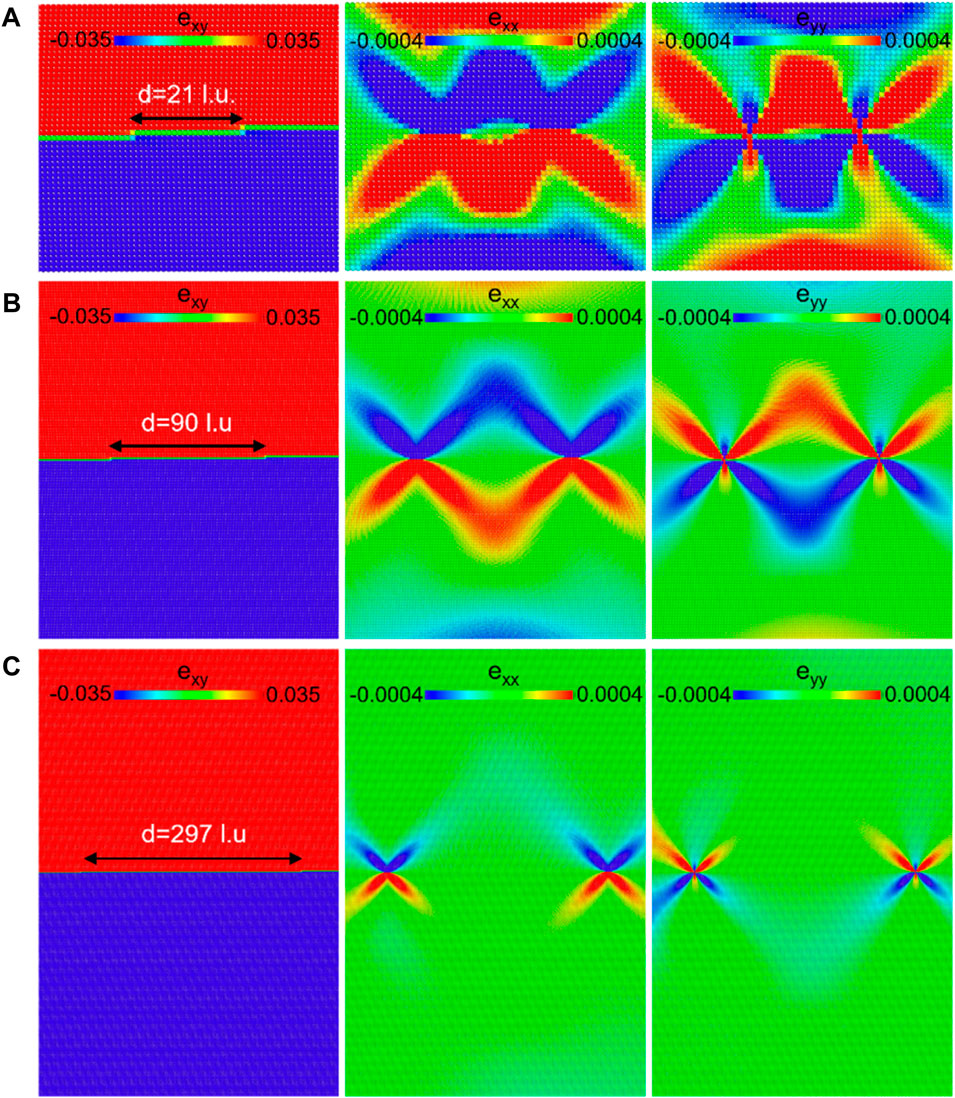
Figure 7. Strain maps of kink-kink configurations inside horizontal wall with equilibrium separation distances resulting from repulsive interactions between kinks. The system sizes in y direction are 51 l. u. in (A), 201 l. u. in (B) and 601 l. u. in (C). Strain colour maps are coded by atomic-level normal strains (exx and eyey) and shear strain (exy).
In our thin, freestanding sample (Figure 8) the interaction energy follows a typical dipole-dipole interaction for distances smaller than the equilibrium distance (Figure 9). The scaling exponent is −2 for this interaction energy E ∼ d-2. The size effect (surface strains) is very large in small systems, and strongly affects the kink-kink interaction energy while it is irrelevant for large system sizes. This scenario applies to small memristive elements where the fast diffusion is constrained to the twin walls. The crossover is at sizes equivalent to around 200 nm which shows that nanoparticles are prone to size effects while large single crystals are not. Similar interactions occur in parallel walls containing kink-antikink pairs.
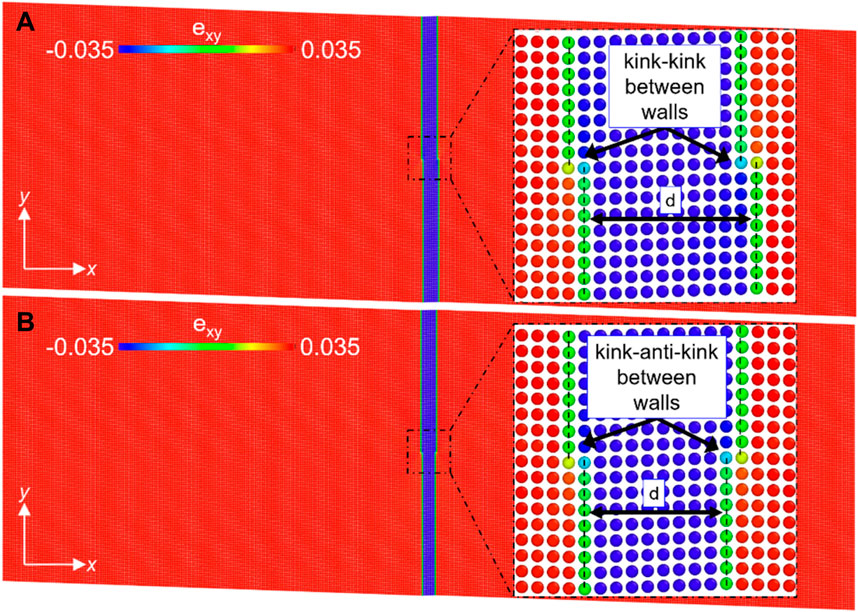
Figure 8. Atomic structure of kink-kink (A) and kink-antikink (B) residing inside two parallel domain walls. The colours are coded by the atomic shear strain (exy). Green atoms (indicated by dashed lines) represent the domain walls with kinks in the insets.
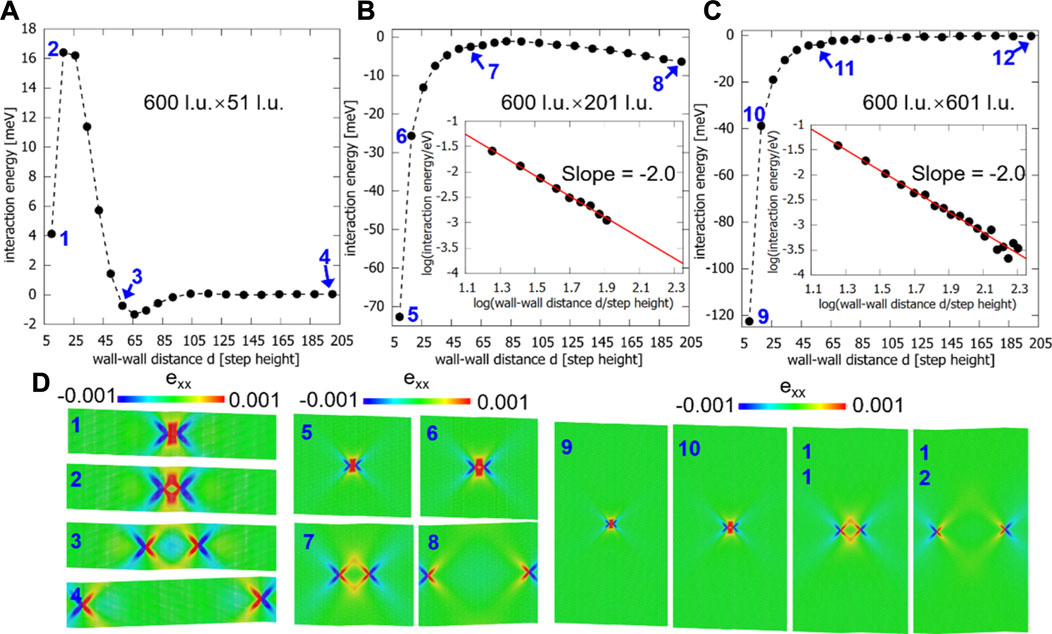
Figure 9. Interaction energy of kink-kink configurations residing inside two parallel walls as function of wall-wall distances. The system size in (A), (B), and (C) are 600 l. u.×51 l. u., 600 l. u.×201 l. u., and 600 l. u.×601 l. u. 1–12 in (A)–(C) indicate the interaction energy of kink-kink configurations with wall-wall distances of 10 l. u., 18 l. u., 58 l. u. and 200 l. u. (D) The corresponding strain maps for each configuration. Insets in (B) and (C) show the scaling exponent E ∼ d-2 between the interaction energy and the wall-wall distances. The colors are coded by atomic-level normal strain exx.
All simulations were performed under open boundary conditions where the sample could change its shape. This approach makes the simulations much more realistic for most ferroelastic materials (Salje, 2012) and particularly for the large group of disordered materials (Salje and Dahmen, 2014) where porosity often plays a major role in the assessment of their elastic deformation (Casals and Salje, 2021). Most ferroelastic minerals, for example, display porosities between 10% and 60% (Salje, 2021b; Salje, 2022) which allows mineral grains to relax their shape when their microstructure changes as a function of temperature or pressure. The simulations highlight that shapes changes occur for small enough samples when kinks are generated in a twin wall. Depending on the kink or antikink configuration, the sample bends in one direction or the opposite. The bents are restricted to a small area near the (anti-)kink position while the rest of the sample simply tilts in two opposite directions. The bent region is ∼10 lattice units wide; the sample tilts continue to the sample surface. In typical crystal structures like perovskites with lattice units of ∼0.4 nm or feldspars with 1.3 nm in the monoclinic b direction these bent regions are some 4–13 nm wide and are hence observable under the transmission electron microscope. The tilt angles are in the order of 1.2° for single kinks and are hence observable.
In contrast to small, freestanding samples, thick samples were shown to have much stronger wall-wall interactions (Pertsev and Salje, 2000). These interactions are long ranging with decay scaling 1/d where d is that distance between kinks. They are very similar to dislocations so that many of the dislocation patterns are transferable to kinked ferroelastic twin walls–notwithstanding that the walls are essentially flat while the dislocations can loop. The size dependence of the wall-wall interaction was investigated by Lu et al. (2023). These authors showed that the fundamental features of the interaction is the same (namely, the lattice bending and the local distortion) but that the weak dipolar interaction in this samples continuously emerges into the much stronger mono-polar interaction (Figure 10).
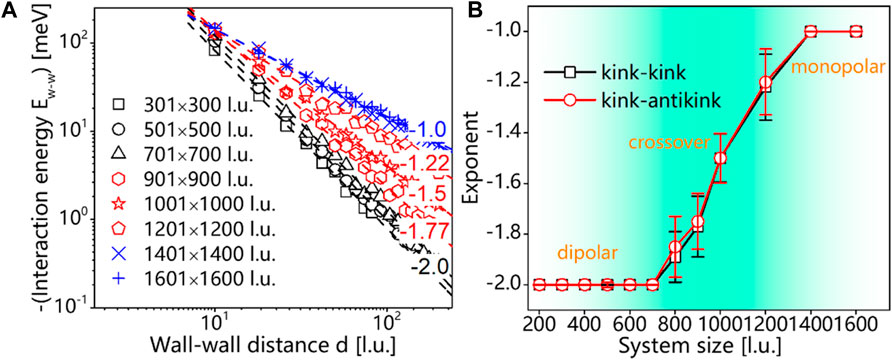
Figure 10. Interaction energies of kink-kink configurations residing inside two parallel walls as a function of the wall-wall distance d. (A) Interaction energy on logarithmic scales with the fitted scaling exponents (B) Scaling exponents as a function of sample sizes. The thickness scaling changes from d-2 for thin samples to d-1 for thick samples.
The thin samples are hence dominated by surface relaxations, similar to the relaxations in dislocations, while such relaxations do not exist in thick samples. Kink-kink interactions in bulk samples interact as “monopoles” with a d-1 dependence when they are separated by the distance d. As the sample size decreases, the interaction for thin samples decays following a characteristic d-2 trend similar to that of dipoles. This behaviour of any singularity (dielectric, dislocations, interstitials, etc.) is commonly described analytically by the concept of “image forces”. The construction is based on the calculation of the surface relaxation as having the same energy as if a fictitious image force was placed outside the sample. Such image forces have also been used to describe the dynamics of dislocation movements (Gurrutxaga-Lerma et al., 2015). Our results clarify the role of a wide crossover regime near d = 1,000 l. u. The exact value of the crossover region depends on the model parameters but the order of magnitude is estimated to be between 200 nm and a few microns. This places the crossover behaviour in the typical region for nano-crystals and small grain devices in neuromorphic computer elements. The results show that the expected self-generated nano-structure differs greatly as a function of size: while larger grains show organized domain walls with the classic patterns of needle domains and junctions, this is not true for small grains where more complex structure with higher wall densities and curved walls are expected.
Discussion
Neuromorphic computing uses physical artificial neurons for computation (Burr et al., 2017; Marković et al., 2020). These neuromorphic elements often operate analogue rather than digital with memristors (Kumar et al., 2022), spintronic memories, threshold switches, transistors (Fuller et al., 2019; He et al., 2021), as attractive physical realisations. Domain boundary-based systems exist in all these options where the relevant elements (like ionic diffusion over interatomic distances, spin flips, charge induces switches and transistor junctions) can be constraint to domain walls. Following this route, we have then to consider how the domain walls form complex networks from ferroelastic stripe pattern to glassy structure (Salje and Carpenter, 2015), Skyrmions (Pantel et al., 2012) and tweed structures (Salje and Parlinski, 1991; Parlinski et al., 1993; Salje et al., 2016a). The fundamental idea is that neuromorphic engineering explores individual neurons, circuits, applications, and overall architectures that are desirable for computation but also the adaptation to fast change (plasticity). This plasticity may partly come from the artificial neuron but also from inter-neuron interactions. In addition, each neuron may have an internal adaptive structure generated by the domain boundaries (Viehland and Salje, 2014). In the approach of Seidel and Sharma (Sharma and Seidel, 2023), only two crossed domain walls are considered. If the domain wall density is much higher in tweed and glassy structures, we expect typical repetition units of the nano-structure of some few unit cells so that the total size of the artificial neuron remains below some 20 nm and still contains a fully adaptive and complex domain boundary array.
We have shown in this paper that one opportunity to ‘tailor’ responsive, plastic systems is to use adaptive domain boundary-based arrays which contain enough complexity to relax an-harmonically when stimulated. Such responses have been observed in test cases like SrTiO3 (Salje et al., 2013; Pesquera et al., 2018; Kustov et al., 2020), where the time constants of the glass relaxation stretch over several decades. The same effect is expected in WO3 where glassy behaviour was observed (Hutchins et al., 2007) and related to the existence of small polarons and low temperature relaxations (Schirmer and Salje, 1980). The smallness of the neuron makes it likely to see domain patterns related to our case of open boundary conditions, which is expected to contain much greater wall densities than under clamped boundary conditions. The exact solution will depend greatly on the interface between the neuron and the substrate which may reduce the relaxation and the image forces. As several different highly conducting interfaces are in use, this issue may need experimental clarification while the possible options for the wall configurations are described in this paper.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.
Author contributions
GL: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing–original draft, Writing–review and editing. ES: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing–original draft, Writing–review and editing.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. National Natural Science Foundation of China (Grant No. 12304130) and the Doctoral Starting Fund of Yantai University (Grant No. 1115- 2222006). EPSRC (EP/P024904/1) and the EU’s Horizon 2020 programme under the Marie Sklodowska-Curie Grant (861153).
Acknowledgments
GL is grateful for the financial support by the National Natural Science Foundation of China (Grant No. 12304130) and the Doctoral Starting Fund of Yantai University (Grant No. 1115-2222006). EKHS is grateful to EPSRC (EP/P024904/1) and the EU’s Horizon 2020 programme under the Marie Sklodowska-Curie Grant (861153).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Aird, A., and Salje, E. K. H. (1998). Sheet superconductivity in twin walls: experimental evidence of WO3-x. J. Phys. Condens. Matter 10, L377–L380. doi:10.1088/0953-8984/10/22/003
Aird, A., and Salje, E. K. H. (2000). Enhanced reactivity of domain walls in with sodium. Eur. Phys. J. B - Condens. Matter Complex Syst. 15, 205–210. doi:10.1007/pl00011037
Balke, N., Choudhury, S., Jesse, S., Huijben, M., Chu, Y. H., Baddorf, A. P., et al. (2009). Deterministic control of ferroelastic switching in multiferroic materials. Nat. Nanotechnol. 4, 868–875. doi:10.1038/nnano.2009.293
Barone, P., Di Sante, D., and Picozzi, S. (2014). Improper origin of polar displacements at CaTiO3 and CaMnO3 twin walls. Phys. Rev. B 89, 144104. doi:10.1103/physrevb.89.144104
Bhatnagar, A., Roy Chaudhuri, A., Heon Kim, Y., Hesse, D., and Alexe, M. (2013). Role of domain walls in the abnormal photovoltaic effect in BiFeO3. Nat. Commun. 4, 2835. doi:10.1038/ncomms3835
Bismayer, U., and Salje, E. (1981). Ferroelastic phases in Pb3(PO4)2-Pb3(AsO4)2; X-ray and optical experiments. Acta Crystallogr. Sect. A 37, 145–153. doi:10.1107/s0567739481000417
Bose, S. K., Mallinson, J. B., Gazoni, R. M., and Brown, S. A. (2017). Stable self-assembled atomic-switch networks for neuromorphic applications. IEEE Trans. Electron Devices 64, 5194–5201. doi:10.1109/ted.2017.2766063
Burr, G. W., Shelby, R. M., Sebastian, A., Kim, S., Kim, S., Sidler, S., et al. (2017). Neuromorphic computing using non-volatile memory. Adv. Phys. X 2, 89–124. doi:10.1080/23746149.2016.1259585
Carpenter, M. A. (2015). Static and dynamic strain coupling behaviour of ferroic and multiferroic perovskites from resonant ultrasound spectroscopy. J. Phys. Condens. Matter 27, 263201. doi:10.1088/0953-8984/27/26/263201
Casals, B., Nataf, G. F., and Salje, E. K. H. (2021). Avalanche criticality during ferroelectric/ferroelastic switching. Nat. Commun. 12, 345. doi:10.1038/s41467-020-20477-6
Casals, B., and Salje, E. K. H. (2021). Energy exponents of avalanches and Hausdorff dimensions of collapse patterns. Phys. Rev. E 104, 054138. doi:10.1103/physreve.104.054138
Casals, B., van Dijken, S., Herranz, G., and Salje, E. K. H. (2019). Electric-field-induced avalanches and glassiness of mobile ferroelastic twin domains in cryogenic SrTiO3. Phys. Rev. Res. 1, 032025. doi:10.1103/physrevresearch.1.032025
Catalan, G., Seidel, J., Ramesh, R., and Scott, J. F. (2012). Domain wall nanoelectronics. Rev. Mod. Phys. 84, 119–156. doi:10.1103/revmodphys.84.119
Chai, X., Jiang, J., Zhang, Q., Hou, X., Meng, F., Wang, J., et al. (2020). Nonvolatile ferroelectric field-effect transistors. Nat. Commun. 11, 2811. doi:10.1038/s41467-020-16623-9
Chen, Y., Gou, B., Xu, X., Ding, X., Sun, J., and Salje, E. K. H. (2023). Multibranches of acoustic emission as identifier for deformation mechanisms in additively manufactured 316L stainless steel. Addit. Manuf. 78, 103819. doi:10.1016/j.addma.2023.103819
Chen, Y., Gou, B., Yuan, B., Ding, X., Sun, J., and Salje, E. K. H. (2022). Multiple avalanche processes in acoustic emission spectroscopy: multibranching of the Energy−Amplitude scaling. Phys. status solidi (b) 259, 2100465. doi:10.1002/pssb.202270008
Christensen, D. V., Dittmann, R., Linares-Barranco, B., Sebastian, A., Le Gallo, M., Redaelli, A., et al. (2022). 2022 roadmap on neuromorphic computing and engineering. Neuromorphic Comput. Eng. 2, 022501. doi:10.1088/2634-4386/ac4a83
Chrosch, J., and Salje, E. K. H. (1999). Temperature dependence of the domain wall width in LaAlO3. J. Appl. Phys. 85, 722–727. doi:10.1063/1.369152
Cipollini, D., Swierstra, A., and Schomaker, L. (2024). Modeling a domain wall network in BiFeO3 with stochastic geometry and entropy-based similarity measure. Front. Mater. 11, 1323153. doi:10.3389/fmats.2024.1323153
Cultrera, A., Milano, G., De Leo, N., Ricciardi, C., Boarino, L., and Callegaro, L. (2021). Recommended implementation of electrical resistance tomography for conductivity mapping of metallic nanowire networks using voltage excitation. Sci. Rep. 11, 13167. doi:10.1038/s41598-021-92208-w
Ding, X., Zhao, Z., Lookman, T., Saxena, A., and Salje, E. K. H. (2012). High junction and twin boundary densities in driven dynamical systems. Adv. Mater. 24, 5385–5389. doi:10.1002/adma.201200986
Everhardt, A. S., Damerio, S., Zorn, J. A., Zhou, S., Domingo, N., Catalan, G., et al. (2019). Periodicity-doubling cascades: direct observation in ferroelastic materials. Phys. Rev. Lett. 123, 087603. doi:10.1103/physrevlett.123.087603
Feigl, L., Yudin, P., Stolichnov, I., Sluka, T., Shapovalov, K., Mtebwa, M., et al. (2014). Controlled stripes of ultrafine ferroelectric domains. Nat. Commun. 5, 4677. doi:10.1038/ncomms5677
Fuller, E. J., Li, Y., Bennet, C., Keene, S. T., Melianas, A., Agarwal, S., et al. (2019). Redox transistors for neuromorphic computing. IBM J. Res. Dev. 63 (9), 1–9. doi:10.1147/jrd.2019.2942285
Ghavasieh, A., and De Domenico, M. (2023). Generalized network density matrices for analysis of multiscale functional diversity. Phys. Rev. E 107, 044304. doi:10.1103/physreve.107.044304
Gonnissen, J., Batuk, D., Nataf, G. F., Jones, L., Abakumov, A. M., Van Aert, S., et al. (2016). Direct observation of ferroelectric domain walls in LiNbO3: wall-meanders, kinks, and local electric charges. Adv. Funct. Mater. 26, 7599–7604. doi:10.1002/adfm.201603489
Gurrutxaga-Lerma, B., Balint, D. S., Dini, D., and Sutton, A. P. (2015). Elastodynamic image forces on dislocations. Proc. R. Soc. A Math. Phys. Eng. Sci. 471, 20150433. doi:10.1098/rspa.2015.0433
Harrison, R. J., and Salje, E. K. H. (2010). The noise of the needle: avalanches of a single progressing needle domain in LaAlO3. Appl. Phys. Lett. 97, 021907. doi:10.1063/1.3460170
Hayward, S. A., and Salje, E. K. H. (1999). Cubic-tetragonal phase transition in SrTiO3 revisited: Landau theory and transition mechanism. Phase Transitions 68, 501–522. doi:10.1080/01411599908224530
He, X., Li, S., Ding, X., Sun, J., Kustov, S., and Salje, E. K. H. (2022). Internal friction in complex ferroelastic twin patterns. Acta Mater. 228, 117787. doi:10.1016/j.actamat.2022.117787
He, X., Li, S., Ding, X., Sun, J., Selbach, S. M., and Salje, E. K. H. (2019). The interaction between vacancies and twin walls, junctions, and kinks, and their mechanical properties in ferroelastic materials. Acta Mater. 178, 26–35. doi:10.1016/j.actamat.2019.07.051
He, Y., Zhu, L., Zhu, Y., Chen, C., Jiang, S., Liu, R., et al. (2021). Recent progress on emerging transistor-based neuromorphic devices. Adv. Intell. Syst. 3, 2000210. doi:10.1002/aisy.202000210
Hochstetter, J., Zhu, R., Loeffler, A., Diaz-Alvarez, A., Nakayama, T., and Kuncic, Z. (2021). Avalanches and edge-of-chaos learning in neuromorphic nanowire networks. Nat. Commun. 12, 4008. doi:10.1038/s41467-021-24260-z
Hutchins, M. G., Abu-Alkhair, O., El-Nahass, M. M., and Abdel-Hady, K. (2007). Electrical conductivity and dielectric relaxation in non-crystalline films of tungsten trioxide. J. Non-Crystalline Solids 353, 4137–4142. doi:10.1016/j.jnoncrysol.2007.06.042
Indiveri, G., Linares-Barranco, B., Legenstein, R., Deligeorgis, G., and Prodromakis, T. (2013). Integration of nanoscale memristor synapses in neuromorphic computing architectures. Nanotechnology 24, 384010. doi:10.1088/0957-4484/24/38/384010
Kim, D. J., Lu, H., Ryu, S., Bark, C. W., Eom, C. B., Tsymbal, E. Y., et al. (2012). Ferroelectric tunnel memristor. Nano Lett. 12, 5697–5702. doi:10.1021/nl302912t
Kim, Y., Alexe, M., and Salje, E. K. H. (2010). Nanoscale properties of thin twin walls and surface layers in piezoelectric WO3-x. Appl. Phys. Lett. 96, 032904. doi:10.1063/1.3292587
Kubel, F., and Schmid, H. (1990). Structure of a ferroelectric and ferroelastic monodomain crystal of the perovskite BiFeO3. Acta Crystallogr. Sect. B 46, 698–702. doi:10.1107/s0108768190006887
Kumar, S., Wang, X., Strachan, J. P., Yang, Y., and Lu, W. D. (2022). Dynamical memristors for higher-complexity neuromorphic computing. Nat. Rev. Mater. 7, 575–591. doi:10.1038/s41578-022-00434-z
Kustov, S., Liubimova, I., and Salje, E. K. H. (2020). Domain dynamics in quantum-paraelectric SrTiO3. Phys. Rev. Lett. 124, 016801. doi:10.1103/physrevlett.124.016801
Lajzerowicz, J., and Levanyuk, A. P. (1994). Fluctuation-induced interaction of domain walls: influence on the commensurate-incommensurate transition. Phys. Rev. B 49, 15475–15484. doi:10.1103/physrevb.49.15475
Lee, W. T., Salje, E. K. H., Goncalves-Ferreira, L., Daraktchiev, M., and Bismayer, U. (2006). Intrinsic activation energy for twin-wall motion in the ferroelastic perovskite CaTiO3. Phys. Rev. B 73, 214110. doi:10.1103/physrevb.73.214110
Liu, Z., Wang, H., Li, M., Tao, L., Paudel, T. R., Yu, H., et al. (2023). In-plane charged domain walls with memristive behaviour in a ferroelectric film. Nature 613, 656–661. doi:10.1038/s41586-022-05503-5
Lu, G., Cordero, F., Hideo, K., Ding, X., Xu, Z., Chu, R., et al. (2024). Elastic precursor softening in proper ferroelastic materials: a molecular dynamics study. Phys. Rev. Res. 6, 013232. doi:10.1103/physrevresearch.6.013232
Lu, G., Ding, X., Sun, J., and Salje, E. K. H. (2022). Wall-wall and kink-kink interactions in ferroelastic materials. Phys. Rev. B 106, 144105. doi:10.1103/physrevb.106.144105
Lu, G., Hideo, K., Ding, X., Xu, Z., Chu, R., Nataf, G. F., et al. (2023). Influence of kinks on the interaction energy between ferroelastic domain walls in membranes and thin films. Microstructures 3, 2023033. doi:10.20517/microstructures.2023.28
Lu, G., Li, S., Ding, X., and Salje, E. K. H. (2019a). Piezoelectricity and electrostriction in ferroelastic materials with polar twin boundaries and domain junctions. Appl. Phys. Lett. 114, 202901. doi:10.1063/1.5092523
Lu, G., Li, S., Ding, X., Sun, J., and Salje, E. K. H. (2019b). Ferroelectric switching in ferroelastic materials with rough surfaces. Sci. Rep. 9, 15834. doi:10.1038/s41598-019-52240-3
Lu, G., Li, S., Ding, X., Sun, J., and Salje, E. K. H. (2019c). Electrically driven ferroelastic domain walls, domain wall interactions, and moving needle domains. Phys. Rev. Mater. 3, 114405. doi:10.1103/physrevmaterials.3.114405
Lu, G., Li, S., Ding, X., Sun, J., and Salje, E. K. H. (2020a). Enhanced piezoelectricity in twinned ferroelastics with nanocavities. Phys. Rev. Mater. 4, 074410. doi:10.1103/physrevmaterials.4.074410
Lu, G., Li, S., Ding, X., Sun, J., and Salje, E. K. H. (2020b). Current vortices and magnetic fields driven by moving polar twin boundaries in ferroelastic materials. npj Comput. Mater. 6, 145. doi:10.1038/s41524-020-00412-5
Lu, G., and Salje, E. K. H. (2024). Multiferroic neuromorphic computation devices. Apl. Mater. 12, 061101. doi:10.1063/5.0216849
Luk’yanchuk, I. A., Schilling, A., Gregg, J. M., Catalan, G., and Scott, J. F. (2009). Origin of ferroelastic domains in free-standing single-crystal ferroelectric films. Phys. Rev. B 79, 144111. doi:10.1103/physrevb.79.144111
Ma, C., Luo, Z., Huang, W., Zhao, L., Chen, Q., Lin, Y., et al. (2020). Sub-nanosecond memristor based on ferroelectric tunnel junction. Nat. Commun. 11, 1439. doi:10.1038/s41467-020-15249-1
Maksymovych, P., Seidel, J., Chu, Y. H., Wu, P., Baddorf, A. P., Chen, L.-Q., et al. (2011). Dynamic conductivity of ferroelectric domain walls in BiFeO3. Nano Lett. 11, 1906–1912. doi:10.1021/nl104363x
Mambretti, F., Mirigliano, M., Tentori, E., Pedrani, N., Martini, G., Milani, P., et al. (2022). Dynamical stochastic simulation of complex electrical behavior in neuromorphic networks of metallic nanojunctions. Sci. Rep. 12, 12234. doi:10.1038/s41598-022-15996-9
Marković, D., Mizrahi, A., Querlioz, D., and Grollier, J. (2020). Physics for neuromorphic computing. Nat. Rev. Phys. 2, 499–510. doi:10.1038/s42254-020-0208-2
Meier, D., and Selbach, S. M. (2022). Ferroelectric domain walls for nanotechnology. Nat. Rev. Mater. 7, 157–173. doi:10.1038/s41578-021-00375-z
Milano, G., Pedretti, G., Montano, K., Ricci, S., Hashemkhani, S., Boarino, L., et al. (2022). In materia reservoir computing with a fully memristive architecture based on self-organizing nanowire networks. Nat. Mater. 21, 195–202. doi:10.1038/s41563-021-01099-9
Moreno, Y., Nekovee, M., and Pacheco, A. F. (2004). Dynamics of rumor spreading in complex networks. Phys. Rev. E 69, 066130. doi:10.1103/physreve.69.066130
Nataf, G. F., Guennou, M., Gregg, J. M., Meier, D., Hlinka, J., Salje, E. K. H., et al. (2020). Domain-wall engineering and topological defects in ferroelectric and ferroelastic materials. Nat. Rev. Phys. 2, 634–648. doi:10.1038/s42254-020-0235-z
Nesterov, O., Matzen, S., Magen, C., Vlooswijk, A. H. G., Catalan, G., and Noheda, B. (2013). Thickness scaling of ferroelastic domains in PbTiO3 films on DyScO3. Appl. Phys. Lett. 103, 142901. doi:10.1063/1.4823536
Pantel, D., Goetze, S., Hesse, D., and Alexe, M. (2012). Reversible electrical switching of spin polarization in multiferroic tunnel junctions. Nat. Mater. 11, 289–293. doi:10.1038/nmat3254
Parlinski, K., Heine, V., and Salje, E. K. H. (1993). Origin of tweed texture in the simulation of a cuprate superconductor. J. Phys. Condens. Matter 5, 497–518. doi:10.1088/0953-8984/5/4/018
Pastor-Satorras, R., and Vespignani, A. (2001). Epidemic spreading in scale-free networks. Phys. Rev. Lett. 86, 3200–3203. doi:10.1103/physrevlett.86.3200
Pertsev, N. A., Novak, J., and Salje, E. K. H. (2000). Long-range elastic interactions and equilibrium shapes of curved ferroelastic domain walls in crystals. Philos. Mag. A 80, 2201–2213. doi:10.1080/01418610008212157
Pertsev, N. A., and Salje, E. K. H. (2000). Thermodynamics of pseudoproper and improper ferroelastic inclusions and polycrystals: effect of elastic clamping on phase transitions. Phys. Rev. B 61, 902–908. doi:10.1103/physrevb.61.902
Pesquera, D., Carpenter, M. A., and Salje, E. K. H. (2018). Glasslike dynamics of polar domain walls in cryogenic SrTiO3. Phys. Rev. Lett. 121, 235701. doi:10.1103/physrevlett.121.235701
Plimpton, S. (1995). Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 117, 1–19. doi:10.1006/jcph.1995.1039
Roitburd, A. L. (1976). Equilibrium structure of epitaxial layers. Phys. status solidi (a) 37, 329–339. doi:10.1002/pssa.2210370141
Salje, E., and Parlinski, K. (1991). Microstructures in high Tc superconductors. Supercond. Sci. Technol. 4, 93–97. doi:10.1088/0953-2048/4/3/002
Salje, E., and Wruck, B. (1983). Specific-heat measurements and critical exponents of the ferroelastic phase transition in Pb3(PO4)2 and Pb3(P1-xAsxO4)2. Phys. Rev. B 28, 6510. doi:10.1103/PhysRevB.28.6510
Salje, E. K. H. (2010). Multiferroic domain boundaries as active memory devices: trajectories towards domain boundary engineering. ChemPhysChem 11, 940–950. doi:10.1002/cphc.200900943
Salje, E. K. H. (2012). Ferroelastic materials. Annu. Rev. Mater. Res. 42, 265–283. doi:10.1146/annurev-matsci-070511-155022
Salje, E. K. H. (2021a). Mild and wild ferroelectrics and their potential role in neuromorphic computation. Apl. Mater. 9, 010903. doi:10.1063/5.0035250
Salje, E. K. H. (2021b). Ferroelastic twinning in minerals: a source of trace elements, conductivity, and unexpected piezoelectricity. Minerals 11, 478. doi:10.3390/min11050478
Salje, E. K. H., Aktas, O., Carpenter, M. A., Laguta, V. V., and Scott, J. F. (2013). Domains within domains and walls within walls: evidence for polar domains in cryogenic SrTiO3. Phys. Rev. Lett. 111, 247603. doi:10.1103/physrevlett.111.247603
Salje, E. K. H., Alexe, M., Kustov, S., Weber, M. C., Schiemer, J., Nataf, G. F., et al. (2016a). Direct observation of polar tweed in LaAlO3. Sci. Rep. 6, 27193. doi:10.1038/srep27193
Salje, E. K. H., and Carpenter, M. A. (2015). Domain glasses: twin planes, Bloch lines, and Bloch points. Phys. status solidi (b) 252, 2639–2648. doi:10.1002/pssb.201552430
Salje, E. K. H., and Dahmen, K. A. (2014). Crackling noise in disordered materials. Annu. Rev. Condens. Matter Phys. 5, 233–254. doi:10.1146/annurev-conmatphys-031113-133838
Salje, E. K. H., Graeme-Barber, A., Carpenter, M. A., and Bismayer, U. (1993). Lattice parameters, spontaneous strain and phase transitions in Pb3(PO4)2. Acta Crystallogr. Sect. B 49, 387–392. doi:10.1107/s0108768192008127
Salje, E. K. H., Hayward, S. A., and Lee, W. T. (2005). Ferroelastic phase transitions: structure and microstructure. Acta Crystallogr. Sect. A 61, 3–18. doi:10.1107/s0108767304020318
Salje, E. K. H., and Ishibashi, Y. (1996). Mesoscopic structures in ferroelastic crystals: needle twins and right-angled domains. J. Phys. Condens. Matter 8, 8477–8495. doi:10.1088/0953-8984/8/44/004
Salje, E. K. H., Li, S., Stengel, M., Gumbsch, P., and Ding, X. (2016b). Flexoelectricity and the polarity of complex ferroelastic twin patterns. Phys. Rev. B 94, 024114. doi:10.1103/physrevb.94.024114
Salje, E. K. H., Wang, X., Ding, X., and Scott, J. F. (2017). Ultrafast switching in avalanche-driven ferroelectrics by supersonic kink movements. Adv. Funct. Mater. 27, 1700367. doi:10.1002/adfm.201700367
Schirmer, O. F., and Salje, E. (1980). Conduction bipolarons in low-temperature crystalline WO3-x. J. Phys. C Solid State Phys. 13, L1067–L1072. doi:10.1088/0022-3719/13/36/005
Seidel, J., Martin, L. W., He, Q., Zhan, Q., Chu, Y. H., Rother, A., et al. (2009). Conduction at domain walls in oxide multiferroics. Nat. Mater. 8, 229–234. doi:10.1038/nmat2373
Selke, W. (1988). The ANNNI model — theoretical analysis and experimental application. Phys. Rep. 170, 213–264. doi:10.1016/0370-1573(88)90140-8
Sharma, P., and Seidel, J. (2023). Neuromorphic functionality of ferroelectric domain walls. Neuromorphic Comput. Eng. 3, 022001. doi:10.1088/2634-4386/accfbb
Stukowski, A. (2010). Visualization and analysis of atomistic simulation data with OVITO–the Open Visualization Tool. Model. Simul. Mater. Sci. Eng. 18, 015012. doi:10.1088/0965-0393/18/1/015012
Van Aert, S., Turner, S., Delville, R., Schryvers, D., Van Tendeloo, G., and Salje, E. K. H. (2012). Direct observation of ferrielectricity at ferroelastic domain boundaries in CaTiO3 by electron microscopy. Adv. Mater. 24, 523–527. doi:10.1002/adma.201103717
Venkatesan, S., Kooi, B. J., De Hosson, J. T. M., Vlooswijk, A. H. G., and Noheda, B. (2007). Substrate influence on the shape of domains in epitaxial PbTiO3 thin films. J. Appl. Phys. 102, 104105. doi:10.1063/1.2815657
Viehland, D. D., and Salje, E. K. H. (2014). Domain boundary-dominated systems: adaptive structures and functional twin boundaries. Adv. Phys. 63, 267–326. doi:10.1080/00018732.2014.974304
Wruck, B., Salje, E. K. H., Zhang, M., Abraham, T., and Bismayer, U. (1994). On the thickness of ferroelastic twin walls in lead phosphate Pb3(PO4)2 an X-ray diffraction study. Phase Transitions 48, 135–148. doi:10.1080/01411599408200357
Yang, Y., Li, S., Ding, X., Sun, J., Weiss, J., and Salje, E. K. H. (2020). Twisting of pre-twinned α-Fe nanowires: from mild to wild avalanche dynamics. Acta Mater. 195, 50–58. doi:10.1016/j.actamat.2020.04.023
Yang, Y., Lin, Y., Ding, X., Sun, J., Butterfield, N. J., Aufort, J., et al. The twin boundary in calcite, its structure and physical properties. Submitted to PRB.
Yang, Y., Zhang, L., Li, S., Ding, X., Sun, J., Weiss, J., et al. (2021). Mild fluctuations in ferroelastic domain switching. Phys. Rev. B 104, 214103. doi:10.1103/physrevb.104.214103
Keywords: ferroelastic materials, twin walls, memristors, wall-wall interactions, surface relaxations, domain walls
Citation: Lu G and Salje EKH (2024) Ferroelastic twin walls for neuromorphic device applications. Front. Mater. 11:1406853. doi: 10.3389/fmats.2024.1406853
Received: 25 March 2024; Accepted: 01 August 2024;
Published: 14 August 2024.
Edited by:
Steven Koester, University of Minnesota Twin Cities, United StatesReviewed by:
Tamalika Banerjee, University of Groningen, NetherlandsPavan Nukala, Indian Institute of Science (IISc), India
Copyright © 2024 Lu and Salje. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Guangming Lu, bHVndWFuZ21pbmcxOTkwQHl0dS5lZHUuY24=; Ekhard K. H. Salje, ZWtoYXJkQGVzYy5jYW0uYWMudWs=
 Guangming Lu1*
Guangming Lu1* Ekhard K. H. Salje
Ekhard K. H. Salje