Characterizing pearlite transformation in an API X60 pipeline steel through phase-field modeling and experimental validation

This study explores the microstructural characterization of pearlite phase transformation in high-strength low-alloy API X60 steel, which is used in pipelines. Understanding the formation, phase percentages, and morphology of the pearlitic phase is crucial since it affects the mechanical properties of the considered steel. In this research, a phase-field model, particularly the Cahn–Hilliard approach, was used in order to simulate the formation and morphology of the pearlite phase in response to different heat treatments. Both double- and triple-well potentials were considered for comprehensively studying pearlite’s morphology in the simulations. The simulation results were then compared with experimental outcomes obtained by metallography and field-emission scanning electron microscopy analyses. Considering the double-well potential can help simulate only two phases, ferrite and cementite, which is less compatible with the experiment results than the triple-well potential, which gives the possibility of simulating a three-phase microstructure, ferrite, cementite, and austenite, and a better match with experimental data. The study revealed that as the cooling rate increases, the interlamellar spacing and layer thickness decrease. Additionally, the difference between experimental and simulation results using triple-well potential was approximately ∼10%. Therefore, triple-well potential formulation predictions have better agreements with experimental results for the development circumstance of pearlitic structures.

1 Introduction

The increasing demand for oil and natural gas has compelled companies to seek out these resources in challenging environments, such as humid or extremely cold weather. Pipeline steels not only need to possess high strength and toughness to withstand these harsh conditions but also provide an economical and safe means for transporting oil and natural gas over long distances (Dong et al., 2010). Consequently, the production, installation, and commissioning of large-diameter pipes, which are used over extensive lengths and under high-pressure conditions, have become critical in terms of economy and safety (Shin et al., 2006; Olivares et al., 2008). For acquiring the required properties, steels should be subjected to various processes, including the austenite–pearlite transformation in low-carbon steels and fine-tuning the microstructure to control steel properties (Dong, 2012). High-strength low-alloy (HSLA) steels are a class of low-carbon steels that are enriched with small amounts of alloying elements like molybdenum, niobium, titanium, and vanadium to increase the strength of steels (DeArdo et al., 2009; Morrison, 2009). Pipeline steels are a group of microalloyed steels that typically have low carbon content (<0.14% weight) and a total alloy content in the range of 2–3 wt% (Collins et al., 1983). The mechanical properties of these steels (Baker, 2016) depend on their microstructure, which makes them suitable for constructing various types of structures. Additionally, the simultaneous improvement of toughness and strength is a key challenge for these steels, especially in working conditions that involve high pressure at low temperatures. To achieve this, engineering the steel’s microstructure is crucial, involving the design of microstructures with multi-phase, metastable, and multi-scale features ranging from micro- to nano-length scales (Yapp and Blackman, 2004; Toloui and Militzer, 2010). These steels require highly controlled processing to achieve the desired strength and toughness through a combination of small grain size and fine precipitate distribution enhanced by using micro-alloying with elements such as Nb, V, and Ti, which leads to grain refinement and precipitation hardening, which significantly increase the strength of the steel (Roy et al., 2020b). Thermo-mechanically controlled processing (TMCP) involves austenite conditioning, controlled rolling, and accelerated cooling to further refine the microstructure and improve the mechanical properties (Gong et al., 2016). Effectiveness of fine particles and precipitates have been proven through applying processes such as mechanical alloying, sintering, or hot pressing in various metal alloy systems (Koch et al., 1999; Darling et al., 2008; Zhang et al., 2016; Chakravarty et al., 2017; Kilmametov et al., 2018; Chakraborty et al., 2019; Roy et al., 2020a; Mathapati et al., 2022; Yan et al., 2023; El-Zaidia et al., 2024). HSLA steels can have various microstructures, including ferrite–pearlite, bainite/acicular ferrite, martensite, and multi-phase structures, and utilize a range of strengthening mechanisms, such as solid-solution strengthening, dislocation substructure, precipitation hardening, and grain refinement. Microstructural evolution in HSLA steels can be initially studied using continuous cooling of austenite after being heat-treated at elevated temperature (Cotterill and Mould, 1976), which indicates to the formation of various microstructural constituents from austinite depending on the cooling rate, the grain size of the austenite, and the chemical composition of the steel. The accurate prediction of the overall transformation in many steels depends on a precise understanding of the kinetics and morphology of pearlite formation. The Fe-C-Mn system is a suitable model for studying the growth and growth rate of well-developed pearlite under a constant growth rate (steady-state or isothermal conditions) or varying growth rates (unsteady or continuous cooling conditions) and related interlamellar spacing. In isothermal conditions, pearlite formation is usually assumed to be of the steady-state type with constant interlamellar spacing (Hagel et al., 1956), while in reality, it encounters with the continuous cooling or non-isothermal conditions and varied interlamellar spacing (Cahn and Hagel, 1963). They observed that pearlite formed in Fe-1C-5Mn (wt%) at a temperature of 680 $℃$ grows with large interlamellar spacing and a decreasing growth rate over time. They argued that pearlite formed in specific ternary alloys above the lower A_e1 temperature must form at a variable growth rate and that the carbon composition of the austenite γ) must continuously change until an equilibrium between pearlite and austenite is achieved.

Understanding the microstructure is essential for predicting and controlling the properties of steels. Therefore, there is a growing need for quantitative models, especially in the field of materials science and engineering, with the increasing complexity of steel microstructures. The phase-field method is a popular modeling technique for simulating the evolution of complex microstructures, including phase transitions and deformation changes, under various conditions. The phase-field method was first introduced in the 1980s by Langer (1980) as a way to describe the movement of solid–liquid interfacial boundaries in alloys. Since then, this method has been utilized for a wide range of problems, including crystal growth, solidification, and phase transformation. This method applies thermodynamic principles and can account for different regions within materials, such as the matrix, the precipitate, and the interface between them, without assigning physical thickness to the boundaries (referred to as “sharp interfaces”). However, this sharp interface approach poses challenges for numerical simulations, particularly in three-dimensional cases, where related numerical codes are complex and less developed (Qin and Bhadeshia, 2010). This methodology describes a microstructure via an assortment of field variables that include both compositional and structural domains, positing continuity of these variables across interfaces. Field variables are usually divided into conserved, whose dynamics are governed by the non-linear Cahn–Hilliard diffusion relation (Cahn and Hilliard, 1958; Cahn, 1961), and non-conserved, which are related to the temporal dynamics designed by the Allen–Cahn relaxation equation (Allen and Cahn, 1972; Allen and Cahn, 1973). Furthermore, the time-dependent non-conserved variables are explicated by the Ginzburg–Landau temporal framework (Landau and Khalatikov, 1963). The Allen–Cahn equation describes the evolution of an order parameter, often representing the concentration of the phases, and is especially known for its use in sharp interface limits, where it can describe the motion by mean curvature. On the other hand, the Ginzburg–Lnadau equation is known for its ability to describe continuous (second-order) phase transformation, where the order parameter changes smoothly (Lee, 2023). Collectively, these kinetic frameworks underpin the core physical principles behind broad phase-field models in the literature. In a study, Steinbach and Apel (2007) used a phase-field model investigating pearlitic phase transformation. The model that Steinbach considered for pearlitic transformation is based on three states: first, the use of an order parameter to form a microstructure and its growth; second, the modified Cahn–Hilliard equation which shows the concentration field throughout the microstructure; and finally, the use of an elasticity field to examine the effect of stress and strain within the microstructure during transformation. They discovered that the interlamellar spacing in the pearlite phase influences the growth of the phase, with reduced growth observed in pearlite phases having minimal interlamellar spacing compared to those with larger spacing. In another study, Ankit et al. (2013) used another formulation for phase-field modeling called the grand potential function. They found observed a logical overlap of the analytically predicted growth rate with the phase-field results in the absence of diffusion in ferrite. However, a slight deviation near the critical interlayer distance was observed, which accounted for diffusion in ferrite and in austenite. Meanwhile, there was a narrowing of the cementite near the growth front which could be caused due to diffusion in ferrite.

In order to characterize the pearlitic transformation in API X60 steel, combined experimental and simulation approaches were established to show the importance of pearlitic phase morphology. Therefore, a heating cycle followed by different cooling rates for producing various pearlitic structures of API X60 steel was designed and executed. Then, by considering the same conditions, the resulted pearlitic structures were predicted using a phase-field model. Finally, the outcomes of simulations were compared with the experimental results.

2 Materials and methods

2.1 Phase-field model and formulation

In this research, it is assumed that the total free energy function is only in chemical form. The standard evolution equation based on the Cahn–Hilliard model is presented as follows.

$\frac{\partial c}{\partial t}=\nabla .M\nabla \left(\frac{\delta F^{CH}}{\delta c}\right),(1)$

where $c$ represents the chemical composition of carbon, $t$ the time, $M$ the mobility, and $F^{CH}$ the total free energy. For $F^{CH}$, the free chemical energy should ideally be selected such that both its analytical and numerical solutions are readily available. Additionally, it should have good congruence with the type of problem solution and the physics governing the phase-field equations. In order to investigate three-phase transformation, we utilized a triple-well potential equation:

$F^{CH}=F_t^{CH}=\int \left[f_{eff}\left(c,T\right)+\frac{{\kappa }_t}{2}{\left|\nabla c\right|}^2\right]dv,(2)$

where $f_{eff}\left(c,T\right)$ is the effective free energy density for a homogenous state (Razumov et al., 2017).

$f_{eff}\left(c,T\right)=\mathit{min}\left\{f_{\alpha }\left(c,T\right),f_{\gamma }\left(c,T\right),f_{\theta }\left(c,T\right)\right\},(3)$

where $f_{\gamma \left(\alpha ,\theta \right)}\left(c,T\right)$ are the local free energy density of austenite (ferrite and cementite) at temperature $T$ and carbon concentration $c$. This model implies that the phase with the lowest energy is realized at a given spatial point for a constant local concentration of carbon. This relationship can resolve two fundamental problems present in the earlier model and discussed in section 3. Now, each of these three local free energy densities has its specific definition, which can be observed in the following sections (Vaks et al., 2011). A symmetrical form of triple-well potential with respect to the Eq. 3 is shown in the Figure 1.

$f_{\gamma }\left(c,T\right)=g_{\gamma }^{PM}-{\displaystyle \underset{0}{\overset{{\stackrel{\sim }{J}}_{\gamma }}{\int }}}Q\left({\stackrel{\sim }{J}}_{\gamma }^{\prime },T\right)d{\stackrel{\sim }{J}}_{\gamma }^{\prime }-T\left(s_0+S_{\gamma }\right),(4)$

$f_{\alpha }\left(c,T\right)=g_{\alpha }^{PM}-{\displaystyle \underset{0}{\overset{{\stackrel{\sim }{J}}_{\alpha }}{\int }}}Q\left({\stackrel{\sim }{J}}_{\alpha }^{\prime },T\right)d{\stackrel{\sim }{J}}_{\alpha }^{\prime }-T{S}_{\alpha },(5)$

Figure 1

Figure 1. Effective potential energy in different concentrations.

where $s_0$ is the temperature limit of the entropy difference between the $\alpha$ and $\gamma$ phases; $S_{\left(\alpha \right)\gamma }$ is the configurational entropy in the α and γ phases, respectively; $Q\left(T\right)\equiv 〈m_0.m_1〉/m^2$ is a temperature-dependent correlation function (Smart and Van Vleck, 1966); and ${\stackrel{\sim }{J}}_{\gamma \left(\alpha \right)}\left(c\right)=g_{\gamma \left(\alpha \right)}^{PM}\left(c\right)-g_{\gamma \left(\alpha \right)}^{FM}\left(c\right)$ represents the exchange energy.

$g_{\gamma }^{PM\left(FM\right)}\left(c\right)={\stackrel{\sim }{g}}_{\gamma }^{PM\left(FM\right)}+{\epsilon }_{\gamma }^{PM\left(FM\right)}c+{\upsilon }_{\gamma }{c}^2/2,(6)$

$g_{\alpha }^{PM\left(FM\right)}\left(c\right)={\stackrel{\sim }{g}}_{\alpha }^{PM\left(FM\right)}+{\epsilon }_{\alpha }^{PM\left(FM\right)}c+{\upsilon }_{\alpha }{c}^2/2.(7)$

The term $g_{\gamma \left(\alpha \right)}^{PM\left(FM\right)}$ refers to the energies of elemental iron in its paramagnetic (ferromagnetic) states (Okatov et al., 2011). The terms ${\epsilon }_{\gamma \left(\alpha \right)}^{PM\left(FM\right)}$ and ${\upsilon }_{\gamma \left(\alpha \right)}$ represent the solution and mixing energies of carbon within the FCC (BCC) iron lattice structure, respectively. The formation of cementite through pearlite transformation (PT) significantly increases the carbon concentration, typically to a value of $c=0.25$. Consequently, the model includes a term proportional to $c^2$ to account for the interactions between carbon atoms, as shown in Eqs 6, 7. It is important to note that in this model, the marked temperature sensitivity of the free energy of alpha iron ($\alpha$-Fe) is attributed more to the enhancement of ferromagnetic ordering as the temperature decreases rather than to phonon entropy contributions (Razumov et al., 2017). Hence, the configurational entropy of carbon within the $\alpha$ and $\gamma$ phases is expressed as follows:

$S_{\alpha }\approx -kc\mathit{ln}\left(\frac{c}{3}\right),(8)$

$S_{\gamma }=-k\left[4c\mathit{ln}\left(4c\right)+\left(1-4c\right)\mathit{ln}\left(1-4c\right)\right]/4.(9)$

Based on the provided explanations and the following reference (Battezzati et al., 2005), the free energy density for cementite can now be expressed as follows:

$f_{\theta }\left(c,T\right)=f_{\alpha Fe}\left(T\right)+∆f_{\alpha \theta }\left(T\right)+∆f_{\theta }^{\left(1\right)}\left(c,T\right).(10)$

In the given context, $f_{\alpha Fe}\left(T\right)=f_{\alpha }\left(0,T\right)$ signifies the free energy density associated with pure $\alpha$ iron, while $∆f_{\alpha \theta }\left(T\right)$ refers to the free energy density related to the formation of stoichiometric cementite originating from pure components (BCC iron and graphite) recognized at $c_{cem}=0.25$, and $∆f_{\theta }^{\left(1\right)}\left(c,T\right)$ denotes the variation in free energy density for cementite arising from any deviation from the calculated stoichiometric state (Steinbach and Apel, 2007). To solve this model, the fast-Fourier transform (FFT) method was utilized, and programming was done in MATLAB software. In the Table 1 the parameters that are used as input for the algorithm is shown. To evaluate the robustness of the phase-field model in predicting the microstructural evolution during pearlitic transformations, sensitivity analyses were conducted by varying key parameters, including thermodynamic factors like free energy coefficients and kinetic factors such as carbon diffusion coefficients, along with boundary conditions like temperature gradients and cooling rates. Significant variations in the model’s predictions in response to these changes indicate its sensitivity and the need for precise parameter selection to ensure accuracy.

Table 1

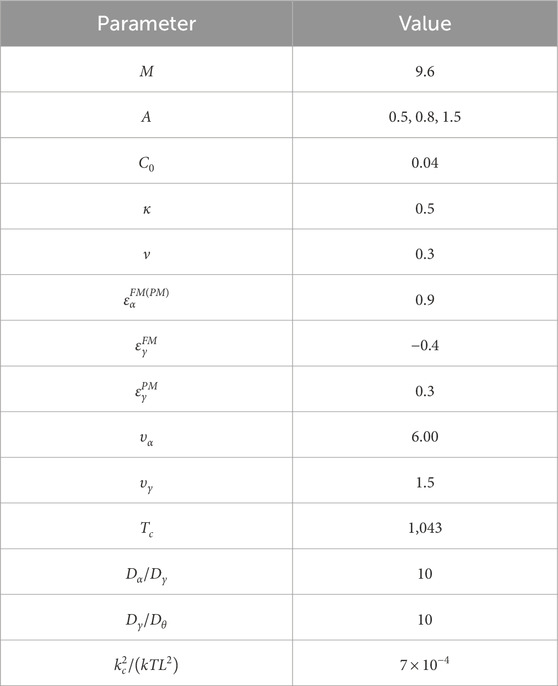
Table 1. Parameters used for phase-field simulation (Razumov, 2017).

2.2 Experimental approach

The chemical composition of API X60 steel, which was the focus of this investigation, was determined using optical emission spectroscopy in accordance with the ASTM E415-17 standard. Specified heat-treatment cycles, illustrated in Figure 2, were used to facilitate the investigation of pearlitic phase transitions under varying cooling rates. These heat treatments include two methodologies aimed at evaluating the morphological evolution of pearlite colonies: 1) after austenitization at 950°C for a duration of 2 hours, isothermal holding at temperatures of $600℃$, $550℃$, and $500℃$ for the initial three samples until the completion of evolution of pearlite colonies, and 2) continuous cooling, wherein subsequent samples underwent quenching via ambient air, water spray, and immersion in water, resulting in temperature gradients of $5$, $15$, and $100℃$ per second, respectively. Subsequent to these heat treatments, the specimens were precisely polished to achieve a reflective finish and thus rendered suitable for microstructural examination via field-emission scanning electron microscopy (FESEM).

Figure 2

Figure 2. Schematic representation of the heat treatment cycle for six samples.

In Figure 3, a phase diagram of API X60 steel, generated using Thermo-Calc software (FEDEMO database), is presented. Table 2 is showing the chemical composition of this steel which is used input of Thermo-Calc software. The diagram reveals that the heat treatment process starts at 950°C, where the microstructure is fully austenitic. As the temperature decreases, the austenite phase transforms into ferrite and pearlite. Due to the low carbon content of this steel, the majority of the resulting microstructure consists of ferrite, with a small fraction of pearlite colonies distributed throughout the matrix.

Figure 3

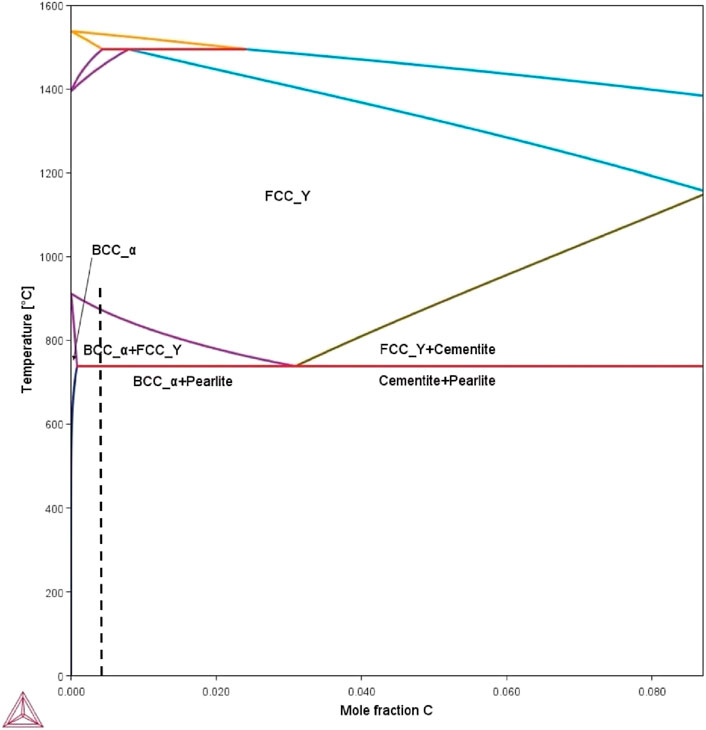
Figure 3. Phase diagram of API X60 steel using Thermo-Calc. The black dashed line shows the 0.003 mol fraction of carbon.

Table 2

Table 2. Chemical composition of API X60 steel.

3 Results and discussion

3.1 Microstructures of isothermal and continuous cooled samples

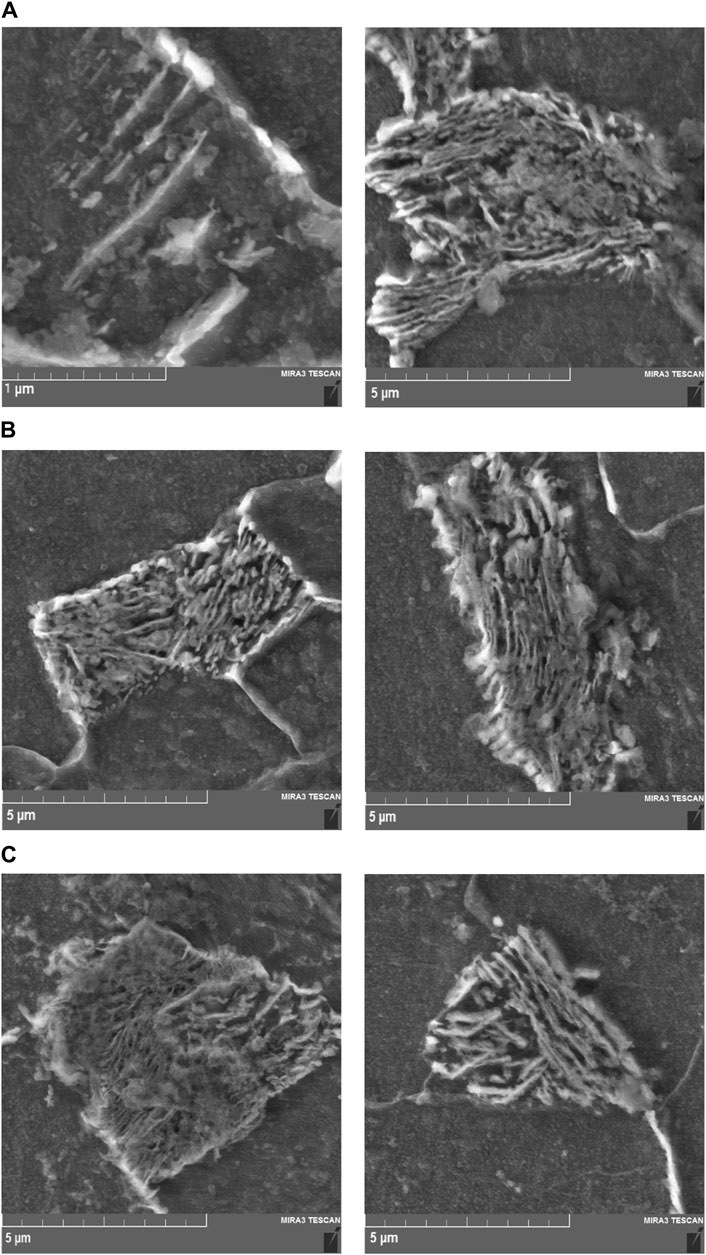
In API X60 steel, characterized by its low carbon content, pearlite appears as very fine layers in the microstructure, making it hard to detect. In Figure 4, the microstructures of the isothermal-treated samples are shown. In this figure, the ferrite domains with pearlitic nucleation occur explicitly along the ferrite grain interfaces. In Figure 4A, there is a clear indication of cementite lamellae, also known as degraded pearlite or divorced pearlite (Pandit and Bhadeshia, 2012). However, in these figures, the pearlite phase is formed between ferrite phases to form the partially divorced-like morphology. In experimental microstructures, the formation of divorced pearlite is influenced by the dynamics between the nucleation and growth kinetics of ferrite and cementite. Divorced pearlite is characterized by randomly distributed cementite particles within a ferrite matrix, differing from the conventional lamellar pearlite structure. This phenomenon is driven by varying nucleation and growth rates under different cooling conditions, as modeled in our phase-field simulations, where cementite nucleation is posited at the austenite–ferrite interface, and pearlite colony growth is dictated by carbon diffusion in the austenite matrix. Slower cooling allows carbon atoms more diffusion time, leading to larger ferrite grains and more dispersed cementite, forming divorced pearlite, whereas faster cooling restricts carbon diffusion, resulting in finer ferrite grains and closely packed cementite, fostering typical lamellar pearlite. The model assumes a constant diffusion coefficient for carbon in austenite, which simplifies the complex reality where this coefficient might vary with temperature and chemical composition, impacting the nucleation and growth dynamics of the phases involved. In Figure 4C, the pearlitic lamellae are finer than other cases of this figure. The observed finer-layered structure of the pearlite phase can be attributed to the low diffusion distance at low-temperature isothermal transformation (Furuhara et al., 2008).

Figure 4

Figure 4. Microstructures of isothermal heat treatment at (A) $\mathbf{600}℃$, (B) $\mathbf{550}℃$, and (C) $\mathbf{500}℃$.

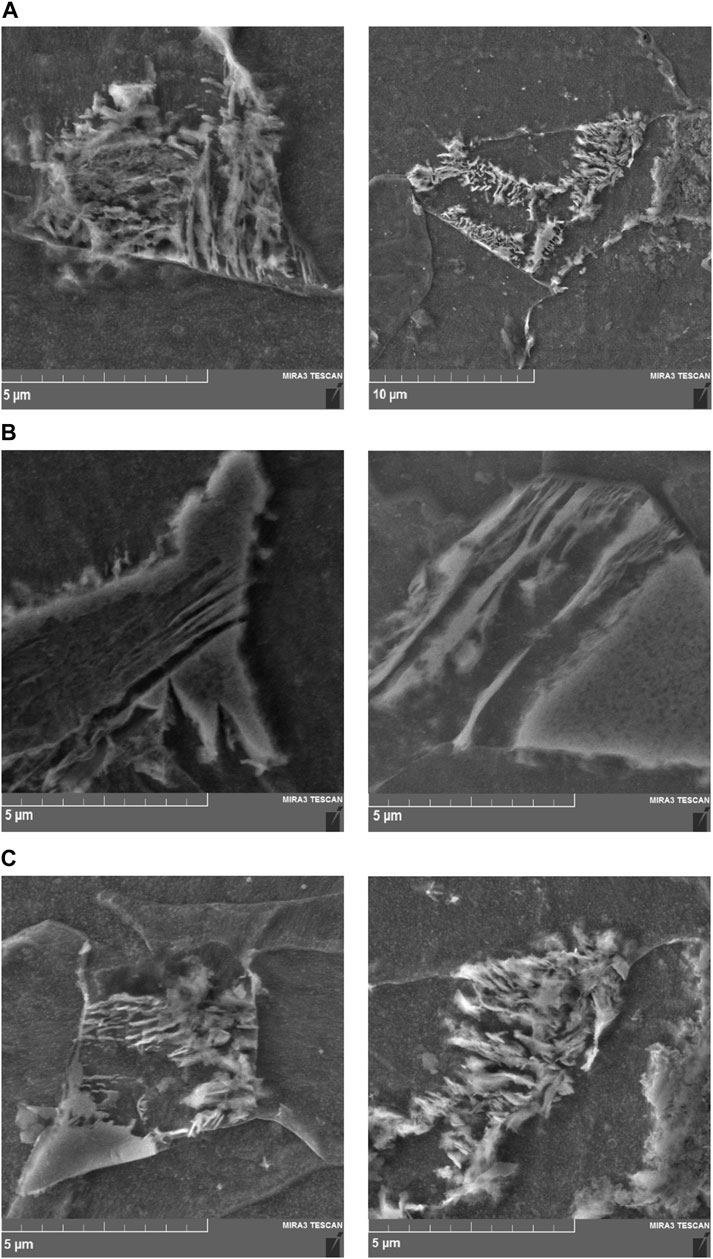
Figure 5A illustrates the outcomes of continuous cooling in air for sample number 4. The resultant microstructural configuration, notably the pearlitic constituents, is frequently observed to exhibit signs of degraded pearlite or divorced pearlite (Pandit and Bhadeshia, 2012). Such degradation is the consequence of an escalated cooling rate relative to isothermal conditions, which surpasses the carbon atom diffusion rate. This rapid cooling causes the renucleation of cementite layers within the same developmental pathway. Figure 5 indicates that the carbon concentration has exerted a significant influence, to the extent that the pearlitic transformation remains incomplete, with pearlite colonies emerging at multiple ferrite grain boundaries. A comparison between Figures 4, 5 demonstrates the formation of a pearlitic structure precisely at a ferrite triple junction. Figure 5B shows that by increasing the cooling rate with water spray, the layers get thinner as compared to cooling of the sample in air, and the layers were divided into two separate layers. In Figure 5C, the morphology of pearlite is like divorced pearlite, but the layered structure can be seen in some parts.

Figure 5

Figure 5. Microstructures of continuous cooling heat treatment at (A) $\mathbf{5}℃/\mathit{s}$, (B) $\mathbf{15}℃/\mathit{s}$, and (C) $\mathbf{100}℃/\mathit{s}$.

3.2 Microstructural products of isothermal transformation predicted by the PFM

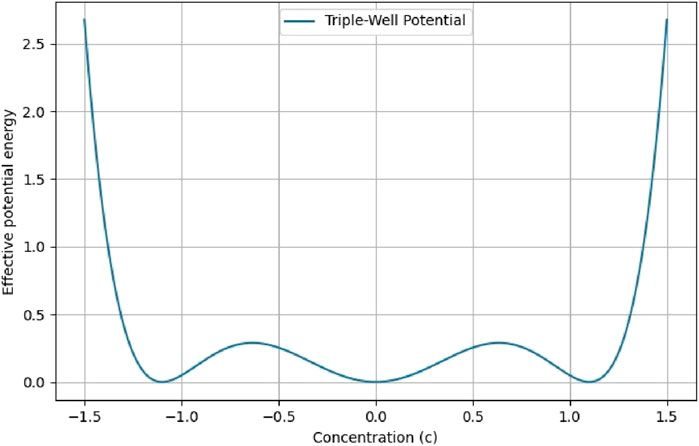
In this section, the results derived from using a triple-well potential are presented. The decision to utilize this modeling approach was based on several key factors, contrasting with the outcomes obtained using a double-well potential that is outlined in the Appendix:

1. The triple-well potential demonstrates enhanced accuracy and aligns well with the experimental data, providing a robust validation of the simulation results.

2. This approach offers computational efficiency, facilitating extensive parametric studies, which are crucial for a thorough exploration of the phase space.

3. It effectively captures the complex energy landscape and phase stability inherent in the system, crucial for accurate phase transformation simulations.

4. It enables the simulation of multi-phase evolution within the material, a critical factor for modeling the sophisticated microstructural changes observed experimentally.

In our phase-field modeling simulations, the primary focus was on the growth kinetics of pearlite colonies, assuming pre-existing nucleation. The computational framework utilized a suite of coupled partial differential equations (PDEs) to model the dynamic changes in phase-field variables and carbon concentration, underpinned by a total free energy functional incorporating chemical free energy, interfacial energy, and elastic strain energy. Pearlite growth was predominantly governed by carbon diffusion within the austenite matrix, with a diffusion coefficient set at $1.0\times {10}^{-9}{m}^2/s$. The phase transformations to ferrite and cementite were regulated by Cahn–Hilliard equations, with consistent mobility coefficients assumed for both phases. Notably, this model simplifies the complexity of the real system by not considering the slower diffusion rates of alloying elements and the varying activation energies, focusing instead on core aspects of pearlite growth and providing insights into phase transformation kinetics and morphological evolution.

Using the formulation of triple-well potential, the diagram shown in Figure 6, the PFM was applied to estimate the evolution of pearlite colonies during isothermal transformation. Examination of different pictures of Figure 6, which belong to the isothermal transformation of API X60 steel at three temperatures of $500℃$, $550℃$, and $600℃$ after dwelling times of $50\mathrm{s}$, $75\mathrm{s}$, and $100\mathrm{s}$, clearly indicates that during high temperatures, isothermal transformation not only widens the interlamellar spacing but also contributes to thickening of the cementite layers. Comparison of the predicted thickness and interlamellar spacing of the pearlite colony isothermally transformed at $500℃$, $550℃$, and $600℃$ showed the lowest spacing for the transformation at $500℃$. Such phenomena are consistent with the underlying mechanics of the pearlitic transformation process, which emphasizes the significance of carbon atom diffusion substantially facilitated by isothermal transformation. In fact, subjecting the sample to isothermal transformation creates favorable conditions for easy and short pathways for carbon diffusion, which implies the reduction of the thermodynamic energy barrier for carbon atom migration and carbon atom mobility (Gaude-Fugarolas, 2002).

Figure 6

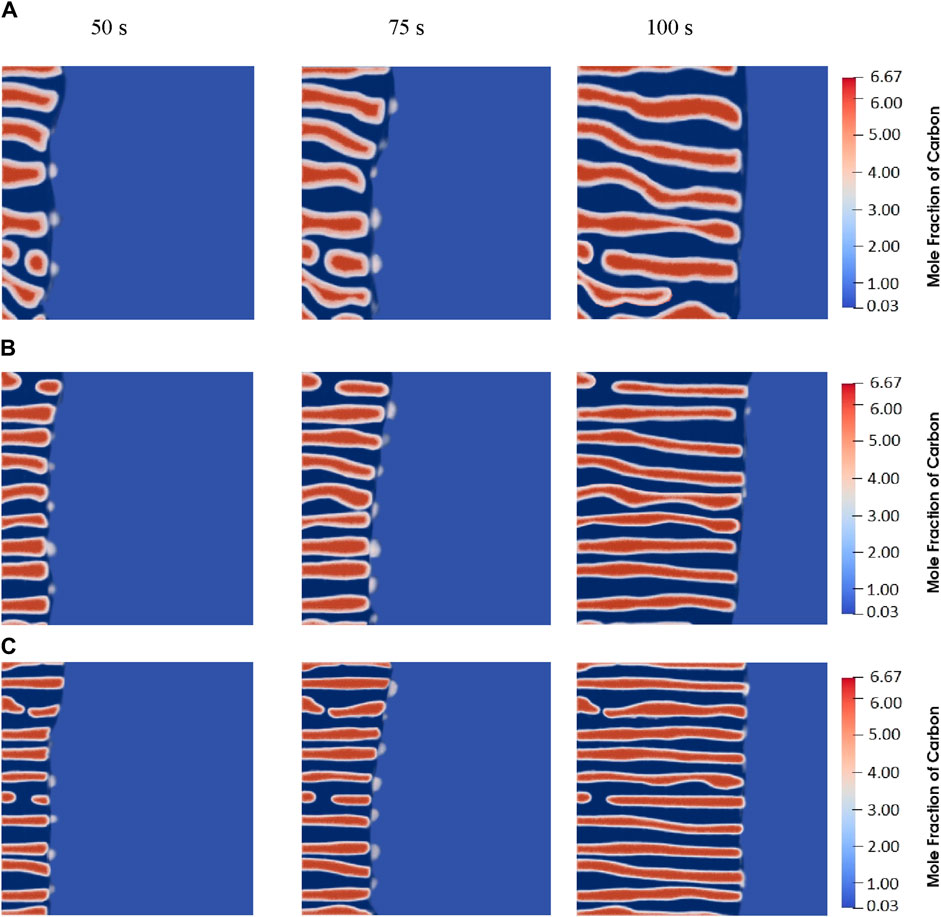
Figure 6. Evolution of the pearlite colony in isothermal cooling at (A) $\mathbf{600}℃$, (B) $\mathbf{550}℃$, and (C) $\mathbf{500}℃$ after 50, 75, and 100 s. The figure is colored by the concentration: red represents cementite, dark blue represents austenite, and light blue represents ferrite.

A noteworthy observation from the simulation outcomes is the phase segregation. Although the heat treatment was conducted under isothermal conditions, carbon segregation in the cementite layers and interlayers was still apparent. Such a phenomenon may facilitate the formation of divorced pearlite (Mathews et al., 2023), as discussed in section 3.1.

3.3 Microstructural products of continuous cooling transformation predicted by the PFM

The results of the continuous cooling PFM simulation showed that from a thermodynamic viewpoint, the increase in the energy barrier confronting carbon atoms during diffusion necessitating diffusion over an extended distance is discernible. This phenomenon restricts the mobility of carbon atoms, thereby leading to a decrease in the thickness of cementite layers. The continuous cooling heat treatment induces a substantial thermal gradient across the cementite layers. In contrast to isothermal transformation, the continuous cooling transformation induces a substantial thermal gradient across the cementite layers with accompanying possible stress fields, which can influence the transformation characteristics. In Figure 7, the evolution of the pearlite colony under continuous cooling at $5℃/s$, 1 $5℃/s$, and $100℃/s$ after $50\mathrm{s}$, $75\mathrm{s}$, and $100\mathrm{s}$ dwell times is shown.

Figure 7

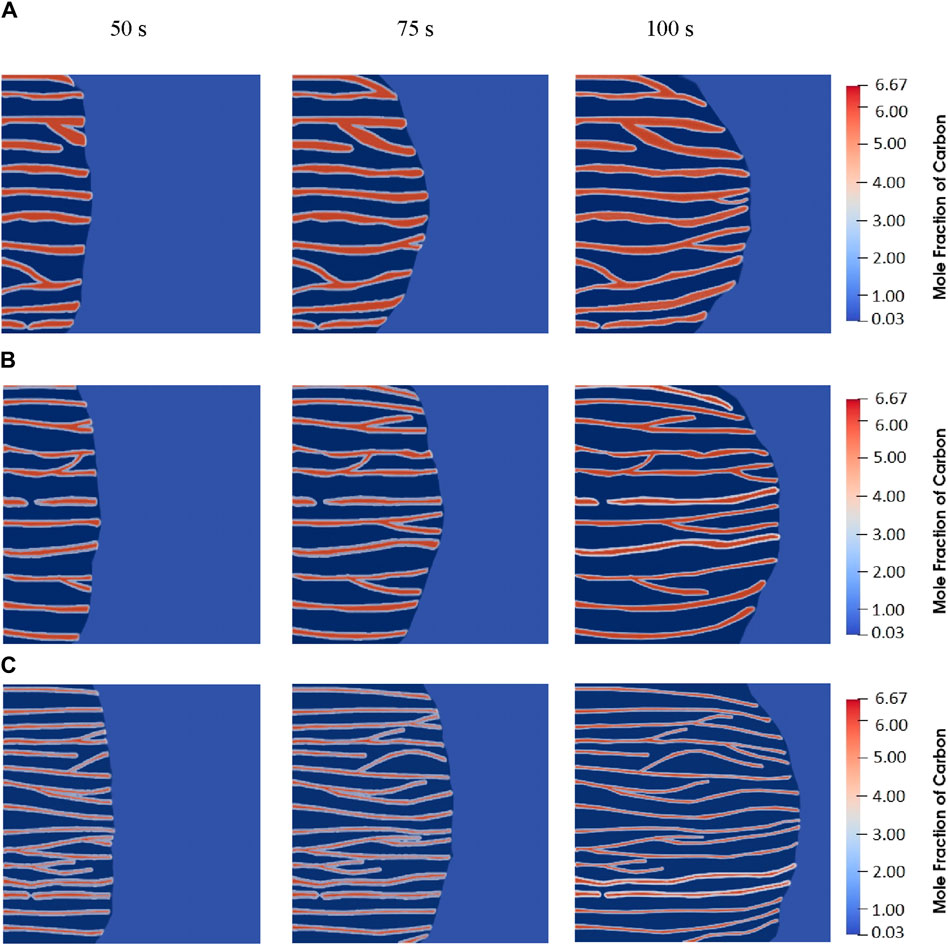
Figure 7. Evolution of the pearlite colony in continuous cooling at (A) $\mathbf{5}℃/\mathit{s}$, (B) $\mathbf{15}℃/\mathit{s}$, and (C) $\mathbf{100}℃/\mathit{s}$ after 50, 75, and 100 s. The figure is colored by the concentration: red represents cementite, dark blue represents austenite, and light blue represents ferrite.

In this figure, the culmination in diverse morphological behaviors, such as bifurcation and amalgamation within the cementite layers, is illustrated. Localized formation of new cementite within a pearlite colony has been observed to prevent the extension of pre-existing layers. Such dynamics suggest that continuous cooling increases the mobility of carbon atoms through short-ranged pathways at an accelerated rate relative to the isothermal conditions. In a broader context, with the temporal evolution of the pearlitic structure at the beginning, an examination of Figure 7A reveals a tendency for the pearlite colony’s constituent layers to coalesce. The existence of the thermal gradient at the front of these layers is notable.

Examination of Figure 7B, representing the water spray cooling methodology, reveals that increasing the cooling rate forces a decrease in the cementite layers’ thickness along with a contraction in the spacing between layers. In comparison with Figure 7A, only a negligible variation in the interlamellar spacing is observed, yet there is a discernible reduction in the cementite layers’ thickness. The degraded cementite morphology is distinctly observed within a layer, a phenomenon attributable to the increased cooling rate and the resulting restricted mobility of carbon atoms. Detailed inspection of Figure 7B elucidates the presence of morphological diversifications, such as branching, fusion of cementite layers, and their mutual alignment, all of which are well-captured in this simulation.

Figure 7C, illustrating the effects of quenching in cold water, shows a pronounced reduction in the thickness of the cementite layers. Concurrently, there is a discernible increment in the quantity of layers, which correlates with the decreased interlamellar spacing within the pearlite structure. The high cooling rate significantly restricts the diffusive process for carbon, thereby inducing an acicular configuration within the layers. Additionally, phenomena such as branching within the cementite structure, degraded cementite, and the suppression of expansion in the pre-existing cementite layers are distinctly identified in this figure.

This study on API X60 steel reveals that isothermal and continuous cooling treatments distinctly affect pearlite formation, aligning with established theoretical and empirical models. Isothermal treatment promotes uniform pearlite growth, controlled by thermodynamics and carbon diffusion, whereas continuous cooling results in varied microstructures due to fluctuating temperatures. Novel observations include the formation of divorced pearlite under certain cooling conditions, suggesting additional factors like local chemical composition and interfacial energy significantly influence pearlite morphology.

In assessing the fidelity of simulation and experimental methodologies in portraying the pearlite phase’s morphology, our focus centered on two principal metrics: layer thickness and interlayer spacing. These parameters were systematically measured across 50 instances within both simulated and actual micrographs, using Digimizer software, providing a robust dataset for comparison. Subsequent statistical analysis employing a two-sample t-test demonstrated no significant variance in either metric between the simulated and experimental data, with p-values of 0.78 for layer thickness and 0.65 for interlayer spacing, confirming the simulation’s effectiveness at a 95% confidence level. This outcome validates the phase-field model’s utility, particularly with the implementation of a triple-well potential, in accurately representing the intricate morphological traits of the pearlite phase.

Figure 8 illustrates the interlamellar spacing and cementite layer thickness, determined through both computational simulations and experiment approaches. In alignment with the discourse of prior sections, these morphological parameters are intricately linked to the thermal gradient experienced during the heat treatment process. These modeling and experimental data indicate a reciprocal relationship between cooling rates and isothermal holding temperatures with the dimensions of the aforementioned microstructural features. It was found that a decrease in both interlamellar spacing and layer thickness is accompanied with increased cooling rates or reduced isothermal temperatures. The comparative analysis between the simulation and experimental findings within the figure yields a significant correlation, with a computed difference of approximately 10.2% on average, underscoring the predictive accuracy and reliability of the simulation model within the accepted margin of deviation.

Figure 8

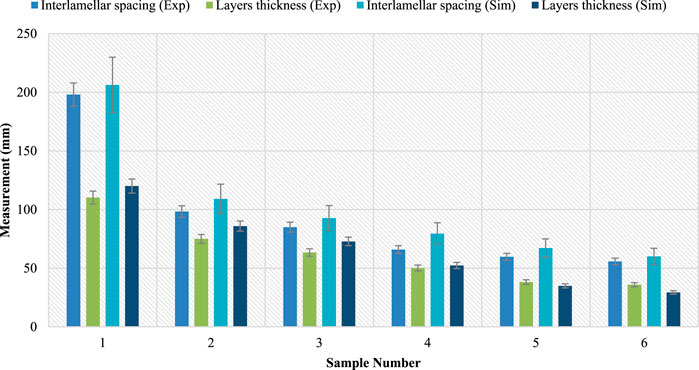
Figure 8. Comparing the data from both simulation and experimental approaches on interlamellar spacing and layer thickness.

4 Conclusion

Within the scope of the present investigation, the impacts of isothermal and continuous cooling treatment with the accompanying temperature gradients on microstructural evolution were analyzed utilizing both computational simulations and experimental methodologies. Phase-field modeling was used to explore phase transformation. The simulation of API X60 steel under continuous cooling conditions highlights the influence of thermodynamic and kinetic factors on the morphological evolution of pearlite colonies. Through the application of a triple-well potential, the simulations show how the free energy landscape shapes the morphology and growth kinetics, with interfacial energy playing a crucial role in determining the structure of pearlite. Additionally, the diffusion of carbon in the austenite matrix, modulated by cooling rates, directly impacts the formation of pearlite, influencing both the coarseness and fineness of its structure. This understanding is pivotal for optimizing heat treatment processes to improve the mechanical properties of steel by controlling pearlite morphology. Given the critical dependency of phase transformations on thermodynamic variables, it is imperative to apply precise and accurate formulations to ensure congruence with empirical data. Through an integrated assessment of outcomes derived from both computational and experimental procedures, the following conclusions have been reached:

1) In the scenario where a triple-well potential is utilized in the phase-field model, the results affirmed the formation of a three-phase microstructure comprising austenite, ferrite, and cementite, which collectively constitute the pearlite colony.

2) The simulation results utilizing the triple-well potential were in good agreement with the experimental findings, as evidenced by 10.2% difference of the thickness and interlamellar spacing derived from the two approaches.

3) The final microstructure obtained from the carried out simulations distinctly exhibited branching patterns, parallel alignment of cementite layers, and a convergence trend among the cementite layers for the continuous cooling heat treatment process.

This comprehensive approach facilitates the customization of heat treatment strategies to improve microstructural features and mechanical properties while minimizing residual stresses, optimizing API X60 steel’s performance for critical structural applications. The phase-field model developed in this study focuses on the thermodynamics and kinetics of pearlitic transformations in API X60 steel, excluding the impact of residual stresses which can significantly influence steel’s mechanical properties. This model has elucidated fundamental aspects, such as the growth of pearlite colonies and the effects of cooling rates on microstructural evolution. Future work will expand on these findings by incorporating the kinetics of phase transformations and the development of thermal- and transformation-induced stresses during cooling.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary material; further inquiries can be directed to the corresponding author.

Author contributions

MA: conceptualization, methodology, writing–original draft, and writing–review and editing. MP: conceptualization, methodology, and writing–review and editing. MG: methodology and writing–original draft. RR: formal analysis and writing–review and editing. HM: writing–review and editing. SX: writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. Financial support for publication was provided by the University of Oklahoma Libraries’ Open Access Fund.

Acknowledgments

The authors want to thank Behzad Sadeghian, Shahab Davoudi, Mostafa Hojati, and S. M. A. Anahid for their support during this research.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The author(s) declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmats.2024.1390159/full#supplementary-material

References

Allen, S. M., and Cahn, J. W. (1972). Ground state structures in ordered binary alloys with second neighbor interactions. Acta Metall. 20 (3), 423–433. doi:10.1016/0001-6160(72)90037-5

CrossRef Full Text | Google Scholar

Allen, S. M., and Cahn, J. W. (1973). A correction to the ground state of fcc binary ordered alloys with first and second neighbor pairwise interactions. Scr. Metall. 7 (12), 1261–1264. doi:10.1016/0036-9748(73)90073-2

CrossRef Full Text | Google Scholar

Ankit, K., Choudhury, A., Qin, C., Schulz, S., McDaniel, M., and Nestler, B. (2013). Theoretical and numerical study of lamellar eutectoid growth influenced by volume diffusion. Acta Mater. 61 (11), 4245–4253. doi:10.1016/j.actamat.2013.03.050

CrossRef Full Text | Google Scholar

Baker, T. N. (2016). Microalloyed steels. Ironmak. Steelmak. 43 (4), 264–307. doi:10.1179/1743281215y.0000000063

CrossRef Full Text | Google Scholar

Battezzati, L., Baricco, M., and Curiotto, S. (2005). Non-stoichiometric cementite by rapid solidification of cast iron. Acta Mater. 53 (6), 1849–1856. doi:10.1016/j.actamat.2004.12.035

CrossRef Full Text | Google Scholar

Cahn, J. W. (1961). On spinodal decomposition. Acta Metall. 9 (9), 795–801. doi:10.1016/0001-6160(61)90182-1

CrossRef Full Text | Google Scholar

Cahn, J. W., and Hagel, W. G. (1963). Divergent pearlite in a manganese eutectoid steel. Acta Metall. 11 (6), 561–574. doi:10.1016/0001-6160(63)90090-7

CrossRef Full Text | Google Scholar

Cahn, J. W., and Hilliard, J. E. (1958). Free energy of a nonuniform system. I. Interfacial free energy. J. Chem. Phys. 28 (2), 258–267. doi:10.1063/1.1744102

CrossRef Full Text | Google Scholar

Chakraborty, S., Gupta, A. K., Roy, D., and Basumallick, A. (2019). Studies on nano-metal dispersed Cu-Cr matrix composite. Mater. Lett. 257, 126739. doi:10.1016/j.matlet.2019.126739

CrossRef Full Text | Google Scholar

Chakravarty, S., Sikdar, K., Singh, S. S., Roy, D., and Koch, C. C. (2017). Grain size stabilization and strengthening of cryomilled nanostructured Cu 12 at% Al alloy. J. Alloys Compd. 716, 197–203. doi:10.1016/j.jallcom.2017.05.093

CrossRef Full Text | Google Scholar

Collins, L. E., Godden, M. J., and Boyd, J. D. (1983). Microstructures of linepipe steels. Can. Metall. Q. 22 (2), 169–179. doi:10.1179/cmq.1983.22.2.169

CrossRef Full Text | Google Scholar

Cotterill, P., and Mould, P. R. (1976). Recrystallization and grain growth in metals.

Google Scholar

Darling, K. A., Chan, R. N., Wong, P. Z., Semones, J. E., Scattergood, R. O., and Koch, C. C. (2008). Grain-size stabilization in nanocrystalline FeZr alloys. Scr. Mater. 59 (5), 530–533. doi:10.1016/j.scriptamat.2008.04.045

CrossRef Full Text | Google Scholar

DeArdo, A. J., Hua, M. J., Cho, K. Gr, and Garcia, C. I. (2009). On strength of microalloyed steels: an interpretive review. Mater. Sci. Technol. 25 (9), 1074–1082. doi:10.1179/174328409x455233

CrossRef Full Text | Google Scholar

Dong, C.-fang, Xiao, K., Liu, Z.-yong, Yang, W.-jing, and Li, X.-gang (2010). Hydrogen induced cracking of X80 pipeline steel. Int. J. Minerals, Metallurgy, Mater. 17, 579–586. doi:10.1007/s12613-010-0360-2

CrossRef Full Text | Google Scholar

Dong, H. (2012). High performance steels: initiative and practice. Sci. China Technol. Sci. 55, 1774–1790. doi:10.1007/s11431-012-4911-9

CrossRef Full Text | Google Scholar

El-Zaidia, M. M., Mai, Z. Z., Abomostafa, H. M., and Taha, M. A. (2024). Comprehensive studies for evaluating promising properties of Cu/Graphene/Fly ash nanocomposites. Sci. Rep. 14 (1), 2236. doi:10.1038/s41598-024-52563-w

PubMed Abstract | CrossRef Full Text | Google Scholar

Furuhara, T., Kikumoto, K., Saito, H., Sekine, T., Ogawa, T., Morito, S., et al. (2008). Phase transformation from fine-grained austenite. ISIJ Int. 48 (8), 1038–1045. doi:10.2355/isijinternational.48.1038

CrossRef Full Text | Google Scholar

Gaude-Fugarolas, D. (2002). “Phase transformations in steel during induction hardening,” in Mathematical modelling and information technologies in welding and related processes (Crimea, Ukraine: Katsiveli), 16–20.

Google Scholar

Gong, P., Palmiere, E. J., and Rainforth, W. M. (2016). Thermomechanical processing route to achieve ultrafine grains in low carbon microalloyed steels. Acta Mater. 119, 43–54. doi:10.1016/j.actamat.2016.08.010

CrossRef Full Text | Google Scholar

Hagel, W. C., Pound, G. M., and Mehl, R. F. (1956). Calorimetric study of the austenite: pearlite transformation. Acta Metall. 4 (1), 37–46. doi:10.1016/0001-6160(56)90107-9

CrossRef Full Text | Google Scholar

Kilmametov, A. R., Ivanisenko, Yu, Mazilkin, A. A., Straumal, B. B., Gornakova, A. S., Fabrichnaya, O. B., et al. (2018). The α→ω and β→ω phase transformations in Ti–Fe alloys under high-pressure torsion. Acta Mater. 144, 337–351. doi:10.1016/j.actamat.2017.10.051

CrossRef Full Text | Google Scholar

Koch, C. C., Morris, D. G., Lu, K., and Inoue, A. (1999). Ductility of nanostructured materials. Mrs Bull. 24 (2), 54–58. doi:10.1557/s0883769400051551

CrossRef Full Text | Google Scholar

Landau, L. D., and Khalatikov, I. M. (1963). The selected works of LD landau. Oxford: Pregamon.

Google Scholar

Langer, J. S. (1980). Instabilities and pattern formation in crystal growth. Rev. Mod. Phys. 52 (1), 1–28. doi:10.1103/revmodphys.52.1

CrossRef Full Text | Google Scholar

Lee, D. (2023). Gradient-Descent-like scheme for the allen–Cahn equation. AIP Adv. 13 (8). doi:10.1063/5.0161876

CrossRef Full Text | Google Scholar

Mathapati, M., Amate, K., Prasad, C. D., Jayavardhana, M. L., and Raju, T. H. (2022). A review on fly ash utilization. Mater. Today Proc. 50, 1535–1540. doi:10.1016/j.matpr.2021.09.106

CrossRef Full Text | Google Scholar

Mathews, J. A., Farahani, H., Sietsma, J., Petrov, R. H., Mecozzi, M. G., and Santofimia, M. J. 2023. “Microstructures in a carburized steel after isothermal pearlitic treatment.” J. Mater. Sci. Technol. 160:66–75. doi:10.1016/j.jmst.2023.03.017

CrossRef Full Text | Google Scholar

Morrison, W. B. (2009). Microalloy steels–the beginning. Mater. Sci. Technol. 25 (9), 1066–1073. doi:10.1179/174328409x453299

CrossRef Full Text | Google Scholar

Okatov, S. V., Gornostyrev, Yu N., Lichtenstein, A. I., and Katsnelson, M. I. (2011). Magnetoelastic coupling in γ-iron investigated within an ab initio spin spiral approach. Phys. Rev. B 84 (21), 214422. doi:10.1103/physrevb.84.214422

CrossRef Full Text | Google Scholar

Olivares, I., Alanis, M., Mendoza, R., Campillo, B., and Juarez-Islas, J. A. (2008). Development of microalloyed steel for pipeline applications. Ironmak. Steelmak. 35 (6), 452–457. doi:10.1179/174328108x318879

CrossRef Full Text | Google Scholar

Pandit, A. S., and Bhadeshia, HKDH (2012). Divorced pearlite in steels. Proc. R. Soc. A Math. Phys. Eng. Sci. 468 (2145), 2767–2778. doi:10.1098/rspa.2012.0115

CrossRef Full Text | Google Scholar

Qin, R. S., and Bhadeshia, H. K. (2010). Phase field method. Mater. Sci. Technol. 26 (7), 803–811. doi:10.1179/174328409x453190

CrossRef Full Text | Google Scholar

Razumov, I. K., Yu, N. G., and Katsnelson, M. I. (2017). Autocatalytic mechanism of pearlite transformation in steel. Phys. Rev. Appl. 7 (1), 014002. doi:10.1103/physrevapplied.7.014002

CrossRef Full Text | Google Scholar

Razumov, I. ’ya K. (2017). Stabilization of growth of a pearlite colony because of interaction between carbon and lattice dilatations. Phys. Solid State 59, 1906–1912. doi:10.1134/s1063783417100304

CrossRef Full Text | Google Scholar

Roy, D., Chakraborty, S., Gupta, A. K., Mallick, A. B., and Koch, C. C. (2020a). Synergistic effect of Nb and Zr addition in thermal stabilization of nano-crystalline Cu synthesized by ball milling. Mater. Lett. 271, 127780. doi:10.1016/j.matlet.2020.127780

CrossRef Full Text | Google Scholar

Roy, D., Gupta, A. K., Alam, Md S., Srikanth, S., and Jha, B. K. (2020b). Enhancement of properties of micro-alloyed low-carbon Ni-added steel by thermomechanical treatment. J. Mater. Eng. Perform. 29 (12), 7952–7963. doi:10.1007/s11665-020-05311-w

CrossRef Full Text | Google Scholar

Shin, S. Y., Hwang, B., Kim, S., and Lee, S. (2006). Fracture toughness analysis in transition temperature region of API X70 pipeline steels. Mater. Sci. Eng. A 429 (1–2), 196–204. doi:10.1016/j.msea.2006.05.086

CrossRef Full Text | Google Scholar

Smart, J. S., and Van Vleck, J. H. (1966). Effective field theories of magnetism. America: American Institute of Physics.

Google Scholar

Steinbach, I., and Apel, M. (2007). The influence of lattice strain on pearlite formation in Fe–C. Acta Mater. 55 (14), 4817–4822. doi:10.1016/j.actamat.2007.05.013

CrossRef Full Text | Google Scholar

Toloui, M., and Militzer, M. (2010). Phase field simulation of austenite grain growth in the HAZ of microalloyed linepipe steel. Int. J. Mater. Res. 101 (4), 542–548. doi:10.3139/146.110308

CrossRef Full Text | Google Scholar

Vaks, V. G., Stroev, A. Yu, Urtsev, V. N., and Shmakov, A. V. (2011). Experimental and theoretical study of the formation and growth of pearlite colonies in eutectoid steels. J. Exp. Theor. Phys. 112, 961–978. doi:10.1134/s1063776111050098

CrossRef Full Text | Google Scholar

Yan, Y.-F., Kou, S.-Q., Yang, H.-Yu, Shu, S.-Li, Qiu, F., Jiang, Q.-C., et al. (2023). Ceramic particles reinforced copper matrix composites manufactured by advanced powder metallurgy: preparation, performance, and mechanisms. Int. J. Extreme Manuf. 5, 032006. doi:10.1088/2631-7990/acdb0b

CrossRef Full Text | Google Scholar

Yapp, D., and Blackman, S. A. (2004). Recent developments in high productivity pipeline welding. J. Braz. Soc. Mech. Sci. Eng. 26, 89–97. doi:10.1590/s1678-58782004000100015

CrossRef Full Text | Google Scholar

Zhang, Yi, Volinsky, A. A., Tran, H. T., Chai, Z., Liu, P., Tian, B., et al. (2016). Aging behavior and precipitates analysis of the Cu–Cr–Zr–Ce alloy. Mater. Sci. Eng. A 650, 248–253. doi:10.1016/j.msea.2015.10.046

CrossRef Full Text | Google Scholar