- 1China First Highway Engineering Co., Ltd., Beijing, China
- 2School of Transportation and Geomatics Engineering, Shenyang Jianzhu University, Shenyang, China
The dynamic modulus of asphalt mixture is an important factor in the design of asphalt pavement, and many scholars have proposed different models for estimating the dynamic modulus of asphalt mixture, but there are almost no studies on the prediction of the dynamic modulus of semi-flexible materials. In order to analyze and estimate the dynamic modulus of semi-flexible materials, we set up a high-performance cementitious paste (HPCP) semi-flexible material and a reference group Stone Mastic Asphalt (SMA-16) under multiple conditions, first measured its dynamic modulus in the laboratory, and analyzed the dynamic modulus characteristics of the material, and then used the equation the estimation equation proposed by Witczak et al. (Witczak1-37A) as a benchmark to introduce a new parameter, grouting mass ratio (Pb) to develop a Witczak-G prediction model to compare and validate the predicted dynamic modulus with the measured values. The results show that compared with SMA-16, HPCP semi-flexible material exhibits higher dynamic modulus and lower phase angle, and its temperature sensitivity and deformation resistance are significantly better than those of SMA-16. Under the influence of porosity and Pb factor, the dynamic modulus is positively correlated with both factors, and the phase angle increases first and then decreases, showing strong elastic properties. In this paper, we propose a dynamic modulus prediction model based on viscosity and Pb, Witczak-G, which predicts the highest coefficient of determination (R2) of the predicted dynamic modulus as high as 0.99 after initial fitting and validation, which indicates that the Witczak-G model is suitable for predicting the dynamic modulus of semi-flexible materials injected with HPCP.
1 Introduction
Semi-flexible pavement (SFP) is a joint-free pavement formed by a special cement grouting material poured into an open-graded asphalt mixture (its void ratio is 20%–30%). PSFP offers benefits such as resistance to high-temperature rutting, reduced cracks, and enhanced pavement material performance. The earliest research on semi-flexible pavement was the construction of a semi-flexible composite pavement test road on an airstrip in France (1954) and the application for a construction patent called “Salviacim” (Guo et al., 2022). In recent years, a large number of studies have been carried out on the properties of SFP, such as Setyawan. (2013), who studied the relationship between the compressive strength of grouting materials and SFP through uniaxial compression tests. Pei et al. (2016) also analyzed the compressive strength and compressive modulus of SFP using uniaxial compression tests. Cai et al. (2017) found that the contribution of grouting material to the whole was much higher than that of matrix asphalt mixture, and found that pouring high-performance cement paste and pure cement paste into matrix asphalt mixture respectively had similar mechanical properties, but high-performance cement paste had better pavement performance and durability, in addition, in order to meet the wettability requirements of densely graded asphalt concrete, the void ratio of matrix asphalt mixture should reach 21% in the injection of high-performance cement paste and 24% in the injection of pure cement paste. Yang et al. (2022) used five kinds of asphalt binders with different binding properties and rheological properties to form SFP, and experimental studies showed that there were obvious differences in the influence of adhesive properties and rheological properties of asphalt binders such as viscosity and bond strength on the crack resistance of SFP.
Studying the dynamic parameters and dynamic characteristics of semi-flexible pavement structure under dynamic load is essential. The dynamic modulus, a crucial performance parameter in the Mechanistic Empirical Pavement Design Guide (MEPDG), represents the ratio of axial stress amplitude to strain amplitude under dynamic load. This parameter aligns more closely with the actual stress conditions of pavement structures (Donald and Bonaquist, 2015). There are three methods to obtain dynamic modulus: laboratory testing using detection equipment, calculation through established empirical formulas, and empirical-based reference to typical values. Currently, the mainstream approach for obtaining the dynamic modulus of pavement materials involves indoor testing using equipment at different temperatures and frequencies. The dynamic modulus is then obtained through fitting based on certain functional relationships, illustrating the main curve depicting its variations with temperature and loading frequency. However, indoor testing for dynamic modulus involves complex conditions, substantial workload, and high experimental costs (Christensen et al., 2003). To streamline the process and reduce the effort in obtaining the dynamic modulus of pavement materials, researchers have conducted numerous experiments, accumulating a wealth of dynamic modulus test data. Based on material characteristics and experimental conditions, predictive models for asphalt mixtures have gradually been established. Among them, the Witczak1-A and Hirsch models are widely recognized predictive models, along with modified Witczak and models proposed by National cooperation Highway Research Program (NCHRP 1-40D), among others (Al-Khateeb et al., 2006), however, the current series of predictive models focus primarily on conventional asphalt mixtures, with limited research on the dynamic modulus of injected semi-flexible material pavements. Existing studies are limited to the exploration of the main curve of dynamic modulus, lacking precise prediction equations. As there is no secondary level for obtaining the dynamic modulus of semi-flexible materials, it has become imperative to seek a simplified method for predicting the dynamic modulus of such materials.
Numerous researchers have established comprehensive asphalt mixture material characteristics and dynamic modulus databases, incorporating climate conditions, test parameters, material properties, etc. This has led to the development of several dynamic modulus estimation models for asphalt mixtures. Previous studies have established a comprehensive database of material characteristics and dynamic modulus of asphalt mixture through a large number of indoor and outdoor tests, and combined with climate, test conditions, material characteristics, etc., a series of dynamic modulus prediction models of asphalt mixture have been proposed. The Witczak1-37A model is one of the most widely used dynamic modulus prediction models, which follows a Sigmoid form, it defines key parameters influencing dynamic modulus, including asphalt content and viscosity, aggregate critical sieve pore passing rate, void ratio, test temperature, loading frequency, etc. However, the model does not consider the viscoelastic properties (Gb*) of asphalt, which significantly deviates from actual asphalt performance and requires adjustment in practical applications. The NCHRP1-40D model is the Witczak1-37A model modified by Bari (2005), which comprehensively considers mixture types, including various asphalt types and aging conditions, by replacing the original model’s viscosity-temperature relationship with shear modulus |Gb*| and phase angle δ, the Witczak model more effectively reflects the deformation characteristics of asphalt mixtures under different load frequencies and temperatures (Ma et al., 2018). The Hirsch model is a semi-empirical formula, which biggest feature is that the dynamic modulus of asphalt mixture is predicted by using the dynamic shear modulus of asphalt binder |Gb*|, voids in mineral aggregate (VMA) and vapor flash aromatics (VFA), so as to better reflect the performance of asphalt mixture. In summary, the previous models are based on the Witczak1-37A model and the Hirsch model modification, so these two commonly used models are selected (Ceylan et al., 2009; Gu et al., 2019; Bi et al., 2021).
With support from the NCHRP 1-40D program, the model has been revised, incorporating additional data and parameters. The updated version demonstrates improved predictive capabilities and stands as one of the most widely applied estimation models today (Salini et al., 2015; Ma et al., 2017a; Ma et al., 2017b; Bueno et al., 2020; Vestena et al., 2023). The dynamic shear modulus |Gb*|, voids in mineral aggregate (VMA), and asphalt saturation (VFA) are utilized for predicting the dynamic modulus of asphalt mixtures. Due to a relatively limited dataset, further validation is required for the reliability of its regression model. Research indicates that the Hirsch model struggles to accurately predict the dynamic modulus of mixtures at high temperatures and low frequencies (Kim et al., 2005; Zhang et al., 2022a; Zhao et al., 2012; Jiang et al., 2022; Kim and Lee, 1995). Noted poor performance of the Hirsch model for |E*| at low temperatures (−10°C), attributing it to extrapolated binder data rather than direct measurements. They also highlighted the Witczak model’s greater effectiveness at colder temperatures compared to warmer ones (Khan et al., 2023; Liu et al., 2023). It is an urgent need to propose an estimation model for the dynamic modulus of semi-flexible materials, which is essential for the design of dynamic parameters and dynamic characteristics of semi-flexible pavement structures under dynamic loading. The practical applicability of the above three typical models is affected by many factors, mainly due to the different environment, temperature, raw material characteristics, experimental working conditions and load frequency standards in different countries, resulting in changes in the applicability of the estimation model, with the development of computer technology, researchers have gradually formed a trend of predicting the modulus of asphalt mixture through numerical simulation of discrete elements (Cheng et al., 2023; Hu et al., 2023).
This paper proposes a dynamic modulus prediction equation for predicting the stiffness of poured semi-flexible material layers. Previous dynamic modulus prediction models were limited to conventional asphalt mixtures, and the study of dynamic modulus for poured semi-flexible materials was restricted to master curve analysis. However, as road materials and structural forms become more diverse, conventional prediction models require modification. The key innovation of this study lies in deviating from the traditional dynamic modulus prediction for typical asphalt mixtures. Instead, focusing on poured-in semi-flexible materials, it introduces the grout-to-mixture mass ratio as a new variable, expanding the material scope for dynamic modulus prediction. This design considers the influence of aggregate and asphalt based on their respective characteristics, distinguishing itself from previous dynamic modulus equations by incorporating the impact of grout. It introduces the grout mass ratio Pb, further proposing a dynamic modulus estimation equation for semi-flexible materials. The equation has been validated, providing a convenient and informative reference for the research and design of semi-flexible pavement materials.
This paper commences with indoor experiments. It sequentially prepares semi-flexible material specimens. The porosity of matrix asphalt is an important factor affecting the dynamic modulus of the mixture, and a specific porosity range is selected as a representative and its change trend is analyzed, and the dynamic modulus characteristics of the entire porosity range can be deduced, which saves a lot of test operation and time (Pan et al., 2023; Zhao et al., 2023). The preparation involves grouting HPCP with varying base asphalt void ratios (20%, 22%, and 24%) and grouting volumes. Additionally, a set of SMA-16 specimens is prepared using the same SBS modified asphalt Following that, the DTS-30 dynamic hydraulic servo testing equipment was employed. The tests were conducted using the Dynamic Modulus American Association of State Highway and Transportation Officials (AASHTO-TP79) method. Single-axis compression dynamic modulus tests were conducted at five different test temperatures and six different loading frequencies. The dynamic modulus and phase angle of two pavement mixtures were measured. Comparatively analyzing their dynamic modulus and phase angle variations with test temperature and loading frequency, we also discuss the impact of base asphalt void ratios and Pb on the dynamic modulus and phase angle of semi-flexible materials. Finally, a comparative analysis of the applicability of Witczak1-A and Hirsch models to PSFP was conducted. A baseline predictive model was selected, and we discussed and introduced grouting material impact parameters. We constructed a semi-flexible material dynamic modulus prediction model and validated it. At present, the main object of dynamic modulus estimation research is ordinary asphalt mixture, and the model used to predict the dynamic modulus of ordinary asphalt mixture is representative, and it is easier and cheaper to obtain or estimate the modulus of asphalt mixture, but these models still have certain limitations in predicting the dynamic modulus of other types of asphalt mixture (such as warm mix asphalt, rubber asphalt, etc.). Therefore, it is necessary to establish an estimation model based on the dynamic modulus test of more types of asphalt mixtures (Peng et al., 2023; Zarei et al., 2023; Dhandapani and Mullapudi, 2023).
2 Materials and methods
2.1 Material selection
Raw materials include: aggregates, mineral powders, SBS modified asphalt, Subote JGM-301 type grout.
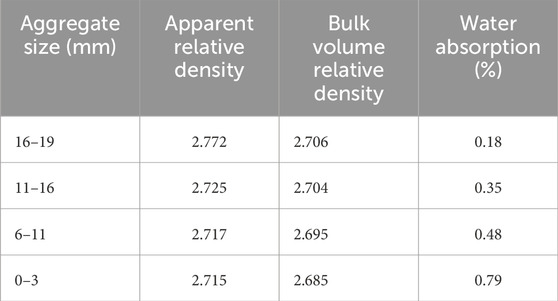
(1) The coarse and fine aggregates used are selected from basalt and limestone respectively, and the filler is made of mineral powder and ground from limestone. The selected aggregates are divided into 4 grades, which are 0∼3 mm, 6∼11 mm, 11∼16 mm, and 16∼19 mm, and the basic index test results are shown in Tables 1, 2.
(2) In this study, SBS modified asphalt was selected, and the test results of various performance parameters are shown in Table 3.
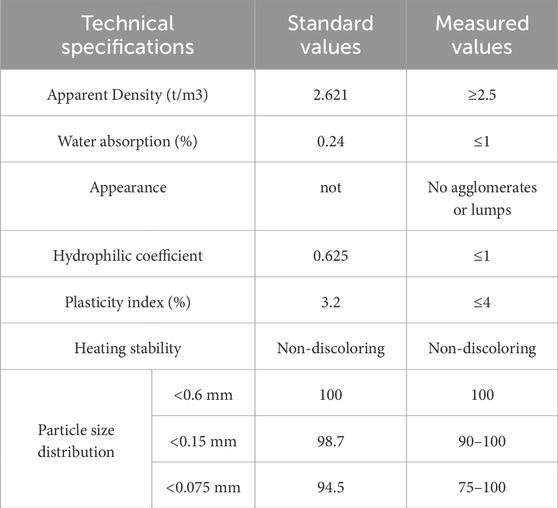
(3) Su Bot JGM-301 semi-flexible pavement grouting was used in this experiment, which is dark brown in color. The water-cement ratio is set at 0.29, using a high-performance cement grout with high fluidity and low expansion characteristics. The basic performance test results of cement and accelerator are shown in Tables 4, 5.
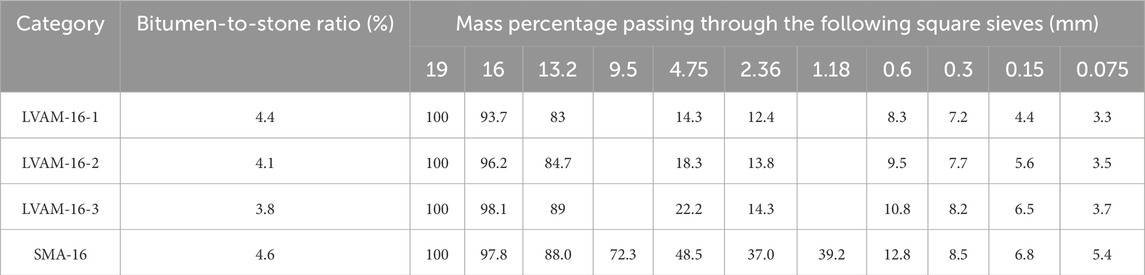
(4) In this paper, three groups of large-void matrix asphalt mixtures with different gradations and one group of SBS modified asphalt SMA-16 were designed, as shown in Table 6.
2.2 Sample preparation
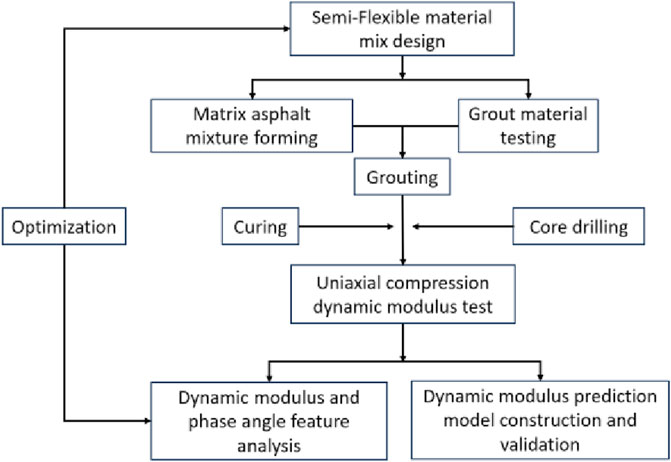
In the laboratory, three types of high void asphalt mix specimens were produced, with four replicate specimens for each type. These specimens were compacted using a gyratory compactor into cylinders with a diameter of 150 mm and a height of 170 mm. Grouting commenced when the specimen temperature reached 50°C, and the grouting continued until bubbling ceased. After the completion of grouting, it is necessary to test the grouting volume for each of the three PSFP mixtures, with each group consisting of four specimens (labeled as PSFP1#1 to PSFP1#4 for the first group, PSFP2#1 to PSFP2#4 for the second group, and PSFP3#1 to PSFP3#4 for the third group, totaling 12 specimens). Table 7 presents the grouting volume (Pb) for each specimen, indicating a relatively uniform grouting amount for each gradation, demonstrating good grouting effectiveness. After the specimens reach the required strength, cores are taken and cut to obtain the target specimens (with a diameter of 100 mm and height of 150 mm). The porosity and asphalt content errors for each specimen are within ±0.5%. The specific process for preparing semi-flexible specimens is illustrated in Figure 1. Finally, a set of four specimens of a general asphalt mixture using the same SBS modified asphalt (labeled as SMA-16#1 to SMA-16#4) is prepared for comparative testing.
2.3 Experimental methods
Firstly, the specimens were cut to prepare specimens conforming to the standard for dynamic modulus testing under uniaxial compression. These specimens are cylindrical asphalt mix specimens with a diameter of 100 mm ± 2 mm and a height of 150 ± 2.5 mm. Figure 2 is the experimental setup multifunctional hydraulic servo pavement material dynamic testing system (DTS-30), which using the AASHTO TP79 method. The testing conditions include five temperatures and six loading frequencies: 10°C, 5°C, 20°C, 35°C, and 50°C. The environmental chamber maintains a temperature control accuracy of ±0.5°C. The tests are conducted in a sequence starting from low to high temperatures, with loading frequencies ranging from 25 Hz to 0.1 Hz. This approach effectively mitigates potential damage to the specimens (Khan et al., 2022a; Liu et al., 2022; Zhao and Yang, 2023). The experiment employs computer control, which measures and records the axial load and axial deformation experienced by the specimen in each loading cycle. It ensures that the axial response strain of the specimen is controlled between 50 and 150 micro-strains (Ling et al., 2022a; Solouki et al., 2022). The test is conducted under the conditions of linear viscoelastic stress, and it provides dynamic modulus values and phase angles for the two materials.
In this paper, the prediction model is fitted on the basis of a large number of experimental data obtained from the above experiments, firstly, the experimental data are analyzed and processed, the dynamic modulus characteristic changes under various factors are analyzed, the benchmark model is discussed and selected, the new parameter Pb is introduced to modify the original model, and the generated prediction equation is verified to be applicable.
3 Results and discussion
3.1 Dynamic modulus and phase angle feature analysis
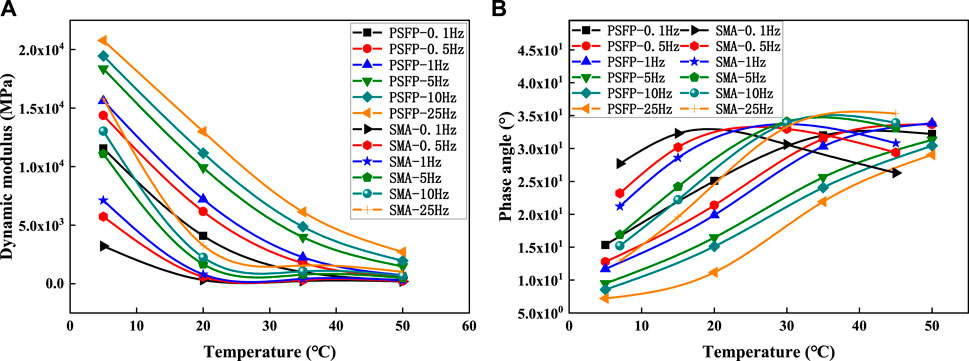
Compared to SMA-16, the semi-flexible material specimens exhibit an overall increase in dynamic modulus values. Additionally, they show a smaller overall phase angle. This implies a substantial reduction in the overall high-temperature viscosity of the material and, simultaneously, an enhancement in low-temperature elasticity through grouting. The outstanding feature of grouted semi-flexible materials lies in the enhancement of the high-temperature dynamic modulus of pavement materials. This improvement is particularly noteworthy. Comparing PSFP and SMA-16 mixtures, Figures 3A, B display the dynamic modulus results at varying test temperatures and loading frequencies. Both materials exhibit a gradual decrease in dynamic modulus with increasing temperature and a gradual increase with higher frequency from 5°C to 35°C, SMA-16 shows a rapid concave decrease in dynamic modulus with rising temperature, while the grouted semi-flexible material tends to exhibit a slower, linear decline. Notably, the dynamic modulus of the grouted semi-flexible material is significantly higher than that of SMA-16, with the former being approximately three times greater than the latter at 20°C. At 50°C, the grouted semi-flexible material is approximately 1.6–2.9 times that of SMA-16.
The conventional view holds that asphalt mixtures are viscoelastic materials. According to Eq. 1, past research has indicated that cos ϕ represents the elastic portion, and a smaller ϕ implies a higher proportion of elastic recovery, indicating better recovery capability after deformation. The imaginary part represented by sin ϕ indicates the viscosity of the material. A larger ϕ suggests a higher proportion of viscous behavior, indicating poorer recovery capability after deformation (Yang et al., 2022; Xiong et al., 2022; Zarei et al., 2022; Davoodi et al., 2022).
where: |E*| is the dynamic modulus, MPa; σo is the axial stress amplitude; εo is the axial strain amplitude; ϕ is the phase angle of strain lagging stress.
During the asphalt mixture experiment, the relationship between phase angle and frequency, as well as temperature in Figure 3, reveals that for SMA-16 at 7°C and 15°C, the phase angle decreases with increasing loading frequency and increases with temperature. At the same time, the relative value of the phase angle is small, indicating that at lower temperatures, the material exhibits more elasticity. At this point, the material’s resistance to temperature and load is jointly borne by the elastic and plastic components. However, at 30°C and 45°C, the phase angle increases with the acceleration of the loading frequency and decreases with the increase in temperature. At this point, the material’s ability to resist temperature and load is more dependent on the elastic component. The overall phase angle of grouted semi-flexible materials is generally smaller than that of SMA-16. The analysis indicates that compared with ordinary asphalt mixture, the high temperature sensitivity of semi-flexible materials is lower, because the pouring of grouting materials forms a three-phase structure of asphalt, aggregate and grout, and the grouting material provides great rigidity at high temperatures, so that it still has good resistance to deformation under high temperature conditions, and the structure still maintains good ductility at low temperatures.
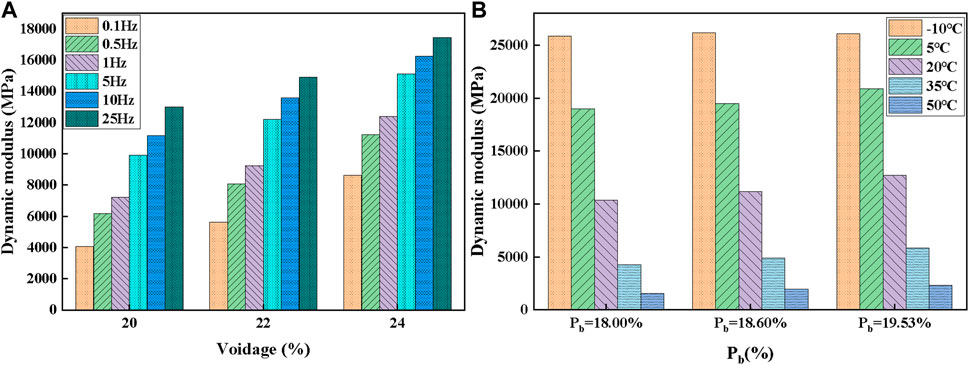
It illustrates the dynamic modulus of PSFP asphalt mixtures with different aggregate void ratios at a temperature of 20°C, which is shown in Figure 4A. Analyses indicates an increase in the dynamic modulus of PSFP with the addition of Pb, and the rate of increase gradually rises. It is evident that within the range of 20%, 22%, and 24% aggregate void ratios in the matrix asphalt mixture, the dynamic modulus of the injected semi-flexible material correlates positively with the aggregate void ratio. Under a loading frequency of 10 Hz, when the aggregate void ratio of the matrix asphalt mixture increases by 2% and 4%, the dynamic modulus increases by 21.7% and 45.6%, respectively. For each 1% increase in the aggregate void ratio of the matrix asphalt mixture, the dynamic modulus of the injected semi-flexible material increases by 10.85% and 11.4%. Figure 4B presents the dynamic modulus of three sets of specimens with the same gradation under a loading frequency of 10 Hz, at different grouting mass ratios. The grouting mass ratios are 18.00%, 18.60%, and 19.53%. At an experimental temperature of 20°C, as Pb increases by 0.6% and 1.53%, the dynamic modulus increases by 8% and 23%, respectively. For each 1% increase in the grouting mass ratio, the dynamic modulus increases by 13.33% and 15.03%. In conclusion, within the void ratios of 20%, 22%, and 24%, the dynamic modulus increases with the addition of grout, and the rate of increase gradually rises, For every 1% increase in grouting rate or void ratio, the dynamic modulus increases by about 10%–15%. Compared with the law that the dynamic modulus of semi-flexible materials increases with the increase of porosity, some studies have shown that the dynamic modulus (PAC-13) of ordinary asphalt mixture increases by about 15.8% on average for every 1% decrease in porosity, he reason for this is that with the increase of porosity, the increase of grouting directly leads to the increase of the dynamic modulus of semi-flexible materials.
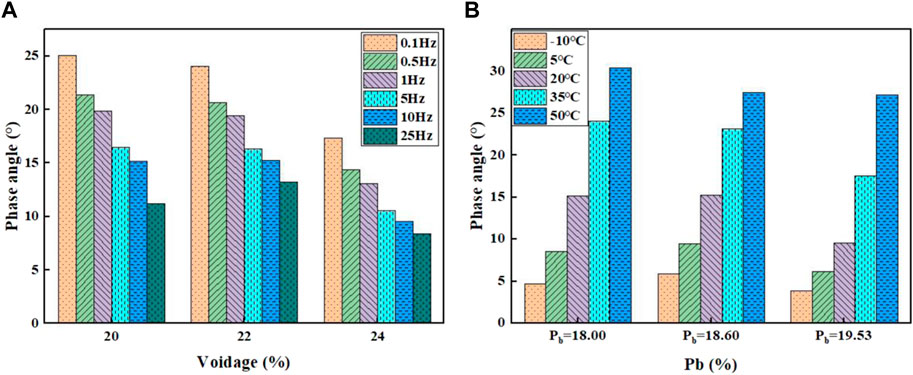
The variations in phase angle with aggregate void ratios and different Pb are shown in Figures 5A, B. Analysis indicates that the phase angle of PSFP doesn't consistently decrease with an increase in aggregate void ratio and Pb. At low temperatures, it initially increases with added Pb and then gradually decreases. Under the same experimental conditions, the phase angle decreases with an increase in aggregate void ratio and increases with more Pb. For a 10 Hz loading frequency, as the aggregate void ratio of the matrix asphalt mixture increases between 20% and 22%, and between 22% and 24%, the phase angle increases by 0.05° and decreases by 7.61°, respectively. At a temperature of 20°C, when Pb of the matrix asphalt mixture increases between 18% and 18.6%, and between 18.6% and 19.53%, the phase angle increases by 0.16° and decreases by 6.12°, respectively, for each 1% increase in the grouting mass ratio. It can be seen that when the porosity gradually increases, the phase angle increases less and decreases more, the larger the porosity, the more obvious the elastic state and the stronger the deformation resistance, the main reason is that the grouting material has the characteristics of a rigid material.
3.2 Construction of dynamic modulus prediction model
3.2.1 Determination of baseline prediction model
In recent years, numerous studies have utilized indoor dynamic modulus tests, which generated a wealth of experimental data. Based on material characteristics and experimental conditions, predictive models for asphalt mixtures have been gradually established. Among them, the Witczak 1–37A and Hirsch models are the most commonly used forecasting models (Zhang et al., 2022b; Zhao and Yang, 2022). The Witczak 1–37A model conforms to the Sigmoidal function form. Developed by Witczak and other researchers over more than 30 years, the Witczak 1–37A model is derived from 2,750 sets of dynamic modulus data obtained through extensive testing of 205 asphalt mixtures. The key influencing factors on modulus include aggregate gradation, asphalt mixture void ratio, optimal asphalt content and viscosity, loading frequency, experimental temperature, etc., (Zhao and Yang, 2022), as represented in Eq. 2.
where: |E*| is the dynamic modulus, MPa; Vbeff is the effective asphalt content of asphalt mixture, %; ƒ is the loading frequency, Hz; η is asphalt viscosity, MPa s; Va is the porosity of the asphalt mixture, %; ρ200 is the percentage of the pass rate of 0.075 sieve holes, %; ρ4, ρ38 and ρ34 are the cumulative sieving percentages of aggregates at 4.75 mm, 9.5 mm and nominal maximum particle size sieve holes, respectively, %; ρ34 is the percentage of mass of the aggregate on the nominal maximum particle size sieve hole, %.
The Hirsch model is a semi-empirical formula (Khan et al., 2022b), which differs significantly from the Witczak 1–37A model by considering voids in mineral aggregate (VMA), shear modulus |Gb*|, and vapor flash aromatics (VFA). The Hirsch model is built using five experimental temperatures, two loading frequencies, and comprises 13 asphalt types and five aggregate gradation types, totaling 206 sets of data (Haibin et al., 2022). The advantage of the Hirsch model is that it simplifies input parameters while also considering the impact of modifiers on the dynamic modulus of asphalt mixtures (Gong et al., 2022). However, numerous studies indicate that the Hirsch model cannot accurately predict the dynamic modulus of mixtures at high temperatures and low frequencies. Even the corrected Hirsch model is limited to regional predictions of dynamic modulus (Fang et al., 2022; Ren et al., 2022). Moreover, its experimental data are significantly fewer than those of the Witczak 1–37A model, as shown in Eqs 3, 4. For grouted semi-flexible materials, the Hirsch model can greatly simplify parameters. However, its notable drawback is that it can only obtain volume indicators of the matrix asphalt. Obtaining indicators for semi-flexible materials themselves is challenging. Therefore, this paper selects the Witczak 1–37A model as the baseline prediction model.
3.2.2 Building prediction model and introducing grouting parameters
The asphalt viscosity η is determined by predicting the viscosity-temperature relationship, which is obtained from the viscosity-temperature curve (Ling et al., 2022b; Spadoni et al., 2022) given by Eq. 5:
where: η is the rotational viscosity of asphalt, mPa s; TR For the test temperature, °C; A is the regression intercept of viscosity-temperature curve; VTS is the regression slope of the viscosity-temperature curve.
From Table 8, it can be observed that as the temperature increases, the viscosity of SBS-modified asphalt gradually decreases. Using the viscosity-temperature relationship Eq. 5 for regression analysis, the final viscosity estimation equation for SBS-modified asphalt at different temperatures is obtained. As shown in Eq. 6, at temperatures below 60°C, the viscosity of SBS-modified asphalt sharply decreases, fluctuating within the range of 5,000 to 3,000.
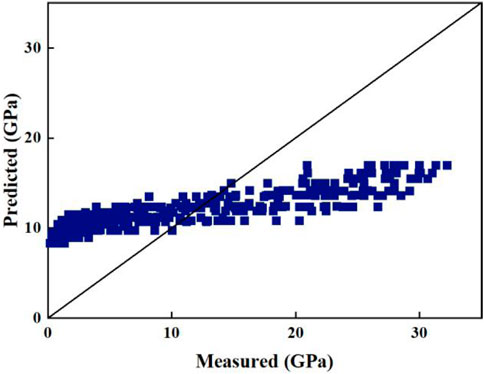
Based on the Witczak 1–37A prediction model described in Eqs 2, 6, the predicted dynamic modulus values are compared to the measured values as shown in Figure 6. The dynamic modulus predicted tends to be lower at high temperatures and low frequencies, with predicted values exceeding the measured values. Conversely, at low temperatures and high frequencies, the predicted dynamic modulus tends to be higher, with predicted values falling below the measured values. The correlation between predicted and measured values is poor, the highest coefficient of determination is only 0.78, indicating that Witczak 1–37A is not suitable for directly estimating the dynamic modulus of semi-flexible materials.
It's evident that the expected accuracy is not achieved when considering the prediction model based on η for PSFP. Both the Witczak1-A and Hirsch models, originally designed for predicting asphalt mixtures, exhibit significant discrepancies when applied to forecast the dynamic modulus of PSFP. This is attributed to the oversight of grout properties’ impact on the dynamic modulus of semi-flexible materials, revealing substantial differences between the assumptions of micro-mechanical models and the actual characteristics of mixtures. Grouting volume plays a crucial role in the stiffness of semi-flexible pavement materials. Studies indicate that with an increase in grouting volume, the stiffness of composite pavement materials increases. However, the low-temperature crack resistance does not proportionally increase with the grouting volume. When the grouting volume exceeds a certain threshold, the low-temperature crack resistance of composite pavement materials deteriorates (Bonicelli et al., 2019; Guo and Hao, 2021). Therefore, the modified model considers Pb as a factor influencing grout performance. This predictive model introduces the indicator of the grouting mass ratio (Pb) and, based on asphalt viscosity, obtains the estimation model through the least squares fitting method, as shown in Eq. 7.
where: |E*| is the dynamic modulus, MPa; Vbeff is the effective asphalt content of asphalt mixture, %; ƒ is the loading frequency, Hz; η is asphalt viscosity, MPa s; Va is the porosity of the asphalt mixture, %; ρ200 is the percentage of the pass rate of 0.075 sieve holes, %; ρ4, ρ38, and ρ34 are the cumulative sieving percentages of aggregates at 4.75 mm, 9.5 mm, and nominal maximum particle size sieve holes, respectively, %; ρ34 is the percentage of mass of the aggregate on the nominal maximum particle size sieve hole, %; Pb is the ratio of the grouting quality of the semi-flexible composite mixture to the total mass of the mixture, and the ratio of the grouting quality, %.
Randomly selecting three gradation sections under five experimental temperatures and six loading frequencies, which based on asphalt mixture material properties and grouting volume performance, the regression coefficients of the modified model were determined through nonlinear regression analysis. Eq. 8 is based on Pb for the Witczak1-37A modified dynamic modulus prediction model, denoted as Witczak-G. Utilizing two-thirds of the randomly selected experimental data from the three gradations, the dynamic modulus values predicted by the modified model are compared with the measured values, as shown in Figure 7. Compared to the improved predictive model in Figure 7A, the prediction accuracy of the modified model is significantly enhanced. The dynamic modulus data are concentrated near the 45° contour, with R2 = 0.99, which indicated a good agreement between predicted and measured values with no significant deviation.
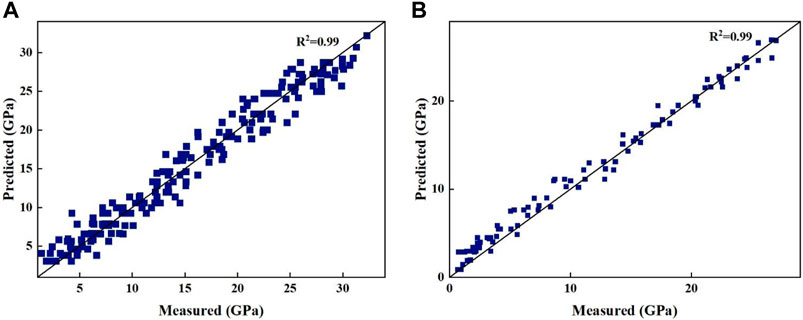
Figure 7. (A) Comparison of the predicted and measured dynamic modulus of the model based on the grouting mass ratio Pb; (B) Validation of the modified predictive model.
The newly developed Witczak-G predictive model was validated, which used the remaining measured dynamic modulus data. Figure 7B presents a comparison between the measured dynamic modulus results and the predicted dynamic modulus values using Eq. 8. With an R2 value of 0.99, indicating a strong correlation between measured and predicted values, the estimation model slightly overestimates the predicted dynamic modulus (low modulus values) under high-temperature, low-frequency conditions. The main reason for this is the significant performance differences between cement grout and asphalt mixture under high-temperature conditions. The majority of dynamic modulus discrepancies fall within ±10%. In the author’s view, the Witczak-G model equation provides a reliable prediction of the dynamic modulus values for grouted semi-flexible materials like HPCP.
3.3 Discussion
The advantage of the Witczak-G model proposed in this study lies in its incorporation of the grouting volume parameter to establish a predictive model for the dynamic modulus of semi-flexible materials. The model demonstrates good predictive capability for the dynamic modulus of high-performance cement grout semi-flexible materials. However, its limitation lies in the fact that while it considers the impact factors of both porous asphalt mixtures and grout, it only accounts for high-performance cement grout for the grouting volume. Further research is needed to explore semi-flexible materials grouted with other types of grout. Initially, this paper introduces several traditional dynamic modulus prediction models for asphalt mixtures, analyzing the characteristics and advantages and disadvantages of each model. Since many models are essentially modifications of the Witczak 1–37A and Hirsch models, these two models were selected as baseline models. Comparative analysis reveals that the predictions of the Hirsch model are unstable at high temperatures and low frequencies, with limited data, thus questioning its reliability. Therefore, the Witczak 1–37A model was chosen as the baseline model. This study verifies the predictive performance of the Witczak 1–37A model for semi-flexible materials and finds it suboptimal, with the highest coefficient of determination (R2) for predicting dynamic modulus reaching only 0.78. Consequently, traditional dynamic modulus prediction models are not suitable for semi-flexible materials. Therefore, based on the Witczak 1–37A model, grouting parameters were proposed. The Witczak-G model was derived by fitting two-thirds of the measured data through the least squares method, resulting in the highest predicted dynamic modulus coefficient of determination (R2) of 0.99. To validate the effectiveness of the proposed model, the remaining measured data were used in the predictive equation, yielding a highest coefficient of determination (R2) of 0.99. Thus, the Witczak-G model proves to be effective.
4 Conclusion
(1) Compared with the ordinary asphalt mixture SMA-16, the temperature sensitivity of the infused HPCP semi-flexible material is lower, and the grouting material promotes the semi-flexible material to have good deformation resistance under high temperature conditions, and the phase angle is at a small value at low temperature, and the elastic properties of the material are significant, and it has good low temperature resistance. Different from the ordinary asphalt mixture, the dynamic modulus decreases with the increase of porosity, and the dynamic modulus of the infused HPCP semi-flexible material increases by more than 10% with the increase of porosity by 1%.
(2) This paper adopts the Witczak 1–37A model as the baseline model, and it establishes the Witczak-G predictive model by introducing Pb and considering different experimental conditions, which included void ratios, asphalt viscosity, test temperature, and loading frequency. Comparative analysis of predicted modulus and measured dynamic modulus, R2 is as high as 0.99, which is a good match and can explain more than 99% of the dynamic modulus variation. The remaining measured dynamic modulus data is used to verify the new equation, and the R2 is still 0.99, so the predicted value is in good agreement with the measured value, and there is no obvious deviation.
Data availability statement
The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found in the article/Supplementary Material.
Author contributions
DW: Conceptualization, Formal Analysis, Investigation, Methodology, Writing–original draft. GL: Formal Analysis, Investigation, Validation, Writing–review and editing. LJ: Formal Analysis, Investigation, Writing–review and editing. HZ: Formal Analysis, Funding acquisition, Writing–review and editing. JZ: Formal Analysis, Investigation, Writing–review and editing. XS: Formal Analysis, Validation, Writing–review and editing.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This research was funded by a technology development project of China First Highway Engineering Co., Ltd., (Contract number: T-SZ-S4GS(J)-SIC-WRL-00-QT-011).
Acknowledgments
The authors are grateful for the support.
Conflict of interest
Authors DW, GL, LJ, and JZ were employed by China First Highway Engineering Co., Ltd.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Al-Khateeb, G., Shenoy, A., Gibson, N., et al. (2006). A new simplistic model for dynamic modulus predictions of asphalt paving mixtures Asphalt Paving Technology: Association of Asphalt Paving Technologists-Proc. Tech. Sess., 2006, 75E.
Bari, J. (2005). Development of a new revised version of the Witczak E* predictive models for hot mix asphalt mixtures. Ariz. State Univ. 2005.
Bi, Y., Guo, F., Zhang, J., Pei, J., and Li, R. (2021). Correlation analysis between asphalt binder/asphalt mastic properties and dynamic modulus of asphalt mixture. Constr. Build. Mater., 276(9):122256. doi:10.1016/j.conbuildmat.2021.122256
Bonicelli, A., Preciado, J., Rueda, A., and Duarte, A. (2019). Semi-flexible material: a solution for high-performance pavement infrastructures. IOP Conf. Ser. Mater. Sci. Eng. 471 (2019), 032062. doi:10.1088/1757-899X/471/3/032062
Bueno, L. D., Schuster, S. L., Specht, L. P., Pereira, D. d. S., Nascimento, L. A. H. d., Kim, Y. R., et al. (2020). Asphalt pavement design optimisation: a case study using viscoelastic continuum damage theory. Int. J. Pavement Eng. 2020 (2), 1070–1082. doi:10.1080/10298436.2020.1788030
Cai, J., Pei, J., Luo, Q., Zhang, J., Li, R., and Chen, X. (2017). Comprehensive service properties evaluation of composite grouting materials with high-performance cement paste for semi-flexible pavement. Constr. Build. Mater. 153, 544–556. doi:10.1016/j.conbuildmat.2017.07.122
Ceylan, H., Schwartz, C. W., Kim, S., and Gopalakrishnan, K. (2009). Accuracy of predictive models for dynamic modulus of hot-mix asphalt .J. Mater. Civ. Eng., 21(6):286–293. doi:10.1061/(ASCE)0899-1561(2009)21:6(286)
Cheng, P., Ma, G., and Li, Y. (2023). Preparation and performance improvement mechanism investigation of high-performance cementitious grout material for semi-flexible pavement. Polymers, 15(12): 2631. doi:10.3390/polym15122631
Christensen, D. W., Pellinen, T., and Bonaquist, R. F. (2003). Hirsch model for estimating the modulus of asphalt concrete . Asphalt Paving Technol. Assoc. Asphalt Paving Technologists-Proceedings Tech. Sess., 72:97–121.
Davoodi, A., Esfahani, M. A., Bayat, M., Mohammadyan-Yasouj, S. E., and Rahman, A. (2022). Influence of nano-silica modified rubber mortar and EVA modified porous asphalt on the performance improvement of modified semi-flexible pavement. Constr. Build. Mater. 337, 127573. doi:10.1016/j.conbuildmat.2022.127573
Dhandapani, B. P., and Mullapudi, R. S. (2023). Design and performance characteristics of cement grouted bituminous mixtures-a review. Constr. Build. Mater. 369, 130586. doi:10.1016/j.conbuildmat.2023.130586
Donald, W., and Bonaquist, R. (2015). Improved Hirsch model for estimating the modulus of hot-mix asphalt. Road Mater. Pavement Des., 16(Suppl. 2):254–274. doi:10.1080/14680629.2015.1077635
Fang, Y., Wang, X., Jia, L., Liu, C., Zhao, Z., Chen, C., et al. (2022). Synergistic effect of polycarboxylate superplasticizer and silica fume on early properties of early high strength grouting material for semi-flexible pavement. Constr. Build. Mater. 319, 126065. doi:10.1016/j.conbuildmat.2021.126065
Gong, M., Xiong, Z., Deng, C., Peng, G., Jiang, L., and Hong, J. (2022). Investigation on the impacts of gradation type and compaction level on the pavement performance of semi-flexible pavement mixture. Constr. Build. Mater. 324, 126562. doi:10.1016/j.conbuildmat.2022.126562
Gu, L., Chen, L., Zhang, W., and Ma, H. (2019). Mesostructural modeling of dynamic modulus and phase angle master curves of rubber modified asphalt mixture. Materials, 12, 1667(10). doi:10.3390/ma12101667
Guo, M., et al. (2022). Review of aging and antiaging of asphalt and asphalt mixtures. China J. Highw. Transp. 35 (4), 41–59.
Guo, X., and Hao, P. (2021). Influential factors and evaluation methods of the performance of grouted semi-flexible pavement (GSP)—a review, Appl. Sci. 11 6700. doi:10.3390/app11156700
Haibin, D., Shungui, W., Yingchen, L., Yinfei, D., and Tangzhong, W. (2022). Matching the color difference between asphalt mixture and cement grouting paste used in semi-flexible pavement. Front. Mater. 9, 816247. doi:10.3389/fmats.2022.816247
Hu, C., Zhou, Z., and Luo, Y. (2023). Study on damage evolution and mechanism of semi-flexible pavement under acid rain erosion. Case Stud. Constr. Mater. 19, e02286. doi:10.1016/j.cscm.2023.e02286
Jiang, D., Wang, D., Chen, Z., Fan, L., and Yi, J. (2022). Research on the mesoscopic viscoelastic property of semi-flexible pavement mixture based on discrete element simulation. Case Stud. Constr. Mater. 17, e01282. doi:10.1016/j.cscm.2022.e01282
Khan, M. I., Khan, N., Hashmi, S. R. Z., Yazid, M. R. M., Yusoff, N. I. M., Azfar, R. W., et al. (2023). Prediction of compressive strength of cementitious grouts for semi-flexible pavement application using machine learning approach. Case Stud. Constr. Mater. 2023, e02370. doi:10.1016/j.cscm.2023.e02370
Khan, M. I., Sutanto, M. H., Khahro, S. H., Zoorob, S. E., Md. Yusoff, N. I., Al-Sabaeei, A. M., et al. (2022a). Fatigue prediction model and stiffness modulus for semi-flexible pavement surfacing using irradiated waste polyethylene terephthalate-based cement grouts. Coatings, 13(1): 76. doi:10.3390/coatings13010076
Khan, M. I., Sutanto, M. H., Khan, K., Iqbal, M., Napiah, M. B., Zoorob, S. E., et al. (2022b). Effective use of recycled waste PET in cementitious grouts for developing sustainable semi-flexible pavement surfacing using artificial neural network (ANN). J. Clean. Prod. 340, 130840. doi:10.1016/j.jclepro.2022.130840
Kim, Y. R., King, M., and Momen, M. (2005). Typical dynamic moduli values of hot mix asphalt in North Carolina and their prediction [C]//CD-ROM. 84th Annu. Meet. TRB., 2005.
Kim, Y. R., and Lee, Y. C. (1995). Interrelationships among stiffnesses of asphalt-aggregate mixtures. J. Assoc. asphalt paving Technol. 1995.
Ling, S., Chen, Z., Sun, D., Ni, H., Deng, Y., and Sun, Y. (2022a). Optimal design of pouring semi-flexible pavement via laboratory test, numerical research, and field validation. Transp. Res. Rec. 2676 (11), 479–495. doi:10.1177/03611981221093631
Ling, S., Hu, M., Sun, D., and Xu, L. (2022b). Mechanical properties of pouring semi-flexible pavement material and engineering estimation on contribution of each phase. Constr. Build. Mater. 315, 125782. doi:10.1016/j.conbuildmat.2021.125782
Liu, W., Jiang, Y., Zhao, Z., Du, R., and Li, H. (2022). Material innovation and performance optimization of multi-solid waste-based composite grouting materials for semi-flexible pavements. Case Stud. Constr. Mater. 17, e01624. doi:10.1016/j.cscm.2022.e01624
Liu, X., Wu, K., Cai, X., Huang, W., and Huang, J. (2023). Influence of the composite interface on the mechanical properties of semi-flexible pavement materials. Constr. Build. Mater. 397 (2023), 132466. doi:10.1016/j.conbuildmat.2023.132466
Ma, T., Wang, H., He, L., Zhao, Y., Huang, X., and Chen, J. (2017b). Property characterization of asphalt binders and mixtures modified by different crumb rubbers. J. Mater. Civ. Eng., 29(7):04017036. doi:10.1061/(ASCE)MT.1943-5533.0001890
Ma, T., Wang, H., Zhang, D., and Zhang, Y. (2017a). Heterogeneity effect of mechanical property on creep behavior of asphalt mixture based on micromechanical modeling and virtual creep test. Mech. Mater. 104 (j a n), 49–59. doi:10.1016/j.mechmat.2016.10.003
Ma, T., Zhang, D., Zhang, Y., Wang, S., and Huang, X. (2018). Simulation of wheel tracking test for asphalt mixture using discrete element modelling .Road Mater. Pavement Des., 19(1-2):367–384. doi:10.1080/14680629.2016.1261725
Pan, B., Zhang, H., Liu, S., Gong, M., and Yang, J. (2023). Dynamic responses of semi-flexible pavements used for the autonomous rail rapid transit. Appl. Sci., 13(6): 3673. doi:10.3390/app13063673
Pei, J., Cai, J., Zou, D., Zhang, J., Li, R., Chen, X., et al. (2016). Design and performance validation of high-performance cement paste as a grouting material for semi-flexible pavement. Constr. Build. Mater. 126, 206–217. doi:10.1016/j.conbuildmat.2016.09.036
Peng, B., Li, J., Ling, T., Li, X., Diao, H., and Huang, X. (2023). Semi-flexible pavement with glass for alleviating the heat island effect. Constr. Build. Mater. 367, 130275. doi:10.1016/j.conbuildmat.2022.130275
Ren, J., Xu, Y., Zhao, Z., Chen, J., Cheng, Y., Huang, J., et al. (2022). Fatigue prediction of semi-flexible composite mixture based on damage evolution. Constr. Build. Mater. 318, 126004. doi:10.1016/j.conbuildmat.2021.126004
Salini, R., Xu, B., and Lenngren, A. C. (2015). Application of artificial intelligence for optimization in pavement management . Int. J. Eng. Technol. Innovation, 5(3).
Setyawan, A. (2013). Asessing the compressive strength properties of semi-flexible pavements. Procedia Eng. 54, 863–874. doi:10.1016/j.proeng.2013.03.079
Solouki, A., Tataranni, P., and Sangiorgi, C. (2022). Thermally treated waste silt as geopolymer grouting material and filler for semiflexible pavements. Infrastructures 7 (8), 99. doi:10.3390/infrastructures7080099
Spadoni, S., Graziani, A., and Canestrari, F. (2022). Laboratory and field investigation of grouted macadam for semi-flexible pavements. Case Stud. Constr. Mater. 16, e00853. doi:10.1016/j.cscm.2021.e00853
Vestena, P. M., Schuster, S. L., Almeida, P. O. B. D., Faccin, C., Specht, L. P., and Pereira, D. d. S. (2023). Dynamic modulus master curve construction of asphalt mixtures: error analysis in different models and field scenarios. Constr. Build. Mater. 301, 124343. 2023-09-04]. doi:10.1016/j.conbuildmat.2021.124343
Xiong, Z., Gong, M., Hong, J., and Deng, C. (2022). The influential factors of semi-flexible pavement cracking performance. J. Wuhan Univ. Technology-Mater. Sci. Ed., 37(5): 953–962. doi:10.1007/s11595-022-2618-8
Yang, Q., Li, Y., Zou, H., Feng, L., Ru, N., Gan, L., et al. (2022). Study of the effect of grouting material strength on semiflexible pavement material. Adv. Mater. Sci. Eng. 2022, 1–18. doi:10.1155/2022/5958896
Zarei, S., Ouyang, J., Alae, M., and Zhao, Y. (2023). Fracture behavior of semiflexible pavement containing cement asphalt emulsion paste. J. Mater. Civ. Eng., 35(5): 04023098. doi:10.1061/JMCEE7.MTENG-14891
Zarei, S., Ouyang, J., and Zhao, Y. (2022). Evaluation of fatigue life of semi-flexible pavement with cement asphalt emulsion pastes. Constr. Build. Mater., 349: 128797, doi:10.1016/j.conbuildmat.2022.128797
Zhang, S., He, Y., Zhang, H., Chen, J., and Liu, L. (2022b). Effect of fine sand powder on the rheological properties of one-part alkali-activated slag semi-flexible pavement grouting materials. Constr. Build. Mater. 333, 127328. doi:10.1016/j.conbuildmat.2022.127328
Zhang, Z., Li, J., and Ni, F. (2022a). Material innovation preparation and performance study of semi-flexible pavement materials. Case Stud. Constr. Mater. 17, e01355. doi:10.1016/j.cscm.2022.e01355
Zhao, W., and Yang, Q. (2022). Influence analysis of performance of semi-flexible pavement based on aggregate distribution characteristics of matrix skeleton. Constr. Build. Mater. 338, 127633. doi:10.1016/j.conbuildmat.2022.127633
Zhao, W., and Yang, Q. (2022). Study on the applicability of asphalt concrete skeleton in the semi-flexible pavement. Constr. Build. Mater. 327, 126923. doi:10.1016/j.conbuildmat.2022.126923
Zhao, W., and Yang, Q. (2023). Life cycle assessment and multi-index performance evaluation of semi-flexible pavement after composite modification by using fly ash, rubber particles, warm mixing asphalt and recycled asphalt pavement. Constr. Build. Mater. 364, 129945. doi:10.1016/j.conbuildmat.2022.129945
Zhao, Y., Tang, J., and Liu, H. (2012). Construction of triaxial dynamic modulus master curve for asphalt mixtures. Constr. Build. Mater., 37(none):21–26. doi:10.1016/j.conbuildmat.2012.06.067
Keywords: HPCP-infused semi-flexible materials, dynamic modulus, phase angle, cement grout mass ratio, predictive model
Citation: Wang D, Li G, Jiang L, Zhang H, Zhang J and Si X (2024) Dynamic modulus characteristics and prediction model of semi-flexible materials filled with high-performance cement paste. Front. Mater. 11:1365896. doi: 10.3389/fmats.2024.1365896
Received: 05 January 2024; Accepted: 08 July 2024;
Published: 31 July 2024.
Edited by:
Jian Zhou, Central South University, ChinaReviewed by:
Gholam Hossein Hamedi, University of Guilan, IranJoel Oliveira, University of Minho, Portugal
Copyright © 2024 Wang, Li, Jiang, Zhang, Zhang and Si. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Huaizhi Zhang, aHVhaXpoaS56aGFuZ0AxNjMuY29t
 Deyong Wang1
Deyong Wang1 Huaizhi Zhang
Huaizhi Zhang Xiaowei Si
Xiaowei Si