Structural and mechanical properties of Cu-SiCp nanocomposites fabricated by accumulative roll bonding (ARB)

In this study, the accumulative roll bonding (ARB) method, a severe plastic deformation (SPD) process, was used to fabricate copper-2 wt% silicon carbide composite strips. The ARB process was successfully conducted for up to nine cycles on pure copper strips with silicon carbide particles distributed between them, as well as on monolithic copper. Equiaxed tensile and Vickers hardness tests were conducted to evaluate the mechanical properties of the samples. SEM was utilized to study the fracture surfaces and to determine the fracture mechanism of ARB processed monolithic copper and composite samples after the tensile test. Texture parameters were calculated through X-ray analysis. The Rietveld method using MAUD software were employed to assess the crystallite size of the samples. Results indicated that average amount of porosity decreased and interface bonding between copper strip layers improved with increasing the number of ARB cycles. Moreover, an increased number of cycles led to homogeneous distribution of SiC particles within the copper matrix. The tensile strength of the fabricated composites improved with an increase in the number of cycles, ultimately reaching 483 MPa after nine cycles, compared to 388 MPa for the composite processed with a single cycle of ARB and 194 MPa for annealed copper strips. Initially, the elongation of the composite samples decreased dramatically to about 6% after applying five cycle of ARB process from the 46% observed for annealed pure copper strip. However, it improved as the process continued, reaching 8.9% after the ninth cycle. Investigation of fracture surfaces after the tensile test using SEM revealed that the dominant failure mode was shear ductile fracture. Analysis of sample textures demonstrated that the dominant texture was (100). Crystallite sizes for pure copper and nine cycles-rolled composites, as determined by Reitveld method, reached 111 nm and 89 nm, respectively.

1 Introduction

Pure copper and its alloys find widespread application in the industry due to their superior properties, including excellent thermal and electrical conductivities, corrosion resistance, and remarkable plasticity (Caron and Sharif, 2017; Ke et al., 2024). Adding ceramic reinforcing particles such as carbides and oxides to copper to fabricate metal matrix composites (MMCs) leads to new microstructure and enhance several properties, including elastic modulus, strength, wear resistance, and high temperature stability (Chawla and Chawla, 2006; Zare et al., 2022; Zhao et al., 2022). The demand for MMCs continues to rise. Cu-SiC composites have been studied since 1996 (Ghaderi et al., 2013). Cu based materials and are being explored as a potential solution to thermal management in advanced electronic devices with increasing power requirements. These is also a need to enhance wear properties of copper alloys (Ghaderi et al., 2013; Chen et al., 2024).

Nanocomposite is applied in various applications such as water treatment, civil, automotive and aerospace industries (Farajpour Mojdehi et al., 2024). Composites including Cu-SiC could be used in electrical contact materials in relays, contactors, switches, circuit breakers and electric brushes in rotating or sliding devices (Ghaderi et al., 2013; Akbarpour et al., 2023a).

The SiC reinforced Copper composites can offer a good compromise between thermo-mechanical properties and high conductivity. They have lower density than copper, very good thermal conductivity, and low coefficient of thermal expansion. A Cu-SiC metal matrix composite (MMC) heat spreader can offer high thermal conductivity between 250 W/mK and 325 W/mK and corresponding adjustable coefficient of thermal expansion between 8.0 ppm/ºC and 12.5 ppm/°C. However, the primary challenges in the manufacturing of Cu-SiC composites is to prevent reaction between copper and silicon carbide during high temperature densification, which can dramatically reduce the thermal conductivity (Bukhari et al., 2011).

The manufacturing methods of these composite materials often include casting, powder metallurgy, selective laser melting, composite electroforming technology, cyclic extrusion and compression, and electrodeposition (Ebrahimi et al., 2021; Akbarpour et al., 2023b). Casting processes for synthesis of Cu-SiC composites have challenges due to poor wettability between copper and reinforcing particles and difficulty in achieving the uniform dispersion. While powder metallurgy is a better option, it has disadvantages such as high working temperature, strong reaction at the interface of the matrix/reinforcement, non-uniform distribution of the second phase, high cost, and limitations in the size of components which can be fabricated.

Ultrafine materials are produced by various methods such as rapid solidification, vapor deposition, mechanical alloying, cryogenic metal forming and severe plastic deformation (SPD). The severe plastic deformation method is one of the most suitable methods for producing ultrafine (UFG) grained materials for industrial applications. In this method, a very high plastic strain is applied to the bulk of the material in order to fabricate bulky materials with ultrafine grain sizes. The main goal of this process is to produce parts with high strength (Azushima et al., 2008). Accumulating rolling (ARB) process is a promising severe plastic deformation process which was invented for mass production of bulk materials by Saito and his colleagues in 1998 (Saito et al., 1998). It has a great potential for integration with manufacturing processes such as tailor rolled blanks (TRBs) (Liu et al., 2024). ARB is a practical processes for continuous production of strips, plates and strips with ultrafine grained structure. The cold roll bonding (CRB) process to produce layered strips and foils has grown rapidly due to its unique characteristics compared to other methods. The CRB process is relatively simple and can be automated. In fact, CRB is a solid-state welding process because the bond is created by plastic deformation of the metals to be joined. When the surfaces of virgin metal encounter each other due to surface expansion, a bond is created. In fact, when the pressure reaches a large enough value to extrude the virgin metal through the cracks of the broken surface layer of the strip, it causes contact and bond between the exposed virgin metal surfaces. The solid state joining method in CRB can be used for a wide variety of materials, which can be either similar with the same properties or even having the widely different metallurgical and mechanical properties (Li et al., 2008).

The ARB process has been successfully carried out on various metals and alloys. In all these cases, the material is severely deformed. The strength of the metal also accumulates due to the increase in strain and increases its hardness. In recent years, ARB has been also used in manufacturing of multilayer composites with dissimilar raw materials such as Al/Cu (Eizadjou et al., 2008), Ti/Al (Luo and Acoff, 2004; Zhang and Acoff, 2007; Yang et al., 2010; Peng et al., 2012), Al/Ni (Min et al., 2006; Mozaffari et al., 2011) and Al/Mg (Chen et al., 2006), due to its versatility of the process and low cost.

It has been observed that ultra-fine grained (UFG) structure or even nano scale microstructure can be achieved in the matrix by applying ARB process, and a composite is fabricated with homogeneous distribution of the reinforcement in the matrix. Strength and hardness also increase with increasing the number of ARB cycles. The production of metal matrix composites with ceramic particle reinforcements is being developed by ARB method. According to the studies conducted in these cases, the composite has been produced with uniform dispersion of reinforcing particles in the matrix and without porosity.

The main novelty of this research lies in the utilization of the Accumulative Roll Bonding (ARB) method, a severe plastic deformation (SPD) process, to fabricate copper-2 wt% silicon carbide composite. This study successfully applied the ARB process for up to nine cycles on pure copper strips with silicon carbide particles distributed between them, as well as on monolithic copper. In view of limitations in the production of metal matrix composites (MMCs) using conventional methods, where achieving uniform distribution of reinforcement are a problem, the ARB process was optimized specifically for copper-silicon carbide composite fabrication to avoid problems with other methods of preparing metal matrix composites cost and energy requirements. Additionally, the investigation focuses on understanding the effect of the number of cycles on the properties of SiCp-reinforced commercially pure copper matrix composites, which is a growing area of interest in various industries.

2 Experimental procedures

2.1 Materials

In this research, commercial pure copper metal with a purity of 99.9% was used. Table 1, gives the chemical composition of the pure copper strip obtained by an optical emission quantometer method. The primary copper sheet with a thickness of 1 mm was cut into strips with a length of 200 mm and a width of 50 mm, and then four small holes were drilled in its corners to fasten the 2 strips to each other during the rolling stage. These strips were annealed at 480°C in the air for 2 h.

Table 1

Table 1. The chemical composition of the copper strip.

Also, silicon carbide (SiC) powder with particle size of 75 µm was used as reinforcement in this research. X-ray diffractometry (XRD, Philips X’pert, Netherlands, CuKa) with scan speed of 3°/min, from 40° to 140°. Figure 1 shows the XRD analysis of the silicon carbide powder.

Figure 1

Figure 1. XRD pattern of the silicon carbide powder.

2.2 Accumulative roll bonding process (ARB)

The ARB process is shown schematically in Figure 2. First, the surfaces of strips that come in contact with each other were subjected to surface treatment in order to create a strong metallurgical bond. At this stage, grease and surface contaminations were removed by acetone, and wire brushing was also done to remove surface oxides and create a suitable roughness. In the first stage of composite fabrication after surface preparation, 0.5 vol% of SiC particles were sprinkled almost uniformly between 2 strips in each cycle, and then the strips were firmly tied together at the corners by steel wires. They were subjected to rolling and then the rolled strips were divided into two-halves by transverse cutting, and the two obtained strips were surface prepared again, the powder was spread between them and rolled. This process continued up to four cycles. Tightening the strips is to prevent them from sliding on each other during the rolling process. In the second stage of composite production, the same process was done for five more cycles without dispersing the particles.

Figure 2

Figure 2. Schematic of accumulative roll bonding process.

It should be noted that the time interval between the surface preparation and rolling operations should be as small as possible to prevent re-oxidation of the surfaces after cleaning and wire brushing, preferably less than 120 s. To apply the roll bonding process with a thickness reduction of 50%, a laboratory rolling machine with a loading capacity of 20 tons, rollers diameter of 127 mm and rolling speed of 3 rpm was performed without the use of lubricant.

To investigate the bonding conditions of rolled layers and reinforcement dispersion during different cycles, the cross-section of ARBed samples in Rolling Direction- Transverse to rolling Direction (RD-TD) and Transverse to rolling Direction- Normal to rolling Direction (TD-ND) plane was examined by optical microscope. After grinding with a sandpaper number 320 to 4,000, the samples were subjected to mechanical polishing using 0.05 μm alumina solution and then observed without etching by optical microscope.

2.3 Microstructural evaluation

Optical microscopy and scanning electron microscopy (SEM) were used to investigate the distribution of SiC powder, and the amount of porosity and agglomerations in different cycles of ARB process in TD-RD, ND-RD and TD-ND sections.

2.4 Mechanical properties

In order to measure the mechanical properties of the samples, tensile test was performed parallel to the rolling direction with an initial strain rate of 1.67 × 10⁻⁴ s^-1 at ambient temperature by Hounsfield H50KS tensile machine according to ASTM E8M standard (Handbooks, 1997; ASTM E8, 2004). The length and width of the tensile test specimen were equal to 25 mm and 6 mm, respectively. Vickers hardness test was also done with a force of 10 kg for 20 s. To measure the hardness, 10 points were randomly selected, and the hardness was measured. The maximum and minimum hardness numbers obtained were ignored and the average hardness of the remaining eight readings was reported as the hardness value.

2.5 Fractography

The fracture surface of the samples after the tensile testing was evaluated by PHTLTPS XL30 scanning electron microscopy (SEM) to determine the failure mechanism in the ARB processed composite and monolithic pure copper.

2.6 Textural studies

The texture of the samples was measured by the texture parameter determination method. ARBed specimens with dimensions of 10 × 5 mm were grounded using sandpaper grit 1,200. Then mechanical polishing was done using 0.05 µm alumina solution. X-ray diffraction patterns with Cukα radiation and a step size of 0.05° and a counting time of 1 s were used to investigate texture parameters. By selecting seven suitable peaks from the diffraction pattern and comparing their intensity with the corresponding peaks in a random sample (perfectly annealed copper powder at 480°C for 2 h) their normalization was done. The texture parameter was denoted by the following Eq. (1) (Wagner et al., 1999).

$T.P=\frac{\frac{I_{hkl}}{I_{hkl}^0}}{\frac{1}{n}{\displaystyle \sum }\frac{I_{hkl}}{I_{hkl}^0}}(1)$

I_hkl: Intensity of peak (hkl).

I⁰_hkl: Intensity of peak (hkl) in the copper powder specimen.

n: Total number of the planes.

2.7 Crystallite size measurement using rietveld method

X-ray Diffraction (XRD) was used to estimate the subgrain size, dislocation density and microstrain in the samples after different cycles of ARB. Because strain anisotropy is not considered in the Williamson-Hall method, this method is not accurate enough to investigate the materials that have undergone SPD process, as severe anisotropy has occurred in these materials.

Therefore, the Ritveld method was used to estimate the microstructural parameters including subgrain size (crystallite size), dislocation density, and microstrain. This method considers various parameters such as the effect of strain anisotropy, texture, cold work, and other parameters. For this purpose, by fitting a curve on the X-ray diffraction pattern of composite and monolithic samples in different cycles of the ARB process were analyzed using MAUD software, which is a Rietveld method computing software based on Java. In this research, the matching of the calculation graphs on the X-ray diffraction patterns of all the composite samples was done with good accuracy by MAUD software, so that the Good of Fit (GOF) factor was less than two in all the samples. The GOF factor is defined to measure the compatibility of the pattern calculated by the software with the actual pattern in the software.

3 Results

3.1 Microstructural evolution during different stages of the process

Figure 3 displays optical microscopy images showcasing the microstructure of the Cu/2 vol% SiC composite in the RD-TD section after various rolling cycles. Following five cycles, noticeable features emerge: large particles, regions lacking dispersed SiC, and clustering of SiC particles within the copper matrix. The extent of powder-free areas and the prevalence of particle clustering are notably high. In general, the distribution of SiC particles in the copper matric is nonuniform (Figures 3A).

Figure 3

Figure 3. The microstructure of the RD-TD cross-section of the rolled Cu/2 vol% SiC composite in the cycles, (A) the fifth cycle, (B) the seventh cycle, and (C) the ninth cycle.

After seven cycles, the large particles free areas have decreased, the number of large SiC particle clusters have reduced, and the distribution of SiC particles has improved (Figures 3B). As the ARB process progressed to the ninth cycle (Figures 3C), both clusters of SiC and regions without particles has significantly decreased.

SEM images of the RD-TD section of composite strips after three, five, and nine cycles are shown in Figure 4. After three and five ARB cycles, contacts between copper and SiC are poor, with most of the porosities observed in SiC clusters (Figures 4A, B). However, as the number of ARB cycles increases, the contacts between copper and SiC becomes more continuous, and the amounts of porosities decreases. Therefore, after nine cycles (Figures 4C), even at high magnifications in SEM imaging hardly any porosity can be observed. It can be said that continuous rolling improves the contact between copper and SiC created in previous cycles and removes porosities.

Figure 4

Figure 4. SEM images of RD-TD section of the composite strips after, (A) three, (B) five, and (C) nine cycles.

Figure 5 displays the OM images of the RD-ND cross-section of Cu/SiC composite strips after different cycles of the ARB process. With an increase in the number of ARB cycles, the layered structure (copper strips and powder layers) transforms into a powder-reinforced composite. In the earlier cycles, layers of silicon carbide and copper are still clearly visible (Figures 5A). By the fourth cycle, the copper layers become thinner, and the particles are embedded in the copper matrix (Figures 5B). By the ninth cycle, the microstructure shows a better distribution of SiC particles in the matrix and an improvement in the contact between the metal and SiC (Figures 5C).

Figure 5

Figure 5. Distribution of reinforcements in the RD-ND cross section of Cu/SiC composite in, (A) third, (B) fourth, and (C) ninth cycles.

3.2 Mechanical properties

The engineering stress-strain diagram of the ARB-ed composite is presented in Figure 6 after various rolling cycles. As the number of cycles increases, the tensile strength of the samples also improved accordingly.

Figure 6

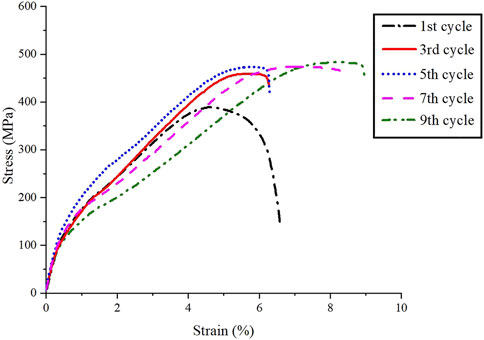
Figure 6. Engineering stress-strain diagrams of ARB processed Cu- 2 vol% SiC composite at different cycles.

The tensile strength of the ARB processed composite was also compared with that of monolithic copper in Table 2, illustrating that the tensile strength of the ARB-ed composite was 2.4 times greater than that of the ARB processed monolithic copper sample (192 MPa) after ARB for same cycles. At the end of the first stage (after four cycles), the tensile strength values for the Cu/2 vol% SiC composite and monolithic copper were 460 MPa and 419 MPa, respectively. However, these values for the composite and monolithic copper were 483 MPa and 444 MPa, respectively, at the end of the second stage of ARB process.

Table 2

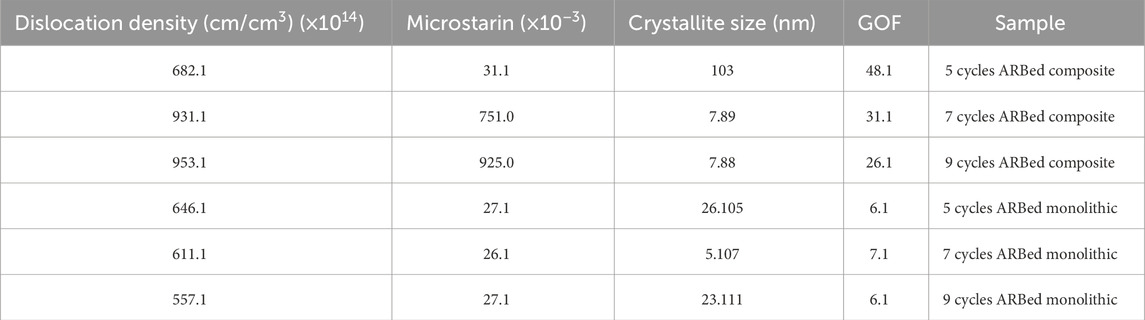
Table 2. Output of MAUD software from the analysis of the diffraction patterns of various ARB processed samples.

The changes in elongation of the metal matrix composite Cu/2 vol% SiC and pure copper fabricated by ARB process after tensile testing, as a function of the number of cycles, are presented in Table 2. In the initial stage of composite production, as the number of ARB cycles increases, the elongation gradually decreases. The elongation decreased from 46.45% for annealed pure copper to about 6.25% at the end of the fourth cycle (the end of the first stage of composite production), but it reached about 8.93% at the end of the second stage. In fact, after nine cycles, the elongation improves, attributed to the uniformity of SiC particles in the matrix, improved contact quality of Cu/SiC interfaces, and reduced porosity. Additionally, the elongation of the monolithic copper was about 8.53% after the first cycle. Subsequently, in the following cycles, this parameter improved to some extent and reached 17.36% in the ninth cycle (Figure 7).

Figure 7

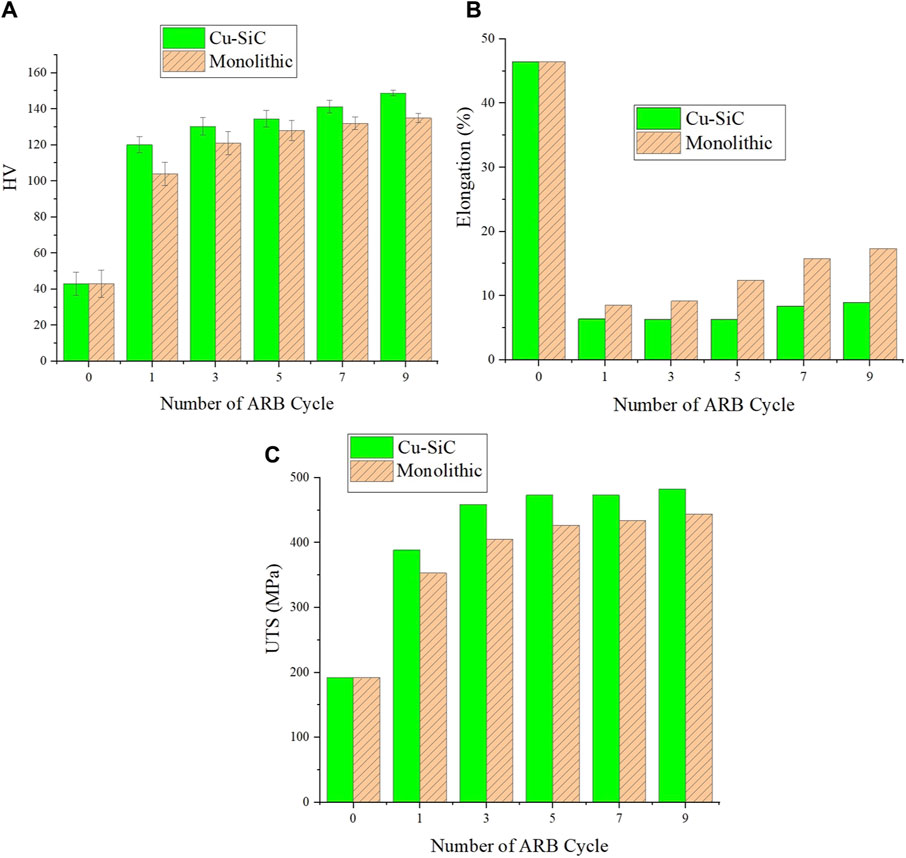
Figure 7. Mechanical properties of ARB processed Cu-2 wt% SiC and monolithic copper samples showing, (A) Vickers hardness, (B) Elongation, and (C) ultimate yield strength.

3.3 Hardness

The hardness values of Cu/SiC composites and monolithic copper processed by ARB in different cycles are depicted in Table 2. The curve demonstrates a rapid increase in hardness during the initial cycles, followed by a more gradual increase until the ninth cycle. After nine ARB cycles, the hardness of the composite increased from 43 Vickers for annealed copper to 148 Vickers. Similarly, the hardness of monolithic ARB copper also rises with increasing cycles, reaching 135 Vickers after nine cycles, indicating a significant level of strain and deformation hardening. The hardness curve for monolithic copper exhibits a similar slope and trend to that of the composite across cycle numbers.

3.4 Fractography

The SEM was used to investigate and identify fracture mechanisms in ARB processed monolithic copper and Cu/2 vol% SiC composite samples. The fracture surfaces of the samples were examined after tensile testing. Pictures of fracture surfaces from the third and ninth cycle samples at low magnification are shown in Figures 8A, B.

Figure 8

Figure 8. SEM images of the fracture surface after tensile testing of samples: (A) the third ARB cycle, (B) the ninth ARB cycle (C), annealed pure copper, (D) composite in the fifth ARB cycle, (E) composite in the ninth ARB cycle, and (F) pure copper in the ninth ARB cycle.

As indicated, in the low cycles, while a 50% reduction in thickness was achieved, a complete contact between copper matrix and SiC particles did not occur, and therefore, during tensile testing, fracture occurred across the interfaces (Figures 8C). As the number of ARB cycles increases, the contact at the interfaces created in previous cycles improves, and fewer discontinuity areas are observed. This can be clearly seen in the SEM image of the fracture surface of the ninth cycle ARB sample (Figures 8D). Therefore, one can say that with the advancement of the ARB process in each cycle, the contact created in previous cycles improve.

To understand the fracture mechanism of samples in different cycles, ARB processed monolithic copper and composite samples were investigated at higher magnification and with more details, as can be seen in the pictures taken in Figures 8C, F. The fracture surface of annealed copper samples has deep concentric dimples (Figures 8C). This appearance is a proof of the ductile fracture mode in most materials and occurs with the formation of microvoids and joining them together (Gabriel, 1998). Inside the dimples related to annealed copper samples, particles can be seen, which Shaabraf (Shaarbaf and Toroghinejad, 2009) demonstrated with EDS analysis to be impurities such as copper oxide. The oxide particles are randomly distributed; if the number of these micro-voids is small and scattered at intervals, the voids they create will be large, and if a large number of micro-voids nucleate and cause the formation of voids, the voids will get caught in the neighboring voids after a little growth and consequently become small.

Figures 8F shows the fracture cross-sectional surface of pure, monolithic copper after nine cycles of the ARB process. In this figure, the ductile shear mechanism is also observed, but the depth of the dimples is greater, and their elongation is less than that of the nine-cycle composite ARB sample. This is consistent with the fact that the tensile strength of the composite sample is higher than that of the pure copper sample, and its percentage of elongation is lower. Voids areas are clearly seen in Figures 8D, E.

3.5 Calculation of microstructural parameters using rietveld method

In the Rietveld method, a significant part of the experimental X-ray diffraction patterns is simulated with computational functions that consider structural parameters and instrumental parameters. In this method, an X-ray diffraction pattern is accurately matched with a series of structural parameters such as cell homogeneity, thermal motions, microstructural parameters such as sub-grain size, microstrain, peak shape, and background parameters. The variables are optimized and corrected by repeating the least-squares method and minimizing the residual parameters (Tsuji et al., 1999; Sahu et al., 2002; Dini et al., 2010). In Figure 9, the experimental XRD analysis image and the curve obtained from the MAUD software for the nine-cycle ARB sample are presented. In Figures 9B, the experimental diffraction pattern is shown in blue, and the plot drawn by the software is in black, and the two can be compared with each other. In Table 2, a summary of the data obtained by the MAUD software from the diffraction patterns of copper and ARB composite samples is presented.

Figure 9

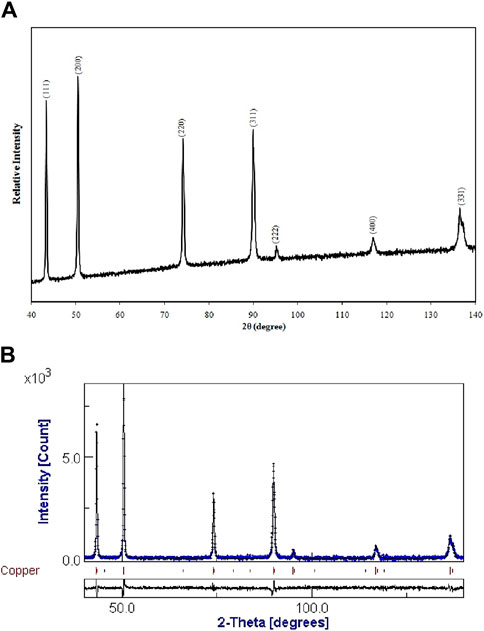
Figure 9. (A) Experimental XRD analysis image and (B) MAUD software output with the fitted curve on the XRD result of the ARB-processed sample with nine cycles and the fitting error curve (lower curve).

3.6 Texture parameters

The texture of the ARB processed samples was investigated using the texture parameter determination method. According to the computational method mentioned before, the texture parameter for each plane in each cycle was obtained. An example of the calculations performed for the (200) and (400) planes is presented in Table 3.

Table 3

Table 3. An example of the calculations performed for the (200) and (400) planes.

The changes in texture parameter for composite samples in different cycles of the accumulative roll bonding (ARB) process are shown in Figures 10A, and the plane of each peak is specified. In this graph, the chart of changes in composite texture in the (200), (400), (220), and (311) planes with respect to the number of cycles is provided. Additionally, Figures 10B shows the change in the texture parameter of different planes of pure copper ARB samples as a function of the number of cycles.

Figure 10

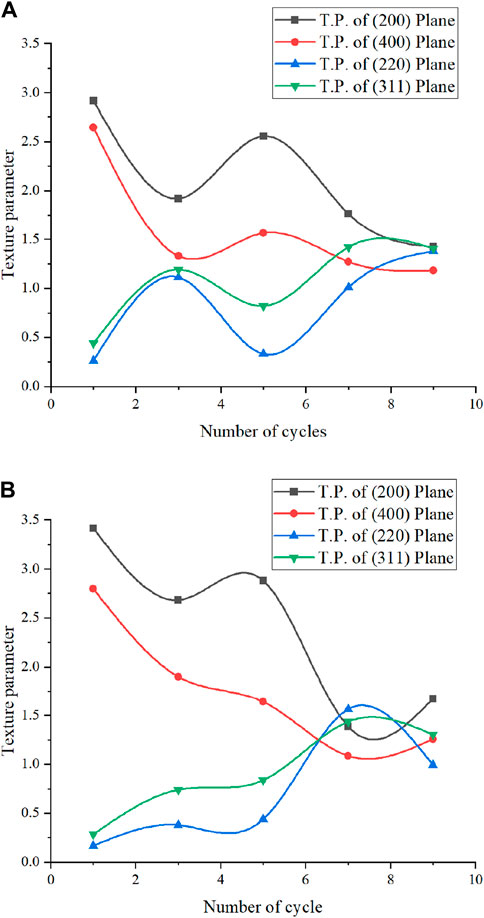
Figure 10. Graph of (A) ARBed composite samples versus the number of cycles and (B) the texture parameter of monolithic copper samples versus the number of cycles.

Considering the trends and changes in the slope of the graphs in Figures 10B, it can be said that a texture transition occurred in the fourth cycle of the process.

4 Discussion

It has been reported that during cold roll bonding, two brittle surface oxide layers in both sides are uniformly broken by surface preparation and the virgin substrate metal is extruded from the cracks created in the surface oxide layers from both sides under rolling pressure and exposed to contact with each other. Also, the metal deforms plastically and flows. In the presence of SiC particles between the strips, the virgin metal of the substrate is extruded towards the particles in the areas where the particles exist, and subsequently, a uniform distribution of the particles in the matrix is obtained. In addition, according to the film theory, copper is found to flow through the widened cracks in the surface oxide layers which causes the interface to be a combination of SiC particles and areas of extruded copper (Li et al., 2008) in contact with SiC. As a result, the cracking of the oxide layer on the surface allows atom-to-atom contact and bond rolling. In addition to the uniformity of the particles in the matrix, the quality of the bonding between the reinforcement and the matrix, and amount of the porosities, are other factors that affect the properties of MMCs.

In general, the distribution of SiC reinforcement with increasing the number of ARB cycles is studied from three perspectives.

a) Increasing the number of copper and SiC interfaces;

b) Extrusion of virgin metal in between agglomeration of particles;

c) Increasing the length of the strips due to rolling.

By continuing the ARB process, the number of copper and SiC interfaces is increased, their thicknesses are reduced, and the distribution of particles in the direction perpendicular to rolling (ND) improves with the distribution of particles in the matrix due to the vertical pressure of rolling. In addition, the matrix extrudes and flows between the agglomerates of SiC particles under the vertical pressure of rolling. As a result, the dense clusters of particles can turn into distributed particles and the distance between the clusters increases, there is a fragmentation of the clusters and consequently an improvement of the distribution of reinforcemnets in the matrix is achieved (Tan and Zhang, 1998; Torralba et al., 2003; Yazdani and Salahinejad, 2011).

In addition, the clusters of particles are stretched in the direction of rolling, which is due to the increase in the length of the sheet, and the transformation of large clusters of particles into smaller clusters, as well as the increase in contact between the metals and particles. This means an increase in the distance between the clusters, the fragmentation of the clusters, a decrease in the areas free of powder, and an improvement in the homogeneity of the structure. There are some agglomerates of particles in which there is no matrix material between the particles (Yazdani et al., 2011; Yazdani and Salahinejad, 2011).

The mechanisms of increasing the number of copper and silicon carbide layers, and metal extrusion among the clusters of particles are active in both TD-ND and RD-ND sections. However, the only difference is the mechanism of increasing the length of strips. During the rolling process, the length increases in the rolling direction, which is a function of the thickness reduction whilst the strain in the transverse direction is assumed to be zero. Therefore, increasing the length of the strip has no contribution to the distribution of particles in the TD-ND plane, because there is no significant increase in the length of the strip in the transverse direction.

The ratio of increased values of tensile strength because of the ARB performed in the first stage was 1.18 times for composite and 1.19 times for monolithic copper, while it was 1.05 times for composite and 1.06 times for pure copper, at the end of the ninth cycle. The big difference between the increased values for the first and second stage is attributed to the reducing the of strengthening effect of factors such as strain hardening and increase in the role of reinforcement in strengthening at the second stage. The slope of the curve is high at the initial cycles and low at the final stage.

It has been reported (Saito et al., 1998; Tsuji et al., 2002; Chen et al., 2006) that changes in tensile strength in the ARB process are controlled by two important strengthening mechanisms: strain hardening by dislocations, and grain refining. In the initial cycles of the ARB, strain hardening or strengthening by dislocations plays the most important role, while in the final stages, higher tensile strength occurs due to grain refining (Hansen et al., 2004). With the formation of co-axial grain boundaries, due to the high rate of dynamic recovery, the reduction of the density of dislocations is accelerated by the grain boundaries surfaces which act as dislocation sinks, and the strengthening mechanism by grain refinement dominates, instead, which results in an increase in flexibility without weakening the strengthening.

During strain hardening, dislocation sources (Frank-Reed sources) are activated and the number of dislocations in the structure increases. Since the dislocations accumulate in the strained areas of the distorted structure, if these areas are close together, they can have a mutual effect on each other which makes it difficult for new dislocations to move in these strained areas. Therefore, with the increase in plastic deformation, the number of dislocations increases, and this leads to a sharp increase in the yield stress. Based on the Eq. (2), the increase in yield stress $\left(∆{\mathrm{\sigma }}_{\text{SH}}\right)$ is proportional to the density of dislocations:

$\mathrm{\sigma }∆=\left(0.1\dots 0.2\right).\mathrm{M}.\mathrm{G}.\mathrm{b}.\mathrm{\surd }\mathrm{\rho }(2)$

where M is the Taylor factor, G is the shear modulus, and b is the Burgers vector (Humphreys and Hatherly, 1995).

The mechanical properties of metallic materials are strongly dependent on grain size. Yield stress increases with decreasing grain size for various groups of metals, following the Hall-Petch relationship. If a dislocation source generates dislocations within a grain, these dislocations accumulate near the grain boundary. The stress at the head of this dislocation pile-up must reach a critical level for the dislocations to continue moving and sliding onto the neighboring grain. Therefore, grain boundaries act as an additional barrier against dislocation movement. Given this, producing materials with fine grains has been of interest due to the increased number of grain boundaries that obstruct dislocation movement (Verlinden et al., 2007).

As the number of cycles increases, the tensile strength of the composite reaches a saturation point in the final cycles. This can be attributed to recrystallization within the composite sheet, as continuous recrystallization occurs due to the increased driving force from dislocation generation by particles during deformation and particle-induced nucleation (Tsuji et al., 2002). Since the presence of particles and the deformed structure near particles facilitate recrystallization nucleation, the kinetics of composite grain recrystallization is very fast, and the tensile strength of the composite reaches saturation. However, the finer the particles, the more they act as barriers against the movement of subgrain boundaries and grain boundaries, delaying recovery, recrystallization, and grain growth of the composite even at high temperatures. Therefore, it is highly likely and predictable that the tensile strength of the MMC will increase more with smaller particles. Another reason for the continuous occurrence of recovery and recrystallization during the accumulative rolling process is the increase in the temperature of the deforming metal (Humphreys and Hatherly, 1995). This temperature increase can be estimated using Eq. 3:

$\Delta \mathrm{T}=\frac{\mathrm{\eta }\mathrm{\delta }\mathrm{\epsilon }}{\mathrm{\rho }\mathrm{c}}(3)$

In η, the coefficient of conversion of mechanical work to thermal energy, δ is the average flow stress, ε is the equivalent strain, ρ is the density, and c is the specific heat of the material undergoing deformation. The density and specific heat of copper are respectively equal to 8.96 g·cm⁻³ and 0.386 J/g·K. Assuming a constant η for copper, as the number of ARB cycles increases, ΔT also increases. The calculated values are likely lower than the actual temperature increases of the sample, as the heat generated from the friction between the rollers and the workpiece is not considered, and the formula is related to adiabatic conditions. As the temperature increases, the likelihood of dynamic recovery in copper increases, and as a result, the elongation increase (Lee et al., 2002a).

Based on Table 2, for monolithic copper, the highest increase in tensile strength is related to the first cycle, and it increases at a slower rate afterwards. The tensile strength increases from 192.7 MPa, related to the primary annealed raw copper, up to about 444 MPa. During the ARB process, the tensile strength of the samples increases with the increasing number of cycles. In the first cycle, the strength increases significantly, reaching 353 MPa, and then continues to increase at a slower pace.

Two mechanisms may be mentioned regarding the increase in tensile strength of the ARBed pure monolithic copper: strain hardening or dislocation strengthening (σ_ρ), and grain refinement or grain boundary strengthening (σ_b). Up to the third cycle, strain hardening plays the most important role, and after that, the formation of sub-grains with ultrafine size or dislocation cells contributes to strengthening. As the number of cycles increases, strain hardening becomes less effective, and in the higher cycles, the number of ultrafine grains with large angle boundaries plays the most important role (Mishra et al., 2007).

On the other hand, it should be noted that in this study, the strengthening of metal matrix composites is influenced by both above mentioned mechanisms and the presence of particles in the matrix. The presence of silicon carbide particles can increase the threshold stress for dislocation slip and generate additional dislocations around SiC particles, reducing dislocation mobility during plastic deformation. These effects lead to an increase in the strength and decrease in the flexibility of the ARB composite. During plastic deformation, Cu/SiC interfaces can be preferred sites for crack initiation and propagation. Therefore, the flexibility of the MMC decreases, and it is well known that a higher volume fraction of particles results in greater strain hardening during mechanical work, thus improving tensile strength while reducing flexibility.

The uniformity in distribution of SiC particles has a significant effect on the tensile strength and elongation. The distribution of silicon carbide particles in the matrix changes towards a more uniform and homogeneous distribution with increasing ARB cycles and the tensile strength and elongation of the MMC increase.

Additionally, the quality of the Cu/SiC interface is the most important factor affecting the tensile strength and percentage of elongation of the composite. In fact, the tensile strength of the interface of the composite plays a crucial role in enhancing strength and flexibility. In the case of metal matrix composites, the fracture mechanism starts with the initiation of cracks at the Copper-SiC interfaces, spreading between the interfaces, and then connecting to the cracks or other reinforcing/substrate interfaces, causing fracture. As the number of ARB cycles increases, the bond between the reinforcement and the substrate is likely to become stronger due to the applied rolling pressure, resulting in increased tensile strength and elongation. One of the reasons for the early fracture (low ductility) of ARB materials is the presence of voids (areas of improper bonding), which act like cracks and cause fracture at low plastic strains. To reduce these voids, any factor that increases the forging force (such as increasing the width and increasing the roughness of external surfaces) can help reduce the number of these voids and consequently increase ductility and strength.

Porosity also has a significant effect on the mechanical properties of metal matrix composites. The presence of porosity in the composite, especially porosity surrounding the reinforcing particles, leads to lower tensile strength and elongation. As the number of ARB cycles increases, porosity in the samples decreases due to the good formability of the copper substrate and rolling pressure, leading to an increase in tensile strength and elongation (Jamaati et al., 2011a).

The difference between the coefficients of thermal expansion (CTE) of copper and the reinforcing particles is another influential factor on tensile strength and elongation percentage. As mentioned, it has been reported that the temperature of the sample increases during plastic deformation. It should be noted that silicon carbide has a low thermal conductivity of 45 W/(m.K). In contrast, the thermal conductivity of copper is high, approximately 350–385 W/(m.K). Therefore, it is expected that the temperature increase due to plastic deformation will be primarily transferred by copper, and the temperature in the copper substrate will rise significantly during plastic deformation (Lee et al., 2002a). Also, the CTE of silicon carbide and copper are approximately 4 × 10⁻⁶ K⁻¹ and 9.16 × 10⁻⁶ K⁻¹, respectively. As a result, after each ARB cycle and during the cooling process, silicon carbide particles and the copper substrate in the sample generate misfits. This is due to the generation of multi-directional thermal stresses at the Cu/SiC interfaces caused by the significant difference in CTE between the substrate and the reinforcement (Jamaati et al., 2011a).

Reduction of elongation at the initial stage of ARB process can be related to the reinforcing role of particles, uniformity, bond quality, and porosity. In other words, in the case of the composite in the initial stage, as the number of cycles increases, the reinforcing role and porosity increase, while uniformity and bond quality decrease. All these changes are related to the addition of SiC particles to the cycle in the initial stage. In addition, strain hardening has the most significant effect on the decrease in elongation in the first stage. Therefore, overall, it results in a reduction in flexibility in the first stage of composite production (Humphreys and Hatherly, 1995; Xing et al., 2002; Hansen et al., 2004; Alizadeh and Paydar, 2010). It has been reported that with an increase in reinforcing particles, due to the increase in the interfacial reinforcement of the matrix, the elongation decreases (Alizadeh and Paydar, 2010).

Regarding the decrease in the flexibility of the ARB copper in the first cycle, it can be said that this is mainly influenced by strain hardening (Tsuji et al., 2002). Furthermore, the inability to establish a proper bond in the last interface created in each cycle also plays a significant role in reducing flexibility (Alizadeh and Paydar, 2010). Tsuji and his colleagues (Tsuji et al., 2002) showed that the occurrence of strain hardening in cases with a grain size smaller than 1 µm after the ARB process is relatively difficult. The decrease in elongation in the ARB copper strips where strain hardening is difficult can be explained by terms of plastic instability. The conditions of plastic instability (necking propagation in the tensile test) are expressed by the Eq. (4):

$\ge \frac{\mathrm{d}\mathrm{\delta }}{\mathrm{d}\mathrm{\epsilon }}\mathrm{\delta }(4)$

where δ and ε represent true stress and true strain, respectively, and dδ/dε is the strain-hardening rate (Tsuji et al., 2002).

As mentioned, the continuous occurrence of recrystallization leads to an increase in the number of grains with large-angle grain boundaries as the strain level increases. Therefore, it is likely that the occurrence of the recrystallization phenomenon is one reason for the increase in elongation in higher cycles. Also, as discussed, factors such as increasing the uniformity of reinforcing particles dispersion, reducing porosities, and improving the quality of interfacial bonding have impacts on the increase in the elongation in higher cycles.

The rapid increase in hardness behavior in the first cycle is due to strain hardening, meaning an increase in dislocation density and interactions between them, which saturates at high strains. The reason for this can be attributed to the establishment of a balance between the generation of dislocations during the ARB process and their annihilation during the dynamic recovery stage, which ultimately results in the dislocation density reaching a stable and saturated state (Lee et al., 2002b; Shaarbaf and Toroghinejad, 2008; Eizadjou et al., 2009).

In the initial cycles, the sample has a layered structure in which SiC powder layers are placed between copper layers. With increasing cycles, the distribution of SiC reinforcing particles in the matrix improves, contributing to increased composite hardness. Additionally, the reduction of porosities in the composite with increasing cycles is another reason for increased hardness. Also, it can be seen that the standard deviation of the measured values decreases as the number of cycles increases. This also supports the claim that uniformity improves with increasing cycles. In terms of structural non-uniformity, some indentations in the hardness test are made on areas devoid of powder, showing low hardness values, while some can be applied to particle clusters, showing high hardness. Therefore, the standard deviation of eight random hardness tests has a high value.

In contrast, for uniform structures, the contribution of the matrix and reinforcement to hardness values is approximately equal in all surface positions examined, resulting in a low standard deviation. Microscopic images and the reduction of standard deviation hardness values with increasing cycles both rely on the fact that structural uniformity improves with increasing cycles. The overall hardness level for monolithic copper is lower than the composite sample, due to the reinforcing effects of SiC particles. In the initial cycles and low strains, the role of work hardening is evident. In contrast, in higher cycles, the slowdown in the hardness increase trend indicates a balance between dislocation creation during the rolling process and their removal by dynamic recovery, causing dislocation density to reach a stable and saturated state.

As can be seen in the experimental XRD analysis image with MAUD software output comparison, these two plots are very closely aligned with each other. The plotted graph at the bottom also includes the residual and unmatched parameters, essentially showing the error in the fit, and it can be observed that the amount of this error is practically negligible. After performing the fitting, microstructural parameters, including microstrain and sub-grain size, were obtained.

It was observed that for the composite, the overall trend of microstrain changes is decreasing, but a significant decrease in microstrain occurred in the seventh cycle, which can be justified considering the occurrence of recovery or continuous recrystallization. Also, overall, the sub-grain size decreased to 7.88 nm after nine cycles. In addition, the average dislocation density can be calculated based on the Eqs 5–7 (Sahu et al., 2002):

$\mathrm{\rho }={\left({\mathrm{\rho }}_{\mathrm{D}}+{\mathrm{\rho }}_{\mathrm{S}}\right)}^{1/2}(5)$

${\mathrm{\rho }}_{\mathrm{D}}=3/{\mathrm{D}}^2(6)$

${\mathrm{\rho }}_{\mathrm{S}}=\mathrm{K}<{\mathrm{\epsilon }}_{\mathrm{L}}{>}^2/{\mathrm{b}}^2(7)$

where,

ρ: dislocations density.

ρ_D: dislocation density related to crystallite size.

ρ_S: dislocation density related to strain.

D: average crystallite size.

ɛ: average microstrain.

K: constant and equal to 6π.

B: burgers vector that is equal to $\frac{\sqrt{2}}{2}\mathrm{a}$ for a face center cubic (FCC) structure.

Shaarbaf, et al., (Shaarbaf and Toroghinejad, 2009), using TEM evaluations on pure copper samples produced by the ARB process, showed that after eight ARB cycles, the copper grain size had reached less than 100 nm. He also demonstrated that the grain boundaries in the fourth ARB cycle sample were formed by dislocation networks, while ultrafine grains after eight cycles were surrounded by distinct but irregular grain boundaries. These extremely small grains are polycrystals with relatively large mismatches relative to each other. It has been reported (Tsuji et al., 1999) that ultrafine grain boundaries produced by severe plastic deformation have non-equilibrium structures. An interesting result is that microstructural changes during ARB and ultrafine grains produced are almost similar for all materials and independent of the material type. However, it should be noted that the average grain size varies greatly depending on the material type.

In another study conducted by Pasebani (Pasebani and Toroghinejad, 2010), a 70/30 brass nanostructured strip was produced by six cycles of the ARB process. The average grain size was measured by TEM and compared with the calculated average grain size by the Rietveld method (using XRD data and MAUD software). Using TEM images in the sixth cycle, it was observed that most grains had become very small, with an average diameter of less than 50 nm. A significant fraction of the ultrafine grains observed in TEM images are coaxial grains with very distinct boundaries, indicating that these grains are the primary grains. The Rietveld method calculations showed that the average sub-grain size in the sixth cycle was about 23 nm. Considering the closeness of the calculated average sub-grain size (23 nm) by the Rietveld method to the average grain diameter measured by TEM, it can be concluded that in the upper cycles of the ARB process and with the increase of strain applied to the material, the sub-grain boundaries turn into high-angle grain boundaries and sub-grains turn into primary grains. Therefore, it can be said that in the upper cycles of the process, the calculations by the Rietveld method are in good agreement with TEM observations, and thus the Rietveld method is a reliable method for calculating microstructural parameters, including grain size.

Therefore, in the present study, considering the presence of reinforcing particles as a factor in the accumulation of dislocations and grain refinement in the Cu/SiC composite, comparing the results obtained by Shirbaf on pure copper and the results from calculations using the Rietveld method, it can be concluded that the grain size related to the produced composite after nine cycles of the ARB process has reached below 100 nm.

The Williamson-Hall (Williamson and Hall, 1953) and Rietveld (Wiles and Young, 1980; Chanda and De, 2000; Evans and Evans, 2021) methods are among the methods used for analyzing X-ray diffraction patterns. It is worth mentioning that the calculated dislocation density value through X-ray diffraction pattern analysis is not an accurate method. In the XRD method, many theoretical concepts, instrumental parameters (such as peak symmetry and peak broadening parameters), lattice defects (such as dislocations, stacking faults, and twinning), texture effects, and sample conditions exist that can affect the measured values, including crystallite size, microstrain, and subsequently calculated dislocation density. However, measuring dislocation densities by TEM image observations faces many difficulties and is somewhat impossible. In fact, obtaining reliable information largely depends on the accuracy of sample preparation and imaging. In some cases, the observed defects in TEM are not related to the original structure but have been created during sample preparation. This is especially the case for materials with unstable or metastable structures. Another limiting factor for TEM capability is the low quality of images obtained from structures with a high percentage of defects such as dislocations, particularly in large deformations. Therefore, the XRD method is accepted for the indirect measurement of dislocation densities.

Considering that a texture parameter less than one indicates a random texture, the texture parameter of the planes that had a value above one was investigated. According to this explanation, it is observed that in the first cycle of the process, only the (200) and (400) planes, which are likely cubic texture components, have led to the formation of texture. As the number of cycles increases to three, the texture parameter of the mentioned planes decreases, and the parameter of the (220) and (311) planes increases, reaching around one. As a result, it can be stated that this cubic texture component is derived from recrystallization (Raei et al., 2010). With further increase in the number of cycles, in the fifth cycle, the texture parameter of the (200) and (400) planes increases again, and the parameter of the (220) and (311) planes decreases. This phenomenon can probably be attributed to the fact that the dominant texture component has changed from cubic to rotated cubic. The rotated cubic component, which is a common component related to the shear texture, appears in the sample after three cycles (Raei et al., 2010). In fact, a texture transition occurs in this sample. However, to make a definitive statement on this matter, it is necessary to examine the images of the orientation distribution functions (ODF). Then, until the ninth cycle, the texture parameters for the (200) and (400) planes continue to decrease, and for the (220) and (311) planes, it increases. The rotated cubic texture becomes the main texture component from the third cycle onwards, and the texture reaches a stable state. As the number of cycles increases, the number of common interfaces increases, and therefore the distance between them decreases. In any case, these common interfaces have a shear texture. Therefore, after a specific number of cycles, due to the increase in the number of common interfaces, the shear texture (rotated cubic) appears as the dominant texture in the sample, and the possibility of the shear component dominating increases with the number of cycles (Raei et al., 2010).

Although it is expected that with increasing the number of ARB cycles, the shear texture easily transforms into the rolling texture, it can be stated that the presence of silicon carbide particles between the strips causes the shear texture to reappear even with an increase in cycles. In other words, during ARB, silicon carbide particles can prevent the conversion of shear texture along the thickness of the sheets (Kim et al., 2005). However, researchers state that a small amount of fine reinforcing particles does not have a significant impact on texture developments. In other words, unlike large reinforcing particles, fine particles cannot prevent the change of shear texture in the thickness of the strips. Texture developments show that after nine cycles, the rotated cubic component becomes the main texture component in all samples, and for all samples, almost all texture components, except for the rotated cubic, are weak (Kim et al., 2005; Kamikawa et al., 2007). This result is related to the presence of large secondary phase particles, which cause the randomization of the texture around these particles (Jamaati et al., 2011b).

Overall, in this case, the most notable point is that the dominant texture parameter related to the (200) plane, which is probably the rotated cubic texture component, remains until the end. One can see that in the first cycle, a cubic texture component is dominant, which indicates that even after the first cycle, the recrystallization texture has not disappeared, but its intensity has decreased.

In this case ARBed monolithic copper, the main texture component is probably a rotated cubic component, which is a shear texture component. The shear texture is formed due to the creation of shear deformation near the surface of the sample. Furthermore, no meaningful change in the type of texture components occurs until the end of the ninth cycle.

In the ARB process, a large amount of excess shear strain is created due to the friction between the rollers and the surface of the strips at the sample surface. Moreover, strips that have experienced a 50% reduction in thickness are cut and then stacked again between cycles, transferring half of the areas that were under severe deformation in the previous cycle to the center of the sample. Therefore, in ARB, unlike the conventional rolling process, shear deformation is not concentrated only in layers close to the surface, but the shear strain is distributed throughout the thickness (Shaarbaf and Toroghinejad, 2009).

5 Conclusion

In this research, the metal matrix composite of copper/silicon carbide was fabricated using the Accumulative Roll Bonding (ARB) method. The main conclusions of this work can be summarized as follows.

1- Nanocrystalline copper and composite samples were produced using nine cycles of the ARB process. The grains sizes for the monolithic Copper and composite samples were estimated to be 111.23 nm and 88.7 nm, respectively, using MAUD software and microstructural evaluation.

2- It was observed in composites that the uniformity in distribution of silicon carbide particles in the copper matrix improved as the process progressed. After nine cycles of the process, no pores were observed at the interface between copper layers or between the particle and the matrix.

3- The tensile strength of the composite made by the ARB method was 2.5 and 1.1 times the tensile strength of the annealed primary copper samples and the pure ARB copper, respectively. The tensile strength of the composite increased in both the first and second stages of the manufacturing process. While the first stage led to a reduction in the percentage of elongation, the second stage increased the percentage of elongation of these composites. A rapid increase in hardness was observed in the early cycles, which continued with a lower slope until the ninth cycle.

4- The fracture mechanism of the ARB composite is of the ductile shear type. Also, it can be seen in the composite samples that the fracture occurred more around the reinforcing particles.

5- The texture parameter studies on the samples produced by the ARB method showed that in the first cycle of the process, only the (200) and (400) planes, which are probably the cubic texture components, have created the texture. In the fifth cycle, the dominant texture component probably changed from cubic to rotated cubic. Overall, in this case, the dominant texture parameter related to the (200) plane, which is probably the same rotated cubic texture component, remains until the end.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

OG: Conceptualization, Data curation, Formal Analysis, Investigation, Methodology, Project administration, Software, Supervision, Validation, Visualization, Writing–original draft, Writing–review and editing. MZ: Software, Writing–review and editing. HS: Writing–review and editing. MT: Conceptualization, Funding acquisition, Project administration, Resources, Supervision, Validation, Visualization, Writing–review and editing. AN: Supervision, Validation, Writing–review and editing. BC: Writing–review and editing. PR: Validation, Writing–review and editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Akbarpour, M. R., Gazani, F., Mousa Mirabad, H., Khezri, I., Moeini, A., Sohrabi, N., et al. (2023a). Recent advances in processing, and mechanical, thermal and electrical properties of Cu-SiC metal matrix composites prepared by powder metallurgy. Prog. Mater. Sci. 140, 101191. doi:10.1016/j.pmatsci.2023.101191

CrossRef Full Text | Google Scholar

Akbarpour, M. R., Mirabad, H. M., Gazani, F., Khezri, I., Ahmadi Chadegani, A., Moeini, A., et al. (2023b). An overview of friction stir processing of Cu–SiC composites: microstructural, mechanical, tribological, and electrical properties. J. Mater. Res. Technol. 27, 1317–1349. doi:10.1016/j.jmrt.2023.09.200

CrossRef Full Text | Google Scholar

Alizadeh, M., and Paydar, M. H. (2010). Fabrication of nanostructure Al/SiCP composite by accumulative roll-bonding (ARB) process. J. Alloys Compd. 492 (1-2), 231–235. doi:10.1016/j.jallcom.2009.12.026

CrossRef Full Text | Google Scholar

ASTM E8 (2004). Tension testing of metallic materials. West Conshohocken, United states: ASTM International

Google Scholar

Azushima, A., Kopp, R., Korhonen, A., Yang, D. Y., Micari, F., Lahoti, G. D., et al. (2008). Severe plastic deformation (SPD) processes for metals. CIRP Ann. - Manuf. Technol. 57 (2), 716–735. doi:10.1016/j.cirp.2008.09.005

CrossRef Full Text | Google Scholar

Bukhari, M., Brabazon, D., and Hashmi, M. J. (2011). “Application of metal matrix composite of CuSiC and AlSiC as electronics packaging materials,” in The 28th international manufacturing conference, Dublin City University, Republic of Ireland, August 2011.

Google Scholar

Caron, R., and Sharif, A. (2017). Copper alloys: properties and applications. Encyclopedia of Materials

Google Scholar

Chanda, A., and De, M. (2000). X-ray characterization of the microstructure of a-CuTi alloys by Rietveld’s method. J. Alloys Compd. 313, 104–114. doi:10.1016/s0925-8388(00)01189-0

CrossRef Full Text | Google Scholar

Chawla, N., and Chawla, K. K. (2006). Metal matrix composites. New York: Springer.

Google Scholar

Chen, M. C., Hsieh, H. C., and Wu, W. (2006). The evolution of microstructures and mechanical properties during accumulative roll bonding of Al/Mg composite. J. Alloys Compd. 416 (1–2), 169–172. doi:10.1016/j.jallcom.2005.09.017

CrossRef Full Text | Google Scholar

Chen, R., Zhao, B., He, T., Tu, L., Xie, Z., Zhong, N., et al. (2024). Study on coupling transient mixed lubrication and time-varying wear of main bearing in actual operation of low-speed diesel engine. Tribol. Int. 191, 109159. doi:10.1016/j.triboint.2023.109159

CrossRef Full Text | Google Scholar

Dini, G., Najafizadeh, A., Monir-Vaghefi, S. M., and Ueji, R. (2010). Grain size effect on the martensite formation in a high-manganese TWIP steel by the Rietveld method. J. Mater. Sci. Technol. 26 (2), 181–186. doi:10.1016/s1005-0302(10)60030-8

CrossRef Full Text | Google Scholar

Ebrahimi, M., Zhang, L., Wang, Q., Zhou, H., and Li, W. (2021). Damping characterization and its underlying mechanisms in CNTs/AZ91D composite processed by cyclic extrusion and compression. Mater. Sci. Eng. A 821, 141605. doi:10.1016/j.msea.2021.141605

CrossRef Full Text | Google Scholar

Eizadjou, M., Danesh Manesh, H., and Janghorban, K. (2009). Microstructure and mechanical properties of ultra-fine grains (UFGs) aluminum strips produced by ARB process. J. Alloys Compd. 474 (1-2), 406–415. doi:10.1016/j.jallcom.2008.06.161

CrossRef Full Text | Google Scholar

Eizadjou, M., Kazemi Talachi, A., Danesh Manesh, H., Shakur Shahabi, H., and Janghorban, K. (2008). Investigation of structure and mechanical properties of multi-layered Al/Cu composite produced by accumulative roll bonding (ARB) process. Compos. Sci. Technol. 68 (9), 2003–2009. doi:10.1016/j.compscitech.2008.02.029

CrossRef Full Text | Google Scholar

Evans, J. S. O., and Evans, I. R. (2021). Structure analysis from powder diffraction data: Rietveld refinement in excel. J. Chem. Educ. 98 (2), 495–505. doi:10.1021/acs.jchemed.0c01016

CrossRef Full Text | Google Scholar

Farajpour Mojdehi, M., Rafie, S. F., Abu-Zahra, N., Saghatchian, O., Shams Ghamsari, Z., Mahmoudi, F., et al. (2024). Exploring the mechanisms of diazinon adsorption onto alpha and beta cyclodextrins through molecular dynamics simulations: insights into environmentally friendly pesticide remediation. Results Eng. 21, 102020. doi:10.1016/j.rineng.2024.102020

CrossRef Full Text | Google Scholar

Gabriel, B. L. (1998). Scanning electron microscopy. Charact. Mater. 2, 1721–1735. doi:10.1002/0471266965.com081.pub2

CrossRef Full Text | Google Scholar

Ghaderi, O., Toroghinejad, M. R., and Najafizadeh, A. (2013). Investigation of microstructure and mechanical properties of Cu–SiCP composite produced by continual annealing and roll-bonding process. Mater. Sci. Eng. A 565, 243–249. doi:10.1016/j.msea.2012.11.004

CrossRef Full Text | Google Scholar

Handbooks, A. (1997). Metals mechanichal testing-elevated and low temperature. West Conshohocken, PA: American Society for Testing and Materials, 1120.

Google Scholar

Hansen, N., Huang, X., Ueji, R., and Tsuji, N. (2004). Structure and strength after large strain deformation. Mater. Sci. Eng. A 387–389, 191–194. doi:10.1016/j.msea.2004.02.078

PubMed Abstract | CrossRef Full Text | Google Scholar

Humphreys, F. J., and Hatherly, M. (1995). Recrystallization and related annealing phenomena. 2nd Ed. Oxford: Pergamon.

Google Scholar

Jamaati, R., Amirkhanlou, S., Toroghinejad, M. R., and Niroumand, B. (2011a). Effect of particle size on microstructure and mechanical properties of composites produced by ARB process. Mater. Sci. Eng. A 528 (4–5), 2143–2148. doi:10.1016/j.msea.2010.11.056

CrossRef Full Text | Google Scholar

Jamaati, R., Toroghinejad, M. R., Hoseini, M., and Szpuna, J. A. (2011b). Texture development in Al/Al₂O₃ MMCs produced by anodizing and ARB processes. Mater. Sci. Eng. A 528, 3573–3580. doi:10.1016/j.msea.2011.01.056

CrossRef Full Text | Google Scholar

Kamikawa, N., Sakai, T., and Tsuji, N. (2007). Effect of redundant shear strain on microstructure and texture evolution during accumulative roll-bonding in ultralow carbon IF steel. Acta Mater. 55 (17), 5873–5888. doi:10.1016/j.actamat.2007.07.002

CrossRef Full Text | Google Scholar

Ke, J. G., Liu, R., Xie, Z. M., Zhang, L. C., Wang, X. P., Fang, Q. F., et al. (2024). Ultrahigh strength, thermal stability and high thermal conductivity in hierarchical nanostructured Cu-W alloy. Acta Mater. 264, 119547. doi:10.1016/j.actamat.2023.119547

CrossRef Full Text | Google Scholar

Kim, H.-W., Kang, S.-B., Tsuji, N., and Minamino, Y. (2005). Elongation increase in ultra-fine grained Al–Fe–Si alloy sheets. Acta Mater. 53 (6), 1737–1749. doi:10.1016/j.actamat.2004.12.022

CrossRef Full Text | Google Scholar

Lee, S. H., Saito, Y., Sakai, T., and Utsunomiya, H. (2002a). Microstructures and mechanical properties of 6061 aluminum alloy processed by accumulative roll-bonding. Mater. Sci. Eng. A 325 (1–2), 228–235. doi:10.1016/s0921-5093(01)01416-2

CrossRef Full Text | Google Scholar

Lee, S. H., Saito, Y., Tsuji, N., Utsunomiya, H., and Sakai, T. (2002b). Role of shear strain in ultragrain refinement by accumulative roll-bonding (ARB) process. Scr. Mater. 46, 281–285. doi:10.1016/s1359-6462(01)01239-8

CrossRef Full Text | Google Scholar

Li, L., Nagai, K., and Yin, F. (2008). Progress in cold roll bonding of metals. Sci. Technol. Adv. Mater. 9 (2), 023001. doi:10.1088/1468-6996/9/2/023001

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, Y., Liu, Y., Wang, T., Wang, Z., and Huang, Q. (2024). Mathematical modeling and analysis of the tailor rolled blank manufacturing process. Int. J. Mech. Sci. 266, 108991. doi:10.1016/j.ijmecsci.2024.108991

CrossRef Full Text | Google Scholar

Luo, J.-G., and Acoff, V. L. (2004). Using cold roll bonding and annealing to process Ti/Al multi-layered composites from elemental foils. Mater. Sci. Eng. A 379 (1–2), 164–172. doi:10.1016/j.msea.2004.01.021

CrossRef Full Text | Google Scholar

Min, G., Lee, J.-M., Kang, S.-B., and Kim, H.-W. (2006). Evolution of microstructure for multilayered Al/Ni composites by accumulative roll bonding process. Mater. Lett. 60 (27), 3255–3259. doi:10.1016/j.matlet.2006.03.001

CrossRef Full Text | Google Scholar

Mishra, A., Kad, B. K., Gregori, F., and Meyers, M. A. (2007). Microstructural evolution in copper subjected to severe plastic deformation: experiments and analysis. Acta Mater. 55 (1), 13–28. doi:10.1016/j.actamat.2006.07.008

CrossRef Full Text | Google Scholar

Mozaffari, A., Hosseini, M., and Manesh, H. D. (2011). Al/Ni metal intermetallic composite produced by accumulative roll bonding and reaction annealing. J. Alloys Compd. 509 (41), 9938–9945. doi:10.1016/j.jallcom.2011.07.103

CrossRef Full Text | Google Scholar

Pasebani, S., and Toroghinejad, M. R. (2010). Nano-grained 70/30 brass strip produced by accumulative roll-bonding (ARB) process. Mater. Sci. Eng. A 527 (3), 491–497. doi:10.1016/j.msea.2009.09.029

CrossRef Full Text | Google Scholar

Peng, J., Liu, Z., Xia, P., Lin, M., and Zeng, S. (2012). On the interface and mechanical property of Ti/Al–6%Cu–0.5%Mg–0.4%Ag bimetal composite produced by cold-roll bonding and subsequent annealing treatment. Mater. Lett. 74, 89–92. doi:10.1016/j.matlet.2012.01.052

CrossRef Full Text | Google Scholar

Raei, M., Toroghinejad, M. R., Jamaati, R., and Szpunar, J. A. (2010). Effect of ARB process on textural evolution of AA1100 aluminum alloy. Mater. Sci. Eng. A 527 (26), 7068–7073. doi:10.1016/j.msea.2010.07.089

CrossRef Full Text | Google Scholar

Sahu, P., De, M., and Kajiwara, S. (2002). Microstructural characterization of stress-induced martensites evolved at low temperature in deformed powders of Fe–Mn–C alloys by the Rietveld method. J. Alloys Compd. 346 (1–2), 158–169. doi:10.1016/s0925-8388(02)00495-4

CrossRef Full Text | Google Scholar

Saito, Y., Tsuji, N., Utsunomiya, H., Sakai, T., and Hong, R. G. (1998). Ultra-fine grained bulk aluminum produced by accumulative roll-bonding (ARB) process. Scr. Mater. 39 (9), 1221–1227. doi:10.1016/s1359-6462(98)00302-9

CrossRef Full Text | Google Scholar

Shaarbaf, M., and Toroghinejad, M. R. (2008). Nano-grained copper strip produced by accumulative roll bonding process. Mater. Sci. Eng. A 473 (1-2), 28–33. doi:10.1016/j.msea.2007.03.065

CrossRef Full Text | Google Scholar

Shaarbaf, M., and Toroghinejad, M. R. (2009). Evaluation of texture and grain size of nanograined copper produced by the accumulative roll bonding process. Metallurgical Mater. Trans. A 40, 1693–1700. doi:10.1007/s11661-009-9851-z

CrossRef Full Text | Google Scholar

Tan, M. J., and Zhang, X. (1998). Powder metal matrix composites: selection and processing. Mater. Sci. Eng. A 224, 80–85. doi:10.1016/s0921-5093(97)00829-0

CrossRef Full Text | Google Scholar

Torralba, J. M., Costa, C. E., and Velasco, F. (2003). P/M aluminum matrix composites: an overview. J. Material Process Technol. 133, 203–206. doi:10.1016/s0924-0136(02)00234-0

CrossRef Full Text | Google Scholar

Tsuji, N., Ito, Y., Saito, Y., and Minamino, Y. (2002). Strength and ductility of ultrafine grained aluminum and iron produced by ARB and annealing. Scr. Mater. 47 (12), 893–899. doi:10.1016/s1359-6462(02)00282-8

CrossRef Full Text | Google Scholar

Tsuji, N., Saito, Y., Utsunomiya, H., and Tanigawa, S. (1999). Ultra-fine grained bulk steel produced by accumulative roll-bonding (ARB) process. Scr. Mater. 40 (7), 795–800. doi:10.1016/s1359-6462(99)00015-9

CrossRef Full Text | Google Scholar

Verlinden, B., Driver, J., Samajdar, I., and Doherty, R. D. (2007). Thermo-mechanical processing of metallic materials. Oxford: Elsevier.

Google Scholar

Wagner, F. (1999). “Texture determination by using X ray diffraction,” in Characterization techniques of glasses and ceramics. Editors J. M. Rincon, and M. Romero (Berlin, Heidelberg: Springer Berlin Heidelberg), 169–186.

CrossRef Full Text | Google Scholar

Wiles, D. B., and Young, R. A. (1980). Application of the Rietveld method for structure refinement with powder diffraction data. Adv. X-ray Analysis 24, 1–23. doi:10.1154/s0376030800007114

CrossRef Full Text | Google Scholar

Williamson, G. K., and Hall, W. H. (1953). X-ray line broadening from filed aluminium and wolfram. Acta Metall. 1 (1), 22–31. doi:10.1016/0001-6160(53)90006-6

CrossRef Full Text | Google Scholar

Xing, Z. P., Kang, S. B., and Kim, H. W. (2002). Structure and properties of AA3003 alloy produced by accumulative roll bonding process. Mater. Sci. 37, 717–722. doi:10.1023/A:1013879528697

CrossRef Full Text | Google Scholar

Yang, D., Cizek, P., Hodgson, P., and Ce, W. (2010). Ultrafine equiaxed-grain Ti/Al composite produced by accumulative roll bonding. Scr. Mater. 62 (5), 321–324. doi:10.1016/j.scriptamat.2009.11.036

CrossRef Full Text | Google Scholar

Yazdani, A., and Salahinejad, E. (2011). Evolution of reinforcement distribution in Al–B4C composites during accumulative roll bonding. Mater. Des. 32 (6), 3137–3142. doi:10.1016/j.matdes.2011.02.063

CrossRef Full Text | Google Scholar

Yazdani, A., Salahinejad, E., Moradgholi, J., and Hosseini, M. (2011). A new consideration on reinforcement distribution in the different planes of nanostructured metal matrix composite sheets prepared by accumulative roll bonding (ARB). J. Alloys Compd. 509 (39), 9562–9564. doi:10.1016/j.jallcom.2011.07.084

CrossRef Full Text | Google Scholar

Zare, M., Maleki, A., and Niroumand, B. (2022). In situ Al-SiOC composite fabricated by in situ pyrolysis of a silicone polymer gel in aluminum melt. Int. J. Metalcasting 16 (3), 1327–1346. doi:10.1007/s40962-021-00658-9

CrossRef Full Text | Google Scholar

Zhang, R., and Acoff, V. L. (2007). Processing sheet materials by accumulative roll bonding and reaction annealing from Ti/Al/Nb elemental foils. Mater. Sci. Eng. A 463 (1–2), 67–73. doi:10.1016/j.msea.2006.06.144

CrossRef Full Text | Google Scholar

Zhao, Y., Sun, Y., and Hou, H. (2022). Core-shell structure nanoprecipitates in Fe-xCu-3.0 Mn-1.5 Ni-1.5 Al alloys: a phase field study. Prog. Nat. Sci. Mater. Int. 32 (3), 358–368. doi:10.1016/j.pnsc.2022.04.001

CrossRef Full Text | Google Scholar