Semi-active inerters: a review of the literature

The inerter was introduced as a mechanical counterpart to the electrical capacitor, completing the force-current analogy. This is a one-port, two-terminal device in which the equal and opposite forces exerted at its terminals are proportional to the relative acceleration between them. Within this relationship, the “inertance” is the coefficient of proportionality and carries the unit of mass. This implies that the inerter can exert an inertial force at its terminals, effectively representing a virtual mass. Due to these properties, inerters have gained popularity, finding applications as components of vibration control systems and energy harvesters. Derived from passive inerters, semi-active inerters are integrated with active control systems to regulate their inertance. Since their introduction, semi-active inerters have been pivotal in situations demanding active monitoring of natural frequency or control force, generally outperforming their passive counterparts. While numerous significant reviews on passive inerters and their applications have been published in respected journals, dedicated literature reviews on semi-active inerters remain scarce. This review seeks to bridge this gap, offering a comprehensive literature review on semi-active inerters and highlighting research challenges and opportunities. Given the novelty of semi-active inerters, they present a fascinating area of study.

1 Introduction

Advancements in the field of mechanical engineering have led to the discovery of innovative mechanical devices and systems. The inerter was proposed in the early 2000s as a mechanical equivalent of the electrical capacitor to complete the force-current analogy. It is a one-port, two-terminal mechanical device in which the equal and opposite force applied at the terminals is proportional to their relative acceleration (Smith, 2002). “Inertance” is the coefficient of proportionality in the relationship between force and acceleration of an inerter. This quantity carries the unit of mass, which implies that the inerter can exert inertial force at both terminals (Smith, 2020; Ma et al., 2021). Inerters are superior to masses since they have two terminals and do not require a ground in the mechanical network like the mass. Furthermore, inerters can emulate the inertial behaviour of a large apparent mass using a device with a much smaller physical mass (Ma et al., 2021).

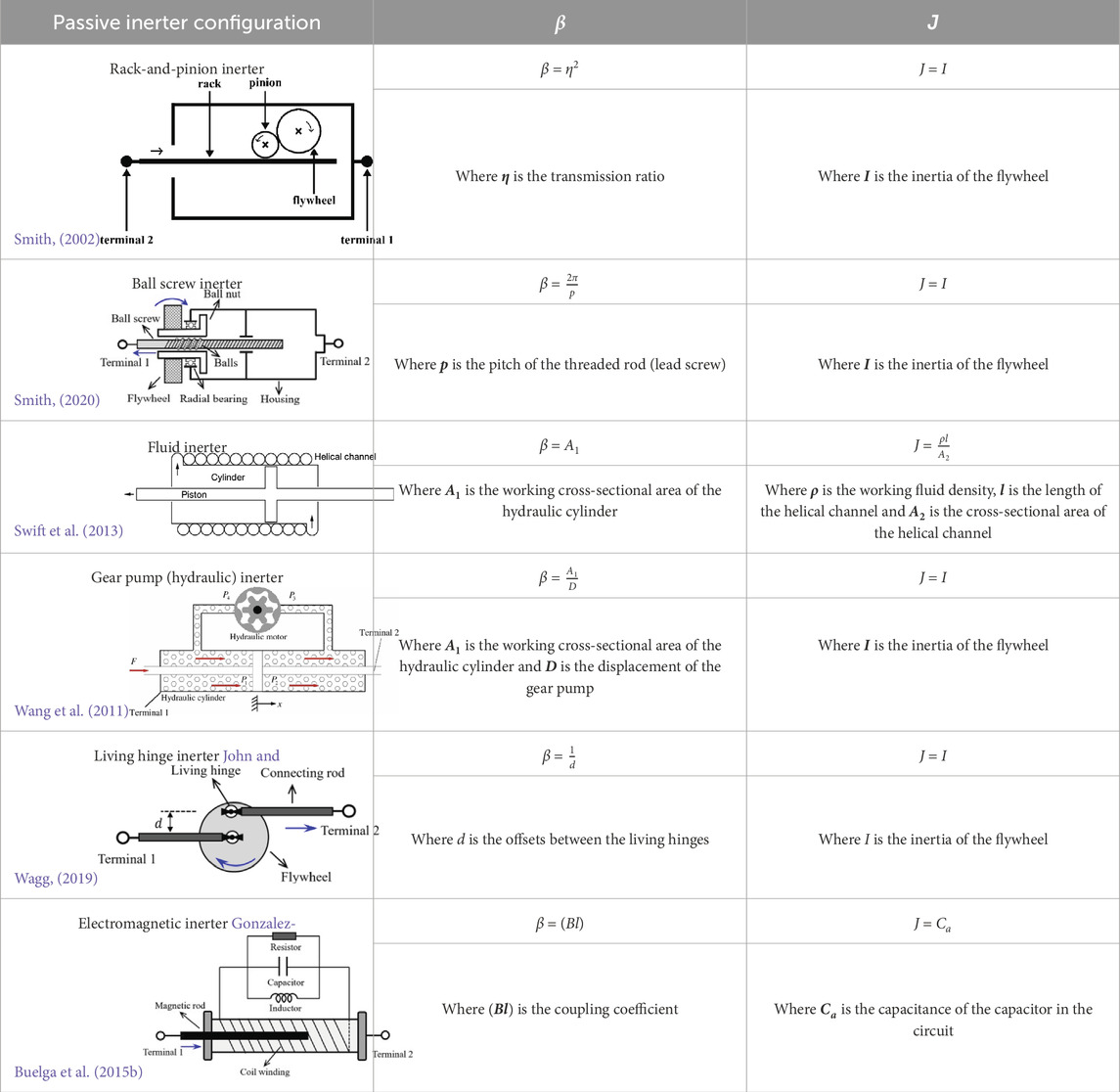
Various physical means can be employed to embody inerters, such as mechanical, hydraulic, or electromagnetic mechanisms. There are numerous examples of these physical embodiments, including the rack and pinion inerter (Smith, 2002), ball screw inerter (Smith, 2020), fluid inerter (Swift et al., 2013), gear pump (hydraulic) inerter (Wang et al., 2011), living hinge inerter (John and Wagg, 2019), electromagnetic inerter (Gonzalez-Buelga et al., 2015a), hydraulic-electric inerter (Shen et al., 2019), and crank inerter (Zhang et al., 2022a). Each configuration possesses unique strengths, rendering them well-suited for specific applications.

Due to their working principles and properties, inerters are particularly attractive in the field of vibration control, where they are integrated into vibration control systems to enhance performance (Ma et al., 2021). Unwanted mechanical vibrations negatively affect the performance, safety, and lifespan of structures and systems. Hence, vibration control systems are purposely designed to exert control forces for mitigating such oscillations (Ma et al., 2021). These systems can be either passive, semi-active, or active (Liu et al., 2021).

Passive vibration control systems utilise passive components such as dashpots, springs, and masses to exert resistive control force. These vibration control systems are reliable and require no energy from external sources (Liu et al., 2021). The introduction of inerters in passive vibration control systems has led to substantial improvements in vibration reduction since inerters are typically effective in controlling low-frequency vibrations (Ma et al., 2021). Applications of this technology have been observed in various areas. Applications such as structural vibration controllers (Ma et al., 2021), automobile suspension (Smith and Wang, 2004; Smith, 2020), train suspension (Wang et al., 2009), motorcycle steering compensators (Evangelou et al., 2007), machining chatter suppression (Dogan et al., 2019), and aircraft shimmy suppression devices (Li et al., 2017) have all benefitted from the incorporation of inerters. While passive vibration control systems are reliable and inexpensive, their performance in vibration attenuation is limited (Karnopp et al., 1974).

Active vibration control systems employ actuators guided by precise control strategies to apply vibration-attenuating forces. Active vibration controllers offer the most superior performance in vibration control. However, they are expensive and consume a lot of energy. Semi-active vibration controllers compromise between passive and active systems as they offer similar performance as active vibration controllers without the complexity and high energy consumption of their active counterparts. These controllers feature active adjustment of formerly passive device’s characteristic parameters such as stiffness and damping coefficient to provide controllable vibration attenuating forces (Garrido et al., 2018). Since inerters can serve as a component of the vibration control system, another type of device for semi-active vibration controllers can be realised. Semi-active inerters are mechanical inerters that feature controllable inertance. These devices employ auxiliary control systems based on sensed variables to actively control their inertance in real time (Garrido et al., 2018). The research around semi-active inerters is burgeoning. Integration of semi-active inerters to semi-active vibration control systems may potentially yield performance closer to active vibration control systems at a low cost and energy consumption, hence its study is of significant interest.

The concept of the semi-active inerter was first conceived by Chen et al. (2014a) in 2014 as a component of a semi-active vehicle suspension system. In 2015, Brzeski et al. (2015) presented the first physical configuration of the semi-active inerter, featuring a continuously variable transmission (CVT) to adjust its inertance. Since then, publications around the semi-active inerter have emerged, presenting new physical embodiments, applications, and improvements that the device has to offer. In 2018, Garrido et al. (2018); Garrido et al. (2019) implemented the principle of duality to define “independently-variable-inertance inerters” and “resettable inertance inerters” as subclasses of semi-active inerters to match with the classification of semi-active springs. This classification has opened a lot of opportunities as the research around resettable inertance inerters is only at its preliminary stage. Research on semi-active inerters has also delved into their nonideal behaviours and instability to examine the behaviour of devices and systems implemented in practice (Hu et al., 2021a; Hu et al., 2022). Most recently, Hu et al. presented the “mechatronic inerter”, a semi-active inerter that features quick and independent control of its inertance (Hu et al., 2023).

Numerous impactful review articles targeting passive inerters and their applications have been published over the past 2 decades. To name a few, Ma et al. presented a state-of-the-art review on inerter-based vibration control systems (Ma et al., 2021). Liu et al. conducted literature review on the inerter and its applications in vibration isolation systems (Liu et al., 2022). Pippi et al. reviewed the use of inerters in structure coupling technique for adjacent building vibration control (de Souza Pippi et al., 2022). Wagg conducted a review on the mechanical inerter, including its historical context, physical realisations, and nonlinear applications (Wagg, 2021). Some mentions of the semi-active inerter were found in these articles. However, literature review articles targeting exclusively semi-active inerters have yet to be published. This article attempts to present a review of published literature around semi-active inerters, aiming to present the fundamentals, characteristics, and applications of the semi-active inerter as well as identify challenges and opportunities in research within this area. Given that research around semi-active inerters has not yet reached maturity, it is essential to highlight these opportunities and challenges to present the current state of the art.

The rest of this article is organised as follows: Section 2 discusses the fundamentals of passive inerters and semi-active inerters. Section 3 presents different configurations of the semi-active inerter. Section 4 reviews the applications of semi-active inerter in the field of vibration control and energy harvesting. Section 5 discusses the research opportunities around semi-active inerters and their applications identified from reviewing published literature. Ultimately, section 6 concludes the article.

2 Fundamentals

2.1 The inerter

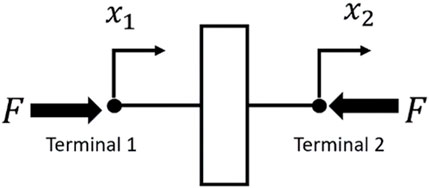
Figure 1 presents the mechanical network diagram of the inerter. The inerter exerts an inertial force that is proportional to the relative acceleration of its terminals, as represented by equation Eq. 1 (Smith, 2002).

$F=b\left({\ddot{x}}_2-{\ddot{x}}_1\right)(1)$

where $F$ is the inertial force exerted at the terminals, $b$ is the inertance of the inerter, ${\ddot{x}}_1$ and ${\ddot{x}}_2$ are the acceleration of the inerter terminals. The inertance $b$ is the constant of proportionality in this relationship. This quantity carries the unit of mass (Smith, 2002), which enables the inerter to represent a two-terminal mass element (Ma et al., 2021). With this property, the inerter can represent a large apparent mass using a light-weight device. Inerters exhibit negative stiffness behaviour, meaning that the force exerted by inerters assists rather than opposing motion (Ma et al., 2021). This property enables inerters to reduce the natural frequency of mechanical systems (Chen et al., 2014b).

Figure 1

Figure 1. Mechanical network diagram of the inerter.

Inerters can be physically realised by coupling a transmission mechanism to an inertial energy storage mechanism. When a force is applied to the terminals causing relative motion, the transmission mechanism transmits kinetic energy to the inertial energy storage mechanism for storage. When the force is released, the stored energy is then released back to the transmission device, inducing relative motion between the inerter’s terminals in the same direction as the previously applied force.

The rack-and-pinion inerter was the first proposed configuration of the mechanical inerter (Smith, 2002; Papageorgiou et al., 2009). This configuration features a gear rack mated with a gear pinion, which is coupled to a flywheel (as depicted in Figure 2). For the rack-and-pinion inerter, terminal 1 is located on the housing of the device, while terminal 2 is located at the rack that is mated with the pinion. Relative motion between the terminals causes the gear rack-and-pinion (the transmission mechanism) to drive the flywheel (the energy storage mechanism), thus creating the inertance effect. The ideal inertance of a rack-and-pinion inerter can be calculated by Eq. 2.

$b={\eta }^{2}I(2)$

where $b$ is the ideal inertance, $\eta$ is the transmission ratio between the rack and pinion and $I$ is the inertia of the flywheel. Over the years, various other configurations of the inerter were proposed, which include but are not limited to ball screw inerter (Smith, 2020), fluid inerter (Swift et al., 2013), gear pump (hydraulic) inerter (Wang et al., 2011), living hinge inerter (John and Wagg, 2019), electromagnetic inerter (Gonzalez-Buelga et al., 2015b), hydraulic-electric inerter (Shen et al., 2019), and crank inerter (Zhang et al., 2022a). By and large, the ideal inertance of an inerter $b$ can be determined by a function of the transmission parameter $\beta$ and inertial parameter $J$, i.e.,

$b={\beta }^{2}J(3)$

where parameter $\beta$ and $J$ respectively relate to the transmission and energy storage mechanisms of the inerter. Eq. 3 has similarity to the general equation for determining the moment of inertia $I$ of a body about an axis, $I=\int r^{2}dm$ where $dm$ is the infinitesimal mass and $r$ is the radius of gyration between such mass and the axis. In Eq. 3, Parameter $\beta$ is the transmission parameter, which is quadratically proportional to the inertance of an inerter. This parameter can be determined by the characteristics of the transmission mechanism in an inerter, and its value depends on specific inerter configurations. For instance, parameter $\beta$ is the transmission ratio between the rack and pinion in a rack and pinion inerter. With the advancement of compact transmission systems with large ratio such as the 3K planetary reducer (Matsuki et al., 2019), designers can take advantages of the quadratic relationship between $\beta$ and $b$ to maximise the inertance while keeping the system compact and lightweight.

Figure 2

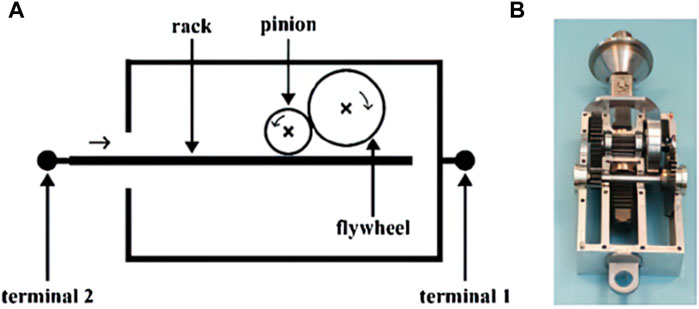
Figure 2. (A) Schematic of the rack-and-pinion inerter; (B) physical prototype of the device (Smith, 2002; Papageorgiou et al., 2009).

Parameter $J$ is the energy storage parameter, which is linearly proportional to the inertance of an inerter. This parameter can be determined by the capability of the energy storage mechanism to store energy, where its value also depends on specific embodiments of the inerter. For example, parameter $J$ can be the inertia of the flywheel in flywheel-based inerters such as the rack and pinion inerter, or the capacitance of the capacitor in an electromagnetic inerter. The value of this parameter generally affects the size and weight of the inerter device. For instance, the inertia of a flywheel is determined by its mass and radius of gyration. Table 1 shows how $\beta$ and $J$ are determined for various configurations of the passive inerter.

Table 1

Table 1. Calculation of $\mathit{\beta }$ and $\mathit{J}$ in various passive inerter configurations.

Realistic devices can only approximate the behaviour of the ideal inerter. Realistic inerter devices must meet specific conditions for accurate behaviour approximations: small physical mass; detachability from physical grounds; specified finite linear travel and adherence to the force-acceleration proportionality when the relative motion of the terminals is reversed (Smith, 2002; Smith, 2020). Inevitable nonlinearities in realistic inerters such as dry friction, viscous damping, backlash, and material compressibility/elasticity can deviate actual performance from ideal models (Wang and Su, 2008; Li et al., 2012; Ma et al., 2021; Chillemi et al., 2023). The deviation between the ideal inertance equation and the actual inertance of inerters was also present (Wen et al., 2017). These nonlinearities negatively affect performance in various inerter applications (Wang and Su, 2008; Brzeski and Perlikowski, 2017; Gonzalez-Buelga et al., 2017).

2.2 Semi-active inerters

Semi-active devices, characterised by controllable characteristic variables, are categorised based on their inherent passivity (Garrido et al., 2018). Inherently passive semi-active devices cannot generate energy, in which the “generated energy” here refers to the energy supplied to their mechanical subsystems by auxiliary actuators (Garrido et al., 2018). Semi-active inerters are inerters that enable active control of their characteristic variable inertance. They are categorised into independently-variable-inertance inerters (IVIIs) and resettable-inertance inerters (RIIs), as shown in Figure 3. IVII-type semi-active inerters offer continuously controllable inertance, while RII-type inerters are inherently passive (Garrido et al., 2019). Unlike IVIIs, RIIs can only increase inertance when the velocity across their terminals is zero and decreases at any time. Therefore, RII-type inerters can be decoupled and stopped to eliminate energy from the system (Garrido et al., 2019).

Figure 3

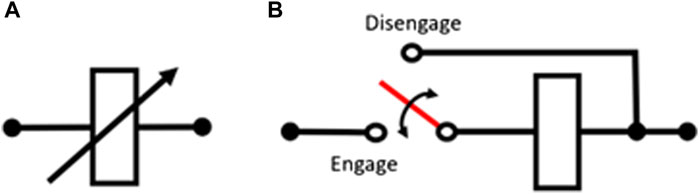
Figure 3. Mechanical network symbols of semi-active inerters (Garrido et al., 2018). Subfigure (A) depicts the IVII, while subfigure (B) depicts the RII.

The research around IVII-type semi-active inerters is more established. From passive inerters, IVII-type semi-active inerters can be derived by incorporating auxiliary mechanisms to actively control inertance, which can involve the control of $\beta$, $J$ or both variables in Eq. 3. IVII-type semi-active inerters exhibit variable negative stiffness behaviour (Ning et al., 2019a). IVII-type semi-active inerters act as adjustable two-terminal mass devices. Along with their variable negative stiffness properties, these semi-active inerters are beneficial for applications that require active control of a system’s natural frequency (Brzeski et al., 2015).

On the other hand, the research around RII-type inerters is still immature. RII-type inerters are embodied by modifying any passive inerter to include mechanisms that actively engage/disengage the inerter from the system and eliminate its energy according to a control law (Garrido et al., 2019). RIIs exhibit negative stiffness behaviour when engaged to systems and dissipate energy when disengaged. They are desirable for their inherent passivity (Garrido et al., 2019), which can be used to realise inherently stable vibration control systems (Garrido et al., 2018). These systems guarantee stability despite errors in control strategies or auxiliary system failures, making them suitable for low-maintenance and educational applications (Garrido et al., 2018).

Semi-active inerters evolved from passive inerters, therefore they inherited nonideal behaviours and nonlinearities from their passive predecessors. Other challenges such as time delays and stability issues have emerged for semi-active inerters when control mechanisms are integrated. Hu et al. (2021a) analysed stability in semi-active inerter-based vibration control systems, revealing potential instability in 1-DOF systems under specific switching state control laws. Their study emphasised that improper control of inertance can induce instability, even when considering inerter nonlinearities. In a subsequent study, Hu et al. (2022) conducted inherent stability analysis for multibody systems with semi-active inerter, identifying conditions for stability by restricting inertance and inertance varying rates within a certain range. From these findings, one must be mindful of potential nonlinearities and stability issues when working with semi-active inerter.

3 Configurations

3.1 Independently-variable-inertance inerters (IVII)

IVII-type semiactive inerters are realised by integrating auxiliary mechanisms to control inertance through the modulation of $\beta$, $J$ or a combination of both parameters in a passive inerter. IVII-type inerters with variable $\beta$ parameter can be realised by integrating mechanisms such as transmission systems with variable ratio, while the subtype with variable $J$ parameter can be realised by employing mechanisms such as the variable inertia flywheel. Since parameter $\beta$ is quadratically proportional to inertance, IVII-type semi-active inerters featuring a controllable $\beta$ parameter would have a larger controllable range of inertance compared to a semi-active inerter with a controllable $J$ parameter, provided that the ranges of controllable parameters in the semi-active inerters are equal. On the other hand, IVII-type semi-active inerters with a controllable $J$ parameter may exhibit better inertance control accuracy due to the constant rate of change of inertance concerning the change in the controllable parameter. To encompass the best traits of both subtypes, IVII-type semi-active inerters where both $\beta$ and $J$ are controllable can be realised by combining the mechanisms used in the former subtypes. Subsections 3.1.1, 3.1.2, and 3.1.3 explore these subtypes of IVII-type semi-active inerters.

3.1.1 IVII-type semi-active inerters featuring controllable $\mathit{\beta }$ parameter

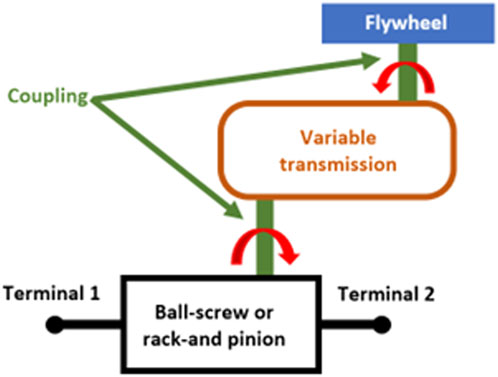
IVIIs derived from flywheel-based passive inerters (such as ball-screw or rack-and-pinion inerters) were integrated with variable transmission mechanisms to control parameter $\beta$. Usually, the input of the variable transmission is coupled to the output of the ball-screw or rack-and-pinion, while the output of the variable transmission is coupled with the flywheel (as shown by Figure 4). By controlling the transmission ratio, the transmission between the translational motion of the inerter’s terminals and the rotation of the flywheel can be altered, which results in inertance control.

Figure 4

Figure 4. Schematic of a typical variable transmission IVII configuration.

Brzeski et al. (2015); Brzeski et al. (2017) proposed an IVII of this type by integrating a continuously variable transmission (CVT) with a rack-and-pinion inerter. Sadeghian et al. (2021) integrated a more compact Continuously Variable Planetary (CVP) transmission device between the ball-screw and flywheel to realise a semi-active ball-screw inerter. Similarly, other researchers have integrated the CVT into their configuration of the flywheel-based IVII (Matsuoka, 2017; Ebrahimnejad and Samani, 2020; Lazarek et al., 2022; Punyakaew, 2022). Apart from CVTs, the parameter $\beta$ of a flywheel-based inerter can be controlled by other means of variable transmission. For example, Tai et al. (2023) presented the “crank train inerter”, where the length of the crank is altered to control the inertance. The incorporation of mechanical variable transmission systems such as CVT, CVP, and planetary variators offers reliable control of inertance for IVII-type semi-active inerters. However, the response time for inertance control relies heavily on the mechanisms used to adjust the transmission ratio. Generally, these mechanisms are mechanically actuated which results in a slower control response time. In addition, nonlinearities and nonideal behaviours associated with the variable transmission systems also present, which may cause unwanted damping effects and deviation from the ideal models.

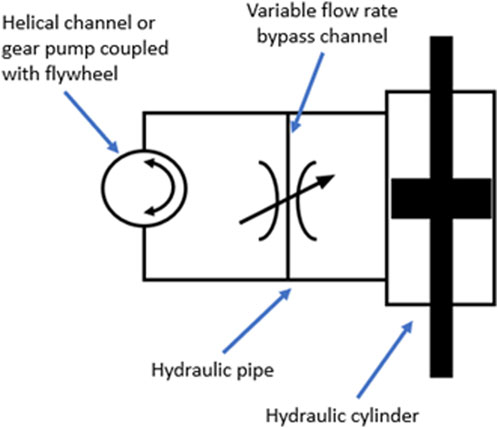
Fluid and hydraulic inerters realise the inertance effect using the flow of fluid and use a hydraulic cylinder to serve as the terminals of the device and drive fluid flow. Fluid inerters utilise the circular motion of a fluid flowing through a helical channel to achieve inertance effect (Swift et al., 2013). On the other hand, hydraulic (gear pump) inerter achieves this by using fluid to drive a hydraulic rotor (Wang et al., 2011). To control parameter $\beta$ for fluid/hydraulic-based IVIIs, one may connect a variable flow rate bypass channel parallel to the hydraulic cylinder and the gear pump or helical channel, as presented in Figure 5. Adjusting the flow rate through the bypass channel controls the flow rate of fluid through the helical channel or the gear pump, resulting in the control of inertance.

Figure 5

Figure 5. Schematic of typical semi-active bypass fluid/hydraulic inerter configuration.

Tipuric et al. (2018); Tipuric et al. (2019) first introduced the concept in their studies, which employs magnetorheological (MR) fluid as the working fluid and a bypass channel with an MR valve to control the inertance. Inspired by this work, Yu et al. (2021) designed a variable bypass gear pump inerter, employing an annular-radial MR valve. In this design, both hydraulic oil and MRF served as working fluids, separated by moveable plates. The working volume around the bypass valve was filled with MR fluid, while the remainder of the working volume was filled with hydraulic oil. Liu et al. (2020a) also adopted the idea of using a bypass channel, but their design only features on-off control, toggling between a high and a low level of inertance. Moreover, one can easily construct a bypass-type semi-active fluid inerter by incorporating a bypass channel with any kind of flow rate control valve.

Fluid or hydraulic inerters are preferred in certain scenarios due to fewer moving parts, less wear, and the ability to handle larger loads compared to mechanical counterparts. However, they present challenges such as higher sealing requirements, exerting larger damping forces (Liu et al., 2022) and susceptibility to unwanted elastic effects often caused by air trapped in the system (Swift et al., 2013; Chillemi et al., 2023). Semi-active inerters derived from passive fluid inerters inherit these undesirable traits. The use of a variable bypass valve to control $\beta$ for a fluid semi-active inerter not only controls inertance but also affects the damping coefficient. This can result in the semi-active inerter behaving more like a variable damper, making it unsuitable for applications requiring purely variable inertance.

3.1.2 IVII-type semi-active inerters featuring controllable $\mathit{J}$ parameter

IVIIs featuring controllable $J$ parameter can be realised by employing variable energy storage mechanisms. For flywheel-based passive inerters (such as ball-screw or gear-pump inerters), their variable inertance counterpart can also be realised by replacing the fixed inertia flywheel with a controllable inertia flywheel. Hu et al. (2016) presented an IVII of this type, employing a controllable inertia flywheel where its inertia can be controlled by controlling the radial position of moveable masses mounted on it. This control is realised by a linkage mechanism actuated by a linear actuator. Therefore, the response time and accuracy in the control of inertance heavily rely on the properties of the linear actuator and its controllers. Figure 6A depicts the schematic of the semi-active inerter presented by the researchers. Similar mechanisms of the controllable inertia flywheel IVII where the radial positions of masses are controlled were also found in published literature (Garrido et al., 2018; Hiramoto and Yamazaki, 2022; Takino and Asai, 2023).

Figure 6

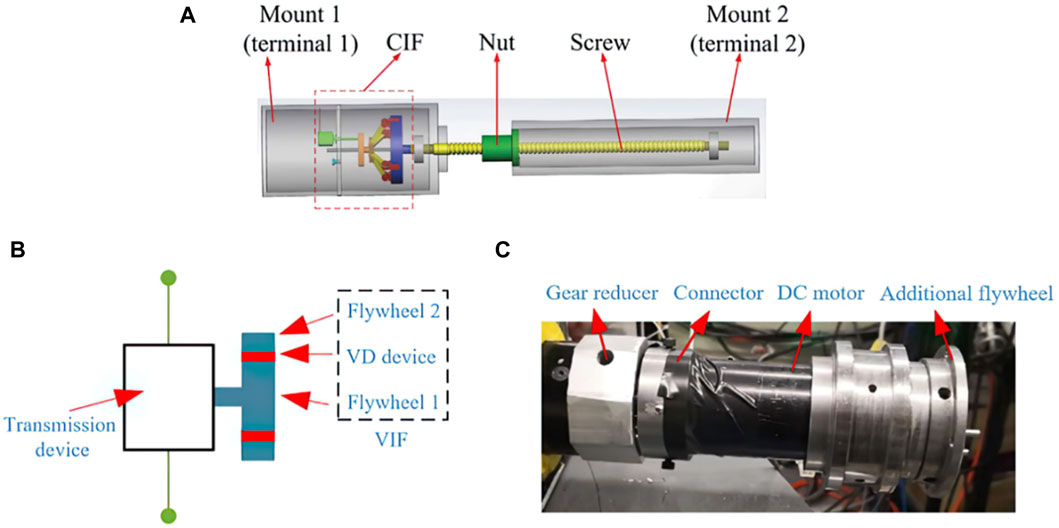
Figure 6. Illustrations of different semi-active inerter configurations equipped with variable inertia flywheels. Subfigure (A): Schematic of the semi-active inerter, Hu et al. (2016); Subfigure (B): Schematic illustrating the semi-active inerter proposed by Ning et al. (2019a); Subfigure (C) experimental prototype of the semi-active inerter, Ning et al. (2019a).

Various other mechanisms have also been proposed to realise the controllable inertia for semi-active inerters. Ning et al. (2019a) implemented an electromagnetic variable damping (VD) mechanism between two concentric flywheels (illustrated by Figure 6B) to adjust the inertia. A prototype was constructed (as depicted in Figure 6C) where a DC motor was utilised as the variable damping mechanism between two flywheels. Similarly, Zhong et al. (2020) integrated a magnetorheological (MR) clutch between concentric flywheels to achieve the same objective. It’s worth noting that the damping-controlled controllable inertia flywheel dissipates some of its rotation energy due to the damping effect between the flywheels. Consequently, this approach of controlling inertance also affects the equivalent damping coefficient of the device, causing the semi-active inerter to function as a combined variable damping and variable inertance device.

Li et al. (2021a) proposed a controllable inertia flywheel that incorporates spring-loaded mechanisms and MR damping. However, controlling the flywheel’s inertia in this design relies on the rotational speed. MATSUOKA and AIZAWA, (2020) introduced a controllable inertia flywheel where inertia can be controlled by altering the dispersion of magnetisable particles within MR fluid, though the range of controllable inertia in this design is limited. Lastly, Tsai and Huang, (2010) presented a device that features controllable equivalent inertia using a magnetic planetary gearbox.

IVII-type inerters with controllable $J$ parameters can also be derived from non-flywheel-based inerters like fluid or electromagnetic inerters. For fluid inerter, $J$ and inertance are actively controlled by adjusting the helical channel length. Zhang et al. (2022b) introduced a semi-active fluid inerter with an “inertance and damping valve” for helical channel length control (Figure 7A). However, controlling inertance may cause disturbances due to hydraulic pressure differences caused by shifting the valve element with force. Electromagnetic inerters can replace the fixed capacitor with a variable capacitor to achieve this inertance control. Hu et al. (2023) presented a “mechatronic inerter” featuring a pulse-width modulation-controlled variable capacitor for quick and independent inertance control (Figure 7B). Yet, the excessive energy consumption of the variable capacitor requires minimisation and power outages may lead to system failure as a continuous power supply is required.

Figure 7

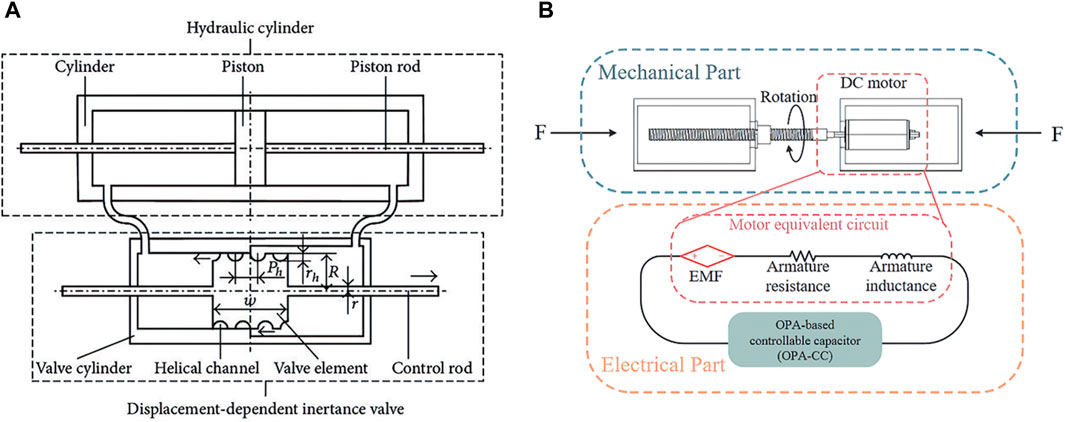
Figure 7. (A) Schematic of the semi-active fluid inerter with displacement-dependent inertance valve; (B) Schematic illustrating the structure of the new mechatronic semi-active inerter, Hu et al. (2023).

3.1.3 IVII-type semi-active inerters featuring combined control of $\mathit{\beta }$ and $\mathit{J}$

More advanced configurations of the IVII can be designed to feature the control of both parameters $\beta$ and $J$. Independently-variable-inertance inerter of this type may have a larger range of controllable inertance as both variables of the ideal inertance equation are actively controlled. It is straightforward to realise an IVII where both parameters are controllable. For example, one may combine the use of continuously variable transmission and controllable inertia flywheel to realise a semi-active rack-and-pinion inerter of this type. In the published literature, Wu et al. have implemented a lever mechanism to improve the controllable inertance range of a flywheel-based semi-active inerter (Wu et al., 2022). Although the lever mechanism was not actively controlled, it can be done by integrating control systems. It is anticipated that more studies featuring configurations of semiactive inerters within this subtype will be published.

3.2 Resettable inertance inerters

Resettable inertance inerters can be developed from any type of passive inerter, as (Garrido et al., 2019) demonstrated in their adaptation from the rack-and-pinion inerter. This configuration employs a clutch to actively engage/disengage the flywheel from the system and a brake to dissipate its energy (illustrated in Figure 8). A similar mechanism can be applied to flywheel-based passive inerters such as ball screw or gear pump (hydraulic) inerter.

Figure 8

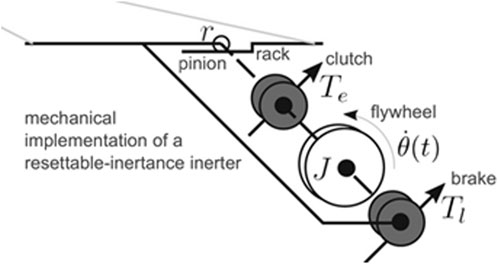
Figure 8. Schematic of the resettable inertance inerter developed from a rack-and-pinion inerter, Garrido et al. (2019).

Fluid or electromagnetic inerters can also be developed into RIIs by the integration of appropriate clutching and braking mechanisms. For fluid inerters, a bypass channel with an on-off flow control valve can be employed to engage/disengage the device, while a flow control valve can be integrated into the helical channel to block the flow and dissipate energy. RIIs can be realised from electromagnetic inerters by incorporating auxiliary mechanisms to disconnect and discharge the capacitor. Smart material technology or electromagnetic damping mechanisms can be employed in the design of these clutching/braking mechanisms to enhance control response and reduce wear. Generators can be enhanced to the RII to facilitate energy harvesting (Garrido et al., 2019). While various ideas exist, no functional prototype of the RII has been presented. Existing devices like the clutching inerter damper (CID) are effective but passive and require two flywheels for bidirectional inertial forces (Makris and Kampas, 2016; Wang and Sun, 2018; Málaga-Chuquitaype et al., 2019). As research on RII-type inerters is preliminary, more studies are expected.

4 Applications of semi-active inerters

The use of semi-active inerters enhances performance in vibration control and energy harvesting applications. In vibration control applications, semi-active inerters are typically employed to manipulate the natural frequency of vibration control systems or to track the desired force, thereby improving vibration attenuation. In energy harvesting applications, these inerters play a crucial role in enhancing the generator’s efficacy in harvesting energy from oscillatory motions, such as waves or vibrations. This section aims to comprehensively review the existing literature on the application of semi-active inerter. In this section, Section 4.1 discusses the research around the applications of semi-active inerters in vibration control, while Section 4.2 analyses the research on the energy harvesting applications of the semi-active inerter.

4.1 Vibration control

Unwanted vibrations are oscillations about an equilibrium point that are detrimental to the performance, longevity, and safety of structures and mechanical systems. Vibration control systems are designed to protect their host structures from these oscillations. These systems are classified into passive, semi-active, and active according to the power generated by their components and the ability to adjust characteristic variables such as mass, spring and stiffness (Karnopp et al., 1974; Garrido et al., 2018). Passive vibration control systems include energy dissipators (ED), dynamic vibration absorbers (DVAs), and vibration isolators (VIs) (Ma et al., 2021).

Inerters are incorporated into structural vibration control systems to enhance their performance. Ma et al. (2021) have demonstrated the advantages of the inerter-based vibration control systems over conventional systems by analysing the equation of motion of a structure with its vibration control system. Suppose we have a n-degree-of-freedom structure, its equation of motion would be (Soong, 1988; Ma et al., 2021):

$\mathit{M}\ddot{\mathit{x}}\left(\mathit{t}\right)+\mathit{C}\dot{\mathit{x}}\left(\mathit{t}\right)+\mathit{K}\mathit{x}\left(\mathit{t}\right)=\mathit{D}{\mathit{f}}_{\mathit{c}}\left(\mathit{t}\right)+\mathit{E}{\mathit{f}}_{\mathit{e}}\left(\mathit{t}\right)(4)$

where $\mathit{M}$, $\mathit{C}$ and $\mathit{K}$ are the mass, damping and stiffness matrices of the structure; $\mathit{x}\left(\mathit{t}\right)$ is the displacement vector of the structure; ${\mathit{f}}_{\mathit{c}}\left(\mathit{t}\right)$ and ${\mathit{f}}_{\mathit{e}}\left(\mathit{t}\right)$ are the vibration control and external force vectors; while $\mathit{D}$ and $\mathit{E}$ are the location matrices of these forces respectively. A conventional vibration control system utilises stiffness and damping components such as dashpots and springs to attenuate structural vibration. An n-degree-of-freedom conventional vibration control system would have its control force represented by (3):

${\mathit{f}}_{\mathit{c}}\left(\mathit{t}\right)={\mathit{C}}_{\mathit{c}}\dot{\mathit{x}}\left(\mathit{t}\right)+{\mathit{K}}_{\mathit{c}}\mathit{x}\left(\mathit{t}\right)+{\mathit{G}}_{\mathit{c}}{\mathit{f}}_{\mathit{e}}\left(\mathit{t}\right)(5)$

where ${\mathit{C}}_{\mathbf{1},\mathit{c}}$ is the damping matrix, ${\mathit{K}}_{\mathbf{1},\mathit{c}}\left(\mathit{t}\right)$ is the stiffness matrix and ${\mathit{G}}_{\mathit{c}}$ is the gain matrices of the external force acting on the control system. An inerter-based vibration control system incorporates the inerter in addition to the stiffness and damping components. The equation of motion of an n-degree-of-freedom inerter-based vibration control system is (Ma et al., 2021):

${\mathit{f}}_{\mathit{c}}\left(\mathit{t}\right)={\mathit{B}}_{\mathit{c}}\ddot{\mathit{x}}\left(\mathit{t}\right)+{\mathit{C}}_{\mathit{c}}\dot{\mathit{x}}\left(\mathit{t}\right)+{\mathit{K}}_{\mathit{c}}\mathit{x}\left(\mathit{t}\right)+{\mathit{G}}_{\mathit{c}}{\mathit{f}}_{\mathit{e}}\left(\mathit{t}\right)(6)$

where $B_c$ is the inertance matrices. To illustrate the advantages of inerter-based vibration control systems over their conventional counterparts, equations Eqs 5, 6 are substituted into equation Eq. 4 to form Eqs 7, 8) respectively. These equations illustrate the equations of motion of n-degree-of-freedom structures with conventional and inerter-based vibration control systems respectively (Ma et al., 2021).

$\mathit{M}\ddot{\mathit{x}}\left(\mathit{t}\right)+\left(\mathit{C}-\mathit{D}{\mathit{C}}_{\mathit{c}}\right)\dot{\mathit{x}}\left(\mathit{t}\right)+\left(\mathit{K}-\mathit{D}{\mathit{K}}_{\mathit{c}}\right)\mathit{x}\left(\mathit{t}\right)=\left(\mathit{E}+\mathit{D}{\mathit{G}}_{\mathit{c}}\right){\mathit{f}}_{\mathit{e}}\left(\mathit{t}\right)(7)$

$\left(\mathit{M}-\mathit{D}{\mathit{B}}_{\mathit{c}}\right)\ddot{\mathit{x}}\left(\mathit{t}\right)+\left(\mathit{C}-\mathit{D}{\mathit{C}}_{\mathit{c}}\right)\dot{\mathit{x}}\left(\mathit{t}\right)+\left(\mathit{K}-\mathit{D}{\mathit{K}}_{\mathit{c}}\right)\mathit{x}\left(\mathit{t}\right)=\left(\mathit{E}+\mathit{D}{\mathit{G}}_{\mathit{c}}\right){\mathit{f}}_{\mathit{e}}\left(\mathit{t}\right)(8)$

According to Eq. 7, the conventional vibration control system only manipulates the damping and stiffness matrices of the structure. As shown by the left-hand side of Eq. 8, inerter-based vibration control system modulates the mass matrix of the structure in addition to the stiffness and damping terms. Therefore, inerter-based vibration control systems can control all the dynamic properties of structures, resulting in better performance (Ma et al., 2021).

A similar argument can be made to justify the use of semiactive inerters within the vibration control systems. Conventional semiactive vibration control systems use devices like variable damping dampers and variable stiffness springs to actively manipulate only the damping and stiffness terms in structures. In contrast, semiactive inerter-based vibration control systems have the additional capability to actively modulate their inertial term for vibration control. Because semi-active inerters share many traits with their passive counterparts, semi-active inerter-based vibration control systems shall be classified similarly. The practical applications of these systems extend to diverse domains, with vehicle suspension and seat suspension being notable examples. Section 4.1 reviews the literature on semi-active inerter-based energy dissipators, dynamic vibration absorbers, and vibration isolators in lower-level subheadings 4.1.1, 4.1.2, and 4.1.3, respectively. Section 4.1.4. Provides an analysis of research focused on the applications of semi-active inerter-based vibration control systems in vehicle and seat suspension.

4.1.1 Energy dissipators (EDs)

Energy dissipators (EDs) safeguard structures by dissipating vibrational kinetic energy into other forms (Ma et al., 2021). Incorporating negative stiffness elements into EDs would enhance motion, which improves energy dissipation and thus vibration suppression performance (Li et al., 2008). Inerters serve as effective negative stiffness components in EDs, with examples like the inertial mass damper (IMD), tuned viscous mass damper (TVMDs) and their variations. An IMD can be realised by connecting an inerter in parallel to a damping component such as a dashpot (Figure 9A) (Ma et al., 2021). A TVMD can be created by placing a tuning spring in series with an IMD (Figure 9B) (Ikago et al., 2012). Variants of these include angular mass dampers (Pradono et al., 2008), gyro-mass dampers (Saitoh, 2012), and clutching inerter dampers (Makris and Kampas, 2016; Wang and Sun, 2018; Málaga-Chuquitaype et al., 2019). Advanced variants such as the electromagnetic inertial mass damper (EIMD) (Zhu et al., 2019) and tuned inertial mass electromagnetic transducer (TIMET) (Asai et al., 2017) can even harvest energy from vibrations using built-in generators.

Figure 9

Figure 9. Mechanical network diagram of (A) Inertial mass damper (Ma et al., 2021) (B) Tuned Viscous Mass Damper (Ikago et al., 2012).

The optimal performance of a TVMD relies on tuning its natural frequency to match that of the host structure, creating resonance for enhanced energy dissipation. Failure to tune this frequency properly can lead to inefficiency or even damage to the structure. Structural vibrations occur at variable frequencies, which indicates the importance of actively tuning the natural frequency of TVMDs. One method to achieve this active control is to replace the passive inerter of the TVMD with an IVII-type semi-active inerter. Sadeghian et al. (2021) integrated a semi-active inerter into a TVMD, creating the “Adaptive Tuned Viscous Mass Damper” (ATVID). Simulations comparing passive control against the ATVMD under sinusoidal excitation demonstrated comparable vibration control performance at the resonance frequency, and the ATVID outperformed the passive system outside this frequency range.

Takino and Asai, (2023) integrated a semi-active inerter into the TIMET, a variant of the TVMD designed for energy harvesting to improve performance. Fast Fourier Transform was implemented to determine the dominant frequency for inertance control; while Static Admittance (SA) and Performance Guaranteed (PG) strategies were used for controlling the current of the electromagnetic transducer. Simulations and experiments under various excitations demonstrated that the semi-active inerter-based TIMET with PG control significantly outperformed passive TIMET in energy harvesting. However, limitations including the time lag of the FFT-based inertance control strategy and issues with the damping components in the mathematical models were noted.

RIIs can function as energy dissipators with the potential for energy harvesting. Garrido et al. (2019) simulated a rack-and-pinion-based RII integrated into a 1-degree-of-freedom host structure, optimising its parameters for energy harvesting. A simple control strategy was developed such that the RII can be engaged to an oscillating system when the relative velocity is zero and disengaged at maximum relative velocity. Their study evaluated RII performance in vibration control, observing force-displacement response under sinusoidal excitation and frequency response in harvested power and structural vibration. The RII exhibited high-frequency oscillations during engagement with the structure due to the high stiffness of its clutching mechanisms. Its energy harvesting capability remained homogenous as the excitation amplitude varied and had a narrow effective frequency range. Simulation results revealed that the RII excelled in vibration control, demonstrating a superior reduction in structure displacement and acceleration at high amplitudes. These findings highlighted the potential of the RIIs and the need for in-depth research into their real-world behaviours and applications.

Applications of the semi-active inerter in energy dissipators have been presented in previous studies. Sadeghian et al. (2021) and Garrido et al. (2019) have shown through simulations that the ATIVD and RII devices can attenuate vibration through energy dissipation. However, their tests were limited to harmonic excitations, and the semi-active inerters lacked comprehensive control strategies. These conditions do not fully replicate the real-world challenges of seismic or weather-induced structural vibrations. In contrast, Takino and Asai (2023) not only used simulations but also validated their results experimentally under sinusoidal and random excitation, leading to more robust conclusions. However, the authors only tested the TIMET’s performance in energy harvesting, omitting its role in vibration control.

4.1.2 Dynamic vibration absorbers (DVAs)

Dynamic Vibration Absorbers (DVAs) attenuate structural vibrations through absorption (Ma et al., 2021), employing an auxiliary inertial member connected to the host structure via connecting elements like springs and dampers (Flannelly, 1967; Roberson, 1952). Tuned Mass Dampers (TMDs) and Tuned Liquid Dampers (TLDs) are common types of DVAs respectively utilising solids and liquids as inertial components (Ma et al., 2021). The optimal performance of DVAs relies on resonance between the natural frequency of the system and host structure (Flannelly, 1967; Roberson, 1952). Improved efficiency is achieved with a large ratio between the auxiliary mass and host structure mass, compromised by the cost of occupiable space and increased construction expenses (Ma et al., 2021). Inerters, integrated into DVAs as coupling members, significantly enhance their vibration control performance (Hu and Chen, 2015). Notable configurations include the Tuned Mass Damper (TMDI) (as presented in Figure 10A) connecting a grounded inerter to the TMD’s auxiliary mass, enhancing mass ratio and thus performance without substantial weight increase (Marian and Giaralis, 2014). The Tuned Inerter Damper (TID), as presented in Figure 10B, innovates further by replacing the TMD’s mass with a grounded inerter, achieving comparable performance to TMD but with significantly reduced weight (Lazar et al., 2014).

Figure 10

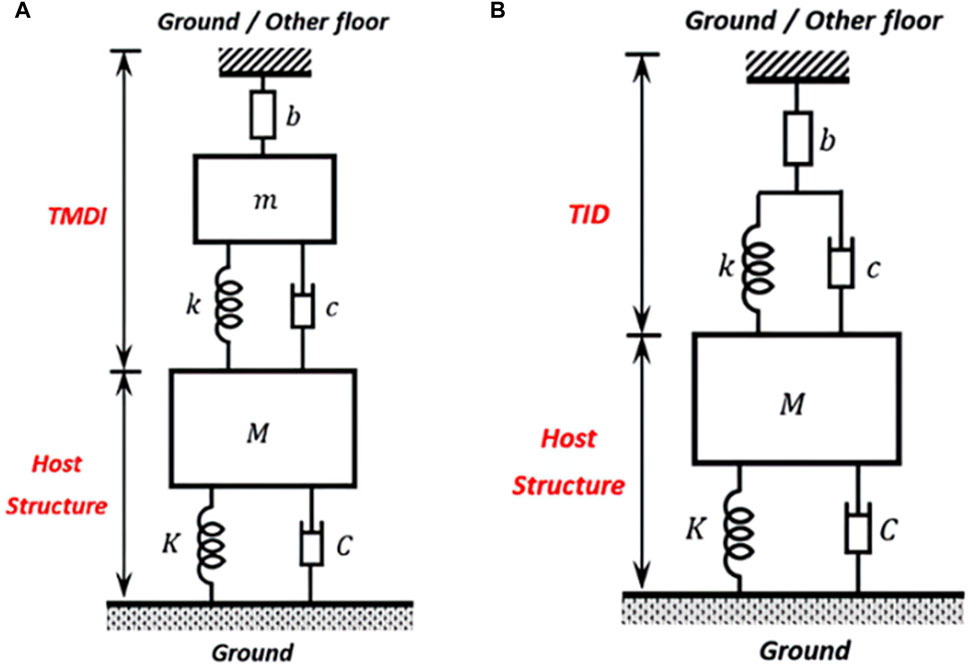
Figure 10. Mechanical network diagrams of (A) Tuned Mass Damper Inerter; (B) Tuned Inerter Damper (Ma et al., 2021).

DVAs have a narrow effective frequency range, which is around the resonance frequency of the host structure that they are tuned to during the design phase. Misalignment between the natural frequencies of DVAs and their host structure can exacerbate structure vibrations (Roberson, 1952; Brzeski et al., 2015). Since structural vibrations can have variable frequencies, it is crucial to extend the effective frequency range of DVAs. To broaden the effective frequency range, solutions like nonlinear springs (Roberson, 1952) or viscous dampers (Den Hartog, 1985) in coupling members are considered, but they compromise performance at the principal resonance frequency (Brzeski et al., 2015). An effective solution involves integrating an IVII-type semi-active inerter to actively control the natural frequency of the DVAs such that it matches with the frequency of excitation. This extends the frequency range without affecting principal resonance frequency performance. Numerous publications have explored the benefits of incorporating this inerter into dynamic vibration absorbers.

Brzeski et al. (2015) integrated a CVT-based IVII-type semi-active inerter into their adaptive TMD, enabling active re-tuning of the natural frequency. This extends the effective frequency range for vibration control without compromising performance at the principal resonance frequency. Simulation results under sinusoidal excitation demonstrated that the adaptive TMD with semi-active inerter effectively attenuated vibration over a wide frequency range. Notably, it achieved significant vibration reduction at the host structure’s resonance frequency. Different configurations of the structure equipped with the adaptive TMD were simulated, where the auxiliary-to-host-structure mass ratio, the inerter’s damping and the structure stiffness were altered. Consistent findings were observed across various structure stiffness properties, eliminating bifurcations in structural displacement caused by nonlinear stiffness (softening and hardening) behaviours of the host structure. Experimental verification by the authors (Brzeski et al., 2017) supported simulation results and validated the mathematical models of the adaptive TMD. Figure 11 presents the experimental setup along with the experimentally determined frequency response of structure displacement of the proposed TMD under sinusoidal excitation. The authors also suggested that increasing the control range of the semi-active inerter would improve the TMD’s performance. Additionally, Brzeski’s group addressed parameter identification (Lazarek et al., 2018) and documented the design and modelling of the belt-drive CVT system for their adaptive TMD (Lazarek et al., 2019). Lazarek et al. (2022), the group also investigated the feasibility of using an off-the-shelf CVT called the “Planetary Variator” for commercial semi-active inerter-based TMD applications.

Figure 11

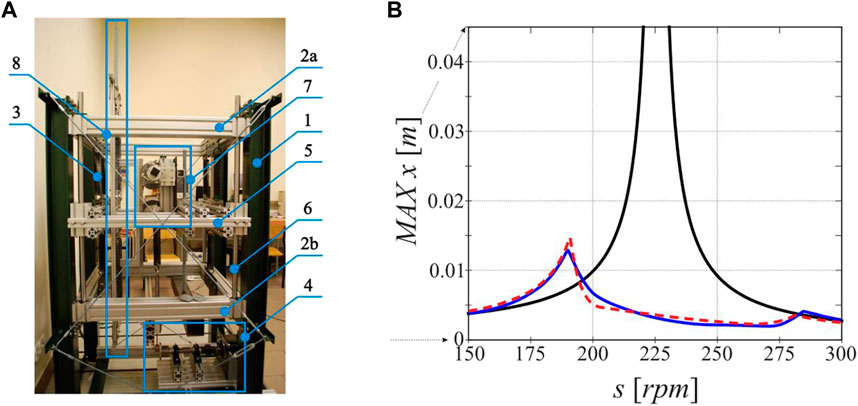
Figure 11. (A) Experimental setup of the semi-active inerter-based tuned mass damper; (B) Experimental and simulated frequency response of the host structure maximum displacement. In subfigure (B), the black curve presents the frequency response of the uncontrolled structure, the blue curve represents simulated results while the dashed red curve represents the experimental results of the novel tuned mass damper. Brzeski et al. (2017).

Aiming to actively control the natural frequency of DVAs, Hu et al. (2016) replaced the passive inerter in a TID with an IVII-type semi-active inerter, introducing the “Semi-active Inerter Adaptive Vibration Absorber” (SIATVA) with an actively controllable natural frequency. Two control methods including frequency-tracker (FT) and phase-detector (PD) were developed to regulate inertance. Experimental results revealed that both methods were effective for the device, though the latter one was more fluctuant. Sadeghian et al. (2022) integrated an IVII-type semi-active inerter as a component of their device, dubbed the “Adaptive Tuned Mass Inerter Damper” (ATMID). Simulations under harmonic excitation at variable frequencies and system properties revealed that the ATMID outperformed the passive controller, with a significant reduction of structure displacement at resonance and superior reduction at other frequencies. Results from Brzeski et al. (2015), Hu et al. (2016), and Sadeghian et al. (2022) have indicated a decrease in the effectiveness of semi-active inerter-based DVA with the increase in parasitic damping coefficient within the inerter. Brzeski et al. (2015) and Sadeghian et al. (2022) found that increasing the mass ratio between the auxiliary mass and the host structure improves DVA performance. Additionally, Sadeghian et al. (2022) indicated that the performance of DVAs can be boosted by increasing the damping coefficient of the host structure.

Several other studies have investigated the use of semi-active inerters in DVAs, exploring a variety of uses and configurations. Punyakaew, (2022) implemented a CVT-based IVII-type semi-active inerter in a DVA, employing a lookup table-based control strategy with Fast Fourier Transform for oscillation frequency measurement. Simulation on a 1-degree-of-freedom structure demonstrated the device’s effectiveness in vibration control across a wide frequency range under varying sinusoidal excitation. Ebrahimnejad and Samani, (2020) developed a semi-active inerter-based Vibration Absorber (IBVA) to mitigate beam vibrations caused by moving loads. Simulations using the Euler-Bernoulli beam model indicated that the IBVA reduced beam vibration by 73% more than a linear DVA with optimised parameters. Despite a longer settling time, the semi-active IBVA showed smaller steady-state beam deflection compared to the linear DVA. Hu et al. (2020) utilised a semi-active inerter to approximate the “Skyhook inerter” configuration, aiming to virtually increase the auxiliary mass of the TMD installed on an offshore wind turbine. Simulations using TurSim data focused on tower deflection and TMD motion, revealing that the ideal skyhook inerter network enhanced vibration control. However, the semi-active inerter approximation offered marginal benefits, suggesting that alternative strategies may offer better control of vibration.

The studies suggest that semi-active inerter-based DVAs offer advantages over their passive counterpart in structure vibration control. They excel in suppressing vibration at resonance frequency and extending the effective frequency range without compromising vibration control effectiveness. To enhance the performance of semi-active inerter-based DVAs, increasing the control range of the semi-active inerter, increasing the mass ratio between the auxiliary system and the structure, reducing internal damping of the semi-active inerter, and boosting the structural damping coefficient are recommended. Notably, it was found that DVAs with semi-active inerters featuring mechanically actuated inertance control tend to have a slower response time, which can be problematic when the excitation frequency fluctuates faster than the system settling time for inertance modulation.

The research on semi-active inerter-based Dynamic Vibration Absorber (DVAs) reveals promising but incompletely explored avenues. While some studies offer experimental validation, most relied on numerical simulations with highly idealised mathematical models that overlooked the nonlinearities and nonideal behaviours of these devices. Sinusoidal excitations, commonly used for testing vibration control systems, provide insights into frequency response but fall short of capturing real-world operating conditions. Control strategy development for semi-active inerters is often deferred, and when explored, is frequently incomplete. This limits the understanding of their transient response and how it affects performance. Concerns about localised damages from localised damage due to excessive control forces in vibration controllers persist, yet studies addressing this issue for semi-active inerter-based DVAs remain unpublished. The majority of studies focused on 1-degree-of-freedom systems, while structural vibrations can happen at multiple degrees of freedom. In addition, there is no research conducted featuring the integration of resettable inertance inerters into DVAs. Despite these limitations, the research signifies the emergence of a promising branch for semi-active inerters in vibration control.

4.1.3 Vibration isolators (VIs)

Structural vibration isolators (VIs) protect their host structures from harsh disturbance by reducing the transmissibility of force and vibration, achieved through shifting the structure’s fundamental frequency away from the dominant excitation frequency (Ma et al., 2021). Comprising a linkage network of stiffness and damping components, VIs suspends their host structures from the surrounding environment and exert vibration control forces to isolate them from external excitations. Linear VIs only effectively isolate vibrations when excitation frequencies exceed $\sqrt{2}$ the structure’s natural frequency, and improper tuning can exacerbate vibrations (Ibrahim, 2008; Ma et al., 2021). To address these challenges, passive inerters can be integrated into VIs.

Historical examples, like the Dynamic Antiresonance Vibration Isolator (DAVI), predated the formal introduction of the inerter and showcased effective vibration isolation through inertial and elastic components (Flannelly, 1967; Wagg, 2021). Figure 12A presents the schematic of the DAVI, along with the frequency response of the host structural displacement (Figure 12B) to illustrate its effectiveness. Subsequent research on inerter-based VIs, following the formal introduction of inerters, has demonstrated their superiority over non-inerter counterparts. For instance, Hu et al. (2015) studied five inerter-based vibration isolation configurations and found that these inerter-based networks outperformed traditional VIs and DVAs with similar mass ratios. Notably, the “parallel-connected inerter” configuration, where the inerter is connected in parallel with a spring and damper between the host structure and the ground, was more attractive (Hu et al., 2015). This configuration widens the effective frequency range and improves vibration isolation at a specific frequency range. As the field progresses, innovations such as inerter-based quasi-zero stiffness VIs (Wang et al., 2020a) or the use of geometrically nonlinear inerters in these systems have emerged (Moraes et al., 2018).

Figure 12

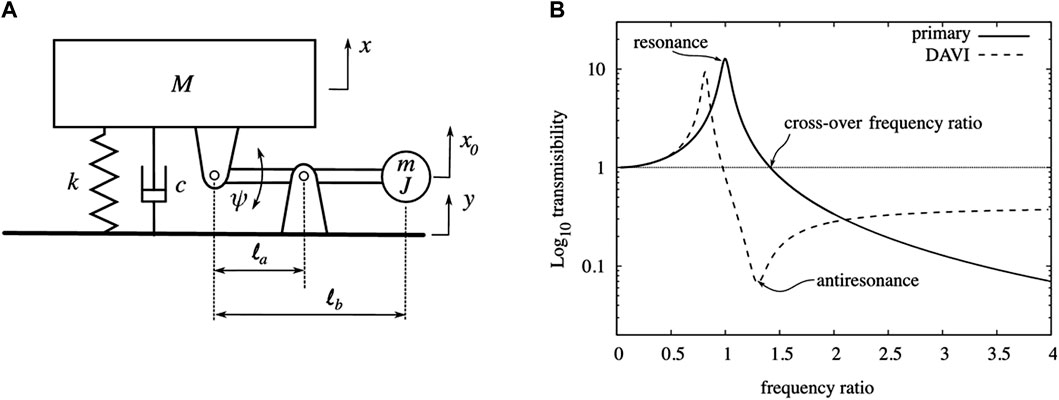
Figure 12. (A) Mechanical network diagram of the Dynamic Anti Resonance Isolator (DAVI); (B) Frequency response of the DAVI, where the dashed line is the response of the DAVI-controlled structure, and the solid line is the response of the uncontrolled structure (Wagg, 2021).

While passive VIs are reliable and inexpensive, they only operate efficiently within a narrow frequency band. Active VIs address the shortcomings of their passive counterparts by using actively controlled actuators to exert prescribed control forces for vibration isolation. However, they are expensive and are notorious for high energy consumption. A compromise between these two is the semi-active VIs, offering improved performance without high energy consumption by featuring semi-active components with actively controllable characteristic parameters. The development of semi-active VIs has seen the integration of semi-active controllers such as variable damping dampers (Karnopp, 1995) and variable stiffness springs (Chen et al., 2022; Jin et al., 2023). With the advent of the semi-active inerter, it has also become an integral component of semi-active VIs.

Various researchers have incorporated the semi-active inerter into structural vibration isolators and studied their performance. Wang et al. (2019) proposed a semi-active inerter-based vibration isolation system where the passive inerter in the “parallel-connected inerter” isolator configuration was replaced with a semi-active inerter. The authors developed the relative-acceleration-relative-velocity (RARV) and relative-acceleration-absolute-velocity (RAAV) control strategies to modulate inertance based on the relative acceleration and relative/absolute velocity between the host structure and the oscillating ground. Simulations conducted using analytical methods demonstrated that the semi-active inerter-based vibration isolator exhibited a broader isolation frequency band and superior reduction in transmissivity and dynamic displacement compared to passive isolators under sinusoidal excitations. Tai et al. (2023) presented a novel “Crank Train Inerter” (CTI) configuration with variable inertance for structural vibration isolation. Simulations and experimental tests showed promising vibration control performance under frequency response tests and in base-isolated structures, with reduced amplitude-frequency response and inter-story drift ratio as well as isolation layer deformations. The CTI was at its preliminary stage of development, thus active control mechanisms for modulating inertance were reserved for future work.

For multiple floor structures, Hiramoto and Yamazaki, (2022) proposed a semi-active inerter-based vibration isolation system to mitigate lateral oscillations. The authors developed a control strategy for the semi-active inerter using LMI-based pole placement method to make the semi-active system perform like its active counterpart. Numerical simulations under seismic excitation showed that the semi-active inerter-based system outperformed the passive inerter-based and active vibration control system, despite a slight increase in first-floor displacement. Wang et al. (2022) introduced a novel semi-active inerter-based vibration isolator to isolate vibrations from the underframe suspended device of a power-decentralised high-speed train. This vibration isolator system features a semi-active inerter and damper configured in the parallel-inerter isolator configuration. A control strategy based on a linear quadratic regulator (LQR) was developed for regulating the inertance and damping coefficient. Simulation results showed that the semi-active inerter-based underframe suspended device excelled in reducing train body vertical accelerations, especially at lower frequencies, thereby offering superior passenger comfort.

Key observations emerged upon reviewing the studies. In general, the integration of the semi-active inerters into vibration isolators significantly improves their performance in vibration isolation. While some studies featured experimental verification, simulation was the primary method for evaluating the performance of semi-active inerter-based vibration isolators, with some simulations relying on idealised models of the semi-active inerter. This raises concerns about the disparity between real-world and simulation results, potentially presenting an overly optimistic view. Another concern is the limited focus on the nonlinearities and nonideal behaviours of semi-active inerters in their control systems, which could deteriorate vibration control performance and introduce stability issues. In addition, all studies revolving around semi-active inerter-based vibration isolators featured the incorporation of independently-variable-inertance inerters. Despite the limitations and shortcomings of current studies, their findings offer a promising start.

4.1.4 Vehicle and seat suspension

Vehicle and seat suspension are one of the practical applications of semi-active inerter-based vibration control systems. These applications have been studied extensively for the past years, given that the inerter was originally invented for vehicle suspension applications.

The vehicle suspension system connects the vehicle’s body to its wheels, allowing relative motion between them (Jazar and Jazar, 2014). It comprises a linkage system of elastic and damping components to exert control forces to isolate vibrations caused by travel surface irregularities to enhance comfort and maintain traction of the vehicle. Key performance indices of these systems include ride comfort, road holding, and suspension deflection, often requiring a design compromise to meet multiple objectives (Gao et al., 2009). The semi-active inerter was applied as a component of semi-active vehicle suspension systems to further enhance their performance. Research in the area has proposed various innovative semi-active inerter-based suspension systems, where control strategies such as active force-tracking (Chen et al., 2014a) and skyhook inerter (Zhang et al., 2018) along with other control strategies have been commonly employed to regulate inertance.

Active force-tracking control strategies are designed for semi-active suspensions to emulate the performance of active suspension systems by minimising the differences between the control forces exerted by active systems and semi-active systems (Chen et al., 2014a). This can be achieved by controlling the characteristic parameters of the semi-active devices such as springs and dampers accordingly. Chen et al. (2014a) introduced the “Semi-active I&D” suspension, integrating a semi-active inerter and a semi-active damper controlled by this control strategy. Simulation results have indicated that the “Semi-active I&D” system outperformed passive systems in ride comfort and road holding. Li et al. (2014) implemented the force-tracking strategy to track the control force of a $H_2$ feedback controlled active system. Through simulations under sinusoidal excitations, the “Semi-active I&D” system demonstrated a reduction of the vehicle body acceleration at the sprung mass’s natural frequency, with small deterioration at the unsprung mass frequency.

The “Skyhook inerter” suspension improves ride comfort by mimicking a loaded vehicle, as a lower sprung mass natural frequency results in improved ride comfort (Zhang et al., 2018). This concept involves connecting a grounded inerter to the sprung mass of the vehicle, mimicking the effect of a loaded vehicle without physically increasing its mass (Hu et al., 2017). Practical implementations of the Skyhook inerter network are impossible due to the nonexistence of a real “sky” grounding point for the inerter. In practice, semi-active inerter-based suspension networks incorporate the inerter between the sprung mass in parallel with other suspension components (as presented by Figure 13), with its inertance controlled by “Skyhook inertance” strategies to emulate the skyhook inerter system.

Figure 13

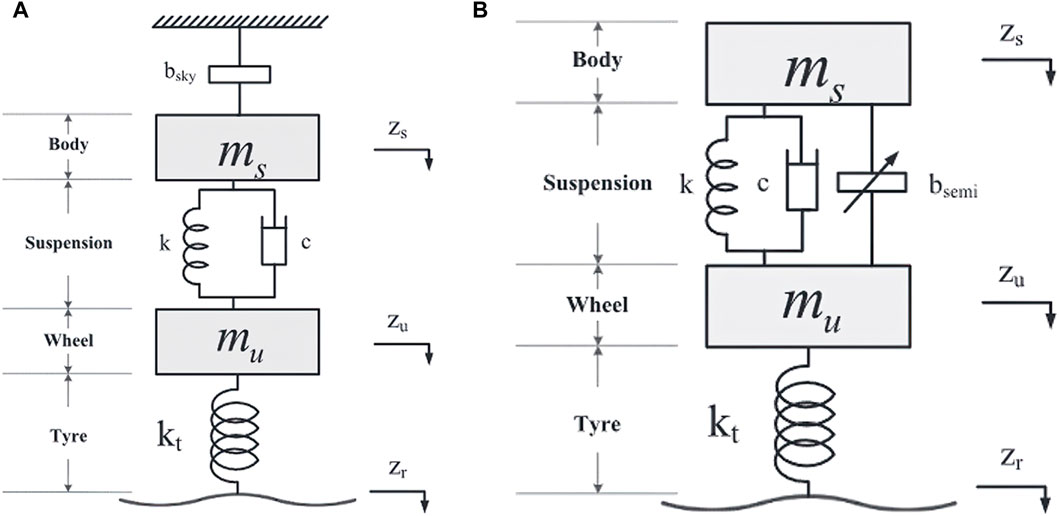
Figure 13. (A) The ideal skyhook inerter vehicle suspension system and (B) its emulation using a semi-active inerter (Hu et al., 2017).

Hu et al. (2017) proposed comfort-oriented skyhook inertance control strategies, with simulation results showing a 10% improvement in ride comfort. However, the authors implemented the ideal model of the semi-active inerter. Zhang et al. (2018) presented a semi-active skyhook inerter suspension with a semi-active fluid inerter. Their quarter car simulation results indicated a reduction of 28.8% in vehicle body acceleration under random road conditions. In their later work, Zhang et al. (2022c) incorporated a semi-active damper to the semi-active Skyhook inerter network, realising the “semi-active double-skyhook” suspension system. Simulations under sinusoidal and random road excitations showed that these semi-active suspensions with double skyhook strategies adapt to road and vehicle loading variations, providing a more constant and comfortable ride compared to single-skyhook and passive suspensions. The independent and damping-based skyhook control strategies favoured ride comfort, while the inertance-based strategies offered a balance between comfort and road holding capacity. Li et al. (2021b) also employed the semi-active damper, realising the semi-active skyhook inerter-spring-damper (ISD) suspension system with innovative control strategies. Via simulations under random excitations, the authors found that combining “Continuous Skyhook” and “Acceleration Driven Damping” control strategies offered superior comfort, reducing sprung mass acceleration by 45.2% compared to passive suspension. However, combinations involving the On-off skyhook control induced chattering oscillations that negatively affected performance.

Other control strategies were also proposed to control semi-active inerter-based vehicle suspension systems. To address the limited high-frequency performance of the skyhook inerter strategies, Wang et al. (2020b) introduced the RARV + - and RARV- + strategies, which were repurposed from the RARV control strategy proposed in their earlier study (Wang et al., 2019). Simulations showed that the RARV + - strategy enhances handling and suspension travel at high frequencies, while the RARV- + improves comfort at all frequencies while sacrificing handling and suspension travel at high frequencies. Fuzzy Proportional Integral Derivative (PID) control strategies, where the PID gains are modulated by a fuzzy algorithm was also implemented for semi-active inerter-based suspension. Li et al. (2021a) implemented this control scheme for controlling the inertance and damping of their “HDMI suspension”, with simulation results showing superior performance in reducing body acceleration and suspension travel.

In addition, research has been conducted on the impact of nonideal behaviours in semi-active inerters on vehicle suspension performance. One prevalent issue encountered in semi-active systems is time delay. Liu et al. (2020b) investigated the stability of a semi-active skyhook-controlled inerter-spring-damper (ISD) suspension considering time delay, revealing that excessive time delay negatively affects the suspension’s performance. Nonetheless, the semi-active ISD suspension still outperformed traditional suspensions. Nonlinearities within passive inerter can hinder inerter-based suspension (Wang and Su, 2008), and this holds for semi-active inerters, given their development from passive predecessors. Liu et al. (2020a) studied how fluid-air mixture in a semi-active inerter affects semi-active skyhook inerter suspension performance. Quarter car simulations under integral white noise road excitation revealed that the fluid-air mixture in a semi-active fluid inerter negatively affects ride comfort, but enhanced suspension working space and dynamic tyre load performance. Nonetheless, the semi-active inerter-based suspension still outperforms traditional suspensions. These findings highlight the importance of not overlooking the nonideal behaviours of semi-active inerters in developing inerter-based suspensions.

Seat suspension systems use components such as dampers, springs, and inerters to exert control forces for isolating the vibrations transmitted from the cabin floor of heavy-duty vehicles to its driver. Unlike vehicle suspension systems, the primary focus of seat suspension systems is to improve ride comfort. Various semi-active inerter-based vehicle seat suspension systems have been explored to enhance comfort and reduce driver fatigue. Ning et al. (2019a) introduced an "Electromagnetic Variable Inertance Device" for seat suspension with $H_{\infty }$ force-tracking control. Figure 14 presents the experimental setup of the semi-active seat suspension, where a GARPEN GSSC7 seat suspension was modified to incorporate the semiactive inerter, along with the bar graphs showing experimental results. Simulations and experiments demonstrated reduced transmissibility under sinusoidal excitation, a 38.8% decrease in Root-Mean-Square (RMS) acceleration, a 35.7% decrease in frequency-weighted RMS acceleration, and a 32% decrease in Vibration Dose Value during random vibration tests. In a subsequent study, Ning et al. (2019b) developed a "Variable Admittance" (VA) device using an MR clutch for inertance control in seat suspension. The results showed a 45.7% reduction in seat acceleration during bump tests and a 43.6% decrease in RMS acceleration during random vibration tests. Despite longer settling times, the VA-based suspension exhibited a 51.8% reduction in vibration dose value, indicating improved comfort.

Figure 14

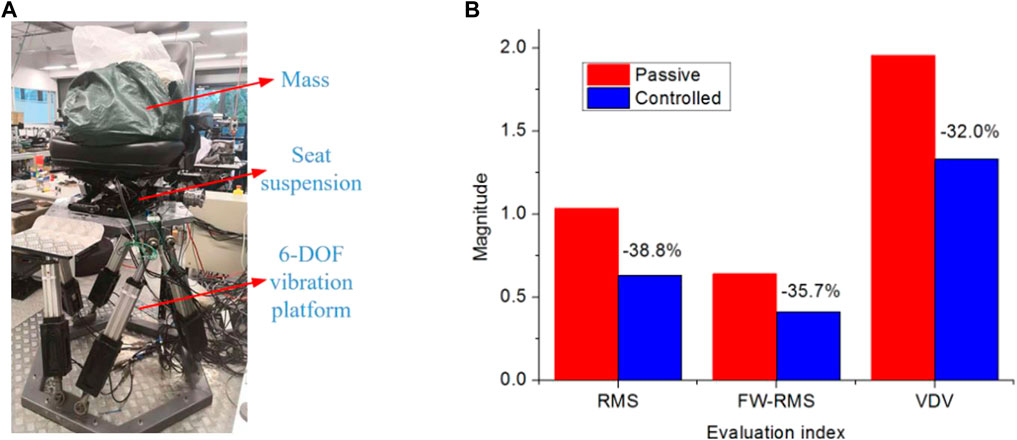
Figure 14. (A) Semi-active seat suspension experimental setup. (B) Performance comparison between semi-active inerter-based (controlled) seat suspension with passive suspension. Column 1 plots the root-mean-square (RMS) seat acceleration, Column 2 plots the frequency-weighted RMS (FW-RMS) seat acceleration, and Column 3 plots the Vibration Dose Value (VDV) (Ning et al., 2019a).

Another development by the authors (Ning et al., 2020) involved a semi-active inerter device with variable damping (VD), variable inertance (VI), and controllable mechanical motion rectifier (CMMR) modes. Seat suspension simulations demonstrated a 39.3% higher vibration reduction in the CMMR mode compared to the VD mode, signifying improved ride comfort. Luan et al. (2023) designed a semi-active inerter-based seat suspension with a "Variable Equivalent Inertance - Variable Damping" device controlled by a force-tracking approach. Sinusoidal and random vibration simulations showed superior performance below 1.5Hz, with a 30.97% reduction in frequency-weighted root-mean-square acceleration and a 29.6% decrease in peak-to-peak acceleration during bump tests. The authors acknowledged the need for further experimental verification of results and the study of time delays.

Research indicates promising benefits from incorporating semi-active inerters into vehicle and seat suspensions across various road conditions. Typically configured in parallel to the spring and damper, these semi-active inerters enhance ride comfort in vehicle suspensions, with up to 45% reduction in sprung mass acceleration reported. These suspension systems primarily improve low-frequency performance, however, control strategies such as RARV can be employed to extend their effective frequency range. In seat suspensions, semi-active inerter-based configurations excel in terms of seat acceleration in various conditions, indicating improved ride comfort. To improve road holding capability in vehicle suspension, semi-active damping can be integrated, as seen in the “Semi-active I&D” suspension with a force-tracking strategy. The inertance-based double-skyhook control strategy strikes an optimal balance between ride comfort and road-holding performance. Despite nonideal behaviours, such as time delay and inerter nonlinearities, semi-active inerter-based suspensions outperform passive counterparts.

The research focusing on semi-active inerter-based suspensions has its limitations. While some studies have incorporated experimental testing of these suspensions, numerical simulations have remained the primary method for performance evaluation. Idealised mathematical models of semi-active inerters have frequently been employed, potentially leading to overly optimistic findings, as experimental results may significantly deviate from simulations. The majority of studies have concentrated on assessing the performance of vehicle suspension systems using the quarter-car model. Although the quarter-car model provides valuable insights, it falls short in representing the vehicle’s practical behaviour by omitting motions such as car body roll and pitch. Limited attention has been given to investigating the nonlinearities and real-life behaviour of these systems. Further research is needed to ensure the real-world applicability of these systems. Additionally, many studies forego discussing the potential drawbacks of semi-active inerter-based suspension systems in comparison to others. These limitations and shortcomings in the current state of the art underscore the need for further studies in the area.

4.2 Energy harvesting

Energy harvesting is the act of harnessing energy from external sources such as solar, thermal, or vibrations to produce electricity (Selvan and Ali, 2016). It plays a crucial role in renewable energy generation, and the development of self-powered systems (Harb, 2011; Liang et al., 2023). Vibration, a significant energy source, can be harvested using transduction mechanisms like electromagnetic, electrostatic, or piezoelectric transducers (Vullers et al., 2009; Harb, 2011). The inerter, an innovation in vibration control, finds applications in energy harvesting. Research has explored the benefits of integrating inerters into energy harvesting systems, with notable studies referenced in Gonzalez-Buelga et al. (2015a); Asai et al. (2017); Petrini et al. (2020); Liu et al. (2021). Optimal vibration energy harvester performance is achieved when the mechanical terminals of their transducers reach maximum oscillation amplitude, which occurs when the mechanical system resonates with the excitation oscillation (Sterken et al., 2004; Vullers et al., 2009). A notable solution to achieve this was proposed by Budar and Falnes’s (Budar and Falnes, 1975), which featured the integration of a semi-active inerter-like device into a wave energy harvester, an approach that predates the formal introduction of inerters by decades. Their design integrated mechanisms that operate a variable-inertia flywheel, whose inertia can be manually adjusted to tune the natural frequency of the energy harvester. The advent of semi-active inerters has further spurred the development of innovative vibration energy harvesters.

Numerous studies have explored the integration of semi-active inerters into energy harvesters, employing various control strategies. A common strategy involves controlling inertance to make the energy harvester resonate with the oscillating excitation frequency. Takino and Asai (Takino and Asai, 2023) applied this to the TIMET energy harvester, utilising Fast Fourier Transform (FFT) and current control method for enhanced energy harvesting. Wave energy harvesters benefit from resonance, as demonstrated by ref (Budar and Falnes, 1975). Nemoto et al. (2022), integrated a semi-active inerter into a point absorber (PA) for natural frequency tuning to pursue resonance. The mechanical network schematic of such a system is illustrated in Figure 15. The authors employed control strategies combining FFT and static admittance. Simulation results showed that the semi-active inerter-based PA outperformed passive variants, especially with frequent FFT updates. Hua et al. (2020) simulated the performance of a two-body PA (TBPA) featuring semi-active inerter to pursue resonance. Their results show that the semi-active inerter-based TBPA achieved a 696% increase in harvested power for regular waves and 746.33% for irregular waves. Similarly, Wang et al. (2020c) showed that employing the semi-active inerter improved the performance of a TBPA, particularly when tuning the lower float to resonate with low-frequency waves under low generator damping.

Figure 15

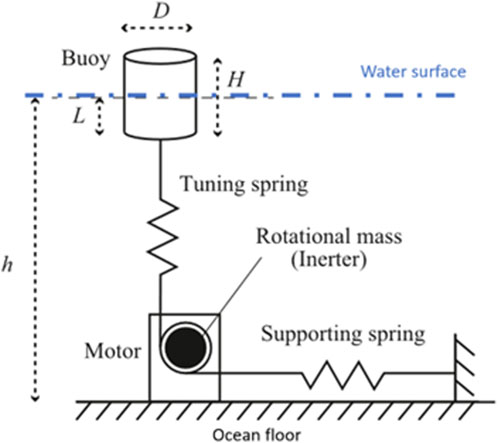
Figure 15. Mechanical network schematic of the semi-active inerter-based point absorber for wave energy harvesting (Nemoto et al., 2022).

Apart from pursuing resonance, other control methods have been proposed for semi-active inerter-based energy harvesters. The force-tracking control strategy commonly found in vibration isolators and vehicle suspension applications can also be employed for energy harvesting applications. Hu et al. (2021b) investigated a two-body PA WEC featuring a semi-active inerter controlled by the force-tracking strategy to enhance performance. An active full-state feedback control strategy with optimised power absorption was developed. Here, the control force determined by the active strategy was to be tracked by the semi-active inerter. Numerical simulations under regular and irregular waves showed that the proposed two-body point absorber enhanced power absorption by 107.42% for the linear time-invariant system and 335.87% for the linear time-varying system. Resettable inertance inerters (RIIs) are technically semi-active inerter-based energy harvesting systems. Garrido et al. (2019) studied the potential of RIIs in energy harvesting. A simple control strategy was developed such that the RII can be engaged to an oscillating system when the relative velocity is zero and disengaged at maximum relative velocity. Discussion about resettable-inertance inerters can be referred back to Sections 3.2, 4.1.2 of this article, with findings showing enhanced energy harvesting capability compared to passive systems.

The integration of semi-active inerters into energy harvesting systems has emerged as a game-changing innovation, indicating a significant development in the field of renewable energy generation. This integration aids in enhancing the efficiency of green energy and reducing dependency on fossil fuels. Studies documented in published literature have reported a substantial improvement in energy harvesting performance with the integration of semi-active inerters into the system, with some results showing up to a 746% increase in harvested power compared to traditional systems (Wang et al., 2020c). It is commonly found that semi-active inerters are more suitable for low-frequency vibration energy harvesting applications, as simulation testing under these conditions tends to yield the most improvement in harvested power. Regarding inertance control strategies, the resonance-pursuing strategy offers superior energy harvesting performance. Variants of this strategy tend to result in better improvements compared to strategies such as force-tracking control.

Critical observations can be identified by synthesising methodologies and findings from related studies. Most studies employed simulations to assess energy harvester performance, with Takino and Asai (Takino and Asai, 2023) being an exception, conducting experimental validation to verify theoretical results. This raise concerns as conclusions drawn solely from simulated results may be overly optimistic if they significantly differ from experimental outcomes. Many authors assume the semi-active inerter is an ideal, zero-order system in simulations, potentially leading to significant differences between experimental and simulated results if the system is experimentally validated. However, Takino and Asai, (2023) demonstrated a small discrepancy between simulated and experimental results, which enhanced confidence in their simulated results. Despite these limitations, the findings offer a promising start, recognising the early stages of semi-active inerter and their applications in energy harvesting.

5 Research opportunities

Section 5 explores various research opportunities arising from the review of semi-active inerter. It addresses common limitations in the state of the art, discusses opportunities and explore applications in vibration control and energy harvesting, and examined the prospect of commercial viability. The section begins by highlighting the need for more experimental research, as there is currently an overrepresentation of simulation studies in the area of semi-active inerters. It also suggests focusing on resettable-inertance inerter (RIIs) alongside independently-variable-inertance inerters (IVIIs) to bridge the gap in research. Secondly, the section proposes developing a near-ideal physical embodiment of the IVII, aiming for more responsive control mechanisms with less nonlinearities, employing smart material technologies such as electrorheological or magnetorheological technologies. Thirdly, the section explores the opportunities in the vibration control and energy harvesting applications. Regarding vibration control, it emphasises the need for further research in these areas, including the integration of semi-active inerters into existing systems. With respect to energy harvesting, there is a potential to explore applications, such as miniature semi-active inerters for self-powered systems. The section concludes with highlighting the important of considering the commercial viability of semi-active inerters. Once the technical aspects are well established, future studies should focus on safety, reliability, maintenance, cost and market integration.

5.1 Addressing common limitations in semi-active inerter research

Reviewing the research on semi-active inerters has unveiled promising opportunities in this field. This section delves into research opportunities concerning the configurations of semi-active inerters and their applications in vibration control and energy harvesting. Throughout the subheadings covered in this article, a notable gap in the research on semi-active inerters has become apparent – specifically, the overrepresentation of simulation studies and a lack of experimental research. This imbalance may potentially result in overly optimistic findings in the studies within the field. Consequently, there is an urgent need for more experimental studies, particularly those involving the exposure of the semi-active inerters, or systems based on them to real-world scenarios such as seismic excitation. In addition, studies featuring independently-variable-inertance inerters (IVIIs) are more prevalent in the research around semi-active inerters compared to resettable-inertance inerters (RIIs). Therefore, future research in the area should delve into studying the performance and application of RIIs in greater depth.

5.2 Configurations of semi-active inerters

Addressing research challenges and opportunities around the configurations of semi-active inerters may involve developing a near-ideal physical embodiment of the IVII. This embodiment should ideally employ a more responsive control mechanism while being subject to fewer nonlinearities (such as parasitic damping) compared to its counterparts. Many studies on semi-active inerters have shown promising results using ideal models of the semi-active inerter. Therefore, creating a near-ideal semi-active inerter could bridge the gap between these findings and practical applications. Implementing strategies such as parameter optimisation can aid in refining the design of such devices.

Another path for future research is the integration of smart material technologies into the design of innovative semi-active inerter configurations. Mechanisms involving smart materials with actively controllable mechanical properties, such as electrorheological (Halsey, 1992) or magnetorheological (De Vicente et al., 2011) fluids could enhance the development of the semi-active inerters. It is anticipated that more embodiments of the IVII and the resettable-inertance inerter (RII) will emerge in the coming years. Additionally, active inerters, realised by actively controlled actuators, can be developed to provide variable inertance devices with superior performance. The concept of the active inerter has not been published in existing literature. In an active inerter, an acceleration sensor measures the relative acceleration of its terminals. A built-in control algorithm of these active inerter then calculates the output force according to instantaneous acceleration data and inertance before sending control signal to the actuator for exerting the inertial force. The inertance of these inerters can be varied by altering the “inertance” as an input variable to the control algorithm. These inerters may offer quick inertance control responses and accurately regulated inertial forces for vibration control, with the expense of a more complicated design and high energy consumption. Such “active inerters” can find applications in advanced vibration control scenarios where expensive design and high energy usage are tolerable.

5.3 Vibration control applications

Applications of semi-active inerters in vibration control include energy dissipators, dynamic vibration absorbers, and isolators. A review of research in semi-active inerter-based structural vibration control systems reveals opportunities in each of these subtypes. A common limitation across studies related to vibration control applications of semi-active inerters is the lack of research in multiple degree-of-freedom scenarios. The fact that structural vibrations act on multiple degrees of freedom indicates an opportunity for more studies where inerter-based vibration control systems are examined in multiple degree-of-freedom scenarios. Future research should also investigate the effect of nonlinearities and the transient response of semi-active inerters on the performance of semi-active inerter-based vibration control, as this is also lacking in current research.

The benefits of integrating semi-active inerters into energy dissipators are evident. However, research in this field is still growing, and the number of publications is limited. There is considerable research potential, especially in applying the RIIs for vibration control and energy harvesting. As of now, working RII prototypes designed for seismic or random disturbances are untested. Additionally, there is a need to explore more applications of the semi-active inerter in the domain of energy dissipators. A promising start could be looking at energy dissipators that require accurate tuning of their natural frequencies and incorporating semi-active inerters into those systems.

Regarding Dynamic Vibration Absorbers (DVAs), there are opportunities for research featuring an in-depth evaluation of the control systems for semi-active inerter-based DVAs. Publications featuring semi-active inerter-based DVAs only studied the effect of incorporating IVII-type semi-active inerters. Therefore, it would be a notable contribution to incorporate the resettable-inertance inerter as a component of DVAs to either improve vibration control or introduce energy harvesting. The semi-active inerter has been extensively incorporated into DVAs resembling the Tuned Mass Dampers, but studies regarding its applications in other types of DVAs are yet to be published, presenting another research opportunity. Finally, research featuring the comparison between semi-active inerter-based DVA against other innovative solutions in structural vibration control can be conducted. This will enable further understanding of semi-active inerter-based DVA and allow engineers to make more informed decisions when designing these systems.

Reviewing the research around semi-active inerter-based vibration isolators revealed several opportunities for future studies. There is a need for more innovative solutions related to semi-active inerter-based building vibration isolators. A promising start would involve integrating the semi-active inerter into established configurations of inerter-based vibration isolators, such as those presented by (3). The semi-active inerter can be integrated to supplement the performance of semi-active isolators featuring semi-active dampers and springs by providing more comprehensive control of vibration. Innovative control strategies, such as those utilising learning-based models can be used. Such a strategy has been implemented for controlling MR elastomer vibration isolators to address issues related to the nonlinearities and hysteresis behaviour of the smart material (Gu et al., 2017).

The research around semi-active inerter-based vehicle and seat suspension also presents opportunities for further explorations. Tailoring semi-active inerter-based suspensions to specific vehicle makes and models holds potential benefits. Testing these customised systems on actual vehicles as case studies would offer insights closest to real-world scenarios. In addition, there is a need for studies to compare the performance of different control strategies, all tailored to a suspension system with the same specifications. These studies would enable engineers to gain deeper insights to inform their designs.

Another promising research avenue involves investigating the effect of nonlinearities and nonideal factors in semi-active inerters on the performance of vibration control systems. This approach allows for studying how these systems perform in real-world settings. While a few studies, such as (Liu et al., 2020a; Liu et al., 2020b), have previously addressed this topic, more research in this area is required to consolidate the findings. Furthermore, innovative solutions such as integrating continuously variable stiffness devices like magnetorheological elastomers or electromagnetic springs can be developed. The theory of vibration control in mechanical systems revolves around the inertial, damping, and stiffness properties of structures (Ma et al., 2021). Therefore, combining variable stiffness devices along with the semi-active inerter and damper can result in a more comprehensive control of vibration and enhanced suspension performance.

5.4 Energy harvesting applications

Research on semi-active inerter-based energy harvesters has predominantly centred around renewable energy generation, with various control strategies being explored. However, this article might not have captured all the potential inertance control strategies that are tailored for energy harvesting. Regarding control strategies, there is an opportunity to conduct studies comparing the performance of different inertance control strategies for energy harvesters. This would provide helpful insights for designers who develop these systems. Since renewable energy generation is just one of many applications of energy harvesting technologies, there is an opportunity to incorporate the semi-active inerter in numerous other energy harvesting applications. A miniature version of the semi-active inerters for energy harvesters in self-powered systems such as robots and biomedical implants can be an interesting path for further advancements. The lack of studies around resettable-inertance inerters has left most of their potentials, characteristics, and shortcomings in energy harvesting undiscovered by research. This opened opportunities for aspiring researchers.

5.5 Commercial viability of semi–active inerters

The nascent state of research on semi–active inerters and their applications means that the primary focus is on their technical performance. Once the technical aspects of semi–active inerter–based applications have been well established by research, the focus should be shifted to their commercial uses. Subsequent studies should delve into the safety, reliability, maintenance, and cost of these systems. In addition, user experience and acceptance of semi–active inerter–based systems should also be studied. It is essential to ensure that semi–active inerter–based systems are not just technologically superior, but also ready for integration into the market.

6 Conclusion

The significance of semi-active inerter in enhancing the performance of mechanical systems has been demonstrated in this literature review. Inerters, which generate forces proportional to the relative acceleration between their terminals, have witnessed innovative augmentation through the introduction of semi-active inerters. Controlled by auxiliary systems, semi-active inerters can actively adjust their inertance. Semi-active inerters are classified into the inherently passive resettable-inertance inerters (RII) and the non-inherently passive independently-variable-inertance inerters (IVII). A diverse variety of physical embodiments of the semi-active inerter were presented, spanning from variable inertia flywheels to operational amplifier-based variable capacitors for the IVII category; and the integration of active clutching and braking mechanisms for the RII-type inerters.

Research has showcased their beneficial applications in areas such as vibration control, and energy harvesting. In general, the integration of semi-active inerters has resulted in superior performance over traditional methodologies. Despite these advancements, the overrepresentation of simulation-based studies in current literature underscores a need for empirical research. Future studies should delve deeper into the nonlinearities and nonideal behaviours of semi-active inerters, exploring their influence on system performance. The nascent state of research around semi-active inerters and their applications underscore the need for more innovations. Potential advancements could include the development of near-ideal semi-active inerters, the integration of intelligent control strategies, or the discovery of new applications of the semi-active inerter. Such innovations would greatly enrich our understanding of the field. As the technical facets of semi-active inerters and their application become matured, the focus must be shifted to studying their commercial viability before the semi-active inerters can be utilised in industries.

Author contributions

KT: Writing–original draft. SJ: Writing–review and editing. LD: Writing–review and editing. HD: Supervision, Writing–review and editing. HQ: Supervision, Writing–review and editing. WL: Supervision, Writing–review and editing.

Funding

The authors acknowledge the financial support provided by the Australian Government Research Training Program (AGRTP) scholarship and Australian Research Council (ARC) Linkage Grant under grant number LP210301054.

Acknowledgments

The authors acknowledged the use of Open AI GPT-3.5 language model for translating foreign journal articles to English, as well as editing the article to meet conciseness and English language requirements.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The author(s) declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Asai, T., Araki, Y., and Ikago, K. (2017). Energy harvesting potential of tuned inertial mass electromagnetic transducers. Mech. Syst. Signal Process. 84, 659–672. doi:10.1016/j.ymssp.2016.07.048

CrossRef Full Text | Google Scholar

Brzeski, P., Kapitaniak, T., and Perlikowski, P. (2015). Novel type of tuned mass damper with inerter which enables changes of inertance. J. Sound Vib. 349, 56–66. doi:10.1016/j.jsv.2015.03.035

CrossRef Full Text | Google Scholar

Brzeski, P., Lazarek, M., and Perlikowski, P. (2017). Experimental study of the novel tuned mass damper with inerter which enables changes of inertance. J. Sound Vib. 404, 47–57. doi:10.1016/j.jsv.2017.05.034

CrossRef Full Text | Google Scholar

Brzeski, P., and Perlikowski, P. (2017). Effects of play and inerter nonlinearities on the performance of tuned mass damper. Nonlinear Dyn. 88, 1027–1041. doi:10.1007/s11071-016-3292-1

CrossRef Full Text | Google Scholar

Budar, K., and Falnes, J. (1975). A resonant point absorber of ocean-wave power. Nature 256 (5517), 478–479. doi:10.1038/256478a0

CrossRef Full Text | Google Scholar

Chen, M. Z., Hu, Y., Huang, L., and Chen, G. (2014b). Influence of inerter on natural frequencies of vibration systems. J. Sound Vib. 333 (7), 1874–1887. doi:10.1016/j.jsv.2013.11.025

CrossRef Full Text | Google Scholar

Chen, M. Z., Hu, Y., Li, C., and Chen, G. (2014a). Semi-active suspension with semi-active inerter and semi-active damper. IFAC Proc. Vol. 47 (3), 11225–11230. doi:10.3182/20140824-6-za-1003.00138

CrossRef Full Text | Google Scholar

Chen, Z., Sun, S., Deng, L., Yang, J., Zhang, S., Du, H., et al. (2022). Investigation of a new metamaterial magnetorheological elastomer isolator with tunable vibration bandgaps. Mech. Syst. Signal Process. 170, 108806. doi:10.1016/j.ymssp.2022.108806

CrossRef Full Text | Google Scholar

Chillemi, M., Furtmüller, T., Adam, C., and Pirrotta, A. (2023). Nonlinear mechanical model of a fluid inerter. Mech. Syst. Signal Process. 188, 109986. doi:10.1016/j.ymssp.2022.109986

CrossRef Full Text | Google Scholar

Den Hartog, J. P. (1985). Mechanical vibrations. Taiwan: Dover Publications.

Google Scholar

A. de Souza Pippi, S. M. Avila, and G. Doz (2022). A review on the use of the inerter device in the structural coupling technique for adjacent building vibration control. Structures (Elsevier).

Google Scholar

De Vicente, J., Klingenberg, D. J., and Hidalgo-Alvarez, R. (2011). Magnetorheological fluids: a review. Soft matter 7 (8), 3701–3710. doi:10.1039/c0sm01221a

CrossRef Full Text | Google Scholar

Dogan, H., Sims, N. D., and Wagg, D. J. (2019). “Investigation of the inerter-based dynamic vibration absorber for machining chatter suppression,” in Journal of Physics: Conference Series. (IOP Publishing).

CrossRef Full Text | Google Scholar

Ebrahimnejad, R., and Samani, F. S. (2020). Novel inerter-based absorbers for suppressing beams vibration under successive moving loads. SN Appl. Sci. 2, 1791–1799. doi:10.1007/s42452-020-03566-5

CrossRef Full Text | Google Scholar

Evangelou, S., Limebeer, D. J., Sharp, R. S., and Smith, M. C. (2007). Mechanical steering compensators for high-performance motorcycles. J. Appl. Mech. 74 (2), 332–346. doi:10.1115/1.2198547

CrossRef Full Text | Google Scholar

Flannelly, W. G. (1967). Dynamic antiresonant vibration isolator. United States: U.S. Patent and Trademark Office.

Google Scholar

Gao, H., Sun, W., and Shi, P. (2009). Robust sampled-data H_∞ control for vehicle active suspension systems. IEEE Trans. control Syst. Technol. 18 (1), 238–245. doi:10.1109/tcst.2009.2015653

CrossRef Full Text | Google Scholar

Garrido, H., Curadelli, O., and Ambrosini, D. (2018). On the assumed inherent stability of semi-active control systems. Eng. Struct. 159, 286–298. doi:10.1016/j.engstruct.2018.01.009

CrossRef Full Text | Google Scholar

Garrido, H., Curadelli, O., and Ambrosini, D. (2019). Resettable-inertance inerter: a semiactive control device for energy absorption. Struct. Control Health Monit. 26 (11), e2415. doi:10.1002/stc.2415

CrossRef Full Text | Google Scholar

Gonzalez-Buelga, A., Clare, L., Neild, S., Burrow, S., and Inman, D. (2015a). An electromagnetic vibration absorber with harvesting and tuning capabilities. Struct. Control Health Monit. 22 (11), 1359–1372. doi:10.1002/stc.1748

CrossRef Full Text | Google Scholar

Gonzalez-Buelga, A., Clare, L. R., Neild, S. A., Jiang, J. Z., and Inman, D. J. (2015b). An electromagnetic inerter-based vibration suppression device. Smart Mater. Struct. 24 (5), 055015. doi:10.1088/0964-1726/24/5/055015

CrossRef Full Text | Google Scholar

Gonzalez-Buelga, A., Lazar, I. F., Jiang, J. Z., Neild, S. A., and Inman, D. J. (2017). Assessing the effect of nonlinearities on the performance of a tuned inerter damper. Struct. Control Health Monit. 24 (3), e1879. doi:10.1002/stc.1879

CrossRef Full Text | Google Scholar

Gu, X., Yu, Y., Li, J., and Li, Y. (2017). Semi-active control of magnetorheological elastomer base isolation system utilising learning-based inverse model. J. Sound Vib. 406, 346–362. doi:10.1016/j.jsv.2017.06.023

CrossRef Full Text | Google Scholar

Halsey, T. C. (1992). Electrorheological fluids. Science 258 (5083), 761–766. doi:10.1126/science.258.5083.761

PubMed Abstract | CrossRef Full Text | Google Scholar

Harb, A. (2011). Energy harvesting: state-of-the-art. Renew. Energy 36 (10), 2641–2654. doi:10.1016/j.renene.2010.06.014

CrossRef Full Text | Google Scholar

Hiramoto, K., and Yamazaki, I. (2022). Semi-active vibration control of structural systems with a variable inerter. IFAC-PapersOnLine. 55 (27), 230–235. doi:10.1016/j.ifacol.2022.10.517

CrossRef Full Text | Google Scholar

Hu, Y., and Chen, M. Z. (2015). Performance evaluation for inerter-based dynamic vibration absorbers. Int. J. Mech. Sci. 99, 297–307. doi:10.1016/j.ijmecsci.2015.06.003

CrossRef Full Text | Google Scholar

Hu, Y., Chen, M. Z., Shu, Z., and Huang, L. (2015). Analysis and optimisation for inerter-based isolators via fixed-point theory and algebraic solution. J. sound Vib. 346, 17–36. doi:10.1016/j.jsv.2015.02.041

CrossRef Full Text | Google Scholar

Hu, Y., Chen, M. Z., and Sun, Y. (2017). Comfort-oriented vehicle suspension design with skyhook inerter configuration. J. Sound Vib. 405, 34–47. doi:10.1016/j.jsv.2017.05.036

CrossRef Full Text | Google Scholar

Hu, Y., Chen, M. Z., Xu, S., and Liu, Y. (2016). Semiactive inerter and its application in adaptive tuned vibration absorbers. IEEE Trans. Control Syst. Technol. 25 (1), 294–300. doi:10.1109/tcst.2016.2552460

CrossRef Full Text | Google Scholar

Hu, Y., Cheng, C., Li, J., Chen, M. Z., and Du, H. (2023). Design and experimental analysis of an operational amplifier circuit based mechatronic semi-active inerter. IEEE Trans. Industrial Electron. 71, 3915–3923. doi:10.1109/tie.2023.3273263

CrossRef Full Text | Google Scholar

Hu, Y., Hua, T., Chen, M. Z., Shi, S., and Sun, Y. (2021a). Instability analysis for semi-active control systems with semi-active inerters. Nonlinear Dyn. 105 (1), 99–112. doi:10.1007/s11071-021-06555-4

CrossRef Full Text | Google Scholar

Hu, Y., Hua, T., Chen, M. Z., Shi, S., and Sun, Y. (2021b). Application of semi-active inerter in a two-body point absorber via force tracking. Trans. Inst. Meas. Control 43 (12), 2809–2817. doi:10.1177/01423312211009374

CrossRef Full Text | Google Scholar

Hu, Y., Hua, T., Chen, M. Z., Shi, S., and Sun, Y. (2022). Inherent stability analysis for multibody systems with semi-active inerters. J. Sound Vib. 535, 117073. doi:10.1016/j.jsv.2022.117073

CrossRef Full Text | Google Scholar

Hua, T., Hu, Y., and Chen, M. Z. (2020). “Dimensionless analysis on the wave energy conversion of a semi-active inerter-based two-body point absorber,” in 2020 Chinese Automation Congress (CAC). (IEEE).

CrossRef Full Text | Google Scholar

Hu, Y., Wang, J., Wang, Z., and Chen, M. Z. (2020). “Structural control for a barge-type floating offshore wind turbine with a skyhook inerter configuration,” in 2020 Chinese Control And Decision Conference (CCDC). (IEEE).

CrossRef Full Text | Google Scholar

Ibrahim, R. (2008). Recent advances in nonlinear passive vibration isolators. J. sound Vib. 314 (3-5), 371–452. doi:10.1016/j.jsv.2008.01.014

CrossRef Full Text | Google Scholar

Ikago, K., Sugimura, Y., Saito, K., and Inoue, N. (2012). Modal response characteristics of a multiple-degree-of-freedom structure incorporated with tuned viscous mass dampers. J. Asian Archit. Build. Eng. 11 (2), 375–382. doi:10.3130/jaabe.11.375

CrossRef Full Text | Google Scholar

Jazar, R. N. (2014). Suspension mechanisms. Vehicle Dynamics: Theory and Application, 497–565.

CrossRef Full Text | Google Scholar

Jin, S., Yang, J., Sun, S., Deng, L., Chen, Z., Gong, L., et al. (2023). Magnetorheological elastomer base isolation in civil engineering: a review. J. Infrastructure Intell. Resil. 2, 100039. doi:10.1016/j.iintel.2023.100039

CrossRef Full Text | Google Scholar

John, E. D., and Wagg, D. J. (2019). Design and testing of a frictionless mechanical inerter device using living-hinges. J. Frankl. Inst. 356 (14), 7650–7668. doi:10.1016/j.jfranklin.2019.01.036

CrossRef Full Text | Google Scholar

Karnopp, D. (1995). Active and semi-active vibration isolation. J. Mech. Des. 117, 177–185. doi:10.1115/1.2836452

CrossRef Full Text | Google Scholar

Karnopp, D., Crosby, M. J., and Harwood, R. (1974). Vibration control using semi-active force generators. J. Eng. Ind. 96 (2), 619–626. doi:10.1115/1.3438373

CrossRef Full Text | Google Scholar

Lazar, I., Neild, S., and Wagg, D. (2014). Using an inerter-based device for structural vibration suppression. Earthq. Eng. Struct. Dyn. 43 (8), 1129–1147. doi:10.1002/eqe.2390

CrossRef Full Text | Google Scholar

Lazarek, M., Brzeski, P., and Perlikowski, P. (2018). Design and identification of parameters of tuned mass damper with inerter which enables changes of inertance. Mech. Mach. Theory 119, 161–173. doi:10.1016/j.mechmachtheory.2017.09.004

CrossRef Full Text | Google Scholar

Lazarek, M., Brzeski, P., and Perlikowski, P. (2019). Design and modeling of the CVT for adjustable inerter. J. Frankl. Inst. 356 (14), 7611–7625. doi:10.1016/j.jfranklin.2018.11.011

CrossRef Full Text | Google Scholar

Lazarek, M., Brzeski, P., and Perlikowski, P. (2022). Modeling dynamics of a planetary variator applied in the adaptive TMDVI. Int. J. Mech. Sci. 231, 107487. doi:10.1016/j.ijmecsci.2022.107487

CrossRef Full Text | Google Scholar

Li, C., Liang, M., Wang, Y., and Dong, Y. (2012). Vibration suppression using two-terminal flywheel. Part I: modeling and characterization. J. Vib. Control 18 (8), 1096–1105. doi:10.1177/1077546311419546

CrossRef Full Text | Google Scholar

Li, H., Liu, M., and Ou, J. (2008). Negative stiffness characteristics of active and semi-active control systems for stay cables. Struct. Control Health Monit. Official J. Int. Assoc. Struct. Control Monit. Eur. Assoc. Control Struct. 15 (2), 120–142. doi:10.1002/stc.200

CrossRef Full Text | Google Scholar

Li, P., Lam, J., and Cheung, K. C. (2014) “Investigation on semi-active control of vehicle suspension using adaptive inerter,” in 21st International Congress on Sound and Vibration 2014, ICSV 2014. ICSV 2014.

Google Scholar

Li, W., Dong, X., Yu, J., Xi, J., and Pan, C. (2021a). Vibration control of vehicle suspension with magneto-rheological variable damping and inertia. J. Intelligent Material Syst. Struct. 32 (13), 1484–1503. doi:10.1177/1045389x20983885

CrossRef Full Text | Google Scholar

Li, Y., Jiang, J. Z., and Neild, S. (2017). Inerter-based configurations for main-landing-gear shimmy suppression. J. Aircr. 54 (2), 684–693. doi:10.2514/1.c033964

CrossRef Full Text | Google Scholar

Liang, Z., He, J., Hu, C., Pu, X., Khani, H., Dai, L., et al. (2023). Next-generation energy harvesting and storage technologies for robots across all scales. Adv. Intell. Syst. 5 (4), 2200045. doi:10.1002/aisy.202200045

CrossRef Full Text | Google Scholar

Li, Y., Han, S., Gao, G., Xiong, J., Zhang, Q., and Shi, J. (2021b). “Vehicle suspension design with semi-active inerter and semi-active damper configuration,” in Tenth International Symposium on Precision Mechanical Measurements. (SPIE).

CrossRef Full Text | Google Scholar

Liu, C., Chen, L., Lee, H. P., Yang, Y., and Zhang, X. (2022). A review of the inerter and inerter-based vibration isolation: theory, devices, and applications. J. Frankl. Inst. 359, 7677–7707. doi:10.1016/j.jfranklin.2022.07.030

CrossRef Full Text | Google Scholar

Liu, C., Chen, L., Zhang, X., and Yang, X. (2020b). Stability analysis of semi-active inerter-spring-damper suspensions based on time-delay. J. Theor. Appl. Mech. 58 (3), 599–610. doi:10.15632/jtam-pl/121975

CrossRef Full Text | Google Scholar

Liu, C., Chen, L., Zhang, X., Yang, Y., and Nie, J. (2020a). Design and tests of a controllable inerter with fluid-air mixture condition. IEEE Access 8, 125620–125629. doi:10.1109/access.2020.3007918

CrossRef Full Text | Google Scholar

Liu, M., Tai, W.-C., and Zuo, L. (2021). Vibration energy-harvesting using inerter-based two-degrees-of-freedom system. Mech. Syst. Signal Process. 146, 107000. doi:10.1016/j.ymssp.2020.107000

CrossRef Full Text | Google Scholar

Luan, G., Liu, P., Ning, D., Liu, G., and Du, H. (2023). Semi-active vibration control of seat suspension equipped with a variable equivalent inertance-variable damping device. Machines 11 (2), 284. doi:10.3390/machines11020284

CrossRef Full Text | Google Scholar

Ma, R., Bi, K., and Hao, H. (2021). Inerter-based structural vibration control: a state-of-the-art review. Eng. Struct. 243, 112655. doi:10.1016/j.engstruct.2021.112655

CrossRef Full Text | Google Scholar

Makris, N., and Kampas, G. (2016). Seismic protection of structures with supplemental rotational inertia. J. Eng. Mech. 142 (11), 04016089. doi:10.1061/(asce)em.1943-7889.0001152

CrossRef Full Text | Google Scholar

Málaga-Chuquitaype, C., Menendez-Vicente, C., and Thiers-Moggia, R. (2019). Experimental and numerical assessment of the seismic response of steel structures with clutched inerters. Soil Dyn. Earthq. Eng. 121, 200–211. doi:10.1016/j.soildyn.2019.03.016

CrossRef Full Text | Google Scholar

Marian, L., and Giaralis, A. (2014). Optimal design of a novel tuned mass-damper–inerter (TMDI) passive vibration control configuration for stochastically support-excited structural systems. Probabilistic Eng. Mech. 38, 156–164. doi:10.1016/j.probengmech.2014.03.007

CrossRef Full Text | Google Scholar

Matsuki, H., Nagano, K., and Fujimoto, Y. (2019). Bilateral drive gear—a highly backdrivable reduction gearbox for robotic actuators. IEEE/ASME Trans. Mechatronics. 24 (6), 2661–2673. doi:10.1109/tmech.2019.2946403

CrossRef Full Text | Google Scholar

Matsuoka, T. (2017). Vibration suppression device that has variable inertia mass using CVT. Trans. JSME (in Japanese) 83 (854), 17–00292. doi:10.1299/transjsme.17-00292

CrossRef Full Text | Google Scholar

Matsuoka, T., and Aizawa, N. Vibration suppression device that has variable moment of inertia using magneto-rheological fluid (Seismic test during switching series inertia mass by reinforcement learning) Transactions of the JSME (in Japanese). 2020;86(886):19–00405. doi:10.1299/transjsme.19-00405

CrossRef Full Text | Google Scholar

Moraes, F. H., Silveira, M., and Gonçalves, P. J. P. (2018). On the dynamics of a vibration isolator with geometrically nonlinear inerter. Nonlinear Dynamics 93, 1325–1340. doi:10.1007/s11071-018-4262-6

CrossRef Full Text | Google Scholar

Nemoto, Y., Takino, M., Tsukamoto, S., and Asai, T. (2022). Numerical study of a point absorber wave energy converter with tuned variable inerter. Ocean Engineering 257, 111696. doi:10.1016/j.oceaneng.2022.111696

CrossRef Full Text | Google Scholar

Ning, D., Christie, M. D., Sun, S., Du, H., Li, W., and Wang, Y. (2020). A controllable mechanical motion rectifier-based semi-active magnetorheological inerter for vibration control. Smart Materials and Structures 29 (11), 114005. doi:10.1088/1361-665x/abb643

CrossRef Full Text | Google Scholar

Ning, D., Sun, S., Du, H., Li, W., Zhang, N., Zheng, M., et al. (2019a). An electromagnetic variable inertance device for seat suspension vibration control. Mechanical systems and signal processing 133, 106259. doi:10.1016/j.ymssp.2019.106259

CrossRef Full Text | Google Scholar

Ning, D., Sun, S., Yu, J., Zheng, M., Du, H., Zhang, N., et al. (2019b). A rotary variable admittance device and its application in vehicle seat suspension vibration control. Journal of the Franklin Institute 356 (14), 7873–7895. doi:10.1016/j.jfranklin.2019.04.015

CrossRef Full Text | Google Scholar

Papageorgiou, C., Houghton, N. E., and Smith, M. C. (2009). Experimental testing and analysis of inerter devices. J. Dyn. Sys., Meas., Control. 131 (1), 011001. doi:10.1115/1.3023120

CrossRef Full Text | Google Scholar

Petrini, F., Giaralis, A., and Wang, Z. (2020). Optimal tuned mass-damper-inerter (TMDI) design in wind-excited tall buildings for occupants’ comfort serviceability performance and energy harvesting. Engineering Structures 204, 109904. doi:10.1016/j.engstruct.2019.109904

CrossRef Full Text | Google Scholar

Pradono, M. H., Iemura, H., Igarashi, A., and Kalantari, A. (2008). Application of angular-mass dampers to base-isolated benchmark building. Structural Control and Health Monitoring The Official Journal of the International Association for Structural Control and Monitoring and of the European Association for the Control of Structures 15 (5), 737–745. doi:10.1002/stc.270

CrossRef Full Text | Google Scholar

Punyakaew, S. (2022). Adaptively tuned vibration absorber using cone based continuously variable transmission. Cogent Engineering 9 (1), 2102044. doi:10.1080/23311916.2022.2102044

CrossRef Full Text | Google Scholar

Roberson, R. E. (1952). Synthesis of a nonlinear dynamic vibration absorber. Journal of the Franklin Institute 254 (3), 205–220. doi:10.1016/0016-0032(52)90457-2

CrossRef Full Text | Google Scholar

Sadeghian, M. A., Yang, J., Wang, F., and Wang, X. (2022). Structural vibration control using novel adaptive tuned mass inertance damper (ATMID) with adjustable inertance. Applied Sciences 12 (8), 4028. doi:10.3390/app12084028

CrossRef Full Text | Google Scholar

M. A. Sadeghian, J. Yang, X.-e. Wang, and F. Wang (2021). Novel adaptive tuned viscous inertance damper (ATVID) with adjustable inertance and damping for structural vibration control. Structures (Elsevier).

Google Scholar

Saitoh, M. (2012). On the performance of gyro-mass devices for displacement mitigation in base isolation systems. Structural Control and Health Monitoring 19 (2), 246–259. doi:10.1002/stc.419

CrossRef Full Text | Google Scholar

Selvan, K. V., and Ali, M. S. M. (2016). Micro-scale energy harvesting devices: review of methodological performances in the last decade. Renewable and Sustainable Energy Reviews 54, 1035–1047. doi:10.1016/j.rser.2015.10.046

CrossRef Full Text | Google Scholar

Shen, Y., Shi, D., Chen, L., Liu, Y., and Yang, X. (2019). Modeling and experimental tests of hydraulic electric inerter. Science China Technological Sciences 62 (12), 2161–2169. doi:10.1007/s11431-019-9546-y

CrossRef Full Text | Google Scholar

Smith, M. C. (2002). Synthesis of mechanical networks: the inerter. IEEE Transactions on automatic control 47 (10), 1648–1662. doi:10.1109/tac.2002.803532

CrossRef Full Text | Google Scholar

Smith, M. C. (2020). The inerter: a retrospective. Annual Review of Control, Robotics, and Autonomous Systems 3, 361–391. doi:10.1146/annurev-control-053018-023917

CrossRef Full Text | Google Scholar

Smith, M. C., and Wang, F.-C. (2004). Performance benefits in passive vehicle suspensions employing inerters. Vehicle system dynamics 42 (4), 235–257. doi:10.1080/00423110412331289871

CrossRef Full Text | Google Scholar

Soong, T. (1988). State-of-the-art review: active structural control in civil engineering. Engineering Structures 10 (2), 74–84. doi:10.1016/0141-0296(88)90033-8

CrossRef Full Text | Google Scholar

T. Sterken, K. Baert, C. Van Hoof, R. Puers, G. Borghs, and P. Fiorini (2004). Comparative modelling for vibration scavengers [MEMS energy scavengers], (IEEE). SENSORS.

Google Scholar

Swift, S., Smith, M. C., Glover, A., Papageorgiou, C., Gartner, B., and Houghton, N. E. (2013). Design and modelling of a fluid inerter. International Journal of Control 86 (11), 2035–2051. doi:10.1080/00207179.2013.842263

CrossRef Full Text | Google Scholar

Tai, Y.-j., Xu, Y.-s., Hua, X.-g., Chen, C., Wang, W.-x., and Chen, Z.-q. (2023). A new type of inerter with easily adjustable inertance and superior adaptability: crank train inerter. Journal of Structural Engineering 149 (6), 04023063. doi:10.1061/jsendh.steng-12154

CrossRef Full Text | Google Scholar

Takino, M., and Asai, T. (2023). Development and performance evaluation of an electromagnetic transducer with a tuned variable inerter. Journal of vibration and control 29 (9-10), 2035–2048. doi:10.1177/10775463221074078

CrossRef Full Text | Google Scholar

Tipuric, M., Wagg, D., and Sims, N. (2018). “Vibration suppression using the concept of a semi-active magnetorheological inerter device,” in proceedings of the International Confernce on Uncertainty in Structural Mechanics.

Google Scholar

M. Tipuric, D. Wagg, and N. Sims (2019). “Magnetorheological bypass valve design for a semi-active inerter,” Active and passive smart structures and integrated systems XIII (SPIE).

CrossRef Full Text | Google Scholar

Tsai, M.-C., and Huang, C.-C. (2010). Development of a variable-inertia device with a magnetic planetary gearbox. IEEE/ASME Transactions on mechatronics. 16 (6), 1120–1128. doi:10.1109/tmech.2010.2077679

CrossRef Full Text | Google Scholar

Vullers, R., van Schaijk, R., Doms, I., Van Hoof, C., and Mertens, R. (2009). Micropower energy harvesting. Solid-State Electronics 53 (7), 684–693. doi:10.1016/j.sse.2008.12.011

CrossRef Full Text | Google Scholar

Wagg, D. J. (2021). A review of the mechanical inerter: historical context, physical realisations and nonlinear applications. Nonlinear Dynamics 104 (1), 13–34. doi:10.1007/s11071-021-06303-8

CrossRef Full Text | Google Scholar

Wang, F.-C., Hong, M.-F., and Lin, T.-C. (2011). Designing and testing a hydraulic inerter. Proceedings of the Institution of Mechanical Engineers, Part C Journal of Mechanical Engineering Science 225 (1), 66–72. doi:10.1243/09544062jmes2199

CrossRef Full Text | Google Scholar

Wang, F.-C., Liao, M.-K., Liao, B.-H., Su, W.-J., and Chan, H.-A. (2009). The performance improvements of train suspension systems with mechanical networks employing inerters. Vehicle System Dynamics 47 (7), 805–830. doi:10.1080/00423110802385951

CrossRef Full Text | Google Scholar

Wang, F.-C., and Su, W.-J. (2008). Impact of inerter nonlinearities on vehicle suspension control. Vehicle system dynamics 46 (7), 575–595. doi:10.1080/00423110701519031

CrossRef Full Text | Google Scholar

Wang, M., and Sun, F. (2018). Displacement reduction effect and simplified evaluation method for SDOF systems using a clutching inerter damper. Earthquake Engineering & Structural Dynamics 47 (7), 1651–1672. doi:10.1002/eqe.3034

CrossRef Full Text | Google Scholar

Wang, Y., Ding, H., and Chen, L.-Q. (2020b). Averaging analysis on a semi-active inerter–based suspension system with relative-acceleration–relative-velocity control. Journal of Vibration and Control 26 (13-14), 1199–1215. doi:10.1177/1077546319891612

CrossRef Full Text | Google Scholar

Wang, Y., Li, H. X., Cheng, C., Ding, H., and Chen, L. Q. (2020a). Dynamic performance analysis of a mixed-connected inerter-based quasi-zero stiffness vibration isolator. Structural Control and Health Monitoring 27 (10), e2604. doi:10.1002/stc.2604

CrossRef Full Text | Google Scholar

Wang, Y., Li, H.-X., Meng, H.-D., and Wang, Y. (2022). Dynamic characteristics of underframe semi-active inerter-based suspended device for high-speed train based on LQR control. Bulletin of the Polish Academy of Sciences Technical Sciences 70 (4), 141722. doi:10.24425/bpasts.2022.141722

CrossRef Full Text | Google Scholar

Wang, Y., Meng, H., Zhang, B., and Wang, R. (2019). Analytical research on the dynamic performance of semi-active inerter-based vibration isolator with acceleration–velocity-based control strategy. Structural Control and Health Monitoring 26 (4), e2336. doi:10.1002/stc.2336

CrossRef Full Text | Google Scholar

Wang, Z., Hu, Y., Xiong, S., Zheng, F., and Wang, H. (2020c). “Application of semi-active inerter in a two-body point absorber wave energy converter,” in 2020 39th Chinese Control Conference (CCC). (IEEE).

CrossRef Full Text | Google Scholar

Wen, H., Guo, J., Li, Y., Liu, Y., and Goh, Y. P. (2017). Research on nonlinear inertance calculation method of ball-screw inerter. Journal of Vibroengineering 19 (6), 4042–4057. doi:10.21595/jve.2017.18047

CrossRef Full Text | Google Scholar

Wu, X., Cui, K., Xiong, Y., and Chen, M. (2022). “Lever-based semiactive inerter and its application in vibration absorbers,” in Journal of Physics: Conference Series. (IOP Publishing).

CrossRef Full Text | Google Scholar

Yu, J., Dong, X., Su, X., Tao, X., and Li, X. (2021). Design and testing of a semi-active inerter with magneto-rheological fluid valve. Smart Materials and Structures 30 (10), 105035. doi:10.1088/1361-665x/ac1ead

CrossRef Full Text | Google Scholar

Zhang, L., Xue, S., Zhang, R., Hao, L., Pan, C., and Xie, L. (2022a). A novel crank inerter with simple realization: constitutive model, experimental investigation and effectiveness assessment. Engineering Structures 262, 114308. doi:10.1016/j.engstruct.2022.114308

CrossRef Full Text | Google Scholar

Zhang, X., Zhu, W., and Nie, J. (2022b). Modelling and experiment of an adjustable device combining an inerter and a damper. Machines 10 (9), 807. doi:10.3390/machines10090807

CrossRef Full Text | Google Scholar

Zhang, X.-L., Zhang, T., Nie, J., and Chen, L. (2018). A semiactive skyhook-inertance control strategy based on continuously adjustable inerter. Shock and Vibration 2018, 1–8. doi:10.1155/2018/6828621

CrossRef Full Text | Google Scholar

Zhang, X. L., Zhu, J., Nie, J., Gene Liao, Y., and Lu, X. (2022c). Analysis of inertance and damping double-skyhook control strategies for a semi-active device combining an adjustable inerter and damper. Structural Control and Health Monitoring 29 (10), e3040. doi:10.1002/stc.3040

CrossRef Full Text | Google Scholar

Zhong, W.-M., Zhu, A.-D., Bai, X.-X. F., Wereley, N. M., and Zhang, N. (2020). Integrated shock absorber with both tunable inertance and damping. Frontiers in Materials 7, 204. doi:10.3389/fmats.2020.00204

CrossRef Full Text | Google Scholar

Zhu, H., Li, Y., Shen, W., and Zhu, S. (2019). Mechanical and energy-harvesting model for electromagnetic inertial mass dampers. Mechanical Systems and Signal Processing 120, 203–220. doi:10.1016/j.ymssp.2018.10.023

CrossRef Full Text | Google Scholar