Estimation of slope stability using ensemble-based hybrid machine learning approaches

Mining is one of the most daunting occupations gain the sector since it entails risk at any point in the operation. In its operation, the main focus is on slope stability. To avoid slope failures, work should be performed in line with both the regulations and the safety criteria. Slope stability is essential in mining activities owing to slope failure putting productivity and safety at risk. Prediction of slope failure is difficult because of the complexity of traditional engineering techniques. Through study, recent technologies have helped mining companies predict slope problems quickly and effectively. In this current research, an ensemble of machine learning intelligence algorithms was used to estimate and assess the Factor of Safety (FOS). In Ostapal Chromicte Mine, India, 79 experimental and failure slope occurrences were tracked to gather in-the-moment field data. The available data were split into training and testing sets at random to build algorithms. The five influenced factors such as the unit weight, the friction angle, the cohesiveness, the mining depth, as well as the slope angle used as input variables to estimate the FOS. Selected machine learning techniques such as Multiple Linear Regression (MLR), Decision Tree, Random Forest (RF), eXtreme Gradient Boosting (XGBoost) and ensemble hybrid model combining eXtreme Gradient Boosting and Random Forest (XGBoost-RF) were developed to evaluate the FOS. The validity and efficiency of created models can be evaluated using standard evaluation parameters such as coefficient of determination (R²), root mean square error (RMSE), mean square error (MSE), normalized root mean square error (NRMSE), mean absolute percentage error (MAPE) and mean absolute deviation (MAD). The most precise model to assess the FOS across all models was discovered to be the XGBOOST-RF ensemble model, which had a high R² of 0.931, MSE of 0.009, NRMSE of 0.069, MAD of 0.037, MAPE of 3.581 and an RMSE of 0.098.

1 Introduction

Given that there is danger involved at every stage of the process, mining is among the most challenging jobs in the industry. The main focus is on stability, which is important. Work should be done according to the guidelines and safety standards to prevent slope collapse. Slope stability is crucial for both safety and profitability in open-pit quarrying and mining operations. Building safe, affordable, and useful dug slopes is essential to achieve a steady state of slope stability. It is commonly accepted that a thorough grasp of geological processes, such as geomorphology, stratigraphy, petrography, weathering, and earthquakes, is necessary to construct a stable slope. The main natural factors that affect how stable slopes are intersections of joints, bedding planes, faults, joints, and shear zones. The devastation of important commodities and the death of individuals can both result from catastrophic rock slope instability. Gravity’s actions on materials cause them to migrate downward, which leads to slope failure. However, it is believed that where joint sets cross is where a rock slope will slide. Failure of a rock mass becomes unavoidable once the shear stress approaches the rock’s shear resistance (Gao et al., 2017). Slope wall failure is still influenced by several factors, such as cracks in the rock mass, weathering, an increase in pore pressure, the existence of decayed clay rock fillers, leaching, a rise in moisture absorption, strain softening, as well as a start changing in the complexities of the groundwater (Sha, 2016). To ensure that the construction of a pit wall continues for such duration of a mine while collecting quite so much ore as securely as well as affordably possible, it is crucial to understand the composition and behaviors of the rock mass. The most frequent type of collapse in rocky slopes is plane collapse. The structure collapses whenever a structural discontinuity surface, such as a bedding plane, has an angle that is greater than the discontinuity surface’s angle of friction but lesser than that of the inclination angle of the slope (Raghuvanshi, 2019). Additionally, the slope may become unstable because of the water forces that are present along the probable collapse plane. The dynamic loading and surcharge forces are cited by Wang and Niu (2009) as additional variables that contribute to the key driving force which results in a collapse in slope stability. In the past few decades, significant progress has been achieved in slope stability scientific studies which looked at the factors that contribute to slope failure and the causes of slope collapse. Sha (2016) splits these components into external and internal factors. Some internal factors that could affect a sloping wall’s stability include the kind of rock, the mineral composition of the stone, and the stone’s structural and geotechnical characteristics. Earthquakes, rain, and weathering are examples of environmental influences that could reduce the strength of a rock mass; in contrast, external causes were primarily the consequence of human activity (Nicholas and Sims, 2000). Slope stability must be considered in mining operations management since slope failure compromises both the production’s financial and security elements. The majority of mines have been designed to extract additional materials through deep and steep mines due to the rise in demand for mineral minerals and the emergence of much better efficient extraction techniques and equipment. These mines are inclined at a greater angle, which raises their risk of experiencing a slope failure. Slope failure could result in worker injuries, mine equipment damage, and operations disruption, all of which have a detrimental effect on the efficiency of the mining process. It is essential to conduct thorough geotechnical investigations to make sure the FOS falls within a reasonable range (less than one) of failure to avoid such danger from happening. Greater focus should be placed on monitoring such slopes to prevent slope failure in situations where the FOS seems to be very low. Open-pit mines frequently experience slope failures, which are inevitable as excavation grows deeper and more challenging to control. Examining previously failed slopes all around the world helps us in a better understanding of the failure modes and variables to consider when regulating the processes that lead to mass material movement in slope design (Sjoberg, 2000). It is crucial to have a full understanding of the properties of rock masses, the impact of underground water pressure, structural geology, and some other local external stressors to reduce the risk of slope failure. There are several reasons why rock slopes collapse, and most of them have previously been discussed in this paper. For maximum operating effectiveness, the walls of the stripping excavation must be made as steep as necessary. Although pre-existing faults and cracks account for the bulk of open pit mining failures, failure may happen if the slope design is excessively steep (Simmons and Simpson, 2006). Different interior structures interact with one another differently as the rock deforms, affecting how the rock behaves generally. Furthermore, to understand the deformation operations in open pit mining sites, a thorough understanding of the situ stress field sequence is required.

1.1 Slope failure accidents in India and other countries

There have been several slope and dump failure accidents taking place in some of the Indian mines to date. Some of the prominent slope failure accidents that took place in Indian mines are summarized in the following Table 1. Although there is sufficient advancement in technology and methodology in foreign countries, several slope and dump failure accidents have taken place in some of the mines till date. Some of the prominent slope failure accidents that took place in the mines across the world are detailed in Table 2.

TABLE 1

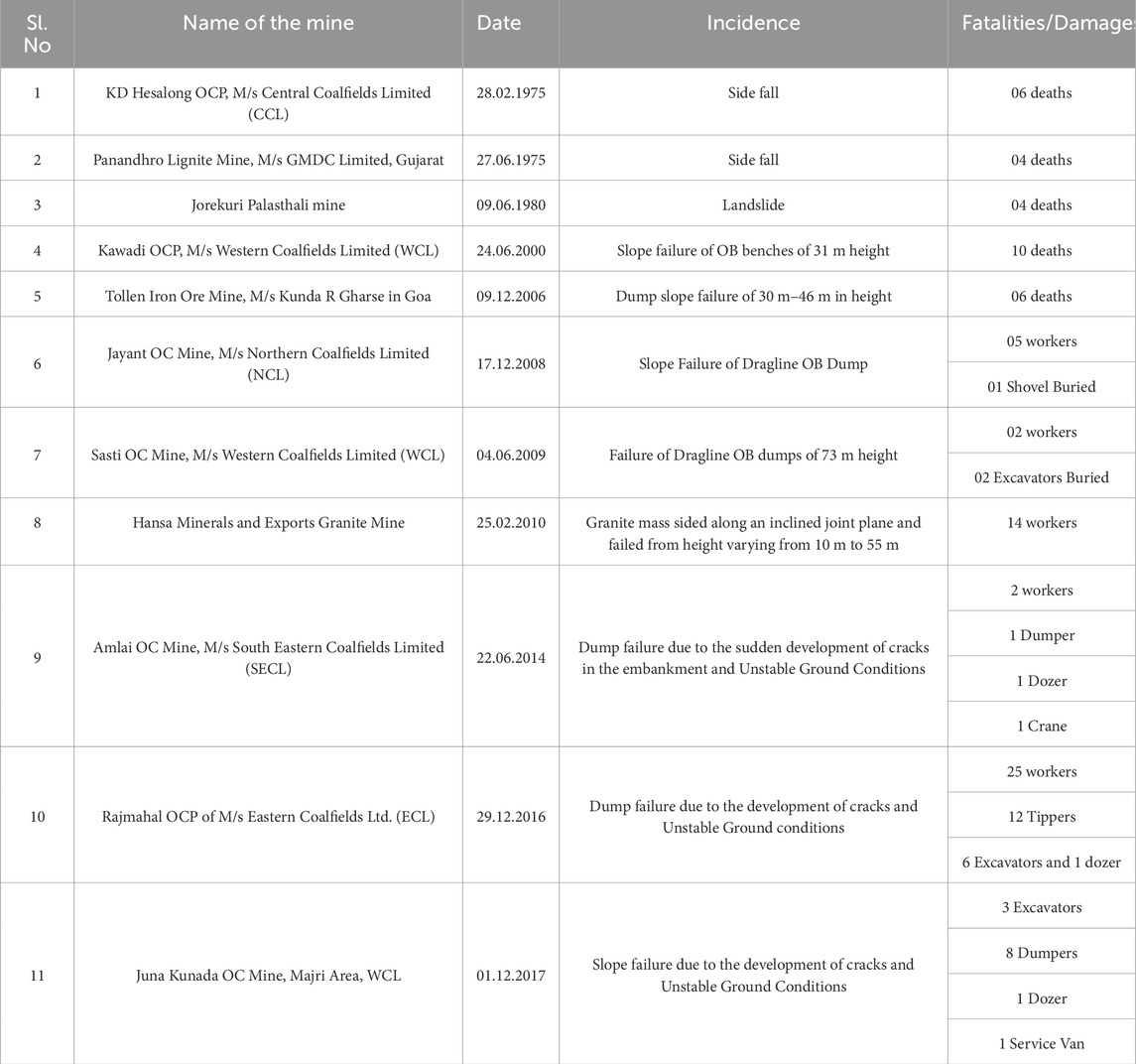
TABLE 1. Some catastrophic mining accidents in Indian opencast mines involved dump and slope failures.

TABLE 2

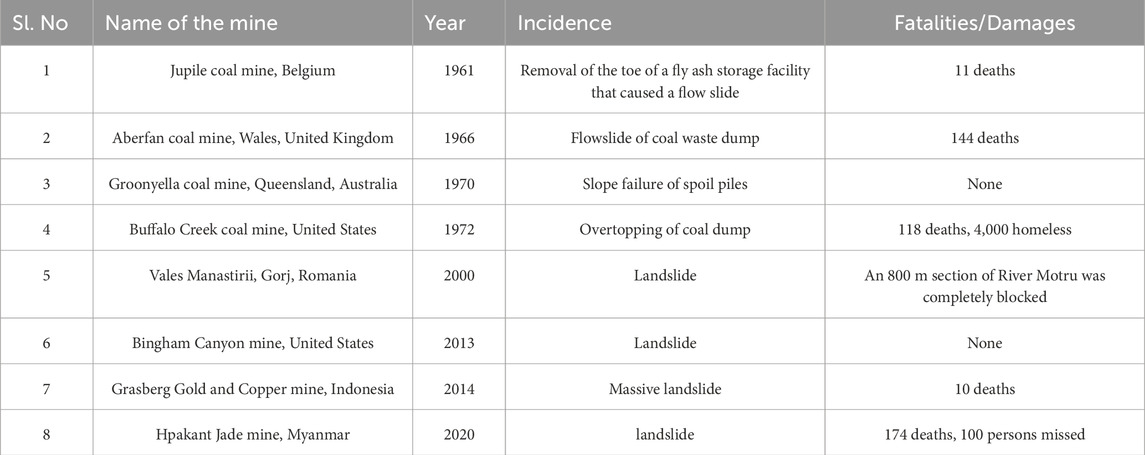
TABLE 2. Some fatality incidents in opencast mines in foreign nations involved dump and slope collapses.

1.2 Input features selection

The most important influenced elements must be determined to forecast the slope’s stability. According to the literature, six variables were chosen as input qualities for this purpose: unit weight (γ), cohesiveness (c), angle of internal friction (ϕ), slope angle (β), and slope height (H). The slope’s status, which may be either stable or unstable, is the model’s output. For the context of this research, stable plains were those that had a FOS greater than one. Variable selection techniques are used to choose the input variables that are relevant for modeling/predicting the variable(s) under consideration. Three separate sets of data—training, testing, and validation sets—are created from the original data collection. The largest dataset, known as the training dataset, is used by neural networks to discover patterns within the data. After that, the general abilities of a purportedly trained network are tested using the testing set. Utilizing the validation set, a full verdict of the trained network’s performance is made. The existing slope’s FOS must be measured and monitored regularly to ensure that working conditions are fully safe. It is possible to quickly calculate the equilibrium circumstances like an uneven slope as well as the likelihood of its own instability using a variety of methodologies, such as numerical modeling and soft computing techniques. In this study, the stability of several of the benches at the Ostapal Chromite open-cast mine in Odisha, India was evaluated using ensemble machine learning methods. For every stone of the slope that the FOS is to be measured, parameters such as slope angle, cohesiveness, bench height, internal angle of friction, lithology, and other factors are first determined. The usual method of evaluating the factor of safety, which takes into account the bench geometric features, cohesiveness, and internal angle of friction of a single rock kind, is the foundation for all of the data sets being used to train the model.

Contributions: Motivated by the existing slope stability issues and its damages in open cast mines, the main contribution in this research paper can be described as follows:

• Slope stability accidents, affecting key factors and types of slope failures discussed with respect to the past research literature and survey.

• In this current work, the prediction of slope failure in open-pit mines is examined using ensemble machine learning methods. It includes the determination of the factor of safety of slope against all possible influence parameters.

• Totally five machine learning (ML) models named MLR, Decision Tree, RF, XGBoost and an ensemble hybrid model combining eXtreme Gradient Boosting and Random Forest (XGBoost-RF) were used to estimate the Slope’s FOS.

• The performance of these ML models can be evaluated by evaluation metrics such as coefficient of determination (R²), RMSE, MSE, NRMSE, MAPE, and MAD.

2 Previous work(s)

To find the slope designs and equilibrium equations that are most feasible, stable, as well as economical, slope stability evaluation is carried out. The ratio of resistive forces acting on an inclined surface to the force that would otherwise cause it to collapse or slide is known as slope stability. The primary issues of slope stability research are observing and reviewing failure processes, identifying critically dangerous slopes, and determining slope vulnerability. When determining the stability of a slope, deterministic and probabilistic methods were combined with engineering concepts to compute the slope’s factor of safety (FOS). The factors that affect the equilibrium and operate on the mass assumed to fail are identified. This technique holds that the weight of the substance in the sliding mass constitutes the outside load on the face and that the slope’s surfaces also contribute to phases that affect mobility. On the surface that is expected to fail, the soil’s shear strength prevents slippage. The resistive moment is calculated based on the overall soil’s shear strength. This is how the safety factor is shown:

$\mathit{F}\mathit{O}\mathit{S}=\frac{\mathit{M}\mathit{o}\mathit{m}\mathit{e}\mathit{n}\mathit{t}\mathit{s}\mathit{R}\mathit{e}\mathit{s}\mathit{i}\mathit{s}\mathit{t}\mathit{i}\mathit{n}\mathit{g}\mathit{t}\mathit{h}\mathit{e}\mathit{S}\mathit{l}\mathit{i}\mathit{d}\mathit{i}\mathit{n}\mathit{g}\left(\mathit{r}\mathit{e}\mathit{s}\mathit{i}\mathit{s}\mathit{t}\mathit{i}\mathit{n}\mathit{g}\mathit{f}\mathit{o}\mathit{r}\mathit{c}\mathit{e}\right)}{\mathit{M}\mathit{o}\mathit{m}\mathit{e}\mathit{n}\mathit{t}\mathit{s}\mathit{C}\mathit{a}\mathit{u}\mathit{s}\mathit{i}\mathit{n}\mathit{g}\mathit{t}\mathit{h}\mathit{e}\mathit{S}\mathit{l}\mathit{i}\mathit{d}\mathit{i}\mathit{n}\mathit{g}\left(\mathit{d}\mathit{r}\mathit{i}\mathit{v}\mathit{i}\mathit{n}\mathit{g}\mathit{f}\mathit{o}\mathit{r}\mathit{c}\mathit{e}\right)}$

Empirical relationships are often employed to measure the component of protection that cannot be strictly relied on just because the models do not take moisture into account. Additionally, the models are strictly observational and the estimation time is too long. They are unable to estimate the risk of loss. Many of these loopholes, however, can be filled using soft computing techniques. Soft computational methods, such as artificial neural networks, rely on prior familiarity with input and output data. In soft-computed methodologies, any uncertainty in the data collection may be accepted. Soft computation is similar to the mechanism of the human brain. It does not depend on binary numbers or crisp values. The mining industry makes extensive use of soft computing techniques for a variety of purposes. Artificial neural networks are systems focused on neurons in the human brain. Several different types of neural networks can be used for a range of purposes and uses such as pattern recognition, detection, classification, voice, vision, and control systems. There are two forms of learning: supervised and unsupervised. The primary soft computing techniques include machine learning, probabilistic reasoning, evolutionary communication, fuzzy algorithms, neural networks, and supporting vector algorithms. Mc Culloh and Pitts (McCulloch and Pitts, 1943) are credited with developing the very first artificial neural network (ANN) which is acknowledged as the ground-breaking breakthrough in artificial intelligence. Any neural network must be constructed so that increasing the number of inputs yields the desired number of outputs.

2.1 Slope stability

The condition known as slope failure occurs when a slope abruptly gives way due to the earth’s reduced ability to hold itself together for a variety of reasons, the two most important of which are precipitation or an earthquake. The sudden failure of the slope can result in casualties and different types of injuries. Such events, as well as their number and duration, are becoming more common by the day. The explanation is obvious, i.e., technical advances in the design of heavy earth-moving machines and rapid drilling, as seen in the mining industry, infrastructural development activities, and so on. The stability of a slope is the capacity of soil-covered slopes to accept and withstand displacement. The slope stability can be evaluated using the interaction of peak strength. A once-stable slope can become conditionally unstable when it is originally affected by preparation conditions. Climate-related phenomena may be the initiating causes of such slope instability since they can purposefully make a slope unstable and trigger mass movements. Increased shear stress, loading, lateral strain, as well as a transient force all contribute to mass displacement. Weathering, variations in pore moisture content, and organic content all lower shear strength. The dynamic and static stability of soil and stone dam slopes, various types of excavated slopes, and naturally occurring slopes in soft rock and soil are all included in the concept of slope stability. Investigation, analysis, and design mitigation of slope stability are assisted by geologists and geotechnical engineers.

2.2 Factors affecting the stability of slope

The stability of slopes in opencast mines is altered by several factors which include geometry of slope, lithology, groundwater and rainfall, geological structure, time, cohesion, internal angle of friction, dynamic forces, and mining methods. The various factors affecting slope stability in opencast mines are shown in Figure 1.

FIGURE 1

FIGURE 1. The geometry of opencast mine and some factors affecting slope stability.

2.2.1 Geometry of slope

The most critical element influencing slope stability is slope geometry. The three primary geometrical slope design factors are the height of the bench, the total angle of the slope, and the extent of the failure surface. The slope stability decreases as the height and slope angle increase. The possible degree of just about any failure towards the back of the crests increases with the overall slope angle, therefore it must be taken into account to prevent soil deformations. The Directorate General of Mines (DGMS) Safety finds an average slope angle of 45° to be secure. Convex segment slope must be avoided in slope design since the slope’s curve does have a significant impact on instability. The slope becomes less stable as it becomes steeper and higher.

2.2.2 Lithology

The stability of the rock mass depends on the types of rocks that make up a wide pit slope and is influenced by faults, discontinuities, bending, old workings, and weathering. The formation of a slope in huge sandstone is an example of reveling, circular, and rock fall instabilities, which are all indicators of weak rock mass strength. Pit slopes with alluvium of soil or weathered rocks on the surface have weak shear strength, which would be lowered further if water drains into it.

2.2.3 Groundwater

Due to its tendency to increase upward push and propel water pressures, groundwater seems to have a detrimental impact on slope stability. Thus, the cohesion, as well as friction of the discontinuities face, will alter due to the physical and chemical impacts of pore water pressure inside the filling materials of joints. Frictional resistances are physically reduced by elevating the joint plane. This lessens the shear resistance across the probable failure plane by lowering the practical normal stress acting on it. The chemical and physical effects of water pressures in rock pores result in a decrease in shear strengths when the confining tension has been lowered.

2.2.4 Geological structure and time

The slope stability in open-pit mines is most affected by the following geological characteristics such as proportions and directions of dips, zones of intra-formational shear, surface joints and fractures and faults. A slope’s standing period after mining also needs to be taken into account. Surface mine slopes must stand for a brief period of time, but they are treated with the same thorough care as civil ventures. In the long run, slope stability is significantly influenced by the pace of incremental strain softening.

2.2.5 Cohesion

A rock or soil’s cohesion is a characteristic that reveals how well it resists breaking or deformation as a result of gravity. Cohesion in soils and rocks is caused by electrostatic repulsion within rigid over hardened clays, gluing with Fe₂O₃, CaCO₃, NaCl, as well as other materials, as well as root cohesion. On the other hand, the evident cohesiveness is brought on by unskilled loading’s negative capillary pressure reaction and pore pressure. Less compacted rocks and/or soils cause slopes to be less stable.

2.2.6 Internal angle of friction

It is the angle formed between the support force and the resulting force when the failure occurs only as a result of shearing stress. Its tangent is the coefficient of sliding friction. The size and sphericity of the particles have an impact on the slope of internal friction. It is also influenced by the presence of quartz. In the lab, the internal angle of friction can be measured using the Direct Shear Test or the Triaxial Shear Test.

2.2.7 Dynamic forces

The dynamic movement of the material temporarily amplifies the effects of friction, blast, and shear loads, making stabilizing the slope face more challenging. It induces rock breaking and earth movement. The consequences of reckless or incorrectly designed blasting may be severe for the stability of the bench. Vibrations due to blasting result in slope failures. With good results, several types of soft blasting have also been proposed to lessen such impacts on minor slopes.

2.3 Types of slope failures

Failures in slopes are significant natural disasters that occur in a variety of locations around the world. Because of their geometry, slopes show two or three free surfaces. Slopes are prone to planar, wedge, toppling, rock fall, and rotational failures. The direction and dispersion of discontinuity planes in relation to the slope face greatly affect the first four, which are far more prevalent in rock slopes. Plane mode failure is common on slopes made by layered sedimentary and meta-sedimentary rock formations. On a rock slope, plane failure occurs when a longitudinal discontinuity plane dips or daylights into the valley at an angle that is larger than the friction angle of the discontinuity surface but less than the slope face angle. The surface’s strike should be nearly parallel to the slope face in order to have the least amount of resistance while sliding, and there should be release surfaces on both sides of the sliding mass. Wedge failure occurs when rock strata cross two intersecting discontinuities and then fall from the edge inclination at an inclination to the cut surface, a wedge-shaped square is created.

2.4 Factor of safety (FOS)

For slope stability analysis, the factor of safety is frequently estimated as the ratio of final shear strength to mobilized shear stress during incipient failure. The FOS can be measured using a variety of methods. The most common approximation for F, expressed in terms of force equilibrium or moment equilibrium, as follows, assumes that the factor of protection is constant along the slip surface:

1. Moment equilibrium is a concept that is frequently applied in the research of rotating landslides. In the event of a slip surface, provides the factor of safety $F_m$ defined in aspects of the moment.

${\mathit{F}}_{\mathit{m}}=\frac{{\mathit{M}}_{\mathit{r}}}{{\mathit{M}}_{\mathit{d}}}$

Where, $M_r$ is the total of his recalcitrant times, $M_d$ is the total driving time. The instant spot for such a spherical failure surface is typically taken to be the circle’s center for the sake of simplicity. Any point for immediate consideration can be used to examine such as a non-circular failure surface.

2. Force equilibrium: Force equilibrium is a translational or rotational failure composed of planar or polygonal slip surfaces. According to force, the safety factor $F_f$ is determined as follows:

${\mathit{F}}_{\mathit{f}}=\frac{{\mathit{F}}_{\mathit{r}}}{{\mathit{F}}_{\mathit{d}}}$

Where, $F_r$ is the total of resisting forces and $F_d$ is the total of driving forces

2.5 Slope stability analysis methods

There are primarily two methods for performing slope stability studies. The successful stress strategy, which is employed in long-term stability investigations when drained conditions are available, is the second technique. Taking into account the overall water level during intense rainstorms, the successful stress approach can be used to evaluate natural slopes as well as slopes in residual soils. The slope stability analysis techniques that have been used and put into effect up to this point include limit equilibrium methods, limit analysis methods, physical modeling, probabilistic approaches, and numerical modeling.

2.5.1 Limit equilibrium methods

Engineers can employ a range of research methods to solve the nonlinear static problem of slope stability. Presently, the majority of soil stabilization analyses are performed utilizing computer technologies. Nevertheless, several of the earliest LEMs are simple to compute manually. More complex techniques have been developed since the invention of computers. Most LEMs are built using slice techniques, which can be either vertical, horizontal, or slanted. In contrast to a strictly mechanical theory, engineering intuition was stressed in the first-slice approach (Fellenius, 1927) (Fellenius, 1927). The slice approaches underwent significant progress in the 1950s and 1960s, which will be discussed below. The most common features of all the methods are briefed below:

a) The sliding body is split into something like a limited number of slices spread well over the failure plane. Typically, the slices are sliced vertically, but lateral and inclined are also used by several scientists and scholars. The differences between various cutting techniques are typically negligible, and most engineers currently favor vertical cuts.

b) To bring the slipping block or body to a limited condition, similar amounts of the slip surface’s strength are mobilized.

c) Interslice force assumptions are used to determine the problem.

d) Equations of a moment or force equilibrium are utilized to estimate the safety factor.

2.5.2 Limit analysis method

The breakdown mechanism, such as inflexible translational/rotational failure mechanisms or block/wedge failure mechanisms, must be predetermined for this approach, much like for LEM. The studies have presumed the failure mechanism because the typical limit analysis approach was utilized to tackle 3D slope issues (Farzaneh and Askari 2003; Michalowski 2010) (Orang and Faradjollah, 2003). Recently, Gao et al. (2012) (Gao et al., 2012) included face and base failures in the research of Michalowski and Drescher (2009) (Michalowski and Drescher, 2009), who utilized a toe failure with something like a rotational failure mechanism in their investigation. Because it is difficult to compute the stress field required by the lower bound limit analysis system, the majority of slope stability analyses only have employed the upper bound limit evaluation technique, which is similar to what was previously stated. This analysis, often referred to as reliability analysis, was initially conducted in the 1930s in relation to aircraft failure. People started to understand the importance of uncertainty in structure engineering after Freudenthal wrote Degree of Safety in Structure in 1946 (Freudenthal, 1947) and then invented risk evaluations in functional engineering design. With the advent of dependability theory and a greater focus on the uncertainties of slope engineering, engineers as well as academics began to pay more attention to slope probabilistic analysis. It was initially utilized in slope engineering in the 1970s. After that, other people conducted additional research and created several methods for probabilistic analysis. The Second Moment Pattern (Cornell, 1969,1971) (Cornell, 1969) was the first statistical instrument. Such methods result in a linearization of the performance function with a mean-centered distribution.

2.6 Numerical modelling

The classic limit equilibrium approach, which gives no data on the actual strain growth, solely considers the system’s ultimate limit state. If the slope fails owing to dynamic processes, designing it exclusively utilizing a limiting equilibrium analysis will fail. Some of the failure masses may likely face considerable stress in the case of a natural slope, mobilizing residual strength in some areas and adding final shear strength to other failure masses. In addition to brittle materials, over-consolidated or fissured clays can also experience this type of gradual collapse. The approximation of such successive failures will be improved more by the use of numerical approaches. The usage of numerical methods in geomechanics has significantly increased during the past 30 years. Using simple slope geometry and clear loading situations, traditional research methodologies have a limited range of applications and insufficient understanding of the mechanisms underlying slope failure. Investigations into slope stability employ the continuum, discontinuum, and hybrid simulation methods of numerical analysis. To optimize their key benefits, hybrid codes combine these two approaches (continuum and discontinuum).

2.7 Hybrid approach

In slope analysis, hybrid techniques are widely used. This may entail joint investigations using limit equilibrium stability analysis, groundwater flow, and finite element modeling, such as those found in the GEO-SLOPE applications package (Geo-Slope 2000). Hybrid computational models, such as coupled boundary/distinct element and paired boundary/finite component solutions, have been used for a very long time in underground rock engineering. Coupled particle flow and finite difference calculations using PFC3D and FLAC3D are two examples of advancements. 2005 (Itasca), for the data analysis, the hybrid technique was employed to characterize the micro-mechanical interactions between the particles and forecast how they will affect stability analyses. To help people understand how complex slope stability is, a soft computing technique model is offered. Since a few years ago, sophisticated machine learning methods have been employed to assess the FOS. Other researchers used a variety of novel soft computing techniques to predict FOS, including Multiple Regression (MR), Genetic Algorithm (GA), Support Vector Machine (SVM), Support Vector Regression (SVR), K-Nearest Neighbors (KNN), Extreme gradient boosting (XGBoost), Random Forest (RF), Decision Tree (DT), and hybrid models, Gradient Boosting Decision Tree was used in several applications, and the results were found to be noticeably superior to those attained by employing traditional techniques. (Marrapu and Jakka, 2017; Lin et al., 2018a; Bui et al., 2020a; Huang et al., 2020; Deris et al., 2021; Jingjing et al., 2021; Kardhani et al., 2021; Sina et al., 2021; Christoph et al., 2022; Feezan et al., 2022; Gagan et al., 2022; Gexue et al., 2022; Zhihao and Zhiwei, 2022; Mahmoodzadeh and Mohammadi, 2023; Xu et al., 2023). Arunav Chakraborty and Diganta Goswami (Arunav and Diganta, 2017) carried out their work on slope stability prediction utilizing artificial neural networks, very advanced modeling methods that can be suitable for modeling highly complicated functions. In this study, an ANN-based prediction method for the slope safety factor was developed. Using Bishop’s Simplified Method, they examined 110 cases with varying geometric and soil conditions. A backpropagation learning algorithm was used as the computational technique in this case for the training procedure.

Farzad Farrokhzad et al. (Choobbasthi et al., 2009) researched the prediction of slope stability using ANN. In this paper, artificial neural networks are utilized to analyze slope stability in a selected area. The findings are then contrasted with earlier research approaches to verify the ANN model validity. Total stress, effective stress, angle of slope, angle of internal friction, cohesion, and slope stability are the relevant input parameters used in this article, and slope stability is the output. Geotechnical engineering is a discipline that, Sakellariou and Ferentinou (Michael and Maria, 2021) submitted work on identifying the nonlinear nature of multidimensional dynamic systems. The training computation was carried out using a back-propagation learning technique. In this article, the source data for the stability of the slope computation are the parameters of the geotechnical and geometrical input variables. The FOS of the slope scenarios under consideration is calculated by the network. According to research by Arunav Chakraborty (Arunav and Diganta, 2016), the influence of specific factors on slope failures can be described using statistical techniques like regression analysis, neural networks, and other techniques. The geotechnical as well as geometrical input parameters are used as the input data for the three-dimensional slope stability computation in this article This study contains the geotechnical and geometrical input characteristics as the input data for the three-dimensional slope stability calculation, and the output data is the 3-D crucial protection factor (FOS). A summary of all researcher’s investigations in the field of FOS estimation and their prediction performances are illustrated in Table 3.

TABLE 3

TABLE 3. An overview of prior studies on the subject of FOS prediction.

Slope stability evaluation is an important problem in construction projects, according to Zhihao and Zhiwei (2020). This study looks into the application of multivariate adaptive regression splines (MARS) to represent this same underlying multidimensional and nonlinear relationship between the factors involved in assessing slope stability. A comparison of backpropagation neural network (BPNN) and MARS-based machine learning approaches were implemented for the evaluation of slope stability. The model was built using a single data set that contained actual slope failure events, and the performance of BPNN and MARS was contrasted. In light of the research results, the BPNN and MARS models will simulate the relationship between both the safety factor and the slope parameters. Erzin and Cetin (2011) (Yusuf and Tulin, 2012) researched the creation of Artificial Neural Network (ANN) and Multiple Regression (MR) models in order to ascertain the critical factor of safety (FOS) value of a typical artificial slope subjected to seismic pressures. This was accomplished by altering the natural subsoil qualities during slope stability tests while maintaining the slope’s structure and the attributes of man-made soil, namely, cohesion, internal angle of friction, bulk unit weight of the crust beneath the ground surface, and seismic coefficient. Maria Ferentinou and Muhammad Fakir (2018) (Maria and Muhammad, 2018) proposed an optimized back-propagation network and trained it on a large collection of 141 open-pit mine case studies from around the world. The extended parameters’ values, which comprise 18 open pit slope stability parameters, are the inputs. The possibility for instability is approximated as a result. As a result, a function approximation is used to simulate the slope stabilization problem. To estimate the future status regime comprehensively, the presentation of a new open-pit mining slope stability index. By contrasting the actual values with the stability status that was observed, these values are verified. A. J. Choobbasti and others (2009) (Choobbasti et al., 2009) based on location inspection data from Nobad, Mazandaran, Iran, this study develops multilayer perceptron network-based ANN systems to forecast slope stability. The input parameters were total stress, effective stress, slope angle, coefficient of cohesion, internal friction angle, and horizontal earthquake coefficient. The output value was slope stability.

Kanule Jason and Ngetich Wilson (2018) (Kanule, 2021) proposed an ANN model to predict the factor of safety of a slope using a set of numerical simulations. To determine the factor of safety for each situation, the author included six slope characteristics: slope angle, cohesion, internal angle of friction, pore water pressure, and water content. These parameters were then fed into a model. More simulations are run under various scenarios to determine the appropriate level of safety for the data acquired. The ANN model is then trained, tested, and validated using these data sets. The results are compromising and the ANN model approximated the factor of safety close to the actual values. In their research on slope stability risk analysis, Prashant K. Nayak et al. (2020) (Paliwal et al., 2022) noted that it is crucial for every mining engineer to offer a reasonable slope safety factor. The study area’s slope face has been separated into cells in this work, each with a homogeneous aspect, a slope angle, rock characteristics, and joint set orientations. This study develops an ANN model and uses a mix of slope geometry and discontinuity characteristics to determine the likelihood of failure. Fattahi Hadi and Mahdi Hasanipanah (2021) developed four improved ANN models include cascaded forward neural network (CFNN) trained by Levenberg-Marquardt algorithm (LMA) and Conjugate gradient back propagation (CGP), radial basis function neural network (RBFNN) was optimized by the Dragonfly Algorithm (DA) and teaching-learning-based optimization (TLBO) to predict the rock fragmentation. The outcomes evident that CFNN-LMA exhibits lowest RMSE over other models (Fattahi and Hasanipanah, 2021). Mahdi Hasanipanah et al. (Hasanipanah et al., 2022a) adopted a novel hybrid ANN based on the adaptive musical inspired optimization methods such as ANN coupled with adaptive dynamical harmony search (ANN-ADHS), ANN coupled by harmony search (ANN-HS) and particle swarm optimization (ANN-PSO) for accurate prediction of fly rock induced by blasting operation in mines. In their study, the results confirmed that ANN-ADHS model shows high predictive performance over other models. Mahadi Hasanipanah et al. (Hasanipanah et al., 2022b) utilized three novel hybrid models named as CFNN-LMA, CFNN-Bayesian regularization (BR), and CFNN-scaled conjugate gradient (SCG) to estimate the rock mass deformation modulus (E_m). The computational outcomes revealed that developed CFNN-LMA model provides better results than other models. Ding et al. (2023a); Ding et al. (2023b)developed improved hybrid models includes CFNN-LMA, CFNN-CGP, RBFNN-DA, RBFNN-TLBO and least squares support vector machine (LSSVM) based gravitational search algorithm (GSM), whale optimization algorithm (WOA), ant bee colony (ABC) for predicting rock fragmentation and fly rock, respectively. The performance of all adopted algorithms were analyzed with various evaluation metrics. The outcome of computational evident that CFNN-LMA and LSSVM-WOA provide better results than other to predict the rock fragmentation and fly rock, respectively. Wang et al. (2023) proposed a novel hybridize adaptive neuro fuzzy inference system (ANFIS) coupled with two optimization algorithms named as differential evolution (DE) and the firefly algorithm (FA) to assess the rock elastic modulus (E). The results conclude that ANFIS-FA algorithm shows superior performance to the ANFIS-DE and ANFIS-NN algorithms.

3 Description of the experimental study region and the data gathered

The Ostapal Chromite Mines is located in the Sukinda Ultramafic Complex to the North of Damsala Nallah. Villag of Gurujanga, taluka of Sukinda, district of Jajpur, and State of Odisha, India. The area is bounded by Latitude 21°0′ to 21°5′ N and Latitude 85°40′ E to 85°53′E. The location of the lease area is under Survey of India, Topo Sheet No. 73 – G/16. Serpentinite, quartzite, pyroxenite, dolerite, nickeliferous limonite, and other lithological units are found in the leasehold area. Serpentinite is the chromite host rock. All over the lease area, the ultrabasic bulk has weathered to a laterite capping of 10–20 m in thickness. Talus and clayey soil cover the lease area’s northern, southern, and western regions. Clayey soil with a thickness ranging from 1 to 3 m cements the detrital deposit. The ultramafic body has a strike length of 15 km in NE–SW direction from Kana to Kalarangi and breadth ranging from 1 to 4 km. The widest part of redefinition is confined to the southwestern part, tapering gradually to the northeast, and dying out entirely against quartzite. The Sukinda ultramafic field’s chromite deposits appear as six more or less parallel bands in Serpentinite. These Chromite bands, known locally as Bands 1, 2, 3, 4, 5, and 6, are separated from one another by Serpentinite/Pyroxenite ranging in thickness from 120 M to 600 M. These chromite bands are exposed intermittently in quarries throughout a 15-km strike length, with the majority of these bands hidden beneath laterite capping. The bottom sequence of the Iron ore super group has been folded structurally into overseas syndrome, which plunges at a low angle of 150–200°. The Sukinda syndrome is formed as an asymmetrical syncline based on the direction obtained from cross beddings, with the apex of the fold centered around Kansa village. The excavated overburden mass of the Ostapal quarry has been placed in a waste dump near the northern limit of the Ostapal Chromite Mines license. The collected data set with ranges were summarized in Table 4.

TABLE 4

TABLE 4. Summary of collected dataset.

Figure 2 presents the current state of the workings as of 9 June 2017. The maximum dump height in the North and the South dumps is approximately 87 and 41 m, respectively. North and South dumps have a maximum of 6 and 3 decks, respectively. The maximum deck height in the North and South dumps is approximately 17 and 15 m, respectively. The mine is located in a subtropical climate. In total, 79 samples were gathered for this current research work. Figure 3 reflects the mine’s plan view as well as the dumps.

FIGURE 2

FIGURE 2. Working at ostapal chromite mine, M/S factor Ltd, odisha.

FIGURE 3

FIGURE 3. Plan view of mine along with dumps.

4 Estimation of FOS using MLR technique

Multiple variables are modeled and examined using this kind of analysis. MLR is a statistical strategy for predicting the outcome of a response variable, often referred to as multiple correlation, may be used. By evaluating the relation between the independent variable (x_i) and the connected variable, a correlation model that gives the researcher access to the dependent variable (y) and helps them to comprehend dependent connection variables and multiple variables may be produced (y) (Lee et al., 2020). The following equation represents the MLR model:

$\mathit{y}={\mathit{\beta }}_{\mathbf{0}}+{\mathit{\beta }}_{\mathbf{1}}{\mathit{x}}_{\mathbf{1}}+{\mathit{\beta }}_{\mathbf{2}}{\mathit{x}}_{\mathbf{2}}+{\mathit{\beta }}_{\mathit{p}}{\mathit{x}}_{\mathit{p}}+\mathit{\epsilon }$

Where, $y$ is the response (predicted) variable, $x_1,x_2,x_3\dots .x_p$ are the predictor inputs, ${\beta }_0$ is called intercept, ${\beta }_1,{\beta }_2,{\beta }_p$ are the coefficient of corresponding predictor epsilon is the error. Table 5 listed the overall analysis of the MLR model. Eventually, an empirical equation was found to assess the FOS, as presented in the following Equation.

$\begin{array}{ll}\hfill \mathit{F}\mathit{O}\mathit{S}& =\mathbf{0.0121}\left(\mathit{U}\mathit{n}\mathit{i}\mathit{t}\mathit{w}\mathit{e}\mathit{i}\mathit{g}\mathit{h}\mathit{t}\right)+\mathbf{0.00593}\left(\mathit{c}\mathit{o}\mathit{h}\mathit{e}\mathit{s}\mathit{i}\mathit{o}\mathit{n}\right)+\mathbf{0.01856}\hfill \\ \hfill & \left(\mathit{f}\mathit{r}\mathit{i}\mathit{c}\mathit{t}\mathit{i}\mathit{o}\mathit{n}\mathit{a}\mathit{n}\mathit{g}\mathit{l}\mathit{e}\right)-\mathbf{0.032}\left(\mathit{s}\mathit{l}\mathit{o}\mathit{p}\mathit{e}\mathit{a}\mathit{n}\mathit{g}\mathit{l}\mathit{e})-\mathbf{0.0026}\right)\hfill \\ \hfill & \left(\mathit{m}\mathit{i}\mathit{n}\mathit{i}\mathit{n}\mathit{g}\mathit{d}\mathit{e}\mathit{p}\mathit{t}\mathit{h}\right)+\mathbf{1.539}\hfill \end{array}$

TABLE 5

TABLE 5. MLR model performance.

Figure 7 shows the correlation relation graph between actual and MLR-predicted FOS. The observed R² of 0.596, is evident that wide scattering compared to actual FOS.

5 Estimation of FOS using ensemble machine learning algorithms

Five machine learning models were developed to estimate the FOS including Decision Tree, Random Forest (RF), eXtreme Gradient Boosting (XGBoost) and an ensemble hybrid model combining eXtreme Gradient Boosting and Random Forest (XGBoost-RF) models. The total database with 79 samples was randomly divided into two parts: (i) 85% for training, and (ii) 15% for testing. All adopted models use similar training and testing datasets. A trial-and-error method was implemented in all used ML models.

5.1 Decision tree regression

Decision Tree Regression model is a tree-like model which is constructed based on Decisions about whether the value of the feature is exceeding a particular value or not. The feature to be considered is selected based on the kind of Information Gain (IG) obtained from the feature. Information Gain is based on the expected reduction of entropy, in other terms reducing the impurity of the data. The features with more Information Gain are chosen and if-then conditions are applied recursively and split the data into smaller regions. This splitting of data is stopped when a certain parameter among the set of parameters is reached. Outputs obtained are the mean or the median of the training values that belong to the particular section. So, the data should be arranged in ascending order. Then after the midpoint of a_i, a_i is found and subsequently, entropy is calculated. The entropy of the probabilities is calculated by:

$\mathit{H}\left(\mathit{p}\right)=-\sum {\mathit{p}}_{\mathit{i}}{\mathit{log}}_{\mathbf{2}}\left({\mathit{p}}_{\mathit{i}}\right)$

Finally, Information Gain is computed by the summation of all the entropies before and after the split of the node.

$\mathit{I}\mathit{n}\mathit{f}\mathit{o}\mathit{r}\mathit{m}\mathit{a}\mathit{t}\mathit{i}\mathit{o}\mathit{n}\mathit{G}\mathit{a}\mathit{i}\mathit{n}=\mathit{H}\left({\mathit{p}}_{\mathit{i}}\right)-\mathit{H}\left({\mathit{p}}_{\mathit{f}}\right)$

Where, $H\left(p_i\right)$ = Entropy at the root node and $H\left(p_f\right)$ = Entropy after the split of the node. Here, Distance is considered the decision-making parameter for the root node and considered a continuous variable. The Information Gain obtained by the Distance feature is 5.21. Different combinations of maximum depth and criterion were tested. The maximum depth of the tree was considered as 6 and the Squared_error criterion (which uses Poisson deviance to find the splits among the data) is used for splitting the values to get the optimum solution. All the other parameters are set to default values. The values of Slope Angle less than or equal to 960 go to the left side, and those of greater than 960 go to the right side. The accuracy score of the training data set is 0.973 and the accuracy score of the testing data is 0.373. The feature importance of various features is listed in the below table (See Table 6). It is observed that the Slope Angle was given more importance, i.e., 0.6961. Figure 8 demonstrates the relation between actual and predicted FOS and R² was observed as 0.893.

TABLE 6

TABLE 6. Key parameters and feature importance of decision tree model.

5.2 Random forest model

The random forest approach, a tree-based ensemble learning technique where every tree is reliant on numerous randomly selected factors, was invented by Leo Breiman (Breiman, 2001). In order to forecast slope stability and landslide susceptibility, the Random Forest has been applied (Youssef et al., 2015; Lin et al., 2018b). Random forest is often considered to be a rival to the boosting and the continuation of bagging (Breiman, 1996). The random forest theory is illustrated in Figure 4. Due to their superior performance, machine learning techniques including support vector machines, random forests, and neural networks are utilized generally nowadays. These function effectively, however, practitioners who consider themselves to be domain-independent frequently do not comprehend how they operate and instead simply input data into these algorithms without considering how they might be used (Vigneau et al., 2018). As a result, this study will begin with an examination of the benefits and drawbacks of the random forest before delving into its applicability. The following questions will be answered as a result of this research: What types of data or forecasts are appropriate for random forests and which are not. This work principal research method is assessing and combining current literature study results.

FIGURE 4

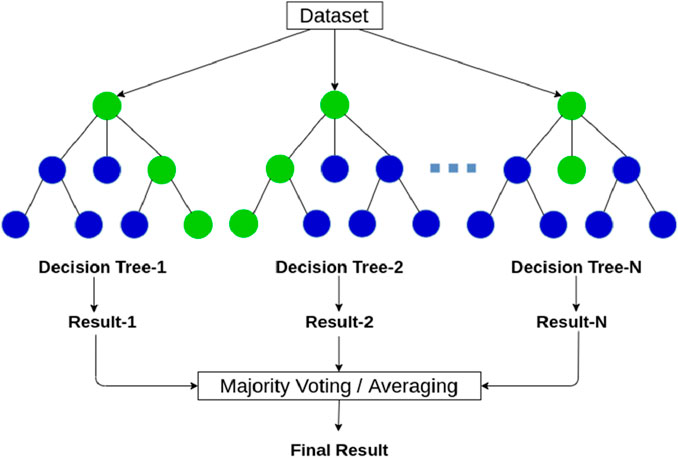
FIGURE 4. Random forest understanding (towardsdatascience, 2022)

The purpose of this research is to assist people who are having trouble choosing a good machine-learning algorithm. Significant RF regression variables including ntree, maximum depth, subsample, and mtry are said to have an impact on the effectiveness of the produced RF model as well as its application for error minimization. (Sharafati et al., 2019; Bui et al., 2020b). A huge proportion of relatively irrelevant models working together as a committee will perform better than any individual constituent model by mitigating and shielding one another from one another’s flaws (Huang and Boutros, 2016). Computational benefits: Issues with classification and regression, such as multi-class classification, can be handled by the astonishingly adaptable and very accurate Random Forest (Zhu, 2020). It is also relatively quick to train and predict. Table 7 presented the key and feature importance parameters considered while optimal results. Finally, the ideal RF model was defined with the Number of estimators was 10, and the maximum depth was selected at 7. Figure 9 declares the plot between actual and predicted FOS. In addition, the recorded R² of 0.886.

TABLE 7

TABLE 7. Key and feature importance parameters used in random forest model.

5.3 XGBOOST model

The XGBoost ensemble method (Zhang et al., 2022) uses a grade-boosting frame and has been extensively employed in the famed Kaggle contests because of its high efficacy and enough stiffness (Chen and Guestrin, 2016; Ragam et al., 2022). The XGBOOST technique, developed in 2016 by Chen and Guestrin, can efficiently construct boosted trees (Chen and Guestrin, 2016). This method’s fundamental premise is that classification or regression trees (RTs) are generated one at a time, and the subsequent model is trained using the residuals from the earlier trees. It combines the calculated values based on the first trained trees to improve the training process. Pruning is required to avoid overfitting, which shrinks the size of the decision tree by deleting nodes that do not significantly contribute to the goal values (Zhang et al., 2022). This is how the prediction was calculated.

${\widehat{\mathit{y}}}_{\mathit{i}}^{\left(\mathit{t}\right)}={\mathit{\Sigma }}_{\mathit{k}-\mathbf{1}}^{\mathit{t}}{\mathit{f}}_{\mathit{k}}\left({\mathit{x}}_{\mathit{i}}\right)={\widehat{\mathit{y}}}_{\mathit{i}}^{\left(\mathit{t}-\mathbf{1}\right)}+{\mathit{f}}_{\mathit{t}}\left({\mathit{x}}_{\mathit{i}}\right)$

Where, ${\widehat{y}}_i^{\left(t\right)}$ represents the finished tree model, ${\widehat{y}}_i^{\left(t-1\right)}$ is the former tree model, $x_i$ represents the features corresponding to the sample i, t is indeed the sum of the number of base tree models, and $f_t\left(x_i\right)$ is the most recently generated tree model. To achieve the best performance, it is essential to choose the right depth and quantity of trees. As a result, the objective function $Ob{j}^{\left(t\right)}$ can be expressed as:

$\mathit{O}\mathit{b}{\mathit{j}}^{\left(\mathit{t}\right)}={\mathit{\Sigma }}_{\mathit{i}=\mathbf{1}}^{\mathit{t}}\mathit{l}\left({\mathit{y}}_{\mathit{i}},{\widehat{\mathit{y}}}_{\mathit{i}}^{\left(\mathit{t}\right)}\right)+{\mathit{\Sigma }}_{\mathit{i}=\mathbf{1}}^{\mathit{t}}\mathit{\Omega }\left(|{\mathit{f}}_{\mathit{i}}\right)$

Where, $y_i$ is the factual value, how well the model fits the training set of data is described by the loss function $l\left(y_i,{\widehat{y}}_i^{\left(t\right)}\right)$, and the punishment term for normalization to prevent overfitting is $\mathrm{\Omega }\left(f_i\right)$ . Following (Friedman, 2000), the objective function can be converted into

$\mathbf{0}\mathit{b}{\mathit{j}}^{\left(\mathit{t}\right)}=\left[{\mathit{g}}_{\mathit{i}}{\mathit{f}}_{\mathit{i}}\left({\mathit{x}}_{\mathit{i}}\right)+\frac{\mathbf{1}}{\mathbf{2}}{\mathit{h}}_{\mathit{i}}{\mathit{f}}_{\mathit{t}}^{\mathbf{2}}\left({\mathit{x}}_{\mathit{i}}\right)\right]+\mathit{\Omega }\left(|{\mathit{f}}_{\mathit{t}}\right)$

Where, $g_i=\partial {\widehat{y}}_i^{\left(t-1\right)}l\left(y_i,{\widehat{y}}_i^{\left(t-1\right)}\right)$ and $h_i=\partial ²{\widehat{y}}_i^{\left(t-1\right)}l\left(y_i,{\widehat{y}}_i^{\left(t-1\right)}\right)$ are the loss function’s first and second-order partial derivations, respectively. To lessen model complexity, prevent overfitting, and enhance generalizability, the penalty term $\mathrm{\Omega }\left(f_t\right)$ is employed. It is predicted by the following equation: $\mathit{\Omega }\left(|{\mathit{f}}_{\mathit{t}}\right)=\mathit{\gamma }\mathit{T}+\frac{\mathbf{1}}{\mathbf{2}}\mathit{\lambda }{‖\mathit{w}‖}^{\mathbf{2}}$

With default values of 1 and 0, respectively, w is the weight assigned to each leaf, T is the total number of leaves, and $\lambda$ and $\gamma$ are the coefficients. The parameters adopted during the selection of optimal results are shown in Table 8. The correlation graph reveals that the R² between actual FOS and predicted FOS was 0.927, as shown in Figure 10.

TABLE 8

TABLE 8. Key and feature importance parameters used in XGBoost model.

5.4 Ensemble hybrid XGBOOST- RF model

Gradient-boosted decision trees and other gradient-boosted models are frequently trained with XGBoost. XGBRF also referred to as the implementation of Random Forest on the Extreme Gradient Boosting Regression, is used to provide improved results and predictions. XGBoost comes under the Boosting Algorithm, while RF comes under the bagging algorithm. Here for the base estimator, RFs are used. The model structure and inference are the same for Random Forests and Gradient-Boosted Decision Trees, but the training methodology is different. Various combinations of Maximum Features, Number of Estimators, and Random State is made to discover the best fit. Optimum accuracy is achieved when the number of estimators is 300, and the maximum depth is considered as 9. All the other parameters are set to default. The accuracy score of the training data set is 0.988 and the accuracy score of the testing data is 0.568. One of the crucial hyperparameters to choose for the XGBoost-RF is the number of trees. Typically, the number of trees is increased until the model performance stabilizes. Intuition might suggest that more trees will lead to overfitting, although this is not the case. Both bagging and RF algorithms appear to be somewhat immune to overfitting the training dataset given the stochastic nature of the learning algorithm. The most crucial element to select for RF could be the number of features that are randomly sampled at each split point. Here, autonomous RF training is the major focus. Since the beginning, provided native APIs for training random forests, and with version 0.82, included a fresh Scikit-Learn wrapper (not included in 0.82). Here, it reserves the right to modify the user interface as necessary because the new Scikit-Learn wrapper is currently in the experimental stage. Important XGBoost-RF ensemble algorithm properties to consider when tuning for the best results and feature importance parameters are illustrated in Tables 9. In addition, Figure 11 includes a comparison of the estimated and actual FOS along with the linear relationship of the XGBoost-RF model. In this process, the R² between the actual and estimated FOS is 0.931. It is inferred that the proposed ensemble hybrid XGBoost-RF model has the ability to estimate the slope FOS close to actual FOS values.

TABLE 9

TABLE 9. Key and feature importance parameters used in XGBoost-RF.

6 Evaluation metrics

Numerous widely used statistical performance evaluation standards can be used to assess the efficacy of developed machine learning algorithms. The coefficient of determination (R²), root mean square error (RMSE), mean square error (MSE), normalized root mean square error (NRMSE), mean absolute percentage error (MAPE), and mean absolute deviation (MAD) are the evaluation statistical measures used in this context are listed in Table 10.

TABLE 10

TABLE 10. List of performance metrics.

7 Results and discussion

FOS is key parameter to measure the slope stability to avoid the mishaps due to slope failure in opencast mines. To determine optimal solution for such failures and analyse the connection between slope failure and its indispensable properties, this current study made an endeavour to propose ensemble based machine learning algorithms which capable of establishing a relationships between FOS and its influenced parameters. In this context, developed and applied ML estimated models such as MLR, Decision Tree, RF, XGBoost, and an ensemble hybrid model XGBoost-RF by taking into account of five input influenced parameters such as unit weight, cohesion, friction angle, slope angle, minimum depth, and one out parameter (FOS). The prediction capabilities of the suggested and developed predictive models must be carefully examined while modeling FOS. Other input variables, however, may have an impact on the slope stability FOS.

7.1 Data exploratory analysis

The optimal strategy to solve the high non-linear issues determine by the behavior of adopted dataset during simulation procedure. Hence, it is essential to aware the statistical dataset description at the pre-processing stage in ML modelling. Table 4 depicts the statistical data and its range in FOS estimation process. Similarly, Figure 5 demonstrates the pair plot correlation coefficient between all variables in the dataset.

FIGURE 5

FIGURE 5. Pair plot correlation coefficient between input and target variable.

The heat map depicting the Pearson correlation is shown in Figure 6. It evaluates the linear connection between two attributes by calculating their values. The Pearson correlation was used to calculate the correlation between the two characteristics. The values of the correlation coefficients varied from −1 to +1. There is less association when the value is closer to 0. A value of 0 indicates no association. A stronger positive or negative correlation is indicated by a number that is closer to 1 or -1, respectively. The Slope Angle and Friction Angle were shown to have the highest positive correlation.

FIGURE 6

FIGURE 6. Heat map of Pearson’s correlation coefficient for all FOS variables.

The key findings of this current work indicate that the ensemble hybrid techniques performed well than the others. The 79 slope stability event values are collected from Ostapal Chromite Mines, India to assess the FOS. All used models were implemented using the same amount of training and testing, i.e., 85% for training and 15% for testing datasets.

7.2 Outcomes of modelling

The accuracy and agreements of the developed ensemble hybrid ML algorithms are analysed using six comparative evaluation metrics such as coefficient of determination (R²), means square error (MSE), root mean square error (RMSE), normalized root mean square error (NRMSE), mean absolute deviation (MAD), and mean absolute percentage error (MAPE). The evaluation error matrix is implemented to show the agreement and accuracy level of developed models. Five algorithms were performed based on training and testing process and evaluated their performance. Table 11 shows the MSE, RMSE, NRMSE, MAD and MAPE values attained by developed ML models. It evident that XGBoost-RF outperformed the other models in predicted the FOS.

TABLE 11

TABLE 11. Parameters evaluation of created prediction models.

In addition, Figures 7–11 demonstrate the correlation graph of predicted FOS of all ML models with actual FOS. The obtained results reveal that the XGBoost-RF hybrid ensemble approach provides high R² (0.931), MSE (0.009), RMSE (0.098), NRMSE (0.069), MAD (0.00370), and MAPE (3.85), among all other ML approaches for accurate prediction of FOS. For better understanding, the stack bar diagram of all attained performance metrics of predicted models shown in Figure 12. From Figure 12, it is observed that the XGBoost-RF model yielded significant performance as compared to the other prediction models to estimate the FOS. The best hyper parameters are tuned using sklearn. model_selection.GridSearchCV. GridSearchCV is a method used to find the hyper parameters that five optimum accuracy using K-Fold Cross Validation technique.

FIGURE 7

FIGURE 7. MLR model.

FIGURE 8

FIGURE 8. Decision tree regression.

FIGURE 9

FIGURE 9. Random forest model.

FIGURE 10

FIGURE 10. XGBoost regression model.

FIGURE 11

FIGURE 11. XGBoost-RF regression model.

FIGURE 12

FIGURE 12. Performance evaluation metrics of all predicting models.

8 Conclusion

The present study in this work is the current research and development trend towards the transformation of traditional mining into intelligent mining. The necessity for transformation is to estimate slope safety (FOS) in open-cast mines. The mine named Ostapal Chromite Mine, M/s Facor Limited in India is selected for carrying out this study and the details of the mine including geological information, mine workings, and data required for the completion of the current study were collected. The following conclusions were drawn from the present investigation. They are:

• In estimating the levels of FOS at Ostapal Chromite Mine, India, ensemble machine learning models outperformed traditional predictor models, according to the study’s main findings. It should be emphasized that on 79 different input datasets, each of the developed machine learning models performed admirably. Particularly, throughout modeling, there were no overfitting issues. A trial-and-error procedure was implemented to get the optimal architecture.

• Machine learning models include MLR, Decision Tree, Random Forest (RF), XGBoost, and ensemble hybrid XGBoost-RF were successfully applied for prediction of slope’s FOS. In this study, five input parameters such as unit weight, cohesion, friction angle, slope angle, minimum depth, and single output parameter i.e., FOS are considered.

• From the obtained results (see Table 11), it interprets that the ensemble hybrid-based XGBoost-RF model showed a significant R² (0.931), MSE (0.009), NRMSE (0.069), MAD (0.037), MAPE (3.581) and least RMSE (0.098) compared with the other ML model analysis.

• For future investigation, complex hybrid metaheuristic architecture algorithms such as PSO-XGBoost, XGBoost optimization with gray wolf, whale, and Bayesian, can be implemented to enhance the XGBoost algorithm performance to assess the FOS.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

PR: Conceptualization, Investigation, Methodology, Writing–original draft, Writing–review and editing. NK: Software, Writing–original draft. AJ: Writing–review and editing. GK: Conceptualization, Data curation, Writing–original draft. VH: Investigation, Resources, Supervision, Writing–review and editing. DS: Software, Validation, Visualization, Writing–review and editing. BR: Formal Analysis, Supervision, Writing–review and editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Arunav, C., and Diganta, G. (2016). State of art: three dimensional(3D) slope stability analysis. Int. J. Geotech. Eng. 10 (5), 1–6. doi:10.1080/19386362.2016.1172807

CrossRef Full Text | Google Scholar

Arunav, C., and Diganta, G. (2017). Prediction of slope stability using multiple linear regression (MLR) and artificial neural network (ANN). Arab. J. Geosci. 10 (17), 385. doi:10.1007/s12517-017-3167-x

CrossRef Full Text | Google Scholar

Breiman, L. (1996). Bagging predictors. Mach. Lear. 24 (2), 123–140. doi:10.1007/bf00058655

CrossRef Full Text | Google Scholar

Breiman, L. (2001). Random forests. Mach. Lear. 45 (1), 5–32. doi:10.1023/a:1010933404324

CrossRef Full Text | Google Scholar

Bui, X. N., Nguyen, H., Choi, Y., Nguyen-Thoi, T., Zhou, J., and Dou, J. (2020a). Prediction of slope failure in open-pit mines using a novel hybrid artificial intelligence model based on decision tree and evolution algorithm. Sci. Rep. 10 (1), 9939–10017. doi:10.1038/s41598-020-66904-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Bui, X. N., Nguyen, H., Le, H. A., Bui, H. B., and Do, N.-H. (2020b). Prediction of blast-induced air over-pressure in open-pit mine: assessment of different artificial intelligence techniques. Nat. Resour. Res. 29 (2), 571–591. doi:10.1007/s11053-019-09461-0

CrossRef Full Text | Google Scholar

Chen, T., and Guestrin, C. (2016). XGBoost: a scalable tree boosting system in proceedings of the 22nd ACM SIGKDD international conference on knowledge discovery and data mining. J. ACM., 785–787. doi:10.1145/2939672.2939785

CrossRef Full Text | Google Scholar

Choobbasthi, A. J., Zad, F., and Barari, A. (2009). Prediction of slope stability using artificial neural network (case study: noabad, Mazandaran, Iran). Arab. J. Geosci. 2 (4), 311–319. doi:10.1007/s12517-009-0035-3

CrossRef Full Text | Google Scholar

Choobbasti, A. J., Farrokhzad, F., and Ami, B. (2009). Prediction of slope stability using artificial neural network (case study: noabad, Mazandaran, Iran). Geosci. 2 (4), 311–319. doi:10.1007/s12517-009-0035-3

CrossRef Full Text | Google Scholar

Christoph, S., Jan, M., Luis, P. S., Patrick, S., and Torsten, W. (2022). Strain-dependent slope stability for earthquake loading. Comput. Geotechnics 152, 105048. doi:10.1016/j.compgeo.2022.105048

CrossRef Full Text | Google Scholar

Cornell, C. A. (1969). A probabilistic based structural code. J. Proc. 66 (12), 974–985. doi:10.14359/7446

CrossRef Full Text | Google Scholar

Deris, A. M., Solemon, B., and Omar, R. C. (2021). A comparative study of supervised machine learning approaches for slope failure production. Yogyakarta: The 8th International Conference on Science and Technology. Available at: https://www.e3s-conferences.org/articles/e3sconf/abs/2021/101/e3sconf_icst2021_01001/e3sconf_icst2021_01001.html.

Google Scholar

Ding, X., Bahadori, M., Hasanipanah, M., and Abdullah, R. A. (2023a). Predicting the rock fragmentation in surface mines using optimized radial basis function and cascaded forward neural network models. Geomech. Eng. 33, 567–581. doi:10.12989/gae.2023.33.6.567

CrossRef Full Text | Google Scholar

Ding, X., Jamei, M., Hasanipanah, M., Abdullah, R. A., and Le, B. N. (2023b). Optimized data-driven models for prediction of flyrock due to blasting in surface mines. Sustainability 15 (May 22), 8424. doi:10.3390/su15108424

CrossRef Full Text | Google Scholar

Fattahi, H., and Hasanipanah, M. (2021). An indirect measurement of rock tensile strength through optimized relevance vector regression models, a case study. Environ. Earth Sci. 80, 748–812. doi:10.1007/s12665-021-10049-2

CrossRef Full Text | Google Scholar

Feezan, A., Xiowei, T., Jiangnan, Q., Piotr, W., Mahmood, A., and Irfan, J. (2022). Prediction of slope stability using Tree Augmented Naive-Bayes classifier: modeling and performance evaluation. Math. Biosci. Eng. 19 (5), 4526–4546. doi:10.3934/mbe.2022209

PubMed Abstract | CrossRef Full Text | Google Scholar

Fellenius, W. (1927). “Erdstatische Berechnungen mit Reibung und Kohasion (Adhasion) und unter Annahme kreiszylindrischer Gleitflachen” Berlin. Germany: W. Ernst and Sohn. Available at: https://www.worldcat.org/title/erdstatische-berechnungen-mit-reibung-und-kohasion-adhasion-und-unter-annahme-kreiszylindrischer-gleitflachen/oclc/18623301.

Google Scholar

Freudenthal, A. (1947). The safety of structures. Trans. Am. Soc. Civ. Eng. 112 (1), 125–159. doi:10.1061/taceat.0006015

CrossRef Full Text | Google Scholar

Friedman, J. H. (2000). Greedy function approximation: a gradient boosting machine. Ann. Stat. 29 (5), 1189–1232. doi:10.1214/aos/1013203451

CrossRef Full Text | Google Scholar

Gagan, G., Sanjay, S. F., and Singh, G. S. P. (2022). Dump slope stability analysis using artificial intelligence. J. Mines Met. Fuels. 70 (3), 129–135. doi:10.18311/jmmf/2022/30445

CrossRef Full Text | Google Scholar

Gao, W., Dai, S., Xiao, T., and He, T. (2017). Failure process of rock slopes with cracks based on the fracture mechanics method. Eng. Geol. 231, 190–199. doi:10.1016/j.enggeo.2017.10.020

CrossRef Full Text | Google Scholar

Gao, Y., Zhang, F., Lei, G. H., Li, D., Wu, Y., and Zhang, N. (2012). Stability charts for 3D failures of homogeneous slopes. J. Geotechnical Geoenvironmental Eng. 139 (9), 1528–1538. doi:10.1061/(asce)gt.1943-5606.0000866

CrossRef Full Text | Google Scholar

Gexue, B., Yunglong, H., Baofeng, W., Ning, A., Yihao, Y., Zheng, T., et al. (2022). Performance evaluation and engineering verification of machine learning based prediction models for slope stability. Appl. Sci. 12 (15), 7890. doi:10.3390/app12157890

CrossRef Full Text | Google Scholar

Hasanipanah, M., Jamei, M., Mohammed, A. S., Amar, M. N., Hocine, O., and Khedher, K. M. (2022b). Intelligent prediction of rock mass deformation modulus through three optimized cascaded forward neural network models. Earth Sci. Inf. 15, 1659–1669. doi:10.1007/s12145-022-00823-6

CrossRef Full Text | Google Scholar

Hasanipanah, M., Keshtegar, B., Thai, D. K., and Troung, N. T. (2022a). An ANN-adaptive dynamical harmony search algorithm to approximate the flyrock resulting from blasting. Eng. Comput. 38, 1257–1269. doi:10.1007/s00366-020-01105-9

CrossRef Full Text | Google Scholar

Huang, B. F. F., and Boutros, P. C. (2016). The parameter sensitivity of random forests. BMC Bioinform 17 (1), 331. doi:10.1186/s12859-016-1228-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Huang, S., Huang, M., and Lyu, Y. (2020). An improved KNN-based slope stability prediction model. Adv. Civ. Eng. 2020 (11), 1–16. doi:10.1155/2020/8894109

CrossRef Full Text | Google Scholar

Jingjing, M., Hans, M., and Jan, L. (2021). Three-dimensional slope stability predictions using artificial neural networks. Int. J. Numer. Anal. Methods Geomech. 45 (13), 1988–2000. doi:10.1002/nag.3252

CrossRef Full Text | Google Scholar

Kanule, J. (2021). Hydro mechanical slope stability analysis: modelling, monitoring and prediction using BP-FF artificial neural networks. Kenya: Ph.D dissertation, University of Eldoret.

Google Scholar

Kardhani, N., Zhou, A., Nazem, M., and Shen, S.-L. (2021). Improved prediction of slope stability using a hybrid stacking ensemble method based on finite element analysis and field data. J. Rock Mech. Geotech. Eng. 13 (1), 188–201. doi:10.1016/j.jrmge.2020.05.011

CrossRef Full Text | Google Scholar

Lee, Y.-S., Wang, J.-R., Zhan, J.-W., and Zhang, J.-M. (2020). Data mining analysis of overall team information based on internet of things. IEEE Access 8, 41822–41829. doi:10.1109/access.2020.2976728

CrossRef Full Text | Google Scholar

Lin, Y., Zhou, K., and Li, J. (2018a). Prediction of slope stability using four supervised learning methods. IEEE Access 6, 31169–31179. doi:10.1109/access.2018.2843787

CrossRef Full Text | Google Scholar

Lin, Y., Zhou, K.-P., and Li, J.-L. (2018b). Prediction of slope stability using four supervised learning methods. IEEE Access 6, 31169–31179. doi:10.1109/access.2018.2843787

CrossRef Full Text | Google Scholar

Mahmoodzadeh, A., and Mohammadi, M. (2023) Forecasting factor of safety of slopes stability using several machine learning techniques. Res. Sq. 23, 2023. doi:10.21203/rs.3.rs-669928/v1

CrossRef Full Text | Google Scholar

Maria, F., and Muhammad, F. (2018). Integrating rock engineering systems device and artificial neural networks to predict stability conditions in an open pit. Eng. Geol. 246 (1), 293–309. doi:10.1016/j.enggeo.2018.10.010

CrossRef Full Text | Google Scholar

Marrapu, B. M., and Jakka, R. S. (2017). Assessment of slope stability using multiple regression analysis. Geomechanics Eng. 13 (2), 237–254. doi:10.12989/gae.2017.13.2.237

CrossRef Full Text | Google Scholar

McCulloch, W. S., and Pitts, W. (1943). A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biol. 5 (4), 115–133. doi:10.1007/bf02478259

CrossRef Full Text | Google Scholar

Michael, S., and Maria, F. (2021). A study of slope stability prediction using neural networks. Geotech. Geol. Eng. 23 (4), 419–445. doi:10.1007/s10706-004-8680-5

CrossRef Full Text | Google Scholar

Michalowski, R. L., and Drescher, A. (2009). Three-dimensional stability of slopes and excavations. Géotechnique 59 (10), 839–850. doi:10.1680/geot.8.p.136

CrossRef Full Text | Google Scholar

Nicholas, D. E., and Sims, D. B. (2000). Collecting and using geologic structure data for slope design,” SLOPESTABILITY in surface mining. Tucson, Arizona, USA: Society for Mining, Metallurgy, and Exploration, 11–26. Available at: https://www.cnitucson.com/publications/2000_ch2_col&using_geol_data_sme_den_ds.pdf.

Google Scholar

Orang, F., and Faradjollah, A. (2003). Three-dimensional analysis of nonhomogeneous slopes. J. Geotechnical Geoenvironmental Eng. 129 (2), 137–145. doi:10.1061/(asce)1090-0241(2003)129:2(137)

CrossRef Full Text | Google Scholar

Paliwal, M., Goswami, H., Ray, A., Bharati, A. K., Rai, R., and Khandelwal, M. (2022). Stability prediction of residual soil and rock slope using artificial neural network. Adv. Civ. Eng. 2022, 1–14. doi:10.1155/2022/4121193

CrossRef Full Text | Google Scholar

Ragam, P., Komalla, A. R., and Kanne, N. (2022). Estimation of blast-induced peak particle velocity using ensemble machine learning algorithms: a case study. Noise Vib. 57, 404–413. doi:10.1177/09574565221114662

CrossRef Full Text | Google Scholar

Raghuvanshi, T. K. (2019). Plane failure in rock slopes – a review on stability analysis techniques. J. King Saud. Univ. Sci. 31 (1), 101–109. doi:10.1016/j.jksus.2017.06.004

CrossRef Full Text | Google Scholar

Sha, L. (2016). Analysis of slope instability factors and protection. Int. J. Multidiscip. Res. Dev. 3 (4), 181–182.

Google Scholar

Sharafati, A., Khosravi, K., Khosravinia, P., Ahmed, K., Salman, S. A., Yaseen, Z. M., et al. (2019). The potential of novel data mining models for global solar radiation prediction. Int. J. Environ. Sci. 16 (11), 7147–7164. doi:10.1007/s13762-019-02344-0

CrossRef Full Text | Google Scholar

Simmons, J. V., and Simpson, P. J. (2006). Composite failure mechanisms in coal measures rock masses-myths and reality. J. South. Afr. Inst. Min. Metall. 106, 459–469.

Google Scholar

Sina, S. H., Sami, S. H., Zong Woo, G., Tae-Hyung, K., Reza, M., Luigi, P., et al. (2021). Application of harmony search algorithm to slope stability analysis. Land 10 (11), 1250. doi:10.3390/land10111250

CrossRef Full Text | Google Scholar

Sjoberg, J. (2000). Failure mechanisms for high slopes in hard rock,” SLOPESTABILITY in surface mining. Tucson, Arizona, USA: Society for Mining, Metallurgy, and Exploration, 71–80. ch. 7.

Google Scholar

towardsdatascience (2022). Understanding random forest-how the algorithm works and why it is so effective. Available at: https://towardsdatascience.com/understanding-random-forest-58381e0602d2.

Google Scholar

Vigneau, E., Courcoux, P., Symoneaux, R., Guerin, L., and Villière, A. (2018). Random forests: a machine learning methodology to highlight the volatile organic compounds involved in olfactory perception. Food Qual. Prefer 68, 135–145. doi:10.1016/j.foodqual.2018.02.008

CrossRef Full Text | Google Scholar

Wang, X., and Niu, R. (2009). Spatial forecast of landslides in three gorges based on spatial data mining. Sensors 9 (1), 2035–2061. doi:10.3390/s90302035

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, Y., Rezaei, M., Abdullah, R. A., and Hasanipanah, M. (2023). Developing two hybrid algorithms for predicting the elastic modulus of intact rocks. Sustainability 15 (Feb 26), 4230. doi:10.3390/su15054230

CrossRef Full Text | Google Scholar

Xu, W., Kang, Y., Chen, L., Wang, L., Qin, C., Zhang, L., et al. (2023). Dynamic assessment of slope stability based on multi-source monitoring data and ensemble learning approaches: a case study of Jiuxianping landslide. Geol. J. 58 (6), 2353–2371. doi:10.1002/gj.4605

CrossRef Full Text | Google Scholar

Youssef, A. M., Pourghasemi, H. R., Pourtaghi, Z. S., and Al-Katheeri, M. M. (2015). Landslide susceptibility mapping using random forest, boosted regression tree, classification and regression tree, and general linear models and comparison of their performance at Wadi Tayyah Basin, Asir Region, Saudi Arabia. Landslides 13 (5), 839–856. doi:10.1007/s10346-015-0614-1

CrossRef Full Text | Google Scholar

Yusuf, E., and Tulin, C. (2012). The use of neural networks for the prediction of the critical factor of safety of an artificial slope subjected to earthquake forces. Sci. Iran. 19 (2), 188–194. doi:10.1016/j.scient.2012.02.008

CrossRef Full Text | Google Scholar

Zhang, W., Li, H., Han, L., Chen, L., and Wang, L. (2022). Slope stability prediction using ensemble learning techniques: a case study in Yunyang County, Chongqing, China. J. Rock. Mech. Geotech. Eng. 14 (4), 1089–1099. doi:10.1016/j.jrmge.2021.12.011

CrossRef Full Text | Google Scholar

Zhihao, L., and Zhiwei, L. (2020). Slope stability evaluation using backpropagation neural networks and multivariate adaptive regression splines. Open Geosci. 12 (1), 1263–1273. doi:10.1515/geo-2020-0198

CrossRef Full Text | Google Scholar

Zhihao, L., and Zhiwei, L. (2022). Slope stability evaluation using backpropagation neural networks and multivariate adaptive regression splines. Open Geosci. 12 (1), 1263–1273. doi:10.1515/geo-2020-0198

CrossRef Full Text | Google Scholar

Zhu, T. (2020). Analysis on the applicability of the random forest. J. Phys. Conf. Ser. 1607 (1), 012123. doi:10.1088/1742-6596/1607/1/012123

CrossRef Full Text | Google Scholar