- College of Civil Engineering, Guizhou University, Guiyang, Guizhou, China
To describe the full-stage creep behavior of layered rock accurately, a new elastic-viscoplastic creep model is proposed based on fractional order theory in this manuscript, which consists of a Hooke elastomer, a fractional Abel dashpot, a Kelvin body, and a new non-linear visco-plastic component. The non-linear creep model can not only describe the changes in three creep stages (primary creep, steady-state creep and accelerating creep) but also reflect the influence of different bedding angles of rock. The constitutive equations of the non-linear creep model are deduced by the empirical model method and plastic theory method, respectively. The parameters of the non-linear creep model are identified using the Levenberg-Marquardt algorithm from Origin. It shows that the creep model in this paper are highly consistent with the experimental data under different load levels, creep stages and bedding angles, and the accuracy and rationality of the model are verified. Moreover, the creep constitutive equations for layered rock derived by the two methods have the same fitting effect on the same set of experimental data.
1 Introduction
Rock rheology refers to the continuous adjustment and recombination of rock and mineral fabric (skeleton) with the growth of time, resulting in the continuous increase and change of its stress and strain state with time (Sun, 2007a). The rheology of rock includes creep, stress relaxation and elastic aftereffects. Especially, the creep characteristics of rock are of great significance to the stability of rock engineering, and the research on this aspect is also of great significance and engineering application value. The study of creep characteristics of rock began in the 1930s, Griggs (Griggs, 1939) carried out a series of creep tests on rocks such as limestone, shale and sandstone in 1939, and concluded that rock creep occurs when the load reaches 12.5%–80.0% of its compressive strength. Several elasto-viscoplastic creep models have been proposed that can well describe the time-dependent behavior of rock under certain conditions (Wu et al., 2018; Brantut et al., 2013; Sone et al., 2014; Xia et al., 2009). In general, the classical rock rheological model theory is mainly limited to linear rheological problems, and there are two main methods to describe non-linear rheological problems of rock. The first method is to replace the linear model theory with a new non-linear rheological theory completely, such as internal time theory, fracture and damage mechanics theory, etc. The other method is to improve the classical model theory by using non-linear components (non-linear spring or non-linear dashpot) instead of linear elements.
The component model is widely used because of its intuitive concept and clear meaning. Classical component combination models include the Maxwell model, Kelvin model, Poyting-Thomson model, Burgers model and Nishihara model. However, the basic element of the classical model is linear, it is still linear whether connection in series or parallel, and can not describe the non-linear creep characteristics of the rock in the accelerating stage. Therefore, establishing a creep model which can describe the non-linear characteristics of the rock creep process has always been a hot and difficult point in the theoretical research of rock mechanics. In the present research, scholars (Cheng et al., 2020; Shan et al., 2020; Wang and Wan, 2016; Yang and Jiang, 2022) having been established different non-linear creep models by introducing creep damage theory (Shen et al., 2023a; Zhang et al., 2022a) and fractional calculus theory. The constitutive model based on fractional calculus theory with fewer parameters and better fitting effect has been widely applied in rock rheological mechanics. A classical example is Koeller (Koeller, 1984) used Riemann–Liouville (R-L) fractional dashpot to replace the traditional Newtonian dashpot in the component model in 1978. The R-L type (Zhou et al., 2018) or Caputo type (Liu et al., 2020) fractional order calculus theory is used to construct fractional dashpot to replace the traditional Newtonian dashpot in the element model, and to establish a creep model that can describe the three stages (primary creep, steady-state creep and accelerating creep) of rock creep. However, it lacks physical significance in the accelerating creep, and it can not well characterize the internal mechanism of accelerating creep of rock. Therefore, damage factors were introduced to describe the accelerating creep of rock, and establish an elasto-viscoplastic creep model reflecting the complete creep process of rock by combining fractional calculus theory and damage theory (Deng et al., 2022; Shen et al., 2022; Wu et al., 2018) becoming a relatively popular study method. In addition, scholars have study the mechanical characteristics about the concrete-rock combination (Shen et al., 2022; Zhang et al., 2019) and other interface (Shen et al., 2023b; Zhang et al., 2023). By comparing the creep model established by fractional calculus theory, it is based on the assumption that there are two stages (hardening and damage) in the creep of rock, and with clear physical significance for describing the accelerating creep stage. However, due to various ways of defining damage factors and increasing model parameters, the calculation is inconvenient.
There are abundant of achievements on creep characteristics for common rock, but few studies on creep characteristics for layered rock. In the basic mechanics study area, Ramamurthy (Ramamurthy, 1993) carried out a study on the physical and mechanical properties of rock with different bedding angles, explored the anisotropy law of strength and deformation. Yong (Yong Tsao, 2000; Yong, 2001) studied the effect of the bedding angle on the strength and elastic modulus for layered rock, proposed corresponding damage guidelines. Fortsakis (Fortsakis et al., 2012) modeled the bedding as separate units and the rock masses as anisotropic materials to investigate the differences in the analysis of isotropic, anisotropic and transverse isotropic analysis methods. Studies has also shown the influence of bedding angles in the basic mechanical properties for layered rock (Celleri et al., 2018; Chang et al., 2020; Hb et al., 2003; Saeidi et al., 2014; Wu et al., 2015; Yang et al., 2021). In the experimental creep study, Dubey (Dubey and Gairola, 2008) investigated the creep properties of salt rocks containing horizontal, vertical and diagonal laminations at different stress levels by uniaxial compression creep tests, and noted that the higher the stress level, the less the laminations affected the anisotropy of the creep properties of salt rocks. In recent years, some scholars (Hu et al., 2019; Liu et al., 2015; Xu et al., 2019; Zhang et al., 2021) have also studied the anisotropic creep law of layered rock by uniaxial compression creep tests and triaxial compression creep tests. In addition, the creep properties of layered rock under the coupling of multiple factors have been studied (Tang et al., 2018). In the study of creep constitutive model for layered rock, an approach is to inductively derive an empirical model from experimental phenomena (Park et al., 2016; Zhang et al., 2022b). It is based on the assumption of constant volume modulus, then to establish a creep constitutive model by identifying the creep parameters in different directions as different mutually independent values. Another approach is the plasticity theory model by assumption of Poisson’s ratio constant (Aravas et al., 1995; Kou et al., 2023; Wang et al., 2018), which to establish the three-dimensional creep constitutive model for transverse isotropic rock by using the transverse isotropic flexibility matrix replace the isotropic flexibility matrix.
Based on the above analysis, the creep mechanics properties of rock has been widely studied, but less for layered rock. Therefore, a non-linear fractional creep model for layered rock was established in this manuscript by introducing a non-linear Abel dashpot. The model connected the Hooke body, non-linear Abel dashpot body, linear Kelvin body and non-linear viscoplastic body in series. Further more, the non-linear elastic-viscoplastic creep constitutive equations for layered rock were derived. A practical method for model parameters identification is proposed, and finally the accuracy and applicability of the model is verified by using different rock compression creep test data from relevant literature.
2 Rock creep processes and basic mechanical models
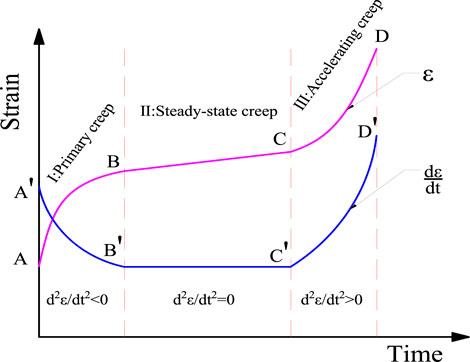
The typical creep curve of rock is shown in Figure 1. The
When a load is applied, the rock then undergoes a transient elastic creep in section
Where
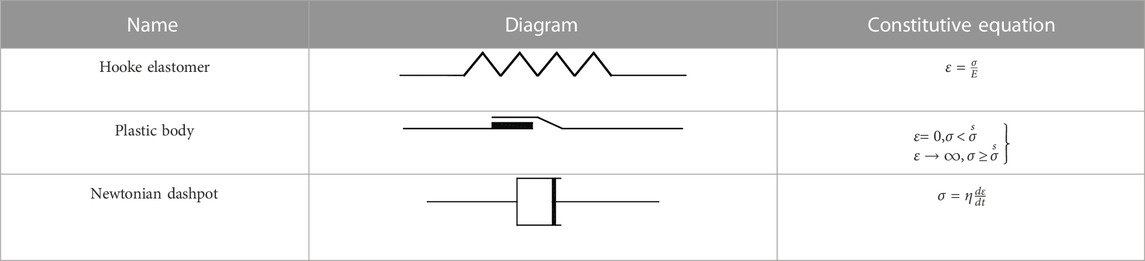
In rheological theory, a rock creep model should be able to characterise the processes of decay creep, steady-state creep and accelerating creep, and reflect the creep characteristics of the rock at different stress levels. The basic units of the rheological model are generally divided into elastic, plastic and viscous elements, and the mechanical model of the three basic units is shown in Table 1.
As the intrinsic relationships of the basic components are linear, the various classical rheological models, such as the Maxwell, Kelvin, Burgers and Nishihara models (Behbahani et al., 2016; Feng, 2021), which consist of basic components connected in series or parallel, are also linear in nature.
3 Establishment of elastic-viscoplastic creep model
3.1 Plastic body elements based on fractional order derivatives
3.1.1 Definition of fractional calculus
Fractional order calculus is an extension of integer order calculus. Since the 1990s, the theory and methods of fractional order calculus have been widely applied to various fields of the natural and social sciences. In the area of viscous fluid mechanics, the introduction of fractional order calculus theory allows for more realistic theoretical models to be developed in the study of mechanical physical problems associated with real fluids, leading to accurate conclusions. The Riemann–Liouville (R-L) type fractional order calculus is commonly used in the theory of rock rheology studies (Zhou et al., 2018), but its fractional order derivatives are hyper-singular and limited in applications in engineering and technology and in physical modeling. In this paper, we use a theory of fractional order derivatives with weak singular properties proposed by the Italian geophysicist Caputo. The Caputo fractional order derivative solves the fractional order initial value problem in the definition of R-L type fractional order calculus and has been widely used in the modeling process of many practical application problems (Liu et al., 2021). The definition of Caputo fractional order derivative is
where
The Caputo fractional operator is shown in Eq. 5:
The Laplace transform formula for the Caputo fractional order derivative is
where
3.1.2 Establishment of fractional order viscoelastic and viscoplastic bodies
The theory of fractional order calculus is applied to the traditional Newtonian dashpot to construct a fractional dashpot, called the Abel dashpot. As shown in Figure 4:
Define the stress-strain equation for the Abel dashpot as
Where η is the viscosity coefficient;
When
In the study of rock creep mechanics,
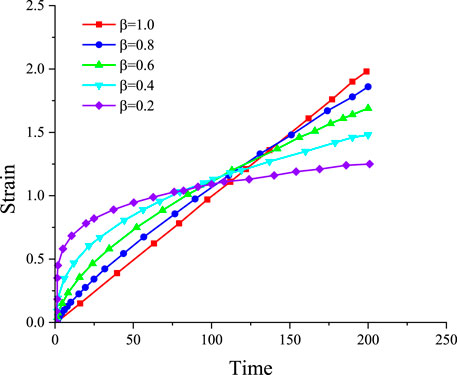
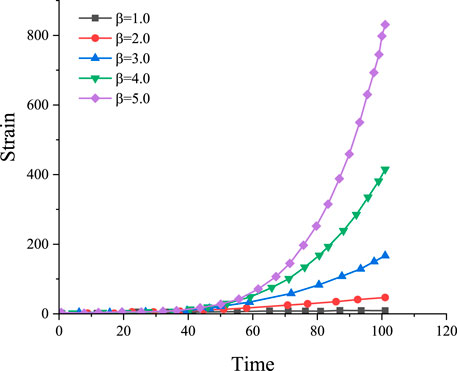
For Eq. 8, if
As shown in Figures 2, 3, the growth rate of
Substituting Eq. 7 into Eq. 9, the fractional order viscoplastic body creep constitutive relationship as:
where
3.2 Elastic-viscoplastic creep model
3.2.1 The elastic-viscoplastic creep model and one-dimensional creep equation
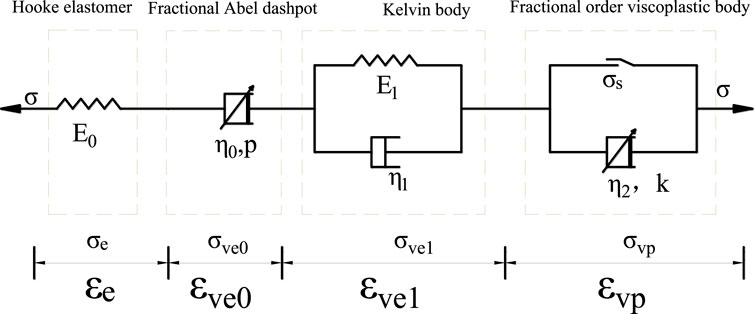
Based on fractional order calculus theory and Boltzmann superposition principle, a six-element non-linear elastic-viscoplastic creep model is proposed as shown in Figure 4 in this paper. The model consists of a Hooke elastomer, an Abel dashpot body, a Kelvin body, and a fractional order viscoplastic body in series. In this case, the instantaneous creep of the rock is characterized by Hooke elastomer. The non-linear decay creep is characterized by the Abel dashpot body. The steady-state creep is approximated by a constant strain with time, as
According to the series-parallel law for the combined element model, when the stress is a constant, the stress-strain relationship for the six-element non-linear elastic-viscoplastic creep model as the following equation shows:
where
(i) When
The creep equation of the Hooke elastomer and Abel dashpot body is
For kelvin body, according to the parallel law, there is
So, the creep constitutive equation of kelvin body is
Solve Eq. 15, obtain the creep equation of the linear kelvin body is
where
Substituting Eqs 13, 16 into Eq. 12, access the equation of
(ii) When
Combining Eq. 10, Eq. 13 and Eq.16 and substituting them into Eq. 18, access the equation of
In summary, the non-linear creep equation for rock in a one-dimensional stress state is as follows:
3.2.2 Three-dimensional creep equation
In geotechnical engineering, rocks are often in a complex three-dimensional stress state. Therefore, in order to reflect the creep properties of rocks in geotechnical engineering more accurately, the three-dimensional creep constitutive equation should be adopted. According to the theory of elasticity, the internal stress tensor
where
Under the condition of the three dimensional stress, assuming the total strain of the non-linear creep model is
In rock creep tests, when the first order stress level applied is less than the long-term strength of the rock, the rock develops transient strain rapidly, and the constitutive relationship at this stage can be described by a Hooke elastomer.
For the Hooke elastomer, the elastic constitutive relation can be expressed by Hooke’s Law as
where
Hence, the strain of the Hooke elastomer can be written as
When the stress keep loading, the rock enters a non-linear decay creep phase, which is described by the Abel dashpot in this paper, and the three-dimensional creep constitutive equation as:
Then, the rock will undergo steady-state creep, use the conventional linear Kelvin body to describe this phase of the rock creep process in this paper. Assuming that the volume change is elastic and the rheological properties are mainly in terms of shear deformation (Sun, 2007b), the three-dimensional creep constitutive equation is
where
When the stress deviator tensor
In a three-dimensional stress state, when stress exceeds the viscoplastic yield surface, a viscoplastic strain will be generated. Based on Perzyna’s limit stress flow law (Perzyna, 1966; Aydan, 2016), the three-dimensional creep equation for fractional order viscoplastic body in the accelerating creep phase can be obtained as
where
Combining Eqs 26–30 into Eq. 23, obtain the three-dimensional creep equation as follow
The classical rock strength criterion includes Mohr-coulomb criterion, Tresca criterion, Von-Mises criterion and Drucker-Prager criterion, et al. However, the Mohr-coulomb and Tresca criterion considers only the maximum and minimum principal stress of the three principal stresses and does not consider the effect of intermediate principal stresses in the material. The Von-Mises criterion does not consider the effect of hydrostatic pressure on yielding and damage. The Drucker-Prager yield criterion improves the corner singularity problem of the Mohr-Coulomb criterion, and is also suitable for describing the yield behavior of rock materials. Therefore, the Drucker-Prager criterion is chosen as the yield criterion for rock creep analysis in this paper. In creep deformation, the creep yield deformation of rock materials mainly results from the deviator stress tensor, and the spherical stress tensor has little effect on yield deformation (Zheng and Kong, 2006), which is defined by
where
In the true triaxial stress environment, the rock is stressed from three directions, and there is
Considering the triaxial creep experiment in the normal triaxial stress status, i.e., σ1 >σ2 = σ3, we can obtain
Substituting Eqs 32–34 into Eq. 31, the full-stage creep strain under the three-dimensional stress state is obtained as follows:
Where
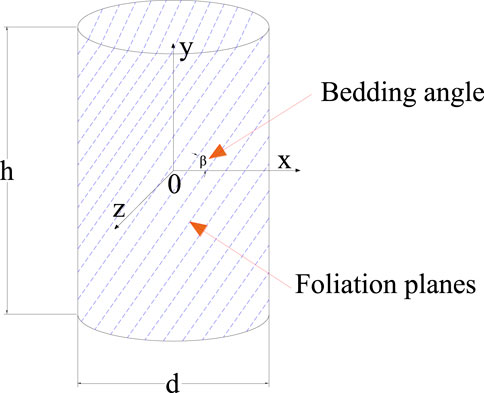
3.3 Non-linear creep model for layered rock
Due to the existence of weak bedding planes, layered rock often shows obvious anisotropy characteristic, specifically transverse isotropic characteristics. According to the results of tests in the available literature (Hu et al., 2019; Liu et al., 2015; Xu et al., 2019; Zhang et al., 2021), the angle of the laminae has a large influence on the creep properties of the rock. For transverse isotropic material creep models, the research literature (Wang et al., 2018) is divided into two main types, namely, empirical models generalized by experiment and theoretical models resolved by plasticity theory. Based on the viscoelastic-plastic creep model established in this paper, the empirical model method and the plasticity theory analytical method are used to derive the intrinsic constitutive equations of the creep model for layered rock, and the relevant experimental data are used for comparative analysis and verification.
3.3.1 Creep equation of empirical model
The establishment method of the empirical model for layered rock creep is based on the model of isotropic materials. The creep equation of layered rock is derived by introducing the influence of laminae on the mechanical properties of rock creep. For example, Tang (Tang et al., 2018) gave the relationship between the elastic modulus, creep rate and bedding angle at the same moisture content by uniaxial compression creep test as
where
The paper introduces functional expressions of elastic modulus and creep rate, and proposes a one-dimensional creep constitutive equation for layered shale based on the Burgers model. However, the creep model for the accelerating creep stage was not given in that paper. Wang (Wang, 2020) obtained the anisotropic characteristics of long-term strength, peak strength and elastic modulus of sandstones with different bedding angles by triaxial creep tests.
In this paper, based on the research, the non-linear elastic-viscoplastic whole process creep equation for layered rock is derived analogously from the isotropic rock material creep model constitutive equation. The one-dimensional creep equation of the elastic-viscoplastic creep of layered rock is
where
Accordingly, with reference to the derivation of the three-dimensional creep equation for isotropic rock materials, the three-dimensional creep equation of the elastic-viscoplastic creep of layered rock is
3.3.2 Creep equation based on plastic theory
The plasticity theory analytical method based on the assumption of constant Poisson’s ratio (Dathe et al., 2001). It is assumed that Poisson’s ratio does not change with time and stress, and is equivalent to the value of elastic stage,
Then, Eq. 20 can be described as
For isotropic rock, the creep compliance substitution method can be used to obtain the basic form of the three-dimensional creep equation of rock as follows (Li et al., 2021):
where
For Eq. 41, scholars (Aravas et al., 1995; Kou et al., 2023) have carried out a detailed solution, which is not repeated in this paper. Based on the creep constitutive model established in this paper, the three-dimensional creep constitutive equation for layered rock is derived as
where
4 Parameter identification and model validation
4.1 Parameter identification of non-layered rock creep model
4.1.1 The one-dimensional non-linear creep model
The uniaxial compression non-linear creep model is shown in Eq. 20, and parameters of the model to be determined are
(i) The parameters of
In the transient elastic creep stage,
(ii) The parameters of
(iii) The parameters of
Selecting the corresponding creep test data of
4.1.2 Three-dimensional non-linear creep model
The triaxial compression non-linear creep model is shown in Eq. 35, and the model parameters to be determined are
then Eq. 35 can be described as
The process of parameter identification is:
(i) The parameters of
Based on the elastic modulus
(ii) The parameters of
The parameter of
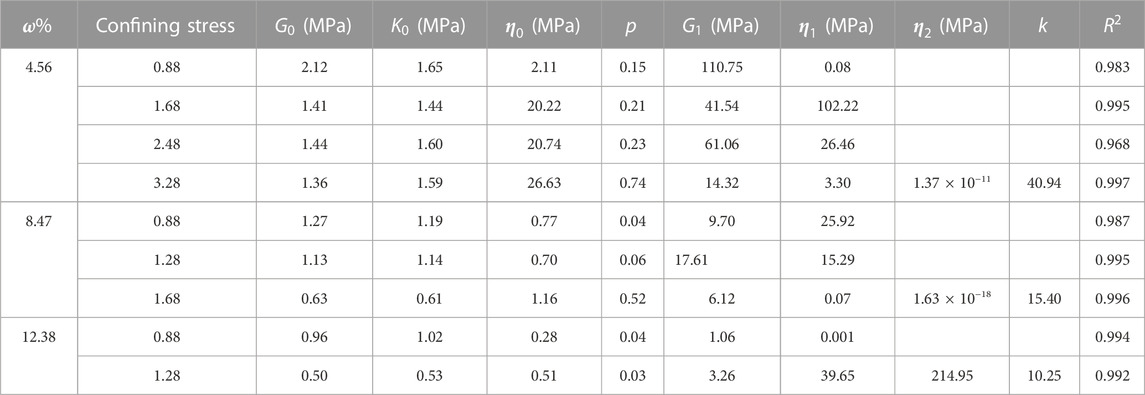
4.2 Parameter identification of layered rock creep model
The non-linear creep model for layered rock is shown in Eqs 37, 38 and Eq. 42, and the parameters identification method is similar to the non-layered rock creep model. In view of space, do not repeat.
4.3 Parameter identification and model validation
4.3.1 One-dimensional non-linear creep model
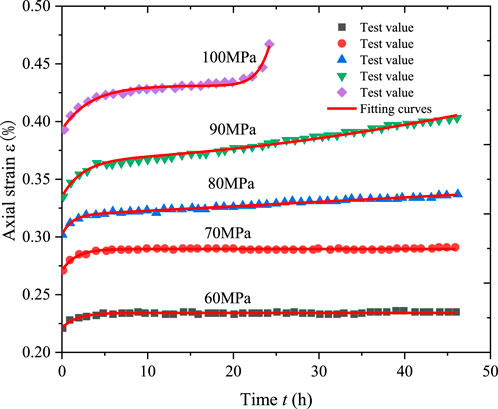
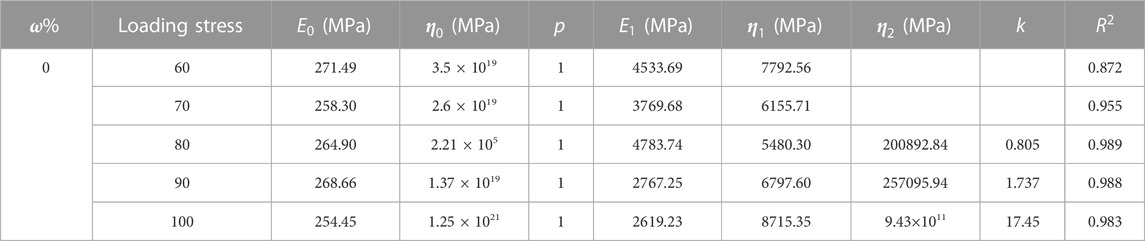
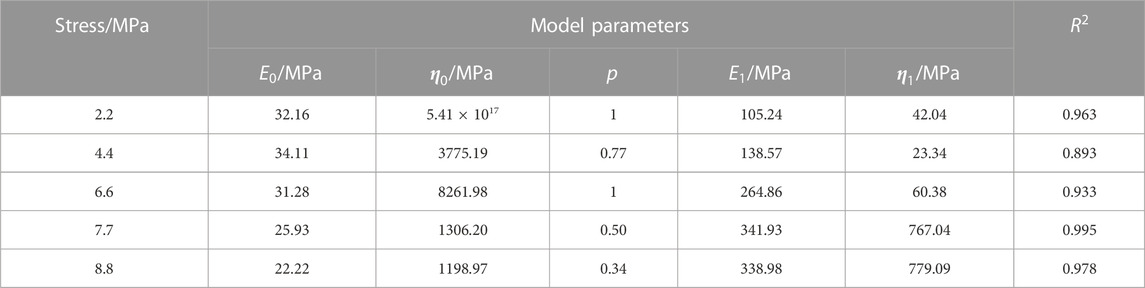
The experimental data used for parameter identification in the one-dimensional creep equation is chosen from Wang (Wang et al., 2020). The test was carried out using the MTS815.02 Multifunctional Servo Test System for uniaxial compression creep testing of sandstone with graded loading, and the long-term strength given in the paper is 70 MPa. In this paper, data from the water content test set
Showing in Figure 7, the proposed creep model can accurately describe the characteristics of three phases of rock creep, the rationality is verified. The parameters of the creep model listed in Table 2.
4.3.2 The three-dimensional non-linear creep model
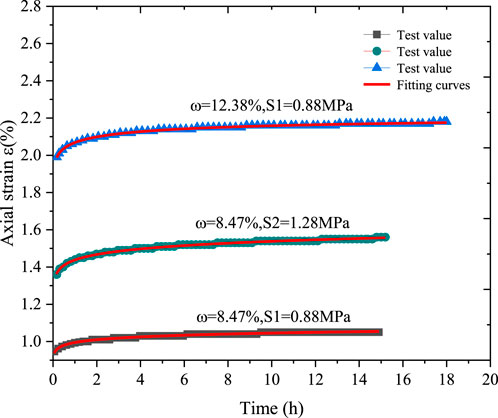
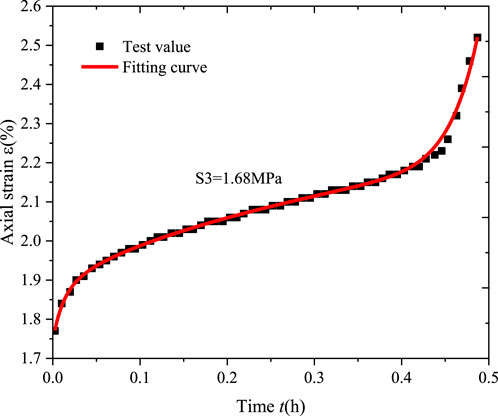
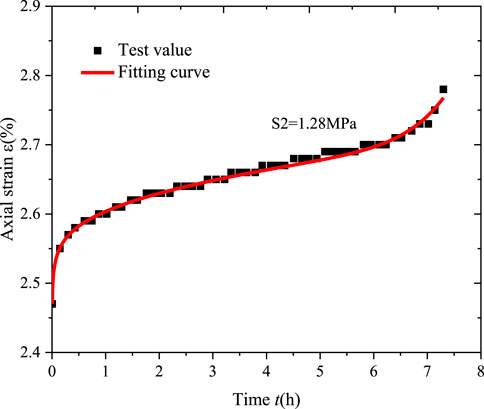
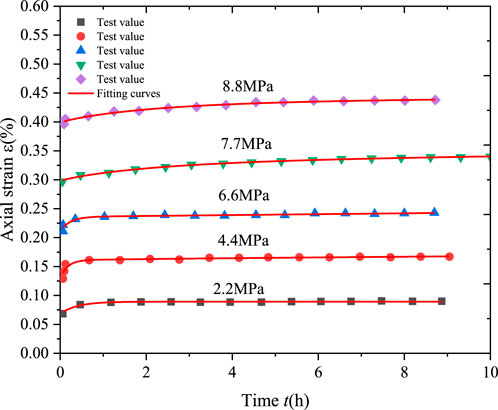
The experimental data used for parameter identification in the three-dimensional creep equation is chosen from Ye (Ye et al., 2022). This test was carried out for triaxial compression creep tests at different water contents
Using the method of the previous Section 4.1.2 for model parameters identification. When the loading stress level is less than the yield strength, the first equation of Eq. 35 is used for nonlinear fitting. The fit of the experimental data to the creep equation was obtained as shown in Figures 8–10.
When the loading stress level is greater than the yield strength, a step-wise non-linear fitting is made by the second equation of Eq. 35. The fitting curve of the moisture content under low-stress level is shown in Figure 8, and the fitting curve of the moisture content of
Analyzing Figures 7, 10, the creep model not only describes the viscoelastic behavior in the decay creep and steady-state creep phases of the rock in uniaxial creep experiment and triaxial creep experiment well under low stress, but also has a good representation of the non-linear mechanical behavior in the accelerating creep phase of the rock under high-stress conditions. Furthermore, as seen in Tables 2, 4, the correlation between experimental data and fitting curves is high. The reasonableness and applicability of the fractional order creep model proposed in this paper are verified.
4.3.3 Creep model for layered rock
(i) Creep Equation of Empirical Model
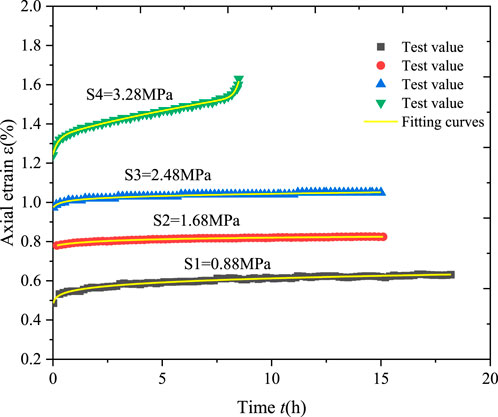
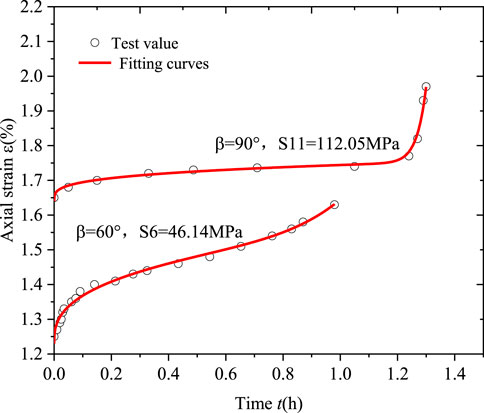
The experimental data used for parameter identification in the one-dimensional creep equation is chosen from Tang (Tang et al., 2018). Selecting the data of
The parameters of the creep model listed in Table 5.
The experimental data used for parameter identification in the three-dimensional creep equation is chosen from Wang (J. Wang et al., 2020). The author took the triaxial compression creep tests on five sets of specimens with bedding angles of
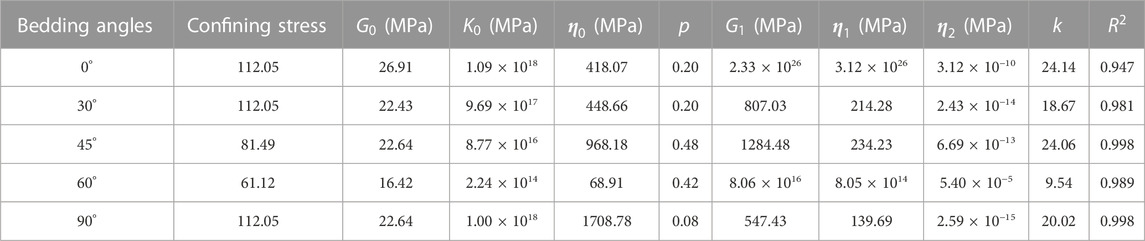
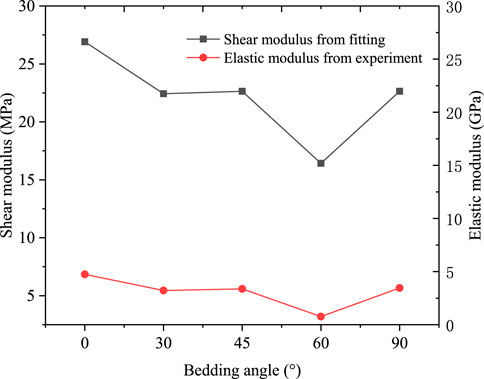
The parameters of the creep model are listed in Table 6.
Based on the parameters from Table 6, giving the plotting of
(ii) Creep Equation of Plasticity Theory
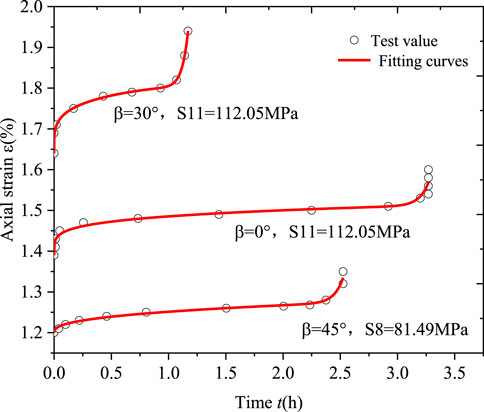
Experimental data were used from the literature (Kou et al., 2023). In the literature, step-wise loading triaxial creep tests of phyllite specimens with three kinds of bedding angles (0°, 45° and 90°) are carried out with the confining pressure of 10 MPa. In this paper, the last stage accelerating creep test data of 0° and 90° layered rock is taken to validate the plasticity theory creep equation and compared with the empirical model creep equation simultaneously. The elastic mechanical parameters of the rock are shown in Table 7. For the bedding angle of 0°, the elastic modulus, poission ratio and long-term strength of rock is
For Eq. 42, let
Then Eq. 42 is expressed as
Substituting the elastic parameters from Table 9 into Eq. 45, then
Substituting Eq. 47 into Eq. 46, fitting the experimental data as shown in Figure 16. For the creep equation of the empirical model, the same set of experimental data was fitted by Eq. 38 using the method described in Section 4.1.2.
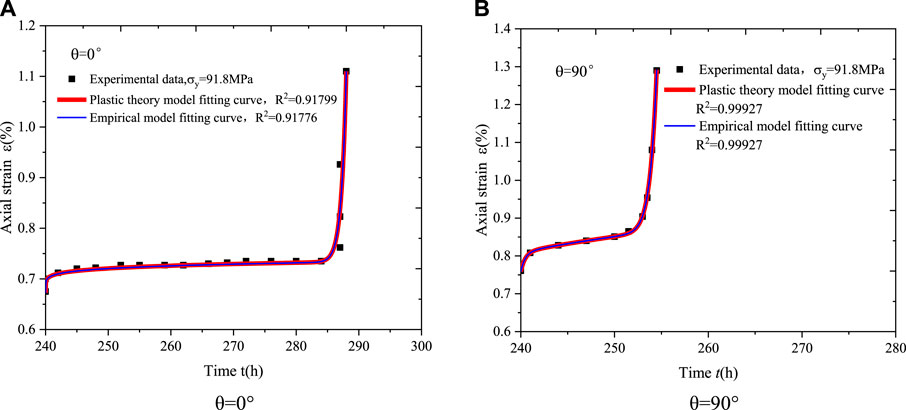
FIGURE 16. Fitting curves of creep equation by empirical model and plastic theory model [(A,B) is the bedding angle of 0°,90° respectively].
The creep constitutive equations for layered rock derived by the above two methods were fitting by the same set of experimental data, and a curve fit of the experimental data to the creep equation was obtained as shown in Figure 16.
The parameters of the two models are shown in Table 7.
As seen in Figure 16 and Table 7, the fitting curves of the creep constitutive equation for layered rock derived by the two methods are almost identical and have the same fitting correlation coefficients.
In summary, the non-linear creep model derived in this paper can not only better characterize the creep properties of layered rock under low and high-stress conditions, but also better reflect the influence of different bedding angles on the creep mechanical properties of rocks. In addition, the empirical creep constitutive equation derived in this paper and the plastic theory creep constitutive equation has almost the same fitting results for the same set of experimental data, which further verifies the accuracy and applicability of the creep constitutive model for layered rock established in this paper.
5 Conclusion
Based on fractional-order calculus theory and rheological element combination model theory, a six-element nonlinear elastic-viscoplastic creep model is given. The model is used as the basis for deriving the non-linear elastic-viscoplastic creep constitutive equation for layered rock, and the accuracy and applicability of the creep constitutive equation are verified by selecting creep experimental data for rocks of different lithologies. The main conclusions are as follows:
(1) Based on fractional calculus theory to introduce the Abel dashpot body, combined with the classical creep strain-time curve of rock for analysis, the Hooke elastomer, Abel dashpot body, Kelvin body and non-linear viscoplastic body are connected in series, and a six-element non-linear elastic-viscoplastic creep model is established. Then, the creep constitutive equation for one-dimensional and three-dimensional are derived respectively.
(2) Analysing the creep experimental data of layered rock, and concluding that the effects of different bedding angles on the creep properties of the rock are mainly the elastic modulus, creep rate and long-term strength, and deriving the full process creep constitutive equation for layered rock by empirical model method and the plastic theory method, respectively.
(3) Based on the Levenberg-Marquardt iterative method of Origin software, a practical identification method of creep model parameters is proposed, and parameters are identified by using rocks of different lithologies under different stress conditions from experimental data.
(4) By fitting the creep experimental data of layered rock with different lithologies to the theoretical curves of the model, it is shown that the model proposed in this paper can not only accurately describe the full-stage creep (primary creep, steady-state creep and accelerating creep) of layered rock, but also better reflect the influence of different bedding angles on the creep properties of rocks. As shown in the tables, the average value of
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author contributions
YL: Data curation, Investigation, Writing–original draft, Writing–review and editing. MS: Investigation, Methodology, Writing–review and editing, Writing–original draft. BD: Funding acquisition, Investigation, Methodology, Resources, Supervision, Writing–review and editing. SY: Investigation, Writing–original draft.
Funding
The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This research was supported by the National Natural Science Foundation of China (No. 52268022). The author BD is the leader of this project.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The reviewer JJ declared a shared affiliation with the authors to the handling editor at the time of review.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Al-Rub, R., Darabi, M. K., Kim, S. M., Little, D. N., and Glover, C. J. (2013). Mechanistic-based constitutive modeling of oxidative aging in aging-susceptible materials and its effect on the damage potential of asphalt concrete. Constr. Build. Mater. 41 (apr), 439–454. doi:10.1016/j.conbuildmat.2012.12.044
Aravas, N., Cheng, C., and Casta Eda, P. P. (1995). Steady-state creep of fiber-reinforced composites: constitutive equations and computational issues. Int. J. Solids Struct. 32 (15), 2219–2244. doi:10.1016/0020-7683(94)00251-Q
Behbahani, H., Ziari, H., and Kamboozia, N. (2016). Evaluation of the visco-elasto-plastic behavior of glasphalt mixtures through generalized and classic burger's models modification. Constr. Build. Mater. 118, 36–42. doi:10.1016/j.conbuildmat.2016.04.157
Celleri, H. M., Martín, S., and Otegui, J. L. (2018). Fracture behavior of transversely isotropic rocks with discrete weak interfaces: fracture behavior of ti rocks with discrete weak interfaces. Int. J. Numer. Anal. Methods Geomech. 42, 2161–2176. doi:10.1002/nag.2849
Chang, X., Zhao, H., and Cheng, L. (2020). Fracture propagation and coalescence at bedding plane in layered rocks. J. Struct. Geol. 141 (2), 104213. doi:10.1016/j.jsg.2020.104213
Cheng, H., Zhou, X., Pan, X., and Berto, F. (2020). Damage analysis of sandstone during the creep stage under the different levels of uniaxial stress using nmr measurements. Fatigue Fract. Eng. Mater. Struct. 44, 719–732. doi:10.1111/ffe.13389
Dathe, A., Eins, S., Niemeyer, J., and Gerold, G. (2001). The surface fractal dimension of the soil-pore interface as measured by image analysis. Geoderma Int. J. Soil Sci. 103 (1/2), 203–229. doi:10.1016/S0016-7061(01)00077-5
Deng, H., Zhou, H., Jia, W., Li, L., and Su, T. (2022). A nonlinear triaxial damage creep model for granite based on atangana–baleanu fractional derivative. Int. J. Appl. Mech. 14. doi:10.1142/S1758825122500685
Dubey, R. K., and Gairola, V. K. (2008). Influence of structural anisotropy on creep of rocksalt from simla himalaya, India: an experimental approach. J. Struct. Geol. 30 (6), 710–718. doi:10.1016/j.jsg.2008.01.007
Feng, Z. Q., Yang, X. J., Liu, J. G., and Chen, Z. Q. (2021). A new fractional nishihara-type model with creep damage considering thermal effect. Eng. Fract. Mech. 242 (1), 107451. doi:10.1016/j.engfracmech.2020.107451
Fortsakis, P., Nikas, K., Marinos, V., and Marinos, P. (2012). Anisotropic behaviour of stratified rock masses in tunnelling. Eng. Geol. 141-142 (none), 74–83. doi:10.1016/j.enggeo.2012.05.001
Hb, M., Nasseri, H., S, K., Rao, , et al. (2003). Anisotropic strength and deformational behavior of himalayan schists. Int. J. Rock Mech. Min. Sci. 40, 3, 23. doi:10.1016/S1365-1609(02)00103-X
Hu, B., Yang, S. Q., Xu, P., and Cheng, J. L. (2019). Cyclic loading–unloading creep behavior of composite layered specimens. Acta geophys. 67, 449–464. doi:10.1007/s11600-019-00261-x
Koeller, R. C. (1984). Applications of fractional calculus to the theory of viscoelasticity. Trans. Asme J. Appl. Mech. 51 (2), 299–307. doi:10.1115/1.3167616
Kou, H., He, C., Yang, W., Wu, F., Zhou, Z., Fu, J., et al. (2023). A fractional nonlinear creep damage model for transversely isotropic rock. Rock Mech. Rock Eng. 56 (56), 831–846. doi:10.1007/s00603-022-03108-y
Li, L., Guan, J., Xiao, M., and Zhuo, L. (2021). Three-dimensional creep constitutive model of transversely isotropic rock. Int. J. Geomech. 21 (8), 21. doi:10.1061/(asce)gm.1943-5622.0002111
Liu, X., Li, D., and Han, C. (2020). A nonlinear damage creep model for sandstone based on fractional theory. Arab. J. Geosci. 13 (6), 246. doi:10.1007/s12517-020-5215-1
Liu, X., Li, D., and Han, C. (2021). A caputo fractional damage creep modeland its experimental validation. Mech. Time-Depend. Mater. 26 (26), 909–922. doi:10.1007/s11043-021-09519-8
Liu, Z. B., Xie, S. Y., Shao, J. F., and Conil, N. (2015). Effects of deviatoric stress and structural anisotropy on compressivecreep behavior of a clayey rock. Appl. Clay Sci. 114, 491–496. doi:10.1016/j.clay.2015.06.039
Moghadam, S. N., Mirzabozorg, H., and Noorzad, A. (2013). Modeling time-dependent behavior of gas caverns in rock salt considering creep, dilatancy and failure. Tunn. Undergr. Space Technol. 33 (Jan.), 171–185. doi:10.1016/j.tust.2012.10.001
Park, K. H., Jung, Y. H., and Chung, C. K. (2016). Evolution of stiffness anisotropy during creep of engineered silty sand in South Korea. KSCE J. Civ. Eng. 21, 2168–2176. doi:10.1007/s12205-016-1105-1
Perzyna, P. (1966). Fundamental problems in viscoplasticity. Adv. Appl. Mech. 9 (2), 243–377. doi:10.1016/S0065-2156(08)70009-7
Saeidi, O., Rasouli, V., Vaneghi, R. G., Gholami, R., and Torabi, S. R. (2014). A modified failure criterion for transversely isotropic rocks. Geosci. Front. 5 (2), 215–225. doi:10.1016/j.gsf.2013.05.005
Shan, R. L., Bai, Y., Ju, Y., Han, T. Y., and Li, Z. L. (2020). Study on the triaxial unloading creep mechanical properties and damage constitutive model of red sandstone containing a single ice-filled flaw. Rock Mech. Rock Eng. 54 (6), 833–855. doi:10.1007/s00603-020-02274-1
Shen, M., Bi, J., Zhao, Y., Wang, C., Wei, T., and Du, B. (2022). Study on the mechanical characteristics and damage evaluation of concrete-rock combination after high temperatures exposure. Constr. Build. Mater. 330, 127278. doi:10.1016/j.conbuildmat.2022.127278
Shen, M., Zhao, Y., Bi, J., Wang, C., Du, B., and Zhang, K. (2023b). In situ experimental study on mechanical properties of interlayer in roller compacted concrete (rcc) dam. Constr. Build. Mater. 379, 131268. doi:10.1016/j.conbuildmat.2023.131268
Shen, M., Zhao, Y., Bi, J., Wang, C., Ning, L., Deng, X., et al. (2023a). Micro-damage evolution and macro-mechanical property of preloaded sandstone subjected to high-temperature treatment based on nmr technique. Constr. Build. Mater. 369, 130638. doi:10.1016/j.conbuildmat.2023.130638
Sun, J. (2007a). Rock rhelogical mechanicals and its advance in engineering applications. Chin. J. Rock Mech. Eng. 26 (6), 1081–1106. doi:10.1097/00000542-199411000-00017
Sun, J. (2007b). Rock rhelogical mechanicals and its advance in engineering applications. Chin. J. Rock Mech. Eng. 26 (6), 1081–1106.
Tang, J., Teng, J., and Zhang, C. (2018). Experimental study of creep characteristics of layered water bearing shale. Rock Soil Mech. 39 (S1), 33–41. doi:10.16285/j.rsm.2017.1709
Wang, J., Meng, L., Liu, T., and Chen, H. (2020). Analysis of the influence of sandstone bedding structure on its mechanical properties. Railw. Stand. Des. 64 (04), 130–135. doi:10.13238/j.issn.1004-2954.201904040003
Wang, X., and Wan, L. (2016). Nonlinear creep model of rock in consideration of damage. Sci. Technol. Eng.
Wang, Y. (2020). Study on uniaxial compression creep test of sandstone and improvement of nishihara model. J. Lanzhou Inst. Technol. 27 (05), 10–14.
Wang, Z., Zong, Z., Qiao, L., and Li, W. (2018). Elastoplastic model for transversely isotropic rocks. Int. J. Geomech. 18 (2), 4017141–4017149. doi:10.1061/(ASCE)GM.1943-5622.0001070
Wu, B., Jia, S. P., and Luo, J. Z. (2015). Anisotropic composite model for layered rock mass based on characteristics of soft interfaces. Material Res. Innovations 19 (1)–S1-245. doi:10.1179/1432891715Z.0000000001478
Wu, F., Jie, C., and Zou, Q. (2018). A nonlinear creep damage model for salt rock. Int. J. Damage Mech. 28, 1281561184. doi:10.1177/1056789518792649
Xu, G., He, C., Yan, J., and Ma, G. (2019). A new transversely isotropic nonlinear creep model for layered phyllite and its application. Bull. Eng. Geol. Environ. 78, 5387–5408. doi:10.1007/s10064-019-01462-w
Yang, X., and Jiang, A. (2022). An improved nonlinear creep damage model of slates considering freeze–thaw damage and bedding damage. Bull. Eng. Geol. Environ. 81, 240–246. doi:10.1007/s10064-022-02740-w
Yang, X. W., Zhang, X. P., Zhang, Q., Li, C. D., and Wang, D. J. (2021). Study on the mechanisms of crack turning in bedded rock. Eng. Fract. Mech. 247, 107630. doi:10.1016/j.engfracmech.2021.107630
Ye, W., Qili, W., Wenjing, L., Xiongyao, X., and Biao, Z. (2022). Compressive creep property and model for unsaturated argillaceous siltstone. J. TONGJI Univ. Sci. 50 (08), 1154–1162. doi:10.11908/j.issn.0253-374x.21326
Yong, M. T., and Tsao, P. F. (2000). Preparation and mechanical properties of artificial transversely isotropic rock. Int. J. Rock Mech. Min. Sci. 37 (6), 1001–1012. doi:10.1016/S1365-1609(00)00024-1
Yong, T., and Kuo, M. C. (2001). A failure criterion for transversely isotropic rocks. Int. J. Rock Mech. Min. Sci. 38, 399–412. doi:10.1016/S1365-1609(01)00007-7
Zhang, J., Zhang, X., Huang, Z., and Fu, H. (2022a). Transversely isotropic creep characteristics and damage mechanism of layered phyllite under uniaxial compression creep test and its application. Environ. Earth Sci. 81 (20), 499–518. doi:10.1007/s12665-022-10585-5
Zhang, J., Zhang, X., Huang, Z., Yi, Y., and Zhao, X. (2021). Energy evolution mechanism of the mechanical and creep properties of layered phyllite under uniaxial compression and creep tests. Arab. J. Geosci. 14 (22), 2437–2513. doi:10.1007/s12517-021-08757-x
Zhang, Z., Jin, X., and Luo, W. (2019). Long-term behaviors of concrete under low-concentration sulfate attack subjected to natural variation of environmental climate conditions. Cem. Concr. Res. 116, 217–230. doi:10.1016/j.cemconres.2018.11.017
Zhang, Z., Pang, K., Xu, L., Zou, Y., Yang, J., and Wang, C. (2023). The bond properties between uhpc and stone under different interface treatment methods. Constr. Build. Mater. 365, 130092. doi:10.1016/j.conbuildmat.2022.130092
Zhang, Z., Zou, Y., Yang, J., and Zhou, J. (2022b). Capillary rise height of sulfate in portland-limestone cement concrete under physical attack: experimental and modelling investigation. Cem. Concr. Compos. 125 (125-), 104299. doi:10.1016/j.cemconcomp.2021.104299
Zheng, Y., and Kong, L. (2006). Generalized plastic mechanics and its application. Eng. Sci. 4 (1), 21–36. doi:10.1007/s11769-005-0030-x
Keywords: layered rock, elastic-viscoplastic creep, constitutive model, fractional calculus, non-linear analysis
Citation: Li Y, Shen M, Du B and Yuan S (2023) An elastic-viscoplastic creep model for describing creep behavior of layered rock. Front. Mater. 10:1286197. doi: 10.3389/fmats.2023.1286197
Received: 31 August 2023; Accepted: 13 October 2023;
Published: 13 November 2023.
Edited by:
Zhongya Zhang, Chongqing Jiaotong University, ChinaReviewed by:
Lei Zhao, Guizhou Communications Polytechnic, ChinaShaoyun Pu, Shaoxing University, China
Jinyu Jiang, Ningbo University, China
Copyright © 2023 Li, Shen, Du and Yuan. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Bin Du, YmluZHUxOTgyQDE2My5jb20=
 Yukun Li
Yukun Li Bin Du
Bin Du Shisong Yuan
Shisong Yuan