- 1Changjiang Institute of Technology, Wuhan, China
- 2Sanya Science and Education Innovation Park, Wuhan University of Technology, Sanya, China
- 3School of Civil Engineering and Architecture, Wuhan University of Technology, Wuhan, China
Rock blasting vibration can cause harm to the surrounding environment. This article aims to investigate the propagation and attenuation of vibration waves in the blasting excavation of porous rock. Similar materials were used to simulate porous rock media and indoor blasting experiments were conducted on 12 porous rock-like models poured to estimate influences of the media material, porosity, moisture conditions, and decoupling coefficient of blast holes on the propagation of blasting stress waves. The results show that: 1) the crack propagation path of vibration waves in foam ceramics similar materials (FC) is not a completely straight line: cracks tend to produce a large deflection during the development process; 2) damage modes of low-porosity similar materials are mainly dominated by crack development, while damage and failure of high-porosity similar materials involve crack expansion and crushed fragments; 3) the peak vibration acceleration presents exponential decay with the distance, which will not vary with changes in the media material, porosity, moisture conditions, and the decoupling coefficient of blast holes; 4) the peak vibration acceleration of cement-based similar materials (SM) demonstrates the exponential decay coefficient of −1.4 ∼ −1.0, the exponential decay coefficient of the peak vibration acceleration for FC is −0.8 ∼ −0.4. The peak vibration acceleration of high-porosity similar material shows a faster decay rate, which is generally 0.3 less than that of the low-porosity similar material; 5) the type of material exerts the most significant controlling effect on the decay coefficient of peak vibration acceleration, followed by the effects of porosity and degree of water saturation; the decoupling coefficient of blast holes does not exert any significant influence on the decay of peak vibration acceleration.
1 Introduction
With the constant development of marine construction projects, it is an urgent demand to excavate underwater rock foundations for projects under construction and to be constructed, such as offshore wind power plants, cross-sea bridges, and deepwater ports. Blasting is the main construction means for excavating rock foundations. Blasting, as an artificial vibration source, may cause vibration in rocks and therefore harm the surrounding environment (Bata, 1971; Takamatsu et al., 1982; Jaroslaw and Andrzej, 2015). This requires that influences of blast vibration be considered during blasting excavation. In the meantime, marine rocks are mainly reef limestone characterized by high porosity and low strength; because reef limestone formations are far from the land and difficult to mine, it is difficult to collect large samples of reef limestone (this itself may harm the marine ecological environment). Considering this, it was necessary to use reef-limestone-like porous materials to replace the original rock to conduct experiments on the decay of the blasting vibration waves.
The propagation of blasting vibration waves in rock media is influenced by multiple factors, such as the type of media, physical and mechanical parameters, and the size and form of the blasting source (s). The propagation characteristics of blasting vibration waves in various media are generally studied through experiments and in situ tests (Yuan et al., 2000), together with numerical simulation (Hu et al., 2021; Yang et al., 2022; Jiang et al., 2023) and theoretical research. In terms of theoretical research (Allen et al., 1980; Murphy, 1982; Murphy, 1984; Knight and Nolen Hoeksema, 1990; Tsw et al., 1995; Cadoret et al., 1998; Knight et al., 1998), although the mathematical theory for the propagation of vibration waves in single-phase media has been mature, it is complicated when applied to resolve the propagation of vibration waves in practical engineering media (including artificial materials, soil, and rocks). Most real-world engineering media exhibit typical porous and multiphase characteristics: solid particles form the solid skeletons, and the pores between the skeletons are filled with liquid or gas with different proportions. Such characteristic allows the presence of pores to exert significant influences on the propagation characteristics of vibration waves in media. With regard to experimental research, researchers have used cement mortar specimens (Chen et al., 2018; Li et al., 2023), autoclaved aerated concrete blocks (Chong et al., 2021) and in situ experiments (Gou et al., 2019) to explore the absorption and decay effects of joints on blasting stress waves. Through such experiments (Zhang et al., 2000; Kahriman, 2002; Kuzu, 2008; Triguerosa et al., 2017; Jayasinghe et al., 2019; Wang et al., 2022), the decay of peak vibration velocity with the distance was studied by researchers based on numerous measurement data. In summary, various similar materials are used to simulate rocks in laboratory experiments to study the decay trend of vibration waves therein. Different empirical equations for the decay of vibration waves for guiding engineering design are mainly fitted using data from in situ experiments through regression of measurement data (Chong et al., 2019).
Combining with previous research results, the research selected cement-based similar materials to simulate low-strength and high-porosity reef limestone and foam ceramic similar materials to simulate high-strength and high-porosity reef limestone. These similar materials are characterized by advantages that enable accurate control of porosity, controllable pore size, and allow rapid preparation of specimens. Vibration acceleration sensors were adopted to acquire abundant measurement data in numerous model tests that resemble field experiments, so as to reveal the decay during the propagation of vibration waves.
2 Theory of wave propagation in media
2.1 Characteristic equations of body waves
The propagation of vibration waves involves the kinetics of the media. Microscopically, a porous medium comprises three phases (solid, liquid and gas). Methods in the continuum mechanics were introduced to the research. Analysis of a continuum assumes that porous multi-phase media are continuous in the space and the three phases (solid, liquid and gas) are completely overlapped and fill the entire medium.
According to previous research results (Xie, 2021), the characteristic equation for p waves in body waves is
The characteristic equation of S waves is
where
where
2.2 Vibration analysis of blasting medium
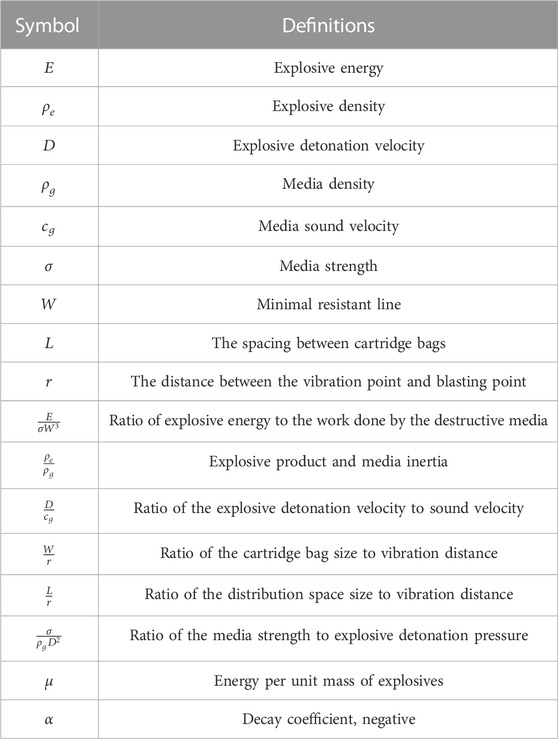
The physical parameters related to vibration of media caused by explosive blasting include
Dimensional analysis indicates that the nine independent physical quantities can constitute six dimensionless similar parameters. To ensure dimensional homogeneity on both sides of the equation, the ratio of two physical parameters (
Assuming that the properties of explosives and media remain unchanged, influences of
According blasting data, Eq. 6 can be fitted through regression analysis:
It can be seen from Eq. 7 that the peak vibration velocity of media has a power-exponential relationship with the distance. In engineering, the vibration velocity
3 Preparation of porous rock-like models
3.1 Preparation of similarity models and experimental conditions
According to previous research results of the authors (Luo et al., 2023), the mix proportions (Table 2) were adopted to prepare the cement-based similarity models. After being poured, the models were cured at the room temperature for 28 days, followed by blasting experiments.
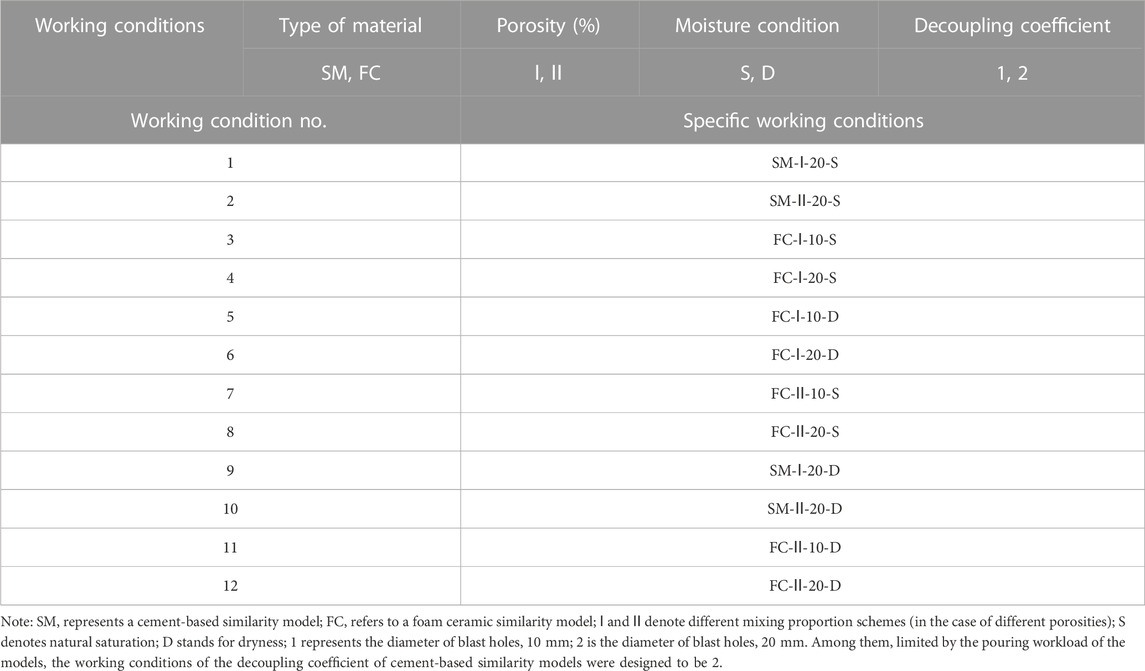
Experiments were conducted on two different types of similarity models prepared by the authors, including cement-based similarity models and foam ceramic similarity models measuring 2000 mm × 300 mm × 150 mm. A total of 12 models were poured, including four cement-based similarity models and eight foam ceramic similarity models, as shown in Figure 1. Four experimental working conditions were designed, which could be combined to 12 working conditions (numbered 1 to 12, Table 3). Meanwhile, for typical commercial explosives, the detonation pressure applied onto the hole walls at the moment of detonation is easily to exceed 10 GPa (Zhu et al., 2007); however, due to the low blast resistance of the two types of similarity models and for the purpose of acquiring better results, detonators (with the charge with a mass of 1 g) were used in the experiments, which were detonated by blasters.
3.2 Physico-mechanical parameter measurement of two types of similarity models
When pouring models, a cylindrical standard specimen measuring 100 mm × 50 mm was prepared for each model sample (Figure 2; Table 4).
3.3 Experimental process
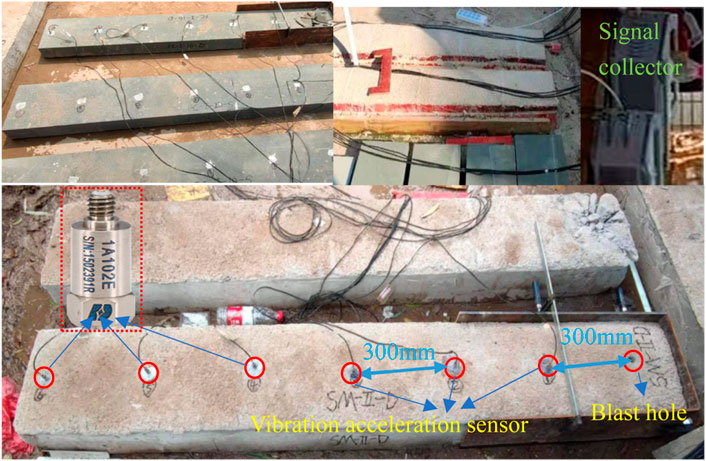
The experiment used the universal piezoelectric acceleration sensor (Model is 1A102E, Maximum range is 5,000 m/s2, Frequency range is 1–10000 Hz) from Jiangsu Donghua Testing Technology Co., Ltd. (Figure 3).
One vibration acceleration sensor was arranged every 300 mm along the model length from the blast hole. After being arranged, the sensors were linked to a signal acquisition device to run and debug, so as to ensure that the signal acquisition device and sensors are connected well and data paths are clear (Figure 3).
The depth of blast holes in each model was 100 mm. Before experiments, detonators measuring 50 mm × 10 mm were placed in the blast holes, which were then stemmed. This can ensure that conditions including the initial blasting load and energy were similar.
The sampling frequency during the experiment is 200 KHZ. The vibrations in an axis parallel to the blasting hole were detected within the measurement range of the acceleration sensor.
4 Blasting experiments and analysis of results
4.1 Analysis of crack propagation and fragmentation effect around blast holes
As shown in Figure 4, cracks tend to propagate along the direction of propagation of blasting stress waves in the experiments on the two materials and standard blasting craters are formed after blasting.
The crack propagation paths are not ideal straight lines in the two types of similarity models, and they are more curved in the foam ceramic similarity models than in the cement-based similarity models. This is probably because foam ceramic similarity models are more anisotropic, so that the stress field is non-uniform. Meanwhile, because foam ceramics have better cementation property and strength, cracks tend to have a large deflection during the development process. Moreover, huge energy is generated at the moment of blasting, while the energy propagation is not symmetrical in the specimens, which may give rise to an unbalanced stress field near the crack tips. Finally, the cracks may deflect from their ideal linear propagation path.
Figure 5 shows that, because high-porosity foam ceramic similarity models have significantly lower strengths than low-porosity foam ceramic similarity models, the crushing effects of the two after blasting differ: many fragments appear in the low-strength similarity models, and the fragments are mainly blocky and are ejected around the blast hole. Damage modes of high-strength similarity models are mainly dominated by crack propagation, with few fragments, manifest as small particles. The crushing effects in the experiments are consistent with the measured strengths (Table 4).
4.2 Analysis of vibration acceleration characteristics for porous rock-like materials
4.2.1 Influence of media material on vibration acceleration
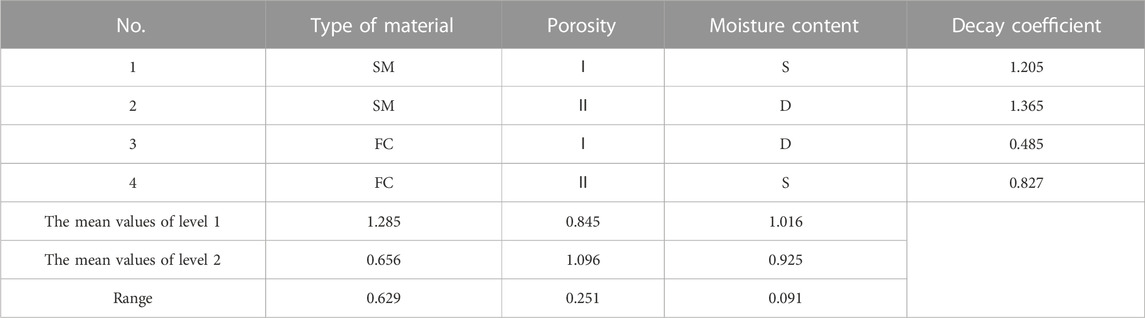
As shown in Figure 6A, the peak vibration acceleration of cement-based similarity models and foam ceramic similarity models both present exponential decay with distance under same porosity, diameter of blast holes and moisture conditions. The correlation coefficients R2 are separately 0.956, 0.993, 0.985, and 0.974.
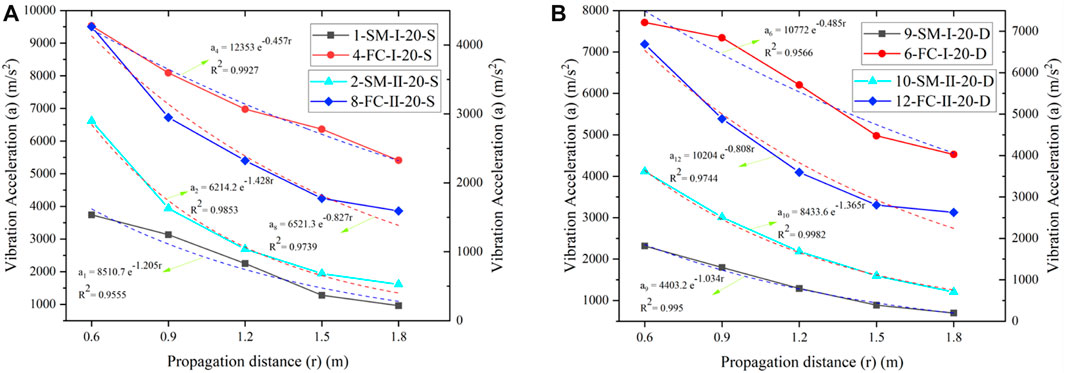
FIGURE 6. The influence of materials on the attenuation of vibration waves. (A) Moisture conditions. (B) Dry conditions.
Taking comparison of the No. 1 and 4 broken lines in the figure as an example, the absolute value of decay coefficient of cement-based similarity models is 1.2 when the porosity is in state Ⅰ (about 50%), the decoupling coefficient is 2 and natural saturation is applied. It is larger than that of foam ceramic similarity models (0.46). This indicates that the vibration waves decay faster in cement-based similarity models than in foam ceramic similarity models. This is because cement-based similarity models have a lower cementation degree than foam ceramic similarity models, so their wave-absorbing capacity is stronger than foam ceramic similarity models. Meanwhile, the results are also consistent with measured speeds of sound (Table 3).
Besides, the No. 2 and 8 broken lines in Figures 6A, B show that peak vibration acceleration exhibits exponential decay with the distance in both cement-based and foam ceramic similarity models under different porosities and moisture conditions. The correlation coefficient R2 exceeds 0.95, suggesting a good correlation. This conforms to the trend shown above; meanwhile, it is found that the decay rate of peak vibration acceleration in cement-based similarity models is faster than in foam ceramic similarity models under all working conditions assessed herein.
According to Figures 6A, B, due to the strong wave-absorbing capacity, cement-based similarity models always show small initial peak vibration acceleration than foam ceramic similarity models. The decay coefficient of peak vibration acceleration in the cement-based similarity models is in the range of −1.4 to −1.0, while it is in the range of −0.83 to −0.46 in foam ceramic similarity models.
4.2.2 Influence of porosity on vibration acceleration
As shown in Figure 7A, the peak vibration acceleration always exhibits exponential decay with the distance in cement-based similarity models with different porosities under conditions of the same material, diameter of blast holes, and moisture conditions. The correlation coefficients R2 are separately 0.956, 0.985, 0.995, and 0.998.
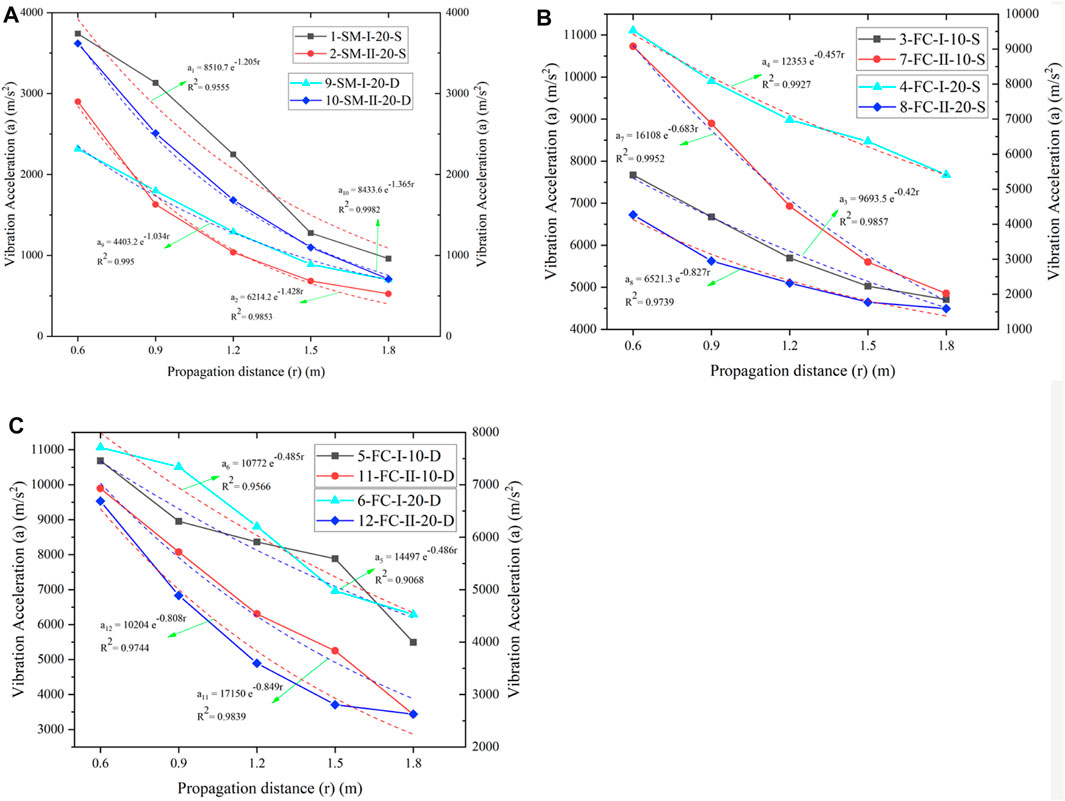
FIGURE 7. The influence of porosity on the attenuation of vibration. (A) Cement-based materials. (B) Foam ceramic materials in moisture conditions. (C) Foam ceramic materials in dry conditions.
The comparison of the No. 1 and 2 broken lines in the figure is taken as an example. The decay coefficient of the low-porosity similar material has an absolute value of 1.2 when the medium is a cement-based material, the decoupling coefficient is 2, and natural saturation is adopted. It is smaller than that of the high-porosity similar material (1.4), which indicates that vibration waves in the high-porosity cement-based similarity models decay faster than in low-porosity cement-based similarity models. This is because the energy of vibration waves is dissipated rapidly in pores when the porosity is high, which reduces the energy propagated as transient vibrations, leading to a reduction of the peak acceleration. Meanwhile, the results also agree with measured speeds of sound (Table 3).
The No. 9 and 10 broken lines in Figure 7A, together with Figures 7B, C demonstrate that the peak vibration acceleration always shows exponential decay with distance in materials of different porosities under conditions of different materials, different decoupling coefficients, and different moisture conditions. The correlation coefficient R2 exceeds 0.90, suggesting a good correlation. Meanwhile, the peak vibration acceleration decays faster in the high-porosity similarity models than in low-porosity similarity models under various working conditions in the experiments.
Figures 7A–C show that the decay coefficient of peak vibration acceleration in high-porosity similarity models is about 0.3 less than that in low-porosity similarity models.
4.2.3 Influence of moisture conditions on vibration acceleration
In the experiments, the similarity model was placed in a blasting crater excavated in advance and natural saturation of the model was achieved by injecting water in the crater and immersing the model for 12 h. It was tested that the saturability of the six naturally saturated similarity models is always below 50%.
As shown in Figure 8A, the peak vibration acceleration of similarity models of different moisture conditions always presents exponential decay with the distance under conditions of same media material, diameter of blast holes and porosity. The correlation coefficients R2 are separately 0.956, 0.995, 0.985, and 0.998.
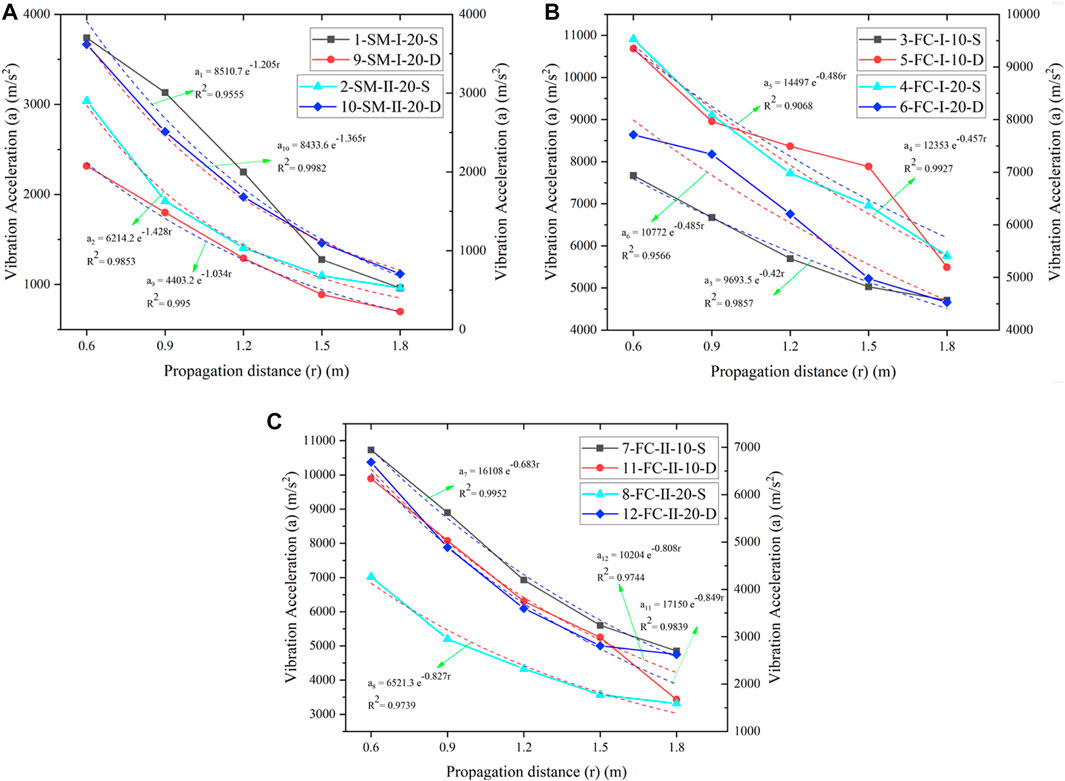
FIGURE 8. The influence of natural saturation on the attenuation of vibration. (A) Cement-based materials. (B) Foam ceramic materials with porosity of Ⅰ. (C) Foam ceramic materials with porosity of Ⅱ.
The comparison of No. 1 and 9 broken lines in the figure is taken as an example. The absolute value of the decay coefficient of naturally saturated similar models is 1.2 when the medium is cement-based materials, the porosity is in state Ⅰ (about 50%), and the decoupling coefficient is 2. It does not differ significantly from that of dry similarity models (1.0). This indicates that the decay of peak vibration acceleration in naturally saturated cement-based similarity models does not differ greatly from that in dry cement-based similarity models. That is, the low saturability (lower than 50%) does not significantly affect the decay of vibration in the cement-based similarity models.
Besides, the No. 2 and 10 broken lines in Figure 8A, together with Figures 8B, C show that the peak vibration acceleration always exhibits exponential decay with the distance in similarity models of different moisture conditions under different media, different decoupling coefficients, and different porosities. The correlation coefficient R2 exceeds 0.90, indicative of a good correlation.
Figure 8A–C show that the decay coefficient of peak vibration acceleration in the low-porosity similarity models is comparable to that in dry similarity models. That is to say, the low saturability (lower than 50%) does not significantly affect the decay of peak vibration acceleration in the similarity models under various working conditions in the experiments.
4.2.4 Influence of the decoupling coefficient of blast holes on vibration acceleration
As shown in Figure 9A, the peak vibration acceleration of foam ceramic similarity models of different decoupling coefficients always exhibits exponential decay with distance under the same media material, moisture conditions and porosity. The correlation coefficients R2 are separately 0.986, 0.993, 0.907, and 0.957.
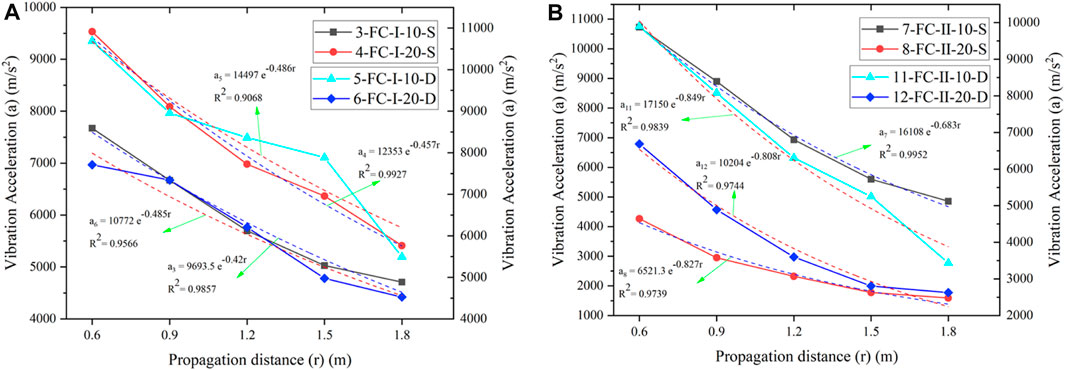
FIGURE 9. The influence of the decoupling coefficient on the attenuation of vibration. (A) Foam ceramic materials with porosity of Ⅰ. (B) Foam ceramic materials with porosity of Ⅱ.
Comparison of the No. 3 and 4 broken lines in the figure is taken as an example. The absolute value of decay coefficient of the similarity models with a decoupling coefficient of 1 is 0.42 when the medium is foam ceramics, the porosity is in state Ⅰ (about 50%), and natural saturation is adopted; this matches results from similarity models with a decoupling coefficient of 2 (0.46). This indicates that the vibration waves differ slightly in similarity models of different decoupling coefficients, that is, the decoupling coefficient does not significantly influence the decay of vibration in the foam ceramic similarity models.
Moreover, the No. 5 and 6 broken lines in Figures 9A, B show that the peak vibration acceleration always exhibits exponential decay with distance in foam ceramic similarity models with different decoupling coefficients under different moisture conditions and different porosities. The correlation coefficient R2 is always greater than 0.90, suggesting a good correlation.
Figures 9A, B show that the decay coefficient of peak vibration acceleration in the foam ceramic similarity models with a decoupling coefficient of 1 is comparable to that with the decoupling coefficient of 2. That is, under various working conditions in the experiments, the decoupling coefficient does not apparently influence the decay of peak vibration acceleration in the foam ceramic similarity models.
4.2.5 Sensitivity analysis of influencing factors for the decay of vibration acceleration
The method of solving the range of various factors is generally used in multi-condition experiments to compare influences of various factors on the results (Dong et al., 2012). The above experimental results demonstrate that the decoupling coefficient of blast holes exerts little influence on the decay of peak vibration acceleration. Combining the actual working conditions in the experiments and the experimental results, the mean and the difference between the maximum and minimum of the decay coefficient corresponding to other three factors at two levels were calculated, that is, the range of a factor for the decay coefficient was ascertained. A large range indicates that the corresponding factor significantly affects the decay coefficient, and the vice versa (Xu et al., 2016). An orthogonal experimental table L4 (23) (Table 5) was designed, and the experimental results are listed in Table 6.
The mean and range of each factor influencing the decay coefficient at each level were calculated, and the results are listed in Table 6; the type of material shows the largest range, followed successively by the porosity and moisture conditions. This indicates that the type of material exerts an obvious controlling effect on the decay coefficient of peak vibration acceleration; porosity exerts a certain controlling effect on the decay coefficient; while the moisture conditions only slightly affect the decay coefficient.
5 Conclusion
Based on previous research into a similarity model of porous reef limestone media, 12 porous rock-like material models were poured. The propagation and decay of blasting vibration waves in porous rock media were experimentally investigated by respectively considering factors such as porous media material, porosity, moisture conditions, and decoupling coefficient of blast holes. The following key conclusions were drawn:
(1) The foam ceramic similarity model has strong heterogeneity, while also exhibiting better cementation and strength than the cement-based similarity model. This gives rise to an uneven stress distribution of the material, causing the stress-wave propagation path to deviate from a straight line, and cracks to tend to undergo a larger deflection. As high-porosity similarity models are weaker, their large fragments after blasting were found to be ejected from surrounding blast holes, which is different from the grain fragments arising from low-porosity similarity models; damage modes of low-porosity similarity models are mainly dominated by crack propagation; while high-porosity similarity models present crack propagation and much more crushing damage;
(2) Through fitting experimental data, the peak blast vibration accelerations of two types of similarity models all show exponential decay with the distance. The correlation coefficient R2 exceed 0.95, suggesting favorable correlation; this trend is unaffected by porosity, moisture conditions, and the decoupling coefficient of blast holes. The decay coefficient of the peak vibration acceleration for the cement-based similarity models is between −1.4 and −1.0, while that for the foam ceramic similarity models lies between −0.8 and −0.4. The decay rate of the peak vibration acceleration in the cement-based similarity models is faster than that in the foam ceramic similarity models; likewise, the decay rate of the peak vibration acceleration in the high-porosity similarity models is faster than that in the low-porosity similarity models: the decay coefficient of the high-porosity similarity models is 0.3 less than that of the low-porosity similarity models;
(3) A range analysis method was used to assess the sensitivity of influencing factors such as media material, porosity, moisture conditions, and the decoupling coefficient of blast holes to blast vibration responses. The results indicate that the type of material exerts a significant controlling effect on the decay coefficient of peak vibration acceleration, followed by the influences of porosity and water saturation; while the decoupling coefficient of blast holes exerts little influence on the decay coefficient of peak vibration acceleration.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
GL: Supervision, Writing–review and editing. YT: Writing–original draft, Writing–review and editing.
Funding
The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This work was supported by the PhD Scientific Research and Innovation Foundation of Sanya Yazhou Bay Science and Technology City (Grant Nos HSPHDSRF-2022-03-026, HSPHDSRF-2022-03-009), the National Natural Science Foundation of China (Grant No. 51979208), the Hainan Natural Science Foundation Innovation Research team project (Grant No. 521CXTD444), the National Key R&D Program of China (Grant No. 2021YFC3100801).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Allen, F. A., Richart, F. E., and Woods, R. D. (1980). Fluid wave propagation in saturated and nearly saturated sands. J. Geotechnical Eng. 106 (3), 235–254. doi:10.1061/ajgeb6.0000931
Bata, M. (1971). Effects on buildings of vibrations caused by traffic. Build. Sci. 6 (4), 221–246. doi:10.1016/0007-3628(71)90014-4
Cadoret, T., Mavko, G., and Zinszner, B. (1998). Fluid distribution effect on sonic attenuation in partially saturated limestones. Geophysics 63 (1), 154–160. doi:10.1190/1.1444308
Chen, X., Zhao, X., Wang, H., Ma, L., and Wang, C. (2018). Model tests and application research on propagation laws of blasting stress wave in jointed and filled rock mass. J. Rock Saf. Sci. Technol. 14 (12), 130–134. doi:10.11731/j.issn.1673-193x.2018.12.021
Chong, Y., Yue, H., Li, H., Xia, X., and Liu, B. (2021). Scale model test study of influence of joints on blasting vibration attenuation. Bull. Eng. Geol. Environ. 80 (1), 533–550. doi:10.1007/s10064-020-01944-2
Chong, Y., Yue, H., Li, H., Zuo, H., Deng, S., and Liu, B. (2019). Study on the attenuation parameters of blasting vibration velocity in jointed rock masses. Bull. Eng. Geol. Environ. 78, 5357–5368. doi:10.1007/s10064-018-01452-4
Dong, J., Yang, J., Yang, G., Wu, F., and Liu, H. (2012). Research on similar material proportationing test of model test based on orthogonal design. J. China Coal Soc. 37 (1), 44–49.
Gou, Y., Shi, X., Qiu, X., Zhou, J., Chen, H., and Huo, X. (2019). Propagation characteristics of blast-induced vibration in parallel jointed rock mass. Int. J. Geomechanics 19 (5), 04019025. doi:10.1061/(asce)gm.1943-5622.0001393
Hu, Y., Yang, Z., Yao, E., Liu, M., and Rao, Y. (2021). Investigation and control of the blasting-induced ground vibration under cold condition. Shock Vib. 2021, 1–13. doi:10.1155/2021/6660729
Jaroslaw, K., and Andrzej, C. (2015). Evaluation of the vibration impacts in the transport infrastructure environment. Archive Appl. Mech. 85, 1331–1342. doi:10.1007/s00419-015-1029-0
Jayasinghe, B., Zhao, Z., Teck Chee, A. G., Zhou, H., and Gui, Y. (2019). Attenuation of rock blasting induced ground vibration in rock-soil interface. J. Rock Mech. Geotechnical Eng. 11, 770–778. doi:10.1016/j.jrmge.2018.12.009
Jiang, N., Lyu, G., Wu, T., Zhou, C., Li, H., and Yang, F. (2023). Vibration effect and ocean environmental impact of blasting excavation in a subsea tunnel. Tunn. Undergr. Space Technol. 131, 104855. doi:10.1016/j.tust.2022.104855
Kahriman, A. (2002). Analysis of ground vibrations caused by bench blasting at can Open-pit Lignite Mine in Turkey. Environ. Geol. 41 (6), 653–661. doi:10.1007/s00254-001-0446-2
Knight, R., Dvorkin, J., and Nur, A. (1998). Acoustic signatures of partial saturation. Geophysics 63 (1), 132–138. doi:10.1190/1.1444305
Knight, R., and Nolen Hoeksema, R. A. (1990). A laboratory study of the dependence of elastic wave velocities on pore scale fluid distribution. Geophys. Res. Lett. 17 (10), 1529–1532. doi:10.1029/gl017i010p01529
Kuzu, C. (2008). The importance of site-specific characters in prediction models for blast-induced ground vibrations. Soil Dyn. Earthq. Eng. 28 (5), 405–414. doi:10.1016/j.soildyn.2007.06.013
Li, Y., Zhu, J., Han, D., Zhao, R., Ma, Y., and Zhou, T. (2023). Experimental study of the dynamic responses of surrounding jointed rock masses and adjacent underground openings and induced ground vibrations subjected to underground explosion. Tunn. Undergr. Space Technol. 135, 105060. doi:10.1016/j.tust.2023.105060
Luo, Y., Tao, Y., Zhang, M., Gong, H., and Li, X. (2023). Experimental study on mix proportions of similar materials to reef limestone. Constr. Build. Mater. 365, 130111. doi:10.1016/j.conbuildmat.2022.130111
Murphy, W. F. (1982). Effects of partial water saturation on attenuation in Massilon sandstone and Vycor porous glass. J. Acoust. Soc. Am. 71 (6), 1458–1468. doi:10.1121/1.387843
Murphy, W. F. (1984). Acoustic measures of partial gas saturation in tight sandstones. J. Geophys. Res. 89 (B13), 11549–11559. doi:10.1029/jb089ib13p11549
Takamatsu, M., Futatsuka, M., Sakurai, T., Matoba, T., Gotoh, M., Aoyama, H., et al. (1982). A study of the extent and scope of local vibration hazards in Japan. Ind. Health 20 (3), 177–190. doi:10.2486/indhealth.20.177
Triguerosa, E., Cánovasb, M., Muñoza, J. M., and Cospedal, J. (2017). A methodology based on geomechanical and geophysical techniques to avoid ornamental stone damage caused by blast-induced ground vibrations. Int. J. Rock Mech. Min. Sci. 93, 196–200. doi:10.1016/j.ijrmms.2016.12.013
Tsw, C., Marsion, D., and Zinszner, B. (1995). Influence of frequency and fluid distribution on elastic wave velocity in partially saturated limestones. J. Geophys. Res. 100 (B6), 9789–9803. doi:10.1029/95JB00757
Wang, X., Li, J., Zhao, X., and Liang, Y. (2022). Propagation characteristics and prediction of blast-induced vibration on closely spaced rock tunnels. Tunn. Undergr. Space Technol. 123, 104416. doi:10.1016/j.tust.2022.104416
Xie, W. (2021). Study on vibration wave propagation mechanism and response characteristics of new cement-based grouting material. Xuzhou: China University of Mining and Technology.
Xu, Y., Su, D., Zhou, B., Liu, Z., and Zhou, C. (2016). Experiment study on similarity ratio of similar material for model test on red-bed soft rock. Rock Soil Mech. 37 (8), 2231–2237. doi:10.16285/j.rsm.2016.08.014
Yang, J., Sun, J., Jia, Y., and Yao, Y. (2022). Energy generation and attenuation of blast-induced seismic waves under in situ stress conditions. Appl. Sci. 12 (18), 9146. doi:10.3390/app12189146
Yuan, L., Feng, C., Xu, Q., Ji, M., and Zhang, J. (2000). Study on propagation characteristics of blasting seismic waves in A rock medium and numerical calculation. Eng. Blasting 6 (3), 1–7.
Zhang, Q., Bai, C., Liu, Q., Zhang, Y., Guo, Y., and Wang, Z. (2000). Experimental research on amplitude change of blasting seismic wave with topography. J. Beijing Inst. Technol. 9 (3), 237–242. doi:10.15918/j.jbit1004-0579.2000.03.003
Keywords: porous rock-like material, model experiment, blasting vibration wave, vibration acceleration, decay law
Citation: Lu G and Tao Y (2023) Experimental study into the propagation and attenuation of blasting vibration waves in porous rock-like materials. Front. Mater. 10:1284158. doi: 10.3389/fmats.2023.1284158
Received: 28 August 2023; Accepted: 24 October 2023;
Published: 07 November 2023.
Edited by:
Giuseppe Saccomandi, University of Perugia, ItalyReviewed by:
Tibor Krenicky, Technical University of Košice, SlovakiaKailu Xiao, Texas A&M University, United States
Copyright © 2023 Lu and Tao. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yuhang Tao, dHloMDcxN0B3aHV0LmVkdS5jbg==
 Ge Lu1
Ge Lu1 Yuhang Tao
Yuhang Tao