A review on the mechanical metamaterials and their applications in the field of biomedical engineering

Wang, Hao; Lyu, Yongtao; Bosiakov, Sergei; Zhu, Hanxing; Ren, Yuanfei

doi:10.3389/fmats.2023.1273961

REVIEW article

Front. Mater., 20 September 2023

Sec. Metamaterials

Volume 10 - 2023 | https://doi.org/10.3389/fmats.2023.1273961

A review on the mechanical metamaterials and their applications in the field of biomedical engineering

Hao Wang¹

Yongtao Lyu^1,2

Sergei Bosiakov³

Hanxing Zhu⁴

Yuanfei Ren⁵*

¹Department of Engineering Mechanics, Dalian University of Technology, Dalian, China
²DUT-BSU Joint Institute, Dalian University of Technology, Dalian, China
³Faculty of Mechanics and Mathematics, Belarusian State University, Minsk, Belarus
⁴School of Engineering, Cardiff University, Cardiff, United Kingdom
⁵The First Department of Hand and Foot Surgery, Dalian Municipal Central Hospital, Dalian, China

Metamaterials are a group of materials/structures which possess novel behaviors not existing in nature. The metamaterials include electromagnetic metamaterials, acoustic metamaterials, mechanical metamaterials, etc. among which the mechanical metamaterials are widely used in the field of biomedical engineering. The mechanical metamaterials are the ones that possess special mechanical behaviors, e.g., lightweight, negative Poisson’s ratio, etc. In this paper, the commonly used mechanical metamaterials are reviewed and their applications in the field of biomedical engineering, especially in bone tissue engineering and vascular stent, are discussed. Finally, the future perspectives of this field are given.

1 Introduction

Metamaterials are a group of materials/structures which possess novel behaviors not existing in nature. Grouped by different professional disciplines, the metamaterials can be classified into electromagnetic metamaterials, acoustic metamaterials, thermal metamaterials, mechanical metamaterials, etc. The concept of metamaterials first appeared in the field of electromagnetism. With the deepening intersection of materials disciplines and other disciplines, many types of metamaterials have been developed and applied (Zhang et al., 2011; Yang et al., 2012; Raimond, 2013; Cui et al., 2017; Xu et al., 2019; Hong et al., 2020; Song et al., 2021; Cheng et al., 2023), as shown in Figure 1.

FIGURE 1

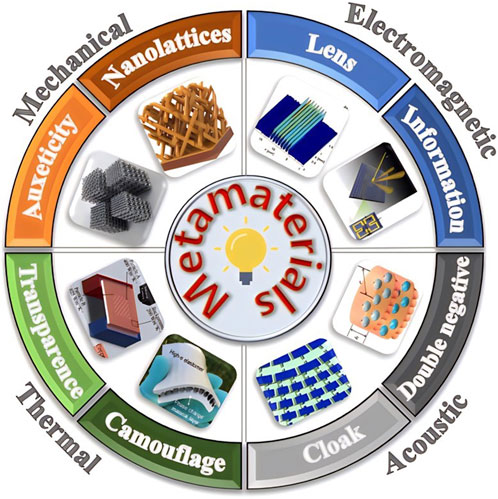
FIGURE 1. The types of metamaterials. [Figure adapted from Refs (Zhang et al., 2011; Yang et al., 2012; Raimond, 2013; Cui et al., 2017; Xu et al., 2019; Hong et al., 2020; Song et al., 2021; Cheng et al., 2023).].

Metamaterials, due to their unique microstructure, exhibit unprecedented performance at the macroscopic that conventional materials do not possess. The original idea of metamaterials was proposed by Veselago, 1968. However, this idea was not taken seriously, due to the lack of technology at that time. Metamaterials have been paid more and more attention since some researchers have proved the negative permittivity and permeability of copper composite materials in the microwave band using ingenious design methods (Pendry et al., 1996; Pendry et al., 1999; Pendry, 2000; Shelby et al., 2001). Thereafter, researchers have carried out in-depth exploration of the principles and properties of metamaterials and have gradually improved the theoretical system of metamaterials.

Electromagnetic metamaterials have a wide range of applications, e.g., perfect lenses, invisible cloaks, antennas, different types of sensors, etc. (Raimond, 2013) As early as the end of the last century, Pendry (Pendry, 2000) began to work on “superlenses,” which were lenses working at visible frequencies and could be realized in the form of a thin slab of silver. Leonhardt (Leonhardt, 2006) and Pendry (Pendry et al., 2006) both proposed the concept and design of a perfect stealth cloak in 2006, and Smith et al. (Schurig et al., 2006) successfully demonstrated the cloak experimentally in the same year. Gradient metamaterial lenses can easily deflect and focus incident plane waves due to the unique properties of tunable particles (Lin et al., 2008). One of the inherent limitations of conventional metamaterials is once prepared, the functionality will be determined, making it difficult to achieve real-time, and wide-scale regulation. Consequently, Cui’s team introduced the concepts of digital encoding and programmable metamaterials in 2014 (Cui et al., 2014), and further expanded the concepts into information metamaterials (Cui et al., 2017; Liu and Cui, 2017; Ma and Cui, 2020). Information metamaterials completely overturn the conventional system of electromagnetic metamaterials characterized by analog material parameters, and they are creatively described using digital coding of the physical units. Besides, by controlling different coding sequences, real-time and wide-scale modulation of electromagnetic wave behavior can be achieved, thereby realizing field programmable metamaterial functions. The metamaterial absorber is a special branch of electromagnetic metamaterials that has attracted interest due to its ability to achieve unity absorptivity of electromagnetic waves (Watts et al., 2012; Huang et al., 2022). The performance of metamaterial absorbers depends on material composition, cell size, and structure, and “perfect” absorption can often be achieved through appropriate design. Since both acoustic and electromagnetic waves conform to the wave equation, they have the same or similar fluctuating properties, and also have the same wave parameters such as wave vector, wave impedance, and energy flow. Researchers were the first to transfer the research methods of electromagnetic metamaterials to the field of acoustics, thus giving birth to acoustic metamaterials (Song et al., 2021; Zheng et al., 2022).

Like electromagnetic metamaterials, acoustic metamaterials are constructed from artificially constructed periodic/aperiodic geometries and the cell size of the structures is much smaller than the wavelength. In 2000, Liu et al., 2000 designed locally resonant structures to fabricate acoustic crystals, breaking the conventional mass-density law of sound transmission, thus initiating the study of acoustic metamaterials. Subsequently, research had been carried out with a focus on negative mass density elastic modulus, double negative acoustic metamaterials, and many theoretical models (Liu et al., 2005; Mei et al., 2006; Mei et al., 2007). A typical application of acoustic metamaterials is the cloaking effect of acoustic waves. The scattering problem was solved using a spherical-Bessel function series expansion method and its perfect cloaking effect was verified (Chen and Chan, 2007). Therefore, the researchers designed a three-dimensional acoustic cloak based on this method (Chen and Chan, 2007; Cummer et al., 2008a; Cummer et al., 2008b). In order to solve the difficult problem of parameters, a two-dimensional cylindrical acoustic cloak was designed by introducing the acoustic transmission line theory, which can realize ultrasonic stealth in a 52–64 kHz wide band (Zhang et al., 2011). An invisible acoustic cloak was realized which was near-perfect three-dimensional, broadband, omnidirectional carpet (Zigoneanu et al., 2014). Recently, there have also been numerous teams optimizing the design of acoustic cloak in different ways to overcome the limitations of various acoustic metamaterials (Chen et al., 2021; Cominelli et al., 2022). Cao et al. (Cao et al., 2021) presented a tunable acoustic metasurface composed of Helmholtz-resonator-like digital-coding meta-atoms to overcome the limitation and realize 3D dynamic wave manipulations. Zhang et al., 2021 realized reconfigurable active acoustic metalen under an active acoustic metasurface platform, scanning the focal point along an arbitrary trajectory in free space. Xiao et al., 2023 proposed a joint amplitude-phase coding acoustic metasurface, which realized simultaneous acoustic wavefront engineering and energy allocation.

Mechanical metamaterials were developed later than the development of the electromagnetic and acoustic metamaterials, and their basic principles and design ideas almost follow those of acoustic metamaterials. However, the design and fabrication of mechanical metamaterials are usually based on lattice or microstructural design, aiming to achieve the desired mechanical properties by controlling the shape of the structure and the composition of the material. The design and fabrication of acoustic metamaterials focus on controlling the propagation, interference, and scattering properties of acoustic waves, allowing them to be conducted, focused, isolated, etc. Although both mechanical and acoustic metamaterials utilize the design of special materials or structures, their goals and fields of application are different. Mechanical metamaterials focus on special properties in the field of mechanical mechanics, while acoustic metamaterials focus on controlling the propagation of acoustic waves. Mechanical metamaterials exhibit unprecedented mechanical properties due to their unusual micro-/nanostructures, such as negative Poisson’s ratio, negative compressibility, tunable stiffness, etc. Researchers have applied these unique mechanical behaviors to different fields. Jiang T-J. et al., 2023 proposed a new mechanical metamaterial that exhibits negative stiffness behavior by merging folded beams with stiffening walls. Iantaffi et al., 2023 investigated the mechanical properties of cubic chiral metamaterials under large plastic strain. The experimental results show auxeticity under large plastic strain, suggesting that such materials may have better energy absorption capabilities. Jiang Y-L. et al., 2023 investigated a new artificial intervertebral disc implant with auxeticity using experimental tests and the finite element method. The results showed that the new artificial intervertebral disc implant exhibited more effective stress transfer and attenuation under practical loading conditions. In the present paper, the mechanical metamaterials will be presented in detail, especially their applications in the field of biomedical engineering.

This paper therefore focuses on the review of mechanical metamaterials and their applications in the field of biomedical engineering, such as bone implants and vascular stents, and future perspectives are concluded finally.

2 Mechanical metamaterials

The mechanical metamaterial is a kind of composite structures/materials constructed by artificial microstructure unit cells, with counterintuitive static/dynamic properties that natural materials do not possess (Yu et al., 2018). The mechanical metamaterials are the ones with special mechanical behaviors, e.g., negative Poisson’s ratio, negative elasticity, negative compressibility, tunable stiffness, etc. The classification criteria are established based on the Young’s modulus E, shear modulus G, bulk modulus K, Poisson’s ratio $υ$ , and mass density $ρ$ of mechanical metamaterials. Based on the fundamental material mechanics, mechanical metamaterials can be broadly classified into lightweight metamaterials ( $E / ρ$ is very large), pattern transformation metamaterials (E is tunable), negative compressibility metamaterials ( $-$ 4G $/$ 3 $<$ K $<$ 0), pentamode metamaterials (G $≪$ K), and auxetic metamaterials (G $≫$ K, $υ < 0$ ) (Yu et al., 2018). Different types of mechanical metamaterials have various features. Both low mass and high stiffness of lightweight materials are ensured by optimizing the structures. The stiffness of pattern transformation metamaterials is switchable. The volume of negative compressibility metamaterials expands under compression and contracts under tension. Pentamode metamaterials are solid materials with fluid properties. The Poisson’s ratio of auxetic metamaterials is below zero.

2.1 Lightweight metamaterials

The lightweight metamaterials are associated with stiffness, which is constructed by optimizing the phase topology of biphasic materials or cellular materials. The biphasic materials or cellular materials have two phases, one of which phase is a void and the other is a solid constituent material (Lu C-X. et al., 2022). Based on their structure, the lightweight metamaterials can be categorized into four groups, namely, micro-/nanolattices metamaterials, chiral metamaterials, origami-inspired metamaterials, and cellular origami metamaterials.

The micro-/nanolattices metamaterials are composed of numerous periodic arrangements of unit cells, and their structures can be beam-based, plate-based, and minimal surface-based (Lu C-X. et al., 2022), as shown in Table 1. The microscopic topology is controlled to achieve the desired macroscopic mechanical properties, thereby increasing the suitability for applications in various fields. The lightweight structures are developed in such a way that stiffness and strength are also guaranteed to be met (Zhang et al., 2020). Some researchers have designed micro-/nanolattice materials, whose density is less than that of water like foam, while they are as stiff and strong as steel (Do Rosário et al., 2015; Bauer et al., 2017; Do Rosário et al., 2017). For example, the large-area multifunctional metal nanolattice fabricated can achieve an ultra-high tensile strength of 257 MPa, which is 2.6 times stronger than the previous porous material, but only has a relative density of 0.298 (Jiang and Pikul, 2021). It has also been recently reported that quasi-BBC nanolattices not only have a high compressive yield strength but also have ultra-high energy absorption capability (Cheng et al., 2023).

TABLE 1

TABLE 1. The types of lightweight mechanical metamaterials.

The chiral material is also a type of lightweight metamaterials, being their mirror image non-overlapped and divided into left-handed and right-handed metamaterials, as shown in Table 1. Prall and Lakes (Prall and Lakes, 1997) were the first to make a hexagonal honeycomb chiral material based on Wojciechowski’s theory (Wojciechowski, 1989). The unit cell consists of a central cylinder as a node and six ligaments connected by axisymmetric rotation around it. In addition, there are anti-chiral structures where the adjacent nodes of the basic unit are on the same side of the same ligament, in other words, the nodes are connected on the opposite side of the ligament, as shown in Table 1. The chiral structures, especially anti-chiral structures, contract the ligaments around the nodes simultaneously under compression loading, and expand them simultaneously under tensile loading so that the materials have a negative Poisson’s ratio, namely, auxeticity (This property will be described in more detail in Section 2.5) (Kolken and Zadpoor, 2017). Several groups have used chiral structures to design 2D and 3D metamaterials with large deployable ratios and ultrafast shape reconfiguration responses, effectively exploiting the bistability and energy transformation capabilities of prestressed shells to achieve compatible spontaneous shape reconfiguration (Liu Y-Z. et al., 2023). However, unlike chiral or anti-chiral structures, hierarchical structural nodes are square, rhombic, or polygonal and have a much higher stiffness (Mousanezhad et al., 2016), as shown in Table 1.

Origami, a word derived from Japanese, is a traditional art about folding paper in Japan. Origami allows for the design of elegant three-dimensional structures due to the complexity and variety resulting from the number, order, and orientation of its folds (Tomohiro, 2013; Lv et al., 2014), as shown in Table 1. Inspired by origami, three lightweight metamaterials have been designed and developed, namely, the Miura-ori pattern (Lv et al., 2014), the non-periodic Ron Resch pattern (Tomohiro, 2013), and the square twist (Silverberg et al., 2015). They are flexible, deformable, and compact. Recently, Han et al., 2023 proposed an origami-based mechanical memory metamaterial that can greatly enhance the capability of vibration suppression of the metamaterial by switching the metamaterials between different memories.

Cellular origami metamaterials are the extensions of origami design principles to three-dimensional cellular materials, resulting in foldable cellular metamaterials. It can also be seen as a combination of origami structure and micro-/nanolattices design. Cellular origami metamaterials are available in two combinations, stacked and interlaced (Schenk and Guest, 2013; Cheung et al., 2014), as shown in Table 1. By stacking cellular metamaterial cells, a new class of origami cellular metamaterials with tunable Poisson’s ratio has been proposed with significant potential applications in vibration isolation devices, acoustic waveguides, and electronic devices (Lyu et al., 2021). Origami interleaved tube cellular materials consist of interleaved tubes with two orthogonal axes, have high interfacial surface area and are deployable (Cheung et al., 2014). The relationship between key geometric parameters and mechanical properties of various origami cellular metamaterial models can provide effective guidance for 3D printing of metallic origami cellular metamaterials (Huan et al., 2022).

The four categories of mechanical metamaterials above are all lightweight metamaterials that have been designed to exhibit excellent and unusual mechanical properties at the macroscopic level through the design of their microstructures. The types of lightweight mechanical metamaterials are summarized in Table 1. Although all four groups of materials are lightweight, they also have many unique features. Micro-/nanolattices metamaterials have a higher strength and stiffness relative to the other groups (Lu C-X. et al., 2022). Chiral metamaterials have bistabilities, large deployable ratios, and ultrafast shape reconfiguration responses (Mousanezhad et al., 2016; Kolken and Zadpoor, 2017). Origami-inspired metamaterials are flexible, deformable, and compact (Lv et al., 2014; Yu et al., 2018). Cellular origami metamaterials have deployable, tunable Poisson’s ratio, and high interfacial surface area (Yu et al., 2018; Han et al., 2023). Therefore, these different features are utilized according to different requirements.

2.2 Pattern transformation metamaterials

Pattern transformation with tunable stiffness is a form of mechanical metamaterial. When a certain threshold of deformation is reached, the material undergoes a variation in its microstructure leading to a macroscopic phase change and thus the material has tunable stiffness. This switchable metamaterial is a phase transition between microstructures. Macroscopic external stress can switch between patterns in the entire metamaterial (Yu et al., 2018). However, pattern transformation and other metamaterials should first be distinguished, especially in the case of auxetic materials, i.e., negative Poisson’s ratio. Under compression, the stiffness of the pattern transformation metamaterial changes in both the axial and normal directions, so the Poisson’s ratio of the material also changes when under compression, and the positive and negative signs of the Poisson’s ratio are uncertain. This is not the same as the auxetic metamaterial, which has a fixed negative Poisson’s ratio. It is also necessary to distinguish between the tunable stiffness of pattern transformation and chiral/anti-chiral metamaterials. The tunable stiffness of the pattern transformation is related to the shape of the holes and the array of holes in the topology.

The shape of the holes can be regular shapes of circles, ovals, and polygons, or irregular shapes, as shown in Figure 2A. The response of mechanical metamaterials can be easily tuned for topological optimization by simply changing the shape of the holes (Kruijf et al., 2007). The incremental stiffness of the structure after optimizing the hole shape can be characterized in terms of the structural stress-strain response (Overvelde and Bertoldi, 2014). As the compressive strain increases, it first goes through the initial linear elastic stiffness phase, and then the incremental stiffness becomes almost zero. Finally, the stiffness increases sharply with the collapse of the hole.

FIGURE 2

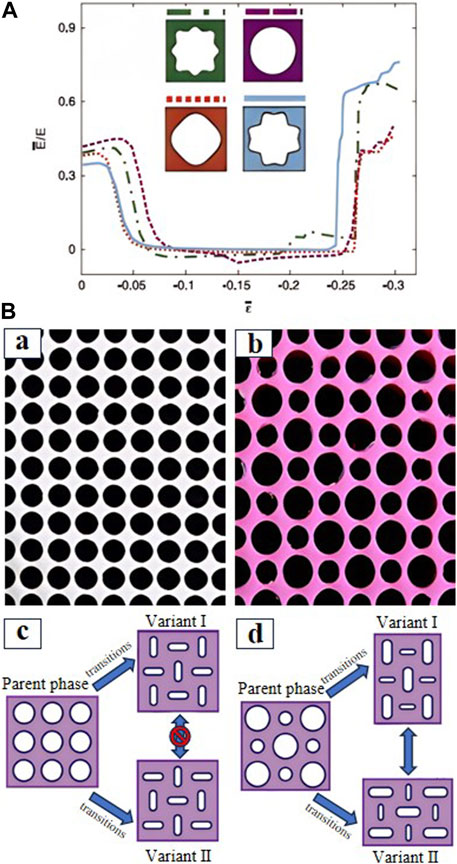
FIGURE 2. Pattern transformation with tunable stiffness. (A) The shape of the holes. (B) The array of holes. (a) Holey sheets. (b) Biholar sheets. (c) The phase transitions of holey sheets. (d) The phase transitions of biholar sheets. [Figure adapted from Refs (Overvelde and Bertoldi, 2014; Bertoldi et al., 2008; Florijn et al., 2014; Yang et al., 2016).].

There are four types of hole arrays: square, triangle, trihexagonal, and rhombitrihexagonal. Topology optimization for pattern transformation can make use of hole arrays with different hole sizes. One with the same hole size is called holey sheet and the other with two different sizes of circular holes is called biholar sheet (Bertoldi et al., 2008; Florijn et al., 2014), as shown in Figure 2B. The holey sheet can also be seen as the periodic elastomeric micro-lattice structure based on beams. The nonlinear stress-strain behavior of the structure can provide superior energy absorption properties. The nonlinear stress-strain behavior exhibited by the material under compressive loading is due to the linear response of the plateau stress caused by the initial structural instability of its microstructure deviating from the development (Bertoldi et al., 2008). The buckling of cellular microstructures usually results in local deformation via the collapse band, progressing through the structure under a relatively constant stress, to a large strain (Chung and Waas, 2002). The biholar sheet is like a programmable mechanical metamaterial with a negative Poisson’s ratio. The biholar mechanical metamaterial breaks the symmetry and occurs as a highly nonlinear deformation coupling in the two main axes (Florijn et al., 2014). Reversible elastic instability can lead to a change in the pattern, and it is possible to switch between variants (Yang et al., 2016). The pattern transformation, therefore, has properties such as tunable stiffness and tunable negative Poisson’s ratio. The negative Poisson’s ratio induced by the pattern transformation plays a key role and there is a critical effective threshold that generates the waisted buckling mode (Cao et al., 2023). Real-time tunable negative stiffness mechanical metamaterial has been designed with multistage pattern transformation for excellent performance in vibration isolation and energy absorption efficiency (Tan et al., 2020). In conclusion, such metamaterials exploit the mechanical instability of periodic porous elastic structures, opening up new avenues for a wide range of applications.

2.3 Negative compressibility metamaterials

Negative compressibility refers to the negative bulk modulus, which means that the material expands during compression or contracts during tension (Baughman et al., 1998; Nicolaou and Motter, 2012). Compressibility is a measure of the relative volume change of a solid or fluid in response to pressure changes, and is usually a positive sign (Xie et al., 2014). This special effect of negative compressibility occurs only when the system moves from one stable state to another metastable state under the force, called negative/inverted compressibility transition (Nicolaou and Motter, 2012; Nicolaou and Motter, 2013). The metamaterials with negative compressibility can be broadly classified into three types, i.e., negative linear compressibility (NLC), negative area compressibility (NAC), and negative thermal expansion (NTE), as shown in Figure 3.

FIGURE 3

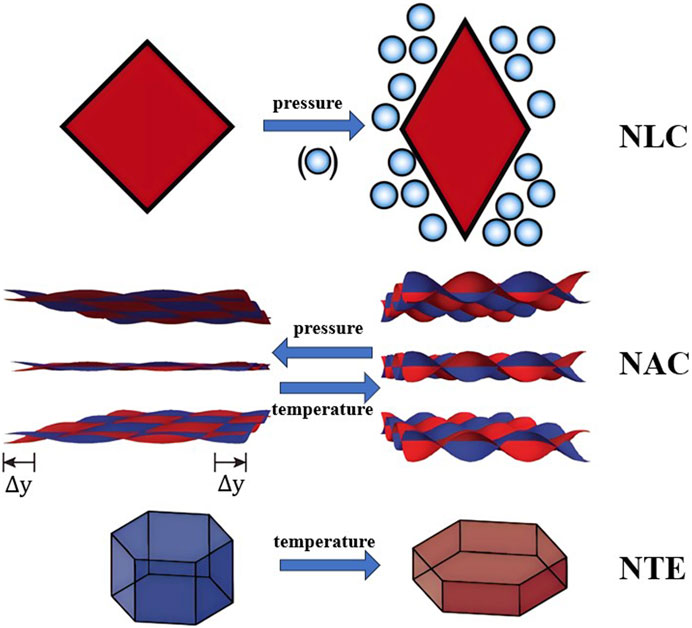
FIGURE 3. Negative compressibility metamaterials. [Figure adapted from Refs (Cairns and Goodwin, 2015; Hodgson et al., 2014; Collings et al., 2014).].

NLC is the bizarre material property in which the system expands in one direction where uniformly compressed (Cairns and Goodwin, 2015). NLC materials include both natural and artificial materials. However, the natural materials found have little negative compressibility, such as R-cristobalite structured BAsO₄ (Haines et al., 2003) and KMn [Ag(CN)₂]₃ (Cairns et al., 2012). The NLC effect of these materials is relatively weak. The artificial materials based on a framework with either wine-rack, honeycomb, or a related topology can be designed with higher values of negative compressibility. Li et al., 2012 developed a 3D hybrid zinc formate framework with the NLC based on metal-organic frameworks (MOFs), [NH₄][Zn(HCOO)₃]. Ghaedizadeh et al. (Ghaedizadeh et al., 2017) proposed two approaches to design and fabricate new composite structures with NLC. The experimental results showed that the designed material structures have NLC behavior due to the compressibility of the filled foam, the pattern of the network elements, and the stiffness ratio between the two constituent materials.

The expansion of compressed crystals in both directions, called NAC, is rare (demonstrated only in a few structures) and even weaker in magnitude compared to NLC (Cai et al., 2015). For example, the densification of layered materials usually proceeds through collapse in the stacking direction, which in turn leads to expansion in two perpendicular directions within the layer (Hodgson et al., 2014). The molecular framework Ag (tcm) (tcm⁻ = tricyclic methanation) expand continuously in two orthogonal directions under hydrostatic compression, and this NAC behavior is caused by the flattening of the honeycomb-like layers during the rapid pressure-driven collapse of the interlayer separation (Hodgson et al., 2014).

NTE refers to the contraction of a material when heated (Collings et al., 2014; Hodgson et al., 2014). NTE metamaterials follow the law of conservation of energy, but when heated, the whole effective structure will contract in one or more directions instead of expanding as usual (Yu et al., 2018). There is evidence for a specific link between anisotropic NTE and NLC/NAC in framework materials (Cairns et al., 2012). Therefore, anisotropic negative thermal expansion (NTE) behavior is also a type of negative compressibility. The researchers exploited the rare properties of negative compressibility for engineering applications. Tortora et al. (Tortora et al., 2021) obtained a metal-organic framework (MOF) by non-wetting liquid intrusion into a flexible porous media, which can have giant negative compressibility. Kim et al., 2023 presented a broadband muffler using a metamaterial consisting of a membrane structure with negative effective density and a Helmholtz resonator with negative effective compressibility. An unprecedented metamaterial muffler with a wide and low frequency performance range is achieved. The mechanical metamaterials with negative compressibility can be applied in engineering to meet specific conditions.

2.4 Pentamode metamaterials

Pentamode metamaterials can be perceived as ideal liquids in which the shear modulus is close to zero (Kadic et al., 2013). Pentamode metamaterials have a three-dimensional structure but exhibit two-dimensional properties, i.e., they are difficult to compress but flow easily (Yu et al., 2018). Due to the vanishing shear modulus, they can also be called metafluid (Kadic et al., 2013). They can easily support five infinitesimal strain modes with only one single stress. Milton (Milton and Cherkaev, 1995) and Sigmund (Sigmund, 1995) conceived and predicted it through theory back in 1995, but it was not made until early 2012. Wegener et al. (Martin et al., 2012; Kadic et al., 2013) proposed a pentamode metamaterial structure consisting of two connected truncated cones of elements, which were further fabricated by the current state-of-the-art lithography, as shown in Figure 4. The unit cell of a pentamode metamaterial generally consists of 16 double-cone elements (Kadic et al., 2012; Martin et al., 2012; Kadic et al., 2013). It is also possible to modify their diameter dimensions to obtain pentamode metamaterials of various structures. Moreover, a series of new pentamode lattice microstructures can be discovered over a range of effective material properties using efficient topology optimization methods (Li Z-Y. et al., 2021). Twenty-four pentamode lattices were developed to demonstrate the effectiveness of the proposed method. In addition, effective wave manipulation of pentamode metamaterial can also be achieved at low frequency conditions below 1,000 Hz underwater (Liang et al., 2023). Increasingly, pentamode metamaterials are being designed to solve problems in various fields, due to their unique mechanical properties.

FIGURE 4

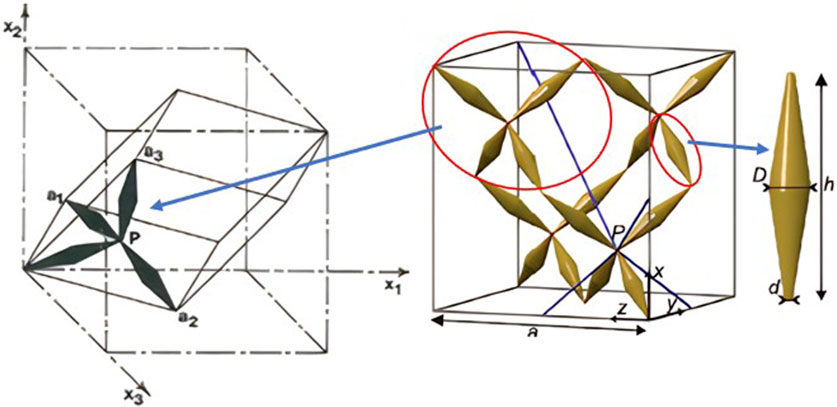
FIGURE 4. Pentamode metamaterials. [Figure adapted from Ref (Kadic et al., 2013).].

2.5 Auxetic metamaterials

Auxetic metamaterials, known as negative Poisson’s ratio materials, exhibit lateral contraction rather than expansion when compressed, and exhibit lateral expansion rather than contraction when stretched (Lu C-X. et al., 2022). Based on the forming structures, the auxetic metamaterials can be grouped into re-entrant structures, chiral structures, rotating rigid structures, and perforated sheet structures which are also called auxetic structures (Kolken and Zadpoor, 2017; Ren et al., 2018; Lu C-X. et al., 2022).

Conventional honeycomb structures are non-auxetic structures, but the re-entrant hexagonal honeycombs have the characteristic of auxeticity, as shown in Table 2. When a conventional honeycomb structure is stretched at both ends of the longitudinal direction, the structure contracts in transverse direction (positive Poisson’s ratio), but when the same stretch is exerted on the re-entrant hexagonal honeycomb structure, the structure expands in transverse direction (negative Poisson’s ratio) (Lu C-X. et al., 2022). In addition to the re-entrant hexagonal honeycomb structure, several other geometric structures have been proven to have re-entrant mechanisms, such as auxetic arrowhead structures (Larsen et al., 1997), Lozenge grids and square grids (Gaspar et al., 2005), and 3-STAR, 4-STAR, and 6-STAR systems (Grima et al., 2005a). In addition, 3D re-entrant structures can be developed from 2D structures (Yang et al., 2012). With the development of additive manufacturing technology, 3D re-entrant structures can be fabricated to deal with specific issues. Yang et al. (Yang et al., 2012) designed and manufactured a Ti–6Al–4V 3D re-entrant lattice auxetic structure using the electron beam melting process. The results showed that this structure possesses superior mechanical performances compared to conventional materials.

TABLE 2

TABLE 2. The types of auxetic mechanical metamaterials.

Chiral structures or anti-chiral structures (mentioned in Section 2.1) also have negative Poisson’s ratios, as shown in Table 2. The cylinder rotates under mechanical loading, causing the ligaments to flex, which results in the unfolding or folding of the ligament under tensile or compressive loading, respectively. Thus, the structures also have auxetic behaviors. However, adding cylinders to form the chiral honeycomb structures will reduce their stiffness relative to the re-entrant hexagonal honeycombs (Alderson et al., 2010a). Moreover, anti-chiral honeycombs are found to exhibit lower moduli than chiral counterparts with the same number of ligaments (Alderson et al., 2010b). To create periodic chiral structures, it is necessary to obey the constraints of rotational symmetry. Therefore, there are only five structures: trichirals, anti-trichirals, tetrachirals, anti-tetrachirals, and hexachirals. The Poisson’s ratio of chiral structures depends on the ligament/cylinder wall thickness-to-cylinder radius ratio and the ligament length-to-cylinder radius ratio (Lu C-X. et al., 2022). Meta-chiral structures do not obey the principle of rotational symmetry, and the combination of chiral structures and anti-chiral structures greatly increases the auxeticity. A meta-tetrachiral structure combines tetrachiral and anti-tetrachiral structures and replaces the nodes from cylindrical to rectangular (Grima et al., 2008a). The Poisson’s ratio of the meta-tetrachiral structure is much less than $-$ 1.0. Furthermore, 3D chiral structures have also been designed (Huang et al., 2016). However, a negative Poisson’s ratio can only be exhibited at small strains.

Rotating structures are usually made of regular geometric shapes connected by hinges, as shown in Table 2. These geometric shapes can be squares and rectangles, as well as triangles, rhombi, and parallelograms. When mechanically loaded, the rigid structure rotates around the hinge point. The overall structure expands in uniaxial tension and contracts in uniaxial compression. Grima and Evans (Grima and Evans, 2000; Grima and Evans, 2006) firstly proposed that the rotating structure have a negative Poisson’s ratio. Both the rotating square structure and the rotating triangular structure exhibit a Poisson’s ratio of $-$ 1.0 (Grima and Evans, 2000; Grima and Evans, 2006). Rotating rectangular structures are generated by replacing squares with rectangles, which are divided into two types depending on the shape of the empty space. The shapes of the empty space of type I are rhombi with the Poisson’s ratio ranging from negative to positive, depending on the rectangular aspect ratio and the angle between adjacent connecting rectangles (Grima et al., 2004). The shapes of the empty space of type Ⅱ are parallelograms, and the mechanisms are similar to that of the rotating square structures, although the connectivity is different (Grima et al., 2005b). The rotating rhombic and rotating parallelogram structures have also been investigated, whose Poisson’s ratios depend on the loading direction, the rotating geometry, and the empty space between them (Grima et al., 2008b; Attard et al., 2009; Attard and Grima, 2008).

Perforated sheet structures are perforated with different patterns of conventional blocks or sheets to form structures with negative Poisson’s ratio (Grima and Gatt, 2010), as shown in Table 2. Grima and Gatt explained the mechanism of auxeticity of perforated sheet structures and indicated that diamond and star perforated sheet structures have negative Poisson’s ratio in both tension and compression (Grima and Gatt, 2010). Although some perforated sheet structures looked like rotating structures, the fabrication method was easier than other auxetic structures (Grima et al., 2010). Most perforated sheet structures were limited in their auxeticity and could not exhibit a wide range of negative Poisson’s ratios. However, a class of highly anisotropic auxetic perforated metamaterials was proposed that exhibited high tunability and had the potential to exhibit a large range of Poisson’s ratios (Mizzi et al., 2021). Recently, the introduction of machine learning models has contributed to a rapid and accurate development of auxetic perforated sheet metamaterials (Wang et al., 2021). A new planar auxetic metamaterial was developed by introducing orthogonally aligned oval-shaped perforations, using the machine learning method. This approach enables an efficient and convenient design.

Besides the aforementioned auxetic metamaterials, there are also structures with negative Poisson’s ratios. Microporous polymers also have auxetic behavior, such as polytetrafluoroethylene (PTFE) (Caddock and Evans, 1989a; Caddock and Evans, 1989b). PTFE is highly anisotropic, with a Poisson’s ratio as low as $-$ 12.0. The microstructure of PTFE consists of disc-shaped particles and fibrils. When PTFE is stretched, the fibrils drive the particles to rotate, so it exhibites auxeticity in macroscopic. Origami metamaterials (mentioned in Section 2.1) also have negative Poisson’s ratio. For example, a negative Poisson’s ratio can be achieved in the Miura-ori origami structure according to its design parameters (Schenk and Guest, 2013; Lv et al., 2014).

With the development of science and technology, there are more and more types of mechanical metamaterials. Based on different criteria and mechanisms, mechanical metamaterials can also be classified in different ways. The types of auxetic mechanical metamaterials are summarized in Table 2.

Each of the five types of mechanical metamaterials presented above has unique mechanical properties and is applied in different fields (Liu et al., 2012; Ren et al., 2018; Yu et al., 2018; Surjadi et al., 2019; Mardling et al., 2020; Lu C-X. et al., 2022). Lightweight metamaterials are primarily used in aerospace, automotive, and construction applications, where they can improve the fuel efficiency of airplanes and automobiles and reduce the weight of buildings. Pattern transformation metamaterials are mainly used in the field of vibration isolation and energy absorption due to tunable stiffness. Negative compression metamaterials are widely used for muffling and vibration prevention, which can effectively isolate the propagation of sound and absorb and disperse vibration energy. Pentamode metamaterials are mostly used in the field of telecommunications and sensors, which can improve the performance and capacity of telecommunications systems, as well as the sensitivity and response speed of sensors. Auxetic metamaterials are typically used in vibration damping and biomedical applications, while their negative Poisson’s ratio properties can reduce vibration and impact forces on structures and equipment and can improve the suitability and effectiveness of medical devices. Therefore, some mechanical metamaterials are typically used in the field of biomedical engineering. For example, lightweight metamaterials and auxetic metamaterials are more commonly used in bone implant applications. Other types of mechanical metamaterials also have potential application in the field of biomedical engineering and deserve to be gradually explored.

3 Applications of mechanical metamaterials in the field of biomedical engineering

The mechanical metamaterials have many unique properties due to different structures. The unique properties of the mechanical metamaterials are particularly favored in the field of biomedical engineering. Therefore, bone implants, vascular stents, and other interesting applications will be reviewed next.

Among different types of metamaterials, the mechanical metamaterials are the most widely used in the field of biomedical engineering. Mechanical metamaterials have unique mechanical properties as described above, which have attracted the attention of researchers in the field of biomedical engineering. It has been shown in the last century that some natural biological tissues have a negative Poisson’s ratio, such as cat skin (Veronda and Westmann, 1970), cancellous bone (Williams and Lewis, 1982), and cow teat skin (Lees et al., 1991). Subsequently, embryonic epithelial tissues (Wiebe and Brodland, 2005; Chen and Brodland, 2009), the nuclei of embryonic stem cells (Pagliara et al., 2014), arteries (Timmins et al., 2010), tendons (Gatt et al., 2015), and the annulus fibrosus of the intervertebral disc (Derrouiche et al., 2019), which are natural tissues, were also reported to have auxetic behaviors. Moreover, cancellous bone has graded pores, and scaffolds can be designed to graded micro-/nanolattices structures (Zhang et al., 2023). Based on these investigations, mechanical metamaterials are mostly used in bone implants, vascular stents, and other biomedical applications.

3.1 Application in bone implants

Mechanical metamaterials have properties such as auxeticity, lightweight structures, tunable stiffness, etc., which can be used in the investigation of bone implants. Not only they are suitable for carrying tensile loads, but also they can show high levels of resistance to shear, energy dissipation, and indentation (Shirzad et al., 2023).

Bone screw is one of the bone implants. When the bone screw is loosened there is an outward pullout force, at which point the radial expansion of the auxetic screw increases the biomechanical interaction between the screw and the bone, thus improving the anti-pullout performance. Yao et al., 2020 designed bone screws with different auxetic unit cells, including re-entrant structures, chiral structures, and rotating structures. Experimentally and computationally, the re-entrant structure was considered to have the greatest stiffness and strength of all designs of auxetic bone screws and had a better performance in auxeticity, as shown in Table 3. Rotating structures have the greatest auxeticity, but the smallest stiffness and strength. Obviously, the re-entrant structures are more suitable for auxetic bone screws. The wall thickness and re-entrant angle of the unit cell are also investigated using a pull-out finite element model (Yao et al., 2021). The change in re-entrant angle significantly alters the mechanical properties of the screw compared to its thickness, especially its auxeticity. As the re-entrant angle changes from 45° to 80°, its Poisson’s ratio decreases slowly from −1.47 to −1.33 at first and then rapidly to −0.24.

TABLE 3

TABLE 3. Example of applications of mechanical metamaterials in bone implants.

The applications of mechanical metamaterials for hip implants are relatively early. The lightweight properties of metamaterials have drawn the attention of the researchers. For example, the triply periodic minimal surface (TPMS) structures are widely applied in bone scaffolds (Huo et al., 2021). The applications of TPMS structures ensure that the bone scaffolds are both lightweight and meet the required mechanical properties. This is also like the properties of natural bone. Kolken et al., 2021a designed acetabular cups based on six different unit cells and demonstrated after bionic compression tests that meta-implants with functional gradient diamond infill had the best space-filling behavior, as shown in Table 3. However, stress shielding and micromotions are two of the most serious problems in the stem of artificial joints (Ghavidelnia et al., 2020). To solve these problems, auxetic mechanical metamaterials are used to design hip implants. Therefore, different types of meta-biomaterials are also designed and additively manufactured with a rational distribution of positive and negative Poisson’s ratios, thereby improving the contact between implant and bone, increasing the implant longevity (Kolken et al., 2018). In addition, heterogeneous structural hip implant stems with the positive and negative Poisson’s ratio are effective in preventing bone implant failure (Liu B. et al., 2023). Furthermore, fatigue performance and fatigue crack initiation and propagation are investigated in auxetic implants (Kolken et al., 2021b; Kolken et al., 2022). These auxetic structures exhibit morphological and mechanical properties suitable for bone implant applications. The structural integrity has been maintained and despite the presence of significant crack growth, but there are no signs of rapid strain accumulation. Auxetic lattice structure stems are introduced to reduce stress shielding, and the Mayo-type stems with a re-entrant angle of 70° have the lowest level of stress shielding revealed by the finite element analysis (Liu B-L. et al., 2023), as shown in Table 3. The load on the hip joint has a bending effect on the implant stem, which causes the implant stem to contract and loosen. The application of auxetic mechanical metamaterials can effectively address this problem. The introduction of 2D or 3D auxetic structures on the lateral side of the implant stems can promote osseointegration in the proximal lateral region of the femur (Singh et al., 2023). These novel solutions regarding metamaterials can improve the survival rate of the implant stem after total hip arthroplasty.

Mechanical metamaterials are not only used in bone screws and hip implants but also there are studies carried out on intervertebral discs. The lumbar spine is an important pillar for the body to carry loads. The lumbar disc herniation is a restriction on mobility for the elderly. The auxetic metamaterials intervertebral disc implants made of polymers are ideally suited as a replacement for natural discs (Martz et al., 2005). The negative Poisson’s ratios of the auxetic structure can provide excellent energy absorption and compression stability. When compressed, the artificial disc will shrink in the transverse plane, and thus the nerves will not be compressed. Artificial intervertebral discs can be made of auxetic foam with re-entrant cellar structures (Baker, 2013). Finite element analysis has shown that the use of a negative Poisson’s ratio artificial disc is a solution to the problem due to the elimination of damage to the surrounding nerves. Jiang Y-L. et al., 2023 compared natural intervertebral discs, conventional 3D implants, and a new designed auxetic implant and the results showed that the new implant had more effective stress transfer and attenuation under physical loading conditions, as shown in Table 3. The artificial intervertebral discs with auxetic structures contract laterally inwards during longitudinal compression, facilitating the relief of herniated discs. Furthermore, the concept of self-aware implants, a revolutionary technology, has recently been proposed by Barri et al., 2022, as shown in Table 3. The self-aware implants were built on rationally designed different triboelectric auxetic microstructures. Integrating nano energy harvesting and mechanical metamaterials, the implanted device can respond to its environment, empower itself and self-monitor its condition. The results showed that self-aware cage implants could use internally generated voltage signals to diagnose the bone healing process. The revolutionary technology can potentially facilitate a better recovery after surgery.

Due to the shortcomings of existing bone fixation devices, metamaterial intramedullary nails are designed to address stress shielding and bone nonunion in the healing of fractured bones. High initial stiffness prevents micromovement of newly formed bone, leading to poor bone healing. Therefore, a novel design of printable tunable stiffness metamaterial is developed for bone healing (Hashemi et al., 2021), as shown in Table 3. The metamaterial structure can exhibit effective bilinear stiffness in one direction, with relative rigidity after a specific amount of compression. It can also provide appropriate micromotion to promote the gradual transformation of callus into bone. Ali et al. (Mehboob et al., 2022) designed two new intramedullary nail structures based on cylinder and pillar and compared them with the one of Mohammad et al. (Hashemi et al., 2021). The results showed that cylindrical intramedullary nails exhibit excellent mechanical properties under different types of loading and have the best healing and bending stiffness at a strain of 10%. The applications of the tunable stiffness metamaterial include, but are not limited to long bone fractures, and it can be used in any application where bilinear stiffness is required.

The manufacture of artificial bone is based on the amazing properties of metamaterials to replace non-working human bone. When severe irreversible and irreparable damages to the bone occur, it needs to be replaced with a suitable substitute. Therefore, artificial bone with a performance similar to that of human bone needs to be designed and manufactured. Li J. et al., 2021 prepared a layered ferroelectric metamaterial with ceramic-like piezoelectric properties and bone-like fracture toughness utilizing low-voltage-assisted 3D printing, as shown in Table 3. The results of the experiments and finite element analysis demonstrated that the developed artificial bone has tunable anisotropic piezoelectric and bone-comparable mechanical properties. In addition, Masoumi Ravandi et al. (Masoumi et al., 2023) have also used 3D printing to fabricate metamaterial bone with porosity. The investigation showed that the 30% optimum porosity has the best mechanical performance and a 5.97% reduction in weight compared to the solid bone sample. These explorations into artificial bone have helped us to find an appropriate replacement for human bone.

As mentioned above, the various types of bone implants have applied metamaterials with different and amazing mechanical properties. Examples of applications of mechanical metamaterials in bone implants are summarized in Table 3.

3.2 Application in vascular stents

In the clinic, the reconfigurable or shape-shifting behavior of vascular stent is crucial for the successful implantation of vascular stent. The radius of the blood vessel is small and varies at different locations, requiring the vascular stent to be small and can be moved to the target region and fixed at that region. The 4D reconfigurable behavior of metamaterials exactly matches this expectation. The stent is shrunk and placed into the target region through minimally invasive surgery, and then expand in the target region to secure in that place. The shape-shifting or reconfigurable materials will change their dimension and structure upon activation (van Manen et al., 2021). Shape memory polymers can recover from a programmed temporary shape to an initial shape in response to external stimuli (e.g., light, heat, magnetism, electricity, etc.) (Wan et al., 2020; Holman et al., 2021; Xia et al., 2021). For example, the polymers are deformed and temporarily “frozen” by cooling to low temperatures, and the temperatures increase to make them flexible and mobile again (Ionov, 2014). Moreover, Hydrogels can also be controlled in terms of swelling by changing the temperature and pH (Ionov, 2014). Although metamaterials have exotic properties, not all of them can be used in vascular stents.

It should be noted that not all types of materials can be reconfigurable and applicable in the field of biomedical engineering. The widely used reconfigurable biomedical materials in vascular stents are shape memory polymers, due to their good biocompatibility and biodegradability. Shape memory polymers can exhibit one permanent shape at room temperature and another deformed shape at high temperatures and this shape can be retained after cooling (Xia et al., 2021). Compared to conventional metal stents, shape memory polymer stents can self-expand in specific locations, which can facilitate drug delivery systems and blood circulation (Wache et al., 2003). Approximately 2 mm shape memory polymer stents were successfully implanted into the femoral artery of porcine animals to prevent damage caused by vessel occlusion (Shin et al., 2019). This resulted in improved patency of the porcine blood vessels and remodeling of the blocked vessels. Liu et al., 2020 also conducted a theoretical study and numerical analysis to improve the mechanical properties of shape memory polymer stents. Simulation results showed that the stents with smaller radii have higher critical buckling loads and smaller buckling displacements. Furthermore, the smaller contact area with the vessel reduced implantation stress and vascular restenosis. The shape memory polymers have characteristics such as deformability and elasticity, good biocompatibility, and controlled degradation properties, making them one of the ideal vascular stent materials.

It should be noted that not only the reconfigurable behaviors of metamaterials are used, but also the auxetic behaviors can also be applied in vascular stents. There are several advantages to applying the auxetic behavior. One of the most important advantages is that the length of the stent increases during radial expansion, allowing for longer vessel coverage compared to conventional stents. Moreover, because of the auxetic structure, when the stent is stretched by an external force, it will expand in the transverse plane and thus the resistance force is increased, and the stent can be firmly fixed at that position. Furthermore, when a vessel becomes narrowed due to a blockage, the stent will be compressed and the auxetic stent also has better stiffness to ensure that the vessel has some space to stop narrowing. A 3D tubular lattice metamaterial with sinusoidal ligaments was applied to the auxetic vascular stents (Jiang et al., 2020; Jiang et al., 2022). The results showed that the designed auxetic stents have better ductility than conventional stents under large compressive deformations. Abbaslou et al., 2023 also designed a novel meta-trichiral auxetic vascular stent using three types of unit cells: re-entrant, trichiral, and anti-trichiral. The effective and parametric design of the stent geometry improve its stiffness, stability, and auxetic effect. What’s more, combining reconfigurable and auxetic behavior creates a new tubular stent structure (van Manen et al., 2021), as shown in Figure 5. Upon activation, arms bending leads to a switch from a re-entrant unit cell (with auxetic behavior) to a conventional honeycomb unit cell (with a positive Poisson’s ratio). The application of auxetic behavior offers a novel option for the treatment of vascular diseases in the biomedical engineering field.

FIGURE 5

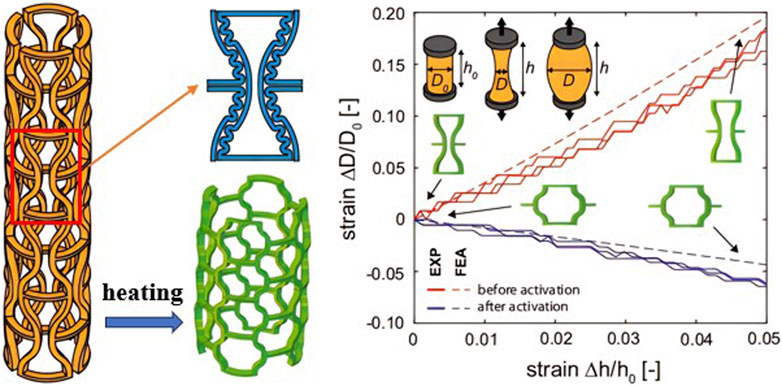
FIGURE 5. Example of the reconfigurable auxetic vascular stent. [Figure adapted from Ref (van Manen et al., 2021).].

3.3 Other applications in the field of biomedical engineering

(1) Mechanical metamaterials in healthcare applications

Mechanical metamaterials can be used in impact protector devices (pads, gloves, helmets, and mats) to exploit better conformability for comfort, support, and protection (Sanami et al., 2014). A cylinder-ligament honeycomb with synclastic curvature was reported, which made this system a candidate core material in sports helmet applications. The material had a double curvature and the cylinders in the honeycomb structure were always aligned perpendicular to the curved surface of the helmet to provide maximum resistance across the thickness of the crushing or impact event. Nowadays, more and more medical insoles are designed using auxetic structures, as the auxetic foam will have better resilience and energy absorption capability under uniaxial compression. Therefore, auxetic foam has been proven to be one of the excellent materials for energy absorbing components and impact protectors.

Mechanical metamaterials have significant potential for textile applications (Wang and Hu, 2014). In the biomedical engineering fields, the fiber or yarn form of metamaterial textiles can be developed in different ways. For example, smart bandage is one of the typical applications (Wang and Hu, 2014). The bandage was made of auxetic filaments with wound-healing agents. When swelling occurred in the wound, the bandage would open and release the agents. When the wound healed, the bandage closed and stopped releasing the agents. Auxetic fabrics can also be used for children’s wear (Wang and Hu, 2014). The children’s body develops quickly and after a few months, the previous clothes are no longer wearable. Therefore, many parents give their children loose-fitting clothes. However, this can be dangerous when the child is playing. Auxetic children’s wear can solve this problem effectively. The auxetic fabric can expand in length and width direction, which allows the clothing to fit the children for a long time. Auxetic fabrics have many other potential applications for metamaterial textiles due to their excellent shape fit and comfort properties.

(2) Mechanical metamaterials in biomedical sensor applications

The superior mechanical properties of the mechanical metamaterials are applied to sensors to improve their sensitivity. Jiang et al., 2018 applied the auxetic behavior of mechanical metamaterials to stretchable strain sensors and achieved a much higher sensitivity of 24 times compared to conventional sensors. The stretchable strain sensors based on tensile metamaterials are used for pulse monitoring in the human radial artery. Due to the high sensitivity, the monitoring results are more accurate and comprehensive compared to conventional sensors. Gu et al., 2021 had developed the piezo-transmittance-based strain sensor using gap control of the auxetic patterned elastomer. The gap opening mechanism in the negative Poisson’s ratio metamaterial with a rotating square structure allows the sensor to achieve a designable response and low stiffness. The metamaterial sensors have great potential for the continuous monitoring of everyday health with high precision and abundant medical detail.

4 Summary and future perspective

In summary, metamaterials have been more and more widely used in the field of biomedical engineering. Due to their unique behaviors, they have been used to enhance the fixation of bone screws, allow for the minimally invasive implantation of vascular stents, enhance the resilience of running shoes, etc. However, the research limit has not been reached and further efforts should be made to improve the performance of biomedical products.

(1) The structures of the metamaterial need to be optimized for design. At present, there are various types of metamaterials, but the selection standard and criterion have not been set up. Structural optimal design can be an approach to set up the procedure to select the optimal structures to maximize the product performance, but this requires extensive consolidated research.

(2) The integrated design-manufacturing approach to minimize product defects and inaccuracy. The complex auxetic structures of the metamaterials pose a huge challenge to the accurate manufacturing of products. Additive manufacturing is a widely used approach to produce such structures but there are always geometry discrepancies and mismatches of the mechanical properties are always present in the produced products (Lu et al., 2020). Therefore, one of the future research efforts will be to reduce manufacturing inaccuracies.

(3) The efficient assessment of the performance of biomedical products in clinic-mimicking scenarios. Biomedical products with metamaterials are intended to be used in the human body. Therefore, the assessment of their performance in the clinic scenarios is crucial. While the in vivo investigation approach is time-consuming and expensive, new approaches, such as the in silico method using musculoskeletal and numerical modeling techniques, should be investigated in the future.

(4) Many advanced methods have been utilized to explore novel structures. At present, almost all metamaterials are periodically arrayed structures. There is still a large room to improve them into bionic structures, such as the non-periodic bone-like structures. However, the applications of some advanced design approaches, such as the machine learning technique (Lu Y-T. et al., 2022), and the Movable Morphable Components (Guo et al., 2016) are required.

Author contributions

HW: Conceptualization, Writing–original draft. YL: Conceptualization, Funding acquisition, Writing–review and editing. SB: Funding acquisition, Resources, Writing–review and editing. HZ: Writing–Review & Editing, Resources, Funding acquisition. YR: Funding acquisition, Resources, Writing–review and editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This research was funded by (The National Natural Science Foundation of China) Grant Number (12072066), (The Liaoning Provincial Natural Science Foundation of China) Grant Number (2022-YGJC-21), (The Dalian Science and Technology Innovation Fund) Grant Number (2022JJ13SN077), (DUT-BSU grant) Grant number (ICR2103) and (The Dalian University of Technology -Cardiff University collaboration and exchange fund) Grant Number (DUT-CU-2023070703).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abbaslou, M., Hashemi, R., and Etemadi, E. (2023). Novel hybrid 3D-printed auxetic vascular stent based on re-entrant and meta-trichiral unit cells: finite element simulation with experimental verifications. Mater. Today Commun. 35, 105742. doi:10.1016/j.mtcomm.2023.105742