The significance of ternary hybrid cross bio-nanofluid model in expanding/contracting cylinder with inclined magnetic field

Significance: Bio-nanofluids have achieved rapid attention due to their potential and vital role in various fields like biotechnology and energy, as well as in medicine such as in drug delivery, imaging, providing scaffolds for tissue engineering, and providing suitable environments for cell growth, as well as being used as coolants in various energy systems, wastewater treatment, and delivery of nutrients to plants.

Objective: The present study proposes a novel mathematical model for the ternary hybrid cross bio-nanofluid model to analyse the behaviour of blood that passes through a stenosed artery under the influence of an inclined magnetic field. The model considers the effect of expanding/contracting cylinder, infinite shear rate viscosity, and bio-nanofluids.

Methodology: The considered model of the problem is bounded in the form of governing equations such as PDEs. These PDEs are transformed into ODEs with the help of similarity transformations and then solved numerically with the help of the bvp4c method.

Findings: The results show that the flow rate and velocity decrease as the inclination angle of the magnetic field increases. Additionally, research has found that the presence of nanoparticles in the bio-nanofluid has a significant impact on the velocity and flow rate. Therefore, the flow rate decreases, in general, as the stenosis becomes more severe.

Advantages of the study: The results obtained from this study may provide insights into the behaviour of blood flow in stenosed arteries and may be useful in the design of medical devices and therapies for the treatment of cardiovascular diseases.

1 Introduction

Bio-nanofluids are a generally modern range of inquiries within the field of biomedicine, and they have been pulled into critical consideration due to their potential applications in well-dignified conveyance, imaging, and detecting. Specifically, the use of bio-nanofluids within the setting of blood has gotten much consideration as these liquids have the potential to upgrade the transport of drugs and other helpful operators within the circulatory system. Bio-nanofluids and suspension of nanoparticles in a natural liquid, such as blood, can essentially modify the physical and chemical properties of the liquid. The involvement of nanoparticles within bio-fluidity can improve the thickness of the liquid and modify the surface properties of the blood cells, which can influence their aptitude with other cells and with the dividers of blood vessels. Moreover, bio-nanofluids can improve the solvency and bio-availability of drugs and other restorative specialists, which can enhance their adequacy and decrease their side impacts. Bio-nanofluids have been utilized to upgrade blood stream in totally different ways. Therefore, it has been shown that adding nanoparticles, such as gold nanoparticles or carbon nanotubes, to the blood can reduce its viscosity and improve blood flow (Conrad and Wang, 2021). This can be achieved by reducing the interparticle spacing and increasing the Brownian motion of the particles. Another method is to modify the surface properties of the blood vessels. Bio-nanoparticles, such as liposomes and dendrimers, can be used to modify the surface properties of the blood vessels, which can reduce the resistance of the blood flow and improve its velocity (Ali et al., 2021). Ige et al. (Ige et al., 2023) made a numerical analysis related to mixed convection of blood flow with the hybrid fluid model under the influence of bio nanoparticles. In this study, Boussinesq approximation and transient Regime are incorporated. Latest studies regarding bio-nanoparticles in blood flow and their characteristics are investigated by (Ige et al., 2022; Yadav et al., 2022; Fatima et al., 2023).

The contracting/expanding stenosed arteries could be a common event in blood vessel maladies, such as atherosclerosis, where the supply route dividers thicken and limit the bloodstream. The harshness of the supply route leads to an increment in speed and turbulence of the bloodstream, which can cause different cardiovascular diseases, including myocardial dead tissue and stroke. Exact modelling of the bloodstream in stenosed courses is, hence, basic for understanding the instruments of these illnesses and creating viable treatment procedures. In the past, numerical models have been created to recreate the bloodstream in stenosed courses and explore the impacts of different components, such as the consistency of blood, the shape and estimate of the stenosis, and the nearness of attractive areas or nanoparticles. Stenosis has been broadly considered within the past few decades, and different computational models have been created to explore its impacts on the bloodstream. We utilised a computational show to re-enact expanding/contracting stenosis in a human carotid course and found that the degree of stenosis and the sufficiency of altered vessel breadth altogether influenced the speed and divider shear stretch of the bloodstream (Bath et al., 1999). Alghamdi et al. (Alghamdi et al., 2023) investigated a hybrid nanofluid to explore the effects of multiple ferromagnetic nanoparticles in co-axial disks for magnetized fluid. A computational study with Oldroyd-B nanofluid flow and magnetized gold-blood particles passing through the blood was conducted by (Tang et al., 2023a). Furthermore, literature regarding magnetized gold-blood nanofluid stenosis narrow arteries, blood flow via arteries with overlapping shaped stenosis, and vertical porous multiple stenoses can be traced by (Zain and Ismail, 2023a; Tang et al., 2023b; El Kot and Abd Elmaboud, 2023).

The magnetic field has appeared to have a critical effect on the conduct of the bloodstream in courses. In the past, we have found that the application of an attractive magnetic field to stenosed courses can improve the bloodstream and decrease the hazard of cardiovascular maladies. The reason behind this enhancement is credited to the impact of attractive areas on the attractive properties of blood cells, which changes the stream conduct of the blood. When an attractive magnetic field is connected at a point to the supply route, the speed and stream rate of blood are influenced, driving changes within the shear push and weight dispersion. These changes can have both positive and negative impacts on the cardiovascular framework, depending on the greatness and course of the attractive field. Hence, it is basic to consider the impacts of slanted attractive areas on the bloodstream in stenosed courses to get the superior potential benefits and dangers of using attractive areas within the treatment of cardiovascular diseases. In the past, there has been developing intrigue in considering the impact of a slanted attractive field on the bloodstream. A few considerations have illustrated that an attractive field can impact the rheological properties of blood, counting its thickness and stream characteristics. For example, a study by Dolui et al. (Dolui et al., 2023) found that an inclined magnetic field could reduce the resistance to flow in blood vessels, potentially improving circulation in patients with cardiovascular disease. Furthermore, Varshney et al. (Varshney et al., 2010) showed that a magnetic field applied at an angle to the direction of blood flow could alter the orientation of red blood cells, leading to changes in their deformation and aggregation behaviour. These findings suggest that an inclined magnetic field could have important implications for the diagnosis and treatment of various cardiovascular disorders. Zain et al. (Zain and Ismail, 2023b) explored the numerical results regarding the effects of MHD on blood flow by taking the mathematical model of power and the law fluid model. The latest study related to the influence of MHD, Dufour, and Soret effects on blood through a stenosed artery and keeping variable viscosity is established by Mishra et al. (Mishra et al., 2023).

1.1 Motivation

The inspiration for the “ternary hybrid cross bio-nanofluid in expanding/contracting stenosed arteries with interminable shear rate thickness and magnetic field” is to create a comprehensive numerical demonstration that considers numerous components that can influence the bloodstream in requisite posited stenosed supply routes. The motivation behind using a cross nanofluid is because of its capability to investigate the flow behaviour at a very high and low shear rate. The behavior of bloodstream flow in stenosed arteries became more understandable via adding the effects of expanding/contracting stenosis geometry, infinite shear rate consistency, and inclined magnetic field. Furthermore, thinking about the bio-nanofluid stream in stenosed supply routes may give bits of knowledge into the conduct of the bloodstream at the nanoscale level and the potential benefits of utilizing nanoparticles within the treatment of cardiovascular illnesses.

1.2 Novelty

The “ternary hybrid cross bio-nanofluid model” considers various factors affecting blood flow in requisite posited stenosed arteries. The stenosis, viscosity, bio-nanofluid flow, and magnetic field influence have been simultaneously explored in the given model. This examination offers a novel model that sheds light on blood flow in narrowed arteries and the advantages of utilizing ternary nanofluids and magnetic fields to treat cardiovascular illnesses.

2 Mathematical formulation

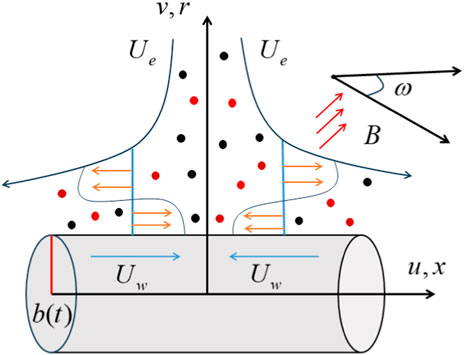
Let us consider the two-dimensional stagnation-point flow of a ternary hybrid cross bio-nanofluids over a permeable expanding/contracting cylinder with influences of the inclined magnetic field. Also, the liquid (blood) is initiated by extension and withdrawal of a stenosed artery having a time-dependent radius $b\left(t\right)=b_0\sqrt{1-\beta t}$. So, $\beta$ is called the constant of the expansion/contraction strength parameter, and the positive consistent b₀ incorporates a length measurement. However, when $\beta$ is positive, the artery’s sweep decreases over time, whereas in the case that $\beta$ is negative, the radius develops as a result. Moreover, the problem is bounded by the corresponding x-axis and r-axis, as delineated in Figure 1. In this situation, the supply route is accepted to be contracting or developing at a rate determined by the time-dependent velocity $U_w\left(x,t\right)=\frac{2cx}{1-\beta t}$, where c may be a positive constant of dimension (time)⁻¹ and the x-axis is the horizontal surface of the cylinder. It is assumed that $T_w$ is the surface (body) temperature of the cylinder, and $T_{\infty }$ is the temperature of the free stream. A non-uniform transverse attractive magnetic field $B\left(t\right)=\frac{B_0}{\sqrt{1-\beta t}}$ is applied perpendicular to the surface of the cylinder. The induced magnetic field is negligible due to a very small Reynolds number. The free stream velocity is denoted by $U_e\left(x,t\right)=\frac{2ax}{\left(1-\beta t\right)}$ where $\beta$ is a positive acceleration and deceleration parameter.

FIGURE 1

FIGURE 1. Physical shape of the flow problem.

The velocity and temperature field vectors are defined as:

$\begin{array}{l}V=\left[v\left(r,x,t\right),0,u\left(r,x,t\right)\right],\\ T=T\left(r,x,t\right).\end{array}(1)$

Furthermore, using the above-stated assumptions, the leading governing equations can take place as follows (see (Sumner et al., 1999; Ali et al., 2020a; Waqas, 2020; Ayub et al., 2022a)):

$\frac{\partial }{\partial x}\left(ru\right)+\frac{\partial }{\partial r}\left(rv\right)=0,(2)$

$\begin{array}{l}\left(\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial r}\right)=U_e\frac{\partial U_e}{\partial x}+\frac{\partial U_e}{\partial t}+\frac{1}{{\rho }_{thnf}}\frac{{\mu }_{thnf}}{r}\frac{\partial u}{\partial r}\left[{\left({\beta }^{*}+\left(1-{\beta }^{*}\right)\left(1+{\left(\mathrm{\Gamma }\frac{\partial u}{\partial r}\right)}^n\right)\right)}^{-1}\right]+\\ \frac{1}{{\rho }_{thnf}}{\mu }_{thnf}\frac{\partial }{\partial r}\left[\frac{\partial u}{\partial r}{\left({\beta }^{*}+\left(1-{\beta }^{*}\right)\left(1+{\left(\mathrm{\Gamma }\frac{\partial u}{\partial r}\right)}^n\right)\right)}^{-1}\right]-\frac{{\sigma }_{thnf}{\sin }^2\left(\omega \right)B^2}{{\rho }_{thnf}}\left(u-U_e\right),\end{array}(3)$

$\rho {\left(C_p\right)}_{thnf}\left[\frac{\partial T}{\partial t}+v\frac{\partial T}{\partial r}+u\frac{\partial T}{\partial x}\right]=\frac{1}{r}\frac{\partial }{\partial r}\left[k_{thnf}^{*}\left(T\right)r\frac{\partial T}{\partial r}\right],(4)$

along with boundary conditions are (see (Ayub et al., 2022a)):

$u=U_w\left(x,t\right)=\frac{2cx}{1-\beta t},v=V_w\left(t\right)=-\frac{a{b}_{0}s}{\sqrt{1-\beta t}},T=T_w,\text{at\hspace{0.17em}}r=b\left(t\right),(5)$

$u\to U_e\left(x,t\right),T\to T_{\infty },\text{as\hspace{0.5em}}r\to \infty .(6)$

Here, ${\beta }^{*}$ is the infinite shear rate viscosity parameter, $u$ and $v$ refer to the velocity components of blood along the axial and radial direction, respectively, $T$ is the temperature of the THN, $s$ is the suction parameter, $b_0$ is the positive constant, and $c$ is called the stretching/shrinking rates. In addition, ${\mu }_{thnf}$ denotes the viscosity of the ternary hybrid nanofluid (THN), ${\sigma }_{thnf}$ refers to the electrical conductivity of the THN, ${\rho }_{thnf}$ represents the density of the THN, and $k_{thnf}^{*}\left(T\right)$ is the variable thermal conductivity (TCN) of the THN model. Also, the term ${\left(C_p\right)}_{thnf}$ is the specific heat. The variable TCN is defined as (see (Kaleem et al., 2022; Nazir et al., 2022; Babu et al., 2023; Bafakeeh et al., 2023)):

$k_{thnf}^{*}\left(T\right)=k_{thnf}\left(1+\epsilon \left(\frac{T-T_{\infty }}{T_w-T_{\infty }}\right)\right),(7)$

where $k_{thnf}$ is the TCN of the THN and its correlation is defined later in the given section, while $\epsilon$ is the thermal conductivity parameter.

Furthermore, the thermo-physical characteristics of the ternary nanofluid model are given as follows:

$\frac{{\mu }_{thnf}}{{\mu }_f}=\frac{1}{{\left(1-{\phi }_{s1}\right)}^{2.5}{\left(1-{\phi }_{s2}\right)}^{2.5}{\left(1-{\phi }_{s3}\right)}^{2.5}},(8)$

$\frac{{\rho }_{thnf}}{{\rho }_f}=\left[\left(1-{\phi }_{s1}\right)\left(1-{\phi }_{s2}\right)\left(1-{\phi }_{s3}\right)+\frac{{\rho }_{s3}}{{\rho }_f}{\phi }_{s3}+\frac{{\rho }_{s2}}{{\rho }_f}{\phi }_{s2}+\frac{{\rho }_{s1}}{{\rho }_f}{\phi }_{s1}\right],(9)$

$\frac{{\left(\rho C_p\right)}_{thnf}}{{\left(\rho C_p\right)}_f}=\left[\left(1-{\phi }_1\right)\left(1-{\phi }_2\right)\left(1-{\phi }_3\right)+\frac{{\left(\rho C_p\right)}_{s3}}{{\left(\rho C_p\right)}_f}{\phi }_{s3}+\frac{{\left(\rho C_p\right)}_{s2}}{{\left(\rho C_p\right)}_f}{\phi }_{s2}+\frac{{\left(\rho C_p\right)}_{s1}}{{\left(\rho C_p\right)}_f}{\phi }_{s1}\right].(10)$

$\frac{k_{thnf}}{k_{hnf}}=\frac{k_{s1}+2k_{hnf}-2{\phi }_{s1}\left(k_{hnf}-k_{s1}\right)}{k_{s1}+2k_{hnf}+{\phi }_{s1}\left(k_{hnf}-k_{s1}\right)},(11)$

$\frac{k_{hnf}}{k_{nf}}=\frac{k_{s2}+2k_{nf}-2{\phi }_{s2}\left(k_{nf}-k_{s2}\right)}{k_{s2}+2k_{nf}+{\phi }_{s2}\left(k_{nf}-k_{s2}\right)},(12)$

$\frac{k_{nf}}{k_f}=\frac{k_{s3}+2k_f-2{\phi }_{s3}\left(k_f-k_{s3}\right)}{k_{s3}+2k_f+{\phi }_{s3}\left(k_f-k_{s3}\right)},(13)$

and the electrical conductivity

$\frac{{\sigma }_{thnf}}{{\sigma }_{hnf}}=\frac{{\sigma }_{s1}+2{\sigma }_{hnf}-2{\phi }_{s1}\left({\sigma }_{hnf}-{\sigma }_{s1}\right)}{{\sigma }_{s1}+2{\sigma }_{hnf}+{\phi }_{s1}\left({\sigma }_{hnf}-{\sigma }_{s1}\right)},(14)$

$\frac{{\sigma }_{hnf}}{{\sigma }_{nf}}=\frac{{\sigma }_{s2}+2{\sigma }_{nf}-2{\phi }_{s2}\left({\sigma }_{nf}-{\sigma }_{s2}\right)}{{\sigma }_{s2}+2{\sigma }_{nf}+{\phi }_{s2}\left({\sigma }_{nf}-{\sigma }_{s2}\right)},(15)$

$\frac{{\sigma }_{nf}}{{\sigma }_f}=\frac{{\sigma }_{s3}+2{\sigma }_f-2{\phi }_{s3}\left({\sigma }_f-{\sigma }_{s3}\right)}{{\sigma }_{s3}+2{\sigma }_f+{\phi }_{s3}\left({\sigma }_f-{\sigma }_{s3}\right)}.(16)$

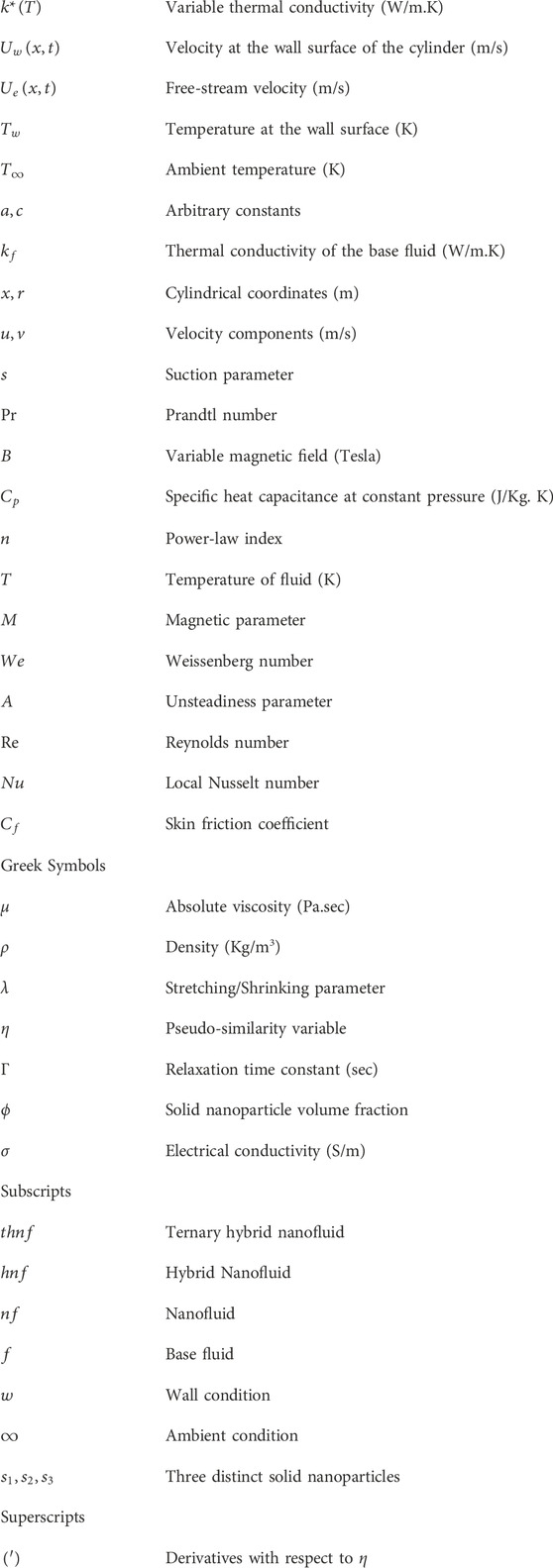
Here, in Equations 8–16, the solid nanoparticles volume fraction is denoted by ${\phi }_{si},$ where $i=\mathrm{1,2,3}$. For this particular case, ${\phi }_{si}=0,\text{for\hspace{0.5em}}i=\mathrm{1,2,3}$; the equations are reduced to the regular base fluid. Moreover, the subscripts $thnf$, $hnf$, $nf$, $f$, and $si,\text{for\hspace{0.5em}}i=\mathrm{1,2,3}$ refer to the THNF, HNF, NF, base fluid, and the solid nanoparticles, respectively. The experimentation physical data of the base (blood) fluid and the three distinct nanoparticles are given in Table 1, see (Das et al., 2021; Tripathi et al., 2021; Sajid et al., 2023a).

TABLE 1

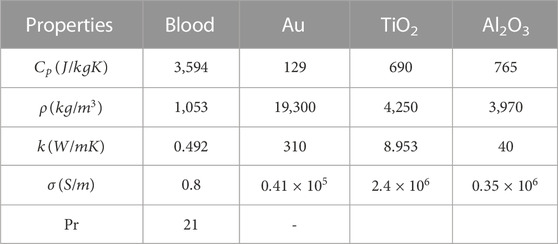
TABLE 1. The thermophysical characteristics of base (blood) fluid and Au, TiO₂, and Al₂O₃ nanoparticles.

3 Solution procedure

Furthermore, to ease the investigation of the problem, the following similarity variants are introduced for the conversion of PDEs into ODEs as:

$u=\frac{2ax}{\left(1-\beta t\right)}{f}^{\prime }\left(\eta \right),v=-\frac{a{b}_0}{\sqrt{1-\beta t}}\frac{f\left(\eta \right)}{\sqrt{\eta }},\eta ={\left(\frac{r}{b_0}\right)}^2{\left(1-\beta t\right)}^{-1},\theta \left(\eta \right)=\frac{T-T_{\infty }}{T_w-T_{\infty }}.(17)$

Substituting Equation 17 in Equations 3, 4, we get the following reduced form of ODEs as:

$\begin{array}{c}\left[{\beta }^{*}+\left(1-{\beta }^{*}\right)\left(1+\left(1-n\right)W{e}^n{\left(f^{″}\right)}^n\right)\right]\eta f^{‴}+\frac{A_1{A}_2}{2}\left(2+\left(1-n\right)W{e}^n{\left(f^{″}\right)}^n\right)f^{″}+\\ A_1{A}_2\mathrm{Re}\left(f{f}^{″}-f^{\prime 2}+1\right){\left(1+W{e}^n{\left(f^{″}\right)}^n\right)}^2-A_1{A}_{2}A\left(\eta f^{″}+f^{\prime }-1\right){\left(1+W{e}^n{\left(f^{″}\right)}^n\right)}^2-\\ M{\mathit{Sin}}^2\left(\omega \right)A_1{A}_2{A}_3\mathrm{Re}{\left(1+W{e}^n{\left(f^{″}\right)}^n\right)}^2\left(f^{\prime }-1\right)=0,\end{array}(18)$

$A_5\left(1+\epsilon \theta \right)\eta {\theta }^{″}+\left(1+\epsilon \theta \right){\theta }^{\prime }-A_4\mathrm{Pr}\mathrm{R}\mathrm{e}f{\theta }^{\prime }=0,(19)$

with BCs are:

$\begin{array}{l}{f}^{\prime }\left(1\right)=\lambda ,f\left(1\right)=s,\theta \left(1\right)=1,\\ \theta \left(\eta \right)\to 0,f^{\prime }\left(\eta \right)\to 1,as\eta \to \infty .\end{array}(20)$

In addition, many different dimensionless parameters that are commonly used in this study are “We” (Weissenberg number), “Re” (Reynold number), “A” (unsteadiness parameter), “s” (suction parameter), and “Pr” (Prandtl number). The parameter obtained due to the ratio between the initial velocity and free stream velocity is $\lambda$; if $\lambda <0$, it is called the shrinking case of the cylinder and $\lambda >0$ is the stretching case of the cylinder.

$\begin{array}{l}\text{Re}=\frac{a{b}_0^2}{2{\upsilon }_f},A=\frac{\beta b_0^2}{4{\upsilon }_f},\mathrm{Pr}=\frac{{\upsilon }_f}{{\alpha }_f},\\ We=\frac{2r\mathrm{\Gamma }{U}_e}{{b_0}^2\left(1-\beta t\right)},M=\frac{{\sigma }_f{\beta }_0^2}{2\rho a},\lambda =\frac{c}{a}.\end{array}(21)$

The skin friction coefficient $C_f$ and local Nusselt number $Nu$ for the practical point of view are defined as:

$C_f=\frac{{\tau }_{rx{|}_{r=b\left(t\right)}}}{\frac{1}{2}\rho U_e^2}\text{and\hspace{0.17em}}Nu=\frac{b\left(t\right)q_w{|}_{r=b\left(t\right)}}{2k\left(T_w-T_{\infty }\right)},(22)$

where ${\tau }_{rx}$ exposes the wall shear stress and $q_w$ is the wall heat flux, and both are defined as:

${\tau }_{rx}={\mu }_{thnf}\frac{\partial u}{\partial r}{\left[\frac{1}{{\beta }^{*}+\left(1-{\beta }^{*}\right)\left[1+{\mathrm{\Gamma }}^n{\left(\frac{\partial u}{\partial r}\right)}^n\right]}\right]}_{r=b\left(t\right)},q_w=-k_{thnf}\frac{\partial T}{\partial r}{|}_{r=b\left(t\right)}.(23)$

Implementing the similarity transformations in the above-stated equations, we get the reduced form of the skin friction and heat transfer rate as follows:

$\begin{array}{l}{C}_{f}Re\frac{x}{b\left(t\right)}=\frac{1}{A_1}\left[\frac{f^{″}\left(1\right)}{{\beta }^{*}+\left(1-{\beta }^{*}\right)\left(1+{\left(We{f}^{″}\left(1\right)\right)}^n\right)}\right]\\ \text{and}\\ Nu=-A_5{\theta }^{\prime }.\end{array}.(24)$

In which:

$A_1=\frac{1}{{\left(1-{\phi }_{s1}\right)}^{2.5}{\left(1-{\phi }_{s2}\right)}^{2.5}{\left(1-{\phi }_{s3}\right)}^{2.5}},A_3=\frac{{\sigma }_{thnf}}{k_f},A_5=\frac{k_{thnf}}{k_f},(25)$

$A_2=\left(1-{\phi }_{s1}\right)\left(1-{\phi }_{s2}\right)\left(1-{\phi }_{s3}\right)+{\phi }_{s3}\frac{{\rho }_{s3}}{{\rho }_f}+{\phi }_{s2}\frac{{\rho }_{s2}}{{\rho }_f}+{\phi }_{s1}\frac{{\rho }_{s1}}{{\rho }_f},(26)$

$A_4=\left(1-{\phi }_{s1}\right)\left(1-{\phi }_{s2}\right)\left(1-{\phi }_{s3}\right)+\frac{{\left(\rho C_p\right)}_{s1}}{{\left(\rho C_p\right)}_f}{\phi }_{s1}+\frac{{\left(\rho C_p\right)}_{s2}}{{\left(\rho C_p\right)}_f}{\phi }_{s2}+\frac{{\left(\rho C_p\right)}_{s3}}{{\left(\rho C_p\right)}_f}{\phi }_{s3}.(27)$

4 Numerical scheme

This portion of the work demonstrates the numerical solution procedure and the accuracy of the code. There are several numerical schemes (Shah et al., 2021; Ayub et al., 2022b; Darvesh et al., 2022; El Din et al., 2022; Khan et al., 2022; Sajid et al., 2022; Wang et al., 2022; Darvesh et al., 2023) used to fetch the numerical results. To investigate such a framework, the bvp4c (Khan et al., 2023; Haider et al., 2021; Ayub et al., 2021a; Ayub et al., 2021b; han et al., 2022; Shah et al., 2021; Ayub et al., 2020) MATLAB command/function is utilized. To begin the process of the code, the boundary value problem (BVP) is changed into the initial value problem (IVP) and after that, bvp4c is utilized to get the unavailable results. This scheme is further based on the RK-4 method (Zaib et al., 2019; Ali et al., 2020b; Botmart et al., 2022a; Botmart et al., 2022b; Ayub et al., 2022c; Goud et al., 2022; Rasool et al., 2022) or finite difference scheme, which is only applicable to solve the initial value problems. Before starting the procedure, the MATLAB syntax is written with the help of the following substitution: $L_1=f$, $L_2=f^{\prime }$, $L_3=f^{″}$, $L_4=\theta$, and $L_5={\theta }^{\prime }$. The MATLAB syntax is written as:

$\left(\begin{array}{l}L{L}_1\\ L{L}_2\end{array}\right)=\left(\begin{array}{c}\frac{\left(\begin{array}{l}-\frac{A_1{A}_2}{2}\left(2+\left(1-n\right)W{e}^n{L_3}^n{L}_3\right)-A_1{A}_2\mathrm{R}\mathrm{e}\left(L_1{L}_3-{L_2}^2+1\right){\left(1+W{e}^n{L_3}^n\right)}^2+\\ A_1{A}_{2}A\left(\eta L_3+L_2-1\right){\left(1+W{e}^n{L_3}^n\right)}^2+MSi{n}^2\left(\omega \right)A_1{A}_2{A}_3\mathrm{R}\mathrm{e}{\left(1+W{e}^n{L_3}^n\right)}^2\left(L_2-1\right)\end{array}\right)}{\left[{\beta }^{*}+\left(1-{\beta }^{*}\right)\left(1+\left(1-n\right)W{e}^n{L_3}^n\right)\right]\eta }\\ \frac{\left(-\left(1+\epsilon L_4\right)L_5+A_4\mathrm{Pr}\mathrm{R}\mathrm{e}{L}_1{L}_5\right)}{\left(A_5\left(1+\epsilon L_4\right)\eta \right)}\end{array}\right)(28)$

and appropriate boundary conditions become:

$\left.\begin{array}{l}{L}_2\left(1\right)=\lambda ,L_1\left(1\right)=s,L_4\left(1\right)=1,\text{at\hspace{0.5em}}\eta =1\\ L_2\left(\eta \right)\to 1,L_4\left(\eta \right)\to 0,\text{as\hspace{0.17em}}\eta \to \infty .\end{array}\right\}(29)$

The procedure mentioned is used to solve Eqs. 28, 29 to find the missing slopes. The step size between two mesh points is 0.01 and the point ${\eta }_{\max }$ representing infinity is chosen appropriately such that BCs are attained in an asymptotic manner. From the figures, it can be seen that all BCs are attained asymptotically, which is a sign of the convergence of results. For further details of the method considered that have been documented by various researchers, see refs. (Shahzad et al., 2022; AlBaidani et al., 2023; Althoey et al., 2023; Assiri et al., 2023; Sajid et al., 2023b; Rafique et al., 2023). Moreover, the authors have utilized the mentioned numerical method for the following reasons:

a) The bvp4c is a robust method capable of solving varied nonlinear differential equations and initial conditions. It uses the finite difference method for stiff problems.

b) The user can adjust the error tolerance as needed when employing this technique.

c) It efficiently solves systems that are challenging to address using analytical methods.

d) Compared to other known methods, this approach significantly cuts the time required to find the solution.

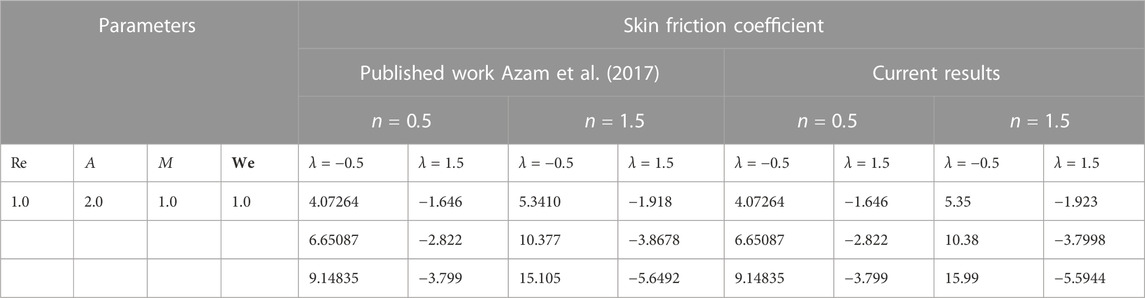
4.1 Validity of the scheme

The current scheme intersects with old literature while fixing some of the influential parameters such as $A_1=A_2=A_3=A_4=1$. This attempt shows that the validity of the mathematical model and numerical scheme used to solve this model are correct. The outcomes of the given work with prior research work are shown in Table 2.

TABLE 2

TABLE 2. The validity of the current model with old literature for limiting cases.

5 Results and discussion

The ternary hybrid cross bio-nanofluid model is a promising approach for studying the fluid dynamics of expanding/contracting cylinders with inclined magnetic field effects. This model combines the three different types of nanoparticles (Cu, Al₂O₃, and TiO₂) with biological components (blood) to create a unique bio-nanofluid. The model also considers the effects of stenosis (narrowing of the artery) and the expansion/contraction of the cylinder, which are important factors that can affect blood flow and lead to considerable cardiovascular diseases. By incorporating these elements, the ternary hybrid cross bio-nanofluid model provides a more realistic and comprehensive understanding of blood flow in stenosed arteries. Furthermore, this model has the potential to inform the development of novel therapies and interventions for cardiovascular diseases, by providing insights into the mechanisms underlying blood flow abnormalities. Overall, the ternary hybrid cross bio-nanofluid model is a valid and valuable tool for studying the fluid dynamics of expanding/contracting stenosed arteries.

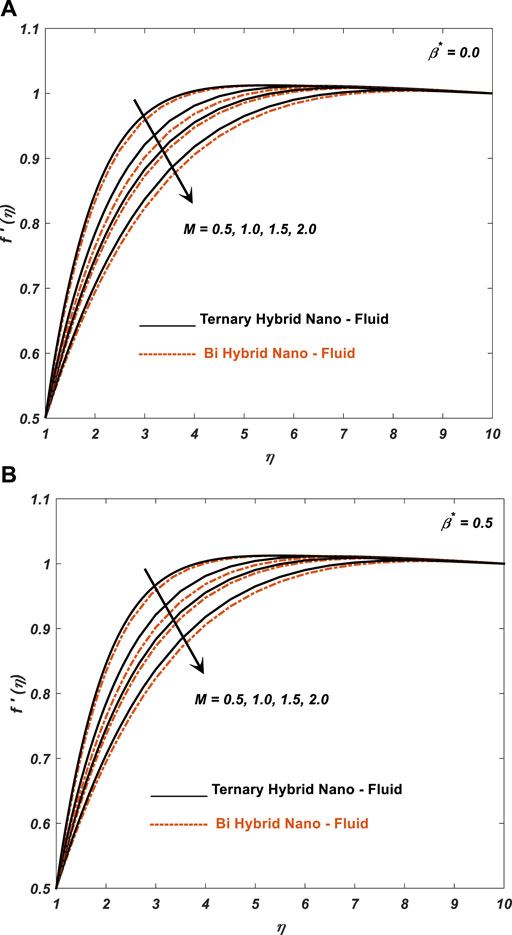
This section investigates the impact of several involved physical parameters on the velocity and temperature of the blood flow in the presence and absence of the infinite shear rate viscosity parameter $\left({\beta }^{*}=0/{\beta }^{*}\ne 0\right)$. Figures 2–7 are established for velocity distribution and Figures 8–10 are presented to discuss the temperature profiles keeping fixed the variation of parameters like $\mathrm{Pr}\in \left[\mathrm{18,21}\right],M\in \left[\mathrm{0.1,5.1}\right]$, $\text{We}\in \left[0.1,4\right]$, $n\in \left[\mathrm{0,1}\right]$ and $\omega ={30}^{\circ },{45}^{\circ },{60}^{\circ },{90}^{\circ }$.

FIGURE 2

FIGURE 2. Pictorial interpretation of physically attached parameter $M$ on f′(η).

FIGURE 3

FIGURE 3. Pictorial interpretation of physically attached parameter $We$ on f′(η).

FIGURE 4

FIGURE 4. Pictorial interpretation of physically attached parameter $n$ on f′(η).

FIGURE 5

FIGURE 5. Pictorial interpretation of physically attached parameter $Re$ on f′(η).

FIGURE 6

FIGURE 6. Pictorial interpretation of physically attached parameter $\omega$ on f′(η).

FIGURE 7

FIGURE 7. Pictorial interpretation of physically attached parameter $A$ on f′(η).

FIGURE 8

FIGURE 8. Pictorial interpretation of physically attached parameter $Re$ on θ′(η).

FIGURE 9

FIGURE 9. Pictorial interpretation of physically attached parameter ε on θ′(η).

FIGURE 10

FIGURE 10. Pictorial interpretation of physically attached parameter of $\omega$ on θ′(η).

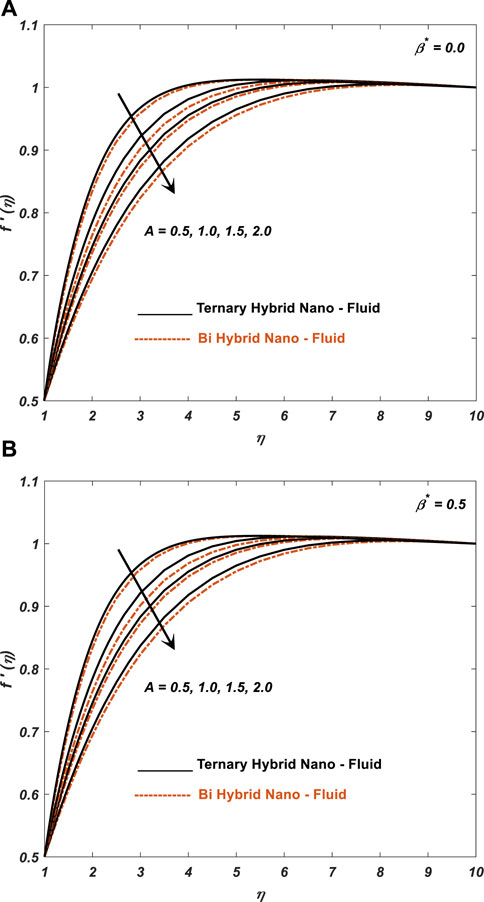
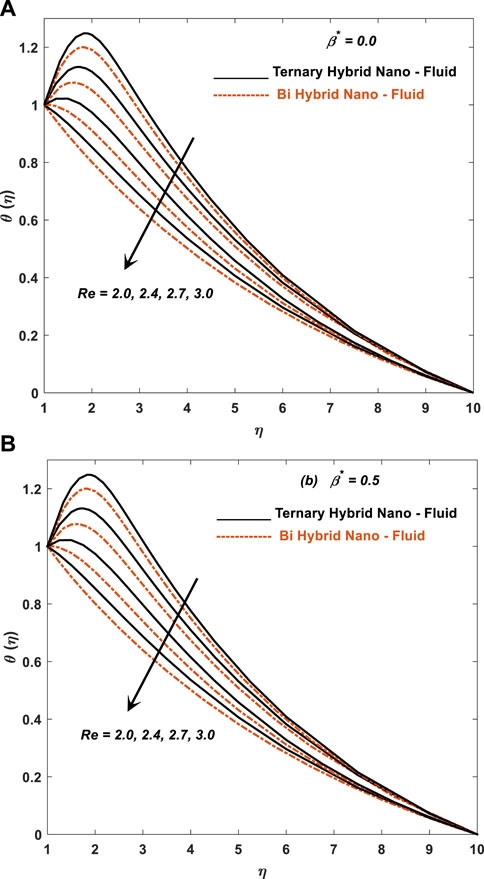
Figures 2–4 give a pictorial interpretation of the physically attached parameter $M$ and We on f′(η). From the pictures, it is seen that a greater value of M, We, and n shows a lower velocity in the presence and absence $\left({\beta }^{*}=0/{\beta }^{*}\ne 0\right)$ of the infinite shear rate viscosity parameter. The magnetic parameter is the strength of the magnetic field. From the physical point of view, the higher magnetic field strengths can lead to a lower blood flow rate as the charged particles in the blood experience Lorentz force and are pushed along more slowly (see Figure 2). However, extremely high magnetic fields can also be harmful to the body, so it is important to use magnetic fields within safe limits.

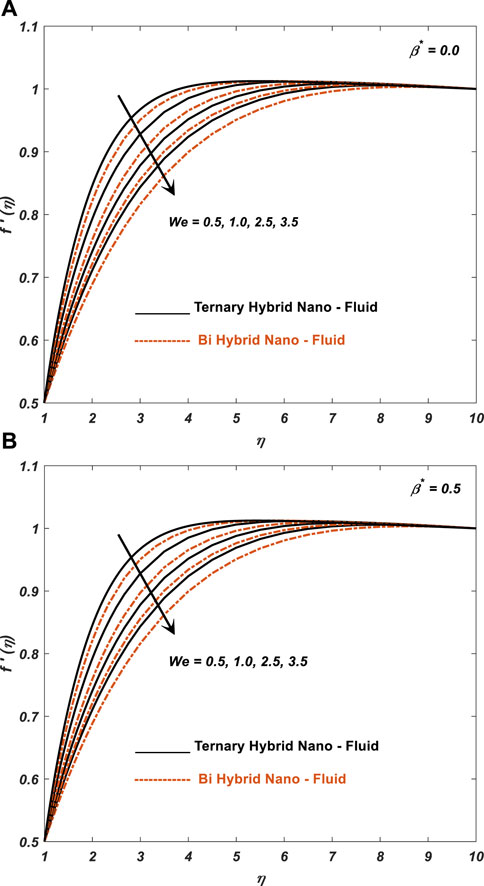
Figure 3 shows that the impact of the Weissenberg number on the blood flow rate will depend on the specific flow conditions and geometry of the blood vessel being considered. In the current study, higher Weissenberg numbers (indicating more elastic fluids) can lead to more complex flow patterns and changes in blood flow rate, especially in regions where the blood vessel is constricted or curved, and as a result, velocity decreases.

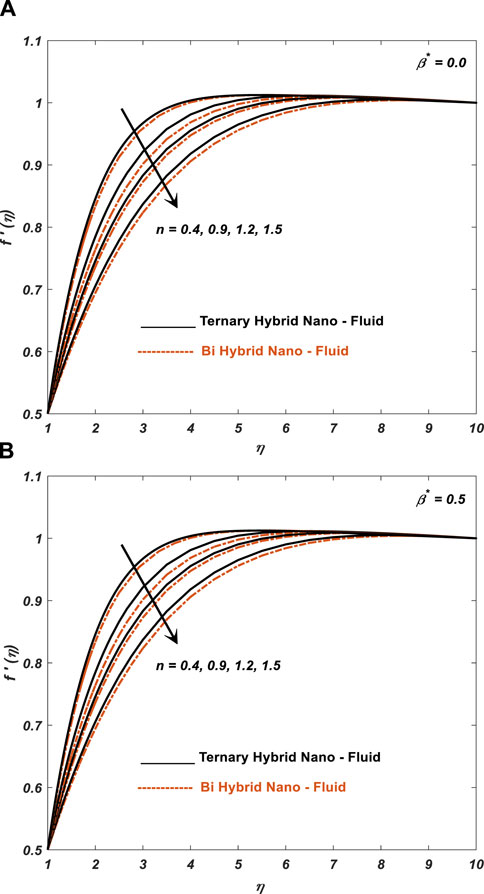
Figure 4 displays that increasing the cross-fluid index (n) by adding a layer of fluid with a higher viscosity to a blood vessel wall can lead to changes in the flow patterns of the blood, including the formation of vortices and eddies, and due to these facts, the velocity of blood decreases. These changes in flow patterns can affect the shear stress experienced by the endothelial cells lining the blood vessel wall, which can in turn impact the development of atherosclerosis and other vascular diseases.

Figure 5 reveals the interpretation of $\mathrm{Re}$ on f′(η). When the Reynolds number is low, viscous forces dominate and the flow is characterized as laminar. When the Reynolds number is high, inertial forces dominate and the flow is characterized as turbulent. Blood flow in the human body is laminar, with low Reynolds numbers. However, in certain situations, such as in regions of high flow rate or where blood vessels are narrowed, the Reynolds number may increase, and blood flow may become turbulent.

Figure 6 shows the attachment of $\omega$ on f′(η). Inclined angle produces Lorentz force and hence flow rate decreases in the presence and absence $\left({\beta }^{*}=0/{\beta }^{*}\ne 0\right)$ of infinite shear rate viscosity parameter. Moreover, the solution gap between the curves is slightly better in the given figure compared to other graphs.

Figure 7 presents the impact of $A$ on f′(η). The unsteadiness of blood flow refers to variations in flow rate and pressure over time. The blood flow in the circulatory system is inherently unsteady due to the pulsatile nature of the heart, as well as other factors such as changes in vessel diameter and blood viscosity. The impact of unsteady flow on blood flow rate is complex and depends on several factors. While unsteady flow is a natural aspect of blood flow, certain conditions, such as disease states or variations in vessel geometry, can lead to increased unsteadiness and potentially negative impacts on the circulatory system.

Figure 8 depicts the impact of $\mathrm{Re}$ on θ′(η). Temperature distribution becomes lower as the value of Re increases in the presence and absence $\left({\beta }^{*}=0/{\beta }^{*}\ne 0\right)$ of infinite shear rate viscosity parameter. Reynolds number has an impact on the temperature profile of blood flow through several mechanisms. When the Reynolds number is high, turbulent flow can cause energy dissipation and mixing within the fluid, leading to decreased heat transfer between the blood and the surrounding tissue. This can result in a more uniform temperature within the fluid.

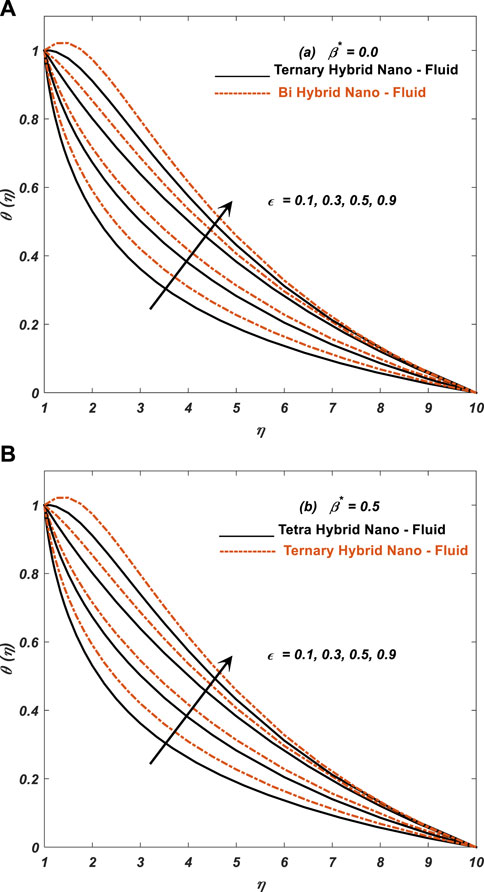
Figure 9 describes the influence of ε on θ′(η). Increased thermal conductivity parameter causes obvious increases in the temperature of blood flow in the presence and absence $\left({\beta }^{*}=0/{\beta }^{*}\ne 0\right)$ of infinite shear rate viscosity parameter. Blood has a relatively low thermal conductivity compared to other materials, such as metals or ceramics. This means that blood is a poor conductor of heat, and heat transfer within the fluid is primarily driven by convective processes.

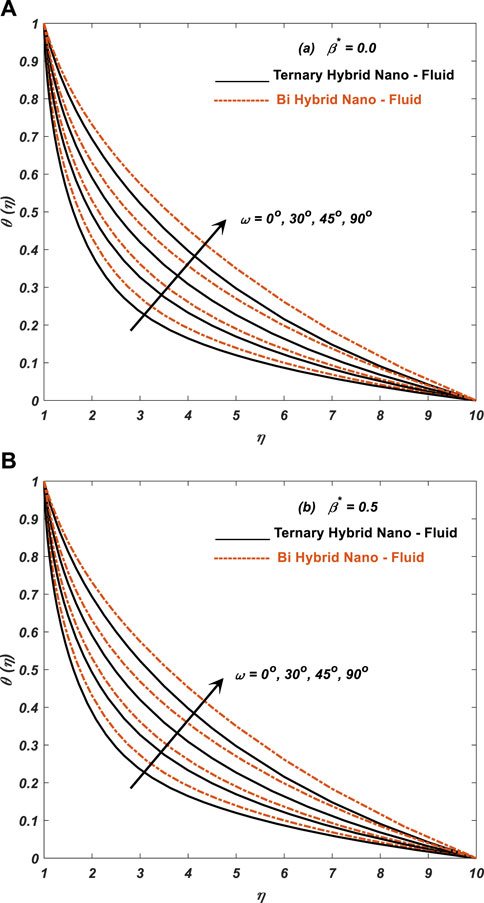
Figure 10 shows the physics of $\omega$ on θ′(η). A gradual increase in the inclined angle reduces velocity and, hence, increases the temperature. When charged particles experience the Lorentz force and move through a magnetic field, they transfer some of their kinetic energy to the surrounding fluid as heat. This process can cause localized heating of the fluid, including the blood.

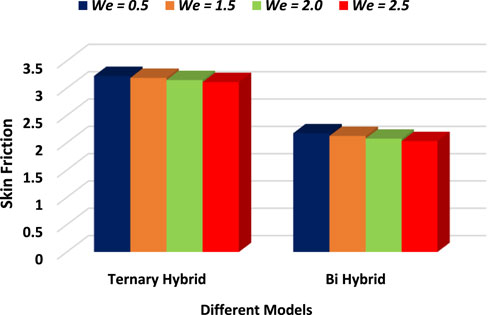
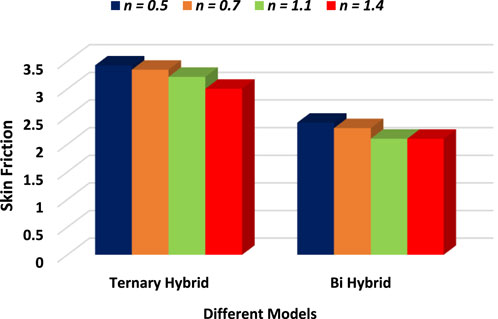
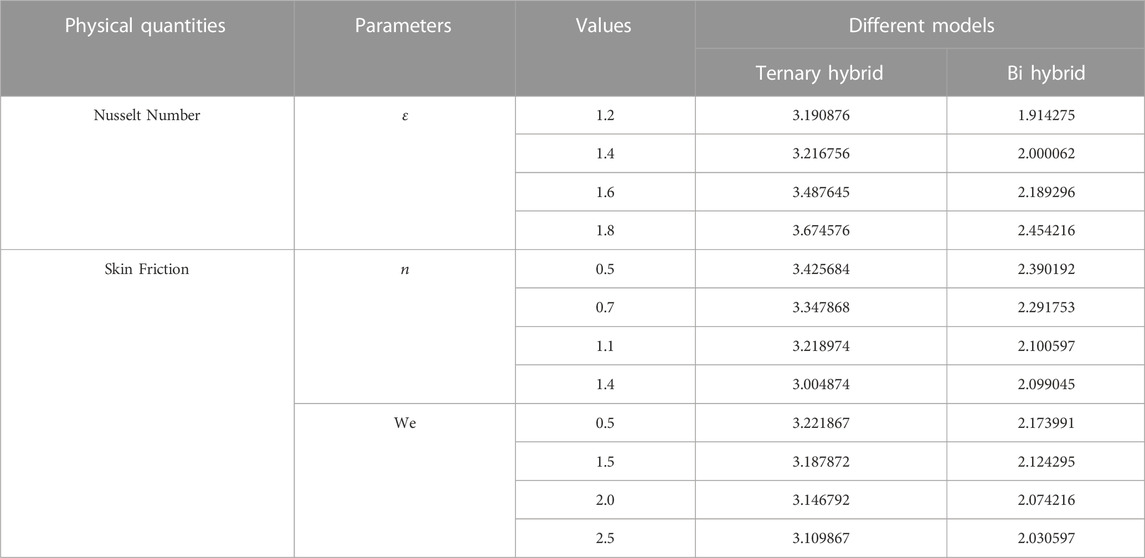
Figures 11, 12 are established for statistical analysis of skin friction and Nusselt number corresponding to Table 3 with different parameters. In blood flow, the Nusselt number can impact the heat transfer between the blood and the vessel walls. This is important because the temperature of the blood can have significant effects on physiological processes, and the heat transfer between blood and the walls of blood vessels can affect the temperature profile. The drag force can impact the flow rate of blood and can have implications for the development of cardiovascular disease. Tabulations of all these results are presented in Table 3. For example, high drag forces can lead to turbulence in the flow of blood, which can increase the likelihood of plaque formation and blockages in blood vessels.

FIGURE 11

FIGURE 11. Statistical interpretation for We on the skin friction coefficient.

FIGURE 12

FIGURE 12. Statistical interpretation for cross fluid index “n” on the skin friction coefficient.

TABLE 3

TABLE 3. Tabular representation of physical quantities.

6 Conclusion

The expanding/contracting stenosed artery refers to the narrowing and widening of an artery due to the accumulation of plaque, which can impede blood flow and lead to cardiovascular disease. The inclusion of an infinite shear rate viscosity suggests that the model is accounting for the high levels of shear stress that occur at the site of a stenosis. Additionally, the inclined magnetic field may suggest that the model is considering the effects of magnetic fields on blood flow, which have been shown to have potential therapeutic applications for cardiovascular diseases. The main outcomes of the considered model are given as follows.

1. Greater value of M, We, and n gives lower velocity in ternary nanofluid compared to bi-hybrid nanofluid. Higher magnetic field strengths can lead to lower blood flow rates, as the charged particles in the blood experience Lorentz force and are pushed along more slowly.

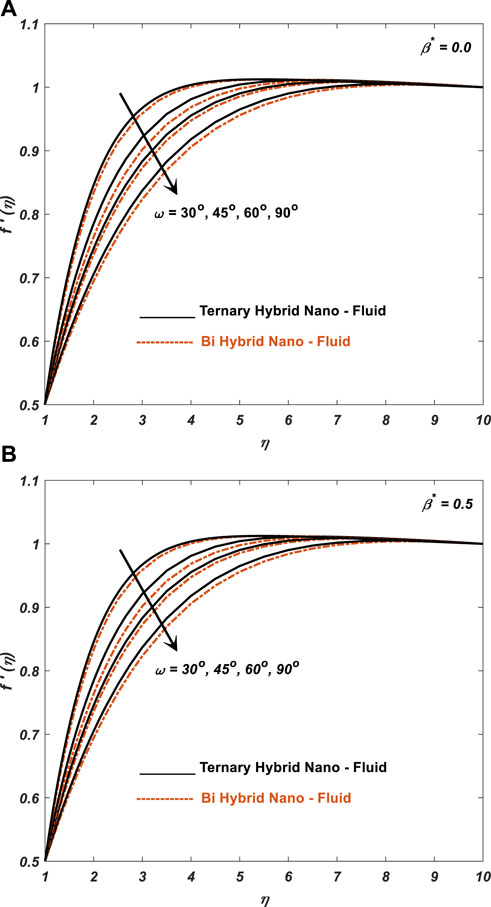
2. Gradual increase in inclined angle reduces velocity and hence increases the temperature in ternary nanofluid compared to bi-hybrid nanofluid.

3. Heat transport is rapid in ternary nanofluid compared to bi-hybrid nanofluid.

4. Higher Weissenberg numbers (indicating more elastic fluids) can lead to more complex flow patterns and changes in blood flow rate.

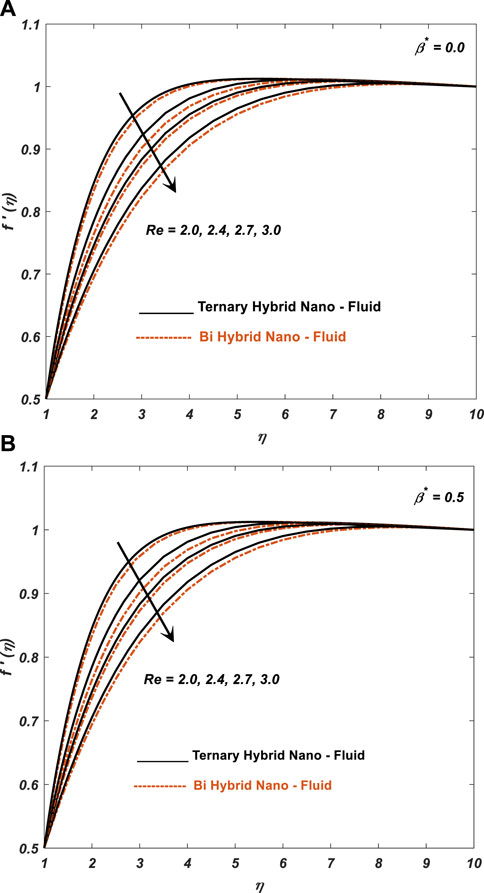
5. When the Reynolds number is low, viscous forces dominate and the fluid flow is characterized as laminar.

6. The inclined angle produces Lorentz force and hence flow rate decreases.

7. When the Reynolds number is high, turbulent flow can cause energy dissipation and mixing within the fluid, leading to decreased heat transfer between the blood and the surrounding tissue.

6.1 Advantages of the significant outcomes

i. Greater heat transport regulates the physiological functions in the human body like temperature regulation (distribution of excess heat generated during physical activity), prevention of overheating, and improved oxygen delivery.

ii. Parameters like M, We, and n give lower velocity of blood and slower blood flow rate within capillaries allowing for more efficient exchange of nutrients, gases, and waste products between the blood and surrounding tissues, and lower blood velocity requires less energy expenditure from the heart.

6.2 Future direction

The current study considers the effects of multiple physical parameters on blood flow in stenosed arteries, but there are many other factors that could also be investigated in future research work which are as follows.

1. The effects of blood rheology, flow rate, and vessel compliance could be explored to gain a more complete understanding of the Casson and Power Law fluidic model.

2. Future research could launch the accuracy and predictive power of the ternary hybrid cross/Carreau bio-nanofluid model with the numerical technique of artificial neural networks.

3. The entropy generation for the non-Newtonian models can also be implemented in future research work.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Acknowledgments

The researchers wish to extend their sincere gratitude to the Islamic University of Madinah, Saudi Arabia for the support provided to this research work.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

AlBaidani, M. M., Mishra, N. K., Ahmad, Z., Eldin, S. M., Haq, E. U., and Ul Haq, E. (2023). Numerical study of thermal enhancement in ZnO-SAE50 nanolubricant over a spherical magnetized surface influenced by Newtonian heating and thermal radiation. Case Stud. Therm. Eng. 45, 102917. doi:10.1016/j.csite.2023.102917

CrossRef Full Text | Google Scholar

Alghamdi, M., Akbar, N. S., Hussain, M. F., Akhtar, S., and Muhammad, T. (2023). Thermodynamic study of hybrid nanofluid to explore synergistic effects of multiple ferromagnetic nanoparticles in co-axial disks for magnetized fluid. Tribol. Int. 188, 108867. doi:10.1016/j.triboint.2023.108867

CrossRef Full Text | Google Scholar

Ali, A., Bukhari, Z., Umar, M., Ismail, M. A., and Abbas, Z. (2021). Cu and Cu-swcnt nanoparticles’ suspension in pulsatile Casson fluid flow via Darcy–forchheimer porous channel with compliant walls: A prospective model for blood flow in stenosed arteries. Int. J. Mol. Sci. 22 (12), 6494. doi:10.3390/ijms22126494

PubMed Abstract | CrossRef Full Text | Google Scholar

Ali, M., Shahzad, M., Sultan, F., Khan, W. A., and Shah, S. Z. H. (2020b). Characteristic of heat transfer in flow of Cross nanofluid during melting process. Appl. Nanosci. 10, 5201–5210. doi:10.1007/s13204-020-01532-6

CrossRef Full Text | Google Scholar

Ali, M., Sultan, F., Khan, W. A., Shahzad, M., and Arif, H. (2020a). Important features of expanding/contracting cylinder for Cross magneto-nanofluid flow. Chaos, Solit. Fractals 133, 109656. doi:10.1016/j.chaos.2020.109656

CrossRef Full Text | Google Scholar

Althoey, F., Akhter, M. N., Nagra, Z. S., Awan, H. H., Alanazi, F., Khan, M. A., et al. (2023). Prediction models for marshall mix parameters using bio-inspired genetic programming and deep machine learning approaches: A comparative study. Case Stud. Constr. Mater. 18, e01774. doi:10.1016/j.cscm.2022.e01774

CrossRef Full Text | Google Scholar

Assiri, T. A., Aziz Elsebaee, F. A., Alqahtani, A. M., Bilal, M., Ali, A., and Eldin, S. M. (2023). Numerical simulation of energy transfer in radiative hybrid nanofluids flow influenced by second-order chemical reaction and magnetic field. AIP Adv. 13 (3). doi:10.1063/5.0141532

CrossRef Full Text | Google Scholar

Ayub, A., Darvesh, A., Altamirano, G. C., and Sabir, Z. (2021b). Nanoscale energy transport of inclined magnetized 3D hybrid nanofluid with Lobatto IIIA scheme. Heat. Transf. 50, 6465–6490. doi:10.1002/htj.22188

CrossRef Full Text | Google Scholar

Ayub, A., Sabir, Z., Shah, S. Z. H., Mahmoud, S. R., Algarni, A., Sadat, R., et al. (2022c). Aspects of infinite shear rate viscosity and heat transport of magnetized Carreau nanofluid. Eur. Phys. J. Plus 137 (2), 247–317. doi:10.1140/epjp/s13360-022-02410-6

CrossRef Full Text | Google Scholar

Ayub, A., Sabir, Z., Wahab, H. A., Balubaid, M., Mahmoud, S. R., Ali, M. R., et al. (2022a). Analysis of the nanoscale heat transport and Lorentz force based on the time-dependent Cross nanofluid. Eng. Comput. 39, 2089–2108. doi:10.1007/s00366-021-01579-1

CrossRef Full Text | Google Scholar

Ayub, A., Sajid, T., Jamshed, W., Zamora, W. R. M., More, L. A. V., Talledo, L. M. G., et al. (2022b). Activation energy and inclination magnetic dipole influences on carreau nanofluid flowing via cylindrical channel with an infinite shearing rate. Appl. Sci. 12 (17), 8779. doi:10.3390/app12178779

CrossRef Full Text | Google Scholar

Ayub, A., Wahab, H. A., Sabir, Z., and Arbi, A. (2020). “A note on heat transport with aspect of magnetic dipole and higher order chemical process for steady micropolar fluid,” in Fluid-structure interaction (London, England: IntechOpen).

Google Scholar

Ayub, A., Wahab, H. A., Shah, S. Z., Shah, S. L., Darvesh, A., Haider, A., et al. (2021a). Interpretation of infinite shear rate viscosity and a nonuniform heat sink/source on a 3D radiative cross nanofluid with buoyancy assisting/opposing flow. Heat. Transf. 50 (5), 4192–4232. doi:10.1002/htj.22071

CrossRef Full Text | Google Scholar

Azam, M., Khan, M., and Alshomrani, A. S. (2017). Unsteady radiative stagnation point flow of MHD Carreau nanofluid over expanding/contracting cylinder. Int. J. Mech. Sci. 130, 64–73. doi:10.1016/j.ijmecsci.2017.06.010

CrossRef Full Text | Google Scholar

Babu, M. S., Sankar, G. R., Velpula, V. R., Chu, Y. M., Khan, M. I., Raju, C. S. K., et al. (2023). Chemically reactive flow of viscous thermophoretic fluid over wedge with variable thermal conductivity and viscosity. Case Stud. Therm. Eng. 45, 102924. doi:10.1016/j.csite.2023.102924

CrossRef Full Text | Google Scholar

Bafakeeh, O. T., Al-Khaled, K., Khan, S. U., Abbasi, A., Ganteda, C., Khan, M. I., et al. (2023). On the bioconvective aspect of viscoelastic micropolar nanofluid referring to variable thermal conductivity and thermo-diffusion characteristics. Bioengineering 10 (1), 73. doi:10.3390/bioengineering10010073

PubMed Abstract | CrossRef Full Text | Google Scholar

Bathe, M., and Kamm, R. D. (1999). A fluid-structure interaction finite element analysis of pulsatile blood flow through a compliant stenotic artery. J. Biomech. Eng. 121, 361–369. doi:10.1115/1.2798332

PubMed Abstract | CrossRef Full Text | Google Scholar

Botmart, T., Ayub, A., Sabir, Z., weera, W., Sadat, R., and Ali, M. R. (2022a). Infinite shear rate aspect of the cross-nanofluid over a cylindrical channel with activation energy and inclined magnetic dipole effects. Waves Random Complex Media, 1–21. doi:10.1080/17455030.2022.2160028

CrossRef Full Text | Google Scholar

Botmart, T., Shah, S. Z. H., Sabir, Z., Weera, W., Sadat, R., Ali, M. R., et al. (2022b). The inclination of magnetic dipole effect and nanoscale exchange of heat of the Cross nanofluid. Waves Random Complex Media, 1–16. doi:10.1080/17455030.2022.2128225

CrossRef Full Text | Google Scholar

Conrad, S. A., and Wang, D. (2021). Evaluation of recirculation during venovenous extracorporeal membrane oxygenation using computational fluid dynamics incorporating fluid-structure interaction. Asaio J. 67 (8), 943–953. doi:10.1097/mat.0000000000001314

PubMed Abstract | CrossRef Full Text | Google Scholar

Darvesh, A., Altamirano, G. C., Sánchez-Chero, M., Zamora, W. R., Campos, F. G., Sajid, T., et al. (2023). Variable chemical process and radiative nonlinear impact on magnetohydrodynamics cross nanofluid: an approach toward controlling global warming. Heat. Transf. 52, 2559–2575. doi:10.1002/htj.22795

CrossRef Full Text | Google Scholar

Darvesh, A., Sajid, T., Jamshed, W., Ayub, A., Shah, S. Z. H., Eid, M. R., et al. (2022). Rheology of variable viscosity-based mixed convective inclined magnetized cross nanofluid with varying thermal conductivity. Appl. Sci. 12 (18), 9041. doi:10.3390/app12189041

CrossRef Full Text | Google Scholar

Das, S., Pal, T. K., Jana, R. N., and Giri, B. (2021). Significance of Hall currents on hybrid nano-blood flow through an inclined artery having mild stenosis: homotopy perturbation approach. Microvasc. Res. 137, 104192. doi:10.1016/j.mvr.2021.104192

PubMed Abstract | CrossRef Full Text | Google Scholar

Dolui, S., Bhaumik, B., and De, S. (2023). Combined effect of induced magnetic field and thermal radiation on ternary hybrid nanofluid flow through an inclined catheterized artery with multiple stenosis. Chem. Phys. Lett. 811, 140209. doi:10.1016/j.cplett.2022.140209

CrossRef Full Text | Google Scholar

El Din, S. M., Darvesh, A., Ayub, A., Sajid, T., Jamshed, W., Eid, M. R., et al. (2022). Quadratic multiple regression model and spectral relaxation approach for carreau nanofluid inclined magnetized dipole along stagnation point geometry. Sci. Rep. 12 (1), 17337–17418. doi:10.1038/s41598-022-22308-8

PubMed Abstract | CrossRef Full Text | Google Scholar

El Kot, M. A., and Abd Elmaboud, Y. (2023). Model of LDL-C concentration of blood flow through a vertical porous microchannel with multiple stenoses: computational simulation. J. Taibah Univ. Sci. 17 (1), 2176194. doi:10.1080/16583655.2023.2176194

CrossRef Full Text | Google Scholar

Fatima, N., Alayyash, K., Alfwzan, W. F., Ijaz, N., Riaz, A., Saleem, N., et al. (2023). Mathematical model for numerical simulations of thermal energy of nano-fluid in a complex peristaltic transport within a curved passage: pharmacological and engineering biomedical application. Case Stud. Therm. Eng. 45, 102897. doi:10.1016/j.csite.2023.102897

CrossRef Full Text | Google Scholar

Goud, J. S., Srilatha, P., Kumar, R. V., Kumar, K. T., Khan, U., Raizah, Z., et al. (2022). Role of ternary hybrid nanofluid in the thermal distribution of a dovetail fin with the internal generation of heat. Case Stud. Therm. Eng. 35, 102113. doi:10.1016/j.csite.2022.102113

CrossRef Full Text | Google Scholar

Haider, A., Ayub, A., Madassar, N., Ali, R. K., Sabir, Z., Shah, S. Z., et al. (2021). Energy transference in time-dependent Cattaneo–Christov double diffusion of second-grade fluid with variable thermal conductivity. Heat. Transf. 50 (8), 8224–8242. doi:10.1002/htj.22274

CrossRef Full Text | Google Scholar

han, U., Zaib, A., Ishak, A., Elattar, S., Eldin, S. M., Raizah, Z., et al. (2022). Impact of irregular heat sink/source on the wall Jet flow and heat transfer in a porous medium induced by a nanofluid with slip and buoyancy effects. Symmetry 14 (10), 2212. doi:10.3390/sym14102212

CrossRef Full Text | Google Scholar

Ige, E. O., Falodun, B. O., Adebiyi, D. O., and Khan, S. U. (2022). Computational analysis of mixed convection in a blood-based hybrid nanoliquid under Boussinesq approximation in a transient Regime. J. Comput. Biophysics Chem. 22, 347–359. doi:10.1142/s2737416523400094

CrossRef Full Text | Google Scholar

Ige, E. O., Falodun, B. O., Adebiyi, D. O., and Khan, S. U. (2023). Computational analysis of mixed convection in a blood-based hybrid nanoliquid under Boussinesq approximation in a transient Regime. J. Comput. Biophysics Chem. 22 (03), 347–359. doi:10.1142/s2737416523400094

CrossRef Full Text | Google Scholar

Kaleem, M. M., Usman, M., Asjad, M. I., and Eldin, S. M. (2022). Magnetic field, variable thermal conductivity, thermal radiation, and viscous dissipation effect on heat and momentum of fractional Oldroyd-B bio nano-fluid within a channel. Fractal Fract. 6 (12), 712. doi:10.3390/fractalfract6120712

CrossRef Full Text | Google Scholar

Khan, U., Zaib, A., Ishak, A., Elattar, S., Eldin, S. M., Raizah, Z., et al. (2022). Impact of irregular heat sink/source on the wall Jet flow and heat transfer in a porous medium induced by a nanofluid with slip and buoyancy effects. Symmetry 14 (10), 2212. doi:10.3390/sym14102212

CrossRef Full Text | Google Scholar

Khan, U., Zaib, A., Ishak, A., Eldin, S. M., Alotaibi, A. M., Raizah, Z., et al. (2023). Features of hybridized AA7072 and AA7075 alloys nanomaterials with melting heat transfer past a movable cylinder with Thompson and Troian slip effect. Arabian J. Chem. 16 (2), 104503. doi:10.1016/j.arabjc.2022.104503

CrossRef Full Text | Google Scholar

Mishra, N. K., Sharma, M., Sharma, B. K., and Khanduri, U. (2023). Soret and Dufour effects on MHD nanofluid flow of blood through a stenosed artery with variable viscosity. Int. J. Mod. Phys. B, 2350266. doi:10.1142/s0217979223502661

CrossRef Full Text | Google Scholar

Nazir, U., Sohail, M., Mukdasai, K., Singh, A., Alahmadi, R. A., Galal, A. M., et al. (2022). Applications of variable thermal properties in Carreau material with ion slip and Hall forces towards cone using a non-Fourier approach via FE-method and mesh-free study. Front. Mater. 9, 1054138. doi:10.3389/fmats.2022.1054138

CrossRef Full Text | Google Scholar

Rafique, K., Mahmood, Z., Saleem, S., Eldin, S. M., and Khan, U. (2023). Impact of nanoparticle shape on entropy production of nanofluid over permeable MHD stretching sheet at quadratic velocity and viscous dissipation. Case Stud. Therm. Eng. 45, 102992. doi:10.1016/j.csite.2023.102992

CrossRef Full Text | Google Scholar

Rasool, G., Shah, S. Z. H., Sajid, T., Jamshed, W., Cieza Altamirano, G., Keswani, B., et al. (2022). Spectral relaxation methodology for chemical and bioconvection processes for cross nanofluid flowing around an oblique cylinder with a slanted magnetic field effect. Coatings 12 (10), 1560. doi:10.3390/coatings12101560

CrossRef Full Text | Google Scholar

Sajid, T., Ayub, A., Shah, S. Z. H., Jamshed, W., Eid, M. R., El Din, E. S. M. T., et al. (2022). Trace of chemical reactions accompanied with arrhenius energy on ternary hybridity nanofluid past a wedge. Symmetry 14 (9), 1850. doi:10.3390/sym14091850

CrossRef Full Text | Google Scholar

Sajid, T., Jamshed, W., Eid, M. R., Altamirano, G. C., Aslam, F., Alanzi, A. M., et al. (2023a). Magnetized cross tetra hybrid nanofluid passed a stenosed artery with nonuniform heat source (sink) and thermal radiation: novel tetra hybrid tiwari and das nanofluid model. J. Magnetism Magnetic Mater. 569, 170443. doi:10.1016/j.jmmm.2023.170443

CrossRef Full Text | Google Scholar

Sajid, T., Jamshed, W., Shahzad, F., Ullah, I., Ibrahim, R. W., Eid, M. R., et al. (2023b). Insightful into dynamics of magneto Reiner-Philippoff nanofluid flow induced by triple-diffusive convection with zero nanoparticle mass flux. Ain Shams Eng. J. 14 (4), 101946. doi:10.1016/j.asej.2022.101946

CrossRef Full Text | Google Scholar

Shah, S. Z. H., Fathurrochman, I., Ayub, A., Altamirano, G. C., Rizwan, A., Núñez, R. A. S., et al. (2021a). Inclined magnetized and energy transportation aspect of infinite shear rate viscosity model of Carreau nanofluid with multiple features over wedge geometry. Heat. Transf. 51, 1622–1648. doi:10.1002/htj.22367

CrossRef Full Text | Google Scholar

Shah, S. Z., Wahab, H. A., Ayub, A., Sabir, Z., haider, A., and Shah, S. L. (2021b). Higher order chemical process with heat transport of magnetized cross nanofluid over wedge geometry. Heat. Transf. 50 (4), 3196–3219. doi:10.1002/htj.22024

CrossRef Full Text | Google Scholar

Shahzad, F., Jamshed, W., Ibrahim, R. W., Aslam, F., Tag El Din, E. S. M., ElSeabee, F. A. A., et al. (2022). Galerkin finite element analysis for magnetized radiative-reactive Walters-B nanofluid with motile microorganisms on a Riga plate. Sci. Rep. 12 (1), 18096. doi:10.1038/s41598-022-21805-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Sumner, D., Wong, S. S. T., Price, S. J., and Paidoussis, M. P. (1999). Fluid behaviour of side-by-side circular cylinders in steady cross-flow. J. Fluids Struct. 13 (3), 309–338. doi:10.1006/jfls.1999.0205

CrossRef Full Text | Google Scholar

Tang, T. Q., Rooman, M., Shah, Z., Jan, M. A., Vrinceanu, N., and Racheriu, M. (2023a). Computational study and characteristics of magnetized gold-blood Oldroyd-B nanofluid flow and heat transfer in stenosis narrow arteries. J. Magnetism Magnetic Mater. 569, 170448. doi:10.1016/j.jmmm.2023.170448

CrossRef Full Text | Google Scholar

Tang, T. Q., Rooman, M., Shah, Z., Jan, M. A., Vrinceanu, N., and Racheriu, M. (2023b). Computational study and characteristics of magnetized gold-blood Oldroyd-B nanofluid flow and heat transfer in stenosis narrow arteries. J. Magnetism Magnetic Mater. 569, 170448. doi:10.1016/j.jmmm.2023.170448

CrossRef Full Text | Google Scholar

Tripathi, J., Vasu, B., Bég, O. A., and Gorla, R. S. R. (2021). Unsteady hybrid nanoparticle-mediated magneto-hemodynamics and heat transfer through an overlapped stenotic artery: biomedical drug delivery simulation. Proc. Institution Mech. Eng. Part H J. Eng. Med. 235 (10), 1175–1196. doi:10.1177/09544119211026095

CrossRef Full Text | Google Scholar

Varshney, G., Katiyar, V., and Kumar, S. (2010). Effect of magnetic field on the blood flow in artery having multiple stenosis: A numerical study. Int. J. Eng. Sci. Technol. 2 (2), 967–982. doi:10.4314/ijest.v2i2.59142

CrossRef Full Text | Google Scholar

Wang, F., Sajid, T., Ayub, A., Sabir, Z., Bhatti, S., Shah, N. A., et al. (2022). Melting and entropy generation of infinite shear rate viscosity carreau model over riga plate with erratic thickness: A numerical keller box approach. Waves Random Complex Media, 1–25. doi:10.1080/17455030.2022.2063991

CrossRef Full Text | Google Scholar

Waqas, M. (2020). Simulation of revised nanofluid model in the stagnation region of cross fluid by expanding-contracting cylinder. Int. J. Numer. Methods Heat Fluid Flow 30 (4), 2193–2205. doi:10.1108/hff-12-2018-0797

CrossRef Full Text | Google Scholar

Yadav, M., Pareek, N., and Vivekanand, V. (2022). “Eggshell and fish/shrimp wastes for synthesis of bio-nanoparticles,” in Agri-waste and microbes for production of sustainable nanomaterials (Amsterdam, Netherlands: Elsevier), 259–280.

CrossRef Full Text | Google Scholar

Zaib, A., Khan, U., Khan, I., Seikh, H., and Sherif, M. (2019). Entropy generation and dual solutions in mixed convection stagnation point flow of micropolar Ti6Al4V nanoparticle along a Riga surface. Processes 8 (1), 14. doi:10.3390/pr8010014

CrossRef Full Text | Google Scholar

Zain, N. M., and Ismail, Z. (2023a). Numerical solution of magnetohydrodynamics effects on a generalised power law fluid model of blood flow through a bifurcated artery with an overlapping shaped stenosis. Plos one 18 (2), e0276576. doi:10.1371/journal.pone.0276576

PubMed Abstract | CrossRef Full Text | Google Scholar

Zain, N. M., and Ismail, Z. (2023b). Numerical solution of magnetohydrodynamics effects on a generalised power law fluid model of blood flow through a bifurcated artery with an overlapping shaped stenosis. Plos one 18 (2), e0276576. doi:10.1371/journal.pone.0276576

PubMed Abstract | CrossRef Full Text | Google Scholar

Nomenclature