Relaxation behavior of biaxially stretched PLA film during the heat setting stage

In this paper, the relaxation behavior of polylactic acid (PLA) film in the heat-setting stage of biaxial stretching was studied. Firstly, the polylactic acid casting films were stretched synchronously in different ratios. We found that the Machine direction (MD) and Transverse direction (TD) stress relaxation curves exhibited a separation trend with the increase in the stretching ratio, and the relaxation amplitude increased gradually. Then, the stress relaxation curves were fitted by the expansion exponential equation (KWW equation). The results showed that the coefficient used to characterize the homogeneity of stress relaxation increased with the increase in the stretching ratio, and the homogeneity in Machine direction was better than that in Transverse direction. Finally, we analyzed the evolution of rheological units and the activation energy spectrum during stress relaxation. We found that the volume of rheological units gradually decreased with the increase in the stretching ratio. The activation energy spectrum exhibited a Gaussian distribution, and the symmetry axis of distribution curves shifted to the high energy. The above results would be of great significance in further understanding the deformation mechanism of polylactic acid film during biaxial stretching and providing theoretical guidance for the preparation of high-performance BOPLA films.

1 Introduction

Polylactic acid (PLA) film has been widely used for packaging food, medical, and other daily necessities due to its excellent moulding processability, biodegradability, and biocompatibility (Wu et al., 2013; Claro et al., 2016; Moradi and Yeganeh, 2020; Fredi et al., 2022; Wu et al., 2022). However, as a result of the unique molecular structure in PLA, it possesses the disadvantages of brittleness and low-impact toughness, which seriously restricts its large-scale application in the high-end packaging industry (Lou et al., 2008; Tenn et al., 2012; Palai et al., 2020; Azlin et al., 2022). In order to expand the application range of PLA film, how to improve its flexibility has become a pressing problem at present.

In recent years, research has found that biaxial stretching technology can promote the crystallization orientation of PLA molecular chains and effectively improve their mechanical properties (Jariyasakoolroj et al., 2015; Kong et al., 2015; Ouchiar et al., 2016; Ren et al., 2020; Ding et al., 2021; Liu et al., 2021; Yoksan et al., 2021; Lin et al., 2022; Zhou et al., 2022). For example, Jariyasakoolroj et al. (Jariyasakoolroj et al., 2015) characterized the microstructure of biaxially oriented PLA (BOPLA) film and found that the small γ-microcrystals with isotropic properties were formed inside the film when the stretching rate and the stretching ratio increased simultaneously. As a result, the toughness of BOPLA film increased sharply, and its elongation at break was nearly four times higher than that of an unstretched film. Ouchiar et al. (Ouchiar et al., 2016) studied the ductile-brittle transition mechanism of biaxially oriented PLA/talc composite film by in-situ small angle scattering (SAXS). They found that there was a correlation between the crack propagation mechanism of the film with the biaxial stretching conditions. Zhou et al. (Zhou et al., 2022) prepared BOPLA film by the method of combining biaxial stretching and constrained annealing. They found that the oriented nanocrystals which were induced by biaxial stretching during annealing can be used as physical crosslinking to strengthen the amorphous chain entanglement network, and further improve the ductility of the film.

The above works show that biaxial stretching technology plays an important role in improving the mechanical properties of the film. However, the coupling relationship between the biaxial stretching process with the mechanical properties of the film and the deformation mechanism of the film during biaxial stretching have not been fully understood. Therefore, the development and large-scale application of high-performance BOPLA films have been restricted.

As a typical viscoelastic material, the mechanical behavior of PLA is closely related to the time, and there are apparent rheological phenomena during biaxial stretching (Yang and Kan, 2013; Li et al., 2016; Liu et al., 2021; Zhang et al., 2021). Therefore, studying the rheological behavior during biaxial stretching is of great significance in understanding the deformation mechanism of PLA films. Nevertheless, there are few studies on the rheological behavior of PLA films. In this paper, the relaxation behavior of biaxially stretched PLA films during the heat setting stage was taken as a breakthrough to explore the deformation mechanism of PLA films during biaxial stretching. The main contents include the following parts. First, the PLA casting films were stretched synchronously in different ratios. Then, the stress relaxation curves were fitted by the expansion exponential equation (KWW equation). Finally, we analyzed the evolution of rheological units and the activation energy spectrum during stress relaxation. This study will provide theoretical guidance for the optimization of the biaxial stretching process and the preparation of high-performance BOPLA films.

2 Materials and methods

2.1 Materials and equipment

PLA: 4032D, molecular weight 130,000, Nature Works, United States of America.

Twin-screw extruder: CTE35 PLUS, Nanjing Kebelong Machinery Co., Ltd.

Vacuum drying oven: DHG101, Shanghai Rundai Automation Equipment Co., Ltd.

Extrusion cast machine: FDHU35, Guangzhou Putong Experimental Analytical Instruments Co., Ltd.

Biaxial tensile testing machine: KARO5, Bruckner, Germany.

2.2 Biaxial stretching with different ratios

The PLA casting films need to be prepared by the extrusion casting method before biaxial stretching. The casting temperature was set to 185–200°C and the screw speed was 20 r/min. The film thickness was controlled at 300–400 μm by adjusting the extrusion speed and the casting roller speed, then the film was cooled on the casting roll at 30°C. After the PLA casting films were obtained, the biaxial stretching experiment was carried out by using the biaxial stretching machine (KARO-5, Bruckner), which can collect the experimental data of load displacement during stretching. In this study, we mainly investigated the effect of the stretching ratio on the relaxation behavior of PLA during the biaxial stretching heat-setting stage. Thus, the stretching ratio was set as a variable in the experimental process, and the other experimental parameters were fixed. Based on this principle, BOPLA films with different ratios of 2 × 2, 3 × 3, 4 × 4, and 5 × 5 were prepared under the conditions of preheating for 30 s, stretching rate of 40 mm/s, and stretching temperature and heat setting temperature of 130°C. To ensure the repeatability of the experimental data, four repeated stretching were performed under each of the above conditions. The stretching diagram is shown in Figure 1, in which MD and TD represent the machine and transverse stretching directions, respectively.

FIGURE 1

FIGURE 1. Schematic diagram of biaxial stretching.

The representative load-time curves with different stretching ratios are shown in Figure 2. It can be seen that the trend of load-time curves in MD and TD directions with different stretching ratios are basically the same. Upon reaching the yield point, the material begins to soften and the load drops briefly, and then, different degrees of rebound (increase in load) appear. The above trends become more apparent with the increase in the stretching ratio. It is worth noting that the load in the TD direction is higher than that in the MD direction with these four stretching ratios. This phenomenon may be related to the different crystal orientations in TD and MD directions. That is, the degree of crystal orientation in the TD direction of PLA films is higher than that in the MD direction during biaxial stretching. So, the mechanical properties of the TD direction are better than those of the MD direction. Meanwhile, it can also be seen that the difference in load between the TD direction and the MD direction shows an increasing trend with the increase in the stretching ratio, indicating that the effect of the stretching ratio on the crystal orientation in the TD direction is greater than that in the MD direction. In addition, when entering the heat setting stage, all four stretching curves show significant relaxation. Moreover, the relaxation amplitude exhibits an increasing trend with the increase in the stretching ratio.

FIGURE 2

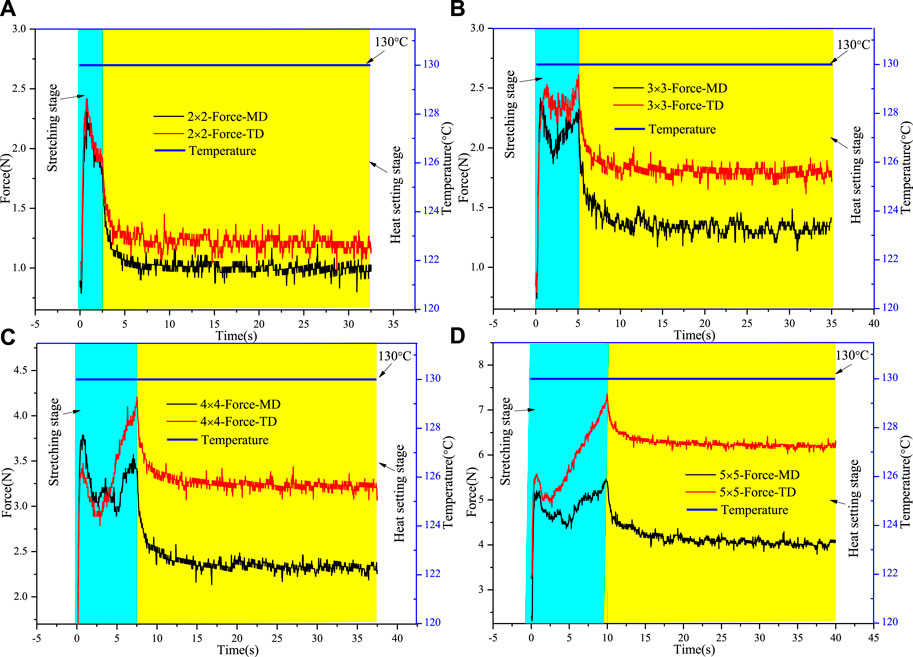
FIGURE 2. Load-time or temperature-time curves during biaxial stretching with different stretching ratios: (A) stretching ratio at 2 × 2, (B) stretching ratio at 3 × 3, (C) stretching ratio at 4 × 4, (D) stretching ratio at 5 × 5.

2.3 The relationship of stress-strain during biaxial stretching

To further study the rheological mechanism of the film during biaxial stretching, the load-displacement (time) relationship was transformed into the stress-strain (time) relationship. In the schematic diagram of biaxial stretching in Figure 1, we set L_M0, d_T0, and h₀ to be the length, width, and height of the film at the beginning of stretching, respectively. F_M and F_T represent the machine and transverse stretching forces. V_M and V_T are the machine and transverse stretching rates. The volume of the film before stretching is expressed as:

$V_0=L_{M0}\times d_{T0}\times h_0(1)$

The machine and transverse lengths in the stretching process can be expressed as:

$L_M=L_{M0}\times \left(1+V_M\times t\right)(2)$

$d_T=d_{T0}\times \left(1+V_T\times t\right)(3)$

So, the area of the film during stretching is expressed as:

$S=L_M\times d_T=L_{M0}\times \left(1+V_M\times t\right)\times d_{T0}\times \left(1+V_T\times t\right)(4)$

For the convenience of calculation, we assume that the volume of the film remains unchanged during stretching, so the thickness during stretching can be expressed as:

$\begin{array}{l}h=V_0/S\\ ={L_M}_0\times {d_T}_0\times h_0/\left[L_{M0}\times \left(1+V_M\times t\right)\times d_{T0}\times \left(1+V_T\times t\right)\right]\\ =h_0/\left[\left(1+V_M\times t\right)\times \left(1+V_T\times t\right)\right]\end{array}(5)$

The machine cross-sectional area of the film during the stretching process can be written as:

$\begin{array}{l}{S}_M=d_T\times h\\ =d_{T0}\times \left(1+V_T\times t\right)\times h_0/\left[\left(1+V_M\times t\right)\times \left(1+V_T\times t\right)\right]\\ =d_{T0}\times h_0/\left(1+V_M\times t\right)\end{array}(6)$

Then, the machine stretching stress can be obtained:

${\mathrm{\sigma }}_M=F_M/S_M=F_M\times \left(1+V_M\times t\right)/\left(d_{T0}\times h_0\right)(7)$

Similarly, the transverse stretching stress can be expressed as:

${\mathrm{\sigma }}_T=F_T/S_T=F_T\times \left(1+V_T\times t\right)/\left(L_{M0}\times h_0\right)(8)$

Using Eqs 7, 8 to calculate the load-time data in Figure 2 and the obtained stress-strain curves during biaxial stretching as shown in Figure 3, it can be seen that the changing trend of the stress-time curve is basically consistent with the load-time curve. In the heat setting stage, with the increase in the stretching ratio, the difference between the stress curves of MD and TD directions gradually increases, and stress relaxation amplitude also increases. The reason for the above phenomenon may be that the large ratio of biaxial stretching accelerates the movement of molecular chains inside the film (Rhee and White, 2002), which leads to a significant change in macroscopic mechanical behavior, but the mechanism needs to be further investigated.

FIGURE 3

FIGURE 3. Stress-time curves of films with different stretching ratios.

To further analyze the rheological behavior during the biaxial stretching process, the stress-time curve of the heat setting stage was extracted separately for analysis, as shown in Figure 4. It can be seen that the stress-time curves with different stretching ratios all decrease sharply at the initial stage of setting, and stress relaxation gradually tends to be gentle with the increase in time, indicating that the film has reached the setting effect within the preset setting time (Salem and Vasanthan, 2009). Meanwhile, the initial stress values of TD and MD both exhibit an increasing trend with the increase in the stretching ratio, and the difference between the two increases gradually. This indicates that the effect of large ratio stretching on the TD direction is more significant.

FIGURE 4

FIGURE 4. Stress-time curves of the heat-setting stage with different stretching ratios.

3 Results and discussion

3.1 Dynamic heterogeneity and activation rate of the rheological unit

In order to further analyze the rheological mechanism of the film during the heat setting stage, the stress relaxation curves with different stretching ratios were fitted by the Kohlrausch-Willianms-Watts (KWW) equation (Wang et al., 2014). The expression of the KWW equation is as follows: the stress-time data of different relaxation curves is inputted and the corresponding σ₀ is substituted for fitting analysis, so the corresponding β can be obtained. The only difference between the fitting of these four sets of curves is the inconsistency in the original stress-time data input under various stretching ratios.

$\sigma ={\sigma }_0\exp \left[-{\left(\frac{t}{{\tau }_c}\right)}^{\beta }\right](9)$

Where σ₀ is the initial stress, and τ_c is the characteristic relaxation time (Aval et al., 2020). The value of the extended exponential parameter β can reflect the dynamic inhomogeneity of the stress relaxation in the film, that is, the smaller β means the more significant dynamic inhomogeneity (Ediger, 2000; Zhao et al., 2015; Duan et al., 2022). The fitting curves for different stretching ratios are shown in Figure 5.

FIGURE 5

FIGURE 5. The Stress-time curve for the heat-setting stage with the KWW formula fitting.

The obtained values of β by using the KWW formula to fit the stress relaxation curves at different stretching ratios are shown in Figure 6. It can be seen that the β in the MD and TD directions shows an increasing trend with the increase in the stretching ratio. Moreover, the values of β in the MD direction are persistently greater than in the TD direction. It indicates that the films become more homogeneous with the stretching ratios increase in the stretching process, and the deformation in the MD direction is more uniform than that in the TD direction, which may be ascribed to the large ratio of stretching that promotes the crystalline orientation of the molecular chains inside the film. As a result, the amorphous region is reduced, resulting in more uniform deformation.

FIGURE 6

FIGURE 6. Parameters β for different stretching ratios obtained by fitting with the KWW formula.

In order to quantitatively analyze the rheological behavior of the PLA film, the flow unit model is introduced, in which the microstructure of the material is composed of hard and soft regions, and the soft is mixed with the hard (Wang et al., 2014). The hard region has a compact molecular structure, while the soft region consists of loosely arranged molecules. As the flow unit, the soft region undertakes the viscoelastic and viscoplastic deformation process of the material. Then, the activation rate of the rheological unit can be defined as n = 1-σ_r/σ0 (Wang et al., 2014), where σr is the equilibrium stress. The values of n under different stretching ratios are shown in Figure 7. It can be seen that n decreases with the increase in the stretching ratio, indicating that the crystallization orientation is promoted and the movement of the molecular chain is inhabited in the film at a larger stretching ratio, which corresponds to the more difficult condition of the transition from the hard region to the soft region in the microstructure of the film. As a result, the proportion of the hard region in which the energy is more stable is larger, and the internal structure of the film reaches a more stable state (Wang et al., 2014). Reference to the result of β is presented in Figure 6. It can be inferred that the activation rate decreasing will further result in a smaller dynamic inhomogeneity of the film.

FIGURE 7

FIGURE 7. Activation rate (n) of rheological units with different stretching ratios.

3.2 The volume of the rheological unit

In practice, the relaxation curves can exhibit a logarithmic variation of stress with time or a non-logarithmic one. The former case has been reported for a range of materials and deformation conditions and corresponds to a relaxation curve of the following equation (Wang et al., 2014):

$\sigma \left(t\right)={\sigma }_0+\frac{-k_{\mathrm{B}}T}{V_{\mathrm{a}}}\ln \left(1+\frac{t}{C_r}\right)(10)$

The relaxation curves at different stretching ratios were fitted and analyzed by the above formula to further calculate the rheological unit volume. Where K_B is Boltzmann constant, ${\tau }_0$ is the initial stress and C_r is a time-related constant. This is different from the free volume which was generated by the space gap between the crystal structure, grain shape, and grain size of the material. The apparent activation volume V_a represents the average volume of the rheological unit and is fully determined by knowing relaxation curves. The fitting curves under different stretching ratios are shown in Figure 8.

FIGURE 8

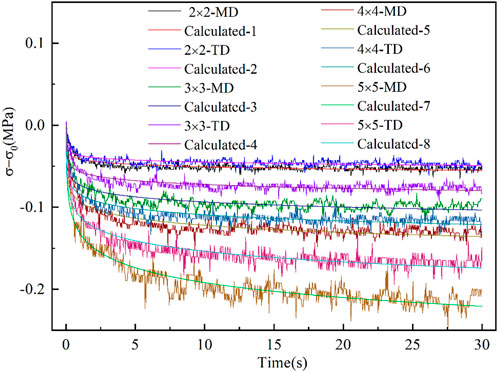
FIGURE 8. The relaxation stress-time curves and the fitting curves with different stretching ratios.

The volumes of the rheological unit which were obtained by fitting the stress relaxation curves under different stretching ratios are shown in Figure 9. As can be seen, the volume of the rheological unit decreases with the increase in the stretching ratio, which is consistent with the trend of activation rate. Combined with the dynamic inhomogeneity during the stress relaxation, it can be inferred that the rheological units of PLA films were mainly transformed from the amorphous region in the internal microstructure, meaning the higher crystallinity fraction with increasing stretching ratios leads to fewer rheological units This rule is consistent with the experimental result of characterizing the free volume by electron annihilation (Jia et al., 2015). Nevertheless, the internal physical mechanism needs to be further investigated.

FIGURE 9

FIGURE 9. The volume of rheological units with different stretching ratios.

3.3 Activation of the energy spectrum

The deformation of the film during biaxial stretching involves the local motion of the flow unit, which needs to cross the corresponding energy barrier to be activated (Gibbs et al., 1983). Due to the change, the activation energy will control the proportion of the rheological units. Thus, the volume of rheological units is also affected by the activation energy. In order to understand the connection between the activation energy and the volume of rheological units during the stress relaxation process of the film, the activation energy spectrum should be further analyzed. The flow units and activation energy in the film are widely distributed during biaxial stretching. The evolution of inelastic strain energy with time can be described by the activation energy spectrum (AES) (Gibbs et al., 1983). The variation of relaxation stress on time can be expressed by an integral equation:

$\Delta \sigma \left(t\right)={\int }_0^{+\infty }P\left(E\right)\theta \left(E,T,t\right)dE(11)$

Where P(E) is the distribution intensity of the activation energy. The θ(E, T, t) is a characteristic function; it can be expressed as follow:

$\theta \left(E,T,t\right)=1-\exp \left(-\frac{t}{\tau }\right)=1-\exp \left[-v_{0}t\exp \left(\frac{E}{K_{\mathrm{B}}T}\right)\right](12)$

Where v0 is an effective attack frequency of the order of the Debye frequency or less. During the heat setting process, the deformation with the characteristic relaxation time less than the experimental time is involved in stress relaxation. On the contrary, the deformation that the characteristic relaxation time is greater than the experimental time does not participate in the relaxation (Zhao et al., 2015). Correspondingly, the flow unit has a critical energy activation. When the activation energy of the flow unit is less than the critical activation energy, it will be activated to participate in the relaxation process; otherwise, it will not. In the frame of step-like approximation, the distribution intensity of the activation energy can be expressed as follows (Qiao et al., 2016):

$P\left(E\right)=\frac{-1}{k_{\mathrm{B}}T}\frac{\mathrm{d}\sigma \left(t\right)}{\mathrm{d}\ln t}(13)$

Where σ(t) is the time function of stress, and T is the temperature. The critical activation energy is calculated by the Arrhenius equation (Yang et al., 2021).

$E=K_{B}T\ln \left(v_{0}t\right)(14)$

Based on Eqs. 13, 14, the activation energy spectrum during stress relaxation can be calculated. It should be pointed out that it is necessary to fit the relaxation stress-time curve with the power law formula before calculating the distribution intensity of the activation energy. The fitting curves are shown in Figure 10. Then, the activation energy spectrum is calculated based on the fitting curves.

FIGURE 10

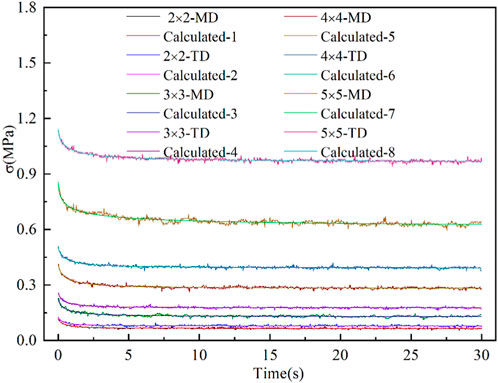
FIGURE 10. The stress relaxation curves under different stretching ratios were fitted by the power law formula.

According to Eqs. 13, 14, the obtained apparent activation energy spectra are presented in Figure 11. It can be seen that the shape of activation energy spectra is close to the Gaussian distribution, and the peak of the spectrum increases with the increase in the stretching ratio. In addition, the symmetry axis of the peak shifted toward the high energy value with the increase in the stretching ratio, indicating that more rheological units with higher energy barriers are activated during inelastic deformation at elevated stretching ratios. The movement of the rheological unit is limited which further results in a decrease in the activation rate. Meanwhile, the proportion of rheological units that can be activated is less, which means that the range of the soft region will gradually be smaller. Reference to the result of V_a is presented in Figure 9 and the value of β is presented in Figure 6. It can be inferred that the decrease in the rheological unit volume and the weaker dynamic inhomogeneity may be related to the high activation energy. This result further confirms that the high activation energy is related to the high crystallinity of the film.

FIGURE 11

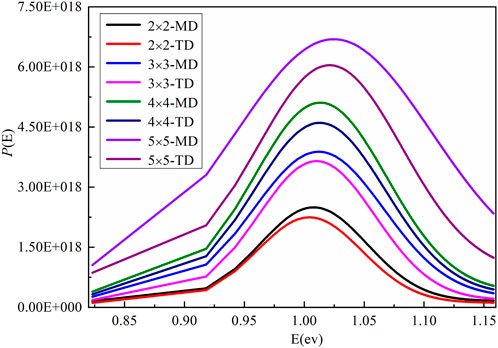
FIGURE 11. Activation energy spectrum of stress relaxation processes with different stretching ratios.

4 Conclusion

In this work, the biaxial stretching test of PLA films with different ratios was carried out with the biaxial stretching machine. Then, the rheological behavior of PLA films during the heat setting stage was investigated; the following results were obtained:

1) The stress calculation expression during biaxial stretching was derived at first, and then the load-time relationship was transformed into the stress-strain curve. We found that the stress relaxation amplitude is greater with the increase in the stretching ratio during the heat-setting stage.

2) The KWW formula was employed to fit and analyze the stress-time curve in the heat-setting stage. It was found that the increase in the stretching ratio led to the augmentation of the expansion index β, suggesting that the larger the stretching ratio, the better the dynamic homogeneity. In addition, the dynamic homogeneity in the MD direction was always better than that in the TD direction.

3) By analyzing the characteristics of the rheological units in the heat setting stage, the results showed that the activated rheological units in the microstructure of PLA films gradually decreased with the increase in the stretching ratios, and the activation energy spectrum curve was similar to the Gaussian distribution curve. In addition, the energy spectrum curve exhibited an apparent trend to a higher energy state with an increasing stretching ratio. Indicating that the greater the stretching ratio, the more energy was required to activate the rheological units.

The above results would provide a theoretical basis for further understanding the biaxial stretching mechanism of thin films.

Data availability statement

The data analyzed in this study is subject to the following licenses/restrictions: contact to author. Requests to access these datasets should be directed to eHp5MDQ1QGZveG1haWwuY29t.

Author contributions

ZX conceptualization, investigation, writing—original draft, review and editing. GL methodology, conceptualization, writing—review and editing. YL methodology, writing—review and editing, funding acquisition. JL formal analysis, writing—review and editing. BL formal analysis, writing—review and editing. LC formal analysis, review and editing. All authors contributed to the article and approved the submitted version.

Funding

This work was supported by the National Natural Science Foundation of China (No. 11872179), the Natural Science Foundation of Hunan Province (No. 2020JJ5136), the Hunan Provincial Education Department (No. 21B0535), and the Supported by Scientific Research and Innovation Foundation of Hunan Province of Technology (CX20231104).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Aval, S. T., Davachi, S. M., Sahraeian, R., Dadmohammadi, Y., Heidari, B. S., Seyfi, J., et al. (2020). Nanoperlite effect on thermal, rheological, surface and cellular properties of poly lactic acid/nanoperlite nanocomposites for multipurpose applications. Polym. Test. 91, 106779. doi:10.1016/j.polymertesting.2020.106779

CrossRef Full Text | Google Scholar

Azlin, M. N. M., Sapuan, S. M., Zuhri, M. Y. M., and Zainudin, E. S. (2022). Mechanical, morphological and thermal properties of woven polyester fiber reinforced polylactic acid (PLA) composites. Fibers Polym. 23 (1), 234–242. doi:10.1007/s12221-021-0139-2

CrossRef Full Text | Google Scholar

Claro, P. I. C., Neto, A. R. S., Bibbo, A. C. C., Mattoso, L. H. C., Bastos, M. S. R., and Marconcini, J. M. (2016). Biodegradable blends with potential use in packaging: A comparison of PLA/chitosan and PLA/cellulose acetate films. J. Polym. Environ. 24 (4), 363–371. doi:10.1007/s10924-016-0785-4

CrossRef Full Text | Google Scholar

Ding, Y. T., Han, A. C., Zhou, H. X., Zhou, Q., Song, H. L., Chen, R., et al. (2021). Preparation of poly(ε-caprolactone) based composites through multistage biaxial-stretching extrusion with excellent oxygen and water vapor barrier performance. Compos. Part a-Applied Sci. Manuf. 149, 106494. doi:10.1016/j.compositesa.2021.106494

CrossRef Full Text | Google Scholar

Duan, Y. J., Zhang, L. T., Qiao, J. C., Wang, Y. J., Yang, Y., Wada, T., et al. (2022). Intrinsic correlation between the fraction of liquidlike zones and the beta relaxation in high-entropy metallic glasses. Phys. Rev. Lett. 129 (17), 175501. doi:10.1103/PhysRevLett.129.175501

PubMed Abstract | CrossRef Full Text | Google Scholar

Ediger, M. D. (2000). Spatially heterogeneous dynamics in supercooled liquids. Annu. Rev. Phys. Chem. 51, 99–128. doi:10.1146/annurev.physchem.51.1.99

PubMed Abstract | CrossRef Full Text | Google Scholar

Fredi, G., Dorigato, A., Dussin, A., Xanthopoulou, E., Bikiaris, D. N., Botta, L., et al. (2022). Compatibilization of polylactide/poly(ethylene 2,5-furanoate) (PLA/PEF) blends for sustainable and bioderived packaging. Molecules 27 (19), 6371. doi:10.3390/molecules27196371

PubMed Abstract | CrossRef Full Text | Google Scholar

Gibbs, M. R. J., Evetts, J. E., and Leake, J. A. (1983). ACTIVATION-ENERGY spectra and relaxation in amorphous materials. J. Mater. Sci. 18 (1), 278–288. doi:10.1007/bf00543836

CrossRef Full Text | Google Scholar

Jariyasakoolroj, P., Tashiro, K., Wang, H., Yamamoto, H., Chinsirikul, W., Kerddonfag, N., et al. (2015). Isotropically small crystalline lamellae induced by high biaxial-stretching rate as a key microstructure for super-tough polylactide film. Polymer 68, 234–245. doi:10.1016/j.polymer.2015.05.006

CrossRef Full Text | Google Scholar

Jia, C. F., Zhang, Q. W., Liao, X., Zhu, J. J., Wu, L. Y., Ni, K., et al. (2015). Hierarchical microstructure changes and the molecular mechanism of polypropylene under a critical failure strain during creep. Polymer 67, 92–100. doi:10.1016/j.polymer.2015.04.057

CrossRef Full Text | Google Scholar

Kong, W. S., Ju, T. J., Park, J. H., Lee, J. W., and Yoon, H. G. (2015). Modification of biaxially oriented polypropylene films using dicyclopentadiene based hydrogenated hydrocarbon resin. J. Polym. Eng. 35 (9), 859–866. doi:10.1515/polyeng-2014-0264

CrossRef Full Text | Google Scholar

Li, H., Cao, Z., Wu, D., Tao, G., Zhong, W., Zhu, H., et al. (2016). Crystallisation, mechanical properties and rheological behaviour of PLA composites reinforced by surface modified microcrystalline cellulose. Plastics Rubber Compos. 45 (4), 181–187. doi:10.1179/1743289815y.0000000040

CrossRef Full Text | Google Scholar

Lin, X. T., Wu, Y. C., Cui, L. N., Chen, X., Fan, S. H., Liu, Y. J., et al. (2022). Crystal structure, morphology, and mechanical properties of biaxially oriented polyamide-6 films toughened with poly(ether block amide). Polym. Adv. Technol. 33 (1), 137–145. doi:10.1002/pat.5497

CrossRef Full Text | Google Scholar

Liu, Y., Liao, G. K., Liu, Y. J., Li, X. G., Liu, X. C., Dong, Y., et al. (2021). Investigation on the creep behavior of PA6 film based on the fractional differential model. J. Elastomers Plastics 53 (6), 599–611. doi:10.1177/0095244320959805

CrossRef Full Text | Google Scholar

Lou, C. W., Yao, C. H., Chen, Y. S., Hsieh, T. C., Lin, J. H., and Hsing, W. H. (2008). Manufacturing and properties of PLA absorbable surgical suture. Text. Res. J. 78 (11), 958–965. doi:10.1177/0040517507087856

CrossRef Full Text | Google Scholar

Moradi, S., and Yeganeh, J. K. (2020). Highly toughened poly(lactic acid) (PLA) prepared through melt blending with ethylene-co-vinyl acetate (EVA) copolymer and simultaneous addition of hydrophilic silica nanoparticles and block copolymer compatibilizer. Polym. Test. 91, 106735. doi:10.1016/j.polymertesting.2020.106735

CrossRef Full Text | Google Scholar

Ouchiar, S., Stoclet, G., Cabaret, C., Addad, A., and Gloaguen, V. (2016). Effect of biaxial stretching on thermomechanical properties of polylactide based nanocomposites. Polymer 99, 358–367. doi:10.1016/j.polymer.2016.07.020

CrossRef Full Text | Google Scholar

Palai, B., Mohanty, S., and Nayak, S. K. (2020). Synergistic effect of polylactic acid(PLA) and Poly(butylene succinate-co-adipate) (PBSA) based sustainable, reactive, super toughened eco-composite blown films for flexible packaging applications. Polym. Test. 83, 106130. doi:10.1016/j.polymertesting.2019.106130

CrossRef Full Text | Google Scholar

Qiao, J. C., Wang, Y. J., Zhao, L. Z., Dai, L. H., Crespo, D., Pelletier, J. M., et al. (2016). Transition from stress-driven to thermally activated stress relaxation in metallic glasses. Phys. Rev. B 94 (10), 104203. doi:10.1103/PhysRevB.94.104203

CrossRef Full Text | Google Scholar

Ren, M. Q., Tang, Y. J., Gao, D. L., Ren, Y. M., Yao, X. R., Shi, H. W., et al. (2020). Recrystallization of biaxially oriented polyethylene film from partially melted state within crystallite networks. Polymer 191, 122291. doi:10.1016/j.polymer.2020.122291

CrossRef Full Text | Google Scholar

Rhee, S., and White, J. L. (2002). Crystal structure and morphology of biaxially oriented polyamide 12 films. J. Polym. Sci. B Polym. Phys. 40, 1189–1200. doi:10.1002/polb.10181

CrossRef Full Text | Google Scholar

Salem, D. R., and Vasanthan, N. (2009). Multiple thermosetting of semicrystalline polymers: polyamide 66 and poly(ethylene terephthalate) fibers. Polymer 50 (7), 1790–1796. doi:10.1016/j.polymer.2009.02.018

CrossRef Full Text | Google Scholar

Tenn, N., Follain, N., Fatyeyeva, K., Poncin-Epaillard, F., Soulestin, J., and Marais, S. (2012). “The increase of barrier performances of PLA films by cold plasma treatments and incorporation of nanoparticles,” in 18th IAPRI world Conference on packaging) (San Luis Obispo: IAPRI), 143–148.

Google Scholar

Wang, Z., Sun, B. A., Bai, H. Y., and Wang, W. H. (2014). Evolution of hidden localized flow during glass-to-liquid transition in metallic glass. Nat. Commun. 5, 5823. doi:10.1038/ncomms6823

PubMed Abstract | CrossRef Full Text | Google Scholar

Wu, J. H., Hu, T. G., Wang, H., Zong, M. H., Wu, H., and Wen, P. (2022). Electrospinning of PLA nanofibers: recent advances and its potential application for food packaging. J. Agric. Food Chem. 70 (27), 8207–8221. doi:10.1021/acs.jafc.2c02611

PubMed Abstract | CrossRef Full Text | Google Scholar

Wu, J. H., Yen, M. S., Wu, C. P., Li, C. H., and Kuo, M. C. (2013). Effect of biaxial stretching on thermal properties, shrinkage and mechanical properties of poly (lactic acid) films. J. Polym. Environ. 21 (1), 303–311. doi:10.1007/s10924-012-0523-5

CrossRef Full Text | Google Scholar

Yang, P. R., Liu, C. X., Guo, Q. Y., and Liu, Y. C. (2021). Variation of activation energy determined by a modified Arrhenius approach: roles of dynamic recrystallization on the hot deformation of Ni-based superalloy. J. Mater. Sci. Technol. 72, 162–171. doi:10.1016/j.jmst.2020.09.024

CrossRef Full Text | Google Scholar

Yang, R. H., and Kan, C. W. (2013). Effect of heat setting parameters on some properties of PLA knitted fabric. Fibers Polym. 14 (8), 1347–1353. doi:10.1007/s12221-013-1347-1

CrossRef Full Text | Google Scholar

Yoksan, R., Dang, K. M., Boontanimitr, A., and Chirachanchai, S. (2021). Relationship between microstructure and performances of simultaneous biaxially stretched films based on thermoplastic starch and biodegradable polyesters. Int. J. Biol. Macromol. 190, 141–150. doi:10.1016/j.ijbiomac.2021.08.206

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, M. N., Yang, E., Zeng, J., Ji, J., Tian, F. C., and Li, L. B. (2021). Numerical study on oblique stretching of viscoelastic polymer film. J. Newt. Fluid Mech. 295, 104597. doi:10.1016/j.jnnfm.2021.104597

CrossRef Full Text | Google Scholar

Zhao, L. Z., Li, Y. Z., Xue, R. J., Wang, W. H., and Bai, H. Y. (2015). Evolution of structural and dynamic heterogeneities during elastic to plastic transition in metallic glass. J. Appl. Phys. 118 (15). doi:10.1063/1.4933343

CrossRef Full Text | Google Scholar

Zhou, L., Xu, P. P., Ni, S. H., Xu, L., Lin, H., Zhong, G. J., et al. (2022). Superior ductile and high-barrier poly(lactic acid) films by constructing oriented nanocrystals as efficient reinforcement of chain entanglement network and promising barrier wall. Chin. J. Polym. Sci. 40 (10), 1201–1212. doi:10.1007/s10118-022-2723-3

CrossRef Full Text | Google Scholar