- 1Department of Mechanical Engineering, University of Ottawa, Ottawa, ON, Canada
- 2Digital Technologies Research Center, National Research Council of Canada, Ottawa, ON, Canada
Machine learning (ML) techniques emerged as viable means for novel materials discovery and target property determination. At the vanguard of discoverable energy materials are perovskite crystalline materials, which are known for their robust design space and multifunctionality. Previous efforts for simulating the discovery of novel perovskites via ML have often been limited to straightforward tabular-dataset models and compositional phase-field representations. Therefore, the present study makes a contribution in expanding ML capability by demonstrating the efficacy of a new deep evolutionary learning framework for discovering stable and functional inorganic materials that adopts the complex
1 Introduction
The discovery of new materials is fundamental to addressing numerous technological challenges. Traditionally, the process consists of experimental synthesization and/or quantum mechanics first-principles calculations. Despite the significant contributions of both approaches, they remain inadequate for substantially large search spaces as they tend to be considerably difficult, unpractical, uneconomical and computationally expensive. In Edisonian experiments, for example, new materials have to be synthesized by reacting chemical participants to produce new chemical compounds. Such experimental effort will strongly depend on experiential knowledge, and in some cases, trial-and-error, thereby limiting their usability over a wider spectrum of design requirements and/or material class. Similarly, first-principles (ab initio) methods are generally known to be computationally expensive due to the heavy price of solving the costly Schrödinger equation on a many-body Hamiltonian system. In this context, data-driven Artificial Intelligence (AI) technologies, that are based on Deep Generative Modeling (DGM), have emerged as potentially more reliable, inexpensive, and more rapid alternatives for the systematic identification of novel (unknown) and complex materials. By solving an inverse design scheme (Fuhr and Sumpter, 2022), DGM processes can efficiently accelerate the search for new materials within a robust chemical combinatorial or design space. In several contemporary studies, DGMs are trained on target-specific material properties by learning from a materials dataset in a semi-supervisory manner. The semi-supervisory approach comprises an unsupervisory algorithm used to regenerate new materials and a supervisory algorithm for conditioning a target-property of interest. A proven semi-supervisory DGM used in solving the inverse design challenge is the Semi-Supervisory Variational AutoEncoder (SS-VAE) (Kingma et al., 2014), which is a variant of the traditional Variational Autoencoder (VAE) (Kingma and Welling, 2013). The SS-VAE is a directed graphical model and operates by projecting a probabilistic distribution of the original data onto a compact latent space. At the same time, the SS-VAE learns a representative labeled data associated with the training dataset during the unsupervised learning process. The latent space itself can be visualized as a hyperdimensional reduced representative form of the original data, whereby explorative and forensic investigations can be conducted (Kamnitsas et al., 2018). Moreover, the efficiency of a SS-VAE model can be influenced by several factors that evolve around the application field of interest and/or hyper-parameter tunings. Within the context of materials discovery, two aspects are of high importance for influencing the performance and design architecture of SS-VAE models. First are material inductive biases, which leverage on the current physicochemical state of the material class. Such biases are known to influence the choice of descriptor design, such as choosing between implementing graph-based modeling (Xie and Grossman, 2018; Mansimov et al., 2019), image-based modeling (Ren et al., 2022; Chenebuah et al., 2023) or phase-field modeling (Jena et al., 2019). Second are target-specific search optimizations. Optimizing for specific target properties is normally conducted in the latent space and, thus, influences the overall modeling architecture and sampling strategy. Customarily, SS-VAE models are instinctive latent space optimizers, which is due to the effect of the incorporated supervisory learning algorithm. The supervisory target-learning network predicts a labeled material’s property of interest in hyperdimension and, as such, organizes the latent space based on inferred knowledge from the prediction process.
In prior studies moreover, the practicality of SS-VAE models has been demonstrated for systematic materials discovery. For instance, as applied in a vanadium oxide (V-O) SS-VAE generator, new polymorphic compounds were successfully identified by target-learning the latent space using features that quantitatively assess stability from a strict formation energy perspective (Noh et al., 2019). In another research, a novel target-property predicting SS-VAE model was combined with a diffusive decoding model for generating thermodynamically stable 2D materials (Lyngby and Thygesen, 2022). Likewise, a Fourier Transformed Crystal Property (FTCP) representation was used to describe a wide stoichiometry of inorganic crystals for simulating the prediction of new stable compounds in a target-learnable SS-VAE latent space (Ren et al., 2022). In as much as SS-VAE models have achieved considerable successes, some technical challenges persist with their target-learning capabilities. Specifically, a common limitation is a phenomenon referred to as posterior collapse (Lucas et al., 2019), whereby the model fails to properly utilize the latent space, and therefore, generates unknown materials that are substantially different from the predefined target objective. Another major challenge is that a significant proportion of generated materials from an explorative sampling strategy are decoded to be chemically infeasible or inaccurate due to overlapping geometrical coordination of constitutive atoms (Ren et al., 2022).
To address the aforementioned challenges, the current study develops an evolutionary-based deep learning materials generator that enhances target-specific search optimization in the latent space while applying a geometrical similarity analysis on atomic coordination for recommending novel materials that are theoretically more likely to be chemically stable. The proposed Evolutionary Variational Autoencoder for Perovskite Discovery (EVAPD) model progressively combines a SS-VAE deconstructive algorithm, an evolutionary-based genetic algorithm (Michalewicz and Schoenauer, 1996), and a one-to-one similarity analysis based on geometrical coordination. Moreover, the study focusses on the discovery of host materials that adopts the perovskite stoichiometry. Perovskites in general are well known for their appealing functionalization, in-demand applications, and robust design space afforded by their chemical flexibility (Johnsson and Lemmens, 2005; Zhang et al., 2022). Common bulk perovskite stoichiometries include the simple ternary structures (
The present study is organized as follows. First, the study highlights the unlimited design space afforded by the perovskite material class and describes the proposed modeling approach used in representing multi-stoichiometrical compounds that adopts the perovskite chemical formula. Second, the performance of the EVAPD model is assessed and the results of the forward and inverse design modeling experiments are presented based on standardized evaluation metrics. Third, the generative modeling approach is demonstrated for some newly predicted host materials and their properties are determined using machine learning and DFT. Finally, the developed EVAPD model is compared to other contemporary design architectures to demonstrate the scientific contribution of the current study.
2 Materials and methods
2.1 Perovskite chemical combinatorial design space
The bulk ternary
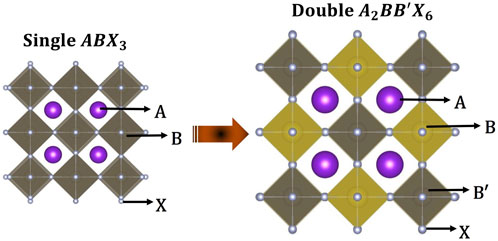
FIGURE 1. The double B-site perovskite crystal structure relative to the single
2.2 Image-based descriptor design
Molecular and organic materials have standard representative forms for feature engineering their chemical structures, such as Simplified Molecular Linear Input Specification (SMILES) representations (Weininger, 1988) and graph-based methods (Mansimov et al., 2019). For crystalline materials however, there currently exists no absolute descriptor design, which is a consequence of material-inductive biases. Modeling descriptor design for crystalline materials will have to take into consideration the crystal material class, the physicochemical state of the material, the stoichiometry, and the periodic effect of the reciprocal lattice. Previous efforts for broadly representing general inorganic crystals have been proposed using the Fourier Transformed Crystal Property (FTCP) (Ren et al., 2022). However, such a broad descriptor design is constrained by local exploitative search mechanisms (e.g., perturbative search operations), in order to randomly capture theoretically feasible materials within a diverse pool of material classes. To address this limitation, the present study constructs a user-interpretable image-based descriptor design for optimizing the explorative search of multi-stoichiometrical perovskite materials. The design consists of two sections that play crucial roles in the modeling objectives of the current study. The first section contains six crystallographic features that include: discretized atomic number (i.e., elemental label), stoichiometrical type, ionic occupancy, lattice parameters, number of atoms in the unit cell, and fractional atomic coordinates. The aforementioned features are essential for generative modeling, as they define the arrangement and bonding of atoms for all newly discovered perovskites. The second section provides thirteen discretized (one-hot encoded) features that comprehensively describe the thermochemistry behavior of all constitutive chemical elements that build the crystal structure. They include group number, row number, electronegativity, covalent radius, valence, ionization, electron affinity, spdf block, molar volume, average ionic radius, polarizability, specific heat, and thermal conductivity. The discretized features are crucial for mapping perovskites to their corresponding target properties (Xie and Grossman, 2018). As such, the thermochemistry properties assist in the organization of the latent space via the target-learning model, in addition to the supportive feedback models that are integrated into the evolutionary learning branch. Figure 2 illustrates the stacking arrangement and matrix array size of all contributing feature embedding. Both distinctive sections are horizontally concatenated, three-dimensionally reshaped, and zero-padded to produce an RGB (image-based) perovskite descriptor with an overall input matrix array of size
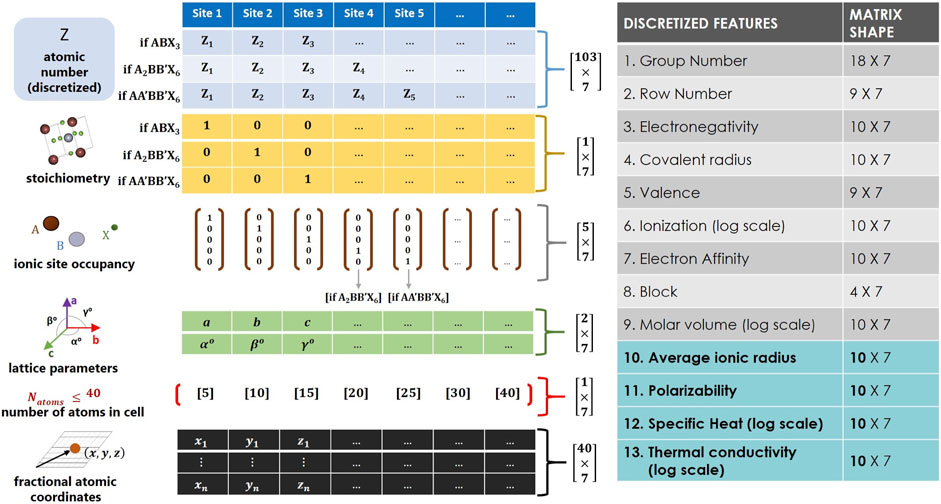
FIGURE 2. Image-based descriptor design for representing
2.3 Semi-supervised variational autoencoder (SS-VAE) model
For generative modeling, a regularized latent space is crucial for smoothly transitioning between data points in hyperdimension. Emerging from Bayes theorem, Variational Autoencoders (VAE) enable such regularization by encoding feed inputs using predefined probability distributions (Kingma and Welling, 2013). For a known set of original perovskite samples (i.e.,
2.4 Developed deep evolutionary learning framework
As illustrated in Figure 3, the deep evolutionary framework implemented in the current study begins by transforming perovskite samples (i.e.,
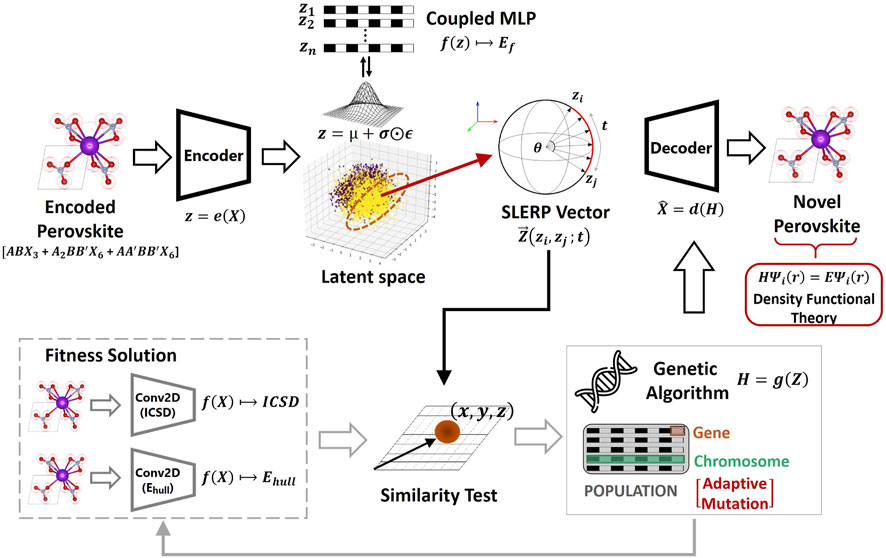
FIGURE 3. Proposed Evolutionary Variational Autoencoder for Perovskite Discovery (EVAPD). The modeling approach progressively combines a Semi-Supervised Variational Autoencoder (SS-VAE), a Genetic Algorithm (GA), two fitness-scoring convolutional neural networks (Conv2D), and a geometrical similarity-screening test to form the deep evolutionary learning framework.
Moreover, the SLERP technique is characterized by its tendency to lean more towards the variety extreme in the variety-validity tradeoff (Ren et al., 2022). Here, validity refers to the price in generating structurally feasible candidates (i.e., exploitation), but at the expense of diversity. Variety on the other hand pertains to diversification in generated candidates (i.e., exploration), but at the expense of feasibility. The present study attempts to manage the higher variety extreme from SLERP by implementing an exploitative similarity test analysis that improves validity. In addition, the present study integrates an evolutionary algorithm for further optimizing the sampled solutions generated from the SLERP process. The evolutionary search algorithm performs metaheuristic search operations and ranks the generated solutions based on a fitness-scoring process. For this purpose, the Genetic Algorithm (GA) is preferred over other similar evolutionary models due to its computational flexibility in allowing user-defined fitness functions and non-derivative problem-solving capability (Michalewicz and Schoenauer, 1996). The GA model searches for the most promising perovskite candidates by conducting dynamic iterative operations over a batch population via a process that is inspired by biologically motivated crossover and mutation of genes (scalars) and chromosomes (vectors). Moreover, the current study modifies the mutation process of the GA model to be quality-adaptive, by flipping the genes of low-quality solutions twice as much as high-quality solutions. To comprehensively search for high-quality candidates, the fitness function of the GA model (
2.5 Variable-cell DFT relaxation using Quantum Espresso
Using the first-principles Density Functional Theory (DFT) simulation technique, the novel candidates emerging from the EVAPD pipeline are chemically and geometrically validated to ascertain their synthesizability potential. For this purpose, the Quantum Espresso (QE) DFT software package (Giannozzi et al., 2009) is used to perform plane-wave Generalized Gradient Approximation (GGA) calculations, as parametrized on a Perdew-Burke-Ernzerhof (PBE) (Perdew et al., 1996) - Projector Augmented Wave (PAW) pseudopotential class (Blöchl, 1994; Kresse and Joubert, 1999). For validating the novel candidates, the current study applies two successive DFT approaches. First, non-spin polarized DFT relaxation is performed on stationary unit cells of the crystal lattice in order to find the most stable three-dimensional configuration of constitutive atoms or ionic positions. The preliminary relaxation exercise saves computational resource by ensuring that only chemically-balanced and atomically-optimized candidates (i.e., novel perovskites with converged total electronic energy) are selected for further investigation. For the second relaxation phase, the overall crystal structure is thoroughly examined by performing variable-cell relaxation (vc-relax) on all axes and angles of previously converged unit cell candidates. Moreover, the second optimization phase includes spin polarized (magnetic) calculation by inducing collinear starting magnetization values on the initially relaxed geometry. Such spin polarization is beneficial for understanding the magnetic behavior of the material, i.e., di-, para-, ferro-magnetism, etc. For both relaxation phases, appropriate K-points grid meshes are used to sample the three-dimensional Brillouin zone of the reciprocal crystal lattice, as recommended by Materials Cloud (Talirz et al., 2020). The Broyden-Fletcher-Goldfarb-Shanno (BFGS) iterative algorithm is applied for ionic and cell optimizations. Self-consistent field (SCF) electronic convergence is achieved by setting energy accuracy, force and pressure at 1.0e-7 Rydberg, 1.0e-3 Rydberg/Bohr, and 0.5 kbar, respectively. The energy cutoff threshold for charge density is set at ten times the corresponding value for wave function from the chemical element pseudopotential’s condition (Prandini et al., 2018). To ensure that a smooth integration of electron occupation occurs across the fermi energy level, Gaussian-smearing technique with low broadening (0.01 Rydberg) is used.
3 Experiment and simulation results
3.1 Perovskite dataset
For training the Evolutionary Variational Autoencoder for Perovskite Discovery (EVAPD) model, the current study uses scientific data from the Materials Project (Jain et al., 2013). Using pymatgen MPRester, the training samples are extracted from the platform by searching for only generic entries that adopt the three interested perovskite stoichiometries, i.e.,
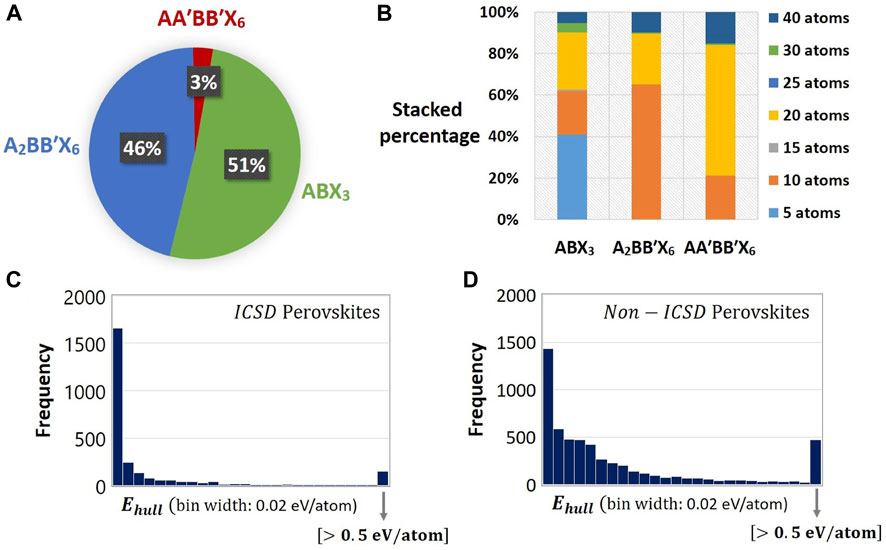
FIGURE 4. Data statistics of
3.2 Preliminary forward design evaluation on target-property prediction
The forward design can be formulated as: given the perovskite crystal structure, find the corresponding target (i.e.,
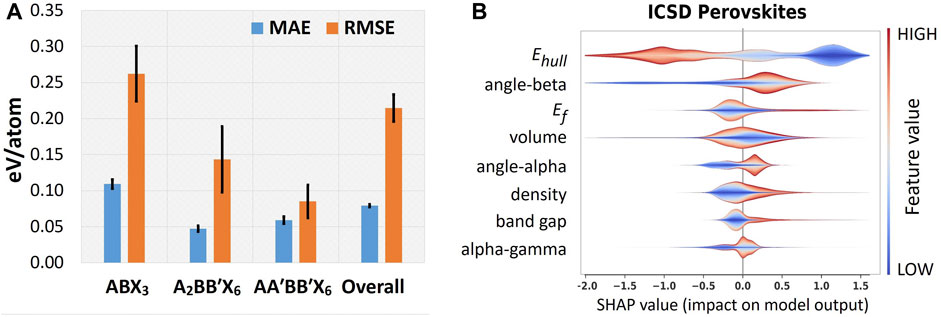
FIGURE 5. Results on forward design modeling. (A) Stoichiometric-specific MAE and RMSE evaluations on the prediction of
3.3 Performance of the SS-VAE inverse design model
The proposed SS-VAE model is used to inversely generate unknown perovskites while using target-learning information from a supervisory Multi-Layer Perceptron (MLP) model. For evaluating the model’s performance, the reconstructive errors from the encoding-decoding phases of important feature embedding is investigated. In addition, the efficacy of the target-learning MLP for organizing the latent space based on predicted formation energy is evaluated. For predicting the formation energy, the latent space vectors (i.e.,
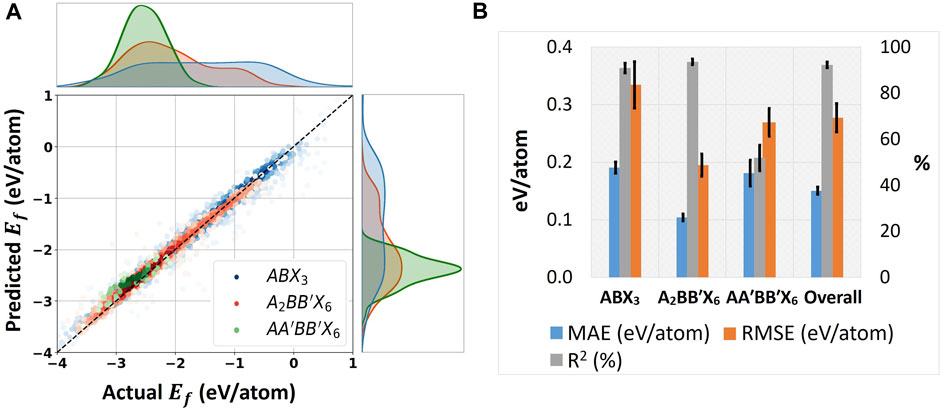
FIGURE 6. Modeling performance of the SS-VAE model for inversely designing perovskites. (A) MLP’s regression fitting on
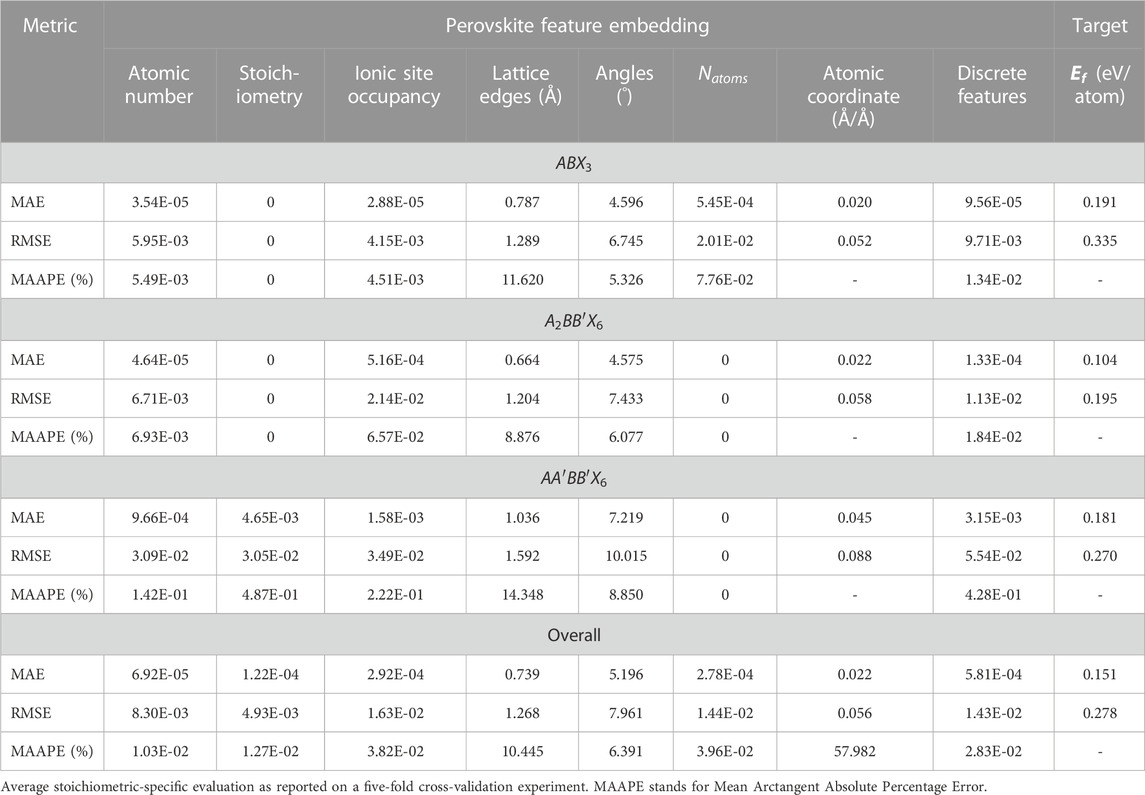
TABLE 1. Reconstruction of important input feature embedding from the image-based descriptor, in addition to formation energy determination from the target-learning arm of the SS-VAE model.
3.4 Generating novel and stable perovskites of the double stoichiometry
The architectural design of the SS-VAE model dimensionally reduces each image-based perovskite into encoded data points of vector length

FIGURE 7. Visualization of the stability-structured latent space. (A) Transformed t-SNE PCA latent space with respect to real

FIGURE 8. Displacement of data points within the interested latent space region corresponding to the 164th versus 179th axis. (A) Stable versus unstable points based on
3.5 Ranking high-quality candidates and geometrical similarity analysis
For ranking high-quality candidates, the SLERP latent vectors are evolutionary learnt using the Genetic Algorithm (GA). The GA model iteratively searches for the most stable and promising perovskite candidates using feedback loops from two pre-trained convolutional neural networks (Conv2D) for updating the fitness function. The first Conv2D model transmits information based on predicted stability for an expected/idealized value of
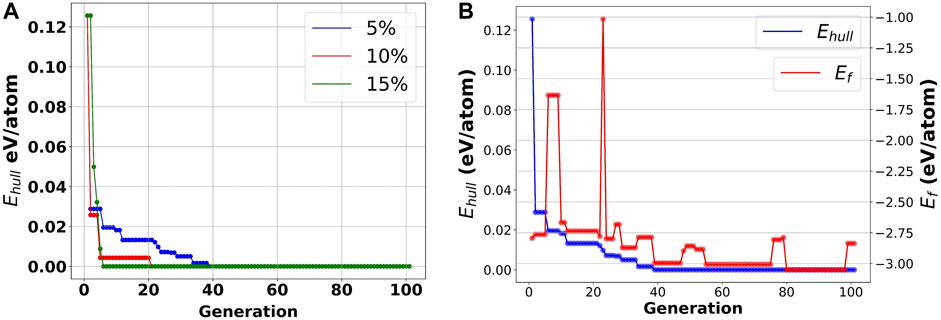
FIGURE 9. Evolutionary learning process for searching for the most optimized solution using the genetic algorithm. (A) Sensitivity analysis on the mutation rate across 100 generations; (B) Predicted
Furthermore, the high-quality solutions emerging from the joint SLERP-GA processes are further screened to ensure their geometrically coordinated environment is consistent with proven standard perovskite forms. As described in Eq. 5, the similarity analytical model measures the deviation in one-to-one atomic coordination between standards and newly generated perovskites. A dissimilarity value of
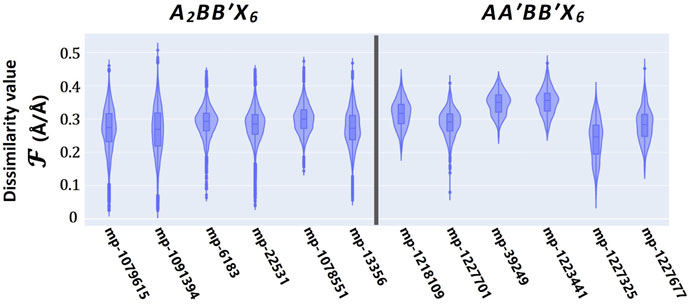
FIGURE 10. Similarity analysis as it relates to the three-dimensional geometrical (atomic) coordination between proven perovskite standards from the Materials Project (MP) database and newly generated perovskite compounds from the SLERP-GA process.
4 Discovered perovskites, analysis and Discussion
4.1 Newly discovered double perovskites and property determination
The present study reports the successful discovery of 114

TABLE 2. Newly discovered double perovskites emerging from the EVAPD model that successfully underwent thorough DFT-relaxation.
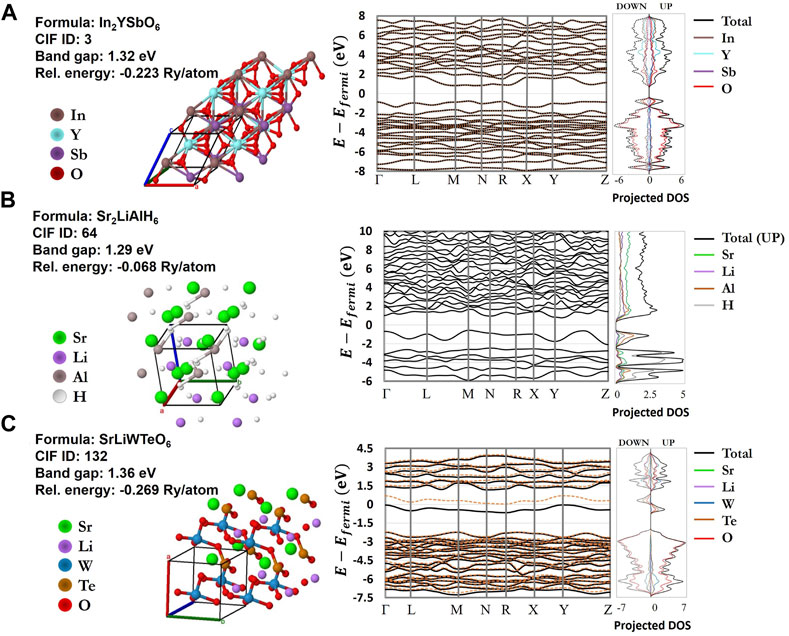
FIGURE 11. Electronic band structure and projected density of states (PDOS) properties for three promising photovoltaic host perovskite materials from the EVAPD model, with idealized band gaps close to 1.3 eV (A)
4.2 Experimental impact of the EVAPD model and future improvements
The unlimited design space afforded by perovskite stoichiometries suggests that data-mining Deep Generative Modeling (DGM) can be a more efficient alternative over first-principles techniques and/or Edisonian experiments for making accelerated discovery. The current study points to this potential advantage by cost-effectively demonstrating the efficacy of a deep evolutionary learning framework for discovering stable and functional perovskites that adopt the
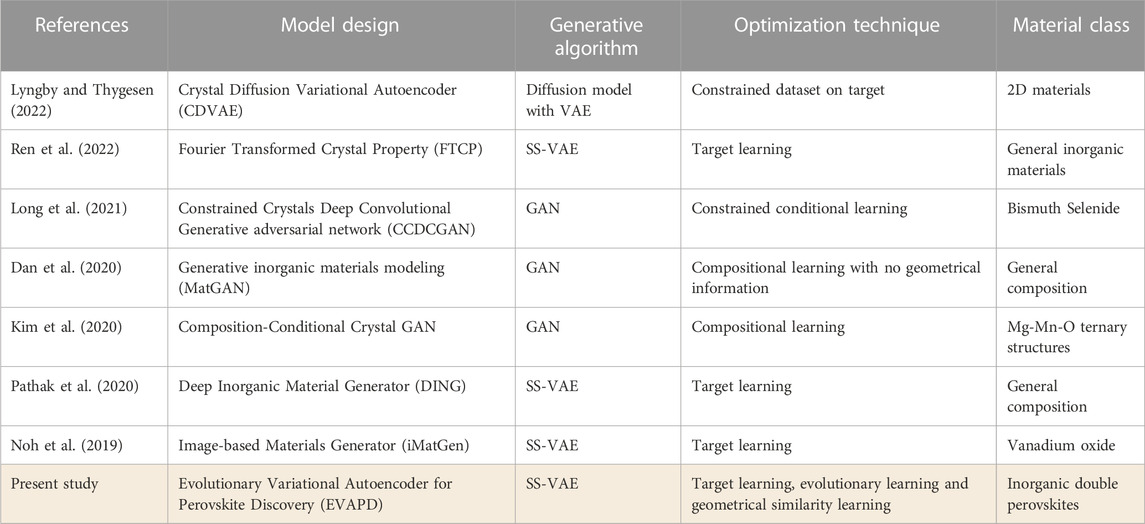
TABLE 3. Proposed model as compared to the prior arts on invertible deep generative modeling (DGM) approaches for accelerated materials discovery.
On the downside, VAE models, including the proposed model, are also prone to several challenges that affect their general performance for generating quality samples in the latent space. In addition to the aforementioned posterior and mode collapse phenomena, other concerns are related to their computational efficiency on high-dimensional data structures. The current study observes such lapses in the higher errors that were realized in reconstructing the lattice edge vectors and inter-axial angles associated with the input image-based descriptor (Table 1). Possible solutions to mitigate such limitations are by replacing the conventional autoencoder with a more efficient Wasserstein autoencoder (Tolstikhin et al., 2017), or by entirely remodeling using a different DGM, e.g., generative adversarial networks (GAN) (Goodfellow et al., 2014) and denoising diffusion models (Sohl-Dickstein, et al., 2015). This is the focus of future studies aiming at improving the EVAPD model by comparing and contrasting the results generated in the current study with other advanced DGM techniques. Another potential improvement is to better integrate DFT in the EVAPD model. In the current design architecture, post-optimizing novel perovskites using DFT validation is performed after generative and sampling processes have taken place. A better design alternative might be by directly integrating on-the-fly first-principles DFT validation and/or laboratory synthesization into the evolutionary learning space to produce an adaptive EVAPD model. This could ensure that novel materials with definitive targets are generated on a more successful rate. This is also an area of future studies.
5 Conclusion
In the present study, an Evolutionary Variational Autoencoder for Perovskite Discovery (EVAPD) model is proposed for accelerating the search for stable and functional perovskite candidates. The perovskite stoichiometries of interest are the complex
Data availability statement
The new materials dataset generated for this study can be found in the NOMAD repository (doi.org/10.17172/NOMAD/2023.05.31-1). The preprocessed dataset used for machine learning, relevant source codes for developing the EVAPD model, and Crystallographic Information Files (CIF) of newly generated materials are made available on GitHub (github.com/chenebuah/EVAPD).
Author contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Funding
This research was supported by the National Research Council of Canada (NRC) through its Artificial Intelligence for Design Program led by the Digital Technologies Research Centre.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmats.2023.1233961/full#supplementary-material
References
Belsky, A., Hellenbrandt, M., Karen, V. L., and Luksch, P. (2002). New developments in the inorganic crystal structure database (ICSD): accessibility in support of materials research and design. Acta Cryst. B58, 364–369. doi:10.1107/S0108768102006948
Berger, R. F., and Neaton, J. B. (2012). Computational design of low-band-gap double perovskites. Phys. Rev. B 86 (16), 165211. doi:10.1103/PhysRevB.86.165211
Blöchl, P. E. (1994). Projector augmented-wave method. Phys. Rev. B 50 (24), 17953–17979. doi:10.1103/PhysRevB.50.17953
Chenebuah, E. T., Nganbe, M., and Tchagang, A. B. (2023). A Fourier-transformed feature engineering design for predicting ternary perovskite properties by coupling a two-dimensional convolutional neural network with a support vector machine (Conv2D-SVM). Mater. Res. Express. 10, 026301. doi:10.1088/2053-1591/acb683
Chenebuah, E. T., Nganbe, M., and Tchagang, A. B. (2021). Comparative analysis of machine learning approaches on the prediction of the electronic properties of perovskites: A case study of ABX3 and A2BB′X6. Mater. Today Commun. 27, 102462. doi:10.1016/j.mtcomm.2021.102462
Dan, Y., Zhao, Y., Li, X., Li, S., Hu, M., and Hu, J. (2020). Generative adversarial networks (GAN) based efficient sampling of chemical composition space for inverse design of inorganic materials. npj Comput. Mater 6, 84. doi:10.1038/s41524-020-00352-0
Draxl, C., and Scheffler, M. (2018). Nomad: the fair concept for big data-driven materials science. MRS Bull. 43, 676–682. doi:10.1557/mrs.2018.208
Emery, A., and Wolverton, C. (2017). High-throughput DFT calculations of formation energy, stability and oxygen vacancy formation energy of ABO3 perovskites. Sci. Data 4, 170153. doi:10.1038/sdata.2017.153
Fuhr, A. S., and Sumpter, B. G. (2022). Deep generative models for materials discovery and machine learning-accelerated innovation. Front. Mater. 9, 865270. doi:10.3389/fmats.2022.865270
Gad, A. F. (2021). PyGAD: an intuitive genetic algorithm Python library. arXiv:2106.06158v1 [cs.NE]. doi:10.48550/arXiv.2106.06158
Giannozzi, P., Baroni, S., Bonini, N., Calandra, M., Car, R., Cavazzoni, C., et al. (2009). Quantum espresso: A modular and open-source software project for quantum simulations of materials. J. Phys.:Condens. Matter. 21 (39), 395502. doi:10.1088/0953-8984/21/39/395502
Goodfellow, I. J., Pouget-Abadie, J., Mirza, M., Xu, B., Warde-Farley, D., Ozair, S., et al. (2014). Generative adversarial networks. arXiv:1406.2661v1 [stat.ML]. doi:10.48550/arXiv.1406.2661
Jain, A., Ong, S. P., Hautier, G., Chen, W., Richards, W. D., Dacek, S., et al. (2013). Commentary: the materials project: A materials genome approach to accelerating materials innovation. Apl. Mater. 1 (1), 011002. doi:10.1063/1.4812323
Jena, A. K., Kulkarni, A., and Miyasaka, T. (2019). Halide perovskite photovoltaics: background, status, and future prospects. Chem. Rev. 119 (5), 3036–3103. doi:10.1021/acs.chemrev.8b00539
Johnsson, M., and Lemmens, P. (2005). Crystallography and chemistry of perovskites. arXiv:cond-mat/0506606v1 [cond-mat.str-el]. doi:10.48550/arXiv.cond-mat/0506606
Kamnitsas, K., Castro, D. C., Le Folgoc, L., Walker, I., Tanno, R., Rueckert, D., et al. (2018). Semisupervised learning via compact latent space clustering. arXiv:1806.02679v2 [cs.LG]. doi:10.48550/arXiv.1806.02679
Kim, C., Huan, T. D., Krishnan, S., and Ramprasad, R. (2017). A hybrid organic-inorganic perovskite dataset. Sci. Data 4, 170057. doi:10.1038/sdata.2017.57
Kim, S., Noh, J., Gu, G. H., Aspuru-Guzik, A., and Jung, Y. (2020). Generative adversarial networks for crystal structure prediction. ACS Cent. Sci. 6 (8), 1412–1420. doi:10.1021/acscentsci.0c00426
Kingma, D. P., Rezende, D. J., Mohamed, S., and Welling, M. (2014). Semi-supervised learning with deep generative models. arXiv:1406.5298v2 [cs.LG]. doi:10.48550/arXiv.1406.5298
Kingma, D. P., and Welling, N. (2013). Auto-encoding variational Bayes. arXiv:1312.6114v11 [stat.ML]. doi:10.48550/arXiv.1312.6114
Kiselyovaa, N. N., Dudareva, V. A., Stolyarenkoa, A. V., Dokukina, A. A., Sen’koc, O. V., Ryazanovc, V. V., et al. (2022). Prediction of space groups for perovskite-like A2IIBIIIB′VO6 compounds. Inorg. Mater Appl. Res. 13 (2), 277–293. doi:10.1134/S2075113322020228
Knapp, M. C., and Woodward, P. M. (2006). A-site cation ordering in AA′BB′O6 perovskites. J. Solid State Chem. 179 (4), 1076–1085. doi:10.1016/j.jssc.2006.01.005
Kresse, G., and Joubert, D. (1999). From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59 (3), 1758–1775. doi:10.1103/PhysRevB.59.1758
Kullback, S., and Leibler, R. A. (1951). On information and sufficiency. JSTOR. 22 (1), 79–86. doi:10.1214/aoms/1177729694
Kwon, Y., Kang, S., Choi, Y. S., and Kim, I. (2021). Evolutionary design of molecules based on deep learning and a genetic algorithm. Sci. Rep. 11, 17304. doi:10.1038/s41598-021-96812-8
Libelli, S. M., and Alba, P. (2000). Adaptive mutation in genetic algorithms. Soft Comput. 4, 76–80. doi:10.1007/s005000000042
Long, T., Fortunato, N. M., Opahle, I., Zhang, Y., Samathrakis, I., Shen, C., et al. (2021). Constrained crystals deep convolutional generative adversarial network for the inverse design of crystal structures. npj Comput. Mater. 7, 66. doi:10.1038/s41524-021-00526-4
Lucas, J., Tucker, G., Grosse, R. B., and Norouzi, M. (2019). Understanding posterior collapse in generative latent variable models. DGS@ICLR.
Lufaso, M. W., and Woodward, P. M. (2004). Jahn–Teller distortions, cation ordering and octahedral tilting in perovskites. Acta Cryst. B 60, 10–20. doi:10.1107/S0108768103026661
Lundberg, S. M., and Lee, S. I. (2017). A unified approach to interpreting model predictions advances in neural information processing systems. arXiv:1705.07874v2 [cs.AI]. doi:10.48550/arXiv.1705.07874
Lyngby, P., and Thygesen, K. S. (2022). Data-driven discovery of 2D materials by deep generative models. npj Comput. Mater 8, 232. doi:10.1038/s41524-022-00923-3
Mansimov, E., Mahmood, O., Kang, S., and Cho, K. (2019). Molecular geometry prediction using a deep generative graph neural network. Sci. Rep. 9, 20381. doi:10.1038/s41598-019-56773-5
Michalewicz, Z., and Schoenauer, M. (1996). Evolutionary algorithms for constrained parameter optimization problems. Evol. Comput. 4 (1), 1–32. doi:10.1162/evco.1996.4.1.1
Mitchell, R., Welch, M., and Chakhmouradian, A. (2017). Nomenclature of the perovskite supergroup: A hierarchical system of classification based on crystal structure and composition. Mineral. Mag. 81 (3), 411–461. doi:10.1180/minmag.2016.080.156
Mukaidaisi, M., Vu, A., Grantham, K., Tchagang, A., and Li, Y. (2022). Multi-objective drug design based on graph-fragment molecular representation and deep evolutionary learning. Front. Pharmacol. 13, 920747. doi:10.3389/fphar.2022.920747
Noh, J., Kim, J., Stein, H. S., Sanchez-Lengeling, B., Gregoire, J. M., Aspuru-Guzik, A., et al. (2019). Inverse design of solid-state materials via a continuous representation. Matter 1 (5), 1370–1384. doi:10.1016/j.matt.2019.08.017
Pathak, Y., Juneja, K. S., Varma, G., Ehara, M., and Priyakumar, U. D. (2020). Deep learning enabled inorganic material generator. Phys. Chem. Chem. Phys. 22, 26935–26943. doi:10.1039/D0CP03508D
Perdew, J. P., Burke, K., and Ernzerhof, M. (1996). Generalized gradient approximation made simple. Phys. Rev. Lett. 77 (18), 3865–3868. doi:10.1103/PhysRevLett.77.3865
Pilania, G., Balachandran, P. V., Kim, C., and Lookman, T. (2016). Finding new perovskite halides via machine learning. Front. Mater 3 (19), 19. doi:10.3389/fmats.2016.00019
Prandini, G., Marrazzo, A., Castelli, I. E., Mounet, N., and Marzari, N. (2018). Precision and efficiency in solid-state pseudopotential calculations. npj Comput. Mater 4, 72. doi:10.1038/s41524-018-0127-2
Ren, Z., Tian, S. I. P., Noh, J., Oviedo, F., Xing, G., Li, J., et al. (2022). An invertible crystallographic representation for general inverse design of inorganic crystals with targeted properties. Matter 5 (1), 314–335. doi:10.1016/j.matt.2021.11.032
Rühle, S. (2016). Tabulated values of the Shockley–Queisser limit for single junction solar cells. Sol. Energy 130, 139–147. doi:10.1016/j.solener.2016.02.015
Saal, J. E., Kirklin, S., Aykol, M., Meredig, B., and Wolverton, C. (2013). Materials design and discovery with high-throughput density functional theory: the open quantum materials database (OQMD). JOM 65, 1501–1509. doi:10.1007/s11837-013-0755-4
Setyawan, W., and Curtarolo, S. (2010). High-throughput electronic band structure calculations: challenges and tools. Comput. Mater. Sci. 49 (2), 299–312. doi:10.1016/j.commatsci.2010.05.010
Shapley, L. S. (1953). “A value for n-person games,” in Contributions to the theory of games, annals of mathematical studies. Editors H. W. Kuhn, and A. W. Tucker (Princeton University Press), 307–317. doi:10.1515/9781400881970-018
Shockley, W., and Queisser, H. J. (1961). Detailed balance limit of efficiency of p-n junction solar cells. J. Appl. Phys. 32 (3), 510–519. doi:10.1063/1.1736034
Shoemake, K. (1985). Animating rotation with quaternion curves. SIGGRAPH Comput. Graph. 19 (3), 245–254. doi:10.1145/325165.325242
Singh, A. K., Montoya, J. H., Gregoire, J. M., and Persson, K. A. (2019). Robust and synthesizable photocatalysts for CO2 reduction: A data-driven materials discovery. Nat. Commun. 10, 443. doi:10.1038/s41467-019-08356-1
Sohl-Dickstein, J., Weiss, E. A., Maheswaranathan, N., and Ganguli, S. (2015). Deep unsupervised learning using nonequilibrium thermodynamics. arXiv:1503.03585v8 [cs.LG]. doi:10.48550/arXiv.1503.03585
Talirz, L., Kumbhar, S., Passaro, E., Yakutovich, A. V., Granata, V., Gargiulo, F., et al. (2020). Materials Cloud, a platform for open computational science. Sci. Data. 7, 299. doi:10.1038/s41597-020-00637-5
Tao, Q., Xu, P., Li, M., and Lu, W. (2021). Machine learning for perovskite materials design and discovery. npj Comput. Mater 7, 23. doi:10.1038/s41524-021-00495-8
Tolstikhin, I., Bousquet, O., Gelly, S., and Schoelkopf, B. (2017). Wasserstein auto-encoders. arXiv:1711.01558v4 [stat.ML]. doi:10.48550/arXiv.1711.01558
Wang, Y., Zhang, H., Zhu, J., Lü, X., Li, S., Zou, R., et al. (2020). Antiperovskites with exceptional functionalities. Adv. Mater. 32, 1905007. doi:10.1002/adma.201905007
Weininger, D. (1988). SMILES, a chemical language and information system. 1. Introduction to methodology and encoding rules. J. Chem. Inf. Comput. Sci. 28 (1), 31–36. doi:10.1021/ci00057a005
Woodward, P. M. (1997). Octahedral tilting in perovskites. I. Geometrical considerations. Acta Cryst. B 53, 32–43. doi:10.1107/S0108768196010713
Xie, T., and Grossman, J. C. (2018). Crystal graph convolutional neural networks for an accurate and interpretable prediction of material properties. Phys. Rev. Lett. 120 (14), 145301. doi:10.1103/physrevlett.120.145301
Zhang, P., Li, M., and Chen, W. C. (2022). A perspective on perovskite solar cells: emergence, progress, and commercialization. Front. Chem. 10, 802890. doi:10.3389/fchem.2022.802890
Keywords: machine learning (ML), deep evolutionary learning, variational autoencoder (VAE), genetic algorithm, inverse design, density functional theory (DFT), perovskite, materials discovery
Citation: Chenebuah ET, Nganbe M and Tchagang AB (2023) An evolutionary variational autoencoder for perovskite discovery. Front. Mater. 10:1233961. doi: 10.3389/fmats.2023.1233961
Received: 03 June 2023; Accepted: 06 September 2023;
Published: 22 September 2023.
Edited by:
Shengli Zhang, Nanjing University of Science and Technology, ChinaReviewed by:
Mykhailo V. Klymenko, RMIT University, AustraliaBo Cai, Nanjing University of Posts and Telecommunications, China
Copyright © 2023 Chenebuah, Nganbe and Tchagang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Ericsson Tetteh Chenebuah, ZWNoZW4wMTNAdW90dGF3YS5jYQ==
 Ericsson Tetteh Chenebuah
Ericsson Tetteh Chenebuah Michel Nganbe
Michel Nganbe Alain Beaudelaire Tchagang
Alain Beaudelaire Tchagang