- 1Unisa Biomedical Engineering Research Group, Department of Mechanical Engineering, School of Engineering, College of Science Engineering and Technology, University of South Africa, Pretoria, South Africa
- 2Council for Scientific and Industrial and Research, Defence and Security Cluster, Pretoria, South Africa
- 3Department of Mechanical Engineering, Faculty of Engineering and the Built Environment, Durban University of Technology, Durban, South Africa
Besides surgery, there are currently no other established methods for routine treatment of tracheal pathologies such a tracheal stenosis or tracheal and airway tumors. Even with several attempts to repair the infected trachea with artificial and natural prostheses, there is a need for the fundamental understanding of the tissue’s mechanical behaviour. The purpose of this study was to investigate the mechanical behaviour of the tracheal tissue under biaxial tensile loading. Furthermore, the study examines the material properties of the tissue through a study of the model parameters for six constitutive models. Materials and methods: The fourteen (n = 14) specimens of sheep trachea (Vleis Merino) measured to be ∼30 × 20 mm where only the effective area of ∼25 × 16 mm was subjected to engineering strain. In this study, we assume that the tracheal tissue is anisotropic and incom-pressible, therefore we apply and study the material parameters from six different constitutive material models. Results: The results show that the tracheal tissue is twice as stiff along the circumferential direction as it is along the longitudinal direction. It is also observed that the material properties are different (non-homogeneous) along the trachea. Conclusion: The findings of this study will benefit computational models for the study of tracheal diseases or injuries. Furthermore, these findings will assist in the development of regenerative medicine for different tracheal pathologies and in the bioengineering of replacement tissue in cases of damage.
1 Introduction
The trachea, commonly known as the windpipe, is a vital part of the respiratory system. It is a flexible tube made up of rings of cartilage, giving it structural support and preventing collapse. The trachea is lined with a specialized type of tissue called respiratory epithelium or pseudostratified ciliated columnar epithelium. This lining consists of ciliated cells, which have tiny hair-like structures called cilia. These cilia help in trapping dust, debris, and microbes, and facilitate their movement upwards towards the throat to be coughed out or swallowed, thereby protecting the lungs from potential infections. Additionally, the trachea also contains glands that produce mucus, aiding in moistening and cleaning the air as it passes through the respiratory tract.
The normal physiological functioning of the trachea has led to more research focussing on the understanding of its mechanical behaviour under normal airflow conditions. As a result, most research has focused on the study of fluid-structure interaction between the air and the tracheal tissue (Koombua and Pidaparti, 2008; Wall and Rabczuk, 2008; Qi et al., 2014; Shukla et al., 2020; DeBoer et al., 2021; Zobaer and Sutradhar, 2021). These studies have examined and analysed how the tracheal wall interact with the air as it gets pulled into and pushed out of the lungs. In such studies the focus has been on understanding tracheal flow by employing computational fluid dynamics methods. However there remains questions on what part of the normal breathing action does the tracheal wall really play or if a damaged but open tracheal wall can still perform its function. When one feels the trachea during deep inhaling and exhaling exercise, the tracheal rings can be sensed moving up and down along the neck which implies that the tracheal muscle plays a part during inhaling and exhaling processes. Such subtle actions of the trachea that make breathing feel normal to an animal are a focus area in the development of replacement material for the tracheal tissue. The understanding of the working mechanisms of native trachea will elucidate the development of the tissue-engineered trachea which remains unclear (Kojima and Vacanti, 2014), however relevant mechanical and biomechanical properties of the trachea are incompletely characterised (Hoffman et al., 2016).
To understand fully the mechanical properties of the soft tissues, it is necessary to understand its mechanical behaviour (Nemavhola et al., 2021a; Ngwangwa et al., 2021; Nemavhola et al., 2021b; Greaney and Niklason, 2021; Ngwangwa and Nemavhola, 2021). Mechanical properties of soft tissues may be utilised in developing detailed computational models to study mechanisms of diseases (Masithulela, 2015a; Masithulela, 2015b; Masithulela, 2015c; Masithulela, 2016a; Masithulela, 2016b; Sáez and Kuhl, 2016). But how the implantation of a replacement material affects the response of the physiological response of a trachea is a challenge. In this study, the mechanical behaviour of the tracheal tissue under biaxial tensile loading is investigated. The stress-strain behaviour of the tissue in the circumferential and longitudinal directions are examined and discussed. Due to its very low physiological loading, often below the limit stresses in the toe region, the strains are kept to within 30% strain.
Besides studying the stress-strain behaviour of the tracheal muscle, the mechanical properties of the tissue are studied by examination of the material parameters and performances of six different constitutive material models. The Fung, Choi-Vito, Holzapfel (2000), Holzapfel (2005), Polynomial (Anisotropic) and Four-Fiber Family hyperelastic constitutive models have been previously utilised in studying mechanical behaviour of the soft tissues (Nemavhola et al., 2021c; Lebea et al., 2021). The material parameters obtained from the selected hyperelastic constitutive models are normally utilised in developing finite element models (Kortsmit et al., 2013; Skatulla et al., 2013; Masithulela, 2015a; Nemavhola, 2017a; Nemavhola, 2019a; Nemavhola, 2019b). It is expected that the analysis of the trachea using constitutive models may improve surgical outcomes. Within the limitations of such a study, there are two very important findings: firstly, the tracheal muscle is stiffer along its circumferential directions probably due to the circular cartilaginous rings (Roberts et al., 1997; Hoffman et al., 2016; Safshekan et al., 2017; Lee et al., 2019) which are more rigid than the adjoining soft tissue around it; secondly, the material is highly random and non-homogeneous as exhibited by the wide margin in the standard deviation of its material parameters across the different test specimens. In drawing the latter conclusion, the authors are mindful of the fact that there could be other factors that may have influenced such a finding although the stringent control conditions under which the testing was carried out may have eliminated such eventualities. The tested tissues showed anisotropy along the circumferential direction at larger strains which is typical for soft tissues (Fung, 1993). Although it might be expected that the same trend would also be true for the longitudinal direction, it is hard to explicitly say so in the present study since it seems that 30% strain was not large enough to stretch the tissue along the longitudinal direction beyond its toe region.
The study is aimed at investigating the mechanical behaviour of the windpipe (trachea) in two directions: aligned along its circumference and in the direction of the airflow. The trachea serves two important purposes primarily as an air conduit into and out of the lungs (Zobaer and Sutradhar, 2021) and secondly as a preconditioner and prefilter for inhaled air. The most common tracheal injury (tracheal stenosis) (Grillo et al., 1995) is usually caused by a tracheotomy intubation with unsuitable pressure. Despite the availability of various treatment procedures, with varying degrees of success, it is reported that even after treatment, the stenosis may reappear especially in cases of serious pathologies (Belsey, 1950; Huang, 2001; Grillo, 2002). Such problematic situations with respect to the total treatment of tracheal injuries makes it necessary to understand its mechanical behaviour.
2 Materials and methods
2.1 Tissue acquisition and preparation for mechanical testing
The trachea was delivered to University of South Africa (Unisa) Biomechanics Laboratory after the slaughtering of sheep (Vleis Merino) of between 40,000 and 42,000 g. The slaughtering of the sheep and dissection of the full length of the trachea were carried out at the local abattoir. Then the full sheep trachea was delivered within 2 h of slaughter from the abattoir in a temperature-controlled bag. The test specimens were excised using sharp surgical equipment in the laboratory. A total length of 280 mm was cut from the trachea’s mid-span from which fourteen 20 mm long specimens were obtained. The remaining pieces at both ends were thrown away to avoid the effect of residual stresses resulting from uncontrolled cutting at the abattoir. The temperature was kept at a maximum of 5°C during transportation. In this study, the microstructural coordinates were not utilised because there was no imaging to ascertain the exact fiber direction. Therefore, two directions were defined as per the coordinate system of the trachea where longitudinal direction was along the length of the trachea and the circumferential direction was defined to be around the circumference of the trachea.
2.2 Biaxial mechanical testing
To capture the mechanical properties of the sheep trachea, the CellScale Biaxial testing system (BioTester 5,000 CellScalle, Wateroo, ON, Canada®) was utilised by performing equi-biaxial testing on the excised trachea tissue (Figure 1). In this study, the microstructural coordinates were not utilised because there was no imaging to ascertain the exact fiber direction. Therefore, two directions were defined as per the coordinate system of the trachea where longitudinal direction was along the length of the trachea and the circumferential direction was defined to be around the circumference of the trachea. The excised tissue was cut in approximately 30 mm and 20 mm in longitudinal and circumferential directions, respectively. The tissues were placed in the biaxial device that has hooks attached to a pully system as reported previously (Nemavhola, 2017b; Nemavhola et al., 2021c; Nemavhola, 2021). Vernier calliper was utilised in capturing and measuring the thickness of the tissue in four different points where the average thickness was then utilised for further processing of engineering stresses and strains. Preconditioning was performed by applying 10 cycles of 10% strain per second. In order to remove tissue slack at the beginning of the tensile test, a preload of 10% at the strain rate of 0.001/second was applied. The values used in the preconditioning and preload were arrived at by trial and error in this on other samples during pre-test preparation. The tensile tester was operated in displacement control at a uniform strain rate of 0.025/second. Saline 0.91% w/v of NaCl was heated to 33 °C before the sample tissue is placed in the bath for mechanical testing (Ndlovu et al., 2020; Lebea et al., 2021; Ndlovu et al., 2021). A 0.005 N equi-biaxial preload was applied to both longitudinal and circumferential directions. Finally, the strain rate of 30% strain/10 s equi-biaxial loading and recovery was applied on the tissue.
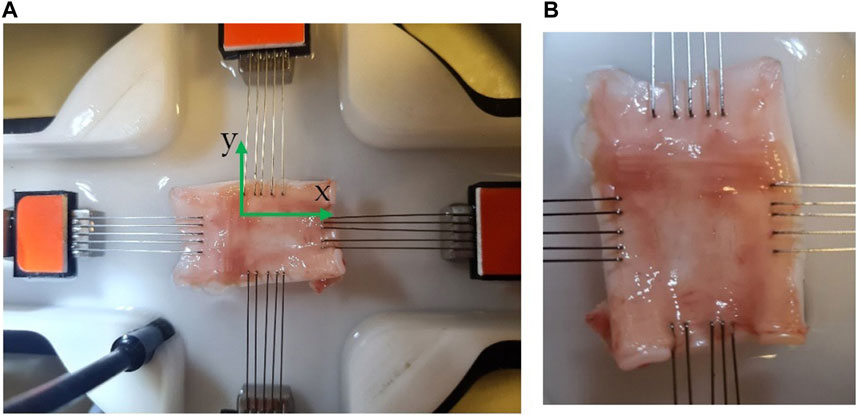
FIGURE 1. Experimental set-up of trachea subjected to biaxial tensile loading. (A) The 30 × 20 mm sheep trachea cut tissue hooked by the CellScale Biaxial testing system (BioTester 5,000 CellScalle, Wateroo, ON, Canada®) submerged in the with Saline 0.91% w/v of NaCl was heated to 33°C before the sample tissue is placed in the bath for mechanical testing (B) magnified sheep trachea cut tissue hooked at ∼ 26 × 15 mm. In (A), x indicates the longitudinal direction while y indicates the circumferential direction.
3 Theoretical formulations
3.1 Tissue stress-strain analysis
In this study the stresses were calculated through the first Piola-Kirchoff stress T in the two-directions using the equation:
The finite strains were calculated by the formula:
Where
FIGURE 2. Digrammatic representation of a body subjected to finite deformation showing (A) an unstretched specimen (B) biaxially stretched specimen and (C) Stress-strain direction undeformed and under different strain rate.
The calculated stress results are cut-off at 30% strain. These stress results however are noisy therefore they were further filtered with an 8-point moving average filter in Excel. The data were resampled and further smoothened using a quadratic function.
3.2 Constitutive modelling
The passive response of a biological soft tissue is more complex than the response of elastic solids due to the fact that they undergo finite deformations under mechanical loads (Fung, 1984; Fung, 1993). Thus, the passive phases of the tissues’ deformations are considered using the nonlinear theory of hyperelasticity. The most useful quantity in deriving the expressions for the passive response of materials that undergo finite deformation is the strain energy function (Fung, 1993). There is a huge number of variations of its implementation in the literature depending on different cases. In this study, we assume that the tracheal tissue is anisotropic and incompressible, therefore we apply and study the material parameters from six models, namely, the Fung, Choi-Vito, Holzapfel (2000), Holzapfel (2005), Polynomial (Anisotropic) and Four-Fiber Family models. In the following sections, these models are presented in terms of their strain energy functions.
3.2.1 The Fung model
The Fung model is a hyperelastic anisotropic material model for stress-strain description of arterial wall. It is phenomenological in nature and its incompressible form is given by (Chuong and Fung, 1983; Fung, 1984).
Where
3.2.2 Choi-Vito model
Choi-Vito model is hyperelastic anisotropic material model developed for canine pericardium. The model is fully phenomenological and formulated through the components of Green-Lagrange strain tensor. The model is implemented in an exponential format and its strain-energy function is expressed as (Choi and Vito, 1990).
Where
3.2.3 The Holzapfel (2000) model
This model is hyperelastic anisotropic material model for stress-strain description of arterial layers. It is constituted by forms of the strain energy function that represent isotropy and anisotropy. Thus, its strain energy function is given by (Holzapfel et al., 2000).
Where
3.2.4 The Holzapfel (2005) model
This model is a variation of the previous model also aimed at modelling stress-strain behaviour of hyperelastic anisotropic materials, specifically the arterial layers. It models the arterial walls as composite material with spirally arranged layers. Its strain energy function is expressed as (Holzapfel et al., 2005)
Where
3.2.5 The four-fiber family model
This model is hyperelastic anisotropic material model for stress-strain description of aortas and aneurysms. The model represents an elastin-dominated amorphous matrix reinforced by four families of (collagen) fibers (in axial, circumferential and diagonal directions) whose strain energy function is expressed as (Baek et al., 2007; Ferruzzi et al., 2011)
This model implements a hybrid polynomial and exponential format where
3.2.6 The polynomial (anisotropic) model
Like its name, this model is hyperelastic anisotropic material model whose strain energy function is expressed as a polynomial series of isotropic and anisotropic strain invariants given as (Bursa et al., 2008).
Where
3.3 Data analysis
In this study, we use the constrained optimisation by linear approximation algorithm (COBYLA (third party: SciPy)) implemented in Hyperfit software for fitting the equi-biaxial tensile experimental data of Fung, Choi-Vito, Holzapfel et al. (2000), Holzapfel et al. (2005), Polynomial (Anisotropic) and Four-Fiber Family hyperelastic constitutive models given in Eqs 3–(8). Five metrics that measure models’ performances are evaluated for each model. These metrics are coefficient of determination, correlation coefficient, Normalized Root Mean Square error, Normalised error, and evaluation index. Their expressions are given in Eqs 9–(14) below.
The coefficient of determination (R2) (also known as Nash-Sutcliffe coefficient) is defined as follows:
Where
The Evaluation Index (EI) is a critical parameter in evaluating how the hyperelastic constitutive model fits the experimental data, and is given by
where,
The Rminimum and Rmaximum represent the R values for poorest and best fitting hyperelastic models, respectively. EI in Eq. 11 is a comparative parameter whose values may span values between 0.0 for poorest fitting models, and 1.0 for best fitting models. Therefore, the higher the coefficient of determination (R2), the higher the model fit (EI).
The correlation coefficient (r) is defined as
Where
The Normalized Root Mean Square error (NRMSE) is defined as
The Normalised error (NE) is expressed as
3.4 Parameter Estimation
Minimisation of the error between the experimental (measured) and estimated stress in both longitudinal and circumferential directions using Eqs 3–(7) was performed to determine the constitutive parameters of each model. Sum of squares of difference (SS) was utilised as the objective function as follows:
With DIFF being the absolute difference:
W3 - is manual weight factor (for individual data-point)
W4 - is automatic weight factor (for normalization between the data-points)
4 Results
Stress-strain curves for the trachea muscle subjected to equi-biaxial tensile loading are plotted in Figure 3. The stress-strain curves for trachea muscle in Figure 3 show that the circumferential direction has a well-defined nonlinear behaviour as the tissue gets stretched from the toe region to 30% strain. At 30% strain, the tissue in the longitudinal direction still appears to be within the toe region with the stress-strain curve showing much more tissue compliance. The tracheal tissue in the longitudinal direction attains 30% strain below 50 kPa while the same level of strain is attained in the circumferential direction at stresses of about 100 kPa (double as much as that in the longitudinal direction). These findings are in line with previous studies by other researchers on the relatively higher stiffness of the tracheal tissue along the circumferential direction (Hoffman et al., 2016; Kaye et al., 2022) as compared to the longitudinal direction. Along the circumferential direction the toe region is only up to 15% strain as opposed to the 30% strain for the circumferential direction. The relationship between the stresses in the circumferential direction and those in the longitudinal direction are strikingly similar to the relationship between these stresses in a pressured thin-walled cylinder theory. The direct application of this theory in this study may be a little bit contentious because of an invalid ratio between the wall thickness and the diameter of the trachea which is approximately 1:2. It is therefore likely that the relationship between the stresses in the circumferential and longitudinal directions may only kick in after the diameter has stretched from the undeformed length of 8 mm to approximately 27 mm. However, in the present study, this was not actually the case, therefore, stiffer circumferential direction may have only been caused by the effect of the cartilaginous ring around the trachea wall which is aligned with the circumferential direction. A previous study (Safshekan et al., 2017) found that the cartilaginous rings in the trachea were stiffer towards the cranial regions than towards the caudal regions.
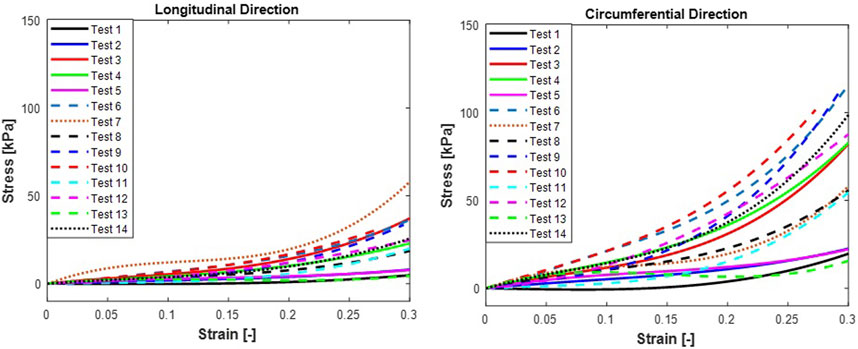
FIGURE 3. N = 14 sheep trachea subjected to equi-biaxial mechanical forces shoing stress vs. strain mechanical properties at 30% strain (A) Longitudinal and (B)Circumferential. Test 7 showing the highest stress and Test 1 showing the lowest stress in the longitudinal direction, respectively. Additionally, test 10 and Test 1 showing highest and lowest tress in the circumferential direction, respectively.
Before performing model fitting, we first examined the nature of the hyperelastic responses to determine a proper form of model for fitting the overall responses. To capture the observed large specimen variability, model fitting was performed for material responses at three stiffness levels, including the mean responses, the upper bound (UB) responses (mean responses + one standard deviations) and lower bound (LB) responses (mean response - one standard deviation). The LB, mean and UB parameter values are plotted in Tables 1–6 for each of the constitutive models in this study. These mean values of parameters were then applied to the respective models to calculate the mean stresses. Figure 4–8 show these model-estimated mean stresses plotted over the measured mean stresses. The results are remarkably close for all the models under study. It is therefore appropriate to examine the metrics such as the coefficient of determination and evaluation index further to see if there are any significant trends in the performances of the six constitutive models.

TABLE 1. Material parameters of Fung hyperelastic constitutive models (b1, b2, b3, b4, b5 and b6) for different samples of sheep trachea subjected to equi-biaxial testing. Normalised Error (NE) and Normalised RMS Error (NRMSE) were also determined for all experimental samples.
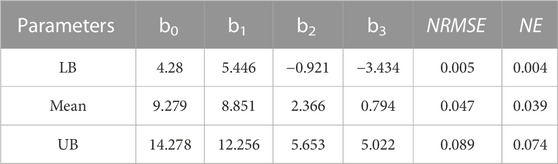
TABLE 2. Material parameters of Choi-Vito hyperelastic constitutive models (bo, b1, b2 and b3) obtained by simultaneous fitting to the mean, UB, and LB responses for diffreent samples of sheep trachea subjected to equi-biaxial testing. Normalised Error (NE) and Normalised RMS Error (NRMSE) were also determined for all experimental samples.

TABLE 3. Material parameters of Polynomial (Anisotropic) hyperelastic constitutive model (a1, a2, a3, b1, b2, b3, c2, c3, c4, c5, c6,
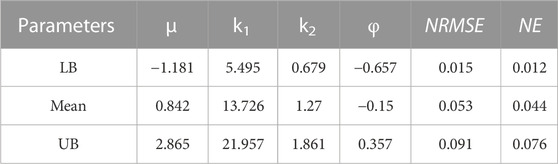
TABLE 4. Material parameters of Holzapfel (2000) hyperelastic constitutive model (

TABLE 5. Material parameters of Holzapfel (2005) hyperelastic constitutive models (

TABLE 6. Material parameters of Four-Fiber Family hyperelastic constitutive models (c, c11, c21, c12, c22, c134, c234 and
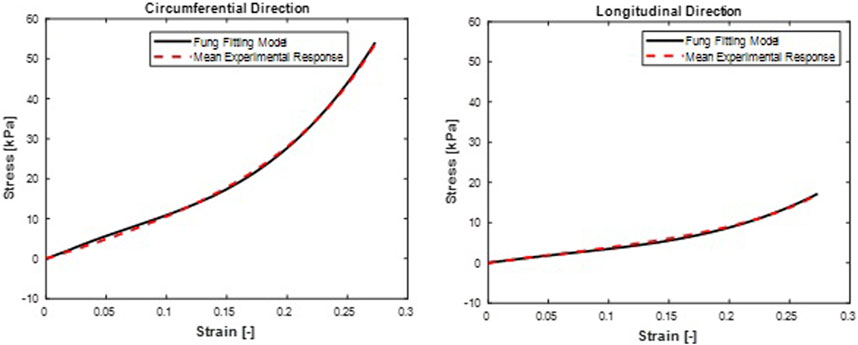
FIGURE 4. Mean stress-time histories in (A) Circumferential and (B) Longitudinal direction. Fung model fit curves were from a mean set of constitutive parameters fitted simultaneously to the averaged responses of all specimens.
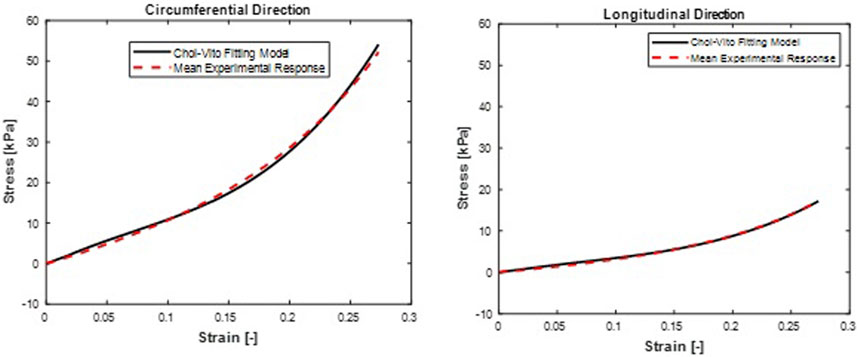
FIGURE 5. Mean stress-time histories in (A) Circumferential and (B) Longitudinal direction. Choi-Vito model fit curves were from a mean set of constitutive parameters fitted simultaneously to the averaged responses of all specimens.
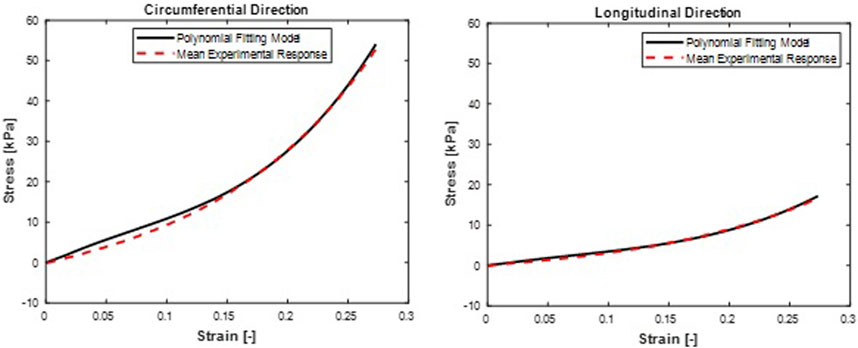
FIGURE 6. Mean stress-time histories in (A) Circumferential and (B) Longitudinal directions. Polynomial (Anisotropic) hyperelastic model fit curves were from a mean set of constitutive parameters fitted simultaneously to the averaged responses of all specimens.
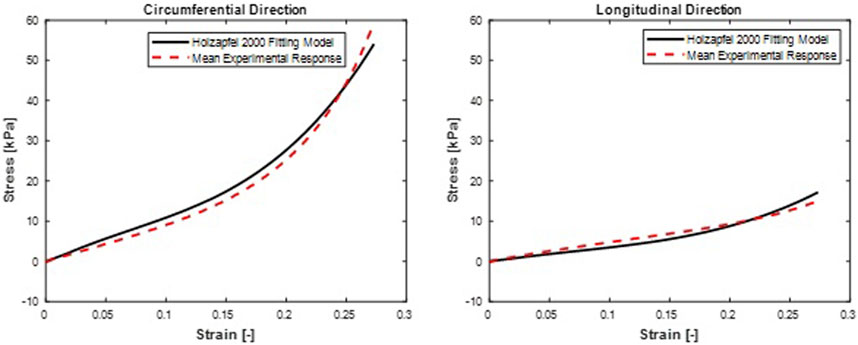
FIGURE 7. Mean stress-time histories in (A) Circumferential and (B) Longitudinal directions. Holzapfel et al. (2000) hyperelastic model fit curves were from a mean set of constitutive parameters fitted simultaneously to the averaged responses of all specimens.
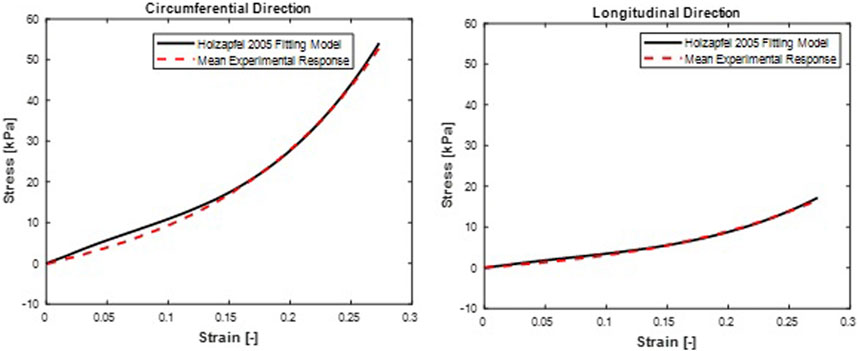
FIGURE 8. Mean stress-time histories in (A) Circumferential and (B) Longitudinal directions. Holzapfel et al. (2005) hyperelastic model fit curves were from a mean set of constitutive parameters fitted simultaneously to the averaged responses of all specimens.
The ranges of the standard deviations as represented by the LB and UB parameter values tabulated in Tables 1–6 show that all the material models vary widely from one test to another over the fourteen tests. The amount of standard deviation calculated for each material model is quite substantial. This emphasizes the probabilistic nature of tracheal tissue which shows that it is very hard to apply material parameters from one experiment to predict the tensile behaviour of a different tracheal tissue. As shown in a previous study by the authors, the most appropriate procedure is to use the average values, though such mean values will certainly yield substantial errors in some cases as can be observed in the wider ranges between LB and UB in this study. It is important however to note that these results were only calculated from the circumferential direction of the tracheal tissue.
In terms of anisotropy, it is extremely difficult to establish from this test the anisotropy of the tissue along the longitudinal direction since it appears that the tissue is still in its toe region. But along the circumferential direction, the tracheal tissue shows anisotropy. The tissue anisotropy grows with strain level in both directions although the circumferential direction is clearly more anisotropic from strain ranges greater than 15% strain. It is not clear what might have caused the extraneous stress-strain bevaviour of the specimen number 7 along the longitudinal direction, although its behaviour along the circumferential direction falls within the ranges of all the other specimen stress-strain curves.
Figures 9, 10 show the average values of the coefficient of determination (R2), the Normalized Root Mean Square Error (NRMSE), and the evaluation index (EI) that were calculated over all the fourteen tests for each of the six different hyperelastic models. The coefficient of detemination measures the correlation between the experimental and model results while the NRMSE gives an indication of the model fitting quality in terms of the fitting error. The EI is a metric that shows how the models fit the experimental results relative to each other. The plotted results show that the polynomial (anisotropic) model performs the best in both the average R2 and NRMSE values. Besides the highest and lowest levels of the mean for the R2 and NRMSE, the polynomial (anisotropic) model also yields the smallest deviations and outliers of its predictions away from the mean line in Figures 9, 10. With the exception of about three outliers, a large proporportion of the predicted results by the polynomial (anisotropic) model fall within the 95% confidence interval bounds.
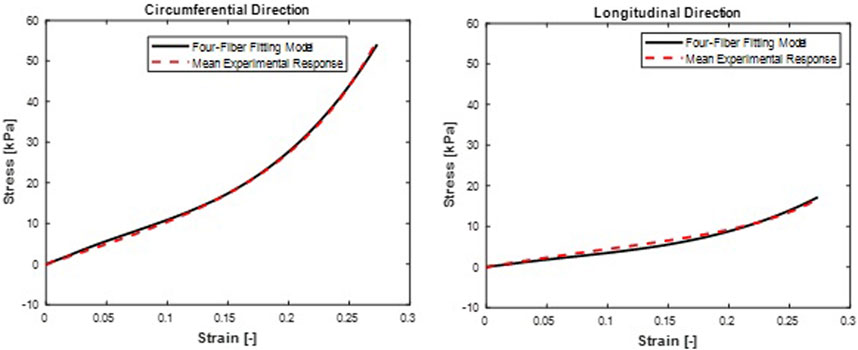
FIGURE 9. Mean stress-time histories in (A) Circumferential and (B) Longitudinal directions. Four-Fiber Family hyperelastic model fit curves were from a mean set of constitutive parameters fitted simultaneously to the averaged responses of all specimens.
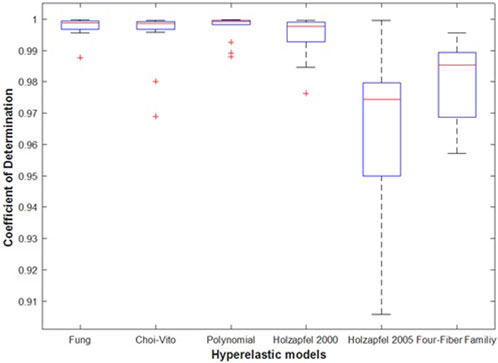
FIGURE 10. Average Coefficient of determination (R2) was determined using Eq. 9 for N = 14 of the sheep trachea soft tissue for Fung, Choi-Vito, Holzapfel et al. (2000), Holzapfel et al. (2005), Polynomial (Anisotropic) and Four-Fiber Family hyperelastic constitutive models. Holzapfel et al. (2005) hyperelastic constitutive model showing the highest variation of the average R2 and Polynomial (Anisotropic) hyperelastic model showing lowest value of variation.
In Figure 11 the average EI values show that the Fung model yields the best performance (at 100% EI) and that it slightly outperforms the polynomial (anisotropic) model (at around 95% EI). It is interesting to note that both models are implemented as polynomial functions of the material parameters. Of course, the Fung model exhibits a wider range of deviations away from the mean value in their predicted results. The Holzapfel (2005) model yields the worst performance with R2 greater than 95%, NRMSE below 20%, and EI equal to zero percent. Since EI is a measure of relative performance of the models, this performance of the Holzapfel (2005) cannot be considered disastrous since it still shows that it is capable of producing correlations above 95% and fitting errors of less than 20%. However, for better accuracy in the predictions of tensile behaviour of the tracheal tissue it might be recommended to apply the Fung or the polynomial (anisotropic) models which yield R2 greater than 99.9%, fitting errors NRMSE less than 5%, and EI above 95%. In Figure 12, the Choi-Vito and Holzapfel (2000) have modest performance in the EI at 70% while the four-fiber family yields EI of approximately 20%.
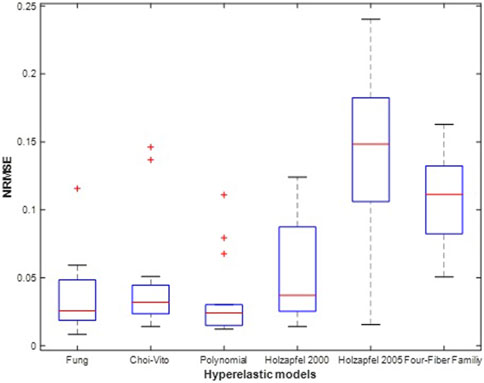
FIGURE 11. Average Normalised RMS Error (NRMSE)was determined using Eq. 13 for N = 14 of the sheep trachea soft tissue for Fung, Choi-Vito, Holzapfel et al. (2000), Holzapfel et al. (2005), Polynomial (Anisotropic) and Four-Fiber Family hyperelastic constitutive models. Holzapfel et al. (2005) hyperelastic constitutive model showing the highest variation of the average R2 and Polynomial (Anisotropic) hyperelastic model showing lowest value of variation.
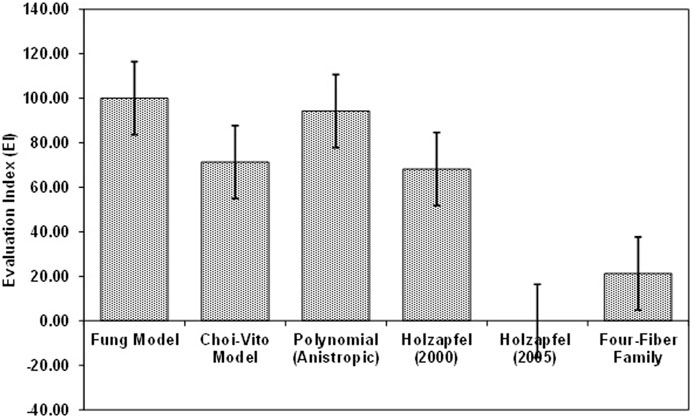
FIGURE 12. Average Evaluation Index (EI) for all Fung, Choi-Vito, Holzapfel et al. (2000), Holzapfel et al. (2005), Polynomial (Anisotropic) and Four-Fiber Family hyperelastic constitutive models. Holzapfel et al. (2005) hyperelastic constitutive model was found to have the lowest EI as compared to the other five model. Additionally, Fung hyperelastic constitutive model was found to have the highest EI when compared to other models. This means that for this biaxial tensile data, the Fung model has produced the best R2.
5 Discussion
The mechanical material properties of the sheep trachea were observed to be nonlinear anisotropic and hyperelastic material, similar to other biological soft tissues (Grillo, 1989). Biaxial testing is a reliable method utilised in understanding the mechanical behaviour of soft tissues (Nemavhola, 2017b; Nemavhola et al., 2021b; Nemavhola et al., 2021c; Nemavhola et al., 2021d; Ngwangwa et al., 2022). The data presented in this study covers the circumferential and longitudinal directions. It is observed that the best performing models are both based on the polynomial implementations having very high numbers of material parameters in their architectures. In our previous studies on soft tissues, the models with exponential implementations such as the two Holzapfel models have yielded much better predictions than the other material models and have always outperformed the Fung model. In this study, the results do not agree with that trend.
Secondly, the performance of the Choi-Vito model with respect to other models within the exponential implementation group is quite remarkable in this study. It performs as well as the Holzapfel et al. (2000) model clearly outperforms the Holzapfel et al. (2005) and the four-fiber family models. Both the Holzapfel et al. (2005) and the four-fiber family models were shown in the oesophagus tissue test to outperform the Choi-Vito model. Thus, for the tracheal tissues, the models that performed poorly in the oesophagus perform much better in the trachea. One of the distinctive features of the trachea is that it consists of rings of cartilaginous tissue embedded within its cylindrical walls. This implies that besides its normal soft tissue which may be dominated by collagen type I, it has other forms of collagen types within its structure. The cartilage tissue is relatively rigid with much less percentage of elongation at fracture. It does not really possess much of the hyperelasticity of the other biological soft tissues. It possesses the property that is desirable for organs that must exhibit some rigidity, elasticity, and lubrication. It is this distinctive property that makes it different from the tensile behaviour of most soft tissues. However, it is not very clear in this study what makes the models such as the Choi-Vito and Fung models perform better than they have in the other soft tissues previously studied by the authors. An understanding of these underlying issues will inform the development of most effective replacement materials for the tracheal tissue.
The performance of the Holzapfel et al. (2005) model over the tracheal tissue is most unreliable. It yields the largest NRMSE value with the widest standard deviation. The polynomial (anisotropic) model produces the most consistent results and therefore is shown to be the most reliable. However, its debilitating character is that it requires the largest number of material parameters which obviously affects its convergence rate, thereby making the model the slowest and most computationally expensive model of the six material models studied in this research. Therefore, a researcher is more likely to opt for the Choi-Vito or the Fung models with relatively fewer numbers of required material parameters than the polynomial (anisotropic) model.
In its normal physiological functioning, the trachea is not subjected to excessive mechanical loads in any of these directions. It is rather subjected to very low gauge pressure which may cause stresses well below the limit of its toe region, which were calculated as 3.3 kPa in tension during inspiration, −5.25 kPa in compression during expiration and 7.2 kPa for mechanical ventilation (Malvè et al., 2011). However, there might be several traumatic situations and illnesses that subject the tracheal tissue to very high stresses in the circumferential, longitudinal, or radial directions. A comprehensive literature study of the published cases of tracheal replacement between 1898 and 2018 on 290 patients reported that a breakdown of large tracheal defects comprised cancerous tumour invasions (60.4%), airway trauma (6.7%), critical airway stenosis (7.8%), congenital stenosis (6.0%), tuberculosis (3.9%), prolonged intubation (3.9%), and other conditions (11.3%) (Greaney and Niklason, 2021; Zobaer and Sutradhar, 2021).
The higher tissue stiffness along the circumferential direction may be attributed to the effect of the rigid cartilaginous tissue which tends to be pulled axially outwards as opposed to the longitudinal direction where this tissue has no effect at all. It is therefore likely that tissue stretching along the longitudinal direction was stopped too early. Thus, differential straining may be a better way of testing the trachea than equi-biaxial stretching of the trachea tissue. This is to ensure that there is a fully developed stress-strain curve along the longitudinal direction. It might also be interesting to determine the impact of the cartilage fiber on the total tensile behaviour of the trachea tissue by testing that fiber alone.
The comprehensive material characterization of trachea, as provided in this study, lays a foundation for further investigations aimed at contrasting healthy and diseased tracheal conditions. Such comparisons offer deeper insights into how the trachea undergoes changes and remodeling in response to various pathological states. By comprehensively examining the material properties, this research significantly contributes to advancing our understanding of tracheal repair mechanisms. Moreover, this knowledge serves as a pivotal guide in exploring innovative strategies for addressing tracheal ailments, potentially revolutionizing treatments and interventions in respiratory health.
The key findings of the study reveal the tracheal tissue’s greater stiffness along the circumferential versus longitudinal direction and regional material property variations. However, regional dependencies of the trachea were not explored. The limitation of the study is the lack of cross-sectional image analysis during experimentation which might lead to testing errors, potentially affecting results. Stress distribution assumptions during biaxial tests and unexamined effects of BioRakes’ hooking positions pose limitations. Quantitative investigation into the influence of cartilaginous rings on circumferential stiffness is lacking. Although not explored, the calculated model parameters offer promise for computational models, regenerative medicine, and bioprinting applications in tracheal tissue replacement. Integrating microstructural study comparisons could further enrich these findings.
6 Patents
This study presents the measured mechanical properties of ex-vivo sheep trachea under biaxial loading. The mechanical data was further utilized for fitting the selected hyperelastic constitutive models. The study has two important findings: firstly, the sheep tracheal tissue is about twice as stiff along its circumferential direction as it is along its longitudinal direction; secondly, the material properties of the sheep tracheal tissue in the different regions are random and different from one another. It would be very interesting if regional dependencies of these material properties were evaluated. Besides the above limitation, the authors believe that the study would have benefitted a lot from correlating these findings with microstructural examinations. Nonetheless, it is believed that the calculated constitutive model parameters will provide more light on the development of accurate computational models for the study of various diseases or medical conditions that affect the trachea. Also, the data presented here will be useful in regenerative medicine and bioprinting of tissue replacements.
Limitations: The detailed cross-sectional image analysis of the trachea was not performed during experimentation. This may have caused or introduced errors during tensile testing since relative slipping of layers could have easily occurred.
During the experiment, uniform stress distribution was assumed in the biaxial tests, but this is highly hypothetical since in reality it is expected that there will be stress concentrations at the hooking positions of the BioRakes whose effects have not been investigated in this study.
The effect of the cartilaginous ring tissue along the circumferential direction has not been quantitatively investigated in this study. It might have contributed to the stiffness in the circumferential direction.
The results in this study were not compared with the results of microstructural studies on sheep tracheal tissue.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.
Ethics statement
The animal study was approved by the UNISA-CAES health research ethics committee - ref 2021/caes_hrec/103. The study was conducted in accordance with the local legislation and institutional requirements.
Author contributions
TP, HN, and FN contributed to conception, design, data acquisition, analysis, and interpretation, drafted the manuscript, HN, TP, and FN contributed to the interpretation of the data and critically revised the manuscript, and finally FN, HN, and TP contributed to conception, design, data analysis, and interpretation, drafted and critically revised the manuscript. All authors contributed to the article and approved the submitted version.
Funding
Support from the National Research Foundation (NRF) Grant number (129380) is gratefully acknowledged. Unisa CAPEX Programme supported the acquisition of biaxial testing machine in the Department of Mechanical Engineering, School of Engineering, College of Science Engineering and Technology.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Baek, S., Gleason, R., Rajagopal, K., and Humphrey, J. (2007). Theory of small on large: potential utility in computations of fluid–solid interactions in arteries. Comput. methods Appl. Mech. Eng. 196 (31-32), 3070–3078. doi:10.1016/j.cma.2006.06.018
Belsey, R. (1950). Resection and reconstruction of the intrathoracic trachea. Br. J. Surg. 38 (150), 200–205. doi:10.1002/bjs.18003815008
Bursa, J., Skacel, P., Zemanek, M., and Kreuter, D. (2008). “Implementation of hyperelastic models for soft tissues in FE program and identification of their parameters,” in Proceedings of the Sixth IASTED International Conference on Biomedical Engineering, Innsbruck, Austria, 13-15 February 2008.
Choi, H. S., and Vito, R. (1990). Two-dimensional stress-strain relationship for canine pericardium. J. biomechanical Eng. 112 (2), 153–159. doi:10.1115/1.2891166
Chuong, C., and Fung, Y. (1983). Three-dimensional stress distribution in arteries. J. biomechanical Eng. 105 (3), 268–274. doi:10.1115/1.3138417
DeBoer, E. M., Kimbell, J. S., Pickett, K., Hatch, J. E., Akers, K., Brinton, J., et al. (2021). Lung inflammation and simulated airway resistance in infants with cystic fibrosis. Respir. Physiology Neurobiol. 293, 103722. doi:10.1016/j.resp.2021.103722
Ferruzzi, J., Vorp, D. A., and Humphrey, J. (2011). On constitutive descriptors of the biaxial mechanical behaviour of human abdominal aorta and aneurysms. J. R. Soc. Interface 8 (56), 435–450. doi:10.1098/rsif.2010.0299
Fung, Y. (1984). Structure and stress-strain relationship of soft tissues. Am. Zoologist 24 (1), 13–22. doi:10.1093/icb/24.1.13
Greaney, A. M., and Niklason, L. E. (2021). The history of engineered tracheal replacements: interpreting the past and guiding the future. Tissue Eng. Part B Rev. 27 (4), 341–352. doi:10.1089/ten.teb.2020.0238
Grillo, H. C. (1989). Notes on the windpipe. Ann. Thorac. Surg. 47 (1), 9–26. doi:10.1016/0003-4975(89)90227-0
Grillo, H. C. (2002). Tracheal replacement: a critical review. Ann. Thorac. Surg. 73 (6), 1995–2004. doi:10.1016/s0003-4975(02)03564-6
Grillo, H. C., Donahue, D. M., Mathisen, D. J., Wain, J. C., and Wright, C. D. (1995). Postintubation tracheal stenosis: treatment and results. J. Thorac. Cardiovasc. Surg. 109 (3), 486–493. doi:10.1016/s0022-5223(95)70279-2
Hoffman, B., Martin, M., Brown, B. N., Bonassar, L. J., and Cheetham, J. (2016). Biomechanical and biochemical characterization of porcine tracheal cartilage. Laryngoscope 126 (10), E325–E331. doi:10.1002/lary.25861
Holzapfel, G. A., Gasser, T. C., and Ogden, R. W. (2000). A new constitutive framework for arterial wall mechanics and a comparative study of material models. J. Elast. Phys. Sci. solids 61 (1), 1–48. doi:10.1023/a:1010835316564
Holzapfel, G. A., Sommer, G., Gasser, C. T., and Regitnig, P. (2005). Determination of layer-specific mechanical properties of human coronary arteries with nonatherosclerotic intimal thickening and related constitutive modeling. Am. J. Physiology-Heart Circulatory Physiology 289 (5), H2048–H2058. doi:10.1152/ajpheart.00934.2004
Huang, C.-J. (2001). Use of the silicone T-tube to treat tracheal stenosis or tracheal injury. Ann. Thorac. Cardiovasc. Surg. 7 (4), 192–196.
Kaye, R., Cao, A., Goldstein, T., Grande, D. A., Zeltsman, D., and Smith, L. P. (2022). Biomechanical properties of the ex vivo porcine trachea: a benchmark for three-dimensional bioprinted airway replacements. Am. J. Otolaryngology 43 (1), 103217. doi:10.1016/j.amjoto.2021.103217
Kojima, K., and Vacanti, C. A. (2014). Tissue engineering in the trachea. Anatomical Rec. 297 (1), 44–50. doi:10.1002/ar.22799
Koombua, K., and Pidaparti, R. M. (2008). Inhalation induced stresses and flow characteristics in human airways through fluid-structure interaction analysis. Model. Simul. Eng. 2008, 1–8. doi:10.1155/2008/358748
Kortsmit, J., Davies, N. H., Miller, R., Macadangdang, J. R., Zilla, P., and Franz, T. (2013). The effect of hydrogel injection on cardiac function and myocardial mechanics in a computational post-infarction model. Comput. Methods Biomechanics Biomed. Eng. 16 (11), 1185–1195. doi:10.1080/10255842.2012.656611
Lebea, L., Ngwangwa, H., Pandelani, T., and Nemavhola, F. (2021). Biomechanical behaviour and hyperelastic model parameters identification of sheep omasum. Res. Square. doi:10.21203/rs.3.rs-1015547/v1
Lee, J. S. J., Park, J., Shin, D. A., Ryu, Y. J., Kim, H. C., Lee, J. C., et al. (2019). Characterization of the biomechanical properties of canine trachea using a customized 3D-printed apparatus. Auris Nasus Larynx 46 (3), 407–416. doi:10.1016/j.anl.2018.10.010
Malvè, M., Pérez del Palomar, A., Trabelsi, O., López-Villalobos, J., Ginel, A., and Doblaré, M. (2011). Modeling of the fluid structure interaction of a human trachea under different ventilation conditions. Int. Commun. heat mass Transf. 38 (1), 10–15. doi:10.1016/j.icheatmasstransfer.2010.09.010
Masithulela, F. (2015a). “The effect of over-loaded right ventricle during passive filling in rat heart: a biventricular finite element model,” in ASME international mechanical engineering congress and exposition (American Society of Mechanical Engineers).
Masithulela, F. (2015b). “Analysis of passive filling with fibrotic myocardial infarction,” in ASME international mechanical engineering congress and exposition (American Society of Mechanical Engineers).
Masithulela, F. (2015c). “The effect of over-loaded right ventricle during passive filling in rat heart: a biventricular finite element model,” in ASME 2015 international mechanical engineering congress and exposition.
Masithulela, F. (2016a). Bi-ventricular finite element model of right ventricle overload in the healthy rat heart. Bio-medical Mater. Eng. 27 (5), 507–525. doi:10.3233/bme-161604
Masithulela, F. J. (2016b). Computational biomechanics in the remodelling rat heart post myocardial infarction.
Ndlovu, Z., Desai, D., Nemavhola, F., and Ngwangwa, H. M. (2021). Sheep sclera soft tissue subjected to mechanical equi-biaxial testing. Preprints, 2021080388. doi:10.20944/preprints202108.0388.v1
Ndlovu, Z., Nemavhola, F., and Desai, D. (2020). Biaxial Mechanical Characterization And Constitutive Modelling Of Sheep Sclera Soft Tissue. Russ. J. Biomechanics/Rossijski Zurnal Biomehaniki 24 (1).
Nemavhola, F. (2017a). Fibrotic infarction on the LV free wall may alter the mechanics of healthy septal wall during passive filling. Bio-medical Mater. Eng. 28 (6), 579–599. doi:10.3233/bme-171698
Nemavhola, F. (2017b). Biaxial quantification of passive porcine myocardium elastic properties by region. Eng. Solid Mech. 5 (3), 155–166. doi:10.5267/j.esm.2017.6.003
Nemavhola, F. (2019a). Detailed structural assessment of healthy interventricular septum in the presence of remodeling infarct in the free wall–A finite element model. Heliyon 5 (6), e01841. doi:10.1016/j.heliyon.2019.e01841
Nemavhola, F. (2019b). Mechanics of the septal wall may be affected by the presence of fibrotic infarct in the free wall at end-systole. Int. J. Med. Eng. Inf. 11 (3), 205–225. doi:10.1504/ijmei.2019.101632
Nemavhola, F. (2021). Study of biaxial mechanical properties of the passive pig heart: material characterisation and categorisation of regional differences. Int. J. Mech. Mater. Eng. 16 (1), 6–14. doi:10.1186/s40712-021-00128-4
Nemavhola, F., Ngwangwa, H. M., and Pandelani, T. (2021a). An investigation of uniaxial mechanical properties of excised sheep heart muscle fibre–fitting of different hyperelastic constitutive models. Preprints, 2021080566 Available at: https://www.preprints.org/manuscript/202108.0566/v1.
Nemavhola, F., Ngwangwa, H., Pandelani, T., Davies, N., and Franz, T. (2021b). Understanding regional mechanics of rat myocardia by fitting hyperelatsic models. Res. Square. Preprint (Version 1). doi:10.21203/rs.3.rs-957393/v1
Nemavhola, F., Ngwangwa, H., Davies, N., and Franz, T. (2021c). Passive biaxial tensile dataset of three main rat heart myocardia: Left ventricle, mid-wall and right ventricle. Preprints, 2021080153. doi:10.20944/preprints202108.0153.v1
Nemavhola, F., Pandelani, T., and Ngwangwa, H. (2021d). FITTING OF HYPERELASTIC CONSTITUTIVE MODELS IN DIFFERENT SHEEP HEART REGIONS BASED ON BIAXIAL MECHANICAL PROPERTIES. Available at: https://www.biorxiv.org/content/10.1101/2021.10.28.466240v1.
Ngwangwa, H., and Nemavhola, F. (2021). Evaluating computational performances of hyperelastic models on supraspinatus tendon uniaxial tensile test data. J. Comput. Appl. Mech. 52 (1), 27–43. doi:10.22059/jcamech.2020.310491.559
Ngwangwa, H., Nemavhola, F., Pandelani, T., Msibi, M., Mabuda, I., Davies, N., et al. (2022). Determination of cross-directional and cross-wall variations of passive biaxial mechanical properties of rat myocardia. Processes 10 (4), 629. doi:10.3390/pr10040629
Ngwangwa, H. M., Pandelani, T., and Nemavhola, F. (2021). The application of standard nonlinear solid material models in modelling the tensile behaviour of the supraspinatus tendon. 2021080298. Preprints Available at: https://www.preprints.org/manuscript/202108.0298/v1/download.
Qi, S., Li, Z., Yue, Y., van Triest, H. J., and Kang, Y. (2014). Computational fluid dynamics simulation of airflow in the trachea and main bronchi for the subjects with left pulmonary artery sling. Biomed. Eng. online 13 (1), 85–15. doi:10.1186/1475-925x-13-85
Roberts, C. R., Rains, J. K., Paré, P. D., Walker, D. C., Wiggs, B., and Bert, J. L. (1997). Ultrastructure and tensile properties of human tracheal cartilage. J. biomechanics 31 (1), 81–86. doi:10.1016/s0021-9290(97)00112-7
Sáez, P., and Kuhl, E. (2016). Computational modeling of acute myocardial infarction. Comput. methods biomechanics Biomed. Eng. 19 (10), 1107–1115. doi:10.1080/10255842.2015.1105965
Safshekan, F., Tafazzoli-Shadpour, M., Abdouss, M., Behgam Shadmehr, M., and Ghorbani, F. (2017). Investigation of the mechanical properties of the human tracheal cartilage. Tanaffos 16 (2), 107–114.
Shukla, R. K., Srivastav, V. K., Paul, A. R., and Jain, A. (2020). Fluid structure interaction studies of human airways. Sādhanā 45, 1–6. doi:10.1007/s12046-020-01460-9
Skatulla, S., Legner, D., Rama, R. R., Mbewu, J., Sansour, C., Davies, N., et al. (2013). “Computational study of the injection therapy for myocardial infarction during the necrotic stage,” in Proceedings of 3rd South-East European conference on computational mechanics, Kos Island, Greece, 12–14.
Wall, W. A., and Rabczuk, T. (2008). Fluid–structure interaction in lower airways of CT-based lung geometries. Int. J. Numer. Methods Fluids 57 (5), 653–675. doi:10.1002/fld.1763
Keywords: biaxial biomechanical behavior, sheep trachea, trachea mechanics, biaxial testing, constitutive material models
Citation: Pandelani T, Ngwangwa H and Nemavhola F (2023) Experimental analysis and biaxial biomechanical behaviour of ex-vivo sheep trachea. Front. Mater. 10:1230789. doi: 10.3389/fmats.2023.1230789
Received: 29 May 2023; Accepted: 04 December 2023;
Published: 22 December 2023.
Edited by:
Luca Valentini, University of Perugia, ItalyReviewed by:
Milos Kojic, Houston Methodist Research Institute, United StatesIrene Chiesa, University of Pisa, Italy
Copyright © 2023 Pandelani, Ngwangwa and Nemavhola. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Thanyani Pandelani, ZXBhbmRldEB1bmlzYS5hYy56YQ==
 Thanyani Pandelani
Thanyani Pandelani Harry Ngwangwa1
Harry Ngwangwa1