- 1Shandong High-Speed Infrastructure Construction Co., Ltd., Jinan, China
- 2School of Qilu Transportation, Shandong University, Jinan, China
- 3Shandong Hi-Speed Jiwei Expressway Co., Ltd., Jinan, China
- 4School of Safety Engineering and Emergency Management, Shijiazhuang Tiedao University, Jinan, China
Early damage to asphalt pavements generally occurs due to the increasing traffic flow and the loads of vehicles, coupled with alternating high- and low-temperature cycles, freeze–thaw cycles, ultraviolet radiation, and other harsh environments. Several types of distress, such as rutting, cracking, and other damage, deteriorate the serviceability of asphalt pavements and shorten the road service life. Thus, the long-term structural mechanical response of asphalt pavements under the influence of loads and the environment is crucial data for the road sector, which provides guidance about road maintenance. Effectively processing the pavement dynamic monitoring data is a prerequisite to obtain the dynamic response of asphalt pavement structures. However, the dynamic monitoring data of pavements are often characterized by transient weak signals with strong noises, making it challenging to extract their essential characteristics. In this study, wavelet decomposition and reconstruction methods were applied to reduce the noise of pavement dynamic response data. The parameters of the signal-to-noise ratio (SNR) and root mean square error (RMSE) were introduced to compare and analyze the effect of the decomposition of two different wavelet functions: the symlet (sym) wavelet function and the Daubechies (db) wavelet function. The results showed that both the sym and db wavelet functions can effectively obtain the average similarity information and the detailed information of the dynamic response signals of the pavement, the SNR after the sym wavelet fixed-threshold denoising process is relatively higher, and the RMSE is smaller than that of the db wavelet. Thus, wavelet transformation exhibits good localization properties in both the time and frequency domains for processing pavement dynamic monitoring data, making it a suitable approach for handling massive pavement dynamic monitoring data.
1 Introduction
The increasing demand for fast and convenient transportation has resulted in the need for intelligent road infrastructure. This infrastructure heavily relies on the application of digital transport systems and road monitoring information support (Wang and Wang, 2019). Previous studies have mainly relied on macroscopic road surface investigations and non-destructive testing techniques to evaluate asphalt pavement performance. However, asphalt pavements are subjected to various factors, such as external loads, temperature, and humidity. To monitor the dynamic response and internal environmental information of pavement structures, researchers have used fiber-optic grating sensors and resistance-type sensors, enabling the monitoring of pavement dynamics and environmental changes. This information helps us in the understanding of the relationship between load and pavement performance, providing valuable insights about road maintenance (Liu and Qin, 1998).
Mechanical parameters, including stress and strain, are essential for the pavement design, according to the Chinese Specifications for Design of Highway Asphalt Pavement (Ministry of Transport of the People’s Republic of China, 2017; Li and Ji, 2019). Researchers have attempted to obtain the mechanical response of asphalt pavement interlayers. Embedded sensors in layered structures have proven effective in monitoring these parameters and capturing their dynamic response. For example, Guan and Zhuang (2012) measured road strain–stress signals using asphalt strain gauges and earth pressure boxes, analyzing the dynamic strain and compressive stress in different layers. Liu and Li (2017) collected asphalt pavement strain data using I-beam strain sensors and developed software for post-processing. Yang and Wang (2010) investigated the dynamic strain response of asphalt layers under heavy loads and temperature effects. Wei and Wang (2009) measured strain data under different loads and analyzed the response using resistance strain sensors. Several other studies have also explored strain sensor arrangements and have developed monitoring systems for asphalt pavements (Tan and Li, 2017; Cornaggia et al., 2022).
Various signal processing techniques have been utilized in pavement research studies. For instance, Hui et al. (2023) and Hui and Yu (2023) used fast Fourier transform (FFT) to analyze acoustic emission signals and characterize asphalt damage patterns. Jiang and Nie (2015) applied wavelet decomposition and reconstruction filtering to reduce vibration noise in the output signal of a fiber-optic gyroscope. Wavelet-based methods have also been utilized in pavement identification, adhesion coefficient estimation, and crack detection (Sun et al., 2011; Golestani et al., 2013; Devi et al., 2022). However, previous studies have lacked effective preprocessing, real-time analysis, and feature extraction methods for handling large-scale pavement monitoring data. Accurate processing of dynamic monitoring data is crucial for the understanding of the dynamic response of asphalt pavements, as road dynamic signals are weak and transient and often accompanied by significant noise. In this context, traditional Fourier filtering techniques are not suitable due to the non-smooth nature of the signals. Wavelet transformation emerges as a suitable approach for processing extensive monitoring data in asphalt pavements.
Symmetrical wavelets, also known as orthogonal wavelets or biorthogonal wavelets, are a class of wavelet functions that exhibit symmetry properties (Powers, 2022). Unlike other types of wavelets, symmetrical wavelets possess both symmetry and anti-symmetry characteristics (Gossler et al., 2022). These wavelets are designed to have equal energy distribution in their positive and negative frequency components (Banerjee and Bhowmik, 2022). The key characteristic of symmetrical wavelets is their ability to provide a balanced representation of both high-frequency and low-frequency components of a signal (Bairwa and Rathod, 2022). This property makes them particularly useful for analyzing signals with symmetric properties or those that require a balanced representation of positive and negative values. In practical terms, the use of symmetrical wavelets in signal processing allows for an accurate and stable analysis of signals, as they can capture both fine details and global trends in a signal (Ghobber and Mejjaoli, 2023). They are commonly utilized in various applications, including image processing, audio and speech analysis, data compression, and time–frequency analysis. The symmetric properties of these wavelets enable efficient filtering of signals, noise reduction, feature extraction, and decomposition of signals into different frequency components. They provide a versatile tool for analyzing and processing signals in both the time and frequency domains (Ke et al., 2023). In the context of pavement engineering and maintenance, the application of symmetrical wavelets in signal processing can help extract meaningful information from dynamic response signals obtained from field testing (Janani et al., 2022). Through symmetrical wavelet analysis, the method proposed in this study can effectively remove noise and enhance the accuracy and clarity of the pavement’s dynamic behavior representation, enabling a better understanding of its performance and facilitating decision-making in pavement engineering practices (Mallat, 1989; Zeng, 2007; Qin, 2014; Shao and Bai, 2014; Zhang, 2016; Tulup, 2021).
This paper focuses on the application of wavelet decomposition and reconstruction techniques to process dynamic response signals obtained from field testing of asphalt pavements. By removing high-frequency noise, the processed signals provide a clearer and more accurate representation of the pavement’s dynamic behavior. We introduce the signal-to-noise ratio (SNR) and root mean square error (RMSE) as evaluation parameters for comparing two different wavelet functions: the symlet (sym) wavelet function and Daubechies (db) wavelet function. The effectiveness of the proposed method is validated through the experimental analysis and comparison with traditional signal processing techniques. The processed data lay a valuable foundation for further analysis and decision-making in pavement engineering and maintenance.
2 Engineering background and data source
2.1 Engineering background
The original monitoring data of this study were collected from an urban road in Jinan, Shandong. Sensors were directly laid on a semi-rigid road base, and asphalt strain gauges were arranged outside of the lane. The applied sensors were coefficient-calibrated, and data acquisition was verified to be stable. The temperature and humidity sensors were, respectively, arranged between a 6-cm AC-20 asphalt mixture layer and an 8-cm AC-25 pavement layer and a 13-cm LSPM-30 base and an 18-cm cement-stabilized gravel base. A spacing of 60 cm was set between the sensors. The pavement structure and sensor layout are illustrated in Figure 1. The asphalt layer bottom sensor is grounded and shielded by the instrument, and the noise base fluctuates by only 1–3 uε to meet the acquisition conditions.

FIGURE 1. Diagram of the road surface structure and sensor placement. (A) Diagram of the asphalt pavement structure; (B) sensor location; and (C) diagram of sensor placement.
2.2 Field testing
The testing vehicle was a 6.8-m two-axle flatbed truck manufactured by Dongfeng, and the tire inflation pressure was 1.2 MPa during the test. A controlled axle weight of 10 t was set for the rear axle of the two-axle truck (single-axle twin wheelset, Figure 2B). The front-axle weight was weighed and recorded (2.8 t). The dynamic response signals of the pavement were recorded using a high-frequency data acquisition system with multiple measurement functions, solid-state relay modules, and scanning speeds of up to 800 channels/second.

FIGURE 2. Field testing area and load-controlled vehicle. (A) Test section; (B) two-axle truck loaded with sand.
2.3 Dynamic pavement response signal acquisition under loading
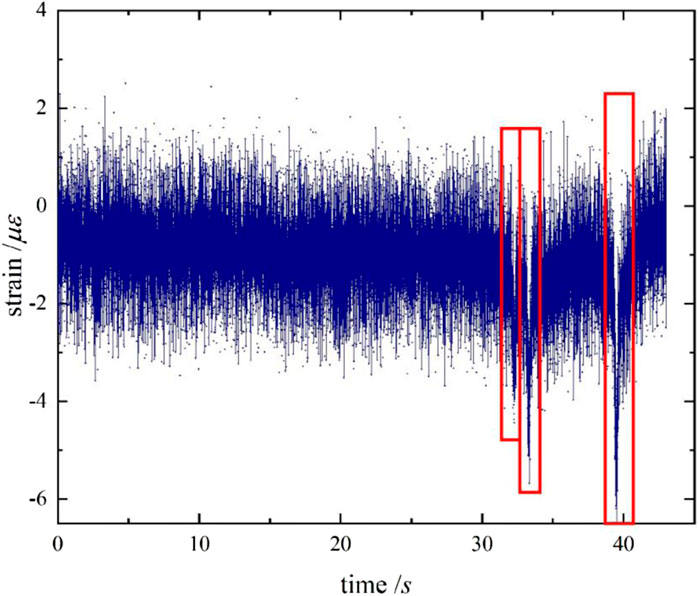
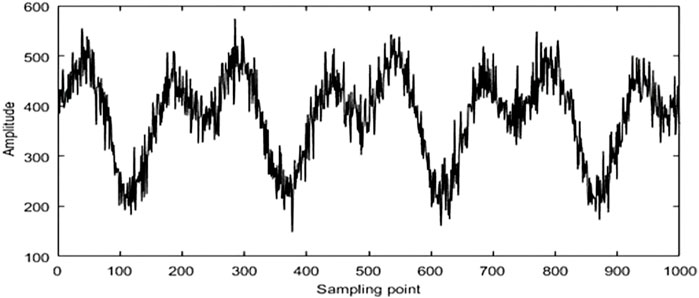
A dynamic load appears when the original signal of the pavement dynamic response amplitude changes with time, as shown in Figure 3. The horizontal coordinate is the time, and the vertical coordinate is the signal amplitude. The waveform graph shows that the collected pavement dynamic response signal base fluctuation is large; the data that appeared in the three peaks are the response signals when the wheels pass through the sensor. The fluctuation region noise interference is more serious, which almost covers the characteristic peak. The noise seriously affects the subsequent pavement monitoring work, which needs to be reduced.
3 Signal processing based on wavelet decomposition and reconstruction
3.1 Wavelet decomposition and reconstruction methods
The wavelet decomposition and reconstruction processing methods have the advantages of low entropy, multi-resolution, and decorrelation (Hui et al., 2023). Wavelet decomposition requires a priori knowledge of the signal frequency to determine the basic functions and decomposition levels, which decomposes the signal into a set of elementary functions called wavelets; these wavelets are obtained by scaling and shifting a prototype wavelet called the mother wavelet (Hui and Yu, 2023). We set the mother wavelet function ψ(t) with a scale factor of a and a translation factor of b; then, the wavelet analysis basis is defined as follows:
(1) Discrete wavelet transformation:
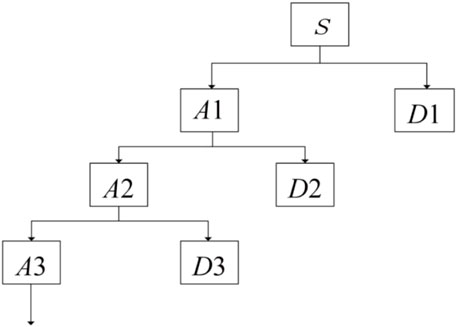
Mallat proposes an efficient algorithm for decomposing signals into approximate and detailed sequences (Sun et al., 2011). The wavelet decomposition process is shown in Figure 4, where S denotes the original signal, A denotes the approximate or low-frequency signal, and D denotes the detailed or high-frequency signal, with each level dividing the low-frequency signal into a high-frequency signal and a low-frequency signal.
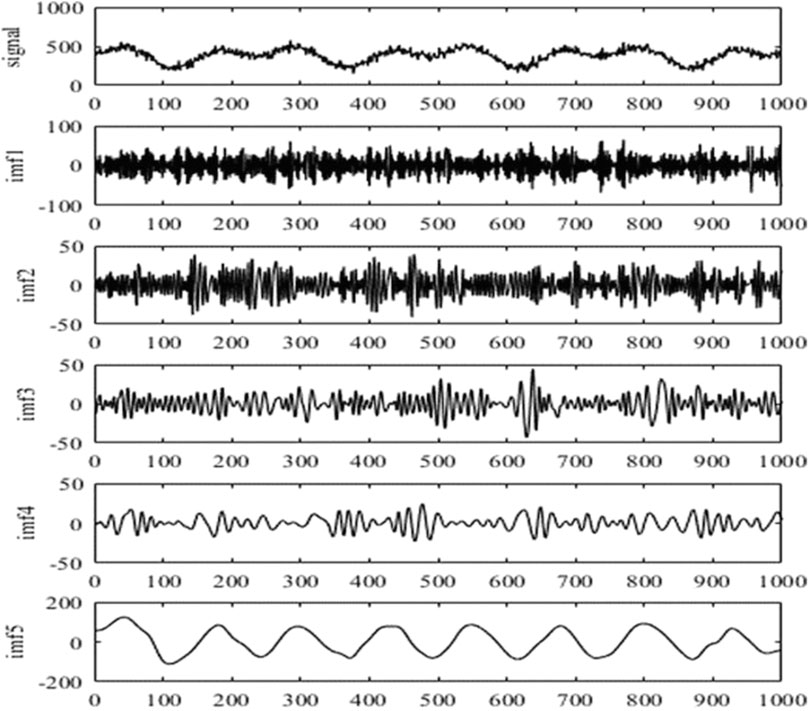
It is noteworthy that the decomposition level L and the number of samples N should satisfy the relationship 2L≤N. The decomposed signal consists of the approximation of level l and the details from level 1 to level l. Figure 5 shows the approximate sequence a containing the lower frequency signal and the detailed sequence d∼f containing the higher frequency signal, obtained after the four-layer wavelet decomposition of the road response monitoring signal collected in this paper. It can be seen that after four layers of wavelet decomposition, the high-frequency noise signal is decomposed layer by layer, and the low-frequency effective pavement response signal obtained retains the whole dynamic response characteristics of the pavement generated by the three-axle truck and can proceed to the next step.
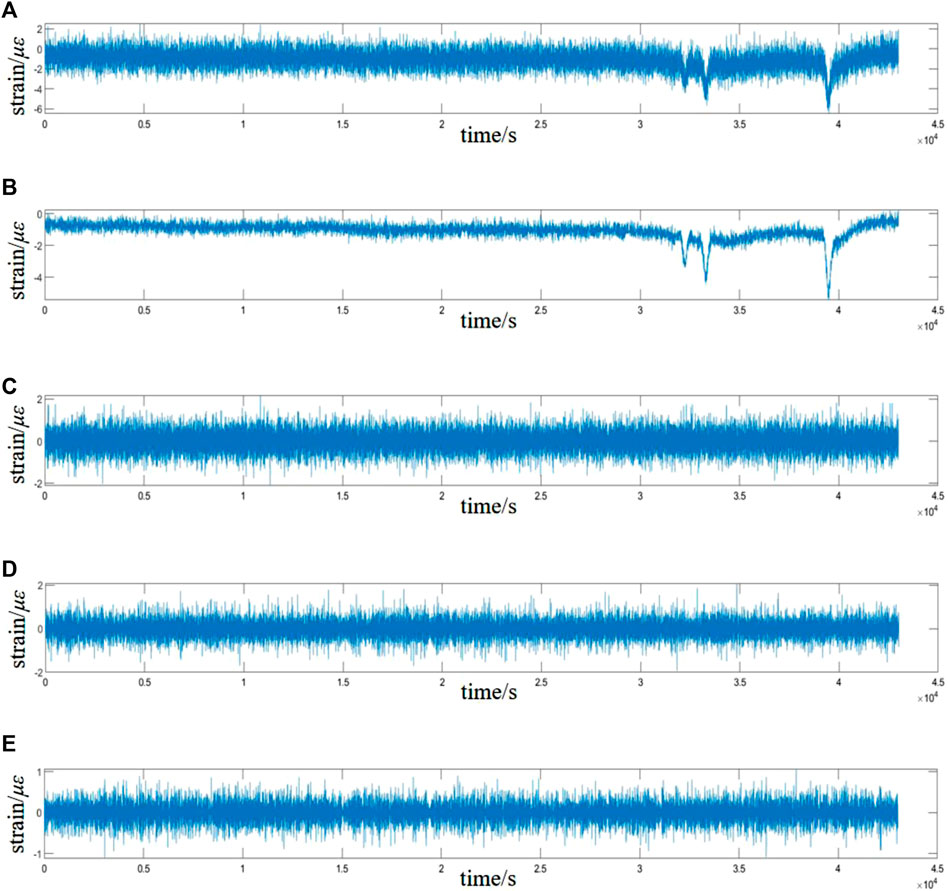
FIGURE 5. Four-layer wavelet decomposition result. (A) Original monitoring data; (B) approximate sequence a; (C) approximate sequence d; (D) approximate sequence e; (E) approximate sequence f.
The discrete wavelet transformation (DWT) discretizes the scale and translation parameters to the power of 2 and averages the time discretization usually using binary wavelet decomposition and reconstruction, with discretized scale times of 2, 4, 6, 8, and 2n (the sampling rate is required to satisfy Nyquist’s sampling theorem), and is commonly used for the multi-resolution analysis of signals and signal decomposition and reconstruction, with the following equation:
At different scales and times, the scale function vector group and the wavelet function vector group are constructed, respectively, for the scale function vector space V and the wavelet function vector space W. At a certain level, the approximate, low-frequency information of the signal is obtained by the convolution of the signal in the scale space V and the detailed, high-frequency information of the signal is obtained by the convolution of the signal in the wavelet space W.
① Scale function:
② Wavelet function:
③ Threshold:
Common threshold selection methods, currently available, include unbiased risk estimation thresholds (rigrsure), fixed thresholds (sqtwolog), heuristic thresholds (heursure), and very large and very small thresholds (minimaxi). There are two categories of the four methods: one of them is the conservative principle; e.g., the rigrsure criterion and the minimaxi criterion are relatively conservative (only some of the coefficients are set to zero), and therefore, the method is suitable for high-frequency information that contains noise. The second is the non-conservative principle; e.g., the sqtwolog and heursure criteria, particularly the fixed-threshold (sqtwolog) method, which removes more noise, is therefore suitable for low-frequency information (Devi et al., 2022).
The mathematical formula for the generic threshold is
where
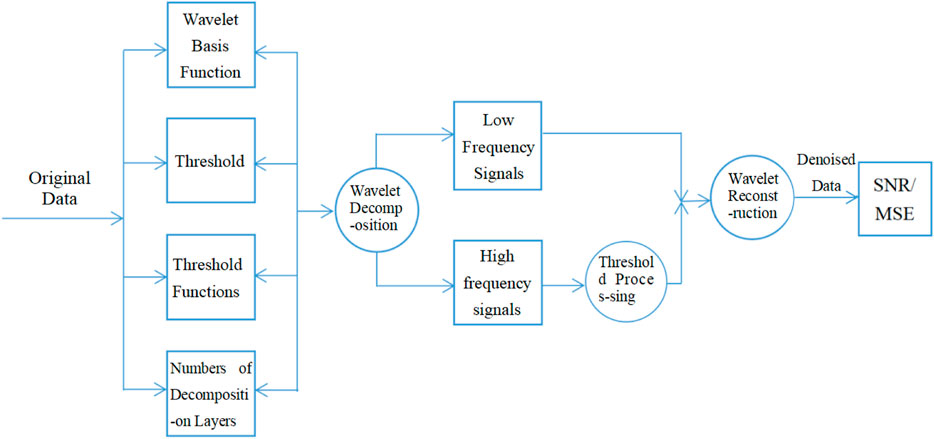
The process of discrete wavelet transformation thresholding denoising is shown in Figure 6. The wavelet basis function, threshold, queue function, and the number of decomposition layers are all key factors affecting the final denoising effect in the process of discrete wavelet transformation thresholding denoising.
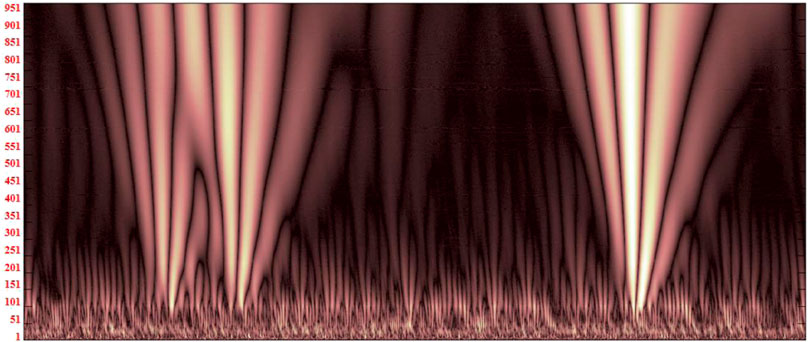
The signal is processed using wavelet decomposition and reconstruction methods, and the wavelet coefficients obtained contain important information about the signal. The effect of wavelet decomposition coefficients on the dynamic response signal of the pavement is shown in Figure 7, which clearly shows the exact location of time discontinuity. The wavelet coefficient of the pavement response monitoring signal is larger after wavelet decomposition, and the wavelet coefficient of the noise is smaller than that of the effective pavement dynamic response signal. An appropriate threshold is selected, and the wavelet decomposition coefficients of each layer are quantified using the threshold function; when the wavelet coefficient is larger than the threshold, the pavement dynamic response signal is considered effective and is retained; if it is smaller than the threshold, it is considered as noise and the wavelet coefficient is set to 0, thus eliminating the noise. The essence of the wavelet decomposition and reconstruction processing method is to suppress the useless noise part of the pavement response monitoring signal and enhance the useful signal part.
The basic steps are as follows:
(i) Step 1: Decomposition: Select wavelets with N layers for the wavelet decomposition of the pavement response monitoring signal.
(ii) Step 2: After wavelet decomposition, select an appropriate threshold and quantify the wavelet decomposition coefficients of each layer using the threshold function.
(iii) Step 3: Reconstruction: Reconstruct the pavement dynamic response signal using the processed wavelet coefficients.
3.2 Comparative selection of wavelet basis functions and thresholds
3.2.1 Selection of wavelet basis functions
The choice of a wavelet basis function is usually based on the combination of support length, vanishing moments, symmetry, regularity, and similarity. As the support length increases, the amount of computation required is usually greater, and the resulting wavelet coefficients are larger. Long support lengths can cause boundary problems, and short support lengths have small vanishing moments, which are detrimental to the concentration of the signal energy. For the underlying wavelet, not only the permissible conditions must be met, but also the “vanishing moments” must be applied to it to minimize wavelet coefficients or non-zero wavelets, thus facilitating data compression and noise removal. As the vanishing moment increases, subway coefficients become smaller. However, as the vanishing moment increases, the support length increases under normal conditions. Therefore, we need to weigh the support length and vanishing moment.
Wavelet basis functions have their characteristics in signal processing, but each type of function focuses on the denoising effect of different types of information. Daubechies and symlet wavelets are the two families of wavelet bases that are better integrated and adapted to the aforementioned principles.
The Daubechies wavelet is a wavelet function proposed by the wavelet analyst Ingrid Daubechies, often abbreviated as dbN, where N represents the number of orders of the wavelet. The support region in the wavelet function Ψ(t) and the scale function φ(t) is 2N-1, and the vanishing moment of Ψ(t) is N. The dbN wavelet has better regularity; in other words, the smooth error introduced by this wavelet as a sparse basis is not easily detectable, making the signal reconstruction process relatively smooth. The characteristics of the dbN wavelet are as follows: as the order increases (sequence N), the order of the vanishing moment becomes larger, where the higher the vanishing moment, the better the smoothness, the stronger the localization ability in the frequency domain, and the better the division of the frequency band; however, it will make the compact support of the wavelet function weaker, and at the same time, the computational effort increases greatly and the real-time performance becomes worse. The sym wavelet is an improvement to the db wavelet. It has better symmetry and, to some extent, reduces phase distortion when analyzing and reconstructing the signal.
3.2.2 Selection of decomposition layers
The second key step in wavelet decomposition and reconstruction is determining the number of decomposition layers. The number of wavelet decomposition layers is essentially related to the characteristics of the signal itself and the sampling frequency. As the number of decomposition layers increases, more signals are obtained, the difference in noise characteristics and signal performance becomes greater, a more complete signal denoising is carried out, and a more beneficial separation effect is observed. However, the higher the number of decomposition layers, the bigger the distortion in the dynamic response signal of the reconstructed pavement, which may result in the loss of the effective signal, and this will affect the final noise reduction effect. Conversely, a lower number of decomposition layers may lead to incomplete denoising. Therefore, special attention should be paid to the conflict between the two functions in the process of application, and an appropriate decomposition ratio should be selected (Powers, 2022). This paper compares and analyses the decomposition effects of the db and sym functions. By comparing their intuitive graphs, detail differences, and signal-to-noise ratios, it is found that the decomposition method using the sym wavelet algorithm is more in line with the objectives.
After wavelet transformations, we adopt three methods to process the signal: hard-threshold denoising, soft-threshold denoising, and fixed-threshold denoising. By setting the appropriate wavelet bases, thresholds, threshold functions, and decomposition layers for wavelet decomposition, the approximate wavelet coefficients and detailed wavelet coefficients are obtained (Gossler et al., 2022).
To carry out the wavelet threshold denoising method, we introduce two metrics: the signal-to-noise ratio and the root mean square error for evaluation, and the pavement structure mechanical response signals are processed separately using different threshold quantization methods. Figure 8 shows the waveform effect of the fixed-threshold wavelet denoising process with a different number of decomposition layers and different wavelet functions. It can be observed from the figure that as the number of decomposition layers increases, the more obvious the waveform is, and the SNR and RMSE obtained are shown in Table 1. The results show that the difference between hard- and soft-thresholding methods is not significant since the mechanical response of an asphalt pavement structure is a one-dimensional signal; the reconstructed signal has less loss compared to the original signal, and the decomposition and reconstruction methods both yield better results. The signal-to-noise ratio is relatively high and the root mean square error value is small after the sym wavelet fixed-threshold denoising process.
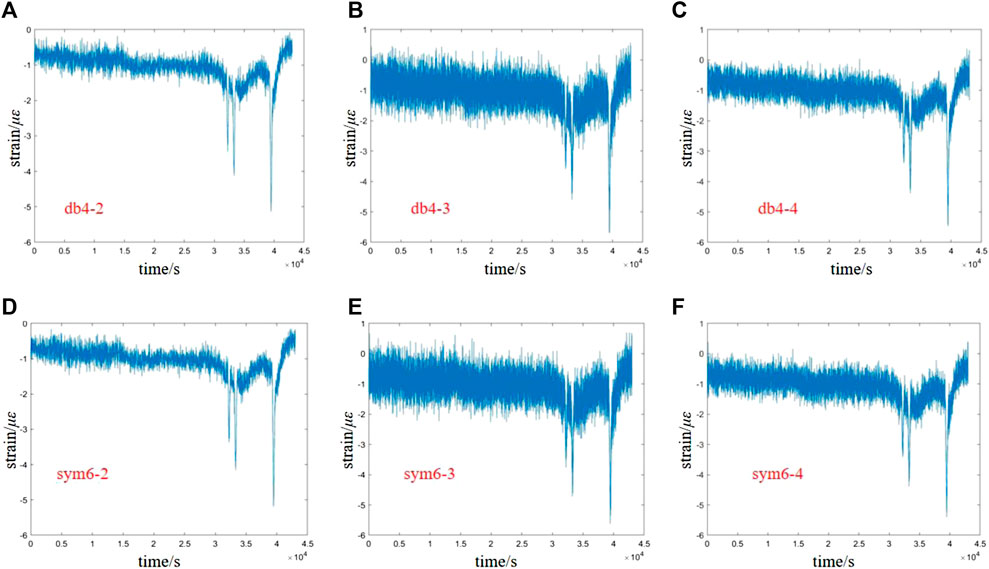
FIGURE 8. Waveform results of wavelet denoising. (A) db4 wavelet two-layer decomposition; (B) db4 wavelet three-layer decomposition; (C) db4 wavelet four-layer decomposition; (D) sym6 wavelet two-layer decomposition; (E) sym6 wavelet three-layer decomposition; and (F) sym6 wavelet four-layer decomposition.
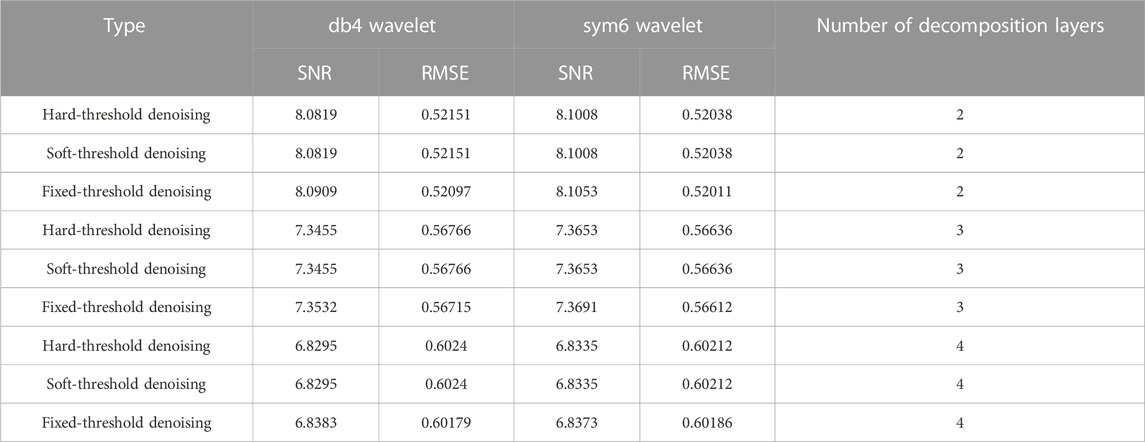
TABLE 1. SNRs and RMSEs of wavelet denoising results with different decomposition layers and wavelet functions.
3.3 Results of wavelet decomposition and reconstruction processing
Figure 9 shows the waveform comparison between the output signal and the original pavement response monitoring signal after the selected sym6 wavelet four-layer decomposition and reconstruction. Wavelet decomposition and reconstruction retain the whole characteristics of the strain signal generated by the three-axle vehicle, where the signal first drops from the baseline to the first trough and then rises, while the second and third axle signals, in turn, pass through the sensor, generating a compression strain and a trough. In addition, the difference in signal amplitude between the wavelet decomposition reconstructed signal and the original pavement response monitoring signal is small. It can be seen that in the wavelet decomposition process, different scales have different temporal and frequency resolutions; thus, the signal contained in different frequency intervals can be separated using wavelet decomposition, and therefore, wavelet decomposition and reconstruction have a powerful local feature portrayal capability.
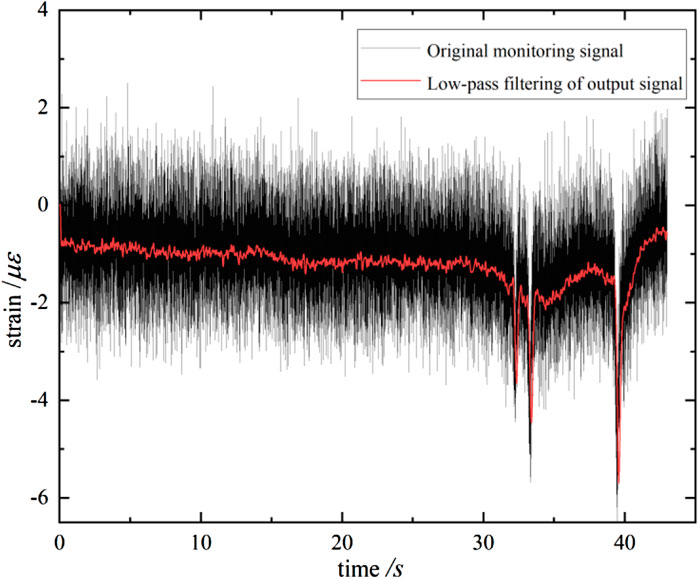
FIGURE 9. Comparison of the effect of wavelet decomposition and reconstruction on the dynamic response signal of the pavement.
3.4 Validation of applicability
In order to validate the effectiveness and applicability of the proposed wavelet decomposition and reconstruction method, a comparative analysis was conducted using a signal from the selected literature titled “Signal Detection and Noise Reduction Method of Massage Chair Based on EMD” (Lu and Yu, 2021). The chosen signal, as shown in Figure 10, is characterized by noisy motor detection data in the context of a massage chair. Figure 11 shows the result of signal denoising in the literature.
The chosen signal was processed using the sym8 wavelet with a decomposition level of 4, consistent with the methodology described in this literature. The wavelet decomposition results were obtained and compared with the denoising results presented in this paper. The obtained results demonstrated a high degree of similarity with the literature, providing evidence for the applicability of our proposed method. Figure 10 illustrates the wavelet decomposition results, showcasing the effectiveness of the sym8 wavelet in reducing noise and preserving useful signal components. These findings validate the suitability of the proposed wavelet transformation approach for processing dynamic monitoring data in pavement applications.
Figure 12 presents the wavelet decomposition and reconstruction results for the selected signal. The comparative analysis was performed based on evaluating the signal-to-noise ratio and the preservation of useful signal characteristics.
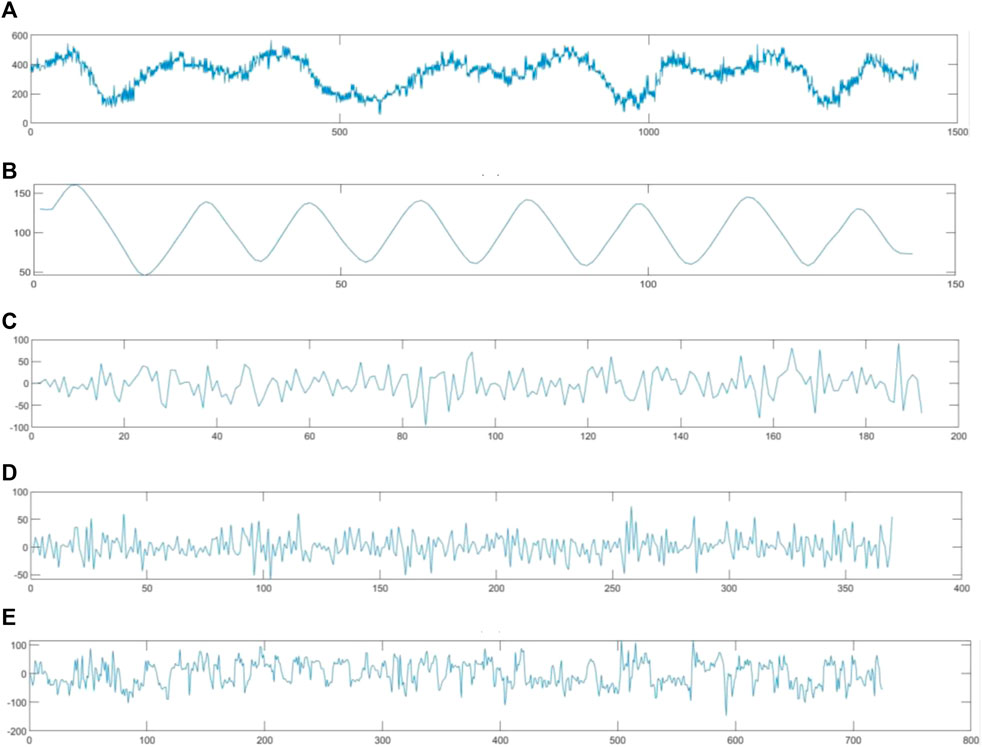
FIGURE 12. Four-layer wavelet decomposition result. (A) Original monitoring data; (B) approximate sequence a; (C) approximate sequence d; (D) approximate sequence e; and (E) approximate sequence f.
This comparative analysis serves as compelling evidence supporting the applicability and effectiveness of the proposed wavelet decomposition and reconstruction method for noise reduction in motor detection signals of massage chairs.
The findings highlight the advantages of using the sym8 wavelet with a decomposition level of 4 for handling noisy motor detection data. This approach exhibits good localization properties in both the time and frequency domains, enabling the extraction of essential characteristics from the dynamic response signals of the motor of the massage chair. The proposed method provides a suitable approach for processing massive motor detection data, which is vital for the effective maintenance and quality control of massage chairs.
4 Conclusion
In this paper, the pavement dynamic response signal is reconstructed via wavelet decomposition, and its working principle and noise reduction process are analyzed in detail. Wavelet transformation is characterized by multiple analyses and is able to analyze local features in both time and frequency domains.
This paper’s results demonstrate the effectiveness of wavelet decomposition and reconstruction techniques in processing pavement dynamic response signals. Consequently, the signal-to-noise ratio of the signal was significantly improved. Noise reduction was successfully achieved by applying these methods, and the signal-to-noise ratio of the signal was significantly improved to obtain a clearer dynamic response signal of the pavement structure. By comparing different wavelet functions, it was found that the sym wavelet method produced good results in terms of signal-to-noise ratio and root mean square error. The wavelet decomposition and reconstruction algorithm is appropriate for the preprocessing of the dynamic response signal between different layers of the pavement.
The selection of the wavelet basis function, decomposition layer, and threshold processing method has a great influence on the denoising results. The difference between hard and soft thresholding is not obvious for wavelet decomposition and reconstruction methods, since the mechanical response of an asphalt pavement structure is a one-dimensional signal. The sym wavelet fixed-threshold denoising results indicated a relatively high signal-to-noise ratio and a small root mean square error.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
Author contributions
SS, project administration; ML, writing—review and editing; YJ, writing—original draft preparation; HW and CB, data curation; ZL, investigation; RZ and HL, funding acquisition; YZ, visualization; ZY and FX, formal analysis. All authors contributed to the article and approved the submitted version.
Funding
The authors acknowledge the financial support of the Qilu Young Scholars Program of Shandong University, Natural Science Foundation of Shandong Province (CN) (No. ZR2020ME244), Innovation Project of Jinan Science and Technology Bureau (202228101), and National Key R&D Program “Transportation Infrastructure” “Reveal the list and take command” project (2022YFB2603300).
Conflict of interest
Authors SS, HW, and ZL were employed by Shandong High-Speed Infrastructure Construction Co., Ltd., and CB, RZ, HL, and YZ were employed by Shandong Hi-Speed Jiwei Expressway Co., Ltd.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Bairwa, B., and Rathod, S. (2022). “Development of fault detection method in cable using arduino UNO,” in IEEE International Conference on Recent Advances and Innovations in Engineering, MANGALORE, India, 01-03 December 2022 (IEEE).
Banerjee, S., and Bhowmik, S. (2022). “Detection and location of fault in microgrid using discrete wavelet transform based technique,” in IEEE International Conference on Condition Assessment Techniques in Electrical Systems, Durgapur, India, 17-19 December 2022 (IEEE).
Cornaggia, A., Ferrari, R., Zola, M., Rizzi, E., and Gentile, C. (2022). Signal processing methodology of response data from a historical arch bridge toward reliable modal identification. Infrastructures 7 (5), 74. doi:10.3390/infrastructures7050074
Devi, R., Kirthika, A., Divya Priyadharshini, M., Ladha, A., Anju, A., Rajesh Kumar, T., et al. (2022). Development of symmetrical fault detection during power swing based on entropy. J. Electr. Eng. 17, 1533–1542. doi:10.1007/s42835-021-00994-0
Ghobber, S., and Mejjaoli, H. (2023). Deformed wavelet transform and related uncertainty principles. Symmetry-Basel 15, 675. doi:10.3390/sym15030675
Golestani, A., Kolbadi, S., and Heshmati, A. A. (2013). Localization and de-noising seismic signals on SASW measurement by wavelet transform. J. Appl. Geophys. 98, 124–133. doi:10.1016/j.jappgeo.2013.08.010
Gossler, F., Queiroz, D., and Villarreal, F. (2022). Design of nearly-orthogonal symmetric wavelet filter banks based on the wavelet orthogonalization process. Circuits Syst. Signal Process. 42, 234–254. doi:10.1007/s00034-022-02111-6
Guan, Z., and Zhuang, C. (2012). Accelerated loading dynamic respond of full-scale asphalt concrete pavement. J. Traffic Transp. Eng. 12 (2), 24–31.
Hui, W., Hu, Zh., Li, J., Zheng, J., and Ren, J. (2023). Effect of loading rate on failure characteristics of asphalt mixtures using acoustic emission technique. Constr. Build. Mater. 364, 129835. doi:10.1016/j.conbuildmat.2022.129835
Hui, W., and Yu, Z. (2023). Fracture characteristics of a cement concrete pavement plate considering subgrade modulus decay based on a meshless finite block metho. Front. Mater. 10, 1157529. doi:10.3389/fmats.2023.1157529
Janani, A., Rezaeieh, S., Darvazehban, A., Keating, S. E., and Abbosh, A. M. (2022). Portable electromagnetic device for steatotic liver detection using blind source separation and shannon wavelet entropy. IEEE J. Electromagn. Rf Microwaves Med. Biol. 6, 546–554. doi:10.1109/jerm.2022.3205247
Jiang, M., and Nie, M. (2015). “Signal processing of fiber optic gyro under vehicle vibration environment,” in 2015 34th Chinese Control Conference (CCC), Hangzhou, China, 28-30 July 2015 (IEEE).
Ke, X., Shi, Y., Fu, X., Song, L., Jing, H., Yang, J., et al. (2023). The nth power fourier spectrum analysis for the generalized seismic wavelets. IEEE Trans. Geoscience Remote Sens. 61, 1–10. doi:10.1109/tgrs.2023.3243184
Li, M., and Ji, S. (2019). The pretreatment methods of pavement strain signals. J. Shandong Univ. Sci. 49 (03), 73–79.
Liu, F., and Li, H. (2017). Post-processing of measured straindata for asphalt pavement structure. Highway 5 (5), 60–63.
Liu, Z., and Qin, R. (1998). The analysis of the effect of overload truck on asphalt pavement. J. Chang Sha Comun. Univ. 15 (2), 59–64.
Lu, L., and Yu, H. (2021). “Signal detection and noise reduction method of massage chair based on EMD,” in Advanced manufacturing and automation X (Spinger).
Mallat, S. (1989). A theory for multiresolution signal decomposition: the wavelet representation. IEEE Trans. Pattern Analysis Mach. Intell. 11 (7), 674–693. doi:10.1109/34.192463
Ministry of Transport of the People’s Republic of China (2017). Specifications for design of Highway asphalt pavement. Beijing, China: China Communications Press.
Powers, N. P. (2022). Power factor in non-sinusoidal and non-symmetrical regimes in three-phase systems. Energies 15, 5130. doi:10.3390/en15145130
Qin, D. (2014). Performance analysis of FFT and DWT. J. Guangdong Polytech. Normal Univ. 35 (07), 12–15.
Shao, T., and Bai, Z. (2014). Decomposition and reconstruction of signal based on DWT. Comput. Technol. Dev. 24 (11), 159–161.
Sun, R., Shan, Y., and Wang, B. (2011). Study of pavement identification approach based on wavelet analysis. Appl. Mech. Mater. 44-47, 3632–3639. doi:10.4028/www.scientific.net/AMM.44-47.3632
Tan, Z., and Li, H. (2017). Study on layout of monitoring system about mechanical response of asphalt pavement. J. Wuhan Univ. Technol. 41 (3), 528–532.
Tulup, A. (2021). Research on application of wavelet analysis in mutation signal processing. Master’s thesis. Urumchi: Xinjiang Normal University.
Wang, L., and Wang, H. (2019). Development and prospect of intelligent pavement. China J. Highw. Transp. 32 (04), 50–72.
Wei, J., and Wang, L. (2009). Asphalt pavement strain gauge data collection and signals proces. Highw. Eng. 34 (2), 45–47.
Yang, Y., and Wang, L. (2010). Typical pavement structure dynamic response data collection and analysis under heavy vehicle loading. J. Highw. Transp. Res. Dev. 27 (5), 11–16.
Zeng, S. (2007). Wavelet denoising and applying in signal processing. Master’s thesis. Tianjin: Tianjin University.
Keywords: asphalt pavement, pavement dynamic response, signal processing, wavelet decomposition and reconfiguration, monitor
Citation: Shang S, Liang M, Wang H, Jiao Y, Liu Z, Bi C, Xu F, Zhang R, Li H, Zhao Y and Yao Z (2023) Pavement dynamic monitoring data processing based on wavelet decomposition and reconfiguration methods. Front. Mater. 10:1221385. doi: 10.3389/fmats.2023.1221385
Received: 12 May 2023; Accepted: 31 July 2023;
Published: 22 August 2023.
Edited by:
Linglin Li, Hefei University of Technology, ChinaReviewed by:
Fuqiang Dong, Hohai University, ChinaYinfei Du, Central South University, China
Jue Li, Chongqing Jiaotong University, China
Copyright © 2023 Shang, Liang, Wang, Jiao, Liu, Bi, Xu, Zhang, Li, Zhao and Yao. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Ming Liang, bGlhbmdAc2R1LmVkdS5jbg==
 Shujie Shang1
Shujie Shang1 Ming Liang
Ming Liang