Flow and heat transfer analysis on micropolar fluid through a porous medium between a clear and Al2O3−Cu/H2O in conducting field

The current study is focused on the flow of micropolar liquid in a saturated permeable medium sandwiched between clear and hybrid nanofluid filled in an inclined channel, with radiation and dissipation effects. Copper and Aluminium oxide nanoparticles is considered along with base (water) fluid. The solution for velocity, micro rotational velocity, and temperature are determined by applying the regular perturbation technique to the dimensionless version of the governing equations. The heat transport rate at the left $y=-1$ and right $y=2$ plate is also calculated, as well as shear stress expressed in terms of skin-friction coefficient and Nusselt number. The result obtained for various physical parameters are analyzed through several graphs and tables. Results reveal that an increase in the material parameter of micropolar fluid, the motion of the fluid flow decreases. The heat transport rate is enhanced and the velocity is degraded by the magnetic parameter. The Hybrid nanofluid temperature is greater when compared to clear and binary hybrid nanofluid. This work establishes the mechanisms for heat transport enhancement on micropolar liquid through a porous medium between a clear and hybrid nanofluid in conducting field.

1 Introduction

Micropolar fluids are special non-Newtonian fluids with microscopic effects like micro rotational and rotational inertia. Eringen has put out the theory of micropolar fluids (Eringen, 1964), (Eringen, 1996). Many academics studied micropolar fluids by outlining many practical uses. Micropolar liquids may be utilized as lubricants since they have lesser friction coefficients than Newtonian liquids (Bansal et al., 2020), (Khonsari, 1990). The significance of micropolar fluids exists in various industries such as the metallic plate cooling, colonial and suspension solutions, liquid crystals, blood (Ikbal et al., 2009), and nuclear power plant (Siddiqa et al., 2021). Recently, nanofluids have so many applications in many industrial sectors, In connection to this, many fluid dynamics experts are currently exhibiting a significant interest in studying them. As the volume percentage of the suspended nanoparticles increases, the thermal conductivity of nanofluids rises (Lee and Eastman, 1999; Wang et al., 1999; Li and Xuan, 2000; Mintsa et al., 2009). Additionally, Wang & Mujumdar’s (Wang and Mujumdar, 2007) comparison of their data with other sources shows that the rate of thermal conduction of nanofluids improves as the size of the particles decreases. As temperature rises, the thermal conductivity likewise rises (Das et al., 2003), (Hayat et al., 2019) and (Gopal et al., 2020). Anwar et al. (Bég et al., 2019) swotted the two-phase stream of a fluids in the presence of a permeable medium. Under the isothermal condition, Kumar et al. (Kumar et al., 2010) carried out the scrutiny of the two-phase stream of micropolar and Newtonian fluid in the channel. The study of two-layered non-miscible liquids in flat mini channels was swotted by Khaled et al. (Khaled and Vafai, 2014) and Umavathi et al. (Umavathi and Anwar Bég, 2020a). Chamkha (Chamkha, 2000) scrutinized the influence of a permeable medium in a two-phase stream of heat-generating or absorbing materials.

Three-phase flows of a couple of stress fluids squeezed between Newtonian fluids are analytically studied by Umavathi et al. (Umavathi et al., 2005). It was noticed that the fluid flow is increased by the pair stress parameter. Umavathi et al. (Umavathi et al., 2008) investigated the three-phase flow of Micropolar fluid. Dragiša et al. (Nikodijevic et al., 2014) analytically studied the three immiscible region flows of Newtonian fluid and all three regions are electrically conducting. Abdul Rauf and Memoona Naz (Abdul and Naz, 2020) investigated the one-dimensional flow of three immiscible region flows in a cylindrical. Hasnain et al. (Hasnain et al., 2022) studied the three-phase flow of Casson liquid with a porous medium squeezed between hybrid nanofluid with clear fluid. They noticed that copper (Cu) nanoparticles increase the temperature. Kumar et al. (Kumar Yadav et al., 2018) analytically studied the three-phase flow of micropolar fluid between clear and hybrid nanofluid. Engineering applications for three-phase flows in porous media include oil production, biofluid transfer, radiator coolant circulation, and more (Dey et al., 2017; Fan et al., 2017; Vamvakidis et al., 2018). Modern methods such as the machine learning are adopted by El-Amin et al. (El-Amin et al., 2023) to study the effect of Nanoparticles in two-phase flow in permeable medium and demonstrated that machine learning approach gives better results than some of the numerical methods. Immiscible fluid flow in different geometries was considered to study flow and heat transfer rate (Umavathi and Anwar Bég, 2020b), (Chen and Jian, 2022). Abdullah et al. (Alzahrani et al., 2023) studied the effect of viscous-Casson fluid in a rotating two-phase flow channel with a chemical reaction and performed a comparative study of different numerical methods.

There is a fascinating new class of sophisticated fluids known as hybrid nanofluids. These nanofluids combine the advantages of traditional nanofluids with those of hybrid materials. They are manufactured by dispersing nanoparticles and other functional components in a base fluid, which results in the creation of a medium that is unique, adaptable, and with increased qualities. In their study, Shamshuddin et al. (Shamshuddin et al., 2023a) educed the HNF model and the development of entropy across a stretchy disk. Shamshuddin et al. (Shamshuddin et al., 2023b) investigated the effects of radiation and other influencing factors on magnetized nanoliquid flow in a permeable cylindrical annulus. They used molybdenum disulfide and magnetite nanoparticles in their research. Shamshuddin et al. (Shamshuddin et al., 2023c) conducted research on a micropolar liquid medium channel while assuming heat radiation and species reactive agents were present. Researchers Shamshuddin et al. (Shahzad et al., 2022) investigated the thermal features of ternary hybrid nanofluids. Additionally, aluminum oxide, copper oxide, silver, and water nano-molecules were used in the research. Taking into account the Hall effect and radiation impacts Shamshuddin et al. (Shamshuddin et al., 2023d) investigated the energy transition that occurs in order to improve the heat transport rate during the flow of a ternary hybrid nanofluid across the surface of a rotating disk. Moreover, this examination is focused on the characteristics of two different kinds of metallic nanoparticles, including Cu and Al₂O₃. In this framework, Cu nanomaterials are used/exercised in a wide variety of products, including heat transfer, antimicrobial materials, catalysts, super solid materials, and sensors [see Refs. (Ahmed et al., 2016; Khan et al., 2021; Khan et al., 2022)]. The advantages or benefits of Cu nanomaterials are competitive, inflated yields under delicate reaction circumstances or situations, and exact reaction durations that seem differently from traditional catalysts (Khan and Alshomrani, 2017). In addition, the Al₂O₃ nanomaterials are widely used in the ceramics, mechanical, and personal care industries (Khan et al., 2017). In recent times, numerous researchers explored the hybrid nanofluids past diverse surfaces (Kavya et al., 2022; Lou et al., 2022; Raju et al., 2022; Upadhya et al., 2022).

In further study, they can use the different nanoparticle with different base fluids. They can study the mass transfer with Soret effect and Dufour effect with non-linear thermal radiation. The aforementioned works’ wide-ranging implications in science and technology have led to the discussion of the three-phase flow of micropolar fluid compressed between transparent fluid and hybrid nanofluid subject to heat radiation and electromagnetic influence. The perturbation technique is carried out to solve the differential equation in our study.

2 Problem formulation

The flow configuration of the problem is schematically shown in Figure 1. In the presence of a magnetic field and electric field, steady and laminar fluid flow through a channel is considered. The fluid flow in the inclined channel is assumed to be a constant pressure gradient. The wall y = −1 is kept at $T_{w2}$, while y = 2 is maintained at $T_{w1}$. The inclined channel is separated into three regions, Region-1 consists of clear fluid and Region-3 consists of a hybrid nanofluid. Both regions are considered in the presence of viscous, Joules and Darcy dissipation region 2 is of a porous medium and consists of micropolar fluid. Density is considered to be constant in all the regions and thermal conductivity and viscosity only with temperature. Copper, Aluminium Oxide—water hybrid nanofluid are considered. The properties of the nanoparticles involved in the study are mentioned in Table 1. Nanoparticles are assumed to be spherical $\left(q=3\right)$ and platelets $\left(q=5.7\right)$ shape for the fluid flow.

FIGURE 1

FIGURE 1. A physical model of the problem.

TABLE 1

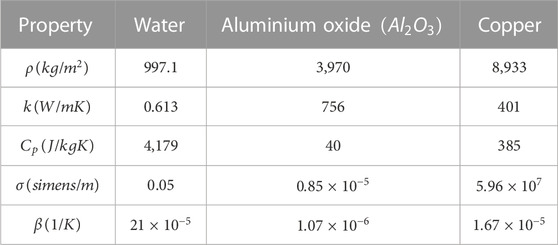
TABLE 1. Thermophysical properties of base fluids and nanoparticles (Hayat and Nadeem, 2017).

These presumptions allow us to write the steady, microrotation velocity, one-dimensional velocity and temperature governing equations (Umavathi et al., 2008), (Ghasemi and Aminossadati, 2009; Muthtamilselvan et al., 2010; Vajravelu et al., 2013) as follows.

Region 1:

${\mu }_f\frac{d^2{u}_1^{\prime }}{d{y^{\prime }}^2}+\left({\rho }_{f}g{\beta }_f\right)\left(T_1-T_{w2}\right)\cos \left(\omega \right)-\frac{\partial p}{\partial x}-{\sigma }_f\left(E_0+B_0{u}_1^{\prime }\right)B_0=0(1)$

$k_f\frac{d^2{T}_1}{d{y^{\prime }}^2}+{\mu }_f{\left(\frac{d{u}_1^{\prime }}{d{y}^{\prime }}\right)}^2-\frac{\partial q^{*}}{\partial y}+{\sigma }_f{\left(E_0+B_0{u_1^{\prime }}_1\right)}^2=0(2)$

Region 2:

$\left({\mu }_{mf}+k\right)\frac{d^2{u}_2^{\prime }}{d{y^{\prime }}^2}+k\frac{dn}{d{y}^{\prime }}+\left({\rho }_{f}g{\beta }_f\right)\left(T_2-T_{w2}\right)\cos \left(\omega \right)-\frac{{\mu }_{mf}}{\kappa }{u}_2^{\prime }-\frac{\partial p}{\partial x}-{\sigma }_{mf}\left(E_0+B_0{u}_2^{\prime }\right)B_0=0(3)$

$\gamma \frac{d^{2}n}{d{y^{\prime }}^2}-k\left(2n+\frac{d{u}_2^{\prime }}{d{y}^{\prime }}\right)=0(4)$

$k_{mf}\frac{d^2{T}_2}{d{y^{\prime }}^2}+{\mu }_{mf}{\left(\frac{d{u}_2^{\prime }}{d{y}^{\prime }}\right)}^2+\frac{{\mu }_{mf}}{\kappa }{u_2^{\prime }}^2-\frac{\partial q^{*}}{\partial y}+{\sigma }_{mf}{\left(E_0+B_0{u}_2^{\prime }\right)}^2=0(5)$

Region 3:

${\mu }_{hnf}\frac{d^2{u}_3^{\prime }}{d{y^{\prime }}^2}+\left({\rho }_{hnf}g{\beta }_{hnf}\right)\left(T_3-T_{w2}\right)\cos \left(\omega \right)-\frac{\partial p}{\partial x}-{\sigma }_{ehnf}\left(E_0+B_0{u}_3^{\prime }\right)B_0=0(6)$

$k_{hnf}\frac{d^2{T}_3}{d{y^{\prime }}^2}+{\mu }_{hnf}{\left(\frac{d{u}_3^{\prime }}{d{y}^{\prime }}\right)}^2-\frac{\partial q^{*}}{\partial y}+{\sigma }_{ehnf}{\left(E_0+B_0{u}_3^{\prime }\right)}^2=0(7)$

Boundary and Interface conditions are assumed to be:

$\begin{array}{ll}\hfill u_1^{\prime }\left(-h\right)=& 0,u_1^{\prime }\left(0\right)=u_2^{\prime }\left(0\right),{\mu }_f\frac{d{u}_1^{\prime }\left(0\right)}{d{y}^{\prime }}={\mu }_{mf}\left(1+K\right)\frac{d{u}_2^{\prime }\left(0\right)}{d{y}^{\prime }}+{\mu }_{mf}K{N}_m,u_2^{\prime }\left(h\right)=u_3^{\prime }\left(h\right),u_3^{\prime }\left(2h\right)\hfill \\ \hfill & =0,{\mu }_{mf}\left(1+K\right)\frac{d{u}_2^{\prime }\left(h\right)}{d{y}^{\prime }}+{\mu }_{mf}K{N}_m={\mu }_{hnf}\frac{d{u}_3^{\prime }\left(h\right)}{d{y}^{\prime }},\frac{d{N}_m\left(0\right)}{dy}=0,\frac{d{N}_m\left(1\right)}{dy}=0\hfill \end{array}$

$T_1\left(-h\right)=T_{w2},T_1\left(0\right)=T_2\left(0\right),k_f\frac{d{T}_1\left(0\right)}{d{y}^{\prime }}=k_{mf}\frac{d{T}_2\left(0\right)}{d{y}^{\prime }},T_2\left(h\right)=T_3\left(h\right),T_3\left(2h\right)=T_{w1},k_{mf}\frac{d{T}_2\left(h\right)}{d{y}^{\prime }}=k_{hnf}\frac{d{T}_3\left(h\right)}{d{y}^{\prime }}(8)$

To convert Eqs 1, 2, 3, 4, 5, 6, 7, 8 into dimensionless equations, we use the following dimensionless parameters

$\begin{array}{c}y=\frac{y^{\prime }}{h},u_i=u_i^{\prime }\left(\frac{{\rho }_f}{{\mu }_f}\right)h,{\theta }_i=\frac{T_i-T_{w2}}{T_{w1}-T_{w2}},G_r=\frac{g{\beta }_f\left(T_{w1}-T_{w2}\right)h^3}{v_f^2}\cos \left(\omega \right),M^2=\frac{B_0^2{h}_1^2\sigma }{{\mu }_f},E=\frac{E_0{\rho }_{f}h}{B_0{\mu }_f},Br=\frac{{\mu }_f^3}{{\rho }_f^2{h}^2\left(T_{w1}-T_{w2}\right)k_f},\sigma =\frac{h}{\sqrt{\kappa }},\hfill \\ P=-\frac{{\rho }_f{h}^3}{{\mu }_f^2}\frac{\partial p}{\partial x},v_f=\frac{{\mu }_f}{{\rho }_f},\frac{\partial q}{\partial y}=4{\alpha }^2\left(T_i-T_{w2}\right),N=2\alpha \frac{h}{{\sqrt{k}}_f},K=\frac{k}{{\mu }_{mf}},n=\frac{Nh}{{\mu }_{mf}}\hfill \end{array}$

The thermophysical properties of hybrid nanofluids are given by (Hayat and Nadeem, 2017):

${\rho }_{hnf}=\left[\left(1-{\varphi }_{s1}\right){\rho }_f+{\varphi }_{s1}{\rho }_{s1}\right]\left(1-{\varphi }_{s2}\right)+{\rho }_{s2}{\varphi }_{s2},{\alpha }_{hnf}=\frac{k_{hnf}}{{\left(\rho C_p\right)}_{hnf}}$

${\left(\rho \beta \right)}_{hnf}=\left[\left(1-{\varphi }_{s1}\right){\left(\rho \beta \right)}_f+{\varphi }_{s1}{\left(\rho \beta \right)}_{s1}\right]\left(1-{\varphi }_{s2}\right)+{\left(\rho \beta \right)}_{s2}{\varphi }_{s2},{\mu }_{hnf}=\frac{{\mu }_f}{\sqrt{{\left(1-{\varphi }_{s1}\right)}^5{\left(1-{\varphi }_{s2}\right)}^5}}$

${\left(\rho C_p\right)}_{hnf}={\left(\rho C_p\right)}_f\left(1-{\varphi }_{s2}\right)\left[\left(1-{\varphi }_{s1}\right)+{\varphi }_{s1}\frac{{\left(\rho C_p\right)}_{s1}}{{\left(\rho C_p\right)}_f}\right]+{\varphi }_{s2}{\left(\rho C_p\right)}_{s2}$

${\sigma }_{hnf}={\sigma }_{nf}\left[\frac{{\sigma }_{s2}+2{\sigma }_{nf}-2{\varphi }_{s2}\left({\sigma }_{nf}-{\sigma }_{s2}\right)}{{\sigma }_{s2}+2{\sigma }_{nf}+{\varphi }_{s2}\left({\sigma }_{nf}-{\sigma }_{s2}\right)}\right],{\sigma }_{nf}={\sigma }_f\left[\frac{{\sigma }_1+2{\sigma }_f-2{\varphi }_1\left({\sigma }_f-{\sigma }_1\right)}{{\sigma }_1+2{\sigma }_f+{\varphi }_1\left({\sigma }_f-{\sigma }_1\right)}\right](9)$

The thermophysical properties of the nanofluid, base fluid and nanoparticles are denoted by the subscripts $nf$, $f$, $s_1$ and $s_2$ respectively. According to Maxwell thermal conductivity of hybrid nanofluid $k_{hnf}$ is considered as:

$k_{hnf}=k_{bf}\left[\frac{k_{s2}+\left(q-1\right)k_{bf}-\left(q-1\right){\varphi }_2\left(k_{bf}-k_{s2}\right)}{k_{s2}+\left(q-1\right)k_{bf}+{\varphi }_2\left(k_{bf}-k_{s2}\right)}\right],k_{bf}=k_f\left[\frac{k_{s1}+\left(q-1\right)k_f-\left(q-1\right){\varphi }_1\left(k_f-k_{s1}\right)}{k_{s1}+\left(q-1\right)k_f+{\varphi }_1\left(k_f-k_{s1}\right)}\right](10)$

2.1 Non—dimensionalized equations

Region 1

$\frac{d^2{u}_1}{d{y}^2}+G_r{\theta }_1+P-M^2\left(E+u_1\right)=0(11)$

$\frac{d^2{\theta }_1}{d{y}^2}+Br{\left(\frac{d{u}_1}{dy}\right)}^2-N^2{\theta }_1+Br{M}^2{\left(E+u_1\right)}^2=0(12)$

Region 2

$\left(1+K\right)\frac{d^2{u}_2}{d{y}^2}+K\frac{d{N}_m}{dy}+G_r{\theta }_2-{\sigma }^2{u}_2+P-M^2\left(E+u_2\right)=0(13)$

$\frac{d^2{\theta }_2}{d{y}^2}+Br\left({\left(\frac{d{u}_2}{dy}\right)}^2+{\sigma }^2{u_2}^2\right)-N^2{\theta }_2+Br{M}^2{\left(E+u_2\right)}^2=0(14)$

$\frac{d^2{N}_m}{d{y}^2}-\frac{2K}{2+K}\left(2N_m+\frac{d{u}_{30}}{dy}\right)=0(15)$

Region 3

$\frac{d^2{u}_3}{d{y}^2}+A_{6}Gr{\theta }_3+A_{41}P-A_{51}{M}^2\left(E+u_3\right)(16)$

$\frac{d^2{\theta }_3}{d{y}^2}+Br{A}_4{\left(\frac{d{u}_3}{dy}\right)}^2-\frac{N^2}{A_3}{\theta }_3+A_{5}Br{M}^2{\left(E+u_3\right)}^2=0(17)$

Boundary and interface conditions are:

$\left.\begin{array}{c}{u}_1\left(-1\right)=0,u_1\left(0\right)=u_2\left(0\right),{\mu }_f\frac{d{u}_1\left(0\right)}{dy}={\mu }_{mf}\left(1+K\right)\frac{d{u}_2\left(0\right)}{dy}+{\mu }_{mf}K{N}_m,u_2\left(1\right)=u_3\left(1\right),\\ {\mu }_{mf}\left(1+K\right)\frac{d{u}_2\left(1\right)}{dy}+{\mu }_{mf}K{N}_m={\mu }_{hnf}\frac{d{u}_3\left(1\right)}{dy},u_2\left(1\right)=0,\frac{d{N}_m\left(0\right)}{dy}=0,\frac{d{N}_m\left(1\right)}{dy}=0\\ {\theta }_1\left(-1\right)=0,{\theta }_1\left(0\right)={\theta }_2\left(0\right),\frac{d{\theta }_1\left(0\right)}{dy}=\frac{k_{mf}}{k_f}\frac{d{\theta }_2\left(0\right)}{dy},{\theta }_2\left(1\right)={\theta }_3\left(1\right),\frac{d{\theta }_2\left(1\right)}{dy}=\frac{k_{hnf}}{k_{mf}}\frac{d{\theta }_3\left(1\right)}{dy},{\theta }_2\left(1\right)=1\end{array}\right\}(18)$

2.2 Solution of the problem

The dimensionless governing Eqs 11, 12, 13, 14, 15, 16, 17 which are nonlinear and coupled are solved using the boundary and interface constraints Eq. 18 for flow. We form an asymptotic analysis by representing the velocity and temperature as:

$u_i\left(y\right)=u_{i0}\left(y\right)+Br{u}_{i1}\left(y\right)+{\left(Br\right)}^2{u}_{i2}\left(y\right)+........(19)$

${\theta }_i\left(y\right)={\theta }_{i0}\left(y\right)+Br{\theta }_{i1}\left(y\right)+{\left(Br\right)}^2{\theta }_{i2}\left(y\right)+........(20)$

The perturbation parameter is assumed to be $Br$, by replacing Eqs 19, 20 in Eqs 11, 12, 13, 14, 15, 16, 17, then equating the same powers and ignoring higher order terms we get:

2.3 Zeroth order equations

Region 1

$\frac{d^2{u}_{10}}{d{y}^2}+G_r{\theta }_{10}+P-M^2\left(E+u_{10}\right)=0(21)$

$\frac{d^2{\theta }_{10}}{d{y}^2}-N^2{\theta }_{10}=0(22)$

Region 2

$\left(1+K\right)\frac{d^2{u}_{20}}{d{y}^2}+K\frac{d{N}_m}{dy}+G_r{\theta }_{20}+P-M^2\left(E+u_{20}\right)-{\sigma }^2{u}_{20}=0(23)$

$\frac{d^2{N}_m}{d{y}^2}-\frac{2K}{2+K}\left(2N_m+\frac{d{u}_{20}}{dy}\right)=0(24)$

$\frac{d^2{\theta }_{20}}{d{y}^2}-N^2{\theta }_{20}=0(25)$

Region 3

$\frac{d^2{u}_{30}}{d{y}^2}+A_{6}Gr{\theta }_{30}+A_{41}P-A_{51}{M}^2\left(E+u_{30}\right)=0(26)$

$\frac{d^2{\theta }_{30}}{d{y}^2}-\frac{N^2}{A_3}{\theta }_{30}=0(27)$

The boundary and interface conditions are

$\left.\begin{array}{c}{u}_{10}\left(-1\right)=0,u_{10}\left(0\right)=u_{20}\left(0\right),{\mu }_f\frac{d{u}_{10}\left(0\right)}{dy}={\mu }_{mf}\left(1+K\right)\frac{d{u}_{20}\left(0\right)}{dy}+{\mu }_{mf}K{N}_m,u_{20}\left(1\right)=u_{30}\left(1\right),\\ {\mu }_{mf}\left(1+K\right)\frac{d{u}_{20}\left(1\right)}{dy}+{\mu }_{mf}K{N}_m={\mu }_{hnf}\frac{d{u}_{30}\left(1\right)}{dy},u_{30}\left(2\right)=0,\frac{d{N}_m\left(0\right)}{dy}=0,\frac{d{N}_m\left(1\right)}{dy}=0,\\ {\theta }_{10}\left(-1\right)=0,{\theta }_{10}\left(0\right)={\theta }_{20}\left(0\right),\frac{d{\theta }_{10}\left(0\right)}{dy}=\frac{k_{nf}}{k_f}\frac{d{\theta }_{20}\left(0\right)}{dy},{\theta }_{20}\left(1\right)={\theta }_{30}\left(1\right),\frac{d{\theta }_{20}\left(1\right)}{dy}=\frac{k_f}{k_{nf}}\frac{d{\theta }_{30}\left(1\right)}{dy},{\theta }_{30}\left(2\right)=1\end{array}\right\}(28)$

2.4 First-order equations

Region 1

$\frac{d^2{u}_{11}}{d{y}^2}+G_r{\theta }_{11}-M^2{u}_{11}=0(29)$

$\frac{d^2{\theta }_{11}}{d{y}^2}+{\left(\frac{d{u}_{10}}{dy}\right)}^2-N^2{\theta }_{11}+M^2{\left(E+u_{10}\right)}^2=0(30)$

Region 2

$G_r{\theta }_{21}+\left(1+K\right)\frac{d^2{u}_{21}}{d{y}^2}-{\sigma }^2{u}_{21}-M^2{u}_{21}=0(31)$

$-\frac{2K}{2+K}\frac{d{u}_{21}}{dy}=0(32)$

$\frac{d^2{\theta }_{21}}{d{y}^2}+{\left(\frac{d{u}_{20}}{dy}\right)}^2+{\sigma }^2{u}_{20}^2-N^2{\theta }_{21}+M^2\left(E^2+u_{20}^2+2E{u}_{20}\right)=0(33)$

Region 3

$\frac{d^2{u}_{31}}{d{y}^2}+A_{6}Gr{\theta }_{31}-A_{51}{M}^2{u}_{31}=0(34)$

$\frac{d^2{\theta }_{31}}{d{y}^2}+A_4{\left(\frac{d{u}_{30}}{dy}\right)}^2-\frac{N^2}{A_3}{\theta }_{31}+A_5{M}^2{\left(E+u_{30}\right)}^2=0(35)$

The boundary and interface conditions are

$\left.\begin{array}{l}{u}_{11}\left(-1\right)=0,u_{11}\left(0\right)=u_{21}\left(0\right),{\mu }_f\frac{d{u}_{11}\left(0\right)}{dy}={\mu }_{mf}\left(1+K\right)\frac{d{u}_{21}\left(0\right)}{dy}+{\mu }_{mf}K{N}_m,u_{21}\left(1\right)=u_{31}\left(1\right),\\ {\mu }_{mf}\left(1+K\right)\frac{d{u}_{21}\left(1\right)}{dy}+{\mu }_{mf}K{N}_m={\mu }_{hnf}\frac{d{u}_{31}\left(1\right)}{dy},u_{31}\left(2\right)=0,\frac{d{N}_m\left(0\right)}{dy}=0,\frac{d{N}_m\left(1\right)}{dy}=0,\\ {\theta }_{11}\left(-1\right)=0,{\theta }_{11}\left(0\right)={\theta }_{21}\left(0\right),\frac{d{\theta }_{11}\left(0\right)}{dy}=\frac{k_{nf}}{k_f}\frac{d{\theta }_{21}\left(0\right)}{dy},{\theta }_{21}\left(1\right)={\theta }_{31}\left(1\right),\frac{d{\theta }_{21}\left(1\right)}{dy}=\frac{k_f}{k_{nf}}\frac{d{\theta }_{31}\left(1\right)}{dy},{\theta }_{31}\left(2\right)=0\end{array}\right\}(36)$

Solving Eqs 21, 22, 23, 24, 25, 26, 27, 29, 30, 31, 32, 33, 34, 35 by using boundary conditions Eqs 28, 36, we obtain.

Region 1

$u_1=u_{10}+Br{u}_{11}$

$u_1=\left(\begin{array}{l}\left(c_7\cosh \left[My\right]+c_8\sinh \left[My\right]\right)-\left(\frac{G_r{c}_1}{N^2-M^2}\cosh \left[Ny\right]+\frac{G_r{c}_2}{N^2-M^2}\sinh \left[Ny\right]-\frac{P}{M^2}+E\right)\\ +Br\left(\begin{array}{l}\left(b_{41}\cosh \left[My\right]+b_{42}\mathrm{Sinh}\left[My\right]\right)-\left(L_{170}\cosh \left[Ny\right]+L_{171}\sinh \left[Ny\right]\right)\\ +\left(\begin{array}{l}{L}_{172}+L_{173}\cosh \left[2My\right]+L_{174}+L_{175}\cosh \left[2My\right]+L_{165}\cosh \left[\left(M-N\right)y\right]\\ +L_{166}\sinh \left[\left(M-N\right)y\right]+L_{167}\sinh \left[\left(M+N\right)y\right]+L_{168}\cosh \left[\left(M+N\right)y\right]\\ +L_{176}-L_{177}\cosh \left[2Ny\right]+L_{169}\sinh \left[2Ny\right]-L_{178}-L_{179}\sinh \left[2Ny\right]-L_{180}\\ -L_{181}\cosh \left[2Ny\right]+L_{182}y\cosh \left[My\right]+L_{183}y\sinh \left[My\right]+L_{184}\sinh \left[2My\right]\\ +L_{185}\cosh \left[Ny\right]+L_{186}y\sinh \left[Ny\right]-L_{187}+L_{188}\sinh \left[Ny\right]+L_{189}y\cosh \left[Ny\right]\end{array}\right)\end{array}\right)\end{array}\right)(37)$

${\theta }_1={\theta }_{10}+Br{\theta }_{11}$

${\theta }_1=\left(\begin{array}{l}\left(c_1\cosh \left[Ny\right]+c_2\sinh \left[Ny\right]\right)+Br\left(b_{11}\cosh \left[Ny\right]+b_{12}\sinh \left[Ny\right]\right)\\ -Br\left(\begin{array}{l}{L}_{76}\left[N^2\cosh \left(2My\right)+4M^2-N^2\right]+L_{77}\left[N^2\cosh \left(2My\right)-4M^2+N^2\right]\\ +\cosh \left[\left(M-N\right)y\right]L_{78}+\sinh \left[My-Ny\right]L_{79}+\sinh \left[\left(M+N\right)y\right]L_{80}\\ +L_{81}\cosh \left[\left(M+N\right)y\right]+L_{82}\left(-3+\cosh \left[2Ny\right]\right)+L_{83}\sinh \left[2Ny\right]\\ +L_{84}\left(3+\sinh \left[2Ny\right]\right)+L_{85}\left(3+\cosh \left[2Ny\right]\right)+L_{86}\left(L_{12}\cosh \left[My\right]+L_{13}\sinh \left[My\right]\right)\\ +L_{87}\left(L_{14}+L_1\right)\sinh \left[2My\right]+L_{881}\left(y\sinh \left[Ny\right]\right)+L_{88}\left(y\cosh \left[Ny\right]\right)+L_{89}\end{array}\right)\end{array}\right)(38)$

Region 2

$u_2=u_{20}+Br{u}_{21}$

$u_2=\left(\begin{array}{l}{c}_9\cosh \left[Z_{9}y\right]+c_{91}\sinh \left[Z_{9}y\right]+c_{10}\cosh \left[Z_{10}y\right]+c_{101}\sinh \left[Z_{10}y\right]+Z_{16}\cosh \left[Ny\right]\\ +Br\left(\begin{array}{l}{Z}_{651}\cosh \left[Ny\right]+Z_{661}\sinh \left[Ny\right]+Z_{671}-Z_{681}\cosh \left(2Z_{9}y\right)-Z_{69}\sinh \left(2Z_{9}y\right)\\ -Z_{70}\cosh \left(Z_9+Z_{10}\right)y+Z_{71}\cosh \left(Z_9-Z_{10}\right)y-Z_{72}\sinh \left(Z_{10}+Z_9\right)y\\ +Z_{73}\sinh \left(Z_9-Z_{10}\right)y-Z_{74}\cosh \left(2Z_{10}y\right)-Z_{75}\sinh \left(2Z_{10}y\right)-Z_{76}\cosh \left(Z_9+N\right)y\\ +Z_{77}\cosh \left(N-Z_9\right)y-Z_{78}\sinh \left(N+Z_9\right)y+Z_{79}\sinh \left(Z_9-N\right)y-Z_{80}\cosh \left(Z_{10}+N\right)y\\ +Z_{81}\cosh \left(N-Z_{10}\right)y-Z_{82}\sinh \left(N+Z_{10}\right)y+Z_{83}\sinh \left(Z_{10}-N\right)y-Z_{84}\cosh \left(2Ny\right)\\ -Z_{85}\sinh \left(y{Z}_9\right)+Z_{86}\sinh \left(2Ny\right)-Z_{87}\mathrm{Cosh}\left(y{Z}_9\right)-Z_{88}\mathrm{Cosh}\left(y{Z}_{10}\right)-Z_{89}\sinh \left(y{Z}_{10}\right)\\ -Z_{90}y\cosh \left[Ny\right]+Z_{91}\sinh \left[Ny\right]-Z_{92}\cosh \left[Ny\right]+Z_{93}y\sinh \left[Ny\right]{+}_{51}\mathrm{Cosh}\left(Z_{96}\right)y\\ +b_{52}\mathrm{Sinh}\left(Z_{96}\right)y\end{array}\right)\end{array}\right)(39)$

${\theta }_2={\theta }_{20}+Br{\theta }_{21}$

${\theta }_2=\left(\begin{array}{l}\left(c_3\cosh \left[Ny\right]+c_4\sinh \left[Ny\right]\right)+Br\left(b_{21}\cosh \left[Ny\right]+b_{22}\sinh \left[Ny\right]\right)\\ -Br\left(\begin{array}{l}{Z}_{36}+Z_{37}\cosh \left(2Z_{9}y\right)+Z_{38}\sinh \left(2Z_{9}y\right)+Z_{39}\cosh \left(Z_9+Z_{10}\right)y-Z_{40}\cosh \left(Z_9-Z_{10}\right)y\\ +Z_{41}\sinh \left(Z_{10}+Z_9\right)y-Z_{42}\sinh \left(Z_9-Z_{10}\right)y+Z_{43}\cosh \left(2Z_{10}y\right)+Z_{44}\sinh \left(2Z_{10}y\right)\\ +Z_{45}\cosh \left(Z_9+N\right)y-Z_{46}\cosh \left(N-Z_9\right)y+Z_{47}\sinh \left(N+Z_9\right)y-Z_{48}\sinh \left(Z_9-N\right)y\\ +Z_{49}\cosh \left(Z_{10}+N\right)y-Z_{50}\cosh \left(N-Z_{10}\right)y+Z_{51}\sinh \left(N+Z_{10}\right)y-Z_{52}\sinh \left(Z_{10}-N\right)y\\ +Z_{53}\cosh \left(2Ny\right)+Z_{54}\sinh \left(y{Z}_9\right)-Z_{55}\sinh \left(2Ny\right)+Z_{56}\mathrm{Cosh}\left(y{Z}_9\right)+Z_{57}\mathrm{Cosh}\left(y{Z}_{10}\right)\\ +Z_{58}\sinh \left(y{Z}_{10}\right)+Z_{59}y\mathrm{Cosh}\left(yN\right)-Z_{60}y\sinh \left(yN\right)\end{array}\right)\end{array}\right)(40)$

Region 3

$u_3=u_{30}+Br{u}_{31}$

$u_3=\left(\begin{array}{l}\left(\begin{array}{l}{c}_{11}\cosh \left[A_{8}y\right]\\ +c_{12}\sinh \left[A_{8}y\right]\end{array}\right)-\left(\frac{Gr{A}_6{c}_5}{{A_7}^2-{A_8}^2}\cosh \left[A_{7}y\right]+\frac{Gr{A}_6{c}_6}{{A_7}^2-{A_8}^2}\sinh \left[A_{7}y\right]-\frac{A_{41}P}{{A_8}^2}+\frac{A_{51}{M}^{2}E}{{A_8}^2}\right)\\ +Br\left(\begin{array}{l}{b}_{61}\cosh \left[A_{53}y\right]+b_{62}\sinh \left[A_{53}y\right]-A_{54}\cosh \left[y{A}_{42}\right]-A_{55}\sinh \left[y{A}_{42}\right]\\ +A_{56}\sinh \left[y{A}_7\right]+A_{57}y\cosh \left[y{A}_7\right]+A_{58}\cosh \left[y{A}_8\right]+A_{59}\cosh \left[y{A}_7\right]\\ +A_{60}y\sinh \left[y{A}_7\right]-A_{61}+A_{62}\sinh \left[2y{A}_7\right]+A_{63}\sinh \left[2y{A}_8\right]+A_{64}\cosh \left[2y{A}_8\right]\\ +A_{65}c\mathrm{o}\mathrm{s}\mathrm{h}\left[2y{A}_7\right]+A_{66}\cosh \left[y\left(A_7+A_8\right)\right]+A_{67}\cosh \left[y\left(A_7-A_8\right)\right]\\ +A_{68}\sinh \left[y\left(A_7+A_8\right)\right]+A_{69}\sinh \left[y\left(A_7-A_8\right)\right]\end{array}\right)\end{array}\right)(41)$

${\theta }_3={\theta }_{30}+Br{\theta }_{31}$

${\theta }_3=\left(\begin{array}{l}\left(c_5\cosh \left[A_{7}y\right]+c_6\sinh \left[A_{7}y\right]\right)+\left(b_{31}\cosh \left[A_{42}y\right]+b_{32}\sinh \left[A_{42}y\right]\right)\\ -Br\left(\begin{array}{l}{A}_{43}y\cosh \left[y{A}_7\right]+A_{44}\cosh \left[y{A}_8\right]+A_{45}+A_{46}y\sinh \left[y{A}_7\right]+A_{47}\sinh \left[2y{A}_7\right]\\ +A_{48}\sinh \left[2y{A}_8\right]+A_{49}\cosh \left[2y{A}_8\right]+A_{50}\cosh \left[2y{A}_7\right]+A_{511}\cosh \left(A_7+A_8\right)y\\ +A_{52}\cosh \left(A_7-A_8\right)y+A_{53}\sinh \left(A_8+A_7\right)y+A_{54}\sinh \left(A_7-A_8\right)y\end{array}\right)\end{array}\right)(42)$

2.5 Derived quantities

2.5.1 Nusselt number

${\left(Nu\right)}_{y=-1}={\left(\frac{d{\theta }_1}{dy}\right)}_{y=-1}=\left(\begin{array}{l}\left(-c_{1}N\sinh \left[N\right]+c_{2}N\cosh \left[N\right]\right)+Br\left(-b_{11}N\sinh \left[N\right]+b_{12}N\cosh \left[N\right]\right)\\ -Br\left(\begin{array}{l}{L}_{76}\left[-2M{N}^2\sinh \left(2M\right)\right]+L_{77}\left[-2M{N}^2\sinh \left(2M\right)\right]\\ -\left(M-N\right)\sinh \left[\left(M-N\right)\right]L_{78}+\left(M-N\right)\cosh \left[M-N\right]L_{79}\\ +\left(M+N\right)\cosh \left[\left(M+N\right)\right]L_{80}-L_{81}\left(M+N\right)\sinh \left[\left(M+N\right)\right]\\ -L_{82}\left(2N\sinh \left[2N\right]\right)+L_{83}2N\cosh \left[2N\right]+L_{84}\left(2N\cosh \left[2Ny\right]\right)\\ -L_{85}2N\left(\sinh \left[2N\right]\right)+L_{86}\left(-L_{12}M\sinh \left[M\right]+L_{13}M\cosh \left[M\right]\right)\\ +L_{87}\left(L_{14}+L_1\right)2M\cosh \left[2M\right]+L_{881}\left(-\sinh \left[N\right]-N\cosh \left[N\right]\right)\\ +L_{88}\left(\cosh \left[N\right]+N\sinh \left[Ny\right]\right)\end{array}\right)\end{array}\right)$

${\left(Nu\right)}_{y=2}=-{\left(\frac{d{\theta }_3}{dy}\right)}_{y=2}=\left(\begin{array}{l}\left(c_5{A}_7\sinh \left[2A_7\right]+c_6{A}_7\cosh \left[2A_7\right]\right)\\ -Br\left(\begin{array}{l}{A}_{43}\left(\cosh \left[2A_7\right]+4A_7\sinh \left[2A_7\right]\right)+A_{44}{A}_8\sinh \left[2A_8\right]\\ +A_{46}\sinh \left[2A_7\right]+4A_{46}{A}_7\cosh \left[2A_7\right]+A_{47}2A_7\cosh \left[4A_7\right]\\ +A_{48}2A_8\cosh \left[4A_8\right]+A_{53}\left(A_8+A_7\right)\cosh \left[2\left(A_8+A_7\right)\right]\\ +A_{511}\left(A_7+A_8\right)\sinh \left[2\left(A_7+A_8\right)\right]+b_{31}{A}_{42}\sinh \left[2A_{42}\right]\\ +A_{52}\left(A_7-A_8\right)\sinh \left[2\left(A_7-A_8\right)\right]+b_{32}{A}_{42}\cosh \left[2A_{42}\right]\\ +A_{49}2A_8\sinh \left[4A_8\right]+A_{50}2A_7\sinh \left[4A_7\right]\\ +A_{54}\left(A_7-A_8\right)\cosh \left[2\left(A_7-A_8\right)\right]\end{array}\right)\end{array}\right)$

2.5.2 Skin friction

${\left(\tau \right)}_{y=-1}={\left(\frac{d{u}_1}{dy}\right)}_{y=-1}=\left(\begin{array}{l}\left(\begin{array}{l}-c_{7}M\sinh \left[M\right]\\ +c_{8}M\cosh \left[M\right]\end{array}\right)-\left(\begin{array}{l}\frac{G_{r}N{c}_1}{N^2-M^2}\sinh \left[N\right]\\ +\frac{G_{r}N{c}_2}{N^2-M^2}\cosh \left[N\right]\end{array}\right)\\ +Br\left(\begin{array}{l}\left(-L_{170}N\sinh \left[N\right]+L_{171}N\cosh \left[N\right]\right)-L_{173}2M\sinh \left[2M\right]\\ -L_{175}2M\sinh \left[2M\right]-L_{165}\left(M-N\right)\sinh \left[\left(M-N\right)\right]\\ +L_{166}\left(M-N\right)\cosh \left[\left(M-N\right)\right]+L_{167}\left(M+N\right)\cosh \left[\left(M+N\right)\right]\\ -L_{168}\left(M+N\right)\sinh \left[\left(M+N\right)\right]+L_{177}2N\sinh \left[2N\right]\\ +L_{169}2N\cosh \left[2N\right]-L_{179}2N\cosh \left[2N\right]+L_{181}2N\sinh \left[2N\right]\\ -b_{41}M\sinh \left[M\right]+L_{182}\left(\cosh \left[M\right]+M\sinh \left[M\right]\right)+b_{42}M\cosh \left[M\right]\\ +L_{183}\left(-\sinh \left[M\right]-M\cosh \left[M\right]\right)+L_{184}2M\cosh \left[2M\right]\\ -L_{185}N\sinh \left[N\right]+L_{186}\left(-\sinh \left[N\right]-N\cosh \left[N\right]\right)+L_{188}N\cosh \left[N\right]\\ +L_{189}\left(\cosh \left[N\right]+N\sinh \left[N\right]\right)\end{array}\right)\end{array}\right)$

${\left(\tau \right)}_{y=2}=-{\left(\frac{d{u}_3}{dy}\right)}_{y=2}=\left(\begin{array}{l}{c}_{11}{A}_8\sinh \left[2A_8\right]+c_{12}{A}_8\cosh \left[2A_8\right]-\frac{Gr{A}_6{A}_7{c}_5}{{A_7}^2-{A_8}^2}\sinh \left[2A_7\right]\\ +Br\left(\begin{array}{l}-\frac{Gr{A}_6{A}_7{c}_6}{Br\left({A_7}^2-{A_8}^2\right)}\cosh \left[2A_7\right]+b_{61}{A}_{53}\sinh \left[2A_{53}\right]+b_{62}{A}_{53}\cosh \left[2A_{53}\right]\\ -A_{54}{A}_{42}\sinh \left[2A_{42}\right]-A_{55}{A}_{42}\cosh \left[2A_{42}\right]+A_{56}{A}_7\cosh \left(2A_7\right)\\ +A_{57}\cosh \left(2A_7\right)+2A_{57}{A}_7\sinh \left(2A_7\right)+A_{58}\left[2A_8\right]\sinh \left[2A_8\right]\\ +A_{62}2A_7\cosh \left[4A_7\right]+A_{59}{A}_7\sinh \left(2A_7\right)+A_{60}\left(\begin{array}{l}\sinh \left(2A_7\right)\\ +A_7\cosh \left(2A_7\right)\end{array}\right)\\ +A_{63}2A_8\cosh \left[4A_8\right]+A_{64}2A_8\sinh \left[4A_8\right]+A_{65}2A_7\sinh \left[4A_7\right]\\ +A_{66}\left(A_7+A_8\right)\sinh \left[2\left(A_7+A_8\right)\right]+A_{67}\left(A_7-A_8\right)\sinh \left[2\left(A_7-A_8\right)\right]\\ +A_{68}\left(A_7+A_8\right)\cosh \left[2\left(A_7+A_8\right)\right]+A_{69}\left(A_7-A_8\right)\cosh \left[2\left(A_7-A_8\right)\right]\end{array}\right)\end{array}\right)$

3 Results and discussions

Before embarking on the discussion of the results, we make some comments on the flow parameters that are considered in this study such as $Gr,Br,E,M,N,\sigma \&Km$ influencing the convective heat and mass transport. The flow is considered as follows the first region consists of clear fluid, the second region has micropolar fluid with porous medium and the third region has hybrid nanofluid. Also, sphere and platelet shapes of nanoparticles are considered in the current study, they have a sphericity $\psi$ as 1 & 0.526 respectively.

Figures 2A, B are the plots of temperature and velocity for varied thermal Grashof number $\left(Gr\right)$ and nanoparticle shape factor $\left(q\right)$ values. Here, as $Gr$ & $q$ upsurges, the temperature and velocity of the fluid flow also increase. The temperature and velocity can be observed to be maximum in region-3. Figure 2A portrays the temperature change, a small difference can be observed in clear fluid & micropolar fluid regions whereas a large difference is observed in the hybrid nanoliquid region, it is due to the higher thermal conductivity property of hybrid nanoliquid which surpasses the property of porous medium and micropolar fluid, hence a major difference is observed in all the regions. The platelet shape of the hybrid nanoparticle exhibits a higher temperature than the sphere shape. A similar observation can be made for a change in velocity from Figure 2B but the sphere shape has a higher velocity than the platelet shape.

FIGURE 2

FIGURE 2. Depicts the effect of thermal grashof number on (A) temperature (B) Velocity.

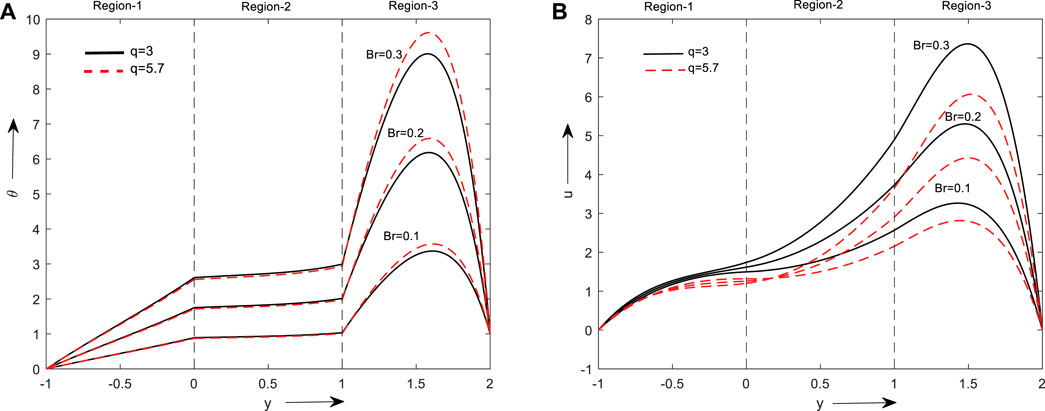
The flow and thermal distributions for different base liquids and nanoparticles is shown in Figures 3A, B. The ratio of heat transfer by viscous dissipation to molecular conduction is Br’s physical interpretation. Consequently, the slowdown the viscous dissipation resulting in greater temperature enhancement due to increase in Br is shown in Figures 3A, B. As Br increases, a velocity increment can be noticed. Furthermore, velocity rise is more prevalent in the hybrid nanofluid region than in the clear & micropolar fluid region, it is due to higher thermal conductivity, temperature enhancement is more and fluid thickness reduction which increases the fluid velocity which is visible in Figure 3B.

FIGURE 3

FIGURE 3. Depicts the effect of Brinkman number on (A) temperature (B) Velocity.

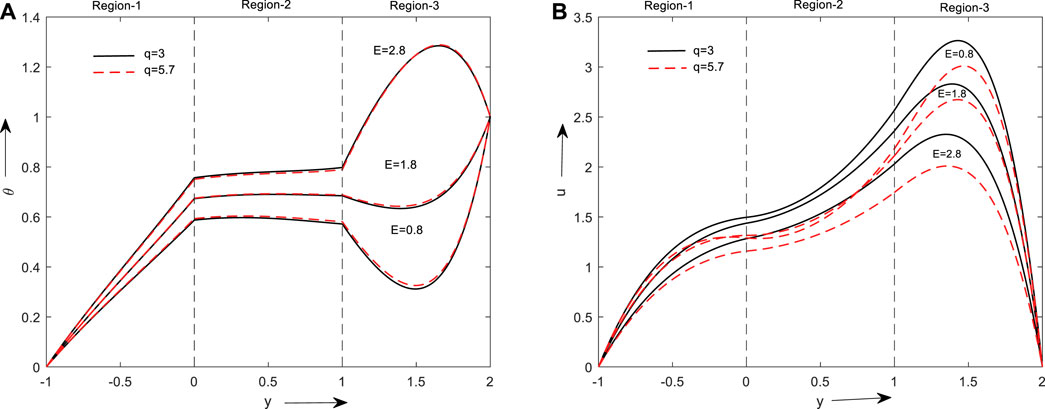
The consequence of the electric field on the temperature and velocity of fluid can be observed in Figures 4A, B. Graphs are plotted for increasing values of electric field & shape factor parameters in both cases. But the outcome of the variation is different in both. Velocity declines and temperature grows with increases in the electric field. Because of the resistance force induced by the electric field, molecules for a group move in a haphazard manner which reduces the velocity and a temperature rise is observed.

FIGURE 4

FIGURE 4. Depicts the effect of the Electric field on (A) temperature (B) Velocity.

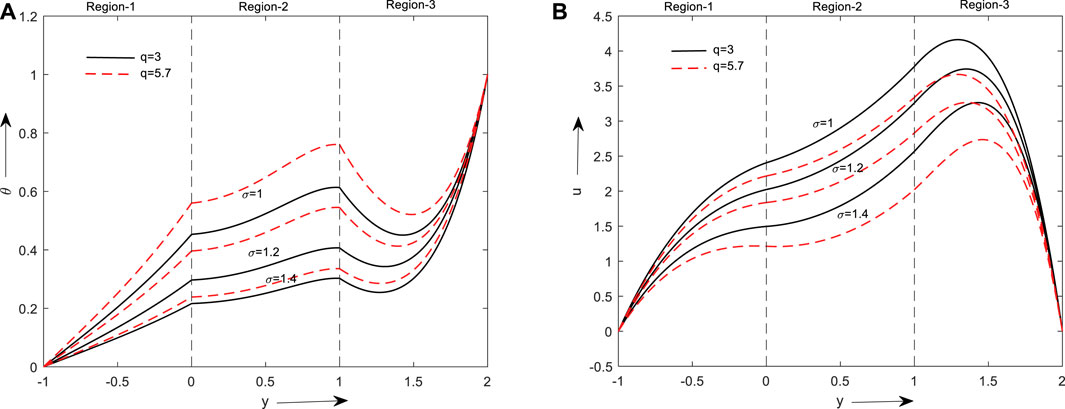
Figures 5A, B reveal the influence of the $\sigma$ on thermal and velocity respectively. Figure 5A exemplifies that the temperature decrement $\sigma$ is increased in all the regions. In contrast to the micropolar and hybrid nanofluid zones, the impact of suppression is dominant in the clear fluid region. This is a typical outcome that is seen when the channels are filled with various fluids that have a wide range of thermal conductivities.

FIGURE 5

FIGURE 5. Depicts the effect of porosity on (A) temperature (B) Velocity.

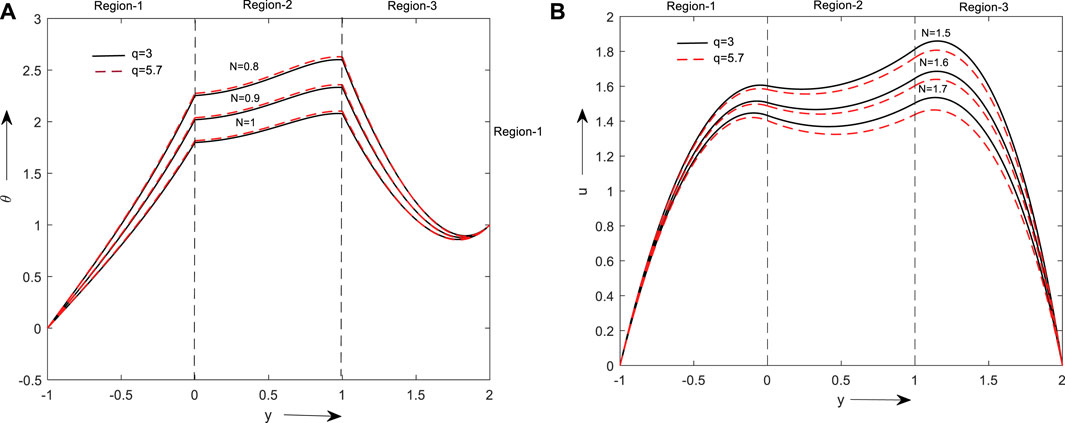
Figures 6A, B show the consequence of thermal radiation on the velocity and thermal behaviours. Here, both the fields within the boundary are seen to decrease with an increase in N. This is for all combinations of nanofluids, thermal conductivity declines as the radiation parameter rise, hence temperature and velocity decrease.

FIGURE 6

FIGURE 6. Depicts the effect of thermal radiation on (A) temperature (B) Velocity.

We examine the effect of Lorentz force on temperature and velocity distribution from Figures 7A, B. The clear fluid zone has a higher momentum compared to the nanofluid region in the velocity profile, which can be seen in Figure 7B. The temperature is enhanced and the velocity is degraded by the magnetic parameter. This is because of the Hartmann effect, which is a ratio of viscous force to electromagnetic force. Thus, as the magnetic field is strengthened, the viscosity also grows, dampening the flow’s velocity and raising its temperature.

FIGURE 7

FIGURE 7. Depicts the effect of magnetic field on (A) temperature (B) Velocity.

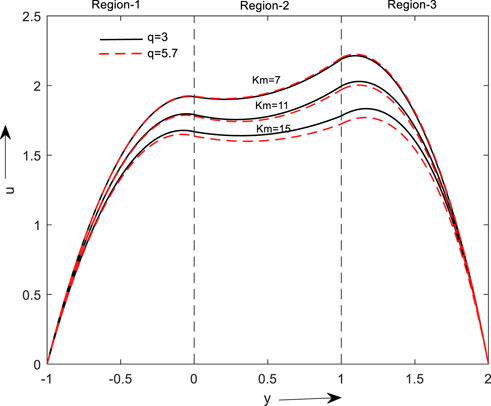
Figure 8 is plotted for the micropolar parameter on velocity. From the above fig, it is noticed that an increase in the material parameter decreases the flow velocity. The flow of regions 1 and 3 don’t affect by an increase in the material parameter value. This is because a material parameter, which only applies to micropolar fluids and specifies the micro rotational features of fluid flow, is the cause of the problem.

FIGURE 8

FIGURE 8. Depicts the effect of micropolar parameter on Velocity.

The outcome of material parameter and magnetic field on micro rotational velocity in region 2 is shown in Figures 9A, B. It is observed that the above y = 0.5, velocity decreases with the material parameter and magnetic parameter, and below y = 0.5 velocity increases with the material parameter and magnetic parameter, this trend is observed on both graphs.

FIGURE 9

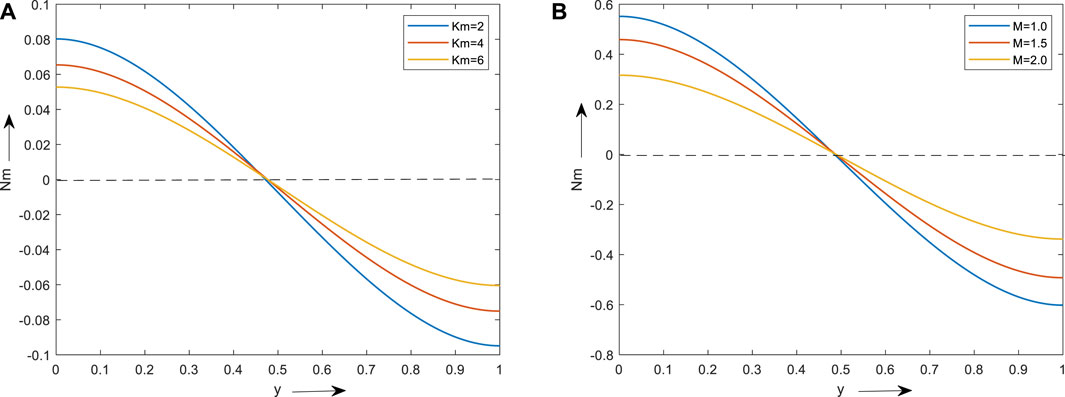
FIGURE 9. Depicts the impact of the material parameter (A) and magnetic parameter (B) on the micro rotational velocity.

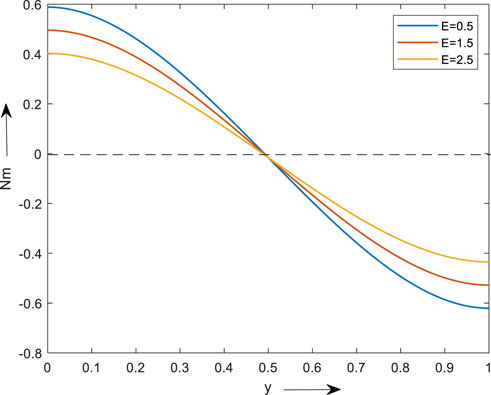
From Figure 10, it is clear that Region 2 is affected by the electric field’s influence on a micropolar fluid’s rotational velocity. Figure 10 illustrates how the electric field changes with micro rotational velocity below and above y = 0.5. Below y = 0.5, it has been noted that a larger value of micro rotational velocity is higher for a lower value of an electric field. For smaller levels of the electric field, the micro rotational velocity reaches a minimum value above y = 0.5.

FIGURE 10

FIGURE 10. Depicts the effect of the Electric field on the micro rotational velocity.

Figures 11A–D display the surface graphs of Nu and $\tau$ for different values of Br and Gr. Figures 11A, B are plotted for y = −1 and Figures 11C, D are plotted for y = 2. Skin friction increases by increasing both Br and Gr for y = −1 and y = 2 respectively. By keeping Gr values constant and increasing Br values, it is observed that the rate of heat transfer is maximum in both plates (y = −1, y = 2).

FIGURE 11

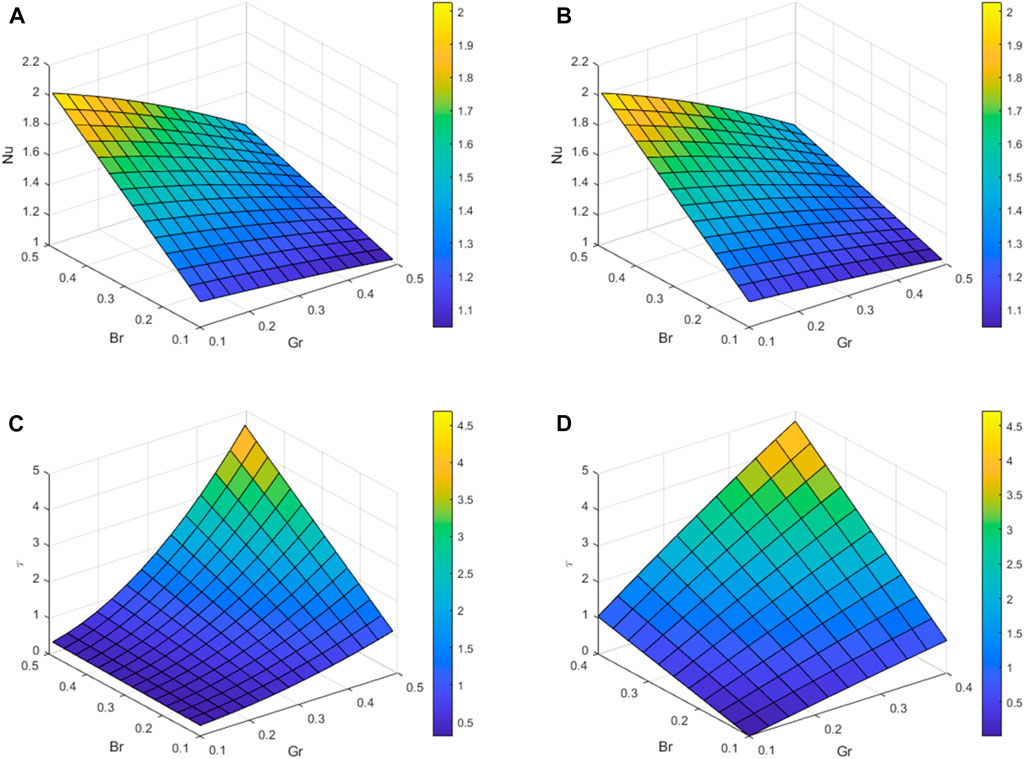
FIGURE 11. Nu graphs for variation in Br and Gr (A) at the left plate (B) at the right plate & Skin friction (C) at the left plate (D) at the right plate.

Nusselt number and skin friction graph for variation in thermal radiation and Electric field are shown in Figures 12A–D. From Figures 12A, B, Nu increases gradually by increasing the values of N and E, at y = −1 and for smaller values of N and E rate of heat transfer is higher at y = 2. By simultaneously increasing the values of N and E, an upward skin friction co-efficient is observed.

FIGURE 12

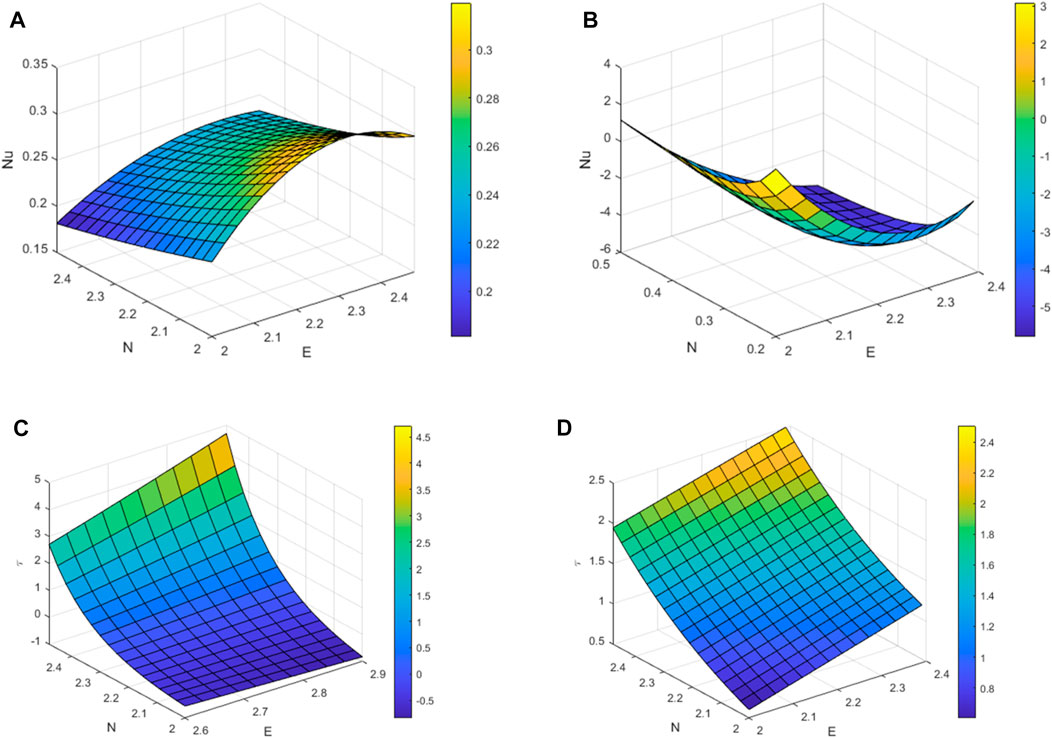
FIGURE 12. Nu graphs for variation in N and E (A) at the left plate (B) at the right plate & Skin friction (C) at the left plate (D) at the right plate.

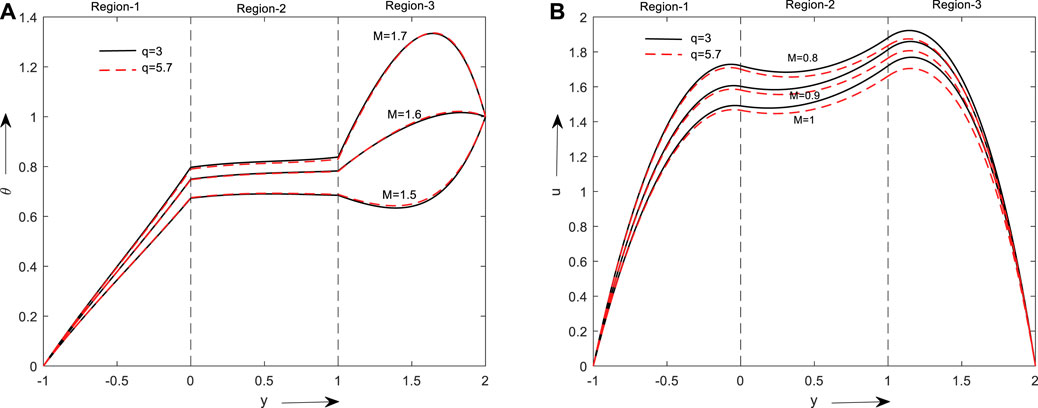
Graphs for Nusselt number and Skin friction for various values of Gr and M are shown in Figures 13A–D. By increasing the values of Gr and M, the rate of heat transfer increases in the left (y = −1) and right plates (y = 2). Figures 13C, D also give similar observations for skin friction.

FIGURE 13

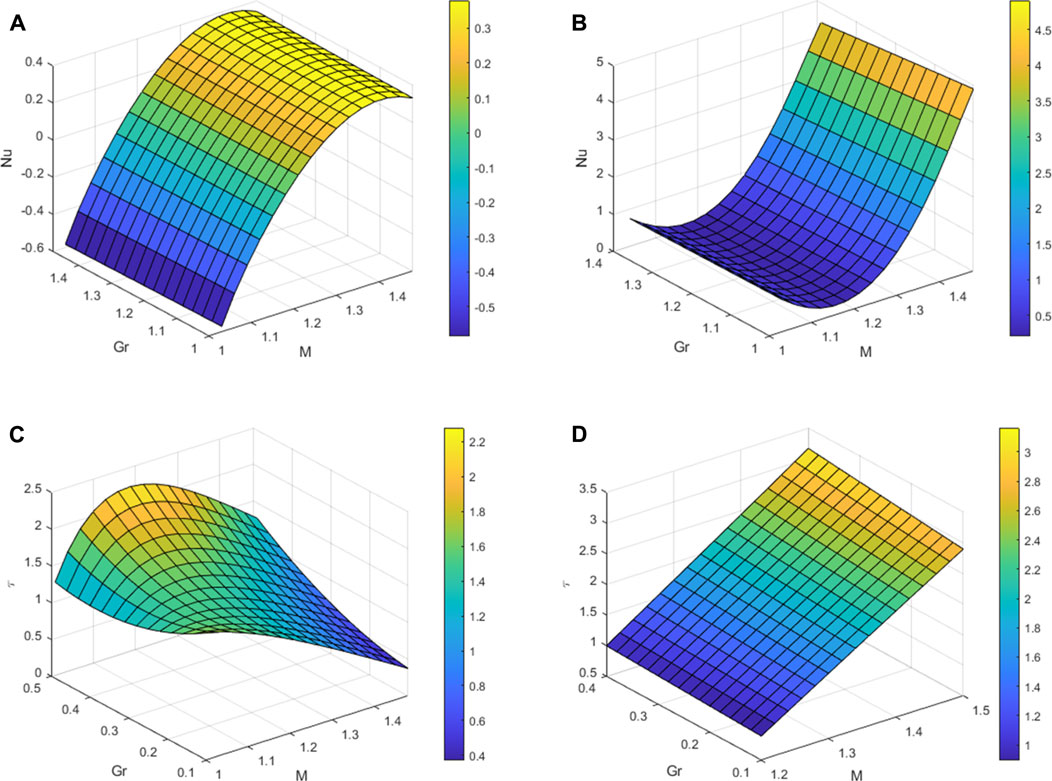
FIGURE 13. Nu graphs for variation in Gr and M (A) at the left plate (B) at the right plate & Skin friction (C) at the left plate (D) at the right plate.

4 Validation of results

validation of the current study is carried out by comparing our results with Kumar et al. (Kumar Yadav et al., 2018). Kumar et al. considered a horizontal channel with three regions with finite lengths where the middle region is micropolar and is bounded by Newtonian fluid. By considering $P=-0.7$, $Gr=0$, $\sigma =1.1$, ${\varphi }_1={\varphi }_2=0$ and, Figures 14A, B are plotted. It is noticed that our results are in good agreement with the Kumar et al. paper.

FIGURE 14

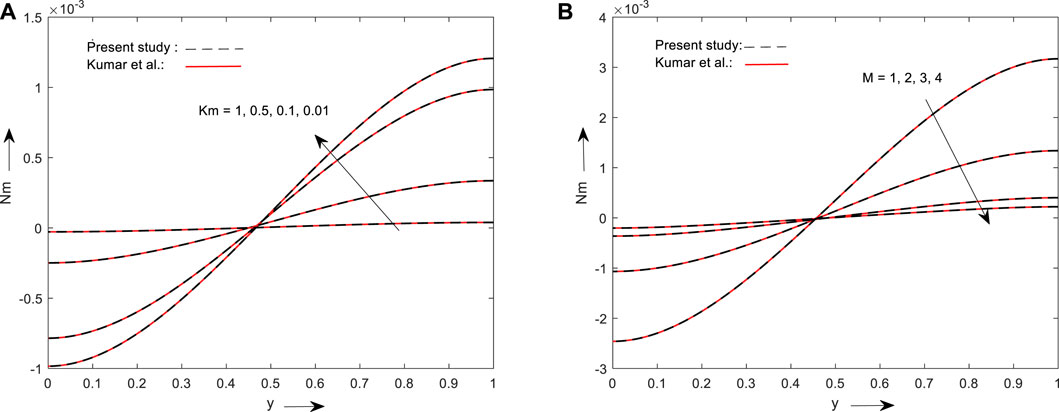
FIGURE 14. Depicts the comparison of the present outcomes for the impact of the material parameter (A) and magnetic parameter (B) on the micro rotational velocity with prior research work.

5 Conclusion

Three-phase flows for clear fluid, micropolar fluid and hybrid nanofluid are studied. Here the effects of the magnetic field, electric field, thermal radiation and permeability parameter on the physical study of fluid’s velocity and temperature profile with the $Cu/H_{2}O$ and $A{l}_2{O}_3/H_{2}O$ hybrid nanoparticles are studied.

Some observations noticed from this study are.

• The electric and magnetic fields decline the velocity and increase the temperature distribution.

• The Hybrid nanofluid temperature is greater when compared to nano and clear fluid.

• By increasing material parameters, the velocity of the micropolar liquid decreases.

• Velocity and thermal profiles of the fluid flow increase by increasing the Grashof number and Brinkman number. By increasing porous parameters and thermal radiation, the fluid’s velocity and temperature distribution decrease.

• The heat transport rate is enhanced by up surging the Grashof number and magnetic field.

• Skin friction can be increased by increasing thermal radiation and electric field.

• The effect of the Brinkman number and Grashof number increases heat flux marginally.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

All authors listed have made a substantial, direct and intellectual contribution to the work and approved it for publication. TNN, LK, KS, SVKV and UK wrote the original draft, E-SMS, AMH, IP and HSG done the mathematical analysis, language editing and study validation.

Funding

This work was funded by the Researchers Supporting Project number (RSP2023R33), King Saud University, Riyadh, Saudi Arabia.

Acknowledgments

The authors are thankful for the support of Researchers Supporting Project number (RSP2023R33), King Saud University, Riyadh, Saudi Arabia.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abdul, R., and Naz, M. (2020). Simultaneous flow of three immiscible fractional Maxwell fluids with the clear and homogeneous porous cylindrical domain. J. Appl. Comput. Mech. 6, 1324–1334. doi:10.22055/JACM.2020.33464.2230

CrossRef Full Text | Google Scholar

Ahmed, J., Begum, A., Shahzad, A., and Ali, R. (2016). MHD axisymmetric flow of power-law fluid over an unsteady stretching sheet with convective boundary conditions. Results Phys. 6, 973–981. doi:10.1016/j.rinp.2016.11.013

CrossRef Full Text | Google Scholar

Alzahrani, A. K., Abbas, Z., and Ullah, M. Z. (2023). Chemically reactive two-phase flow of viscous-Casson fluids in a rotating channel. Alexandria Eng. J. 62, 403–413. doi:10.1016/j.aej.2022.07.036

CrossRef Full Text | Google Scholar

Bansal, P., Saraswat, M., Sharma, K., and Chauhan, N. (2020). Effect of Poisson’s ratio for liner material on performance of journal bearing under micropolar lubrication. Int. J. Eng. Trends Technol. 68 (8), 58–61. doi:10.14445/22315381/IJETT-V68I8P211S

CrossRef Full Text | Google Scholar

Bég, O. A., Zaman, A., Ali, N., Gaffar, S. A., and Bég, E. T. (2019). Numerical computation of nonlinear oscillatory two-immiscible magnetohydrodynamic flow in dual porous media system: FTCS and FEM study. Heat Transfer-Asian Res. 48 (4), 1245–1263. doi:10.1002/htj.21429

CrossRef Full Text | Google Scholar

Chamkha, A. J. (2000). Flow of two-immiscible fluids in porous and nonporous channels. J. Fluids Eng. 122 (1), 117–124. doi:10.1115/1.483233

CrossRef Full Text | Google Scholar

Chen, X., and Jian, Y. (2022). Entropy generation minimization analysis of two immiscible fluids. Int. J. Therm. Sci. 171, 107210. doi:10.1016/j.ijthermalsci.2021.107210

CrossRef Full Text | Google Scholar

Das, S. K., Putra, N., Thiesen, P., and Roetzel, W. (2003). Temperature dependence of thermal conductivity enhancement for nanofluids. J. Heat. Transf. 125 (4), 567–574. doi:10.1115/1.1571080

CrossRef Full Text | Google Scholar

Dey, C., Baishya, K., Ghosh, A., Goswami, M. M., Ghosh, A., and Mandal, K. (2017). Improvement of drug delivery by hyperthermia treatment using magnetic cubic cobalt ferrite nanoparticles. J. Magn. Magn. Mater 427, 168–174. doi:10.1016/j.jmmm.2016.11.024

CrossRef Full Text | Google Scholar

El-Amin, M., Alwated, B., and Hoteit, H. (2023). Machine learning prediction of nanoparticle transport with two-phase flow in porous media. Energies (Basel) 16 (2), 678. doi:10.3390/en16020678

CrossRef Full Text | Google Scholar

Eringen, A. C. (1996). Theory of micropolar fluids. J. Math. Mech. 16, 1–18. doi:10.1512/iumj.1967.16.16001

CrossRef Full Text | Google Scholar

Eringen, A. C. (1964). Simple micro fluids. Int. J. Eng. Sci. 2 (2), 205–217. doi:10.1016/0020-7225(64)90005-9

CrossRef Full Text | Google Scholar

Fan, H., Xing, X., Yang, Y., Li, B., Wang, C., and Qiu, D. (2017). Triple function nanocomposites of porous silica-CoFe ₂ O ₄ -MWCNTs as a carrier for pH-sensitive anti-cancer drug-controlled delivery. Dalton Trans. 46 (43), 14831–14838. doi:10.1039/C7DT02424J

PubMed Abstract | CrossRef Full Text | Google Scholar

Ghasemi, B., and Aminossadati, S. M. (2009). Natural convection heat transfer in an inclined enclosure filled with a water-cuo nanofluid. Numeri Heat. Transf. A Appl. 55 (8), 807–823. doi:10.1080/10407780902864623

CrossRef Full Text | Google Scholar

Gopal, D., Naik, S. H. S., Kishan, N., and Raju, C. S. K. (2020). The impact of thermal stratification and heat generation/absorption on MHD carreau nano fluid flow over a permeable cylinder. SN Appl. Sci. 2 (4), 639. doi:10.1007/s42452-020-2445-5

CrossRef Full Text | Google Scholar

Hasnain, J., Abid, N., O Alansari, M., and Zaka Ullah, M. (2022). Analysis on Cattaneo-Christov heat flux in three-phase oscillatory flow of non-Newtonian fluid through porous zone bounded by hybrid nanofluids. Case Stud. Therm. Eng. 35, 102074. doi:10.1016/j.csite.2022.102074

CrossRef Full Text | Google Scholar

Hayat, T., and Nadeem, S. (2017). Heat transfer enhancement with Ag–CuO/water hybrid nanofluid. Results Phys. 7, 2317–2324. doi:10.1016/j.rinp.2017.06.034

CrossRef Full Text | Google Scholar

Hayat, T., Nadeem, S., and Khan, A. U. (2019). Numerical analysis of Ag–CuO/water rotating hybrid nanofluid with heat generation and absorption. Can. J. Phys. 97 (6), 644–650. doi:10.1139/cjp-2018-0011

CrossRef Full Text | Google Scholar

Ikbal, Md. A., Chakravarty, S., and Mandal, P. K. (2009). Two-layered micropolar fluid flow through stenosed artery: Effect of peripheral layer thickness. Comput. Math. Appl. 58 (7), 1328–1339. doi:10.1016/j.camwa.2009.07.023

CrossRef Full Text | Google Scholar

Kavya, S., Nagendramma, V., Ahammad, N. A., Ahmad, S., Raju, C. S. K., and Shah, N. A. (2022). Magnetic-hybrid nanoparticles with stretching/shrinking cylinder in a suspension of MoS4 and copper nanoparticles. Int. Commun. Heat Mass Transf. 136, 106150. doi:10.1016/j.icheatmasstransfer.2022.106150

CrossRef Full Text | Google Scholar

Khaled, A.-R. A., and Vafai, K. (2014). Heat transfer enhancement by layering of two immiscible co-flows. Int. J. Heat. Mass Transf. 68, 299–309. doi:10.1016/j.ijheatmasstransfer.2013.09.040

CrossRef Full Text | Google Scholar

Khan, M., and Alshomrani, A. S. (2017). Numerical simulation for flow and heat transfer to carreau fluid with magnetic field effect: Dual nature study. J. Magnetism Magnetic Mater. 443, 13–21. doi:10.1016/j.jmmm.2017.06.135

CrossRef Full Text | Google Scholar

Khan, U., Waini, I., Ishak, A., and Pop, I. (2021). Unsteady hybrid nanofluid flow over a radially permeable shrinking/stretching surface. J. Mol. Liq. 331, 115752. doi:10.1016/j.molliq.2021.115752

CrossRef Full Text | Google Scholar

Khan, U., Zaib, A., Ishak, A., Waini, I., Raizah, Z., Prasannakumara, B. C., et al. (2022). Dynamics of bio-convection agrawal axisymmetric flow of water-based Cu-TiO2 hybrid nanoparticles through a porous moving disk with zero mass flux. Chem. Phys. 561, 111599. doi:10.1016/j.chemphys.2022.111599

CrossRef Full Text | Google Scholar

Khan, Z. H., Qasim, M., Haq, R. U., and Al-Mdallal, Q. M. (2017). Closed form dual nature solutions of fluid flow and heat transfer over a stretching/shrinking sheet in a porous medium. Chin. J. Phys. 55, 1284–1293. doi:10.1016/j.cjph.2017.07.001

CrossRef Full Text | Google Scholar

Khonsari, M. M. (1990). On the self-excited whirl orbits of a journal in a sleeve bearing lubricated with micropolar fluids. Acta Mech. 81 (3–4), 235–244. doi:10.1007/BF01176991

CrossRef Full Text | Google Scholar

Kumar, J. P., Umavathi, J. C., Chamkha, A. J., and Pop, I. (2010). Fully-developed free-convective flow of micropolar and viscous fluids in a vertical channel. Appl. Math. Model 34 (5), 1175–1186. doi:10.1016/j.apm.2009.08.007

CrossRef Full Text | Google Scholar

Kumar Yadav, P., Jaiswal, S., Asim, T., and Mishra, R. (2018). Influence of a magnetic field on the flow of a micropolar fluid sandwiched between two Newtonian fluid layers through a porous medium. Eur. Phys. J. Plus 133 (7), 247. doi:10.1140/epjp/i2018-12071-5

CrossRef Full Text | Google Scholar

Lee, S. U. S. ChoiS. Li, and Eastman, J. A. (1999). Measuring thermal conductivity of fluids containing oxide nanoparticles. J. Heat. Transf. 121 (2), 280–289. doi:10.1115/1.2825978

CrossRef Full Text | Google Scholar

Li, Q., and Xuan, Y. (2000). Heat transfer enhancement of nanofluids. Int. J. Heat. Fluid Flow. 21, 58–64. doi:10.1016/s0142-727x(99)00067-3

CrossRef Full Text | Google Scholar

Lou, Q., Ali, B., Rehman, S. U., Habib, D., Abdal, S., Shah, N. A., et al. (2022). Micropolar dusty fluid: Coriolis force effects on dynamics of MHD rotating fluid when Lorentz force is significant. Mathematics 10 (15), 2630. doi:10.3390/math10152630

CrossRef Full Text | Google Scholar

Mintsa, H. A., Roy, G., Nguyen, C. T., and Doucet, D. (2009). New temperature dependent thermal conductivity data for water-based nanofluids. Int. J. Therm. Sci. 48 (2), 363–371. doi:10.1016/j.ijthermalsci.2008.03.009

CrossRef Full Text | Google Scholar

Muthtamilselvan, M., Kandaswamy, P., and Lee, J. (2010). Heat transfer enhancement of copper-water nanofluids in a lid-driven enclosure. Commun. Nonlinear Sci. Numer. Simul. 15 (6), 1501–1510. doi:10.1016/j.cnsns.2009.06.015

CrossRef Full Text | Google Scholar

Nikodijevic, D., Stamenkovic, Z., Jovanovic, M., Kocic, M., and Nikodijevic, J. (2014). Flow and heat transfer of three immiscible fluids in the presence of uniform magnetic field. Therm. Sci. 18 (3), 1019–1028. doi:10.2298/TSCI1403019N

CrossRef Full Text | Google Scholar

Raju, C. S. K., Ahammad, N. A., Sajjan, K., Shah, N. A., Yook, S.-J., and Kumar, M. D. (2022). Nonlinear movements of axisymmetric ternary hybrid nanofluids in a thermally radiated expanding or contracting permeable Darcy Walls with different shapes and densities: Simple linear regression. Int. Commun. Heat Mass Transf. 135, 106110. doi:10.1016/j.icheatmasstransfer.2022.106110

CrossRef Full Text | Google Scholar

Shahzad, F., Jamshed, W., El Din, S. M., Shamshuddin, M., Ibrahim, R. W., Raizah, Z., et al. (2022). Second-order convergence analysis for Hall effect and electromagnetic force on ternary nanofluid flowing via rotating disk. Sci. Rep. 12 (1), 18769. doi:10.1038/s41598-022-23561-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Shamshuddin, M. D., Akkurt, N., Saeed, A., and Kumam, P. (2023d). Radiation mechanism on dissipative ternary hybrid nanoliquid flow through rotating disk encountered by Hall currents: HAM solution. Alexandria Eng. J. 65, 543–559. doi:10.1016/j.aej.2022.10.021

CrossRef Full Text | Google Scholar

Shamshuddin, M. D., Mabood, F., Khan, W. A., and Rajput, G. R. (2023c). Exploration of thermal Péclet number, vortex viscosity, and Reynolds number on two-dimensional flow of micropolar fluid through a channel due to mixed convection. Heat. Transf. 52 (1), 854–873. doi:10.1002/htj.22719

CrossRef Full Text | Google Scholar

Shamshuddin, M. D., Saeed, A., Asogwa, K. K., and Jamshed, W. (2023a). A semi-analytical approach to investigate the entropy generation in a tangent hyperbolic magnetized hybrid nanofluid flow upon a stretchable rotating disk. J. Magn. Magn. Mater 574, 170664. doi:10.1016/j.jmmm.2023.170664

CrossRef Full Text | Google Scholar

Shamshuddin, M. D., Salawu, S. O., Asogwa, K. K., and Srinivasa Rao, P. (2023b). Thermal exploration of convective transportation of ethylene glycol based magnetized nanofluid flow in porous cylindrical annulus utilizing MOS2 and Fe3O4 nanoparticles with inconstant viscosity. J. Magn. Magn. Mater 573, 170663. doi:10.1016/j.jmmm.2023.170663

CrossRef Full Text | Google Scholar

Siddiqa, S., Begum, N., Hossain, Md. A., Abrar, M. N., Gorla, R. S. R., and Al-Mdallal, Q. (2021). Effect of thermal radiation on conjugate natural convection flow of a micropolar fluid along a vertical surface. Comput. Math. Appl. 83, 74–83. doi:10.1016/j.camwa.2020.01.011

CrossRef Full Text | Google Scholar

Umavathi, J. C., and Anwar Bég, O. (2020a). Effects of thermophysical properties on heat transfer at the interface of two immisicible fluids in a vertical duct: Numerical study. Int. J. Heat. Mass Transf. 154, 119613. doi:10.1016/j.ijheatmasstransfer.2020.119613

CrossRef Full Text | Google Scholar

Umavathi, J. C., and Anwar Bég, O. (2020b). Effects of thermophysical properties on heat transfer at the interface of two immisicible fluids in a vertical duct: Numerical study. Int. J. Heat. Mass Transf. 154, 119613. doi:10.1016/j.ijheatmasstransfer.2020.119613

CrossRef Full Text | Google Scholar

Umavathi, J. C., Chamkha, A. J., Manjula, M. H., and Al-Mudhaf, A. (2005). Flow and heat transfer of a couple-stress fluid sandwiched between viscous fluid layers. Can. J. Phys. 83 (7), 705–720. doi:10.1139/p05-032

CrossRef Full Text | Google Scholar

Umavathi, J. C., Kumar, J. P., and Chamkha, A. J. (2008). Flow and heat transfer of a micropolar fluid sandwiched between viscous fluid layers. Can. J. Phys. 86 (8), 961–973. doi:10.1139/p08-022

CrossRef Full Text | Google Scholar

Upadhya, S. M., Raju, S. V. S. R., Raju, C. S. K., Shah, N. A., and Chung, J. D. (2022). Importance of entropy generation on Casson, Micropolar and Hybrid magneto-nanofluids in a suspension of cross diffusion. Chin. J. Phys. 77, 1080–1101. doi:10.1016/j.cjph.2021.10.016

CrossRef Full Text | Google Scholar

Vajravelu, K., Prasad, K. V., and Abbasbandy, S. (2013). Convective transport of nanoparticles in multi-layer fluid flow. Appl. Math. Mech. 34 (2), 177–188. doi:10.1007/s10483-013-1662-6

CrossRef Full Text | Google Scholar

Vamvakidis, K., Mourdikoudis, S., Makridis, A., Paulidou, E., Angelakeris, M., and Dendrinou-Samara, C. (2018). Magnetic hyperthermia efficiency and MRI contrast sensitivity of colloidal soft/hard ferrite nanoclusters. J. Colloid Interface Sci. 511, 101–109. doi:10.1016/j.jcis.2017.10.001

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, X.-Q., and Mujumdar, A. S. (2007). Heat transfer characteristics of nanofluids: A review. Int. J. Therm. Sci. 46 (1), 1–19. doi:10.1016/j.ijthermalsci.2006.06.010

CrossRef Full Text | Google Scholar

Wang, X., Xu, X., and Choi, S. U. S. (1999). Thermal conductivity of nanoparticle - fluid mixture. J. Thermophys. Heat. Trans. 13 (4), 474–480. doi:10.2514/2.6486

CrossRef Full Text | Google Scholar

Nomenclature