Fatigue failure and energy evolution of double-stepped fissures contained marble subjected to multilevel cyclic loads: a lab-scale testing

The instability of rock mass induced by the deterioration and failure of rock bridge is often encountered in hard rock engineering. Under engineering disturbance, a steep and gentle stepped sliding surface is prone to forming along the rock bridges between the intermittent rock joints, which directly controls the rock mass instability modes. In order to reveal the influence of fissure angle on the fatigue deterioration and energy evolution mechanism of stepped double-flawed hard rock, the multilevel cyclic loading mechanical test were carried out on flawed marble samples with fissure angle of 10°, 30°, 50°, and 70° angles. The testing shows that rock strength, fatigue lifetime, peak strain and dissipated energy increase with increasing fissure angle and the increase rate of them becomes sharply in the high cyclic level. In addition, the increase of dissipated energy accelerates with the increase of cyclic loading level, and shows a sudden increase trend in the last cyclic loading stage. When the joint fissure angle is 10°, the dissipated energy is the smallest and the dissipated energy is the largest at 70°. Moreover, a damage evolution model based on dissipated energy is established to describe the characteristics of damage accumulation. The model is in good agreement with the experimental data and reflects the nonlinear characteristics of damage accumulation.

1 Introduction

Rock is the basic material for building large rock projects such as mines, tunnels, slopes, water conservancy and underground spaces (Cerfontaine and Collin, 2018). The interior of the rock contains abundant fractures, pores and other micro defects. These randomly distributed microdefects accumulate, expand and penetrate under dynamic loads such as impact, earthquake, engineering blasting and vehicle loading (Erarslan and Williams, 2012; Yin et al., 2018; Orozco et al., 2019). These actions may then lead to damage and fracture of the rock, which in turn induces many catastrophic accidents in rock engineering. Especially in the hard rock projects, such as the Jiama Copper Polymetallic Mine in Tibet and Baiyunebo Iron Ore Mine, China, the rock bridge is likely to be communicated under engineering disturbances such as unloading, excavation and blasting. It is very easy to form a stepped slip surface, resulting in the deterioration and failure of the rock bridge, thus causing the slope destabilization and huge catastrophic losses. Therefore, it is of great importance to investigate the fracture and energy evolution characteristics of stepped marble under multi-stage fatigue loading, in order to maintain the long-term stability of rock engineering.

Nowadays, many scholars in the field of rock mechanics have conducted a lot of researches on the fatigue mechanical properties of rocks under cyclic loading, and have obtained a large number of research results (Ray et al., 1999; Momeni et al., 2015; Erarslan, 2021; Faradonbeh et al., 2021). In terms of rock deformation law under cyclic loading, Zhao et al. (2014) studied the fatigue characteristics of limestone under cyclic loading at different frequencies by using the MT S810 dynamic testing machine. The results clarified that the linear relationship between the fatigue life of limestone and the loading frequency satisfied the double logarithmic coordinate system, and the fatigue life increased with the increase of loading frequency. Afterwards, they proposed a fatigue life calculation model based on the average strain increment. By studying the fatigue mechanical properties of rock materials, Xiao et al. (2011) pointed out that the higher the upper limit stress, the higher the stress amplitude, the higher the loading frequency, the shorter the fatigue life of the rock, etc. However, the essence of rock damage is driven by energy conversion (Wang and Zheng, 2015; Peng et al., 2019), and the fracture mechanism is influenced by many factors. The commonly used mechanical indicators are hard to describe the damage evolution and fracture process of rocks. Therefore, employing energy analysis to describe the damage evolution during rock deformation is effective to reveal the damage mechanism under cyclic fatigue loading (Erarslan and Williams, 2012; Wang et al., 2020; Bai et al., 2021; Shirani Faradonbeh et al., 2021; Zhou et al., 2021; Bai et al., 2022; 2023; Wang et al., 2023a; Wang et al., 2023b; Wang et al., 2023c; Wang et al., 2023d). Xie et al. (2005, 2008) pointed out that energy dissipation caused rock damage and led to structural deterioration and loss of strength. At the same time, energy release was intrinsically responsible for triggering the sudden destruction of the rock as a whole. Finally, the overall connection between rock strength and energy dissipation and release was established. Zhang et al. (2014) carried out conventional triaxial tests on marble, limestone and sandstone to study the characteristics of energy nonlinear evolution of rock deformation process. It was shown that most of the external work was converted into elastic strain energy stored inside the rock specimens before failure, and the dissipated energy increased little, and the dissipated energy increased rapidly after the yielding point, and the elastic energy increased slowly. Wang et al. (2020) investigated the anisotropic fracture and energy dissipation characteristics of interbedded marble under multistage cyclic loading, they found that the dissipated energy was impacted by the interbed angle. Li et al. (2017) analyzed and developed a theoretical model between axial strain and number of cycles under cyclic loading and unloading conditions by conducting uniaxial graded cyclic loading and unloading tests on two sets of sandstone specimens, and derived an evolution equation for damage variables to evaluate the degree of rock damage. Wang et al. (2023a) performed triaxial alternative cyclic loading and unloading confining pressure tests to investigate the influence of prior damage and rock macro-meso failure characteristics, and they found that the energy-driven failure evolution of rock is strongly impacted by the previous damage degree.

Although plenty of studies have been achieved on rock damage evolution investigations, there are fewer studies on the fracture and energy evolution characteristics of rock double-stepped fissure contained rock. As a result, a series of multilevel fatigue loading tests were carried out in this work to reveal the fracture and energy evolution characteristics of pre-flawed rock samples. This study is focusing on the effects of fissure angle on rock peak strain, fatigue strength, and dissipated energy evolution pattern. The results are of great significance for revealing the mechanical properties of double stepped fissure contained rock mass under fatigue disturbance.

2 Testing methods

2.1 Rock specimen preparation

The tested rock material was obtained from an open pit slope located at the Jiama Copper Polymetallic Mine in Tibet, China, as shown in Figures 1A, B. The stepped fissures can be clearly observed and the information of rock structure is obtained by using 3D laser detection technology in Figures 1C, D. According to the method recommended by ISRM (Ulusay, 2015), the rock mass obtained from the open pit slope was prepared into a cylinder with a diameter (D) of 50 mm and a height (H) of 100 mm. Both ends of the specimens were polished to ensure that the non-uniformity error is less than 0.05 mm and the parallelism is less than 0.1 mm. Two parallel fissures were prefabricated on the specimens using a precision carving machine as shown in Figure 2A. The angle between the fissure and the horizontal plane was set to be 10°, 30°, 50°, and 70°, respectively. For all the prepared rock specimens, the angle and length of the rock bridge between the two fissures were the same. Typical marble specimens with different fissure angle used in this work are shown in Figure 2B.

FIGURE 1

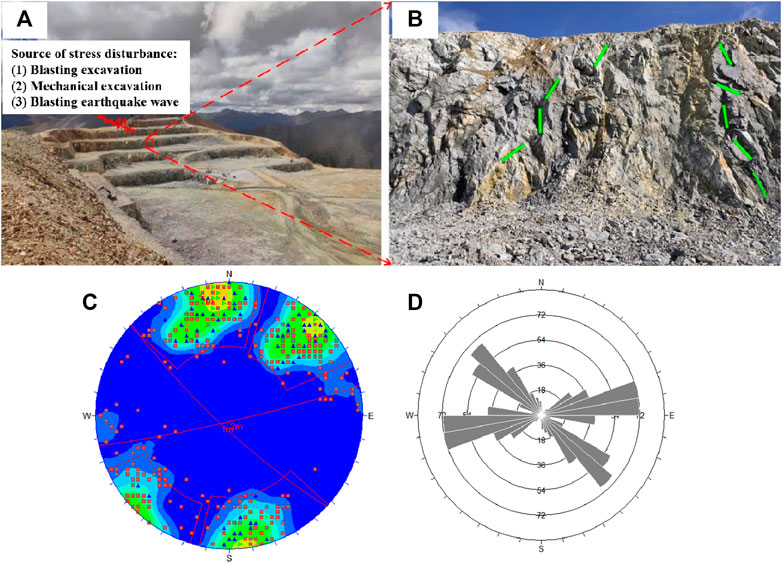
FIGURE 1. Description of the slope rock mass structure of the jiama copper polymetallic mine in tibet (A) Schematic diagram of stress disturbance; (B) Stepped rock bridge structure; (C) Result of stereographic projection; [(D) Rose diagram of dominant joints in rock mass].

FIGURE 2

FIGURE 2. Preparation of marble specimens with two pre-existing flaws (A) Working diagram of rock engraving machine; [(B) Marble specimens with double stepped fissures].

2.2 Testing scheme

All mechanical tests were conducted in an electro-hydraulic servo-controlled rock testing system RDST 1000, which can apply the dynamic loading frequencies in the range of 0–10 Hz. During rock deformation, the axial strain and lateral strain were continuously measure using grating sensors installed at the longitudinal and circumferential of rock specimens. The information of axial stress, axial strain, and lateral strain were recorded by computer at the same loading sampling frequency. The following gives the detailed experimental procedures.

(1) Static loading stage: Loading to 15 MPa using a constant loading rate which the loading rate was 0.06 mm/min (1.0 × 10⁻⁵ s⁻¹).

(2) Fatigue loading stage: Based on the field monitoring data of blasting and tramcar loads, the testing was conducted using a cyclic load applied at a dynamic frequency of 0.2 Hz. During the cyclic loading process, the stress amplitude increases by 5 MPa for each cyclic loading phase and is controlled by the sine wave stress cyclic loading. During each dynamic cyclic loading stage, 30 cycles were applied to the specimens. Stress cycling was performed using this multi-stage approach until the specimen were finally damaged. The loading paths are shown in Figure 3.

FIGURE 3

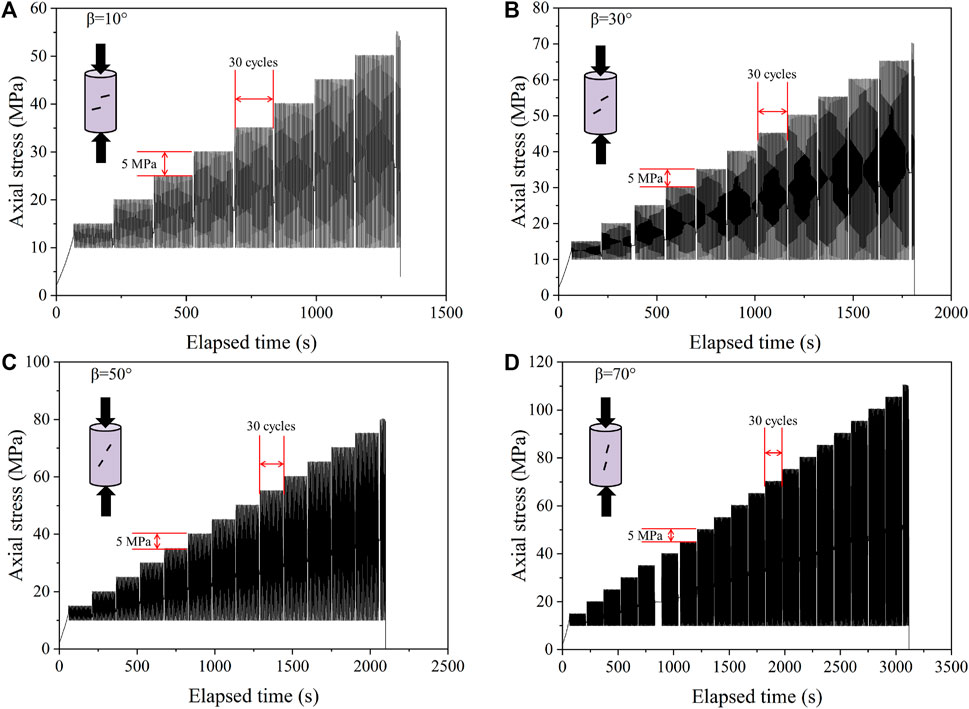
FIGURE 3. Loading paths of marble specimens with different fissure angles [(A–D) Rock specimens with fissure angles of 10°, 30°, 50°, and 70°, respectively].

According to the loading path, it can be found that different flaw angles greatly affect the duration of the test. The test duration increases significantly with the increase of the fissure angles. The fatigue strength of the rocks with fissure angles of 10°, 30°, 50°, and 70° are 55.21 MPa, 70.32 MPa, 80.24 MPa, and 110.55 MPa, respectively. The rock specimens are subjected to different stages of fatigue loading until destruction, going through 9, 12, 14, and 20 loading stages, respectively. The total number of loading cycles for the four sets of specimens varied due to the different fissure angles, which are 244, 334, 398, and 582, respectively. The number of cyclic loading increases with the increase of the fissure angles, indicating that the fissure angles have a significant effect on the strength and strain of the rock.

2.3 Energy conversion during rock failure

According to the energy dissipation and release theory proposed by Xie et al. (2011), the process of compressive deformation and damage of rocks contains energy input, accumulation of releasable elastic strain energy, and continuous energy dissipated and release. The whole process is very complex. Assuming that in an energy-independent closed environment, the rock unit is subjected to external work to produce damage strain, and according to the law of conservation of energy and transformation, the following relationship exists between each strain energy:

$E_n=E_{n_e}+E_{n_d}(1)$

Where: $E_n$ is the total energy; $E_{n_e}$ is the elastic energy; $E_{n_d}$ is the dissipated energy used for rock damage as well as irreversible strain to drive crack initiation, extension and coalescence.

According to the studies of Solecki and Conant (2003), Formula 1 can be converted in terms of energy density, as shown in Formula 2:

$\int UdV=\int U_{e}dV+\int U_{d}dV(2)$

Where: V is the volume of the rock, U is the total strain energy density, U_e is the elastic energy density, U_d is the dissipated energy density.

The total energy, elastic energy, and dissipated energy are calculated as follows:

$U={\displaystyle \underset{{\epsilon }_1}{\overset{{\epsilon }_{\max }}{\int }}}\sigma d\epsilon ={\displaystyle \sum _{i=1}^n}\frac{1}{2}\left({\sigma }_i+{\sigma }_{i+1}\right)\left({\epsilon }_{i+1}-{\epsilon }_i\right)(3)$

$U_e={\displaystyle \underset{{\epsilon }_1}{\overset{{\epsilon }_{\max }}{\int }}}\sigma d\epsilon ={\displaystyle \sum _{i=1}^n}\frac{1}{2}\left({\sigma }_i+{\sigma }_{i+1}\right)\left({\epsilon }_{i+1}^e-{\epsilon }_i^e\right)(4)$

$U_d=U-U_e={\displaystyle \underset{{\epsilon }_1}{\overset{{\epsilon }_{\max }}{\int }}}\sigma d\epsilon -{\displaystyle \underset{{\epsilon }_2}{\overset{{\epsilon }_{\max }}{\int }}}\sigma d\epsilon (5)$

The calculation process of total energy (U), elastic energy (U_e) and dissipated energy (U_d) are shown in Figure 4A. The area of the ABCD region under the loading curve represents the total energy (Wang et al., 2021). The area of the EFDC region under the unloading curve represents the elastic energy released during the unloading process. The dissipated energy is the difference between the total energy and the elastic energy area.

FIGURE 4

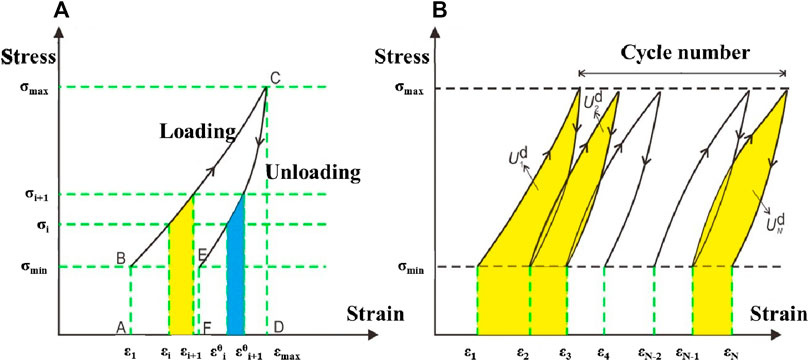
FIGURE 4. Calculation of strain energy density, adopted from Wang et al. (2021) [(A): Schematic diagram of strain energy calculation: (B) N cycles cumulative dissipated strain energy].

In cyclic loading tests, the study of fatigue damage variables for accumulative damage evolution is essential for the prediction of fatigue instability. The damage variables can be defined in terms of different physical-mechanical parameters such as elastic modulus, acoustic emission, density, damping, dissipated energy, etc. Xiao et al. (2010) used six common definition methods to obtain damage variables, revealing the advantages and disadvantages of these methods. In this work, the dissipated energy is used to define the fatigue damage variable, as shown in Formula (6):

$D_{FL}={\displaystyle \sum _{i=1}^{N_i}}{U}_i^d/{\displaystyle \sum _{i=1}^{N_f}}{U}_i^d(6)$

Where: $D_{FL}$ is the damage variable caused by fatigue loading, $N_i$ is the stage number, $N_f$ is the number of stages in the failure of the rock, $U_i^d$ is the dissipated energy of the i-th stage.

3 Results and discussions

3.1 Typical stress strain responses

For multi-stage fatigue loading tests on rock specimens with different fissure angles, the axial and lateral stress and strain curves can be obtained as shown in Figures 5A, B. It can be found that as the test time increases, the loading curve and unloading curve no longer coincide due to the plastic deformation of the specimen’s interior, thus forming a hysteresis loop. The form of the hysteresis loop varies with the loading time, and for each fatigue loading stage before specimen damage, the hysteresis loop exhibits a change from sparse to dense. The sparse morphology of the hysteresis curve is due to the increase in stress amplitude, which causes a large plastic strain. Subsequently the formed cracks are gradually closed, resulting in the hysteresis curve becoming dense. Compared with the hysteresis curves of the previous fatigue loading stage, the final stage of fatigue loading shows violent crack development, a significant increase in dissipated energy, and a significant increase in deformation of the specimen during the compressive yielding stage. Therefore, the hysteresis curve in this stage becomes increasingly sparse until the specimen failure.

FIGURE 5

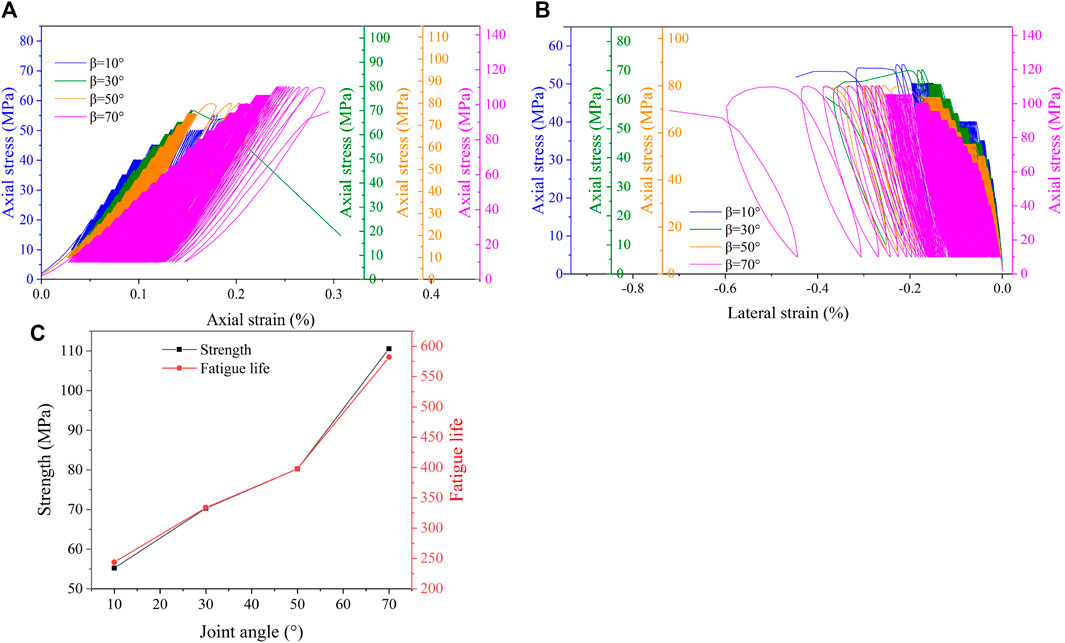
FIGURE 5. Stress-strain curves, strength and fatigue life curves ofmarble specimens with different fissure angles [(A) Axial strain; (B) Lateral strain; (C) Changes of strength and fatigue life of marble specimens with different fissure angles].

In order to study the effect of different fissure angles on marble specimens, the effect of different fissure angles on the strength and fatigue life of marble specimens are analyzed, as shown in Figure 5C. It can be visualized from the Figure 5C that the strength as well as the lifetime of the marble specimens increases gradually with the increase of the fissure angles under the fatigue loading condition.

In order to describe more intuitively the effect of fissure angles on the marble specimens fatigue responses, the loading path (Figure 3) and the stress strain curves (Figure 5) are combined to obtain the damage characteristics of the marble specimens under fatigue loading conditions, detailed mechanical parameters as shown in Table 1.

TABLE 1

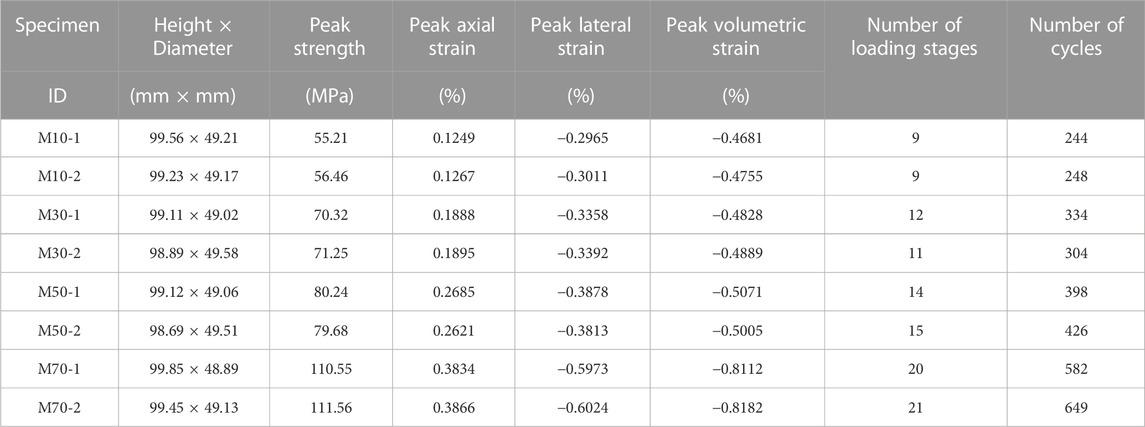
TABLE 1. Mechanical parameters of marble specimens with different fissure angles under fatigue loads.

3.2 Specimen deformation characteristics

The form of the hysteresis loops at each fatigue loading stage reflects the changes in the internal microstructure of the rock, which is closely related to the crack extension behavior. Afterwards, the relationship curves of the maximum axial strain with the number of fatigue cycles for marble specimens with different fissure angles are plotted, as shown in Figure 6. It can be observed that the axial strain increases with the increase in the number of cycles and exhibits a significantly different trend at the beginning of cyclic loading than at the middle and the end. At the beginning of each loading stage, the strain increases rapidly and then tends to become stable until the last cyclic loading stage. At the same time, the sudden increase in stress amplitude also leads to larger axial deformation, and the accumulative plastic strain increases continuously with the cyclic loading stage, and the axial strain increases sharply at the last fatigue loading stage until the specimens are damaged.

FIGURE 6

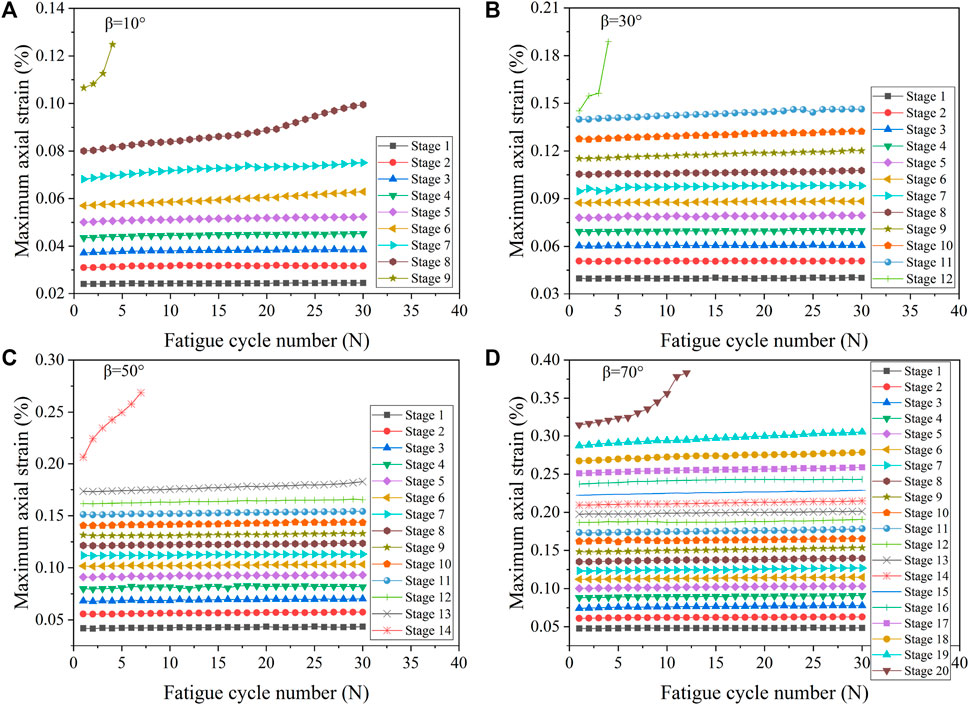
FIGURE 6. Variation diagram of axial strain of marble specimens with different fissure angles during fatigue strain [(A–D) Rock specimens with fissure angles of 10°, 30°, 50°, and 70°, respectively].

In order to further analyze the relationship between lateral strain and fissure angle during the whole fatigue loading process, the relationship curves between the lateral strain and the number of fatigue cycles during the fatigue loading process of the marble specimens with different fissure angles are plotted as shown in Figure 7. It can be found that the lateral strain increases significantly faster at the end of cyclic loading relative to the earlier loading stages, and the radial strain increases suddenly at the last loading level until the damage of the rock. Meanwhile, in order to be able to better describe the effect of axial and lateral strains on the volume change of the specimen, the volumetric strain is calculated from the axial and lateral strains. The volumetric strain reflects the volume change of the rock during deformation and is also a good indicator to reveal the fracture behavior of the rock. The relationship curves between the volumetric strain and the number of fatigue cycles are shown in Figure 8. Combining Figures 7, 8, it can be found that the trends of lateral strain and volumetric strain are very similar, which indicates that the lateral strain of the rock has a greater effect on the fatigue damage of the rock.

FIGURE 7

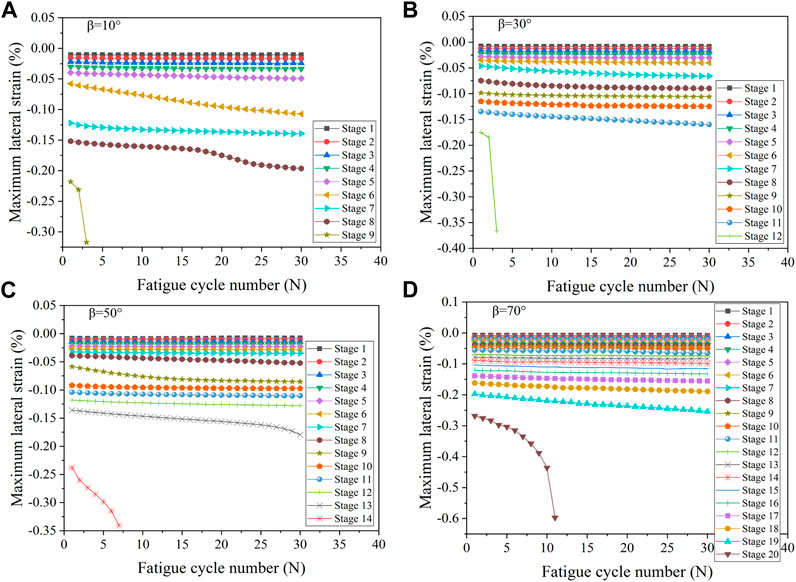
FIGURE 7. Radial strain curves of marble specimens with different fissure angles during fatigue strain [(A–D) Rock specimens with fissure angles of 10°, 30°, 50°, and 70°, respectively].

FIGURE 8

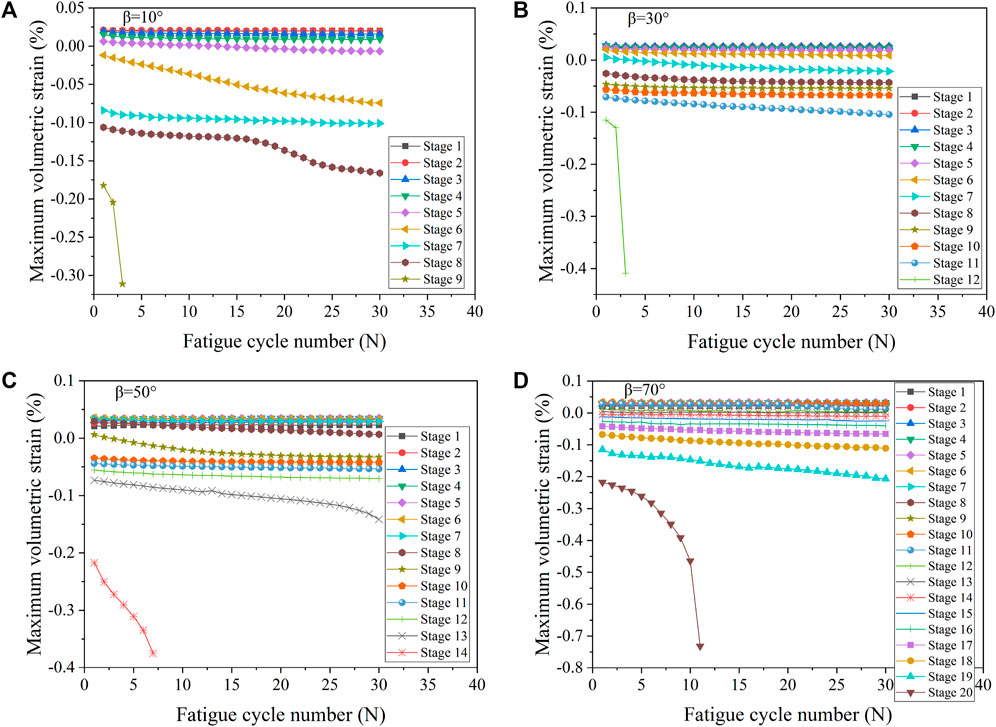
FIGURE 8. Volumetric strain curves of marble specimens with different fissure angles during fatigue strain [(A–D) Rock specimens withfissure angles of 10°, 30°, 50°, and 70°, respectively].

The relationship curves between axial, lateral and volumetric strains and fatigue loading stages can be more intuitive to see that with the increasing loading stages, the axial, lateral and volumetric strains gradually become larger, and in the final stage of fatigue loading, they all increase sharply. In addition, the peak axial strain, peak lateral strain and peak volumetric strain of the marble specimens with different fissure angles under fatigue loading conditions are obtained as shown in Figure 9D. It can be found that each peak strain gradually increases with the increasing angle of the joint. Meanwhile, with the increase of cyclic loading stage, the volumetric strain changes from positive to negative, as shown in Figure 9C. The phenomenon indicates that the rock specimens underwent a process of compression followed by expansion. The results also further illustrate that the degree of damage as well as the damage form of different marble specimens of fissure angles under fatigue loading conditions are different.

FIGURE 9

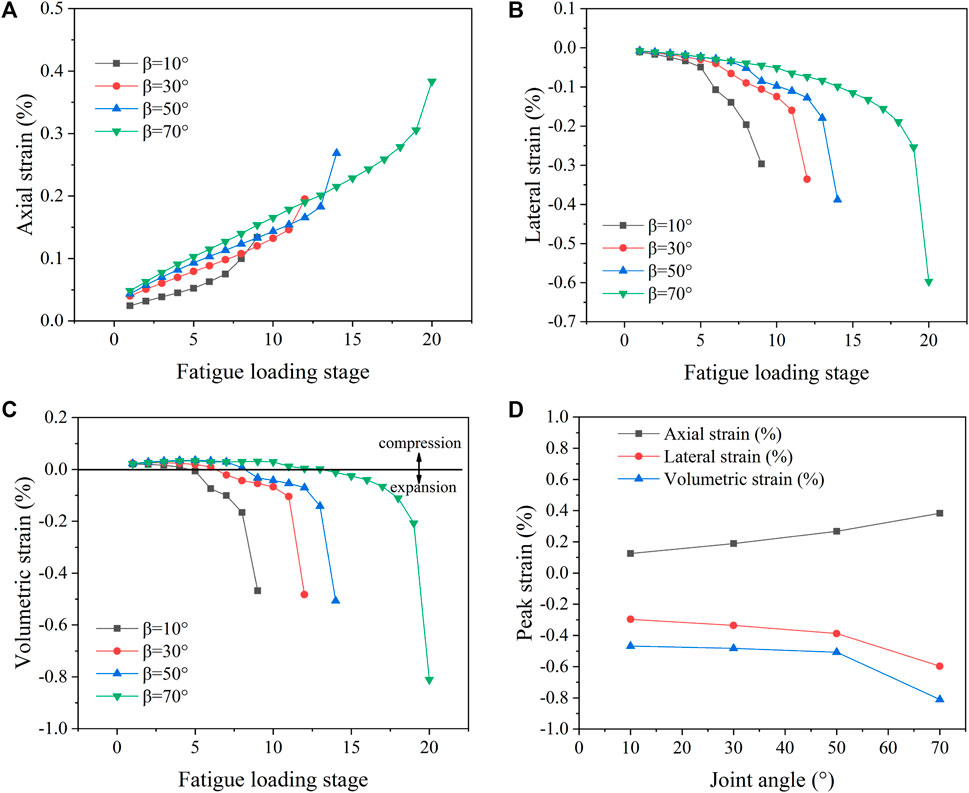
FIGURE 9. Relationship between strain and fatigue loading stage and variation trend of peak strain [(A–C) Relationship between axial, lateral and volumetric and fatigueloading stage; (D) Variation trend of peak strain of marble specimens under different fissure angles].

3.3 Energy evolution characteristics

The relationship between the total input energy, elastic energy, dissipated energy and the number of cycles is plotted using Eqs 3–5, as shown in Figures 10A–D. The results show that the overall trend of the energy curves is similar under the effect of static loading. During the initial cyclic loading stage, the total input energy is almost entirely converted into elastic energy and stored in the interior of the rock. At this time, the damage of the rock is smaller, so the dissipated energy is also smaller, the total energy curve and the elastic energy curve basically overlap, and the dissipated energy is almost zero.

FIGURE 10

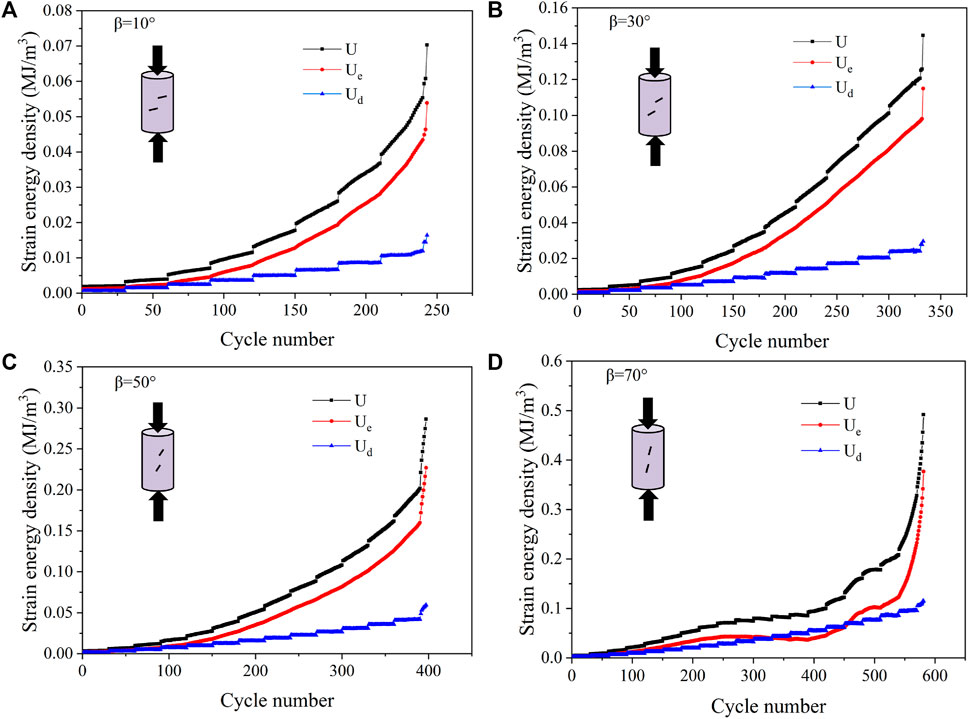
FIGURE 10. Variation of total strain energy, elastic energy and dissipated energy of marble specimens with the cycle number [(A–D)Rocks pecimens with fissure angles of 10°, 30°, 50°, and 70°, respectively].

As the number of fatigue cycles increases, damage occurs inside the rock, the accumulation of damage gradually increases, and part of the input energy is consumed to produce cracks, so the elastic energy curve no longer coincides with the total energy curve. As the number of fatigue cycles gradually increases, the dissipated energy also begins to increase, and the growth rate accelerates. It can be found that the increase of dissipated energy within the same cyclic loading stage is not obvious. When the stress amplitude increases, the dissipated energy increases suddenly. In the final fatigue loading stage, the dissipated energy increases faster and faster until the rock is damaged (Figure 10). The results show that fatigue loading causes further damage to the marble specimens, but the damage accumulation is not severe, while the increasing stress amplitude accelerates the damage deterioration of the rock. Meanwhile, the overall increasing trend in dissipated energy prior to damage of the marble specimens accelerates, indicating a continued increase in the energy required to drive crack expansion and a gradual increase in the degree of rock damage.

In order to investigate the effects of different fissure angles on the damage extension and the corresponding energy release and dissipation of marble specimens under fatigue loading conditions, the evolution process between the total energy, elastic energy, dissipated energy and the number of cycles of marble specimens with different angles of joint is analyzed and obtained as shown in Figures 11A–C. It can be visualized from the figure that the input energy is converted into elastic energy and dissipated energy, and the proportion of dissipated energy increases with the increase of cyclic loading stage. During the fatigue deformation of the marble specimens, most of the energy is released from the elastic energy, and the accumulation of damage caused by fatigue loading is increasing, which in turn leads to an increase in dissipated energy. The dissipated energy increases slowly at the initial stage of fatigue loading, but increases rapidly near the failure of the specimen, and increases sharply at the last fatigue loading stage until the specimen is damaged. The sharp increase of dissipated energy indicates the unstable propagation and coalescence mode of the crack. The dissipated energy is maximum for a fissure angle of 70° and minimum for a fissure angle of 10°. The dissipated energy for different fissure angles are 0.016 MJ/m³, 0.030 MJ/m³, 0.059 MJ/m³ and 0.115 MJ/m³, respectively.

FIGURE 11

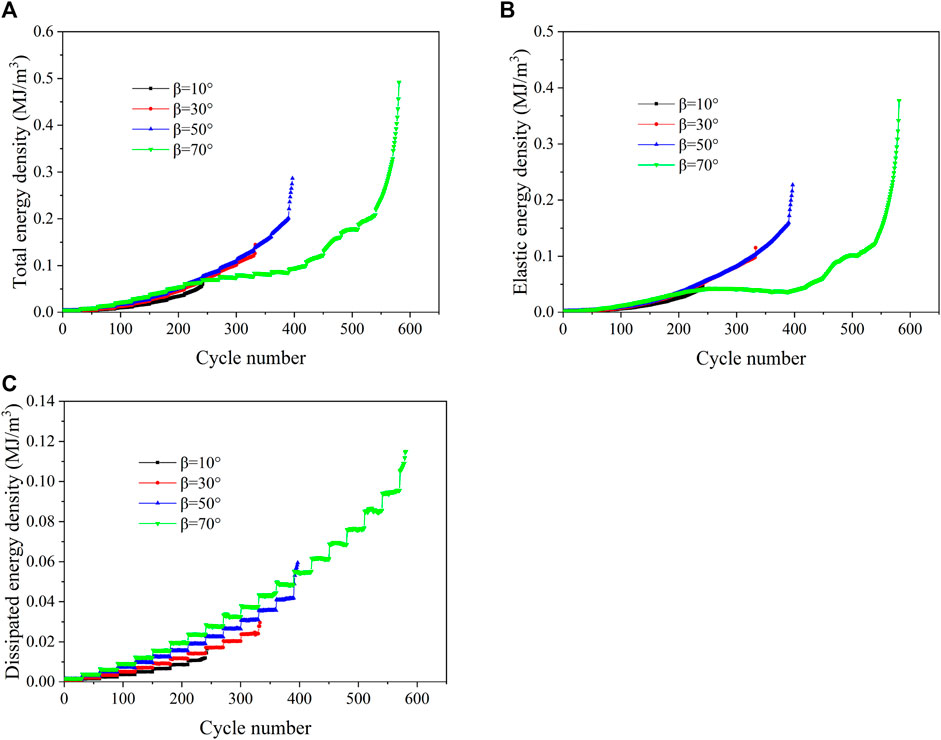
FIGURE 11. Relationship between the strain energy and fatigue loading stage [(A–C) Respectively the relationship between total strain energy, elastic energy and dissipated energy and the number of cycles].

The energy curves exhibit a stepped growth mode, and the energy increment is larger when the stress amplitude increases abruptly. The results indicate that the number of cycles of fatigue loading and the fatigue loading stage greatly affect the dissipation and release characteristics of rock energy. The relationship between the total energy, elastic energy, dissipated energy and maximum axial stress of the rock specimens are shown in Figures 12A–D. The curve fitting method is adopted to reveal the relationship between strain energy density and the upper limit of stress amplitude. The fitting results show that during each fatigue loading, the total energy, elastic energy and dissipated energy of four groups of marble specimens with different fissure angles increase with the increase of the upper limit of axial stress, and the increasing rate is gradually accelerated. In addition, a significant non-linear increasing trend is observed, and the data satisfies a power function with high correlation. The fitting results are listed in Table 2.

FIGURE 12

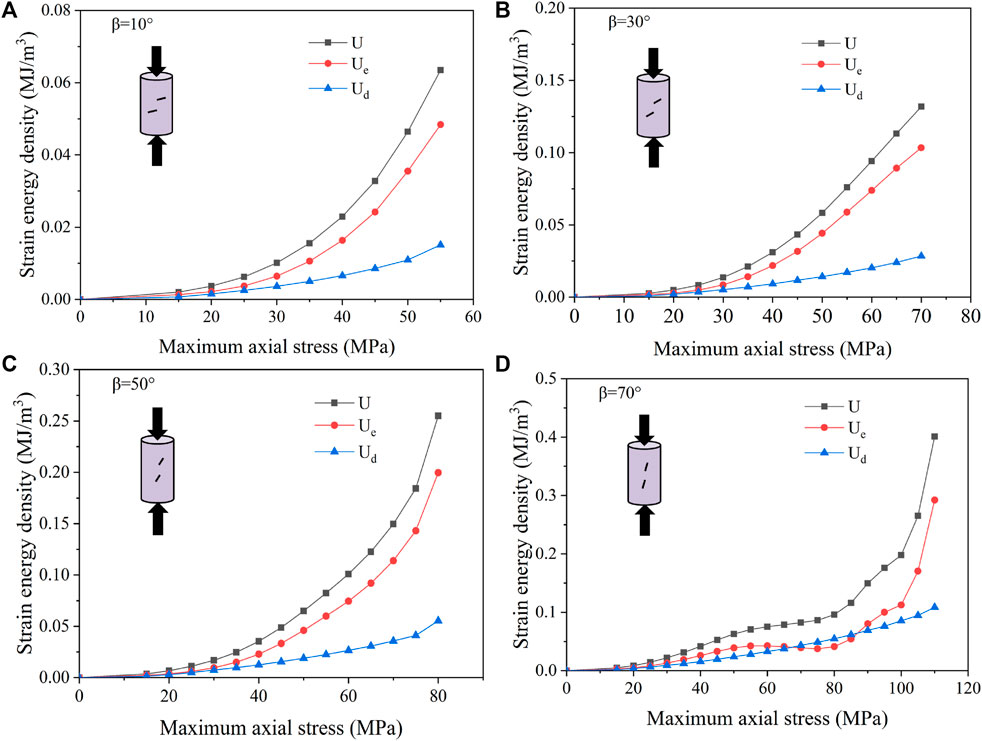
FIGURE 12. Relationship between strain energy density and the maximum axial stress [(A–D) Rock specimens with fissure angle of 10°, 30°, 50°, and 70°, respectively].

TABLE 2

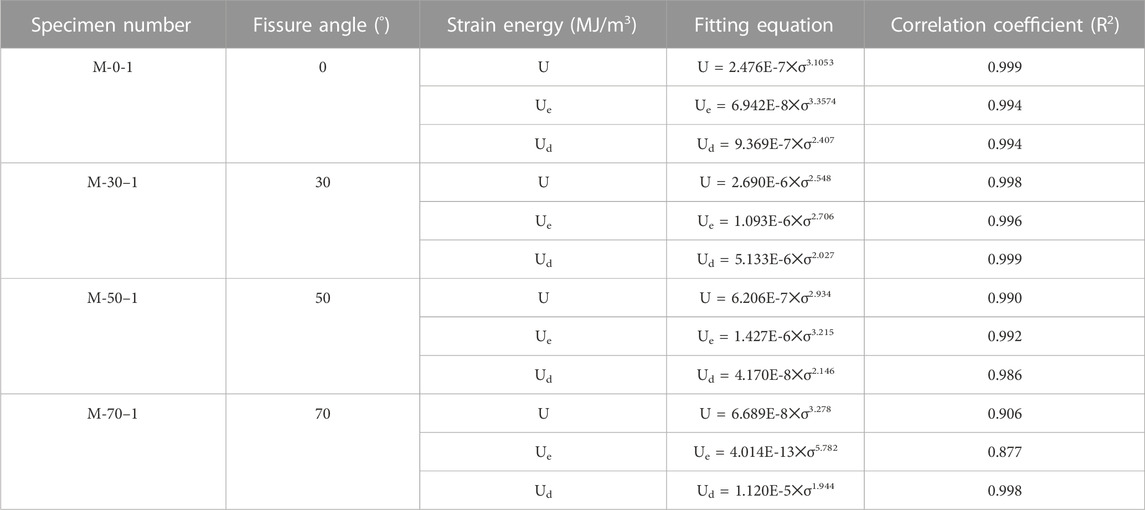
TABLE 2. Fitting results of strain energy and maximum axial stress of marble specimens with different fissure angles.

After investigation, it is found that there is a non-linear damage accumulation law in rocks under multi-stage fatigue cyclic loading conditions, and the previous models are not suitable for describing the damage evolution characteristics of rocks under this loading path (Figure 13). As rock damage and fracture is energy-driven, in my opinion, the energy index is better than other parameters to express damage propagation. In addition, the energy parameter contains rock stress and strain information, it is the comprehensive reflection of rock failure. According to Formula 6, a new dissipated energy-based damage accumulation model is proposed to describe the damage process of rocks by using dissipated energy to calculate the damage variables (Wang Y et al., 2020) which is shown in Formula 7.

$D=1-{\left(1-{\left(n/N_f\right)}^a\right)}^b(7)$

FIGURE 13

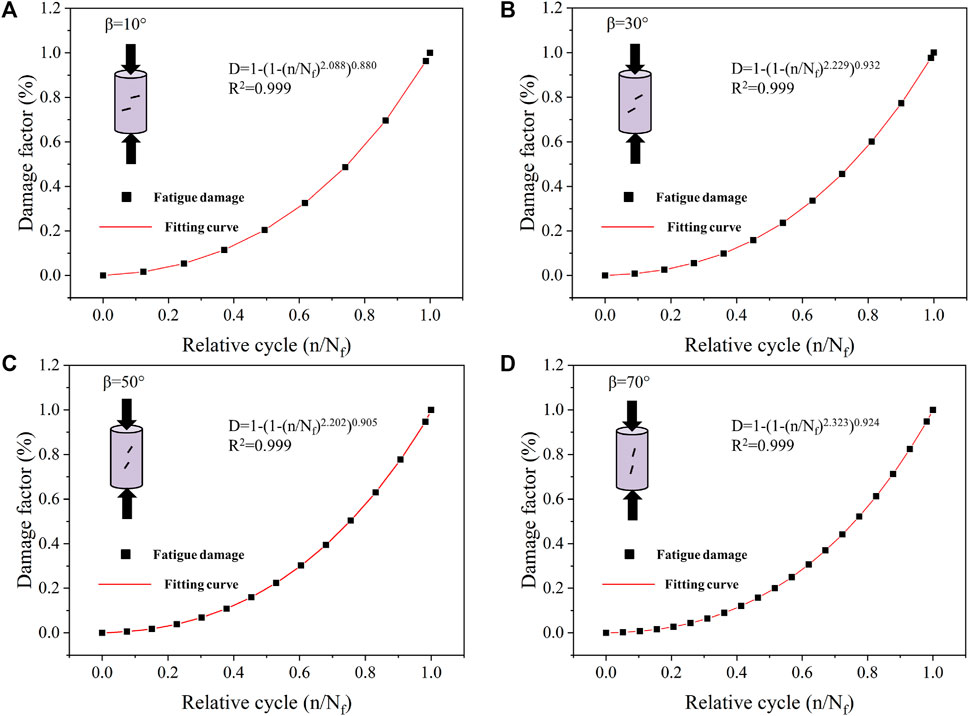
FIGURE 13. Damage evolution modeling of the marble specimens under multiple level cyclic loading [(A–D) Rock specimens with fissure angles of 10°, 30°, 50°, and 70°, respectively].

Where: D is the damage variable caused by dissipative energy, when n is 0, D is 0, when n is N_f, D is 1; N is the number of total cycles; N_f is the fatigue lifetime; a and b are the material related parameters.

According to the fitting results and the value of R², it can be seen that the accumulative damage curves show a trend of slow increasing and then fast increasing, and have obvious non-linear characteristics as well as high correlation.

3.4 Failure morphology analysis

Since rock crack initiation and fracture evolution are essentially energy-driven, and the different joint angle may lead to different capacities for energy storing and releasing in stepped marble, which causes differences in the damage forms and fracture morphology of the specimens. The macroscopic fracture forms of the typical marble specimens after destruction are shown in Figure 14. It can be clearly observed that the joints play a dominant and controlling role in the crack expansion path of the whole specimen. The crack extension paths of the four groups of typical marble specimens have similarities. The crack extensions of the specimens at the time of damage all start from the end of the fracture, and the development direction of the rock bridge is consistent with that of the joint. All of them develop through along the rock bridge starting fracture and are similar to the wing crack, and the crack extension direction gradually approaches 90° and gradually converges to the maximum principal stress direction. When the angles of the joint vary, there are also some differences. From Figure 14, it can be found that the cracks gradually transition from tension failure to shear failure as the angles of the joint increases. When β is 10°, in the longitudinal, the specimen shows vertical splitting cracks with some secondary cracks. When β is 30°, 50°, and 70° respectively, the upper and lower main crack tips are obviously controlled by the maximum principal stress. The angle between the main crack and the maximum principal stress is basically the same, showing a symmetric development trend. The expansion path of “X” conjugate crack is formed by the expansion from the tip of the joints.

FIGURE 14

FIGURE 14. Typical failure modes of rock specimens with different fissure angles [(A–D) Rock specimens with fissure angle of 10°, 30°, 50°, and 70°, respectively].

4 Conclusion

Multilevel cyclic loading tests were carried out on marble specimens with double-stepped fissures with angle of 10°, 30°, 50°, and 70°, respectively. The dynamic fracture and energy evolution properties of rocks are studied experimentally. The main conclusions are summarized as follows.

(1) The peak strain, strength, lifetime, and dissipated energy of the rock are all influenced by the fissure angle. With the increase of the fissure angle, the increasing rate of those mechanical parameters becomes dramatically at high fatigue loading level. The formation of the hysteresis loop further reveals the plastic deformation characteristics. It is found that rock volumetric strain increases slowly during the first few cyclic stages and increases sharply near to fatigue failure.

(2) The total input energy, elastic energy and dissipated energy all increase with the increase of the fissure angle. Meanwhile, the proportion of dissipated energy using to drive crack propagation increases rapidly with increasing cycles, indicating a coalescence pattern of crack network.

(3) An obvious nonlinear damage accumulation law for rock subjected to multilevel cyclic loading was revealed. A model of rock damage evolution is developed based on dissipated energy, which can fit well with testing data and can be used to describe the nonlinear damage accumulation.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

DW and ZL: Experiments, data analysis; HX and SG: Methodology, conceptualization; PL and JL: Visualization, data curation, resources; YW: Supervision, funding acquisition, project administration. All authors contributed to the article and approved the submitted version.

Funding

This study was supported by the National Natural Science Foundation of China (52174069), Beijing Natural Science Foundation (8202033) and the Fundamental Research Funds for the Central Universities (FRF-TP-20-004A2).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bai, B., Bai, F., Li, X., Nie, Q., Jia, X., and Wu, H. (2022). The remediation efficiency of heavy metal pollutants in water by industrial red mud particle waste. Environ. Technol. Innovation 28, 102944. doi:10.1016/j.eti.2022.102944

CrossRef Full Text | Google Scholar

Bai, B., Zhou, R., Cai, G., Hu, W., and Yang, G. (2021). Coupled thermo-hydro-mechanical mechanism in view of the soil particle rearrangement of granular thermodynamics. Comput. Geotechnics 137, 104272. doi:10.1016/j.compgeo.2021.104272

CrossRef Full Text | Google Scholar

Bai, B., Zhou, R., Yang, G., Zou, W., and Yuan, W. (2023). The constitutive behavior and dissociation effect of hydrate-bearing sediment within a granular thermodynamic framework. Ocean. Eng. 268, 113408. doi:10.1016/j.oceaneng.2022.113408

CrossRef Full Text | Google Scholar

Cerfontaine, B., and Collin, F. (2018). Cyclic and fatigue behaviour of rock materials: Review, interpretation and research perspectives. Rock Mech. Rock Eng. 51 (2), 391–414. doi:10.1007/s00603-017-1337-5

CrossRef Full Text | Google Scholar

Erarslan, N. (2021). Experimental and numerical investigation of plastic fatigue strain localization in brittle materials: An application of cyclic loading and fatigue on mechanical tunnel boring technologies. Int. J. Fatigue 152, 106442. doi:10.1016/j.ijfatigue.2021.106442

CrossRef Full Text | Google Scholar

Erarslan, N., and Williams, D. J. (2012). The damage mechanism of rock fatigue and its relationship to the fracture toughness of rocks. Int. J. Rock Mech. Min. Sci. 56, 15–26. doi:10.1016/j.ijrmms.2012.07.015

CrossRef Full Text | Google Scholar

Faradonbeh, R. S., Taheri, A., and Karakus, M. (2021). Failure behaviour of a sandstone subjected to the systematic cyclic loading: Insights from the double-criteria damage-controlled test method. Rock Mech. Rock Eng. 54, 1–21.

Google Scholar

Li, X. M., Liu, C. Y., and Speng, S. (2017). Fatigue deformation characteristics and damage model of sandstone subjected to uniaxial step cyclic loading. J. China Univ. Min. Technol. 46 (1), 8–17.

Google Scholar

Momeni, A., Karakus, M., Khanlari, G. R., and Heidari, M. (2015). Effects of cyclic loading on the mechanical properties of a granite. Int. J. Rock Mech. Min. Sci. 77, 89–96. doi:10.1016/j.ijrmms.2015.03.029

CrossRef Full Text | Google Scholar

Orozco, L. F., Delenne, J. Y., Sornay, P., and Radjai, F. (2019). Discrete-element model for dynamic fracture of a single particle. Int. J. Solids Struct. 166, 47–56. doi:10.1016/j.ijsolstr.2019.01.033

CrossRef Full Text | Google Scholar

Peng, K., Wang, Y. Q., Zou, Q. L., Liu, Z. P., and Mou, J. H. (2019). Effect of crack angles on energy characteristics of sandstones under a complex stress path. Eng. Fract. Mech. 218, 106577. doi:10.1016/j.engfracmech.2019.106577

CrossRef Full Text | Google Scholar

Ray, S. K., Sarkar, M., and Singh, T. N. (1999). Effect of cyclic loading and strain rate on the mechanical behaviour of sandstone. Int. J. Rock Mech. Min. Sci. 36 (4), 543–549. doi:10.1016/s0148-9062(99)00016-9

CrossRef Full Text | Google Scholar

Shirani Faradonbeh, R., Taheri, A., and Karakus, M. (2021). Post-peak behaviour of rocks under cyclic loading using a double-criteria damage-controlled test method. Bull. Eng. Geol. Environ. 80, 1713–1727. doi:10.1007/s10064-020-02035-y

CrossRef Full Text | Google Scholar

Solecki, R., and Conant, R. J. (2003). Advanced mechanics of materials. London: Oxford University Press.

Google Scholar

R. Ulusay (Editor) (2015). The ISRM suggested methods for rock characterization, testing and monitoring, 2007–2014.

Google Scholar

Wang, C., He, B., Hou, X., Li, J., and Liu, L. (2020). Stress–energy mechanism for rock failure evolution based on damage mechanics in hard rock. Rock Mech. Rock Eng. 53, 1021–1037. doi:10.1007/s00603-019-01953-y

CrossRef Full Text | Google Scholar

Wang, Y., Tang, P. F., Han, J. Q., and Li, P. (2023d). Influence of dynamic disturbed frequency on rock failure characteristics under triaxial cyclic and multistage unloading confining pressure loads. Fatigue Fract. Eng. Mater Struct. 46, 1527–1544. doi:10.1111/ffe.13946

CrossRef Full Text | Google Scholar

Wang, Y., Yan, M. Q., and Song, W. B. (2023c). The effect of cyclic stress amplitude on macro-meso failure of rock under triaxial confining pressure unloading. Fatigue & Fract. Eng. Mater. Struct. 31 (12), 3008–3025. doi:10.1111/ffe.13993

CrossRef Full Text | Google Scholar

Wang, Y., Cao, Z., Li, P., and Yi, X. (2023b). On the fracture and energy characteristics of granite containing circular cavity under variable frequency-amplitude fatigue loads. Theor. Appl. Fract. Mech. 125, 103872. doi:10.1016/j.tafmec.2023.103872

CrossRef Full Text | Google Scholar

Wang, Y. F., and Zheng, X. J. (2015). Energy evolution mechanism in deformation and destruction process of grit stone. J. Henan Polytech. Univ. 34 (1), 30–34.

Google Scholar

Wang, Y., Han, J., Ren, J., and Li, C. (2021). Anisotropic fracture and energy dissipation characteristics of interbedded marble subjected to multilevel uniaxial compressive cyclic loading. Fatigue & Fract. Eng. Mater. Struct. 44 (2), 366–382. doi:10.1111/ffe.13365

CrossRef Full Text | Google Scholar

Wang, Y., Tang, P., Han, J., and Li, P. (2023a). Energy-driven fracture and instability of deeply buried rock under triaxial alternative fatigue loads and multistage unloading conditions: Prior fatigue damage effect. Int. J. Fatigue 168, 107410. doi:10.1016/j.ijfatigue.2022.107410

CrossRef Full Text | Google Scholar

Xiao, J. Q., Feng, X. T., Ding, D. X., and Jiang, F. L. (2011). Investigation and modeling on fatigue damage evolution of rock as a function of logarithmic cycle. Int. J. Numer. Anal. Methods Geomechanics 35 (10), 1127–1140. doi:10.1002/nag.946

CrossRef Full Text | Google Scholar

Xiao, J. Q., Ding, D. X., Jiang, F. L., and Xu, G. (2010). Fatigue damage variable and evolution of rock subjected to cyclic loading. Int. J. Rock Mech. Min. Sci. 47 (3), 461–468. doi:10.1016/j.ijrmms.2009.11.003

CrossRef Full Text | Google Scholar

Xie, H. P., Ju, Y., and Li, L. Y. (2008). Energy mechanism of deformation and failure of rock masses. Chin. J. Rock Mech. Eng. 27 (9), 12.

Google Scholar

Xie, H. P., Li, L. Y., Ju, Y., Peng, R. D., and Yang, Y. M. (2011). Energy analysis for damage and catastrophic failure of rocks. Sci. China Technol. Sci. 54 (1), 199–209. doi:10.1007/s11431-011-4639-y

CrossRef Full Text | Google Scholar

Xie, H. P., Ju, Y., and Li, L. Y. (2005). Criteria for strength and structural failure of rocks based on energy dissipation and energy release principles. Chin. J. Rock Mech. Eng. 24 (17), 3003–3010.

Google Scholar

Yin, P., Ma, H. C., Liu, X. W., Bi, J., Zhou, X. P., and Berto, F. (2018). Numerical study on the dynamic fracture behavior of 3D heterogeneous rocks using general particle dynamics. Theor. Appl. Fract. Mech. 96, 90–104. doi:10.1016/j.tafmec.2018.04.005

CrossRef Full Text | Google Scholar

Zhang, L. M., Gao, S., and Wang, Z. Q. (2014). Rock elastic strain energy and dissipated strain energy evolution characteristics under conventional triaxial compression. J. China Coal Soc. 39 (7), 1238–1242.

Google Scholar

Zhao, K., Qiao, C. S., and Luo, F. R. (2014). Experimental study of fatigue characteristics of limestone samples subjected to uniaxial cycle loading with different frequencies. Chin. J. Rock Mech. Eng. 33, 3466–3475.

Google Scholar

Zhou, Y., Zhao, D., Li, B., Wang, H., Tang, Q., and Zhang, Z. (2021). Fatigue damage mechanism and deformation behaviour of granite under ultrahigh-frequency cyclic loading conditions. Rock Mech. Rock Eng. 54 (9), 4723–4739. doi:10.1007/s00603-021-02524-w

CrossRef Full Text | Google Scholar