Electron beams near surfaces: the concept of partial intensities for surface analysis and perspective on the low energy regime

Electron beam techniques are indispensable tools for the analysis of surfaces in fundamental as well as applied fields of science and technology. Significant improvements have been made in the past decades in the quantitative understanding of electron spectra, particularly with respect to the near-surface transport of signal electrons. The concept of partial intensities is a simple approach providing physical insight into transport of electrons in solids, a numerically convenient means for spectrum modelling and an essential ingredient for spectrum interpretation. The energy-dissipation process of energetic electrons in solids is discussed from the perspective of the partial intensities, offering a unified model for any type of electron beam technique, be it in the quasi-elastic (QE) or the continuous slowing down (CSD) regime. Examples are given for modelling and analysis of electron spectra such as X-ray photoelectron spectra (XPS), Elastic peak electron spectra (EPES) and electron energy-loss spectra (EELS). The physical model as well as the quantities for electron beam interaction with solids are reviewed, and methods for spectrum modelling and analysis are presented. The examples considered demonstrate the high level of accuracy nowadays attainable for characterisation of surfaces and nanostructures employing techniques using medium energy electrons ($>$100 eV). This is in contrast to the low energy regime, where a number of problems prevent a similar level of understanding. The topic of low energy electrons (LEEs) is rapidly gaining importance since in this energy range the involved electrons not only act as signal carriers, but also actively participate in electrochemical processes of importance in fields ranging from nanotechnology to life sciences. Issues of future importance in the field of LEEs are discussed and recent developments such as the 2-dimensional electron cascade in the scanning field electron microscope are highlighted.

1 Introduction

The chemical composition of a solid surface as well as electron induced chemical processes taking place in its vicinity, are of immense importance for our daily lives: webecome evermore dependent on nanostructured microelectronic devices, while electron beam induced chemical processes are not only important for nanotechnology Kozawa and Tagawa (2010); Kozawa and Tamura (2021), they are also taking place in living organisms, and are highly relevant to our very wellbeing Gao et al. (2021); McKee et al. (2019); Barrios et al. (2002); Zheng et al. (2008). Since it is impossible to obtain the desired information on the spot, i.e., inside the solid, one must employ techniques inducing a signal which travels from the location of interest to the surface, into vacuum. This signal can be a mere information-carrier, or it can actively participate in the electrochemical processes of interest. The first part of the present article deals with a simple but highly effective approach describing the transport of electrons in solids and the surface analysis techniques relying on this knowledge to extract the desired information about chemistry from an electron spectrum.

The physical model for the transport of medium energy electrons ($>$100 eV) in surface electron spectroscopy and microscopy is outlined in the next section. This mainly concerns the energy dissipation process in the course of multiple scattering events, which will be presented from the perspective of the partial intensity approach (PIA) Werner (2001). The PIA is an effective approach for electron spectroscopy and microscopy which mainly concerns the quasi-elastic (QE) energy regime of energy losses small compared to the initial energy, but can simply be extended to the true slowing down (SD) regime, providing a unified approach to the slowing down of electrons for any electron beam technique Werner (1997); Wagner and Werner (1998). Theoretical methods for obtaining quantities relevant to spectrum simulation and interpretation are discussed, with emphasis on, but not limited to, numerical modelling using the Monte Carlo (MC) technique. Applications to a variety of electron beam techniques are presented such as Elastic Peak Electron Spectroscopy (EPES) Powell and Jabłonski (1999); Werner (2005), Reflection Electron Energy Loss Spectroscopy (REELS) Tougaard and Chorkendorff (1987); Werner (2010) and X-ray Photoelectron Spectroscopy (XPS) Werner and Powell (2021). It is shown that when appropriate analysis techniques are applied, a satisfactory level of consistency is obtained between data derived from widely different approaches, different laboratories and techniques. This is in stark contrast to the situation several decades ago when for many applications the accuracy of quantification of surface atomic composition, calibration of length dimensions on the nanoscale, etc., was typically beyond ∼50%.

For energies below ∼100 eV many applications nowadays are unable to model all relevant observables with an accuracy comparable to that in the medium energy range. This applies both to experiment as well as to the physical models used for the electron-solid interaction and the methods for testing and verifying the latter, as well as the physical quantities appearing in any model. The main problems in quantitative understanding of the near-surface diffusion of low energy electrons (LEEs) and emission of secondary electrons (SEs), are outlined and potential methods to overcome them are discussed.

2 Physical model of the electron-solid interaction

Individual electrons in a beam are characterised by their momentum and spin, quantities which are subject to changes brought about by scattering processes. Since energy and momentum are both conserved quantities, a change in the magnitude of the momentum (an energy loss) and its direction (a deflection) strictly speaking always occur simultaneously. However, deflections are mainly due to the interaction with the screened Coulomb potential of the ionic cores (nuclei), while energy losses are almost exclusively caused by excitations of valence electrons to unoccupied states of the solid. While in the case of a valence electron excitation the projectile rest mass (i.e., of the incoming electron) is comparable to the mass of the interaction partner, it is always much smaller than that of the ionic cores. Therefore, the distinction between elastic scattering (deflections without significant energy loss) by the ionic cores and inelastic scattering (energy losses without significant deflection) by valence electrons represents a good approximation in many situations. Changes in the spin can be brought about by elastic as well as inelastic processes but will not be treated in the present paper, i.e., spin-resolved techniques are disregarded.

The binary collision model will be adopted for most of the remainder of this paper, i.e., coherent scattering (diffraction effects) will be neglected. This represents a very good approximation in the medium energy range as long as the samples investigated are not perfectly prepared single crystals. For medium energies this approximation is then justified by the fact that the electron wavelength is generally smaller than the interatomic distance. For energies just above the vacuum level, the typical energy range of secondary electrons (SEs), this is no longer true and yet the emission of SEs can be successfully modelled by means of the MC technique. The explanation is that the electron wavelength changes upon crossing of the surface potential barrier. The inner potential U_i is typically of the order of 10 eV for most materials. An electron with a vacuum energy close to zero therefore still has an appreciable energy within the solid, and hence a sufficiently small wavelength to justify the binary collision approximation. This constitutes a distinct physical difference between secondary electrons with a small energy in vacuum and hot electrons inside the solid with an energy between the Fermi level and the vacuum level.

An important further aspect of the kinematics of inelastic electron scattering is also related to the finite electron rest mass: electrons have an appreciable momentum even at low energies. The scattering kinematics then allows an electron to partially transfer its momentum to the interaction partner. This gives rise to multiple inelastic (as well as elastic) electron scattering, where subsequent interactions are independent of each other Werner et al. (2011; 2013b). The fact that multiple scattering is characterised by a Markov-chain of binary collisions makes it possible to treat the electron transport within a Boltzmann-type kinetic equation which can be solved by means of Monte Carlo (MC) simulations Shimizu and Ding (1992); Dubus et al. (1993) or linear transport theory Tilinin et al. (1997); Beilschmidt et al. (1994); Dubus et al. (2000); Tilinin and Werner (1993, 1992).

Elastic scattering processes can be modelled on the basis of the differential elastic scattering cross section (DECS), dσ(θ_s)/dΩ, representing the distribution of polar scattering angles θ_s in an individual deflection. For a spherically symmetric potential of the ionic cores, the azimuthal scattering angles are uniformly distributed. The DECS can be obtained by means of the partial wave expansion method Salvat et al. (2005): an incoming plane wave is expanded into a series of spherical waves with a different angular momentum and the phase shift experienced by each partial wave is calculated for a relevant atomic potential (e.g., a Dirac-Hartree-Fock-Slater-potential). The amplitude of the outgoing spherical wave is then constructed by superposition of the partial waves. A part of the DECS for 500 eV electrons incident on Au is shown by the green curve in Figure 8C below. The DECS is generally characterised by a prominent forward scattering peak and deep minima, the so–called generalised Ramsauer-Townsend minima, which are formed by interference between the incoming plane wave and the outgoing spherical wave Schattschneider (1986). These oscillations are more prominent for lower energies and higher atomic number.

The average distance between successive elastic collisions, the elastic mean free path (EMFP, λ_e) is obtained by integrating the cross section over the unit sphere Salvat et al. (2005). In many situations the most relevant quantity in an elastic process is the transferred momentum. The so–called transport mean free path (TRMFP, λ_tr) which measures the momentum transfer along the initial direction and is obtained by integrating the cross section over the unit sphere with a weighting factor (1 − cos θ_s). This weighting factor corresponds exactly to the fraction of the momentum transferred along the incoming direction, emphasising large scattering angles (θ_s > π/2). Therefore, mainly those deflections contribute to the transport mean free path for which the transferred momentum is of the order of the original momentum: the transport mean free path is the typical distance travelled by a particle before it “forgets” its original direction and represents the characteristic length for momentum relaxation. This is the main phenomenon related to elastic scattering and explains why one can use atomic potentials to model medium-energy elastic scattering in solids: solid state effects mainly influence the weakly bound (solid state) electrons far away from the nucleus, corresponding to large angular momenta, giving rise to small angle scattering. While small angle scattering is important for the elastic mean free path, the average distance between large angle deflections, the transport mean free path is virtually unaffected by solid state effects.

Energy losses in the course of an inelastic process occur via interaction of the probing electron with the (delocalised) solid state electrons. The solid is originally electrically neutral and the field of the particle strongly perturbs the solid, polarising the solid state electrons. The polarisation field induced by the incoming particle eventually decelerates it. The susceptibility of the solid to become polarised is described by the dielectric function ɛ(ω, q). Within the linear response formalism Landau et al. (1984), the energy dissipation of charged particles inside solids is governed by the energy loss function Im[−1/ɛ(ω, q)] and the quantities ℏq and ℏω are then identified as the momentum transfer and energy loss in an inelastic interaction. Near an interface between two media with different dielectric functions, the boundary conditions in Maxwell’s equations give rise to additional modes of inelastic scattering, so-called surface excitations, which, being dipole modes, have a lower resonance frequency than the bulk modes. Bulk (monopole) and surface (dipole) scattering are the most important types of inelastic processes for electron spectroscopy, while in the field of plasmonics, for complex nano-structured morphologies, higher orders of the multipole expansion of the field also become important de Abajo (2010), but their resonance energies are again lower and these features are not regularly resolvable in typical surface analysis methods. A third type of energy loss process relevant for photoelectron emission are so-called intrinsic excitations. Here the polarisation of the solid state electrons is set up by the sudden appearance of the core hole, rather than by the outgoing photoelectron. The photoelectron then continues to produce extrinsic excitations along its trajectory inside the solid. The three types of inelastic processes are illustrated in Figures 1A–C.

FIGURE 1

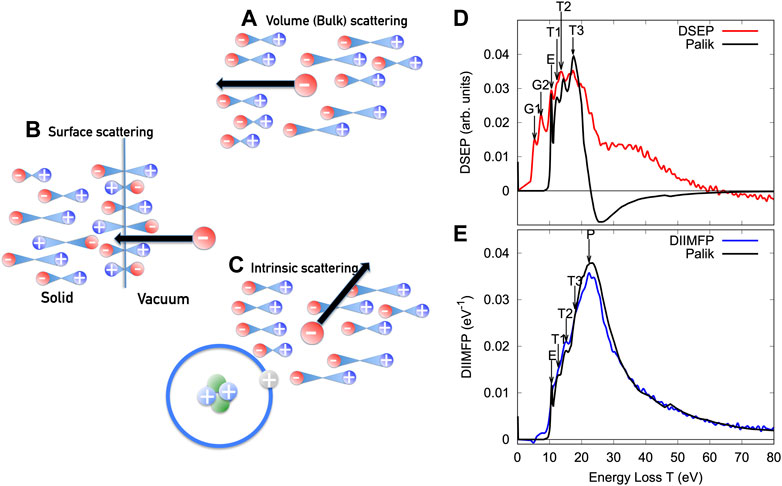
FIGURE 1. Schematic illustration of the three types of inelastic scattering: (A) bulk or volume inelastic scattering; (B) surface excitations; and (C) intrinsic excitations. The black curve in (D) represents the differential surface excitation probability (DSEP) for SiO₂; (E) normalised differential inverse inelastic mean free path (DIIMFP) for SiO₂ calculated using optical constants in Palik’s book Palik (1985), Palik (1991); the red and blue curves were derived from the experimental REELS spectra shown in Figure 7B.

Since inelastic scattering is essentially a many-body process, the distribution of energy losses per unit path length is used as a fundamental quantity describing energy losses. This quantity, commonly referred to as differential inverse inelastic mean free path (DIIMFP) can be calculated within the first Born approximation from the dielectric function of a solid ɛ using classical electrodynamics Landau et al. (1984), taking into account the electronic structure of the solid in the collision kinematics. For surface losses, the distribution of energy losses during a single surface crossing, the so-called differential surface excitation probability (DSEP) is a convenient description, it can also be calculated on the basis of optical data taking into account the boundary conditions of Maxwell’s equations at an interface between two media with a different susceptibility Tung et al. (1994);Salvat-Pujol and Werner (2013).

The DIIMFP (normalised to unity area) for SiO₂ is compared in Figure 1EAstašauskas et al. (2020) with data based on optical constants in Palik’s books Palik (1985; 1991); Figure 1D displays the differential surface excitation probability (DSEP). The most prominent feature in the DIIMFP is the peak at ∼22 eV (indicated by the label “P”) which is due to the excitation of a plasmon, a longitudinal oscillation of the electron gas Schattschneider (1986). The peaks labelled “T” are commonly assigned to interband transitions, the peak labelled “E” is the exciton in SiO₂, while the peaks labelled “G” are gap states created near the surface by defect formation in the course of the sample cleaning procedure with Ar⁺-ion sputtering Astašauskas et al. (2020). The negative excursion in the DSEP is due to the so-called “Begrenzungs”-effect Ritchie (1957), the complementarity of surface and bulk excitations.

The total electron inelastic mean free path (IMFP) is a quantity of fundamental importance for any electron beam technique. This quantity is defined as “the average distance an electron travels in between successive inelastic collisions, measured along its trajectory.” The IMFP is obtained by integrating the DIIMFP over all kinematically allowed energy losses. For non-conducting materials and non-relativistic energies it can be expressed as Boutboul et al. (1996); Shinotsuka et al. (2022)

${\lambda }_i{\left(E\right)}^{-1}=\frac{1}{\pi \left(E-E_g\right)}\underset{E_g}{\overset{E-\left(\mathrm{\Delta }{E}_v+E_g\right)}{\int }}d\omega \underset{q_{-}}{\overset{q_{+}}{\int }}\frac{dq}{q}\mathrm{I}\mathrm{m}\left[\frac{-1}{ϵ\left(\omega ,q\right)}\right].(1)$

where E is the incoming energy, E_g is the band gap energy and ΔE_v denotes the width of the valence band. The upper and lower bounds of the momentum transfer in the case of parabolic bands are given by energy conservation as:

$q_{\pm }=\left(\sqrt{2\left(E-E_g\right)}\pm \sqrt{2\left(E-\omega -E_g\right)}\right)(2)$

Here atomic units have been used (ℏ = m_e = e ≡ 1). The corresponding formulae for conducting materials are obtained by setting E_g = 0 and replacing the upper limit of the integration over the energy loss by ω_max = E − E_F.

Typical values for the characteristic pathlengths are shown in Figure 2 for polymethylmetacrylate (PMMA). The blue dash-dotted curve represents the elastic mean free path, being considerably smaller than the transport mean free path (green), which in turn is larger than the inelastic mean free path (black). The IMFP was calculated with Eq. 1 by Shinotsuka Shinotsuka et al. (2022). For energies above ∼100 eV, the IMFP lies below the TRMFP, while for smaller energies the IMFP increases rapidly, since the phase space available for electronic transitions becomes exhausted when the primary energy approaches the vacuum level, in particular when it becomes of the order of the band gap for an insulator. The red dashed curve represents the IMFP according to the TPP-2M semiempirical formula of Ref. Shinotsuka et al. (2022). The absolute value of the pathlengths for energies E in the range 100 < E < 2000eVare all of the order of a few monolayers, implying that the signal in the characteristic peaks of, e.g., a photoelectron spectrum originates from a depth range of the order of a few monolayers, explaining the superior surface sensitivity of electron spectroscopy techniques and underscoring the necessity for having accurate IMFP values at one’s disposal in order to quantify electron spectroscopic data.

FIGURE 2

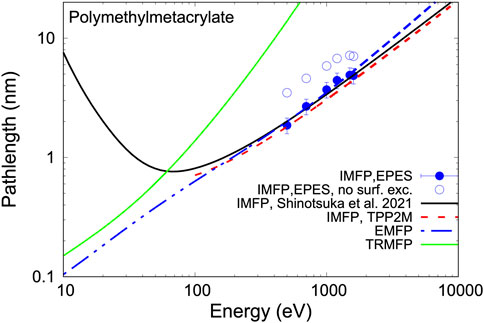
FIGURE 2. Characteristic pathlengths for polymethylmetacrylate (PMMA). Blue curve: elastic mean free path (EMFP, λ_e); Green curve: transport mean free path (TRMFP, λ_tr); Black curve: inelastic mean free path (IMFP, λ_i); Red dashed curve: IMFP according to the TPP-2M semiempirical formula of Shinotsuka et al. (2022); The data points are results of IMFP measurements using EPES Werner et al. (2022b) with (filled symbols) and without (open symbols) correction for surface excitations (see Figure 6 below).

3 The electron energy dissipation process and the partial intensity approach

A photoelectron spectrum obtained by irradiating a Si substrate with a 52 nm thick Al overlayer with linearly polarised x-rays of an energy of hν = 7936 eV is shown in Figure 3. While the main photopeak of the overlayer signal is very prominent, and accompanied on the low kinetic energy side with energy losses due to multiple plasmon excitation in Al, the zero loss peak of the substrate is hardly discernible and, surprisingly, it is also accompanied by multiple plasmon losses. The plasmon energy losses in the Si-substrate spectrum also correspond to the plasmon energy of Aluminium, i.e., the overlayer Kinoshita et al. (2007). The solid curves in Figures 3A,B as well as the datapoints in (c) represent results of Monte Carlo simulations carried out using the NIST standard reference database SRD-100 Simulation of Electron Spectra for Surface Analysis (SESSA) Werner et al. (2014c); Smekal et al. (2005).

FIGURE 3

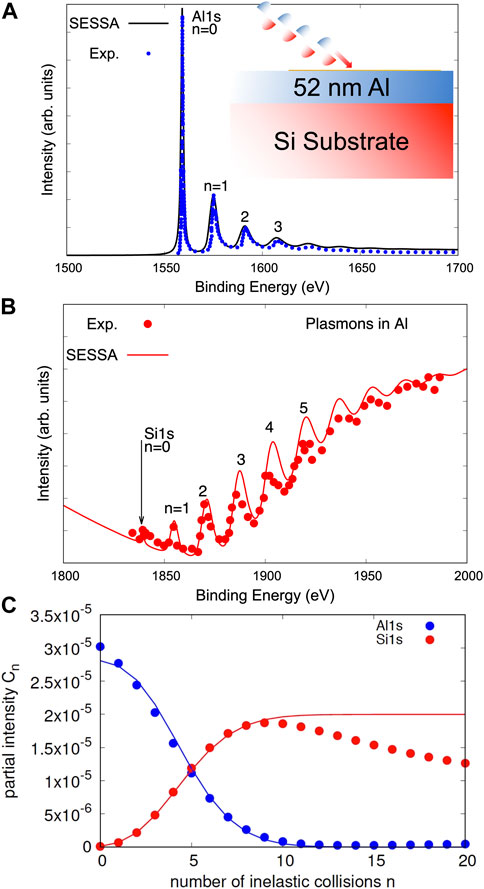
FIGURE 3. Hard x-ray photoelectron spectra of a 52 nm Al overlayer on a Si substrate excited with polarized x-rays with hν =7936 eV; Kinoshita et al. (2007)(A) SESSA simulation of the Al 1s overlayer signal compared with experiment; (B) same as (A) for the Si 1s-signal; (C) partial intensities for overlayer and substrate signal; data points: SESSA, solid lines: Eq. 5.

A simple and effective interpretation of these features is provided by the concept of the partial intensities Werner (2001, 1997, 2005). Obviously, the presented photoelectron spectra consist of characteristic peaks superimposed on an inelastic background caused by multiple energy losses (plasmon excitations) of the signal electrons. The number of electrons within the group of n-fold inelastically scattered electrons are the so-called partial intensities, which, for a particular application are defined in the ISO 18115-1 document on Surface Chemical Analysis as the “number of electrons in an electron spectrum that reach the detector after participating in a given number of inelastic interactions of a given type.” For the rather high kinetic energies in the presented example, one can neglect deflections in the course of elastic scattering processes in a first approximation. For a photoelectron, the pathlength travelled inside the solid until it reaches vacuum and gets detected is then equal to the depth at which it was created. In other words, the distribution of pathlengths is equal to the compositional depth profile. In the binary collision model, the average number of inelastic processes ⟨n⟩ experienced after travelling the pathlength s is just s/λ_i, and the probability for n-fold scattering is given by the Poisson stochastic process Werner (1997, 2005). Then, the number of inelastic collisions for a given pathlength is given as:

$W_n^{QE}\left(s\right)={\mathrm{P}}_n\left(s\right)\equiv \frac{e^{-s/{\lambda }_i}}{n!}{\left(\frac{s}{{\lambda }_i}\right)}^n,(3)$

and the number of n-fold plasmon excitations is expressed in terms of the distribution of travelled pathlengths, Q(s), as:

$C_n=\underset{0}{\overset{\infty }{\int }}{W}_n\left(s\right)Q\left(s\right)ds.(4)$

The quantities C_n per definition represent the partial intensities. If the pathlength distribution is essentially equal to the compositional depth profile c(z), Q(s)=δ(s− c(z)), the simple case of an overlayer between the depths z = 0 and z = d, on a semi-infinite substrate yields the partial intensities by partial integration of Eq. 4 as:

$C_n=\left\{W_n\left(z_1\right)-W_n\left(z_2\right)\right\}+C_{n-1},(5)$

where for the overlayer z₁ = 0, z₂ = d while for the substrate partial intensities one has z₁ = d and z₂ = ∞ and it is assumed for simplicity that the IMFPs in the substrate and overlayer are identical. Figure 3C compares the Al 1s and Si 1s partial intensities calculated by a Monte Carlo simulation using SESSA accounting for elastic scattering (data points) with the simple model, Eq. 5, discussed above (solid curves). The agreement is reasonable, except for large values of n > 10 (large depths) where the influence of elastic electron scattering becomes more noticeable.

The simulated spectra, shown as solid curves in Figures 3A,B are simply obtained by multiplying the partial intensities with the energy distribution after n losses and summing over all collision orders:

$Y\left(E\right)=\sum _{n=0}^N{C}_n{L}_n\left(\omega \right)\otimes f_0\left(E+\omega \right),(6)$

the quantities L_n(ω) are the so-called partial energy loss distributions, i.e., the distribution of energy losses after n collisions, which are given by the n-fold self convolution of the normalised DIIMFP, w_b(ω)Werner (2001):

$\begin{array}{cc}\hfill L_1\left(\omega \right)& \equiv w_b\left(\omega \right)\hfill \\ \hfill L_n\left(\omega \right)& =\int L_{n-1}\left(\omega -{\omega }^{\prime }\right)w_b\left({\omega }^{\prime }\right)d{\omega }^{\prime },\hfill \end{array}(7)$

The first few partial loss distributions for Al are shown in Figure 4A.

FIGURE 4

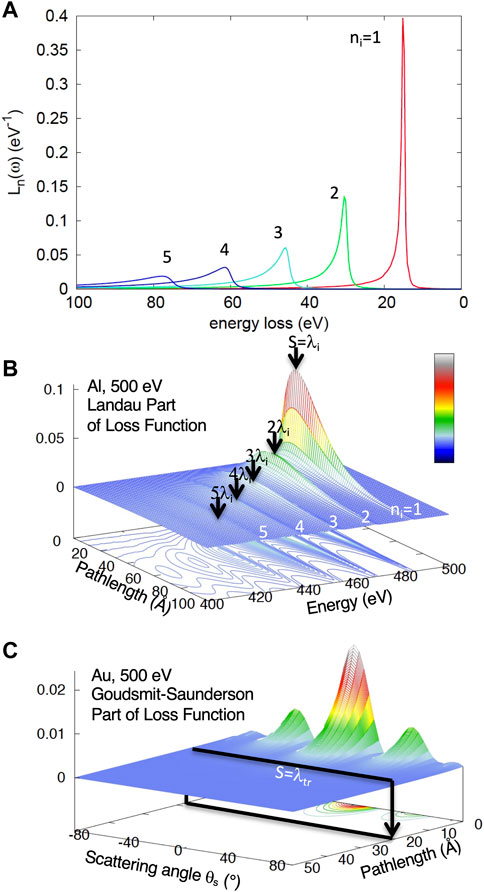
FIGURE 4. (A) Partial energy loss distributions L_n(ω) for Al, i.e., multiple self convolutions of the DIIMFP. (B) the Landau part of the LGS loss function, i.e., the distribution of energy losses as a function of the travelled path length for 500 eV electrons in Al. (C) Goudsmit-Saunderson part of the LGS loss function for 500 eV electrons in Au for scattering angles between 0° and 80°.

The energy distribution after n energy losses, F_n(E), is obtained by convoluting (denoted by the symbol “⊗”) the source energy distribution f₀(E) with the loss distributions:

$F_n\left(E\right)=f_0\left(E+\omega \right)\otimes L_n\left(\omega \right),$

Eq. 6 represents the spectrum written in the partial intensity approach. Overall, the comparison in Figure 3 demonstrates the ability of the PIA to predict relative intensities and spectral shapes. In particular, the shape and intensity of the inelastic background accompanying the Si 1s peak (in Figure 3B) reproduces the experimental data quite well, while similar simulations for Al film thicknesses 10% above and below the nominal specimen thickness (not shown) yield distinctly different shapes of the inelastic background. This result not only gives confidence in the reliability of the databases in SESSA, but also suggests a simple way to measure film thicknesses using the spectral shape of the inelastic background.

To see the connection of Eq. 6 with Landaus celebrated loss function, note that for a given pathlength s, the particle can participate in an arbitrary number of interactions n, with a relative probability described by the stochastic process W_n(s). On the other hand, fluctuations in the energetic degree of freedom after a number of interactions are given by the partial loss distributions L_n(ω) (Eq. 7). For a fixed value of n the energy fluctuation after travelling a given pathlength is therefore a product of the functions W_n(s) and L_n(ω). Summing over all collision orders, gives:

$G\left(s,\omega \right)=\sum _{n=0}^N{W}_n\left(s\right)L_n\left(\omega \right),(8)$

which is exactly Landau’s loss function Landau (1944) written in the form of a collision number expansion Werner (2005). The Landau loss function is shown in the left panel of Figure 4B for 5 keV electrons in Al. Inspection of the energy loss distribution at any particular pathlength shows that the energy dissipation process is dominated by energy fluctuations described by the partial loss distributions. In the case of Al, these can be clearly distinguished in the loss function as multiple plasmon loss peaks (cf. Figure 4A). On the other hand, for fixed energies corresponding to a multiple plasmon loss, the distribution of the travelled pathlengths corresponds to the Poisson stochastic process.

In complete analogy to the above considerations, the distribution of pathlengths for an infinite solid can be expressed in terms of multiple selfconvolutions of the elastic scattering cross section on the unit sphere ${\mathrm{\Gamma }}_{n_e}(\mathrm{\Omega })$ and the stochastic process for elastic scattering Werner (2005):

$Q^{\infty }\left(s,\mathrm{\Omega }\right)=\sum _{n_e=0}^{\infty }{W}_{n_e}\left(s\right){\mathrm{\Gamma }}_{n_e}\left(\mathrm{\Omega }\right).(9)$

where Ω = (θ, ϕ) is the direction of motion. Since elastic and inelastic scattering are independent processes, one can combine the above results into the Landau-Goudsmit-Saunderson (LGS) loss function for an infinite medium

$G\left(s,\omega ,\mathrm{\Omega }\right)=\sum _{n=0}^{\infty }{W}_n\left(s\right)L_n\left(\omega \right)\sum _{n_e=0}^{\infty }{W}_{n_e}\left(s\right){\mathrm{\Gamma }}_{n_e}\left(\mathrm{\Omega }\right)(10)$

The backward Goudsmit–Saunderson part of the LGS loss function is shown in Figure 4C for 500 eV electrons in Au. Note that for small travelled pathlengths of the order of the elastic mean free path, the loss function bears a strong resemblance with the differential elastic scattering cross section (cf. Figure 8C). For pathlengths exceeding the transport mean free path, the distribution of polar directions of motion becomes broad and featureless, implying that the particle has lost any memory of its initial direction of motion after travelling pathlengths larger than the TRMFP. This demonstrates that the transport mean free path is indeed the characteristic length for momentum relaxation.

Beyond the QE–regime, when the energy dependence of the (inelastic) mean free pathlength can no longer be neglected, the stochastic process is accurately described by the following effective approximation Werner (1997):

$W_n^{\mathit{CSD}}\left(s\right)={\mathrm{W}}_n\left(s\right)\equiv \frac{{\lambda }_n}{{\mathrm{\Lambda }}_n}\frac{e^{-s/{\mathrm{\Lambda }}_n}}{n!}{\left(\frac{s}{{\mathrm{\Lambda }}_n}\right)}^n,(11)$

where λ_n is the mean free path after n energy losses and Λ_n = ∑λ_n/(n + 1) is its average value. By replacing the Poisson stochastic process with the above stochastic process valid in the slowing down regime, the partial intensity approach effectively unifies the continuous slowing down approximation (CSDA) and the quasi-elastic approximation, and enables one to correctly account for energy fluctuations in the CSDA Werner (1997), one of the deficiencies of the CSDA as it is commonly used.

Perhaps the greatest advantage of the PIA formalism is that it allows different types of inelastic processes to be modelled in a straightforward way. This is particularly important within the context of electron spectroscopy for the treatment of surface excitations. Surface excitations take place in a shallow zone at both sides of the solid-vacuum interface, are depth-dependent, and exhibit an asymmetry with respect to the surface crossing direction Yang et al. (2019); Ding (1998); Kwei et al. (1998, 1993); Tung et al. (1994), effects which have been experimentally verified Salvat-Pujol et al. (2014); Werner et al. (2013a). An effective approximation is obtained by observing that the width of the surface scattering zone is typically of the order of the thickness of a monolayer, and is generally much smaller than the transport mean free path. In consequence, transport across the surface scattering zone is approximately rectilinear, implying that the partial intensities for surface and volume scattering are uncorrelatedWerner (2003a,b).

$C_{n_b,n_s}=C_{n_b}\times C_{n_s},(12)$

where the subscripts “s” and “b” in the collision numbers indicate surface and bulk scattering, respectively. The partial intensities for surface excitations approximately obey Poisson statistics:

$C_{n_s}=\frac{{\langle n_s\rangle }^{n_s}}{n_s!}{e}^{-\langle n_s\rangle },(13)$

where ⟨n_s⟩ represents the average number of surface excitations in a single surface crossing. Semiempirical relationships have been proposed to estimate ⟨n_s⟩ for arbitrary materials via:

$⟨n_s\left(E,\theta \right)⟩=\frac{a_s}{\sqrt{E}\cos \theta },(14)$

where a_s is a material parameter, the so–called surface excitation parameter Werner et al. (2001b) and cos θ is the polar direction of surface crossing.

The distribution of energy losses in a single surface crossing, the so-called differential surface excitation probability (DSEP) can be derived from the dielectric function, e.g., using the model proposed by Tung and coworkers Tung et al. (1994). An example for the DSEP is shown for SiO₂ in Figure 1D. The partial loss distributions for surface scattering $L_{n_s}(\omega )$ can be calculated in complete analogy to the bulk case using Eq. 7 and the spectrum can then be generalised to take into account surface excitations as followsWerner (2006):

$Y\left(E\right)=\sum _{n_b=0}^{\infty }\sum _{n_s=0}^{\infty }{C}_{n_b}{C}_{n_s}{L}_{n_b}\left({\omega }^{\prime }\right)\otimes L_{n_s}\left(\omega \right)\otimes f_0\left(E+\omega +{\omega }^{\prime }\right)(15)$

Introducing the reduced partial intensities,

${\gamma }_{n_b,n_s}=\frac{C_{n_b}{C}_{n_s}}{C_{n_b=0}{C}_{n_s=0}},(16)$

the expression for the reduced energy loss spectrum becomes:

$y\left(E\right)=\sum _{n_b=1}^{\infty }\sum _{n_s=1}^{\infty }{\gamma }_{n_b}{\gamma }_{n_s}{L}_{n_b}\left({\omega }^{\prime }\right)\otimes L_{n_s}\left(\omega \right)\otimes f_0\left(E+\omega +{\omega }^{\prime }\right),(17)$

where the lower limit of summation indicates that the elastic peak (n_s = n_b = 0) has been removed from the spectrum.

4 Spectrum analysis procedures

Two particularly important spectrum analysis techniques are 1) eliminating the inelastic background in order to accurately quantify peak intensities, e.g., in a photoemission spectrum; and 2) obtaining information on the inelastic scattering characteristics of a solid, or, in other words, the optical properties of solids. The latter is related to, and can be extracted from, the DIIMFP Werner et al. (2009).

The former problem of background subtraction assumes that the inelastic scattering characteristics (i.e., the DIIMFP and DSEP) as well as the partial intensities are known. For materials where the DIIMFP is unknown, Tougaard has proposed a universal inelastic cross section Tougaard (1997), representing a reasonable approximation for background subtraction in most cases. Accurate inelastic background subtraction is important for quantitative surface analysis since the application of semi-empirical background subtraction procedures, such as the popular Shirley method Shirley (1972), can introduce significant errors of 20% or more in surface composition. Tougaard and Sigmund (1982) introduced a rigorous background subtraction method based on the Landau loss function, significantly improving quantitation. The most general procedure is based on the partial intensity approach Werner (1995b, 2001), which offers the great advantage that it can be applied to cases where different types of scattering need to be separated from an experimental spectrum.

Elimination of a given type (e.g., bulk, surface, intrinsic) of multiple inelastic scattering from a spectrum (e.g., a photoemission spectrum) can be achieved by iteratively eliminating single, double and higher-order inelastic scattering until the considered energy range is free of multiple scattering effects Werner (1995b, 2001, 1995a). Denoting the spectrum from which k–fold scattering has been eliminated by Y_k, this can be achieved using the formula Werner (2001); Werner et al. (2001a); Werner (1995a).

$Y_{k+1}\left(E\right)=Y_k\left(E\right)-q_{k+1}\int Y_k\left(E+\omega \right)L_{k+1}\left(\omega \right)d\omega (18)$

The coefficients q_k are functions of the reduced bulk partial intensities γ_n = C_n/C_n=0 given in Table 1. The fact that the subscripts of the coefficients q_k in Table 1 are just given by the partitions of the natural numbers Ahlgren and Ono (2001) has a clear physical explanation Werner et al. (2002). The above equation is thus a means of separating the contributions to a spectrum from different types of energy losses, such as surface and volume scattering, scattering in different layers, etc., which represents one of the great advantages of the PIA.

TABLE 1

TABLE 1. The first few oefficients q_k in Equation (18) for spectrum deconvolution.

Retrieval of the differential scattering properties, such as the DIIMFP or DSEP, can be achieved by analysis of reflection electron energy loss spectra (REELS) using a primary beam with a narrow energy distribution. Since REELS always contain contributions from both surface and bulk scattering, it is necessary to analyse two spectra with different relative contributions from surface and bulk scattering to disentangle the two types of inelastic scattering Werner (2006; 2010). Experimentally, measuring spectra with different relative contributions of surface and bulk scattering can be achieved by using different primary energies and/or different geometrical configurations (see Eq. 14).

The procedure for retrieving the DIIMFP and DSEP can be summarized as follows: First the elastic peak is removed from the spectra and they are divided by the area under the elastic peak [in units of eV (!)], giving the loss spectra y_1,2(ω) in absolute units of reciprocal eV. In other words, it is brought into the form of Eq 17. In a next step, the intermediate spectra $y_{\mathrm{1,2}}^{*}(\omega )$ are derived from the measured loss spectra by applying the Tougaard-Chorkendorff procedure Tougaard and Chorkendorff (1987):

$y_{\mathrm{1,2}}^{*}\left(\omega \right)=y_{\mathrm{1,2}}\left(\omega \right)-\underset{0}{\overset{\omega }{\int }}{y}_{\mathrm{1,2}}\left(\omega -{\omega }^{\prime }\right)y_1^{*}\left({\omega }^{\prime }\right)d{\omega }^{\prime }(19)$

The normalised DIIMFP and DSEP can then be retrieved to first order by means of the series expansion:

$w_{s,b}\left(\omega \right)=u_{10}{y}_1^{*}\left(\omega \right)+u_{01}{y}_2^{*}\left(\omega \right)+u_{11}{y}_1^{*}\otimes y_2^{*}\left(\omega \right)\dots ,(20)$

Where the expansion coefficients are different for the surface and bulk (subscripts “s” and “b,” below) single scattering loss distributions. The expansion coefficients are functions of the partial intensities Werner (2010), which can be calculated by means of MC calculations. Having derived the differential scattering properties from REELS in this way, one can then extract the optical constants (mainly in the VIS-XUV-regime of energies) by fitting an appropriate model dielectric function to the DIIMFP Werner et al. (2009, 2008b, 2007); Ridzel et al. (2022).

Alternative approaches to the retrieval of optical data from REELS have been proposed by several authors, applying inverse modelling schemes to the analysis of a single spectrum, where the optical constants are directly optimised in the retrieval procedure. Various types of modelling REELS spectra are used in these approaches such as the MC method, the method of invariant embedding and others Afanas’ev et al. (2017); Chen et al. (2022); Cohen-Simonsen et al. (1997); Tahir and Tougaard (2012); Ding et al. (2002).

5 Monte Carlo algorithms for electron beam techniques

Monte Carlo (MC) calculations of particle transport for spectrum simulation are conventionally performed by following trajectories of individual particles from their point of origin through the solid to the detector. Simulation of individual trajectories proceeds by explicitly modelling the physics of each interaction leading to a change of the particles kinetic parameters such as momentum and spin. Detailed descriptions about the simulation of individual electron trajectories can be found in excellent reviews of this subject Kyser and Murata (1974); Gibarua et al. (2022); Shimizu and Ding (1992); Ding (1990); Wagner (2001); Werner (2001).

Several techniques to speed up the simulation of Auger-Meitner or photoelectron spectra in the quasi-elastic (QE) regime have been proposed in the literature Gries and Werner (1990); Werner et al. (1991); Cumpson (1993); Alkemade (1995; 1997). As shown in the previous sections, all spectral features in the QE-regime can be conveniently derived from the pathlength distribution within the formalism of partial intensities. The most important improvement in computational efficiency in the calculation of this quantity is the trajectory reversal method Gries and Werner (1990); Werner et al. (1991). It is based on Case’s reciprocity theorem of one-speed particle transport Case and Zweifel (1967), allowing one to avoid futile calculations of trajectories which do not lead to detection (see Figure 5) either because the electron does not leave the solid at all (trajectory type II. in Figure 5) or leaves the solid in a direction not seen by the analyser (type I.). Instead, the trajectory is started in the analyser and its history is traced back inside the solid. At each point along the trajectory, a contribution to the spectrum is calculated by weighting the pathlength travelled up to that point with the source strength for signal electron emission along the direction of motion at the considered location:

$\mathrm{\Delta }{C}_n\left(\mathrm{\Delta }s\right)=\sigma \underset{s}{\overset{\mathrm{\Delta }s}{\int }}{W}_n\left(s\right)Q\left(s\right)ds,(21)$

where Δs represents the part of a trajectory between succesive deflections and σ represents the source strength along the considered interval (e.g., the photoelectron cross section, the concentration of the considered element in the solid at a certain depth, etc.). The contribution to the partial intensities of all desired orders is then summed along the trajectory. A trajectory is terminated either when the pathlength becomes too large to give a sizeable contribution to the partial intensity, or when it leaves the solid. It is obvious that the described algorithm can lead to substantial increase in performance, in particular when the considered solid angle of detection is small.

FIGURE 5

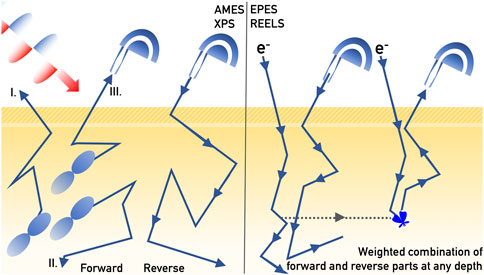
FIGURE 5. Left panel: Schematic illustration of the conventional “forward” Monte Carlo scheme for Auger-Meitner or photoelectron emission and the “reverse” trajectory algorithm which increases computational efficiency by orders of magnitude. Right panel: reverse trajectory scheme for electron reflection, elastic peak electron spectroscopy (EPES) and reflection electron energy loss spectroscopy (REELS).

For a reflection experiment (EPES, REELS), forward and reverse trajectories can be generated for the incoming and outgoing directions, which can be combined at any depth by weighting them with the probability for the appropriate deflection to take place at the considered depth, i.e., the elastic scattering cross section Werner (2005). In this way, the pathlength distribution can be obtained and the spectrum can be calculated using Eq. 6. Accounting for surface excitations can be achieved retrospectively by using Eqs 12–17.

6 Applications

6.1 Elastic peak electron spectroscopy

Elastic reflection of low energy electrons is used extensively to determine the structure of crystalline surfaces Pendry (1974); Hove et al. (2012). If coherent scattering can be disregarded, the diffraction pattern resembles the single atom diffraction pattern, or in other words, the DECS Schmid (1982). The backscattered intensity is determined by the value of the DECS for the considered experimental configuration and the inelastic mean free path. Since calculations of the DECS for realistic atomic potentials are believed to be sufficiently accurate it has been proposed Schilling and Webb (1970); Schmid (1982); Oswald et al. (1993); Oswald (1992); Gergely et al. (1995); Jabłonski (2000); Werner et al. (2001d,c); Powell and Jabłonski (1999) to experimentally determine values of the IMFP by measuring the elastic reflection coefficient. Measurement of the IMFP represents a task which is very difficult to achieve accurately by other means since earlier methods, such as the overlayer method, suffer from a number of serious drawbacks Powell and Jabłonski (1999). Gergely and Jabłonski developed this technique in a series of works Jabłonski et al. (1984); Gergely (1986); Gergely et al. (1995, 2007). As a first approximation, a single scattering approximation was used to relate the backscattering coefficient to the IMFP. This was later improved upon by an elegant analytical expression taking into account multiple elastic scattering, the so-called Oswald-Kasper-Gaukler (OKG) model Oswald et al. (1993); Oswald (1992); Werner (2005). In the mean time, it has become commonly accepted to employ MC calculations to accurately calculate the dependence of the elastic backscattering coefficient on the IMFP Powell and Jabłonski (1999). Experimental data for the elastic backscattering coefficient are compared with the OKG-model and MC calculations in Figure 8C for 500 eV electrons backscattered from a Gold surface for the geometrical configuration illustrated in Figure 8A.

Since one is interested in the elastic peak intensity, the number of inelastic collisions should be set to zero in Eq. 6, yielding for the elastic peak intensity, i.e., the zero order partial itensity:

$C_0\left({\lambda }_i\right)=\underset{0}{\overset{\infty }{\int }}Q\left(s\right)\exp \left(-s/{\lambda }_i\right)ds.(22)$

Eq. 22 explains the sensitivity of the zero-loss peak to the value of the IMFP: for small values of λ_i, the exponential function in Eqn. 22 is small and electron reflection without loss is rather unlikely while for large values of λ_i the exponential function is close to unity and an appreciable elastic reflection coefficient results. Calibration curves can be established via Eq. 22 by calculating the pathlength distribution Q(s) for the considered energy, material and experimental geometrical configuration, and evaluating the zero order partial intensities for a range of values of λ_i. The value of the IMFP can then be read-off this calibration curve by finding that IMFP value that matches the measured elastic reflection coefficient.

Since it is difficult to perform absolute measurements of the elastic reflection coefficient, reference measurements are usually performed under identical experimental conditions on materials for which the IMFP is assumed to be known. An example of this procedure is shown in Figure 6 for polymethylmetacrylate (PMMA) Werner et al. (2022b). Panel (a) shows the measured elastic peaks, together with a fit to a Gaussian, from which the peak area can be accurately determined, the calibration curve for 1,000 eV is shown in panel (b) and the retrieved values of the IMFP with and without correction for surface excitations are indicated by the arrows labelled accordingly. The reference material used was Si. It turns out Werner et al. (2022a) that the surface excitation probability for polymers is negligible compared to that of metals Werner et al. (2001b), leading to a strong correction of the retrieved IMFP values after accounting for surface excitations in the reference material. The final result, shown as filled data points in Figure 2, is in good agreement with the values derived from optical data by Shinotsuka and coworkersShinotsuka et al. (2022).

FIGURE 6

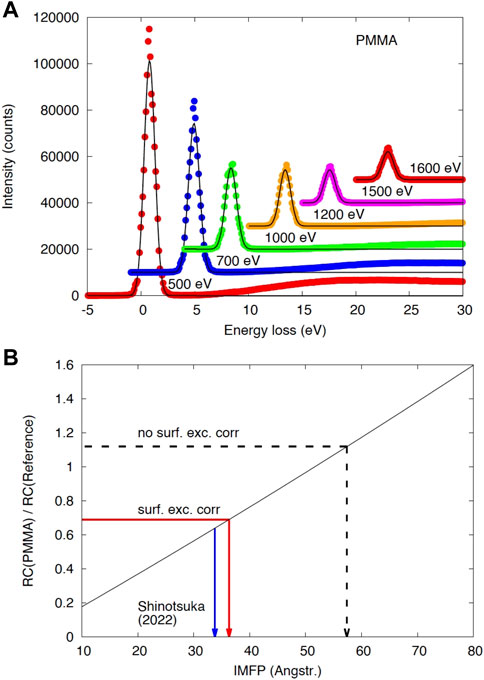
FIGURE 6. (A) Elastic peak spectra of PMMA (data points) for the employed energies shown together with the fit to a Gaussian function (black curves) for the indicated energies. (B) Calibration curve for the IMFP using the Si reference for PMMA, for 1,000 eV. Black solid curve: polynomial fit of the result of the ratio of the reflection coefficient of the unknown and the reference sample calculated with the MC technique. Red arrow: experimental result after correction for surface excitations; black dash-dotted arrow: without surface excitation correction; The blue arrow indicates the IMFP value of Ref. Shinotsuka et al. (2022). The resulting values for the IMFP are shown as data points in Figure 2.

This type of comparison has been performed for many materials in the recent past Powell and Jabłonski (1999) and a comparable consistency between IMFP values derived from optical constants and EPES measurements is generally obtained. This is a very important observation, since it implies that the accuracy in the IMFP values has dramatically improved since the early days of electron spectroscopy where a large variation (of up to 50% !) of IMFP values cited in the literature was seen Seah and Dench (1979). Since the IMFP is a quantity of paramount importance not only for quantification of surface concentrations, but also for nanoscale calibration of film thickness by means of electron beam attenuation, it implies a serious advancement of the field of electron spectroscopy.

6.2 Reflection electron energy loss spectroscopy

Figure 7 illustrates the analysis of two REELS spectra to retrieve the inelastic scattering characteristics, from which the optical constants can eventually be derived Astašauskas et al. (2020). The spectra in Figure 7B were measured at two different energies, 500 and 3,000 eV, both taken at normal incidence with an emission angle of 60°, corresponding respectively to larger and smaller contributions of surface excitations (see Eq. 14). The surface was cleaned by 4 keV Ar⁺-ion sputtering, the elastic peak was subtracted from the measured spectra which were divided by the elastic peak intensities to give the reduced loss spectrum in absolute units corresponding to Eq 17.

FIGURE 7

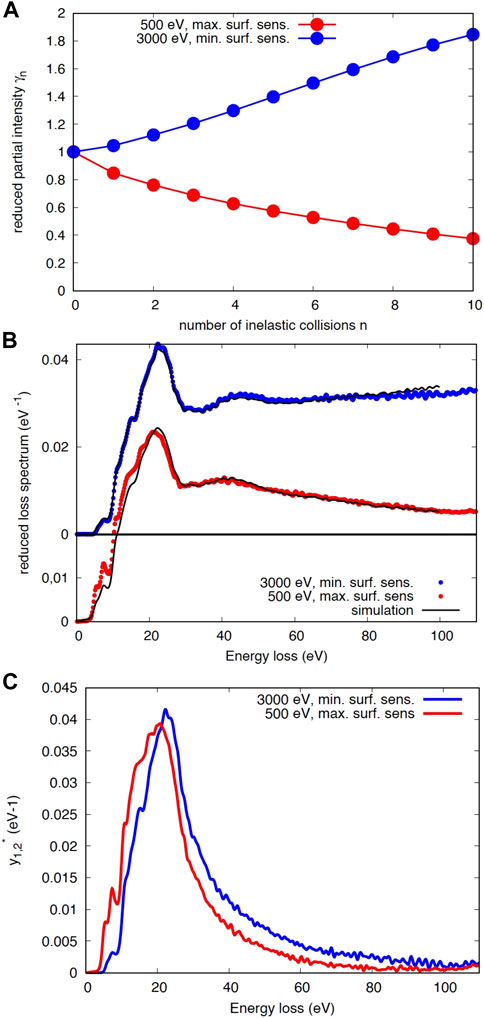
FIGURE 7. (A) reduced partial intensities for electron backscattering from a SiO₂-surface for maximum (500-eV, red) and minimum (3000-eV, blue) surface sensitivity; (B) experimental spectra, the black curve represents the simulation using the partial intensities shown in (A) and the DIIMFP and DSEP shown in Figure 1 using Eq. 17. (C) result of the Tougaard-Chorkendorff procedure, Eq. 19; Tougaard and Chorkendorff (1987).

The partial intensities, calculated with the trajectory reversal MC technique are presented in panel (a) and are seen to be qualitatively different, slowly increasing for 3,000 eV, and monotonically decreasing for 500 eV, a difference caused by the different ratio of the elastic and inelastic mean free path. The experimental spectra, shown in panel (b) clearly reflect this trend. The result of the Tougaard-Chorkendorff algorithm, shown in panel (c), exhibits a greater intensity of low energy losses, for the spectrum taken at 500 eV. The surface sensitive spectrum also exhibits more intensity in the band gap region below ∼10 eV. Applying the procedure summarised by Eq. 20 to the spectra in panel (c) leads to the DIIMFP and DSEP shown in Figure 1D,E. The black curves in panel (b) are simulated spectra using the partial intensities in (a) and the retrieved inelastic scattering characteristics. The consistency between these experimental results and the data in Palik’s books obtained with optical means is again quite satisfactory.

In an experiment proposed by Novak Werner et al. (2013a), it has been possible to demonstrate that energy losses in a reflection experiment not only occur when an electron is inside the solid, but also in vacuum, before or after the surface crossing, a process referred to as super-surface scattering. This makes it possible to uncover the Landau-Goudsmit-Saunderson loss function in the quasi-elastic regime. The experimental configuration is illustrated in Figure 8A: 500-eV electrons are incident on an Au surface with an incidence angle of 70° w.r.t. the surface normal. Angular resolved REELS spectra were measured by rotating an electrostatic analyser around the surface in the range of scattering angles between 40° and 170°. An example of a spectrum obtained in this way is shown in Figure 8B, for the case of normal emission. The contribution of bulk scattering was removed from the spectra by applying Eq 18. Multiple surface excitations were subsequently removed, resulting in the spectrum represented by the blue curve, which agrees reasonably well with earlier measurements taken under significantly different experimental conditions (green curve) Werner et al. (2007; 2009). The area under this curve represents the average number of surface excitations in a single surface crossing ⟨n_s⟩. The angular distribution of the average number of surface excitations is shown as data points in panel (d) of Figure 8. This experiment is a special case, where the angular distribution comprises deep minima in the differential elastic cross section, in which case deflections experienced during inelastic surface excitations can not be neglected Werner et al. (2013a). This is confirmed by the red curves representing surface scattering in vacuum with (solid) and without (dashed) taking into account deflections during surface scattering. The theory accounting for deflections during super-surface scattering are seen to agree quite well with the experimental data points. Note that the comparison in Figure 8D is in absolute units. The blue curves represent surface excitations taking place inside the medium.

FIGURE 8

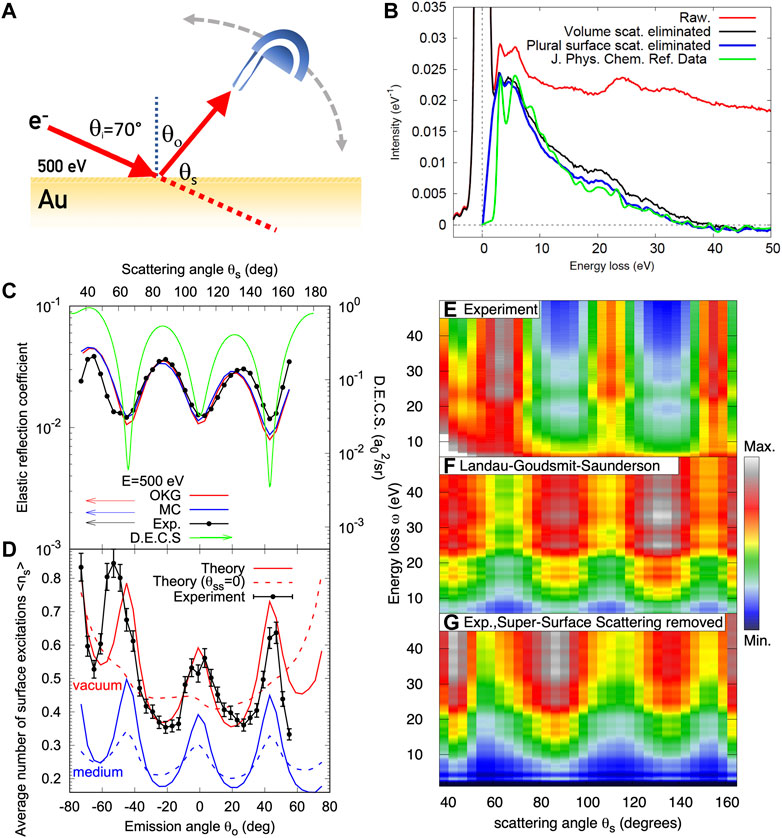
FIGURE 8. (A) Illustration of the experiment to measure the angular distribution of REELS of an Au surface. (B) Spectrum measured at normal emission (red); black curve: raw data after elimination of multiple bulk scattering; the blue curve is the distribution of energy losses in a single surface excitation; green curve: earlier results obtained under different experimental conditions Werner et al. (2009). The area under the blue curve is the average number of surface excitations ⟨n_s⟩. (C) Angular distribution of the elastic peak intensity (data points). The green curve represents the corresponding portion of the elastic scattering cross section; The red and blue curves are simulations using MC calculations (blue) and the Oswald-Kasper-Gaukler model (red) Oswald et al. (1993). (D) Data points: experimental angular distribution of ⟨n_s⟩, the red curves represent theory with (solid) and without (dashed) deflections in the course of a surface excitation taking place in vacuum; blue curves represent theory for surface excitations taking place inside the medium; (E) experimental angular-resolved energy loss distribution; (F) Landau-Goudsmit-Saunderson loss function calculated with (Eq. 10); (G) angular-resolved energy loss distribution after elimination of super-surface scattering.

The raw experimental angular energy loss distribution is presented in panel (e) and compared with the Landau-Goudsmit-Saunderson (LGS) loss function (panel (f)) according to theory in the QE-case calculated using (Eq. 10). Surprisingly, it can be seen that the two data sets are anti-correlated: minima in the experiment correspond to maxima in theory. The apparent contradiction is resolved by noting that the LGS loss function was calculated on the basis of volume scattering only. After eliminating the contribution of surface scattering from the experimental data, the result in panel (g) is obtained, which compares well with LGS theory. Elimination of surface scattering was again performed with Eq. 18, just as for the data shown in Figure 8D, but with an appropriate choice of the required input parameters, i.e., by using the surface partial intensities, Eq. 13, and the DSEP, instead of the bulk parameters used in Figure 8D. The ability of the partial intensity approach to decompose a spectrum into its constituents is one of its major merits and in the present example makes it possible to directly experimentally observe the LGS loss function in the QE regime.

6.3 X-ray photoelectron spectroscopy

The NIST standard reference database SESSA (Simulation of Electron Spectra for Surface Analysis) is a useful tool for quantitative interpretation of Auger-Meitner-electron and X-ray photoelectron spectra (AMES/XPS) for surface analysis and to improve the accuracy of quantitation in routine analysis Werner et al. (2014c); Smekal et al. (2005). For this purpose, the database contains physical data required to perform quantitative interpretation of an electron spectrum for a specimen with a given composition. Retrieval of relevant data is performed by a powerful expert system that queries the comprehensive databases. A trajectory reversal MC simulation module based on the partial intensity approach is available within SESSA that can be used to rapidly calculate peak intensities as well as the energy and angular distribution of the emitted electron flux. SESSA contains data for many parameters required in quantitative AMES and XPS, such as the differential inverse inelastic mean free paths, total inelastic mean free paths, differential elastic-scattering cross sections, total elastic-scattering cross sections, transport cross sections, photoelectric cross sections, photoelectric asymmetry parameters, electron-impact ionisation cross sections, photoelectron lineshapes, Auger-Meitner-electron lineshapes, fluorescence yields and Auger-Meitner electron backscattering factors. Electron spectra can be simulated not only for semi-infinite surfaces, but also for layered samples and for nanostructures such as core-shell nanoparticles, islands, nanowires, spheres, and layered spheres on surfaces. Simulations can be performed for arbitrary incident photon and electron energies in the range of 50 eV–30 keV, polarised x-ray beams, and arbitrary experimental geometrical configurations.

The comparison of the experimental hard X-ray spectra with SESSA simulations, shown in Figure 3, demonstrates that the spectral shape in XPS can be accurately modelled within the PIA. The ability of SESSA to accurately predict peak intensities is demonstrated in Figure 9, which compares experimental peak intensities of two types of ionic liquids with SESSA simulations Holzweber et al. (2019). Ionic liquids are easy to prepare, have an extremely low vapor pressure and after casting a drop on a sample holder exhibit an extremely flat and smooth surface. They are furthermore good conductors, have photopeaks in the energy range of interest for XPS and are inert to oxidation and irradiation by X-rays. These properties make them ideal test samples for XPS, and by comparing experimental peak intensities with simulated ones, the transmission function of the experimental apparatus can be calibrated. Figure 9 compares SESSA simulations for the peak intensities of the class of 1, 3-dialkylimidazolium ionic liquids with bis(tri-fluoromethylsulfonyl)imide as counterion, [C_xC₁im][NTf₂], for different values of x. These multi-elemental samples exhibit five intensive photoemission peaks, F1s, O1s, N1s, C1s, and S2p, in an energy window from 1,600 to 700 eV on the binding energy scale. This is the most important range for applications of quantitative XPS for surface chemical analysis of soft matter. Spectra of these ILs were recorded at different laboratories with different instruments for which the transmission function was calibrated using the UNIFIT software Hesse et al. (2005). It was found that the ILs with x = 2, 3, i.e., the ionic liquids with an ethyl or propyl-group are best suited as reference materials since they exhibit the best homogeneity within the information depth of XPS. The excellent consistency between the SESSA simulations and the experimental results of this interlaboratory study demonstrates the high level of accuracy in the model for the signal generation and transport, as well as the physical parameters entering the model, as presently incorporated in the SESSA databases.

FIGURE 9

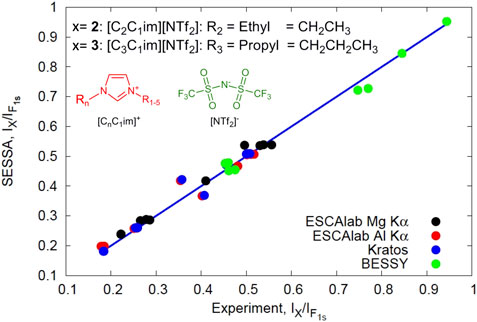
FIGURE 9. Experimental XPS peak intensities of carbon, oxygen, nitrogen and sulfur signals measured on an ionic liquid measured in different laboratories compared with corresponding intensities obtained by SESSA. All peak intensities were normalised by the F1s signal. The straight line has unity slope and passes through the origin, the data points show evaluations of data from different laboratories, as indicated in the legend Holzweber et al. (2019).

Chemical characterisation of core-shell NPs (CSNPs) is nowadays very important for nanotechnological applications. The present version of the SESSA software V2.2 Werner et al. (2014c) is using the PENGEOM package Almansa et al. (2016) to simulate XPS intensities and spectra for surfaces with complex nanomorphologies. These include core-shell particles, multi-shell particles, nanowires, and islands on layered planar surfaces. SESSA has been succesfully employed in the field of nanoparticle characterisation by means of XPS Werner et al. (2014b,a); Chudzicki et al. (2015); Belsey et al. (2016); Powell et al. (2016, 2018); Müller et al. (2019); Cant et al. (2020).

For example, the commonly made assumption that the XPS signal from a powder-like aggregate of nanoparticles can be treated as the signal coming from a single nanoparticle Kuipers et al. (1986), has been verified by SESSA simulations Werner W. S. et al. (2014). A comparison has also been made with the semi-empirical “T_NP”-formula by Shard. Shard (2012), a simple predictive formula to calibrate shell thicknesses from measured core/shell XPS-intensity ratios. SESSA has been used to investigate the range of validity of several approaches developed for NP characterisation with XPS Chudzicki et al. (2015) and has been instrumental in the INNANOPART project Alex G Shard (2014) with the objective to develop techniques to characterise the chemical structure of CSNPs. A recent publication Cant et al. (2021) summarises a technical report International Organization for Standardization (2021) from the International Organization for Standardization with guidelines and recommendations for the quantification of XPS data and for the analysis of nanoparticles with coatings.

Self-assembled monolayers (SAMs) of alkanethiols on flat gold surfaces are a widely employed model system in nanotechnology due to their well-defined structure and surface properties. Numerous studies deal with the synthesis, characterisation, thermodynamics, and reactivity of alkanethiols on flat gold surfaces but there are still many open questions regarding basic properties of SAMs on highly curved surfaces Biebuyck et al. (1994); Hansen et al. (1992); Folkers et al. (1992); Luedtke and Landman (1998); Love et al. (2005); Daniel and Astruc (2004). Techane et al. (2011) conducted a quantitative analysis of the SAM-layer thickness of 16-mercaptohexadecanoic acid (C₁₆COOH) on flat gold and on 14 nm diameter gold nanospheres using XPS. With SESSA, simulation of XPS spectra is possible for different aggregates of CSNPs (see Figure 10) with an arbitrary number of shells simply by defining the compositions, thicknesses, and atomic densities of each layer in the CSNP. The spectra in Figure 10 show SESSA simulations performed for three different nanomorphologies Chudzicki et al. (2015): 1) SAM on a flat gold surface (red); 2) CSNPs formed by SAMs on gold NP-cores (blue); and 3) a single SAM/Gold-CSNP (orange). The experimental spectra, corrected for the transmission function of the analyser, measured by Techane et al. are also shown and agree satisfactorily with SESSA simulations. The analysis allowed the authors not only to evaluate the internal structure of this type of CSNP, but also to quantify the length of a single CH₂ group in the aliphatic chain of the SAM to be between 0.10 and 0.11 nm. It should also be noted that the ratio of peak intensities for the single CSNP model and the powder model are identical, justifying the commonly employed single nanoparticle hypothesis for powders of NPs Kuipers et al. (1986). On the other hand, the shape of the inelastic background is distinctly different, suggesting the use of inelastic background analysis for NP-characterisation Müller et al. (2019); Hansen et al. (1992). Indeed, analysis of the shape of the inelastic background, as well as angle resolved XPS are nowadays highly popular means to obtain information on the compositional depth profile near surfaces as well as their nanomorphology Tougaard (2021); Tasneem et al. (2010).

FIGURE 10

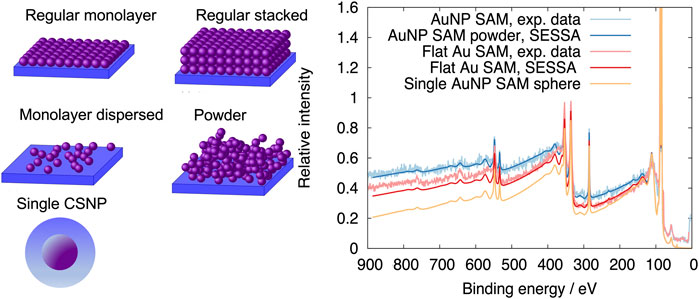
FIGURE 10. Left panels illustrate typical aggregates of core shell nanoparticles (CSNPs) which can be modelled with SESSA. The presented spectra compare transmission-function corrected data for self-assembled monolayers (SAMs) of 16-mercaptohexadecanoic acid (C₁₆COOH) (1) on a flat gold surface and (2) CSNPs formed by SAMs on gold NP-cores with the corresponding simulations. In addition, (3) the simulated spectrum for a single CSNP is also shown. The peak intensity ratios for the single CSNP and powder model are identical, but the shape of the inelastic background is distinctly different.

Summarising the above, good consistency between data assessed using very different approaches has been demonstrated for quasi-elastic electron transport in the medium energy range. This is true for the IMFP values calculated from optical constants and EPES measurements (cf. Figures 2, 6), for the analysis of REELS spectra for SiO₂, from which the dielectric function was extracted in satisfactory agreement with optical measurements (cf. Figures 1D,E, 7). The powerful method to decompose the spectrum into its constituents (Eq. 18) proves the existence of supersurface scattering in a reflection geometry (Figure 8), and made it possible to experimentally uncover the LGS loss function (Eq. 10), which, from the theoretical point of view constitutes the core of the energy dissipation process. The various examples considered for XPS also showed satisfactory agreement, typically within 10%–15%. This typical error estimate is comparable to the uncertainty in the IMFP values, which is still the parameter giving the greatest contribution to the error in quantification of electron beam techniques. Looking back several decades, when the uncertainty in the IMFP was 50% rather than 15% Seah and Dench (1979); Briggs and Seah (1983), one can say that the quantitative understanding of electron spectra has seen a remarkable development: many authors have dedicated a lot of careful work to improve both the model for electron transport near surfaces as well as the input parameters required by them, and have devised appropriate experiments to benchmark the employed models and physical parameters.

6.4 Low energy electrons

Unfortunately, the situation in the low energy regime ($<$100 eV) is presently far less satisfactory. The main reasons seem to be the following: 1) The model for electron transport needs to be extended to take into account additional physical phenomena which are less important in the medium energy range; 2) The physical parameters entering any model are not known with an accuracy anywhere comparable to the case of medium energies; 3) Experiments with low energy electrons are generally more difficult and the necessity of using extremely well-defined surfaces is even more stringent in the low energy case; and 4) Falsification of any of the models found in the literature is complicated by the lack of benchmark data acquired by specifically designed experiments.

While the theoretical description of SE emission has advanced considerably since the early days of the field Kanter (1961); Schou (1980); Seiler (1983); Ganachaud and Mokrani (1995); Ganachaud and Cailler (1979); Rösler and Brauer (1992); Moller and Mohamed (1982); Rösler and Brauer (1981); Devooght et al. (1998); Kuhr and Fitting (1999); Chung and Everhart (1977); Dubus et al. (1987), important questions regarding the model for electron transport remain unanswered. Concerning elastic scattering, the Mott-cross sections for elastic scattering seem to be adequate above 200 eV, but for lower energies it becomes necessary to account for exchange and polarisation effects as well as absorption and solid state effects. These phenomena all have a significant quantitative impact on the physics of elastic scattering Salvat et al. (2005); KESSEL (2022). It is difficult to experimentally determine the required corrections or even to asses the ranges of validity of any approach. Below about 100 eV, measurements of the elastic reflectivity from surfaces no longer agree quantitatively with atomic cross sections even for a noble metal such as Au Ridzel (2019). Furthermore, phonon scattering needs to be taken into account at these energies, for which several models have been proposed Ziman (1960, 1972); Schreiber (2001); Fitting et al. (2001); Schreiber and Fitting (2002); Pop et al. (2004); Akkerman and Murat (2015); Sparks et al. (1981); Fischetti and Laux (1996); Gibarua et al. (2022), leading to widely different values for the transport mean free path for phonon scattering. Again, it is not easy to experimentally decide which of these models yields the best description and usually that model is chosen for which the required parameters are the most readily available.

For medium energies, optical data used in linear response theory yield consistent results between experiment and theory for inelastic scattering (see Figure 2). In the low energy range, several authors have proposed different approaches but the consistency of the results is rather poor and comparison with experiment is not convincing Bourke and Chantler (2010); Chantler and Bourke (2019); Nguyen-Truong (2017, 2016); de Vera and Garcia-Molina (2019). The latter fact is summarily illustrated in Figure 11, showing the IMFP values for the noble metal Au in panel (a) as datapoints, exhibiting a significant scatter for energies below ∼100 eV. Experimental SE yields, i.e., the number of detected electrons upon impact of a single primary electron, as a function of the incident energy are presented in Figure 11BRidzel et al. (2020). Again, a significant scatter in the experimental SE yield curves is observed, even for a noble metal, which is comparably easy to prepare with a well-defined clean surface.

FIGURE 11

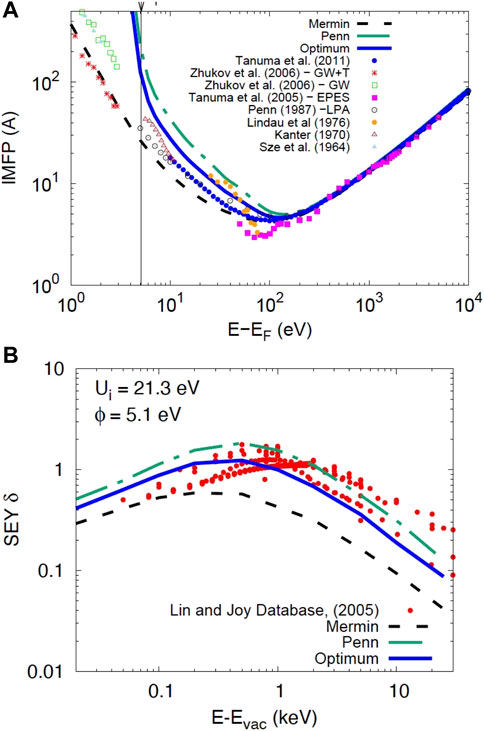
FIGURE 11. (A) Data points: Experimental IMFP values for Gold taken from the literature Penn (1987); Shinotsuka et al. (2019); Kanter (1970); Lindau et al. (1974); Tanuma et al. (2005); Zhukov et al. (2006), compared with IMFPs obtained via analysis of SEY data shown in (B) (solid blue line); Dashed black line: IMFPs calculated using the Mermin dielectric function; Dashdotted green line: Penn’s SSPA algorithm. For energies above ∼100 eV the IMFP from different sources agrees almost perfectly. The symbol ϕ indicates the work function of Gold, U_i is the inner potential Ridzel et al. (2020). (B) Comparison of results of the MC calculation for SEYs using IMFP data shown in Figure 1A with experimental data Brohnstein and Freiman (1968); Joy (2003); Lin and Joy (2005) (data points). Note that the SE-yield above∼100 eV changes significantly when the IMFP for energies below 100 eV is varied within the limits shown in panel (A).

The green dash-dotted and the black dashed curve in Figure 11A represent calculations of the IMFP using two different physical models, the Mermin Mermin (1970) and the Penn model Penn (1987), which were chosen here exclusively because they give widely different values for the IMFP in the low energy range, while for high energies these two models yield practically identical IMFP values. The green, blue and black curves in Figure 11B represent MC-calculations of the SE-yield. The only difference between these calculations is the energy dependence of the IMFP for energies below 200 eV, as shown in panel (a). The calculations for the yield values at higher energies is seen to depend quite significantly (up to a factor of three) on the low energy IMFP values. It should be emphasised again that apart from IMFP values below 200 eV the model to calculate the dashed and dash-dotted curves was identical. The explanation is that, no matter how energetic the primary particle is and to what depth the secondary cascade extends, a limiting factor of SE emission is always the ability of the SE cascade to penetrate the surface and hence the SE yield at arbitrarily high energies is always sensitive to the low energy transport.

This fact was employed to obtain information about the low energy IMFP energy dependence from the high energy part of the yield curve. The IMFP energy dependence was varied in between the two extreme cases labelled “Mermin” and “Penn” and the least squares deviation between experimental and simulated yield curve was minimised giving the optimum IMFP energy dependence in the low energy regime. This optimum is represented in Figure 11 by the blue solid curve in panel (b), the corresponding IMFP values are shown in blue in panel (a). This result suggests that for Au, the Penn algorithm Penn (1987) yields IMFP values which give the best match between simulated SE-yields and the available experimental data. Since the experimental data exhibit a significant scatter and the employed model to simulate the SE-yield contains a number of additional parameters also fraught with errors which are difficult to quantify, it is still difficult to state with certainty which model for the IMFP is best, but it does show that the entire SEY-curve contains information about the low energy transport.

While the sensitivity of the high energy part of the yield curve to the physics of low energy transport is fundamentally interesting and could indeed be utilised to obtain information about the low energy transport, it is clear that this would first require reliable measurements with sufficiently small error bars of the SE-yield curve. To ensure reproducibility and intercomparability of literature data it is not only necessary to produce accurate data, but also to use extremely well-defined surfaces.

The latter point is also of paramount importance for a final phenomenon essential for low energy electrons near surfaces: the escape over the surface potential barrier. The model for the crossing of the potential barrier needs a more careful treatment for electron energies close to the vacuum level. Moreover, it is difficult to find adequate parameters describing the potential barrier for arbitrary materials, in particular for insulating materials. Cazaux (2010b,a, 1999, 2006); Kuhr and Fitting (1999); KESSEL (2022); Astašauskas (2019). Special care must also be taken in experimental work in this connection, since minute changes in the work function and inner potential can lead to dramatic changes in the SE yield.

For energies close to the vacuum level, the electronic structure of the investigated materials also needs to be taken into account. Electron reflectivity at very low energies is modulated by the available density of final states, in particular energy gaps above the vacuum level cause maxima in the reflectivity Bellissimo et al. (2020); Bellissimo (2019); Bronold and Fehske (2022), while minima are observed for energies with available final states. In multilayered graphene samples, oscillations in the reflectivity are observed which are caused by the presence of interlayer resonances in the electronic structure Feenstra et al. (2013). These oscillations occur when electrons are multiply reflected by the π-bound layers in van der Waals materials Jobst et al. (2015); Frank et al. (2011); Mikmekova et al. (2013). This gives rise to a strong anisotropy of the involved phenomena such as an unexpected dependence of the transverse IMFP on the number of layers Geelen et al. (2019). Generally, on well-prepared crystalline surfaces, the band structure causes strong features in the angular-energy distribution of the SE emission close to the vacuum level Willis et al. (1971); Willis (1975).

Perhaps the most important problem in connection with SE emission from surfaces is that it is very difficult to falsify any of the models which can be found in the literature. The point is that the experimental data which are generally used to validate any model, such as SE-yield curves, backscattering coefficients as well as the energy spectrum of SEs are all essentially featureless. None of these quantities exhibits strong characteristics allowing to infer the mechanism leading to SE-generation and their escape from the surface.

This difficulty can be overcome by electron coincidence measurements, i.e., spectroscopy with correlated electron pairs, two electrons which have interacted with each other. By correlating the arrival times of electrons in two detectors Berakdar and Kirschner (2004); Voreades (1976), the spectrum of emitted SEs can be recorded, differential with respect to a certain given energy loss of the primary particle. In other words, in this way one can establish a causal relationship between a certain energy lost by the primary particle and the spectrum of electrons emitted as a result of this specifically considered energy loss.

The double differential secondary electron-electron energy loss spectrum (SE2ELCS) for 100 eV primary electrons incident on a SiO₂ surface is shown in Figure 12C on a false color scale. The DIIMFP of SiO₂ (cf; Figure 1B) is shown for comparison by the white curve. Each pixel in the coincidence spectrum represents the intensity of electron pairs with energies (E₁, E₂). For each energy of the fast electron (E₁), the intensity along the E₂ axis gives the secondary electron spectrum caused specifically by primary electrons that have lost the considered energy ΔE = E₀ − E₁. As expected, these exhibit considerably more structure and characteristic features than the singles spectra.

FIGURE 12

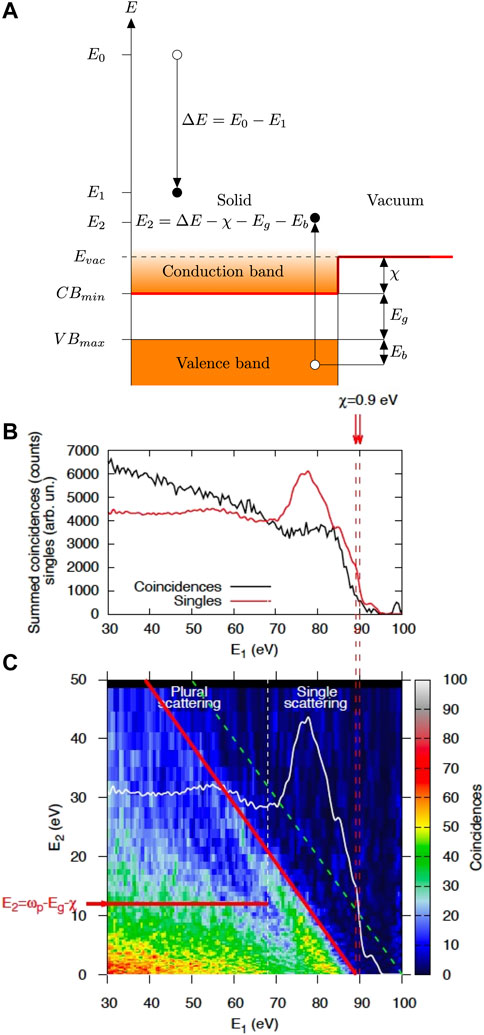
FIGURE 12. (A) Electronic structure model for an insulator explaining the method to determine the electron affinity using two-particle spectroscopy; χ: electron affinity, E_g: band gap energy. It is seen that the smallest energy loss ΔE_min required for emission of a secondary electron just above the vacuum level is: ΔE_min = E_g + χ. (B) Comparison of the (singles) reflection electron energy loss spectrum (REELS, red curve) with the coincidence spectrum shown in (C) summed over all energies E₂ of the second electron; (C) Double differential coincidence spectrum of SiO₂ overlayed with the REELS spectrum (white curve). Emission from the top of the valence band is indicated by the diagonal red line. The dashed green line corresponds to energy conservation E₁+ E₂= E₀.

Generally, since the energy and momentum of all particles involved in the interaction (the incident and the detected electrons) are fixed by the experimental conditions in coincidence spectroscopy, the kinematics of the interaction giving rise to emission of the SE is fully determined. In other words, the initial state of the emitted electron in terms of its binding energy and momentum in the solid, can be reconstructed from coincidence measurements using energy and momentum conservation. In this way, the electronic transition leading to the SE emission is pinpointed and the mechanism for SE creation can be studied Werner et al. (2020).

This type of measurement has contributed substantially to the understanding of low energy electron transport and emission of SEs. First of all, early coincidence measurements were able to establish the causality between the energy loss of the primary and the emission of secondaries Voreades (1976). Secondly, the fact that the transport of the primary can be seen as a Markov-chain of binary collisions was later unambiguously verified Werner et al. (2011). Furthermore, the conjecture that the decay of plasmons leads to emission of secondaries von Koch (1970), which was later supported by theoretical calculations Chung and Everhart (1977) was directly verified by means of coincidence measurements Werner et al. (2008a). This can be clearly seen for the case of SiO₂ in Figure 12C where the plasmon feature in the white curve in the single scattering regime gives rise to a strong peak in the coincidence intensity for energies E₁ between ∼70 eV and ∼85 eV. It was also found that plasmon-decay leads to emission of a single SE while coherent multiple plasmon excitation could not be observed Werner et al. (2013b); Bellissimo (2019), corroborating the Markov-chain model also for low energy transport. Even when the primary electron is approaching the surface, but still in vacuum, the Coulomb interaction with the surface leads to surface losses, which cause emission of SEs which are directly observable in coincidence data Werner et al. (2013b). Coincidence spectroscopy was also used to resolve the (π + σ)-plasmon spectrum of graphite with respect to the electronic interband transitions involved in its decay Werner et al. (2020).

The cited examples show that coincidence data provide essential benchmarks for the validation of low energy electron transport models. In fact, in a recent work Werner et al. (2020) coincidence spectroscopy also gave the explanation of a prominent feature in the singles (i.e., non-coincident) spectrum of highly oriented pyrolitic graphite, commonly referred to as “X″-peak in graphite Ueno et al. (2001). The “X″-peak is a strong resonance in the SE spectrum of graphite, with a well-defined characteristic energy of 3.7 eV above vacuum. It occurs when the (π + σ)-plasmon in graphite decays, thereby breaking the symmetry of the system and hybridising the interlayer states with atomic like σ-states. The hybrid state has both a high density of states and mobility, and couples strongly to vacuum. In other words, a channel for low energy electron escape opens up with a characteristic energy determined by the final state electronic structure. This should be compared with the characteristic energies of Auger-Meitner or photoelectrons, which are determined by the initial state binding energies of the involved electronic levels. This characteristic peak in the singles SE spectrum of graphite can be very useful to calibrate the energy scale near the vacuum level in any experimental apparatus.

Coincidence data not only provide benchmark data for models of SE generation and transport, but also directly contain important information about the electronic structure of a material. This particularly concerns electron refraction of escaping SEs at the surface potential barrier of an insulator Samarin et al. (2004). In a first approximation, the crossing of the surface barrier can be treated within a simple one-dimensional Schrödinger equation with a potential barrier. While the parallel component of the momentum is conserved, the perpendicular component of the momentum k_⊥,in is increased inside the solid:

$\frac{k_{\perp ,in}^2}{2}=\frac{k_{\perp ,out}^2}{2}+U_i,(23)$

where U_i is the inner potential, which, in the case of insulators is taken to be given by the electron affinity, the energetic distance between the bottom of the conduction band and the vacuum level (see Figure 12A). The inner potential thus leads to refraction at the surface and the critical angle of refraction θ_c defines the opening angle of the cone of electrons inside the solid which are allowed to escape:

$\mathrm{\Delta }\mathrm{\Omega }=2\pi \left(1-\cos {\theta }_c\right)=2\pi \left(1-\sqrt{\frac{U_i}{E}}\right),(24)$

where, for simplicity, the classical transmission probability was used. For energies E ∼ U_i, the energy dependence of the opening angle of the escape cone defines the energy distribution, i.e., the typical (featureless) shape, of the secondary electron spectrum, just above the vacuum level. Moreover, the escape cone has a strong influence on the SE emission yield, for any primary energy.

The electron affinity can be directly read-off from coincidence data, as explained in Figure 12A: the smallest energy loss possible in an insulator is equal to the band gap, which can be found by inspection of the onset of losses in the singles energy loss spectrum. The smallest possible energy loss for which a second electron, a secondary, can reach the vacuum level is given by the sum of the band gap and the electron affinity, and corresponds to the onset of energy losses in the coincidence spectrum. The difference between these two values then gives the electron affinity. In Figure 12B the singles energy loss spectrum is compared with the spectrum obtained by summing the coincidences over E₂. The shift in the onset of losses between the singles and the coincidence spectrum is ${\chi }_{Si{O}_2}=$0.9 eV, in good agreement with the literature value. Beyond the single scattering regime, the Markov-chain type plural scattering regime of the primaries, i.e., non-coherent multiple plasmon excitation, also leads to SE emission with (secondary) energies E₂ approximately limited by the red horizontal line, which is given by E₂ = ω_p − E_g − χ, where ω_p is the energy of the plasmon.

For crystalline materials, the change of the wavelength upon surface crossing can be monitored by analysis of the vacuum energies at which Bragg diffraction occurs Werner et al. (2020). There seems to be no consensus in the literature how this can be achieved for non-crystalline insulators, making it difficult to properly define the reference energy of electrons inside this class of materials. It would be interesting to see how the inner potential values obtained at high energies, using electron holography measurements Dunin-Borkowski et al. (2023) compare with data for energies close to the vacuum level, such as the ones shown in Figure 12. The holography data could potentially be an extensive and extremely useful database for the inner potential.

6.5 2-Dimensional electron cascade in the scanning field emission microscope

Any textbook on electron microscopy contains an illustration of the three-dimensional electron cascade defining the “pear-shaped” interaction volume, in which the generation of various signals takes place which are employed in electron microscopy, such as fluorescent x-rays, backscattered electrons, SEs and Auger-Meitner electrons Kyser and Murata (1974); Goldstein et al. (1992); Reimer (1985). Conventional electron microscopy uses rather massive electron-optical components to focus a beam to the desired nanoscale dimensions, which can then be used to either get information about the surface structure, but also to modify the nanomorphology of a surface, as in focussed electron beam induced deposition (FEBID) Huth et al. (2012). Obviously, for nanotechnological applications, a tool for nano-characterisation and modification with microscopic dimensions offers significant advantages. Such a tool is realised by the scanning field emission microscope (SFEM) Young et al. (1971); Bertolini et al. (2017), a scanning tunneling microscope (STM) operated in the field emission mode, by retracting the tip from the sample surface to distances of a few to a few tens of a nanometre. By applying a negative bias of a few to a few tens of a volt to the tip, a lensless microscope is realised. The strong field in the tip-sample junction focusses the field emitted electrons to a nanometre sized spot on the surface from which electrons are reflected and SEs are emitted. By scanning the tip, images of the topographic contrast as well as the magnetic signal of a sample have been obtained Pietro et al. (2017). The SFEM is a development of the topographiner, pioneered by Young some decades ago Young et al. (1971). The mechanism of contrast formation in the SFEM has posed a riddle in the past, since preliminary calculations of electron trajectories in vacuum Cabrera (2016) show that the field in the tip-sample junction pushes all electrons at the impact position back into the surface, preventing them to reach the detector.

This apparent paradox was resolved by means of model calculations in which electron trajectories in vacuum are described in a deterministic way, by numerical integration of the Newtonian equations of motion Radlicka et al. (2018), while upon reentry into the surface, the conventional MC approach for electron reflection and creation of secondary electrons as well as their escape over the surface barrier was employed Ridzel et al. (2020). The results led to a paradigm shift in electron microscopy: the formation of a two-dimensional electron cascade, which propagates along the surface in the field between the electron source, the sample and the (biased) detector Werner et al. (2019). While elastically and inelastically backreflected electrons reaching the detector originate from locations close to the impact position, the detected secondary electrons are created far away, typically several tens or hundreds of a micron (!).

The main simulation results leading to this conclusion are presented in Figure 13, showing trajectories of electrons emitted from a tip leading to a cascade of secondary electrons. From top to bottom (a)-(e), the field of view is zoomed out from nanoscale dimensions (panel (a)) to macroscopic dimensions (panel (e)) as indicated by the yellow size bars. The orange annulus in panel (e) represents the detector in the considered configuration. Trajectories depicted in blue color indicate primary electrons, the light blue color indicates first generation SEs created by energy loss processes of the primaries. These first generation SEs in turn create second generation SEs (green), and so on, ultimately forming the cascade. The left column represents a side view of the surface with the black solid line indicating the solid-vacuum interface. Above the surface, in vacuum, mainly reflected electrons (blue) are visible, their trajectories clearly showing the influence of the strong field in the tip-surface junction. Inside the solid, the trajectories exhibit the typical shape commonly observed in MC results of particle transport, but the essential feature to note is that the lateral extent of the cascade is huge, spanning a macroscopic range, while the maximum extension along the depth coordinate is merely some tens of a nanometre, i.e., the SE cascade is essentially two-dimensional.

FIGURE 13

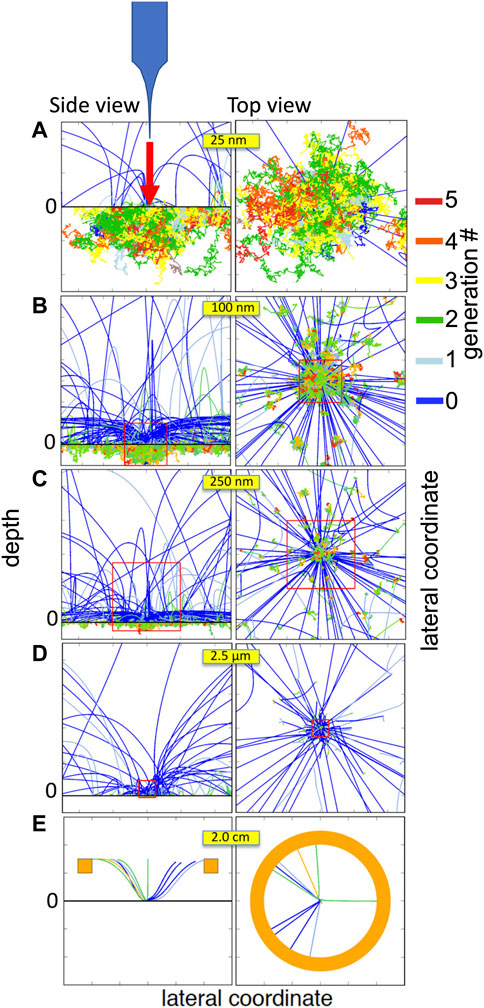
FIGURE 13. Electron trajectories in and above a Silver target for a tip located 20 nm above the surface. Left column: side view, with the label “0″ indicating the interface between the solid (below the horizontal black line) and vacuum (above). Right column: top view. From top to bottom (A–E), the field of view is zoomed out as indicated by the yellow size bars. The color scale indicates the generation of the secondaries (see the text).

Analysis of the spectrum of electrons reaching the detector reveals that the low energy part of the spectrum, i.e., the peak of secondary electrons, originates far away (microns) from the impact position under the tip. The green diffuse features around the origin, but rather far away from it (best seen in the top view of panel (b) and (c)) indicate positions where these SEs are mainly created. These SEs obviously carry no information on the sample properties at the investigated location under the tip Werner et al. (2019). On the other hand, the elastically and inelastically backscattered electrons reaching the detector originate from the tip location and carry information about the sample structure. These are best seen as blue trajectories in the top view of panel (b)-(e), which reach the detector (blue trajectories in panel (e)). This behaviour has in the mean time been experimentally verified by energy filtered SFEM Thamm et al. (2022). In this way, the existence of a 2-dimensional cascade in the SFEM, predicted by the presented MC calculations has been shown to exist in reality.

7 Summary

The concept of partial intensities is a simple but effective description of the electron energy dissipation process. In the quasi-elastic regime where energy fluctuations dominate the energy dissipation, it can be used to accurately model the shape and intensity of electron spectra. The main tools for spectrum analysis, make it possible to decompose the spectrum into its constituents corresponding to different types of scattering or even collisions taking place in different layers of the sample (Eq. 18) or to extract information on the optical properties from electron spectra (Eq. 20). Note that Eqs 6 and 18 are not only mathematically speaking their mutually inverse operations but are also numerically robust, Eqs 6 and 18 can be applied consecutively multiple times, retaining the original data within all digitally representable digits.

The usefulness of the partial intensity approach is not limited to spectrum analysis, such as deconvolution of XPS spectra Cserny et al. (2000); Werner et al. (2002), analysis of REELS data Werner (2010); Werner et al. (2009), but can also be employed to increase the efficiency of Monte Carlo calculations, both in the quasi-elastic regime Werner (2001) as well as in the true slowing down regime Wagner and Werner (1998); Werner (1997).

The presented applications demonstrate the level of consistency between the theoretical description of electron transport based on linear response theory using optical constants, and experiments analysed without using any of the elements of this theory or optical constants. This leads to satisfactory agreement between IMFP values using the two approaches and also leads to good agreement between optical constants derived from electron spectra and optical measurements. Applying the spectrum decomposition tools, the theoretical core of the energy dissipation, the Landau-Goudsmit-Saunderson loss function has been exposed in experimental data. Accurate quantification and nanomorphology determination has also been demonstrated. It should again be emphasised that the accuracy of both, compositional quantification as well as calibration of length dimensions on the nanoscale hinges critically on the availability of accurate IMFP values. In summary, in the medium energy range, the quantitative understanding of electron transport and the typical accuracy of experimental data are of comparable magnitude, a rather satisfactory situation.

In the low energy regime ($<$100 eV), which is of growing interest owing to its importance for nanotechnology, there is still a lot of space for improvement. The main problems have been indicated and, where possible, routes towards improvement have been outlined. It has been pointed out that one can obtain valuable information about low energy electron transport by performing measurements at high energies, and several types of measurements can provide good benchmark data helpful for experimental work, such as the “X”-peak in graphite and the relationship between the band structure and the low energy electron reflectivity. Spectroscopy with correlated electron pairs has been proposed as an experimental technique to overcome the limitations posed by the typical data used for validation of models for low energy electron transport, such as the SE-yield curves, the backscattering coefficient and the energy spectrum of emitted SEs. The point is that the latter are all essentially featureless and devoid of any characteristics useable to quantitatively validate any separate physical phenomenon. Devising experiments to quantitatively validate specific physical parameters, such as the IMFP, phonon mean free paths, etc., has been identified as an issue of high priority. This is deemed as one of the most important routes towards improvement, since it could potentially be used to falsify (or, what is the same, “validate”) existing models.

In closing it should be emphasised that in spite of certain deficiencies in the quantitative understanding of low energy electron transport, the usefulness of state of the art models in this field is undisputed. The available models are indispensable for the advancement of nanotechnology in that they can help to explain contrast mechanisms in various electron beam techniques, to improve industrial production processes, such as electron beam lithography, and even semi-quantitative model calculations can be enlightening for interpretation of results obtained with electron beam techniques. A case in point is the prediction of the 2-dimensional electron cascade in the SFEM, which is expected to play a significant role in future nanotechnological applications.

Author contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Funding

Financial support by the Horizon 2022 Marie-Curie Actions Initial Training Network (ITN) EUSpeclab (Grant No. 101073486), 14IND12 EMPIR project InNanoPart within the European Union’s Horizon 2020 research and innovation programme and by the FP7 People: Marie-Curie Actions Initial Training Network (ITN) SIMDALEE2 (Grant No. PITN 606988) is gratefully acknowledged.

Acknowledgments

The computational results presented have been achieved using the Vienna Scientific Cluster (VSC). The authors acknowledge TU Wien Bibliothek for financial support through its Open Access Funding Programme.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Afanas’ev, V. P., Gryazev, A. S., Efremenko, D. S., and Kaplya, P. S. (2017). Differential inverse inelastic mean free path and differential surface excitation probability retrieval from electron energy loss spectra. Vacuum136, 146–155. doi:10.1016/j.vacuum.2016.10.021

CrossRef Full Text | Google Scholar

Ahlgren, S., and Ono, K. (2001). Addition and counting: The arithmetic of partitions. Notices Am. Math. Soc.48, 978.

CrossRef Full Text | Google Scholar

Akkerman, A., and Murat, M. (2015). Electron-phonon interactions in silicon: Mean free paths, related distributions and transport characteristics. Nucl. Instr. Meth. Phys. Res. B350, 49–54. doi:10.1016/j.nimb.2015.03.024

CrossRef Full Text | Google Scholar

Alex G Shard (2014). Innanopart euramet empir project. http://empir.npl.co.uk/innanopart/.

Google Scholar

Alkemade, P. F. A. (1995). Fast simulation of xps and aes spectra by transformation of electron trajectories. Surf. Interface Anal.23, 251.

CrossRef Full Text | Google Scholar

Alkemade, P. F. A. (1997). Trajectory weighting: A fast Monte Carlo method for calculating large numbers of XPS/AES spectra. Surf. Interface Anal.25, 275–284. doi:10.1002/(sici)1096-9918(199704)25:4<275::aid-sia234>3.0.co;2-4

CrossRef Full Text | Google Scholar

Almansa, J., Salvat-Pujol, F., Díaz-Londoño, G., Carnicer, A., Lallena, A. M., and Salvat, F. (2016). Pengeom—A general-purpose geometry package for Monte Carlo simulation of radiation transport in material systems defined by quadric surfaces. Comput. Phys. Commun.199, 102–113. doi:10.1016/j.cpc.2015.09.019

CrossRef Full Text | Google Scholar

Astašauskas, V., Bellissimo, A., Kuksa, P., Tomastik, C., Kalbe, H., and Werner, S. M. W. (2020). Optical and electronic properties of amorphous silicon dioxide by single and double electron spectroscopy. J. Electron Spectrosc. Rel. Phen.241, 146829. doi:10.1016/j.elspec.2019.02.008

CrossRef Full Text | Google Scholar

Astašauskas, V. (2019). Emission of low energy electrons from solid surfaces studied by means of spectroscopy with individual as well as correlated electrons. Technische Universität Wien. Ph.D. thesis.

Google Scholar

Barrios, R., Skurski, P., and Simons, J. (2002). Mechanism for damage to DNA by low-energy electrons. J. Phys. Chem. B106, 7991–7994. doi:10.1021/jp013861i

CrossRef Full Text | Google Scholar

Beilschmidt, H., Tilinin, I. S., and Werner, W. S. M. (1994). Inelastic mean free path of medium energy electrons in au, pt, ni and al determined by elastic peak electron spectroscopy. Surf. Interface Anal.22, 120–123. doi:10.1002/sia.740220129

CrossRef Full Text | Google Scholar

Bellissimo, A. (2019). Multiparameter analysis of genesis and evolution of secondary electrons produced in the low energy regime. ”Università degli Studi Roma Tre”. Ph.D. thesis. doi:10.5281/zenodo.3924096

CrossRef Full Text | Google Scholar

Bellissimo, A., Pierantozzi, G.-M., Ruocco, A., Stefani, G., Ridzel, O. Y., Astašauskas, V., et al. (2020). Secondary electron generation mechanisms in carbon allotropes at low impact electron energies. J. Electron Spectrosc. Rel. Phen.241, 146883. doi:10.1016/j.elspec.2019.07.004

CrossRef Full Text | Google Scholar

Belsey, N. A., Cant, D. J. H., Minelli, C., Araujo, J. R., Bock, B., Brüner, P., et al. (2016). Versailles project on advanced materials and standards interlaboratory study on measuring the thickness and chemistry of nanoparticle coatings using XPS and LEIS. J. Phys. Chem. C120, 24070–24079. doi:10.1021/acs.jpcc.6b06713

PubMed Abstract | CrossRef Full Text | Google Scholar

Berakdar, J., and Kirschner, J. (2004). Correlation spectroscopy of surfaces, thin films, and nanostructures. Weinheim, Germany: Wiley VCH.

Google Scholar

Bertolini, G., Pietro, L. D., Bähler, T., Cabrera, H., Gürlü, O., Pescia, D., et al. (2017). Spin-polarised electrons in a one-magnet- only mott spin junction. Sci. Rep.7, 13237–13245.

PubMed Abstract | Google Scholar

Biebuyck, H., Bain, C., and Whitesides, G. (1994). Comparison of organic monolayers on polycrystalline gold spontaneously assembled from solutions containing dialkyl disulfides or alkanethiols. Langmuir10 (6), 1825–1831. doi:10.1021/la00018a034

CrossRef Full Text | Google Scholar

Bourke, J. D., and Chantler, C. T. (2010). Measurements of electron inelastic mean free paths in materials. Phys. Rev. Lett.104, 206601. doi:10.1103/physrevlett.104.206601

PubMed Abstract | CrossRef Full Text | Google Scholar

Boutboul, T., Akkerman, A., Breskin, A., and Chechik, R. (1996). Electron inelastic mean free path and stopping power modelling in alkali halides in the 50 eV-10 keV energy range. J. Appl. Phys.79, 6714–6721. doi:10.1063/1.361491

CrossRef Full Text | Google Scholar

Briggs, D., and Seah, M. P. (1983). Practical surface analysis. Chichester: Wiley.

Google Scholar

Brohnstein, I. M., and Freiman, B. S. (1968). Vtorichnaya elektronnaya emissi. Moscow: Nauka. (in Russian).

Google Scholar

Bronold, F. X., and Fehske, H. (2022). Invariant embedding approach to secondary electron emission from metals. J. Appl. Phys.131, 113302. doi:10.1063/5.0082468

CrossRef Full Text | Google Scholar

Cabrera, H. (2016). ETH zcurich research collection. ETH Zürich. Ph.D. thesis. Ph.D. thesis.

Google Scholar

Cant, D. J. H., Müller, A., Clifford, C. A., Unger, W. E. S., and Shard, A. G. (2021). Summary of ISO/TC 201 Technical Report 23173 Surface chemical analysis Electron spectroscopies Measurement of the thickness and composition of nanoparticle coatings. Surf. Interface Analysis53, 893–898. doi:10.1002/sia.6987

CrossRef Full Text | Google Scholar

Cant, D. J., Minelli, C., Sparnacci, K., Müller, A., Kalbe, H., Stöger-Pollach, M., et al. (2020). Surface-energy control and characterization of nanoparticle coatings. J. Phys. Chem. C124, 11200–11211. doi:10.1021/acs.jpcc.0c02161

CrossRef Full Text | Google Scholar

Case, K. M., and Zweifel, P. F. (1967). Linear transport theory. Reading, MA: Addison-Wesley.

Google Scholar

Cazaux, J. (2010a). Calculated influence of work function on SE escape probability and Secondary Electron Emission yield. Appl. Surf. Sci.257, 1002–1009. doi:10.1016/j.apsusc.2010.08.007

CrossRef Full Text | Google Scholar

Cazaux, J. (2006). E-Induced secondary electron emission yield of insulators and charging effects. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. Atoms244, 307–322. doi:10.1016/j.nimb.2005.10.006

CrossRef Full Text | Google Scholar

Cazaux, J. (2010b). Secondary electron emission and fundamentals of charging mechanisms in XPS. J. Electron Spectrosc. Relat. Phenom.178-179, 357–372. doi:10.1016/j.elspec.2009.03.007

CrossRef Full Text | Google Scholar

Cazaux, J. (1999). Some considerations on the secondary electron emission, δ, from e⁻–irradiated insulators. J. Appl. Phys.85, 1137–1147. doi:10.1063/1.369239

CrossRef Full Text | Google Scholar

Chantler, C. T., and Bourke, J. D. (2019). Low-energy electron properties: Electron inelastic mean free path, energy loss function and the dielectric function. Recent measurements, applications, and the plasmon-coupling theory. Ultramicroscopy201, 38–48. doi:10.1016/j.ultramic.2019.03.014

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, H., Zou, Y., Mao, S., Khan, M. S. S., Tokesi, K., and Ding, Z. J. (2022). Influence of energy loss function to the Monte Carlo simulated electron backscattering coefficient. Nature12, 18201. doi:10.1038/s41598-022-20466-3

CrossRef Full Text | Google Scholar

Chudzicki, M., Werner, W. S., Shard, A. G., Wang, Y. C., Castner, D. G., and Powell, C. J. (2015). Evaluating the internal structure of core-shell nanoparticles using X-ray photoelectron intensities and simulated spectra. J. Phys. Chem. C119, 17687–17696. doi:10.1021/acs.jpcc.5b04517

PubMed Abstract | CrossRef Full Text | Google Scholar

Chung, M. S., and Everhart, T. E. (1977). Role of plasmon decay in secondary electron emission in the nearly-free-electron metals. application to aluminum. Phys. Rev. B15, 4699–4715. doi:10.1103/PhysRevB.15.4699

CrossRef Full Text | Google Scholar

Cohen-Simonsen, A., Yubero, F., and Tougaard, S. (1997). Quantitative model of electron energy loss in xps. Phys. Rev.B56, 1612–1619. doi:10.1103/physrevb.56.1612

CrossRef Full Text | Google Scholar

Cserny, K., Kőver, L., Werner, W. S. M., and Kvr, L. (2000). Electron scattering correction of x-ray excited ni and cu kll auger spectra emitted from thin and thick metallic samples. Surf. Interface Anal.29, 126–130. doi:10.1002/(sici)1096-9918(200002)29:2<126::aid-sia704>3.0.co;2-x

CrossRef Full Text | Google Scholar

Cumpson, P. (1993). Elastic scattering corrections in aes and xps: I two rapid Monte Carlo methods for calculating the depth distribution function. Surf. Interface Anal.20, 727–741. doi:10.1002/sia.740200818

CrossRef Full Text | Google Scholar

Daniel, M.-C., and Astruc, D. (2004). Gold nanoparticles: Assembly, supramolecular chemistry, quantum-size-related properties, and applications toward biology, catalysis, and nanotechnology. Chem. Rev.104, 293–346. doi:10.1021/cr030698+

PubMed Abstract | CrossRef Full Text | Google Scholar

de Abajo, F. J. G. (2010). Optical excitations in electron microscopy. Rev. Mod. Phys.82, 209–275. doi:10.1103/revmodphys.82.209

CrossRef Full Text | Google Scholar

de Vera, P., and Garcia-Molina, R. (2019). Electron inelastic mean free paths in condensed matter down to a few electronvolts. J. Phys. Chem. C123, 2075–2083. doi:10.1021/acs.jpcc.8b10832

CrossRef Full Text | Google Scholar

Devooght, J., Dehaes, J. C., Dubus, A., Ganachaud, J. P., and Cailler, M. (1998). Theoretical description of secondary electron emission induced by electron or ion beams impinging on solids. Berlin Heidelberg New York: Springer Verlag.

Google Scholar

Ding, Z.-J. (1990). Fundamental studies on the interactions of kV electrons with solids for application to electron spectroscopies. Japan: Osaka University. Ph.D. thesis.

Google Scholar

Ding, Z.-J., Li, H. M., Pu, Q. R., Zhang, Z. M., and Shimizu, R. (2002). Reflection electron energy loss spectrum of surface plasmon excitation of ag: A Monte Carlo study. Phys. Rev.B66, 085411. doi:10.1103/physrevb.66.085411

CrossRef Full Text | Google Scholar

Ding, Z.-J. (1998). Self-energy in surface electron spectroscopy: Ii surface excitation on real metal surfaces. J. Phys. Condens Matter10, 1753–1765. doi:10.1088/0953-8984/10/8/010

CrossRef Full Text | Google Scholar

Dubus, A., Dehaes, J.-C., Ganachaud, J.-P., Hafni, A., and Cailler, M. (1993). Monte Carlo evaluation of the influence of the interaction cross sections on the secondary-electron-emission yields from polycrystalline aluminum targets. Phys. Rev. B47, 11056–11073. doi:10.1103/physrevb.47.11056

PubMed Abstract | CrossRef Full Text | Google Scholar

Dubus, A., Devooght, J., and Dehaes, J. C. (1987). Improved age-diffusion model for low-energy electron transport in solids. II. Application to secondary emission from aluminum. Phys. Rev.B36, 5110–5119. doi:10.1103/physrevb.36.5110

PubMed Abstract | CrossRef Full Text | Google Scholar

Dubus, A., Jabłonski, A., and Tougaard, S. (2000). Evaluation of theoretical models for elastic electron backscattering from surfaces. Prog. Surf. Sci.63, 135–175. doi:10.1016/s0079-6816(99)00018-0

CrossRef Full Text | Google Scholar

Dunin-Borkowski, R. E., McCartney, M. R., and Smith, D. J. (2023). “Electron holography of nanostructured materials,” in Encyclopedia of nanoscience and nanotechnology. Editors H. S. Nalwa (American scientific publisher), 41–99.

Google Scholar

Feenstra, R. M., Srivastava, N., Gao, Q., Widom, M., Diaconescu, B., Ohta, T., et al. (2013). Low-energy electron reflectivity from graphene. Phys. Rev. B - Condens. Matter Mater. Phys.87, 041406–41414. doi:10.1103/PhysRevB.87.041406

PubMed Abstract | CrossRef Full Text | Google Scholar

Fischetti, M. V., and Laux, S. E. (1996). Band structure, deformation potentials, and carrier mobility in strained si, ge, and sige alloys. J. Appl. Phys.80, 2234–2252. doi:10.1063/1.363052

CrossRef Full Text | Google Scholar

Fitting, H.-J., Schreiber, E., Kuhr, J.-C., and von Czarnowski, A. (2001). Attenuation and escape depths of low-energy electron emission. J. Electron Spectrosc. Rel. Phen.119, 35–47. doi:10.1016/s0368-2048(01)00232-8

CrossRef Full Text | Google Scholar

Folkers, J., Laibinis, P., and Whitesides, G. (1992). Self-assembled monolayers of alkanethiols on gold: Comparisons of monolayers containing mixtures of short-and long-chain constituents with methyl and hydroxymethyl terminal groups. Langmuir8 (5), 1330–1341. doi:10.1021/la00041a015

CrossRef Full Text | Google Scholar

Frank, L., Hovorka, M., Konvalina, I., Mikmekova, S., and Müllerova, I. (2011). Very low energy scanning electron microscopy. Nucl. Instrum. Methods A645, 46–54. doi:10.1016/j.nima.2010.12.214

CrossRef Full Text | Google Scholar

Ganachaud, J. P., and Cailler, M. (1979). A Monte-Carlo calculation of the secondary electron emission of normal metals. Surf. Sci.83, 519–530. doi:10.1016/0039-6028(79)90060-8

CrossRef Full Text | Google Scholar

Ganachaud, J. P., and Mokrani, A. (1995). Theoretical study of the secondary electron emission of insulating targets. Surf. Sci.334, 329–341. doi:10.1016/0039-6028(95)00474-2

CrossRef Full Text | Google Scholar

Gao, Y., Zheng, Y., and Sanche, L. (2021). Low-energy electron damage to condensed-phase DNA and its constituents. Int. J. Mol. Sci.22, 7879–7932. doi:10.3390/ijms22157879

PubMed Abstract | CrossRef Full Text | Google Scholar

Geelen, D., Jobst, J., Krasovskii, E. E., van der Molen, S. J., and Tromp, R. M. (2019). Non-universal transverse electron mean free path through few-layer graphene. Phys. Rev. Lett.123, 086802. doi:10.1103/physrevlett.123.086802

PubMed Abstract | CrossRef Full Text | Google Scholar

Gergely, G. (1986). Elastic peak electron spectroscopy: Elastic peak electron spectroscopy. Scanning8, 203–214. doi:10.1002/sca.4950080503

CrossRef Full Text | Google Scholar

Gergely, G., Menyhard, M., Pentek, K., Sulyok, A., Jabłonski, A., Lesiak, B., et al. (1995). Experimental determination of the inelastic mean free path (IMFP) of electrons in Cr, Mo, Ge and Si based on the elastic peak intensity ratio with a Ni reference sample. Surf. Sci.331, 1203–1207. doi:10.1016/0039-6028(95)00070-4

CrossRef Full Text | Google Scholar

Gergely, G., Menyhard, M., Sulyok, A., Gurban, S., Lesiak, B., Jablonski, A., et al. (2007). Evaluation of the inelastic mean free path (IMFP) of electrons in polyaniline and polyacetylene samples obtained from elastic peak electron spectroscopy (EPES). Open Phys.5, 188–200. doi:10.2478/s11534-007-0012-y

CrossRef Full Text | Google Scholar

Gibarua, Q., Inguimbert, C., Belhaj, M., Raine, M., and Lambert, D. (2022). Monte-carlo simulation and experimental study of the effect of internal charging on the electron emission yield of amorphous sio2 thin films. J. Electron Spectrosc. Rel. Phen.261, 147265. doi:10.1016/j.elspec.2022.147265

CrossRef Full Text | Google Scholar

Goldstein, J., Newbury, D. E., Echlin, P., Joy, D. C., Romig, A. D., Lyman, C. E., et al. (1992). Scanning electron microscopy and X-ray microanalysis. New York, London: Plenum.

Google Scholar

Gries, W. H., and Werner, W. S. M. (1990). Take-off angle and film thickness dependences of the attenuation length of X-ray photoelectrons by a trajectory reversal method. Surf. Interface Anal.16, 149–153. doi:10.1002/sia.740160129

CrossRef Full Text | Google Scholar

Hansen, H., Tougaard, S., and Biebuyck, H. (1992). The adsorption of alkanethiols on gold studied quantitatively by xps inelastic background analysis. J. Electron Spectrosc. Rel. Phen.58, 141–158. doi:10.1016/0368-2048(92)80013-x

CrossRef Full Text | Google Scholar

Hesse, R., Streubel, P., and Szargan, R. (2005). Improved accuracy of quantitative xps analysis using predetermined spectrometer transmission functions with unifit 2004. Surf. Interface Analysis37, 589–607. doi:10.1002/sia.2056

CrossRef Full Text | Google Scholar

Holzweber, M., Lippitz, A., Hesse, R., Denecke, R., Werner, W. S., and Unger, W. E. (2019). The use of ionic liquids for the determination of the spectrometer transmission function in X-ray photoelectron spectroscopy (XPS). J. Electron Spectrosc. Relat. Phenom.233, 51–56. doi:10.1016/j.elspec.2019.03.008

CrossRef Full Text | Google Scholar

Hove, M. A., Weinberg, W. H., and Chan, C.-M. (2012). Low-energy electron diffraction experiment, theory and surface structure determination. Berlin, Heidelberg: Springer. doi:10.1007/978-3-642-82721-1

CrossRef Full Text | Google Scholar

Huth, M., Porrati, F., Schwalb, C., Winhold, M., Sachser, R., Dukic, M., et al. (2012). Focused electron beam induced deposition: A perspective. Beilstein J. Nanotechnol.3, 597–619. doi:10.3762/bjnano.3.70

PubMed Abstract | CrossRef Full Text | Google Scholar

International Organization for Standardization (2021). ISO/TR 23713: 2021 surface chemical analysis -electron spectroscopies- measurement of the thickness and composition of nanoparticle coatings. Geneva: International Organization for Standardization.

Google Scholar

Jabłonski, A. (2000). Determination of the IMFP from electron elastic backscattering probability. Surf. Interface Anal.29, 582–595. doi:10.1002/1096-9918(200009)29:9<582::aid-sia903>3.0.co;2-x

CrossRef Full Text | Google Scholar

Jabłonski, A., Mrozek, P., Gergely, G., Menhyard, M., and Sulyok, A. (1984). The inelastic mean free path of electrons in some semiconductor compounds and metals. Surf. Interface Anal.6, 291–294. doi:10.1002/sia.740060609

CrossRef Full Text | Google Scholar

Jobst, J., Kautz, J., Geelen, D., Tromp, R. M., and Van Der Molen, S. J. (2015). Nanoscale measurements of unoccupied band dispersion in few-layer graphene. Nat. Commun.6, 8926–6. doi:10.1038/ncomms9926

PubMed Abstract | CrossRef Full Text | Google Scholar

Joy, D. C. (2003). A database of electron-solid interactions. http://pciserver.bio.utk.edu/metrology/download/E-solid/database.doc.

Google Scholar

Kanter, H. (1970). Slow-electron mean free paths in aluminum, silver, and gold. Phys. Rev. B11, 522–536. doi:10.1103/physrevb.1.522

CrossRef Full Text | Google Scholar

Kanter, M. (1961). Phys. Rev.121, 1677.

Kessel, L. C. P. M. V. (2022). Physics and applications of electron-matter interaction simulations. Technische Universiteit Delft. Ph.D. thesis.

Google Scholar

Kinoshita, T., Ikenaga, E., Kim, J., Ueda, S., Kobata, M., Harries, J. R., et al. (2007). How is it possible to obtain buried interface information through very thick films using a hard-X-ray PEEM?Surf. Sci.601, 4754–4757. doi:10.1016/j.susc.2007.05.043

CrossRef Full Text | Google Scholar

Kozawa, T., and Tagawa, S. (2010). Radiation chemistry in chemically amplified resists. Jpn. J. Appl. Phys.49, 030001. doi:10.1143/JJAP.49.030001

CrossRef Full Text | Google Scholar

Kozawa, T., and Tamura, T. (2021). Relationship between blurring factors and interfacial effects in chemically amplified resist processes in photomask fabrication. Jpn. J. Appl. Phys.60, 126504. doi:10.35848/1347-4065/ac33cd

CrossRef Full Text | Google Scholar

Kuhr, J. C., and Fitting, H. J. (1999). Monte Carlo simulation of electron emission from solids. J. Electron Spectrosc. Rel. Phen.105, 257–273. doi:10.1016/s0368-2048(99)00082-1

CrossRef Full Text | Google Scholar

Kuipers, H. P. C. E., van Leuven, H. C. E., and Visser, W. M. (1986). The characterization of heterogeneous catalysts by XPS based on geometrical probability 1: Monometallic catalysts. Surf. Interface Anal.8, 235–242. doi:10.1002/sia.740080603

CrossRef Full Text | Google Scholar

Kwei, C. M., Chen, Y., Tung, C. J., and Wang, C. Y. (1993). Electron inelastic mean free paths for plasmon excitations and interband transitions. Surf. Sci.293, 202–210. doi:10.1016/0039-6028(93)90314-a

CrossRef Full Text | Google Scholar

Kwei, C. M., Wang, C. Y., and Tung, C. J. (1998). Surface excitation parameters of low-energy electrons crossing solid surfaces. Surf. Interface Anal.26, 682–688. doi:10.1002/(sici)1096-9918(199808)26:9<682::aid-sia415>3.0.co;2-7

CrossRef Full Text | Google Scholar

Kyser, D. F., and Murata, K. (1974). Quantitative electron microprobe analysis of thin films on substrates. IBM J. Res. Dev.18, 352–363. doi:10.1147/rd.184.0352

CrossRef Full Text | Google Scholar

Landau, L. D., Lifshitz, E. M., and Pitaevski, L. P. (1984). Electrodynamics of continuous media. 2nd edition. Oxford, New York: Pergamom Press. Translated by J. B. Sykes, J. S. Bell and M. J. Kearsley.

Google Scholar

Landau, L. D. (1944). On the energy loss of fast particles by ionization. J. Phys. (Mosc.8, 201.

Google Scholar

Lin, Y., and Joy, D. C. (2005). A new examination of secondary electron yield data. Surf. Interface Anal.37, 895–900. doi:10.1002/sia.2107

CrossRef Full Text | Google Scholar

Lindau, I., Pianetta, P., Doniach, S., and Spicer, W. E. (1974). X-ray photoemission spectroscopy. Nature250, 214–215. doi:10.1038/250214a0

CrossRef Full Text | Google Scholar

Love, J. C., Estroff, L., Kriebel, J., Nuzzo, R., and Whitesides, G. (2005). Self-assembled monolayers of thiolates on metals as a form of nanotechnology. Chem. Rev.105, 1103–1169. doi:10.1021/cr0300789

PubMed Abstract | CrossRef Full Text | Google Scholar

Luedtke, W., and Landman, U. (1998). Structure and thermodynamics of self-assembled monolayers on gold nanocrystallites. J. Phys. Chem. B102, 6566–6572. doi:10.1021/jp981745i

CrossRef Full Text | Google Scholar

McKee, A. D., Schaible, M. J., Rosenberg, R. A., Kundu, S., and Orlando, T. M. (2019). Low energy secondary electron induced damage of condensed nucleotides. J. Chem. Phys.150, 204709. doi:10.1063/1.5090491

PubMed Abstract | CrossRef Full Text | Google Scholar

Mermin, N. D. (1970). Lindhard dielectric function in the relaxation-time approximation. Phys. Rev. B1, 2362–2363. doi:10.1103/PhysRevB.1.2362

CrossRef Full Text | Google Scholar

Mikmekova, E., Bouyanfif, H., Lejeune, M., Müllerova, I., Hovorka, M., Uncovsky, M., et al. (2013). Very low energy electron microscopy of graphene flakes. J. Microsc.251, 123–127. doi:10.1111/jmi.12049

PubMed Abstract | CrossRef Full Text | Google Scholar

Moller, P. J., and Mohamed, M. H. (1982). An experimental study of the energy dependence of the total yield due to the incidence of low-energy electrons onto graphite surfaces. J. Phys. C Solid State Phys.15, 6457–6462. doi:10.1088/0022-3719/15/31/021

CrossRef Full Text | Google Scholar

Müller, A., Heinrich, T., Tougaard, S., Werner, W. S., Hronek, M., Kunz, V., et al. (2019). Determining the thickness and completeness of the shell of polymer core-shell nanoparticles by X-ray photoelectron spectroscopy, secondary ion mass spectrometry, and transmission scanning electron microscopy. J. Phys. Chem. C123, 29765–29775. doi:10.1021/acs.jpcc.9b09258

CrossRef Full Text | Google Scholar

Nguyen-Truong, H. T. (2017). Electron inelastic mean free path at energies below 100 eV. J. Phys. Condens. Matter29, 215501. doi:10.1088/1361-648X/aa6b9d

PubMed Abstract | CrossRef Full Text | Google Scholar

Nguyen-Truong, H. T. (2016). Low-energy electron inelastic mean free path in materials. Appl. Phys. Lett.108, 172901. doi:10.1063/1.4948248

CrossRef Full Text | Google Scholar

Oswald, R., Kasper, E., and Gaukler, K. (1993). A multiple scattering theory of elastic electron backscattering from amorphous surfaces. J. Electron Spectrosc. Rel. Phen.61, 251–274. doi:10.1016/0368-2048(93)80019-i

CrossRef Full Text | Google Scholar

Oswald, R. (1992). Numerische Untersuchung der elastischen Streuung von Elektronen an Atomen und ihrer Rückstreuung an Oberflächen amorpher Substanzen im Energiebereich unter 2000 eV. Tübingen: Eberhard-Karls-Universität Tübingen. Ph.D. thesis.

Google Scholar

Palik, E. D. (1985). Handbook of optical constants of solids. New York: Academic Press.

Google Scholar

Palik, E. D. (1991). Handbook of optical constants of solids II. New York: Academic Press.

Google Scholar

Pendry, J. B. (1974). Low energy electron diffraction. London, New York: Academic Press.

Google Scholar

Penn, D. R. (1987). Electron mean free path calculations using a model dielectric function. Phys. Rev.B35, 482–486. doi:10.1103/physrevb.35.482

PubMed Abstract | CrossRef Full Text | Google Scholar

Pietro, L. D., Bertolini, G., Peter, Q., Cabrera, H., Vindigni, A., Gürlü, O., et al. (2017). Spin-polarised electrons in a one-magnet- only mott spin junction. Sci. Rep.7 (1), 13237–13245. doi:10.1038/s41598-017-13453-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Pop, E., Dutton, R. W., and Goodson, K. E. (2004). Analytic band Monte Carlo model for electron transport in si including acoustic and optical phonon dispersion. J. Appl. Phys.96, 4998–5005. doi:10.1063/1.1788838

CrossRef Full Text | Google Scholar

Powell, C. J., and Jabłonski, A. (1999). Evaluation of calculated and measured electron inelastic mean free paths near solid surfaces. J. Phys. Chem. Ref. Data28, 19–62. doi:10.1063/1.556035

CrossRef Full Text | Google Scholar

Powell, C. J., Werner, W. S. M., Kalbe, H., Shard, A. G., and Castner, D. G. (2018). Comparisons of analytical approaches for determining shell thicknesses of core–shell nanoparticles by X-ray photoelectron spectroscopy. J. Phys. Chem. C122, 4073–4082. doi:10.1021/acs.jpcc.7b12070

CrossRef Full Text | Google Scholar

Powell, C. J., Werner, W. S. M., Shard, A. G., and Castner, D. G. (2016). Evaluation of two methods for determining shell thicknesses of core–shell nanoparticles by X-ray photoelectron spectroscopy. J. Phys. Chem. C120, 22730–22738. doi:10.1021/acs.jpcc.6b07588

CrossRef Full Text | Google Scholar

Radlicka, T., Uncovsky, M., and Oral, M. (2018). In lens bse detector with energy filtering. Ultramicroscopy189, 102–108. doi:10.1016/j.ultramic.2018.03.015

PubMed Abstract | CrossRef Full Text | Google Scholar

Reimer, L. (1985). Scanning electron microscopy. Berlin Heidelberg New York: Springer Verlag.

Google Scholar

Ridzel, O. Y., Astašauskas, V., and Werner, W. S. M. (2020). Low energy (1 - 100 eV) electron inelastic mean free path (IMFP) values determined from analysis of secondary electron yields (SEY) in the incident energy range of 0.1 - 10 keV. J. Electron Spectrosc. Rel. Phen.241, 146824. doi:10.1016/j.elspec.2019.02.003

CrossRef Full Text | Google Scholar

Ridzel, O. Y. (2019). Interaction of slow electrons with matter for nanoscale characterisation of solids. Technische Universität Wien. Ph.D. thesis.

Google Scholar

Ridzel, O. Y., Kalbe, H., Astašauskas, V., Kuksa, P., Bellissimo, A., and Werner, W. S. M. (2022). Optical constants of organic insulators in the UV-range extracted from reflection electron energy loss spectra. Surf. Interface Anal.54, 487–500. doi:10.1002/sia.7055

CrossRef Full Text | Google Scholar

Ritchie, R. H. (1957). Plasma losses by fast electrons in thin films. Phys. Rev.106, 874–881. doi:10.1103/physrev.106.874

CrossRef Full Text | Google Scholar

Rösler, M., and Brauer, W. (1992). “Theory of electron emission from nearly–free–electron metals by proton and electron bombardment,” in Particle induced electron emission I. Editor G. Höhler (Heidelberg: Springer), 122, 1–65. chap. 1.

Google Scholar

Rösler, M., and Brauer, W. (1981). Theory of secondary electron emission. i. general theory for nearly-free-electron metals. Phys. Stat. Sol.104, 161–175. doi:10.1002/pssb.2221040117

CrossRef Full Text | Google Scholar

Salvat, F., Jablonski, A., and Powell, C. J. (2005). Elsepa - Dirac partial-wave calculation of elastic scattering of electrons and positrons by atoms, positive ions and molecules. Comp. Phys. Com.165, 157–190. doi:10.1016/j.cpc.2004.09.006

CrossRef Full Text | Google Scholar

Salvat-Pujol, F., Werner, W. S. M., Jiricek, M. N. P., and Zemek, J. (2014). In-out asymmetry of surface excitations in reflection-electron-energy-lossspectra of polycrystalline al. Phys. Rev.B89, 205435. doi:10.1103/physrevb.89.205435

CrossRef Full Text | Google Scholar

Salvat-Pujol, F., and Werner, W. S. M. (2013). Surface excitations in electron spectroscopy. Part i: Dielectric formalism and Monte Carlo algorithm. Surf. Interface Anal.45, 873–894. doi:10.1002/sia.5175

PubMed Abstract | CrossRef Full Text | Google Scholar

Samarin, S., Berakdar, J., Suvorova, A., Artamonov, O., Waterhouse, D., Kirschner, J., et al. (2004). Secondary-electron emission mechanism of lif film by (e,2e) spectroscopy. Surf. Sci.548, 187–199. doi:10.1016/j.susc.2003.11.003

CrossRef Full Text | Google Scholar

Schattschneider, P. (1986). Fundamentals of inelastic electron scattering. New York, Vienna: Springer.

Google Scholar

Schilling, J. S., and Webb, M. B. (1970). Low-energy electron diffraction from liquid Hg: Multiple scattering, scattering factor, and attenuation. Phys. Rev. B22, 1665–1676. doi:10.1103/physrevb.2.1665

CrossRef Full Text | Google Scholar

Schmid, R. (1982). Ph.D. thesis. Germany: University of Tübingen.

Google Scholar

Schou, J. (1980). Transport theory for kinetic emission of secondary electrons from solids. Phys. Rev.B22, 2141–2174. doi:10.1103/physrevb.22.2141

CrossRef Full Text | Google Scholar

Schreiber, E., and Fitting, H.-J. (2002). Monte Carlo simulation of secondary electron emission from the insulator SiO₂. J. Electron Spectrosc. Rel. Phen.124, 25–37. doi:10.1016/s0368-2048(01)00368-1

CrossRef Full Text | Google Scholar

Schreiber, E. (2001). Monte-Carlo Simulationen des elektronischen Hochfeld-transportes in dielektrischen Schichten. Universität Rostock. Ph.D. thesis.

Google Scholar

Seah, M. P., and Dench, W. A. (1979). Quantitative electron spectroscopy of surfaces: A standard data base for electron inelastic mean free paths in solids. Surf. Interface Anal.1, 2–11. doi:10.1002/sia.740010103

CrossRef Full Text | Google Scholar

Seiler, H. (1983). Secondary electron emission in the scanning electron microscope. J. Appl. Phys.54, R1–R18. doi:10.1063/1.332840

CrossRef Full Text | Google Scholar

Shard, A. G. (2012). A straightforward method for interpreting xps data from core-shell nanoparticles. J. Phys. Chem. C116, 16806–16813. doi:10.1021/jp305267d

CrossRef Full Text | Google Scholar

Shimizu, R., and Ding, Z. (1992). Monte Carlo modelling of electron–solid interactions. Rep. Prog. Phys.55, 487–531. doi:10.1088/0034-4885/55/4/002

CrossRef Full Text | Google Scholar

Shinotsuka, H., Tanuma, S., and Powell, C. J. (2022). Calculations of electron inelastic mean free paths. xiii. data for 14 organic compounds and water over the 50 ev to 200 kev range with the relativistic full penn algorithm. Surf. Interface Anal.49, 534–560. doi:10.1002/sia.7064

CrossRef Full Text | Google Scholar

Shinotsuka, H., Tanuma, S., Powell, C. J., and Penn, D. R. (2019). Calculations of electron inelastic mean free paths. XII. Data for 42 inorganic compounds over the 50 eV to 200 keV range with the full Penn algorithm. Surf. Interface Anal.51, 427–457. doi:10.1002/sia.6598

PubMed Abstract | CrossRef Full Text | Google Scholar

Shirley, D. A. (1972). High-resolution X-ray photoemission spectrum of the valence bands of gold. Phys. Rev. B55, 4709–4714. doi:10.1103/physrevb.5.4709

CrossRef Full Text | Google Scholar

Smekal, W., Werner, W. S. M., and Powell, C. J. (2005). Simulation of electron spectra for surface analysis (SESSA): A novel software tool for quantitative auger-electron spectroscopy and X-ray photoelectron spectroscopy. Surf. Interface Anal.37, 1059–1067. doi:10.1002/sia.2097

CrossRef Full Text | Google Scholar

Sparks, M., Mills, D. L., Warren, R., Holstein, T., Maradudin, A. A., Sham, L. J., et al. (1981). Theory of electron-avalanche breakdown in solids. Phys. Rev. B24, 3519–3536. doi:10.1103/physrevb.24.3519

CrossRef Full Text | Google Scholar

Tahir, D., and Tougaard, S. (2012). Electronic and optical properties of selected polymers studied by reflection electron energy loss spectroscopy. J. Appl. Phys.111, 054101. doi:10.1063/1.3688327

CrossRef Full Text | Google Scholar

Tanuma, S., Shiratori, T., Kimura, T., Goto, K., Ichimura, S., and Powell, C. (2005). Experimental determination of electron inelastic mean free paths in 13 elemental solids in the 50 to 5000 ev energy range by elastic-peak electron spectroscopy. Surf. Interface Anal.37, 833–845. doi:10.1002/sia.2102

CrossRef Full Text | Google Scholar

Tasneem, G., Werner, W. S. M., Smekal, W., and Powell, C. J. (2010). Simulation of parallel angle-resolved X-ray photoelectron spectroscopy data. Surf. Interface Anal.42, 1072–1075. doi:10.1002/sia.3321

CrossRef Full Text | Google Scholar

Techane, S., Gamble, L. J., and Castner, D. G. (2011). Multi-technique characterization of self-assembled carboxylic acid terminated alkanethiol monolayers on nanoparticle and flat gold surfaces. J. Phys. Chem. C Nanom. Interfaces115, 9432–9441. doi:10.1021/jp201213g

CrossRef Full Text | Google Scholar

Thamm, A.-K., Wei, J., Zhou, J., Walker, C. G. H., Cabrera, H., Demydenko, M., et al. (2022). Hallmark of quantum skipping in energy filtered lensless scanning electron microscopy. Appl. Phys. Lett.120, 052403. doi:10.1063/5.0077503

CrossRef Full Text | Google Scholar

Tilinin, I. S., Jabłonski, A., and Werner, W. S. M. (1997). Quantitative surface analysis by auger and x-ray photoelectron spectroscopy. Prog. Surf. Sci.52, 193–335. doi:10.1016/0079-6816(96)00008-1

CrossRef Full Text | Google Scholar

Tilinin, I. S., and Werner, W. S. M. (1993). Angular and energy distribution of auger and photoelectrons escaping from non-crystalline solid surfaces. Surf. Sci.290, 119–133. doi:10.1016/0039-6028(93)90594-a

CrossRef Full Text | Google Scholar

Tilinin, I. S., and Werner, W. S. M. (1992). Escape probability of Auger electrons from noncrystalline solids: Exact solution in the transport approximation. Phys. Rev.B46, 13739–13746. doi:10.1103/physrevb.46.13739

PubMed Abstract | CrossRef Full Text | Google Scholar

Tougaard, S., and Chorkendorff, I. (1987). Differential inelastic electron scattering cross sections from experimental reflection electron-energy-loss spectra: Application to background removal in electron spectroscopy. Phys. Rev.B35, 6570–6577. doi:10.1103/physrevb.35.6570

PubMed Abstract | CrossRef Full Text | Google Scholar

Tougaard, S. (2021). Practical guide to the use of backgrounds in quantitative XPS. J. Vac. Sci. Technol. A39, 011201. doi:10.1116/6.0000661

CrossRef Full Text | Google Scholar

Tougaard, S., and Sigmund, P. (1982). Influence of elastic and inelastic scattering on energy spectra of electrons emitted from solids. Phys. Rev.B25, 4452–4466. doi:10.1103/physrevb.25.4452

CrossRef Full Text | Google Scholar

Tougaard, S. (1997). Universality classes of inelastic electron scattering cross sections. Surf. Interface Anal.25, 137–154. doi:10.1002/(sici)1096-9918(199703)25:3<137::aid-sia230>3.0.co;2-l

CrossRef Full Text | Google Scholar

Tung, C. J., Chen, Y. F., Kwei, C. M., and Chou, T. L. (1994). Differential cross sections for plasmon excitations and reflected electron-energy-loss spectra. Phys. Rev.B49, 16684–16693. doi:10.1103/physrevb.49.16684

PubMed Abstract | CrossRef Full Text | Google Scholar

Ueno, N., Yamane, H., Okudaira, K. K., Setoyama, H., and Kera, S. (2001). Low-energy electron transmission experiments on graphite. Phys. Rev. B - Condens. Matter Mater. Phys.64, 113407–113414. doi:10.1103/PhysRevB.64.113407

CrossRef Full Text | Google Scholar

von Koch, C. V. (1970). Evidence of plasmons in secondary electron emission spectra. Phys. Rev. Lett.25, 792–794. doi:10.1103/physrevlett.25.792

CrossRef Full Text | Google Scholar

Voreades, D. (1976). Secondary electron emission from thin carbon films. Surf. Sci.60, 325–348. doi:10.1016/0039-6028(76)90320-4

CrossRef Full Text | Google Scholar

Wagner, H. W. (2001). PhD thesis. Ph.D. Thesis. Vienna: Vienna University of Technology.

Google Scholar

Wagner, H. W., and Werner, W. S. M. (1998). Calculation of ionization depth distributions and backscattering coefficients applying a new Monte Carlo simulation approach. X-Ray Spectrom.27, 373–380. doi:10.1002/(sici)1097-4539(199811/12)27:6<373::aid-xrs283>3.0.co;2-t

CrossRef Full Text | Google Scholar

Werner, W. S., Chudzicki, M., Smekal, W., and Powell, C. J. (2014a). Interpretation of nanoparticle X-ray photoelectron intensities. Appl. Phys. Lett.104, 243106. doi:10.1063/1.4884065

CrossRef Full Text | Google Scholar

Werner, W. S. M., Ambrosch-Draxl, C., and Glantschnig, K. (2009). Optical constants and inelastic electron scattering data for 17 elemental metals. J. Phys. Chem. Ref. Data38 (4), 1013–1092. doi:10.1063/1.3243762

CrossRef Full Text | Google Scholar

Werner, W. S. M., Astašauskas, V., Ziegler, P., Bellissimo, A., Stefani, G., Linhart, L., et al. (2020). Secondary electron emission by plasmon-induced symmetry breaking in highly oriented pyrolytic graphite. Phys. Rev. Lett.196603, 196603. doi:10.1103/PhysRevLett.125.196603

PubMed Abstract | CrossRef Full Text | Google Scholar

Werner, W. S. M., Cabela, T., Zemek, J., and Jiricek, P. (2001a). On line shape analysis in x-ray photoelectron spectroscopy. Surf. Sci.470, 325–336. doi:10.1016/s0039-6028(00)00877-3

CrossRef Full Text | Google Scholar

Werner, W. S. M., Chudzicki, M., Smekal, W., and Powell, C. J. (2014b). Interpretation of nanoparticle x-ray photoelectron intensities. Appl. Phys. Lett.104, 243106. doi:10.1063/1.4884065

CrossRef Full Text | Google Scholar

Werner, W. S. M. (2006). Differential surface and volume excitation probability of medium-energy electrons in solids. Phys. Rev. B74, 075421. doi:10.1103/physrevb.74.075421

CrossRef Full Text | Google Scholar

Werner, W. S. M. (2001). Electron transport in solids for quantitative surface analysis. Surf. Interface Anal.31, 141–176. doi:10.1002/sia.973

CrossRef Full Text | Google Scholar

Werner, W. S. M., Gries, W. H., and Störi, H. (1991). Analytical expression describing the attenuation of Auger electrons and photoelectrons in solids. Surf. Interface Anal.17, 693–704. doi:10.1002/sia.740171003

CrossRef Full Text | Google Scholar

Werner, W. S. M., Helmberger, F., Schürrer, M., Ridzel, O., Stöger-Pollach, M., and Eisenmenger-Sittner, C. (2022b). Electron inelastic mean free path (imfp) values of kapton, polyethylene (pe), polymethylmethacrylate (pmma), polystyrene (ps) and polytetrafluoroethylene (ptfe) measured with elastic peak electron spectroscopy (epes). Surf. Interface Analysis54, 855–863. doi:10.1002/sia.7098

CrossRef Full Text | Google Scholar

Werner, W. S. M., Helmberger, F., Schürrer, M., Ridzel, O. Y., Stöger-Pollach, M., and Eisenmenger-Sittner, C. (2022a). Measurement of the surface excitation parameter of kapton, polyethylene (pe), polymethylmethacrylate (pmma), polystyrene (ps) and polytetrafluoroethylene (ptfe). Surf. Interface Anal.54, 681–687. doi:10.1002/sia.7080

CrossRef Full Text | Google Scholar

Werner, W. S. M. (1995a). Influence of multiple elastic and inelastic scattering on photoelectron lineshape. Phys. Rev.B52, 2964–2975. doi:10.1103/physrevb.52.2964

PubMed Abstract | CrossRef Full Text | Google Scholar

Werner, W. S. M., Kőver, L., Tóth, J., and Varga, D. (2002). Line shape analysis of high energy x-ray induced auger and photoelectron spectra of thin cu and ni films. J. Electron Spectrosc. Rel. Phen.122, 103–114. doi:10.1016/s0368-2048(01)00347-4

CrossRef Full Text | Google Scholar

Werner, W. S. M., Novak, M., Salvat-Pujol, F., Zemek, J., and Jiricek, P. (2013a). Electron supersurface scattering on polycrystalline Au. Phys. Rev. Lett.110, 086110. doi:10.1103/physrevlett.110.086110

PubMed Abstract | CrossRef Full Text | Google Scholar

Werner, W. S. M. (2003a). Obtaining quantitative information on surface excitations from reflection electron energy-loss spectroscopy (REELS). Surf. Interface Anal.35, 347–353. doi:10.1002/sia.1540

CrossRef Full Text | Google Scholar

Werner, W. S. M., Oral, M., Radlicka, T., Zelinka, J., Müllerova, I., Bellissimo, A., et al. (2019). Scanning tunneling microscopy in the field-emission regime: Formation of a two-dimensional electron cascade. Appl. Phys. Lett.115, 251604. doi:10.1063/1.5128300

CrossRef Full Text | Google Scholar

Werner, W. S. M. (1995b). Partial intensity analysis (PIA) for quantitative electron spectroscopy. Surf. Interface Anal.23, 737–752. doi:10.1002/sia.740231103

CrossRef Full Text | Google Scholar

Werner, W. S. M., and Powell, C. J. (2021). Applications of the national institute of standards and technology (nist) database for the simulation of electron spectra for surface analysis for quantitative x-ray photoelectron spectroscopy of nanostructures. J. Vac. Sci. Technol. A39, 063205. doi:10.1116/6.0001261

CrossRef Full Text | Google Scholar

Werner, W. S. M., Salvat-Pujol, F., Bellissimo, A., Khalid, R., Smekal, W., Novak, M., et al. (2013b). Secondary-electron emission induced by in vacuo surface excitations near a polycrystalline al surface. Phys. Rev.B88, 201407. doi:10.1103/physrevb.88.201407

CrossRef Full Text | Google Scholar

Werner, W. S. M., Salvat-Pujol, F., Smekal, W., Khalid, R., Aumayr, F., Störi, H., et al. (2011). Contribution of surface plasmon decay to secondary electron emission from an Al surface. Appl. Phys. Lett.99, 184102. doi:10.1063/1.3658455

CrossRef Full Text | Google Scholar

Werner, W. S. M. (2010). Simple algorithm for quantitative analysis of reflection electron energy loss spectra (REELS). Surf. Sci.604, 290–299. doi:10.1016/j.susc.2009.11.019

CrossRef Full Text | Google Scholar

Werner, W. S. M. (1997). Slowing down of medium energy electrons in solids. Phys. Rev.B55, 14925–14934. doi:10.1103/physrevb.55.14925

CrossRef Full Text | Google Scholar

Werner, W. S. M., Smekal, W., and Powell, C. J. (2014c). NIST database for simulation of electron spectra for surface analysis SRD100. Gaithersburg (MD), US: National Institute of Standards and Technology (NIST. Version 2.2.

Google Scholar

Werner, W. S. M., Smekal, W., Tomastik, C., and Störi, H. (2001b). Surface excitation probability of medium energy electrons in metals and semiconductors. Surf. Sci.486, L461–L466. doi:10.1016/s0039-6028(01)01091-3

CrossRef Full Text | Google Scholar

Werner, W. S. M., Smekal, W., Winter, H., Ruocco, A., Offi, F., Iacobucci, S., et al. (2008a). Role of surface and bulk plasmon decay in secondary electron emission. Phys. Rev.B78, 233403. doi:10.1103/physrevb.78.233403

CrossRef Full Text | Google Scholar

Werner, W. S. M. (2003b). Surface and bulk plasmon coupling observed in reflection electron energy loss spectra. Surf. Sci.526/3, L159–L164. doi:10.1016/s0039-6028(02)02684-5

CrossRef Full Text | Google Scholar

Werner, W. S. M., Tomastik, C., Cabela, T., Richter, G., and Störi, H. (2001c). Elastic electron reflection for determination of the inelastic mean free path of medium energy electrons in 24 elemental solids for energies between 50 and 3400 ev. J. Electron Spectrosc. Rel. Phen.113, 127–135. doi:10.1016/s0368-2048(00)00280-2

CrossRef Full Text | Google Scholar

Werner, W. S. M., Tomastik, C., Cabela, T., Richter, G., and Störi, H. (2001d). Electron inelastic mean free path measured by elastic peak electron spectroscopy for 24 solids between 50 and 3400 ev. Surf. Sci.470, L123–L128. doi:10.1016/s0039-6028(00)00858-x

CrossRef Full Text | Google Scholar

Werner, W. S. M. (2005). Trajectory reversal approach for electron backscattering from solid surfaces. Phys. Rev. B71, 115415. doi:10.1103/physrevb.71.115415

CrossRef Full Text | Google Scholar

Werner, W. S. M., Went, M. R., Vos, M., Ambrosch-Draxl, C., and Glantschnig, K. (2008b). Measurement and density functional calculations of optical constants of Ag and Au from infrared to vacuum ultraviolet wavelengths. Phys. Rev. B B77, R161404. doi:10.1103/physrevb.77.161404

CrossRef Full Text | Google Scholar

Werner, W. S. M., Went, M. R., and Vos, M. (2007). Surface plasmon excitation at a au surface by 150–40000 ev electrons. Surf. Sci.601, L109–L113. doi:10.1016/j.susc.2007.06.076

CrossRef Full Text | Google Scholar

Willis, R. (1975). Angular-resolved secondary-electron—emission spectra from tungsten surfaces. Phys. Rev. Lett.34, 670–674. doi:10.1103/physrevlett.34.670

CrossRef Full Text | Google Scholar

Willis, R., Feuerbacher, B., and Fitton, B. (1971). Experimental investigation of the band structure of graphite. Phys. Rev.B4, 2441–2452. doi:10.1103/physrevb.4.2441

CrossRef Full Text | Google Scholar

Yang, L. H., Tőkési, K., Tóth, J., Da, B., Li, H. M., and Ding, Z. J. (2019). Optical properties of silicon and germanium determined by high-precision analysis of reflection electron energy loss spectroscopy spectra. Phys. Rev. B100, 245209. doi:10.1103/PhysRevB.100.245209

CrossRef Full Text | Google Scholar

Young, R., Ward, J., and Scire, F. (1971). Observation of metal-vacuum-metal tunneling, field emission, and the transition region. Phys. Rev. Lett.27, 922–924. doi:10.1103/physrevlett.27.922

CrossRef Full Text | Google Scholar

Zheng, Y., Hunting, D. J., Ayotte, P., and Sanche2, L. (2008). Role of secondary low-energy electrons in the concomitant chemoradiation therapy of cancer. Phys. Rev. Lett.100, 198101. doi:10.1103/physrevlett.100.198101

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhukov, V., Chulkov, E., and Echenique, P. (2006). Lifetimes and inelastic mean free path of low-energy excited electrons in fe, ni, pt, and au: Ab initio gw+t calculations. Phys. Rev. B73, 125105. doi:10.1103/physrevb.73.125105

CrossRef Full Text | Google Scholar

Ziman, J. M. (1960). “Electrons and phonons: The theory of transport phenomena in solids,” in The international series of monographs on physics (Oxford (UK): Oxford University Press).

Google Scholar

Ziman, J. M. (1972). “Theoretical solid state physics,” in International series in natural philosophy (Oxford: Pergamon Press), Vol. 2.

Google Scholar