
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Mater., 07 June 2023
Sec. Semiconducting Materials and Devices
Volume 10 - 2023 | https://doi.org/10.3389/fmats.2023.1193423
In this work, a new model is described for the case of interference between thermal, plasma and elastic waves in a non-local excited semiconductor medium. The governing equations have been put under the influence of moisture diffusion in one dimension (1D) when the moisture thermal conductivity of the non-local medium is taken in variable form. Linear transformations were used to describe the dimensionless model. The photo-thermoelasticity theory according to moisture diffusivity was applied to describe the governing equations using Laplace transforms to obtain analytical solutions. In the time domain, complete solutions are obtained linearly when the conditions are applied (thermal ramp type and non-Gaussian plasma shock) to the surface through numerical methods of inverse Laplace transforms. Numerical simulation is used to display the basic physical quantities under study graphically. The current research has yielded several specific examples of great significance. Many comparisons are made under the influence of fundamental physical variables such as relaxation times, variable thermal conductivity, non-local parameters, and reference moisture parameters through graphing and describing them theoretically.
The combination of the “electronic deformation” in the semiconducting medium, based on the photogeneration theory in the crystal lattice, and the “thermoelastic mechanism” owing to the integral photothermal process characterizes an important thermoelastic fact. When atoms are perturbed, they migrate from a high-density to a low-density area. The mechanical defects and internal strains make this form of transportation conceivable. When temperatures climb to the point where materials begin to melt, atomic spacing increases. In a similar vein, moisture transfer takes place when an existing concentration gradient forms as a result of the presence of unequal amounts of moisture. Temperature and humidity levels of the substance change depending on location and time. In this respect, the theories of heat transmission and moisture transfer are essentially identical. Mechanically applied stressors have the potential to significantly alter the distribution of temperature and moisture. That’s why it is important to determine exactly how mechanical deformation relates to diffusion due to changes in humidity and temperature. Many practical engineering problems involve the interplay of moisture, heat, and deformation. When heat and moisture act on solids, a phenomenon known as hygrothermoelasticity takes place. Szekeres (2000); Szekeres (2012) examined how generalized heat transmission is affected by moisture. It has been suggested by Gasch et al. (2016) that changes in humidity and temperature could do more damage than mechanical loadings. Using a fundamental comparison between heat and moisture, (Szekeres and Engelbrecht, 2000) formulated equations governing coupled hygrothermoelasticity.
Photothermal (PT) analysis of semiconductor materials’ thermal and electrical properties has grown in popularity. Semiconductors, used in sensors, solar cells, and advanced medical devices, have been extensively studied. Most renewable energy generation requires semiconductor knowledge. Semiconductors are dielectric and non-conductive. When optical energy activates semiconductor surface holes and electrons, electronic deformation occurs. The optical energy of light accelerates excited electrons to the surface, creating an electron cloud-like convective density or plasma waves. Photo-excitation and heat effect cause thermoelastic deformation. Thus, semiconductors are studied using thermoelasticity and photothermal theories. Numerous authors have developed novel methods to study photoacoustic spectroscopy’s sensitivity when a laser beam hits a semiconductor sample (Gordon et al., 1964; Kreuzer, 1971). Photothermal approaches in several physical tests verified the nano-composite semiconductor materials’ real temperatures, inner displacements, thermal diffusion, and other electrical properties (Tam, 1983; Tam, 1986; Tam, 1989; Todorovic et al., 1999; Song et al., 2010). Photo-excitation directly affects electronic deformation by causing elastic oscillations in the material’s internal structures. Hobiny and Abbas (2016) studied photothermal waves in an unbounded medium using a semiconductor-filled cylindrical cavity. Two-temperature theory and strain-stresses in a semiconducting material under photothermal waves with hydrostatic starting stress are problematic (Abo-dahab and Lotfy, 2017; Lotfy, 2017). Lotfy (2016) applied the photo-thermoelasticity hypothesis to semiconductor media thermal-plasma-elastic waves under a magnetic field and rotation.
Alterations to a material’s mechanical and thermal characteristics are often seen after a temperature change. The influence of the temperature gradient has been taken into consideration by several researchers after being ignored in previous studies of the expanded theory of thermoelasticity (Hasselman and Heller, 1980a; Youssef and Abbas, 2007a; Abouelregal and Marin, 2020; Marin et al., 2020). It is crucial to consider how temperature affects material characteristics (Marin et al., 2015) because the qualities of a material cannot be considered to have constant values under the effect of temperature change. The thermoelasticity theory emerged from discussions of coupled and uncoupled theories, both of which conflict with physical experiments. Biot (1956) introduced the unique hypothesis of linked thermoelasticity, which explained the anomaly. Infinite-speed thermal wave propagation was investigated using the CD theory. Lord and Shulman (1967) (LS) introduced a new concept when the heat equation was still in its infancy, by adding one relaxation period. Two relaxation periods were included in the heat conduction equation by Green and Lindsay (1972) (GL). The generalized thermoelasticity theory (GL) has been used by several writers (Chandrasekharaiah, 1986; Hosseini et al., 2013). Applications of the extended thermoelasticity theory including the interaction of thermal waves, electromagnetic fields, and mechanical waves in a thermoelastic solid medium are many.
Eringen (1972); Eringen and Edelen (1972) found that strain is defined as the gradient of the inner products of non-local deformations on non-local and local continuum components. This is a logical conclusion of the continuum theory of physics. Non-local thermoelastic theory (Eringen and Edelen, 1972) bridges the theoretical gap between the lattice-building theory and the classical continuum hypothesis. The classical continuum hypothesis allows for the investigation of constitutive relations between the atomic structure of lattices and the propagation of phonons. According to photomechanical waves and a moisture diffusivity process, (Alhashash et al., 2022) investigated the two-temperature thermoelasticity theory of a semiconductor model.
Physical characteristics of materials have been shown to depend on the temperature in recent studies. Deformation and thermo-mechanical behavior are both affected by the temperature dependency of these materials. The temperature-dependent thermal conductivity has a greater impact on thermal and mechanical behavior. Therefore, the thermal stress analysis is affected by the varying thermal conductivity. A thermoelastic hollow cylinder was an issue that Suhara investigated around the turn of the last century. Since then, several elastic and inelastic media issues have included the medium’s temperature-dependent physical features (Hasselman and Heller, 1980b). Youssef (2005) used the state-space technique to the solution of the generalized thermoelasticity issue involving a spherical cavity where the thermal conductivity is temperature-dependent under ramp-type heating. Youssef and El-Bary (2006) have included variable thermal conductivity in the generalized thermoelasticity with thermal shock layers. Youssef and Abbas (2007b) have solved the generalized thermoelasticity issue for an infinitely long annular cylinder with variable thermal conductivity. Nano-energy uses rely heavily on the effects of size. For the first time, a new gradient theory is presented to characterize the nonlocal equation of motion (elastic nonlocality) in nano-scale materials during the coupled between electrons and thermoelastic fields (Allen, 2014; Khamis et al., 2021). On the other hand, the nanoscale systems are very complex, therefore, we contented ourselves with studying the non-local equation of motion only.
In this research, the moisture diffusivity property is used to study the wave propagation in a non-local semiconductor medium with photo-thermoelasticity. The work is investigated in one dimension (1D) while a photothermal transport process is going on, affected by specific mechanical forces and the diffusivity upon being hit by a non-Gaussian laser pulse. The problem has been addressed at the free surface of a non-local semiconducting material when the thermal conductivity of the medium depends on the heat. By applying Laplace transforms to the time variable, the governing equations for the most important fundamental physical quantities may be solved analytically. Numerical inversion is carried out on a computer using powerful and efficient software. As a final step, normal force stress, normal displacement, carrier density, temperature distribution, and moisture concentration were all calculated numerically with the different values of thermal memory, thermal conductivity, moisture reference and nonlocality parameters.
The carrier density
The non-local motion equation for diffusivity semiconductor medium may be written as:
The nonlocal elastic parameter in length is denoted by
The stress equation in terms of plasma, temperature, strain and moisture concentration can be written as follows:
In all equations in this work a “comma” before an index implies space-differentiation and a “dot” above a symbol refers to the time-differentiation.
Take into account the moisture thermal conductivity, which is variable and may be chosen as a linear function of temperature. Non-local semiconductor material’s changing moisture thermal conductivity under the effect of a light heat source is represented as a function of temperature as shown in (Hasselman and Heller, 1980b; Alhashash et al., 2022):
When the medium is independent of temperature, the constant thermal conductivity (reference) is
Considering that the values of all physical quantities are unrelated to the
The motion Eq. 4 has the following structure (Hasselman and Heller, 1980b):
Where
Several methods of differentiation provide Eqs. 7, 8 for the map transform, which may be used to the fundamental equations to derive the thermal conductivity, which is a variable in the original computations, as:
Using the same technique, the time-differentiating from the first order for diffusivity is:
As a result applying the map transform to Eq. 1, which
The last term in the first half of Eq. 13 in the preceding equation may be extended as follows if the non-linear components are disregarded:
Leibniz integral rule is applied to Eq. 13, which yields:
Rewriting the heat Eq. 2 and moisture diffusion Eq. 3 after using the map transform yields the following:
According to the map transform, the equation of motion (4) takes the form:
With neglecting the non-linear term, yields:
According to relation (19), the mapped motion Eq. 18 can be rewritten as:
On the other hand, the constitutive equation for the non-local medium can be rewritten in 1D as:
The following are additional non-dimensional values we may provide for use in simplifying expressions:
Using the dimensionless Eq. 22, the mapped Eqs. 15–17 and Eqs. 20, 21 can be reduced in the following form:
Where
To aid in finding a mathematical solution when the system is initially at rest, below are the initial conditions:
To simplify the definition of partial differential equations, the Laplace transform is used, which is defined as:
Eq. 29 is used to convert Eqs. 23–27 as follows:
where,
Eliminating technique is used for the quantities
By conducting calculations using computer programs such as Mathematica, the basic coefficients can be calculated in Eq. 35, whose values are deduced as follows:
Eq. 35 can be solved using the factorization method, which yields:
To acquire roots in the positive real part at
It is possible to express the solutions in terms of the other variables as follows:
The quantities
Assume that the elastic non-local semiconductor medium is exposed to thermal loads of the thermal ramp type under conditions of heat, plasma, and mechanical loading. These conditions are applied to the free outside surface of the non-local medium. In every scenario, Laplace transformations are used (Vlase et al., 2017; Sladek et al., 2020).
(I) Type ramp heating is used for the thermal boundary condition at
The time of pulse heat flux is
(II) A mechanical load is applied to the surface at
Laplace transformation is used, which yields:
(III) During the diffusion phase, the carriers’ plasma density, which can be quantified with the help of the plasma excitation function
Maximum plasma shock loading caused by a laser pulse occurs at a time
(Ⅳ) The boundary condition for displacement on the free surface at
Or:
To obtain the relation between the temperature
In the same way, moisture diffusivity can be obtained.
The inverse Laplace-transform is calculated using the Riemann-sum approximation method; [see ref. (Honig and Hirdes, 1984)] for additional information. Therefore, the following expressions may be used to derive the field’s time-domain variables based on Fourier series expansion. For a Laplace-domain function
where
The following relationship may be found by expanding for the function
Where
To further demonstrate the theoretical findings from the preceding part, we will now provide numerical data. Numerical values of physical characteristics such as thermal, displacement, plasma, moisture concentration, and the normal distribution of stress obtained from this problem under the impact of variable thermal conductivity over a short time may now be graphically represented in MATLAB for the researched physical fields. In the theoretical investigation, n-type silicon (Si) acts as the non-local semiconductor solid material in the device. Table 1 uses SI units for the following Si physical parameters: (Lotfy et al., 2017; Ezzat, 2020; Mondal and Sur, 2021; Zhao et al., 2022a; Zhao et al., 2022b).
Three thermoelasticity models with various relaxation times are analyzed in Figure 1A–D (the first group). When
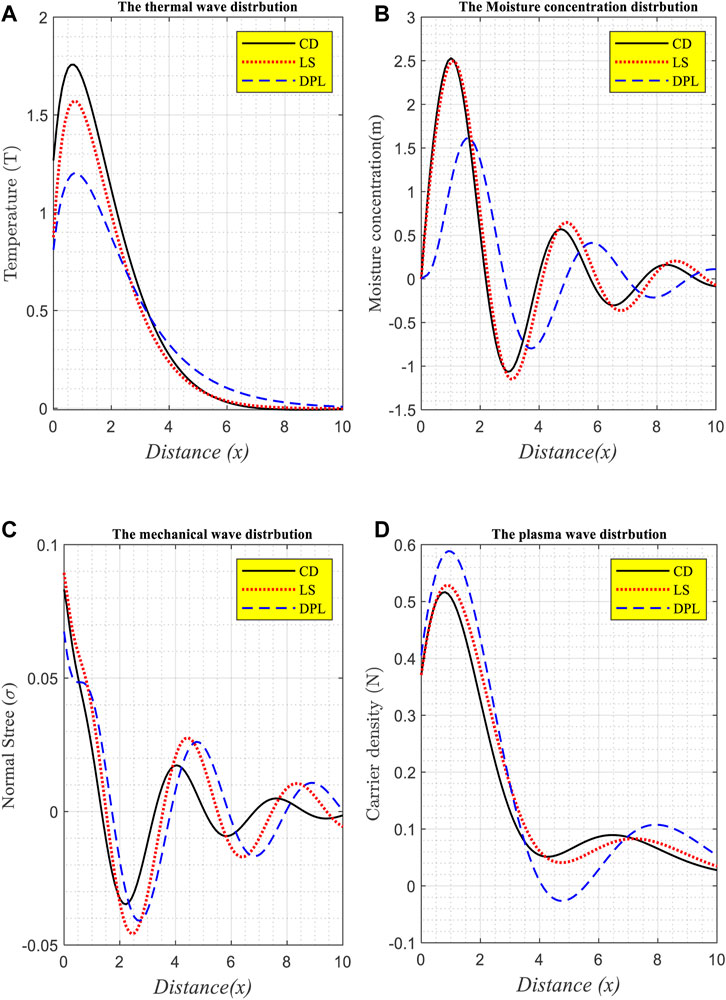
FIGURE 1. (A–D) The wave propagation of the physical fields distribution against the distance according to the variation of thermal relaxation times under the effect of variable thermal conductivity and moisture field for non-local Si material.
Figure 2A–D (the second category) presents a representation of the physical quantities plotted against a horizontal distance and accompanied by several reference moisture constant values. Under the impact of laser pulses and variable thermal conductivity
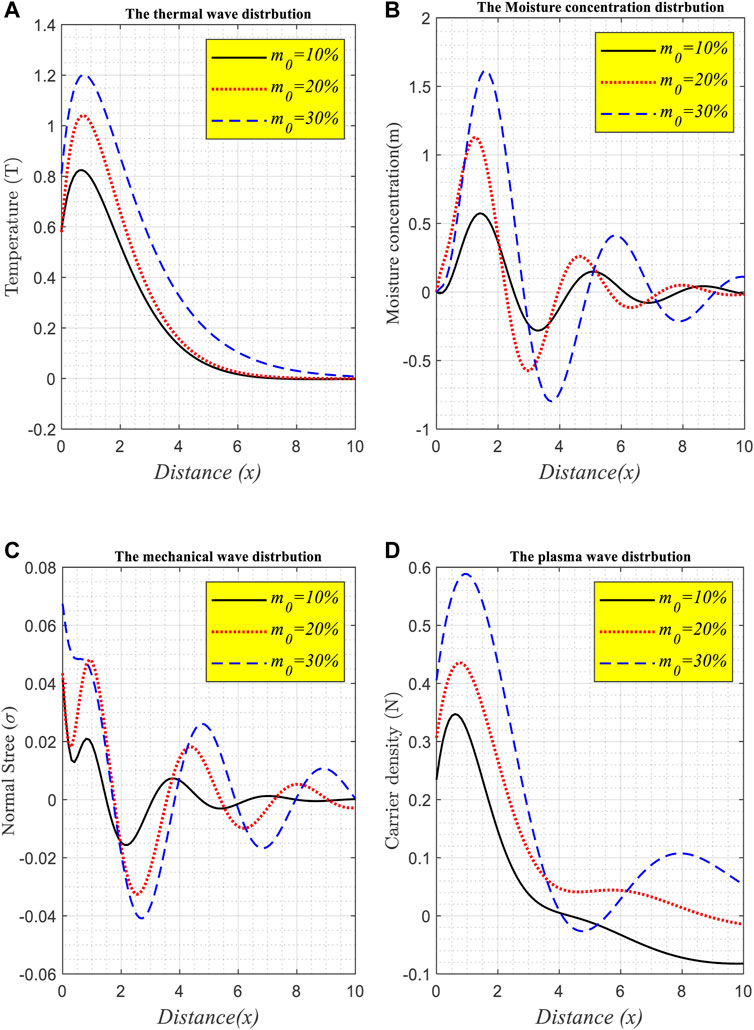
FIGURE 2. (A–D) The wave propagation of the physical fields distribution against the distance according to the different values the reference moisture
According to the kind of thermal ramp and the three constant values of
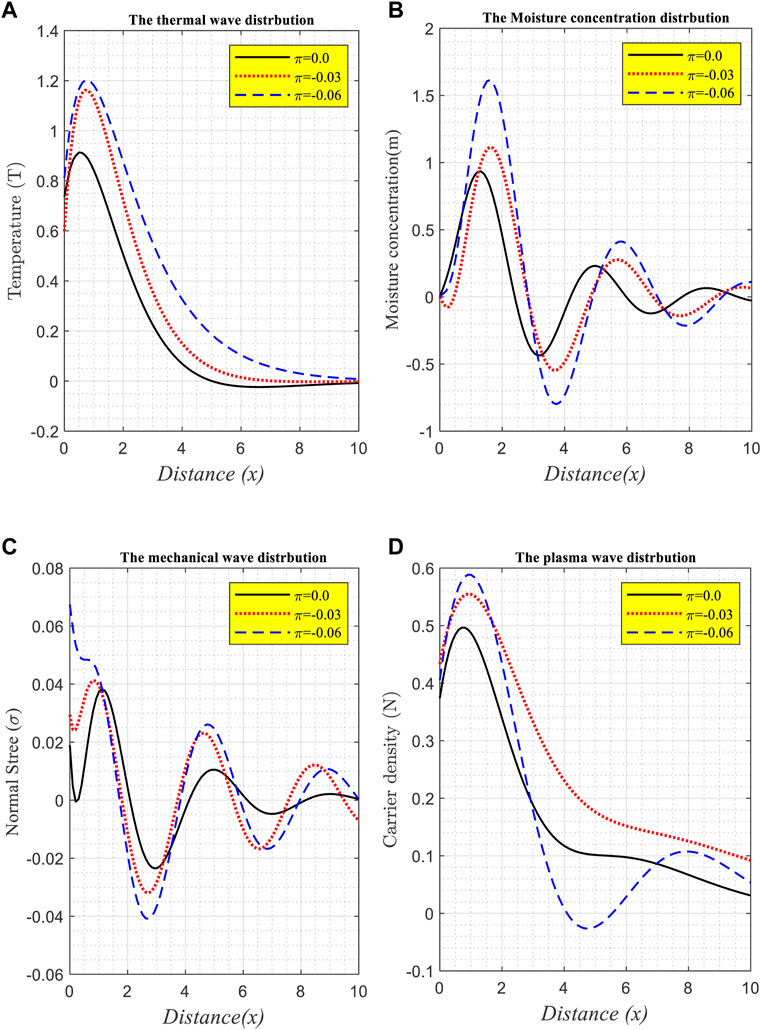
FIGURE 3. (A–D) The wave propagation of the physical fields distribution against the distance according to the variation of thermal conductivity under the effect of moisture field for non-local Si material using the DPL model.
At a constant value of time (
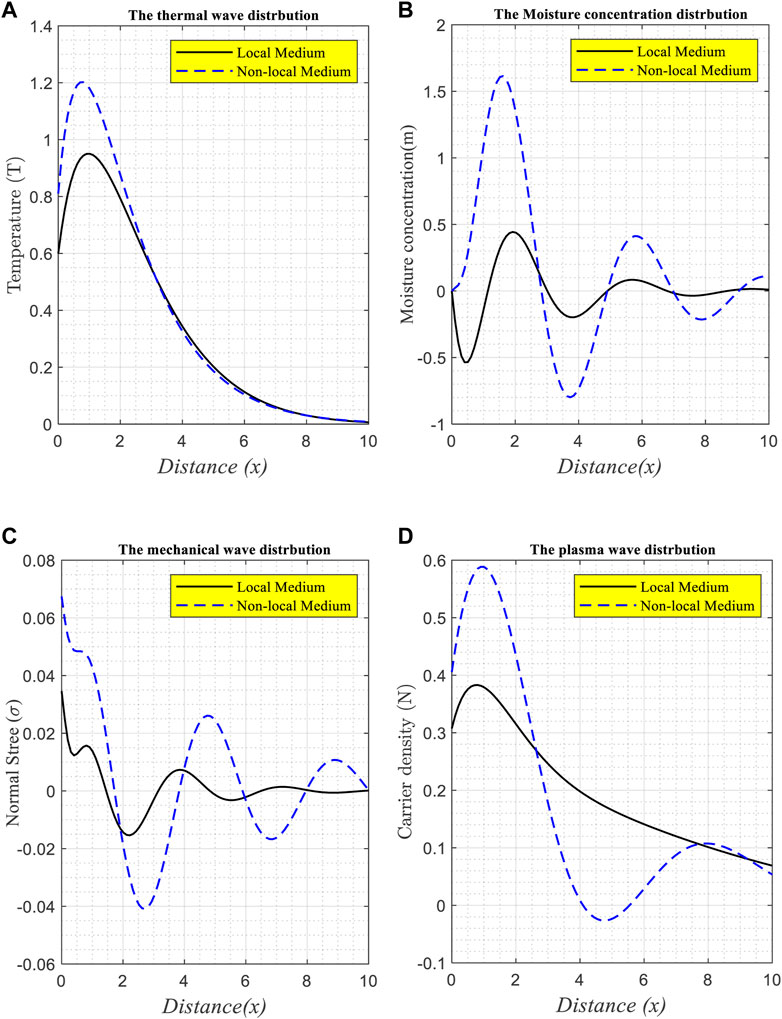
FIGURE 4. (A–D) The wave propagation of the physical field distribution against the distance according to the local and non-local parameters under the effect of variable thermal conductivity and moisture field for Si material.
In this study, we investigate how several external conditions, such as ramp-type heating, laser shock, moisture, and mechanical forces, might affect the propagation of photothermal-elastic waves in a solid non-local semiconducting medium. Electron-elastic deformations ignite elastic waves inside the non-local semiconductor, resulting in a fluctuating deformation potential. One may get the 1D case now. There is hope that the photo-thermoelasticity theories may focus attention on the peculiarities of wave motion in non-local semiconductor media. Considerable graphical analysis has been performed to investigate the significance of thermal memory, the variable thermal conductivity effect, nonlocality, and the moisture reference. As a result of its clarity and precision, the photothermal theory may be used to explain de-excitation in materials and the absorption of light. The plots show that the thermal memory, thermal conductivity, moisture content, and nonlocality of the medium have a major impact on all the considered domains. The research might help scientists learn more about how waves behave in a wide range of environments and temperatures. There is a clear correlation between the thermal conductivity, moisture content, and nonlocality of the field quantities, as the amplitude of these values varies (increasing or decreasing) with the thermal memory. Recent research has shown that semiconductors may be utilized to convert solar energy into electricity while also withstanding exposure to laser pulses, demonstrating the vital role that semiconductors play in today’s cutting-edge technologies. Modern technology relies heavily on semiconductors in a variety of devices, such as solar cells, displays, and transistors. Several fields of mechanical and electrical engineering employ them as nanomaterials. Thermomechanical, sensor, resonator, medical, and accelerometer researchers should all be able to make use of the study’s findings in their own ongoing and future investigations. At the opposite end of the spectrum, microwave and radio frequency emitters make it possible for people to communicate wirelessly. Visible and infrared diode lasers are at the center of the information technology industry. The method presented here has potential application to a wide range of photo-thermoelasticity and thermodynamic issues.
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.
KL: Supervision, conceptualization, methodology, software, data curation. SE-S: Writing—original draft preparation. HC: Visualization, investigation. AE-B: Software, validation, NB: New Software; writing—reviewing and editing.
Authors extend their appreciation to Princess Nourah bint Abdulrahman University for fund this research under Researchers Supporting Project number (PNURSP2023R154) Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.
The authors extend their appreciation to the Deanship of Scientific Research at Northern Border University, Arar, KSA for funding this research work through the project number “NBU-FFR-2023-0027”.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Abo-dahab, S., and Lotfy, Kh. (2017). Two-temperature plane strain problem in a semiconducting medium under photothermal theory. Waves Ran. Comp. Med. 27 (1), 67–91. doi:10.1080/17455030.2016.1203080
Abouelregal, A., and Marin, M. (2020). The response of nanobeams with temperature-dependent properties using state-space method via modified couple stress theory. Symmetry 12 (8), 1276. doi:10.3390/sym12081276
Alhashash, A., Elidy, E., El-Bary, A., Tantawi, R., and Lotfy, Kh. (2022). Two-temperature semiconductor model photomechanical and thermal wave responses with moisture diffusivity process. Crystals 12, 1770. doi:10.3390/cryst12121770
Allen, P. B. (2014). Size effects in thermal conduction by phonons. Phys. Rev. B 90, 054301. doi:10.1103/physrevb.90.054301
Biot, M. A. (1956). Thermoelasticity and irreversible thermodynamics. J. Appl. Phys. 27, 240–253. doi:10.1063/1.1722351
Brancik, L. “Programs for fast numerical inversion of Laplace transforms in MATLAB language environment,” in Proceedings of the 7th Conf. MATLAB’99, Czech Republic Prague, November 1999, 27–39.
Chandrasekharaiah, D. S. (1986). Thermoelasticity with second sound: A review. Appl.Mech. Rev. 39, 355–376. doi:10.1115/1.3143705
Eringen, A., and Edelen, D. (1972). On nonlocal elasticity. Int. J. Eng. Sci. 10, 233–248. doi:10.1016/0020-7225(72)90039-0
Eringen, A. (1972). Nonlocal polar elastic continua. Int. J. Eng. Sci. 10, 1–16. doi:10.1016/0020-7225(72)90070-5
Ezzat, M. (2020). Hyperbolic thermal-plasma wave propagation in semiconductor of organic material. Waves Rand. Comp. media 32, 334–358. doi:10.1080/17455030.2020.1772524
Gasch, A., Malm, R., and Ansell, A., 2016, Coupled hygro-thermomechanical model for concrete subjected to variable environmental conditions, Int. J. Solids Struct., 91, 143–156.
Gordon, J. P., Leite, R. C. C., Moore, R. S., Porto, S. P. S., and Whinnery, J. R. (1964). Long-transient effects in lasers with inserted liquid samples. Bull. Am. Phys. Soc. 119, 501.
Hasselman, D., and Heller, R. (1980). Thermal stresses in severe environments. New York, USA: Plenum Press.
Hasselman, D., and Heller, R. (1980). Thermal stresses in severe environments. New York, NY, USA: Plenum Press.
Hobiny, A., and Abbas, I. A. (2016). A study on photothermal waves in an unbounded semiconductor medium with cylindrical cavity. Mech. Time-Depend Mater 6, 61–72. doi:10.1007/s11043-016-9318-8
Honig, G., and Hirdes, U. (1984). A method for the numerical inversion of Laplace transforms Transforms. Comp. Appl. Math. 10 (1), 113–132. doi:10.1016/0377-0427(84)90075-x
Hosseini, S. M., Sladek, J., and Sladek, V. (2013). Application of meshless local integral equations to two dimensional analysis of coupled non-Fick diffusion-elasticity. Eng. Analysis Bound. Elem. 37 (3), 603–615. doi:10.1016/j.enganabound.2013.01.010
Huang, M., Wei, P., Zhao, L., and Li, Y. (2021). Multiple fields coupled elastic flexural waves in the thermoelastic semiconductor microbeam with consideration of small scale effects. Compos. Struct. 270, 114104. doi:10.1016/j.compstruct.2021.114104
Khamis, A., Lotfy, Kh., El-Bary, A., Mahdy, A., and Ahmed, M. (2021). Thermal-piezoelectric problem of a semiconductor medium during photo-thermal excitation. Waves Random Complex Media 31 (6), 2499–2513. doi:10.1080/17455030.2020.1757784
Kreuzer, L. B. (1971). Ultralow gas concentration infrared absorption spectroscopy. J. Appl. Phys. 42, 2934–2943. doi:10.1063/1.1660651
Liu, J., Han, M., Wang, R., Xu, S., and Wang, X. (2022). Photothermal phenomenon: Extended ideas for thermophysical properties characterization. J. Appl. Phys. 131, 065107. doi:10.1063/5.0082014
Lord, H., and Shulman, Y. (1967). A generalized dynamical theory of thermoelasticity. J. Mech. Phys. Solids 15, 299–309. doi:10.1016/0022-5096(67)90024-5
Lotfy, Kh., Hassan, W., and Gabr, M. E. (2017). Thermomagnetic effect with two temperature theory for photothermal process under hydrostatic initial stress. Results Phys. 7, 3918–3927. doi:10.1016/j.rinp.2017.10.009
Lotfy, Kh. (2017). Photothermal waves for two temperature with a semiconducting medium under using a dual-phase-lag model and hydrostatic initial stress. Waves Ran. Comp. Med. 27 (3), 482–501. doi:10.1080/17455030.2016.1267416
Lotfy, Kh., and Tantawi, R. (2020). Photo-thermal-elastic interaction in a functionally graded material (FGM) and magnetic field. Silicon 12, 295–303. doi:10.1007/s12633-019-00125-5
Lotfy, Kh. (2016). The elastic wave motions for a photothermal medium of a dual-phase-lag model with an internal heat source and gravitational field. Can. J. Phys. 94, 400–409. doi:10.1139/cjp-2015-0782
Marin, M., Ellahi, R., Vlase, S., and Bhatti, M. (2020). On the decay of exponential type for the solutions in a dipolar elastic body. J. Taibah Univ. Sci. 14 (1), 534–540. doi:10.1080/16583655.2020.1751963
Marin, M., Vlase, S., and Paun, M. (2015). Considerations on double porosity structure for micropolar bodies. AIP Adv. 5 (3), 037113. doi:10.1063/1.4914912
Mondal, S., and Sur, A. (2021). Photo-thermo-elastic wave propagation in an orthotropic semiconductor with a spherical cavity and memory responses. Waves Random Complex Media 31 (6), 1835–1858. doi:10.1080/17455030.2019.1705426
Scutaru, M., Vlase, S., Marin, M., and Modrea, A. New analytical method based on dynamic response of planar mechanical elastic systems, Bound. Value Probl., 2020, 1, 104, doi:10.1186/s13661-020-01401-9
Sladek, J., Sladek, V., Repka, M., and Pan, E. (2020). A novel gradient theory for thermoelectric material structures. Int. J. Solids Struct. 206, 292–303. doi:10.1016/j.ijsolstr.2020.09.023
Song, Y. Q., Todorovic, D. M., Cretin, B., and Vairac, P. (2010). Study on the generalized thermoelastic vibration of the optically excited semiconducting microcantilevers. Int. J. Sol. Struct. 47, 1871–1875. doi:10.1016/j.ijsolstr.2010.03.020
Szekeres, A. (2000). Analogy between heat and moisture. Comput. Struct. 76, 145–152. doi:10.1016/s0045-7949(99)00170-4
Szekeres, A., 2012, Cross-coupled heat and moisture transport: Part 1 theory, J. Therm. Stresses, 35, 248–268.
Szekeres, A., and Engelbrecht, J., 2000, Coupling of generalized heat and moisture transfer, Period. Polytech. Ser. Mech. Eng., 44, (1), 161–170.
Tam, A. C. (1986). Applications of photoacoustic sensing techniques. Rev. Mod. Phys. 58, 381–431. doi:10.1103/revmodphys.58.381
Tam, A. C. (1989). Photothermal investigations in solids and fluids. Boston, Unites States: Academic Press, 1–33.
Todorovic, D. M., Nikolic, P. M., and Bojicic, A. I. (1999). Photoacoustic frequency transmission technique: Electronic deformation mechanism in semiconductors. J. Appl. Phys. 85, 7716–7726. doi:10.1063/1.370576
Vlase, S., Năstac, C., Marin, M., and Mihălcică, M. (2017). A method for the study of the vibration of mechanical bars systems with symmetries. Acta Tech. Napoc. Ser. Appl. Math. Mech. Eng. 60 (4), 539–544.
Youssef, H., and Abbas, I. (2007). Thermal shock problem of generalized thermoelasticity for an infinitely long annular cylinder with variable thermal conductivity. Comp. Meth. Sci. Tech. 13, 95–100. doi:10.12921/cmst.2007.13.02.95-100
Youssef, H., and Abbas, I. (2007). Thermal shock problem of generalizedthermoelasticity for an infinitely long annular cylinder with variable thermal conductivity. Comput. methods Sci. Technol. 13 (2), 95–100. doi:10.12921/cmst.2007.13.02.95-100
Youssef, H., and El-Bary, A. (2006). Thermal shock problem of a generalized thermoelastic layered composite material with variable thermal conductivity. Math. Problems Eng. 2006, 1–14. doi:10.1155/mpe/2006/87940
Youssef, H. (2005). State-space on generalized thermoelasticity for an infinite material with a spherical cavity and variable thermal conductivity subjected to ramp-type heating. J. CAMQ, Appl. Math. Inst. 13, 369–390.
Zhao, L., Wei, P., Huang, M., and Xu, Y. (2022). Electro-Thermo-Mechanical multiple fields coupled wave propagation through piezoelectric semiconductor sandwich structure. Compos. Struct. 288, 115358. doi:10.1016/j.compstruct.2022.115358
Zhao, L., Wei, P., Huang, M., and Xu, Y. (2022). Reflection and transmission of coupled elastic waves by a semiconduction interlayer with consideration of photothermal effects. J. Acoust. Soc. Am. 151 (3), 1816–1828. doi:10.1121/10.0009674
Keywords: photothermal theory, non-local semiconductor, moisture diffusivity, thermal conductivity, thermal ramp, silicon
Citation: El-Sapa S, El-Bary AA, Chtioui H, Becheikh N and Lotfy K (2023) Photothermal excitation in non-local semiconductor materials with variable moisture thermal conductivity according to moisture diffusivity. Front. Mater. 10:1193423. doi: 10.3389/fmats.2023.1193423
Received: 24 March 2023; Accepted: 24 May 2023;
Published: 07 June 2023.
Edited by:
Karin Larsson, Uppsala University, SwedenReviewed by:
P. J. Wei, University of Science and Technology Beijing, ChinaCopyright © 2023 El-Sapa, El-Bary, Chtioui, Becheikh and Lotfy. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Nidhal Becheikh, bmlkaGFsLmJlY2hlaWtoQG5idS5lZHUuc2E=; Khaled Lotfy, a2hsb3RmeUB6dS5lZHUuZWc=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.