Exploration of the slope effect on the uplift capacity of single straight and belled piles supporting transmission towers

Single piles are normally used to support the transmission tower in mountain areas. Uplift capacity of piles is a key factor in the engineering design to increase the stability of transmission tower foundation. This study numerically investigated the uplift capacity of single straight and belled piles in the sloping ground which consisted of a clay layer underlain by medium weathered sandstone. A non-linear 3D finite element model was proposed to describe the uplift behavior of single piles and was calibrated against a field test on single piles subjected to uplift loading. A parametric study was conducted to investigate the effect of the slope angle (θ) on the uplift behavior of single piles. The uplift capacity decreased as θ increased for either straight piles or belled piles. Moreover, the range of the equivalent plastic strain was greatest for single piles in the level ground. For piles in the sloping ground, the range of equivalent plastic strain was wider at the position of the downstream slope than that at the position of the upstream slope when the uplift load of single piles reached the maximum. As the expansion angle increased to 30° and 45°, the uplift capacity of belled piles (R_u) was increased by 100% and 180% with respect to that of straight piles, respectively. The increase percentage in R_u was independent of θ. A practical method was proposed to quantify the slope effect on R_u.

1 Introduction

Plenty of transmission towers have been built in mountainous areas in the world. Thus, most of the transmission towers are located in the sloping ground (Jiang et al., 2022). Strong wind and earthquake pose a significant threat to the stability of transmission towers (Qu et al., 2018a; 2019; Xu et al., 2017b; 2021). Because of the variability in the direction of winds, the pile foundations of transmission towers could be subjected to uplift, compression, and horizontal loads. (Xu et al., 2023; Xu et al., 2013; Xu et al., 2017a; Qu et al., 2018b). In the engineering design, the uplift capacity is one of the significant factors to be considered for the pile of transmission towers. Moreover, Figure 1 shows the potential threat of the slope instability to the pile foundations of transmission towers in Guilin City of China. Thus, it is of great necessity to explore the uplift capacity of single piles in sloping ground.

FIGURE 1

FIGURE 1. Potential threat of the slope instability to the pile foundations of transmission towers in Guilin City of China: (A) scene 1 and (B) scene 2 (photos from the investigation of authors).

Over the last several decades, investigators have analyzed the uplift behavior of single piles in various soils. A simplified semi-empirical model was developed to estimate the uplift capacity of single piles embedded in sands (Shanker et al., 2007). The effect of arch on the uplift capacity of single piles and pile groups was investigated by Shelke and Patra (2009) and Shelke and Mishra (2010), respectively. Plenty of model tests were performed to investigate the effect of various factors on the uplift capacity of single piles in sand, that is, the slenderness ratio (Verma and Joshi., 2010; Faizi et al., 2015), relative density of soil, and embedment depth of piles (Gavver, 2013; Saravanan et al., 2017). Kyung and Lee (2019) investigated the influence of installation condition on the uplift capacity of micropiles in sand. Emirler et al. (2017) numerically investigated the effect of relative density of sand and the embedment depth on the uplift behavior of single piles. There are also plenty of studies on how to evaluate the uplift capacities of single piles in clayey soils. A few model tests have been conducted to evaluate the uplift capacity of concrete piles in clay under uplift loading (Mohan and Chandra, 1961; Turner, 1962; Sowa, 1970). Shin et al. (1993) experimentally evaluated the uplift capacity of rigid piles embedded in a compacted near-saturated clayey soil. Lai and Jin (2010) carried out a field-scale model test to investigate the load transfer mechanism of PHC piles in soft soil under uplift loading. However, little research is conducted to investigate the uplift behavior of piles embedded in the mountain areas, where the ground frequently consists of not only clay or sand but also weathered rocks. For these piles, a primary concern is leading to the interaction between the pile and the weathered rock under uplift loading because the weathered rock provides majority of soil resistance (Wang et al., 2021a).

To increase the capability of single piles to resist the uplift loading, the base of piles is expanded. Belled pile is a typical expanded pile to be used in engineering practice. The failure mechanism behind uplift belled piles in the level ground is sufficiently studied (Sawwaf and Nazir, 2006; Hong and Chim, 2015; Schafer and Madabhushi, 2020; Abdelgwad et al., 2022). Moreover, many scholars have studied various influential factors on the uplift capacity of belled piles in the level ground, for example, sand density (Ilamparuthi and Dickin, 2001; HondaHirai and Sato, 2011), diameter of the expanded base, embedment depth of piles (Tanaya and Sujit, 2019; Kang and Kang, 2022), and different bell space ratios (Sun et al., 2022). Moayedi and Mosallanezhad (2017) experimentally found that increasing the number of wings of multi-belled piles does necessarily improve the uplift resistance of single piles embedded in loose sands. The influence of various parameters, for example, the bell angle and the diameter of expanded base, on the uplift capacity of belled piles in sands was numerically studied (Liu et al., 2020; Yang and Qiu, 2020). Wang et al. (2021b) reported that the pile embedment and rock strength significantly affect the uplift resistance of belled piles (Yang et al., 2018). Chae et al. (2012) reported that the bell shape is more significant on the pile displacement than on the uplift capacity of belled piles in weathered rocks through both model tests and numerical analyses. Hu et al. (2022) experimentally explored the failure mechanism of the uplift belled piles in a layered ground which consists of sand and rock. However, previous studies mainly focus on the uplift behavior of single straight and belled piles in the level ground. Little work has been conducted on single piles in the sloping ground, especially in the mountain areas where the ground was composed of clay layer underlain by weathered sandstone.

This study numerically investigated the uplift capacity of single piles in the sloping ground which consisted of a clay layer underlain by medium weathered sandstone. The uplift behavior of single piles was described by a proposed non-linear 3D finite element model calibrated against a field test on single piles under uplift loading. A parametric study was conducted to investigate the effect of the slope angle (θ) on the uplift behavior of single straight and belled piles. Moreover, the influence of the expansion angle on the uplift capacity (R_u) of belled piles was discussed. Finally, a practical method was proposed to quantify the slope effect.

2 Numerical modeling

2.1 Proposed finite element model

Figure 2A shows a field test on a single bored pile under uplift loading in the level ground, as reported by Wang et al., 2021a. The site was composed of a silty clay layer underlain by medium weathered sandstone. The diameter (D) of the pile was 0.8 m, and the embedment depth of the pile in the sandstone was 2.4 m. The thickness of the clay layer was 3.0 m. There was a gap between the pile and the clay via casing shown in Figure 2A.

FIGURE 2

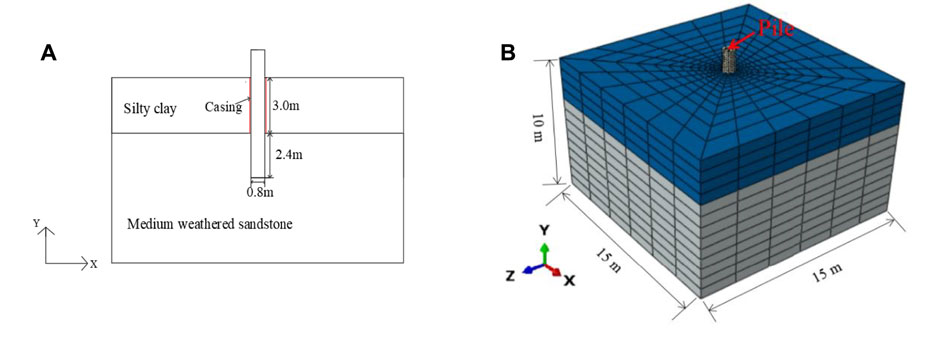
FIGURE 2. 3D finite element modeling of the uplift pile: (A) single pile in the layered ground consisting of silty clay and medium weathered sandstone and (B) finite element mesh.

Figure 2B shows the 3D finite element model with gradient mesh for the single pile under uplift loading in a finite element software ABAQUS (Systèmes, 2007). Both the soil and the pile were modeled by C3D8R elements. The C3D8R element is a general-purpose linear brick element with reduced integration (Systèmes, 2007). The size of the finite element mesh ranged from 0.05 m to 2.5 m. Fine mesh was used for soils surrounding the pile to ensure the sufficient accuracy of finite element analyses. To simulate the pullout behavior of piles in the finite element analysis, the pile–soil contact was considered by selecting “penalty function” and “hard contact” for tangential behavior and normal behavior, respectively. The default values suggested by the software were used for contact parameters. When the pile is separated from the soil, the contact pressure at the interface decreases to zero (AlIsawi et al., 2019). Note that the casing was not considered in the finite element modeling because it has an insignificant effect on the uplift capacity of piles.

Table 1 gives the input parameters for the pile and the soils.

TABLE 1

TABLE 1. Parameters of the pile–soil model.

In this study, the pile was assumed to be elastic. The elastic–plastic behavior of soils was described by the Drucker–Prager (DP) model (Drucker and Prager, 1952). The yielding function and the plastic potential function g for the linearly extended DP model were given by

$F=t-p\tan \beta -d=0,(1)$

$g=t_0-p\tan \psi ,(2)$

$t_0=\frac{q}{2}\left[1+\frac{1}{k}-\left(1-\frac{1}{k}\right){\left(\frac{r}{q}\right)}^3\right],(3)$

where q is the Mises equivalent stress; p is the equivalent pressure stress; r is the third invariant of deviatoric stress; β is the friction angle, which reflects the slope of the yield surface in the stress space; d is the cohesion of soils; k controls the dependence of the yield surface on the value of the intermediate principal stress and ranges from 0.778 to 1; and ψ is the dilation angle. In the study, k is taken as an average value of the range.

The distance between the lateral side and the pile to was set at 10 D to eliminate the boundary effect. In this study, initial stress analysis was performed before the uplift loading was applied to the pile to provide the initial stress of soils for the analysis of uplift piles. The displacements at the base and both two lateral sides of the model were zero.

2.2 Model verification

Figure 3 shows the measured and simulated uplift load (R)–vertical displacement (u_y) curves of single piles under uplift loading. The calculated displacement was generally lower than that measured from the test when the uplift load was smaller than approximately 4500 kN. Nevertheless, the calculated R_max was consistent with that obtained from the field tests. Moreover, the R_max was underestimated by approximately 4% if the initial stress was not considered. Thus, it is suggested that the initial stress can be taken into account in the analysis of the uplift pile.

FIGURE 3

FIGURE 3. Calculated and measured uplift load–displacement curves of single piles.

Moreover, an additional case (i.e., Case 1) was used to explore the influence of the contact between the pile and the clay on the uplift behavior of single piles in this study. Figure 3 also shows that the contact between the pile and the clay caused a 16% increase in the maximum uplift load. Case 1 was used as a bench mark model for the parametric study in the next section.

3 Results and discussion

The effect of slope angle (θ) on the uplift behavior of both straight pile and belled pile was investigated. Figure 4 schematically shows the slope angle (θ) and the belled pile with various base diameters by changing the expansion angle (α), where α is the angle that the pyramidal or conical surface makes against the vertical. Moreover, the effect of α on the uplift behavior of belled piles was studied accordingly. In this study, θ varied between 0° and 20°, and α ranged from 0° to 45°. Table 2 lists all cases in the finite element analyses of this study.

FIGURE 4

FIGURE 4. Schematic view of cases with different θ and α.

TABLE 2

TABLE 2. Cases in the finite element analyses of this study.

3.1 Influence of slope angle on straight piles

Figure 5 shows the influence of θ on the R–u_y curves of single piles. The effect of θ on the R–u_y curve was minimal when the uplift load was lower than approximately 4000 kN. However, the maximum uplift load (R_max) decreased as the slope angle increased.

FIGURE 5

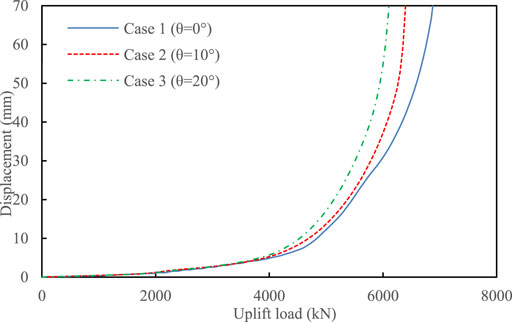
FIGURE 5. Uplift load–vertical displacement curves of uplift straight piles under different slope angles (θ).

Moreover, Figure 6 further shows the maximum equivalent plastic strain (${\epsilon }^{\text{pl}}$) distributed at the soils surrounding the pile. The equivalent plastic strain is defined as ${\epsilon }^{\text{pl}}=\int {\dot{\epsilon }}^{\text{pl}}\mathrm{d}t$, where ${\dot{\epsilon }}^{\text{pl}}=\mathbf{\sigma }:{\epsilon }^{\text{pl}}/\overline{\sigma }$ in the DP model, $\mathbf{\sigma }$ is the stress tensor, and $\overline{\sigma }$ is a function including hardening and rate-dependent effects (Systèmes, 2007). For the pile in the level ground, the equivalent plastic strain was symmetric about the uplift pile (see Figure 6A). Moreover, the range of equivalent plastic strain was wider at the position of the downstream slope than that at the position of the upstream slope when the uplift load reached the maximum Figures 6B, C. This was because of the lower yield strength of the soils at the downstream side of the slope, leading to relatively greater equivalent plastic strain at such position.

FIGURE 6

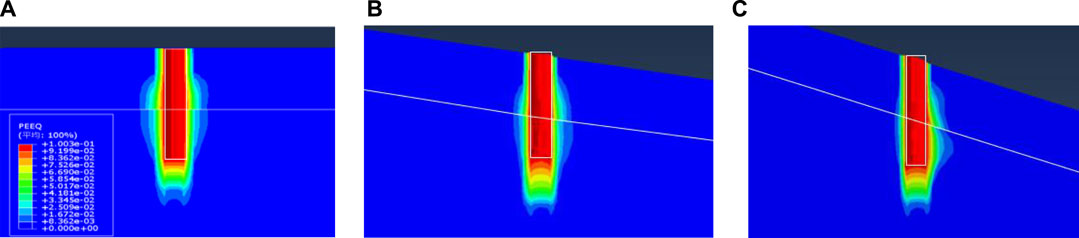
FIGURE 6. Effect of θ on the distribution of equivalent plastic strain surrounding the straight pile: (A) θ = 0°, (B) θ = 10°, and (C) θ = 20°.

3.2 Influence of slope angle on belled piles

Similar to the straight pile, Figure 7 shows that the calculated R_max decreased as θ increased. The same tendency was also found for other cases (see Figure 8A).The effect of θ on the R–u_y curve was minimal when the uplift load was lower than a critical value of approximately 9000 kN. The equivalent plastic strain range was much greater in soils surrounding belled piles than that in the case of straight piles (see Figure 9; Figure 6). Moreover, the range of equivalent plastic strain was also wider at the position of the downstream slope than that at the position of the upstream slope when the uplift load of belled piles reached the maximum.

FIGURE 7

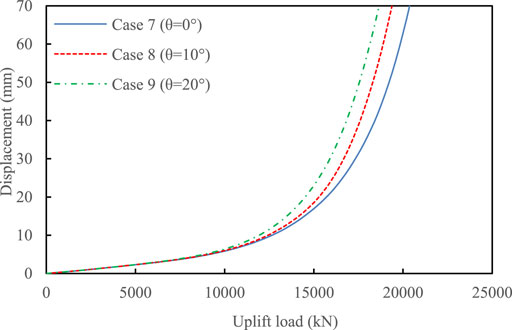
FIGURE 7. Uplift load–vertical displacement curve of belled piles (α = 45°) under different slope angles.

FIGURE 8

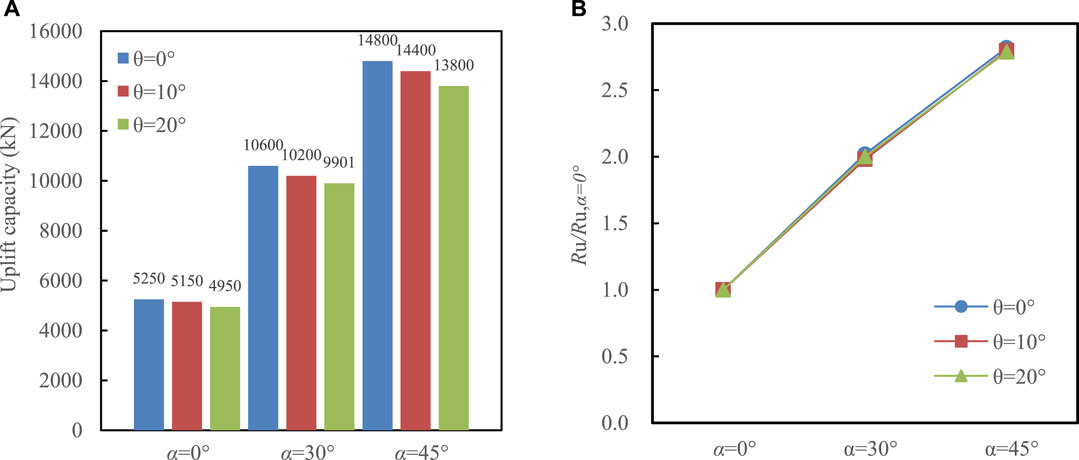
FIGURE 8. Effect of α on (A) the uplift capacity and (B) the normalized uplift capacity of single piles at different slope angles.

FIGURE 9

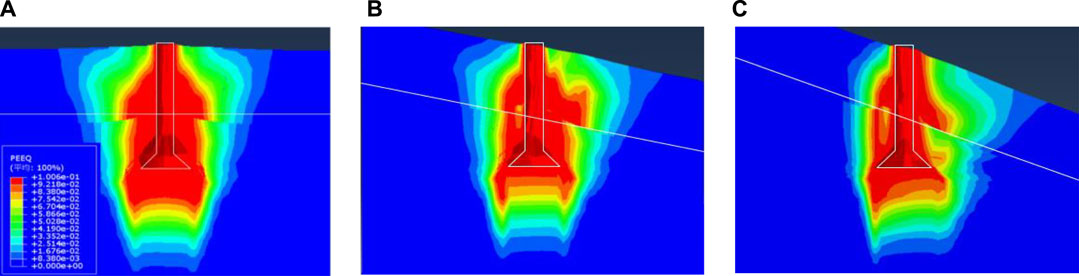
FIGURE 9. Effect of θ on the distribution of equivalent plastic strain surrounding the belled pile with α = 45°: (A) θ = 0°, (B) θ = 10°, and (C) θ = 20°.

3.3 Influence of the expansion angle of belled piles

To illustrate the effect of the expansion angle α, the uplift capacity (R_u) of belled piles was selected as an index and was obtained from the calculated R–u_y curve. Wang et al. (2020) suggested that Ru is the uplift load corresponding to a critical displacement (V_cri) of 2% D for the belled pile under uplift loading. Tang and Chen (2015) suggested V_cri = 2.5% D for rock-socketed piles under uplift loading. Wang et al. (2021b) suggested V_cri = 3% D for straight bored piles. In this study, V_cri = 2% D was used as a criterion for estimating R_u in this study.

Figure 8A also illustrates that R_u generally increased as α increased. Figure 8B further presents the R_u normalized to the uplift capacity (R_{u, α=0°}) of straight piles. As α increased to 30° and 45°, R_u was increased by 100% and 180% with respect to that of straight piles, respectively. Thus, increasing the expansion angle was an effective measure to increase R_u. Moreover, the increase percentage in R_u was independent on the slope angle (see Figure 8B). It should be stressed that the uplift capacity should be almost the same for the same bottom area of the belled piles with various expansion angles because the height of the expansion was assumed to be the same in this study.

3.4 Practical method for quantifying the slope effect on R_u

《Technical code for design of foundation of overhead transmission line 》 (DL/T5219-2014) is used for estimating R_u in China by the following equation. However, the equation is only used for piles in the level ground and cannot be used for the piles in the sloping ground.

$R_{\mathrm{u}}=A_{1}c{h_t}^2+A_2{\gamma }_s{h_t}^3+{\gamma }_s\left(A_3{h_t}^3-V_0\right)+G_f;h_t\le h_c.(4)$

Eq. 4 is used when h_t ≤ h_c, where ht is the embedment depth of the uplift pile and was taken as 5.4 m, as shown in Figure 2A, and h_c is the critical uplift depth and was taken as 3D, as suggested by the code (NEA, 2015); A₁, A₂, and A₃ refer to dimensionless parameters suggested by the code (NEA, 2015) and were determined by the shape of sliding surface, friction angle of soils, and the ratio of the embedment depth of the uplift pile to its base diameter; c stands for the soil cohesion, which was taken as the weighted average based on the thickness of two layers in this study; γ_s is the weighted average weight of soil above the tip of piles; and V₀ is the volume of piles within the embedment depth. G_f is the self-gravity of the foundation. Table 3 gives input parameters for calculating R_u.

TABLE 3

TABLE 3. Input parameters for estimating the uplift capacity of belled piles in the level ground.

Table 3 also shows the comparison between the results calculated from Eq. 4 and finite element analyses for belled piles in the level ground in the cases of α = 30° and α = 45°. The results indicated that the uplift capacity calculated from Eq. 4 was generally greater than the uplift capacity determined from finite element analyses. The discrepancy was mainly due to two reasons: 1) the critical displacement (V_cri) influenced P_u in finite element analyses. Particularly, the discrepancy was decreased with the increasing V_cri because of an increase in P_u and 2) Eq. 4 was proposed for the uniform layer. Thus, the application of Eq. 4 to the layered ground in this study caused certain errors and further contributed to the discrepancy. Nevertheless, as α increased from 30° to 45°, the calculated increase percentage (i.e., ∼26%); in R_u obtained from the proposed numerical model agreed reasonably well with that (i.e., ∼40%) of calculated from Eq. 4.

To estimate the influence of slope angle on R_u, a practical method was proposed in this study and was given by

$R_{\mathrm{u},\theta }=\beta R_{\mathrm{u}}(5)$

where β is a reduction factor and defined as the ratio of R_u to R_u, θ=0_°, and R_u, θ=0° denotes R_u at θ = 0°. Thus, β = 1 when R_u = R_u,θ=0°. Figure 10 illustrates that the reduction factor decreased as θ increased. Moreover, a linear relationship can be used to correlate the reduction factor with the slope angle for all data shown in Figure 8.

$\beta =-0.0071\theta +\mathrm{1.0;0}°\le \mathrm{\theta }\le 20°.(6)$

FIGURE 10

FIGURE 10. Effect of slope angle on the reduction factor at different expansion angles.

4 Conclusion

The effect of slope on the uplift capacity of single straight and belled piles supporting transmission towers was explored via a proposed numerical model which was calibrated against a field test. The following conclusions can be obtained:

(1) The calculated R_max from the 3D finite element model was consistent with that obtained from the field tests. Moreover, considering initial stress was recommended for analyses of uplift piles.

(2) The uplift capacity decreased as the slope angle θ increased for either straight piles or belled piles. Moreover, the range of the equivalent plastic strain was greatest for single piles in the level ground (i.e., θ = 0°).

(3) For piles in the sloping ground, the range of equivalent plastic strain was wider at the position of the downstream slope than that at the position of the upstream slope when the uplift load of single piles reached the maximum.

(4) As the expansion angle α increased to 30° and 45°, R_u was increased by 100% and 180% with respect to straight piles, respectively. Moreover, the increase percentage in R_u was independent on the slope angle.

(5) A practical method was proposed to quantify the slope effect on R_u.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

Conceptualization, software, validation, and writing—original draft: MB; methodology: SQ; investigation: JP and JL; and data curation: XZ.

Funding

The authors declare that this study received funding from Electric Power Research Institute of Guangxi Power Grid Co. Ltd. of China (Grant number: GXKJXM20210299). The funder was not involved in the study design, collection, analysis, interpretation of data, the writing of this article, or the decision to submit it for publication.

Conflict of interest

MB, SQ, JP, JL, and XZ were employed by the Electric Power Research Institute of Guangxi Power Grid Co., Ltd.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abdelgwad, A., Nasr, A., and Azzam, W. (2022). Utilization of enlarged base to improve the uplift capacity of single pile in sand—Model study. Innov. Infrastruct. Solutions 7, 317. doi:10.1007/S41062-022-00922-9

CrossRef Full Text | Google Scholar

Al-Isawi, A. T., Collins, P. E. F., and Cashell, K. A. (2019). Fully non-linear numerical simulation of a shaking table test of dynamic soil-pile-structure interactions in soft clay using ABAQUS. Virginia, United States: American Society of Civil Engineers.

Google Scholar

Chae, D., Cho, W., and Na, H. Y. (2012). Uplift capacity of belled pile in weathered sandstones. Int. J. Offshore Polar Eng. 22, 297–305.

Google Scholar

Drucker, D. C., and Prager, W. (1952). Soil mechanics and plastic analysis or limit design. Quart. Appl. Math. 10, 157–165. doi:10.1090/qam/48291

CrossRef Full Text | Google Scholar

Emirler, B., Emirler, M., and Yildiz, A. (2017). 3D numerical response of a single pile under uplift loading embedded in sand. Geotechnical Geol. Eng. 37, 4351–4363. doi:10.1007/s10706-019-00913-1

CrossRef Full Text | Google Scholar

Faizi, K., Armaghani, D. J., Sohaei, H., Rashid, A. S. A., and Nazir, R. (2015). Deformation model of sand around short piles under pullout test. Measurement 63, 110–119. doi:10.1016/j.measurement.2014.11.028

CrossRef Full Text | Google Scholar

Gaaver, K. E. (2013). Uplift capacity of single piles and pile groups embedded in cohesionless soil. Alexandria Eng. J. 52, 365–372. doi:10.1016/j.aej.2013.01.003

CrossRef Full Text | Google Scholar

HondaHirai, Y., and Sato, E. (2011). Uplift capacity of belled and multibelled piles in dense sand. Soils Found. 51, 483–496. doi:10.3208/sandf.51.483

CrossRef Full Text | Google Scholar

Hong, W. P., and Chim, N. (2015). Prediction of uplift capacity of a micropile embedded in soil. J. Civ. Eng. 19, 116–126. doi:10.1007/s12205-013-0357-2

CrossRef Full Text | Google Scholar

Hu, Z. B., Qu, S. Y., Wang, Q. K., Guo, Y. J., Ji, Y. K., and Ma, J. L. (2022). Pullout behaviour of belled piles under axial and oblique pull in soil-rock composite ground: An experimental study. Int. J. Civ. Eng. 2022, 00778. doi:10.1007/s40999-022-00778-1

CrossRef Full Text | Google Scholar

Ilamparuthi, K., and Dickin, E. A. (2001). The influence of soil reinforcement on the uplift behaviour of belled piles embedded in sand. Geotext. Geomembranes 19, 1–22. doi:10.1016/S0266-1144(00)00010-8

CrossRef Full Text | Google Scholar

Jiang, J. H., Huang, X. L., Shu, X. R., Ning, X., Qu, Y., and Xiong, W. L. (2022). Application of a damage constitutive model to pile–slope stability analysis. Front. Mater. 9, 1082292. doi:10.3389/FMATS.2022.1082292

CrossRef Full Text | Google Scholar

Kang, J. G., and Kang, G. O. (2022). Experimental and semitheoretical analyses of uplift capacity of belled pile in sand. Int. J. Geomechanics 22, 04022217. doi:10.1061/(ASCE)GM.1943-5622.0002511

CrossRef Full Text | Google Scholar

Kyung, D., and Lee, J. (2019). Uplift load-carrying capacity of single and group micropiles installed with inclined conditions. J. geotechnical geoenvironmental Eng. 143, 04017031. doi:10.1061/(ASCE)GT.1943-5606.0001700

CrossRef Full Text | Google Scholar

Lai, Y., and Jin, G. F. (2010). Uplift behavior and load transfer mechanism of prestressed high-strength concrete piles. J. Central South Univ. Technol. 17, 136–141. doi:10.1007/s11771-010-0022-6

CrossRef Full Text | Google Scholar

Liu, G., Zhang, Z. H., Cui, Q., Peng, J., and Cai, M. (2020). Uplift behavior of belled piles subjected to static loading. Arabian J. Sci. Eng. 46, 4369–4385. doi:10.1007/s13369-020-04779-x

CrossRef Full Text | Google Scholar

Moayedi, H., and Mosallanezhad, M. (2017). Uplift resistance of belled and multi-belled piles in loose sand. Measurement 109, 346–353. doi:10.1016/j.measurement.2017.06.001

CrossRef Full Text | Google Scholar

Mohan, D., and Chandra, S. (1961). Frictional resistance of bored piles in expansive clays. Geotechnique 11, 294–301. doi:10.1680/geot.1961.11.4.294

CrossRef Full Text | Google Scholar

National Energy Administration (NEA) (2015). Technical code for design of foundation of overhead transmission line. Beijing, Chain. (DL/T 5219-2014).

Google Scholar

Qu, C. X., Yi, T. H., Li, H. N., and Chen, B. (2018a). Closely spaced modes identification through modified frequency domain decomposition. Measurement 128, 388–392. doi:10.1016/j.measurement.2018.07.006

CrossRef Full Text | Google Scholar

Qu, C. X., Yi, T. H., and Li, H. N. (2019). Mode identification by eigensystem realization algorithm through virtual frequency response function. Struct. Con-trol Health Monit. 26, e2429. doi:10.1002/stc.2429

CrossRef Full Text | Google Scholar

Qu, C. X., Yi, T. H., Zhou, Y. Z., Li, H. N., and Zhang, Y. F. (2018b). Frequency identification of practical bridges through higher order spectrum. J. Aerosp. Engineering-ASCE 31, 04018018. doi:10.1061/(asce)as.1943-5525.0000840

CrossRef Full Text | Google Scholar

Saravanan, R., Arumairaj, P. D., and Subramani, T. (2017). Experimental model study on ultimate uplift capacity of vertical pile in sand. Water Energy Int. 60, 58–66.

Google Scholar

Sawwaf, M. E., and Nazir, A. (2006). The effect of soil reinforcement on pullout resistance of an existing vertical anchor plate in sand. Comput. Geotechnics 4, 167–176. doi:10.1016/j.compgeo.2006.04.001

CrossRef Full Text | Google Scholar

Schafer, M., and Madabhushi, S. P. G. (2020). Uplift resistance of enlarged base pile foundations. Indian Geotech. J. 50, 426–441. doi:10.1007/s40098-019-00369-3

CrossRef Full Text | Google Scholar

Shanker, K., Basudhar, P. K., and Patra, N. R. (2007). Uplift capacity of single piles: Predictions and performance. Geotechnical Geol. Eng. 2, 151–161. doi:10.1007/s10706-006-9000-z

CrossRef Full Text | Google Scholar

Shelke, A., and Mishra, S. (2010). Uplift capacity of single bent pile and pile group considering arching effects in sand. Geotechnical Geol. Eng. 28, 337–347. doi:10.1007/s10706-009-9295-7

CrossRef Full Text | Google Scholar

Shelke, A., and Patra, N. R. (2009). Effect of arching on uplift capacity of single piles. Geotechnical Geol. Eng. 27, 365–377. doi:10.1007/s10706-008-9236-x

CrossRef Full Text | Google Scholar

Shin, E. C., Das, B. M., Puri, V. K., Yen, S. C., and Cook, E. E. (1993). Ultimate uplift capacity of model rigid metal piles in clay. Geotechnical Geol. Eng. 11, 203–215. doi:10.1007/BF00531251

CrossRef Full Text | Google Scholar

Sowa, V. A. (1970). Pulling capacity of concrete cast in situ bored piles. Can. Geotechnical J. 7, 482–493. doi:10.1139/t70-060

CrossRef Full Text | Google Scholar

Sun, T., Cui, X. Z., and Sun, Y. F. (2022). Model tests on uplift capacity of double-belled pile influenced by distance between bells. J. Central South Univ. Technol. 29, 1630–1640. doi:10.1007/S11771-022-5018-5

CrossRef Full Text | Google Scholar

Systèmes, D. (2007). Abaqus analysis user’s manual. Providence, RI, USA: Simulia Corp., 40.

Google Scholar

Tanaya, D., and Sujit, K. P. (2019). Comparison of uplift capacity and nonlinear failure surfaces of single-belled anchor in homogeneous and layered sand deposits. Adv. Civ. Eng. 23, 1–23. doi:10.1155/2019/4672615

CrossRef Full Text | Google Scholar

Tang, M. X., and Chen, D. A. (2015). Computational method of ultimate capacity of uplift piles in basement rock. Rock Soil Mech. 36, 633–638.

Google Scholar

Turner, E. Z. (1962). Uplift resistance of transmission tower footing. J. Power Div. ASCE 88, 17–33. doi:10.1061/JPWEAM.0000339

CrossRef Full Text | Google Scholar

Verma, A. K., and Joshi, P. K. (2010). Uplift load carrying capacity of piles in sand. Mumbai: Indian Geotechnical Conference, 857–860.

Google Scholar

Wang, Q. K., Ma, J. L., Ji, Y. K., and Cao, S. (2021a). Calculation method and influencing factors of uplift bearing capacity of rock-socketed pedestal pile. Arabian J. Geosciences 14, 1–15. doi:10.1007/S12517-021-06567-9

CrossRef Full Text | Google Scholar

Wang, Q. K., Ma, J. L., Wang, M. T., and Ji, Y. K. (2021b). Field test on uplift bearing characteristics of transmission tower foundation in mountainous areas of Western China. Environ. Earth Sci. 80, 745. doi:10.1007/S12665-021-09851-9

CrossRef Full Text | Google Scholar

Wang, Q. K., Ma, J. L., Xiao, Z. L., Chen, W., and Ji, Y. (2020). Field test on uplift bearing capacity of rock-socketed belled piles. J. Civ. Eng. 24, 2353–2363. doi:10.1007/s12205-020-2011-0

CrossRef Full Text | Google Scholar

Xu, L. Y., Cai, F., Wang, G. X., Chen, G. X., and Li, Y. Y. (2017b). Nonlinear analysis of single reinforced concrete piles subjected to lateral loading. KSCE J. Civ. Eng. 21, 2622–2633. doi:10.1007/s12205-017-1010-2

CrossRef Full Text | Google Scholar

Xu, L. Y., Cai, F., Wang, G. X., and Chen, G. X. (2017a). Nonlinear analysis of single laterally loaded piles in clays using modified strain wedge model. Int. J. Civ. Eng. 15, 895–906. doi:10.1007/s40999-016-0072-8

CrossRef Full Text | Google Scholar

Xu, L. Y., Cai, F., Wang, G. X., and Ugai, K. (2013). Nonlinear analysis of laterally loaded single piles in sand using modified strain wedge model. Comput. Geotechnics 51, 60–71. doi:10.1016/j.compgeo.2013.01.003

CrossRef Full Text | Google Scholar

Xu, L. Y., Chen, W. Y., Cai, F., Song, Z., Pan, J. M., and Chen, G. X. (2023). Response of soil–pile–superstructure–quay wall system to lateral displacement under horizontal and vertical earthquake excitations. Bull. Earthq. Eng. 21, 1173–1202.doi:10.1007/S10518-022-01572-Z

CrossRef Full Text | Google Scholar

Xu, L. Y., Song, C. X., Chen, W. Y., Cai, F., Li, Y. Y., and Chen, G. X. (2021). Liquefaction-induced settlement of the pile group under vertical and horizontal ground motions. Soil Dyn. Earthq. Eng. 144, 106709. doi:10.1016/J.SOILDYN.2021.106709

CrossRef Full Text | Google Scholar

Yang, B., Ma, J. L., Chen, W. L., and Yang, Y. X. (2018). Uplift behavior of belled short piles in weathered sandstone. Math. Problems Eng. 8, 1–8. doi:10.1155/2018/8614172

CrossRef Full Text | Google Scholar

Yang, Y. S., and Qiu, L. C. (2020). MPM simulation of uplift resistance of enlarged base piles in sand. Soils Found. 60, 1322–1330. doi:10.1016/j.sandf.2020.08.003

CrossRef Full Text | Google Scholar