Reliable machine learning for the shear strength of beams strengthened using externally bonded FRP jackets

All over the world, shear strengthening of reinforced concrete elements using external fiber-reinforced polymer jackets could be used to improve building sustainability. However, reports issued by the American Concrete Institute called for heavy scrutiny before actual field implementation. The very limited number of proposed shear equations lacks reliability and accuracy. Thus, further investigation in this area is needed. In addition, machine-learning techniques are being implemented successfully to develop strength models for complex problems including shear, flexure, and torsion. This study aims to provide a reliable machine-learning model for reinforced concrete beams strengthened in shear using externally reinforced fiber polymer sheets. The proposed model was developed and validated against the experimental database and the very limited models in existing literature. The model showed better agreement with the experimentally measured strength compared to the previous models, which accounted for the effect of various parameters including but not limited to: the element geometry, strengthening details, and configurations. The model could guide the further developments of design codes and mechanical models.

1 Introduction

The significant shear acts upon reinforced concrete (RC) elements in many buildings. Various shear failures of RC buildings have been reported in previous research papers (Whittle, 2013). The shear failure of RC beams is brittle (Chalioris and Karayiannis, 2009; Karayannis et al., 2018; Deifalla et al., 2020a; Deifalla et al., 2020b), and the elevated cost of replacing infrastructure has driven research into strengthening techniques. Shear strength is vital in many projects (Gosbell and Meggs, 2002; FIB. FRP Reinforcement in RC Structures, 2007; Oller et al., 2021). The fiber-reinforced polymer (FRP) sheets have various benefits over steel plates. Thus, research has been conducted to investigate the behavior of FRP externally and internally in RC beams (De Lorenzis and Nanni, 2001; Deifalla, 2020a; Kotynia et al., 2021). FRP has been used effectively in the automotive and aerospace industries for a few decades. It has been used for new structural elements in recent years, particularly in aggressive environments including but not limited to chemical plants because it is corrosion free (Deifalla, 2015; Deifalla, 2020b; Deifalla et al., 2021). In addition, FRP can be used in situations where the use of steel would be impossible or impractical (Hassan and Deifalla, 2016; Salem and Deifalla, 2022). For instance, it can be formed on-site to fit any irregular shape. FRP fabrics can be wrapped around curves (i.e., beams’ sides, columns’ corners, or beams’ soffits). It is lighter in weight than steel but has the same strength, (Deifalla et al., 2013), and it is easy to handle and cut to the required length.

Worldwide, there is a lack of consensus on the shear strength contribution of externally bonded (EB)-FRP jackets. Several design guidelines and codes exist worldwide (fib Task group 5.1, 2019; ACI Committee 440, 2017; Construction C–AC on TR for. CNR-DT 200 R1/2013, 2013; TR-55 CSTR, 2012; JSCE Japanese Society of Civil Engineers, 2000; Abuodeh et al., 2020; Ly et al., 2020; Chalioris et al., 2020; Benzeguir and Chaallal, 2021; Kim, 2021; Isleem et al., 2021). The lack of consensus is due to the following reasons:

• The shear strength and mechanism are complex.

• The premature debonding failure is difficult to predict for several EB-FRP strengthening schemes.

• The EB-FRP is linear to the brittle failure, while no yield is observed.

• The interaction between the concrete, internal steel reinforcements, and the EB-FRP reinforcement.

• The shear strengthening using EB-FRP can be executed in different patterns:

1) Fully wrapping the sheets around the cross-section (full jacket).

2) Bonding L-shaped EB-FRP sheets to the bottom or the sides of the cross-section (U-jacket).

3) Bonding EB-FRP sheets to the sides of the cross-section (side jacket).

The sheets can be adhesively bonded in a continuous or discrete configuration. However, both U-jacket and side-jacket schemes are vulnerable to premature debonding failure, which occurs once a critical shear crack opens and widens. In this case, the EB-FRP bonded length is not adequate to provide anchorage for the transfer of the tensile force between the FRP and the concrete; thus, the EB-FRP fails by debonding prematurely, which can be prevented using appropriate anchorage devices. The shear strength of EB-FRP beams can be calculated as the summation of the shear resistance of the transverse steel (if any), the concrete, and the EB-FRP. In addition, several guidelines add the resistance of the EB-FRP to the shear capacity of the un-strengthened element (fib Task group 5.1, 2019; ACI Committee 440, 2017; Construction C–AC on TR for. CNR-DT 200 R1/2013, 2013; TR-55 CSTR, 2012; JSCE Japanese Society of Civil Engineers, 2000). However, previous studies have shown that EB-FRP jackets will affect the effective stress level of internal steel. Thus, this superposition approach could lead to non-conservative results (Pellegrino and Modena, 2002; Bousselham and Chaallal, 2006; Bousselham and Chaallal, 2008; Chen et al., 2010; Pellegrino and Vasic, 2013). The lack of conservative results could be because of changes in concrete diagonal cracking, diagonal strut orientation, or transverse reinforcement stress.

The engineering community is increasingly using EB-FRP systems to improve the strength of existing RC beams. Recent studies have led to a worldwide execution of this technique. However, debonding of EB-FRP sheets has been the main issue for EB-FRP RC beams in shear and torsion. For EB-FRP RC beams, premature failure by EB-FRP debonding is generally a sudden type of failure; therefore, for EB-FRP RC beams, debonding is an unwanted failure mode. Two types of EB-FRP debonding were observed by Deifalla (Deifalla et al., 2013), namely end or intermediate debonding, as shown in Figure 1, which are caused by either cover spalling or concrete cracking. Although beams are rarely subjected to pure shear and shear is often accompanied by flexure, beams are usually heavily reinforced in order to avoid the effect of flexure.

FIGURE 1

FIGURE 1. FRP end and intermediate debonding.

The anchorage systems of EB-FRP jackets have no rational and reliable design rules. Thus, FRP design codes and guidelines specify that physical experimental testing should be conducted as a supplement for the implementation of these machine-learning techniques(fib Task group 5.1, 2019; ACI Committee 440, 2017; Construction C–AC on TR for. CNR-DT 200 R1/2013, 2013; TR-55 CSTR, 2012; JSCE Japanese Society of Civil Engineers, 2000). However, the procedure for experimental testing is not specified by existing guidelines and design codes (Pellegrino and Modena, 2002; Sas et al., 2009a; Pellegrino and Vasic, 2013). In addition, because of the time and budget constraints of projects, it is rarely possible to perform such testing. Thus, the potential benefits of FRP anchorages are usually substituted by using an additional increase in the EB-FRP, which is not economical. The experimental studies conducted in this area are limited by case dependency and usually use a small-scale model; thus, it has a small impact in understanding the behavior of the FRP.

The contribution of EB-FRP to the resistance of RC beams is affected by EB-FRP type, direction, arrangement, and allocation. The efficacy of EB-FRP is boosted by attaching the EB-FRP in a direction parallel to the maximum tensile stress. Therefore, EB-FRP arrangements change the shear capacity of strengthened RC beams. A comprehensive investigation into the shear strength of EB-FRP RC beams is rare, and many queries regarding the mechanisms involved are not yet resolved. With the following exception, many researchers have proposed idealized models similar to that used for the internal steel stirrups, which is only valid if the shear contribution of EB-FRP comes from the tensile fiber capacity at a strain close to the ultimate tensile strain of the EB-FRP.

If full FRP wrapping is not feasible, to achieve the full design capacity, anchorage systems can be used for EB-FRP-strengthened beams using FRP (Mofidi and Chaallal, 2011a; Mofidi and Chaallal, 2014). The European fib (fib Task group 5.1, 2019) code suggests that anchorage systems should be at the compressive zone of the EB-FRP RC beams; however, no further details were provided. On the other hand, the ACI (TR-55 CSTR, 2012) indicated that anchorage systems at the termination points of EB-FRP will produce larger tensile stress transfer. However, the efficiency of these anchorage systems and the developed level of tensile stress before failure should be validated using experimental testing of a scaled model before execution (TR-55 CSTR, 2012). A study by Mofidi (Mofidi and Chaallal, 2011a; Mofidi and Chaallal, 2011b; Mofidi and Chaallal, 2014) concluded that experimental testing is needed to validate the proposed anchorage factors for the end-anchorage systems. Kalfat (Kalfat et al., 2013) demonstrated the validity of upgrading the shear strength with anchoring systems for EB-FRP materials. However, there remains a lack of sufficient research in this area. A more recent review by Godat (Godat et al., 2020) has shown that further research is essential to enhance the reliability of the shear strength predictions of EB-FRP RC beams. The interaction between the FRP shear strength, strain, and parameters is required for robust design equations.

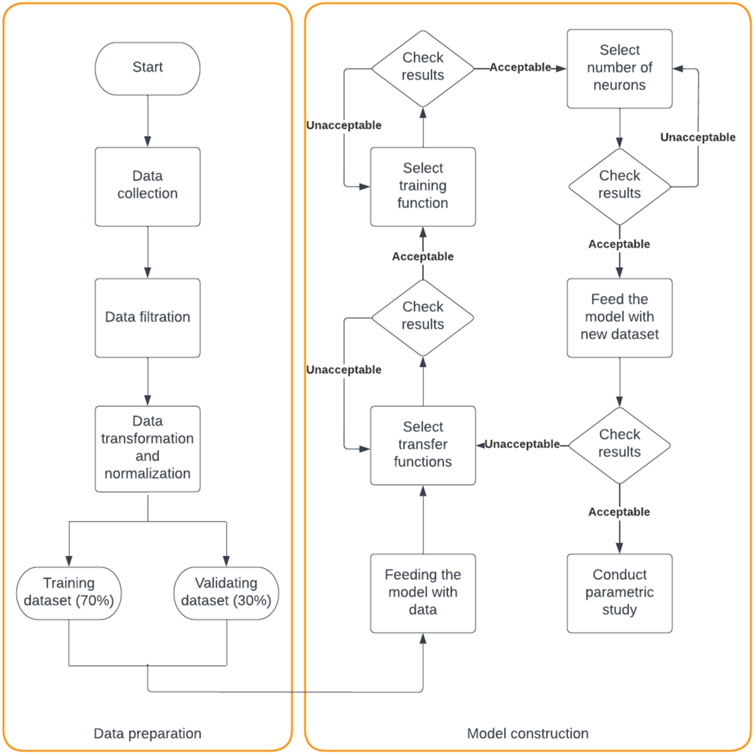
Machine learning is being implemented in various applications because it can capture the actual behavior for complex problems involving many parameters (Deifalla, Salem). This research investigation aims at developing a reliable and accurate strength model based on advanced machine-learning techniques. An extensive database was collected and used to train and validate the model, as shown in Figure 2. A machine learning model was developed and compared with available models from the existing literature. Concluding remarks were outlined.

FIGURE 2

FIGURE 2. Work scheme.

2 Research significance

The reliability of the existing strength models for concrete elements under shear is being questioned by many researchers, where investigations have shown a significant discrepancy and large scattering between the measured and predicted strength of the existing models, especially those used in current design guidelines (Colotti and Swamy, 2011; Lima and Barros, 2011; Isleem et al., 2022; Qaidi et al., 2022; SuhadAbd et al., 2022; Isleem et al., 2023). Thus, existing models are deemed to be inadequate and need further improvement. That shortcoming has motivated comprehensive investigations in all aspects related to shear. This current study investigates the implementation of artificial intelligence in the shear of strengthened concrete elements, which could guide further developments of design codes and mechanical models.

3 Previous studies

Relatively limited detailed studies have investigated the shear strength of RC beams; in addition, many questions regarding the strength mechanism, especially the usage of anchorage devices, are yet to be resolved. Many studies have idealized the EB-FRP jacket in a manner similar to that of steel shear reinforcements with the assumption that the contribution of the EB-FRP to shear capacity arises from the capacity of the EB-FRP to resist tensile stresses at a strain, which is less than or equal to the FRP ultimate tensile strain (Salem and Deifalla, 2022; Deifalla et al., 2013; fib Task group 5.1, 2019). Numerous experimental tests have been conducted in this field of research, and existing design codes and guidelines were available for designing EB-FRP elements (fib Task group 5.1, 2019; ACI Committee 440, 2017; Construction C–AC on TR for. CNR-DT 200 R1/2013, 2013; TR-55 CSTR, 2012; JSCE Japanese Society of Civil Engineers, 2000). Both the empirical evidence and code suggested that performance enhancement can be attained by using the EB-FRP; however, more detailed work is required to quantify its contribution to the strength of the beams under shear (fib Task group 5.1, 2019; ACI Committee 440, 2017; Construction C–AC on TR for. CNR-DT 200 R1/2013, 2013; TR-55 CSTR, 2012; JSCE Japanese Society of Civil Engineers, 2000). Many parameters influence the effective FRP strain for shear-strengthened RC beams, including but not limited to: 1) The type of fibers in terms of Young’s Modulus; 2) The fiber orientation in terms of the inclination angle to the beam longitudinal axis; 3) The fiber distributions in terms of the number of plies and thickness of the FRP fabrics; 4) The FRP bond schemes in terms of the sides the FRP is bonded to (i.e., side bonding U-jacket, and full wrapping); 5) The concrete compressive strength; 6) The usage of anchorage devices.

4 Experimental database

An extensive database of 200 beams collected from existing literature was strengthened using an EB-FRP jacket under shear. The database contains results from more than 80 experimental studies. In addition, this database includes EB-FRP beams available in existing literature (Pellegrino and Vasic, 2013; Colotti and Swamy, 2011; Sas et al., 2009b; Kotynia, Oller, Mari, Kaszubska). Although the data is available in existing databases, all data was validated using the original study.

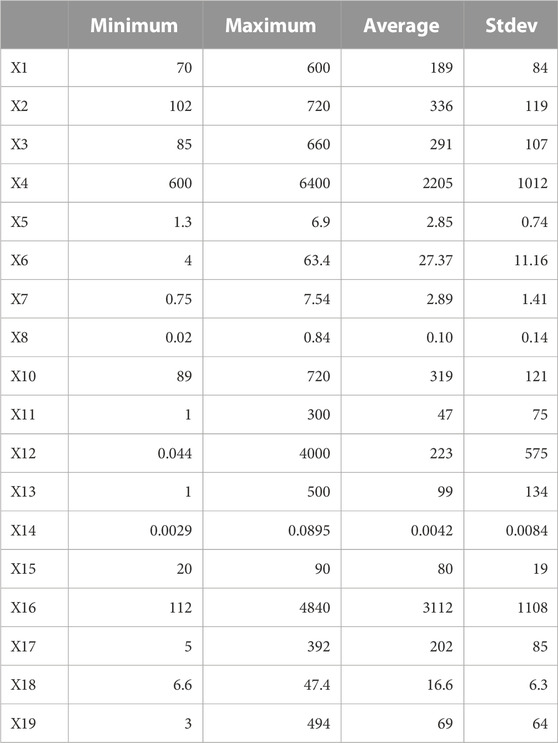
Collected parameters were related to the beam and the FRP jacket as follows: Width of beam cross-section (X1), beam height (X2), the effective depth of beam cross-section (X3), beam span (X4), shear span to depth ratio (X5), concrete compressive strength (X6), steel flexure reinforcement ratio (X7), steel shear reinforcement ratio (X8), strength technique (X9), FRP jacket height (X10), the width of FRP jacket (X11), the thickness of FRP jacket (X12), spacing between FRP strips (X13), FRP reinforcement ratio (X14), angle of fiber orientation (X15), ultimate stress of FRP in GPa (X16), FRP young’s modulus in GPa (X17), FRP rupture strain (X18), and shear strength in kN (X19). Table 1 shows the statistical measures for all parameters.

TABLE 1

TABLE 1. Statistical measures for all parameters.

5 Parameters selection

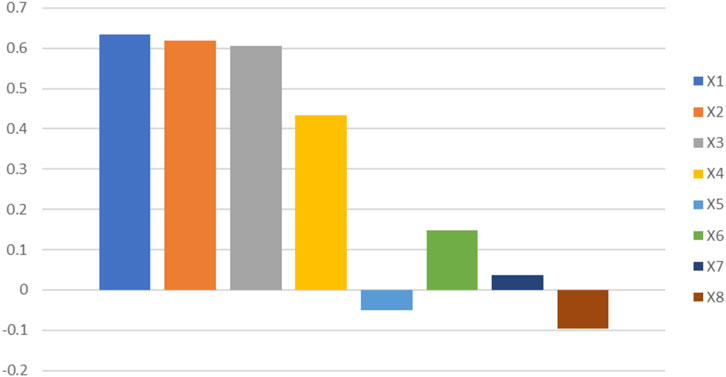
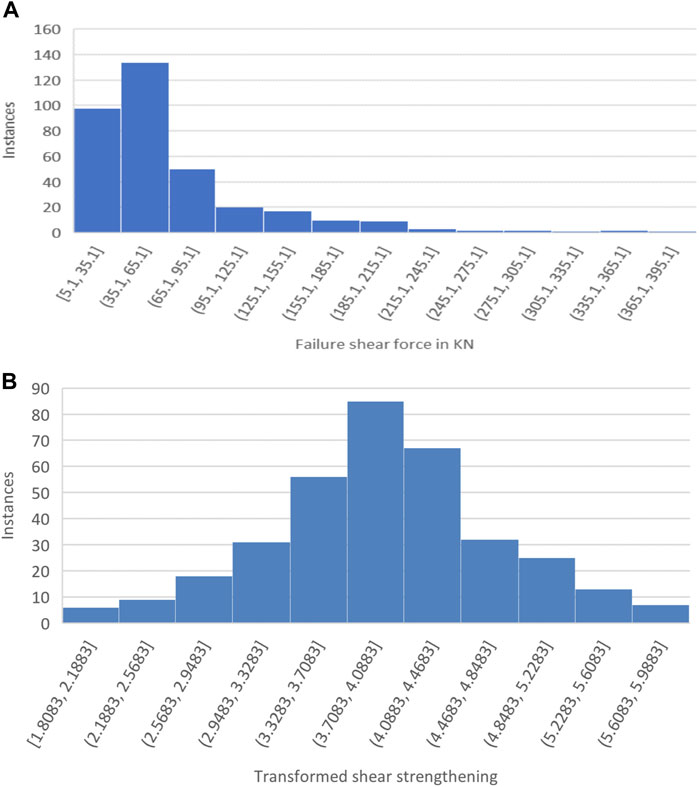
Pearson parametric method was used to determine the influence of beam details on the FRP shear strength, as shown in Figure 3. The selected parameters included X1, X2, and X3, while parameters X4, X5, X6, X7, and X8 were not chosen as they had a lower Pearson coefficient. For a more efficient and faster training and validating process, the input parameters have been normalized to be between zero and one, according to Equation 1, while FRP’s shear strength (model’s output) has been transformed according to Equation 2 for better output distribution, as shown in Figure 4.

$X_{i,norm}=\frac{X_i-X_{min}}{X_{\mathit{max}}-X_{\mathit{min}}}(1)$

where i is the number index for each input parameter, $X_{i,norm}$ is the normalized value for the input parameter; $X_i$ is the value of the input parameter before normalization; $X_{\mathit{max}}$ and $X_{\mathit{min}}$ are the values of the maximum and minimum values of the input parameter $X_i$.

$S^T=\mathit{ln}\left(S+1\right)(2)$

FIGURE 3

FIGURE 3. Results of Pearson variables study on FRP shear strength.

FIGURE 4

FIGURE 4. Distribution of the shear force failure (A) before and (B) after transformation.

S is the value of the added shear strength by FRP in kN while S^T is its transformed value; the input parameter for the proposed model data has been filtered and transformed to follow a normal distribution curve for a better training process to build the model, as shown in Figure 4.

6 Model development

A script has been developed to generate more than 6750 different artificial neural network (ANN) models to compare and boost the developed model performance using MATLAB. In addition, different combinations of various parameters have been tested, as shown in Figure 5.

FIGURE 5

FIGURE 5. Combination of different model parameters.

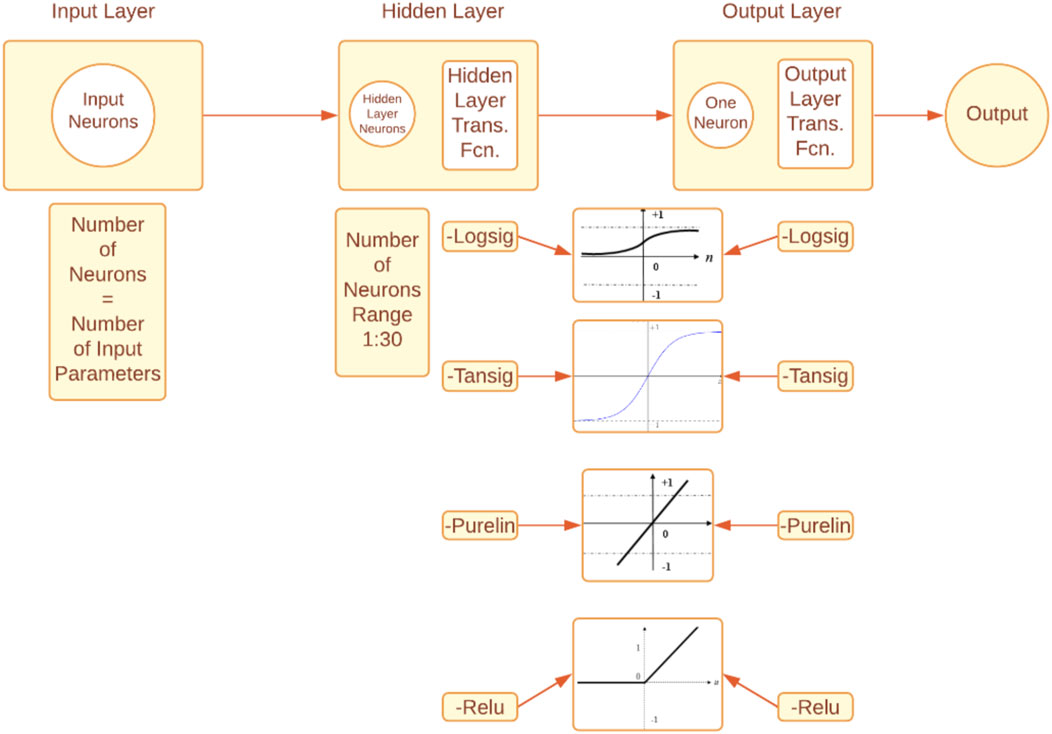
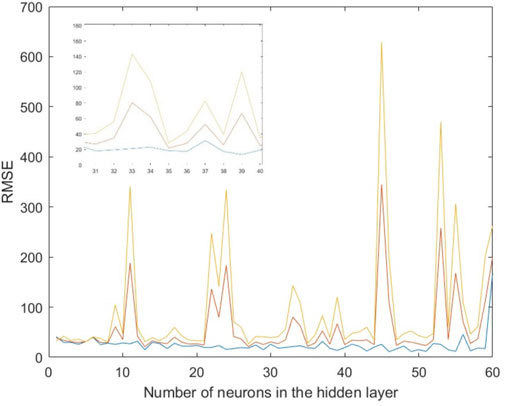
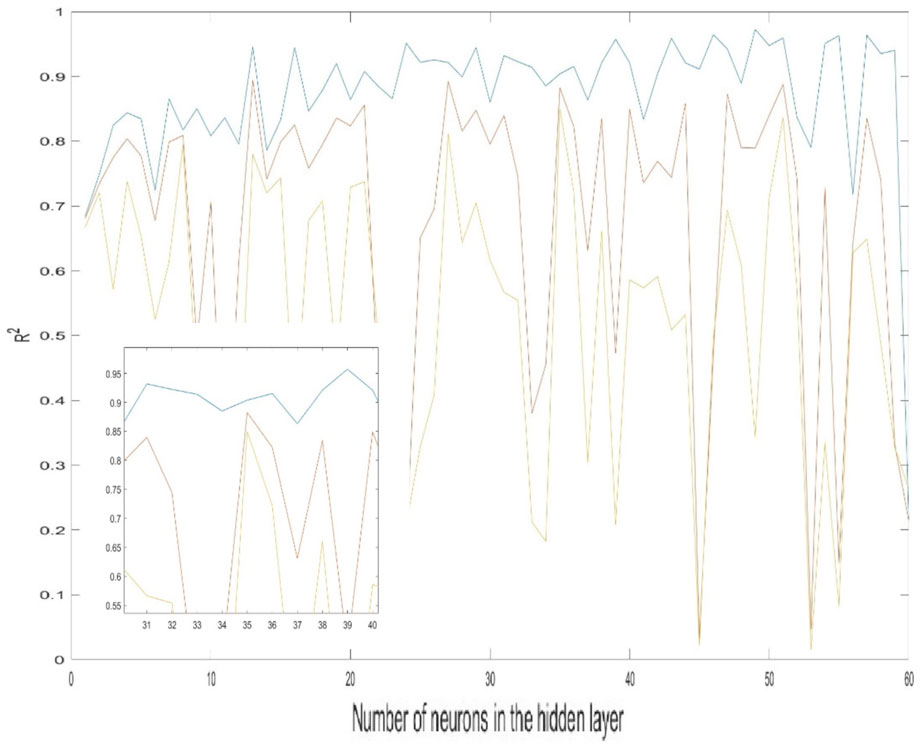
During the model construction, the transfer function of the hidden and output layers were the first parameters to be determined. Then, the training function and the number of neurons in the hidden layer were optimized by plotting the number of neurons versus the correlation coefficient (R²) and root mean square error (RMSE), as shown in Figures 6, 7.

FIGURE 6

FIGURE 6. Number of neurons in the hidden layer versus RMSE.

FIGURE 7

FIGURE 7. Number of neurons in the hidden layer versus R².

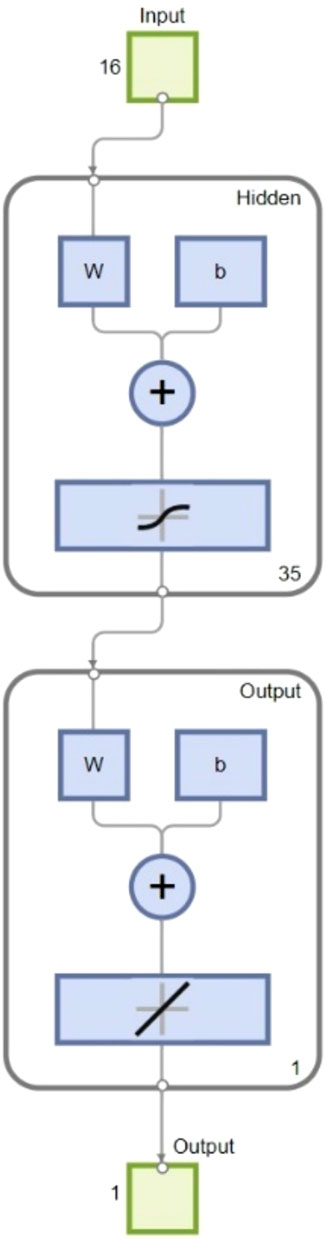
The number of neurons was optimized to be 35 neurons in the hidden layer, while the transfer functions were TANSIG and PURELIN for the hidden and output layers, respectively (Figure 8). Based on the constricted model, a mathematical equation has been developed to predict the shear strength added by the FRP (Equation 3).

$S=\mathit{Exp}\left[PURELIN\left[{\displaystyle \sum _{i=1}^N}{W}_{2i}TANSIG\left({\displaystyle \sum _{j=1}^J}{W}_{1j}\times \frac{X_j-X_{avg}}{X_{\mathit{max}}-X_{\mathit{min}}}+b_{1i}\right)\right]+b_2\right]-1(3)$

where Exp is the exponential function, N is the number of neurons in the hidden layer, which has been optimized to be 35 neurons; W2i is the weight of the output layer; J is the number of input variables; W1 is the weight of the hidden layer; Xj is the value of the input variable (strength configuration, X1, X2, X3, X9, X10, X11, X12, X13, X14, X15, X16, X17, and X18); b1 is the bias of the hidden layer; b2 is the bias of the output layer.

FIGURE 8

FIGURE 8. The proposed ANN model architecture.

The values of the input parameters go through the input layer to be multiplied by the weights that connect the input layer with the hidden layer. The bias of the first layer is added to the multiplication results before they transform through the activation function of the hidden layer (TANSIG). The outcome of the transfer function is then multiplied by the weights of the output layer and added to the bias of the hidden layer. Finally, the product goes through the output layer’s transfer function (PURELIN) to give the predicted value of the shear strength in kN.

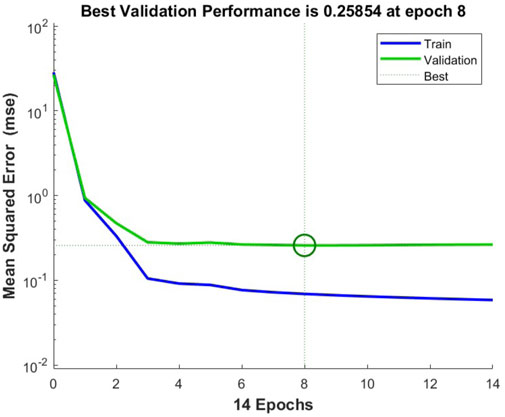
Later, the performance of the ANN model was boosted by 1000 epochs; the best model outcome was found to be at the 8th epoch; then, the validation check stopped the training process at the 14th epoch, as shown in Figure 9.

FIGURE 9

FIGURE 9. Epochs versus Mean square error.

7 Model validation

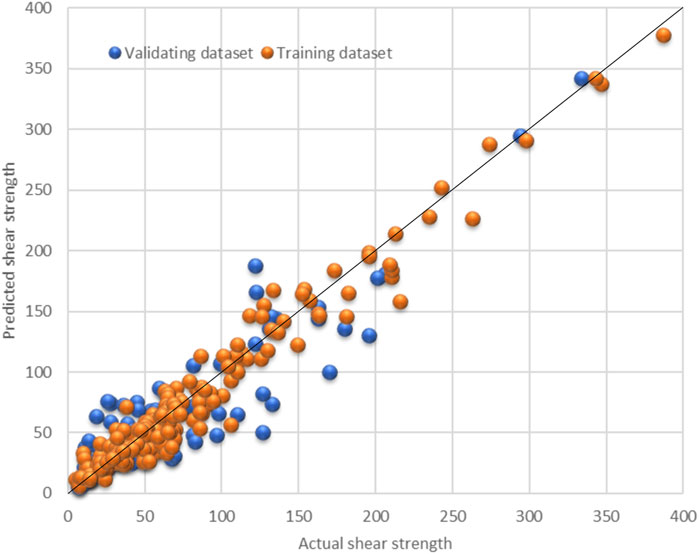
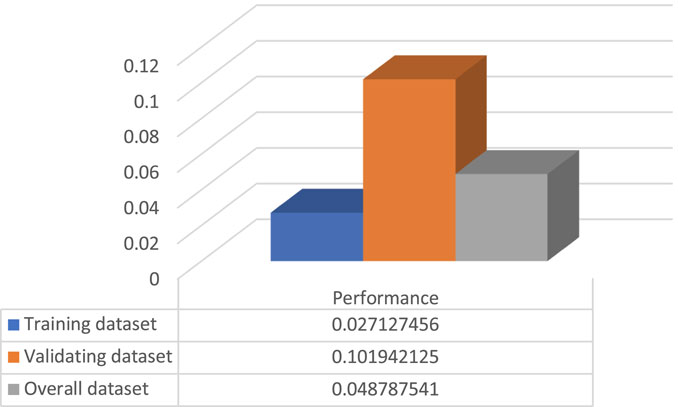
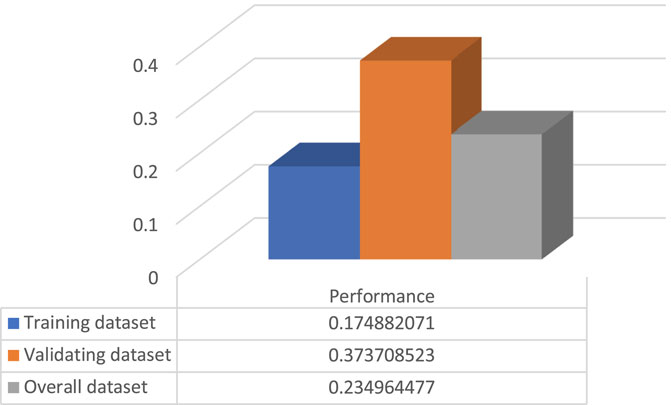
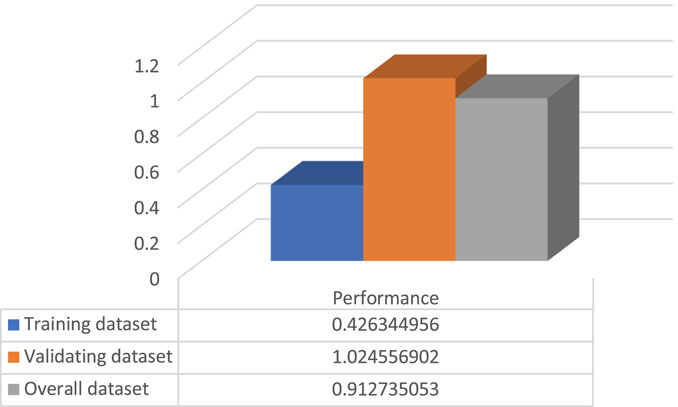
After the model construction, the model was used to predict the shear strength for FRP in kN; then, the predicted value versus the actual values was plotted, as shown in Figure 10. In addition, statistical tests have been conducted to test the accuracy of the newly developed model. Training, validating, and overall datasets have been evaluated using average relative error (ARE), average absolute relative error (AARE), relative deviation (RD), standard deviation (SD), RMSE, and R2 according to equations three to eight. Also, a comparison between the actual and predicted values is presented in Figure 11 Figure 12. Moreover, the ratio between the predicted and actual values has been calculated according to Equation 9 for both the training and validating datasets and is presented in Figure 13.

$ARE=\left(\frac{1}{N}\times {\displaystyle \sum _{i=1}^N}\frac{S^{Predicted}-S^{Actual}}{S^{Actual}}\right)\times 100(4)$

$AARE=\left(\frac{1}{N}\times {\displaystyle \sum _{i=1}^N}\left|\frac{S^{Predicted}-S_i^{Actual}}{S_i^{Actual}}\right|\right)\times 100(5)$

$RD=\frac{S^{Predicted}-S^{Actual}}{S^{Actual}}\times 100(6)$

$SD={\left\{\frac{1}{N-1}\times {\displaystyle \sum _{i=1}^N}{\left(\frac{S^{Predicted}-S^{Actual}}{S^{Actual}}\right)}^2\right\}}^{0.5}(7)$

$RMSE={\left\{\frac{1}{N}\times {\displaystyle \sum _{i=1}^N}{\left(S^{Predicted}-S^{Actual}\right)}^2\right\}}^{0.5}(8)$

$R^2=1-\frac{{\displaystyle \sum _{i=1}^N}{\left(S^{Predicted}-S^{Actual}\right)}^2}{{\left(S_{Actual}^{Mean}-S^{Actual}\right)}^2}(9)$

$Ratio=\frac{F^{Predicted}}{F^{Actual}}(10)$

where N is the number of tested data points, S^Predicted is the predicted shear strength value in kN; S^Actual is the corresponding actual shear strength value in kN; $S_{Actual}^{Mean}$ is the average of the actual shear strength value in kN.

FIGURE 10

FIGURE 10. Actual versus predicted shear strength value in kN.

FIGURE 11

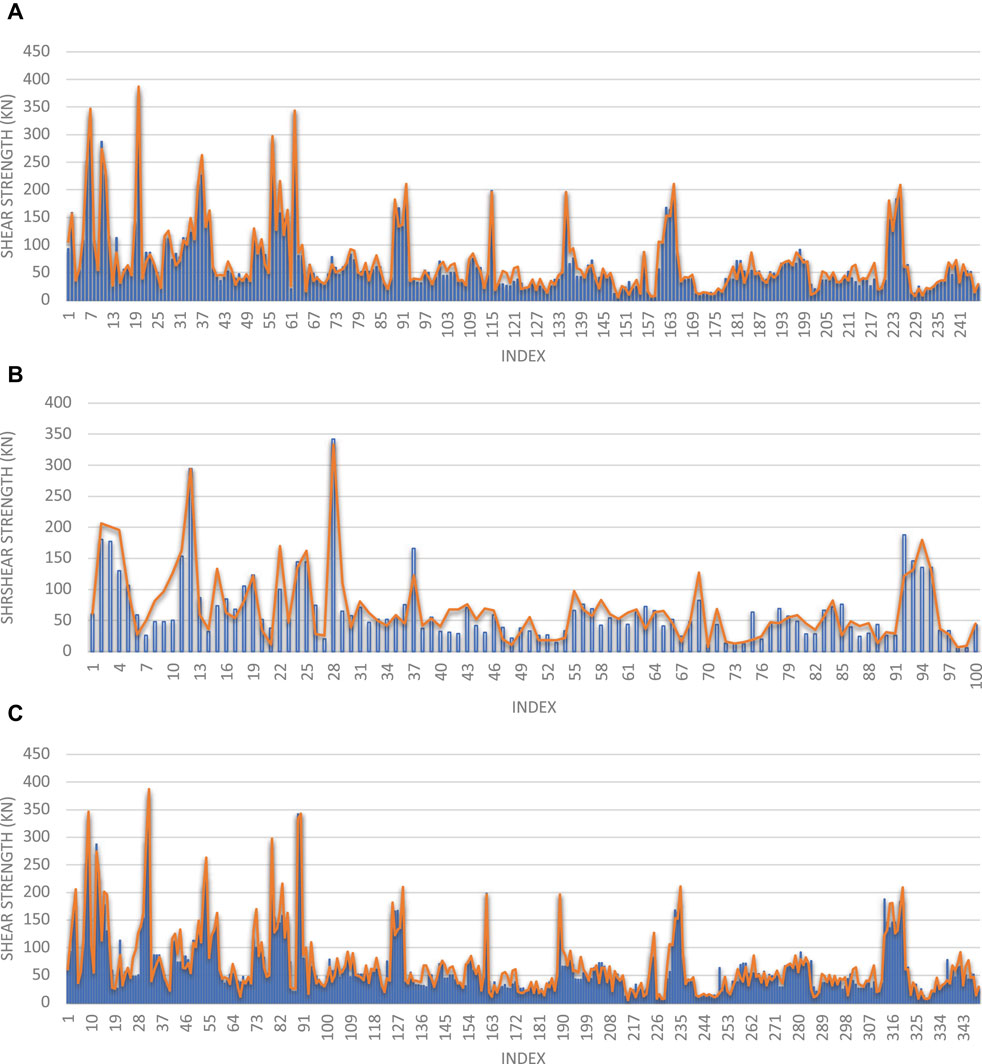
FIGURE 11. Comparing the actual and predicted shear strength values in kN for the (A) training dataset, (B) validating dataset, and (C) overall dataset.

FIGURE 12

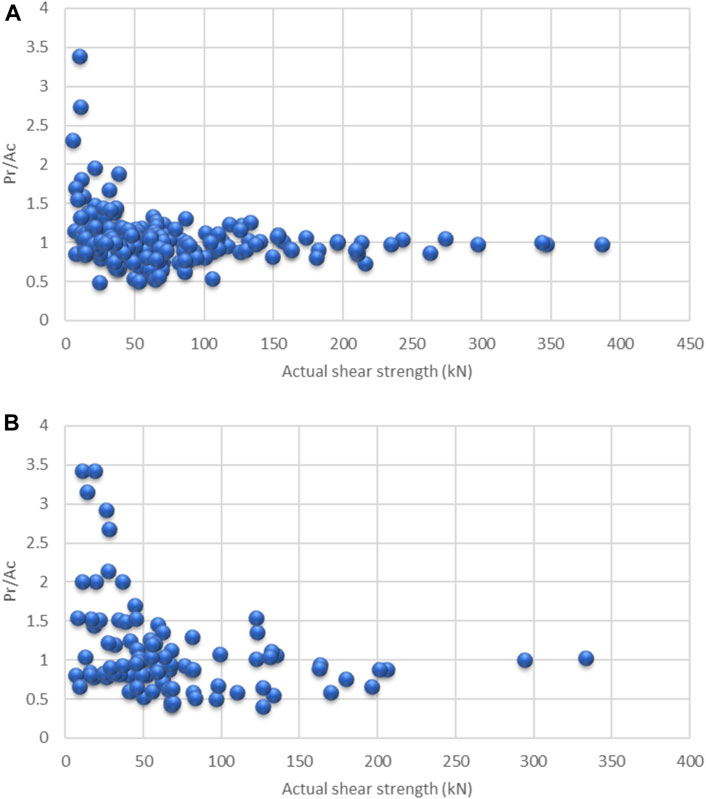
FIGURE 12. The ratio between predicted to actual shear strength versus the actual shear strength value in kN for the (A) training dataset and (B) validating dataset.

FIGURE 13

FIGURE 13. R² for training, validating, and overall datasets.

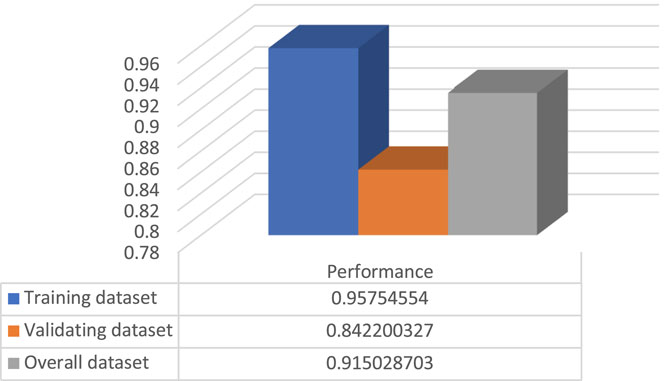
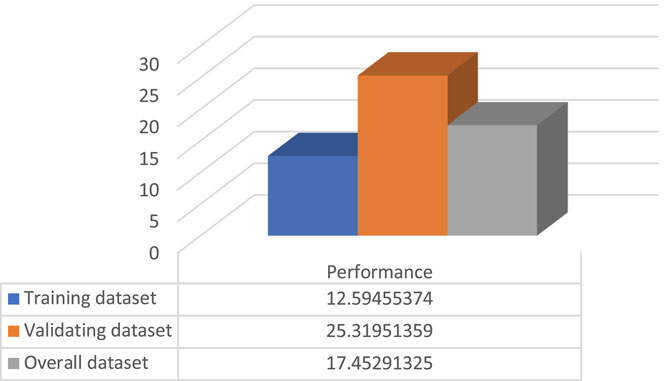
The model showed excellent performance as it has R² and RMSE of 0.91 and 17.45 for the overall dataset, respectively. The R², RMSE, ARE, AARE, and SD statistical tests are summarized and listed in Figures 13–17, respectively. In addition, the results of the different datasets were compared to check the fitting of the proposed model, while RD versus the actual shear strength was plotted and is presented in Figure 18.

FIGURE 14

FIGURE 14. RMSE for training, validating, and overall datasets.

FIGURE 15

FIGURE 15. ARE for training, validating, and overall datasets.

FIGURE 16

FIGURE 16. AARE for training, validating, and overall datasets.

FIGURE 17

FIGURE 17. SD for training, validating, and overall datasets.

FIGURE 18

FIGURE 18. RD versus the testing point index for (A) training and (B) validating datasets.

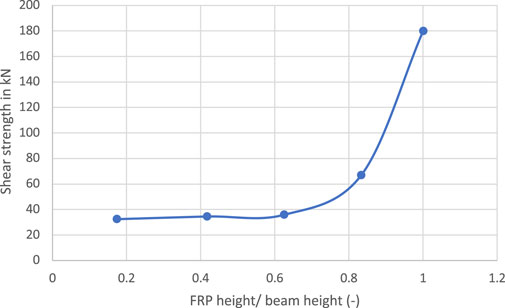
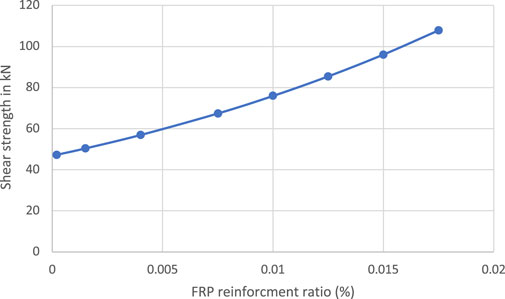
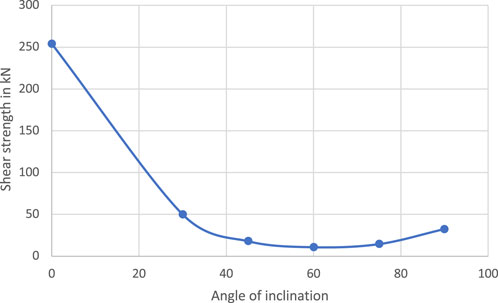
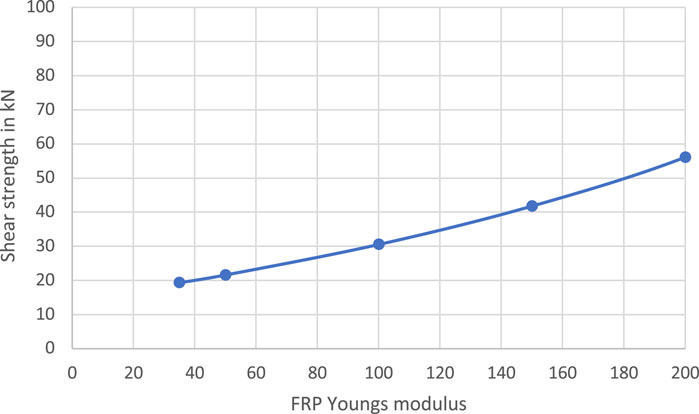
After validating the model and demonstrating its credibility in predicting the shear strength value added by the FRP, the model was then used to conduct a parametric study to study the impact of each parameter individually. When investigating a certain parameter, the rest of the variables were set to a constant at their average value while changing the value of the tested parameter. X10, X14, X15, and X17 were investigated, and their values versus the model outcome were plotted, as shown in Figures 19–22.

FIGURE 19

FIGURE 19. The effect of X10 on shear strength value.

FIGURE 20

FIGURE 20. The effect of X14 on the shear strength.

FIGURE 21

FIGURE 21. The effect of X15 on shear strength value.

FIGURE 22

FIGURE 22. The effect of X17 on shear strength value.

8 Comparisons between the proposed model and existing machine models

In 2020, machine learning was used to predict the FRP shear strength capacity with a certain accuracy [50]. In this work, the proposed model performance has been evaluated and compared to the models from the existing literature. R² is one of the essential statistical parameters that can determine the accuracy of any model regardless of the values of the used data. R² for the overall datasets and the number of data used in developing the new model have been compared with their corresponding values from the previous model, as shown in Figure 23. The model from this work was constructed using a larger number of dataset points, giving the model a wide range of applicability. In addition, R² shows better performance and more accurate results than the models from the existing literature for all datasets.

FIGURE 23

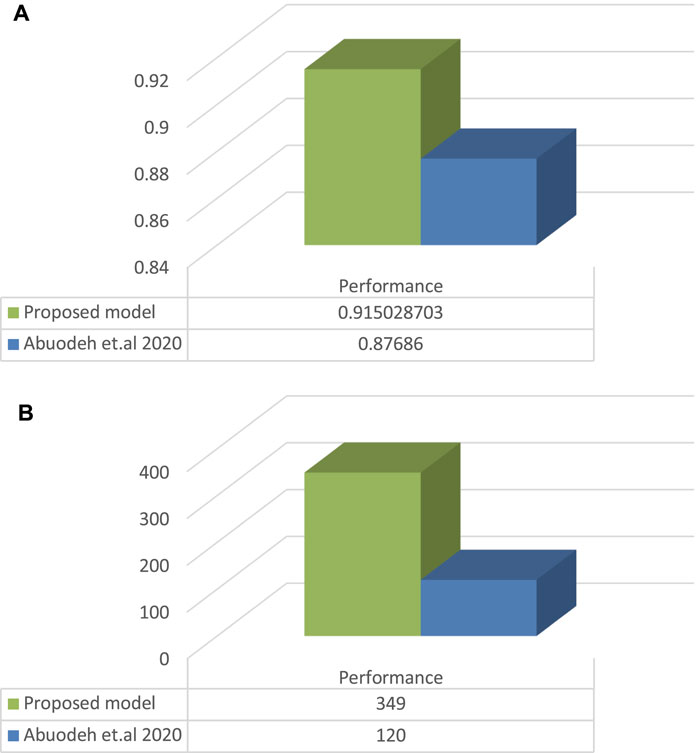
FIGURE 23. Comparison between the existing models from previous literature and the proposed model based on (A) R² and (B) the number of data points used.

9 Comparison between the existing design codes and guidelines and the proposed model

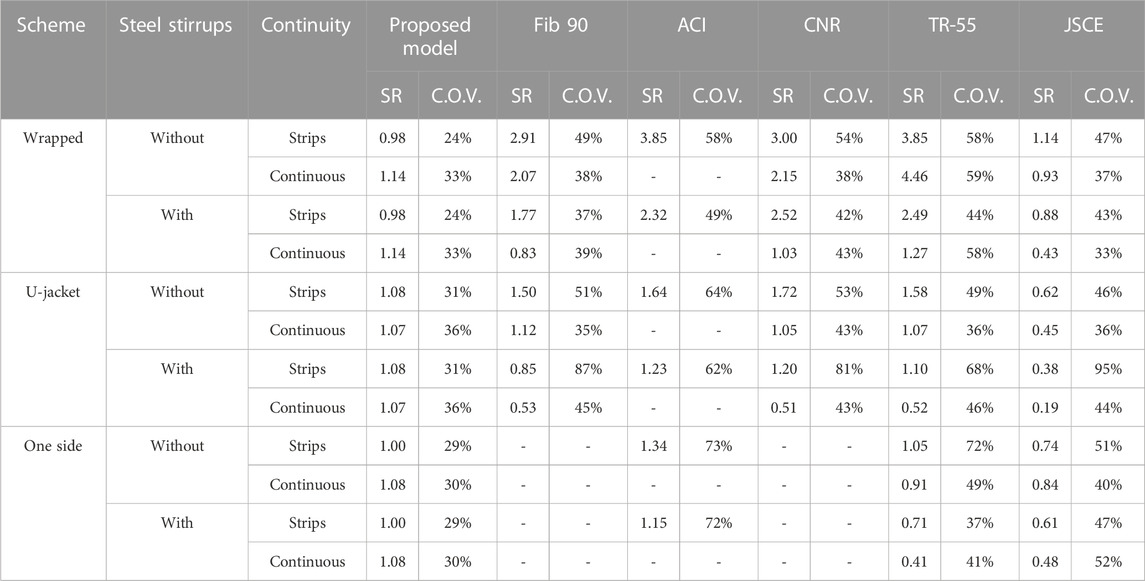
Table 2 shows the statistical measures for various selected models’ safety ratios, namely average and coefficient of variation. The safety ratio was defined as the ratio between the measured and the calculated FRP contribution. At the same time, selected models include the proposed model, the Fib 90 (fib Task group 5.1, 2019), the ACI (ACI Committee 440, 2017), the CNR (Construction C–AC on TR for. CNR-DT 200 R1/2013, 2013), the TR-55 (TR-55 CSTR, 2012), and the JSCE (JSCE Japanese Society of Civil Engineers, 2000). The proposed model captured the behavior of FRP-strengthened beams and precited the FRP contribution accurately and consistently. The range of the average was from 0.98 to 1.14, and the range of the coefficient of variation was from 24% to 36%. The range of the selected models’ average was from 0.48 to 4.46, and the range of the coefficient of variation was from 35% to 95%.

TABLE 2

TABLE 2. Statistical measures for proposed and selected model’s a/d ≥ 2.5.

10 Recommendations

Based on the findings from this current study, the following is recommended:

- The use of artificial intelligence methods to predict the true strength as it provides more accurate strength compared to other methods.

- The implementation of an FRP Jacket with a height of at least 80% of the element height.

11 Future studies

Based on the findings from this current study, the following are recommended for the strength modeling of shear-strengthened beams:

- Using anchorage strengthening schemes.

- Using near-surface mounted techniques.

- Using advanced materials.

- Using design equations and the relationship between parameters.

12 Conclusion

An artificial intelligence model for the shear strength of FRP-strengthened elements was proposed, which accounts for the following parameters: the width of the beam cross-section, beam height, the effective depth of beam cross-section, strength technique, FRP jacket height, the width of FRP jacket, the thickness of FRP jacket, spacing between FRP strips, angle of fiber orientation, ultimate stress of FRP, FRP young’s modulus, and FRP rupture strain. The model’s accuracy compared to the existing model is superior, where statistical tests R², RMSE, ARE, AARE, and SD were found to be 0.91, 17.45, 0.048, 0.23, and 0.91, respectively, for the overall dataset. A parametric study was conducted to study the influence of the FRP jacket height, the width of the FRP jacket, the thickness of the FRP jacket, spacing between FRP strips, angle of fiber orientation, ultimate stress of FRP, FRP young’s modulus, and FRP rupture strain.

Data availability statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found in the article/Supplementary Material.

Author contributions

Conceptualization, MG, OM, AD, and TE; methodology, MG, OM, AD, and TE; software, MG, OM, AD, and TE; validation, AD; formal analysis, MG, OM, AD, and TE; investigation, MG, OM, AD, and TE; resources, MG, OM, AD, and TE; data curation, MG, OM, AD, and TE; writing—original draft preparation, MG, OM, AD, and TE; writing—review and editing, MG, OM, AD, and TE; visualization, AD; supervision, TE and AD; funding acquisition, TE. All authors have read and agreed to the published version of the manuscript.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Construction C– AC on TR for. CNR-DT 200 R1/2013 (2013). Guide for the design and construction of externally bonded FRP systems for strengthening existing structures. Rome, Italy.

Google Scholar

Abuodeh, O. R., Abdalla, J. A., and Hawileh, R. A. (2020). Prediction of shear strength and behavior of RC beams strengthened with externally bonded FRP sheets using machine learning techniques. Compos. Struct. 234, 111698. doi:10.1016/j.compstruct.2019.111698

CrossRef Full Text | Google Scholar

ACI Committee 440 (2017). ACI 440.2r-17, guide for the design and construction of externally bonded FRP systems for strengthening concrete structures. Michigan, USA: Farmington Hills.

Google Scholar

Benzeguir, Z. E. A., and Chaallal, O. (2021). Size effect in FRP shear-strengthened RC beams: Design models versus experimental data. CivilEng 2, 874–894. doi:10.3390/civileng2040047

CrossRef Full Text | Google Scholar

Bousselham, A., and Chaallal, O. (2006). Behavior of reinforced concrete t-beams strengthened in shear with carbon fiber-reinforced polymer-an experimental study. ACI Struct. J. 103, 339–347.

Google Scholar

Bousselham, A., and Chaallal, O. (2008). Mechanisms of shear resistance of concrete beams strengthened in shear with externally bonded FRP. J. Compos Constr. 12:499–512. doi:10.1061/(asce)1090-0268(2008)12:5(499)

CrossRef Full Text | Google Scholar

Chalioris, C. E., and Karayiannis, C. (2009). Effectiveness of the use of steel fibres on the torsional behaviour of flanged concrete beams. Cem. Concr. Compos. 31, 331–341. doi:10.1016/j.cemconcomp.2009.02.007

CrossRef Full Text | Google Scholar

Chalioris, C. E., Zapris, A. G., and Karayannis, C. G. (2020). U-jacketing applications of fiber-reinforced polymers in reinforced concrete T-beams against shear—tests and design. Fibers 8, 13. doi:10.3390/fib8020013

CrossRef Full Text | Google Scholar

Chen, G. M., Teng, J. G., Chen, J. F., and Rosenboom, O. A. (2010). Interaction between steel stirrups and shear strengthening FRP strips in RC beams. J. Compos Constr. 14, 498–509. doi:10.1061/(ASCE)CC.1943-5614.0000120

CrossRef Full Text | Google Scholar

Colotti, V., and Swamy, R. N. (2011). Unified analytical approach for determining shear capacity of RC beams strengthened with FRP. Eng. Struct. 33, 827–842. doi:10.1016/j.engstruct.2010.12.005

CrossRef Full Text | Google Scholar

De Lorenzis, L., and Nanni, A. (2001). Characterization of FRP rods as near-surface mounted reinforcement. J. Comp. Constr. 5 (2), 114–121. doi:10.1061/(asce)1090-0268(2001)5:2(114)

CrossRef Full Text | Google Scholar

Deifalla, A. (2020). Refining the torsion design of fibered concrete beams reinforced with FRP using multi-variable non-linear regression analysis for experimental results. Eng. Struct. 224, 111394. doi:10.1016/j.engstruct.2020.111394

CrossRef Full Text | Google Scholar

Deifalla, A., Awad, A., and El-Garhy, M. (2013). Effectiveness of externally bonded CFRP strips for strengthening flanged beams under torsion: An experimental study. Eng. Struct. 56, 2065–2075. doi:10.1016/j.engstruct.2013.08.027

CrossRef Full Text | Google Scholar

Deifalla, A., Awad, A., Seleem, H., and AbdElrahman, A. (2020). Experimental and numerical investigation of the behavior of LWFC L-girders under combined torsion. Structures 26, 362–377. doi:10.1016/j.istruc.2020.03.070

CrossRef Full Text | Google Scholar

Deifalla, A., Awad, A., Seleem, H., and AbdElrahman, A. (2020). Investigating the behavior of lightweight foamed concrete T-beams under torsion, shear, and flexure. Eng. Struct. 219, 110741. doi:10.1016/j.engstruct.2020.110741

CrossRef Full Text | Google Scholar

Deifalla, A. F., Zapris, A. G., and Chalioris, C. E. (2021). Multivariable regression strength model for steel fiber-reinforced concrete beams under torsion. Materials 14, 3889. doi:10.3390/ma14143889

PubMed Abstract | CrossRef Full Text | Google Scholar

Deifalla, A., and Salem, N. M. (2022). A machine learning model for torsion strength of externally bonded FRP-reinforced concrete beams. Polymers 14, 1824. doi:10.3390/polym14091824

PubMed Abstract | CrossRef Full Text | Google Scholar

Deifalla, A. (2020). Torsion design of lightweight concrete beams without or with fibers: A comparative study and a refined cracking torque formula. Structures 28, 786–802. doi:10.1016/j.istruc.2020.09.004

CrossRef Full Text | Google Scholar

Deifalla, A. (2015). Torsional behavior of rectangular and flanged concrete beams with FRP reinforcements. J. Struct. Eng. 141, 04015068. doi:10.1061/(asce)st.1943-541x.0001322

CrossRef Full Text | Google Scholar

fib Task group 5.1 (2019). FIB Bulletin 90, Externally applied FRP reinforcement for concrete structures. Lausanne, Switzerland.

Google Scholar

FIB. FRP Reinforcement in RC Structures (2007). Technical report prepared by a working party of Task group 9.3; FIB bulletin 40. Lausanne, Switzerland: International Federation for Structural Concrete, 151.

Google Scholar

Godat, A., Hammad, F., and Chaallal, O. (2020). State-of-the-art review of anchored FRP shear-strengthened RC beams: A study of influencing factors. Compos. Struct. 254 112767, doi:10.1016/j.compstruct.2020.112767

CrossRef Full Text | Google Scholar

Gosbell, T., and Meggs, R. (2002). in Proceedings of the IABSE symposium (Melbourne, Australia.West gate bridge approach spans FRP strengthening Melbourne

Google Scholar

Hassan, M. M., and Deifalla, A. (2016). Evaluating the new CAN/CSA-S806-12 torsion provisions for concrete beams with FRP reinforcements. Mat. Struct. 49, 2715–2729. doi:10.1617/s11527-015-0680-9

CrossRef Full Text | Google Scholar

Isleem, H. F., Augustino, D. S., Mohammed, A. S., Najemalden, A. M., Jagadesh, P., Qaidi, S., et al. (2023). Finite element, analytical, artificial neural network models for carbon fibre reinforced polymer confined concrete filled steel columns with elliptical cross sections. Front. Mat. 9, 1115394. doi:10.3389/fmats.2022.1115394

CrossRef Full Text | Google Scholar

Isleem, H. F., Jagadesh, P., Qaidi, S., Althoey, F., Rahmawati, C., Najm, H. M., et al. (2022). Finite element and theoretical investigations on PVC–CFRP confined concrete columns under axial compression. Front. Mater 9, 1055397. doi:10.3389/fmats.2022.1055397

CrossRef Full Text | Google Scholar

Isleem, H. F., Abid, M., Alaloul, W. S., Shah, M. K., Zeb, S., Musarat, M. A., et al. (2021). Axial compressive strength models of eccentrically-loaded rectangular reinforced concrete columns confined with FRP. Materials 14, 3498. doi:10.3390/ma14133498

PubMed Abstract | CrossRef Full Text | Google Scholar

JSCE Japanese Society of Civil Engineers (2000). Recommendations for upgrading of concrete structures with use of continuous fiber sheets.

Google Scholar

Kalfat, R., Al-Mahaidi, R., and Smith, S. (2013). Anchorage devices used to improve the performance of reinforced concrete beams retrofitted with FRP composites: State-of-the-art review. J. Compos. Constr. 17 (1), 14–33. doi:10.1061/(asce)cc.1943-5614.0000276

CrossRef Full Text | Google Scholar

Karayannis, G., Kosmidou, K., and Chalioris, E. (2018). Reinforced concrete beams with carbon-fiber-reinforced polymer bars—experimental study. Fibers 6, 99. doi:10.3390/fib6040099

CrossRef Full Text | Google Scholar

Kim, S.-W. (2021). Prediction of shear strength of reinforced high-strength concrete beams using compatibility-aided truss model. Appl. Sci. 11, 10585. doi:10.3390/app112210585

CrossRef Full Text | Google Scholar

Kotynia, R., Oller, E., Mari, A. R., and Kaszubska, M. Efficiency of shear strengthening of RC beams with externally bonded FRP materials – state-of-the-art in the experimental tests Compos Part B Eng.

Google Scholar

Kotynia, R., Oller, E., Marí, A., and Kaszubska, M. (2021). Efficiency of shear strengthening of RC beams with externally bonded FRP materials – state-of-the-art in the experimental tests. Compos. Struct. 267, 113891. doi:10.1016/j.compstruct.2021.113891

CrossRef Full Text | Google Scholar

Lima, J. L., and Barros, J. A. (2011). Reliability analysis of shear strengthening externally bonded FRP models. Proc. Inst. Civ. Eng. Struct. Build. 164 (SB1), 43–56. doi:10.1680/stbu.9.00042

CrossRef Full Text | Google Scholar

Ly, H.-B., Le, T.-T., Vu, H.-L., Tran, V. Q., Le, L. M., and Pham, B. T. (2020). Computational hybrid machine learning based prediction of shear capacity for steel fiber reinforced concrete beams. Sustainability 12, 2709. doi:10.3390/su12072709

CrossRef Full Text | Google Scholar

Mofidi, A., and Chaallal, O. (2011). Shear strengthening of RC beams with EB FRP: Influencing factors and conceptual debonding model. J. Compos Constr. 15, 62–74. doi:10.1061/(ASCE)CC.1943-5614.0000153

CrossRef Full Text | Google Scholar

Mofidi, A., and Chaallal, O. (2011). Shear strengthening of RC beams with externally bonded FRP composites: Effect of strip-width-to-strip-spacing ratio. J. Compos Constr. 15, 732–742. doi:10.1061/(ASCE)CC.1943-5614.0000219

CrossRef Full Text | Google Scholar

Mofidi, A., and Chaallal, O. (2014). Tests and design provisions for reinforced-concrete beams strengthened in shear using FRP sheets and strips. Int. J. Concr. Struct. Mater 8, 117–128. doi:10.1007/s40069-013-0060-1

CrossRef Full Text | Google Scholar

Oller, E., Kotynia, R., and Antonio Marí, A. (2021). Assessment of the existing models to evaluate the shear strength contribution of externally bonded frp shear reinforcements. Compos. Struct. 264, 113641. doi:10.1016/j.compstruct.2021.113641

CrossRef Full Text | Google Scholar

Pellegrino, C., and Modena, C. (2002). Fiber reinforced polymer shear strengthening of reinforced concrete beams with transverse steel reinforcement. J. Compos Constr. 6:104–111. doi:10.1061/(asce)1090-0268(2002)6:2(104)

CrossRef Full Text | Google Scholar

Pellegrino, C., and Vasic, M. (2013). Assessment of design procedures for the use of externally bonded FRP composites in shear strengthening of reinforced concrete beams. Compos Part B Eng. 45, 727–741. doi:10.1016/j.compositesb.2012.07.039

CrossRef Full Text | Google Scholar

Qaidi, S., Al-Kamaki, S., Al-Mahaidi, R., Mohammed, A. S., Ahmed, H. U., Zaid, O., et al. (2022). Investigation of the effectiveness of CFRP strengthening of concrete made with recycled waste PET fine plastic aggregate. PLOS ONE 17 (7), e0269664. doi:10.1371/journal.pone.0269664

PubMed Abstract | CrossRef Full Text | Google Scholar

Salem, N. M., and Deifalla, A. (2022). Evaluation of the strength of slab–column connections with FRPs using machine learning algorithms. Polymers 14, 1517. doi:10.3390/polym14081517

PubMed Abstract | CrossRef Full Text | Google Scholar

Sas, G., Täljsten, B., Barros, J., Lima, J., and Carolin, A. (2009). Are available models reliable for predicting the FRP contribution to the shear resistance of RC beams? J. Compos Constr. 13, 514–534. doi:10.1061/(ASCE)CC.1943-5614.0000045

CrossRef Full Text | Google Scholar

Sas, G., Täljsten, B., Barros, J., Lima, J., and Carolin, A. (2009). Are available models reliable for predicting the FRP contribution to the shear resistance of RC beams. J. Compos. Constr. 13, 514–534. doi:10.1061/(ASCE)CC.1943-5614.0000045

CrossRef Full Text | Google Scholar

SuhadAbd, M., Mhaimeed, I. S., Tayeh, B. A., Mohammed Najm, H., and Qaidi, S. (2022). Flamingo technique as an innovative method to improve the shear capacity of reinforced concrete beam. Case Stud. Constr. Mater. 17 (2022), e01618. ISSN 2214-5095. doi:10.1016/j.cscm.2022.e01618

CrossRef Full Text | Google Scholar

TR-55 CSTR (2012). Design guidance for strengthening concrete structures using fiber composite materials. London, Great Britain.

Google Scholar

Whittle, R. Failures in concrete structures—case studies in reinforced and prestressed concrete; FL 33487-2742; CRC Press: Boca Raton, FLorida, USA; Taylor and Francis Group, Abingdon, UK, 2013; 140 pp.

Google Scholar