Simulation studies of secondary electron yield with electron transport from Cu (110) surfaces containing C2, N2, CO2, or NO2 adsorbates

Secondary electron yields of (110) copper surfaces, covered with either carbon, nitrogen, or their dioxides, have been studied by employing combined first principles methods for the material properties and Monte Carlo simulations for electron transport. Furthermore, by studying electron transport inside the Cu system and modeling the power loss taking account of the inelastic electron scattering within the material, changes in the thermal energy of the system have been modeled. The physical reasons behind the increase and decrease of the yield for each system from an electronic perspective are discussed. In agreement with results observed in studies of secondary electron emission, it is shown that the formation of C₂ and N₂ monolayers reduce the secondary electron yields, while CO₂ and NO₂ increase the yield significantly. It is demonstrated that in the case of C₂ and N₂ formation, changes in the surface electronic barrier reduce the probability of electron escape from the Cu surface, resulting in lower secondary electron emission. Formation of CO₂ and NO₂, on the other hand, reduce the electronic barrier effects. In addition, due to weak bonding of the CO₂ layer with the Cu host, the surface provides an additional source of secondary electrons resulting in higher electronic emission yield. Moreover, the NO₂ adsorbate creates a surface electric field that changes the surface electron energy and increases the electron escape probability. Additionally, it is verified that thermal change in the system is negligible and so during secondary electron emission measurements, negligible (if any) surface adsorption or desorption could occur.

1 Introduction

Secondary electron emission (SEE) is the process in which secondary electrons are emitted from a surface when it is bombarded by charged particles. SEE can cause a variety of effects that are detrimental to both experiments and devices. For instance in particle accelerators, SEE can be generated by the walls of the particle accelerator and can create electron clouds and heat that infringe on the accelerator’s experimental success (Cimino and Demma, 2014; Schulte et al., 2020). Another issue associated with the synchronized feedback from electron avalanches arising from SEE, known as the multipactor effect (Vaughan, 1988; Fil et al., 2016; Montero et al., 2020; Brown et al., 2022b), can lead to failure in high energy radio frequency devices and high power microwave components in space aplications, detuning of resonant cavities, and generation of excessive noise in communication satellites. Understanding the variety of factors that affect SEE for different materials is thus important, and can allow for better designs to help improve the performance for both experiments and practical devices.

The ratio of secondary electrons emitted by the bombardment of a system to the primary (incident) electrons is known as the secondary electron yield (SEY) (Seiler, 1983). The SEY of materials depends on both the physical properties such as the work function, electron mean free path, and stopping power, and on the surface morphology of the system, such as the surface’s roughness, defects, and coverage with different adsorbates. The latter affects the material properties, electronic energy barriers, permittivity, etc., causing an increase or decrease of the system SEY. For example, experimental studies of Cu surface covered with O, (Petit et al., 2019), C (Larciprete et al., 2013), or N (Kuzucan, 2011; Kuzucan et al., 2012) confirmed that the SEY reduced significantly. However, adsorption of CO or CO₂ (Kuzucan, 2011; Kuzucan et al., 2012) has the opposite effect and increases the SEY with respect to the clean Cu surface. Most SEY studies of materials have been carried out at or above room temperature (Baglin et al., 2000; Hilleret et al., 2003; Patino et al., 2018) and rarely at cryogenic temperatures (Kuzucan, 2011; Kuzucan et al., 2012; Fang et al., 2022), which is the region of interest for the Large Hadron Collider (LHC). More importantly, there have been no systematic studies of physisorbed gases that have a significant effect on the SEY of systems. The aim of this work is to use Monte-Carlo and first-principles calculations to study the influence of physisorbed gases like N₂, NO₂, and CO₂ on the SEY of Cu systems, which represents a common electrode material.

In the work presented here it is demonstrated that, in agreement with experimental observation, formation of C₂ (Larciprete et al., 2013) and N₂ (Kuzucan, 2011; Kuzucan et al., 2012) decreases the SEY of Cu systems. Furthermore, the effect on SEY due to the presence of CO₂ or NO₂ is also probed since the adsorption of O₂ by C and N could form carbon dioxide and nitrogen dioxide molecules covering the Cu surface. For a monolayer (1 ML) surface coverage for either CO₂ or NO₂, the SEY is predicted to increase with respect to the clean surface. Interestingly, in spite of the increase of the work function of NO₂ by about 2.15 eV with respect to clean surface, its SEY increase turns out to be the highest among all of the systems studied in this work.

Our study of the charge density of the C₂ and N₂ pairs on Cu surface confirms the creation of an excess charge density which acts as an electronic barrier that can reduce the escape probability of electrons from the Cu surface as explained later, resulting in a lower SEY. Calculated adsorption energy and total density of states of the CO₂/Cu system show that the CO₂ layer is weakly bonded to the surface, creating an additional source for generating secondary electrons and increasing the SEY of the system. However, for the NO₂/Cu system, the electric dipole (electric field) created by NO₂ is the main reason for the increase in the SEY of the system. In addition, by calculating the electron penetration depth (range) and the energy loss of the primary electrons in the system, the thermal changes in Cu during SEY measurements have been studied here.

This work consists of the following sections: In Section 2 all computational details including the first-principles and Monte Carlo simulations are discussed. Details of the effects of the carbon pair, nitrogen pair, carbon dioxide, and nitrogen dioxide on the SEY of Cu, as well as the temperature stability of the Cu system are given in Section 3. Finally, Section 4 summarizes the results of this work and highlights the important findings.

2 Details of calculations

The first-principles calculations in this work were performed using VASP (Vienna Ab initio Simulation Package), with the projector augmented-wave technique (Kresse and Hafner, 1993; Blöchl, 1994; Kresse and Furthmüller, 1996; Kresse and Joubert, 1999), and the generalized-gradient approximation (GGA) to the exchange-correlation potential, as parameterized by Perdew, Burke, and Ernzerhof (Perdew et al., 1996). The X/Cu (110) surfaces are modeled by a slab made up of ten layers and 40 host Cu atom periodic supercells with a calculated equilibrium bulk lattice constant of 3.63 Å comparable to the experimental value of 3.61 Å (Lihl and Ebel, 1967). For all the systems, the bottom six layers were held fixed while the remaining top layers were allowed to relax. It is worth noting that it has been shown that increasing the number of layers of the slab beyond eight, the calculated value of the work function of the system converges and does not significantly change (Wang et al., 2020). After studying several energy cutoffs and k-point sampling (Table 1) a kinetic energy cutoff of 600 eV and k-point sampling of 5 × 5 × 1 Monkhorst Pack mesh (Monkhorst and Pack, 1976) were used for all of the systems studied here.

TABLE 1

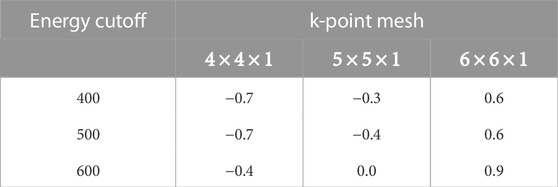
TABLE 1. Calculated total energy difference (meV/atom) for Cu (110) system for different energy cutoffs (eV) and k-point meshes. The calculated total energy with 600 eV cutoff energy and k-point sampling of 5 × 5 × 1 were used as the reference energy.

Using the crystal structure and parameters mentioned, the input parameters for Monte Carlo simulations such as total densities of states, the work function, and dielectric functions that are needed for calculations of mean free paths and stopping power were calculated.

For Monte Carlo simulations of SEY in this study, 100,000 primary electrons with incident energy between 5 and 1,000 eV were used. Treatment of the inelastic scattering was based on the approach introduced by Penn (1987) and also discussed by Ding et al. (2001), Ding et al. (2008). As the generated secondary electrons travel across the Cu surface, there is a possibility that they might be reflected by the potential barrier of the surface. This barrier is the material’s work function. The probability of transmission is given by

$T\left(E,\theta \right)=\left\{\begin{array}{cc}\frac{4\sqrt{1-\left(\frac{U_0}{Eco{s}^2\theta }\right)}}{{\left(1+\sqrt{1-\left(\frac{U_0}{Eco{s}^2\theta }\right)}\right)}^2},\hfill & \text{for}Eco{s}^2\theta >U_0,\hfill \\ 0,\hfill & \text{otherwise},\hfill \end{array}\right.(1)$

where θ is the electron ejection angle measured normal to the surface. This energy-dependent transmission probability is used in the Monte Carlo scheme based on the approach by Azzolini et al. (Azzolini et al., 2019). The inner potential U₀ is

$U_0=E_F+\phi (2)$

where E_F is the Fermi energy. The total density of states of each system yields that system’s respective E_F. The work function φ is the energy required to remove an electron from a material. It is given by

$\phi =E_v-E_F.(3)$

Where E_v is the vacuum level energy at a point far enough away from the surface that the emitted electron would not experience any electrostatic effects.

The electrons are emitted at the angle θ, defined in terms of the polar angle of the scattering electron as $\sqrt{E^{\prime }}$ sin${\theta }^{\prime }=\sqrt{E}$ sinθ. When the externally emitted electrons cross the interface between surface and vacuum, they lose energy. As a result they have the energy E′ = E − U₀.

The stopping power (dE/dR) is one of the essential parameters which is needed in order to determine the secondary electron yield within the simulation. This stopping power is the energy loss per unit length experienced by an electron along its path length, R, and is given by

$\frac{dE}{dR}=\frac{\hslash }{\pi a_{0}E}{\int }_0^{\frac{E}{\hslash }}\left(\hslash \omega \right)d\left(\hslash \omega \right)Im\left(\frac{-1}{\epsilon \left(\omega \right)}\right)\ln \left(\frac{\sqrt{E}+\sqrt{E-\hslash \omega }}{\sqrt{E}-\sqrt{E-\hslash \omega }}\right).(4)$

Where ℏ, $a_0=\frac{4\pi {\epsilon }_0{\hslash }^2}{m_e{e}^2}=5.29\times 10^{-11}$ m, and E are, respectively, the Planck constant, Bohr radius, and electron energy. Calculation of the stopping power can be simplified by making use of a wavevector-independent form of the dielectric function [i.e., ɛ(q, ω) ≡ɛ(ω)].

The inelastic mean free path (IMFP) is another critical input parameter that is used in Monte Carlo simulation of SEY. In order to determine the IMFP, the extended Mermin method with harmonic correction was used. The inverse-IMFP (λ⁻¹) is given by

${\lambda }_{\mathit{harm}}^{-1}=\frac{1}{\pi a_{0}E}{\int }_0^{\infty }d\left(\hslash \omega \right)Im\left[\frac{-1}{\epsilon \left(q,\omega \right)}\right]\ln \left[\frac{2\sqrt{E-E_F-\hslash \omega }}{\sqrt{E}-\sqrt{E-2\hslash \omega }}\right],(5)$

The above calculation of inelastic scattering relies on an evaluation of the dielectric function based on Density Functional Theory. It was first shown that a model of the SEE in pure normal metals requiring a description of inelastic collisions with the jellium can be devised by making use of dielectric theory (Ganachaud and Cailler, 1979). Though the Lindhard function (Lindhard, 1954) has been used for this purpose to quantify the principal properties of the delocalized electrons in a normal metal, improvements could be made to account for the correlation and exchange effects, as well as the finite lifetime of the elementary excitations. This aspect of the problem was first studied almost 50 years ago (Ganachaud, 1977). More recent analysis (Ashley, 1991) has included exchange effect in the calculations of excitation function. It was shown that the excitation function is smaller in values, for kinetic energies <100 eV, when compared with that without including exchange term. Also, the overall result was smaller stopping powers and larger inelastic mean free paths for the slow electrons. However, in the present analysis, these details have been overlooked since such effects play a role mainly at low energies, while the secondary electron emission is influenced more by higher energy particles. However, it may be mentioned for completeness that other modeling studies on SEY have included some of these aspects (Ding and Shimizu, 1996).

It is well known that the Mermin approach with harmonic correction to IMFP overestimates the experimental measurements and that without that correction those results are underestimated. The overestimation has also been observed in other works (Ritchie and Howie, 1977). An extended Mermin method based on (Da et al., 2014) was introduced to deal with this effect, where the corrected IMFP (λ_e) takes the form

${\lambda }_e={\lambda }_{\mathit{harm}}\left[1-e^{-E/B}\right],(6)$

Here, E is the electron kinetic energy and B is a material-dependent parameter which should be determined accordingly. After studying several values for B and comparing the calculated IMFP with experimental measurements, it was determined that B = 50 eV gives the best result. Therefore the harmonic correction with a B = 50 eV was implemented for the systems in this work. In addition, elastic scattering was taken into account based on the Mott theory (Mott, 1929), as discussed in our previous reports (Brown et al., 2022a; Brown et al., 2022c). Elastic scattering is the result of interactions between electrons and atomic nuclei, in which negligible energy exchange takes lace due to the large mass difference between the interacting species and only directional changes are assumed to occur. Other details of a Monte Carlo implementation of elastic scattering based on tabulated Mott scattering cross section data are available in the literature (Browning et al., 1994; Chang et al., 2018). For completeness, it may be mentioned that elastic scattering becomes more important for higher atomic number targets, such as gold, and would not be as significant here.

3 Results and discussion

3.1 Secondary electron emission

In order to study any system, it is essential to find the most stable (lowest energy) structure. Using first-principles calculations and investigating the energy of several configurations, it was determined that a C₂ monolayer would be parallel to the surface and the N₂ pairs would be almost perpendicular to the surface (Figure 1). Also, as shown in the figure, the C₂ and N₂ pairs occupy hollow and top adsorption sites respectively. Furthermore, formation of C₂ pairs, contrary to N₂ pairs, creates internal strain that causes surface reconstruction, driving the surface Cu atoms to new sites different from the ideal face center cubic (FCC) sites.

FIGURE 1

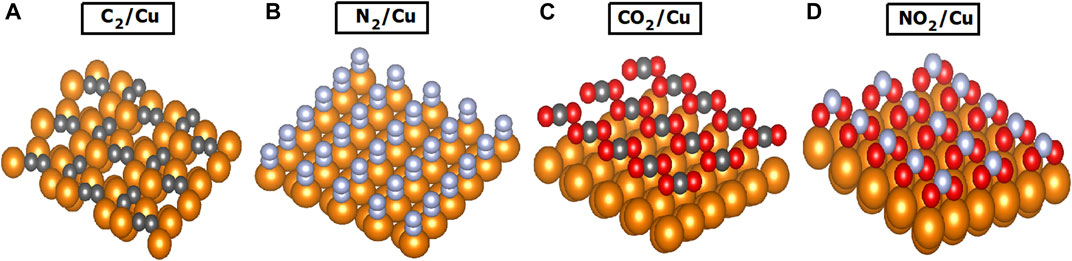
FIGURE 1. Surface coverage of Cu (gold spheres) with (A) C₂ (dark gray spheres), (B) N₂ (light gray spheres), (C) CO₂ (dark gray, red spheres), and (D) NO₂ (light gray, red spheres). The C₂ pairs are parallel to the Cu surface while the N₂ pairs are almost perpendicular to the surface (88.5°). The bond angles between carbon and oxygen atoms are 180° and between nitrogen and oxygen 117.8°.

As a result of O₂ adsorption, the existing surface N or C atoms can form CO₂ and NO₂ molecules covering the Cu surface. The most energetic stable structures of 1 monolayer (ML) of CO₂ and NO₂ were determined and are shown in Figure 1. The CO₂ layer is a two-dimensional structure parallel to the surface, similar to an isolated CO₂ molecule (a linear molecule with 180° bond angle). In contrast, the NO₂ monolayer has a non-linear structure with a bond angle of 117.8°. The neutral NO₂ has a bond angle of 134.3°, while for ${{\mathrm{N}\mathrm{O}}_2}^{-}$, the O-N-O bond angle is reduced further to 115.4°(Gillespie and Hargittai, 1991), comparable to the calculated angle for a monolayer. The reduction of the bond angle is due to the electron gain for O atoms from the Cu surface atoms.

The stability of each adsorbate was verified by calculating the cohesive energy of each system. The cohesive energies are given in Table 2 and were obtained using

$\mathrm{\Delta }{H}_{\mathit{coh}}=E_{\mathit{sys}}-E_{\mathit{clean}}-E_{ML},(7)$

where E_sys, and E_clean are the energy of the entire system, and energy of clean Cu (110) surface, respectively. Here E_ML is the energy of each adsorbate monolayer.

TABLE 2

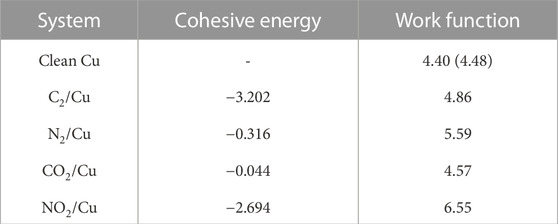
TABLE 2. Calculated cohesive energies ΔH_coh (eV/molecule), and calculated work functions φ (eV) for clean Cu (110). The experimental work function for clean Cu (110) is provided in parentheses and is from Reference (Gartland et al., 1972).

Calculated work function and total density of states were used as part of input parameters for SEY simulations. The diagonal elements of the computed dielectric constant tensor were used to find the average ɛ(ω) [Figure 2) required for calculating the stopping power and IMFP (Eqs. 4, 5)] that are also needed as inputs for SEY simulations. As can be seen from Figure 3, there is comparable agreement between calculated clean surface, C₂/Cu, and the experimental measurement (Larciprete et al., 2013). However, for N₂/Cu, the agreement between the SEY of calculated and experimental values (Kuzucan, 2011; Kuzucan et al., 2012) begins to reduce and gets progressively worse beyond 500 eV primary electron energy. One can explain this deviation based on the weak bonding (small cohesive energy) between the N₂ layer and the Cu surface (Table 2). It was shown that when primary electrons with high energy irradiate the surface, the N₂ molecule can desorb (Kuzucan, 2011). Since the N₂ binding is much stronger than N₂/Cu, after the desorption process the atoms can bond together and create layers of N₂. For that reason, experimental studies of 1–6 ML of N₂ systems (Kuzucan, 2011) produced similar SEY at higher energies (400–1,000 eV), while at lower energies their maximum energies are different, as was expected. In any case, our result of SEY lowering with adsorbed nitrogen is in agreement with experiments where laser processing in nitrogen-rich environments were reported to reduce SEY (Calatroni et al., 2020).

FIGURE 2

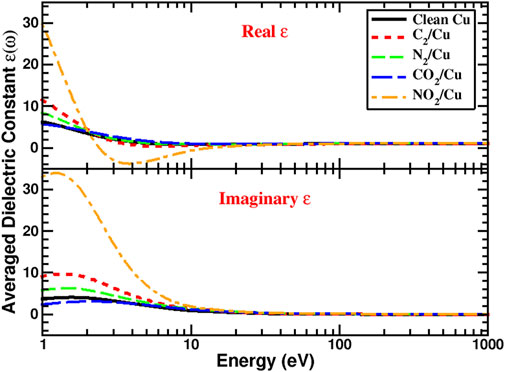
FIGURE 2. Calculated real and imaginary part of the averaged dielectric constants for the clean Cu (110), C₂/Cu (110), N₂/Cu (110), CO₂/Cu (110), and NO₂/Cu (110) surfaces.

FIGURE 3

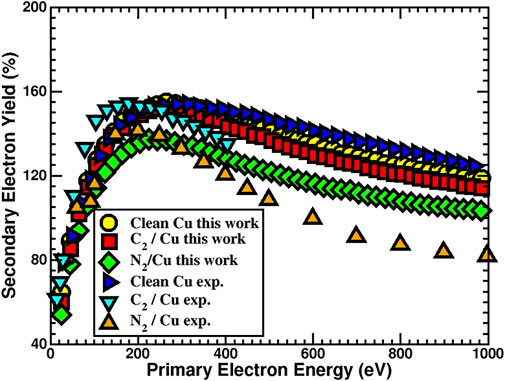
FIGURE 3. Calculated secondary electron yield for the clean Cu (110), C₂/Cu (110), and N₂/Cu (110) surfaces and their comparison with 1.00 ML coverages. Experimental measurements for C₂/Cu (Larciprete et al., 2013) and N₂/Cu (Kuzucan, 2011; Kuzucan et al., 2012) systems are provided for comparison.

From our calculations, adsorption of C₂ and N₂ reduced the SEY of clean Cu system by 2% and 11.5%, respectively. In order to explain the significant reduction of SEY for the N₂ layer, one needs to consider the nature of bonding between adsorbate and Cu surface atoms. The Cu atom has electronegativity of 1.850 on the Allen scale (Allen, 1989), which is lower than the N (3.066) and C (2.544) atoms. Therefore, electrons from the Cu surface atoms are likely to transfer to C and N atoms based on energetics. Bader charge analysis (Henkelman et al., 2006; Sanville et al., 2007; Tang et al., 2009; Yu and Trinkle, 2011) confirms that on the average C and N surface atoms receive about 0.56 and 2.18 electrons from their surrounding atoms, respectively. Charge density studies of clean Cu, C₂/Cu, and N₂/Cu also confirm that the N₂ monolayer has the most surface changes with respect to the clean Cu surface, resulting in creation of regions with higher electron density (Figure 4). Formation of these excess electrons created due to C₂ and N₂ monolayers repels the secondary electrons generated in the Cu back into the system. This repulsive interaction reduces the probability of electrons escaping from the surface. Therefore, because of the higher charge transfer and the creation of an electronic barrier, the SEY for the N₂/Cu system is reduced significantly with respect to the C₂/Cu monolayer and clean Cu surface.

FIGURE 4

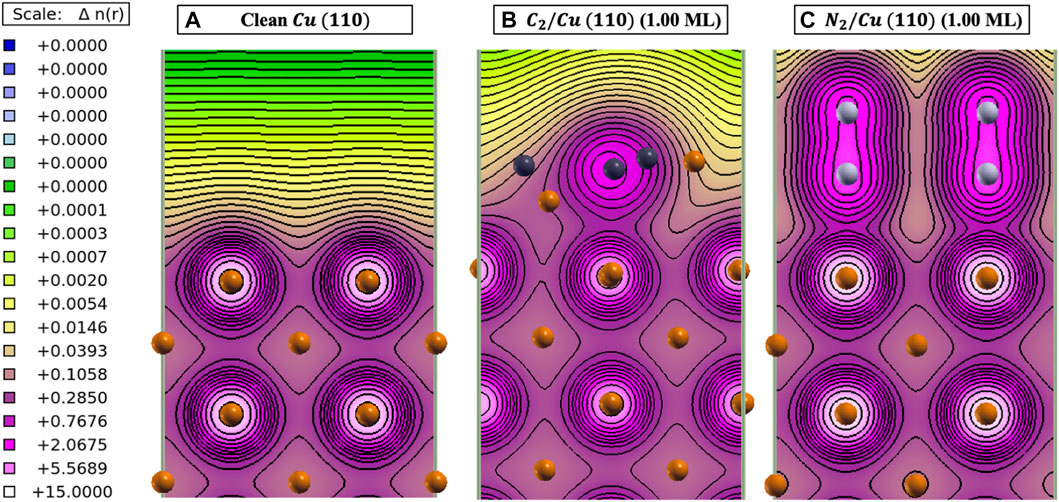
FIGURE 4. Calculated charge density [n(r)] contour plots (Kokalj, 1999) for (A) clean Cu (110), (B) 1.00 ML C₂/Cu, and (C) 1.00 ML N₂/Cu structures. Gold, dark gray, and light gray spheres represent the Cu, C, and N atoms, respectively.

Dissociation of Cu-N and Cu-C bonds and formation of CO₂ and NO₂ weaken the excess electronic barrier created by N₂ and C₂ atoms, and so one should then expect the SEY of the CO₂ and NO₂ systems to increase. Calculated SEY for both systems and their comparison with available experimental measurements (Kuzucan, 2011; Kuzucan et al., 2012) are given in Figure 5. Although for both systems the SEY increases, there are very different physical reasons behind such changes. In the case of CO₂, calculated cohesive energy (Table 2) suggests that the monolayer is not as strongly bonded to the surface. Furthermore, a comparison between calculated total density of states (TDOS) between clean Cu and CO₂/Cu (Figure 6) confirms that CO₂, similar to a CO monolayer (Brown et al., 2022a), is weakly bonded to the surface, and shows no evidence of strong orbital hybridization between the Cu and CO₂ layers. Our TDOS study of the CO₂ layer showed that the DOS contribution in the range from about −9.5 to −9.0 eV is solely due to the CO₂ monolayer. As can be seen from Figure 6, the CO₂ layer increased the TDOS of system and, analogous to CO (Brown et al., 2022a), acted as an additional source for the generation of secondary electrons. Additionally, since the work function did not change significantly with respect to the clean surface, the SEY increased.

FIGURE 5

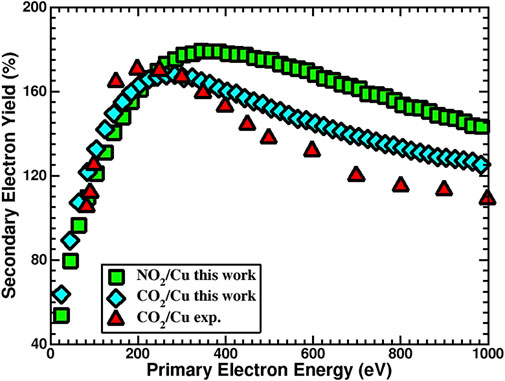
FIGURE 5. Calculated secondary electron yield for the 1.00 ML of NO₂/Cu (110) (green squares) and CO₂/Cu (110) (blue diamonds). Experimental measurement for CO₂/Cu (110) (red triangles) is provided for comparison (Kuzucan, 2011; Kuzucan et al., 2012).

FIGURE 6

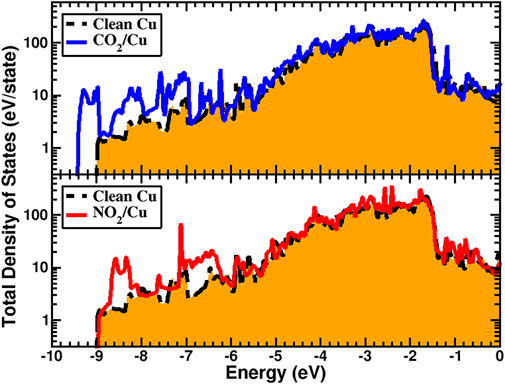
FIGURE 6. Calculated total density of states for CO₂/Cu (top) and NO₂/Cu (bottom), and their comparison with clean Cu. The CO₂ layer shows a weaker bonding to Cu surface compared to NO₂. The Fermi energy level is set at zero for all systems.

For the NO₂/Cu system, on the other hand, Cu surface atoms are predicted to bond with O instead of the N atoms. As a result, the excess surface charge is reduced. Additionally, because of orientational bonding of N with O atoms (as in Figure 1D), an electric dipole above the Cu surface is created. The normal component of a dipole with an electric field toward the surface applies an additional force on secondary generated electrons. This electric field increases the energy of secondary electrons close to the surface and in spite of the system work function having increased significantly, the SEY of the system is effectively enhanced with respect to the clean surface.

In order to estimate the contribution of the NO₂ dipole in increasing the surface electron energy, the following model was used (Diaz et al., 2023): As a first approximation, the electric field due to the normal component of the dipole moment was assumed to be uniform. The energy increase of an electron corresponding to such a uniform electric field (E) is calculated by the following equation

$U_e=e\mathbf{E}\cdot \mathbf{d},(8)$

where e and d are the charge of the electron and the distance between the N and O atoms along the crystal axis. The magnitude of the uniform electric field E was calculated using σ/ɛ₀ with the value of the charge density σ taken from the Bader charge analysis. Using calculated values of σ = 0.45 C/m² and d = 6.64 × 10⁻¹¹ m, the estimated energy gain by electrons would be about 3.40 eV. Comparison between the estimated electric energy (3.40 eV) and the increase of the work function (by 2.15 eV) confirms that the electric field (created by the normal component of the dipole) is responsible for increasing the SEY of the NO₂ system.

3.2 Electron and heat transport

During SEY measurements, the system of interest gains energy from the bombardment of primary electrons, which causes an increase in temperature both on the surface and inside the material. This temperature increase can lead to changes in the adsorption and/or desorption kinetics of gases and thus affect the outcome of SEY measurements. Lowering the intensity and duration of the primary electron beam would decrease this effect, but could give unreliable results from a statistical standpoint. For the above reason, it becomes important to understand how the intensity and pulse time might affect the temperature of the system and ascertain whether SEY measurements are reliable with minimal adsorption and desorption of gases. The SEY Monte Carlo, as previously discussed, was used to track electron transport inside the material. In Figure 7 the results of Monte Carlo simulation of electron range in clean Cu and its comparison with available data (NIST, 2022) are given. Since there is no data available for the low energy region, calculations were carried out for energies between 500 and 20,000 eV for incident primary electrons.

FIGURE 7

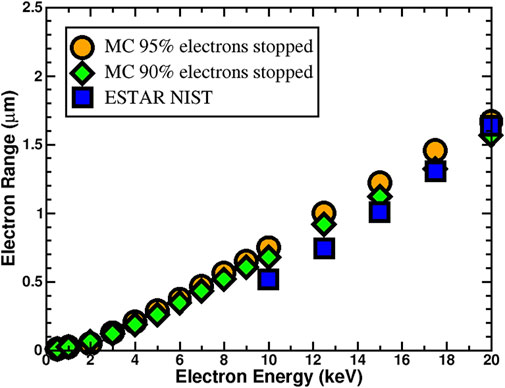
FIGURE 7. Electron range in clean Cu calculated from Monte Carlo simulations with lower limit of 90% (solid green diamonds) and upper limit of 95% (solid orange circles) of stopped electrons are compared with the ESTAR (blue solid squares) database provided by National Institute of Standards and Technology (NIST, 2022).

The penetration depth is defined as the distance such that 90%–95% of incident electrons are stopped. For the calculated electron range shown in Figure 7, both the lower 90% and upper and 95% limits were considered. As it can be seen from Figure 7, calculated electron range with the lower limit is in better agreement with available data for the Cu system.

By modifying the Monte Carlo simulation to also track where the electrons lose their energy within the copper host, the heating profile for the system was determined. Calculated energy loss of electrons as a function of depth was converted to a power dissipation density and used as the source term in a one-dimensional heat transport equation to model the position-dependent variation of temperature at the surface and inside the Cu. The governing heat flow equation is given by

$\rho C_p\frac{\partial T\left(z,t\right)}{\partial t}-k\frac{{\partial }^{2}T\left(z,t\right)}{\partial z^2}=S\left(z\right)(9)$

where ρ, C_p, k, and S(z) are the mass density, specific heat, thermal conductivity, and heat source power density of the system, respectively. The power loss per area (W/A) at the surface layer due to thermal radiation was accounted for according to the Stefan-Boltzmann law

$W/A=ϵ\sigma \left(T^4-T_c^4\right)(10)$

Where ϵ, σ, T_c, and T are the respective emissivity of the material, Stefan-Boltzmann constant, surrounding temperature, and temperature of surface at time t. The bottom layer of the system was maintained at the ambient temperature.

The calculated heat source density corresponding to power loss of electrons with 1,000 eV incident energy, 0.1 nC/mm² electron flux, and 2 ms beam pulse exposure (Kuzucan et al., 2012) is shown in Figure 8. The surface temperature was chosen as the experimental value of 4.7 K (Kuzucan et al., 2012). As shown in the Figure 8 inset, during the beam exposure the changes in the Cu temperature were negligible. It should be emphasized that because of the small flux of primary electrons, a small amount of energy was deposited into the system, causing an insignificant amount of variation of temperature on the surface and across the Cu crystal axis. However, in the case of a large flux of electrons as might occur in high power systems or microwave generators, the temperature could rise to several hundred Kelvin, causing serious possible damage to the system, removing the surface adsorbates, or driving outgassing from the system.

FIGURE 8

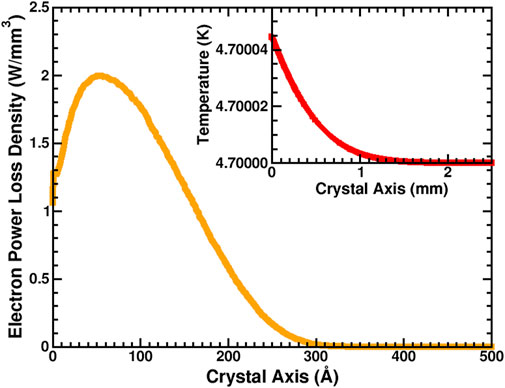
FIGURE 8. Calculated electron power loss density, S(z) (solid orange line), and (top right corner) temperature distribution (solid red line) along crystal axis.

4 Summary

The effects of C₂ pair, N₂ pair, CO₂ and NO₂ layers on the SEY of the Cu (110) surface were studied by employing the first-principles method and Monte Carlo simulations. The required input parameters for Monte Carlo simulations such as the work functions, total densities of states, and dielectric functions were calculated using first principles methods. It was shown that, in agreement with experiments, the C₂ (Larciprete et al., 2013) and N₂ (Kuzucan, 2011; Kuzucan et al., 2012) surface coverage reduced the SEY of Cu system, while adsorption of CO₂ (Kuzucan, 2011; Kuzucan et al., 2012) resulted in a higher SEY with respect to the clean Cu surface. Studying the charge density of C₂/Cu and N₂/Cu confirmed the formation of an electronic barrier as a result of bonding (charge transfer) between the Cu surface and C or N atoms. The electronic barrier reduced the probability for electrons to escape from the surface. Since formation of N₂ created a higher electron barrier, the SEY of the Cu was significantly reduced. In contrast, formation of surface carbon and nitrogen dioxides increased the SEY of the Cu. It was demonstrated that CO₂ weakly bonded to the surface and acted as an additional source of electrons that contributed to the generation of secondary electrons. Meanwhile, NO₂ was shown to bond strongly to the surface and created a large work function in addition to an electric dipole. It was shown that calculated energy gain due to the electric field of the dipole was higher than the increased work function, resulting in a higher SEY. The present method is general and could be used to investigate other emitter materials and/or surface absorbates as well. Some possible scenarios might be the formation of graphitic carbon during irradiation meant for surface treatment (Larciprete et al., 2013), or the presence of carbon-free oxidized (Cu₂O) copper (Petit et al., 2019), or the role of surface water vapor. By modeling the heat transfer for the Cu system, it was verified that thermal increases under conditions typically encountered in SEY measurements are negligible, and so there should be no desorption due to the very minor increase of the surface temperature. The thermal transport model presented in this work can be used for optimizing the beam characteristics for SEY measurements.

It is important to mention that the adsorbates studied in this work are considered to be uniformly distributed on the surface, which is an ideal case. Furthermore, first principles calculations are done at 0 Kelvin, different from finite temperature. Even with these limitations, first principles calculations can give us insight into the electronic perspective of the system which is difficult for experimental measurements of such systems. In addition, most previous reports on SEY (Browning et al., 1994; Chang et al., 2018) have focused on bulk materials. Here we specifically look at the role of surface adsorbates. This opens up a new direction and could be used to model realistic electrode surfaces containing graphitic carbon produced during irradiation or device operation, or the presence of oxidized copper (Cu₂O), or the role of surface water vapor. The information could even be used to select parameters for surface cleaning treatments (e.g., laser wavelengths) to selectively target cleaning of certain undesirable adsorbates and molecules from the surface.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

The authors confirm contribution to the paper as follows: study conception and design: RJ and MS; data collection: MS, MM, ND, and YP; analysis and interpretation of results: RJ and MS; draft manuscript preparation: RJ, MS, MM, and ND All authors reviewed the results and approved the final version of the manuscript.

Funding

This work was supported in part by grants from the Air Force Office of Scientific Research (No. FA9550-19-1-0056) and the Office of Naval Research (No. N00014-22-1-2483).

Acknowledgments

We acknowledge the generous amounts of computer time provided by Texas Tech University High Performance Computer Center.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Allen, L. C. (1989). Electronegativity is the average one-electron energy of the valence-shell electrons in ground-state free atoms. Phys. Rev. St. Accel. Beams 111 (25), 9003–9014. doi:10.1021/ja00207a003

CrossRef Full Text | Google Scholar

Ashley, J. C. (1991). Energy-loss probabilities for electrons, positrons, and protons in condensed matter. J. Appl. Phys. 69 (2), 674–678. doi:10.1063/1.347348

CrossRef Full Text | Google Scholar

Azzolini, M., Angelucci, M., Cimino, R., Larciprete, R., Pugno, N. M., Taioli, S., et al. (2019). Secondary electron emission and yield spectra of metals from Monte Carlo simulations and experiments. J. Phys. Condens. Matter 31 (5), 055901. doi:10.1088/1361-648x/aaf363

PubMed Abstract | CrossRef Full Text | Google Scholar

Baglin, V., Bojko, J., Gröbner, O., Henrist, B., Hilleret, N., Scheuerlein, C., et al. (2000). “The secondary electron yield of technical materials and its variation with surface treatments,” in Proceedings of EPAC 2000, Vienna, Austria, 217–221.

Google Scholar

Blöchl, P. (1994). Projector augmented-wave method. Phys. Rev. B 50 (24), 17953–17979. doi:10.1103/physrevb.50.17953

CrossRef Full Text | Google Scholar

Brown, M., Diaz, L., Aslan, A., Sanati, M., Portillo, S., Schamiloglu, E., et al. (2022a). Carbon-oxygen surface formation enhances secondary electron yield in Cu, Ag and Au. Sci. Rep. 12 (1), 15808. doi:10.1038/s41598-022-19924-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Brown, M., Milestone, W., and Joshi, R. P. (2022b). Numerical analysis for suppression of charge growth using nested grooves in rectangular waveguides. J. Appl. Phys. 132 (21), 213304. doi:10.1063/5.0123925

CrossRef Full Text | Google Scholar

Brown, M., Sanati, M., and Joshi, R. P. (2022c). Combined first-principles-Monte Carlo analysis to evaluate the effect of surface hydrogen on the secondary electron yield of nickel. J. Appl. Phys. 131 (1), 103301. doi:10.1063/5.0080721

CrossRef Full Text | Google Scholar

Browning, R., Li, T., Chui, B., Ye, J., Pease, R., Czyzewski, Z., et al. (1994). Empirical forms for the electron/atom elastic scattering cross sections from 0.1 to 30 kev. J. Appl. Phys. 76 (4), 2016–2022. doi:10.1063/1.357669

CrossRef Full Text | Google Scholar

Calatroni, S., Garcia-Tabares Valdivieso, E., Perez Fontenla, A. T., Taborelli, M., Neupert, H., Himmerlich, M., et al. (2020). Optimization of the secondary electron yield of laser-structured copper surfaces at room and cryogenic temperature. Phys. Rev. Accel. Beams 23 (3), 033101. doi:10.1103/physrevaccelbeams.23.033101

CrossRef Full Text | Google Scholar

Chang, H. Y., Alvarado, A., and Marian, J. (2018). Calculation of secondary electron emission yields from low-energy electron deposition in tungsten surfaces. Appl. Surf. Sci. 450, 190–199. doi:10.1016/j.apsusc.2018.04.155

CrossRef Full Text | Google Scholar

Cimino, R., and Demma, T. (2014). Electron cloud in accelerators. Int. J. Mod. Phys. A 29 (17), 1430023. doi:10.1142/s0217751x14300233

CrossRef Full Text | Google Scholar

Da, B., Shinotsuka, H., Yoshikawa, H., Ding, Z. J., and Tanuma, S. (2014). Extended Mermin method for calculating the electron inelastic mean free path. Phys. Rev. Lett. 113 (6), 063201. doi:10.1103/physrevlett.113.063201

PubMed Abstract | CrossRef Full Text | Google Scholar

Diaz, L., Albers, R. C., Saxena, A., and Sanati, M. (2023). Dipolar effects on the work function of an alkali-iodide overlayer (XI, X= Li, Na, K, Rb, and Cs) on tungsten surfaces. Phys. Scr. 98, 035823. doi:10.1088/1402-4896/acba54

CrossRef Full Text | Google Scholar

Ding, Z. J., and Shimizu, R. (1996). A Monte Carlo modeling of electron interaction with solids including cascade secondary electron production. Scanning 18 (2), 92–113. doi:10.1002/sca.1996.4950180204

CrossRef Full Text | Google Scholar

Ding, Z. J., Tang, X. D., and Shimizu, R. (2001). Monte Carlo study of secondary electron emission. J. Appl. Phys. 89 (1), 718–726. doi:10.1063/1.1331645

CrossRef Full Text | Google Scholar

Ding, Z. J., Li, H. M., Shimizu, R., and Goto, K. (2008). On the energy distribution of secondary electrons emitted from metals. J. Surf. Anal. 15 (2), 186–194. doi:10.1384/jsa.15.186

CrossRef Full Text | Google Scholar

Fang, J., Hong, Y., Wang, S., Wang, Y., Zhu, B., Zhang, W., et al. (2022). Cryogenic secondary electron yield measurements on structural materials applied in particle accelerators. Nucl. Ins. Meth. Phys. A 1027, 166292. doi:10.1016/j.nima.2021.166292

CrossRef Full Text | Google Scholar

Fil, N., Belhaj, M., Hillairet, J., and Puech, J. (2016). Multipactor threshold sensitivity to total electron emission yield in small gap waveguide structure and TEEY models accuracy. Phys. Plasmas 23 (12), 123118. doi:10.1063/1.4972571

CrossRef Full Text | Google Scholar

Ganachaud, J. P., and Cailler, M. (1979). A Monte Carlo calculation of the secondary electron emission of normal metals. Surf. Sci. 83 (2), 519–530. doi:10.1016/0039-6028(79)90060-8

CrossRef Full Text | Google Scholar

Ganachaud, J. P. (1977). Thèse d’Etat. Nantes, France: Nantes University Press.

Google Scholar

Gartland, P. O., Berge, S., and Slagsvold, B. J. (1972). Photoelectric work function of a copper single crystal for the (100), (110), (111), and (112) faces. Phys. Rev. Lett. 28 (12), 738–739. doi:10.1103/physrevlett.28.738

CrossRef Full Text | Google Scholar

Gillespie, R. J., and Hargittai, I. (1991). The VSEPR model of molecular geometry. Boston: Allyn and Bacon, 85–87.

Google Scholar

Henkelman, G., Arnaldsson, A., and Jønsson, H. (2006). A fast and robust algorithm for Bader decomposition of charge density. Comput. Mat. Sci. 36 (3), 354–360. doi:10.1016/j.commatsci.2005.04.010

CrossRef Full Text | Google Scholar

Hilleret, N., Scheuerlein, C., and Taborelli, M. (2003). The secondary-electron yield of air-exposed metal surfaces. Appl. Phys. A 76 (7), 1085–1091. doi:10.1007/s00339-002-1667-2

CrossRef Full Text | Google Scholar

Kokalj, A. (1999). XCrySDen—A new program for displaying crystalline structures and electron densities. J. Mol. Mod. Grph. Model. 17 (3-4), 176–179. doi:10.1016/s1093-3263(99)00028-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Kresse, G., and Furthmüller, J. (1996). Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54 (16), 11169–11186. doi:10.1103/physrevb.54.11169

PubMed Abstract | CrossRef Full Text | Google Scholar

Kresse, G., and Hafner, J. (1993). Ab initio molecular dynamics for liquid metals. Phys. Rev. B 47 (1), 558–561. doi:10.1103/physrevb.47.558

PubMed Abstract | CrossRef Full Text | Google Scholar

Kresse, G., and Joubert, D. (1999). From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59 (3), 1758–1775. doi:10.1103/physrevb.59.1758

CrossRef Full Text | Google Scholar

Kuzucan, A., Neupert, H., Taborelli, M., and Störi, H. (2012). Secondary electron yield on cryogenic surfaces as a function of physisorbed gases. J. Vac. Sci. Tech. A 30 (5), 051401. doi:10.1116/1.4736552

CrossRef Full Text | Google Scholar

Kuzucan, A. (2011). Secondary electron yield on cryogenic surfaces as a function of physisorbed gases. Ph.D. thesis. Vienna: Vienna University of Technology. available at: https://cds.cern.chCERN-THESIS-2011-057.

Google Scholar

Larciprete, R., Grosso, D. R., Commisso, M., Flammini, R., and Cimino, R. (2013). Secondary electron yield of Cu technical surfaces: Dependence on electron irradiation. J. Am. Chem. Soc. 16 (1), 011002. doi:10.1103/physrevstab.16.011002

CrossRef Full Text | Google Scholar

Lihl, F., and Ebel, H. (1967). A handbook of lattice spacings and structures of metals and alloys. Editor W. B. Pearson (Oxford: Pergamon), 2, 234.

Google Scholar

Lindhard, J. (1954). On the properties of a gas of charged particles, 28. det kgl. danske videnskabernes selskab. Matematisk-fysiske meddelelser.8

Google Scholar

Monkhorst, H. J., and Pack, J. D. (1976). Special points for Brillouin-zone integrations. Phys. Rev. B 13 (12), 5188–5192. doi:10.1103/physrevb.13.5188

CrossRef Full Text | Google Scholar

Montero, I., Olano, L., Aguilera, L., Dávila, M. E., Wochner, U., Raboso, D., et al. (2020). Low-secondary electron emission yield under electron bombardment of microstructured surfaces, looking for multipactor effect suppression. J. Electron Spectrosc. Relat. Phenom. 241, 146822. doi:10.1016/j.elspec.2019.02.001

CrossRef Full Text | Google Scholar

Mott, N. F. (1929). The scattering of fast electrons by atomic nuclei. Proc. Roy. Soc. Lond. Ser. A, Contain. Pap. Math. Phys. Charact. 124 (794), 425–442. doi:10.1098/rspa.1929.0127

CrossRef Full Text | Google Scholar

National Institute of Standards and Technology (2022). ESTAR. available at: https://physics.nist.gov/PhysRefData/Star/Text/ESTAR.html.

Google Scholar

Patino, M. I., Wirz, R. E., Raitses, Y., and Koel, B. E. (2018). Angular, temperature, and impurity effects on secondary electron emission from Ni(110). J. Appl. Phys. 124 (9), 093301. doi:10.1063/1.5025344

CrossRef Full Text | Google Scholar

Penn, D. R. (1987). Electron mean-free-path calculations using a model dielectric function. Phys. Rev. B 35 (2), 482–486. doi:10.1103/physrevb.35.482

PubMed Abstract | CrossRef Full Text | Google Scholar

Perdew, J. P., Burke, K., and Ernzerhof, M. (1996). Generalized gradient approximation made simple. Phys. Rev. Lett. 77 (18), 3865–3868. doi:10.1103/physrevlett.77.3865

PubMed Abstract | CrossRef Full Text | Google Scholar

Petit, V., Taborelli, M., Neupert, H., Chiggiato, P., and Belhaj, M. (2019). Role of the different chemical components in the conditioning process of air exposed copper surfaces. Rev. Accel. Beams 22 (8), 083101. doi:10.1103/physrevaccelbeams.22.083101

CrossRef Full Text | Google Scholar

Ritchie, R. H., and Howie, A. (1977). Electron excitation and the optical potential in electron microscopy. Philos. Mag. J. Theor. Exp. Appl. Phys. 36 (2), 463–481. doi:10.1080/14786437708244948

CrossRef Full Text | Google Scholar

Sanville, E., Kenny, S. D., Smith, R., and Henkelman, G. (2007). Improved grid-based algorithm for Bader charge allocation. J. Comp. Chem. 28 (5), 899–908. doi:10.1002/jcc.20575

PubMed Abstract | CrossRef Full Text | Google Scholar

Schulte, S., Hartung, G., Kröger, J., Himmerlich, M., Petit, V., and Taborelli, M. (2020). Energy-resolved secondary-electron emission of candidate beam screen materials for electron cloud mitigation at the Large Hadron Collider. Phys. Rev. Accel. Beams 23 (10), 103101. doi:10.1103/physrevaccelbeams.23.103101

CrossRef Full Text | Google Scholar

Seiler, H. (1983). Secondary electron emission in the scanning electron microscope. J. Appl. Phys. 54 (11), R1–R18. doi:10.1063/1.332840

CrossRef Full Text | Google Scholar

Tang, W., Sanville, E., and Henkelman, G. (2009). A grid-based Bader analysis algorithm without lattice bias. J. Phys. Condens. Mat. 21 (8), 084204. doi:10.1088/0953-8984/21/8/084204

PubMed Abstract | CrossRef Full Text | Google Scholar

Vaughan, J. R. M. (1988). Multipactor. IEEE Trans. Electron Devices 35 (7), 1172–1180. doi:10.1109/16.3387

CrossRef Full Text | Google Scholar

Wang, Y., Xu, L., Hsu, H., Leung, T., and Lin, M. (2020). First-principles study of clean tungsten surface work function under electric field. J. Vac. Sci. Technol. B 38 (2), 022209. doi:10.1116/1.5140750

CrossRef Full Text | Google Scholar

Yu, M., and Trinkle, D. R. (2011). Accurate and efficient algorithm for Bader charge integration. J. Chem. Phys. 134 (6), 064111. doi:10.1063/1.3553716

PubMed Abstract | CrossRef Full Text | Google Scholar