Comparative investigation of fractional bioconvection and magnetohydrodynamic flow induced by hybrid nanofluids through a channel

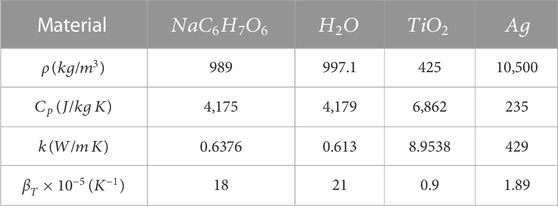
The functional effects of medications, such as those that slow down and calm the body, have been investigated for the polarized diffusion coefficient based on the subsequent increase through magnetism. This study examines generalized Mittag–Lefer kernel-based fractional derivatives in MHD Brinkman-type fluids under bioconvection that contain hybrid titanium dioxide (TiO₂) and silver (Ag) nanoparticles with water (H₂O) and sodium alginate (NaC₆H₇O₆) as the base fluids. Atangana–Baleanu (AB) and Caputo–Fabrizio (CF) fractional derivatives, which are two contemporary definitions of fractional-order derivatives with a memory effect, were used to explore the modified fractional model utilizing the Laplace transformation and certain numerical algorithms. The impacts of restrictions on various nanoparticles were investigated and graphically displayed. We observed that the volumetric fraction improvement controls the fluid velocity by slowing it down. The water-based hybrid nanofluid has a greater influence on the temperature and momentum fields than the sodium alginate-based hybrid nanofluid due to the physical characteristics of the explored nanoparticles and base fluids. Additionally, the memory effect causes a higher substantial value for the AB-fractional derivative of the velocity profile than the CF-fractional derivative.

1 Introduction

Channel flow has been applied in various industrial fields including chemical reactors in pharmacological manufacturing and thermal exchangers in energy plants. Although various natural phenomena and Newtonian actions in equal stages may be named two-phase movements, there are many related applications where the constant fluid segment displays non-Newtonian movement characteristics. In the last two decades, the impact of numerous heat transfer behaviors in the industry and engineering sectors has benefited from and been improved by nanofluid science. The development of a hybrid nanofluid is another recent advancement in nanotechnology. This new product combines at least two substances with various physical and chemical features such as heat flow and thermal conductivity. In essence, the development of a hybrid nanofluid has completely transformed this new product. Numerous researchers have become interested in nanofluids due to their thermal solid conductivity performance. Examples abound in the biomedical, biochemical, and food distribution industries (Bräuer et al., 2021). Zheng et al. (2021) explored how a vortex maker formed affected fluids and the thermal conversion of HNFs in a channel. D’Ippolito et al. (2021) evaluated the systematic scale conflict of channel movement caused by vegetation. Using the CF derivative, Haq et al. (2020) developed MHD’s fractional viscid fluid impact in a channel across a permeable surface.

The exceptional perception of nanoscience to increase the amount of heat sources has motivated researchers due to the constantly growing requirement for heat storage. For example, thermal transmission properties are claimed in fields ranging from biomedical to manufacturing industries. Improvements in thermal efficiency provide an advantage for plasma research, electronic equipment like computer chips, nuclear reactors, electricity generation, space cooling, and many others. The macroscopic fluid convection motion phenomenon, which is known as “bioconvection,” is caused by the thickness angle formed by the mass of directional swimming microorganisms. Bioconvection was a fundamental principle introduced by Plat in 1961. Bioconvection is used, among other things, in the manufacturing of biological polymers in biotechnology and biosensors and in the testing and lab equipment sectors (Platt, 1961; Asjad et al., 2021). Sisko’s three-dimensional radiative bioconvective stream was used by Ge-JiLe et al. (2021) to analyze nanofluids containing moving microorganisms. Ramzan et al. (2021) showed the occurrence of bioconvection in a three-dimensional meandering hyperbolic partially ionized magnetized nanofluid stream with Cattaneo–Christov heat flux and activation vitality. An examination of magneto-bioconvective enhancement and thermal conductivity in a nanofluid stream containing gyrotactic microorganisms was conducted by Alhussain et al. (2021). Farooq et al. (2021) adjusted Cattaneo–Christov equations and exponential space-based heat sources to account for a thermally radioactive Carreau nanofluid bioconvection flow. Yusuf et al. (2021) investigated the role of gyrotactic bacteria and entropy generation in the movement of Williamson nanofluids across an inclined plate. A Brinkman-type fluid (BTF) fractional model utilizing hybrid nanoparticles was examined by Saqib et al. (2020). Danish Ikram et al. considered the heat transfer of an exponentially moving vertical plate over a viscous fluid containing clay nanoparticles. Using a hybrid fractional operator, Asjad et al. (2020) looked into the thermophysical characteristics of clay nanofluids. Using a constant and proportional Caputo fractional operator, Ikram et al. (2021) established a fractional model of a Brinkman-type fluid transporting hybrid nanoparticles in a confined microchannel.

A specific or isolated nanomaterial might exhibit extraordinary thermophysical or rheologic properties in addition to the excellent and typical requirements for a certain use. HNF is controlled to maintain different properties despite the multiple applications. An advanced NF, which is called a hybrid nanofluid, combines “two or more distributed NPs in the base liquid.” The purpose of examining HNFs is to improve various thermal processes, such as heat transfer, highly well-organized heat conductivity, and solidity, by balancing the benefits and drawbacks of remarkable suspensions. Examples of these processes include the refrigeration of generators, cooling systems for machines, electric refrigeration, refrigeration of converters, and atomic structure refrigeration. HNFs’ capacities to improve thermal conductivity offers an opportunity to account for them in real-valued energy models. An HNF was tested over a porous surface in motion along with alumina NPs in Waini et al. (2019), and studies of the volume fraction for copper NPs were confirmed. To simulate the HNF, two NPs were included in the composite along with water. To study the mobility of HNF (Al₂O₃-CuO/H₂O), Ashwinkumar et al. (2021) used radiation passing through a vertical plate and cone. Their research focused on contrasting two different forms and the characteristics of HNF flow. Samrat et al. (2022) considered heat transmission when analyzing the movement of NF and HNF due to the stretched surface. Characteristic groundwork investigations completed on HNFs have also been conducted (Raza et al., 2019; Anuar et al., 2020; Sulochana et al., 2020; TÜRKYILMAZOĞLU, 2021; Ibraheem et al., 2022; Raza et al., 2022; Turkyilmazoglu, 2022; Zhang et al., 2022; Turkyilmazoglu and Altanji, 2023).

The field of fractional calculus is rapidly expanding due to the wide variety of processes that it can be applied to every day. Numerous definitions of fractional derivatives have been published in the literature due to the curiosity of academics. A fractional-order derivative based on an exponential function was created by Caputo–Fabrizio (CF) to address the challenges with earlier research on the singularity problem of the kernel. However, the fractional model of Caputo and Fabrizio lacks a specific kernel. This idea of fractional order has received significant attention in recent studies in the area of fractional calculus. Understanding the viscoelastic and rheologic properties of HNFs in detail are difficult due to the self-similar properties and memory-taking capacities of fractional operators. They provide a reasonable explanation for the behavior and heat efficiency of nanofluids. These operators have frequently been used to mimic and examine the specifics of various natural formations over the past few years. Fractional derivatives are widely applicable in signal processing, epidemiology, population modeling, economics, dynamic structures, fluid dynamics, electrochemistry, and many other fields. The three most fundamental standard fractional operators in fractional calculus depend on the convolution of regular derivatives and distinctive kernels. The two leading derivatives in this hierarchy are Riemann-Liouville and Caputo’s derivatives, where the first operator complicates a power-law kernel (Podlubny, 1999). Due to its widespread use, the definition of CF has been used by numerous researchers for a variety of scientific inquiries. The kernel’s non-locality, which is a difficulty in the definition of CF, was addressed by Atangana and Nieto (2015) in a new formulation. The most current explanation of fractional derivatives without these problems was given by Atangana (2016). AB derivatives are rarely used in research, and this word is brand-new. Arif et al. (2019) used this most recent concept of AB-fractional derivatives to compare these two ideas, and the current issue is also applied to CF-fractional derivatives. In addition, this study solves the well-known pair stress fluid model with an external pressure gradient in a closed-form channel. Even though they employed the Caputo and CF-fractional model, Akhtar (2016) estimated the closed-form solutions (CSF) in channels. To avoid these obstacles, Atangana and Baleanu produced a novel operator whose mathematical expansion encompasses the convolution of the regular derivative and a general kernel, which is included in the Mittag–Leffler function (Atangana and Baleanu, 2016). Currently, in perceiving the worth of fractional-order operators, an extensive range of investigators has explored real-life phenomena in fractional situations rather than in regular contexts. Asjad et al. (2022) investigated the fractional bioconvection nanofluid solution moving through a channel. Investigations on heat transfer and fluid problems were conducted using local and non-local kernel approaches by Ali et al. (2022a) and Ali et al. (2022b). Tarasov explained how a novel rebellion, “memory revolution,” occurred in present mathematical economics just because of fractional derivatives and corresponding integrals. The investigation of neurology has also been impacted by the initiation of fractional calculus (Tarasov, 2019; Riaz et al., 2022).

In the absence of fractional bioconvection, those previously mentioned were carried out by or lacking fractional approaches. However, the fundamental purpose is to combine these two fascinating topics: bioconvection and fractional operators. In the previous literature, we did not find any investigation on the focus of fractional bioconvection of an applied magnetic field on a naturally occurring Brinkman-type flow of a hybrid nanofluid over two parallel plates with CF- and AB-fractional derivative approaches. Consequently, we applied the Laplace transform method to solve the thermal transmission and fluid flow problems of bioconvection. In addition, graphical analysis was applied to present a graphical description of the diverse flow parameters.

2 Description of the problem

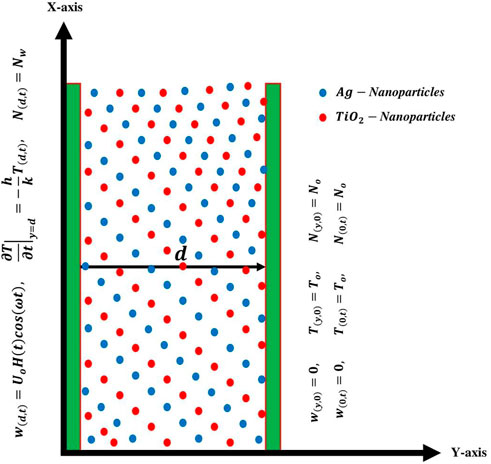
Suppose an incompressible, unsteady, and free convective Brinkman-type hybrid nanofluid moves along the path of two parallel plates with characteristics of mass diffusion and temperature gradient, as described in Figure 1. Both plates are fixed in the xy-plane at a distance d that is vertical to the y-axis and parallel to the x-axis. The whole system, including the fluid and any relevant limitations, is initially at $t=0$ in the rest position. One plate starts to move at time $t>0^{+}$ as a result of the imposed time-dependent shear force. The hybrid nanofluid made of water and sodium alginate begins to flow between the poured plates as a result of oscillations and the rise in temperature. The flowing fluid is subjected to a consistent magnetic field with an inclination angle of $\vartheta$. For this flow model, the following suppositions are used.

• The length of the parallel plates is infinite with width d.

• The poured plates are vertical to the y-axis and oriented in the x-direction.

• At $t\le 0,$ both temperature and bioconvection have constant values as $T_d$ and $N_d$, respectively.

• Different nanoparticles in the mixed hybrid nanofluid accelerate in the x-direction.

• The constant magnetic field of strength $B_o$ is applied to the flowing fluid.

FIGURE 1

FIGURE 1. Flow geometry.

By utilizing Boussinesq’s (Mayeli and Sheard, 2021) and Roseland approximations (Chu et al., 2020), the governed partial differential equations can be formulated as follows (Asjad et al., 2022):

${\rho }_{hnf}\frac{\partial w_{\left(y,t\right)}}{\partial t}+{\rho }_{hnf}{\beta }_1^{*}{w}_{\left(y,t\right)}={\mu }_{hnf}\frac{{\partial }^2{w}_{\left(y,t\right)}}{\partial y^2}-{\sigma }_{hnf}{B}_o^2\mathit{sin}\left(\theta \right)w_{\left(y,t\right)}-\frac{{\mu }_{hnf}{\phi }_{hnf}}{K}{w}_{\left(y,t\right)}+g\left({\left(\rho {\beta }_T\right)}_{hnf}\left(T_{\left(y,t\right)}-T_o\right)-\gamma \left({\rho }_m-\rho \right)\left(N_{\left(y,t\right)}-N_o\right)\right),(1)$

${\left(\rho C_p\right)}_{hnf}\frac{\partial T_{\left(y,t\right)}}{\partial t}=k_{hnf}\frac{{\partial }^2{T}_{\left(y,t\right)}}{\partial y^2},(2)$

$\frac{\partial N_{\left(y,t\right)}}{\partial t}=D\frac{{\partial }^2{N}_{\left(y,t\right)}}{\partial y^2},(3)$

where ${\rho }_{hnf},{\mu }_{hnf},{\sigma }_{hnf},{\left(\rho C_p\right)}_{hnf},k_{hnf}$ and $D$ represent the dynamic density viscosity, electrical conductivity, volumetrically thermal expansion, heat capacitance of the nanofluid, thermal conductivity, and thermal diffusion coefficient, respectively. Its corresponding boundary conditions are as follows:

$w_{\left(y,0\right)}=0,T_{\left(y,0\right)}=T_o,N_{\left(y,0\right)}=N_o;\forall y\ge 0(4)$

$w_{\left(0,t\right)}=0,T_{\left(0,t\right)}=T_o,N_{\left(0,t\right)}=N_o;y=0(5)$

$w_{\left(d,t\right)}=U_{o}H\left(t\right)\mathit{cos}\left(\omega t\right),{\left.\frac{\partial T}{\partial y}\right|}_{y=d}=-\frac{h}{k}{T}_{\left(d,t\right)},N_{\left(d,t\right)}=N_w(6)$

The initial conditions of the entire system are considered in Eq. 4 at $t=0$, where in Eq. 5, the boundary conditions are taken at $y=0$ in which the whole system is in a rest position for $y=0$, where in the last boundary condition (6) at $y=d$, the rate of shear stress and the Newtonian heating effect are considered with the constant bioconvection parameter. Now that the following dimensionless variables have been included, the linked governed equations may not be analyzed with the dimension of influence of all influencing parameters as follows:

$w^{*}=\frac{d}{{\nu }_f}w,t^{*}=\frac{\nu t}{d^2},y^{*}=\frac{y}{d},T^{*}=\frac{T_{\left(y,t\right)}-T_o}{T_w-T_o},N^{*}=\frac{N_{\left(y,t\right)}-N_o}{N_w-N_o},{\lambda }_{hnf}=\frac{k_{hnf}}{k_f},$

$Sc=\frac{\nu }{D},M=\frac{{\sigma }_f{d}^2{B}_o^2}{{\mu }_f},Gr=\frac{g{\beta }_T{d}^3\left(T_w-T_o\right)}{{\nu }^2},Ra=\frac{\gamma \left({\rho }_m-\rho \right)\left(N_w-N_o\right)}{{\rho }_f{\left({\beta }_T\right)}_f\left(T_w-T_o\right)},N=\frac{Gm}{Gr},$

$K_{eff}=\frac{\nu \phi }{K^{*}{U}_o^2},\mathit{Pr}=\frac{{\mu }_f{C}_p}{k_f},Gm=\frac{g{\beta }_C\left(N_w-N_o\right)d^3}{{\nu }^2},{\varphi }_o=\left(1-\phi \right)+\phi \frac{{\rho }_s}{{\rho }_f},$

${\varphi }_1=\frac{1}{{\left(1-\phi \right)}^{2.5}},{\varphi }_2=1+\frac{3\left(\frac{{\sigma }_s}{{\sigma }_f}-1\right)\phi }{\left(\frac{{\sigma }_s}{{\sigma }_f}+2\right)-\left(\frac{{\sigma }_s}{{\sigma }_f}-1\right)\phi },{\varphi }_3=\left(1-\phi \right)+\phi \frac{{\left(\rho {\beta }_T\right)}_s}{{\left(\rho {\beta }_T\right)}_f},$

${\mathrm{\Lambda }}_o=\left(1-\phi \right)+\phi \frac{{\left(\rho {\beta }_C\right)}_s}{{\left(\rho {\beta }_T\right)}_f},{\mathrm{\Lambda }}_1=\frac{{\nu }_f}{D_{hnf}},$

and utilizing the aforementioned none-dimensional constraints in the governed equations and conditions (1)–(6), one can obtain the following results by adjusting the abovementioned dimensionless variables while ignoring the ″*″ symbols:

${\varphi }_o\frac{\partial w_{\left(y,t\right)}}{\partial t}={\varphi }_1\frac{{\partial }^2{w}_{\left(y,t\right)}}{\partial y^2}-{\beta }_1{w}_{\left(y,t\right)}-\left({\varphi }_{2}Msin\left(\theta \right)+K_{eff}\right)w_{\left(y,t\right)}+Gr\left({\varphi }_3{T}_{\left(y,t\right)}-Ra{N}_{\left(y,t\right)}\right),(7)$

${\mathrm{\Lambda }}_o\frac{\partial T_{\left(y,t\right)}}{\partial t}=\frac{{\partial }^2{T}_{\left(y,t\right)}}{\partial y^2},(8)$

${\mathrm{\Lambda }}_1\frac{\partial N_{\left(y,t\right)}}{\partial t}=\frac{{\partial }^2{N}_{\left(y,t\right)}}{\partial y^2},(9)$

with consistent dimensionless circumstances

$w_{\left(y,0\right)}=0,T_{\left(y,0\right)}=0,N_{\left(y,0\right)}=0,(10)$

$w_{\left(0,t\right)}=0,T_{\left(0,t\right)}=0,N_{\left(0,t\right)}=0,(11)$

$w_{\left(d,t\right)}=H\left(t\right)\mathit{cos}\left(\omega t\right),{\left.\frac{\partial T}{\partial t}\right|}_{y=d}=-\left(1+T_{\left(d,t\right)}\right),N_{\left(d,t\right)}=1,(12)$

where $M,Gr,{\beta }_1,K_{eff},Gm,Ra$ stand for the applied magnetic field constraint, heat Grashof number, Brinkman fluid parameter, porosity, mass Grashof number, and the dimensionless bioconvection Rayleigh number, respectively. The hybrid nanofluid model, base material, and solid nanoparticles’ thermal characteristics are listed in Tables 1 and 2.

TABLE 1

TABLE 1. Quantities of hybrid nanofluids’ thermophysical properties.

TABLE 2

TABLE 2. Thermal features of nanoparticles and regular fluids.

3 Basic preliminaries

In the fractional modeling of the set, as mentioned previously for the governing equations, the ABC (Atangana and Baleanu, 2016) and CF (Caputo and Fabrizio, 2015) formulations are employed, and these temporal derivatives are specified as follows:

${}_{ABC}{\mathfrak{D}}_t^{\beta }f\left(y,t\right)=\frac{1}{1-\beta }\underset{0}{\overset{t}{{\displaystyle \int }}}{E}_{\beta }\left(\frac{\beta {\left(t-\tau \right)}^{\beta }}{1-\beta }\right)\frac{\partial f\left(y,\tau \right)}{\partial \tau }d\tau ,$

with its LT

$\mathcal{L}{\{}^{ABC}{\mathfrak{D}}_t^{\beta }f\left(y,t\right)\}=\frac{q^{\beta }\mathcal{L}\left\{f\left(y,t\right)\right\}-q^{\beta -1}f\left(y,0\right)}{\left(1-\beta \right)q^{\beta }+\beta }.(13)$

The mathematical form of the CF-fractional derivative is (Caputo and Fabrizio, 2015)

${}_{CF}{\mathfrak{D}}_t^{\alpha }g\left(y,t\right)=\frac{1}{1-\alpha }\underset{0}{\overset{t}{{\displaystyle \int }}}\mathit{exp}\left(\frac{\alpha \left(1-\tau \right)}{1-\alpha }\right)g^{\prime }\left(\tau \right)d\tau ,$

and the LT of the CF-fractional derivative is

$\mathcal{L}{\{}^{CF}{\mathfrak{D}}_t^{\alpha }g\left(y,t\right)\}=\frac{s\mathcal{L}\left\{g\left(y,t\right)\right\}-g\left(y,0\right)}{\left(1-\alpha \right)s+\alpha }.(14)$

4 Solution with the AB-fractional derivative

4.1 Solution of the temperature profile

The solution of the non-dimensional equation of the temperature field can be represented as follows in the sense of the AB-time fractional derivative:

${\mathrm{\Lambda }}_o^{ABC}{\mathfrak{D}}_t^{\beta }{T}_{\left(y,t\right)}=\frac{{\partial }^2{T}_{\left(y,t\right)}}{\partial y^2},$

with

${\left.\frac{\partial T}{\partial y}\right|}_{y=d}=-\left(1+T_{\left(1,t\right)}\right),T_{\left(0,t\right)}=0.$

The result of the temperature field can be found by applying the Laplace transformation to the abovementioned equation and utilizing the relevant conditions as follows:

${\overline{T}}_{\left(y,q\right)}=\frac{1}{q\left(\sqrt{\frac{{\mathrm{\Lambda }}_o{q}^{\beta }}{\left(1-\beta \right)q^{\beta }+\beta }}-1\right)}\frac{\mathit{Sinh}\left[y\sqrt{\frac{{\mathrm{\Lambda }}_o{q}^{\beta }}{\left(1-\beta \right)q^{\beta }+\beta }}\right]}{\mathit{Sinh}\left[\sqrt{\frac{{\mathrm{\Lambda }}_o{q}^{\beta }}{\left(1-\beta \right)q^{\beta }+\beta }}\right]}.(15)$

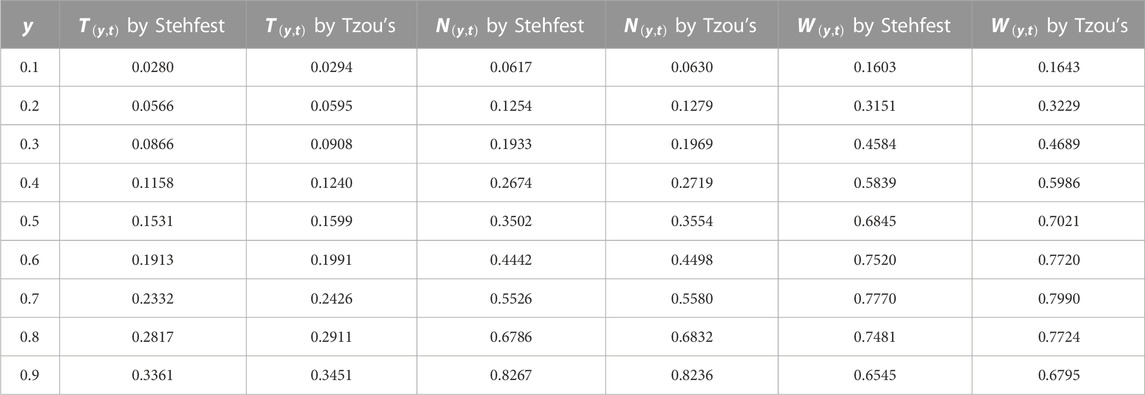
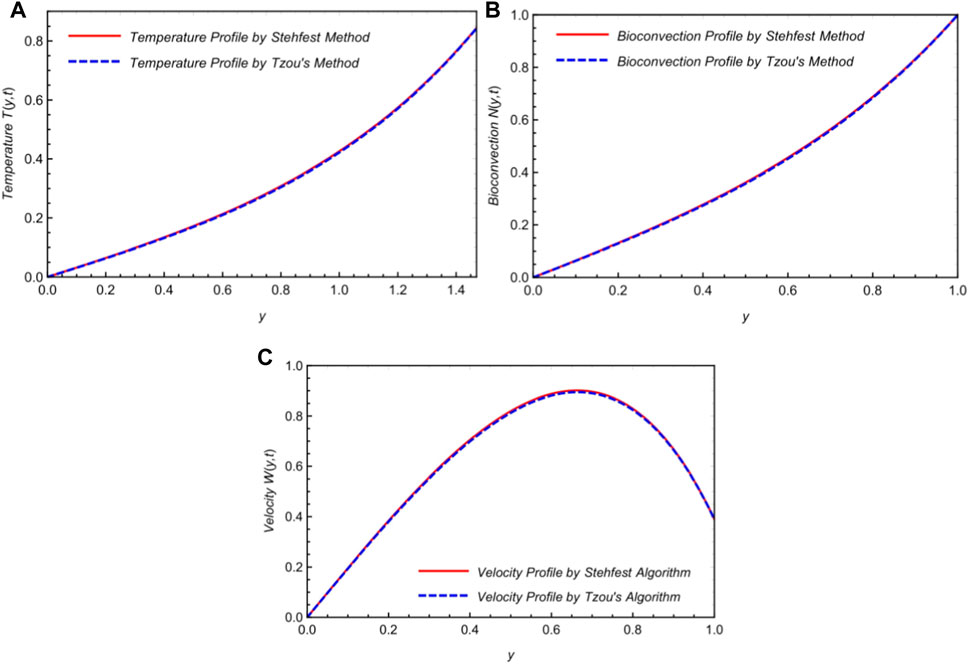
The Laplace inverse of the solution, as described previously, will be numerically evaluated using Stehfest and Tzou’s methods in Tables 3–5.

TABLE 3

TABLE 3. Numerical analysis of numerical algorithms at different times.

TABLE 4

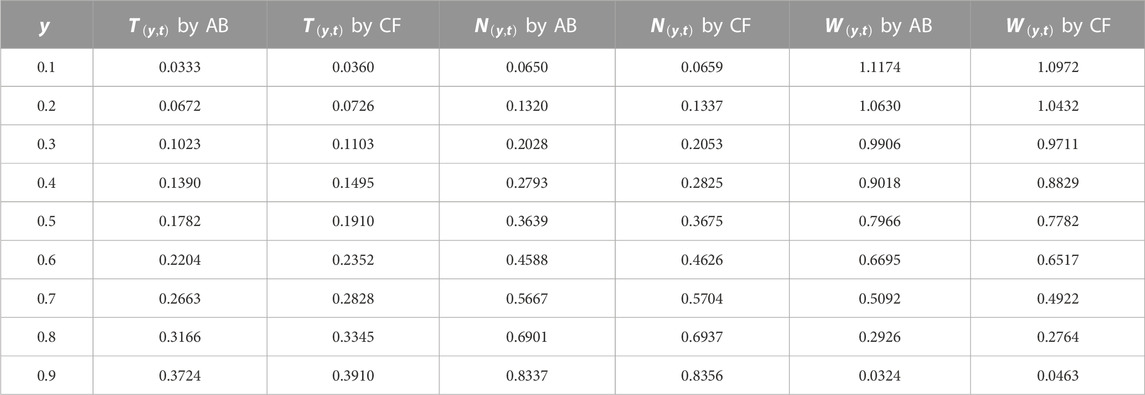
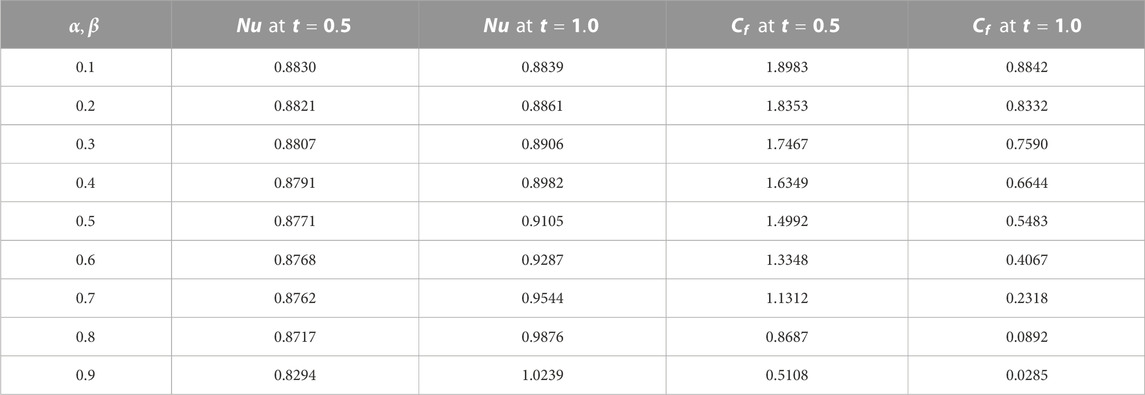
TABLE 4. Numerical analysis of governed solutions with the AB- and CF-fractional derivatives at t = 0.5

TABLE 5

TABLE 5. Numerical analysis of the Nusselt number and skin friction coefficient at different times.

4.2 Solution of the bioconvection profile

In terms of the AB-time fractional derivative, the solution of a non-dimensional equation of the bioconvection profile may be attained by employing the Laplace transformation on the governed equations in terms of the AB-time fractional derivative, and we get

${\mathrm{\Lambda }}_1\left(\frac{q^{\beta }}{\left(1-\beta \right)q^{\beta }+\beta }\right){\overline{N}}_{\left(y,q\right)}=\frac{{\partial }^2{\overline{N}}_{\left(y,q\right)}}{\partial y^2},(16)$

with the corresponding conditions

${\overline{N}}_{\left(1,q\right)}=\frac{1}{q},{\overline{N}}_{\left(0,q\right)}=0.$

By using the aforementioned conditions and Eq. 16, the solution of the bioconvection profile can be derived as

${\overline{N}}_{\left(y,q\right)}=\frac{1}{q}\frac{Sinhy\left[\sqrt{\frac{{\mathrm{\Lambda }}_1{q}^{\beta }}{\left(1-\beta \right)q^{\beta }+\beta }}\right]}{\mathit{Sinh}\left[\sqrt{\frac{{\mathrm{\Lambda }}_1{q}^{\beta }}{\left(1-\beta \right)q^{\beta }+\beta }}\right]}.(17)$

The Laplace inverse of the aforementioned Eq. 17 will be analyzed numerically in Tables 3–5 with numerical algorithms.

4.3 Solution of the velocity profile

For the solution of the velocity profile by employing the LT on the non-dimensional governed equation of the velocity field in Eq. 7,

$\frac{{\partial }^2{\overline{w}}_{\left(y,q\right)}}{\partial y^2}-\frac{1}{{\varphi }_1}\left({\varphi }_{2}Msin\left(\theta \right)+K_{eff}+{\beta }_1+{\varphi }_{o}q\right){\overline{w}}_{\left(y,q\right)}=-\frac{Gr}{{\varphi }_1}\left({\varphi }_3{\overline{T}}_{\left(y,q\right)}-Ra{\overline{N}}_{\left(y,q\right)}\right),(18)$

with

${\overline{w}}_{\left(d,q\right)}=\frac{q}{q^2+{\omega }^2}$ and ${\overline{w}}_{\left(0,q\right)}=0.$With the help of the aforementioned conditions, the solution of the momentum profile is as follows:

$\begin{array}{c}{\overline{w}}_{\left(y,q\right)}=\frac{\mathit{Sinh}\left(y\sqrt{\frac{1}{{\varphi }_1}\left({\varphi }_{2}Msin\left(\theta \right)+K_{eff}+{\beta }_1+{\varphi }_{o}q\right)}\right)}{\mathit{Sinh}\left(\sqrt{\frac{1}{{\varphi }_1}\left({\varphi }_{2}Msin\left(\theta \right)+K_{eff}+{\beta }_1+{\varphi }_{o}q\right)}\right)}\hfill \\ (\frac{{\varphi }_{3}Gr}{q{\varphi }_1\left(\sqrt{{\mathrm{\Lambda }}_o{q}^{\beta }}-\sqrt{\left(1-\beta \right)q^{\mathrm{\beta }}+\mathrm{\beta }}\right)}\frac{\sqrt{\left(1-\beta \right)q^{\mathrm{\beta }}+\mathrm{\beta }}}{\frac{{\mathrm{\Lambda }}_o{q}^{\beta }}{\left(1-\beta \right)q^{\mathrm{\beta }}+\mathrm{\beta }}-\frac{1}{{\varphi }_1}\left({\varphi }_{2}Msin\left(\theta \right)+K_{eff}+{\beta }_1+{\varphi }_{o}q\right)}+\frac{Gm}{q{\varphi }_1}\frac{1}{\frac{{\mathrm{\Lambda }}_1{q}^{\beta }}{\left(1-\beta \right)q^{\mathrm{\beta }}+\mathrm{\beta }}-\frac{1}{{\varphi }_1}\left({\varphi }_{2}Msin\left(\theta \right)+K_{eff}+{\beta }_1+{\varphi }_{o}q\right)}\hfill \\ +\frac{q}{q^2+{\omega }^2})-\frac{{\varphi }_{3}Gr}{q{\varphi }_1\left(\sqrt{{\mathrm{\Lambda }}_o{q}^{\beta }}-\sqrt{\left(1-\beta \right)q^{\mathrm{\beta }}+\mathrm{\beta }}\right)}\frac{\sqrt{\left(1-\beta \right)q^{\mathrm{\beta }}+\mathrm{\beta }}}{\frac{{\mathrm{\Lambda }}_o{q}^{\beta }}{\left(1-\beta \right)q^{\mathrm{\beta }}+\mathrm{\beta }}-\frac{1}{{\varphi }_1}\left({\varphi }_{2}Msin\left(\theta \right)+K_{eff}+{\beta }_1+{\varphi }_{o}q\right)}\frac{\mathit{Sinh}\left(y\sqrt{\frac{{\mathrm{\Lambda }}_o{q}^{\beta }}{\left(1-\beta \right)q^{\mathrm{\beta }}+\mathrm{\beta }}}\right)}{\mathit{Sinh}\left(\sqrt{\frac{{\mathrm{\Lambda }}_o{q}^{\beta }}{\left(1-\beta \right)q^{\mathrm{\beta }}+\mathrm{\beta }}}\right)}+\frac{Gm}{q{\varphi }_1}\frac{1}{\frac{{\mathrm{\Lambda }}_1{q}^{\beta }}{\left(1-\beta \right)q^{\mathrm{\beta }}+\mathrm{\beta }}-\frac{1}{{\varphi }_1}\left({\varphi }_{2}Msin\left(\theta \right)+K_{eff}+{\beta }_1+{\varphi }_{o}q\right)}\frac{\mathit{Sinh}\left(y\sqrt{\frac{{\mathrm{\Lambda }}_1{q}^{\beta }}{\left(1-\beta \right)q^{\mathrm{\beta }}+\mathrm{\beta }}}\right)}{\mathit{Sinh}\left(\sqrt{\frac{{\mathrm{\Lambda }}_1{q}^{\beta }}{\left(1-\beta \right)q^{\mathrm{\beta }}+\mathrm{\beta }}}\right)}.\hfill \end{array}(19)$

5 Solution with the CF-fractional derivative

5.1 Solution of the temperature field

The following representation shows the evaluation of the non-dimensional temperature field solution using the CF-time fractional derivative

${\mathrm{\Lambda }}_o{}_{CF}{\mathfrak{D}}_t^{\alpha }{T}_{\left(y,t\right)}=\frac{{\partial }^2{T}_{\left(y,t\right)}}{\partial y^2}$

with

${\left.\frac{\partial T}{\partial y}\right|}_{y=d}=-\left(1+T_{\left(1,t\right)}\right),T_{\left(0,t\right)}=0.$

The solution of the temperature field will be obtained by applying Laplace to the preceding equation and employing the appropriate conditions as follows:

${\overline{T}}_{\left(y,s\right)}=\frac{\sqrt{\left(1-\alpha \right)s+\alpha }}{s\left(\sqrt{{\mathrm{\Lambda }}_{o}s}-\sqrt{\left(1-\alpha \right)s+\alpha }\right)}\frac{\mathit{Sinh}\left[y\sqrt{\frac{{\mathrm{\Lambda }}_o{\mathrm{b}}_{1}s}{1+\left({\mathrm{b}}_1-1\right)s}}\right]}{\mathit{Sinh}\left[\sqrt{\frac{{\mathrm{\Lambda }}_o{\mathrm{b}}_{1}s}{1+\left({\mathrm{b}}_1-1\right)s}}\right]}.(20)$

Using Stehfest and Tzou’s techniques in Tables 3–5, the Laplace inverse of the aforementioned solution will be numerically examined.

5.2 Solution of the bioconvection field

By using the Laplace transformation on the guided equations in terms of the CF-time fractional derivative, we gain the solution of a non-dimensional equation of the bioconvection profile as follows:

${\mathrm{\Lambda }}_1\left(\frac{s}{\left(1-\alpha \right)s+\alpha }\right){\overline{N}}_{\left(y,s\right)}=\frac{{\partial }^2{\overline{N}}_{\left(y,s\right)}}{\partial y^2},$

with the following conditions

${\overline{N}}_{\left(1,s\right)}=\frac{1}{s},{\overline{N}}_{\left(0,s\right)}=0.$

By using the aforementioned conditions, the solution of the bioconvection profile in terms of the CF-fractional derivative can be derived as follows:

${\overline{N}}_{\left(y,s\right)}=\frac{1}{s}\frac{Sinhy\left[\sqrt{\frac{{\mathrm{\Lambda }}_1{\mathrm{b}}_{1}s}{1+\left({\mathrm{b}}_1-1\right)s}}\right]}{\mathit{Sinh}\left[\sqrt{\frac{{\mathrm{\Lambda }}_1{\mathrm{b}}_{1}s}{1+\left({\mathrm{b}}_1-1\right)s}}\right]}.(21)$

The Laplace inverse of Eq. 21 will be numerically analyzed using the techniques in Tables 3–5.

5.3 Solution of the velocity profile

The solution of the velocity profile is obtained by employing the LT on the non-dimensional governed equation of the velocity field (Eq. 7):

${\varphi }_1\frac{{\partial }^2{\overline{w}}_{\left(y,s\right)}}{\partial y^2}-\left({\beta }_1+{\varphi }_{o}s\right){\overline{w}}_{\left(y,s\right)}-\left({\varphi }_{2}Msin\left(\theta \right)+K_{eff}\right){\overline{w}}_{\left(y,s\right)}+Gr\left({\varphi }_3{\overline{T}}_{\left(y,s\right)}-Ra{\overline{N}}_{\left(y,s\right)}\right)=0,(22)$

with

${\overline{w}}_{\left(d,s\right)}=\frac{s}{s^2+{\omega }^2}$ and ${\overline{w}}_{\left(0,s\right)}=0$

$\begin{array}{c}{\overline{w}}_{\left(y,s\right)}=\frac{\mathit{Sinh}\left(y\sqrt{\frac{1}{{\varphi }_1}\left({\varphi }_{2}Msin\left(\theta \right)+K_{eff}+{\mathrm{\Theta }}_{1}s\right)}\right)}{\mathit{Sinh}\left(\sqrt{\frac{1}{{\varphi }_1}\left({\varphi }_{2}Msin\left(\theta \right)+K_{eff}+{\mathrm{\Theta }}_{1}s\right)}\right)}\hfill \\ \left(\frac{{\varphi }_{3}Gr}{s{\varphi }_1\left(\sqrt{\frac{{\mathrm{\Lambda }}_o\mathrm{s}}{\left(1-\alpha \right)\mathrm{s}+\mathrm{\alpha }}}-1\right)}\frac{1}{\frac{{\mathrm{\Lambda }}_o\mathrm{s}}{\left(1-\alpha \right)\mathrm{s}+\mathrm{\alpha }}-\frac{1}{{\varphi }_1}\left({\varphi }_{2}Msin\left(\theta \right)+K_{eff}+{\mathrm{\Theta }}_{1}s\right)}+\frac{Gm}{s{\varphi }_1}\frac{1}{\frac{{\mathrm{\Lambda }}_1\mathrm{s}}{\left(1-\alpha \right)\mathrm{s}+\mathrm{\alpha }}-\frac{1}{{\varphi }_1}\left({\varphi }_{2}Msin\left(\theta \right)+K_{eff}+{\mathrm{\Theta }}_{1}s\right)}+\frac{s}{s^2+{\omega }^2}\right)\hfill \\ -\frac{{\varphi }_{3}Gr}{s{\varphi }_1\left(\sqrt{\frac{{\mathrm{\Lambda }}_o\mathrm{s}}{\left(1-\alpha \right)\mathrm{s}+\mathrm{\alpha }}}-1\right)}\frac{1}{\frac{{\mathrm{\Lambda }}_o\mathrm{s}}{\left(1-\alpha \right)\mathrm{s}+\mathrm{\alpha }}-\frac{1}{{\varphi }_1}\left({\varphi }_{2}Msin\left(\theta \right)+K_{eff}+{\mathrm{\Theta }}_{1}s\right)}\frac{\mathit{Sinh}\left(y\sqrt{\frac{{\mathrm{\Lambda }}_o\mathrm{s}}{\left(1-\alpha \right)\mathrm{s}+\mathrm{\alpha }}}\right)}{\mathit{Sinh}\left(\sqrt{\frac{{\mathrm{\Lambda }}_o\mathrm{s}}{\left(1-\alpha \right)\mathrm{s}+\mathrm{\alpha }}}\right)}+\frac{Gm}{s{\varphi }_1}\frac{1}{\frac{{\mathrm{\Lambda }}_1\mathrm{s}}{\left(1-\alpha \right)\mathrm{s}+\mathrm{\alpha }}-\frac{1}{{\varphi }_1}\left({\varphi }_{2}Msin\left(\theta \right)+K_{eff}+{\mathrm{\Theta }}_{1}s\right)}\frac{\mathit{Sinh}\left(y\sqrt{\frac{{\mathrm{\Lambda }}_1\mathrm{s}}{\left(1-\alpha \right)\mathrm{s}+\mathrm{\alpha }}}\right)}{\mathit{Sinh}\left(\sqrt{\frac{{\mathrm{\Lambda }}_1\mathrm{s}}{\left(1-\alpha \right)\mathrm{s}+\mathrm{\alpha }}}\right)}.\hfill \end{array}(23)$

Analyzing the results of the momentum, concentration, and temperature profiles is difficult. We also employed numerical approaches for the Laplace inverse, specifically Stehfest and Tzou’s numerical schemes, as numerous authors have previously performed. The mathematical formulations of these algorithms (Raza et al., 2021a; Raza et al., 2021b; Guo et al., 2021) can be characterized as

$U\left(y,t\right)=\frac{\mathit{ln}\left(2\right)}{t}{\displaystyle \sum }_{n=1}^N{v}_n\overline{U}\left(y,n\frac{\mathit{ln}\left(2\right)}{t}\right),$

$v_n={\left(-1\right)}^{n+\frac{N}{2}}{\displaystyle \sum }_{r=\left[\frac{q+1}{2}\right]}^{\mathit{min}\left(q,\frac{N}{2}\right)}\frac{r^{\frac{N}{2}}\left(2r\right)!}{\left(\frac{N}{2}-r\right)!r!\left(r-1\right)!\left(q-r\right)!\left(2r-q\right)!},$

and

$U\left(y,t\right)=\frac{e^{4.7}}{t}\left[\frac{1}{2}\overline{U}\left(r,\frac{4.7}{t}\right)+Re\left\{{\displaystyle \sum }_{j=1}^N{\left(-1\right)}^k\overline{U}\left(r,\frac{4.7+k\pi i}{t}\right)\right\}\right].$

6 Discussion of the results

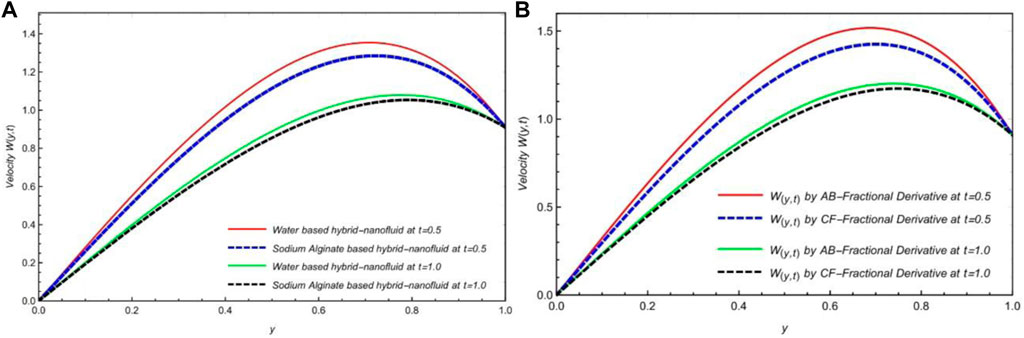
Bioconvection is investigated by employing the combined effects of porosity and the applied magnetic field on a naturally occurring Brinkman-type flow of a viscous and incompressible HNF (Ag-TiO₂-H₂O and Ag-TiO₂-C₆H₉NaO₇) over two parallel plates. The thermal transmission and fluid flow model is fractionalized with two fractional techniques (AB- and CF-fractional derivatives). The Laplace transformation approach is utilized to solve the governing equations. The impact of different constraints has been analyzed graphically with their ranges as follows: $0.1<\alpha ,\beta <0.9;0.01<\phi <0.04;0.1<K_{eff}<2.0;4.0<Gr<12.0;2.0<Gm<10;0.5<M<2.0;0<\theta <\frac{\pi }{2};\mathrm{a}\mathrm{n}\mathrm{d}0.5<{\beta }_1<2.5$. Finally, graphical representations are applied to clarify the physical impacts of flow parameters in Figures 2–14.

FIGURE 2

FIGURE 2. $N_{\left(y,t\right)}$ due to variation in fractional parameters with $\phi =0.02\mathrm{a}\mathrm{n}\mathrm{d}t=0.8$.

FIGURE 3

FIGURE 3. $T_{\left(y,t\right)}$ due to variation in fractional parameters with $\phi =0.02\mathrm{a}\mathrm{n}\mathrm{d}t=0.8$.

FIGURE 4

FIGURE 4. $W_{\left(y,t\right)}$ due to variation in $\alpha ,\beta$ with $\phi =0.02,M=1.65,Ra=1.2,K_{eff}=0.7,Gr=8.0,Gm=6.3,{\beta }_1=1.5,\theta =\pi /4,\mathrm{a}\mathrm{n}\mathrm{d}t=0.8$.

FIGURE 5

FIGURE 5. $W_{\left(y,t\right)}$ due to variation in $\phi$ with $\alpha ,\beta =0.5,M=1.65,Ra=1.2,K_{eff}=0.7,Gr=8.0,Gm=6.3,{\beta }_1=1.5,\theta =\pi /4,\mathrm{a}\mathrm{n}\mathrm{d}t=0.8$.

FIGURE 6

FIGURE 6. $W_{\left(y,t\right)}$ due to variation in $K_{eff}$ with $\alpha ,\beta =0.5,\phi =0.02,M=1.65,Ra=1.2,Gr=8.0,Gm=6.3,{\beta }_1=1.5,\theta =\pi /4,\mathrm{a}\mathrm{n}\mathrm{d}t=0.8$.

FIGURE 7

FIGURE 7. $W_{\left(y,t\right)}$ due to variation in $Gr$ with $\alpha ,\beta =0.5,\phi =0.02,M=1.65,Ra=1.2,K_{eff}=0.7,Gm=6.3,{\beta }_1=1.5,\theta =\pi /4,\mathrm{a}\mathrm{n}\mathrm{d}t=0.8$.

FIGURE 8

FIGURE 8. $W_{\left(y,t\right)}$ due to variation in $Gm$ with $\alpha ,\beta =0.5,\phi =0.02,M=1.65,Ra=1.2,K_{eff}=0.7,Gr=8.0,{\beta }_1=1.5,\theta =\pi /4,\mathrm{a}\mathrm{n}\mathrm{d}t=0.8$.

FIGURE 9

FIGURE 9. $W_{\left(y,t\right)}$ due to variation in $M$ with $\alpha ,\beta =0.5,\phi =0.02,Ra=1.2,K_{eff}=0.7,Gr=8.0,Gm=6.3,{\beta }_1=1.5,\theta =\pi /4,\mathrm{a}\mathrm{n}\mathrm{d}t=0.8$.

FIGURE 10

FIGURE 10. $W_{\left(y,t\right)}$ due to variation in $\theta$ with $\alpha ,\beta =0.5,\phi =0.02,M=1.65,Ra=1.2,K_{eff}=0.7,Gr=8.0,Gm=6.3,{\beta }_1=1.5,\mathrm{a}\mathrm{n}\mathrm{d}t=0.8$.

FIGURE 11

FIGURE 11. $W_{\left(y,t\right)}$ due to variation in ${\beta }_1$ with $\alpha ,\beta =0.5,\phi =0.02,M=1.65,Ra=1.2,K_{eff}=0.7,Gr=8.0,Gm=6.3,\theta =\pi /4,\mathrm{a}\mathrm{n}\mathrm{d}t=0.8$.

FIGURE 12

FIGURE 12. Comparison of $W_{\left(y,t\right)}$ for AB- and CF-fractional derivatives at $\left(\mathbf{A}\right)t=0.5$ and $\left(\mathbf{B}\right)t=1.0$.

FIGURE 13

FIGURE 13. Comparison of governed equations for different numerical schemes.

FIGURE 14

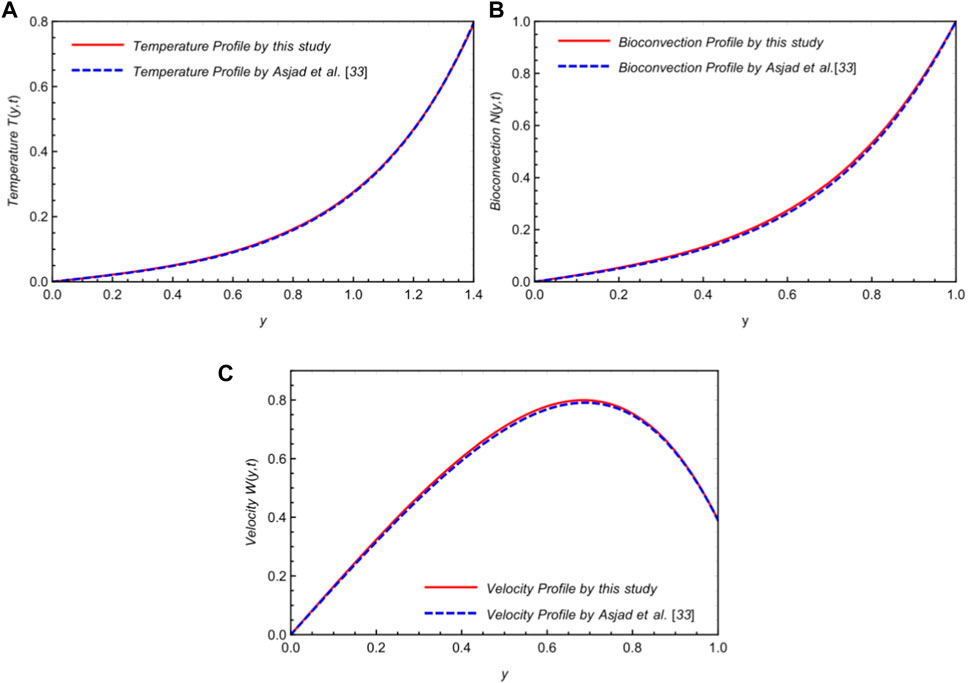
FIGURE 14. Comparison of the validity of governed equations with the attained results of Asjad et al. (2022).

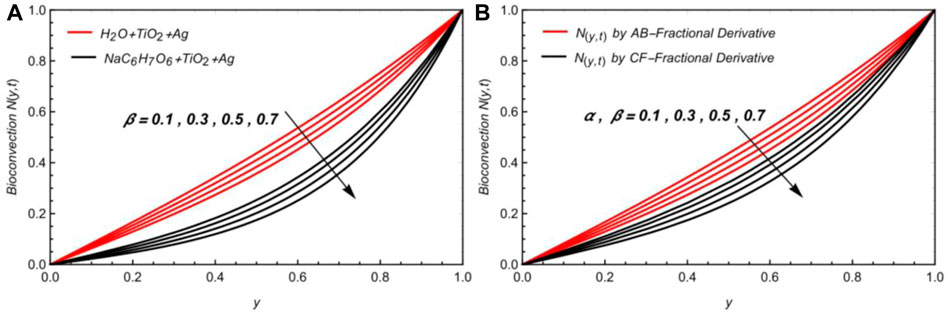
Figure 2A illustrates the influence of the fractional parameter β on bioconvection. The growing value of β causes a decline in bioconvection. This results in a decrease in bioconvection as the boundary layer enlarges. Figure 2B shows the effects of $\alpha ,\beta$ and both AB and CF-fractional operators on bioconvection, and we noted that bioconvection is also reduced by increasing the fractional parameters $\alpha$ and $\beta$. Moreover, the effect of the AB derivative approach is higher than the CF derivative approach, which is due to the different kernels (Mittage–Leffler and exponential-based kernels) of both fractional operators. In fluid mechanics, we usually see that a fractional method is better for controlling the boundary layer viscosity of fluid characteristics. In addition, we found that compared to a silver–titanium dioxide sodium alginate HNF, the bioconvection profile for HNF based on water and silver titanium dioxide has a comparatively larger impact.

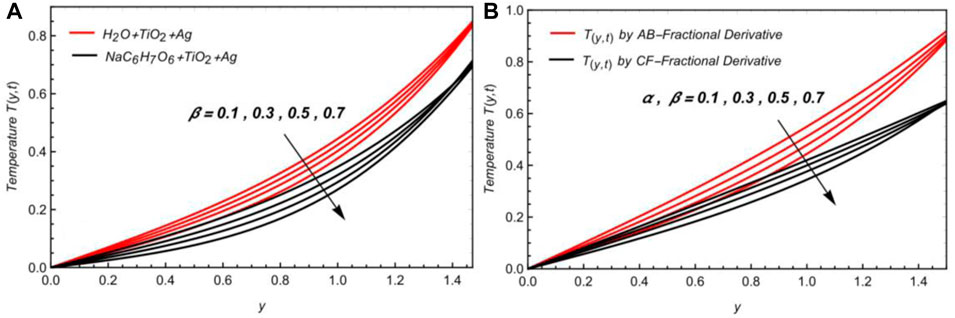
Figure 3A shows that the temperature field declined by increasing β. As the boundary layer becomes extensive, the temperature reduces, which is expected. Figure 3B shows the effects of $\alpha ,\beta$ and both AB and CF-fractional operators on the temperature field and notes that the thermal profile is also reduced by increasing fractional parameters $\alpha$ and $\beta$. Furthermore, the AB derivative approach has a more substantial impact than the CF approach, which is also a result of the different kernels used by the relevant fractional operators (Mittage–Leffler and exponential-based kernels). Additionally, we discovered that the heat profile for silver–titanium dioxide sodium alginate HNF has a substantially less significant impact than the temperature profile for water–silver–titanium dioxide-based HNF.

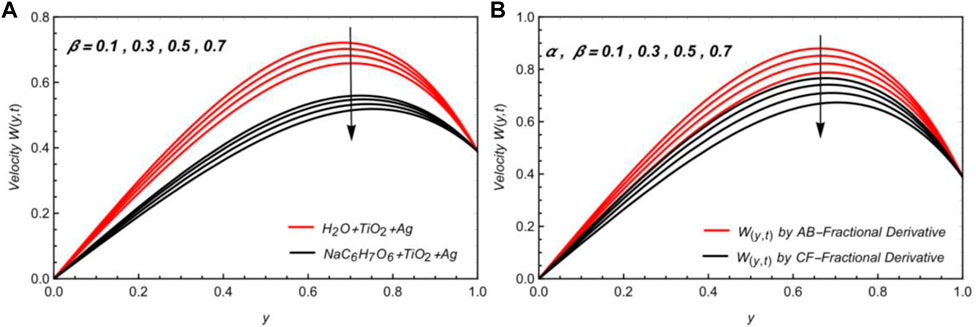
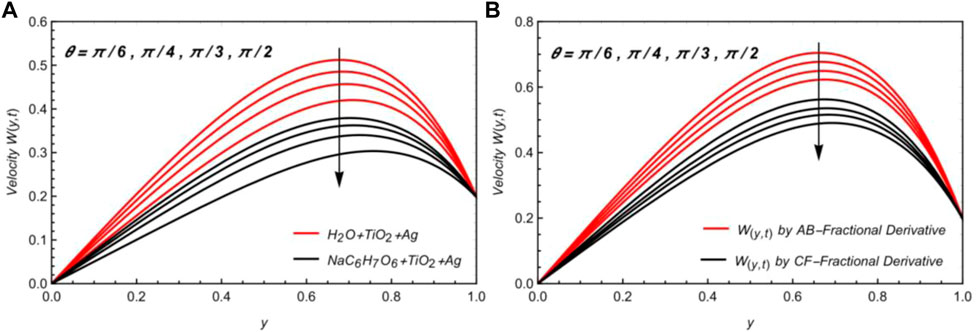
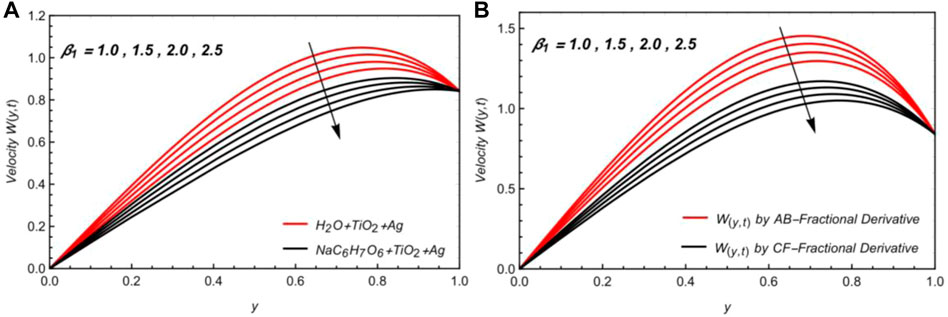
Figure 4A shows that the velocity profile is reduced by increasing β, which is due to the effect of the Mittage–Leffler kernel. Figure 4B shows the effects of $\alpha ,\beta$ and both AB and CF-fractional operators on the velocity profile, and the velocity profile is also reduced by increasing the fractional parameters $\alpha$ and $\beta$. This is because as the boundary layer widens, bioconvection and thermal and momentum fields decrease. Typically, a fractional method is preferable in fluid dynamics for adjusting the boundary layer thickness of the fluid characteristics. Furthermore, the effect of the AB approach is higher than the CF approach, which is also due to the different kernels of involved fractional operators. Additionally, we detected that the velocity profile for water–silver–titanium dioxide-based HNF has a relatively more substantial effect than silver–titanium dioxide sodium alginate HNF. The consequence of HNF is represented in Figures 5A, B. The velocity is reduced for a more considerable value of $\phi$. Actually, for greater $\phi ,$ the velocity is lessened due to the dominance of viscous effects. It was found that the temperature might rise with larger $\phi$ values and velocity-indicated drops. In the velocity field, the nanofluid density is significant. When the base fluid and nanoparticles are combined, the resulting hybrid nanofluids become thicker, which reduces the velocity and increases the temperature.

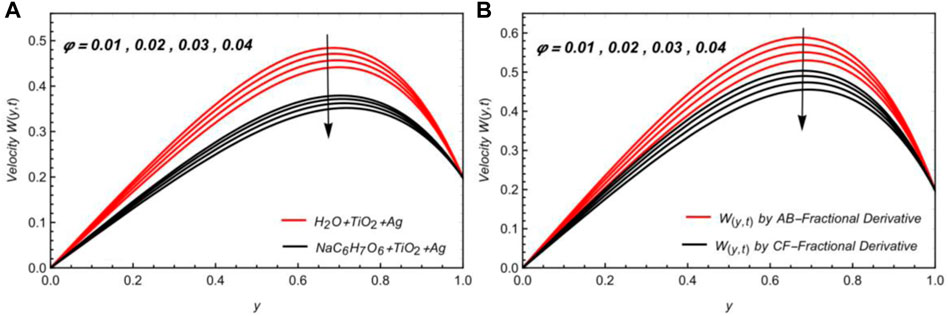
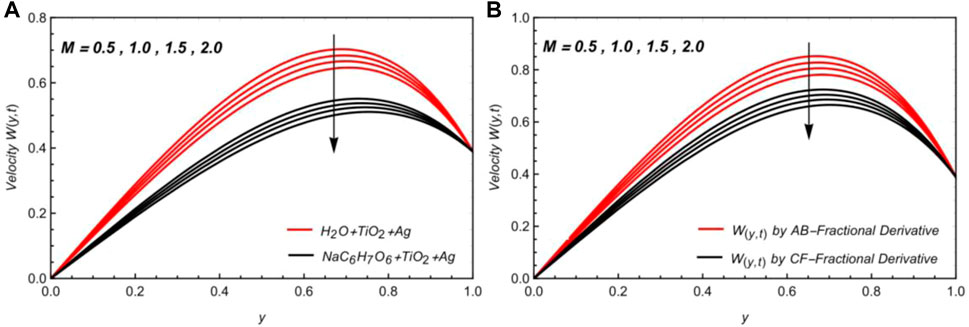
Figures 6A, B represent the velocity diagrams to understand the influence of $K_{eff}$. The velocity displays a lessening trend for larger values of $K_{eff}$. When the holes in a porous media are incredibly sufficient, the porous medium’s resistance can be disregarded. Consequently, the velocity increases as the porous surface develops resistance to the liquid. The impact of $Gr$ is shown in Figures 7A, B, and it was revealed that growing $Gr$ (more bouncy influence) boots the fluid speed. Since the buoyancy forces increase as Gr rises, the fluid velocity also rises. The velocity is also increased with $Gm,$ as observed in 8a and b. A higher Gm improves the concentration gradient, which raises the buoyant forces, and therefore, the fluid flow rises. Figures 9A, B indicate that the velocity is decreased as we increase the values of $M$. Physically, it responds to the drag force, which affects the velocity that faces the fluid speed. This is true for large values of M because M strengthens the Lorentz forces, which tend to slow down the velocity. The Lorentz forces are closest to the channel walls and weakest in the center. As a result, the velocity is zero at the channel’s edges and maximal in the middle, and therefore, the velocity declines. Figures 10A, B show that the momentum profile is inversely proportional to the inclination angle θ.

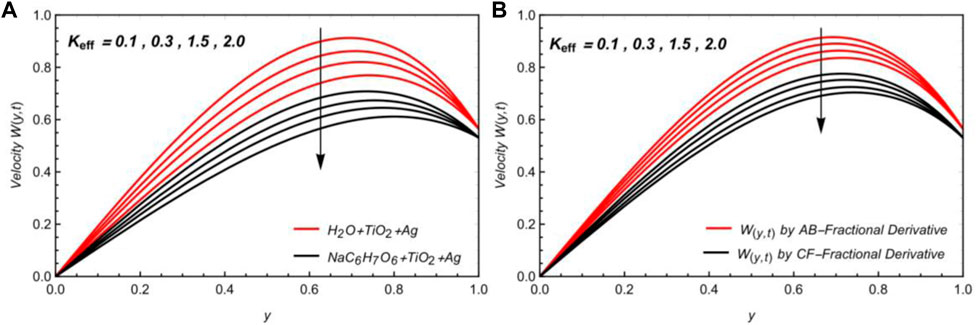
The Brinkman parameter ${\beta }_1$ impacts the momentum, and the field is presented in Figures 11A, B. The velocity decreases as the value of ${\beta }_1$ is enlarged. This occurs by growing the estimations of ${\beta }_1$, and the drag forces are stronger so that the velocity decreases. Figures 12A, B indicate the comparison of the momentum profiles for diverse HNFs (Ag-TiO₂-H₂O and Ag-TiO₂-C₆H₉NaO₇) at different times. We see that Ag-TiO₂-H₂O-based HNF has a significant effect on the velocity profile compared to Ag-TiO₂-C₆H₉NaO₇-based HNF. By adding different NPs in the base fluid, the consequent HNF develops significantly thicker and reduces the velocity. Moreover, it is prominent that the bioconvection, temperature, and momentum profiles for water-based HNF have a relatively progressive value compared to the sodium alginate-based HNF. Furthermore, the effect of the AB approach is higher than the CF approach on the bioconvection, temperature, and velocity fields, which is also due to the different kernels of both fractional operators. To find the numerical inverse Laplace for the temperature, bioconvection, and velocity fields, Figures 13A–C represent a comparison of Tzou and Stehfest approaches and an overall decent agreement was initiated. Furthermore, to check the reliability of our results, Asjad et al. (2022) examined the consequences for the temperature and bioconvection profiles, as compared in Figures 14A, B. The diagrams indicate that the consequences we accomplished overlap with those obtained by Asjad et al. (2022). Table 3 shows the numerical assessment of the bioconvection, temperature, and momentum fields using various computational techniques. Table 4 provides a numerical analysis of the attained solutions with AB- and CF-fractional derivatives. The numerical possessions of the Nusselt number and skin friction coefficient are shown in Table 5. Table 6 shows the numerical analysis of obtained results with ordinary and published work (Asjad et al., 2022).

TABLE 6

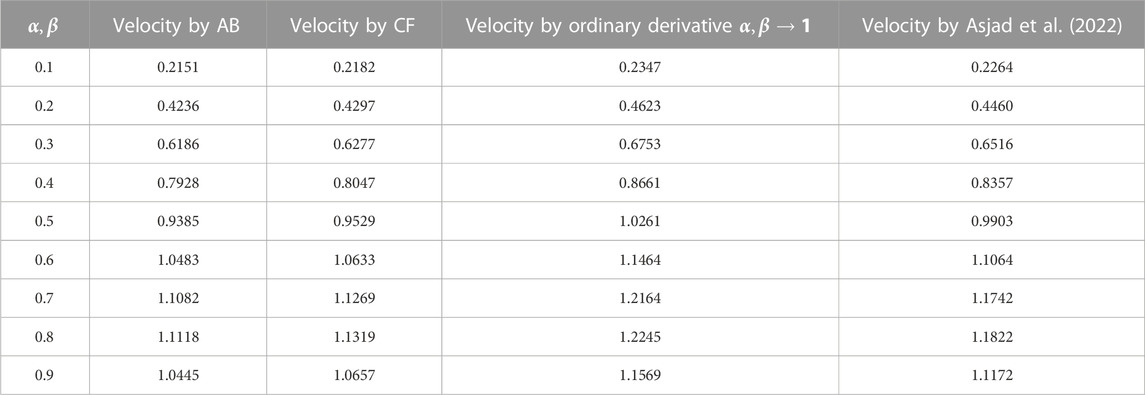
TABLE 6. Numerical analysis of attained results with the ordinary derivative and Asjad et al. (2022).

7 Conclusion

The free convective flow of an unsteady and incompressible Brinkman-type flow mixed with $\left(Ag,Ti{O}_2\right)$ hybrid nanofluid was studied flowing through two parallel poured plates. A fractional model was developed with the recent definitions of fractional derivative, i.e., AB and CF-fractional derivatives, and solved with the help of the Laplace transformation. The impact of different constraints on the attained results of temperature, bioconvection, and the momentum profile was analyzed graphically and numerically. Some remarkable conclusions of this work can be summarized as follows:

• This approach may be broadened to include more varied physical science categories with intricate geometries.

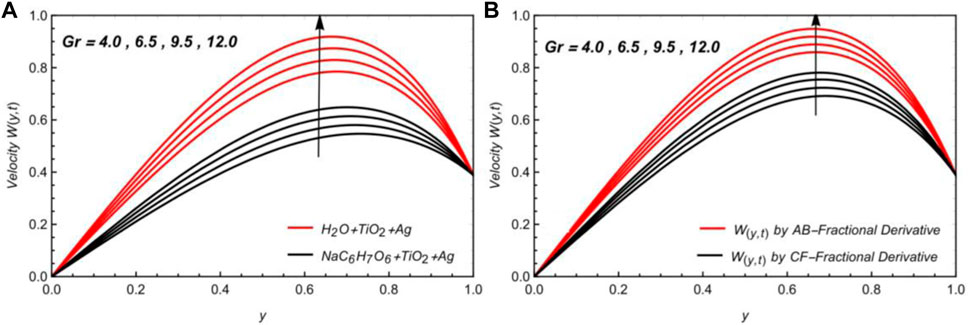
• The enhancing value of $P{r}_{eff}$ decelerates both the momentum and thermal profiles.

• The bioconvection profile also decelerates by enhancing the value of fractional constraints.

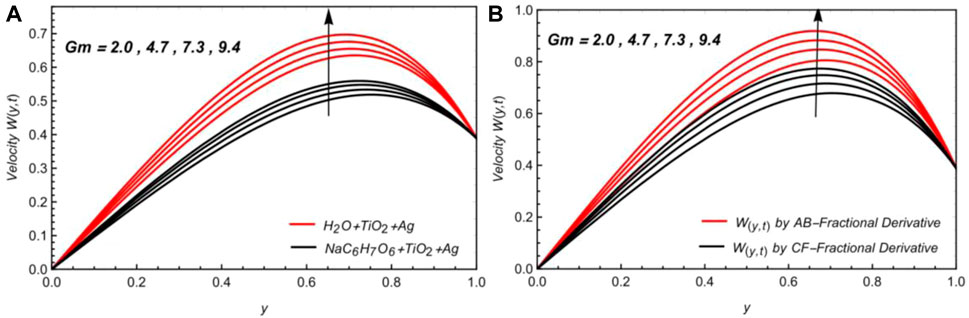
• The momentum field is enhanced by the parameter $Gr,Gm$, while declarations are due to $M$ and ${\beta }_1$.

• The fractional parameter can control the momentum and thermal boundary layer thickness.

• The discovered solutions can aid in accurately interpreting actual data and serve as a tool for testing potential approximations of solutions as necessary.

• The results of Asjad et al. (2022) and the overlap of both curves from the numerical scheme verify the conclusions of this investigation.

The subsequent recommendations are based on methods, expansions, geometries, and analyses and are intended to indicate a future extension of the issue that this study examines. For example, a horizontal plate of constant length and linear velocity may be used to assess the current issue. A Keller Box scheme analysis of the same issue is also possible.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

Conceptualization, SME, SE, AR, and UK; methodology, SE, AR, and UK; software, NN, SE, AA, and UK; validation, NN, SE, AR, and UK; formal analysis, AR, SE, and AA; investigation, UK and AA; resources, AR; data curation, AR; writing—original draft preparation, NN, SME, UK, and SE; writing—review and editing, NN, SME, and AA; visualization, SME; supervision, UK; project administration, AA and SE; funding acquisition, SE and AA. All authors have read and agreed to the published version of the manuscript.

Funding

This work received support from Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2023R163), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia. In addition, this study is also funded by Prince Sattam bin Abdulaziz University project number (PSAU/2023/R/1444).

Acknowledgments

The authors are thankful for the support of Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2023R163), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia. Also, this work is supported via funding from Prince Sattam bin Abdulaziz University project number (PSAU/2023/R/1444).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Abbreviations

$W$, fluid velocity $\left(m/s\right)$; $t$, times $\left(s\right)$; $g$, gravity acceleration $\left(m/s^2\right)$; $k_{nf}$, thermal conductivity of the nanofluid $\left(\frac{W}{mk}\right)$; $C_f$, skin friction $\left(-\right)$; ${\rho }_{nf}$ nanofluid density $\left(\frac{Kg}{m^3}\right)$; $U_0$, characteristic velocity $\left(m{s}^{-1}\right)$; $\theta$, angle of magnetic inclination $\left(-\right)$; $Gm$, mass Grashof number $\left(-\right)$; ${\mu }_{nf}$, dynamic viscosity $\left(\frac{Kg}{ms}\right)$; ${\mathit{Pr}}_{eff}$, Prandtl number $\left(-\right)$; $T_w$, wall temperature, $\left(K\right)$; $Gr$, heat Grashof number $\left(-\right)$; $T_d$, ambient temperature $\left(K\right)$; $\alpha ,\beta$, fractional parameters $\left(-\right)$; $Sc$, Schmidt number $\left(-\right)$; $M$, magnetic field $\left(-\right)$; $D$, thermal diffusion coefficient $\left(-\right)$; ${\left(\rho C_p\right)}_{nf}$, heat capacitance of the nanofluid $\left(-\right)$; $B_o$, magnetic field strength $\left(Kg/s^2\right)$; $C_p$, specific heat at constant pressure $\left(J/kgK\right)$; ${\beta }_T$, thermal expansion coefficient $\left(1/k\right)$; $\sigma$, electrical conductivity $\left(-\right)$; $Nu$, Nusselt number $\left(-\right)$; $Sh$, Sherwood number $\left(-\right)$.

References

Akhtar, S. (2016). Flows between two parallel plates of couple stress fluids with time-fractional Caputo and Caputo-Fabrizio derivatives. Eur. Phys. J. Plus 131 (11), 401–413. doi:10.1140/epjp/i2016-16401-3

CrossRef Full Text | Google Scholar

Alhussain, Z. A., Renuka, A., and Muthtamilselvan, M. (2021). A magneto-bioconvective and thermal conductivity enhancement in nanofluid flow containing gyrotactic microorganism. Case Stud. Therm. Eng. 23, 100809. doi:10.1016/j.csite.2020.100809

CrossRef Full Text | Google Scholar

Ali, Q., Al-Khaled, K., Khan, M. I., Khan, S. U., Raza, A., Oreijah, M., et al. (2022). Diffusion phenomenon for natural convection flow of classical hartmann problem due to a cylindrical tube by generalized fourier’s theories: A fractional analysis. Int. J. Mod. Phys. B, 2350104. doi:10.1142/s0217979223501047

CrossRef Full Text | Google Scholar

Ali, Q., Al-Khaled, K., Omar, J., Raza, A., Khan, S. U., Khan, M. I., et al. (2022). Analysis for advection–diffusion problem subject to memory effects and local and nonlocal kernels: A fractional operators approach. Int. J. Mod. Phys. B, 2350099. doi:10.1142/s0217979223500996

CrossRef Full Text | Google Scholar

Anuar, N. S., Bachok, N., Turkyilmazoglu, M., Arifin, N. M., and Rosali, H. (2020). Analytical and stability analysis of MHD flow past a nonlinearly deforming vertical surface in Carbon Nanotubes. Alexandria Eng. J. 59 (1), 497–507. doi:10.1016/j.aej.2020.01.024

CrossRef Full Text | Google Scholar

Arif, M., Ali, F., Sheikh, N. A., Khan, I., and Nisar, K. S. (2019). Fractional model of couple stress fluid for generalized Couette flow: A comparative analysis of atangana–baleanu and caputo–fabrizio fractional derivatives. IEEE Access 7, 88643–88655. doi:10.1109/access.2019.2925699

CrossRef Full Text | Google Scholar

Ashwinkumar, G., Samrat, S., and Sandeep, N. (2021). Convective heat transfer in MHD hybrid nanofluid flow over two different geometries. Int. Commun. Heat Mass Transf. 127, 105563. doi:10.1016/j.icheatmasstransfer.2021.105563

CrossRef Full Text | Google Scholar

Asjad, M. I., Ikram, M. D., Ali, R., Baleanu, D., and Alshomrani, A. S. (2020). New analytical solutions of heat transfer flow of clay-water base nanoparticles with the application of novel hybrid fractional derivative. Therm. Sci. 24 (1), 343–350. doi:10.2298/tsci20s1343a

CrossRef Full Text | Google Scholar

Asjad, M. I., Ikram, M. D., Sarwar, N., Muhammad, T., Sivasankaran, S., and Subaihi, S. A. A. (2022). Analysis of fractional bioconvection with hybrid nanoparticles in Channel flow. Math. Problems Eng. 2022, 1–14. doi:10.1155/2022/8600591

CrossRef Full Text | Google Scholar

Asjad, M. I., Sarwar, N., Ali, B., Hussain, S., Sitthiwirattham, T., and Reunsumrit, J. (2021). Impact of bioconvection and chemical reaction on MHD nanofluid flow due to exponential stretching sheet. Symmetry 13 (12), 2334. doi:10.3390/sym13122334

CrossRef Full Text | Google Scholar

Atangana, A., and Baleanu, D. (2016). New fractional derivatives with nonlocal and non-singular kernel: Theory and application to heat transfer model. arXiv preprint arXiv:1602.03408.

Google Scholar

Atangana, A., and Nieto, J. J. (2015). Numerical solution for the model of RLC circuit via the fractional derivative without singular kernel. Adv. Mech. Eng. 7 (10), 168781401561375. doi:10.1177/1687814015613758

CrossRef Full Text | Google Scholar

Atangana, A. (2016). On the new fractional derivative and application to nonlinear Fisher’s reaction–diffusion equation. Appl. Math. Comput. 273, 948–956. doi:10.1016/j.amc.2015.10.021

CrossRef Full Text | Google Scholar

Bräuer, F., Trautner, E., Hasslberger, J., Cifani, P., and Klein, M. (2021). Turbulent bubble-laden channel flow of power-law fluids: A direct numerical simulation study. Fluids 6 (1), 40. doi:10.3390/fluids6010040

CrossRef Full Text | Google Scholar

Caputo, M., and Fabrizio, M. (2015). A new definition of fractional derivative without singular kernel. Prog. Fract. Differ. Appl. 1 (2), 73–85.

Google Scholar

Chu, Y. M., Bilal, S., and Hajizadeh, M. R. (2020). Mathematical methods in the applied sciences.Hybrid ferrofluid along with MWCNT for augmentation of thermal behavior of fluid during natural convection in a cavity

CrossRef Full Text | Google Scholar

D’Ippolito, A., Calomino, F., Alfonsi, G., and Lauria, A. (2021). Flow resistance in open channel due to vegetation at reach scale: A review. Water 13 (2), 116. doi:10.3390/w13020116

CrossRef Full Text | Google Scholar

Farooq, U., Waqas, H., Khan, M. I., Khan, S. U., Chu, Y.-M., and Kadry, S. (2021). Thermally radioactive bioconvection flow of Carreau nanofluid with modified Cattaneo-Christov expressions and exponential space-based heat source. Alexandria Eng. J. 60 (3), 3073–3086. doi:10.1016/j.aej.2021.01.050

CrossRef Full Text | Google Scholar

Ge-JiLe, H., Waqas, H., Khan, S. U., Khan, M. I., Farooq, S., and Hussain, S. (2021). Three-dimensional radiative bioconvective flow of a sisko nanofluid with motile microorganisms. Coatings 11 (3), 335. doi:10.3390/coatings11030335

CrossRef Full Text | Google Scholar

Guo, B., Raza, A., Al-Khaled, K., Khan, S. U., Farid, S., Wang, Y., et al. (2021). Fractional-order simulations for heat and mass transfer analysis confined by elliptic inclined plate with slip effects: A comparative fractional analysis. Case Stud. Therm. Eng. 28, 101359. doi:10.1016/j.csite.2021.101359

CrossRef Full Text | Google Scholar

Haq, S. U., Khan, M. A., Khan, Z. A., and Ali, F. (2020). MHD effects on the channel flow of a fractional viscous fluid through a porous medium: An application of the Caputo-Fabrizio time-fractional derivative. Chin. J. Phys. 65, 14–23. doi:10.1016/j.cjph.2020.02.014

CrossRef Full Text | Google Scholar

Ibraheem, G. H., Turkyilmazoglu, M., and Al-Jawary, M. (2022). Novel approximate solution for fractional differential equations by the optimal variational iteration method. J. Comput. Sci. 64, 101841. doi:10.1016/j.jocs.2022.101841

CrossRef Full Text | Google Scholar

Ikram, M. D., Asjad, M. I., Akgül, A., and Baleanu, D. (2021). Effects of hybrid nanofluid on novel fractional model of heat transfer flow between two parallel plates. Alexandria Eng. J. 60 (4), 3593–3604. doi:10.1016/j.aej.2021.01.054

CrossRef Full Text | Google Scholar

Mayeli, P., and Sheard, G. J. (2021). Buoyancy-driven flows beyond the boussinesq approximation: A brief review. Int. Commun. Heat Mass Transf. 125, 105316. doi:10.1016/j.icheatmasstransfer.2021.105316

CrossRef Full Text | Google Scholar

Platt, J. R. (1961). Bioconvection patterns" in cultures of free-swimming organisms. Science 133 (3466), 1766–1767. doi:10.1126/science.133.3466.1766

PubMed Abstract | CrossRef Full Text | Google Scholar

Podlubny, I. (1999). An introduction to fractional derivatives, fractional differential equations, to methods of their solution and some of their applications. Math. Sci. Eng. 198, 340.

Google Scholar

Ramzan, M., Gul, H., Kadry, S., and Chu, Y.-M. (2021). Role of bioconvection in a three dimensional tangent hyperbolic partially ionized magnetized nanofluid flow with Cattaneo-Christov heat flux and activation energy. Int. Commun. Heat Mass Transf. 120, 104994. doi:10.1016/j.icheatmasstransfer.2020.104994

CrossRef Full Text | Google Scholar

Raza, A., Almusawa, M. Y., Ali, Q., Haq, A. U., Al-Khaled, K., and Sarris, I. E. (2022). Solution of water and sodium alginate-based casson type hybrid nanofluid with slip and sinusoidal heat conditions: A prabhakar fractional derivative approach. Symmetry 14 (12), 2658. doi:10.3390/sym14122658

CrossRef Full Text | Google Scholar

Raza, A., Khan, I., Farid, S., My, C. A., Khan, A., and Alotaibi, H. (2021). Non-singular fractional approach for natural convection nanofluid with Damped thermal analysis and radiation. Case Stud. Therm. Eng. 28, 101373. doi:10.1016/j.csite.2021.101373

CrossRef Full Text | Google Scholar

Raza, A., Khan, S. U., Khan, M. I., Farid, S., Muhammad, T., Khan, M. I., et al. (2021). Fractional order simulations for the thermal determination of graphene oxide(GO)and molybdenum disulphide(MoS2)nanoparticles with slip effects. Case Stud. Therm. Eng. 28, 101453. doi:10.1016/j.csite.2021.101453

CrossRef Full Text | Google Scholar

Raza, A., Khan, U., Eldin, S. M., Alotaibi, A. M., Elattar, S., Prasannakumara, B. C., et al. (2019). Significance of free convection flow over an oscillating inclined plate induced by nanofluid with porous medium: The case of the prabhakar fractional approach. Micromachines 13 (11), 2019. doi:10.3390/mi13112019

CrossRef Full Text | Google Scholar

Riaz, S., Amir, M., Memon, I. Q., Ali, Q., and Abro, K. A. (2022). A comparative study for solidification of nanoparticles suspended in nanofluids through non-local kernel approach. Arabian J. Sci. Eng., 1–19. doi:10.1007/s13369-022-07493-y

CrossRef Full Text | Google Scholar

Samrat, S., Ashwinkumar, G., and Sandeep, N. (2022). Simultaneous solutions for convective heat transfer in dusty-nano-and dusty-hybrid nanoliquids. Proc. Institution Mech. Eng. Part E J. Process Mech. Eng. 236 (2), 473–479.

Google Scholar

Saqib, M., Shafie, S., Khan, I., Chu, Y.-M., and Nisar, K. S. (2020). Symmetric MHD channel flow of nonlocal fractional model of BTF containing hybrid nanoparticles. Symmetry 12 (4), 663. doi:10.3390/sym12040663

CrossRef Full Text | Google Scholar

Sulochana, C., Aparna, S., and Sandeep, N. (2020). Magnetohydrodynamic MgO/CuO-water hybrid nanofluid flow driven by two distinct geometries. Heat. Transf. 49 (6), 3663–3682. doi:10.1002/htj.21794

CrossRef Full Text | Google Scholar

Tarasov, V. E. (2019). On history of mathematical economics: Application of fractional calculus. Mathematics 7 (6), 509. doi:10.3390/math7060509

CrossRef Full Text | Google Scholar

Turkyilmazoglu, M., and Altanji, M. (2023). Fractional models of falling object with linear and quadratic frictional forces considering Caputo derivative. Chaos, Solit. Fractals 166, 112980. doi:10.1016/j.chaos.2022.112980

CrossRef Full Text | Google Scholar

Türkyilmazoğlu, M. (2021). Magnetohydrodynamic moving liquid plug within a microchannel: Analytical solutions. J. BIOMECHANICAL ENGINEERING-TRANSACTIONS ASME 143 (1), 011012. doi:10.1115/1.4048713

CrossRef Full Text | Google Scholar

Turkyilmazoglu, M. (2022). Transient and passage to steady state in fluid flow and heat transfer within fractional models. Int. J. Numer. Methods Heat Fluid Flow 33, 728–750. no. ahead-of-print. doi:10.1108/hff-04-2022-0262

CrossRef Full Text | Google Scholar

Waini, I., Ishak, A., and Pop, I. (2019). Hybrid nanofluid flow and heat transfer past a vertical thin needle with prescribed surface heat flux. Int. J. Numer. Methods Heat Fluid Flow 29 (12), 4875–4894. doi:10.1108/hff-04-2019-0277

CrossRef Full Text | Google Scholar

Yusuf, T. A., Mabood, F., Prasannakumara, B., and Sarris, I. E. (2021). Magneto-bioconvection flow of Williamson nanofluid over an inclined plate with gyrotactic microorganisms and entropy generation. Fluids 6 (3), 109. doi:10.3390/fluids6030109

CrossRef Full Text | Google Scholar

Zhang, J., Raza, A., Khan, U., Ali, Q., Zaib, A., Weera, W., et al. (2022). Thermophysical study of oldroyd-B hybrid nanofluid with sinusoidal conditions and permeability: A prabhakar fractional approach. Fractal Fract. 6 (7), 357. doi:10.3390/fractalfract6070357

CrossRef Full Text | Google Scholar

Zheng, Y., Yang, H., Mazaheri, H., Aghaei, A., Mokhtari, N., and Afrand, M. (2021). An investigation on the influence of the shape of the vortex generator on fluid flow and turbulent heat transfer of hybrid nanofluid in a channel. J. Therm. Analysis Calorim. 143 (2), 1425–1438. doi:10.1007/s10973-020-09415-2

CrossRef Full Text | Google Scholar