Analysis of free and forced convections in the flow of radiative viscous fluid with oxytactic microorganisms

The prime intend behind the current effort is to explicate flow attributes of magnetically influenced Newtonian fluids toward a stretchable sheet under the novel physical impact of oxytactic microorganisms in a comparative manner for free and forced convections. In addition, modified Fourier and Fick’s laws are implemented to examine the change in temperature and concentration distributions in a more realistic manner by accounting thermal and mass relaxation parameters in the flow. The obtained PDEs are reduced into the non-linear ODEs by employing similarity variables. Due to the complexity of parametrically based differential equations, a numerical scheme based on a finite-difference approach is implemented via the MATLAB built-in routine known as BVP4C. Flow-controlling parameter effects on associated distributions are evaluated through graphs and tables. Subsequently, the influence of flow-controlling parameters on associated distributions is revealed through pictures in a comparative manner for different convection regimes. Additionally, the quantities such as heat and mass fluxes along with the density of motile microorganisms are also illustrated. From the thorough analysis of the current investigation, it is inferred that velocity distribution enhances for free and forced convections, whereas the temperature of the fluid diminishes against the mentioned convective regimes. It is manifested that the Nusselt number is more in the situation of free convection instead of the forced convection situation. The magnitude of the skin friction factor is more in case of free convection as compared to the forced convection regime. It is also reported that by uplifting the magnitudes of concentration and thermal relaxation parameters, depreciation in associated heat and mass transfer rate arises. In addition, it is also reported that with the increment in the magnetic field, buoyancy ratio, bioconvection parameters, and Rayleigh number skin friction accelerate, while the behavior is quite opposite in case of stretching the ratio parameter.

1 Introduction

The region in the flow domain where the local velocity of the fluid tends to zero while the pressure is at its maximum is defined as the stagnation point. The existence of the stagnation region in the flow process over the stretchable surface has received valuable utilization in multiple engineering processes such as cooling of a nuclear reactor, coating dynamics, and vapor deposition. In addition, it is worthwhile to mention that two diversified situations of velocity distribution occur in the neighborhood of the stagnation point due to the relation of the free stream and stretching velocity ratio. In view of the extensive utilization of fluid flow in the stagnant region, several enthusiastic researchers have conducted studies in this direction. We initialize from the work done by Hiemenz (1911) in which he analyzed 2D stagnant flow toward a static semi-infinite wall by heeding an analytical solution. The axisymmetric stagnant flow over a static semi-infinite wall was discussed by Homann (1936). The stagnant flow of the viscous fluid past a deformable stretched sheet was discussed by Mahapatra and Gupta (Ibrahim et al., 2013). They reported that if the stretching velocity dominates the free stream velocity, the boundary layer thickness exceeds. In addition, they observed that by uplifting the magnitude of the stagnant point parameter, the velocity of the fluid increases. A similarity solution for Navier–Stokes equations was obtained by Mahapatra and Gupta (2003). The formulation of the Navier–Stokes equation for the stagnant flow in the form of partial differential equations was manifested by Wang (2008). Later on, Wang constructed a set of similar variables to transform PDEs into ODEs. A two-dimensional stagnant flow over a stretchable surface was explored by Lok et al. (2011) by accounting the quadratic velocity distribution. The non-orthogonal stagnant flow of the viscous incompressible fluid toward a stretchable sheet was demonstrated by Ishak et al. (2010) and measured for the formation of streamline patterns in the flow distribution. In addition, they also reported that the inclination angle affects the shiftiness of the stagnation point. The stagnation point flow of the non-Newtonian fluid also possesses promising utilization in numerous procedures. In view of its extensive effectiveness, researchers have presented theoretical and experimental studies in recent years. For example, the stagnant flow of the shear thinning fluid flowing toward a stretchable sheet under the action of the magnetic field was demonstrated by Hashim et al. (2019). They reported that the thickness of the thermal boundary layer accelerates for uplifting both the magnetic field and non-Newtonian fluid parameters. Multiple solutions for the velocity profile within the critical range of the stagnation point parameter over the stretching/shrinking surface in the rotating frame were heeded by Khan et al. (2022). The evaluation of homogeneous and heterogeneous reactions in the stagnant flow of the viscous fluid over a stretching surface was carried out by Abbas et al. (2015). It was reported by them that solutions for velocity and concentration profiles exist only for specific values of the velocity ratio parameter. The 2D boundary layer flow of the viscous incompressible fluid toward a stretchable sheet was explored by Chamkha (2015). The results for the impacts of both variable thickness and radiation parameters on the fluid flow were obtained by them. The stagnation point flow of the viscous fluid in a stratified medium along with permeability aspects was evaluated by Khashi’ie et al. (2020).

The process in which molecules diffuse from the region of higher to lower thermal convective potential is called heat convection. Mesmerizing applications of the thermal exchange procedure are revealed in electronic device cooling, nuclear reactor cooling, generation of power, production of energy, and so forth as referred (Mirzaei and Mehdi, 2012; Hosseinzadeh et al., 2013; Dehghan and Abbaszadeh, 2016; Shirvan et al., 2017a; Shirvan et al., 2017b; Dehghan and Abbaszadeh, 2017; Ellahi et al., 2017; Esfahani et al., 2017; Kamranian et al., 2017; Rashidi et al., 2017). In the past, the propagation of heat was considered with infinite speed in accordance with the Fourier law of heat conduction principle (Fourier JBJ., 1822). However, due to the formation of thermal singularities and more passive use of controlled heat in different phenomena, Cattaneo–Christov (Cattaneo and Calore, 1948) modified the existing law by adding the thermal relaxation term (Christov, 2009). This new development has opened new arenas for researchers to work, and nowadays, researchers are incorporating modified laws instead of using old version of laws. Bilal et al. (2021) scrutinized heat and mass transfer characteristics in the Maxwell fluid by obliging modified Fourier and Fick’s laws. The effectiveness of heat and mass transfer control via implementing modified laws in cooling procedures was evaluated by Lyu et al. (2022). Heat transfer in an annulus by varying the shape and number of fins was explored by Madhavadas et al. (2021). They deduced that the efficiency of the heat exchanger is conclusively dependent on the orientation of fins. Formation of thermal boundary layer thickness in hydrothermal flow of viscous fluid over a vertical surface along with advection phenomenon was investigated by (Zhao et al., 2022).

Density differences generated due to the diffusion of microorganisms is known as bioconvection. Hydrothermal characteristics of poorly conducting liquids are improved by the swimming of microorganisms. The inclusion of microorganisms in the flow field increased their utility in the biotechnological field such as in biofuel production and fertilizer production. The phenomenon discussing the motion of microorganisms is known as gyrotaxis. Since most microorganisms are sensitive to oxygen and light, they are characterized into gyrotactic and oxytactic. Tremendous effort has been taken in the direction of bioconvective flow in recent years due to overwhelming utilizations. The influence of the radiative heat flux and gyrotactic microorganism on the fluid flow toward a stretchable sheet was explored by Chamkha et al. (2017). Khan (2018) highlighted the effects of gyrotactic microorganisms on the second-grade stratified nanofluid. The influence of gyrotactic microorganisms on the Powell–Eyring nanofluid was illustrated by Pal et al. (2019). The behavior of the magneto Jeffery fluid toward a vertical cone accompanied with nanoparticles and gyrotactic microorganisms was explored by Saleem et al. (2019). The influence of gyrotactic microorganisms on the power law fluid over a stretchable sheet was explored by Ferdows et al. (2019). Numerical solutions for a water-based nanofluid over a stretchable surface along with the effects of motile gyrotactic microorganisms were explored by De (2019). Later on, Kuznetsov (2011) explored biothermal characteristics on the suspension of nanoparticles along with gyrotactic microorganisms. The impact of velocity slip and thermal radiation on the MHD hybrid nanofluid flow over a permeable sheet was investigated by Wahid et al (2020). Mustafa (2021a) investigated the stagnant flow toward a stretchable sheet or a circular cylinder. The prime intend behind this investigation was to target the exact solution for both momentum and thermal fields. It was also reported that the axial velocity and thermal distributions got suppressed under the stretching impacts. The influence of the MHD steady 2D mixed convective flow due to the non-linear surface in carbon nanotubes was investigated by Mustafa et al. (Syazana et al., 2020). A mathematical demonstration about enhancement in the rate of heat transfer by considering the stretching surface was explored by Mustafa (2021b). Some latest studies on the bioconvective flow are those of Khan et al. (2014), Cao et al. (2022), Sajid et al. (2022), and Prasad et al. (2023).

From the aforementioned literature, the current work comprises the novel influence of the oxytactic microorganism species, variable molecular diffusivity, and Cattaneo–Christov diffusion on the stagnant flow of the viscous fluid flowing toward a stretchable sheet. Oxytactic microorganisms such as bacteria are used for water purification in the drinking water treatment system. Removal of contaminants from water through bioconvection and biodegradation is a life savior. In addition, consideration of the Cattaneo–Christov heat flux model is helpful in controlling heat and mass transfer in the HVAC industry, fire alarms and distinguishers, fuel production, food preservation, and so many other areas. This model makes the study of different systems’ working in daily life more realistic. Lastly, the disclosure of variable molecular diffusivity instead of assuming it linear is more appropriable because in thermosolutal diffusion, the particles move randomly instead of moving on a linear path. So, it is highly important to assume it variable. In view of the aforementioned originality and significance, the present study is conducted.

2 Mathematical modeling

Let us consider the 2D incompressible mixed convective steady and stagnant flow of the viscous fluid over a stretching sheet. The sheet is stretched along the x-axis. The process of mixed convection is taken into account due to the transfer of heat. The effects of oxytactic microorganisms and modified Fourier and Fick’s law are encompassed, respectively.

The mass flux equation for the considered problem is represented as follows:

$\frac{\partial \mathrm{u}}{\partial \mathrm{x}}+\frac{\partial \mathrm{v}}{\partial \mathrm{y}}=0.(1)$

Governing momentum equations by employing the boundary layer approach are shown as follows, as in Cao et al. (2022) and Prasad et al. (2023):

$\mathrm{u}\frac{\partial \mathrm{u}}{\partial \mathrm{x}}+\mathrm{v}\frac{\partial \mathrm{u}}{\partial \mathrm{y}}={\mathrm{U}}_{\infty }\frac{\partial {\mathrm{U}}_{\infty }}{\partial \mathrm{x}}+\mathrm{\nu }\frac{{\partial }^2\mathrm{u}}{\partial {\mathrm{y}}^2}+\frac{{\mathrm{\sigma }\mathrm{B}}_0^2}{{\mathrm{\rho }}_{\mathrm{f}}}\left({\mathrm{U}}_{\infty }-\mathrm{u}\right)+\frac{\mathrm{g}}{{\mathrm{\rho }}_{\mathrm{f}}}\left[{\mathrm{\beta }\mathrm{\rho }}_{\mathrm{f}}\left(1-{\mathrm{C}}_{\infty }\right)\left(\mathrm{T}-{\mathrm{T}}_{\infty }\right)-\left({\mathrm{\rho }}_{\mathrm{p}}-{\mathrm{\rho }}_{\mathrm{f}}\right)\left(\mathrm{C}-{\mathrm{C}}_{\infty }\right)-\left({\mathrm{\rho }}_{\mathrm{m}}-{\mathrm{\rho }}_{\mathrm{f}}\right)\left(\mathrm{N}-{\mathrm{N}}_{\infty }\right)\right].(2)$

Modeled energy, concentration, and motile microorganism mass density equations are expressed as follows, referring to Prasad et al. (2023):

$\mathrm{u}\frac{\partial \mathrm{T}}{\partial \mathrm{x}}+\mathrm{v}\frac{\partial \mathrm{T}}{\partial \mathrm{y}}+{\mathrm{\lambda }}_{\mathrm{E}}{\mathrm{\phi }}_{\mathrm{E}}=\mathrm{\alpha }\frac{{\partial }^2\mathrm{T}}{\partial {\mathrm{y}}^2}-\frac{1}{{\mathrm{\rho }\mathrm{c}}_{\mathrm{p}}}\frac{\partial {\mathrm{q}}_{\mathrm{r}}}{\partial \mathrm{y}},(3)$

$\mathrm{u}\frac{\partial \mathrm{C}}{\partial \mathrm{x}}+\mathrm{v}\frac{\partial \mathrm{C}}{\partial \mathrm{y}}+{\mathrm{\lambda }}_{\mathrm{C}}{\mathrm{\phi }}_{\mathrm{C}}=\mathrm{D}\frac{{\partial }^{2}C}{\partial y^2},(4)$

$\mathrm{u}\frac{\partial \mathrm{N}}{\partial \mathrm{x}}+\mathrm{v}\frac{\partial \mathrm{N}}{\partial \mathrm{y}}={\mathrm{D}}_{\mathrm{m}}\frac{{\partial }^2\mathrm{N}}{\partial {\mathrm{y}}^2}-\frac{{\text{bW}}_{\mathrm{c}}}{{\mathrm{C}}_{\mathrm{w}}-{\mathrm{C}}_{\infty }}\frac{\partial }{\partial \mathrm{y}}\left(\mathrm{N}\frac{\partial \mathrm{C}}{\partial \mathrm{y}}\right),(5)$

where ${\mathrm{\lambda }}_{\mathrm{E}}$ and ${\mathrm{\lambda }}_{\mathrm{C}}$ are the dimensional thermal and concentration relaxation parameters derived from Cattaneo–Christov heat and mass flux relations.

Associated boundary conditions are as follows:

$\mathrm{u}={\mathrm{u}}_{\mathrm{w}}=\text{ax},\mathrm{v}=0,\mathrm{T}={\mathrm{T}}_{\mathrm{w}},\mathrm{C}={\mathrm{C}}_{\mathrm{w}},\mathrm{N}={\mathrm{N}}_{\mathrm{w}}\text{at}\mathrm{y}=0\text{and}\mathrm{u}\to {\mathrm{U}}_{\infty }=\text{bx},\mathrm{T}\to {\mathrm{T}}_{\infty },\mathrm{C}\to {\mathrm{C}}_{\infty },\mathrm{N}\to {\mathrm{N}}_{\infty }\text{as}\mathrm{y}\to \infty .(6)$

Here, ${\mathrm{u}}_{\mathrm{w}}=\mathrm{a}\mathrm{x}$ is the stretching sheet velocity. The sheet is stretched along the horizontal axis, and the velocity away from the sheet is ${\mathrm{u}}_{\infty }=\mathrm{b}\mathrm{x}$. The temperature at the sheet surface is ${\mathrm{T}}_{\mathrm{w}}$, concentration at the wall is described by ${\mathrm{C}}_{\mathrm{w}}$, and density for motile microorganisms is signified by ${\mathrm{N}}_{\mathrm{w}}$, while the temperature, concentration, and motile microorganisms at infinity are represented by ${\mathrm{T}}_{\infty }$, ${\mathrm{C}}_{\infty }$, and ${\mathrm{N}}_{\infty }$, respectively.

Here,

${\varphi }_{\mathrm{E}}=\left({\mathrm{u}}^2\frac{{\partial }^2\mathrm{T}}{\partial {\mathrm{x}}^2}+{\mathrm{v}}^2\frac{{\partial }^2\mathrm{T}}{\partial {\mathrm{y}}^2}+2\text{uv}\frac{{\partial }^2\mathrm{T}}{\partial \mathrm{x}\partial \mathrm{y}}\right)+\left[\left(\mathrm{u}\frac{\partial \mathrm{u}}{\partial \mathrm{x}}+\mathrm{v}\frac{\partial \mathrm{u}}{\partial \mathrm{y}}\right)\frac{\partial \mathrm{T}}{\partial \mathrm{x}}+\left(\mathrm{u}\frac{\partial \mathrm{v}}{\partial \mathrm{x}}+\mathrm{v}\frac{\partial \mathrm{v}}{\partial \mathrm{y}}\right)\frac{\partial \mathrm{T}}{\partial \mathrm{y}}\right],(7)$

and

${\varphi }_{\mathrm{C}}=\left({\mathrm{u}}^2\frac{{\partial }^2\mathrm{C}}{\partial {\mathrm{x}}^2}+{\mathrm{v}}^2\frac{{\partial }^2\mathrm{C}}{\partial {\mathrm{y}}^2}+2\text{uv}\frac{{\partial }^2\mathrm{C}}{\partial \mathrm{x}\partial \mathrm{y}}\right)+\left[\left(\mathrm{u}\frac{\partial \mathrm{u}}{\partial \mathrm{x}}+\mathrm{v}\frac{\partial \mathrm{u}}{\partial \mathrm{y}}\right)\frac{\partial \mathrm{C}}{\partial \mathrm{x}}+\left(\mathrm{u}\frac{\partial \mathrm{v}}{\partial \mathrm{x}}+\mathrm{v}\frac{\partial \mathrm{v}}{\partial \mathrm{y}}\right)\frac{\partial \mathrm{C}}{\partial \mathrm{y}}\right].(8)$

The mathematical expression for the radiative heat flux is given as

${\mathrm{q}}_{\mathrm{r}}=-\frac{4{\mathrm{\sigma }}^{*}\partial {\mathrm{T}}^4}{3{\mathrm{k}}^{*}\partial \mathrm{y}},(9)$

where

${\mathrm{T}}^4=4{\mathrm{T}}_{\infty }^3\mathrm{T}-3{\mathrm{T}}_{\infty }^4,(10)$

where $k^{*}$ represents the mean absorption coefficient and ${\sigma }^{*}$ highlights the Stefan–Boltzmann constant.

Similarity transformations are used to convert PDEs into ODEs.

$\mathrm{\Psi }=\sqrt{\mathrm{a}\mathrm{\upsilon }}\text{xf}\left(\mathrm{\eta }\right),\mathrm{\eta }=\sqrt{\frac{\mathrm{a}}{\mathrm{\upsilon }}}\mathrm{y},\mathrm{\theta }\left(\mathrm{\eta }\right)=\frac{\mathrm{T}-{\mathrm{T}}_{\infty }}{{\mathrm{T}}_{\mathrm{w}}-{\mathrm{T}}_{\infty }},\varphi \left(\mathrm{\eta }\right)=\frac{\mathrm{C}-{\mathrm{C}}_{\infty }}{{\mathrm{C}}_{\mathrm{w}}-{\mathrm{C}}_{\infty }},\mathrm{\chi }\left(\mathrm{\eta }\right)=\frac{\mathrm{N}-{\mathrm{N}}_{\infty }}{{\mathrm{N}}_{\mathrm{w}}-{\mathrm{N}}_{\infty }},(11)$

where the stream function is represented by $\mathrm{\Psi }$ and is defined as $u=\frac{\partial \mathrm{\Psi }}{\partial y}$ and $v=-\frac{\partial \mathrm{\Psi }}{\partial x}$.

After applying the similarity transformation, the following system of ODEs is obtained:

${\mathrm{f}}^{‴}+{\text{ff}}^{\prime }-{{\mathrm{f}}^{\prime }}^2+\mathrm{M}\left(\mathrm{A}-{\mathrm{f}}^{\prime }\right)+{\mathrm{A}}^2+\mathrm{\Lambda }\left[\mathrm{\theta }-\text{Nr}\varphi -\text{Rb}\mathrm{\chi }\right]=0,(12)$

$\left(1+\text{Rd}\right){\mathrm{\theta }}^{″}-\mathrm{Pr}{\mathrm{\delta }}_1\left[{\mathrm{f}}^2{\mathrm{\theta }}^{″}+{\text{ff}}^{\prime }{\mathrm{\theta }}^{\prime }\right]+{\text{Prf}\mathrm{\theta }}^{\prime }=0,(13)$

${\mathit{\varphi }}^{″}+\mathbf{S}\mathbf{c}\mathbf{f}{\mathit{\varphi }}^{\prime }-\mathbf{S}\mathbf{c}{\mathbf{\delta }}_{\mathbf{2}}\left[{\mathbf{f}}^{\mathbf{2}}{\mathit{\varphi }}^{″}+\mathbf{f}{\mathbf{f}}^{\prime }{\mathit{\varphi }}^{\prime }\right]=\mathbf{0},(14)$

${\mathrm{\chi }}^{″}+{\text{Lbf}\mathrm{\chi }}^{\prime }-\text{Pe}\left[\left(\mathrm{\sigma }+\mathrm{\chi }\right){\varphi }^{″}+{\mathrm{\chi }}^{\prime }{\varphi }^{\prime }\right]=0.(15)$

After using similarity transformation, boundary conditions are reduced as follows:

$\mathrm{\eta }=0:\mathrm{f}\left(\mathrm{\eta }\right)=0,{\mathrm{f}}^{\prime }\left(\mathrm{\eta }\right)=1,\mathrm{\theta }\left(\mathrm{\eta }\right)=1,\varphi \left(\mathrm{\eta }\right)=1,\mathrm{\chi }\left(\mathrm{\eta }\right)=1,\mathrm{\eta }\to \infty :{\mathrm{f}}^{\prime }\left(\mathrm{\eta }\right)\to \mathrm{A},\mathrm{\theta }\left(\mathrm{\eta }\right)\to 0,\varphi \left(\mathrm{\eta }\right)\to 0,\mathrm{\chi }\left(\mathrm{\eta }\right)\to 0.(16)$

Dimensionless parameters that appear in ODEs are of great importance for the results and discussion section. These parameters are mathematically highlighted by the following expressions:

$\begin{array}{ll}\hfill \mathrm{Pr}& =\frac{\mathrm{\upsilon }}{\mathrm{\alpha }},\text{Sc}=\frac{\upsilon }{D},\text{Rd}=\frac{16{\mathrm{\sigma }}^{*}{\mathrm{T}}_{\infty }^3}{3{\mathrm{k}}^{*}\mathrm{k}},\mathrm{\sigma }=\frac{{\mathrm{N}}_{\infty }}{{\mathrm{N}}_{\mathrm{w}}-{\mathrm{N}}_{\infty }},\text{Lb}=\frac{\mathrm{\upsilon }}{{\mathrm{D}}_{\mathrm{m}}},\text{Pe}=\frac{{\text{bW}}_{\mathrm{c}}}{{\mathrm{D}}_{\mathrm{m}}},{\mathrm{\delta }}_1={\mathrm{a}\mathrm{\lambda }}_{\mathrm{E}},{\mathrm{\delta }}_2={\mathrm{a}\mathrm{\lambda }}_{\mathrm{C}},\hfill \\ \hfill & \mathrm{\Lambda }=\frac{\text{Gr}}{{\text{Re}}_{\mathrm{x}}^2},\text{Nr}=\frac{\left({\mathrm{\rho }}_{\mathrm{p}}-{\mathrm{\rho }}_{\mathrm{f}}\right)\left({\mathrm{C}}_{\mathrm{w}}-{\mathrm{C}}_{\infty }\right)}{\left(1-{\mathrm{C}}_{\infty }\right){\mathrm{\rho }}_{\mathrm{f}}\mathrm{\beta }\left({\mathrm{T}}_{\mathrm{w}}-{\mathrm{T}}_{\infty }\right)},\text{Rb}=\frac{\left({\mathrm{\rho }}_{\mathrm{m}}-{\mathrm{\rho }}_{\mathrm{f}}\right)\left({\mathrm{N}}_{\mathrm{w}}-{\mathrm{N}}_{\infty }\right)}{\left(1-{\mathrm{C}}_{\infty }\right){\mathrm{\rho }}_{\mathrm{f}}\mathrm{\beta }\left({\mathrm{T}}_{\mathrm{w}}-{\mathrm{T}}_{\infty }\right)},\mathrm{M}=\frac{{\mathrm{\sigma }\mathrm{B}}_0^2}{{\mathrm{\rho }}_{\mathrm{f}}\mathrm{a}},\mathrm{A}=\frac{\mathrm{b}}{\mathrm{a}},\hfill \end{array}(17)$

where $\mathrm{\Lambda }=\frac{Gr}{R{e}_x^2}$ highlights the mixed convection parameter. The Grashof number is represented by $Gr$, which is the ratio of buoyancy to the viscous forces.

The mathematical expression for skin frictions is defined as follows:

$C{f}_x=\frac{\tau }{\frac{U_w^2}{2}}.(18)$

The dimensionless form is given as

$\frac{1}{2}C{f}_{x}R{e}_x^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}=-f^{″}\left(0\right).(19)$

The expression for the Nusselt number is given as follows:

${\text{Nu}}_{\mathrm{x}}=\frac{{\text{xq}}_{\mathrm{w}}}{{\mathrm{k}}_{\mathrm{f}}\left({\mathrm{T}}_{\mathrm{w}}-{\mathrm{T}}_{\infty }\right)},(20)$

where $q_w$ denotes the heat flux, and the mathematical expression for the heat flux is given by the relation

${\mathrm{q}}_{\mathrm{w}}=-\mathrm{k}\frac{\partial \mathrm{T}}{\partial \mathrm{y}}-\frac{4{\mathrm{\sigma }}^{*}\partial {\mathrm{T}}^4}{3{\mathrm{k}}^{*}\partial \mathrm{y}}.(21)$

The dimensionless form of the heat transfer rate is represented by the following expression:

${\text{Nu}}_{\mathrm{x}}{\text{Re}}_{\mathrm{x}}^{-\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}=-\left(1+\text{Rd}\right){\mathrm{\theta }}^{\prime }\left(0\right).(22)$

The mathematical expression for the mass transfer rate is represented as

${\text{Sh}}_{\mathrm{x}}=\frac{{\text{xq}}_{\mathrm{m}}}{{\mathrm{D}}_{\mathrm{B}}\left({\mathrm{C}}_{\mathrm{w}}-{\mathrm{C}}_{\infty }\right)},(23)$

where $q_m$ denotes the mass flux, which is represented by

${\mathrm{q}}_{\mathrm{m}}=-{\mathrm{D}}_{\mathrm{B}}\frac{\partial \mathrm{C}}{\partial \mathrm{y}}.(24)$

The dimensionless form of the mass transfer is represented by the expression

${\text{Sh}}_{\mathrm{x}}{\text{Re}}_{\mathrm{x}}^{-\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}=-{\varphi }^{\prime }\left(0\right).(25)$

Here, the Reynolds number is highlighted by $Re$, that is, the ratio of inertial to the viscous forces. The density of the motile microorganism profile is highlighted by

${\text{Nn}}_{\mathrm{x}}=\frac{{\text{xq}}_{\mathrm{n}}}{{\mathrm{D}}_{\mathrm{m}}\left({\mathrm{N}}_{\mathrm{w}}-{\mathrm{N}}_{\infty }\right)},(26)$

where

${\mathrm{q}}_{\mathrm{n}}=-{\mathrm{D}}_{\mathrm{m}}\frac{\partial \mathrm{\chi }}{\partial \mathrm{y}},(27)$

and the dimensionless form is given by

${\text{Nn}}_{\mathrm{x}}{\text{Re}}_{\mathrm{x}}^{-\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}=-{\mathrm{\chi }}^{\prime }\left(0\right).(28)$

3 Solution methodology

The translated coupled non-linear ODEs are not easy to solve. It is impossible to solve these equations analytically. Therefore, the approximate solution of these equations along with the associated boundary conditions is attained by using the BVP4C built-in technique. To use the BVP4C technique, higher-order ODEs are reduced into ODEs of the first order by considering new variables $f=y_1,f^{\prime }=y_2,f^{″}=y_3,{\mathrm{f}}^{‴}=y_3^{\prime },\theta =y_4,{\theta }^{\prime }=y_5,{\theta }^{″}=y_5^{\prime },\varphi =y_6,{\varphi }^{\prime }=y_7,{\varphi }^{″}=y_7^{\prime },\chi =y_8,{\chi }^{\prime }=y_9,{\chi }^{″}=y_9^{\prime }$. So, the translated first-order ODEs are

$\begin{array}{c}{\mathrm{y}}_1^{\prime }={\mathrm{y}}_2,{\mathrm{y}}_2^{\prime }={\mathrm{y}}_3,{\mathrm{y}}_3^{\prime }=-{\mathrm{y}}_1{\mathrm{y}}_3+{\mathrm{y}}_2^2-\mathrm{M}\left(\mathrm{A}-{\mathrm{y}}_2\right)-{\mathrm{A}}^2-\mathrm{\Lambda }\left[{\mathrm{y}}_4-{\text{Nry}}_6-{\text{Rby}}_8\right],y_4^{\prime }=y_5,\hfill \\ {\mathrm{y}}_5^{\prime }=\frac{\mathrm{Pr}{\mathrm{\delta }}_1{\mathrm{y}}_1{\mathrm{y}}_2{\mathrm{y}}_5-\mathrm{Pr}{\mathrm{y}}_1{\mathrm{y}}_5}{\left(1+\text{Rd}\right)-\mathrm{Pr}{\mathrm{\delta }}_1{\mathrm{y}}_1^2},{\mathrm{y}}_6^{\prime }={\mathrm{y}}_7,{\mathrm{y}}_7^{\prime }=\frac{{\text{Sc}\mathrm{\delta }}_2{\mathrm{y}}_1{\mathrm{y}}_2{\mathrm{y}}_7-{\text{Scy}}_1{\mathrm{y}}_7}{1-{\text{Sc}\mathrm{\delta }}_2{\mathrm{y}}_1^2},{\mathrm{y}}_8^{\prime }={\mathrm{y}}_9,{\mathrm{y}}_9^{\prime }=\text{Pe}\left[\left(\mathrm{\sigma }+{\mathrm{y}}_8\right){\mathrm{y}}_7^{\prime }+{\mathrm{y}}_7{\mathrm{y}}_9\right]-{\text{Lby}}_1{\mathrm{y}}_9,\hfill \end{array}$

where boundary conditions are

$\eta =0:y_1\left(\eta \right)=0,y_2\left(\eta \right)=1,y_4\left(\eta \right)=1,y_6\left(\eta \right)=1,y_8\left(\eta \right)=1,\eta \to \infty :y_2\left(\infty \right)\to A,y_4\left(\infty \right)\to 0,y_6\left(\infty \right)\to 0,y_8\left(\infty \right)\to 0.$

4 Results and discussion

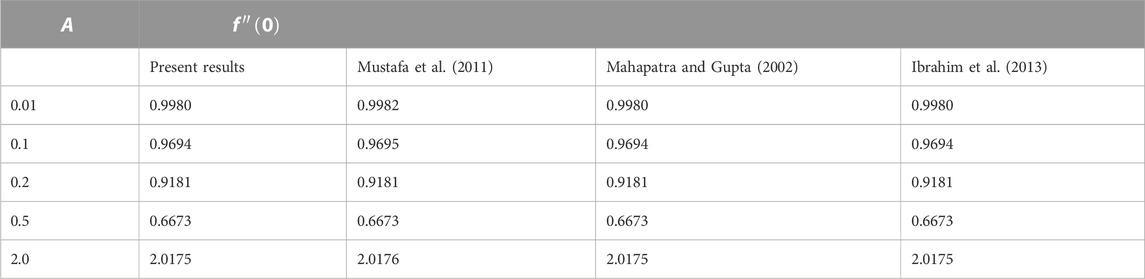
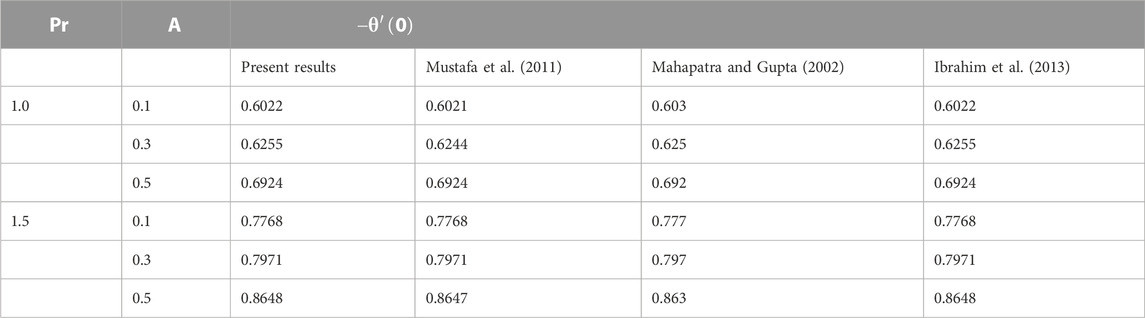
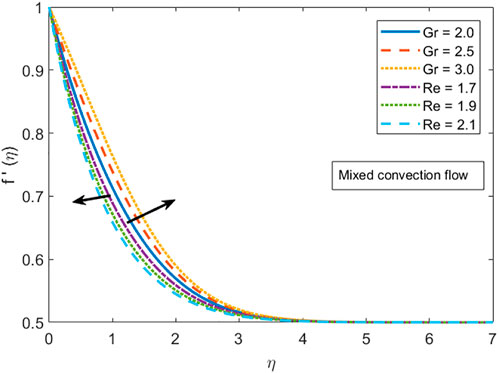
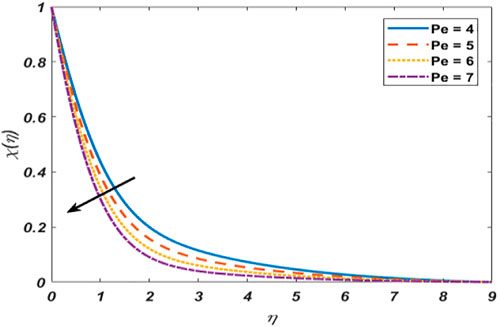
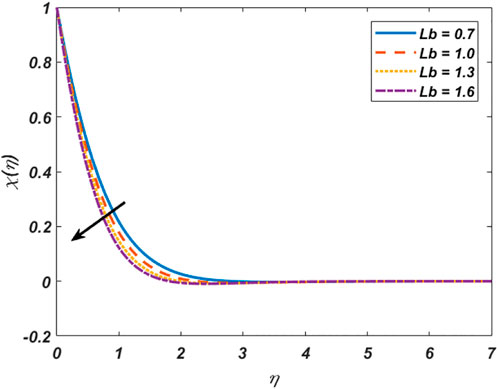
This section comprises the graphical representation of impacts of different rheological parameters on the velocity, temperature, concentration, and motile microorganism profile. The results for the skin friction, Nusselt number, Sherwood, and motile density of microorganism numbers are also tabulated. Validation of the implemented numerical scheme and computed results is given in Table 1 by constructing a comparison with the results published by authors Mahapatra and Gupta (2002), Mustafa et al. (2011), and Ibrahim et al. (2013). From the attained data mentioned in Table 1, variation in the skin friction coefficient is noticed against the stagnation parameter (A) by fixing $M=\mathrm{\Lambda }=Nr=Rb=Rd=\mathrm{Pr}={\delta }_1=Sc=Lb=Pe=\sigma =0$. Here, a complete agreement in derived and available values is found, which shows a complete agreement of results. Subsequently, in Table 2, variations are found in the Nusselt number against the stagnation point parameter (A) for Pr = 1 and 1.5 along with restriction on other parameters like $M=\mathrm{\Lambda }=Nr=Rb=Rd=\mathrm{Pr}={\delta }_1=Sc=Lb=Pe=\sigma =0.$ Again, a good match between the presently computed and existing studies has been delineated. Deviation in the skin friction coefficient (${\mathrm{f}}^{″}\left(0\right)$) for free and forced convections is enumerated in Table 3. The impact of the buoyancy ratio parameter $Nr$ on the shear stress at the wall for mentioned regimes is manipulated in this table. It is observed that skin friction is more in the case of free convection $\left(\mathrm{\Lambda }>1\right)$ in comparison to forced convection $\left(\mathrm{\Lambda }<1\right)$. It is because of the fact that in the case of $\mathrm{\Lambda }>1$, the magnitude of buoyancy forces dominates over inertial forces. Due to this reason, less movement is generated, and the force exerted by the wall on fluid particles is more than in other cases. The change in the heat flux coefficient against the radiation parameter (Rd) for free convection $\left(\mathrm{\Lambda }>1\right)$ and forced convection $\left(\mathrm{\Lambda }<1\right)$ in a comparative manner is evaluated in Table 4. It is seen that the heat flux is more in case of free convection compared to forced convection. It is due to the fact that for $\mathrm{\Lambda }>1$, the magnitude of Gr > Re, which shows that the temperature difference between hot and cold regions rises and, thus, as a consequence, heat flux generates in the domain. The influence of various dimensionless parameters on the skin friction coefficient is illustrated in Table 5. It is shown that the skin friction coefficient amplifies for the uplifting magnetic parameter $M$, buoyancy ratio parameter $Nr$, and bioconvection Rayleigh number $Rb$, while the behavior of the skin friction coefficient is quite opposite for the remaining parameters. Table 6 is formulated by examining the impacts of various dimensionless parameters on the Nusselt number, Sherwood number, and motile microorganism density number by keeping $A=0.1,$ $M=0,$ $Nr=0.5,$ $Rb=1.5$, and $\mathrm{\Lambda }=0.05.$ It is reported that the Nusselt number amplifies for surging the values of the thermal and concentration relaxation time parameters ${\delta }_1,$ ${\delta }_2,$ the radiation parameter $Rd$, the Schmidt number $Sc$, the bioconvection Lewis number $Lb$, the Peclet number $Pe$, and microorganism concentration diffusion parameter $\sigma .$ The Sherwood number amplifies for higher values of the radiation parameter $Rd$, Schmidt number $Sc$, bioconvection Lewis number $Lb$, Peclet number $Pe$, and microorganism concentration diffusion parameter $\sigma$ but decreases for higher values of thermal and concentration relaxation time parameters ${\delta }_1$ and ${\delta }_2.$ The motile microorganism density enhances for the uplifting radiation parameter $Rd$, Schmidt number $Sc$, bioconvection Lewis number $Lb$, Peclet number $Pe$, and microorganism concentration diffusion parameter $\sigma$ but depreciates for higher values of thermal and concentration relaxation time parameters ${\delta }_1$ and ${\delta }_2.$

TABLE 1

TABLE 1. Comparison of the magnitude of the skin friction coefficient with the existing literature.

TABLE 2

TABLE 2. Comparison of the magnitude of the Nusselt number with existing studies.

TABLE 3

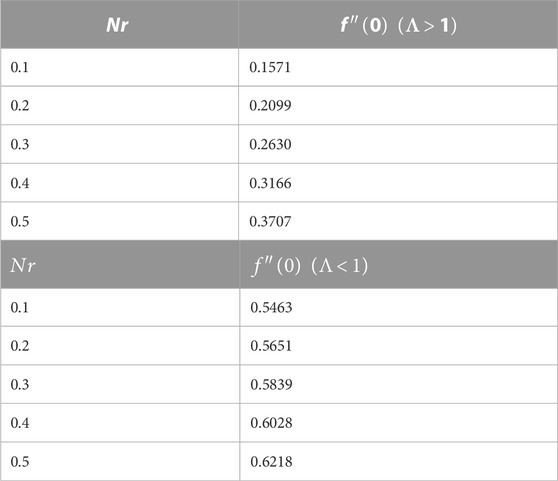
TABLE 3. Variations in skin friction against the buoyancy ratio parameter for forced ($\mathrm{\Lambda }<1$) and free ($\mathrm{\Lambda }>1$) convections.

TABLE 4

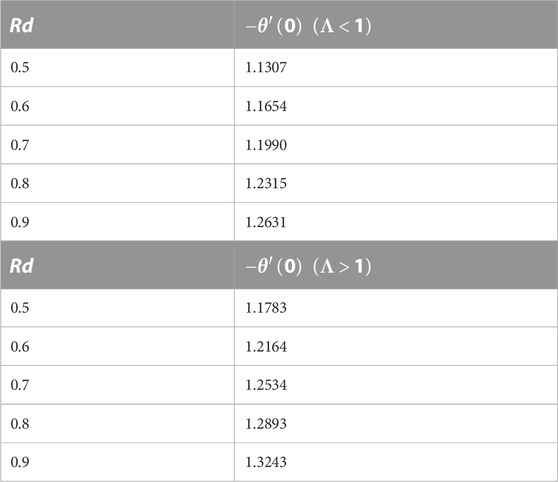
TABLE 4. Variations in the Nusselt number against the radiation parameter Rd for forced ($\mathbf{\Lambda }<1$) and free ($\mathbf{\Lambda }>1$) convections.

TABLE 5

TABLE 5. Variations in skin friction against different parameters.

TABLE 6

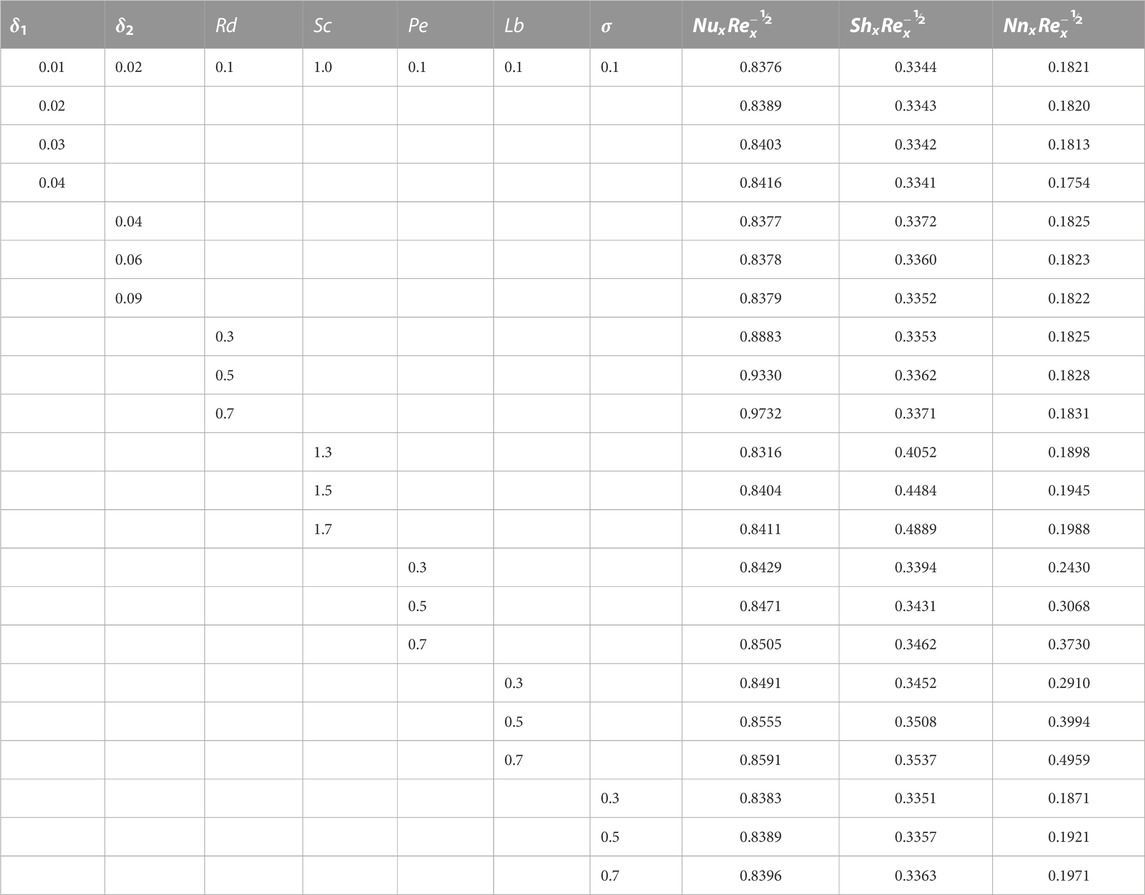
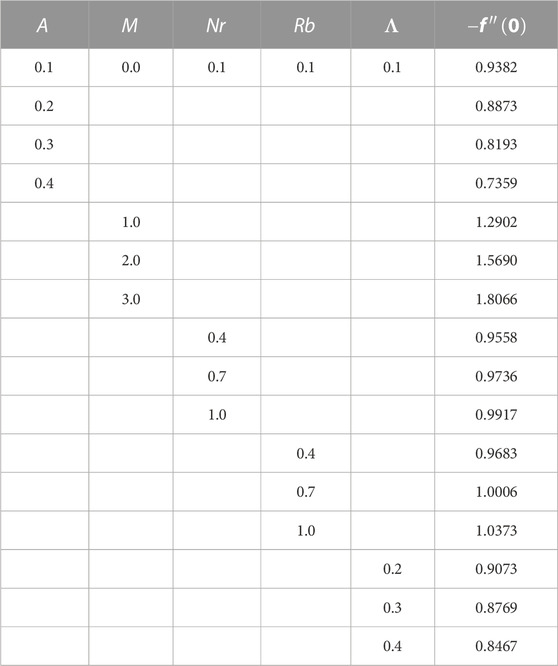
TABLE 6. Variations in the Nusselt, Sherwood, and motile microorganism density numbers against various parameters.

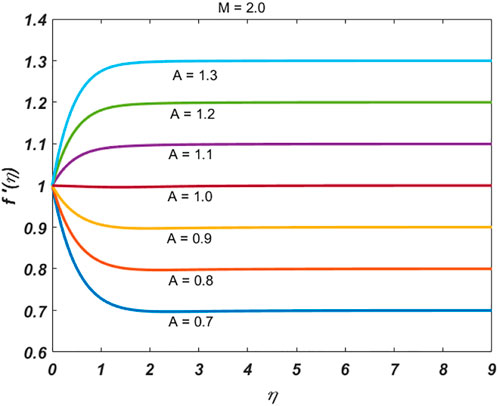
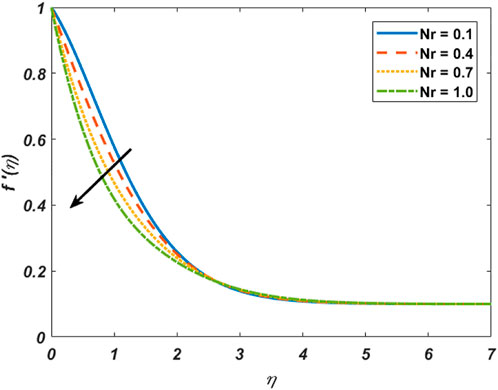
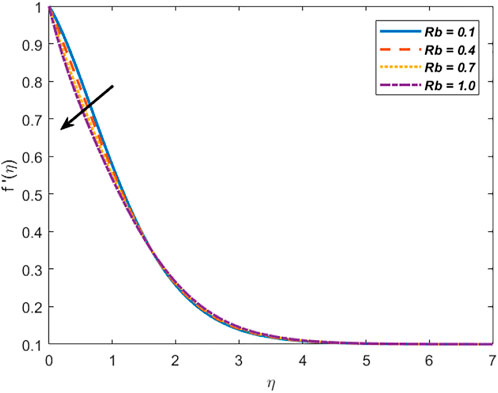
Figure 1 depicts the effect of the stretching ratio parameter $A$ on $f^{\prime }\left(\eta \right)$. It is reported that when the stretching velocity is more than the free stream velocity $\left(A<1\right)$, the velocity of the fluid as well as the boundary layer thickness depreciates. However, in the case when the stretching sheet velocity is less than the free stream velocity $\left(A>1\right)$, the fluid velocity accelerates while the thickness of the boundary layer depreciates. The influence of the magnetic parameter $M$ on the velocity field $f^{\prime }\left(\eta \right)$ is represented in Figure 2. It is reported that for surging $M$, fluid velocity depreciates. This whole phenomenon arises due to the opposing behavior of the Lorentz force. The impact of the Grashof number $\left(Gr\right)$ on the momentum distribution for the forced convective regime is illustrated in Figure 3. Since, in the present study, the effects of convection are considered, to exemplify the influence of forced convection on the velocity profile, the Reynolds number $\left(Re\right)$ is fixed at 2.5 and the Grashof number $\left(Gr\right)$ is varied from 2.0 to 3.2. Here, the buoyancy ratio parameter will take the form $\left(\mathrm{\Lambda }<1\right)$ for forced convection. It is found that by increasing the Grashof number $\left(Gr\right)$, the velocity field enhances. It is because of the fact that for $\left(\mathrm{\Lambda }<1\right)$, the impact of inertial forces is dominant over that of buoyancy forces; thus, as an outcome momentum of fluid accelerates. The influence of the Grashof number $\left(Gr\right)$ on the velocity distribution for the free convective regime is addressed in Figure 4. For interpretation about the change in the velocity distribution in the free convection situation, the Reynolds number $\left(Re\right)$ is fixed at 1.5 and the Grashof number $\left(Gr\right)$ varies from 3 to 4.2. So, the buoyancy ratio parameter will take the form $\left(\mathrm{\Lambda }>1\right)$ for free convection. It is reported that by upsurging the Grashof number $\left(Gr\right)$, the momentum field accelerates. Physically, buoyancy forces dominate inertial by uplifting the Grashof number $\left(Gr\right).$ As a result, the velocity of the fluid accelerates. Figure 5 shows the behavior of the momentum profile for the mixed convective regime including the aspects of forced $\left(\mathrm{\Lambda }<1\right)$ and free $\left(\mathrm{\Lambda }>1\right)$ convection. It is noted that for higher values of the Grashof number $\left(Gr\right)$, the velocity profile accelerates, whereas for higher magnitude of the Reynolds number $\left(Re\right)$, momentum distributions depreciate. Figure 6 depicts the impact of the Grashof number $\left(Gr\right)$ on the temperature profile for the forced convection regime. It is found that intensification in the Grashof number $\left(Gr\right)$ caused decrement in the temperature field. To depict the concerned behavior, the Reynolds number $\left(Re\right)$ is fixed at 3.5 and the Grashof number $\left(Gr\right)$ varies from 2 to 11, which shows the dominancy of the Reynolds number $\left(Re\right)$, i. e., $\left(\mathrm{\Lambda }<1\right).$ The effect of the Grashof number $\left(Gr\right)$ on the temperature profile for the free convection regime is illustrated in Figure 7. Here, the Reynolds number $\left(Re\right)$ is fixed with a value of 1.5, and the Grashof number $\left(Gr\right)$ is varied from 3 to 12, i. e., $\left(\mathrm{\Lambda }>1\right).$ It is reported that by uplifting the magnitude of the Grashof number $\left(Gr\right)$, temperature distributions depreciate. Figure 8 illustrates the behavior of temperature distributions for the mixed convective regime for forced $\left(\mathrm{\Lambda }<1\right)$ and free $\left(\mathrm{\Lambda }>1\right)$ convection. It is noted that for higher values of the Grashof number $\left(Gr\right)$, the temperature profile depreciates, while the opposite behavior is reported in the case of the Reynolds number $\left(Re\right)$. The influence of the buoyancy ratio parameter $Nr$ on $f^{\prime }\left(\eta \right)$ is highlighted in Figure 9. A boosting behavior of $Nr$ depreciates the fluid velocity. Figure 10 shows the influence of the bioconvection Rayleigh number $Rb$ on $f^{\prime }\left(\eta \right).$ In the process of bioconvection, the microorganism, whose density is smaller than fluid density, escapes toward the upper layer due to which the viscosity of the upper layer increases, and as a result, the fluid velocity depreciates. The influence of the radiation parameter $Rd$ on the profile of temperature is highlighted in Figure 11. When high temperature is required, thermal radiation is used in devices such as nuclear reactors and combustion reactors. Physically, the fluid absorbed these radiations to kill harmful microorganisms due to which the heat transfer rate increases. Radiation also carried energy due to which temperature increased. The influence of the thermal relaxation time parameter ${\delta }_1$ on the temperature profile is depicted in Figure 12. For uplifting ${\delta }_1$, the temperature profile depreciates. Physically, the time taken by the fluid to regain its original shape after removing shear stress is the relaxation time. The energy of the fluid depreciates with the passage of time, due to which the temperature field decelerates. The effect of the Schmidt number $Sc$ on the mass transfer is depicted in Figure 13. $Sc$ is the ratio of the momentum to the mass diffusivity. Diffusion is the process of transfer of molecules from a higher-concentration to lower-concentration region. The transfer of mass from the higher-concentration region to the lower one is termed as mass diffusion, where $Sc$ is inversely proportional to the mass diffusion phenomenon. Therefore, for higher values of $Sc$, the rate of mass transfer and concentration of fluid depreciates. The behavior of the motile microorganism profile $\chi \left(\eta \right)$ against the Peclet number $Pe$ is highlighted in Figure 14. It is reported that microorganism motion in the fluid is controlled by $Pe.$ $Pe$ is the ratio of the convection rate to the diffusion rate caused by the transfer of heat. For higher values of $Pe$, the convection phenomenon dominates the diffusion phenomenon. For higher values of $Pe$, the motion of microorganisms present in the fluid decreases, due to which the motile microorganism profile decreases. The impact of the bioconvection Lewis number $Lb$ on $\chi \left(\eta \right)$ is depicted in Figure 15. It is noted that with the increase in the values of $Lb,$ $\chi \left(\eta \right)$ decreases. Physically, the bioconvection phenomenon occurs in the fluid due to the collection of microorganisms. As a result, for higher values of $Lb$ density, the boundary layer thickness depreciates.

FIGURE 1

FIGURE 1. Influence of the stretching parameter $A$ on $f^{\prime }\left(\eta \right)$.

FIGURE 2

FIGURE 2. Influence of the magnetic parameter $M$ on $f^{\prime }\left(\eta \right)$.

FIGURE 3

FIGURE 3. Influence of the Grashof number $\mathit{G}\mathit{r}$ on ${\mathit{f}}^{\prime }\left(\mathit{\eta }\right)$.

FIGURE 4

FIGURE 4. Influence of the Grashof number $\mathit{G}\mathit{r}$ on ${\mathit{f}}^{\prime }\left(\mathit{\eta }\right)$.

FIGURE 5

FIGURE 5. Influence of the bioconvection Rayleigh number $Rb$ on $f^{\prime }\left(\eta \right)$.

FIGURE 6

FIGURE 6. Influence of the Grashof number $\mathit{G}\mathit{r}$ on $\mathit{\theta }\left(\mathit{\eta }\right)$.

FIGURE 7

FIGURE 7. Influence of the Grashof number $\mathit{G}\mathit{r}$ on $\mathit{\theta }\left(\mathit{\eta }\right)$.

FIGURE 8

FIGURE 8. Influence of the thermal relaxation time parameter ${\mathit{\delta }}_1$ on $\mathit{\theta }\left(\mathit{\eta }\right)$.

FIGURE 9

FIGURE 9. Influence of the buoyancy ratio parameter $Nr$ on $f^{\prime }\left(\eta \right)$.

FIGURE 10

FIGURE 10. Influence of the bioconvection Rayleigh number $Rb$ on $f^{\prime }\left(\eta \right)$.

FIGURE 11

FIGURE 11. Influence of the radiation parameter $Rd$ on $\theta \left(\eta \right)$.

FIGURE 12

FIGURE 12. Influence of the thermal relaxation time parameter ${\delta }_1$ on $\theta \left(\eta \right)$.

FIGURE 13

FIGURE 13. Influence of the Schmidt number.

FIGURE 14

FIGURE 14. Influence of the Peclet number $Sc$ on $\varphi \left(\eta \right).$ $Pe$ on $\chi \left(\eta \right)$.

FIGURE 15

FIGURE 15. Influence of bioconvection Lewis number $Lb$ on $\chi \left(\eta \right)$.

5 Conclusion

The effect of mixed convection, thermal radiation, and motile microorganism on the stagnant flow of the viscous fluid toward a stretchable sheet is examined. The governing PDEs are translated into ODEs by employing suitable similarity transformations. For the solution of the problem, the BVP4C technique is used. The central findings are as follows:

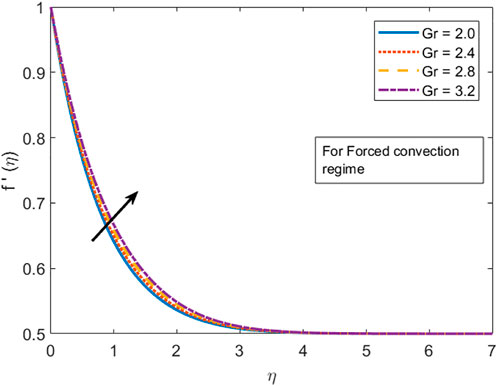
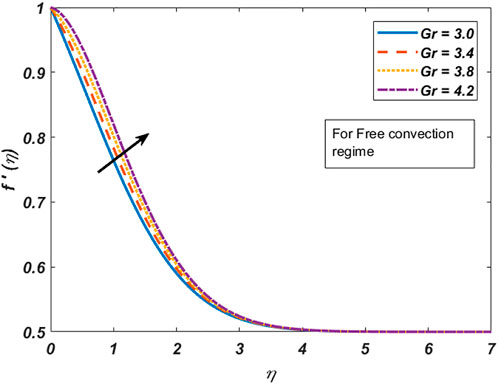
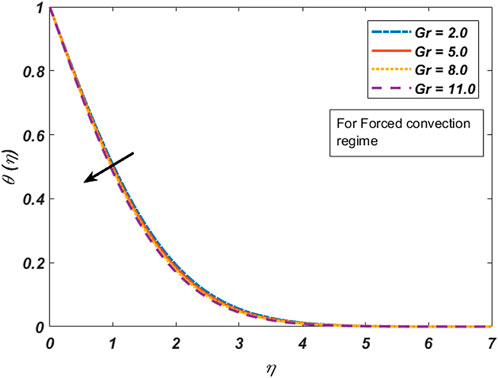
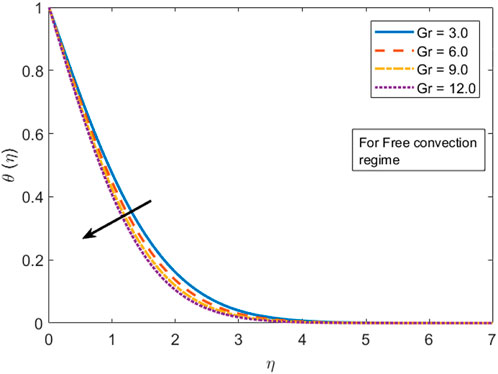
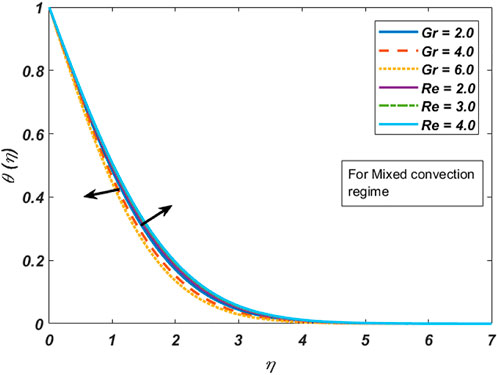
i) By uplifting the Grashof number, the velocity field accelerates, whereas the temperature profile depreciates in both forced and free convection cases

ii) The skin friction coefficient is higher in forced convection $\left(\mathrm{\Lambda }<1\right)$ than in free convection $\left(\mathrm{\Lambda }>1\right)$ due to the effective role of inertial forces

iii) Heat flux is higher in the situation of free convection $\left(\mathrm{\Lambda }>1\right)$ than in forced convection $\left(\mathrm{\Lambda }<1\right)$ due to the production of temperature gradients

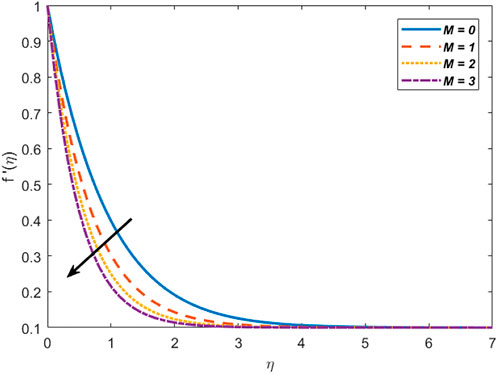
iv) The velocity decelerates for uplifting magnetic and bioconvection parameters

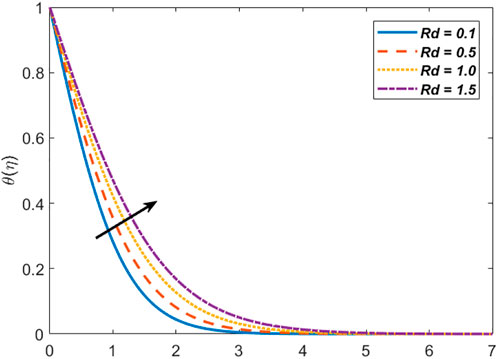
v) The temperature profile amplifies for uplifting the radiation parameter $Rd$ and depreciates for uplifting the thermal relaxation parameter ${\delta }_1$

vi) It is delineated that $Pe$ (Peclet number) controls bioconvection in the motile microorganism $\chi \left(\eta \right)$

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

SB (Conceptualization, extraction of results and discussion, write up). AU (Results validation, discussion of resutls) MIA ( Write up, results discussion, code validation).MYA (Discussion of results, conclusions, results extraction). SE (Write up of results, discussion of results, funds acquisition). IS (New results findings, discussion of new results, addition of review comments response).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Abbreviations

$A$, velocities ratio parameter; $N{u}_x$, Nusselt number; $M$, magnetic parameter; $q_m$, mass flux; $\mathrm{\Lambda }$, buoyancy ratio parameter; $S{h}_x$, Sherwood number; $Nr$, buoyancy ratio parameter; $N{n}_x$, motile microorganism density number; $Rb$, bioconvection Rayleigh number; ${\sigma }^{*}$, Stefan–Boltzmann constant; $\mathit{Pr}$, Prandtl number; $u_w$, stretching velocity; $Rd$, radiation parameter; $T_w$, temperature at the surface; $C_w$, concentration at the surface; $Sc$, Schmidt number; $N_w$, density of the motile microorganism ; $Pe$, Peclet number of the microorganism at the surface; $Lb$, bioconvection Lewis number; $T_{\infty }$, temperature far away from; $\sigma$, microorganism concentration parameter at the surface; $q_w$, surface heat flux; $C_{\infty }$, concentration far away from the surface; $k^{*}$, mean absorption coefficient; $N_{\infty }$, density of the motile microorganism far away from the surface; ${\delta }_1,{\delta }_2$, thermal and concentration relaxation time parameter; $q_r$, radiative heat flux; $U_{\infty }$, free stream velocity; $\upsilon$, kinematic viscosity; $\mathrm{\Psi }$, stream function; $\alpha$, thermal diffusivity.

References

Abbas, Z., Sheikh, M., and Pop, I. (2015). Stagnation-point flow of a hydromagnetic viscous fluid over stretching/shrinking sheet with generalized slip condition in the presence of homogeneous–heterogeneous reactions. J. Taiwan Inst. Chem. Eng. 55, 69–75. doi:10.1016/j.jtice.2015.04.001

CrossRef Full Text | Google Scholar

Bilal, M., Mazhar, S. Z., Ramzan, M., and Mehmood, Y. (2021). Time-dependent hydromagnetic stagnation point flow of a Maxwell nanofluid with melting heat effect and amended Fourier and Fick's laws. Heat. Transf. 50 (5), 4417–4434. doi:10.1002/htj.22081

CrossRef Full Text | Google Scholar

Cao, W., Animasaun, I. L., Yook, S. J., Oladipupo, V. A., and Xianjun, J. (2022). Simulation of the dynamics of colloidal mixture of water with various nanoparticles at different levels of partial slip: Ternary-hybrid nanofluid. Int. Commun. Heat Mass Transf. 135, 106069. doi:10.1016/j.icheatmasstransfer.2022.106069

CrossRef Full Text | Google Scholar

Cattaneo, C., and Calore, S. C. (1948). Sulla condizione del Calore. Atti Semin. Mat. Fis. Univ. Modena Reggio Emilia 3, 83–101. doi:10.1007/978-3-642-11051-1_5

CrossRef Full Text | Google Scholar

Chamkha, A. J., Rashad, A. M., Kameswaran, P. K., and Abdou, M. M. M. (2017). Radiation effects on natural bioconvection flow of a nanofluid containing gyrotactic microorganisms past a vertical plate with streamwise temperature variation. J. Nanofluids 3, 587–595. doi:10.1166/jon.2017.1351

CrossRef Full Text | Google Scholar

Chamkha, Ali. (2015). Stagnation-point flow of a viscous fluid towards a stretching surface with variable thickness and thermal radiation. Int. J. Ind. Math. 7, 77–85.

Google Scholar

Christov, C. I. (2009). On frame indifferent formulation of the Maxwell–Cattaneo model of finite-speed heat conduction. Mech. Res. Commun. 36 (4), 481–486. doi:10.1016/j.mechrescom.2008.11.003

CrossRef Full Text | Google Scholar

De, P. (2019). Impact of dual solutions on nanofluid containing motile gyrotactic micro-organisms with thermal radiation. Bio Nano Sci. 1, 13–20. doi:10.1007/s12668-018-0584-6

CrossRef Full Text | Google Scholar

Dehghan, M., and Abbaszadeh, M. (2017). A finite element method for the numerical solution of Rayleigh–Stokes problem for a heated generalized second grade fluid with fractional derivatives. Eng. Comput. 33 (3), 587–605. doi:10.1007/s00366-016-0491-9

CrossRef Full Text | Google Scholar

Dehghan, M., and Abbaszadeh, M. (2016). Proper orthogonal decomposition variational multiscale element free Galerkin (POD-VMEFG) meshless method for solving incompressible Navier–Stokes equation. Comput. Methods Appl. Mech. Eng. 311, 856–888. doi:10.1016/j.cma.2016.09.008

CrossRef Full Text | Google Scholar

Ellahi, R., Muzammal, H. T., Mohsan, H., and Vafai, K. (2017). On boundary layer nano-ferroliquid flow under the influence of low oscillating stretchable rotating disk. J. Mol. Liq. 229, 339–345. doi:10.1016/j.molliq.2016.12.073

CrossRef Full Text | Google Scholar

Esfahani, J. A., Akbarzadeh, M., Rashidi, S., Rosen, M. A., and Ellahi, R. (2017). Influences of wavy wall and nanoparticles on entropy generation over heat exchanger plat. Int. J. Heat Mass Transf. 109, 1162–1171. doi:10.1016/j.ijheatmasstransfer.2017.03.006

CrossRef Full Text | Google Scholar

Ferdows, M., Reddy, M. G., Sun, S., and Alzahrani, F. (2019). Two-dimensional gyrotactic microorganisms flow of hydromagnetic power law nanofluid past an elongated sheet. Adv. Mech. Eng. 11, 168781401988125. doi:10.1177/1687814019881252

CrossRef Full Text | Google Scholar

Fourier Jbj., T. A. (1822). Theorie analytique de la chaleur. Paris: Cambridge University Press.

Google Scholar

Hashim, H., Mohamed, M. K. A., Ishak, N., Sarif, N. M., and Salleh, M. Z. (2019). Thermal radiation effect on MHD stagnation point flow of Williamson fluid over a stretching surface. J. Phys. Conf. Ser. 1366, 012011. doi:10.1088/1742-6596/1366/1/012011

CrossRef Full Text | Google Scholar

Hiemenz, K. (1911). Die Grenzschicht an einem in den gleichförmigen Flüssigkeitsstrom eingetauchten geraden Kreiszylinder. Dingler’s Polytech. J. 326, 321–324.

Google Scholar

Homann, F. (1936). Der Einfluss grosser Zahigkeit bei der Stromung um den Zylinder und um die Kugel. Z Angew. Math. Mech. 16, 153–164. doi:10.1002/zamm.19360160304

CrossRef Full Text | Google Scholar

Hosseinzadeh, H., Mehdi, D., and Mirzaei, D. (2013). The boundary elements method for magneto-hydrodynamic (MHD) channel flows at high Hartmann numbers. Appl. Math. Model. 37 (4), 2337–2351. doi:10.1016/j.apm.2012.05.020

CrossRef Full Text | Google Scholar

Ibrahim, W., Shankar, B., and Nandeppanavar, M. M. (2013). MHD stagnation point flow and heat transfer due to nanofluid towards a stretching sheet. Int. J. heat mass Transf. 1-2, 1–9. doi:10.1016/j.ijheatmasstransfer.2012.08.034

CrossRef Full Text | Google Scholar

Ishak, A., Lok, Y. Y., and Pop, I. (2010). Stagnation-point flow over a shrinking sheet in a micropolar fluid. Chem. Eng. Comm. 197, 1417–1427. doi:10.1080/00986441003626169

CrossRef Full Text | Google Scholar

Kamranian, M., Mehdi, D., and Mehdi, T. (2017). An adaptive meshless local Petrov–Galerkin method based on a posteriori error estimation for the boundary layer problems. Appl. Numer. Math. 111, 181–196. doi:10.1016/j.apnum.2016.09.007

CrossRef Full Text | Google Scholar

Khan, N. S. (2018). Bioconvection in second grade nanofluid flow containing nanoparticles and gyrotactic microorganisms. Braz. J. Phys. 3, 227–241. doi:10.1007/s13538-018-0567-7

CrossRef Full Text | Google Scholar

Khan, U., Naveed, A., Ullah Khan, S. I., and Tauseef, S. M. D. (2014). Thermo-diffusion effects on MHD stagnation point flow towards a stretching sheet in a nanofluid. Propuls. Power Res. 3, 151–158. doi:10.1016/j.jppr.2014.07.006

CrossRef Full Text | Google Scholar

Khan, U., Zaib, A., Abu Bakar, S., Ishak, A., Baleanu, D., Sherif, E. S. M., et al. (2022). Computational simulation of cross-flow of Williamson fluid over a porous shrinking/stretching surface comprising hybrid nanofluid and thermal radiation. AIMS Math. 7 (4), 6489–6515. doi:10.3934/math.2022362

CrossRef Full Text | Google Scholar

Khashi’ie, N. S., Arifin, N. M., Rashidi, M. M., Hafidzuddin, E. H., and Wahi, N. (2020). Magnetohydrodynamics (MHD) stagnation point flow past a shrinking/stretching surface with double stratification effect in a porous medium. J. Therm. Analysis Calorim. 139 (6), 3635–3648. doi:10.1007/s10973-019-08713-8

CrossRef Full Text | Google Scholar

Kuznetsov, A. V. (2011). Non-oscillatory and oscillatory nanofluid bio-thermal convection in a horizontal layer of finite depth. Eur. J. Mechanics-B/Fluids 302, 156–165. doi:10.1016/j.euromechflu.2010.10.007

CrossRef Full Text | Google Scholar

Lok, Y. Y., Ishak, A., and Pop, I. (2011). MHD stagnation-point flow towards a shrinking sheet. Int. J. Numer. Meth Heat. Fluid Flow. 21, 61–72. doi:10.1108/09615531111095076

CrossRef Full Text | Google Scholar

Lyu, J., Chang, S., Gao, L., Xing, Z., and Bai, M. (2022). Experimental investigation on the heat transfer enhancement of wall modification inside a piston cooling gallery. Exp. Heat. Transf. 2022, 1–22. doi:10.1080/08916152.2022.2151056

CrossRef Full Text | Google Scholar

Madhavadas, V., Das, D., Mohta, K. A., and Prabu, S. S. (2021). Comparative analysis on heat transfer of various fin profile using solid works: A systematic review. IOP Conf. Ser. Earth Environ. Sci. 850, 012029. doi:10.1088/1755-1315/850/1/012029

CrossRef Full Text | Google Scholar

Mahapatra, T. R., and Gupta, A. S. (2002). Heat transfer in stagnation-point flow towards a stretching sheet. Heat Mass Transf. 6, 517–521. doi:10.1007/s002310100215

CrossRef Full Text | Google Scholar

Mahapatra, T. R., and Gupta, A. S. (2003). Stagnation-point flow towards a stretching surface. Can. J. Chem. Eng. 81, 258–263. doi:10.1002/cjce.5450810210

CrossRef Full Text | Google Scholar

Mirzaei, D., and Mehdi, D. (2012). New implementation of MLBIE method for heat conduction analysis in functionally graded materials. Eng. analysis Bound. Elem. 36 (4), 511–519. doi:10.1016/j.enganabound.2011.11.007

CrossRef Full Text | Google Scholar

Mustafa, M., Hayat, T., Pop, I., Asghar, S., and Obaidat, S. (2011). Stagnation-point flow of a nanofluid towards a stretching sheet. Int. J. Heat Mass Transf. 54, 5588–5594. doi:10.1016/j.ijheatmasstransfer.2011.07.021

CrossRef Full Text | Google Scholar

Mustafa, T. (2021). Heat transfer enhancement feature of the Non-Fourier Cattaneo–Christov heat flux model. J. Heat Transf. 9, 4051671. doi:10.1115/1.4051671

CrossRef Full Text | Google Scholar

Mustafa, T. (2021). Stagnation-point flow and heat transfer over stretchable plates and cylinders with an oncoming flow: Exact solutions. Chem. Eng. Sci. 238, 116596. doi:10.1016/j.ces.2021.116596

CrossRef Full Text | Google Scholar

Pal, D., Mondal, S. K., and Mondal, H. (2019). Entropy generation on MHD Jeffrey nanofluid over a stretching sheet with nonlinear thermal radiation using spectral quasilinearisation method. Int. J. Ambient Energy 42, 1712–1726. doi:10.1080/01430750.2019.1614984

CrossRef Full Text | Google Scholar

Prasad, K. V., Rajashekhar, C., Hanumesh, V., Ashwini, B., and Animasaun, I. L. (2023). Analysis of couple stress nanofluid flow under convective condition in the temperature-dependent fluid properties and Lorentz forces. Heat. Transf. 1, 216–235. doi:10.1002/htj.22692

CrossRef Full Text | Google Scholar

Rashidi, S., Esfahani, J. A., and Ellahi, R. (2017). Convective heat transfer and particle motion in an obstructed duct with two side by side obstacles by means of DPM model. Appl. Sci. 7, 431. doi:10.3390/app7040431

CrossRef Full Text | Google Scholar

Sajid, T., Jamshed, W., Shahzad, F., Mohamed, R. E., Sohail, M., and Ullah, I. (2022). Influences of Fourier and Fick's relations in stagnation point flow of Reiner-Philippoff fluid containing oxytactic-microorganisms with variable molecular diffusivity. Waves Random Complex Media 2022, 1–22. doi:10.1080/17455030.2022.2148013

CrossRef Full Text | Google Scholar

Saleem, S., Rafiq, H., Al-Qahtani, A., El-Aziz, M. A., Malik, M. Y., and Animasaun, I. L. (2019). Magneto Jeffery nanofluid biconvection over a rotating verticle cone due to gyrotactic microorganism. Math. Problem Eng. 2019, 1–11. doi:10.1155/2019/3478037

CrossRef Full Text | Google Scholar

Shirvan, K. M., Ellahi, R., Mamourian, M., and Moghiman, M. (2017). Effects of wavy surface characteristics on natural convection heat transfer in a cosine corrugated square cavity filled with nanofluid. Int. J. Heat Mass Transf. 107, 1110–1118. doi:10.1016/j.ijheatmasstransfer.2016.11.022

CrossRef Full Text | Google Scholar

Shirvan, K. M., Mamourian, M., Mirzakhanlari, S., and Ellahi, R. (2017). Numerical investigation of heat exchanger effectiveness in a double pipe heat exchanger filled with nanofluid: A sensitivity analysis by response surface methodology. Powder Technol. 313, 99–111. doi:10.1016/j.powtec.2017.02.065

CrossRef Full Text | Google Scholar

Syazana, A. N., Norfifah, B., Mustafa, T., Arifin, N. M., and Haliza, R. (2020). Analytical and stability analysis of MHD flow past a nonlinearly deforming vertical surface in Carbon Nanotubes. Alexandria Eng. J. 59, 497–507. doi:10.1016/j.aej.2020.01.024

CrossRef Full Text | Google Scholar

Wahid, N. S., Arifin, N. M., Mustafa, T., Mohd, E. H. H., and Rahmin, N. A. A. (2020). MHD hybrid Cu-Al2O3/water nanofluid flow with thermal radiation and partial slip past a permeable stretching surface: Analytical solution. J. Nano Res. 64, 75–91. doi:10.4028/www.scientific.net/jnanor.64.75

CrossRef Full Text | Google Scholar

Wang, C. Y. (2008). Stagnation flow towards a shrinking sheet. Int. J. Non Linear Mech. 43, 377–382. doi:10.1016/j.ijnonlinmec.2007.12.021

CrossRef Full Text | Google Scholar

Zhao, Y., Zhuotong, N., Hailong, J., and Zhao, L. (2022). Convective heat transfer of spring meltwater accelerates active layer phase change in Tibet permafrost areas. Cryosphere 16 (3), 825–849. doi:10.5194/tc-16-825-2022

CrossRef Full Text | Google Scholar