Energy multi-scale method to analyze the scale effect of soil particles

As a common geological material, soil is a key aspect of construction engineering. Soil has typical multi-scale characteristics, but current multi-scale methods analyze these characteristics only in regard to geometric space. More exploration of the coupling influence mechanism of the basic properties of particles on the microstructure and macroscopic properties of soil is needed. This study analyzed the influence of geometric scale and mineral composition on the surface energy of particles at the microscopic level for development of the energy multi-scale method. Experiments were performed to determine the influence of mineral composition and particle size on the plasticity index (I_p) of the soil, and experimental results are discussed and interpreted quantitatively using the energy multi-scale method. The conclusions derived from this work are as follows: 1) the mineral composition and particle size of the soil can cause interface and surface effects; 2) the comprehensive ratio of micro-force to weight (CRFW) of the particles can be determined using the energy multi-scale method and quantitatively reflects the influence of particle size and mineral composition on the microscopic properties of the soil; and 3) the energy multi-scale method explains the mechanism of the plasticity index of soil and has allowed identification of a new division of soil plasticity. When the CRFW was used as the control index, the plasticity index of the three materials was practically the same, even if the mineral composition and particle sizes of the three materials were different.

1 Introduction

Soil is one of the most common geological materials and it has clear effects on human life; slope slides, debris flow, and the collapse of building foundations are all due to soil failure (Guzzetti and Peruccacci, 2008; Pham and Kim, 2018; Li and Zhao, 2022; Samprada Pradhan and Toll, 2022; Liang and Ge, 2023). Particles in soils span about five orders of magnitude in size, from rubble to clay, and show obvious cross-scale characteristics in geometric space. Soil particles also show mineral composition diversity, with varying ratios that indicate differences in primary and secondary minerals. These particles, with irregular shapes, different sizes, and varying mineral content, accumulate to form the complex spatial structure of soil (Mitchell and Soga, 2005). During the soil deformation process, particles of different sizes and different mineral composition in different scale-spaces vary in mechanical and deformation performance. Therefore, there is an obvious size effect on soil behavior (Fang and Bo, 2016; Yang and Liu, 2017).

A series of studies showed that particles with different size and mineral composition influenced the force transmission and coordination of deformation between particles at the contact surface between particles at the micro-level and demonstrated the properties of soils at the macro-level. Monkul and Ozden (2007) found that, in the microstructure of fine mixed sand, the interactions between fine and coarse particles affected the overall stress–strain behavior of soils. Chang and Yin (2010) also suggested that the soil was an assembly of particles and that the stress–strain relationship of the assembly was determined by integrating the behavior of the interparticle contacts in all orientations. Sabbar and Chegenizadeh (2017) found that fine soil particles formed a certain structure to reduce the pores between the particles, thereby changing the soil’s resistance to liquefaction. Dai and Yang (2015) revealed that the occurrence of liquefaction and temporary reduction of soil strength was mainly ascribed to loss of support from the contacts between fine particles, as well as those between fine and large particles. Li and Zhang (2016) used CT images and FEM to demonstrate that the first cracks usually appeared at soil–gravel interfaces, which is the weak part of a soil–rock mixture. Chen and Fang (2019) found that the diffuse double layers formed on particle surfaces at the microscopic level affected the effective pore for seepage, thereby leading to non-Darcy flow in some clay soils. Gong and Nie (2019) analyzed the type of contact between particles, including coordination number and normal contact force, at the microscopic level, to reveal the contribution of each contact type to the residual shear strength of the soil. Ni and Huang (2020) indicated that, according to the electric double layer theory, mineral particles have an important impact on the properties of soil due to their strong surface electrical characteristics. Phan and Bui (2021) suggested that the shear resistance of the soil is governed mainly by particle contact type and the current fractions of those types. Zhu and Zhang (2020) believed that larger particles were more likely to form an occlusal structure and provide higher frictional force, and that sand was more likely to slide when the particle size was smaller. Bai and Zhou (2021) built a coupled thermo-hydro-mechanical mechanism to explore the soil particle rearrangement of granular thermodynamics. Chen and Tong (2022) found that the charges on particle surfaces adsorb water into the pores, thereby affecting surface characteristics between the particles and thus the permeability characteristics of the soil. Therefore, it is necessary to establish a multi-scale research method linking macro and micro scales to explore the microcosmic mechanism behind the complex scale phenomenon of soil; this endeavor has become the frontier of current geotechnical field research (Mingjing, 2019).

Scholars have proposed different multi-scale methods to research the scale phenomenon of soil. First, the strain gradient theory and the couple stress theory (Cosserat, 1909; Ashby, 1970) were proposed to solve the problem of the granularity of materials and rotation of particles, as well as the discontinuity in the stress and strain transformation between the contact interface of the particles when entering a certain microscopic space scale. Researchers continued to improve these two theories for use in soil. For example, Mühlhaus (1989) derived a continuous model of regular structures within the framework of the Cosserat theory. Based on this model, the ultimate load problem of tunnel statics was solved by using the finite element method. After homogenization, Mühlhaus and Oka (1996) introduced continuous concepts, such as stress and couple stress, to directly homogenize discrete motion equations to obtain a general continuous model for granular media. Oda and Iwashita (2000), through tests on sand, found that couple stresses existed in a shear band in a manner consistent with the change of the particle rotation gradient from negative to positive. The presence of small couple stress still plays an important role in the development of microstructure in shear bands. Wang and Zhang (2003) theoretically analyzed the stability and instability sliding of an elastic rock mass in a shear zone and introduced the strain gradient plasticity theory, which allowed determination of the theoretical relationship between shear stress and the relative displacement of the upper and lower walls of a shear zone. Lu and Cui (2003) processed numerical simulation to investigate the influences of shear strain gradient and other factors on the evolution of a shear band. In the framework of a Cosserat continuum, Gudehus and Nuebel (2004) explored the evolution of a sand shear band trough using a numerical method, and the results showed that shear bands can evolve spontaneously in the interior of a granular body, even under homogeneous stress or displacement boundary conditions. Riahi and Curran (2009) used the finite element method to implement the adopted Cosserat formulation in buckling analysis of three-dimensional layered continua. Research in this area has continued to increase (Chu and Yu, 2012; Tang and Song, 2015; Tang and Wei, 2020; Tang and Wei, 2021; Borst and Alizadeh, 2022). The couple stress and strain gradient theories may be used to solve some problems with scale effects of the soil caused by the change in research scale, but these theories are based on the continuum; therefore, the anisotropy problem caused by granularity and mineral composition are not solvable using the same methods.

The discrete element method (DEM) takes the soil particle as the basic research unit, clearly describes the particle properties of the soil, and describes the macroscopic properties of the soil through the interaction of particle groups (Thornton, 2000). This method has become popular for studying multi-scale phenomena of soil. Zeghal and Shamy (2008) analyzed the liquefaction of saturated soil particles in loosely cemented sediments through the coupling of discrete elements and continuous elements. Li and Wan (2011) combined the DEM with the finite element method (FEM) and proposed a method for multi-scale analysis of granular materials at two macroscopic levels. Nguyen and Combe (2014) proposed a multi-scale modeling method for cohesive granular materials; at the micro-level, the DEM was used to simulate dense particle accumulation, and at the macro level, the numerical solution was obtained through the FEM. Zhao and Feng (2017) conducted a 3D numerical study on the formation of landslide dams in open fluid channels by using the DEM combined with computational fluid dynamics. Additionally, Liu and Zhixiang (2021) constructed a numerical model capable of reproducing the estimation of the impact of debris flow by coupling FEM and DEM, Zhang and Zhang (2022) conducted DEM simulations to quantify the relationship between fine particle loss and upscaling from particle to cell and then revealed the multi-scale response of seepage erosion in sandy strata, and Fang and Yang (2023) analyzed the progressive failure process of the stratified rock mass through the analysis of contact fracture events and the evolution of contact forces using the DEM-FEM numerical method. DEM and the DEM-FEM coupling method can intuitively display the particle properties of soil. However, limited by current computing capability, the scale of DEM or DEM-FEM models is generally small (Yang and Wang, 2023) and the particles in the models are greatly simplified. For example, for fine-grained sand–gravel mixed soil, the DEM method only models large particles and simplifies fine particles into contact parameters between particles to reduce the amount of calculation required. Clearly, this method cannot reflect the effect of gradation of particles on soil properties. In addition, due to the unclear mechanism of the coupling effects of factors such as particle size and mineral composition on the particle contact surface, the various mineral compositions and the complex contact properties between the particles result in cumbersome calibration of contact parameters in the DEM that ultimately lacks credibility.

The multi-scale phenomenon of soil has long been known, and a variety of multi-scale analysis methods have been developed. However, there are still defects in these methods when used for solving some multi-scale problems with soil. Regardless of the kind of model that is constructed to connect the macro and micro, the transmission of force between particles, the coordination of strain, and even the construction of soil microstructure are realized through the contact surface. The impact of various characteristics of soil particles at the microscopic level on soil engineering properties should be directly reflected on the contact surface between particles, and the surface energy of soil particles determines the surface of particles and the contact surface between particles. Therefore, in this study, the comprehensive ratio of micro-force to weight was proposed to quantitatively analyze the coupled influence of size and mineral composition of particles on the surface energy of soil particles. We used this energy multi-scale method of analysis to reveal the mechanism of the soil plasticity index. Our results are significant as they support accurate calibration of contact parameters of the DEM method and in promoting the application of the DEM method in soil.

2 Energy multi-scale method

2.1 Energy multi-scale property of soil

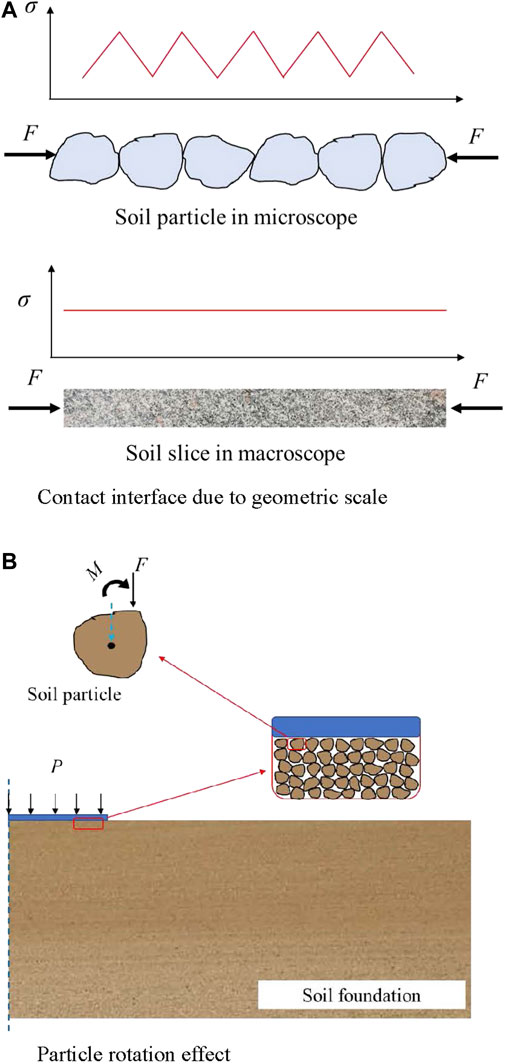
Materials are not infinitely separable, and the intrinsic properties of a particle in the internal length range will affect the mechanical properties of the microstructure. Interface effects and surface effects are ignored at the macroscopic level, but they play important roles at the microscopic level (Chiu and Chen, 2011; Li and Mi, 2019; Lu and Guo, 2019; Wang and Zhang, 2019). Soil shows a typical multi-scale property; that is, the stress and deformation of soil are different in each scale space. A continuous soil slice at the macroscopic level is shown in Figure 1A, which demonstrates that the stress distribution in the soil slice is nearly uniform under the load. However, at the microscopic level, where the research focus is a single soil particle, contact surface discontinuity causes the stress to appear abruptly on the contact surfaces of the particles. In Figure 1B, the cross-scale deformation behavior of the foundation from the macro-level to the micro-level is illustrated. At the macroscopic level, the foundation produced continuous compressive deformation under uniform load, whereas at the microscopic level, the soil particles showed an obvious rotational effect. Microscopically, the particles appeared in individual forms and the contact between particles was highlighted. However, macroscopically, the number of particles in a soil slice is huge and the individuality of particles is weakened; therefore, particle groups are treated as a continuous medium and the contact between particles is no longer considered. In general, the effects of interface properties between particles on soil properties change at different scales.

FIGURE 1

FIGURE 1. Scale effect of soil.

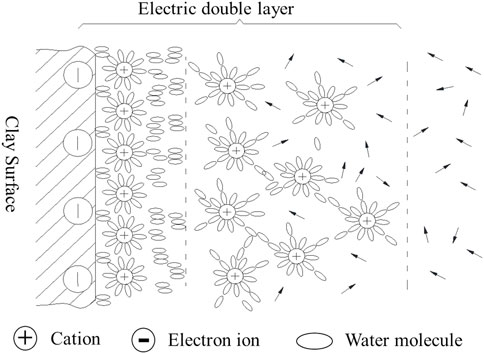
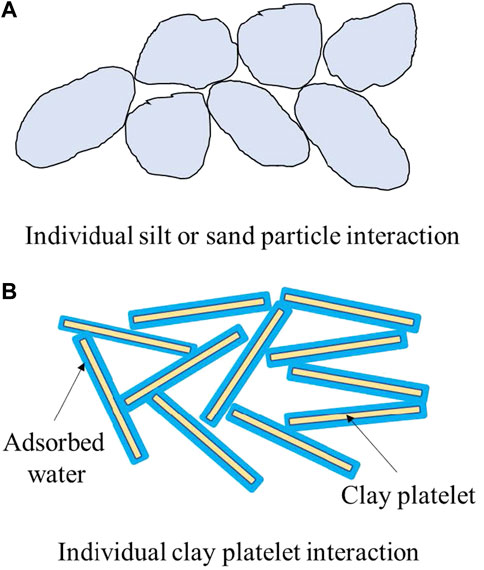
For soil particles, when particle size decreases, the specific surface area of particles and the proportion of charges on the surface of particles increase gradually; thus, the ability to adsorb ions and water molecules increases. As a result, the adsorbed water and the electric double layer formed on the surface of the particles are more obvious, which in turn affects the contact surface between the particles. At the same time, a typical soil mixture contains clay minerals and non-clay minerals. Most clay minerals have excess negative charges on the surface of particles due to isomorphous replacement. The negative charges adsorb the polar water molecules and cations to form an electric double layer (Figure 2). Clay particles tend to be smaller in size and have a larger specific surface area; therefore, the volume of adsorbed water and the electric double layer on the surface of particles is considerably larger than the volume of the particles. When clay particles are in contact, the contacts occur mainly between the water films on the particle’s surface. For non-clay minerals, the ability to adsorb ions and water molecules is very weak because the excess charges on the surface of the non-clay minerals are less; the adsorbed water on the surface of such mineral particles is so thin that the contact between particles is mainly direct contact between mineral crystals. For soil materials, both particle size and mineral composition influence the properties of the particle surface, thereby affecting the contact surface between particles, as shown in Figure 3. Therefore, as a granular medium, soil particles also exhibit the surface effects and interface effects.

FIGURE 2

FIGURE 2. Diffuse electric double layer.

FIGURE 3

FIGURE 3. Contact states of different particles.

The surface and interface effects of soil particles affect the soil microstructure (Guo and Yu, 2019) and thereby affect the soil engineering properties at the macroscopic level, which is the basis for the soil-scale phenomenon. For example, particle size affects the occlusion between sand particles; increased coarse particle content leads to increased microstructure rolling and increased internal friction angle of the soil at the macroscopic level; the electric double layer (DEL) and the adsorbed water on the surface of clay particles result in a cohesive effect among the particles with increased cohesive force and increased clay mineral content; the balance between the microscopic force and the gravity of the particles affects the formation of the microscopic and macroscopic structure of the soil; at the same time, the mineral components have different adsorption water states on the surface, which will also directly affect the state of the liquid flowing over its surface, thereby affecting the permeability characteristics of the soil.

2.2 Energy multi-scale equation for soil particles

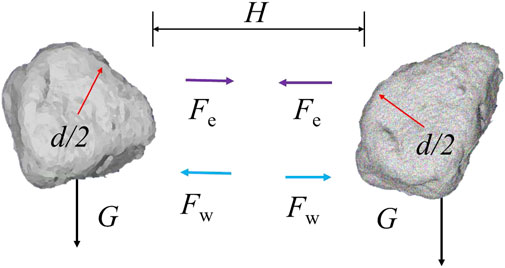
The surface state of a particle is largely determined by the particle’s ability to adsorb water or other ions, and this ability is called the particle’s surface energy. This adsorption energy is mainly manifested as the van der Waals force between particles and the electric field force generated by the excess charges on the particle surface. At the micro-level, the forces with high size factor power, such as gravity and inertial force, are relatively small; while the forces with low size factor power, such as surface tension, van der Waals force, and electric field force, are relatively large, as shown in Figure 4. The surface and contact interface features of the particles are produced mainly by the direct action of these forces. Among these forces, gravity, van der Waals force, and Coulomb force can be used to characterize both the particle size and the mineral composition of soil particles.

FIGURE 4

FIGURE 4. Microscopic force between particles.

In this study, a relationship between gravity, van der Waals force, and Coulomb force was established. As introduced previously, these forces can be used to characterize the adsorption energy of the particle surface. Therefore, our energy multi-scale method involves calculation of the ratio of the micro-Coulomb force to gravity and the ratio of the micro-van der Waals force to gravity. The equations used for these calculations are expressed as follows:

${\lambda }_e=\frac{F_e}{G}=\frac{1}{4\pi {\epsilon }_0}\frac{q_1{q}_2}{r^2}/\frac{\rho g\pi d^3}{6}=\frac{3q_1{q}_2}{2{\pi }^2{\epsilon }_0{r}^2\rho g{d}^3},(1)$

${\lambda }_w=\frac{F_w}{G}=\frac{Ad}{24H^2}/\frac{\rho g\pi d^3}{6}=\frac{A}{4\rho g\pi d^2{H}^2},(2)$

where λ_e and λ_w are the ratio of micro-Coulomb force to gravity and the ratio of micro-van der Waals force to gravity, respectively, F_e is Coulomb force, F_w is van der Waals force, G is gravity, ε₀ is vacuum permittivity, q₁ and q₂ are particle charge, r is particle center spacing, ρ is the particle density, d is the particle diameter, A is the Hamaker constant, and H is the clear particle spacing. Soil particles exist mainly in a water environment, and the amount of charge associated with the particles can be obtained according to colloid and interface chemistry and electrostatic theory (Helmy, 1998; Missana and Adell, 2000):

$q=2\pi {\epsilon }_0{\varphi }_0,(3)$

where φ₀ is the particle surface potential and the clay particle surface potential can be determined by the cation exchange capacity (CEC) method. For the convenience of calculation and the unification of measurement indicators, the adjustment coefficient α is used to combine λ_e and λ_w as one parameter, and this parameter is called the comprehensive ratio of micro-force to weight (CRFW). The expression of λ is as follows:

$\lambda =\alpha {\lambda }_e+\left(1-\alpha \right){\lambda }_w=\alpha \frac{F_e}{G}+\left(1-\alpha \right)\frac{F_w}{G}.(4)$

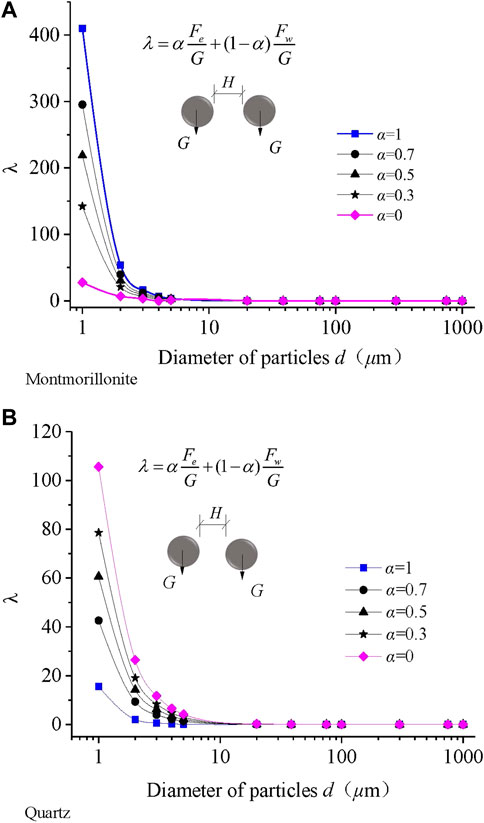
The adjustment coefficient α must be determined according to the properties of the material. Taking the common soil minerals montmorillonite and quartz as examples, the CRFW of these two mineral particles were calculated. When the value of the adjustment coefficient α was varied, the CRFW of montmorillonite and quartz particles also changed according to particle size; these data are displayed in Figure 5. As shown in the figure, when α is 0 the λ degenerates as λ_w and when α is 1 the λ degenerates as λ_e, respectively.

FIGURE 5

FIGURE 5. Relationship of CRFW with particle diameter.

Figure 5 demonstrates that the relationships between λ and the particle sizes of quartz and montmorillonite were basically the same, and when particle size decreased, λ increased gradually. The specific surface area of particles is relative to particle size. As a result, the amount of negative charge on the particle surface increased and the surface energy increased; therefore, the thickness of the water film on the particle surface became larger and the interface between particles was mainly soft contact between water layers. In contrast, with increased particle size, the effect of adsorbed water on the particle surface decreased, and the contact between particles was mainly hard contact between mineral crystals. It is reasonable to use the CRFW to describe the variation of soil properties with particle size. At the same time, it can be seen from Figure 5 that, although the particle size of two different mineral particles is the same, their CRFW values can be very different. As demonstrated previously, compared with non-clay minerals, the isomorphic replacement of clay minerals is more obvious, and the negative charge density of particle surfaces is higher, so the surface effect is more obvious. This also shows the rationality of the formula for CRFW. In summary, the CRFW in the energy multi-scale method reflects the mechanism of property changes based on particle size and mineral composition at the micro-level.

3 The plasticity index of soil explained by the energy multi-scale method

3.1 Experimental plan

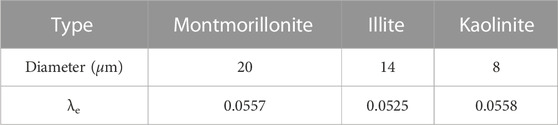
The plasticity index of soil is important for engineering endeavors involving soils such as clay and silty clay. A large number of studies have found that the shear strength, permeability coefficient, and liquefaction index of plastic soils were directly or indirectly related to the plasticity index of soil. Furthermore, the plasticity index of plastic soil reflects the water adsorption capacity of the surface of the particles, which is a direct reflection of the surface energy of the particles. At the same time, the mineral composition and the diameter of the soil particle are the main factors in the calculation of the CRFW by the energy multi-scale method. Therefore, in this study, the surface potential and the diameter of the particles were tested first. Next, the samples with different mineral compositions and relative content, as well as different particle sizes, were prepared to assess the plasticity index of the soil. In terms of soil mineral composition, three typical clay minerals, montmorillonite, kaolinite, and illite, and two non-clay minerals, quartz and feldspar, were selected for these experiments. Due to the high purity of commercial soil minerals, customized commercial soil mineral powders were selected as test material. Samples with clay mineral content of 100%, 60%, 40%, 20%, and 0% were assessed, and the diameter of all mineral particles was 2 μm. Sample characteristics are summarized in Table 1.

TABLE 1

TABLE 1. Sample characteristics.

The dried mineral powders were mixed evenly according to the designed mass ratio, then a small amount of water was added to wet the mineral particles of the soil; the samples were left to stand overnight. Finally, the liquid and plastic limits of the aforementioned soil samples were measured using a liquid–plastic limit tester, and the plasticity index of each group of samples was calculated using the liquid and plastic limit data.

3.2 Results and discussion

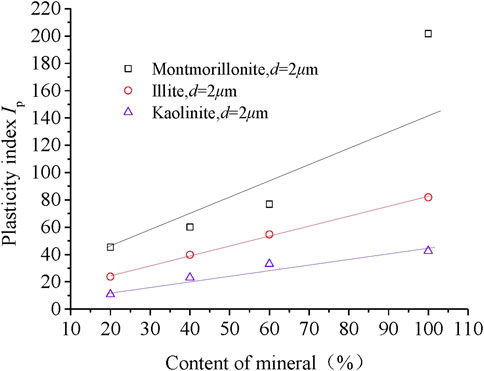
After the liquid–plastic test, the plasticity index (I_p) of each sample was assessed, as shown in Figure 6; the I_p of all soil samples increased with increased clay mineral content, but the three clay mineral samples had substantially different I_p values despite having the same particle size and content.

FIGURE 6

FIGURE 6. Influence of soil mineral content on sample plasticity index.

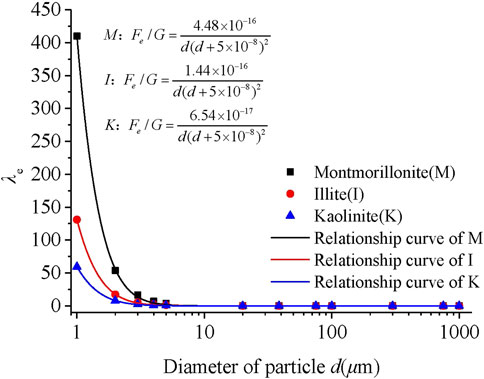
According to the energy multi-scale method, the ratio of micro-Coulomb force to gravity and the ratio of micro-van der Waals force to gravity can be calculated using equations 1 and 2 and the elements from the literature (Huang, 2018). When d = 2 μm, λ_e, and λ_w of the three materials could be calculated and is shown in Table 2; the λ_e values of montmorillonite and illite were 6.91 and 2.1 times the value of kaolinite, respectively, whereas the λ_w values of montmorillonite and illite were 0.73 and 0.79 times that of kaolinite, respectively, and the I_P values of montmorillonite and illite were 4.8 and 1.68 times that of kaolinite, respectively. The difference in λ_w between these minerals was not large. All samples were composed of clay minerals; therefore, the adjustment coefficient α could be set to 1 for the test. As showed in Figure 5, the λ_e is bigger than λ_w for montmorillonite , while λ_e is samller than λ_w for Quartz ,within a certain particle size range. These data indicate that, in clay, the Coulomb force of particles has a greater influence on the particle surface adsorption energy, and the contribution value of λ_e to λ is larger for clay.

TABLE 2

TABLE 2. CRFW and I_p of three types of mineral particles (d = 2 μm).

As described previously, the surface state and interface state are the basis of stress transfer and deformation coordination, and the surface state and contact state of the particles at the microscopic level determine the internal structure and engineering properties of the soil. The adsorbed water and the electric double layer are mainly caused by the negative charges on the surface of the particles. The more charges on the particle surface, the stronger the surface adsorption energy of the particle, and the relatively thicker the adsorbed water layer. For clay minerals, the charge density of the particles is high, and the particle size is small, so the thickness of the adsorbed water layer on the surface of the particles is relatively large for a particle with such a tiny diameter. Currently, the properties of the interface between particles are generally determined by the adsorbed water layer. Therefore, many engineering properties of clay soils are affected by the adsorbed water layer. The plasticity index of clay minerals in this study was typical, and the plasticity index refers to the relative water content of plastic soil from the plastic state to the flowing state. It is an important index for measurement of surface adsorption capacity of mineral particles to free water in the soil, and it is also a typical measure of performance of the microscopic adsorption energy of mineral particles at the macroscopic level. The surface charge density of clay mineral particles such as montmorillonite is largest, illite has the second largest, and kaolinite has the smallest, so the plasticity index of each of the three minerals decreases accordingly, as shown in Figure 6. As shown in Table 2, λ_e of montmorillonite is the largest, that of illite is the second largest, and that of kaolinite is the smallest. These data indicate that the energy multi-scale method quantitatively reflects the adsorption capacity of the microscopic surface of particles. The adsorbed water layer discussed in this paper is relatively thick compared to the particle diameter. When the particle size is large, even if the adsorbed water layer on the surface of the particle is of the same thickness as that of a smaller particle, the relative thickness can be easily ignored compared to the huge particle size. Therefore, using the energy multi-scale method, both λ_e and λ_w decreased with increased particle size, as shown in Figure 5. In addition, we assessed the plasticity index of each of the three clay minerals when the λ_e parameter was controlled. First, according to Eq. 1 and Eq. 2, the relationship curves between the λ_e and particle size of each of the three materials were calculated, as shown in Figure 7.

FIGURE 7

FIGURE 7. Relationship of λ_e with particle size.

The particle diameters of montmorillonite, illite, and kaolinite were set to 20 μm, 14 μm, and 8 μm, respectively, and the λ_e of each of the three materials were caculated from the fitted equation in Figure 7 and the results were shoud in Table 3.

TABLE 3

TABLE 3. λ_e of mineral particles with different diameters.

Figure 8 indicates that the plasticity indices of these three clay minerals, calculated using the energy multi-scale method, are very close to each other and nearly on the same straight line. Therefore, there are benefits to use of this method to classify clay soil samples, as the parameter λ in the energy multi-scale method accounts for the influence of mineral composition and particle size on the microscopic surface and interface states of the particles.

FIGURE 8

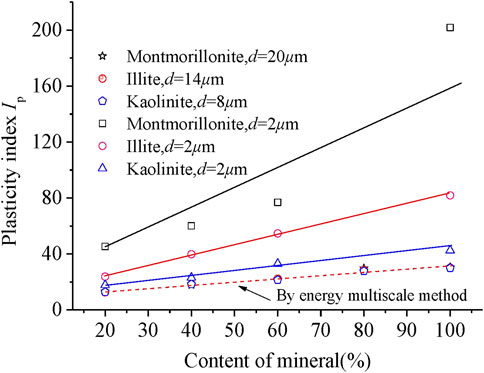
FIGURE 8. Plasticity index of soil samples with different mineral contents using the energy multi-scale method.

4 Conclusion

Soil has an obvious scale effect, and the microscopic characteristics of particles affect the macroscopic properties of soil. This study proposed an energy multi-scale method based on the microscopic properties of particles and established a formula for calculating the CRFW. Additionally, the mechanism of clay plasticity index change was quantitatively explained by the CRFW. The conclusions of this study are as follows:

(1) Both mineral composition and particle size can influence the surface energy of particles and cause interface and surface effects. Higher clay content is associated with greater surface charge of the soil, which results in greater surface adsorption energy and greater relative thickness of the adsorbed water layer on the particle surface. At the same time, when soil particle size is very small, the specific surface area of the particles is large and the thickness of the adsorbed water layer is large. At the microscopic level, the interaction between particles occurs primarily at the contact interface, so these two factors affect the surface characteristics of the particle and thereby affect macroscopic soil properties.

(2) The CRFW of the particles calculated using the energy multi-scale method quantitatively reflects the influence of particle size and mineral composition on the microscopic properties of the soil. The energy multi-scale method takes the microscopic force of the particle as the research object and establishes the CRFW. When the particle size increases, the CRFW of the particle decreases. When the type of the particle changes, the CRFW increases with an increase in particle surface charge.

(3) The energy multi-scale method explains the mechanism of the plasticity index of plastic soil and allowed identification of a new division of soil plasticity. The CRFW quantitatively predicts the influence of mineral composition on the soil plasticity index. When the CRFW is used as the control index, even if mineral composition and particle size of materials are different, the plasticity index of the materials is the same. The multi-scale method may also solve the scale effect of soils in terms of energy scale.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material; further inquiries can be directed to the corresponding author.

Author contributions

Conceptualization, JC and FY; methodology, JC; resources, HT; data curation, XH; writing—original draft preparation, JC; writing—review and editing, JY; supervision, YF; funding acquisition, JY.

Funding

The study was supported by the following fundations: Guangdong Basic and Applied Basic Research Fundation No.20223A1515030051 Funder:JY. Guangdong Basic and Applied Basic Research Fundation No.2022A1515110793 Funder: JC.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ashby, M. F. (1970). The deformation of plastically non-homogeneous materials. Philos. Mag. 21 (170), 399–424. doi:10.1080/14786437008238426

CrossRef Full Text | Google Scholar

Bai, B., Zhou, R., Cai, G., Hu, W., and Yang, G. (2021). Coupled thermo-hydro-mechanical mechanism in view of the soil particle rearrangement of granular thermodynamics. Comput. Geotechnics 137 (8), 104272. doi:10.1016/j.compgeo.2021.104272

CrossRef Full Text | Google Scholar

Borst, R. D., Alizadeh, S. S., and Hageman, T. (2022). Non-associated Cosserat plasticity. Int. J. Mech. Sci. 230, 107535. doi:10.1016/j.ijmecsci.2022.107535

CrossRef Full Text | Google Scholar

Chang, C. S., Yin, Z. Y., and Hicher, P. Y. (2010). Micromechanical analysis for interparticle and assembly instability of sand. J. Eng. Mech. 137 (3), 155–168. doi:10.1061/(asce)em.1943-7889.0000204

CrossRef Full Text | Google Scholar

Chen, J., Fang, Y., Gu, R., Shu, H., Ba, L., and Li, W. (2019). Study on pore size effect of low permeability clay seepage. ARABIAN J. GEOSCIENCES 12 (7), 238. doi:10.1007/s12517-019-4375-3

CrossRef Full Text | Google Scholar

Chen, J., Tong, H., Chen, J., Tong, H., Yuan, J., et al. (2022), Permeability prediction model modified on kozeny-carman for building foundation of clay soil. Buildings 12(11), 1798. doi:10.3390/buildings12111798

CrossRef Full Text | Google Scholar

Chiu, M., and Chen, T. (2011). Higher-order surface stress effects on buckling of nanowires under uniaxial compression. Procedia Eng. 10, 397–402. doi:10.1016/j.proeng.2011.04.067

CrossRef Full Text | Google Scholar

Chu, X., Yu, C., and Xu, Y. (2012). The dilatancy and numerical simulation of failure behaviorof granular materials based on Cosserat model. Interact. Multiscale Mech. Int. J. 5 (2), 157–168. doi:10.12989/imm.2012.5.2.157

CrossRef Full Text | Google Scholar

Cosserate, E. (1909). Théorie de corps deformable. Pairs: Herman.

Google Scholar

Dai, B., and Yang, J. (2015). A numerical analysis of the shear behavior of granular soil with fines. Particuolog 2015(4), 13. doi:10.1016/j.partic.2014.08.010

CrossRef Full Text | Google Scholar

Fang, X., Yang, J., Zhang, X., Zhang, C., Wang, S., and Xie, Y. (2023). Numerical modeling of open TBM tunneling in stratified rock masses using a coupled FDM-DEM method. Comput. Geotechnics 156, 105251. doi:10.1016/j.compgeo.2023.105251

CrossRef Full Text | Google Scholar

Fang, Y. G., and Bo, L. (2016). Multiscale problems and analysis of soil mechanics. Mech. Mater. 103, 55–67. doi:10.1016/j.mechmat.2016.09.003

CrossRef Full Text | Google Scholar

Gong, J., Nie, Z., Zhu, Y., Liang, Z., and Wang, X. (2019). Exploring the effects of particle shape and content of fines on the shear behavior of sand-fines mixtures via the DEM. Comput. Geotechnics 10, 161–176. doi:10.1016/j.compgeo.2018.10.021

CrossRef Full Text | Google Scholar

Gudehus, G., and Nuebel, K. (2004). Evolution of shear bands in sand. Geotechnique 54 (3), 187–201. doi:10.1680/geot.54.3.187.36346

CrossRef Full Text | Google Scholar

Guo, Y., and Yu, X. (2019). "A holistic computational model for prediction of clay suspension structure." Int. J. Sediment Res. 34 (34), 345. doi:10.1016/j.ijsrc.2018.12.002

CrossRef Full Text | Google Scholar

Guzzetti, F., Peruccacci, S., Rossi, M., and Stark, C. P. (2008). The rainfall intensity–duration control of shallow landslides and debris flows: An update. Landslides 5 (1), 3–17. doi:10.1007/s10346-007-0112-1

CrossRef Full Text | Google Scholar

Helmy, A. K. (1998). The limited swelling of montmorillonite. J. Colloid & Interface Sci. 207 (1), 128–129. doi:10.1006/jcis.1998.5739

CrossRef Full Text | Google Scholar

Huang, X. (2018). Division of energy scale and analysis of engineering properties for soil granular group. Guangzhou: South China University of Technology.

Google Scholar

Li, C. S., Zhang, D., Du, S. S., and Shi, B. (2016). Computed tomography based numerical simulation for triaxial test of soil–rock mixture. Comput. Geotechnics 73, 179–188. doi:10.1016/j.compgeo.2015.12.005

CrossRef Full Text | Google Scholar

Li, X., and Mi, C. (2019). Effects of surface tension and Steigmann–Ogden surface elasticity on Hertzian contact properties. Int. J. Eng. Sci. 145, 103165. doi:10.1016/j.ijengsci.2019.103165

CrossRef Full Text | Google Scholar

Li, X., and Wan, K. (2011). A bridging scale method for granular materials with discrete particle assembly – Cosserat continuum modeling. Comput. Geotechnics 38 (8), 1052–1068. doi:10.1016/j.compgeo.2011.07.001

CrossRef Full Text | Google Scholar

Li, Z., Zhao, G., Deng, X., Zhu, J., and Zhang, Q. (2022). Further development of distinct lattice spring model for stability and collapse analysis of deep foundation pit excavation. Comput. geotechnics 144, 104619. doi:10.1016/j.compgeo.2021.104619

CrossRef Full Text | Google Scholar

Liang, X., Ge, Y., Zeng, L., Lyu, L., Sun, Q., Sun, Y., et al. (2023). Debris flow susceptibility based on the connectivity of potential material sources in the Dadu River Basin. Eng. Geol. 312, 106947. doi:10.1016/j.enggeo.2022.106947

CrossRef Full Text | Google Scholar

Liu, C., Zhixiang, Y., and Zhao, S. (2021). A coupled SPH-DEM-FEM model for fluid-particlestructure interaction and a case study of Wenjia gully debris flow impact estimation. Landslides 18 (7), 2403–2425. doi:10.1007/s10346-021-01640-6

CrossRef Full Text | Google Scholar

Lu, L., Guo, X., and Zhao, J. (2019). A unified size-dependent plate model based on nonlocal strain gradient theory including surface effects. Appl. Math. Model. 68, 583–602. doi:10.1016/j.apm.2018.11.023

CrossRef Full Text | Google Scholar

Lu, X., and Cui, P. (2003). The influence of strain gradient on the shear band in a saturated soil. Iran. J. Sci. Technol. Transaction B Eng. 27 (1), 57–62.

Google Scholar

Mingjing, J. (2019). New paradigm for modern soil mechanics: Geomechanics from micro to macro. Chin. J. Geotechnical Eng. 41 (2), 195–254. doi:10.11779/CJGE201902001

CrossRef Full Text | Google Scholar

Missana, T., and Adell, A. (2000). On the applicability of DLVO theory to the prediction of clay colloids stability. J. Colloid Interface Sci. 230 (1), 150–156. doi:10.1006/jcis.2000.7003

PubMed Abstract | CrossRef Full Text | Google Scholar

Mitchell, J. K., and Soga, K. (2005). Fundamentals of soil behavior. Hoboken: John Wiley & Sons.

Google Scholar

Monkul, M. M., and Ozden, G. (2007). Compressional behavior of clayey sand and transition fines content. Eng. Geol. 89 (3-4), 195–205. doi:10.1016/j.enggeo.2006.10.001

CrossRef Full Text | Google Scholar

Mühlhaus, Dr. (1989). Application of Cosserat theory in numerical solutions of limit load problems. Ingenieur-Archiv 59 (2), 124–137. doi:10.1007/bf00538366

CrossRef Full Text | Google Scholar

Mühlhaus, H. B., and Oka, F. (1996). Dispersion and wave propagation in discrete and continuous models for granular materials. Int. J. Solids Struct. 33 (19), 2841–2858. doi:10.1016/0020-7683(95)00178-6

CrossRef Full Text | Google Scholar

Nguyen, T. K., Combe, G., Caillerie, D., and Desrues, J. (2014). FEM × DEM modelling of cohesive granular materials: Numerical homogenisation and multi-scale simulations. Acta Geophys. 62 (5), 1109–1126. doi:10.2478/s11600-014-0228-3

CrossRef Full Text | Google Scholar

Ni, H., and Huang, Y. (2020). Rheological study on influence of mineral composition on viscoelastic properties of clay. Appl. Clay Sci. 187, 105493. doi:10.1016/j.clay.2020.105493

CrossRef Full Text | Google Scholar

Oda, M., and Iwashita, K. (2000). Study on couple stress and shear band development in granular media based on numerical simulation analyses. Int. J. Eng. Sci. 38 (15), 1713–1740. doi:10.1016/s0020-7225(99)00132-9

CrossRef Full Text | Google Scholar

Pham, K., Kim, D., Choi, H. J., Lee, I. M., and Choi, H. (2018). A numerical framework for infinite slope stability analysis under transient unsaturated seepage conditions. Eng. Geol. 243, 36–49. doi:10.1016/j.enggeo.2018.05.021

CrossRef Full Text | Google Scholar

Phan, Q. T., Bui, H. H., Nguyen, G. D., and Bouazza, A. (2021). Effect of particle rolling resistance on drained and undrained behaviour of silty sand. Acta Geotech. 16 (3), 2657–2682. doi:10.1007/s11440-020-01128-y

CrossRef Full Text | Google Scholar

Riahi, A., Curran, J. H., and Bidhendi, H. (2009). Buckling analysis of 3D layered structures using a Cosserat continuum approach. Comput. Geotechnics 36 (7), 1101–1112. doi:10.1016/j.compgeo.2009.03.012

CrossRef Full Text | Google Scholar

Sabbar, A. S., Chegenizadeh, A., and Nikraz, H. (2017). Static liquefaction of very loose sand-slag-bentonite mixtures. Soils Found. -Tokyo- 57 (3), 341–356. doi:10.1016/j.sandf.2017.05.003

CrossRef Full Text | Google Scholar

SampradaPradhan, T., Toll, D. G., Rosser, N. J., and Brain, M. J. (2022). An investigation of the combined effect of rainfall and road cut on landsliding. Eng. Geol. 307, 106787. doi:10.1016/j.enggeo.2022.106787

CrossRef Full Text | Google Scholar

Tang, H., and Song, C. (2015). Cosserat continuum model and its application to the studies of progressive failure. Jpn. Geotech. Soc. Spec. Publ. 2 (18), 703–708. doi:10.3208/jgssp.chn-57

CrossRef Full Text | Google Scholar

Tang, H., Wei, W., Liu, F., and Chen, G. (2020). Elastoplastic Cosserat continuum model considering strength anisotropy and its application to the analysis of slope stability. Comput. Geotechnics 117, 103235. doi:10.1016/j.compgeo.2019.103235

CrossRef Full Text | Google Scholar

Tang, H., Wei, W., Song, X., and Liu, F. (2021). An anisotropic elastoplastic Cosserat continuum model for shear failure in stratified geomaterials. Eng. Geol. 293 (1), 106304. doi:10.1016/j.enggeo.2021.106304

CrossRef Full Text | Google Scholar

Thornton, C. (2000). Numerical simulations of deviatoric shear deformation of granular media. Geotechnique 50 (1), 43–53. doi:10.1680/geot.2000.50.1.43

CrossRef Full Text | Google Scholar

Wang, X., and Zhang, Z. (2003). Unified criterion for stability failure of rock specimens subject to uniaxial tension, direct shear and uniaxial compression based on gradient-dependent plasticity. Rock Soil Mech. 24S, 138–142. doi:10.16285/j.rsm.2003.s2.032

CrossRef Full Text | Google Scholar

Wang, Y., Zhang, B., Zhang, X., Liu, J., and Shen, H. (2019). Two-dimensional fretting contact analysis considering surface effects. Int. J. Solids Struct. 170, 68–81. doi:10.1016/j.ijsolstr.2019.04.027

CrossRef Full Text | Google Scholar

Yang, T., Liu, H. Y., and Tang, C. (2017). Scale effect in macroscopic permeability of jointed rock mass using a coupled stress–damage–flow method. Eng. Geol. 228, 121–136. doi:10.1016/j.enggeo.2017.07.009

CrossRef Full Text | Google Scholar

Yang, W., Wang, S., Kang, W., Yu, T., and Li, Y. (2023). A unified high-order model for size-dependent vibration of nanobeam based on nonlocal strain/stress gradient elasticity with surface effect. Int. J. Eng. Sci. 182, 103785. doi:10.1016/j.ijengsci.2022.103785

CrossRef Full Text | Google Scholar

Zeghal, M., and Shamy, U. E. (2008). Liquefaction of saturated loose and cemented granular soils, Powder Technol., 184 254–265.doi:10.1016/j.powtec.2007.11.032

CrossRef Full Text | Google Scholar

Zhang, D., Zhang, X., and Du, W. (2022). DEM-FEM based numerical analysis on mechanical responses of sandy soil and pipeline to seepage erosion. Eng. Geol. 310 (5), 106868. doi:10.1016/j.enggeo.2022.106868

CrossRef Full Text | Google Scholar

Zhao, T., and Feng, D., (2017). Coupled DEM-CFD investigation on the formation of landslide dams in narrow rivers. Landslides 14 (1), 189–201. doi:10.1007/s10346-015-0675-1

CrossRef Full Text | Google Scholar

Zhu, Z., Zhang, F., Dupla, J. C., Canou, J., and Foerster, E. (2020). Investigation on the undrained shear strength of loose sand with added materials at various mean diameter ratios. Soil Dyn. Earthq. Eng. 137, 106276. doi:10.1016/j.soildyn.2020.106276

CrossRef Full Text | Google Scholar