- Department of Mechanical Engineering, Rowan University, Glassboro, NJ, United States
The advent of acoustic metasurfaces (AMs), which are the two-dimensional equivalents of metamaterials, has opened up new possibilities in wave manipulation using acoustically thin structures. Through the interaction between the acoustic waves and the subwavelength scattering, AMs exhibit versatile capabilities to control acoustic wave propagation such as by steering, focusing, and absorption. In recent years, this vibrant field has expanded to include tunable, reconfigurable, and programmable control to further expand the capacity of AMs. This paper reviews recent developments in AMs and summarizes the fundamental approaches for achieving tunable control, namely, by mechanical tuning, active control, and the use of field-responsive materials. An overview of basic concepts in each category is first presented, followed by a discussion of their applications and details about their performance. The review concludes with the outlook for future directions in this exciting field.
1 Introduction
Controlling the propagation of sound has long been a desirable goal in science and engineering. The emergence of acoustic metamaterials, which are artificial structures composed of meta-atoms, offers unprecedented capabilities in acoustic wave engineering. These metamaterials are designed based on their constitutive unit cells and behave like a continuous material with unconventional properties in the bulk. Over the past two decades, research on acoustic metamaterials has demonstrated a plethora of fascinating phenomena ranging from negative refractive indices to acoustic cloaking (Liu et al., 2000; Lee et al., 2010; Liang and Li, 2012; Cummer et al., 2016; Liao et al., 2021).
In recent years, the community has witnessed strong growth in the development of two-dimensional (2D) equivalent acoustic metamaterials. These structures, termed acoustic metasurfaces (AMs), are capable of providing non-trivial local phase shifts, amplitude modulation, and extraordinary sound absorption. Thanks to their thinness which is usually in the sub-wavelength, AMs have added value and functionalities in comparison with other acoustic metamaterials with small footprint (Xie et al., 2014; Cheng et al., 2015; Zhao et al., 2017; Assouar et al., 2018; Quan and Alu, 2019). Numerous exotic acoustic phenomena such as sound cloaking (Faure et al., 2016; Ma et al., 2019; Fan et al., 2020; Zhou et al., 2020), sound splitting (Zhai et al., 2018; Ding et al., 2021), sound absorption (Ma et al., 2014; Song et al., 2019; Liu et al., 2021; Li et al., 2022a; Guo et al., 2022), anomalous reflection or refraction (Diaz-Rubio and Tretyakov, 2017; Li et al., 2019a; Zhu and Lau, 2019; Li et al., 2020a; Chiang et al., 2020; Song et al., 2021), sound focusing (Zhu et al., 2016a; Lombard et al., 2022), one-way sound propagation (Zhu et al., 2015; Jiang et al., 2016), and medical ultrasound (Tian et al., 2017; Hu et al., 2022) have been proposed and demonstrated using AMs. AMs possess unusual features, including selective focusing and negative refraction, are enabled by the generalized Snell’s law, which adds a new degree of freedom to control the behavior of transmitted or reflected waves by incorporating a lateral momentum (Yu et al., 2011) (see Figure 1). In this approach, conventional AMs modulate the phase change inside the unit cells by changing the effective spatial path of waves via space-coiling structures or by generating a phase delay through resonance.
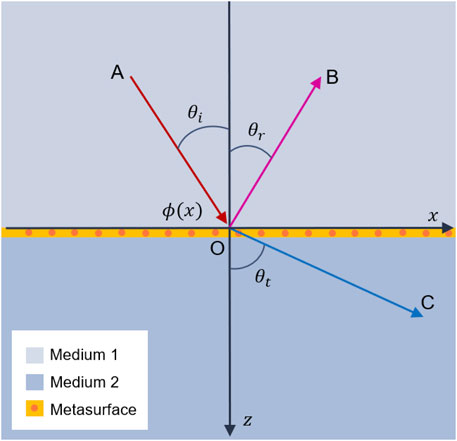
FIGURE 1. Schematic of the generalized Snell’s law and AM where
While these AMs provide unparalleled potential to control acoustic waves, they generally have fixed configurations and cannot be easily altered. As such, research efforts have been devoted to make them tunable, reconfigurable, and programmable to further expand their capacities. Tunability adds another degree of freedom to control the sound transmission like tuning the dispersion or frequency, wavenumber, and topological states of acoustic waves (Tian et al., 2020). Incorporating tunable structures that can operate at different frequencies can also increase the bandwidth of the devices (Peng et al., 2022). There are a few approaches to achieve the desired tunable control of AMs. For example, origami and kirigami, the art of paper folding and cutting, can increase the ultimate strain on the sheets and applications have produced aerodynamic benefits through wing surface texturing (Gamble et al., 2020). These principles have been utilized in AM design by introducing reconfigurable geometries.
The approach of geometrical tuning can be also exemplified by asymmetric structures via rotation. For instance, rotatable anisotropic three-component resonators have been proposed to induce non-degenerate dipolar resonance, which further leads to an evident phase change in low frequencies (Li et al., 2020b). Active designs where electroacoustic transducers and circuits are used, on the other hand, represent another efficient way to realize tunable AMs (Li et al., 2022b). As an example, this has been implemented in acoustic cloaking which enables sound to flow around an obstacle without the trace of reflections using programmable AMs (Li et al., 2019b). The ongoing development of tunable, reconfigurable, and programmable AMs has opened up new possibilities for controlling the behavior of sound in different acoustic media.
This review aims to provide insights into the recent development of tunable, reconfigurable, and programmable AMs. While these notations have all been used extensively and sometimes interchangeably in the literature, a tunable AM should refer to a structure that exhibits some form of tunability. In contrast, reconfigurable and programmable AMs usually denote metasurfaces with more advanced controllability in which the functionality or application can be tailored to meet specific requirements. Here, the main approaches to achieve tunable control are summarized and divided into three main categories: mechanical tuning, active control, and field-responsive material. The principles and mechanism for these approaches are reviewed, and demonstrations of typical applications are presented. At the end, we point out a few pressing questions in the current research and provide an outlook for growth in this burgeoning field.
2 Mechanical tuning
To perform certain functions, AMs typically have a fixed microstructure that can regulate the local scattering of acoustic waves. As such, mechanical tuning manifests itself as a straightforward way to provide tunable functionality by leveraging geometric changes of the microstructures or the overall profile of the metasurface. When propagating through or interacting with these tunable AMs, different phase delays or amplitudes can be achieved, which together represent the tunability of the AMs.
2.1 Geometric tuning via mechanical actuation
Mechanical actuators can change the geometry, the phase, and the cavity size of AMs which permits a variety of interactions and ensures programmable functionality of AMs. A simple yet efficient way to achieve that is to use a mechanical rotation or translation to change the overall configuration of the metasurface. This mechanism can be applied macroscopically to the entire metasurface such that the overall configuration is changed, or microscopically at the unit cell level to modify the constitutive structures. For example, Helmholtz resonators (Li et al., 2017; Xia et al., 2018; Gong et al., 2019; Tian et al., 2019; Gong et al., 2021), fan-shaped (Wang et al., 2020), space-coiling (Yuan et al., 2015), gap-tunable (Liu and Jiang, 2018; Tao et al., 2022), and tunable broadband (Fang et al., 2016; Zhang et al., 2020; Chen et al., 2021; Duan et al., 2021; Mostaan and Saghaei, 2021; Xu et al., 2021) are all working methods for tuning acoustic waves. Tian et al. (2019) obtained versatile wave manipulation functions with the help of Helmholtz resonators as illustrated in Figure 2A. As a result, it was substantiated that by gradually changing the cavity size of a shunted Helmholtz resonator, the sub-wavelength unit cell can continuously modulate the phase and amplitude of transmission acoustic waves. Similarly, a Helmholtz resonator with a continuously varying slit width can also lead to a full 2π phase shift of the unit cell for realization of a tunable AM (Gong et al., 2019). The cavity size can be continuously tuned by adding or withdrawing water using a fluidic pumping system. A space-coiling structure was designed and tested for tuning an AM experimentally and numerically (Wang et al., 2020). In this procedure, a tunable AM was constructed by cascading two parallel metasurfaces to create a negative refractive index. An AM gradient was applied by Liu and Jiang (2018) to produce a system with controllable asymmetric transmission by switching from symmetric transmission to asymmetric transmission at a specific gap value (Figure 2B). Based on the tunable gap between the two layers, the metasurface could switch from high transmission to total reflection in a certain incident direction, while in the opposite direction, the incidence always maintained high transmission, which is typically the controllable asymmetric transmission. Tunable components can also be used to address the limitations in bandwidth associated with many AMs. For example, Helmholtz resonance exhibits excellent sound absorption with a small footprint. Adding rubber coating and a tunable embedded neck provided sufficient elasticity and damping to achieve tunable low-frequency and perfect ultra-broadband absorption, while maintaining the external morphology and fixing the thickness at the deep subwavelength scale (Duan et al., 2021).
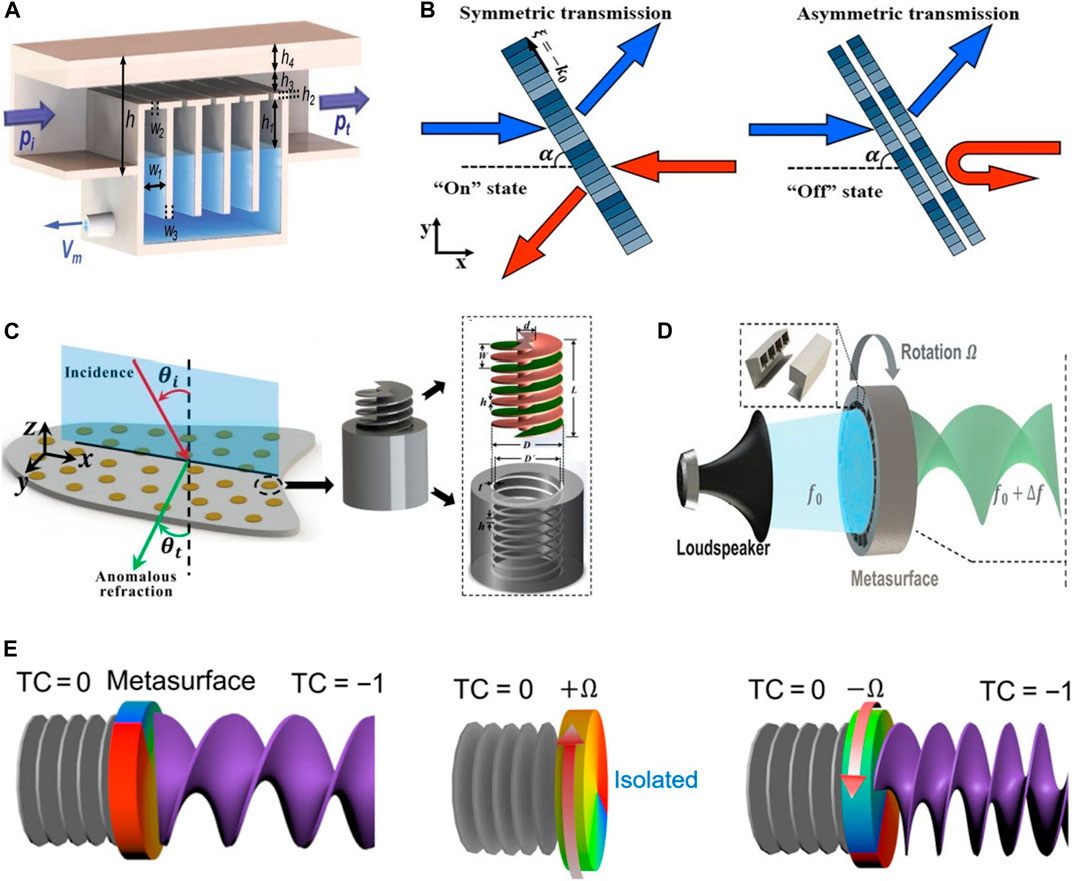
FIGURE 2. Examples of mechanical tuning. (A) Mechanism of programmable acoustic metasurface composed of a straight channel and five shunted Helmholtz resonators (Tian et al., 2019). (B) Controllable acoustic asymmetric transmission with an adjustable gap distance (Liu and Jiang, 2018). (C) Tunable metasurface design based on the screw and nut mechanism (Zhao et al., 2018). (D) Schematic of frequency convertor by rotation. The frequency of the acoustic wave will be converted to a new frequency after passing through a specifically designed rotating metasurface (Wang et al., 2022a). (E) Schematic diagram of the static condition without the rotational Doppler effect (left). When the metasurface and the vortex rotate in the same direction, the incident source is turned off without energy transmission (middle); when the metasurface and the vortex rotate in the opposite direction, the incident source usually propagates (right) (Wang et al., 2022b).
Along this line, helical structures have also been exploited to achieve tunable and multifunctional effects by configuring their orientations and rotation angles in a quasi-static manner (Zhu et al., 2016b; Esfahlani et al., 2017; Fan et al., 2019; Chen et al., 2020; Liang et al., 2020; Xie et al., 2020; Gong et al., 2022). As shown in Figure 2C, different transmission or phase delay properties were achieved by varying the helical unit cells such as by using a screw-nut mechanism to allow the length of the spiral channel to be changed to slow down the propagating waves in a tunable manner (Zhao et al., 2018). This concept was later extended to the dynamic rotation process by leveraging structures and effects such as with nested resonant rings (He et al., 2022), a passive linear vortex (Wang et al., 2022a), electrically pumped carbon nanotubes (Jia et al., 2022), rotational Doppler effect (Wang et al., 2022b), and a tunable perfect sound absorption metasurface (Liu et al., 2021). There have been some research reports dealing with this issue, such as that of Liang et al. (2020), who presented a systematic strategy to control AMs based on helical-structured metamaterials. This method had dispersion-free properties and high transmission efficiency for bands greater than one-octave. A rotating passive linear vortex metasurface was utilized to convert low-frequency waves into audible ones with high efficiency (Figure 2D) (Wang et al., 2022a). In this procedure, a rotational system drives the metasurface to rotate steadily such that the phase-adjustable and high-transmittance units are periodically arranged along the azimuthal direction, forming a spiral phase distribution for the incident plane. Jia et al. (2022) constructed an AM decorated with carbon nanotube patches as spatiotemporal modulators to function as a hybrid mode frequency division multiplexer. Dynamically tuning the thermo-acoustic phase generation was proposed with the help of manipulation of the electric phase delays, and it was substantiated that the acoustic pressure amplitude remained uniform, while its phase accumulation doubled the electrical one. Wang et al. (2022b) introduced the rotational Doppler effect to acquire non-reciprocal control of the non-topological charge beam (Figure 2E). Based on the rotational Doppler effect, the wave vector of the transmitted wave was obtained along with positive and negative transition flexibly by rotating the metasurface at a specific angular velocity. A tunable perfect sound absorption metasurface was proposed by Liu et al. (2021), which dynamically and continuously tuned AMs. In this pathway, the overall sound absorption could be enhanced or weakened by changing the angle in which the rotation of the rotatable plate modified the interior and exterior size of the cavity, modifying the coupling relations between the first and second resonances.
2.2 Origami and kirigami
Another way to leverage mechanical tuning is by using origami and kirigami principles. A Miura-ori deforms only at the folding creases, which is known as rigid origami behavior; spatial over-constrained linkages are known as kirigami. In this pathway, an origami structure is folded from the initial planar state into a compact volume, whereas a kirigami structure is stretched from the initial state into an expanded configuration (Hong et al., 2020; Lie et al., 2020; Cao et al., 2022). Compared to continuous thin sheets, the kirigami sheet enables more freedom and flexibility by shape-shifting through local or global deformation between the cut units. Origami and kirigami have been found useful in many scenarios, especially structural applications. For example, origami can produce a negative Poisson’s ratio (Yasuda and Yang, 2015; He et al., 2020), multi-stability (Fang et al., 2020), and band-gap phononic crystals (Thota et al., 2017), while kirigami can be used in aircraft structures for morphing thickness in airfoils (Sun et al., 2016) and making deployable solar panels (Wang et al., 2021).
Origami/kirigami methods have been applied by the acoustic community to the design and realization of tunable AMs. Pratapa et al. (2018) investigated the utilization of Miura-ori patterns in a Bloch-wave analysis framework with acoustic bandgaps, by making the pattern part of a non-analysis framework. By making the pattern a non-uniform one, in which mass and axial rigidity of alternating unit cells in the origami panels changed relatively, tunable bandgaps were realized. Based on the kirigami structure, an elastic metamaterial was designed by Zhu et al. (2018) to gain anisotropic mass density for sub-wavelength flexural wave propagation in a thin plate (Figure 3A). The plate was constructed without any perforations that could degrade the strength of the pristine plate by attaching resonant kirigami structures. As illustrated in Figure 3B, a reconfigurable acoustic waveguide was proposed using origami principles (Babaee et al., 2016). Different wave radiation patterns were extracted with the help of origami methodology and acoustic responses over a large frequency range were presented. Pyramidal core kirigami cells were also used with smart systems to acquire tunable structural components (See Figure 3C) (Ouisse et al., 2016). Based on kinematic folding, Zou et al. (2018) reconfigured the geometry of tessellated origami facets (Figure 3D). Rayleigh’s integral was used to quantify the acoustic pressure, and the numerical validation boundary element method was utilized to prove the effectiveness of reconfigurable origami tessellations in comparison to traditionally phased arrays.
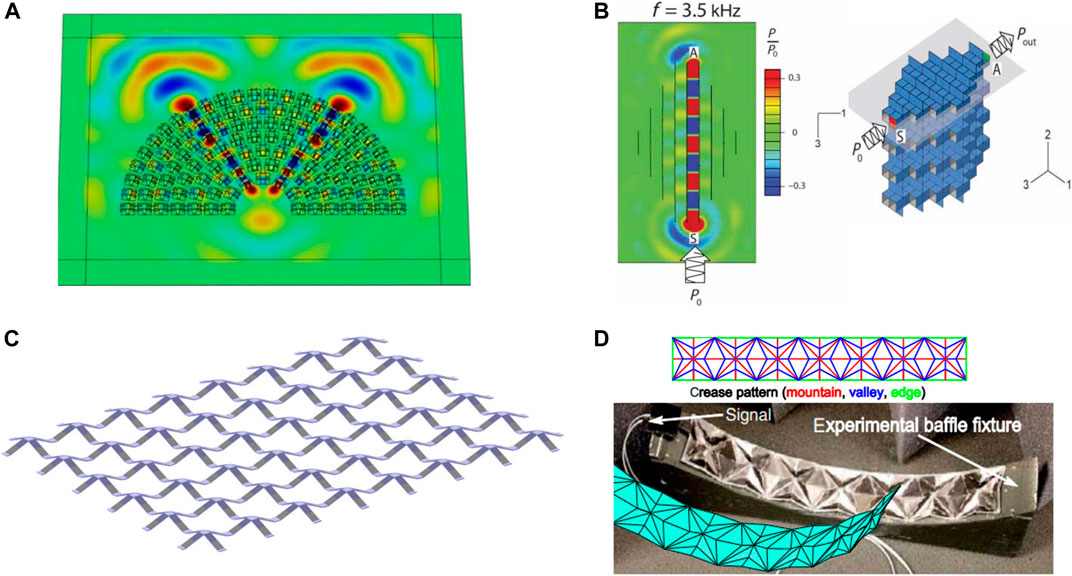
FIGURE 3. Examples of origami and kirigami. (A) Design of kirigami elastic hyperlens for flexural wave field (Zhu et al., 2018). (B) Propagation of sound waves in origami-inspired waveguides (Babaee et al., 2016). (C) Piezocomposite kirigami auxetic lattice for adaptive elastic wave filtering (Ouisse et al., 2016). (D) Crease pattern of foldable tessellations for efficient guiding of acoustic waves (Zou et al., 2018).
3 Active control
Actively controlled metasurfaces have taken center stage in recent years since they provide elegant ways to effectively control and manipulate AMs after fabrication. In comparison with passive AMs that have a fixed functionality once fabricated, the implementation of active elements affords great flexibility and convenience in tuning their responses with reconfigurable electronic circuits. The most common application of such an approach is in membrane-type AMs where, depending on their type and nature, properties such as surface tension can be easily tuned by applying an external voltage (Cheng et al., 2018; Shen et al., 2019; Zhai et al., 2019; Akl and Baz, 2021; Zhang et al., 2021; Kovacevich and Popa, 2022; Peng et al., 2022). Zhang et al. (2016), proposed smart AM designs which exhibit wave reflection at low frequencies with high efficiency (See Figure 4A). As presented in Figure 4B, a tunable AM was proposed in which composite sheets of PVDF membrane and polyimide tape were inserted into the cavity (Li et al., 2022c). Some studies showed that by using a direct voltage applied to the membrane, the eigen-frequencies of AMs could be tuned, and therefore, the wave transmission phase could be tuned as well (Kumar and Lee, 2019). In the case of an alternating voltage applied to the membrane, the vibrations of the membrane AMs resulting from such excitation could be greatly enhanced or suppressed, which could help achieve a variety of functionalities such as acoustic switches with high on/off ratios and phase modulations (Xiao et al., 2015), changing the effective modulus (Li et al., 2019c), as an anomalous acoustic reflector (Zhai et al., 2021), for steerable reflections over a wide frequency band (Lissek et al., 2018), and for asymmetric transmission (Geib et al., 2021; Zhou and Baz, 2023).
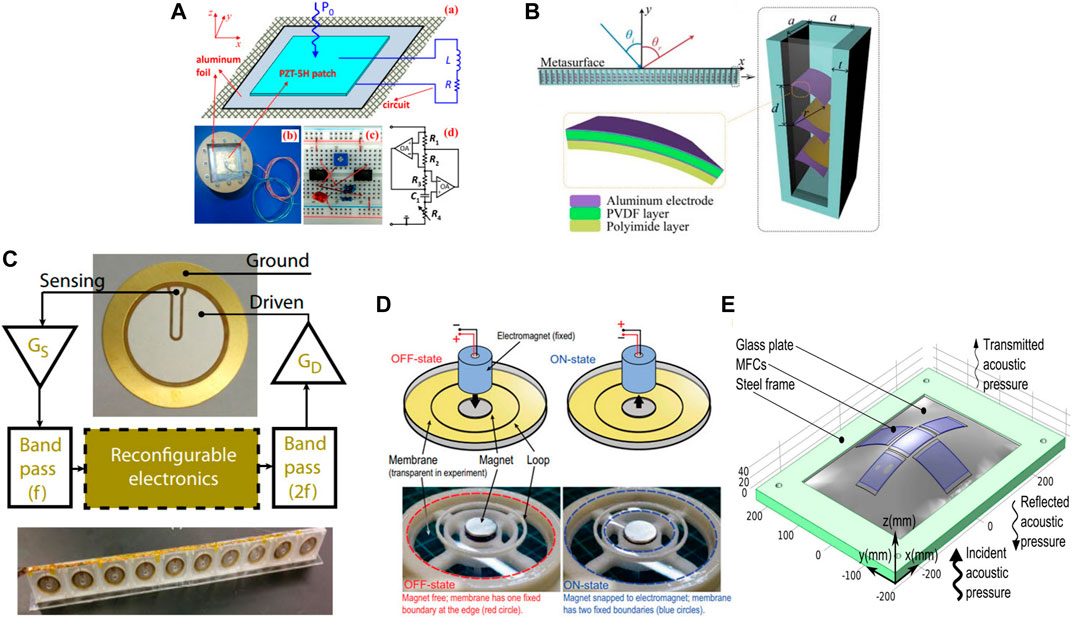
FIGURE 4. Examples of active control. (A) Schematic of smart AM (Zhang et al., 2016). (B) Tunable AM based on tunable units composed of polyimide unimorph sheets (Li et al., 2022c). (C) Reconfigurable piezoelectric membrane controlled by electronics (Popa et al., 2015). (D) Membrane can be electrically switched between on and off states (Ma et al., 2018). (E) Sound shielding system consists of a curved glass plate and piezoelectric MFC actuators (Steiger et al., 2016).
These active approaches have been applied to the design and realization of reconfigurable AMs. For example, Popa et al. (2015) proposed a metamaterial slab in which the metamaterials can play multiple roles simultaneously and have application in non-linear imaging applications (Figure 4C).Tang et al. (2019) attempted to create a versatile wave-front manipulation device by designing an ultrathin membrane-type active acoustic metasurface. The local sound intensity could be actively reconfigured by dc voltage control of electromagnets attached to the membrane-type metamaterial. This concept has been used to perform spatial sound modulation to harness the degrees of freedom that underlie reverberating sound by combining metamaterials and wave-field shaping (Figure 4D) (Ma et al., 2018). Utilizing an adaptive AM approach, a noise shielding device was designed by Steiger et al. (2016) (Figure 4E) to compensate for the acoustic transmission loss of the sound transmitted through adaptive AMs. Also, the precise electronic feedback control of values was presented to overcome capacitance matching with a fixed adjustment of parameters. Sound barriers can also be designed by utilizing acoustic bianisotropic materials which contain non-zero strain-to-momentum coupling by leveraging active components. Basically, compact active meta-atoms that display local responses to external sound can help achieve better properties in terms of bandwidth, attenuation, and shielded volume (Popa et al., 2018).
4 Field-responsive materials
Apart from mechanical and electrical tuning, another method of achieving programmable AMs is by using field-responsive materials. In this approach, either the property or the shape of these materials changes when an external field is applied, and wave–matter interactions are changed in ways that correspond to the property or shape changes, which produces a tunable or programmable metasurface. In general, the use of magnetoactive materials and temperature changes has been proposed as a solution. These have conspicuous advantages like low-frequency wave manipulation (Chen et al., 2014; Chen et al., 2017; Liu et al., 2020), switching on and off of topological states (Lee et al., 2022), and production of negative modulus and density (Xia et al., 2016) which leads to the acquisition of a wider acoustic band, better adjustability, and more balanced performance.
4.1 Magnetoactive material
Magnetoactive materials are adjustable and controllable to act as the tunable part of AM. They can deform under a specific magnetic field and are considered an efficient way to achieve non-contact control of materials. This property can be leveraged to design structures that undergo a certain geometric change by modulation of the applied field. The mechanics of magnetic control is classified into two subcategories of single and multi-film structures, with multi-film magnetic AMs exhibiting better performance and a wider bandwidth with regard to sound insulation (Yu et al., 2018; Lee et al., 2020; Lee et al., 2022; Xia et al., 2022). To exemplify, Lee et al. (2022) proposed a class of magnetoactive acoustic topological transistors capable of switching topological states on and off and reconfiguring topological edges on-demand with external magnetic fields. As presented in Figure 5A, a class of active metamaterials was inspired by shark skin denticles whose configuration can be switched on demand by untethered magnetic fields to enable wave guiding, reciprocity, and logic operation (Lee et al., 2020). A massive block of lead was incorporated into a magnetic field to enhance low frequency sound insulation, and the adjustability of the magnetic field to control materials was proven (Xia et al., 2022).

FIGURE 5. Examples of field-responsive material. (A) Acoustic transmission of samples, vertical Mie resonator pillar array (left), pillar array with two pillars bent by a magnetic field (middle), and pillar array when the magnetic field is turned off (right) (Lee et al., 2020). (B) Schematic diagram of temperature-controlled focusing system (left), acoustic pressure distribution of transmission unit at different temperatures (middle), and acoustic pressure distribution of plane wave in seven reflection units at different temperatures (Wu et al., 2021).
4.2 Thermo-responsive materials
Exploiting the effect of temperature change and its influence on the behavior of AMs has emerged as another way to provide new functionalities and possibilities in the metamaterial domain, such as by enlarging the frequency operating range in some devices or enhancing the acoustic properties in others (Figure 5B) (Wu et al., 2021). Some researchers introduced acoustic transmission line methods to investigate the effect of varying the temperature of the medium by introducing liquid water into a structured metamaterial consisting of multiple Helmholtz resonators with a duct. The variation in water temperature altered its properties and thus the properties of the material used in the structure, which affected the behavior of the entity and modified the local resonant band gap and the negative bulk modulus of the metamaterial (Xia et al., 2016). Zhao et al. (2022) proposed using heat to create a thermal distribution on the metamaterial surface, which can alter the material’s properties, such as the bulk modulus or Young’s modulus, and create a novel gradient metamaterial that can change its own acoustic properties.
5 Conclusion and future outlook
The objective of this review was to provide fresh insights into the fundamental concepts and applications of tunable, reconfigurable, and programmable AMs. To this end, recent advancements achieved in the design and development of AMs were highlighted. Main strategies to achieve tunable, reconfigurable, and programmable AMs were summarized in three main categories: mechanical tuning, active control, and field-responsive materials. In the past decade, AMs have emerged as a new generation of acoustic metamaterials due to their functionalities and mechanical properties. Although much progress has been made in AMs, some promising directions have yet to be fully explored because of technological gaps between large-scale practical applications and lab-scale research. For instance, mechanical tuning provides a reliable means to achieve the required reconfigurable wave control effects by leveraging the geometrical change of the structures. However, this approach typically allows only a relatively slow tuning rate. This poses challenges to apply the approach to applications such as communication in which dynamic tuning is desired. A large degree of change in geometry may also prevent its application in a confined space.
The implementation of active elements affords great flexibility and convenience in being able to quickly regulate their response by fast electronic circuits with high tunability. Despite the great convenience offered by active control, the requirement of conversions between acoustic and electrical signals as well as the relatively complicated feed circuity can still create a bottleneck for many practical applications. Therefore, there is a critical need for further engineering developments in simple yet efficient circuits and electroacoustic systems for a variety of functionalities. Field-responsive materials can adjust and control AMs in a non-contact and reconfigurable manner, which could help solve some of the existing issues requiring sophisticated tuning mechanisms. Nevertheless, their usage is still limited at this moment and more work needs to be carried out in this direction to make them applicable to a real-world setup. For example, they use very specific materials that can induce acoustic interactions and also need the excitation of an external field which could also limit their broad application. While it is evident that tunable and programmable AMs are a relatively new field and are promising in acoustic wave manipulation, more research needs to be carried out, especially in realizing real-time reconfigurable properties with simple tuning mechanisms. It is hoped that both conceptual research and rapid development will be carried on to increase their application in industry.
Author contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Funding
This work was supported by the National Science Foundation under Grant No. CMMI-2137749.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Akl, W., and Baz, A. (2021). Active control of the dynamic density of acoustic metamaterials. Appl. Acoust. 178, 108001. doi:10.1016/j.apacoust.2021.108001
Assouar, B., Liang, B., Wu, Y., Li, Y., Cheng, J. C., and Jing, Y. (2018). Acoustic metasurfaces. Nat. Rev. Mat. 3, 460–472. doi:10.1038/s41578-018-0061-4
Babaee, S., Overvelde, J. T. B., Chen, E. R., Tournat, V., and Bertoldi, K. (2016). Reconfigurable origami-inspired acoustic waveguides. Sci. Adv. 2, e1601019. doi:10.1126/sciadv.1601019
Cao, P., Ou, W., Su, Y., Yin, Y., Dong, E., Song, Z., et al. (2022). Acoustic switch via kirigami metasurface. Phys. Rev. Appl. 18, 054040. doi:10.1103/PhysRevApplied.18.054040
Chen, A., Tang, Q., Wang, H., Zhao, S., and Wang, Y. (2020). Multifunction switching by a flat structurally tunable acoustic metasurface for transmitted waves. Sci. China. Phys. Mech. 63, 244611. doi:10.1007/s11433-019-1498-2
Chen, T., Li, W., and Yu, D. (2021). A tunable gradient acoustic metamaterial for acoustic sensing. Extreme. Mech. Lett. 49, 101481. doi:10.1016/j.eml.2021.101481
Chen, X., Liu, P., Hou, Z., and Pei, Y. (2017). Magnetic-control multifunctional acoustic metasurface for reflected wave manipulation at deep subwavelength scale. Sci. Rep. 7, 9050. doi:10.1038/s41598-017-09652-w
Chen, X., Xu, X., Ai, S., Chen, H., Pei, Y., and Zhou, X. (2014). Active acoustic metamaterials with tunable effective mass density by gradient magnetic fields. Appl. Phys. Lett. 105, 071913. doi:10.1063/1.4893921
Cheng, Y., Li, X., Nassar, H., Hu, G., and Huang, G. (2018). A programmable metasurface for real time control of broadband elastic rays. Smart. Mat. Struct. 27, 115011. doi:10.1088/1361-665X/aae27b
Cheng, Y., Zhou, C., Yuan, B. G., Wu, D. J., Wei, Q., and Liu, X. J. (2015). Ultra-sparse metasurface for high reflection of low-frequency sound based on artificial Mie resonances. Nat. Mat. 14, 1013–1019. doi:10.1038/nmat4393
Chiang, Y., Oberst, S., Melnikov, A., Quan, L., Marburg, S., Alu, A., et al. (2020). Reconfigurable acoustic metagrating for high-efficiency anomalous reflection. Phys. Rev. Appl. 13, 064067. doi:10.1103/PhysRevApplied.13.064067
Cummer, S. A., Christensen, J., and Alu, A. (2016). Controlling sound with acoustic metamaterials. Nat. Rev. Mat. 1, 16001. doi:10.1038/natrevmats.2016.1
Diaz-Rubio, A., and Tretyakov, S. A. (2017). Acoustic metasurfaces for scattering-free anomalous reflection and refraction. Phys. Rev. B 96, 125409. doi:10.1103/PhysRevB.96.125409
Ding, H., Fang, X., Jia, B., Wang, N., Cheng, Q., and Li, Y. (2021). Deep learning enables accurate sound redistribution via nonlocal metasurfaces. Phys. Rev. Appl. 16, 064035. doi:10.1103/physrevapplied.16.064035
Duan, M., Yu, C., Xing, F., and Lu, T. J. (2021). Tunable underwater acoustic metamaterials via quasi-helmholtz resonance: From low-frequency to ultra-broadband. Appl. Phys. Lett. 118, 071904. doi:10.1063/5.0028135
Esfahlani, H., Lissek, H., and Mosig, J. R. (2017). Generation of acoustic helical wavefronts using metasurfaces. Phys. Rev. B 95, 024312. doi:10.1103/PhysRevB.95.024312
Fan, S., Zhao, S., Cap, L., Zhu, Y., Chen, A., Wang, Y., et al. (2020). Reconfigurable curved metasurface for acoustic cloaking and illusion. Phys. Rev. B 101, 024104. doi:10.1103/PhysRevB.101.024104
Fan, S., Zhao, S., Chen, A., Wang, Y., Assouar, B., and Wang, Y. (2019). Tunable broadband reflective acoustic metasurface. Phys. Rev. Appl. 11, 044038. doi:10.1103/PhysRevApplied.11.044038
Fang, H., Chang, T., and Wang, K. W. (2020). Magneto-origami structures: Engineering multi-stability and dynamics via magnetic elastic coupling. Smart. Mat. Struct. 29, 015026. doi:10.1088/1361-665X/ab524e
Fang, X., Wen, J., Yin, J., Yu, D., and Xiao, Y. (2016). Broadband and tunable one-dimensional strongly nonlinear acoustic metamaterials: Theoretical study. Phys. Rev. E. 94, 052206. doi:10.1103/PhysRevE.94.052206
Faure, C., Richoux, O., Félix, S., and Pagneux, V. (2016). Experiments on metasurface carpet cloaking for audible acoustics. App. Phys. Lett. 108, 064103. doi:10.1063/1.4941810
Gamble, L., Lamoureux, A., and Shtein, M. (2020). Multifunctional composite Kirigami skins for aerodynamic control. Appl. Phys. Lett. 117, 254105. doi:10.1063/5.0024501
Geib, N., Sasmal, A., Wang, Z., Zhai, Y., Popa, B., and Grosh, K. (2021). Tunable nonlocal purely active nonreciprocal acoustic media. Phys. Rev. B 103, 165427. doi:10.1103/PhysRevB.103.165427
Gong, K., Wang, X., Ouyang, H., and Mo, J. (2019). Tuneable gradient Helmholtz-resonator-based acoustic metasurface for acoustic focusing. J. Phys. D. Appl. Phys. 52, 385303. doi:10.1088/1361-6463/ab2b85
Gong, K., Zhou, X., and Mo, J. (2022). Continuously tuneable acoustic metasurface for high order transmitted acoustic vortices. Smart. Mat. Struct. 31, 115001. doi:10.1088/1361-665X/ac9265
Gong, K., Zhou, X., Ouyang, H., and Mo, J. (2021). Continuous manipulation of acoustic wavefront using a programmable acoustic metasurface. J. Phys. D. Appl. Phys. 54, 305302. doi:10.1088/1361-6463/abfe81
Guo, J., Zhang, X., Fang, Y., and Qu, R. (2022). An extremely-thin acoustic metasurface for low-frequency sound attenuation with a tunable absorption bandwidth. Int. J. Mech. Sci. 213, 106872. doi:10.1016/j.ijmecsci.2021.106872
He, J., Liang, Q., Lv, P., Wu, Y., and Chen, T. (2022). Tunable broadband multi-function acoustic metasurface by nested resonant rings. Appl. Acoust. 197, 108957. doi:10.1016/j.apacoust.2022.108957
He, Y. L., Zhang, P. W., You, Z., Li, Z. Q., Wang, Z. H., and Shu, X. F. (2020). Programming mechanical metamaterials using origami tessellations. Comput. Sci. Tech. 189, 108015. doi:10.1016/j.compscitech.2020.108015
Hong, Y., Chi, Y., Wu, S., Li, Y., Zhu, Y., and Yin, J. (2020). Boundary curvature guided programmable shape-morphing kirigami sheets. Nat. Commun. 13, 530. doi:10.1038/s41467-022-28187-x
Hu, Z., Yang, Y., Xu, L., Hao, Y., and Chen, H. (2022). Binary acoustic metasurfaces for dynamic focusing of transcranial ultrasound. Front. Neurosci. 16, 984953. doi:10.3389/fnins.2022.984953
Jia, Y., Liu, Y., Hu, B., Xiong, W., Bai, Y., Cheng, Y., et al. (2022). Orbital angular momentum multiplexing in space-time thermoacoustic metasurfaces. Adv. Mat. 34, 2202026. doi:10.1002/adma.202202026
Jiang, X., Liang, B., Zou, X., Yang, J., Yin, L., Yang, J., et al. (2016). Acoustic one-way metasurfaces: Asymmetric phase modulation of sound by subwavelength layer. Sci. Rep. 6, 28023. doi:10.1038/srep28023
Kovacevich, D. A., and Popa, B. (2022). Programmable bulk modulus in acoustic metamaterials composed of strongly interacting active cells. Appl. Phys. Lett. 121, 101701. doi:10.1063/5.0097468
Kumar, S., and Lee, H. P. (2019). Recent advances in active acoustic metamaterials. Int. J. Appl. Mech. 11, 1950081. doi:10.1142/S1758825119500819
Lee, K., Baʼbaʼa, H., Yu, K., Li, K., Zhang, Y., Du, H., et al. (2022). Magnetoactive acoustic topological transistors. Adv. Sci. 9, 2201204. doi:10.1002/advs.202201204
Lee, K., Yu, K., Baʼbaʼa, H., Xin, A., Feng, Z., and Wang, Q. (2020). Sharkskin-inspired magnetoactive reconfigurable acoustic metamaterials. Research 2020, 4825185. doi:10.34133/2020/4825185
Lee, S. H., Park, C. M., Seo, Y. M., Wang, Z. G., and Kim, C. K. (2010). Composite acoustic medium with simultaneously negative density and modulus. Phys. Rev. Mat. 104, 054301. doi:10.1103/PhysRevLett.104.054301
Li, P., Chang, Y., Du, Q., Xu, Z., Liu, M., and Peng, P. (2020). Continuously tunable acoustic metasurface with rotatable anisotropic three-component resonators. Appl. Phys. Express. 13, 025507. doi:10.35848/1882-0786/ab6f27
Li, X., Rosendo-Lopez, M., Zhu, Y., Fan, X., Torrent, D., Liang, B., et al. (2019). Ultrathin acoustic parity-time symmetric metasurface cloak. Research 2019, 8345683. 10.48550/arXiv.1812.05845. doi:10.34133/2019/8345683
Li, X., Wang, Y., Chen, A., and Wang, Y. (2020). An arbitrarily curved acoustic metasurface for three-dimensional reflected wave-front modulation. J. Phys. D. Appl. Phys. 53, 195301. doi:10.1088/1361-6463/ab7327
Li, X., Wang, Y., Chen, A., and Wang, Y. (2019). Modulation of out-of-plane reflected waves by using acoustic metasurfaces with tapered corrugated holes. Sci. Rep. 9, 15856. doi:10.1038/s41598-019-52441-w
Li, X., Zhou, Y., Yang, Z., Zou, X., and Cheng, J. (2022). Tunable acoustic metasurface based on PVDF/polyimide unimorph sheets. Appl. Phys. Express. 15, 014001. doi:10.35848/1882-0786/ac414b
Li, Y., Shen, C., Xie, Y., Li, J., Wang, W., Cummer, S. A., et al. (2017). Tunable asymmetric transmission via lossy acoustic metasurfaces. Phys. Rev. Lett. 119, 035501. doi:10.1103/PhysRevLett.119.035501
Li, Y., Wang, S., Peng, Q., Zhaou, Z., Yang, Z., He, X., et al. (2019). Active control of graphene-based membrane-type acoustic metamaterials using a low voltage. Nanoscale 11, 16384–16392. doi:10.1039/C9NR04931B
Li, Z., Fei, C., Yang, S., Hou, C., Zhao, J., Li, Y., et al. (2022). Coding piezoelectric metasurfaces. Adv. Funct. Mat. 32, 2209173. doi:10.1002/adfm.202209173
Li, Z., Zhai, W., Li, X., Yu, X., Guo, Z., and Wang, Z. (2022). Additively manufactured dual-functional metamaterials with customisable mechanical and sound-absorbing properties. Virtual. Phys. Prototyp. 17, 864–880. doi:10.1080/17452759.2022.2085119
Liang, S., Liu, T., Gao, H., Gu, Z., An, S., and Zhu, J. (2020). Acoustic metasurface by layered concentric structures. Phys. Rev. Res. 2, 043362. doi:10.1103/PhysRevResearch.2.043362
Liang, Z., and Li, J. (2012). Extreme acoustic metamaterial by coiling up space. Phys. Rev. Lett. 108, 114301. doi:10.1103/PhysRevLett.108.114301
Liao, G., Luan, C., Wang, Z., Liu, J., Yao, X., and Fu, J. (2021). Acoustic metamaterials: A review of theories, structures, fabrication approaches, and applications. Adv. Mat. Technol. 6, 2000787. doi:10.1002/admt.202000787
Lie, K., Novelino, L. S., Gardoni, P., and Paulino, G. H. (2020). Big influence of small random imperfections in origami-based metamaterials. Proc. Roy. Soc. A 476, 2241. doi:10.1098/rspa.2020.0236
Lissek, H., Rivet, E., Laurence, T., and Fleury, R. (2018). Toward wideband steerable acoustic metasurfaces with arrays of active electroacoustic resonators. J. Appl. Phys. 123, 091714. doi:10.1063/1.5011380
Liu, B., and Jiang, Y. (2018). Controllable asymmetric transmission via gap-tunable acoustic metasurface. Appl. Phys. Lett. 112, 173503. doi:10.1063/1.5023852
Liu, P., Chen, X., Xu, W., and Pei, W. (2020). Magnetically controlled multifunctional membrane acoustic metasurface. J. Appl. Phys. 127, 185104. doi:10.1063/1.5145289
Liu, X., Wu, J., and Ma, F. (2021). Dynamic tunable acoustic metasurface with continuously perfect sound absorption. J. Phys. D. Appl. Phys. 54, 365105. doi:10.1088/1361-6463/ac0ab9
Liu, Z., Zhang, X., Mao, Y., Zhu, Y. Y., Yang, Z., Chan, C. T., et al. (2000). Locally resonant sonic materials. Science 289, 1734–1736. doi:10.1126/science.289.5485.1734
Lombard, O., Kumar, R., Mondain-Monval, O., Brunet, T., and Poncelet, O. (2022). Quasi flat high index acoustic lens for 3D underwater ultrasound focusing. Appl. Phys. Lett. 120, 221701. doi:10.1063/5.0088503
Ma, F., Xu, Y., and Wu, J. H. (2019). Shell-type acoustic metasurface and arc-shape carpet cloak. Sci. Rep. 9, 8076. doi:10.1038/s41598-019-44619-z
Ma, G., Fan, X., Sheng, P., and Fink, M. (2018). Shaping reverberating sound fields with an actively tunable metasurface. PNAS 115, 6638–6643. doi:10.1073/pnas.1801175115
Ma, G., Yang, M., Xiao, S., Yang, Z., and Sheng, P. (2014). Acoustic metasurface with hybrid resonances. Nat. Mat. 13, 873–878. doi:10.1038/nmat3994
Mostaan, S. M. A., and Saghaei, H. (2021). A tunable broadband graphene-based metamaterial absorber in the far-infrared region. Opt. Quant. Electron. 53, 96. doi:10.1007/s11082-021-02744-y
Ouisse, M., Collet, M., and Scarpa, F. (2016). A piezo-shunted kirigami auxetic lattice for adaptive elastic wave filtering. Smart. Mat. Struct. 25, 115016. doi:10.1088/0964-1726/25/11/115016
Peng, Y., Chen, J., Yang, Z., Zou, X., Tao, C., and Cheng, J. (2022). Broadband tunable acoustic metasurface based on piezoelectric composite structure with two resonant modes. Appl. Phys. Exp. 15, 014004. doi:10.35848/1882-0786/ac444a
Popa, B., Shinde, D., Konneker, A., and Cummer, S. A. (2015). Active acoustic metamaterials reconfigurable in real-time. Phys. Rev. B 91, 220303. doi:10.1103/PhysRevB.91.220303
Popa, B., Zhai, Y., and Kwon, K. (2018). Broadband sound barriers with bianisotropic metasurfaces. Nat. Commun. 9, 5299. doi:10.1038/s41467-018-07809-3
Pratapa, P. P., Suryanarayana, P., and Paulino, G. H. (2018). Bloch wave framework for structures with nonlocal interactions: Application to the design of origami acoustic metamaterials. J. Mech. Phys. Solids. 118, 115–132. doi:10.1016/j.jmps.2018.05.012
Quan, L., and Alu, A. (2019). Hyperbolic sound propagation over nonlocal acoustic metasurfaces. Phys. Rev. Lett. 123, 244303. doi:10.1103/PhysRevLett.123.244303
Shen, Y., Zhu, X., Cai, F., Ma, T., Li, F., Xia, X., et al. (2019). Active acoustic metasurface: Complete elimination of grating lobes for high-quality ultrasound focusing and controllable steering. Phys. Rev. Appl. 11, 034009. doi:10.1103/PhysRevApplied.11.034009
Song, A., Li, J., Peng, X., Shen, C., Zhu, X., Chen, T., et al. (2019). Asymmetric absorption in acoustic metamirror based on surface impedance engineering. Phys. Rev. Appl. 12, 054048. doi:10.1103/PhysRevApplied.12.054048
Song, X., Chen, T., Huang, W., and Chen, C. (2021). Frequency-selective modulation of reflected wave fronts using a four-mode coding acoustic metasurface. Phys. Lett. A 394, 127145. doi:10.1016/j.physleta.2021.127145
Steiger, K., Psota, P., Dolecek, R., Vapenka, D., Mokry, P., Vaclavik, J., et al. (2016). Adaptive acoustic metasurfaces for the active sound field control. Proc. Mtgs. Acoust. 28, 065004. doi:10.1121/2.0000472
Sun, J., Scarpa, F., Liu, Y., and Leng, J. (2016). Morphing thickness in airfoils using pneumatic flexible tubes and Kirigami honeycomb. J. Intell. Mat. Syst. Struct. 6, 755–763. doi:10.1177/1045389X15580656
Tang, Y. F., Liang, B., Yang, J., and Cheng, J. C. (2019). Voltage-controlled membrane-type active acoustic metasurfaces with ultrathin thickness. Appl. Phys. Express. 12, 064501. doi:10.7567/1882-0786/ab1277
Tao, Z., Ren, X., Zhao, A. G., Sun, L., Zhang, Y., Jiang, W., et al. (2022). A novel auxetic acoustic metamaterial plate with tunable bandgap. Int. J. Mech. Sci. 226, 107414. doi:10.1016/j.ijmecsci.2022.107414
Thota, M., Li, S., and Wang, K. W. (2017). Lattice reconfiguration and phononic band-gap adaptation via origami folding. Phys. Rev. B 95, 064307. doi:10.1103/PhysRevB.95.064307
Tian, Y., Wei, Q., Cheng, Y., and Liu, X. (2017). Acoustic holography based on composite metasurface with decoupled modulation of phase and amplitude. Appl. Phys. Lett. 110, 191901. doi:10.1063/1.4983282
Tian, Z., Shen, C., Li, J., Reit, E., Backman, H., Socolar, J. E. S., et al. (2020). Dispersion tuning and route reconfiguration of acoustic waves in valley topological phononic crystals. Nat. Commun. 11, 762. doi:10.1038/s41467-020-14553-0
Tian, Z., Shen, C., Li, J., Reit, E., Gu, Y., Fu, H., et al. (2019). Programmable acoustic metasurfaces. Adv. Funct. Mat. 29, 1808489. doi:10.1002/adfm.201808489
Wang, C., Li, J., and Zhang, D. (2021). Optimization design method for kirigami-inspired space deployable structures with cylindrical surfaces. Appl. Math. Model. 89, 1575–1598. doi:10.1016/j.apm.2020.07.005
Wang, Q., Zhou, Z., Liu, D., Ding, H., Gu, M., and Li, Y. (2022). Acoustic topological beam nonreciprocity via the rotational Doppler effect. Sci. Adv. 8, eabq4451. doi:10.1126/sciadv.abq4451
Wang, W., Hu, C., Ni, J., Ding, Y., Weng, J., Liang, B., et al. (2022). Efficient and high-purity sound frequency conversion with a passive linear metasurface. Adv. Sci. 9, 2203482. doi:10.1002/advs.202203482
Wang, X., Yang, J., Liang, B., and Cheng, J. (2020). Tunable annular acoustic metasurface for transmitted wavefront modulation. Appl. Phys. Express. 13, 014002. doi:10.7567/1882-0786/ab59a5
Wu, L., Fan, Y., Wang, H., Zhang, L., Sheng, Y., Wang, Y., et al. (2021). Research on the processing method of acoustic focusing cavities based on the temperature gradient. Appl. Sci. 11, 5737. doi:10.3390/app11125737
Xia, B., Chen, N., Xie, L., Quin, Y., and Yu, D. (2016). Temperature-controlled tunable acoustic metamaterial with active band gap and negative bulk modulus. Appl. Acoust. 112, 1–9. doi:10.1016/j.apacoust.2016.05.005
Xia, J., Zhang, X., Sun, H., Yuan, S., Qian, J., and Ge, Y. (2018). Broadband tunable acoustic asymmetric focusing lens from dual-layer metasurfaces. Phys. Rev. Appl. 10, 014016. doi:10.1103/PhysRevApplied.10.014016
Xia, P., Lai, Y., and Liu, X. (2022). Adjustable magnetic-control design of a metasurface for sound insulation. Front. Mech. Eng. 7, 829149. doi:10.3389/fmech.2021.829149
Xiao, S., Ma, G., Li, Y., Yang, Z., and Sheng, P. (2015). Active control of membrane-type acoustic metamaterial by electric field. Appl. Phys. Lett. 106, 091904. doi:10.1063/1.4913999
Xie, S., Fang, X., Li, P., Huang, S., Peng, Y., Shen, Y., et al. (2020). Tunable double-band perfect absorbers via acoustic metasurfaces with nesting helical tracks. Chin. Phys. Lett. 37, 054301. doi:10.1088/0256-307X/37/5/054301
Xie, Y., Wang, W., Chen, H., Konneker, A., Popa, B., and Cummer, S. A. (2014). Wavefront modulation and subwavelength diffractive acoustics with an acoustic metasurface. Nat. Commun. 5, 5553. doi:10.1038/ncomms6553
Xu, Z., Meng, H., Chen, A., Yang, J., Liang, B., and Cheng, J. (2021). Tunable low-frequency and broadband acoustic metamaterial absorber. J. Appl. Phys. 129, 094502. doi:10.1063/5.0038940
Yasuda, H., and Yang, J. (2015). Reentrant origami-based metamaterials with negative Poisson’s ratio and bistability. Phys. Rev. Lett. 114, 185502. doi:10.1103/PhysRevLett.114.185502
Yu, K., Fang, N. X., Huang, G., and Wang, Q. (2018). Magnetoactive acoustic metamaterials. Adv. Mat. 30, 1706348. doi:10.1002/adma.201706348
Yu, N., Genevet, P., Kats, M. A., Aieta, F., Tetienne, J., Capasso, F., et al. (2011). Light propagation with phase discontinuities: Generalized laws of reflection and refraction. Science 334, 333–337. doi:10.1126/science.1210713
Yuan, B., Cheng, Y., and Liu, X. (2015). Conversion of sound radiation pattern via gradient acoustic metasurface with space-coiling structure. Appl. Phys. Lett. 8, 027301. doi:10.7567/APEX.8.027301
Zhai, S., Song, K., Ding, C., Wang, Y., Dong, Y., and Zhao, X. (2018). Tunable acoustic metasurface with high Q spectrum splitting. Materials 11, 1976. doi:10.3390/ma11101976
Zhai, Y., Kwon, H., and Popa, B. (2019). Active Willis metamaterials for ultracompact nonreciprocal linear acoustic devices. Phys. Rev. B 99, 220301. doi:10.1103/PhysRevB.99.220301
Zhai, Y., Kwon, H., and Popa, B. (2021). Anomalous reflection with omnidirectional active metasurfaces operating in free space. Phys. Rev. B 16, 034023. doi:10.1103/PhysRevApplied.16.034023
Zhang, C., Cao, W., Wu, L., Ke, J., Jing, Y., Cui, T., et al. (2021). A reconfigurable active acoustic metalens. Appl. Phys. Lett. 118, 133502. doi:10.1063/5.0045024
Zhang, H., Xiao, Y., Wen, J., Yu, D., and Wen, X. (2016). Ultra-thin smart acoustic metasurface for low-frequency sound insulation. Appl. Phys. Lett. 108, 141902. doi:10.1063/1.4945664
Zhang, Y. Y., Gao, N. S., and Wu, J. H. (2020). New mechanism of tunable broadband in local resonance structures. Appl. Acoust. 169, 107482. doi:10.1016/j.apacoust.2020.107482
Zhao, S., Chen, A., Wang, Y., and Zhang, C. (2018). Continuously tunable acoustic metasurface for transmitted wavefront modulation. Phys. Rev. Appl. 10, 054066. doi:10.1103/PhysRevApplied.10.054066
Zhao, X., Cai, L., Yu, D., Lu, Z., and Wen, J. (2017). A low frequency acoustic insulator by using the acoustic metasurface to a Helmholtz resonator. AIP Adv. 7, 065211. doi:10.1063/1.4989819
Zhao, Z., Cui, X., Li, Y., and Li, M. (2022). Thermal tuning of vibration band gaps in homogenous metamaterial plate. Int. J. Mech. Sci. 225, 107374. doi:10.1016/j.ijmecsci.2022.107374
Zhou, H., and Baz, A. (2023). A simple configuration of an actively synthesized gyroscopic-nonreciprocal acoustic metamaterial. J. Vib. Acoust. 145, 021004. doi:10.1115/1.4055103
Zhou, H., Fan, S., Li, X., Fu, W., Wang, Y., and Wang, Y. (2020). Tunable arc-shaped acoustic metasurface carpet cloak. Smart. Mat. Struct. 29, 065016. doi:10.1088/1361-665X/ab87e4
Zhu, R., Yasuda, H., Huang, G. L., and Yang, J. K. (2018). Kirigami-based elastic metamaterials with anisotropic mass density for subwavelength flexural wave control. Sci. Rep. 8, 483. doi:10.1038/s41598-017-18864-z
Zhu, X., and Lau, S. (2019). Perfect anomalous reflection and refraction with binary acoustic metasurfaces. J. Appl. Phys. 126, 224504. doi:10.1063/1.5124040
Zhu, X., Li, K., Zhang, P., Zhu, J., Zhang, J., Tian, C., et al. (2016). Implementation of dispersion-free slow acoustic wave propagation and phase engineering with helical-structured metamaterials. Nat. Commun. 7, 11731. doi:10.1038/ncomms11731
Zhu, Y., Fan, X., Liang, B., Yang, J., Yang, J., Yin, L., et al. (2016). Multi-frequency acoustic metasurface for extraordinary reflection and sound focusing. AIP Adv. 6, 121702. doi:10.1063/1.4968607
Zhu, Y., Zou, X., Liang, B., and Cheng, J. (2015). Acoustic one-way open tunnel by using metasurface. Appl. Phys. Lett. 107, 113501. doi:10.1063/1.4930300
Keywords: acoustic metasurfaces, acoustic waves, mechanical tuning, active control, field-responsive materials
Citation: Zabihi A, Ellouzi C and Shen C (2023) Tunable, reconfigurable, and programmable acoustic metasurfaces: A review. Front. Mater. 10:1132585. doi: 10.3389/fmats.2023.1132585
Received: 27 December 2022; Accepted: 16 February 2023;
Published: 02 March 2023.
Edited by:
Giuseppe Failla, Mediterranea University of Reggio Calabria, ItalyReviewed by:
Nansha Gao, Northwestern Polytechnical University, ChinaYong Li, Tongji University, China
Bogdan Popa, University of Michigan, United States
Copyright © 2023 Zabihi, Ellouzi and Shen. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Chen Shen, c2hlbmNAcm93YW4uZWR1
 Ali Zabihi
Ali Zabihi Chadi Ellouzi
Chadi Ellouzi Chen Shen
Chen Shen