Optical inspection of the braid formation zone during manufacturing of preforms from reinforcement fibers for defect detection purposes

Braiding is a highly automated process for manufacturing preforms directly from reinforcement yarns at large production volumes. The quality of braided textiles and the stability of the process can however be negatively affected by defects that occur during braiding. If such defects can be detected from fine process anomalies early during their formation, the process can be interrupted and countermeasures can be introduced before the defect aggravates and gets braided into the product. Current sensor modules for defect detection during braiding however involve problems of either late response times, process impairments or a lack of applicability to braiding of composite parts. In an effort to overcome these drawbacks, the paper at hand proposes to optically monitor the braid formation zone by means of a single camera (no process impairments). An associated image analysis algorithm creates a measure for the angular distance of each individual braiding yarn to its neighboring yarns and tracks the yarns as they rotate around the overbraidable mandrel (typical for braiding of composite parts). Since braiding yarns typically exhibit distinct curvatures as they span from the bobbins towards the center of the braiding machine due to frictional yarn-yarn interaction, a change in yarn curvature and thus in angular yarn distance is an early sign of a defect-characteristic anomaly in yarn tension (early response). If implemented on a real-time capable computing device, an apparatus according to the presented method can be retrofitted to existing production lines for braiding process monitoring. It then contributes to the reduction of error correction times since countermeasures are quicker to implement as long as the defect has not aggravated, yet. Furthermore, scrap material rates can be reduced as anomalies can be detected before they manifest in the braided structure.

1 Introduction

Having been practiced as a social art of bonding strands of human hair in a pleasant fashion for at least 22.000–30.000 years (Kohen, 1946; White, 2006), the principle of braiding is nowadays applied as a textile production process with applications in a wide range of economic sectors such as the marine industry (e.g., mooring ropes or fishing nets), the sports and leisure industry [e.g., climbing ropes or parachute cords (Michael et al., 2016)], electrical engineering and oil hydraulics (e.g., electric shielding or protection of hoses) or medical technology [e.g., stents (Aibibu et al., 2016)]. More specifically, braiding of reinforcement fibers in order to manufacture preforms for composite parts has well-known applications in the automotive [e.g., pillars for passenger compartments (Hill, 2003; Bulat et al., 2016)], aviation [e.g., helicopter landing gears (Thuis, 2004a; 2004b)], space [e.g., rocket nozzles (van Ravenhorst and Akkerman, 2016b; van Ravenhorst, 2018)] as well as in the sports and leisure industry [e.g., lightweight bicycle rims (Kind and Drechsler, 2015; Bulat et al., 2016; Zuurendonk, 2018)]. During braiding of these often hollow structures that may be curved and show a varying cross-section, typical defects such as a generally “fuzzy” braid due to frictional yarn abrasion, yarn loops due to a loss in tension of a single yarn or local yarn gaps and yarn breakages due to an increased tension of an individual yarn may occur (Ebel et al., 2013; Ebel et al., 2016). A particular process anomaly, namely the fibrous ring, is regarded as the most relevant cause for braiding defects. A fibrous ring is an accumulation of broken carbon filaments at the bobbin (braiding spool) which impedes the yarn from unwinding properly from the spool (Ebel et al., 2016; Mierzwa et al., 2016). This causes an increase in tension of the respective yarn that may eventually lead to a distortion of the regular braid structure in the form of a local yarn gap and eventually to a breakage of the yarn. Mierzwa et al. (2018) and Mierzwa (2019) investigated the effect of local yarn gaps in biaxially braided multilayer specimens on their strength. They found a deterioration of up to 36% in tensile and of up to 33% in compressive strength when the braided preforms with local yarn gaps were infiltrated with resin by the Vacuum Assisted Process. By contrast, they did not find significant effects when the preforms were injected with resin by means of the Resin Transfer Molding (RTM) Process. The authors concluded that an excessive fiber undulation in the braided plies on top of the yarn gap was created when a flexible upper tooling (here: vacuum bag) was used during resin infusion and caused the excessive knock-down in strength. In case of a rigid upper tooling (here: RTM tool), a local yarn gap did not cause additional fiber undulation and hence no significant knock-down in strength. Ebel et al. (2013); Ebel et al. (2016) conducted endurance braiding tests in order to quantify the extent of machine downtime due to the necessity of manually rethreading yarns that had broken because of fibrous rings at the braiding spools. In an extreme case scenario with unsuitable parameters during rewinding of the yarns on the braiding spools, they observed a downtime of 26% of the total duration of a test. Despite of these investigations constituting extreme cases, the above figures show that monitoring systems for the braiding process can on the one hand serve as quality assurance and on the other hand as a measure to increase production output and reduce scrap material rates during braiding. The latter point is particularly valid because a process anomaly can often be resolved with little effort if it is detected early (e.g., removal of a fibrous ring with scissors by hand). If an anomaly has evolved through various stages to a major failure event (e.g., a yarn breakage), the braided preform usually needs to be scrapped and time-consuming effort is required to reset the machine to an acceptable state (e.g., rethreading of a broken yarn).

2 Current sensor modules for braiding process monitoring

In order to detect braiding process anomalies, several approaches already exist. Most widely used sensors are rudimentary, stationary switches that jut into the tracks of the bobbin carriers (c.f. Maidl et al., 2018). Upon breakage of a yarn, a movable member of the yarn tensioning unit of the bobbin carrier, e.g., a lever or a slider, changes its position and/or orientation compared to the usual operating mode. When the defective carrier passes by a stationary sensor, the switch gets pushed and a control signal to stop the braiding machine is generated. This approach comes with particularly low installation effort and costs. However, it is only capable of detecting an anomaly when a yarn has already broken. It does not give an early warning which could be used as a trigger to intervene and avoid a larger failure event.

An approach that allows the generation of an early warning comprises a force sensor with a skid attached to it (Lenkeit, 1997). The skid gets in contact with the braiding yarns as they pass by and the force sensor measures the induced reaction force. This way, yarns with increased tension that are about to break can be identified as can yarns with a reduced tension that may lead to a yarn loop in the braid. A disadvantage of this approach is however that the additional yarn contact may cause additional yarn damage, particularly when the braiding machine operates at high speeds which imply a high relative velocity between the yarn and the skid. When brittle reinforcement fibers such as carbon or glass are braided, it is generally agreed that unnecessary yarn contact needs to be avoided for reasons of an accumulation of yarn damage.

Branscomb (2007) and Branscomb and Beale (2011) proposed an optical inspection of the movement of the braiding point. The braiding point is the point in the center of a braiding machine where, during braiding of a rope or a cord, the braiding yarns meet and form the braided strand. During regular braiding, the braiding point rests stationary in the center of the machine due to a balance of forces from the circularly arranged braiding yarns. If a yarn tension anomaly is present, the braiding point moves outside the center of the machine because of imbalanced yarn forces. This optical inspection also works without any additional yarn contact and therefore incurs no additional yarn damage. The problem of this approach is however that during braiding of composite preforms, a distinct braiding point that is free to move does not exist in most cases. Instead, the reinforcement fibers are usually braided onto rigidly guided mandrels (e.g., by a robot). Hence, the described concept cannot be applied for braiding of composite structures.

Nevertheless, there are optical inspection approaches of the braid formation zone that can be applied in composites braiding (cf. Figure 1 for a view of the braid formation zone). The underlying detection concept is based on the fact that braiding yarns are slightly curved as they span from the bobbin towards the center of the machine due to frictional interaction between yarns that circulate through the machine in opposite directions (van Ravenhorst and Akkerman, 2016a; van Ravenhorst, 2018). When a braiding yarn shows an increased tension, its curvature is reduced. When a yarn shows a reduced tension, its curvature is in turn more pronounced. Brockmanns et al. (2014) conclude in their patent application that from a force sensor with a skid attached to it according to Lenkeit (1997) not only the force amplitude created by the passing-by of each yarn but also the time interval between the force impulses can be measured. Furthermore, yarn contact and thus yarn damage can be avoided by measuring the time intervals between circulating braiding yarns by means of an optical sensor. Due to natural process fluctuations such as vibrating yarns, such a discrete distance measurement was however experimentally determined by means of a light barrier in the braid formation zone to be prone to false positive and false negative defect detections (Maidl et al., 2022).

FIGURE 1

FIGURE 1. Braid formation zone during braiding with $n_{yarn}=64$ 24 k carbon yarns; curvature of one yarn indicated by a tangential white-dotted line; yarn with purposefully increased tension marked by two solid white lines; increased distance to the preceding yarn marked by blue color; reduced distance to the succeeding yarn marked by orange color; image taken from (Maidl et al., 2022) and adapted.

The paper at hand is therefore intended to provide a solution for an optical inspection of the braid formation zone that

• is capable of giving an early warning before defective braid is produced,

• incurs no additional yarn damage,

• is suitable for the use case of braiding of composite structures on a mandrel and

• allows a robust process monitoring by eradicating false positive or false negative defect detections that may stem from natural process fluctuations.

3 Materials and methods

The fact that braiding yarns do not follow a straight line but exhibit a curved shape instead is indicated in Figure 1. A straight dotted line that is tangential to one of the yarns shows an increasing distance to the respective yarn the closer the yarn is to the center of the braid formation zone. Additionally, another yarn marked by two solid lines is purposefully set under an anomalously high tension in Figure 1, thereby resembling a situation that occurs when a braiding defect, such as a fibrous ring, is present. The consequence is that the curvature of this yarn is reduced, resulting in an increased angular distance to its succeeding yarn (cf. blue area in Figure 1) and a reduced angular distance to its preceding yarn (cf. orange area in Figure 1). This deviation in angular yarn distances results in different time intervals of the circulating braiding yarns passing by a discrete sensor that is placed close to the center of the braid formation zone (e.g., a light barrier of which the red laser is visible in Figure 1). Brockmanns et al. (2014) propose to use such a deviation from regular time intervals as a defect detection criterion. Since this was—given natural process fluctuations—shown to be an unreliable criterion (Maidl et al., 2022), a video camera and an associated image analysis algorithm are applied to track the yarns during the braiding process in the paper at hand. The idea behind this approach is that a yarn distance measurement is not only carried out at a discrete position in the braid formation zone but that distance measurements for each yarn are constantly made as the yarns circulate around the center of the machine (ideally at each video frame). This way, a multitude of yarn distance measurements is available for each braiding yarn as it completes a full 360° revolution through the machine. An averaging over several yarn distance measurements is then able to even out naturally occurring process fluctuations (e.g., vibrations or temporary stick-slip movement of the yarns).

In order to validate the above-described detection principle and to illustrate a possible way on how to determine over how many video frames the yarn distance measurements need to be averaged, the following experimental study was conducted. A cylindrical mandrel with a diameter of $d=65mm$ and a length of $l=2.5m$ was overbraided with Tenax®-E HTS40 carbon yarns from Teijin Carbon Europe GmbH under a braiding angle of $\phi ={45}^{°}$. The RF 1/128–100 braiding machine from HERZOG GmbH that was used for the experiments was set to a speed of horn gear rotation of $r=130rpm$. For an optimal spreading of the braiding yarns, the braiding ring was mechanically actuated by shaker motors at a frequency of approximately 13 Hz. The number of braiding yarns was varied between $n_{yarn}=32$ and $n_{yarn}=64$. The reason for varying the yarn number was to evaluate the effect of less overall curvature of the braiding yarns on the detection principle. If a comparatively low number of braiding yarns (here: $n_{yarn}=32$) is used, the overall frictional interaction between the yarns is reduced because there are less yarn crossing points in the braid formation zone. This results in less yarn curvature compared to the use of a larger yarn number (here: $\left.n_{yarn}=64\right)$, making it potentially more difficult to detect a change in angular yarn distances. Furthermore, the filament count of the yarns was varied between 6 k (400 tex), 12 k (800 tex) and 24 k (1600 tex). Similar to the variation in yarn number, the idea behind varying the thickness of the threads was to capture a potential change in frictional yarn interaction. When thinner yarns (here: 6 k) are used, the deflection of each yarn at a crossing point and also the contact area between two touching yarns is smaller compared to the case of thicker braiding yarns (here: 12 k or 24 k). This may result in less overall frictional interaction, less yarn curvature and consequently to a more difficult defect detection by angular yarn distances. The sizing material for the 12 k and 24 k yarns was of the type F13 (epoxy) and of the type E13 (polyurethane) for the 6 k yarns because Teijin Carbon Europe GmbH does not deliver the three thicknesses of HTS40 yarns with the exact same type of sizing. Moreover, the tension of the braiding yarns was varied. During regular braiding without any replication of a defect (reference experiments), the tension of all braiding yarns was set to ∼4 N by applying standard 350 g-yarn tension springs as delivered by HERZOG GmbH in the bobbin carriers. In order to be able to repeatedly create the same level of process anomaly, the tension of a single braiding yarn was increased to ∼20 N, ∼35 N and >45 N by means of a barrel tensioner that was attached to one bobbin carrier (cf. Figure 2) and by changing the tension spring inside the respective bobbin carrier to ratings of 600 g and 950 g. The above-described test plan was carried out full factorially. Given the large number of braiding tests and the amount of data generated from each test, each experiment configuration was tested once.

FIGURE 2

FIGURE 2. Barrel tensioner screwed onto a bobbin carrier in order to create a consistent level of elevated tension of a single yarn during the braiding experiments with a simulated defect.

For the recording the braiding experiments, a Nikon D3300 SLR camera with a resolution of 1920 × 1080 pixels and a frame rate of $framerate=25fps$ was aligned with the mandrel axis and placed at a distance of about 3.3 m to the braiding machine. No obstruction of the camera view on the braid formation zone was present during the experiments discussed in the paper at hand. For considerations on an obstruction of the camera view, e.g., by support structures, the mandrel or another handling robot, the reader is referred to the outlook section of this article. A ring light as backlight illumination (cf. Figure 3) in combination with an ISO value of the camera of 400 and an aperture setting of $\frac{1}{8}$ eliminated any disturbing light reflections from the shimmering sizing of the carbon yarns. The exposure time of the camera was set to 0.002 s in order to obtain video frames without significant motion blur of the yarns. This value was calculated by allowing an error due to motion blur of 1 pixel at the outside edge of the ring light (outside Ø 252.5 mm). The circumferential yarn speed at the outside edge of the ring light was calculated from the set speed of horn gear rotation and linear down-scaling by intercept theorems. A possible vibration of the braiding yarns was neglected in the calculation of the exposure time of the camera. A visual inspection of the acquired video frames did not show any motion blur of the braiding yarns and therefore legitimized this simplification.

FIGURE 3

FIGURE 3. Experimental setup of the RF 1/128–100 braiding machine from HERZOG GmbH equipped with a ring light behind the braid formation zone, a cylindrical mandrel that is overbraided with carbon yarns and a camera that monitors the illuminated braid formation zone.

4 Image analysis algorithm

Figure 4A shows an exemplary video frame acquired by the above-described camera setup during braiding with $n_{yarn}=64$ 12 k braiding yarns at a speed of horn gear rotation of $r=130rpm$. Due to the camera settings, all parts of the image that are not illuminated by the ring light appear dark. Additionally, the braiding yarns distinctly shadow the ring light without any motion blur or disturbing light reflections. Figure 4B depicts the working principle of the image analysis algorithm, which was implemented in MATLAB R2021a. In a preprocessing step, the image is first complemented by the “imcomplement”-function and then binarized by the “imbinarize”-function. After that, all parts of the video frame that are not illuminated by the ring light are cropped from the image by white masks. This makes the braiding yarns appear as white objects in Figure 4B.

FIGURE 4

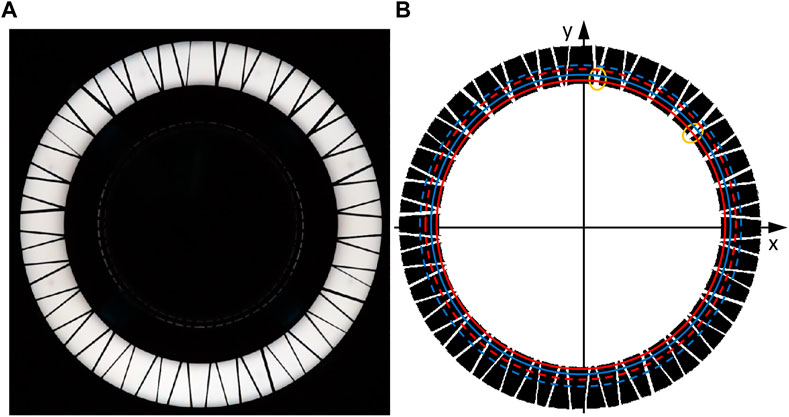
FIGURE 4. Exemplary video frame acquired by the camera that monitors the braid formation zone (A); identical video frame after preprocessing by the image analysis algorithm (B); two pairs of imaginary circles (solid and dashed circles) drawn-in for a visualization of the working principle of the main processing of the algorithm; two orange ellipses mark areas where the circle in solid blue intersects with yarn crossing points.

During the subsequent main processing, a first pair of imaginary concentric circles close to the inner edge of the ring light is drawn into the image (cf. solid red and blue circles in Figure 4B). The outer circle of this pair is 10 pixels larger in radius than the inner circle. It is then checked if both circles intersect with a white object as many times as there are braiding yarns in the braiding test. Three cases may result from this check. The first case is that the number of intersections equals the number of braiding yarns for both circles. In this case, the measurement algorithm can continue. The second case is that the number of intersections only equals the number of braiding yarns for the outer circle. In this case, the outer circle is taken as the new inner circle and a new outer circle is drawn that is 10 pixels larger in radius than the new inner circle (previous outer circle). Then, the check for the number of intersections is run again. In the third case, the number of yarn intersections does not equal the number of braiding yarns for the outer circle. This is the case in Figure 4B. Two orange ellipses mark areas where the outer circle only intersects with one white object where in fact two braiding yarns cross each other. The number of intersections for the outer circle is in this case 62, which is two less than the number of braiding yarns $n_{yarn}=64$. In this case, a whole new pair of circles is drawn into the image, whereby the inner circle of the new pair is 10 pixels larger in radius than the previous outer circle (cf. dashed red and blue circles in Figure 4B). The check for the number of yarn intersections is carried out in a loop until the first case of the yarn number being equal to the number of braiding yarns $n_{yarn}$ is reached or until no new outer circle can be drawn because the algorithm has reached the outer edge of the ring light with its imaginary circles. If the algorithm has reached the outer edge of the ring light without reaching the first case, the respective video frame is dropped and cannot be taken into account for the analysis. If the first case could be reached with a video frame, then the next step of measuring the angular yarn distances can be carried out.

For each of the intersection objects of inner and outer circle, their centroid is calculated by the “regionprops”-function. Exemplary intersection objects and their centroids are depicted in Figure 5. For each centroid on the inner circle, the corresponding centroid on the outer circle, which originates from the same yarn as the respective centroid on the inner circle, is found by means of a nearest neighbor search (“knnsearch”-function). Plausibility checks in the form that the distance between corresponding centroids must not exceed 11 pixels or be less than 9 pixels are implemented in order to avoid wrong assignments of centroids that are located closely to points of yarn intersections. This is of particular importance because in the next step, the decision whether a yarn circulates in clockwise or in counterclockwise direction through the braiding machine is based on the difference in polar angles $\left.\theta \in ]-\pi ;+\pi \right]$ of corresponding centroids from the inner and outer circle. In Figure 5, the polar angles $\theta$ with respect to the center of the braiding machine are drawn in for a pair of corresponding centroids from the inner (red dot) and outer circle (blue dot). Since the polar angle $\theta$ of the point on the inner circle is smaller than the one of the point on the outer circle, this pair of centroids is stipulated to originate from a counterclockwise yarn. If the polar angle $\theta$ from the point on the inner circle was larger than the one of the corresponding point on the outer circle, then the pair of centroids would be stipulated to originate from a clockwise yarn. Exceptions for the case of two corresponding centroids being located on different sides of the negative x-axis (transition $-\pi \to \pi$) are taken account of in the implementation of the image analysis algorithm. After all pairs of corresponding centroids are assigned to a direction of rotation, a further plausibility check is implemented in the form that there must be $\frac{n_{yarn}}{2}$ assignments for each of the two directions of yarn rotation. If this plausibility check cannot be passed, the respective video frame is dropped and the algorithm continues with the next video frame. If this plausibility check is passed, the polar angles $\theta$ for the centroids on the inner circle of both directions of rotation are separately sorted in ascending order. The angular distances of the yarns of both directions of rotation are then calculated by the difference between adjacent polar angles $\theta$ in the two sorted arrays for the two directions of rotation. In Figure 5, the angular distance of two adjacent centroids from a counterclockwise (CC) yarn is exemplarily indicated by $∆{\theta }_{1,CC}$.

FIGURE 5

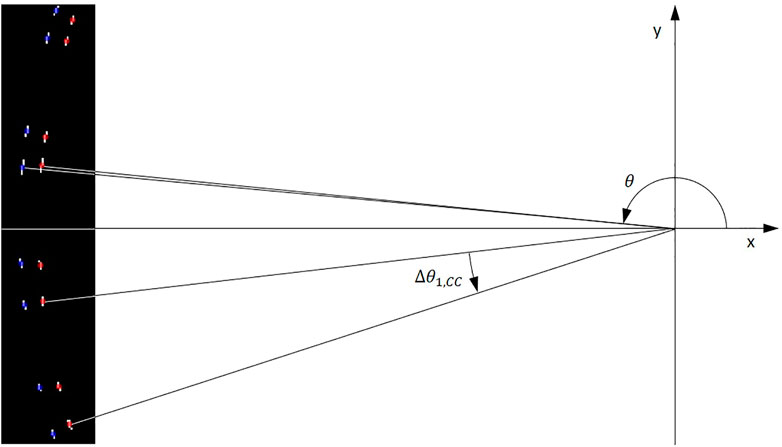
FIGURE 5. Close-up of white intersection objects resulting from the video frame in Figure 4; centroids of inner and outer intersection objects marked by red and blue dots, respectively; exemplary measurement of the polar angle $\theta$ of two intersection objects that originate from the same yarn for an identification of the direction of yarn rotation; exemplary visualization of the angular yarn distance $∆{\theta }_{1,CC}$ between two neighboring yarns of counterclockwise (CC) direction of rotation.

The final post processing comprises the two steps of averaging the yarn distance measurements per direction of rotation over several video frames and a visualization of the defective yarn in the acquired video frames. Figure 6 exemplarily shows angular yarn distance measurements of the counterclockwise yarns during braiding with the 12 k yarns and an increased tension of a single yarn of ∼35 N for the first nine video frames that passed all plausibility checks described above and therefore could be evaluated. Apart from a general scatter in the data, which reflects the nature of the braiding process and caused a stationary light barrier to be found to be unsuitable for braiding process monitoring (Maidl et al., 2022), a distinct pattern of a particular larger yarn distance directly followed by a smaller yarn distance appears to propagate from yarn distance numbers 24–25 in frame 1 to yarn distance numbers 27–28 in frame 15. This distinct propagating pattern reflects the fact that a yarn with an elevated tension, which creates a systematic deviation in yarn distances, moves in counterclockwise direction through the braiding machine. The distinct pattern moves from left to right through the diagrams in Figure 6 because the calculated yarn distances appear sorted from polar angles of $-\pi$ to $+\pi$ (counterclockwise direction in Figure 4) along the x-axes in the diagrams. However, the pattern is not always clearly distinguishable from the natural process scatter (particularly frames 2, 5 and 15) or are not visible at all (particularly frames 7 and 10). This is why an averaging over several video frames is crucial for a stable process monitoring. This averaging is carried out by shifting the x-axes in the diagrams in Figure 6 according to the speed of horn gear rotation of the braiding machine so that the distinct defect-characteristic pattern, graphically speaking, remains stationary (at the same x-axis value) in the diagrams. This shifting is carried out by the following operations: At first, the polar angle of the yarn in the third quadrant that is closest to the negative x-axis in the first video frame of a braiding experiment is calculated (“first yarn”, $i=1$). An isolated measurement of the angle ${\theta }_{i=1,CC,n_{frame}=1}$ would however be subject to yarn vibrations. This is why, for a more exact calculation, the actual position of each yarn ${\theta }_{i,CC,n_{frame}=1}$ is measured, corrected by the theoretical yarn spacing and then averaged.

$\begin{array}{l}{\theta }_{i=1,CC,n_{frame}=1,mean}=mean\left({\theta }_{i,CC,n_{frame}=1}-\frac{2\pi }{\frac{n_{yarn}}{2}}\bullet \left(i-1\right)\right),\\ wherebyi=\left\{1;2;\dots ;\frac{n_{yarn}}{2}\right\}\end{array}(1)$

Secondly, the expected position of the “first yarn” at frame number $n_{frame}$ due to its movement is calculated by

$\begin{array}{l}{\theta }_{i=1,CC,n_{frame},expected}\\ =wrapToPi\left({\theta }_{i=1,CC,n_{frame}=1,mean}+\frac{\frac{n_{frame}}{framerate}}{t_{360°}}\bullet 2\pi \right)\end{array}(2)$

whereby $t_{360°}$ is the time it takes a yarn to complete a full 360° revolution around the center of the braiding machine according to the set machine speed. The function “wrapToPi” is applied in order to project the obtained value from the function argument to the interval $\left]-\pi ;+\pi \right]$. Thirdly, of all the polar angles in the nth frame ${\theta }_{i,CC,n_{frame}}$, the closest match to the expected position of the “first yarn” ($i=1)$ from the first frame of the experiment is calculated by means of the “knnsearch”-function.

$\begin{array}{l}Inde{x}_{n_{frame}}=knnsearch\left({\theta }_{i,CC,n_{frame}},{\theta }_{i=1,CC,n_{frame},expected}\right),\\ wherebyi=\left\{1;2;\dots ;\frac{n_{yarn}}{2}\right\}\end{array}(3)$

FIGURE 6

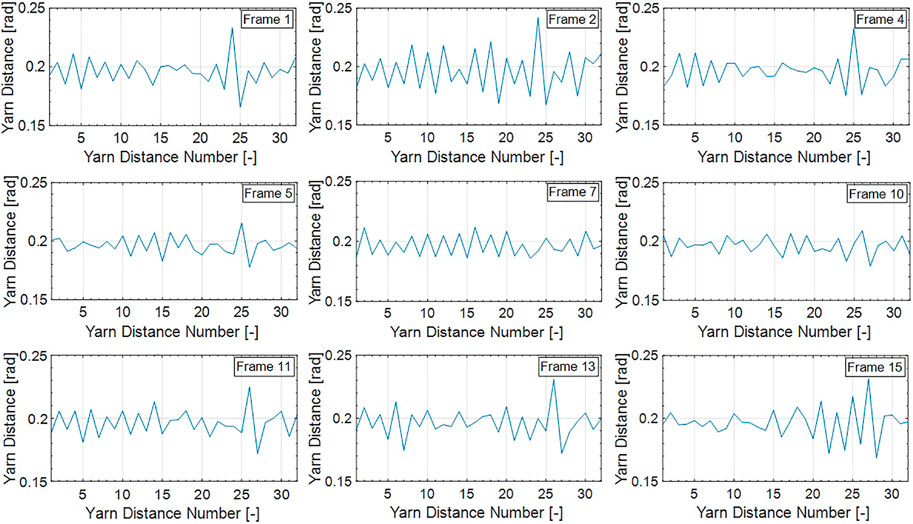
FIGURE 6. Yarn distance measurement results of counterclockwise yarns of the first 15 frames of the braiding experiment with $n_{yarn}=64$ 12 k yarns and an elevated tension of a single counterclockwise yarn of ∼35 N.

The index of the closest match minus 1 then equals the offset of the measured angular yarn distances from the nth frame compared to the first video frame of the experiment.

$offse{t}_{n_{frame}}=Inde{x}_{n_{frame}}\left(1\right)-1(4)$

The negative of this offset value is then applied in the “circshift”-function to shift the sorted array of angular yarn distances in a way that each position of the array corresponds to the same yarn throughout the monitoring process. The above formulae are written and explained for the case of monitoring counterclockwise (CC) yarns. In case clockwise (C) yarns shall be monitored, the “+“-sign in Formula 2 needs to be replaced by a “−“-sign. Additionally, not the negative but the positive offset value from Formula 4 needs to be applied in the “circshift” function in order to keep a moving defective yarn and its corresponding yarn distance measurements at the same position in the array of angular yarn distance values over the duration of the braiding experiment.

Once each position in the array of angular yarn distance values corresponds to the distance between the same two yarns for all acquired video frames, an average in yarn distance can be calculated for each pair of yarns over a certain number of video frames (length of averaging window). The result of such an averaging over the nine diagrams from Figure 6 that represent measurements from counterclockwise yarns is illustrated in Figure 7. It can be observed that random deviations in angular yarn distances have significantly evened out. Furthermore, between yarn distance number 24 and 25, a distinct defect-characteristic spike has formed in the diagram. The prominence of this defect-characteristic spike is marked with a double arrow. This measure is used in the following results section as a value to compare the deviation in yarn distances over the different experiment variants.

FIGURE 7

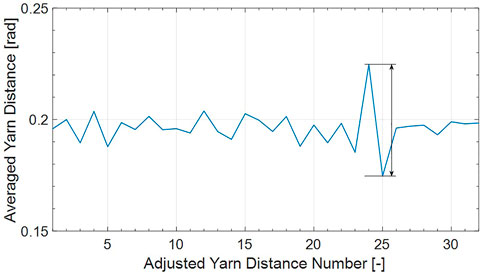
FIGURE 7. Averaged yarn distance measurements calculated from the nine diagrams shown in Figure 6 after shifting the x-axis by Formula 1 through Formula 4; prominence of defect-characteristic pattern indicated by a double arrow.

From the position of the defect-characteristic pattern in Figure 7, the yarn with anomalously high tension can be identified to be the 25th counterclockwise yarn in the first video frame of the experiment counting from the negative x-axis in mathematically positive direction. Figure 8 shows a visualization of the detection result of the above-described image analysis algorithm for the first nine analyzable video frames of the braiding experiment already illustrated in Figure 6. The clockwise yarns are marked by red dots and the counterclockwise yarns are marked by blue dots. The defective yarn as identified by the algorithm is marked by a yellow dot. It can be observed that the marks lie at different radial distances from the center of the camera view. This is due to the fact that the image analysis algorithm had to apply different radii for the pair of circles in order that both circles intersect one-to-one with each braiding yarn. Furthermore, it can be seen that the defective yarn moves in counterclockwise direction through the sequence of images. On close inspection by eye, one can even correlate distinct deviations in angular yarn distances from the diagrams in Figure 6 to the distances of the yellow-marked yarn to its neighboring yarns in the respective frames in Figure 8.

FIGURE 8

FIGURE 8. Video frames corresponding to the yarn distance diagrams from Figure 6; clockwise yarns marked by red dots; counterclockwise yarns marked by blue dots; defective yarn as identified from the characteristic pattern in Figure 7 marked by a yellow dot.

5 Results and discussion

The prominences of the defect-characteristic pattern as marked in Figure 7 were analyzed for the different variants of the braiding experiments. For the diagram shown in Figure 9, all available video frames of a braiding experiment were taken into account for the averaging step. The standard deviations are not drawn-in on purpose because they would not provide any meaningful information given the natural scatter of the angular yarn distances as described above. Additionally, no data is shown for the 6 k yarns and elevated tensions of ∼35 N and >45 N, respectively. The reason for this is that these thin yarns could not sustain these high elevated tensions and broke during the braiding tests. It can be observed that the defect-characteristic spike in the averaged yarn distance measurement is generally more pronounced if $n_{yarn}=64$ braiding yarns are used compared to $n_{yarn}=32$ yarns. Furthermore, a trend towards a stronger deviation in angular yarn distances at the defective yarn can be identified the thicker the braiding yarns are. Only the variant with $n_{yarn}=64$ 6 k yarns and an elevated tension of a single yarn of ∼20 N does not comply with this trend. Moreover, within an experiment group of the same yarn number $n_{yarn}$ and the same yarn thickness, a trend towards an increasing prominence of the defect-characteristic spike in the averaged angular yarn distance measurement is observable the higher the level of the yarn tension anomaly is. However, several experiments with an elevated tension of ∼35 N do not monotonously fit into this trend. Nevertheless, the overall picture of the trend towards stronger deviations in angular yarn distances with increasing yarn tension anomaly is still maintained because the variant with the highest tension (>45 N) consistently creates stronger deviations than the variant with the least yarn tension anomaly (∼20 N).

FIGURE 9

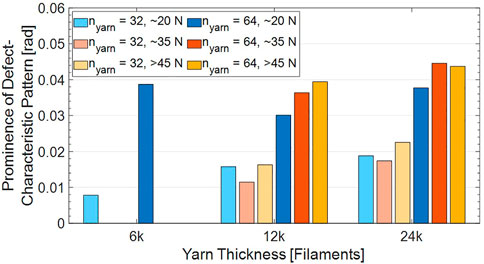
FIGURE 9. Prominence of the defect-characteristic pattern after averaging over the complete duration of each braiding experiment with a simulated defect.

The fact that in variants with $n_{yarn}=64$ yarns the deviations in yarn distances that are more clearly identifiable than in variants with $n_{yarn}=32$ yarns is well explainable by a higher level of frictional interaction in the braid formation zone when $n_{yarn}=64$ yarns are used. A higher number of yarns creates a higher number of yarn crossing points, higher frictional forces between the yarns and thus a more pronounced curvature of the yarns during regular braiding. If the yarns exhibit a more pronounced curvature, the principle of detecting a change in curvature due to changes in yarn tension is better applicable. A similar explanation relying on different levels of frictional interaction between the braiding yarns can also be provided for the trend of increasing prominence of the defect-characteristic pattern the thicker the yarns are. Thicker yarns cause the yarns to be deflected by a larger angle at each yarn crossing point in the braid formation zone. Additionally, the contact area at crossing points between thicker yarns is larger compared to thinner yarns. The overall trend of a more pronounced defect-characteristic pattern the stronger the deviation in tension of a single yarn is can be expected from the detection principle. The curvature of the defective yarn is reduced due to its increased tension, leading to the detectable deviations in angular yarn distances. A reason for the fact that the variants with an elevated tension of a single yarn of ∼35 N do not monotonously fit into the overall trend can be that a screw-on barrel tensioner was used on the respective bobbin carrier to achieve a significant portion of the elevated tension. Given the fact that the yarn tension slightly varies on an unmodified carrier depending on the filling degree of the bobbin, a multiplication of slight yarn tension inputs to the barrel tensioner may lead to more pronounced variations in yarn tension output according to the Euler-Eytelwein frictional law (frictional rope equation). Furthermore, environmental variables such as moisture could not be controlled in the manufacturing laboratory, which are also known to influence frictional yarn interaction during braiding.

In Figure 9, all available video frames of an experiment variant were taken into account for the calculation of the prominence of the defect-characteristic pattern. From a process monitoring perspective, it is however of interest how long the averaging window of video frames actually needs to be in order to reliably detect a defect. This relation is analyzed at the example of the group of experiments with the 12 k yarns in Figure 10. On the x-axis, the number of video frames taken into account for the averaging step described in Section 4 is varied. It can be observed that the smaller the averaging window is, the more pronounced the maximum of random yarn distance variations from flawless reference measurements appears in the diagram (cf. curves labeled as “Max Diff Reference”). With increasing length of the sliding averaging window, random deviations in yarn distances are increasingly evened out. By contrast, the minimum deviation in angular yarn distance that results from the defective yarn increases with increasing length of the averaging window (cf. curves labeled as “Min Diff Error”). For the case of $n_{yarn}=64$ braiding yarns, the curve of maxima of random deviations in angular yarn distance during regular braiding intersects with the lowest curve of minima of systematic deviations in yarn distances due to a process error at a length of an averaging window of 200 video frames. At 200 frames and beyond, a blue-marked area is opened up where the maximum curve of random deviations during regular braiding lies below the curve of minima of systematic deviations during defective braiding. This means if a combination of length of averaging window and detection threshold in terms of difference in angular yarn distance between neighboring yarns from the blue-marked area was chosen, no false positive or false negative defect detections occurred during the conducted braiding tests.

FIGURE 10

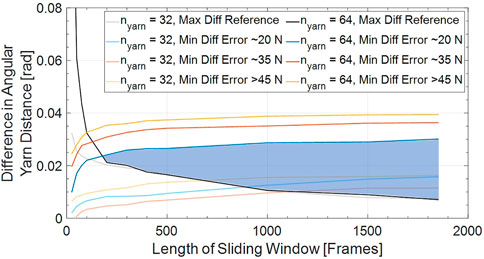
FIGURE 10. Comparison of maximum difference in angular yarn distance resulting from random process fluctuations during flawless reference measurements with minimum of defect-characteristic pattern during measurements with a replicated defect over different lengths of sliding averaging windows for the braiding experiments with 12 k yarns; blue-marked area indicates combinations of lengths of averaging windows and differences in angular yarn distances as possible detection thresholds for a defect detection without any false negative or false positive detections for $n_{yarn}=64$ 12 k yarns.

Given the fact that a minimum length of the averaging window of 200 frames is required for a reliable defect detection at a frame rate of $framerate=25fps$ for the case of $n_{yarn}=64$, a latency of 8 s is incurred in the presented monitoring approach. The set speed of horn gear rotation of $r=130rpm$ and a number of 32 horn gears in the braiding machine results in $t_{360°}=7.38s$ for a full 360° revolution of a yarn through the braiding machine. Within this context, a lead time of 8 s, corresponding to about one full revolution of the braiding machine, can be regarded as acceptable, particularly given the fact that already a comparatively small yarn tension increase of ∼20 N is reliably detected in the braiding experiments. Such small increases in yarn tension do not lead to yarn breakages that are time-consuming to resolve. The picture is however different for the case of $n_{yarn}=32$ braiding yarns. Only at a length of the averaging window of about 1100 frames and beyond, no false positive or false negative defect detections would have occurred in the conducted experiments. This results in approximately 44 s of lead time and thus six full revolutions of the braiding machine that need to be taken into account for an averaging of measured yarn distances. From practical experience and also from the data presented by Maidl et al. (2018) and Maidl et al. (2020), it may well be the case that a yarn with a fibrous ring at its braiding spool has already broken within this time period and has caused the braided preform to be defective due to a missing yarn.

Even though it is a positive finding that a biaxial braid of at least $n_{yarn}=64$ braiding yarns can reliably be monitored by the proposed approach without any false positive or false negative defect detections, the authors would like to point out that it is not absolutely necessary to avoid false negative detections at all costs. This is because the defect detection algorithm is programmed to work on sliding averaging windows. Sticking with the example of a window length of 200 frames, it may for instance be the case that a defect is not detected (false negative) on video frames 1–200. However, when the algorithm takes frames 2–201 into account, the defect might get detected, resulting in a time delay of only 0.04 s (one frame). Figure 11 illustrates this relation for the exemplary case of $n_{yarn}=64$ 12 k braiding yarns and a length of the averaging window of 200 frames. As lower boundary, the maximum of random deviations in yarn distances from flawless reference measurements is drawn-in. Any detection threshold below this value would have resulted in false positive defect detections in the conducted experiments. Given the comparatively high number of 25 fps, even small percentages of false positive detections are not acceptable because this would cause an alarm every few seconds and make a productive braiding impossible. For a length of the averaging window of 200 frames, the upper boundary of the blue-marked area in Figure 10 lies at 0.025 radians. The diagram in Figure 11 however shows that even if higher detection thresholds are chosen, the defect is still detected but only missed for a small number of frames. If, for instance, a level of yarn tension increase of ∼20 N shall be detected, a detection threshold of 0.026 radians would have led to the defect being detected with a maximum delay of only 10 frames. If the detection threshold was set to 0.036 radians, this level of process anomaly would not be detected at all (saturation of the curve at total number of frames per braiding experiment). Nevertheless, the highest level of yarn tension increase (>45 N) would still be detected at this threshold. The detection of such a high level of process anomaly is then only delayed by a maximum of 8 frames. This shows that whereas the lower boundary in Figure 10 needs to be regarded as a “strict” boundary, the upper boundary of the blue-marked area in Figure 10 can be seen as a “soft” boundary. It is therefore advisable to choose a detection threshold that is well above the “strict” lower boundary to avoid false positive defect detections due to process scatter and rather accept a limited number of false negative defect detections.

FIGURE 11

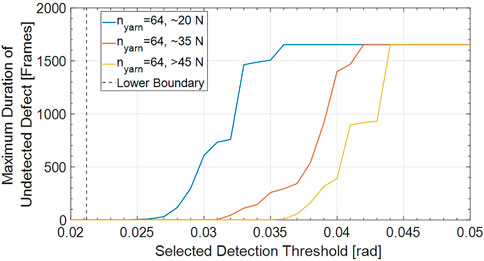
FIGURE 11. Duration of an undetected defect depending on different levels of yarn tension anomalies over selected difference in angular yarn distance as detection threshold for the case of $n_{yarn}=64$ 12 k yarns.

6 Conclusion and outlook

A newly developed camera-based monitoring approach for a simultaneous tracking of all braiding yarns during the process was presented in the paper at hand. As a principle for anomaly detection, the associated image processing algorithm relies on an analysis of angular yarn distances of braiding yarns of the same direction of circulation through the machine. In an experimental study comprising flawless reference braiding tests and braiding tests with purposefully introduced yarn tension anomalies of varying severity as well as a variation of yarn number $n_{yarn}$ and yarn thickness, the new method was shown to be in principle capable of reliably identifying an anomalously tensed yarn during braiding of preforms for composite parts. Also, since the method is purely optical, no additional yarn contact and thus yarn damage is induced. It was found that the method can even out naturally occurring process fluctuations and distinguish them from systematic process anomalies by applying an averaging window over several video frames. In case of $n_{yarn}=64$ 12 k carbon yarns and a moderate yarn tension anomaly of ∼20 N, an averaging window of 200 frames (8 s given the applied frame rate of 25 fps) was sufficient in order not to create any false positive or false negative defect detections. Given such a short averaging window and thus latency time, a braiding defect, such as for instance the fibrous ring mentioned in the beginning of this article, can therefore be detected early during its formation. The braiding machine can be stopped before an eventual yarn breakage occurs and the production of defective braid can be prevented. Due to the fact that the above-described algorithm allows a precise identification of the defective yarn, operating personnel may be provided with a light signal in order to avoid a time-consuming search for the defective yarn among a potentially large number of braiding yarns. The error can swiftly be spotted, its cause can be found and manually be resolved. A limitation to the provided proof of concept is however that the presented method of measuring angular yarn distances as a sign of process anomalies only works if there is sufficient friction between the braiding yarns that creates significant yarn curvature. In the conducted braiding experiments, this prerequisite could not be maintained if only $n_{yarn}=32$ braiding yarns were used. If more than the investigated $n_{yarn}=64$ braiding yarns shall be monitored, the approach is expected to function even better because frictional interaction and thus yarn curvature is even more pronounced due to the further increased number of yarn crossings in the braid formation zone. However, if for instance $n_{yarn}=128$ braiding yarns and more shall be monitored, the authors recommend the use of a ring light that is larger in diameter than the chosen one (outside Ø 252.5 mm) in order to be able to monitor the angular yarn distances at a greater radial distance from the center of the braiding machine. This is necessary for high numbers of braiding yarns $n_{yarn}$ because the yarns are spaced too closely together at small radial distances from the center of the machine. This would cause the imaginary circles of the image analysis algorithm to constantly intersect with yarn crossing points and the criterion of as many yarn intersections of the pair of imaginary circles as there are yarns in the machine would never be possible to satisfy.

For reasons of providing a proof of concept, the experiments in the paper at hand only cover braiding of a cylindrical mandrel. The strength of the braiding process, particularly in comparison to filament winding, is however that also parts that are curved can be produced. If such curved parts need to be braided, the camera view to parts of the braid formation zone may be obstructed by a curved mandrel. A similar obstruction of the camera view occurs when a second handling robot is used so that the overbraidable mandrel is grabbed at both ends. The algorithm presented in the paper at hand does however not require a full view on the braid formation zone. The criterion that the imaginary circles of the image analysis algorithm need to intersect with yarns as many times as there are yarns in the braiding machine can be modified with limited effort. It is for instance possible to let the algorithm operate independently on four quarters of the braid formation zone. In such a modification of the algorithm, the number of yarn intersections of the imaginary circles in a quarter needs to equal $\frac{n_{yarn}}{4}$. It is furthermore not required that it is always the same quarter of the braid formation zone that the view is obstructed to, e.g., in case of a complex path of the guiding robots. Each individual braiding yarn can still be tracked and its distances to neighboring yarns can still be correctly averaged over the independent quarters of the braid formation zone according to Formula 1 through Formula 4. Hence, it is possible to deploy the proposed image analysis algorithm on real-time capable computing devices and retrofit the optical monitoring to existing braiding machines also for the production of complexly shaped preforms. The proposed modification of the algorithm of operating only on sections of the braid formation zone can also be used as a method in order not to be forced exclude entire video frames from the analysis if the respective frames fail to pass the plausibility checks introduced in Section 4. Instead, only the areas of the braid formation zone in a video frame that cannot unambiguously be analyzed can be excluded from the analysis (e.g., due to unfavorable locations of the yarn crossing points with respect to the imaginary circles). The remaining areas can then still be taken into account for the analysis and potentially reduce the required length of the averaging window and thus latency time of the detection method.

As discussed, the detection principle relies on frictional interaction between the braiding yarns. If other yarns than dry carbon yarns also with potentially different types of sizing shall be braided (e.g., glass or aramid fibers) it may be the case that their frictional properties vary from those of carbon yarns. This is why further experiments with these different types of yarn materials are required to assess the defect detection capabilities of the proposed approach. Furthermore, there may be yarns that are partly transparent for the ring shaped backlight illumination (e.g., glass fibers). The brightness thresholds for the binarization during the image preprocessing may have to be modified for such yarn types. Finally, it needs to be acknowledged that if triaxial braids with additional 0°-fibers compared to the investigated biaxial braid shall be monitored, the algorithm as presented is not functional since neighboring intersection objects would not exclusively correspond to moving braiding yarns. The current distinction between clockwise and counterclockwise yarns by comparison of polar angles $\theta$ as illustrated in Figure 5 needs to be amended for the case of 0°-yarns, e.g., by introducing a third case if the polar angles $\theta$ of intersection objects originating from the same yarn on the inner and outer imaginary circle are similar.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

SM Conceptualization, Methodology, Software, Validation, Formal analysis, Investigation, Writing—original draft, Writing—review and editing, Visualization, Project administration, Funding acquisition. MH Conceptualization, Methodology, Writing—review and editing. KK Writing—review and editing, Supervision. KD Resources, Writing—review and editing, Supervision.

Funding

The authors thankfully acknowledge the funding provided by the German Federal Ministry for Economic Affairs and Climate Action under the scheme “Zentrales Innovationsprogramm Mittelstand (ZIM)” for the project “IMoFlecht: Inline Monitoringsystem zur Überwachung hochqualitativer Flechtprodukte” (Funding Code: ZF4004324HB9).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Aibibu, D., Hild, M., and Cherif, C. (2016). “An overview of braiding structure in medical textile: Fiber-based implants and tissue engineering,” in Advances in braiding technology: Specialized techniques and applications. Editor Y. Kyosev (Duxford: Woodhead Publishing), 171–190.

CrossRef Full Text | Google Scholar

Branscomb, D. J. (2007). A machine vision and sensing system for braid defect detection, diagnosis and prevention during manufacture. Master Thesis, Auburn, United States of America: Auburn University.

Branscomb, D. J., and Beale, D. G. (2011). Fault detection in braiding utilizing low-cost USB machine vision. J. Text. Inst. 102, 568–581. doi:10.1080/00405000.2010.498174

CrossRef Full Text | Google Scholar

Brockmanns, K.-J., Kümpers, F.-J., Baumgart, G., and Leifeld, M. (2014). Radialflechtmaschine. German patent application DE102012223127A1.

Google Scholar

Bulat, M., Ahlborn, H., Gnädinger, F., and Michaelis, D. (2016). “Braided carbon fiber composites,” in Advances in braiding technology: Specialized techniques and applications. Editor Y. Kyosev (Duxford: Woodhead Publishing), 383–394.

CrossRef Full Text | Google Scholar

Ebel, C., Brand, M., and Drechsler, K. (2013). “Effect of fiber damage on the efficiency of the braiding process,” in 11th Composites Week @ Leuven and TexComp-11 Conference, Leuven, Belgium.

Google Scholar

Ebel, C., Mierzwa, A., and Kind, K. (2016). “Yarn damage during braiding of reinforcement fibers for composites,” in Advances in braiding technology: Specialized techniques and applications. Editor Y. Kyosev (Duxford: Woodhead Publishing), 319–354.

CrossRef Full Text | Google Scholar

Hill, J. (2003). Adhesively bonded structural composites for Aston Martin vehicles. Available at: https://www.audiclubsouthafrica.co.za/yabbfiles/Attachments/b01.pdf (Accessed October 31, 2021).

Google Scholar

Kind, K., and Drechsler, K. (2015). Method for the production of braided CFRP bicycle rims, 15. Amiens, France: SAMPE Europe Conference.

Google Scholar

Kohen, M. (1946). The venus of willendorf. Am. Imago 3, 49–60.

Google Scholar

Lenkeit, J. (1997). Verfahren zur Zugkraftmessung an laufenden Fäden einer Fadengruppe sowie Vorrichtung zur Ausübung des Verfahrens. German Patent Specification DE19730965C1. Germany: Tensometric-Meßtechnik Ströhmann & Co GmbH.

Google Scholar

Maidl, S., Fernández Villalba, Á., Kind, K., and Drechsler, K. (2020). Development of sensor integrated braiding rings for the automated detection of braiding defects. Mater. Today Proc. 34, 74–81. doi:10.1016/j.matpr.2020.01.194

CrossRef Full Text | Google Scholar

Maidl, S., Putze, L., Kind, K., and Drechsler, K. (2022). “Automated detection of yarn gaps during radial braiding of carbon fiber by means of light barriers,” in ECCM20 - 20th European Conference on Composite Materials, Lausanne, Switzerland.

Google Scholar

Maidl, S., Sabieraj, M., Mierzwa, A., Ebel, C., and Drechsler, K. (2018). Investigating the unwinding behavior of technical yarns and development of a new sensor system for the braiding process. IOP Conf. Ser. Mater. Sci. Eng. 406, 012065. doi:10.1088/1757-899X/406/1/012065

CrossRef Full Text | Google Scholar

Michael, M., Kern, C., and Heinze, T. (2016). “Braiding process for braided ropes,” in Advances in braiding technology: Specialized techniques and applications. Editor Y. Kyosev (Duxford: Woodhead Publishing), 225–243.

CrossRef Full Text | Google Scholar

Mierzwa, A., Ebel, C., and Drechsler, K. (2018). Auswirkungen lokaler Garnlücken auf die mechanischen Eigenschaften geflochtener Kohlenstofffaser-Kunststoff-Verbunde. Zeitschrift Kunststofftechnik/J. Plastics Technol. 14, 146–173. doi:10.3139/o999.02012018

CrossRef Full Text | Google Scholar

Mierzwa, A., Ebel, C., Harbers, T., and Drechsler, K. (2016). “Investigation on creation of fibrous rings and their influence on the braided preform quality,” in ECCM17 - 17th European Conference on Composite Materials, Munich, Germany.

Google Scholar

Mierzwa, A. (2019). Zur Entstehung und Auswirkung von Garnlücken in Carbonbiaxialgeflechten. Dissertation. Munich, Germany: Technical University of Munich.

Google Scholar

Thuis, H. (2004a). “Composite landing gear components for aerospace applications,” in ICAS 2004 - 24th International Congress of the Aeronautical Sciences, Yokohama, Japan.

Google Scholar

Thuis, H. (2004b). The development of composite landing gear components for aerospace applications. https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.157.3791&rep=rep1&type=pdf (Accessed October 31, 2021).

Google Scholar

van Ravenhorst, J. H., and Akkerman, R. (2016a). A yarn interaction model for circular braiding. Compos. Part A Appl. Sci. Manuf. 81, 254–263. doi:10.1016/j.compositesa.2015.11.026

CrossRef Full Text | Google Scholar

van Ravenhorst, J. H., and Akkerman, R. (2016b). “Overbraiding simulation,” in Advances in braiding technology: Specialized techniques and applications. Editor Y. Kyosev (Duxford: Woodhead Publishing), 431–455.

CrossRef Full Text | Google Scholar

van Ravenhorst, J. H. (2018). Design tools for circular overbraiding of complex mandrels. Dissertation. Twente, Netherlands: University of Twente.

Google Scholar

White, R. (2006). The women of brassempouy: A century of research and interpretation. J. Archaeol. Method Theory 13, 250–303. doi:10.1007/s10816-006-9023-z

CrossRef Full Text | Google Scholar

Zuurendonk, B. (2018). Carbon fibre composite rim: An automation feasibility study. Master Thesis. Delft, Netherlands: Delft University of Technology.

Google Scholar