Effects of Newtonian heating and heat generation on magnetohydrodynamics dusty fluid flow between two parallel plates

Dusty fluids are utilized to minimize heat in systems like gas-freezing systems and nuclear-powered reactors, among other places. The present study aims to investigate the effect of Newtonian heating on dusty fluid flow. Between two parallel plates, the two-phase MHD fluctuating flow of the dusty fluid is considered. The dust particles inside the fluid are thought to be spherical and uniformly distributed. The generation and absorption of heat were also taken into consideration. The motion of the fluid is due to the motion of the right plate with free stream velocity $U\left(t\right)$. Partial differential equations are utilized to represent the flow regime. The Poincare-Light Hill Technique is used to find exact solutions. The impact of parameters on the temperature and velocity profiles are shown graphically. Skin friction and rate of heat transfer, two essential fluid parameters for engineers, are also evaluated in tabular form. The velocity of the fluid is shown to decrease with increasing magnetic field. The Newtonian heating phenomena has an effect on the plate’s heating.

1 Introduction

Fluid is a material that constantly deforms (flows) when shear (tangential) stress is applied. Water, honey, oil, and air are a few examples of fluids. In the universe, there are numerous fluids. Non-Newtonian fluids and Newtonian fluids are two types of fluids based on their rheologies. Engineering procedures, industry (thermal power plants, nuclear power plants, refrigerators, air conditioners, and so on), and medical science all use these fluids. Many physical phenomena are not properly described by Newtonian viscous fluids. Non-Newtonian fluids are essential in a wide range of engineering operations, industrial processes, and biological applications. There are several types of non-Newtonian fluids. Non-Newtonian fluids include differential type fluids, rate type fluids, and viscoelastic fluids. Casson fluid and other differential viscoelastic fluids are frequently employed in everyday life. According to the Casson Fluid Definition a fluid that shear-thins to zero viscosity has a yield stress below which no flow occurs and zero viscosity at an infinite rate of shear (Rundora, 2021). The study of viscoelastic Casson fluids cannot be adequately handled by a single governing equation due to their complicated rheology (Makinde, 2009). Some of the Casson fluid’s applications include coal in water, synthetic petroleum products, China clay, paints, biological products fluid, jelly, and fibrinogen (Pramanik, 2014). The Casson first presented the Casson fluid model in “1959” (Casson, 1959). Oka (1971) was the first to investigate Casson fluids in tubes. According to Mukhopadhyay (2013), thermal radiation over the stretched surface has an impact on the unstable Casson viscoelastic fluid flow. In a curved sheet that is stretching exponentially with MHD, Kumar et al. (2020) scrutinized the influence of radiation of heat on a viscoelastic Casson fluid. By Gangadha et al. (2021), a dual solution analysis for MHD Casson fluid and Newtonian heating travelling through a decreasing sheet was presented. Reddy et al. investigated the effect of radiant heat on the MHD viscous dissipation of a Casson fluid flow across an oscillation parallel plate in their work described in Reddy et al. (2018). Rafiq et al. (2020) examine the influence of variable viscosity on the asymmetric flow of a non-Newtonian fluid driven via an expanding/constricting conduit with porous walls. The flow of a non-Newtonian (Casson) fluid between parallel discs travelling in opposite directions on a plane is being investigated (Abbas et al., 2020). Jyothi et al. (2021a) proposed the Casson fluid, which is driven between parallel plates and acts as a heat source or sink as well as a thermophoretic particle deposition. Ramesh et al. (2022) investigated the relationship between the transportation of aluminium alloy particles over parallel plates and chemical reaction and activation energy. Madhukesh et al. (2021) gained scientific insight into heat and mass transfer in a Riga plate with thermophoresis and brownian atomic diffusion in a Casson hybrid flow of nanofluid. Jyothi et al. (2021b) scrutinized the effect of Stefan blowing on Casson nanofluid flow and heat transmission through a moving thin needle. Furthermore, several scholars investigate the relationships between Casson fluid flow, heat transmission, and Mewton’s equation of cooling (Obalalu et al., 2020; Obalalu, 2021).

According to Newton’s rule of cooling (or heating), the heat loss rate of a body is directly proportional to the temperature differential between the system and its surroundings (Hussain et al., 2018). In forced air or pushed fluid cooling (or heating), when fluid properties do not considerably fluctuate with temperature, Newton’s Law of heating (or cooling) is obeyed. However, buoyancy-driven convection, where flow velocity grows with temperature difference, only roughly follows this law. Finally, Newton’s law of cooling (or heating) only holds for very small temperature differences when heat is transmitted by thermal radiation. When modeling MHD two-phase fluctuation flows between parallel plates, ramped wall temperatures or constant surface heat flux assumptions and constant surface temperature are commonly used (O’Sullivan, 1990; Khalid et al., 2015; Ali et al., 2019a; Das et al., 2021; Krishna et al., 2021). Further from that, the assumptions above fail in a variety of real-world situations where heat transport is inversely proportional to surface temperature and the Newtonian heating condition (NHC) is required. It was Merkin (1994) who was the first to explore four forms of temperature distributions on walls, one of which being NHC. Newtonian heating conditions are used in heat exchangers, the oil industry, solar radiation, and conjugated heat transfer around fins. The impacts of NHC, magnetic field, chemical reaction and heat generation on viscoelastic Casson fluid free convection flow among the vertical plates are reported by Khan et al. (2019). Hussanan et al. (2017a) investigated the impact of Newtonian heating on viscoelastic Casson fluid flow between oscillating vertical plates. Hussanan et al. (2017b) investigated the viscoelastic Casson fluid flow (CFF) with heat transfer and Newtonian heating between porous materials. Loganathan et al. (2021) investigated the viscoelastic CFF over a cylinder with NHC and heat absorption effects. Hussanan et al. (2016) investigated the effects of NHC and magnetic field on the CFF of a two-dimensional travelling through a stretched sheet. Manjula and Sekhar (2021) investigated how heat transport and thermal expansion affect the CFF of a vertical surface with NHC.

Magnetohydrodynamics is the analysis of the magnet properties and performance of electrically conducting fluids. Liquid metals, salt water, plasmas, and electrolytes are examples of magnetofluids. MHD flow with free convection has a wide range of applications in fluid engineering issues such as flow metres, blood flow, gas cooling system heat transfer improvement, MHD generators, and accelerators (Ali et al., 2020). In the existence of a chemical reaction, Afikuzzaman et al. (2018) reported heat transfer and free convective flow across an upright plate with MHD. Dusty fluid in an annulus with hydrodynamic velocity behavior was studied by Jha and Gambo (2022). A magnetic field was found to impact Couette flow. It was found that viscosity, heat transfer, and thermal conductivity had a significant effect on the movement of dusty fluids with MHD. Using thermal radiation and MHD, Mabood et al. (2016) examined and analysed the influence of melting heat transfer on Casson fluid flow in a porous media over a moving surface. Sayed-Ahmed et al. (2011) explore the effect of a time-dependent pressure gradient and heat transfer in unsteady Casson fluid flow with MHD. Newtonian heating (or cooling) and thermal radiation, according to (Jalil et al., 2017), can influence MHD flow with an induced magnetic field. Gireesha et al. (2012) investigated the effects of heat transfer, magnetic field, and viscous dissipation on MHD dusty flow using a stretched sheet. Upadhya et al. investigated the radiative MHD flow of suspended Casson fluid within a conical gap (Upadhya et al., 2022). Raju et al. (2021) demonstrated MHD radiated flow in a thermal convective condition using Casson fluid. Hamid et al. (2021) investigate Casson fluid MHD flow with Hall current and homogeneous-heterogeneous interactions. Ali et al. (2019b), Hussain et al. (2021) explore the thermal and magnetic impacts of a bi-viscosity fluid contained in a triangular chamber using finite element analysis. The heat and flow across a revolving disc that is being affected by a constant horizontal magnetic field are investigated by Turkyilmazoglu (2022). Furthermore, several scholars investigate the MHD flow, dusty fluid with analytical solution (Anuar et al., 2020; Wahid et al., 2020).

Dusty fluid flow occurs when a fluid (liquid or gas) has a solid particle distribution (Ezzat et al., 2010). For example, in fluidization problems, dusty air motion the motion and the process of chemical reactions by which raindrops are formed by the coalescence of particles. Dusty fluid flow (multiphase flow) is used in powder technology, nuclear reactor cooling, paint spray, solid fuel rock nozzle performance, dust collecting, and guidance systems (Chanson, 2004). Archimedes of Syracuse invented multi stage flow when he proposed the Principle of Buoyant force, which evolved into the well-known Archimedes principle, which is used in multiphase flow modelling (Khan et al., 2022). The most common type of multiphase flow is two-phase flow (Miwa and Hibiki, 2022). While remaining interested in two-phase flows, several scientists worked on the dusty flow model for a variety of flow configurations and physical situations. Despite the system of quadratic solutions’ challenges, nothing effort has been made to improve a perfect approach. Saffman (1962) was the first to do study on dusty fluid flow laminar. The importance of partial slip caused by lateral velocity and viscous dissipation is investigated using numerical solutions to the partial differential equations are reported by Koriko et al. (2021). The Casson dusty nanofluid: The role of the magnetic field, the non-Fourier heat flow model are discussed by Rehman et al. (2022).

In the above-mentioned literature, the researchers examined non-Newtonian, incompressible, electrically conducting dusty fluids that have been moving with free convection and MHD. Following the Light-Hill technique, no study has been published to our knowledge that combines the fluids energy equation with the dust particles energy equation for a viscoelastic Casson dusty fluid using the fluids energy equation and the dust particles energy equation. Using a distinct equation of heat for the dust particles, this study investigates the impact of NHC on the two-phase MHD fluctuation flow of Casson fluid and dust particles between two vertical plates with suspended electrically conducting particles. The scientific findings of the current study also show that Casson dusty fluid is a very complicated phenomena with a wide range of engineering and product-making uses, such as the usage of Casson dusty fluids in nuclear reactors and gas cooling systems to reduce system temperature. Consequently, the goal of the current work is to ascertain how Newtonian heating affects Casson dusty fluid flow. Additionally, using a graphical representation, this study investigates the impact of various physical characteristics on the Casson dusty fluid flow.

2 Mathematical formulation

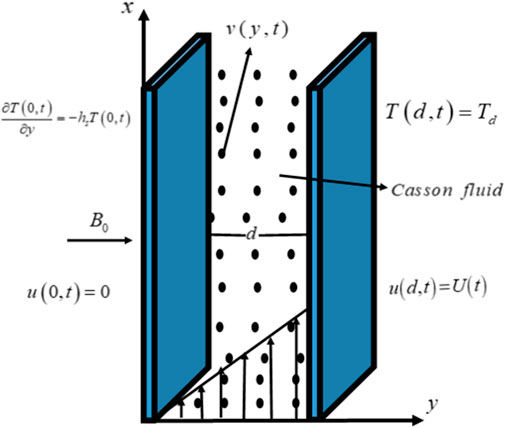
Take electrically conducting, the incompressible, unidirectional, unsteady, two-phase fluctuating flow of MHD Casson fluid with dust particles between two vertical plates. A transverse magnetic field is applied to the flow. The motion of the fluid is due to the motion of the right plate with free stream velocity $U\left(t\right)$, while the left plate is static as shown in Figure 1. The left plate is taken heated with the Newtonian heating condition, while $T_d$ is the temperature of the right plate, and $T_p$ is the particle temperature. Heat generation is only considered in the fluid and not for the particle energy equation. Furthermore, the influence of the particle concentration parameter and the particle energy equation are taken into account. The mass concentration equation for both the fluid and particle is not considered.

FIGURE 1

FIGURE 1. Flow configuration.

The velocity and temperature fields are shown below (Ali et al., 2020):

$\overrightarrow{\mathit{V}}=\left(u\left(y,t\right),\mathrm{0,0}\right)(1)$

$T=T\left(y,t\right)(2)$

The Casson fluid’s constitutive equations are (Ali et al., 2020).

$\nabla .\mathit{V}=0(3)$

$\rho \frac{d\mathit{V}}{dt}=\mathit{s}+\rho .\mathit{b}+\mathit{div}\left({\mathit{\tau }}_{ij}\right)(4)$

By using Maxwell law, generalized ohm’s law and Boussinesqs approximation, the body and surface forces in Eq. 4 becomes (Ali et al., 2020).

$\rho .\mathit{b}=\rho g{\beta }_T\left(T-T_d\right)+J\times B=g\rho {\beta }_T\left(T-T_d\right)-\sigma B_0^{2}u\left(y,t\right)(5)$

$\mathit{s}=-K_0{N}_0\left(u\left(y,t\right)-v\left(y,t\right)\right)(6)$

The rheological equation for unsteady Casson fluid flow is established and derived by Casson (1959) and is denoted by Rehman et al. (2022).

${\tau }_{ij}=\left\{\begin{array}{cc}\left({\mu }_{ϵ}+\frac{p_y}{\sqrt{{2\pi }_1}}\right){2e}_{ij},& {\pi }_1>{\pi }_e\\ \left({\mu }_{ϵ}+\frac{p_y}{\sqrt{{2\pi }_e}}\right){2e}_{ij},& {\pi }_1<{\pi }_e\end{array}\right\}(7)$

${\mathit{e}}_{ij}=-p\mathit{I}+\mu {\mathit{A}}_{\mathit{1}}(8)$

$\mathit{div}\left({\tau }_{ij}\right)=\left({\mu }_{ϵ}+\frac{p_y}{\sqrt{{2\pi }_1}}\right)\frac{{\partial }^{2}u}{\partial y^2}(9)$

Equation 4 may be stated in component form using Eqs 5–9 and Eq. 1 as (Ali et al., 2020).

$\left.\frac{\partial u\left(y,t\right)}{\partial t}=\upsilon \left(1+\frac{1}{\beta }\right)\frac{{\partial }^{2}u\left(y,t\right)}{\partial y^2}+\frac{K_0{N}_0}{\rho }\left(v\left(y,t\right)-u\left(y,t\right)\right)-\frac{\sigma B_0^{2}u}{\rho }+{\beta }_{T}g\left(T-T_d\right)\right\}(10)$

$\left.\frac{\partial v\left(y,t\right)}{\partial t}=\frac{K_0}{m}\left(u\left(y,t\right)-v\left(y,t\right)\right)\right\}(11)$

$\frac{\partial T\left(y,t\right)}{\partial t}=\left(\frac{k}{\rho c_p}\right)\frac{{\partial }^{2}T\left(y,t\right)}{\partial y^2}-\left(\frac{{\rho }_p{c}_s}{\rho c_p{\gamma }_T}\right)\left(T_p\left(y,t\right)-T\left(y,t\right)\right)-\left(\frac{Q_0}{\rho c_p}\right)\left(T\left(y,t\right)-T_d\left(y,t\right)\right)(12)$

${\gamma }_T.\frac{\partial T_p\left(y,t\right)}{\partial t}=\left(T\left(y,t\right)-T_d\left(y,t\right)\right)(13)$

The physical conditions are as follows (Khan et al., 2019).

$\left.\begin{array}{l}u\left(0,t\right)=0\\ u\left(d,t\right)=U\left(t\right)\\ \frac{\partial T\left(0,t\right)}{\partial y}=-h_{s}T\left(0,t\right)\\ T\left(d,t\right)=T_d\end{array}\right\}(14)$

Where, $U\left(t\right)=u_0\left(1+\frac{\epsilon }{2}\left(e^{i\omega t}+e^{-i\omega t}\right)\right)$.

Assume you obtained the result to Eq. 11 through PLHT (Nayfeh, 2008).

$v\left(y,t\right)=e^{i\omega t}{v}_0\left(y\right)(15)$

from Eq. 15, the solution is obtained.

$v\left(y,t\right)=K_0\left(\frac{u\left(y,t\right)}{K_0+mi\omega }\right)(16)$

Equation 10 in view of Eq. 16 becomes.

$\frac{\partial u\left(y,t\right)}{\partial t}=\left(1+\frac{1}{\beta }\right)\upsilon \frac{{\partial }^{2}u\left(y,t\right)}{\partial y^2}+\frac{K_0{N}_0}{\rho }\left\{\left(\frac{K_0}{mi\omega +K_0}\right)-1\right\}u\left(y,t\right)-\frac{\sigma B_0^{2}u\left(y,t\right)}{\rho }+g{\beta }_T\left(T\left(y,t\right)-T_d\left(y,t\right)\right)(17)$

The following dimensionless variables are used in the process of non-depersonalization;

$\left.y^{*}=y{h}_s,u^{*}=\frac{u}{u_0},t^{*}=\upsilon h_s^{2}t,{\theta }^{*}=\frac{T-T_d}{T_d},{{\theta }_p}^{*}=\frac{T_p-T_d}{T_d}\right\}(18)$

Using Eq. 18, Eqs 12, 13, 17 become;

$\frac{\partial u}{\partial t}={\beta }_1\frac{{\partial }^{2}u}{\partial y^2}-\left(M+K_1-K_2\right)u+Gr\theta (19)$

$\frac{\partial \theta \left(y,t\right)}{\partial t}=-\varphi \theta \left(y,t\right)+\frac{1}{Pe}\left(\frac{{\partial }^2\theta \left(y,t\right)}{\partial y^2}+R\left({\theta }_p\left(y,t\right)-\theta \left(y,t\right)\right)\right)(20)$

$\frac{\partial {\theta }_p\left(y,t\right)}{\gamma \partial t}=\left(\theta \left(y,t\right)-{\theta }_p\left(y,t\right)\right)(21)$

The dimensionless criteria are as follows (the (*) sign has been removed for clarity):

$\left.\begin{array}{l}u\left(0,t\right)=0\\ u\left(1,t\right)=1+\epsilon \left(\frac{e^{i.\omega .t}+e^{-i.\omega .t}}{2}\right)\\ \frac{\partial \theta \left(0,t\right)}{\partial y}=\left(-1-\theta \left(0,t\right)\right)\\ \theta \left(1,t\right)=0\end{array}\right\}(22)$

The dimensionless quantities are;

$M=\frac{\sigma B_0^2}{\rho \upsilon h_s^2},Gr=\frac{g{\beta }_T{T}_{\infty }}{u_0\upsilon h_s^2},K_2=\frac{K_0^2{N}_0}{\rho \upsilon h_s^2\left(mi\omega +K_0\right)},K_1=\frac{K_0{N}_0}{\rho \upsilon h_s^2},Pe=\frac{\upsilon \rho c_p}{k}$

${\beta }_1=1+\frac{1}{\beta },\gamma =\frac{1}{\upsilon h_s^2{\gamma }_T},R=\frac{{\rho }_p{c}_s}{k{h}_s^2{\gamma }_T},\varphi =\frac{Q_0}{\upsilon h_s^2\rho c_p}$

Assume you derived the solution to Eq. 21 using the PLHT (Nayfeh, 2008).

${\theta }_p\left(y,t\right)={\theta }_{p_0}\left(y\right)e^{i\omega t}(23)$

Results in:

${\theta }_p\left(y,t\right)=\gamma \left(\frac{1}{\gamma +i\omega }\right)\theta \left(y,t\right)(24)$

Equation 20 in observation of Eq. 24 converts;

$\frac{\partial \theta \left(y,t\right)}{\partial t}=P{e}^{-1}\frac{{\partial }^2\theta \left(y,t\right)}{\partial y^2}+\frac{R}{Pe}\left(\left(\frac{\gamma }{i\omega +\gamma }\right)-1\right)\theta \left(y,t\right)-\varphi \theta \left(y,t\right)(25)$

3 Solution of the energy equation

To solve Eq. 25, the following periodic solution is assumed (Nayfeh, 2008):

$\theta \left(y,t\right)={\theta }_0\left(y\right)+{\theta }_1\left(y\right)e^{i\omega t}(26)$

Now by using Eq. 26 in Eq. 25, and then using the corresponding conditions from Eq. 22, the following solutions is achieved:

$\theta \left(y,t\right)=\frac{\sinh \left(\sqrt{m_0}-y\sqrt{m_0}\right)}{\sqrt{m_0}\cosh \left(\sqrt{m_0}\right)-\sinh \left(\sqrt{m_0}\right)}(27)$

Equation 17 in view of Eq. 27 becomes;

$\frac{\partial u\left(y,t\right)}{\partial t}={\beta }_1\frac{{\partial }^{2}u\left(y,t\right)}{\partial y^2}-\left(M+K1-K2\right)u\left(y,t\right)+Gr\left\{\frac{\sinh \left(\sqrt{m_0}-y\sqrt{m_0}\right)}{\sqrt{m_0}\cosh \left(\sqrt{m_0}\right)-\sinh \left(\sqrt{m_0}\right)}\right\}(28)$

4 Solution of the velocity profile

To solve Eq. 28, the following periodic solution is assumed (Comstock, 1972) and (Nayfeh, 2008).

$u\left(y,t\right)={\psi }_0\left(y\right)+\frac{\epsilon }{2}\left({\psi }_1\left(y\right)e^{i\omega t}+{\psi }_2\left(y\right)e^{-i\omega t}\right)+O\left({\epsilon }^2\right)(29)$

$\left.\begin{array}{l}{\psi }_0\left(0\right)=0,{\psi }_0\left(1\right)=1\\ {\psi }_1\left(0\right)=0,{\psi }_1\left(1\right)=1\\ {\psi }_2\left(0\right)=0,{\psi }_2\left(1\right)=1\end{array}\right\}(30)$

Now obtain the following values ${\psi }_0\left(y\right),{\psi }_1\left(y\right),and{\psi }_2\left(y\right)$ by putting Eq. 29 into Eq. 28;

$\left.\begin{array}{r}{\psi }_0\left(y\right)=\left(\frac{\left(1+H\cosh \left(\sqrt{A_1}\right)\right).\sinh \left(y\sqrt{A_1}\right)}{\sinh \left(\sqrt{A_1}\right)}\right)-H\cosh \left(y\sqrt{A_1}\right)+Gr.A_1\left\{\frac{\sinh \left(\sqrt{m_0}-y\sqrt{m_0}\right)}{\sqrt{m_0}\cosh \left(\sqrt{m_0}\right)-\sinh \left(\sqrt{m_0}\right)}\right\}\\ {\psi }_1\left(y\right)=\frac{\sinh \left(y\sqrt{m_2}\right)}{\sinh \left(\sqrt{m_2}\right)}\\ {\psi }_2\left(y\right)=\frac{\sinh \left(y\sqrt{m_3}\right)}{\sinh \left(\sqrt{m_3}\right)}\end{array}\right\}(31)$

Where,

$\begin{array}{l}{m}_0=\frac{Ri\omega +Pe\varphi \left(i\omega +\gamma \right)}{i\omega +\gamma },A=M+K_1-K_2,A_1=\frac{A}{{\beta }_1}\\ H=\frac{A_1\cdot Gr\cdot \sinh \left(\sqrt{m_0}\right)}{\sqrt{m_0}\cosh \left(\sqrt{m_0}\right)-\sinh \left(\sqrt{m_0}\right)},m_2=\frac{A+i\omega }{{\beta }_1},m_3=\frac{A-i\omega }{{\beta }_1}\end{array}$

$\begin{array}{l}{H}_1=\frac{A\cdot Gr\cdot \sinh \left(\sqrt{m_0}\right)}{\sqrt{m_0}\cosh \left(\sqrt{m_0}\right)-\sinh \left(\sqrt{m_0}\right)}\\ A=M+K_1-K_2,m_4=A+i\omega ,m_5=A-i\omega \end{array}$

In last putting the values ${\psi }_0\left(y\right),{\psi }_1\left(y\right),and{\psi }_2\left(y\right)$ into Eq. 29, becomes:

$\left.\begin{array}{l}u\left(y,t\right)=-H\cosh \left(\sqrt{A_1}.y\right)+\left(\frac{1+H\cosh \left(\sqrt{A_1}\right)}{\sinh \left(\sqrt{A_1}\right)}\right).\sinh \left(\sqrt{A_1}.y\right)+A_1.Gr\left\{\frac{\sinh \left(\sqrt{m_0}-y\sqrt{m_0}\right)}{\sqrt{m_0}\cosh \left(\sqrt{m_0}\right)-\sinh \left(\sqrt{m_0}\right)}\right\}\\ +\frac{\epsilon }{2}\left(\frac{\sinh \left(y\sqrt{m_2}\right)}{\sinh \left(\sqrt{m_2}\right)}\right)e^{i\omega t}+\frac{\epsilon }{2}\left(\frac{\sinh \left(y\sqrt{m_3}\right)}{\sinh \left(\sqrt{m_3}\right)}\right)e^{-i\omega t}\end{array}\right\}(32)$

It is worth noting that the obtained general solution that is Eq. 32 satisfies all the imposed physical boundary conditions.

5 Limiting case; Flow of Newtonian viscous fluid

New use of the Casson parameter $\beta \to \infty$, we get the dimensionless form by putting ${\beta }_1=1$ it into Eq. 19.

$\frac{\partial u}{\partial t}=\frac{{\partial }^{2}u}{\partial y^2}-\left(M+K_1-K_2\right)u+Gr\theta (33)$

$\frac{\partial u}{\partial t}=\frac{{\partial }^{2}u}{\partial y^2}-A.u+Gr.\theta (34)$

To solve Eq. 34, the following periodic solution is (Comstock, 1972; Nayfeh, 2008)

$u\left(y,t\right)={\psi }_{01}\left(y\right)+\frac{\epsilon }{2}\left({\psi }_{12}\left(y\right)e^{i\omega t}+{\psi }_{23}\left(y\right)e^{-i\omega t}\right)(35)$

$\left.\begin{array}{l}{\psi }_{01}\left(0\right)=0,{\psi }_{01}\left(1\right)=1\\ {\psi }_{12}\left(0\right)=0,{\psi }_{12}\left(1\right)=1\\ {\psi }_{23}\left(0\right)=0,{\psi }_{23}\left(1\right)=1\end{array}\right\}(36)$

New obtain the following values ${\psi }_{01}\left(y\right),{\psi }_{12}\left(y\right),and{\psi }_{23}\left(y\right)$ by putting Eqs 35, 36 into Eq. 34;

$\left.\begin{array}{l}{\psi }_{01}\left(y\right)=-H_1\cosh \left(y\sqrt{A}\right)+\left(\frac{\left(1+H_1\cosh \left(\sqrt{A}\right)\right).\sinh \left(y\sqrt{A}\right)}{\sinh \left(\sqrt{A}\right)}\right)+Gr.A\left\{\frac{\sinh \left(\sqrt{m_0}-y\sqrt{m_0}\right)}{\sqrt{m_0}\cosh \left(\sqrt{m_0}\right)-\sinh \left(\sqrt{m_0}\right)}\right\}\\ {\psi }_{12}\left(y\right)=\frac{\sinh \left(y.\sqrt{m_4}\right)}{\sinh \left(\sqrt{m_4}\right)}\\ {\psi }_{23}\left(y\right)=\frac{\sinh \left(y.\sqrt{m_5}\right)}{\sinh \left(\sqrt{m_5}\right)}\end{array}\right\}(37)$

In last putting the values ${\psi }_{01}\left(y\right),{\psi }_{12}\left(y\right),and{\psi }_{23}\left(y\right)$ into Eq. 35, become;

$u\left(y,t\right)=\left\{\begin{array}{l}-H_1\cosh \left(y\sqrt{A}\right)+\left(\frac{\left(1+H_1\cosh \left(\sqrt{A}\right)\right).\sinh \left(y\sqrt{A}\right)}{\sinh \left(\sqrt{A}\right)}\right)+Gr.A\left\{\frac{\sinh \left(\sqrt{m_0}-y\sqrt{m_0}\right)}{\sqrt{m_0}\cosh \left(\sqrt{m_0}\right)-\sinh \left(\sqrt{m_0}\right)}\right\}\\ +\frac{\epsilon }{2}\left(\frac{\sinh \left(y\sqrt{m_4}\right)}{\sinh \left(\sqrt{m_4}\right)}\right)e^{i\omega t}+\frac{\epsilon }{2}\left(\frac{\sinh \left(y\sqrt{m_5}\right)}{\sinh \left(\sqrt{m_5}\right)}\right)e^{-i\omega t}\end{array}\right\}(38)$

The results obtained in Eq. 38 are the same as those obtained by Khan et al. (2022). As a result, this validates the validity of the current research.

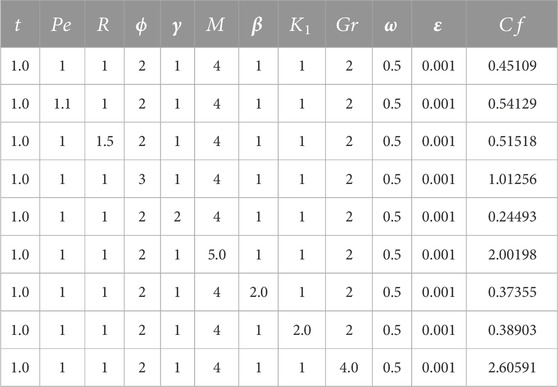
6 Skin friction and nusselt number

Casson fluid shear stress can be defined as (Nayfeh, 2008),

$\tau =\mu \left(1+\frac{1}{\beta }\right)\frac{\partial u\left(y,t\right)}{\partial y}(39)$

By using a dimensionless variable from Eq. 10 and ignore the (*) sign;

$Cf={\left.{\beta }_1\frac{\partial u\left(y,t\right)}{\partial y}\right|}_{y=0}={\beta }_1\left\{\begin{array}{l}\left(\sqrt{A_1}\right)\left(\frac{1+H\cosh \left(\sqrt{A_1}\right)}{\sinh \left(\sqrt{A_1}\right)}\right)-A_1.Gr\left(\frac{\sqrt{m_0}\cosh \left(\sqrt{m_0}\right)}{\sqrt{m_0}\cosh \left(\sqrt{m_0}\right)-\sinh \left(\sqrt{m_0}\right)}\right)\\ +\frac{1}{2}\left(\frac{\epsilon .\sqrt{m_2}}{\sinh \left(\sqrt{m_2}\right)}{e}^{i\omega t}+\frac{\epsilon .\sqrt{m_3}}{\sinh \left(\sqrt{m_3}\right)}{e}^{-i\omega t}\right)\end{array}\right\}(40)$

The heat transfer rate is (Saffman, 1962)

$Nu=-{\left.\frac{\partial \theta \left(y,t\right)}{\partial y}\right|}_{y=0}=\sqrt{m_0}.\left(\frac{\cosh \left(\sqrt{m_0}\right)}{\sqrt{m_0}\cosh \left(\sqrt{m_0}\right)-\sinh \left(\sqrt{m_0}\right)}\right)(41)$

7 Physical interpretations and graphical results

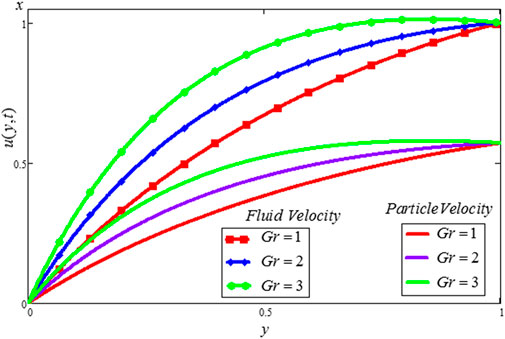
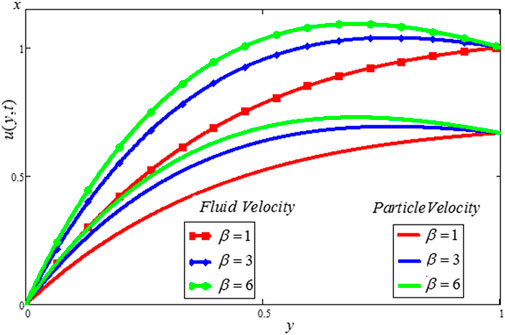
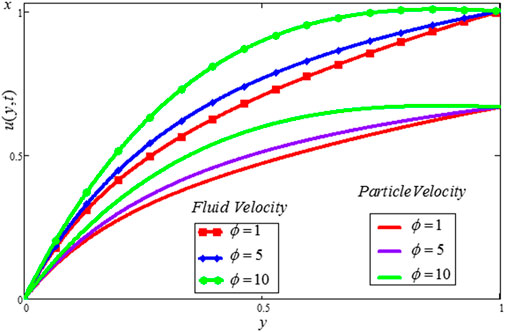
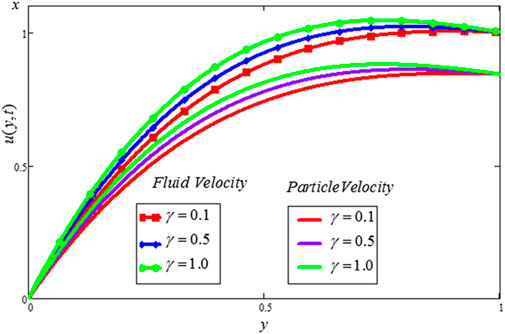
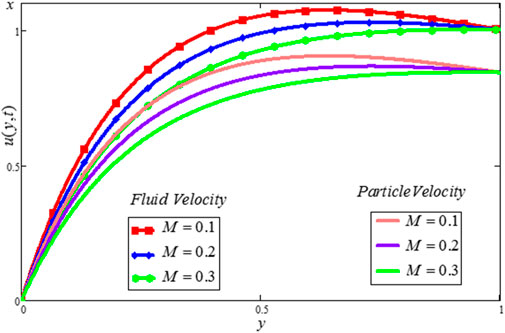
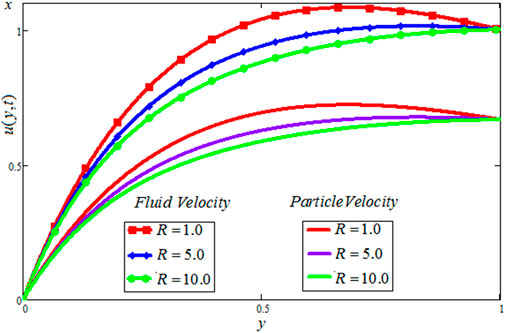
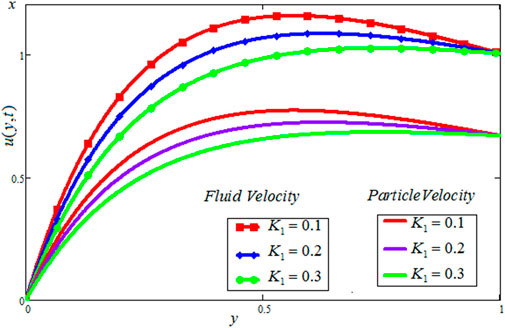
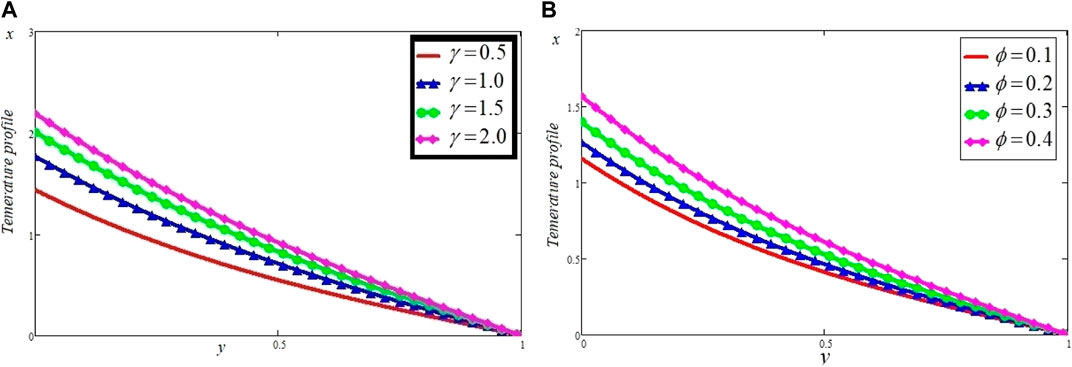
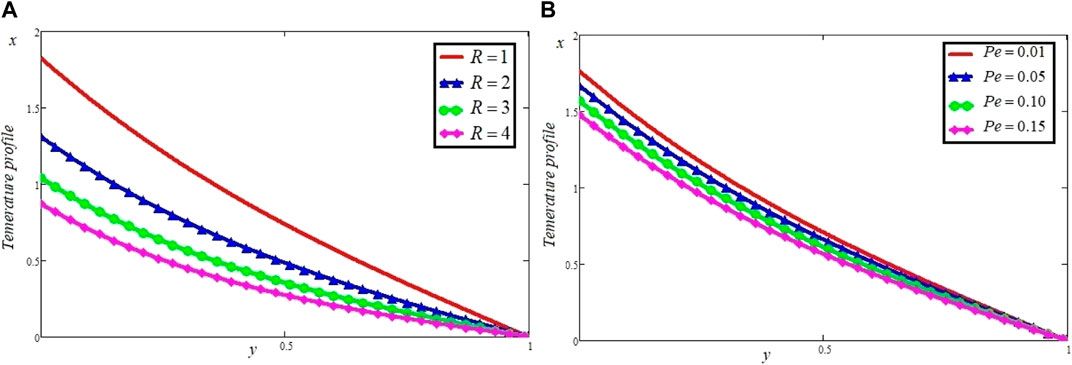
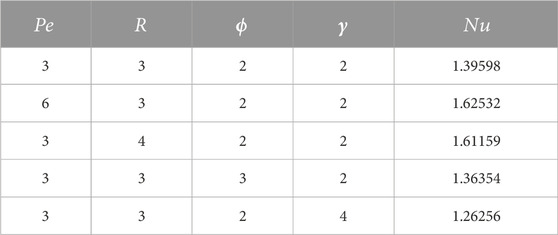
The Casson dusty fluid velocity distribution, particle velocity, skin friction, and heat transfer rate are covered in this section, along with the influence of different dimensionless variables on these parameters. The velocity distribution of the Casson fluid, the velocity distribution of the dust particles, and the temperature profile are all affected by different physical characteristics, as shown in Figures 2–11. Tables 1, 2 discuss the $Nu$, and $Cf$, respectively.

FIGURE 2

FIGURE 2. Effect of $Gr$ on $u\left(y,t\right)$ and $v\left(y,t\right)$. When $\begin{array}{l}Pe=2,R=1,\varphi =2,\gamma =1,M=0.5,K_1=1\\ Gr=5,t=1,\omega =0.5and\epsilon =0.001\end{array}$.

FIGURE 3

FIGURE 3. Effect of $\beta$ on $u\left(y,t\right)$ and $v\left(y,t\right)$. When $\begin{array}{l}Pe=2,R=1,\varphi =2,\gamma =1,M=0.5,K_1=1\\ Gr=5,t=1,\omega =0.5and\epsilon =0.001\end{array}$.

FIGURE 4

FIGURE 4. Effect of $\varphi$ on $u\left(y,t\right)$ and $v\left(y,t\right)$. When $\begin{array}{l}Pe=2,R=1,\varphi =2,\gamma =1,M=0.5,K_1=1\\ Gr=5,t=1,\omega =0.5and\epsilon =0.001\end{array}$.

FIGURE 5

FIGURE 5. Effect of $\gamma$ on $u\left(y,t\right)$ and $v\left(y,t\right)$. When $\begin{array}{l}Pe=2,R=1,Gr=5,\gamma =1,M=0.5,K_1=1\\ \beta =0.5,t=1,\omega =0.5and\epsilon =0.001\end{array}$.

FIGURE 6

FIGURE 6. Effect of $M$ on $u\left(y,t\right)$ and $v\left(y,t\right)$. When $\begin{array}{l}Pe=2,R=1,Gr=5,\varphi =2,\gamma =1,K_1=1\\ \beta =0.5,t=1,\omega =0.5and\epsilon =0.001\end{array}$.

FIGURE 7

FIGURE 7. Effect of $R$ on $u\left(y,t\right)$ and $v\left(y,t\right)$. When $\begin{array}{l}Pe=2,M=0.5,Gr=5,\varphi =2,\gamma =1,K_1=1\\ \beta =0.5,t=1,\omega =0.5and\epsilon =0.001\end{array}$.

FIGURE 8

FIGURE 8. Effect of $K_1$ on $u\left(y,t\right)$ and $v\left(y,t\right)$. When $\begin{array}{l}Pe=2,M=0.5,Gr=5,\varphi =2,\gamma =1,K_1=1\\ \beta =0.5,t=1,\omega =0.5and\epsilon =0.001\end{array}$.

FIGURE 9

FIGURE 9. Effect of $\gamma$ and $\varphi$ on $\theta \left(y,t\right)$. When When $Pe=2,R=3 \varphi =2,and\gamma =2$.

FIGURE 10

FIGURE 10. Effect of $R$ and $Pe$ on $\theta \left(y,t\right)$. When $Pe=2,R=3\varphi =2,and\gamma =2$.

FIGURE 11

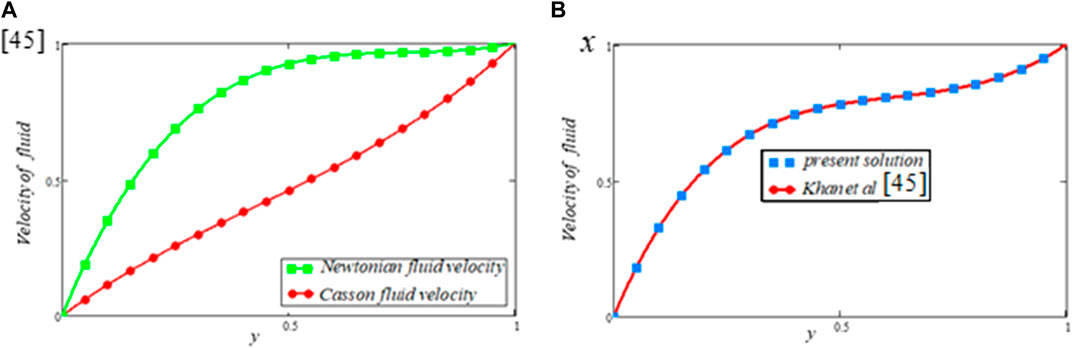
FIGURE 11. Comparison of the present study with (Wahid et al., 2020).

TABLE 1

TABLE 1. Influence of different parameters on $Nu$.

TABLE 2

TABLE 2. Effect of different parameters on skin friction.

Graphical representations of the $Gr$ behavior of both the velocities are shown in Figure 2. The buoyancy-to-viscous force ratio is denoted by $Gr$. Increasing $Gr$, rises buoyancy forces and reduces viscous forces which causes both velocities enhanced. The $\beta$ has an important impact on both the velocity profiles shown in Figure 3. The greater the $\beta$, the thinner the boundary layer becomes, which slows decrease both the velocities profiles. Figure 4 demonstrations the outcome of $\varphi$ on both the velocities profiles. It is clear from these graphs that both the velocities profiles increase. This is true because the thermal forces strengthen as heat generation increases, which cause an increment in both the velocities. The increasing values of temperature time relaxation parameter, enhance both the velocities profiles. More physically, this comportment is that $\gamma$ has inverse relation with dynamic viscosity. As the values of rise, the dynamic viscosity reduces, causing both velocities to increase, as seen in Figure 5. Figure 6 depicts the influence of the magnetic parameter $M$ on the velocity’s profiles for both the velocities profiles. This is due to the fact that Lorentz forces become stronger as $M$ increases which act as resistive forces, and therefore retard the flow. Figure 7 displays the influence of $R$ on the both velocities profiles. The increasing the particle concentration parameter causes extra collisions in the dusty phase, which increase the internal resistive forces, and thus increase both the velocities profiles. The effect of $K_1$ on both velocities is shown from Figure 8. The figure makes it obvious that both velocities decrease as the values of $K_1$ rise. This performance is truthful, as by Stocks drag formula ($K_1=6\pi r\mu$), it is clear that increasing $K_1$ viscous forces increase which resist the flow and consequently decrease the both velocities. The increasing values of temperature time relaxation parameter, enhance temperature profile. The physics is that, the temperature time relaxation parameter $\gamma$ is inverse relation to viscous force, when increases the temperature time relaxation parameter, and reduces viscous forces which causes both velocities enhanced. Figure 9A shows that when the values of $\gamma$ increase, the dynamic viscosity drops and the temperature profile rises as a result. The increasing values of, enhance $\theta \left(y,t\right)$. The physics behind this behavior is that $\varphi$ has direct relation with heat generation. When the values of heat generation parameter $\varphi$ increase the heat generation increases that consequently increase $\theta \left(y,t\right)$ as shown in Figure 9B. The impact of $R$ on $\theta \left(y,t\right)$ is sketched in Figure 10A. By rising the values of $R$, the $\theta \left(y,t\right)$ is decreased. The physics behind this behavior is that the particle concentration parameter $R$ has inverse relation conductivity of thermal. The fluid’s conductivity of thermal decreases as the values $R$ rise, which lowers the temperature distribution. The effect of $P_e$ on $\theta \left(y,t\right)$ is sketched in Figure 10B. By rising the values of $P_e$ the $\theta \left(y,t\right)$ is decreased. The physics behind this behavior is that $P_e$ has the inverse relation thermal conductivity. When the values of $P_e$ increase the thermal conductivity of the fluid decrease therefore, decrease $\theta \left(y,t\right)$; Figure 11A compres Newtonian fluid velocity to viscoelastic Casson fluid velocity. It can be noticed that the viscoelastic Casson fluid has an extremely low velocity than the Newtonian fluid. The greater the Casson parameter $\beta$, the thinner the boundary layer becomes, which slow retard Casson fluid velocity. The value of $\beta \to \infty$ then $\frac{1}{\beta }=0$ has been used for Newtonian fluid. Just for comparison, the Newtonian fluid velocity is much larger than the Casson fluid velocity in this case. Finally; Figure 11B depicted the correlation between the current solutions and (Wahid et al., 2020). Our current solution is reduced to (Wahid et al., 2020) solution by taking ${\beta }_1=1$ into account.

Table 1; Table 2 plot the effect of various parameters on $Nu$ and $Cf$. Table 1 shows the variation $Nu$ with rising values of $Pe$ and $R$. The $Pe$ and $R$ illustrates a direct relation with the $Nu$ that is by increasing $Pe$ and $R$ an enhances in $Nu$, while the $\varphi$ and $\gamma$ depicts an inverse relation with the $Nu$ that is by increasing $\varphi$ and $\gamma$ a decrease in $Nu$. It can be seen that raising $M$, $Pe$, $R$, $\gamma$ and $\varphi$ enhances the numerical value of $Cf$, whereas increasing $Gr$, and $\beta$ decreases the numerical value of $Cf$ because these parameters decrease viscous forces, which reduces the $Cf$.

8 Conclusion

The unsteady MHD flow of an incompressible Casson fluid with dust particles between two parallel plates is analytically investigated when the effects of Newtonian heating are taken into consideration. Using the Lighthill perturbation technique, the perturb solutions for both velocities (fluid and dust) are obtained. Similarly, solutions to the Casson dusty fluid and particle energy equations are obtained separately. To define the impact of $\beta$ and $M$ on the Casson fluid motion, some numerical and graphical results are reported in the Figures 2–11 for various values of physical parameters. The main outcomes are:

• The effect of $M,R$ and $Gr$ on the $u\left(y,t\right)$, and $v\left(y,t\right)$ studied in detail.

• The dusty fluid and particle velocities are declining function for $M$, because of the Lorentz force, the magnetic parameter retards fluid motion.

• The Casson parameter $\beta$ increases then both velocities are enhanced, which also increases the $Cf$.

• Both the velocities (fluid and dust particle velocities) and temperature profile are enhanced when the temperature relaxation time parameter is increased.

• The temperature relaxation time parameter should be increased to manage the rate of heat transfer in fluid.

• The Newtonian heating phenomenon affects the heating on the plate.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

FA conceptualization, formulation, supervision, GA Analysis, and writing draft, AK: Calculations and results, IK software, writing the draft, supervision, ETE: supervision, conceptualization, funding. MA data analysis, revision.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abbas, Z., Jafar, M. A., and Hasnain, J. (2020). Analysis of asymptotic solutions for non-Newtonian fluid flow between two parallel discs with dissimilar in-plane motion. European Journal of Mechanics-B/Fluids 84, 129–138. doi:10.1016/j.euromechflu.2020.06.002

CrossRef Full Text | Google Scholar

Afikuzzaman, M., Biswas, R., Mondal, M., and Ahmmed, S. (2018). MHD free convection and heat transfer flow through a vertical porous plate in the presence of chemical reaction. Frontiers in Heat and Mass Transfer (FHMT) 11 (1), 1–23. doi:10.5098/hmt.11.13

CrossRef Full Text | Google Scholar

Ali, F., Bilal, M., Gohar, M., Khan, I., Sheikh, N. A., and Nisar, K. S. (2020). A report on fluctuating free convection flow of heat absorbing viscoelastic dusty fluid past in a horizontal channel with MHD effect. Scientific Reports 10 (1), 8523–8615. doi:10.1038/s41598-020-65252-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Ali, F., Bilal, M., Sheikh, N. A., Khan, I., and Nisar, K. S. (2019). Two-phase fluctuating flow of dusty viscoelastic fluid between non-conducting rigid plates with heat transfer. IEEE Access 7, 123299–123306. doi:10.1109/access.2019.2933529

CrossRef Full Text | Google Scholar

Ali, N., Nazeer, M., Javed, T., and Razzaq, M. (2019). Finite element analysis of bi-viscosity fluid enclosed in a triangular cavity under thermal and magnetic effects. The European Physical Journal Plus 134 (1), 2–20. doi:10.1140/epjp/i2019-12448-x

CrossRef Full Text | Google Scholar

Anuar, N. S., Bachok, N., Turkyilmazoglu, M., Arifin, N. M., and Rosali, H. (2020). Analytical and stability analysis of MHD flow past a nonlinearly deforming vertical surface in Carbon Nanotubes. Alexandria Engineering Journal 59 (1), 497–507. doi:10.1016/j.aej.2020.01.024

CrossRef Full Text | Google Scholar

Casson, N. (1959). “A flow equation for pigment-oil suspensions of the printing in ink type.” in Rheology of disperse Systems, Editor C. C. Mill (Oxford: Pergamon Press), 84–104. doi:10.4236/wjm.2018.810030

CrossRef Full Text | Google Scholar

Chanson, H. (2004). Hydraulics of open channel flow. Amsterdam, Netherlands: Elsevier.

Google Scholar

Comstock, C. (1972). The Poincaré–Lighthill perturbation technique and its generalizations. SIAM Review 14 (3), 433–446. doi:10.1137/1014069

CrossRef Full Text | Google Scholar

Das, S., Banu, A. S., and Jana, R. N. (2021). Delineating impacts of non-uniform wall temperature and concentration on time-dependent radiation-convection of Casson fluid under magnetic field and chemical reaction. World Journal of Engineering 18, 780–795. doi:10.1108/wje-11-2020-0607

CrossRef Full Text | Google Scholar

Ezzat, M. A., El-Bary, A. A., and Morsey, M. M. (2010). Space approach to the hydro-magnetic flow of a dusty fluid through a porous medium. Computers and Mathematics with Applications 59 (8), 2868–2879. doi:10.1016/j.camwa.2010.02.004

CrossRef Full Text | Google Scholar

Gangadhar, K., Kannan, T., Jayalakshmi, P., and Sakthivel, G. (2021). Dual solutions for MHD Casson fluid over a shrinking sheet with Newtonian heating. International Journal of Ambient Energy 42 (3), 331–339. doi:10.1080/01430750.2018.1550018

CrossRef Full Text | Google Scholar

Gireesha, B. J., Ramesh, G. K., and Bagewadi, C. S. (2012). Heat transfer in MHD flow of a dusty fluid over a stretching sheet with viscous dissipation. Advances in Applied Science Research 3 (4), 2392–2401.

Google Scholar

Hamid, A., Naveen Kumar, R., Punith Gowda, R. J., Varun Kumar, R. S., Khan, S. U., Ijaz Khan, M., et al. (2021). Impact of Hall current and homogenous–heterogenous reactions on MHD flow of GO-MoS2/water (H2O)-ethylene glycol (C2H6O2) hybrid nanofluid past a vertical stretching surface. Waves in Random and Complex Media 3 (1), 1–18.

CrossRef Full Text | Google Scholar

Hussain, F., Nazeer, M., Altanji, M., Saleem, A., and Ghafar, M. M. (2021). Thermal analysis of Casson rheological fluid with gold nanoparticles under the impact of gravitational and magnetic forces. Case Studies in Thermal Engineering 28, 101433. doi:10.1016/j.csite.2021.101433

CrossRef Full Text | Google Scholar

Hussain, S. M., Jain, J., Seth, G. S., and Rashidi, M. M. (2018). Effect of thermal radiation on magneto-nanofluids free convective flow over an ac-celerated moving ramped temperature plate. Scientia Iranica 25 (3), 1243–1257.

Google Scholar

Hussanan, A., Salleh, M. Z., and Khan, I. (2016). Effects of Newtonian heating and inclined magnetic field on two dimensional flow of a casson fluid over a stretching sheet. 5th World Con-ference on Applied Sciences, Engineering & Technology, HCMUT, Vietnam. 251–255.

Google Scholar

Hussanan, A., Salleh, M. Z., Khan, I., and Tahar, R. M. (2017a). Heat transfer in magnetohydrodynamic flow of a Casson fluid with porous medium and Newtonian heating. Journal of nanofluids 6 (4), 784–793. doi:10.1166/jon.2017.1359

CrossRef Full Text | Google Scholar

Hussanan, A., Salleh, M. Z., Khan, I., and Tahar, R. M. (2017b). Heat transfer in magnetohydrodynamic flow of a Casson fluid with porous medium and Newtonian heating. Journal of Nanofluids 6 (4), 784–793. doi:10.1166/jon.2017.1359

CrossRef Full Text | Google Scholar

Jalil, M., Asghar, S., and Yasmeen, S. (2017). An exact solution of MHD boundary layer flow of dusty fluid over a stretching surface. Mathematical Problems in Engineering 2017, 5. doi:2307469doi:10.1155/2017/2307469

CrossRef Full Text | Google Scholar

Jha, B. K., and Gambo, D. (2022). Hydrodynamic behaviour of velocity of applied magnetic field on unsteady MHD Couette flow of dusty fluid in an annulus. The European Physical Journal Plus 137 (1), 67–20. doi:10.1140/epjp/s13360-021-02284-0

CrossRef Full Text | Google Scholar

Jyothi, A. M., Kumar, R. N., Gowda, R. P., and Prasannakumara, B. C. (2021). Significance of Stefan blowing effect on flow and heat transfer of Casson nanofluid over a moving thin needle. Communications in Theoretical Physics 73 (9), 095005. doi:10.1088/1572-9494/ac0a65

CrossRef Full Text | Google Scholar

Jyothi, A. M., Varun Kumar, R. S., Madhukesh, J. K., Prasannakumara, B. C., and Ramesh, G. K. (2021). Squeezing flow of Casson hybrid nanofluid between parallel plates with a heat source or sink and thermophoretic particle deposition. Heat Transfer 50 (7), 7139–7156. doi:10.1002/htj.22221

CrossRef Full Text | Google Scholar

Khalid, A., Khan, I., Khan, A., and Shafie, S. (2015). Unsteady MHD free convection flow of Casson fluid past over an oscillating vertical plate embedded in a porous medium. Engineering Science and Technology, An International Journal 18 (3), 309–317. doi:10.1016/j.jestch.2014.12.006

CrossRef Full Text | Google Scholar

Khan, D., Ali, G., Kumam, P., and ur Rahman, A. (2022). A scientific outcome of wall shear stress on dusty viscoelastic fluid along heat absorbing in an inclined channel. Case Studies in Thermal Engineering 30, 101764–101771. doi:10.1016/j.csite.2022.101764

CrossRef Full Text | Google Scholar

Khan, D., Khan, A., Khan, I., Ali, F., ul Karim, F., and Tlili, I. (2019). Effects of relative magnetic field, chemical reaction, heat generation and Newtonian heating on convection flow of Casson fluid over a moving vertical plate embedded in a porous medium. Scientific Reports 9 (1), 400–418. doi:10.1038/s41598-018-36243-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Koriko, O. K., Adegbie, K. S., Shah, N. A., Animasaun, I. L., and Olotu, M. A. (2021). Numerical solutions of the partial differential equations for investigating the significance of partial slip due to lateral velocity and viscous dissipation: The case of blood-gold carreau nanofluid and dusty fluid. Numerical Methods for Partial Differential Equations 2021, 1–29. doi:10.1002/num.22754

CrossRef Full Text | Google Scholar

Krishna, M. V., Ahamad, N. A., and Chamkha, A. J. (2021). Hall and ion slip impacts on unsteady MHD convective rotating flow of heat generating/absorbing second grade fluid. Alexandria Engineering Journal 60 (1), 845–858. doi:10.1016/j.aej.2020.10.013

CrossRef Full Text | Google Scholar

Kumar, K. A., Sugunamma, V., and Sandeep, N. (2020). Effect of thermal radiation on MHD Casson fluid flow over an exponentially stretching curved sheet. Journal of Thermal Analysis and Calorimetry 140 (5), 2377–2385. doi:10.1007/s10973-019-08977-0

CrossRef Full Text | Google Scholar

Loganathan, K., Sivakumar, M., Mohanraj, M., and Sakthivel, P. (2021). Thermally radiative casson fluid flow over a cylinder with Newtonian heating and heat generation/absorption. Journal of Physics: Conference Series, 1964 (2), 022001. doi:10.1088/1742-6596/1964/2/022001

CrossRef Full Text | Google Scholar

Mabood, F., Abdel-Rahman, R. G., and Lorenzini, G. (2016). Effect of melting heat transfer and thermal radiation on Casson fluid flow in porous medium over moving surface with magnetohydrodynamics. Journal of Engineering Thermophysics 25 (4), 536–547. doi:10.1134/s1810232816040111

CrossRef Full Text | Google Scholar

Madhukesh, J. K., Alhadhrami, A., Naveen Kumar, R., Punith Gowda, R. J., Prasannakumara, B. C., and Varun Kumar, R. S. (2021). Physical insights into the heat and mass transfer in Casson hybrid nanofluid flow induced by a Riga plate with thermophoretic particle deposition. Proceedings of the Institution of Mechanical Engineers, Part E: Journal of Process Mechanical Engineering 3 (2), 1–19.

CrossRef Full Text | Google Scholar

Makinde, O. D. (2009). On thermal stability of a reactive third-grade fluid in a channel with convective cooling the walls. Applied Mathematics and Computation 213 (1), 170–176. doi:10.1016/j.amc.2009.03.003

CrossRef Full Text | Google Scholar

Manjula, V., and Sekhar, K. C. (2021). Heat and mass transfer analysis of MHD Casson fluid flow over a permeable vertical surface with thermal radiation and Newtonian heating AIP Conference Proceedings. AIP Publishing LLC 2375 (1), 030010. doi:10.1063/5.0066543

CrossRef Full Text | Google Scholar

Merkin, J. H. (1994). Natural-convection boundary-layer flow on a vertical surface with Newtonian heating. Int. J. Heat Fluid Flow 15 (5), 392–398. doi:10.1016/0142-727x(94)90053-1

CrossRef Full Text | Google Scholar

Miwa, S., and Hibiki, T. (2022). Inverted annular two-phase flow in multiphase flow systems. International Journal of Heat and Mass Transfer 18 (6), 122340–122354. doi:10.1016/j.ijheatmasstransfer.2021.122340

CrossRef Full Text | Google Scholar

Mukhopadhyay, S. (2013). Effects of thermal radiation on Casson fluid flow and heat transfer over an unsteady stretching surface subjected to suction/blowing. Chinese Physics B 22 (11), 114702–114714. doi:10.1088/1674-1056/22/11/114702

CrossRef Full Text | Google Scholar

Nayfeh, A. H. (2008). Perturbation methods. Hoboken, NJ, USA: John Wiley & Sons.

Google Scholar

Obalalu, A. M. (2021). Heat and mass transfer in an unsteady squeezed Casson fluid flow with novel thermophysical properties: Analytical and numerical solution. Heat Transfer 50 (8), 7988–8011. doi:10.1002/htj.22263

CrossRef Full Text | Google Scholar

Obalalu, A. M., Wahaab, F. A., and Adebayo, L. L. (2020). Heat transfer in an unsteady vertical porous channel with injection/suction in the presence of heat generation. Journal of Taibah University for Science 14 (1), 541–548. doi:10.1080/16583655.2020.1748844

CrossRef Full Text | Google Scholar

Oka, S. (1971). An approach to α unified theory of the flow behavior of time-independent non-Newtonian suspensions. Japanese Journal of Applied Physics 10 (3), 287–298. doi:10.1143/jjap.10.287

CrossRef Full Text | Google Scholar

O’Sullivan, C. T. (1990). Newton’s law of cooling—a critical assessment. American Journal of Physics 58 (10), 956–960. doi:10.1119/1.16309

CrossRef Full Text | Google Scholar

Pramanik, S. (2014). Casson fluid flow and heat transfer past an exponentially porous stretching surface in presence of thermal radiation. Ain Shams Engineering Journal 5 (1), 205–212. doi:10.1016/j.asej.2013.05.003

CrossRef Full Text | Google Scholar

Rafiq, S., Abbas, Z., Sheikh, M., and Hasnain, J. (2020). Effects of variable viscosity on asymmetric flow of non-Newtonian fluid driven through an expanding/contracting channel containing porous walls. Arabian Journal for Science and Engineering 45 (11), 9471–9480. doi:10.1007/s13369-020-04798-8

CrossRef Full Text | Google Scholar

Raju, C. S. K., Upadhya, S. M., and Seth, D. (2021). Thermal convective conditions on MHD radiated flow with suspended hybrid nanoparticles. Microsystem Technologies 27 (5), 1933–1942. doi:10.1007/s00542-020-04971-x

CrossRef Full Text | Google Scholar

Ramesh, G. K., Madhukesh, J. K., Prasannakumara, B. C., and Roopa, G. S. (2022). Significance of aluminium alloys particle flow through a parallel plates with activation energy and chemical reaction. Journal of Thermal Analysis and Calorimetry 147 (12), 6971–6981. doi:10.1007/s10973-021-10981-2

CrossRef Full Text | Google Scholar

Reddy, G. J., Raju, R. S., and Rao, J. A. (2018). Influence of viscous dissipation on unsteady MHD natural convective flow of Casson fluid over an oscillating vertical plate via FEM. Ain Shams Engineering Journal 9 (4), 1907–1915. doi:10.1016/j.asej.2016.10.012

CrossRef Full Text | Google Scholar

Rehman, S. U., Fatima, N., Ali, B., Imran, M., Ali, L., Shah, N. A., et al. (2022). The Casson dusty nanofluid: Significance of Darcy–forchheimer law, magnetic field, and non-Fourier heat flux model subject to stretch surface. Mathematics 10 (16), 2877. doi:10.3390/math10162877

CrossRef Full Text | Google Scholar

Rundora, L. (2021). Unsteady magnetohydrodynamic mixed convective flow of a reactive casson fluid in a vertical channel filled with a porous medium, Defect and Diffusion Forum. 408, 33–49. doi:10.4028/www.scientific.net/DDF.408.33

CrossRef Full Text | Google Scholar

Saffman, P. G. (1962). On the stability of laminar flow of a dusty gas. Journal of Fluid Mechanics 13 (1), 120–128. doi:10.1017/s0022112062000555

CrossRef Full Text | Google Scholar

Sayed-Ahmed, M. E., Attia, H. A., and Ewis, K. M. (2011). Time dependent pressure gradient effect on unsteady mhd Couette flow and heat transfer of a Casson fluid. Engineering 3 (1), 38–49. doi:10.4236/eng.2011.31005

CrossRef Full Text | Google Scholar

Turkyilmazoglu, M. (2022). Flow and heat over a rotating disk subject to a uniform horizontal magnetic field. Zeitschrift für Naturforschung A 77 (4), 329–337. doi:10.1515/zna-2021-0350

CrossRef Full Text | Google Scholar

Upadhya, S. M., Raju, C. S. K., Vajravelu, K., Sathy, S., and Farooq, U. (2022). Significance of radiative magnetohydrodynamic flow of suspended PEG based ZrO2 and MgO2 within a conical gap. Waves in Random and Complex Media 8 (2), 4575–4599.

Google Scholar

Wahid, N. S., Arifin, N. M., Turkyilmazoglu, M., Hafidzuddin, M. E. H., and Abd Rahmin, N. A. (2020). MHD hybrid Cu-Al2O3/water nanofluid flow with thermal radiation and partial slip past a permeable stretching surface: Analytical solution, Journal of Nano Research, 64. 75–91. doi:10.4028/www.scientific.net/JNanoR.64.75

CrossRef Full Text | Google Scholar

Glossary

$h_s$ Heat transfer coefficient ($m^{-1}$)

$B_0$ Applied Magnetic Field ($N.s/C.m$)

$K_0$ Stock’s Resistance Coefficient

$K_1$ Dusty fluid parameter

$K_2$ Dusty fluid parameter

$N_0$ Number Density of the Dust Particles

$P_p$ Density of the dust particle ($kg/m^3$)

$T_d$ Ambient Temperature K)

$c_p$ Specific heat capacity of fluid ($j\cdot k{g^{-}}^1\cdot {K^{-}}^1$)

$\overrightarrow{s}$ Surface forces N)

$u_0$ Constant Velocity ($m/s$)

${\beta }_T$ Coefficient of Thermal Expansion

${\gamma }_T$ Temperature relaxation time

c_s Specific heat capacity of the dust particle

R Particle concentration parameter

T_∞ Ambient temperature K)

ϕ Heat absorption coefficient

$Cf$ Skin friction.

$Gr$ Grashof Number

$M$ Non-dimensional Magnetic Parameter

$Nu$ Nusslet number

$P$ Pressure (kg·m⁻¹ s⁻²)

$Pe$ Pectlet Number

$T$ Temperature of the Fluid K)

$d$ is the distance between parallel plates($m$)

$g$ Gravitational Acceleration ($m{s}^{-2}$ )

$k$ Thermal Conductivity of the Fluid $\left(W/mK\right)$.

$m$ Mass of particles $\left(kg\right)$

$t$ Time ($s$)

$u\left(y,t\right)$ Velocity of the base fluid ($m/s$)

$v\left(y,t\right)$ Velocity of the particle ($m/s$)

$\beta$ Casson fluid parameter

$\theta$ Dimensionless Temperature of the fluid

$\mu$ Dynamic Viscosity ($\mathrm{k}\mathrm{g}.{{\mathrm{m}}^{-}}^1{s^{-}}^1$)

$\rho$ Fluid Density ($kg/m^3$)

$\rho \overrightarrow{b}$ Body Forces

$\sigma$ Electrical Conductivity $\left(S/m\right)$

$\upsilon$ Kinematic Viscosity $\left(kg/m^3\right)$.