
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Mater., 24 February 2023
Sec. Colloidal Materials and Interfaces
Volume 10 - 2023 | https://doi.org/10.3389/fmats.2023.1114665
This article is part of the Research TopicThermodynamics of Newtonian and non-Newtonian Nanofluids with Recent AdvancementsView all 13 articles
 Qasim Ali1
Qasim Ali1 Muhammad Amir1
Muhammad Amir1 Ali Raza1,2
Ali Raza1,2 Umair Khan3,4
Umair Khan3,4 Sayed M. Eldin5*
Sayed M. Eldin5* Abeer M. Alotaibi6
Abeer M. Alotaibi6 Samia Elattar7
Samia Elattar7 Ahmed M. Abed8,9
Ahmed M. Abed8,9The significance of thermal conductivity, convection, and heat transportation of hybrid nanofluids (HNFs) based on different nanoparticles has enhanced an integral part in numerous industrial and natural processes. In this article, a fractionalized Oldroyd-B HNF along with other significant effects, such as Newtonian heating, constant concentration, and the wall slip condition on temperature close to an infinitely vertical flat plate, is examined. Aluminum oxide (Al2O3) and ferro-ferric oxide (Fe3O4) are the supposed nanoparticles, and water (H2O) and sodium alginate (C6H9NaO7) serve as the base fluids. For generalized memory effects, an innovative fractional model is developed based on the recently proposed Atangana–Baleanu time-fractional (AB) derivative through generalized Fourier and Fick’s law. This Laplace transform technique is used to solve the fractional governing equations of dimensionless temperature, velocity, and concentration profiles. The physical effects of diverse flow parameters are discussed and exhibited graphically by Mathcad software. We have considered
With the addition of nanometer-sized particles in various base fluids, thermophysical characteristics may improve in energy transfer schemes. This process signals an expansion in the thermal conductivity for base fluids, making it more reliable and ongoing. These significant fluids define nanofluids (NFs) with an extensive series of suggestions in several areas of science, as well as technology, with nuclear devices, heat exchangers, solar plates, vehicle heaters, and biotic and organic devices (Usman et al., 2018; Khan et al., 2022a; Khan et al., 2022b; Ahmed et al., 2022; Hassan et al., 2022; Khan et al., 2022c). First, Lee and Eastman presented the idea of NFs in 1995 (Lee et al., 1999). Numerous applications of NFs are discoursed by Kaufui et al. (Wong and Omar De Leon., 2010). Mahian et al. (2019) proposed important ideas and reflected novel innovations to completely explain the NFs. They were obsessed with innovative expansions in this field, comprehensive explanations of the thermophysical characteristics, and imitation of thermal transmission in NF flow. Waini et al. (2019) used a numerical scheme to discuss an unsteady thermal transmission flow past a shrinking sheet in an HNF. They presented different applications of NFs in numerous branches of science along with appreciated recommendations. NFs have achieved significant consideration from researchers due to their improved heat conversion characteristics. The rheological presentation of an NF using a revolving rheometer was proposed by Vallejo et al. (2019a). Different rheological characteristics of NFs are discussed in Vallejo et al. (2019b). Currently, NFs have been characterized as HNFs in several mechanisms (Rashad et al., 2018). HNFs are developed by mixing two dissimilar nanoparticles in the base liquid. Its main inspiration is to increase the thermal features of NFs. The variable thermal transmission of HNFs through magnetic influence was examined in Mohebbi et al. (2019). The heat transmission in the non-Newtonian HNF composed with entropy generation was discussed in Shahsavar et al., 2018). Furthermore, Farooq et al. (2018) deliberated on the entropy in the HNF flow in a stretching sheet.
Asogwa et al. (2021) discussed chemical reactions and heat sinks over a ramped temperature. The analytical solution of governing equations was found with the Laplace transform. Asogwa et al. (2022a) used the Laplace approach to discuss a water-based NF containing aluminum oxide and copper in a moving plate and proved that thermal absorption causes a decline in aluminum oxide NF’s thermal and momentum profiles with a copper NF. Shankar Goud et al. (2022) used the Keller–box scheme for the numerical solution along with thermal effects, momentum, and solutal slip on the thermal transmission with a description of the magnetohydrodynamic (MHD) flow of Casson fluid and an exponential porous surface with Dufour, chemical reaction, and Soret impacts. Khan et al. (2022d) studied a fractionalized electro-osmotic flow based on the Caputo operator of a Casson NF containing sodium alginate nanoparticles over a vertical microchannel with MHD effects. They proved that the inclination angle boosts the velocity. Asogwa et al. (2022b) and Asogwa et al. (2022c) considered the stimulation significance of the thermal transmission with the MHD flow of a NF through an extending sheet with MATLAB bvp4c. Furthermore, they investigated the radiative features of the MHD flow with collective heat transportation characteristics on a reactive stretching surface with the Casson NF numerically using MATLAB bvp4c. Goud et al. (2022) applied the bvp4c scheme to study the convection flow via an infinite porous plate on thermal transmission, as well as mass transmission. Asogwa et al. (2022d) discussed the influences of the movement of nanoparticles in NFs by an exponentially enhanced Riga plate. Reddy et al. (2022) calculated the effect of activation energy on a second-grade MHD NF flow over a convectively curved heated stretched surface by considering the Brownian motion and generation/absorption, and thermophoresis. They have shown that velocity and thermal profiles suggestively increase with the concurrent increasing estimation of the fluid parameter.
The fractional calculus (FC) has obtained substantial consideration from experts in previous decades. The important inventions have newly been presented in the application of the FC, where new derivatives, as well as integral operators, are hired (Awan et al., 2019). The new anticipated operators contain the generalized Mittag–Leffler function (MLF), and these features intensify the innovative constructions to achieve numerous attractive properties that are recognized in important outcomes. Subsequently, Atangana and Dumitru (2016) anticipated, the innovative and applicable time-fractional operator, which is expansively hired in numerous branches of science and engineering. It is exposed that the MLF is a more operative and vigorous screening apparatus than the exponential and power laws, constructing the AB-fractional operator, in terms of Caputo, an effective arithmetic procedure to simulate progressively perilous complex tasks. Due to their extensive implications, such fractional models are extensively identified for deriving fractional differential equations (FDEs) with no manufactured irregularities, as for Caputo, Riemann–Liouville (RL), and Caputo–Fabrizio (CF) derivatives, because of their characteristic non-orientation (Ali et al., 2021; Ali et al., 2022a; Raza et al., 2022; Zhang et al., 2022). We also perceived interest in these fractional derivatives on the topic of mathematical approaches, although scientifically approximating these operators' outcomes to compute different problems (Martyushev and Sheremet, 2012; Ali et al., 2022b).
Batool et al. (2022) discussed the thermal and mass transmission processes of a micropolar NF under magnetic and buoyancy effects across an inclusion. Rasool et al. (2022a) examined the significance of the MHD Maxwell NF flow and obtained the solution to this problem by employing the homotopy analysis technique for diverse physical parameters. Moreover, they studied an electro-magneto-hydrodynamic NF flow in a permeable medium with heating boundary conditions. Furthermore, they applied Buongiorno’s method for the flow of radiating thixotropic NFs over a horizontal surface by considering the retardational effects of Lorentz forces and using the influence of Brownian and thermophoresis diffusions (Rasool et al., 2022b; Rasool et al., 2023).
In this paper, a fractionalized Oldroyd-B HNF flow is examined by the recent definitions of the AB time-fractional derivative having a Mittage–Leffler kernel along with Newtonian heating, constant concentration, and the wall slip condition on temperature close to an infinite vertical flat plate. The AB fractional operator is introduced in the governing equations of temperature and diffusion by employing the generalized types of Fourier and Fick’s law. The developed non-dimensional fractional model is solved using the Laplace transform method. Graphical illustrations are used to depict the physical behavior of fractional derivatives and the consequence of diverse flow parameters on velocity, thermal, and concentration fields. Furthermore, for validation of our attained results, some limiting cases are considered to recover fractional derivatives, as well as classical models of Maxwell and Newtonian fluids. The impacts of diverse flow parameters on variable profiles are achieved and presented graphically with significant conclusions.
Consider an unsteady and an incompressible Oldroyd-B HNF flow close to an infinite vertical flat plate. Initially, consider that the fluid and plate are at a relaxation position, with constant temperature
By Boussinesq’s estimation (Ali et al., 2021), the governing equations for an Oldroyd-B HNF are discussed by Martyushev and Sheremet (2012). The equation of motion is as follows:
The energy balance equation is as follows (Awan et al., 2019):
The Fourier law (Zhang et al., 2022) for thermal conduction is as follows:
The diffusion equation (Awan et al., 2019) for
The Fick law is as follows (Awan et al., 2019):
The appropriate initial and boundary conditions are as follows:
Table 1 shows the properties of thermal and under-conversation fluids and nanoparticles.
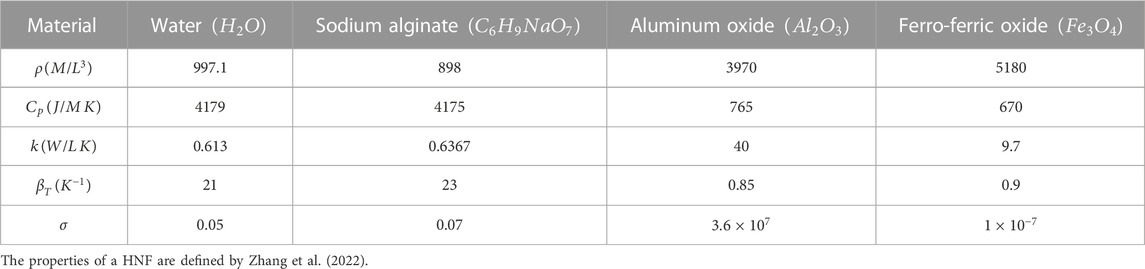
TABLE 1. Thermal characteristics of base fluids and nanoparticles (Raza et al., 2022; Zhang et al., 2022).
The following are a set of non-dimensional parameters:
By utilizing the aforementioned variables in Eqs. 1–8 and after dropping the
where
Now, we develop a fractional Oldroyd-B HNF using Fourier and Fick’s law based on the AB-fractional operator (Atangana and Dumitru, 2016), which is explained as the following expression for a function
and the kernel Mittage–Leffler function
The Laplace transform is
with
The governing equations for the AB-fractional derivative are obtained by substituting the ordinary derivative with the AB derivative operator
Using the Laplace transform on Eqs. 25, 26 and corresponding conditions (15)2-(17)2, we have
where
The solution of Eq. (29) by using Eq. (30) and with conditions in Eq. (31) is
Eq. (32) can be written as
where
The Laplace inverse of Eq. (33) is shown numerically in Table 2.
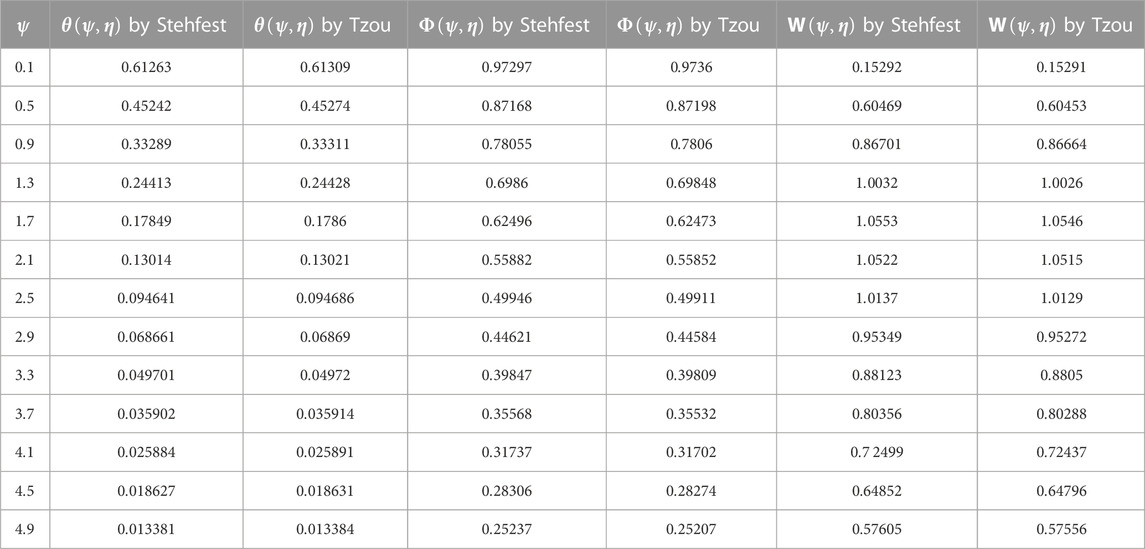
TABLE 2. Numerical comparison of energy, concentration, and velocity profiles by different numerical methods.
By employing the Laplace transform on Eqs. 27, 28 with associated conditions defined in Eqs. (15)3– (17)3, we have
The solution of Eq. (34) by using Eq. (35) and conditions in Eq. (36) is
Eq. (37) may be written as
where
The Laplace inverse of Eq. (38) is computed numerically in Table 2 by invoking diverse numerical methods.
Taking the Laplace transform on Eq. (24) with related conditions in Eqs. (15)1– (17)1, we have
By using temperature values from Eq. (37) and concentration from Eq. (38) and with conditions of Eq. (40), we obtain the solution of the velocity field for Eq. (40) as
where
Our achieved solutions of variable profiles are complex to find analytically. Different researchers employed varied numerical approaches; so to compute Laplace inversion, we also employed numerical techniques, i.e., Stehfest and Tzou numerical methods. These algorithms are defined as follows (Stehfest, 1970; Tzou, 2014):
where
and
Case I. Classical Oldroyd-B fluidBy substituting
Case II. Fractionalized Maxwell fluidBy substituting
Case III. Ordinary Maxwell fluidBy substituting
Case IV. Fractionalized Newtonian fluidBy substituting
Case V. Ordinary Newtonian fluidBy substituting
In this article, the natural convection flow of the Oldroyd-B HNF flowing close to an infinite vertical flat plate is examined. Aluminum oxide–magnetite–water (Al2O3–Fe3O4–H2O) and aluminum oxide–magnetite–sodium alginate (Al2O3–Fe3O4–
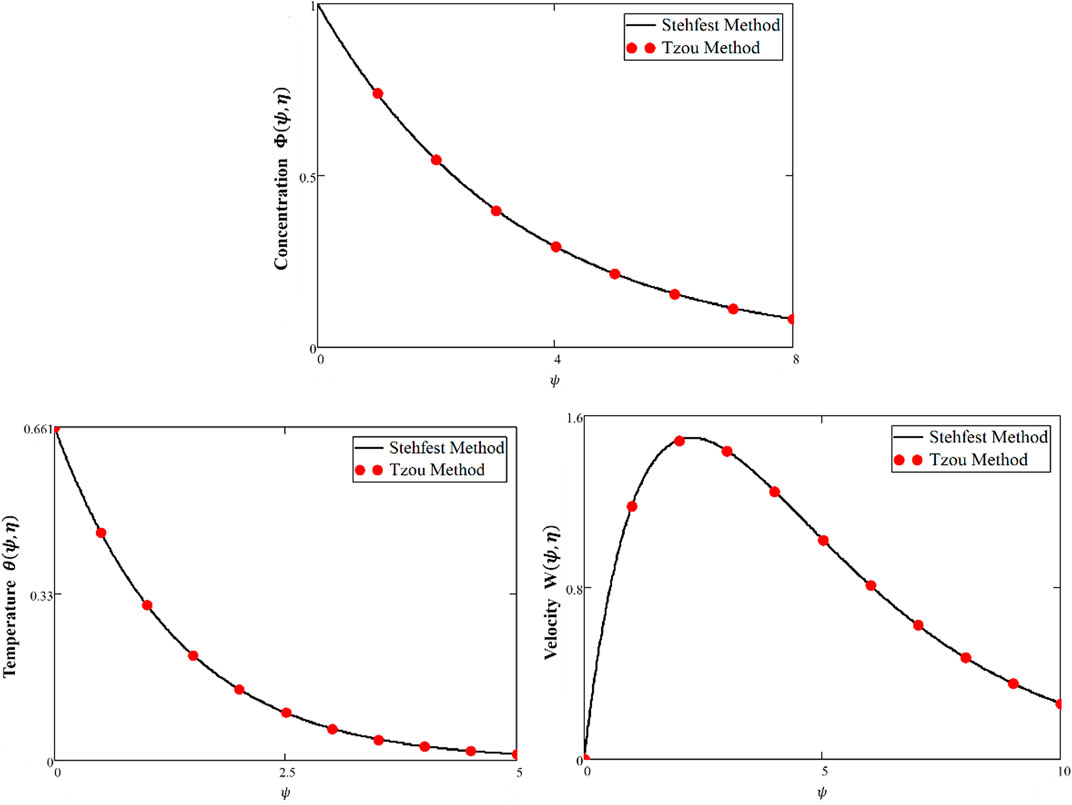
FIGURE 14. Simulation to explain the concentration, temperature, and velocity for the comparison of different inversion numerical algorithms.
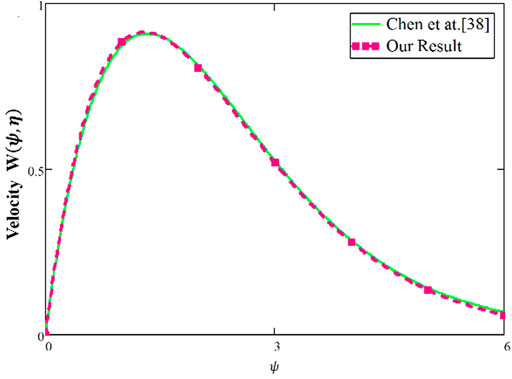
FIGURE 15. Comparison of our results with the results by Chen et al. (2022) for validation.
Figure 2 shows the influence of
The fluid velocity declines as we increase
Figure 8 shows the influence of
Figure 12 shows a comparison of different fluid models. It is observed that the solutions of Maxwell nanofluids for both ordinary and fractional cases have developed curves as compared to Oldroyd-B and viscous nanofluids. Figure 13 shows the velocity for the slip and no-slip conditions. It can be seen that the slip condition shows a lesser profile for velocity than the no-slip conditions. Figure 14 shows the temperature and velocity behaviors for the comparison of diverse numerical techniques (Stehfest and Tzou’s algorithm). The overlapping of profiles shows that these algorithms are strongly validated with each other. Figure 15 shows the validation of our results with Chen et al. (2022). By overlapping both curves, it is observed from these graphs that our achieved results match those developed by Chen et al. (2022). The numerical comparison of energy, concentration, and velocity profiles by different numerical methods is shown in Table 2. Table 3 shows the numerical results of the Nusselt number, Sherwood number, and skin friction. The comparison of the momentum profile with the work of Chen et al. (2022) is shown in Table 4.
This article examines the investigations of the unsteady, convective flow of the Oldroyd-B HNF flowing over a flat plate with wall slip conditions on temperature and constant concentration. The model is developed using the AB-fractional operator and solved with the Laplace transform method. The Laplace inversion is computed with the well-known Stehfest and Tzou numerical schemes. Finally, the effect of diverse flow parameters is planned to estimate the physical clarification of the achieved results of governed equations. The main results from the previous section are summarized in the following:
❖ For a short time, the temperature and momentum profile decayed for a larger value of
❖ By increasing
❖ By increasing
❖ The velocity decreases with increasing
❖ The energy and velocity profiles are larger for a water-based HNF than those of the sodium alginate-based HNF.
❖ The graphs of Maxwell nanofluids for both classical and fractional models have more advanced curves than Oldroyd-B and viscous nanofluids.
❖ The slip condition shows a lower profile for velocity than the no-slip condition.
❖ The comparison of diverse numerical algorithms (Stehfest and Tzou) strongly validated our study’s solutions.
❖ Chen et al. (2022), the overlapping of both curves validate the achieved results of our study.
For extension of this fractional problem examined in this article, we idolized the following proposal based on investigation, approaches, extensions, and geometries, as demarcated in the following:
• The same problem can also be considered over a horizontal plate by using Prabhakar’s time-fractional approach with an MHD effect in a porous medium.
• A comparative study of this study can be solved by the natural and Laplace transform methods.
• The same problem may be discussed by the Keller–box scheme.
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
Conceptualization, SME, AR, QA, MA, and UK; methodology, SME, AR, and UK; software, MA, QA, SME, AR, and UK; validation, SME, AR, UK, SE, MA, and AhA; formal analysis, AbA, SE, AR, and AhA; investigation, UK, AbA, SE, and AhA; resources, AbA; data curation, QA; writing—original draft preparation, MA, SME, QA, UK, AbA, SE, and AhA; writing—review and editing, AbA, QA, MA, and AhA; visualization, AR, AhA, and SE; supervision, UK; project administration, SE; funding acquisition, SE. All authors have read and agreed to the published version of the manuscript.
This work received support from Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2023R163), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia. In addition, this study is also funded by Prince Sattam bin Abdulaziz University project number (PSAU/2023/R/1444).
The authors are thankful for the support of Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2023R163), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia. Also, this work is supported via funding from Prince Sattam bin Abdulaziz University project number (PSAU/2023/R/1444).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Ahmed, Awais, Alhowaity, Sawsan, and Mohamed, E. (2022). Ghoneim, fehmi gamaoun, elsayed tag-eldin, mansour F. Yassen, and mahnoor sarfraz. "Material and wave relaxation phenomena effects on the rheology of Maxwell nanofluids. Front. Phys. 10, 886.
Ali, Qasim, Al-Khaled, Kamel, Ijaz Khan, M., Khan, Sami Ullah, Ali, Raza, Oreijah, Mowffaq, et al. (2022). Diffusion phenomenon for natural convection flow of classical hartmann problem due to a cylindrical tube by generalized fourier’s theories: A fractional analysis. Int. J. Mod. Phys. B 13, 2350104. doi:10.1142/s0217979223501047
Ali, Qasim, Al-Khaled, Kamel, Omar, Jiyan, Ali, Raza, Khan, Sami Ullah, Ijaz Khan, M., et al. (2022). Analysis for advection–diffusion problem subject to memory effects and local and nonlocal kernels: A fractional operators approach. Int. J. Mod. Phys. B 15, 2350099. doi:10.1142/s0217979223500996
Ali, Qasim, Riaz, Samia, Aziz Ullah, Awan, and Ali Abro, Kashif (2021). A mathematical model for thermography on viscous fluid based on damped thermal flux. Z. für Naturforsch. A 76 (3), 285–294. doi:10.1515/zna-2020-0322
Asogwa, Kanayo K., Bilal, Sardar M., Animasaun, Isaac L., and Mebarek-Oudina, Fateh M. (2021). Insight into the significance of ramped wall temperature and ramped surface concentration: The case of Casson fluid flow on an inclined Riga plate with heat absorption and chemical reaction. Nonlinear Eng. 10 (1), 213–230. doi:10.1515/nleng-2021-0016
Asogwa, Kanayo Kenneth, Goud, B. Shankar, Shah, Nehad Ali, and -Jin Yook, Se (2022). Rheology of electromagnetohydrodynamic tangent hyperbolic nanofluid over a stretching riga surface featuring dufour effect and activation energy. Sci. Rep. 12 (1), 14602. doi:10.1038/s41598-022-18998-9
Asogwa, Kanayo Kenneth, Goud, B. Shankar, Yanala Dharmendar Reddy, , and Ibe, Amarachukwu A. (2022). Suction effect on the dynamics of EMHD casson nanofluid over an induced stagnation point flow of stretchable electromagnetic plate with radiation and chemical reaction. Results Eng. 15 (2022), 100518. doi:10.1016/j.rineng.2022.100518
Asogwa, Kanayo Kenneth, Prasad, K. C. Rajendra, Kumar, Raman, Murtugudde, Gururaj, and Punith Gowda, R. J. (2022). Transient electromagnetohydrodynamic Nanofluid flow traveling through a moving Riga plate subject to radiation and heat absorption. Int. J. Mod. Phys. B 09, 2350168. doi:10.1142/s0217979223501680
Asogwa, Kanayo K., Mebarek-Oudina, F., and Animasaun, I. L. (2022). Comparative investigation of water-based Al2O3 nanoparticles through water-based CuO nanoparticles over an exponentially accelerated radiative Riga plate surface via heat transport. Arabian J. Sci. Eng. 47 (7), 8721–8738. doi:10.1007/s13369-021-06355-3
Atangana, Abdon, and Dumitru, Baleanu (2016). New fractional derivatives with nonlocal and non-singular kernel: Theory and application to heat transfer model. arXiv Prepr. arXiv:1602.03408 21.
Awan, Aziz Ullah, Shah, Nehad Ali, Ahmed, Najma, Ali, Qasim, and Riaz, Samia (2019). Analysis of free convection flow of viscous fluid with damped thermal and mass fluxes. Chin. J. Phys. 60, 98–106. doi:10.1016/j.cjph.2019.05.006
Batool, Saima, Rasool, Ghulam, Alshammari, Nawa, Khan, Ilyas, Kaneez, Hajra, and Hamadneh, Nawaf (2022). Numerical analysis of heat and mass transfer in micropolar nanofluids flow through lid driven cavity: Finite volume approach. Case Stud. Therm. Eng. 37 (2022), 102233. doi:10.1016/j.csite.2022.102233
Chen, C., Rehman, A. U., Riaz, M. B., Jarad, F., and Sun, X.-E. (2022). Impact of Newtonian heating via fourier and Fick’s laws on thermal transport of Oldroyd-B fluid by using generalized mittag-leffler kernel. Symmetry 14 (4), 766. doi:10.3390/sym14040766
Farooq, U., Afridi, M. I., Qasim, M., and Lu, D. C. (2018). Transpiration and viscous dissipation effects on entropy generation in hybrid nanofluid flow over a nonlinear radially stretching disk. Entropy 20 (9), 668. doi:10.3390/e20090668
Goud, B. Shankar, Reddy, Y. Dharmendar, and Kenneth Asogwa, Kanayo (2022). Inspection of chemical reaction and viscous dissipation on MHD convection flow over an infinite vertical plate entrenched in porous medium with Soret effect. Biomass Convers. Biorefinery 29, 1–12. doi:10.1007/s13399-022-02886-3
Hassan, Ali, Hussain, Azad, Arshad, Mubashar, Gouadria, Soumaya, Jan, Awrejcewicz, Galal, Ahmed M., et al. (2022). Insight into the significance of viscous dissipation and heat generation/absorption in magneto-hydrodynamic radiative casson fluid flow with first-order chemical reaction. Front. Phys. 10, 605. doi:10.3389/fphy.2022.920372
Khan, Dolat, Kenneth Asogwa, Kanayo, Akkurt, Nevzat, Kumam, Poom, Watthayu, Wiboonsak, and Sitthithakerngkiet, Kanokwan (2022). Development of generalized fourier and Fick’s law of electro-osmotic MHD flow of sodium alginate based casson nanofluid through inclined microchannel: Exact solution and entropy generation. Sci. Rep. 12 (1), 18646. doi:10.1038/s41598-022-21854-5
Khan, Muhammad Naveed, Ahammad, N. Ameer, Ahmad, Shafiq, and Mohamed Abdelghany, Elkotb (2022). Elsayed Tag-eldin, Kamel Guedri, Khaled A. Gepreel, and Mansour F. Yassen. "Thermophysical features of Ellis hybrid nanofluid flow with surface-catalyzed reaction and irreversibility analysis subjected to porous cylindrical surface. Front. Phys. 10, 795.
Khan, M. N., Alhowaity, S., Wang, Z., Alqahtani, A. M., Tag-eldin, E., and Yassen, M. F. (2022). Alqahtani, Elsayed Tag-eldin, and Mansour F. Yassen. "Significance of multiple solutions on the dynamics of ethylene glycol conveying gold and copper nanoparticles on a shrinking surface. Front. Phys. 10, 928.
Khan, Umar, Ahmed, Naveed, and Khan, Ilyas (2022). Heat transfer evaluation in MgZn6Zr/C8H18 [(Magnesium-Zinc-Zirconium)/Engine oil] with non-linear solar thermal radiations and modified slip boundaries over 3-dimensional convectively heated surface. Front. Energy Res. 12, 351.
Lee, S., Choi, S. U.-S, Li, S., and Eastman, J. A (1999). Measuring thermal conductivity of fluids containing oxide nanoparticles 2, 280–289.
Mahian, Omid, Kolsi, Lioua, Amani, Mohammad, Estellé, Patrice, Ahmadi, Goodarz, Kleinstreuer, Clement., et al. (2019). Recent advances in modeling and simulation of nanofluid flows-Part I: Fundamentals and theory. Phys. Rep. 790, 1–48. doi:10.1016/j.physrep.2018.11.004
Martyushev, Semen G., and Sheremet, Mikhail A. (2012). Characteristics of Rosseland and P-1 approximations in modeling nonstationary conditions of convection-radiation heat transfer in an enclosure with a local energy source. J. Eng. Thermophys. 21 (2), 111–118. doi:10.1134/s1810232812020026
Mohebbi, Rasul, Mehryan, S. A. M., Izadi, Mohsen, and Mahian, Omid (2019). Natural convection of hybrid nanofluids inside a partitioned porous cavity for application in solar power plants. J. Therm. Analysis Calorim. 137, 1719–1733. doi:10.1007/s10973-019-08019-9
Rashad, A. M., Chamkha, Ali J., Ismael, Muneer A., and Taha, Salah. (2018). Magnetohydrodynamics natural convection in a triangular cavity filled with a Cu-Al2O3/water hybrid nanofluid with localized heating from below and internal heat generation. J. Heat Transf. 140, 7. doi:10.1115/1.4039213, no.
Rasool, Ghulam, Ahammad, N. Ameer, Ali, Mohamed R., Shah, Nehad Ali, Wang, Xinhua, Shafiq, Anum, et al. (2023). Hydrothermal and mass aspects of MHD non-Darcian convective flows of radiating thixotropic nanofluids nearby a horizontal stretchable surface: Passive control strategy. Case Stud. Therm. Eng. 42 (2023), 102654. doi:10.1016/j.csite.2022.102654
Rasool, Ghulam, Shafiq, Anum, Hussain, Sajjad, Zaydan, Mostafa, Wakif, Abderrahim, Ali, J., et al. (2022). Significance of rosseland’s radiative process on reactive Maxwell nanofluid flows over an isothermally heated stretching sheet in the presence of Darcy–forchheimer and Lorentz forces: Towards a new perspective on buongiorno’s model. Micromachines 133, 368. doi:10.3390/mi13030368, no.
Rasool, G., Ali Shah, N., El-Zahar, E. R., and Wakif, A. (2022). Numerical investigation of EMHD nanofluid flows over a convectively heated riga pattern positioned horizontally in a Darcy-Forchheimer porous medium: Application of passive control strategy and generalized transfer laws. Waves Random Complex Media 17, 1–20.
Raza, A., Almusawa, M. Y., Ali, Q., Haq, A. U., Al-Khaled, K., and Sarris, I. E. (2022). Solution of water and sodium alginate-based casson type hybrid nanofluid with slip and sinusoidal heat conditions: A prabhakar fractional derivative approach. Symmetry 1412, 2658. doi:10.3390/sym14122658, no.
Reddy, S. C., Asogwa, K. K., Yassen, M. F., Adnan, , Iqbal, Z., M-Eldin, S., et al. (2022). Dynamics of MHD second-grade nanofluid flow with activation energy across a curved stretching surface. Front. ENERGY Res. 10. doi:10.3389/fenrg.2022.1007159
Shahsavar, Amin, Moradi, Mehdi, and Bahiraei, Mehdi (2018). Heat transfer and entropy generation optimization for flow of a non-Newtonian hybrid nanofluid containing coated CNT/Fe3O4 nanoparticles in a concentric annulus. J. Taiwan Inst. Chem. Eng. 84, 28–40. doi:10.1016/j.jtice.2017.12.029
Shankar Goud, B., Dharmendar Reddy, Y., and Kenneth Asogwa, Kanayo (2022). Chemical reaction, Soret and Dufour impacts on magnetohydrodynamic heat transfer Casson fluid over an exponentially permeable stretching surface with slip effects. Int. J. Mod. Phys. B, 2350124. doi:10.1142/s0217979223501242
Stehfest, Harald. (1970). Algorithm 368: Numerical inversion of Laplace transforms [D5]. Commun. ACM 13 (1), 47–49. doi:10.1145/361953.361969
Tzou, Da Yu (2014). Macro-to microscale heat transfer: The lagging behavior.Hoboken, NJ, USA John Wiley & Sons.
Usman, M., Hamid, M., Zubair, T., Ul Haq, Rizwan, and Wang, Wei. (2018). Cu-AlO/Water hybrid nanofluid through a permeable surface in the presence of nonlinear radiation and variable thermal conductivity via LSM. Int. J. Heat Mass Transf. 126, 1347–1356. doi:10.1016/j.ijheatmasstransfer.2018.06.005
Vallejo, Javier P., Zyla, G., Fernandez-Seara, J., and Lugo, L. (2019). Influence of six carbon-based nanomaterials on the rheological properties of nanofluids. Nanomaterials 9 (2), 146. doi:10.3390/nano9020146
Vallejo, J. P., Álvarez-Regueiro, E., Cabaleiro, D., Fernández-Seara, J., Fernández, J., and Lugo, L. (2019). Functionalized graphene nanoplatelet nanofluids based on a commercial industrial antifreeze for the thermal performance enhancement of wind turbines. Appl. Therm. Eng. 152, 113–125. doi:10.1016/j.applthermaleng.2019.02.046
Waini, Iskandar, Ishak, Anuar, and Pop, Ioan (2019). Unsteady flow and heat transfer past a stretching/shrinking sheet in a hybrid nanofluid. Int. J. heat mass Transf. 136, 288–297. doi:10.1016/j.ijheatmasstransfer.2019.02.101
Wong, Kaufui V., and Omar De, Leon (2010). Applications of nanofluids: Current and future. Adv. Mech. Eng. 2, 519659. doi:10.1155/2010/519659
Keywords: fractionalized hybrid Oldroyd-B fluid, AB time-fractional derivative, Newtonian heating, Laplace transform method, hybrid nanofluid
Citation: Ali Q, Amir M, Raza A, Khan U, Eldin SM, Alotaibi AM, Elattar S and Abed AM (2023) Thermal investigation into the Oldroyd-B hybrid nanofluid with the slip and Newtonian heating effect: Atangana–Baleanu fractional simulation. Front. Mater. 10:1114665. doi: 10.3389/fmats.2023.1114665
Received: 02 December 2022; Accepted: 07 February 2023;
Published: 24 February 2023.
Edited by:
Noor Saeed Khan, University of Education Lahore, PakistanReviewed by:
Ghulam Rasool, Beijing University of Technology, ChinaCopyright © 2023 Ali, Amir, Raza, Khan, Eldin, Alotaibi, Elattar and Abed. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Sayed M. Eldin, c2F5ZWQuZWxkaW4yMkBmdWUuZWR1LmVn
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.