Mixed convective eyring-powell ferro magnetic nanofluid flow suspension towards a stretching surface with buoyancy effects through numerical analysis

This article examines the impact of buoyancy on the magnetic Eyring-Powell nanofluid flow toward a stretching surface. Coupled similarity equations are created from the governing flow equations. For the particular instance of pure fluid flow, the numerically computed self-similar results are matched with the available literature and found to be in acceptable harmony. The shooting approach was used to arrive at numerical computations to the constitutive ordinary differential equations. The impacts of different fluid flow parameters, nano concentration parameters and heat transfer, are shown graphically for both aiding and opposing flows. It has been discovered that for both aiding and opposing problems, the skin friction is less affected by the buoyant force brought on by temperature differences. Under buoyancy, the rate of heat transfer increments for aiding flow problem while it declines for opposing flow.

1 Introduction

Water, oil, and other common fluids have relatively low thermal conductivities. As a result, heat transport analysis via these common fluids has been difficult for many years. The concept of raising the solid volume percentage in a fluid-solid mixture to increase thermal conductivity was initially proposed by Maxwell (Maxwell, 1873). These combinations contained particles of dimensions of millimeters and micrometers. Even though these fluids have improved thermal performance, they are nevertheless prone to a number of difficulties such abrasion, clogging, and pressure loss. According to Choi (Choi et al., 1995), a nanofluid is a type of fluid that has a tiny concentration of nanoparticles (about 100 nm) dispersed in the base fluid. Such nanoparticles’ thermal performance is dramatically altered by dispersion in common fluids. The study of magneto-hydrodynamic flow is crucial since it is used in various technical phenomena, such as the production of electrical energy and geo-physics. The MHD impact on a free convection heat transport was modeled by Sparrow et al. (Sparrow and Cess, 1961). They discovered that the presence of a magnetic field has a major impact on free convection. In a stretched surface with fixed given velocity and temperature, Chen and Strobel (Chen and Strobel, 1980) investigated the buoyancy effect in a laminar boundary layer. The magnetic field impact flow model of a Newtonian fluid for stretching wall due to unvarying temperature was taken into consideration by Chakrabarti and Gupta (Chakrabarti and Gupta, 1979). The unsteady flow case of a non-Newtonian fluid above a revolving disc was investigated by Attia (Attia, 2014). View more recent literature by visiting Refs. (Xu et al., 2007; Buongiorno, 2010; Vajravelu et al., 2011; Ibrahim and Shanker, 2012; Aly and Vajravelu, 2014; Akbar et al., 2015; Khan et al., 2021; Khan et al., 2022; Waini et al., 2022).

When performing a heat transfer analysis on a steady MHD boundary layer extent, Mukhopadhyay (Mukhopadhyay, 2013) noticed that the expanse of the skin friction parameter rises in the extant of a magnetic impact, which results in a decrease in velocity. Stretching surfaces have recently come under the attention of many researchers due to their widespread use in engineering processes. Nadeem et al. (Nadeem et al., 2014) used numerical evaluation to interpret the MHD boundary layer extent of a nanoparticle-saturated Maxwell non-Newtonian fluid past a stretched surface. The heat transfer with radiation impacts, chemical reactions of nth order and viscous effects, Makinde (Makinde, 2011) looked into the modeling of heat and mass flux for a non-Newtonian Boussinesq fluid over a vertically held porous sheet. Ibrahim and Makinde (Ibrahim and Makinde, 2013) had investigated the issue of boundary layer extent and heat transmission caused by a nano-fluids across a vertical surface with double stratification. When analyzing the transport equations, Brownian movement, thermo-phoresis, solutal layer and thermal layer characteristics were all taken into account. Akbar et al. (Akbar et al., 2014) had used a homogeneous model to discuss the stagnation-point flow problem for carbon nanotubes flow over a stretching surface using base flow as water with slip and convective constraints. The constitutive boundary layer modeling of nanofluid is streamlined via similarity transformations. Through Refs. (Ebaid et al., 2013; Ellahi et al., 2015; Ibrahim and Makinde, 2015; Sheikholeslami et al., 2015; Anuar et al., 2020; Turkyilmazoglu, 2020; Wahid et al., 2020; Rostami et al., 2021; Turkyilmazoglu, 2021), more recent research material can be reviewed.

The influence of buoyancy on the MHD flow problem of Eyring Prandtl nanofluid toward a stretching wall has been investigated in this work. Coupled similarity equations are created from the governing flow equations. For the particular instance of pure fluid flow, the numerically evaluated self-similar results are matched with the accessible literature and established to be in good harmony. The impacts of different fluid flow, heat flux, and nano particles concentration parameters are shown graphically for each aiding and adhesive flows. It has been discovered that for each aiding and opposite flow problems, the skin friction is less affected by the buoyant force brought on by temperature differences. Under buoyancy, the rate of heat flux rises for aiding flow and decreases for opposite flow. The results from the base fluid’s limiting case comparison are in good accord with those from the literature. Although the aforementioned studies point to the fact that the Eyring–Powell model has been extensively studied in different flow configurations with the consideration of a number of different geometries. The prime motivation here is to discuss the non-Newtonian Eyring–Powell fluid model with buoyancy and nanofluid effects. Therefore, the objective is to solve the momentum, thermal and concentration equations and attempt to find numerical solutions representing the flow, temperature and concentration fields. The rheology of the Eyring–Powell fluid as associated to the Newtonian fluid is mined from the exact average velocity expression.

2 Mathematical model

According to (Akbar et al., 2015), the constitutive modelling for the Eyring-Powell fluid non-Newtonian model is provided as.

$\overline{S}=\mu \mathit{\nabla }\overline{\mathit{V}}+\frac{1}{{\beta }_1}\mathit{sin}{h}^{-1}\left(\frac{1}{c}\mathit{\nabla }\overline{V}\right)(1)$

$\mathit{sin}{h}^{-1}\left(\frac{1}{\mathit{c}}\mathit{\nabla }\overline{\mathit{V}}\right)\approx \frac{1}{\mathit{c}}\mathit{\nabla }\overline{V}-\frac{1}{6}{\left(\frac{1}{c}\mathit{\nabla }\overline{V}\right)}^3,\left|\frac{1}{c}\mathit{\nabla }\overline{V}\right|\approx 1.(2)$

3 Mathematical formulation

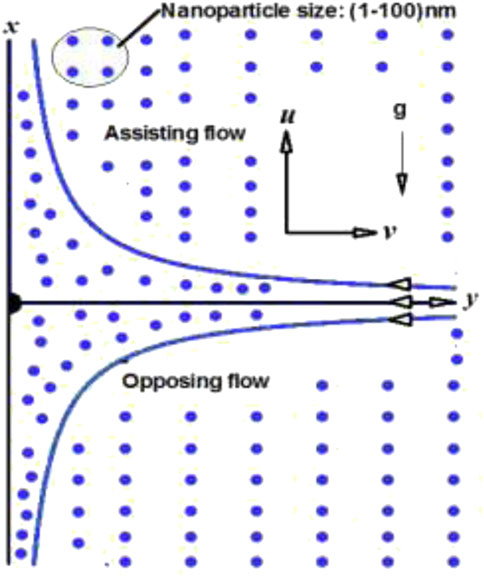
We talk about a constant, two-dimensional flow over a wall that coincides with the flow’s confinement plane of an incompressible, non-Newtonian, Eyring-Powell fluid. The linear stretching is what causes the flow (see Figure 1).

FIGURE 1

FIGURE 1. Geometry of the problem.

Following the application of boundary layer approximations, the constitutive equations for the Eyring-Powell nanofluid model with buoyancy effects can be defined as follows.

$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0,(3)$

$u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}=\left(\nu +\frac{1}{\rho {\beta }_{1}c}\right)\frac{{\partial }^{2}u}{\partial y^2}-\frac{1}{2\rho {\beta }_1{c}^3}{\left(\frac{\partial u}{\partial y}\right)}^2\left(\frac{{\partial }^{2}u}{\partial y^2}\right)-\frac{\sigma B^2}{\rho }u\pm \left(1-{\phi }_{\infty }\right)\frac{1}{\rho }{\rho }_{f\infty }\left[g{\beta }_T\left(T-T_{\infty }\right)+g\beta c\left(C-C_{\infty }\right)\right],(4)$

$\left(u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}\right)=\alpha \frac{{\partial }^{2}T}{\partial y^2}+\tau \left[D_B\frac{\partial T}{\partial y}\frac{\partial C}{\partial y}+\left(\frac{D_T}{T_{\infty }}\right){\left(\frac{\partial T}{\partial y}\right)}^2\right],(5)$

$\left(u\frac{\partial C}{\partial x}+v\frac{\partial C}{\partial y}\right)=D_B\frac{{\partial }^{2}C}{\partial y^2}+\left(\frac{D_T}{T_{\infty }}\right)\frac{{\partial }^{2}T}{\partial y^2},(6)$

The final term in Eq. 2’s right-hand side denotes the effect of the thermal buoyancy effect on the flow profile, having "+" and "-" notations denotes, respectively, the buoyancy-assist and the opposing flow areas.

By using cross-differentiation, we can take p out of Eqs 4, 5. For this issue, the similarity transformations can be expressed as

$u=ax{f}^{\prime }\left(\eta \right),v=-\sqrt{\left(a\nu \right)}f\left(\eta \right),\eta =\sqrt{\left(\frac{a}{\nu }\right)}y,\theta \left(\eta \right)=\frac{T-T_{\infty }}{T_w-T_{\infty }},\phi \left(\eta \right)=\frac{C-C_{\infty }}{C_w-C_{\infty }},(7)$

The following ordinary (similarity) differential equations are produced using the similarity transformation 7).

$\left(1+\gamma \right)f^{‴}-{\left(f^{\prime }\right)}^2+f{f}^{″}-\gamma \beta f^{″}{\left(f^{″}\right)}^2-M^2{f}^{\prime }\pm G_r\left(\theta +Nc\phi \right)=0,(8)$

$\frac{1}{P_r}{\theta }^{″}+f{\theta }^{\prime }+N_b{\varphi }^{\prime }{\theta }^{\prime }+N_t{\theta }^{\prime 2}=0,(9)$

${\phi }^{″}+L_{e}f{\phi }^{\prime }+\frac{N_t}{N_b}{\theta }^{″}=0,(10)$

depending on the boundary constraints

$\begin{array}{l}f\left(0\right)=0,f^{\prime }\left(0\right)=1,\theta \left(0\right)=1,\phi \left(0\right)=1\\ f^{\prime }\to 0,\theta \to 0,\phi \to 0,as\eta \to \infty \end{array},(11)$

primes indicate differentiation with relation to $\eta$

$\begin{array}{ll}\hfill M^2& =\frac{\sigma {B_0}^2}{\rho a},R_{ax}=\frac{u_w\left(x\right)x}{\nu },G_T=\frac{\left(1-{\phi }_{\infty }\right){\rho }_{f\infty }g{x}^3{\beta }_T\left(T_w-T_{\infty }\right)}{{\nu }^2},G_r=\frac{G_T}{{R_{ax}}^2},B_C=\frac{\left(1-{\phi }_{\infty }\right)\left({\rho }_{f\infty }\right)g{x}^3{\beta }_C\left(C_w-C_{\infty }\right)}{{\nu }^2},B_r=\frac{B_C}{{R_{ax}}^2},\hfill \\ \hfill & N_c=\frac{B_r}{G_r}=\frac{B_C}{G_T}=\frac{{\beta }_C\left(C_w-C_{\infty }\right)}{{\beta }_T\left(T_w-T_{\infty }\right)},\mathit{Pr}=\frac{\nu }{\alpha },N_b=\frac{\tau D_B\left({\phi }_w-{\phi }_{\infty }\right)}{\nu },L_e=\frac{\alpha }{D_s},\gamma =\frac{1}{\mu {\beta }_{1}c},N_t=\frac{\tau D_T\left(T_w-T_{\infty }\right)}{\nu T_{\infty }},\beta =\frac{{\left(ax\right)}^3}{2x\nu c^2},\hfill \\ \hfill & \alpha =\frac{k}{{\left(\rho c\right)}_p},\tau =\frac{{\left(\rho c\right)}_p}{{\left(\rho c\right)}_f}\hfill \end{array}(12)$

Expressions for the Sherwood Number, Nusselt Number, and the Skin friction are considered by:

$\begin{array}{ll}\hfill C_f& =\frac{{\tau }_w}{\rho {u_w}^2},Nu=\frac{x{q}_w}{\alpha \left(T_w-T_{\infty }\right)},Sh=\frac{x{q}_m}{\alpha \left(C_w-C_{\infty }\right)},{\tau }_w=\left(1+\frac{1}{{\beta }_{1}c}\right)\frac{\partial u}{\partial y}-\frac{1}{6{\beta }_1{c}^3}{\left(\frac{\partial u}{\partial y}\right)}^3,q_w=-\alpha \left(\frac{\partial T}{\partial y}\right),q_m=-\alpha \left(\frac{\partial C}{\partial y}\right),\hfill \\ \hfill & \sqrt{Re}{c}_f={\left[\left(1+\gamma \right)f^{″}-\frac{\beta \gamma }{3}{\left(f^{″}\right)}^3\right]}_{\eta =0},R{e}_x^{\frac{-1}{2}}N{u}_x=-{\theta }^{\prime }\left(0\right),R{e}_x^{\frac{-1}{2}}S{h}_x=-{\gamma }^{\prime }\left(0\right)\hfill \end{array}(13)$

4 Numerical method

The shooting approach was used to arrive at numerical computations to the constitutive Ordinary Differential Eqs 8–10 with the boundary constraints in Eq (11). The (BVP) Boundary value Problem was first converted into an initial value problem (IVP), and the far field boundary condition was given an appropriate finite value, such as, say i.e., $\eta \to \infty$, say ${\eta }_{\infty }$., the values for $f^{″}\left(0\right)$, ${\theta }^{\prime }\left(0\right)$ and ${\phi }^{\prime }\left(0\right)$ are required to solve the IVP, although they are not provided before the computation. The Fourth Order Runge-Kutta technique is used to find a numerical result using the initial guess values of $f^{″}\left(0\right)$, ${\theta }^{\prime }\left(0\right)$ and ${\phi }^{\prime }\left(0\right)$. We compared the estimated values of $f^{\prime }\left(\eta \right)$, $\theta \left(\eta \right)$ and ${\phi }^{\prime }\left(\eta \right)$ at the away from surface boundary condition ${\eta }_{\infty }\left(=20\right)$ with the given boundary conditions $f^{\prime }\left({\eta }_{\infty }\right),\theta \left({\eta }_{\infty }\right),\gamma \left({\eta }_{\infty }\right),\zeta \left({\eta }_{\infty }\right)\to 0$, respectively, and then corrected the values of $f^{″}\left(0\right)$, ${\theta }^{\prime }\left(0\right)$ and ${\phi }^{\prime }(0$ using the Secant technique for proper and good solution approach. The step-size is set at $\Delta \eta =0.01$, and the 5th decimal place accuracy serves as the convergence criteria.

5 Results and discussion

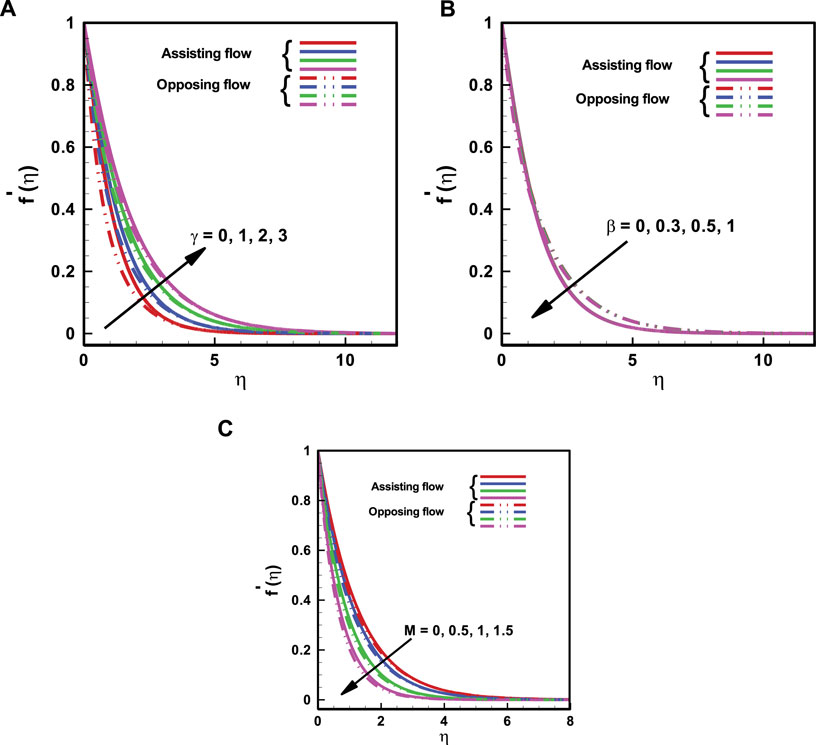
The Eyring-Powell nanofluid numerical solutions for stretching sheets are shown here with graphs that show the buoyancy effects. Figs $\left(2a\right)$ to $\left(2c\right)$ are generated to show how different fluid parameters affect the velocity profile. These graphs show how the buoyant force caused by the temperature differential $G_r$ and ɤ, β have an impact on the dimensionless velocity. The impact of ɤ, β on the velocity profile are shown in Fig. $2\left(a\right)$. With an uplift in ɤ, β, the velocity profile and boundary layer extent both rises. Figure 2B illustrates how the Eyring-Powell fluid parameter affects the velocity profile and the flow profile is reduced. But as the value of $\beta$ grows, the extent of the boundary layer increases. The influence of Hartmann number M on flow is shown in Figure 2C. Figures show that as Hartmann number M is raised, velocity profile declines but boundary layer thickness rises. Additionally, it has been found that the flow profile behaviour for the Eyring-Powell fluid parameters is the same for both helpful and opposing flows.

FIGURE 2

FIGURE 2. Plot of velocity profile for (A) $\gamma$, (B) $\beta$ and (C) $M$.

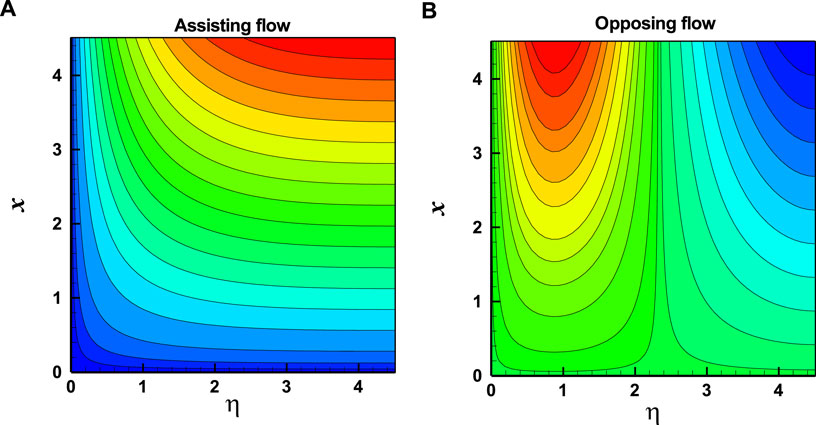
In Figures 3A–C, the influence of the flow parameters on the dimensionless heat flux is explored. Both helpful and opposing flows are covered by Figures 3A–C. The thermal boundary layer thickness is generally increased by Prandtl number, the ratio of buoyancy forces on the rescaled nano-particles volume fraction, and the thermophoresis parameter, whereas temperature profile increases with an increase in the ratio of buoyancy forces on the rescaled nanoparticle concentration and the thermophoresis parameter and decreases with an uplift in $P_r$. In each scenario, it is discovered that opposing flows have thicker thermal boundary layers.

FIGURE 3

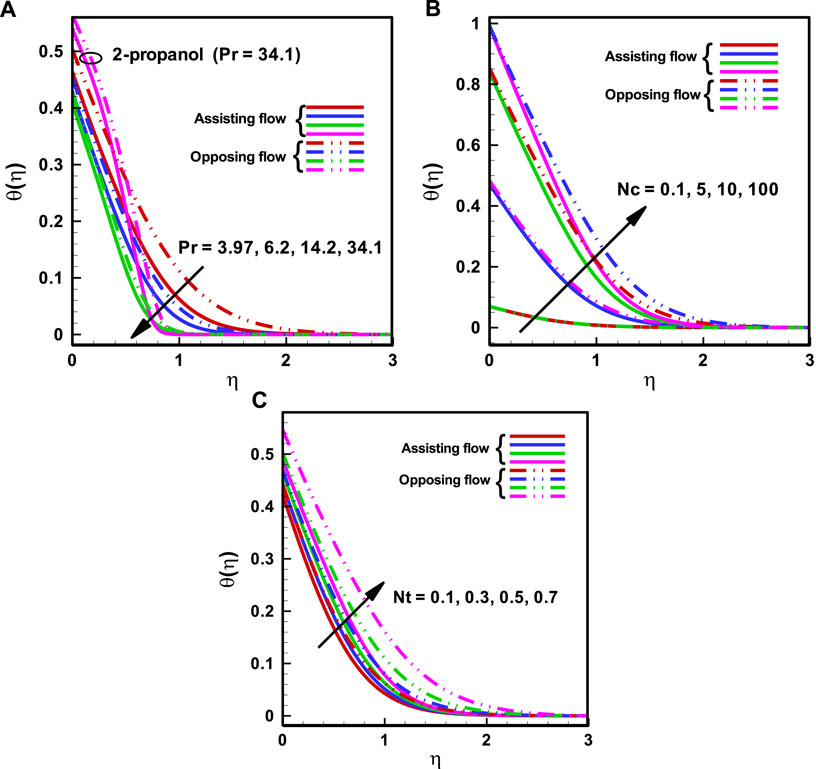
FIGURE 3. Variation of Temperature Profile for (A) $P_r$, (B) The ratio of buoyancy forces on the rescaled nanoparticle volume fraction $N_c$ (C) The thermophoresis parameter $N_t$.

Figures 4A, and Figure 5B) illustrate how the $N_c$ is affected by $N_b$; $N_t$; $P_r$, and the ratio of buoyancy influences. The $N_t$; $N_b$ parameter,; $P_r$ all reduce the rescaled nanoparticle volume percentage for each favourable and opposite flows, as illustrated in Figures 4A, 5B). However, the volume fraction of rescaled nanoparticles tends to grow when the buoyancy forces ratio increases see Figure 5B. In contrast to aiding flow, the fraction of nanoparticles is higher in opposing flow.

FIGURE 4

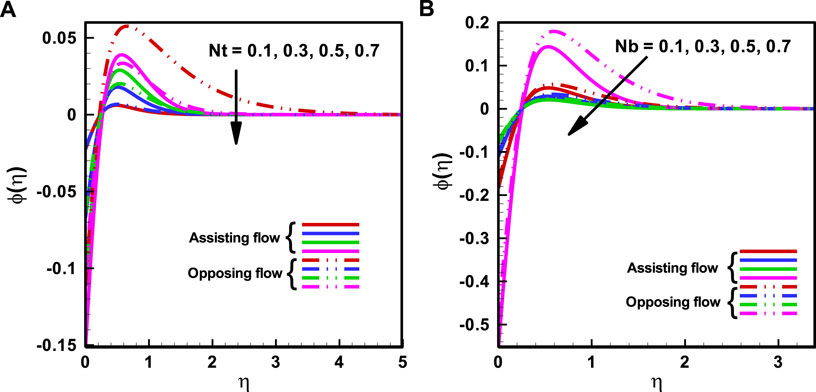
FIGURE 4. Variation of nanoparticles fraction profile (A). The Thermo-Phoresis Parameter $N_t$. (B) The Brownian Motion Parameter $N_b$.

FIGURE 5

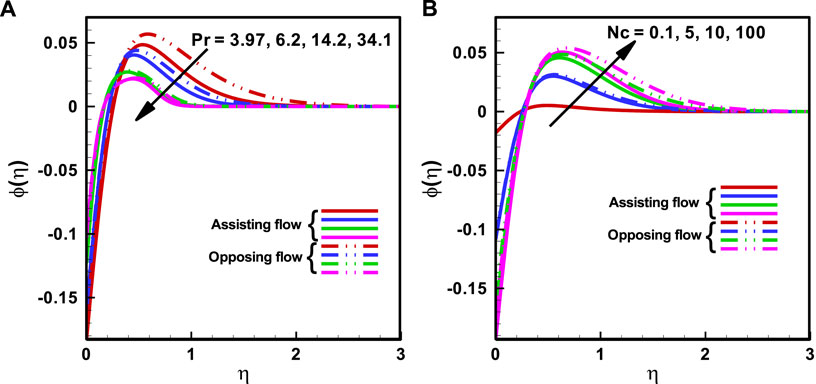
FIGURE 5. Variation of nanoparticles fraction profile for (A) Prandtl number Pr (B) The ratio of buoyancy forces on the rescaled nanoparticle volume fraction Nc.

As seen in the Figures 6A–C), the $N_u$ rises with the Hartmann number $M$ and the Eyring-Powell fluid parameters but falls with an increment in the latter. The $N_t$; $P_r$ both have an impact on the skin friction coefficient; Figures 7A, B illustrates how skin friction coefficient increases for aiding flow but diminishes for opposite flow when Prandtl number and thermophoresis parameter increase. The graph in Figure 7C demonstrates that the skin friction coefficient uplifts for opposing flow but lowers for assisting flow depending on the buoyancy forces on the rescaled nanoparticle volume fraction $N_c$. Additionally, it can be seen that for all flow parameters, the skin friction coefficient is larger in the case of opposing flow than aiding flow.

FIGURE 6

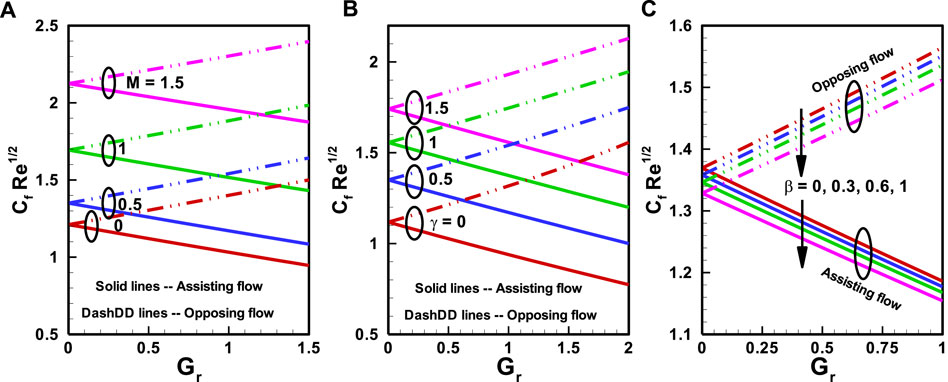
FIGURE 6. Variation of Coefficient for Skin friction (A) Hartmann number $M$, (B) Eyring-Powell fluid parameter $\gamma$ and (C) Eyring-Powell fluid parameter $\beta$.

FIGURE 7

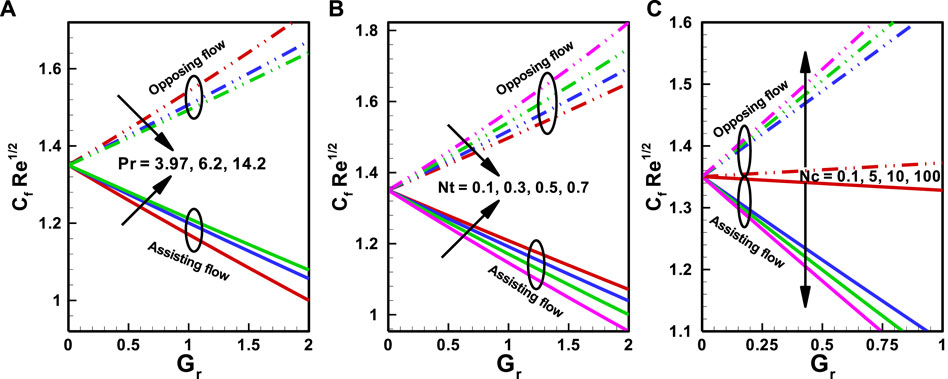
FIGURE 7. Variation of Coefficient for Skin friction (A) Prandtl number $P_r$, (B) The thermophoresis parameter $N_t$ (C) The ratio of buoyancy forces on the rescaled nanoparticle volume fraction $N_c$.

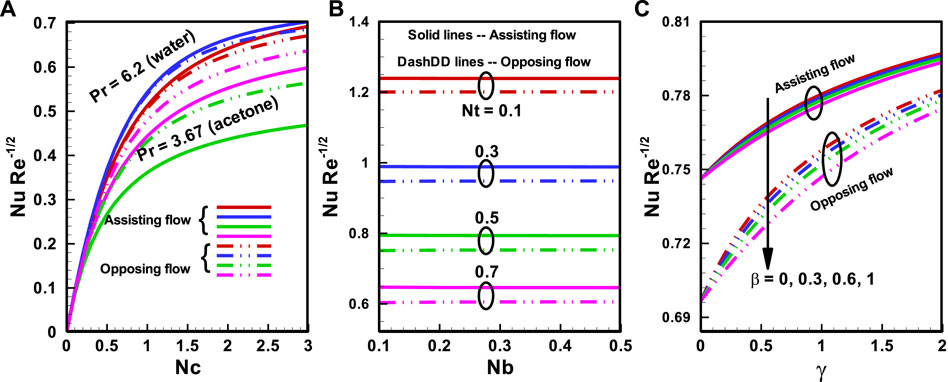
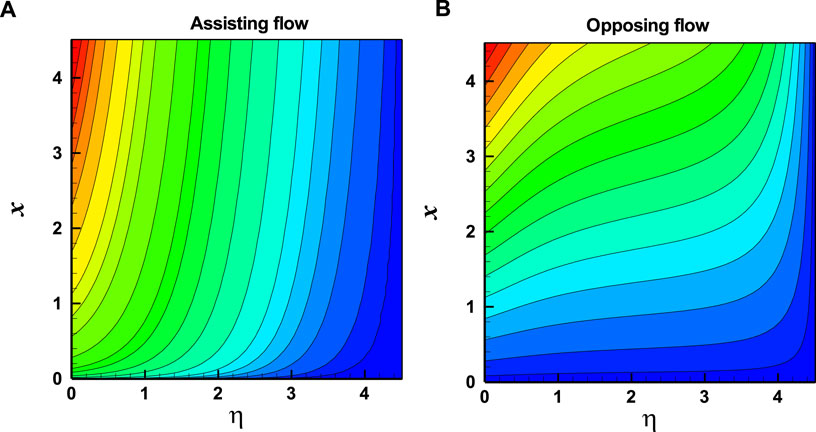
In Figures 8A, and Figure 9B), both for aiding and opposing flows, the influences of various factors on $N_u$ are shown. In every instance; $N_u$ for aiding flows is shown to have a high magnitude. The local Nusselt number for both assisting and opposing flows increases with an uplift in $P_r$, whereas a decrease in the thermophoresis parameter $N_t$ and the Eyring-Powell fluid parameter causes a decrease in the local Nusselt number for each favourable and opposite flows, as displayed in Figures 8A–C. The local $N_u$ is increased for assisting flow and decreased for opposing flow due to the buoyancy force caused by temperature differential $G_r$ and the ratio of buoyancy forces on the rescaled nanoparticle volume fraction $N_c$ (see Figures 9A, B).

FIGURE 8

FIGURE 8. Alteration of $Nu$ for (A) $P_r$ (B) $N_t$ (C) $\beta$.

FIGURE 9

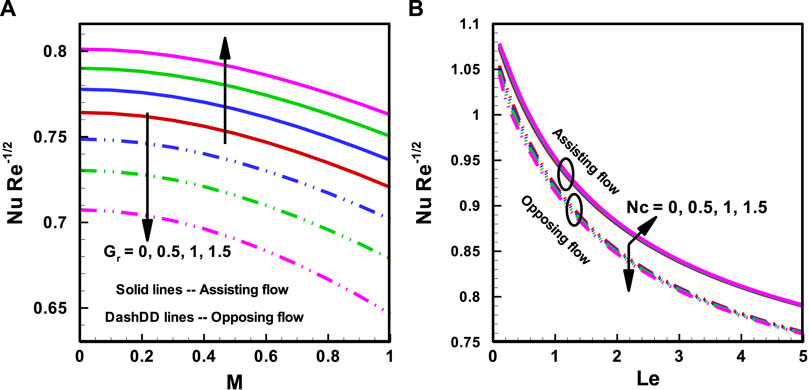
FIGURE 9. Nusselt number for (A) buoyancy influence via Temperature Difference $G$_r, (B) The ratio of Buoyancy forces on the rescaled concentration of nano-particles $N_c$.

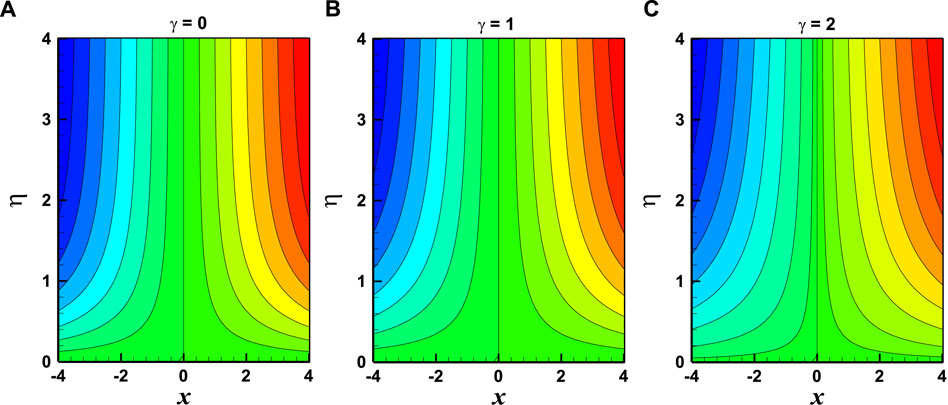
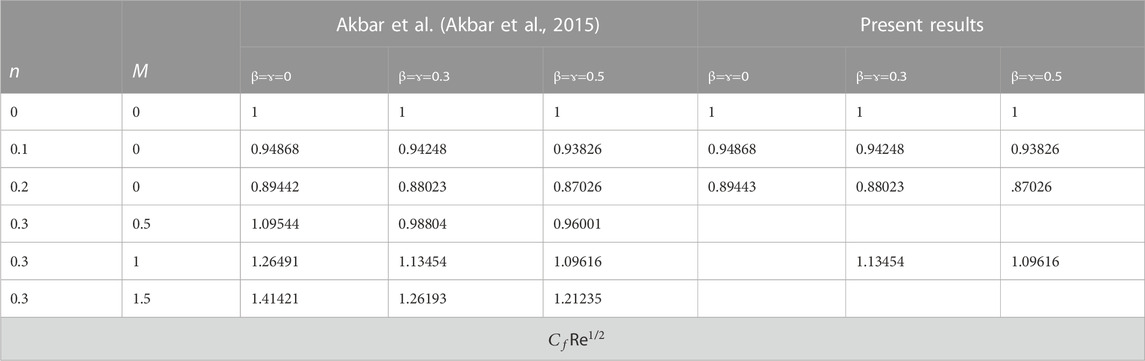
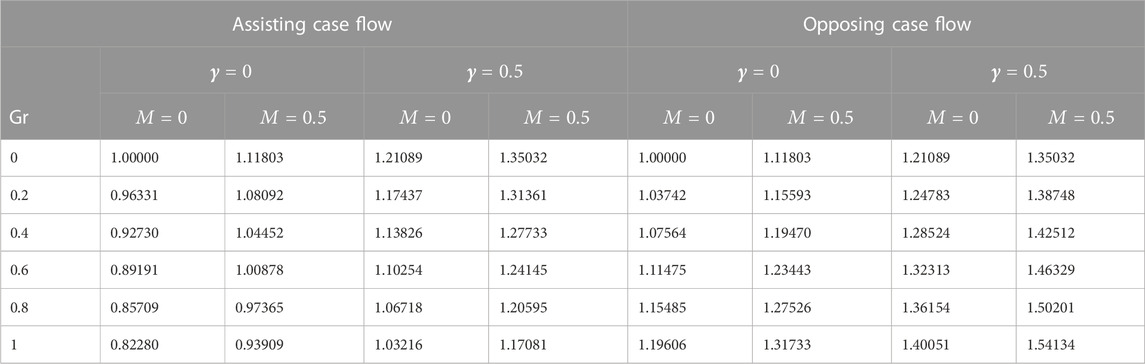
Streamlines and isotherms have been displayed in the Figure 10, and Figure 12) to aid in understanding the fluid flow behaviour. The streamlines will be close to the sheet’s axis when we increase the Eyring-Powell fluid parameter, as shown in Figure 10. In contrast to the aiding flow, opposing flow streams are being confined and moving toward the sheet’s axis. When compared to streamlines, isotherm outcomes are, however, the opposite. In contrast to the opposing flow, isotherms lines for aiding flows are contained and moving in the direction of the sheet’s axis, as seen in the Figure 11, and Figure 12. Table 1 compares the results of the current study to the body of prior research. The skin friction coefficient’s numerical values are provided in Table 2.

FIGURE 10

FIGURE 10. Variation of streamlines for $Nb=0.3,Nt=0.5,Le=1,\mathit{Pr}=3.97,\beta =0.3,Nc=0.5,Gr=0.5,M=0.5.$

FIGURE 11

FIGURE 11. Variation of streamlines for assisting and opposing flow with $Nb=0.3,Nt=0.5,Le=1,\mathit{Pr}=3.97,\beta =\gamma =0.3,Nc=0.5,Gr=0.5,M=0.5.$

FIGURE 12

FIGURE 12. Variation of Isotherms for assisting and opposing flow with $Nb=0.3,Nt=0.5,Le=1,\mathit{Pr}=3.97,\beta =\gamma =0.3,Nc=0.5,Gr=0.5,M=0.5.$

TABLE 1

TABLE 1. Comparison of coefficient of skin friction with [*] for $G_r=0$.

TABLE 2

TABLE 2. Coefficient of skin friction for helping and obstructing flow.

6 Conclusion

The influence of buoyancy forces on a magnetic Eyring-Powell nano-fluid flow over a vertical stretching wall is numerically analysed. The linear stretching case is considered for this incompressible non-Newtonian Eyring-Powell fluid flow problem. The major outcomes of this work are presented as follows.

• The extent of the boundary layer and the velocity profile each rise with an uplift in the Eyring-Powell fluid parameter. The boundary layer becomes thicker as the value of $\beta$ rises.

• The Eyring-Powell flow characteristics and velocity profile behavior is the same for both favorable and adverse flows.

• The $P_r$ often uplifts the thermal boundary layer extent. When the buoyancy pressures on the rescaled nanoparticle concentration and the thermophoresis parameter are increased, the heat flux profile rises, whereas when the $P_r$ is raised, the profile falls. We find that the thermal boundary layers of opposing flows are thicker in each case.

• It is clear that for all flow values, opposing flow has a higher skin friction coefficient than helping flow.

• When we increase the Eyring-Powell fluid parameter, the streamlines will be near to the axis of the sheet. Opposing flow streams are constrained and travelling in the direction of the sheet’s axis in contrast to the assisting flow. However, the results of isotherms are the opposite of streamlines. Isotherms lines for assisting flows are contained and travelling in the direction of the sheet’s axis, in contrast to the opposing flow.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

FD model the problem NS Done the writeup of the manuscript and done solution methodology SS Write introduction and prepared graphs All three authors done the proof reading.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Akbar, N. S., Ebaid, A., and Khan, Z. H. (2015). Numerical analysis of magnetic field effects on Eyring-Powell fluid flow towards a stretching sheet. J. Magnetism Magnetic Mater. 382, 355–358. doi:10.1016/j.jmmm.2015.01.088

CrossRef Full Text | Google Scholar

Akbar, N. S., Nadeem, S., and Hayat Khan, Z. (2014). The combined effects of slip and convective boundary conditions on stagnation-point flow of CNT suspended nanofluid over a stretching sheet. J. Mol. Liq. 196, 21–25. doi:10.1016/j.molliq.2014.03.006

CrossRef Full Text | Google Scholar

Aly, E. H., and Vajravelu, K. (2014). Exact and numerical solutions of MHD nano boundary-layer flows over stretching surfaces in a porous medium. Appl. Math. Comput. 232, 191–204. doi:10.1016/j.amc.2013.12.147

CrossRef Full Text | Google Scholar

Anuar, N. S., Bachok, N., Turkyilmazoglu, M., MdArifina, N., and Rosali, H. (2020). Analytical and stability analysis of MHD flow past a nonlinearly deforming vertical surface in Carbon Nanotubes. Alexandria Eng. J. 59, 497–507. doi:10.1016/j.aej.2020.01.024

CrossRef Full Text | Google Scholar

Attia, H. A. (2014). Unsteady flow of a non-Newtonian fluid above a rotating disk with heat transfer. Int. J. Heat Mass Transf. 46 (14), 2695–2700. doi:10.1016/s0017-9310(03)00029-2

CrossRef Full Text | Google Scholar

Buongiorno, J. (2010). Convective transport in nanofluids. J. Heat Transf. Am. Soc. Mech. Eng. 128 (3), 240–250. doi:10.1115/1.2150834

CrossRef Full Text | Google Scholar

Chakrabarti, A., and Gupta, A. S. (1979). Hydromagnetic flow and heat transfer over a stretching sheet. Quart. Appl. Math. 37, 73–78. doi:10.1090/qam/99636

CrossRef Full Text | Google Scholar

Chen, T. S., and Strobel, F. A. (1980). Buoyancy effects in boundary layer adjacent to a continuous, moving horizontal flat plate. Trans. ASME J. Heat. Transf. 102, 170–172. doi:10.1115/1.3244232

CrossRef Full Text | Google Scholar

Choi, S. U. S. (1995). “Enhancing thermal conductivity of fluids with nanoparticles,” in Developments and applications of non-Newtonian flows. Editors D. A. Siginer, and H. P. Wang (New York: ASME), 66, 99–105.

Google Scholar

Ebaid, A., El-arabawy, H. A., and Nader, Y. (2013). New exact solutions for boundary-layer flow of a nanofluid past a stretching sheet. Int. J. Diff. Eq. 10 (11), 2591–2594. doi:10.1166/jctn.2013.3253

CrossRef Full Text | Google Scholar

Ellahi, R., Hassan, M., and Zeeshan, A. (2015). Shape effects of nanosize particles in Cu–H2O nanofluid on entropy generation. Int. J. Heat Mass Transf. 81, 449–456. doi:10.1016/j.ijheatmasstransfer.2014.10.041

CrossRef Full Text | Google Scholar

Ibrahim, W., and Makinde, O. D. (2015). Double-diffusive in mixed convection and MHD stagnation point flow of nanofluid over a stretching sheet. J. Nanofluids 4, 28–37. doi:10.1166/jon.2015.1129

CrossRef Full Text | Google Scholar

Ibrahim, W., and Makinde, O. D. (2013). The effect of double stratification on boundary-layer flow and heat transfer of nanofluid over a vertical plate. Comput. Fluids 86, 433–441. doi:10.1016/j.compfluid.2013.07.029

CrossRef Full Text | Google Scholar

Ibrahim, W., and Shanker, B. (2012). Unsteady MHD boundary-layer flow and heat transfer due to stretching sheet in the presence of heat source or sink. Comput. Fluids 70, 21–28. doi:10.1016/j.compfluid.2012.08.019

CrossRef Full Text | Google Scholar

Khan, U., Zaib, A., Ishak, A., Bakar, S. A., Animasaun, I. L., Yook, S. J., et al. (2022). Insights into the dynamics of blood conveying gold nanoparticles on a curved surface when suction, thermal radiation, and Lorentz force are significant: The case of Non-Newtonian Williamson fluid. case Newt. Williamson fluid Math. Comput. Simul. 193, 250–268. doi:10.1016/j.matcom.2021.10.014

CrossRef Full Text | Google Scholar

Khan, U., Ishak, A., and Zaib, A. (2021). Simulation of MHD CuO–water nanofluid flow and convective heat transfer considering Lorentz forces. Chin. J. Phys. 74, 350–364.

Google Scholar

Makinde, O. D. (2011). Mhd mixed-convection interaction with thermal radiation and nth order chemical reaction past A vertical porous plate embedded in A porous medium. Chem. Eng. Commun. 198 (4), 590–608. doi:10.1080/00986445.2010.500151

CrossRef Full Text | Google Scholar

Maxwell, J. C. (1873). Electricity and magnatism. Oxford: Clarendon Press.

Google Scholar

Mukhopadhyay, S. (2013). MHD boundary layer flow and heat transfer over an exponentially stretching sheet embedded in a thermally stratified medium. Alexandiria Eng. J. 52, 259–265. doi:10.1016/j.aej.2013.02.003

CrossRef Full Text | Google Scholar

Nadeem, S., Ul Haq, R., and Khan, Z. H. (2014). Numerical study of MHD boundary layer flow of a Maxwell fluid past a stretching sheet in the presence of nanoparticles. J. Taiwan Inst. Chem. Eng. 45 (1), 121–126. doi:10.1016/j.jtice.2013.04.006

CrossRef Full Text | Google Scholar

Rostami, S., Ellahi, R., Oztop, H. F., and Goldanlou, A. S. (2021). A study on the effect of magnetic field and the sinusoidal boundary condition on free convective heat transfer of non-Newtonian power-law fluid in a square enclosure with two constant-temperature obstacles using lattice Boltzmann method. J. Therm. Analysis Calorim. 144 (6), 2557–2573. doi:10.1007/s10973-020-10202-2

CrossRef Full Text | Google Scholar

Sheikholeslami, M., Ganji, D. D., Younus Javed, M., and Ellahi, R. (2015). Effect of thermal radiation on magnetohydrodynamics nanofluid flow and heat transfer by means of two phase model. J. Magnetism Magnetic Mater. 374, 36–43. doi:10.1016/j.jmmm.2014.08.021

CrossRef Full Text | Google Scholar

Sparrow, E. M., and Cess, R. D. (1961). The effect of a magnetic field on free convection heat transfer. Int. J. Heat. Mass Tran. 3 (4), 267–274. doi:10.1016/0017-9310(61)90042-4

CrossRef Full Text | Google Scholar

Turkyilmazoglu, M. (2020). Eyring-Powell fluid flow through a circular pipe and heat transfer: Full solutions. Int. J. Numer. Methods Heat Fluid Flow 30, 4765–4774. doi:10.1108/hff-12-2019-0925

CrossRef Full Text | Google Scholar

Turkyilmazoglu, M. (2021). Stagnation-point flow and heat transfer over stretchable plates and cylinders with an oncoming flow: Exact solutions. Chem. Eng. Sci. 238, 116596. doi:10.1016/j.ces.2021.116596

CrossRef Full Text | Google Scholar

Vajravelu, K., Prasad, K. V., Lee, J., Lee, C., Pop, I., and Gorder, R. A. V. (2011). Convective heat transfer in the flow of viscous Ag-water and Cu-water nanofluids over a stretching surface. Int. J. Therm. Sci. 50, 843–851. doi:10.1016/j.ijthermalsci.2011.01.008

CrossRef Full Text | Google Scholar

Wahid, N. S., Turkyilmazoglu, M., Hafidzuddin, M. E. H., Abd Rahmin, N. A., Wahid, N. S., Arifin, N. M., et al. (2020). MHD hybrid Cu-Al<sub>2</sub>O<sub>3</sub>/water nanofluid flow with thermal radiation and partial slip past a permeable stretching surface: Analytical solution. J. Nano Res. 64, 75–91. doi:10.4028/www.scientific.net/jnanor.64.75

CrossRef Full Text | Google Scholar

Waini, I., Khan, U., Zaib, A., Ishak, A., and Pop, I. (2022). Inspection of TiO2-CoFe2O4 nanoparticles on MHD flow toward a shrinking cylinder with radiative heat transfer. J. Mol. Liq. 361, 119615. doi:10.1016/j.molliq.2022.119615

CrossRef Full Text | Google Scholar

Xu, H., Liao, S. J., and Pop, I. (2007). Series solutions of unsteady three-dimensional MHD flow and heat transfer in the boundary layer over an impulsively stretching plate. Eur. J. Mech. - B/Fluids 26, 15–27. doi:10.1016/j.euromechflu.2005.12.003

CrossRef Full Text | Google Scholar

Nomenclature

($\mathit{x},\mathit{y}$) coordinate axes

${\mathit{L}}_{\mathit{e}}$ lewis number

$\mathit{\gamma }$ $\beta$ eyring-powell fluid parameters

$\mathit{\alpha }$ thermal diffusivity

$\overline{\mathit{\tau }}$ extra stress tensor

$\mathit{\Gamma }$ time-dependent material constant

${\mathit{f}}^{\prime }$ dimensionless velocity

$\mathit{C}$ concentration

$\mathit{\rho }$ density of nanofluid

${\mathit{\beta }}_{\mathit{T}}$ thermal expansion coefficient

$\mathit{\tau }$ effective heat capacity of the nanoparticle ratio to heat capacity of the fluid

$\mathit{M}$ hartmann number

${\mathit{N}}_{\mathit{b}}$ brownian motion parameter

${\mathit{N}}_{\mathit{c}}$ the ratio of buoyancy forces

${\mathit{G}}_{\mathit{r}}$ buoyancy force owing to the temperature distribution

${\mathit{B}}_{\mathit{c}}$ solutal grashoff number

($\mathit{u},\mathit{v}$) velocity field

${\mathit{P}}_{\mathit{r}}$ prandtl number

$\mathit{C}$ concentration within the boundary layer

${\mathit{C}}_{\mathbf{\infty }}$ free stream concentration

${\mathit{\mu }}_{\mathbf{\infty }}$ infinite shear rate viscosity

${\mathit{\mu }}_0$ zero shear rate viscosity

$\mathit{T}$ fluid temperature within the boundary layer

${\mathit{T}}_{\mathbf{\infty }}$ free stream temperature

$\mathit{g}$ acceleration due to gravity

${\mathit{\beta }}_{\mathit{C}}$ coefficient of nanoparticle volumetric expansion

${\mathit{D}}_{\mathit{B}}$ brownian diffusion coefficient

${\mathit{D}}_{\mathit{T}}$ thermophoretic diffusion coefficient

${\mathit{N}}_{\mathit{t}}$ thermophoresis parameter

${\mathit{B}}_{\mathit{r}}$ ratio between the buoyancy force due to concentration difference

${\mathit{G}}_{\mathit{T}}$ thermal grashoff number

${\mathit{R}}_{\mathit{a}\mathit{x}}$ local reynolds number