Automated, high-accuracy classification of textured microstructures using a convolutional neural network

Crystallographic texture is an important descriptor of material properties but requires time-intensive electron backscatter diffraction (EBSD) for identifying grain orientations. While some metrics such as grain size or grain aspect ratio can distinguish textured microstructures from untextured microstructures after significant grain growth, such morphological differences are not always visually observable. This paper explores the use of deep learning to classify experimentally measured textured microstructures without knowledge of crystallographic orientation. A deep convolutional neural network is used to extract high-order morphological features from binary images to distinguish textured microstructures from untextured microstructures. The convolutional neural network results are compared with a statistical Kolmogorov–Smirnov tests with traditional morphological metrics for describing microstructures. Results show that the convolutional neural network achieves a significantly improved classification accuracy, particularly at early stages of grain growth, highlighting the capability of deep learning to identify the subtle morphological patterns resulting from texture. The results demonstrate the potential of a convolutional neural network as a tool for reliable and automated microstructure classification with minimal preprocessing.

1 Introduction

Major advances inmaterials informatics, from the introduction of integrated computational materials engineering Allison et al. (2006) to the high-throughput Materials Project database Jain et al. (2013), have provided a new way for materials scientists to explore structure/properties/processing relationships. In particular, these advances have motivated the development of advanced materials characterization tools Park et al. (2017) and facilitated multiscale modelling efforts aimed at advanced materials design Weber et al. (2020); Weber et al. (2022) and failure prediction Talebi et al. (2014). At the forefront of this field is the pressing need for automated frameworks that can quickly and accurately process material information to advance the materials discovery process. While great advances have been made in high-throughput analysis of material properties and processing conditions Wei et al. (2019); Ma et al. (2020); Wang and Adachi (2019), an outstanding challenge in this field is advanced quantitative microstructure characterization. Conventional methods in the field of materials development require manual input (e.g., grain size measurement by the lineal intercept method ASTM (1996)); as such, they are subject to run-to-run variability and are insufficient for reliable and repeatable microstructural analysis. This conventional method was improved by the implementation of particle segmentation via image analysis Igathinathane et al. (2008), however this technique is highly susceptible to variation in data quality and even grain shape Arasan et al. (2011). Recently, there have been exciting advances in automated microstructure characterization employing computer vision (CV) methods to classify based on visual features within a micrograph DeCost and Holm (2015); Ling et al. (2017); DeCost et al. (2017); Kitahara and Holm (2018). However, with the advancement of modern material characterization tools, it is becoming increasingly clear that macroscale material properties are functions of the non-trivial spatial arrangement of various microstructural metrics collected at varying length scales Kalindindi and DeGraef (2015), beyond visual features that can be distinguished qualitatively. This motivates the need to extract high-order metrics of a material’s hierarchical microstructure.

One such abstract metric is the degree of crystallographic texture, which refers to preferential grain orientation within a microstructure. Significant crystallographic texture in the microstructure of a material can greatly alter its bulk properties and behavior. Some examples include anisotropic fracture toughness and other mechanical properties Zhang et al. (2019); Messing et al. (2017), improved current density in textured superconductors Maeda et al. (2004), heightened magnetic anisotropy in magnetic materials Maeda et al. (2003), and superior electromechanical coupling coefficients in piezoelectrics Yilmaz et al. (2003); Ahn et al. (2009). In an effort to control and exploit these properties, scientists have long been investigating methods of inducing texture during materials, including cold rolling and extrusion Chao et al. (2011), templated grain growth Seabaugh et al. (1997); Seabaugh et al. (2004), and the application of an external field (electrical, magnetic) during powder processing Sugiyama et al. (2003); Maeda et al. (2003); Molodov and Sheikh-Ali (2004). While there is great interest in the fabrication and functional properties of textured materials, it remains a challenge to quantifiably characterize texture with a single metric. For the last 20 years, electron backscatter diffraction (EBSD) has been used for quantitative texture classification and characterization. Although advances in indexing and camera hardware have improved its efficiency and capability of collecting large datasets Winiarski et al. (2021), this technique remains both labor- and time-intensive because it necessitates extensive sample preparation, point by point data collection, and data post-processing. In the present work, we pose an alternative to this classical method of texture classification: machine learning of abstract, high-order microstructural descriptors to identify texture based only on images of the grains. In particular, we believe there to be a correlation between texture and grain boundary network structure, an abstract metric which is currently non-trivial to quantify experimentally. In this work, we will demonstrate the capability of a convolutional neural network (CNN) to learn this metric and classify textured microstructures that are otherwise unable to be classified by conventional morphological metrics.

Machine learning (ML) methods use simulated and/or experimental data to learn relationships that may be indeterminate via traditional analysis methods, and for scientific discovery tasks where fundamental understanding of the underlying physical process still remains elusive Mjolsness and DeCoste (2001). In recent literature, ML methods have been used for microstructure quantification tasks which are challenging to accomplish with traditional data processing methods, including microstructure classification Gola et al. (2019), identifying morphological features of interest such as dendrites Chowdhury et al. (2016), and abnormal grain growth prediction from simulated data Cohn and Holm (2021), among others. Many ML methods use a training dataset to learn a non-linear mapping between inputs and outputs. The mapping is learned through an optimization process. Most ML tasks are either classification (discrete output labels such as category of animals) or regression (continuous output labels such as stock prices) tasks.

In prior work, statistical/machine learning microstructure classification has consisted of two parts: feature extraction from raw data followed by a classification methodology. This feature extraction is typically conducted by experts in the field, and is thus limited by prior knowledge. Subsequently, ML methods such as support vector machine (SVM) Boser et al. (1992) or random forests (RF) Breiman (2001) have been used for microstructure classification. However, these methods still rely on a human expert for designing the classification methodology, and as such may be subject to biases and inaccuracies. Recently, deep learning (DL), which is a subset of ML, has been applied to microstructure analysis LeCun et al. (2015) to address these challenges. The common DL methods, such as deep neural networks (DNN), take in raw data directly without the need for any feature extraction as opposed to other ML methods. DL methods extract non-linear representations between the raw data and the ground truth (output) through multiple non-linear transformations stacked sequentially, learning spatiotemporal trends and relationships that may be otherwise indecipherable.

The present work investigates the potential of DL techniques for advanced microstructure characterization by classifying crystallographically textured and untextured microstructures from binary micrographs (i.e., no orientation information) with a CNN. The CNN technique is used to classify micrographs collected from alumina-monoliths with and without crystallographic texture at different stages of grain growth. It was previously proposed that microstructure evolution of textured alumina diverges from untextured alumina because of its unique hierarchical grain boundary network structure. Here, we demonstrate that the microstructures of the untextured and textured materials can be easily classified with reasonable accuracy (≥80%) by grain morphological features like grain area and aspect ratio after long heat treatment exposures. However, these grain features cannot be used to accurately classify the microstructures at early stages of grain growth. In contrast, we demonstrate that CNN can accurately classify the microstructures at all stages of grain growth (≥90%). The significance of these results is twofold: 1) they indicate an experimentally indeterminate difference in the grain boundary network structure of a textured material, and 2) they demonstrate the potential of deep learning methods for advanced microstructural characterization by recognition of non-trivial, spatiotemporal metrics.

2 Materials and methods

The workflow of this investigation consists of textured and untextured material fabrication, processing, and microstructure characterization, followed by the classification of textured and untextured microstructures via the CNN and, for comparison, Kolmogorov-Smirnov goodness-of-fit tests using conventional microstructure metrics. The details of these steps are described in detail in the subsequent subsections.

2.1 Material fabrication and characterization

Calcia-doped alumina (Al₂O₃) is employed as a model material for this investigation, as it is known to exhibit unique microstructural properties Rodel and Glaeser (1989); Akiva et al. (2014); Conry et al. (2022). To induce crystallographic texture in our microstructures, we use a magnetic slip-casting technique to induce significant crystallographic texture in the as-cast green body Suzuki et al. (2006). Details of this technique and the experimental procedure are described in a previous work Conry et al. (2022). Briefly, two pellets of 300 ppm calcia-doped alumina were prepared by slip casting in and outside a 9 T magnetic field, respectively. Both pellets (19 mm diameter, 5 mm thickness) were sintered in air for 1 h at 1,600°C. The pellets were sectioned into smaller specimens and then heated isothermally for 8 h, 16 h, 32 h, and 64 h. To ensure a smooth surface for analysis, the specimens underwent metallographic polishing from an initial 320 grit grinding paper down to a 0.25 μm vibratory final polish.

Data used for training and testing of the CNN were collected via EBSD (EDAX, Mahwah, NJ, United States) in a Tescan MIRA3 scanning electron microscope (SEM) at each of the aforementioned heat treatment durations. Previous EBSD measurements found that all samples that were slip cast in the magnetic field had a texture index of two or greater, while the samples slip cast outside the magnetic field comprise grains of random orientations (texture index of 1) regardless of the heat treatment duration. Therefore, the microstructures are labeled as “textured” for those slip cast in the magnetic field and “untextured” for those prepared outside of the magnetic field. A minimum of 10 textured and untextured EBSD maps, comprising roughly 400 grains per map, were collected for each heat treatment duration (an exception is the textured microstructure at 16 h, for which only six maps were collected due to data collection limitations). The maps were collected from multiple locations spatially distributed across each polished sample surface. EBSD is a technique that allows pixel-by-pixel determination of crystal orientation of a specimen under an electron beam; neighboring pixels of similar orientation ($<$5° misorientation) are grouped together to define a grain (i.e., grain segmentation). Representative microstructures from each stage of grain growth are presented in Figure 1 for reference. It should be noted that specimens heated for extended durations underwent significant grain growth. As such, some EBSD data from longer heat treatments were collected at a lower magnification than that collected from samples exposed to shorter heat treatments to encompass a useful number of grains. This variation in magnification is significant in our analysis and is discussed in subsequent sections.

FIGURE 1

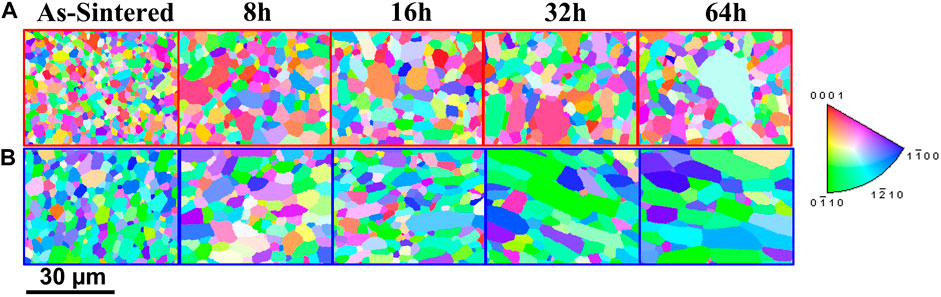
FIGURE 1. Representative EBSD micrographs for each heat treatment from the (A) untextured and (B) textured microstructures. Shown micrographs are scaled to the same magnification for ease of visual comparison.

Raw EBSD data processing was done using EDAX’s OIM analysis software, including noise clean-up and rough grain segmentation steps. Further post-processing was done using DREAM.3D Groeber and Jackson (2014) to convert the default EDAX file type (ANG) into hierarchical data format (HDF5) via a processing pipeline. Additionally, the hexagonal-grid EBSD data was converted to a square grid, during which step the pixel resolution was defined as 0.3 μm for each dataset to mitigate resolution variation that may influence the CNN. For comparative statistical analysis (discussed in a subsequent section), conventional microstructural descriptors were extracted from all datasets using MATLAB’s MTEX toolbox Bachmann et al. (2011).

2.2 Classification

For our task, the 2D image of the microstructure consists of a spatially arranged pattern of grain boundaries. A CNN is a DL architecture commonly used for image recognition tasks in many domains Krizhevsky et al. (2017), which assumes a spatial structure in the data O’Shea and Nash (2015). Since the spatial arrangement of advanced metrics has been posed as an important parameter in advanced microstructural characterization, the CNN is a good choice for texture identification and classification. Recently, CNN methods have been proposed for tasks such as microstructural classification Holm et al. (2020); Azimi et al. (2018) and morphological feature identification Baskaran et al. (2020).

Figure 2 illustrates the CNN-based workflow for a representative sample. The prepared data (a binarized patch such that a value of 0 indicates a pixel within a grain interior and a value of one indicates a pixel located at the grain boundary) is input into a three-layer CNN, in which the information is compressed into three dense layers to output the texture classification. We quantify the classification performance via the classification accuracy (fraction of input patches classified correctly) on a test set. The details of this approach are presented below.

FIGURE 2

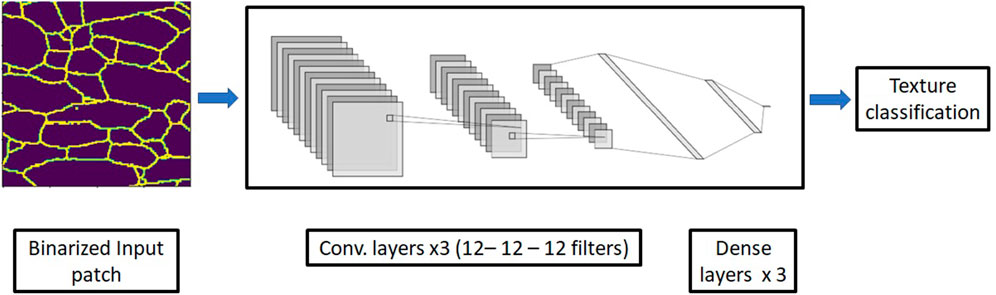
FIGURE 2. Illustration showing the CNN-based approach for microstructural classification via texture identification.

2.2.1 Data preparation

The datasets for the textured and untextured microstructures are formed using EBSD maps collected from all five heat treatments. The “texture” label was based on the processing method of the sample (i.e., magnetic-field during slip casting) and verified by the texture index produced from the EBSD data. The EBSD maps are divided into a training set (80% of EBSD maps) and a test set (20% of EBSD maps collected). Of the training set, 20% is held out as a validation set to validate the model training process. This is common practice in machine learning. The training and testing datasets are assembled with data from all heat treatments. The EBSD micrographs are converted into binary images. From each image, we extract 100 random patches of fixed dimensions to ensure compatibility with the network training process. Patch dimensions in this study are varied from 60 × 60 to 140 × 140 (pixels × pixels).

2.2.2 Texture classification via deep learning

The most common DL method is a fully connected deep neural network (DNN). A DNN consists of multiple hidden layers connected in sequence via parameters (called weights and biases). This enables the DNN to learn non-linear mappings from input to output LeCun et al. (2015), which is crucial for our task of microstructure classification. Each hidden layer has multiple nodes. The input-output mapping of a single output hidden layer node can be expressed as

$y=f\left(\sum _i{w}_i\cdot x_i+b\right),(1)$

where y is the output hidden layer node value, f is a function chosen to learn the non-linearities for that particular hidden layer, w_i are the multiplicative weights (trainable parameter) for the nodes in the input hidden layer, x_i is the value at the ith input hidden layer node, and b is the additive bias value (trainable parameter) for the output hidden layer node. The trainable parameters [w; b] are different for each node and hence Eq. 1 is calculated separately for each hidden layer nodes. In summary, the weighted sum of the input hidden layer node values is passed through a non-linear activation function to obtain the hidden layer node output. In a DNN, all nodes in the hidden layer are connected to each node in the next hidden layer (fully connected layer). The input data is passed through multiple such hidden layers stacked sequentially to learn the non-linear relationships between the input data and output labels for the chosen task.

In contrast with the fully connected neural network, a CNN layer consists of multiple trainable matrices denoted as filters. Each filter in the convolutional layer learns distinct features of interest for a task. Note that each filter has partial spatial invariance (i.e., a filter picks up a particular feature of interest, such as an object’s edge, regardless of its location in the image). This is an advantage over the fully connected dense layer. The filter output can be expressed as,

$y=f\left(w*x+b\right),(2)$

where * is the convolution operation. Similar to a fully connected layer, the filter output is given by the activation function applied to the convolution of the input with the filter weights. A filter has a fixed kernel size (size of the trainable weight matrix). Kernel sizes of 3–7 are commonly used Iandola et al. (2016). The multiple features are summed together and inputted to the next convolutional layer. Subsequent convolutional layers learn increasingly abstract descriptors from the inputs. Having multiple convolutional layers stacked sequentially increases the receptive field (size of the convolutional layer input that the filter is affected by). A max pooling operation (pooling nearby input values and computing their maximum value to get a single scalar value) is commonly used for reducing the dimensionality of the convolutional layer inputs.

2.2.3 Learning to classify

The training data is of supreme importance to the implementation and analysis of ML/DL algorithms. For both fully connected layers (Eq. 1) and the convolutional layers (Eq. 2), the trainable parameters [w; b] are learned through an optimization process. At the network output, an objective function is optimized, usually reducing some error between the output and ground truth knowledge. This error or loss is back-propagated through the network to update the trainable weights in each layer. For microstructural classification, we use the binary cross-entropy loss (BCE), which is commonly used for binary classification tasks. BCE is defined as,

$\mathrm{B}\mathrm{C}\mathrm{E}=-\frac{1}{N}\sum _{i=1}^N{y}_i\text{log}\left(p\left(y_i\right)\right)+\left(1-y_i\right)\text{log}\left(1-p\left(y_i\right)\right),(3)$

where N is the dataset size, y_i is the ground truth, and p (y_i) is the probability that the network predicts label y_i.

2.2.4 Implementation details

We use three convolutional layers followed by four dense (fully connected) layers in the CNN. Each of the three convolutional layers have 12 filters (kernel size = 3). The dense layers have a decreasing number of nodes (800 → 200 → 40 → 2). The network parameters are chosen to maximize classification performance. We use max-pooling (factor = 2) after every convolutional layer. Max-pooling is a commonly used strategy to reduce the input dimensionality by choosing the max value from a input area.

Every layer, except the last, has the ReLU activation function,

$f\left(x\right)=\text{max}\left(0,x\right),(4)$

where x is the input to the layer. We use the softmax activation function in the last layer for binary classification. This is expressed as,

$f\left(z_i\right)=\frac{e^{z_i}}{{\sum }_{j=1}^K{e}^{z_j}},(5)$

where z_i is the ith output layer node and K is the number of possible output labels (K = 2 for the texture prediction task). The softmax function converts the network output values into a vector of pseudo classification probabilities. The two output nodes correspond to either a textured classification or an untextured classification. When testing the CNN, the node with the larger value is identified as the classification output for that segment of microstructure.

A dropout strategy in the dense layers was employed to avoid certain network nodes from having high values (overfitting) Srivastava et al. (2014). Dropout randomly drops out nodes in the network during training process with a user-defined probability (p = 0.2). We use the Adam optimization strategy for learning parameters of the network (weights and biases of the network layers). We train the CNN for n = 25 epochs with a batch size of 16. Table 1 shows the CNN architecture parameters. All the CNN and training hyperparameters are manually chosen to optimize for classification performance. Of the training set, 20% is held out as a validation set to validate the model training process. The validation and training curves (loss and accuracy) are shown in the supplementary material (Supplementary Figure S1). The training and validation curves follow each other closely indicating no overfitting on the training data.

TABLE 1

TABLE 1. CNN architecture.

2.2.5 Texture classification via grain morphology metrics

To compare with the CNN classification results, metrics of the microstructure morphology were extracted from the EBSD data from all microstructures and heat treatment durations to perform a similar classification task. Classification was performed via a two-sample Kolmogorov–Smirnov (K-S) tests to quantify goodness-of-fit of randomly sampled test data Massey (1951). A one-sample K-S analysis is used to compare two distributions, where the null hypothesis is that one of the distributions, the sample distribution, is drawn from the other, the reference distribution. To test this null hypothesis, the difference between the sample distribution of size n and the reference distribution is quantified via the K-S statistic

$D_n={\text{sup}}_x|F_n\left(x\right)-F\left(x\right)|.(6)$

where F_n(x) is the sample distribution and F(x) is the reference distribution. According to the Glivenko-Cantelli theorem Howard (1959), if the sample distribution comes from the reference distribution, D_n will converge to 0 as n approaches ∞. Thus, smaller a value of D_n indicates statistical similarity between sample and reference distributions.

We use the following morphological metrics to classify textured samples with the K-S test.

1. Grain area (μm²): Area comprising a grain, calibrated to the image magnification.

2. Grain caliper diameter (μm): The longest distance between two endpoints of a grain.

3. Grain aspect ratio: The ratio of major to minor axis of an ellipse best fit to a grain (via the linear least squares approach described in Mulchrone and Choudhury (2004)).

4. Grain pixel area: The number of pixels assigned to a grain.

The distributions of these morphological metrics is shown in Figure 3. The grain pixel area and aspect ratio are considered uncalibrated because they are calculated independent of length scale (i.e., they do not consider the number of pixels per unit length). The grain area and grain caliper diameter are considered calibrated because the calculations take into account the magnification and resolution. This distinction between calibrated and uncalibrated metrics is important since the CNN is trained and tested with uncalibrated microstructures, which have been collected at variable magnifications 1) between different heat treatment durations, and 2) among maps collected at individual heat treatment durations. Respectively, these variations are reflected by 1) a range of mean view field area from 3,265 μm² (as-sintered microstructures) to 8,099 μm² (64 h microstructures), and 2) a range of standard deviations in the mean map area from 8.970 μm² (untextured 64 h microstructure) to 2,771 μm² (textured 16 h micrsotructure).

FIGURE 3

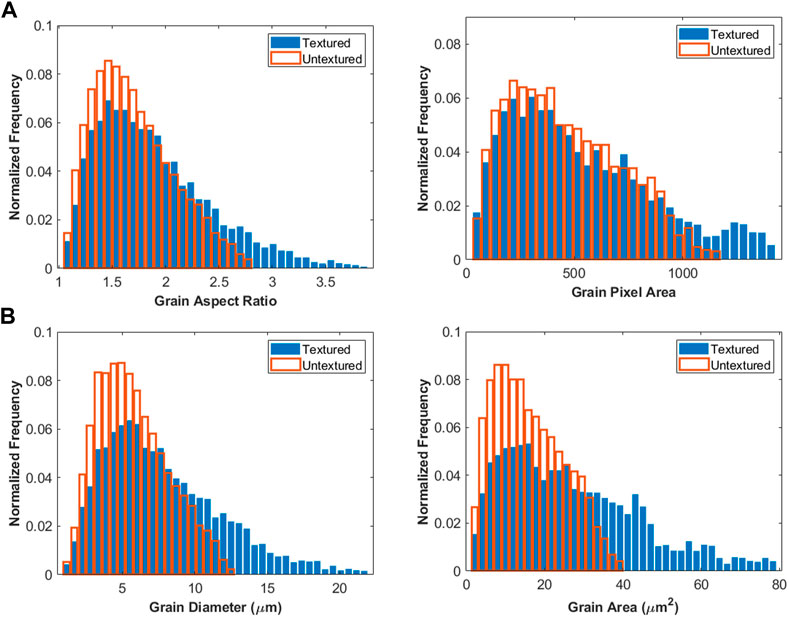
FIGURE 3. Normalized histograms for (A) uncalibrated and (B) calibrated morphological metrics form all heat treatment durations.

For each morphological metric, accuracies for the K-S test are established by comparing the two D_n values calculated for the same sample distribution with two different reference distributions: textured and untextured. For each metric, the reference distributions include the data from all heat treatment durations. Similar to the CNN tests, K-S test reference distributions are obtained from ≈80% of grains in the full dataset for each of textured/untextured (7,500 and 10,000 grains, with 1,500 and 2,000 grains per heat treatment duration, respectively). The sample distributions are extracted from a specific heat treatment duration or combination of heat treatment durations, as specified. The sample distribution is classified as textured or untextured by which reference distribution produces the lower D_n value, i.e., smallest deviation between distributions. As the true texture is known in the sample distribution, the accuracy can be calculated as the fraction of sample distributions that are classified correctly. For the KS testing, test data consists of 100 sample distributions generated with sizes correlating to the mean number of grains input to the CNN at patch size 100 × 100 as in Table 2 (50 sample distributions each for textured and untextured).

TABLE 2

TABLE 2. Mean number of grains per heat treatment duration at patch size 100 × 100.

The effect of patch size on accuracy values was tested in the CNN and, for comparison, required a similar change in the number of grains used in the sample distributions for the K-S test. For each patch size, the average number of grains per patch was extracted to be used for generating K-S test sample distributions. However, after extended heat treatment, the average number of grains varied significantly for the textured and untextured microstructures for each individual duration. Therefore, we grouped the as-sintered and 8 h datasets to form an early stage grain growth dataset, which produced similar average number of grains per patch for the textured and untextured datasets as seen in Table 3 and thus produced a more balanced classification test. The sample distributions were then generated by randomly sampling the number of grains specified in Table 3 from the early stage grain growth data. Test data consists of 100 sample distributions (50 each for textured and untextured). Note that no change was made to the reference distributions.

TABLE 3

TABLE 3. Mean number of early-stage grains per CNN patch.

3 Results

For each of the studies introduced, we present texture classification accuracy from the CNN method and compare with those obtained via the K-S test. In almost all cases, we report superior classification accuracy from the CNN-based method than from the K-S testing method. Table 3.

3.1 Classification at individual stages of grain growth

Classification test accuracy using the CNN method at individual heat treatments with patch size 100 × 100 is reflected in Figure 4. Across all heat treatments, a mean accuracy of 0.91 ± 0.03 is reported. All stages of grain growth can be classified with greater than 0.90 accuracy except for the 8 h heat treatment (0.85), which is attributed to the fact that the 8 h textured microstructure is the least textured of all heat treatment durations Conry et al. (2022). Overall, there is no apparent accuracy trend with heat treatment duration, indicating that the high-order experimentally indeterminate feature learned by the CNN is equally present at both early stages of grain growth, before morphological differences are more apparent, and later stages of grain growth.

FIGURE 4

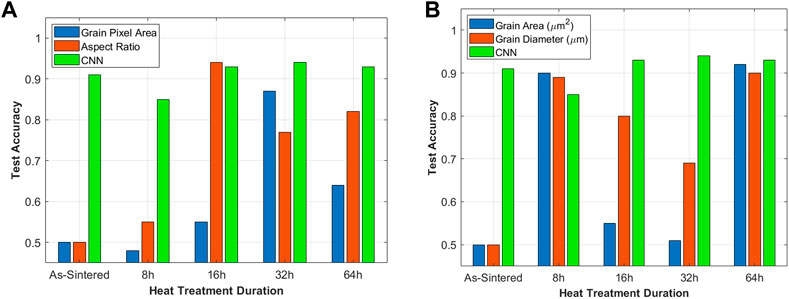
FIGURE 4. Classification accuracy with test data from individual stages of grain growth, considering (A) uncalibrated and (B) calibrated metrics. CNN classification accuracy from the same experiment is included for comparison.

Classification accuracy using the K-S test at individual heat treatments is also shown in Figure 4. We observe that in general, the accuracy of the K-S tests in classifying microstructures as textured or untextured is highly variable and dependent on the heat treatment duration of the tested microstructure for both the calibrated and uncalibrated metrics. For the uncalibrated metrics (Figure 4A), the K-S test accuracy values for longer heat-treatment durations are generally greater than shorter heat-treatment durations. Aspect ratio shows the most consistently high classification accuracy at longer heat-treatments, but cannot classify the as-sintered microstructures (where accuracy is almost the same as random, 0.5). For the calibrated metrics (Figure 4B), although the 64 h microstructures yield the highest accuracy classification, there is no clear trend with change in heat treatment duration. The 8 h microstructures exhibit unexpectedly high accuracy, even greater than the CNN; this result is discussed below. In general, the grain diameter provides equal or better accuracies than grain area, except in the as-sintered case in which both calibrated and uncalibrated metrics are close to random.

We compare the results of the CNN with two other common machine learning classifiers: random forest Breiman (2001) and support vector machine Boser et al. (1992). Each classifier is trained with two separate sets of features: 1) 100 random values of all four grain-level metrics used in the K-S test concatenated together into a 1D vector (concat method) and 2) a flattened version of the same data used by the CNN (flatten method). The results of these methods are shown in the supplementary section.

The methods are compared using standard classification metrics including precision, recall, and F1-score. The comparison in the supplementary section (Supplementary Tables S1–S10) shows that the proposed CNN method is consistently able to achieve superior performance overall (mean F1 score = 0.92) as compared to the support vector machine (mean F1 score = 0.73), random forest (mean F1 Score = 0.72), and KS test with best performing morphological parameter—aspect ratio (mean F1 score = 0.74).

Overall, none of these approaches (except of the CNN), regardless of classifier or feature set, perform well on the binary classification problem. The failure of the grain-level metrics show that these traditional metrics are alone insufficient for describing material texture. The failure of the flattened morphological data highlights the importance of local morphological information in identifying texture.

3.2 Classification with varying input data size

Figure 5 shows the test accuracy for the CNN when varying the patch size. The CNN shows a monotonically increasing trend in classification accuracy with increasing patch size, from 0.72 at patch size 60 to 0.94 at patch size 140. This result seems to indicate that there is a high-order feature being learned, as increasing patch size provides more information from the grain boundary network structure used for the CNN training and testing.

FIGURE 5

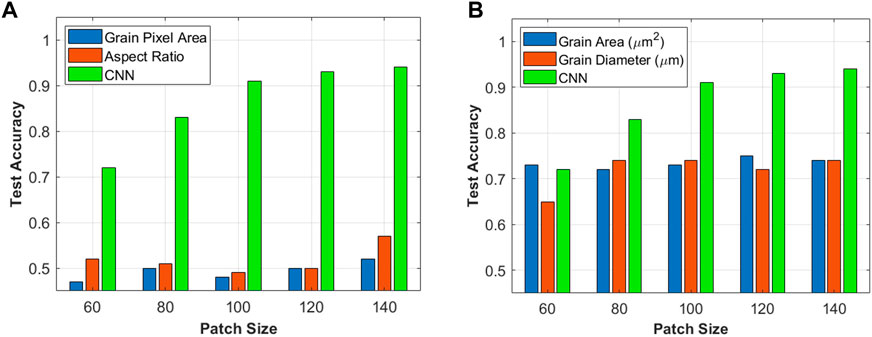
FIGURE 5. Test accuracy with early-stage grain growth data from (A) uncalibrated and (B) calibrated morphological metrics, corresponding to CNN patch size. CNN classification accuracy from the same experiment is included for comparison.

The analogous K-S classification accuracies for the uncalibrated (Figure 5A) and calibrated (Figure 5B) metrics are presented for comparison. Here, only grains from the early stage dataset (combined as-sintered and 8 h), as mentioned in Section 2.2.5, are used in the analysis. Using the calibrated metrics yields a mean accuracy of 0.73 ± 0.03 across all patch sizes. This accuracy is significantly greater than random, and the accuracy using grain area is, in fact, greater than that from the CNN at patch size 60. K-S classification using the uncalibrated metrics, for which there is no information about the data length scale, yields an essentially random mean accuracy of 0.51 ± 0.03. It should be noted that this data is most reflective of the CNN, as the binarized input patches used for training and testing are uncalibrated. In both cases, the monotonic increase is not present with increasing patch size. This may indicate that the spatial arrangement and connectivity of the high-order metrics, which is not reflected in random grain sampling, is an important factor in classifying the micrsotructures.

4 Discussion

Overall, we report superior classification accuracy of textured microstructures by CNN than by K-S classification of grain morphology metrics, regardless of input data dimensions. This finding demonstrates the potential of our CNN-based method as a powerful tool for reliable, automated microstructure classification. In particular, it requires minimal data processing without the need for manual feature extraction. Therefore, it eliminates the dependence on an expert to hand-craft relevant features, which is time-consuming and can lead to human biases. Below, we discuss the potential implications of the consistently high CNN accuracy values on microstructure characterization.

4.1 CNN classifies texture by high-order descriptor of microstructure

The consistent accuracy of CNN predictions at all heat treatment durations for a constant patch size suggests that CNN is learning a feature that is equally present at both early and late stages of grain growth. This feature is, by definition of the CNN test, different between the textured and untextured microstructures. The inconsistency of the K-S tests’ accuracy further suggest that the CNN-identified feature is not grain diameter, grain area (calibrated or uncalibrated), or aspect ratio because none of these metrics can be used to distinguish the microstructures at both early and late stages of grain growth. Similarly to the other microstructural metrics discussed here, the dihedral angles (2D projections from EBSD maps) at triple junctions were also incapable of distinguishing the textured from untextured microstructures at all stages of grain growth as discussed in the supplementary material.

In contrast to the CNN, the microstructural differences between grain growth stages, rather than the crystallographic texture, inhibit the K-S tests’ ability to classify textured from untextured. The K-S tests were designed to reflect the CNN training by assembling data from all heat treatment durations into the reference distributions. However, the tested morphological metrics (grain diameter, area, and aspect ratio) change with increasing heat treatment duration, and their changes are greater than the difference between the textured and untextured microstructures at the same grain growth stage. This can be seen by comparing, for example, the average grain diameters for each heat treatment duration reported in Table 4. The average grain diameter of the textured microstructures varies from 3.2 µm to 7.6 µm, which totally encompasses the diameter range exhibited by the untextured grains. Apart from the as-sintered case, the grain diameter is a defining metric for a microstructure of a certain texture and heat treatment duration but cannot be used to classify all the textured microstructures from the untextured ones. Table 4 also demonstrates why the accuracy of the K-S test for grain diameter in the 8 h samples is high: the average grain diameters of the textured and untextured microstructures for 8 h most closely resemble the average grain diameters of their respective total populations.

TABLE 4

TABLE 4. The average grain diameter (in μm) for untextured and textured microstructures at each heat treatment duration.

This variation in metrics with heat treatment duration does not negatively affect the CNN classification accuracy. The most obvious example of this is the extremely accurate (≥0.9) classification in the as-sintered condition. These are morphologically very similar microstructures (Figure 1; Table 4) and thus very challenging to classify by classical methods, as reflected by the near-random test accuracy with both uncalibrated and calibrated metrics. We pose that the excellent classification ability of the CNN at this initial condition is strong evidence that high-order, experimentally indeterminate microstructural metrics associated with texture are being learned and applied to make the classification.

The improvement in accuracy with increase in patch size further suggests that the CNN is indeed learning a feature that is, although currently indeterminate, of spatiotemporal nature. We report a 31% improvement in CNN classification accuracy at early stages of grain growth by introducing only ≈200 grains per patch. This increase in number of grains does not affect the K-S test accuracy. Instead, we propose that increasing the patch size, rather than increasing the number of patches, improves the CNN accuracy because it provides more information needed for detecting spatiotemporal features. Potential features of importance may be the arrangement of high aspect ratio grains or dihedral angles at the triple junctions (see discussion in Supplementary Material).

4.2 Implications of CNN classification on microstructure characterization

The ability of the CNN to classify crystallographic texture accurately from a relatively small number of binary images has significant implications for both collecting and mining microstructural data. First, the binary images classified by CNN can be collected with simple imaging techniques, either with optical or electron microscopy. Such imaging is faster and simpler than EBSD, which requires labor-intensive sample preparation to remove surface damage and expensive equipment. Furthermore, many grains, at least 2,500–3,00 grains ASTM (1996) and more for heterogeneous microstructures to account for spatial inhomogeneity, are required to statistically differentiate microstructures with conventional grain metrics. In the present work, the trained CNN used no more than ≈250 grains for any experiment to make high-accuracy classifications based on high-order, spatiotemporal features. This finding holds great promise for the future of grain growth and microstructural analysis, as it forecasts the ability to make statistically significant conclusions with far less intensive data collection and analysis than traditionally required.

Moreover, the high-accuracy classification ability of the CNN with uncalibrated, binary microstructure images is powerful, and holds implications towards the potential of generating large microstructural databases. Specifically, it would allow microstructural data to be pulled from across the literature regardless of scale bar, greatly facilitating the large-scale data mining needed to generate such a database. A recent review of materials data science highlights the importance of microstructure databases for the future of advanced materials design Kalindindi and DeGraef (2015). As a specific example, recent work on DL microstructure classification parsed a database of Ti alloy microstructures to classify grain morphologies as a function of processing Baskaran et al. (2020). We pose that CNN methods open the door to data-mining a wide range of complex grain images, advancing hierarchical microstructural characterization and, thus, multiscale modeling of polycrystalline materials.

4.3 Future directions

A natural extension of this work is to use the CNN to classify the degree of crystallographic texture, which is not a binary metric. In future work, we will vary the magnetic field strength during slip casting to change the texture index of the as-sintered microstructures. Varying the texture index of the input data will also provide insight into the sensitivity of CNN classification when the texture index is between 1 and 2, which was not tested here.

Future efforts are focused on identifying what physical descriptors are being learned and used by the CNN to classify texture. Previously, an interpretability analysis has been done for the classification error Oviedo et al. (2019). A future research direction is to similarly perform an interpretability analysis of the intermediate CNN features to obtain high order descriptors of textured grain classification. Interpretations of these high-order descriptors can then be used to guide efforts in elucidating grain growth or predicting microstructure-controlled material behavior.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

IK, BC, AK, and JH contributed to the conception and design of this study. BC collected and processed the experimental data. IK trained and tested the convolutional neural network, and conducted the K-S analysis. BC and IK contributed equally to the writing of the manuscript. All authors contributed to manuscript revision, read and approved the submitted version.

Funding

The authors gratefully acknowledge support from the U.S. Department of Energy, Office of Science, United States (Grant No. DE-SC0020384). BC’s work is further supported by the National Science Foundation Graduate Research Fellowship Program, United States under Grant No. AWD04512–1842473.

Acknowledgments

Additionally, we are grateful to the staff of the Nanoscale Research Facility (NRF) at the University of Florida, at which all EBSD data was collected for this work.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Author Disclaimer

Any opinions, findings, and conclusion or recommendations expressed in this material are those of the author (s) and do not necessarily reflect the views of the National Science Foundation.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmats.2023.1086000/full#supplementary-material

References

Ahn, C. W., Jeong, E. D., Kim, Y. H., Lee, J. S., Chung, G. S., Lee, J. Y., et al. (2009). Piezoelectric properties of textured bi3.25la0.75ti2.97v0.03o12 ceramics fabricated by reactive templated grain growth method. J. Electroceramics 23, 392–396. doi:10.1007/s10832-008-9474-6

CrossRef Full Text | Google Scholar

Akiva, R., Katsman, A., and Kaplan, W. (2014). Anisotropic grain boundary mobility in undoped and doped alumina. J. Am. Ceram. Soc. 97, 1610–1618. doi:10.1111/jace.12787

CrossRef Full Text | Google Scholar

Allison, J., Backman, D., and Christodoulou, L. (2006). Integrated computational materials engineering: A new paradigm for the global materials profession. Jom 58, 25–27. doi:10.1007/s11837-006-0223-5

CrossRef Full Text | Google Scholar

Arasan, S., Akbulut, S., and Hasiloglu, A. S. (2011). Effect of particle size and shape on the grain size distribution using image analysis. Int. J. Civ. Struct. Eng. 1, 968–985. doi:10.6088/ijcser.00202010083

CrossRef Full Text | Google Scholar

ASTM (1996). Standard test methods for determining average grain size. West Conshohocken, PA, USA: designation, 112–196.

Google Scholar

Azimi, S. M., Britz, D., Engstler, M., Fritz, M., and Mücklich, F. (2018). Advanced steel microstructural classification by deep learning methods. Sci. Rep. 8, 1–14. doi:10.1038/s41598-018-20037-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Bachmann, F., Hielscher, R., and Schaeben, H. (2011). Grain detection from 2d and 3d ebsd data — Specification of the mtex algorithm. Ultramicroscopy 111, 1720–1733. doi:10.1016/j.ultramic.2011.08.002

PubMed Abstract | CrossRef Full Text | Google Scholar

Baskaran, A., Kane, G., Biggs, K., Hull, R., and Lewis, D. (2020). Adaptive characterization of microstructure dataset using a two stage machine learning approach. Comput. Mater. Sci. 177, 109593. doi:10.1016/j.commatsci.2020.109593

CrossRef Full Text | Google Scholar

Boser, B. E., Guyon, I. M., and Vapnik, V. N. (1992). A training algorithm for optimal margin classifiers. Proc. fifth Annu. workshop Comput. Learn. theory, 144–152.

CrossRef Full Text | Google Scholar

Breiman, L. (2001). Random forests. Mach. Learn. 45, 5–32. doi:10.1023/a:1010933404324

CrossRef Full Text | Google Scholar

Chao, H., Yang, Y., Wang, X., and Wang, E. (2011). Effect of grain size distribution and texture on the cold extrusion behavior and mechanical properties of az31 mg alloy. Mater. Sci. Eng. A 528, 3428–3434. doi:10.1016/j.msea.2011.01.020

CrossRef Full Text | Google Scholar

Chowdhury, A., Kautz, E., Yener, B., and Lewis, D. (2016). Image driven machine learning methods for microstructure recognition. Comput. Mater. Sci. 123, 176–187. doi:10.1016/j.commatsci.2016.05.034

CrossRef Full Text | Google Scholar

Cohn, R., and Holm, E. (2021). Neural message passing for predicting abnormal grain growth in Monte Carlo simulations of microstructural evolution. arXiv preprint arXiv:2110.09326.

Google Scholar

Conry, B., Harley, J., Tonks, M., Kesler, M., and Krause, A. (2022). Engineering grain boundary anisotropy to elucidate grain growth behavior in alumina. J. Eur. Ceram. Soc. 42, 5864–5873. doi:10.1016/j.jeurceramsoc.2022.06.059

CrossRef Full Text | Google Scholar

DeCost, B., Francis, T., and Holm, E. (2017). Exploring the microstructure manifold: Image texture representations applied to ultrahigh carbon steel microstructures. Acta Mater. 133, 30–40. doi:10.1016/j.actamat.2017.05.014

CrossRef Full Text | Google Scholar

DeCost, B., and Holm, E. (2015). A computer vision approach for automated analysis and classification of microstructural image data. Comput. Mater. Sci. 110, 126–133. doi:10.1016/j.commatsci.2015.08.011

CrossRef Full Text | Google Scholar

Gola, J., Webel, J., Britz, D., Guitar, A., Staudt, T., Winter, M., et al. (2019). Objective microstructure classification by support vector machine (svm) using a combination of morphological parameters and textural features for low carbon steels. Comput. Mater. Sci. 160, 186–196. doi:10.1016/j.commatsci.2019.01.006

CrossRef Full Text | Google Scholar

Groeber, M., and Jackson, M. (2014). Dream.3d: A digital representation environment for the analysis of microstructure in 3d. Integrating Mater. Manuf. Innovation 3, 56–72. doi:10.1186/2193-9772-3-5

CrossRef Full Text | Google Scholar

Holm, E. A., Cohn, R., Gao, N., Kitahara, A. R., Matson, T. P., Lei, B., et al. (2020). Overview: Computer vision and machine learning for microstructural characterization and analysis. Metallurgical Mater. Trans. A 51, 5985–5999. doi:10.1007/s11661-020-06008-4

CrossRef Full Text | Google Scholar

Howard, T. (1959). A generalization of the glivenko-cantelli theorem. Ann. Statistics 30, 828–830. doi:10.1214/aoms/1177706212

CrossRef Full Text | Google Scholar

Iandola, F. N., Han, S., Moskewicz, M. W., Ashraf, K., Dally, W. J., and Keutzer, K. (2016). Squeezenet: Alexnet-level accuracy with 50x fewer parameters and< 0.5 mb model size. arXiv preprint arXiv:1602.07360.

Google Scholar

Igathinathane, C., Pordesimo, L., Columbus, E., Batchelor, W., and Methuku, S. (2008). Shape identification and particles size distribution from basic shape parameters using imagej. Comput. Electron. Agric. 63, 168–182. doi:10.1016/j.compag.2008.02.007

CrossRef Full Text | Google Scholar

Jain, A., Ong, S., Hautier, G., Chen, W., Richards, W., Dacek, S., et al. (2013). Commentary: The materials project: A materials genome approach to accelerating materials innovation. Apl. Mater. 1, 011002. doi:10.1063/1.4812323

CrossRef Full Text | Google Scholar

Kalindindi, S., and DeGraef, M. (2015). Materials data science: Current status and future outlook. Annu. Rev. Mater. Res. 45, 171–193. doi:10.1146/annurev-matsci-070214-020844

CrossRef Full Text | Google Scholar

Kitahara, A., and Holm, E. (2018). Microstructure cluster analysis with transfer learning and unsupervised learning. Integrating Mater. Manuf. Innovation 7, 148–156. doi:10.1007/s40192-018-0116-9

CrossRef Full Text | Google Scholar

Krizhevsky, A., Sutskever, I., and Hinton, G. E. (2017). Imagenet classification with deep convolutional neural networks. Commun. ACM 60, 84–90. doi:10.1145/3065386

CrossRef Full Text | Google Scholar

LeCun, Y., Bengio, Y., and Hinton, G. (2015). Deep learning. nature 521, 436–444. doi:10.1038/nature14539

PubMed Abstract | CrossRef Full Text | Google Scholar

Ling, J., Hutchinson, M., Antono, E., DeCost, B., Holm, E., and Meredig, B. (2017). Building data-driven models with microstructural images: Generalization and interpretability. Mater. Discov. 10, 19–28. doi:10.1016/j.md.2018.03.002

CrossRef Full Text | Google Scholar

Ma, W., Kautz, E., Baskaran, A., Chowdhury, A., Josji, V., Yener, B., et al. (2020). Image-driven discriminative and generative machine learning algorithms for establishing microstructure-processing relationships. J. Appl. Phys. 128, 134901. doi:10.1063/5.0013720

CrossRef Full Text | Google Scholar

Maeda, H., Ohya, K., Sato, M., Motokawa, M., Chen, W., Watanbe, K., et al. (2004). Fitting an ellipse to an arbitrary shape: Implications for strain analysis. J. Struct. Geol. 26, 143–153. doi:10.1016/S0191-8141(03)00093-2

CrossRef Full Text | Google Scholar

Maeda, H., Sastry, P., Trociewitz, U., Schwartz, J., Ohya, K., Chen, M. S. W., et al. (2003). Effect of magnetic field strength in melt-processing on texture development and critical current density of bi-oxide superconductors. Phys. C 386, 115–121. doi:10.1016/S0921-4534(02)02237-2

CrossRef Full Text | Google Scholar

Massey, F. (1951). The Kolmogorov-smirnov test for goodness of fit. J. Am. Stat. Assoc. 46, 68–78. doi:10.1080/01621459.1951.10500769

CrossRef Full Text | Google Scholar

Messing, G., Poterala, S., Chang, Y., Poterala, T., Kupp, E., Watson, B., et al. (2017). Texture-engineered ceramics - property enhancements through crystallographic tailoring. J. Mater. Res. 32, 3219–3241. doi:10.1557/jmr.2017.207

CrossRef Full Text | Google Scholar

Mjolsness, E., and DeCoste, D. (2001). Machine learning for science: State of the art and future prospects. science 293, 2051–2055. doi:10.1126/science.293.5537.2051

PubMed Abstract | CrossRef Full Text | Google Scholar

Molodov, D., and Sheikh-Ali, A. (2004). Effect of magnetic field on texture evolution in titanium. Acta Mater. 52, 4377–4383. doi:10.1016/j.actamat.2004.06.004

CrossRef Full Text | Google Scholar

Mulchrone, K., and Choudhury, K. R. (2004). Fitting an ellipse to an arbitrary shape: Implications for strain analysis. J. Struct. Geol. 26, 143–153. doi:10.1016/S0191-8141(03)00093-2

CrossRef Full Text | Google Scholar

O’Shea, K., and Nash, R. (2015). An introduction to convolutional neural networks. arXiv preprint arXiv:1511.08458.

Google Scholar

Oviedo, F., Ren, Z., Sun, S., Settens, C., Liu, Z., Hartono, N. T. P., et al. (2019). Fast and interpretable classification of small x-ray diffraction datasets using data augmentation and deep neural networks. npj Comput. Mater. 5, 60–69. doi:10.1038/s41524-019-0196-x

CrossRef Full Text | Google Scholar

Park, J.-S., Zhang, X., Kenesei, P., Wong, S. L., Li, M., and Almer, J. (2017). Far-field high-energy diffraction microscopy: A non-destructive tool for characterizing the microstructure and micromechanical state of polycrystalline materials. Microsc. Today 25, 36–45. doi:10.1017/s1551929517000827

CrossRef Full Text | Google Scholar

Rodel, J., and Glaeser, A. (1989). “Anisotropy of grain growth in alumina,” in 91st Annual Meeting of the American Ceramic Society (Basic Science Division).

Google Scholar

Seabaugh, M. M., Cheney, G. L., Hasinska, K., Azad, A. M., Sabolsky, E. M., Swartz, S. L., et al. (2004). Development of a templated grain growth system for texturing piezoelectric ceramics. J. Intelligent Material Syst. Struct. 15, 209–214. doi:10.1177/1045389X04040131

CrossRef Full Text | Google Scholar

Seabaugh, M., Kerscht, I., and Messing, G. (1997). Texture development by templated grain growth in liquid-phase-sintered α-alumina. J. Am. Ceram. Soc. 80, 1181–1188. doi:10.1111/j.1151-2916.1997.tb02961.x

CrossRef Full Text | Google Scholar

Srivastava, N., Hinton, G., Krizhevsky, A., Sutskever, I., and Salakhutdinov, R. (2014). Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 15, 1929–1958.

Google Scholar

Sugiyama, T., Tahashi, M., Sassa, K., and Asai, S. (2003). The control of crystal orientation in non-magnetic metals by imposition of a high magnetic field. ISIJ Int. 43, 855–861. doi:10.2355/isijinternational.43.855

CrossRef Full Text | Google Scholar

Suzuki, T., Uchikoshi, T., and Sakka, Y. (2006). Control of texture in alumina by colloidal processing in a strong magnetic field. Sci. Technol. Adv. Mater. 7, 356–364. doi:10.1016/j.stam.2006.01.014

CrossRef Full Text | Google Scholar

Talebi, H., Silani, M., Bordas, S. P., Kerfriden, P., and Rabczuk, T. (2014). A computational library for multiscale modeling of material failure. Comput. Mater. 53, 1047–1071. doi:10.1007/s00466-013-0948-2

CrossRef Full Text | Google Scholar

Wang, Z.-L., and Adachi, Y. (2019). Property prediction and properties-to-microstructure inverse analysis of steels by a machine-learning approach. Mater. Sci. Eng. A 744, 661–670. doi:10.1016/j.msea.2018.12.049

CrossRef Full Text | Google Scholar

Weber, G., Pinz, M., and Ghosh, S. (2020). Machine learning-aided parametrically homogenized crystal plasticity model (phcpm) for single crystal ni-based superalloys. Jom 72, 4404–4419. doi:10.1007/s11837-020-04344-9

CrossRef Full Text | Google Scholar

Weber, G., Pinz, M., and Ghosh, S. (2022). Machine learning-enabled self-consistent parametrically-upscaled crystal plasticity model for ni-based superalloys. Comput. Methods Appl. Mech. Eng. 402, 115384. doi:10.1016/j.cma.2022.115384

CrossRef Full Text | Google Scholar

Wei, J., Chu, X., Sun, X.-Y., Xu, K., Deng, H.-X., Chen, J., et al. (2019). Machine learning in materials science. Mach. Learn. Mater. Sci. 1, 338–358. doi:10.1002/inf2.12028

CrossRef Full Text | Google Scholar

Winiarski, B., Gholinia, A., Mingard, K., Gee, M., Thompson, G., and Withers, P. (2021). Correction of artefacts associated with large area ebsd. Ultramicroscopy 226, 113315. doi:10.1016/j.ultramic.2021.113315

PubMed Abstract | CrossRef Full Text | Google Scholar

Yilmaz, H., Trolier-McKinstry, S., and Messing, G. (2003). Reactive templated grain growth of textured sodium bismuth titanate (na1/2bi1/2tio3– batio3) ceramics—Ii dielectric and piezoelectric properties. J. Electroceramics 11, 217–226. doi:10.1023/b:jecr.0000026376.48324.21

CrossRef Full Text | Google Scholar

Zhang, Z., Duan, X., Qiu, B., Yang, Z., Cai, D., He, P., et al. (2019). Preparation and anisotropic properties of textured structural ceramics: A review. J. Adv. Ceram. 38, 289–332. doi:10.1007/s40145-019-0325-5

CrossRef Full Text | Google Scholar