Metal foams: A review for mechanical properties under tensile and shear stress

Due to their mechanical properties, metal foams are used in various fields. The aim of the present research is to collect different studies about the important mechanical properties of metal foams, such as Young’s modulus, tensile and shear strength, relative density, etc. under tensile and shear loading. Gaps were identified in the methodological embodiments of the experiments due to the use of different standards, as well as in the calculation of mechanical properties through mathematical relations in tensile and shear, which led to deviations between the experimental results and these. Furthermore, this work records sequences and connections between experimental results of different tasks as well as solutions to the aforementioned issues.

Introduction

Metal foams are man-made materials that replicate structures of nature such as bones or woods, etc. that exhibit interesting physical and mechanical properties with high range of applications in the industry (Zhao et al., 2017; Patel et al., 2018). A lot of research on the history of metal foams has been published in the last years (Singh and Bhatnagar, 2017; Rajak and Gupta, 2020). An extensive historical record for metal foams was presented by Banhart (2013). The first recorded mention of metal foams was in 1925 by Meller, while during the following years no recorded new attempts on that field were seen until 1951, when John Elliott improved the preparation method described by Meller. Since then, there has been an increase in research activity in the field. In 1985 Shinko Wire Co. Ltd. developed one of the most important techniques for metal foams (Alporas foam) (Miyoshi et al., 1998). Four years later the patent for the Alcan foam technique/type was published (Jin et al., 1990). From then until now there was significant development in research and applications of metal foams. This is connected to the improved and scaled up manufacturing of metal foams in the form of constituents of structural components and filters that was recorded in the last couple of decades, as shown in Figure 1 (Google Ngram Viewer, 2022). shows the references in the literature for metal foams during years.

FIGURE 1

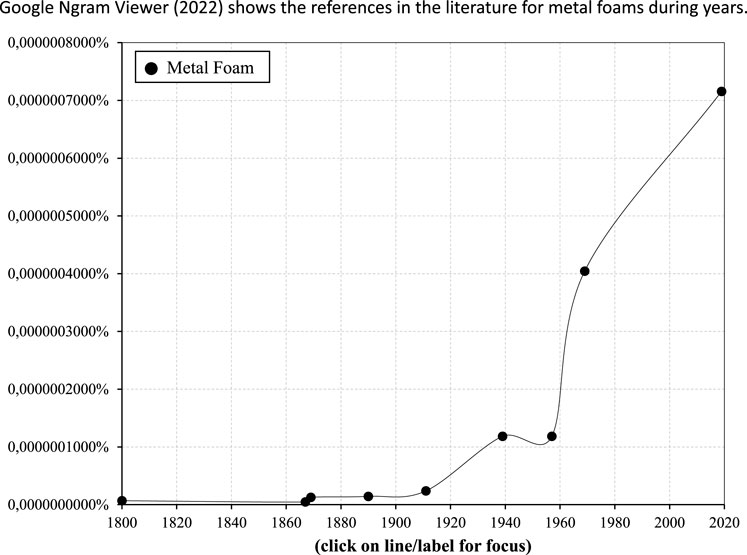
FIGURE 1. References about metal foams in past 220 years (Google Ngram Viewer, 2022).

Applications of metal foams are now found in several areas, such as the automotive industry (Bisht et al., 2019; Carranza et al., 2019; Sun et al., 2019; Buonomo et al., 2022; Sunder Sharma et al., 2022), building construction (Salimon et al., 2005; Bisht et al., 2019; Farhadi et al., 2020; Chibani et al., 2021; Song et al., 2021), aerospace (García-Moreno, 2016; Murugesan and Mansuri, 2018; Zhu et al., 2018; Madhavan et al., 2019; Liu et al., 2022) and chemical industry (Sajid Hossain and Shabani, 2015; Allioux et al., 2020; Du et al., 2020; Hu et al., 2021; Chen et al., 2023), bio-medical (Singh et al., 2013; Maimouni et al., 2020; Tong et al., 2020; Alavi et al., 2021; Rodriguez-Contreras et al., 2021), energy storage (Lafdi et al., 2008; Huang et al., 2019; Lei et al., 2021; Galvagnini et al., 2022; MERT et al., 2022), the list not being exhaustive. The uptake from the industry is still low though, due to relatively costly scaling production issues and the absence of reliable mechanical property evaluation.

To date, the development and manufacture of metal foams are based on various techniques and methods. Metal foams can be manufactured with different methods and combinations of metals such as steel, nickel, lead, and aluminium. Metal foams, metal hollow spheres, or other porous metal products result from the combination of production techniques and the architecture of the cellular structure or casts. Of course, not all methods can be applied for all metal alloys. Some methods use similar techniques for foaming aqueous or polymer liquids, others developed techniques based on a specific characteristic of materials, such as the action during sintering or the agent they can deposit electrically (Banhart, 2013; Mahadev et al., 2018; Kulshreshtha and Dhakad, 2020; Parveez et al., 2022). The basic processing techniques of cellular materials are summarized in Ashby et al. (2000a), with the main categories: liquid metallurgy, coating techniques, and powder metallurgy.

The cellular materials are divided according to the following criteria: a) state of the metal processed, b) the foaming technique, and c) the methods of pore formation.

Focusing on metal foams applications that require reliable mechanical properties, in order to increase commercial uptake, it is essential to develop trustworthy test protocols to evaluate and reproduce representative material strengths and stiffnesses for quality control purposes, but also for material design enhancement.

The study of metal foams under compressive loading is the most common. The mechanical properties under compression are probably the most well studied for metal foams and porous metals, as indicated by the publication of a standard method for compression of porous metals (ISO 13314:2011, 2011). Gibson and Ashby (1997) collected and presented rules for the mechanical properties of cellular materials. This type of material has distinctively different behaviour than solid metals, especially in compression. Compression tests offer essential insights exhibiting three distinct regions on the stress-strain curve (Ashby, 1983) (Figure 2). The first region (linear elasticity region) is a combination of elastic and plastic deformation. This indicates that irreversible deformation can occur at low stress for metal foams. The second region (collapse region) occurs due to successive crush bands of cells collapsing and leading to plastic deformation. The third region (densification region), due to the collapse of the cells, is marked by stiffening behaviour.

FIGURE 2

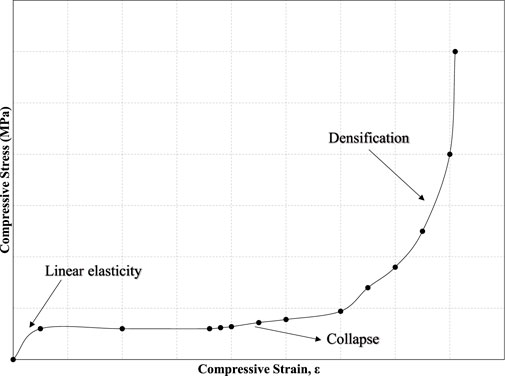
FIGURE 2. Typical diagram for metal foam under compression stress. Divided into three regions a) plastic-elastic deformation (linear elasticity) b) Plastic deformation (collapse) c) densification. (Ashby, 1983).

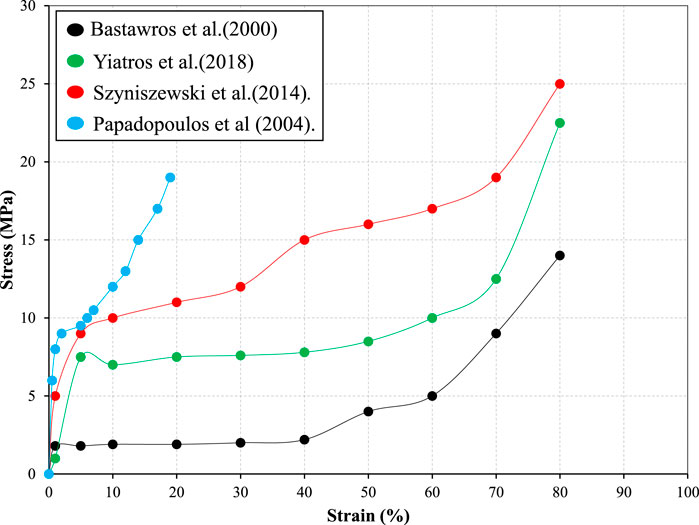
More recent investigations confirm the existing results. Some research works are summarized as follows: Papadopoulos et al. (2004) produced pure $Al$ foam and studied metal foams’ mechanical properties under compressions, such as Young’s modulus and the plateau strength. This experimental result agrees with theoretical and other investigators results (Gibson and Ashby, 1997).

Bastawros et al. (2000) investigated the deformation mechanics of $Al$ alloy close cell foam. They recorded three different stages of deformation of foam. The first stage detected plastic deformation on cell nodes. The second shows discrete cell bands with plastic buckling, increasing, and forming new bands in the following areas. In the last stages, the collapse of some of these bands is recorded.

Szyniszewski et al. (2014) reported four types of compressive tests (no unloading, single unloading in the inelastic region, unloading every 0.5%–1.0% strain, no unloading, reduced cross-section). Foam deformation is characterized by three areas: linear elastic, yield plateau, and abrupt increasing stress.

Yiatros et al. (2018) investigated the compressive properties of steel hollow spheres assembled of different diameters bonded with a thermosetting epoxy. The result of that was specimens with different relative densities between them. Relative density is the ratio of the density of a specimen to the density of a given reference material (Kai Li, 2000). The models with higher relative density had higher first maximum strength, which is the ability to produce force (Stone et al., 2003). The compression behaviour of specimens agrees with the stress-strain diagram in Figure 2.

Figure 3 assembles the stress-strain curves of the above works. The curves’ shape agrees with Gibson and Ashby (1997) curve, Figure 2, but compressive stress is significantly higher. This relates to the different structures of specimens. Also, hollow sphere structures show better behaviour under compression stress compared with the other structures, perhaps due to the more regular cell size and dispersion of porosity within materials compared to other metal foams. A recent extensive literature review on experimental methods for metal foams and porous metal in compression has been reported in Völlmecke et al. (2021) and in Nisa et al. (2022).

FIGURE 3

FIGURE 3. The stress-strain curves from above mentioned works.

The only test method that has a dedicated standard for investigating the mechanical properties of porous metals is under uniaxial compression. The use of the different standards is observed to study the mechanical properties of porous metals in tension and shear. The most typical standard for tensile tests is the ASTM-E8 (2010). This is a standard test for tension testing of metallic materials, so it does not consider the cell structure of the metallic foams and the role this plays in the mechanical properties of the metallic foams. For the investigation of mechanical properties in shear used, a large number of different standard as ASTM-C273-C273M-11 (2011), etc.

This article aims to assemble and review the work done in the experimental evaluation of the properties of metal foam under the two types of loading: tension and shear. Specifically, the work is aimed at research that explored Young’s Modulus in tension that is a mechanical property that measures the tensile stiffness of a solid material when force is applied longitudinally (Biswas, 2022), shear modulus that is a measure of the elastic shear stiffness of a material (Uy, 2021), tensile and shear strengths of porous metals that is the strength of a material or component against the type of yield or structural failure when the material or component fails in tensile or shear (Hibbeler and Yap, 2018), and hollow spheres of different origins of materials and relative densities. The assembly of all this work here allows the mapping of important data related to the mechanical properties of these materials and, most importantly, highlights any gaps in the material space and the experimental procedures for structurally related metal foams.

Properties of metal foams

Before embarking on this review, it is essential to mention that in 2000, Ashby et al. (2000b), drawing parallels from other works in porous materials, connected the characteristics and properties of metal foams with two different sets of parameters. The first describes the geometric structure of the foam, that is, relative density or porosity, size, and shape of the cell. The second is related to the properties of the cell wall material. The most common properties are Young’s modulus, density, plastic, and fracture yield strength (Gibson and Ashby, 1997).

Some approximate mathematical relations for mechanical properties of metal foams have been presented in the past and are also highlighted in Table 1:

TABLE 1

TABLE 1. Mathematical relations for mechanical properties of metal foams (Ashby et al., 2000a).

The symbols with a subscript in the table represent the property of the solid metal of which the foam is made. The properties for $E_s$ and relative density ( $\raisebox{1ex}{$\rho $}\!\left/ \!\raisebox{-1ex}{${\rho }_s$}\right.$ ) are between 0.0026 and 200 (GPa) and 0.02–0.35, respectively, depending from the material (Gibson and Ashby, 1997). The mentioned mathematical relations are based in part on experimental data (Gibson and Ashby, 1997) and in part on empirical adaptations.

Mechanical properties under tension

Tensile tests (Davis, 2004; Iowa State University of Science and Technology, 2020) are used to determine the following mechanical properties: Young’s modulus, Poisson’s ratio, ultimate tensile strength, yield strength, etc. The primary curve produced from a tensile test is a direct stress-strain curve. Figure 4 shows a typical stress-strain curve for metal foams. The curve includes two points of interest: the yield strength and ultimate tensile strength point, and the quasi-elastic initial stiffness.

FIGURE 4

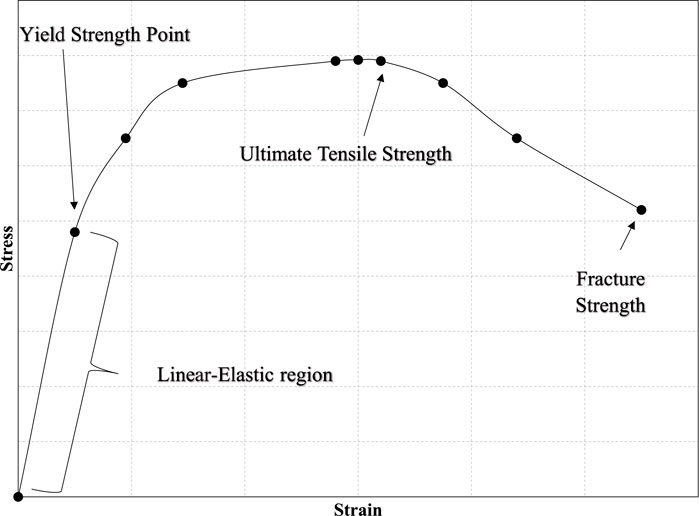
FIGURE 4. Typical stress-strain curve for metal foams (Davis, 2004).

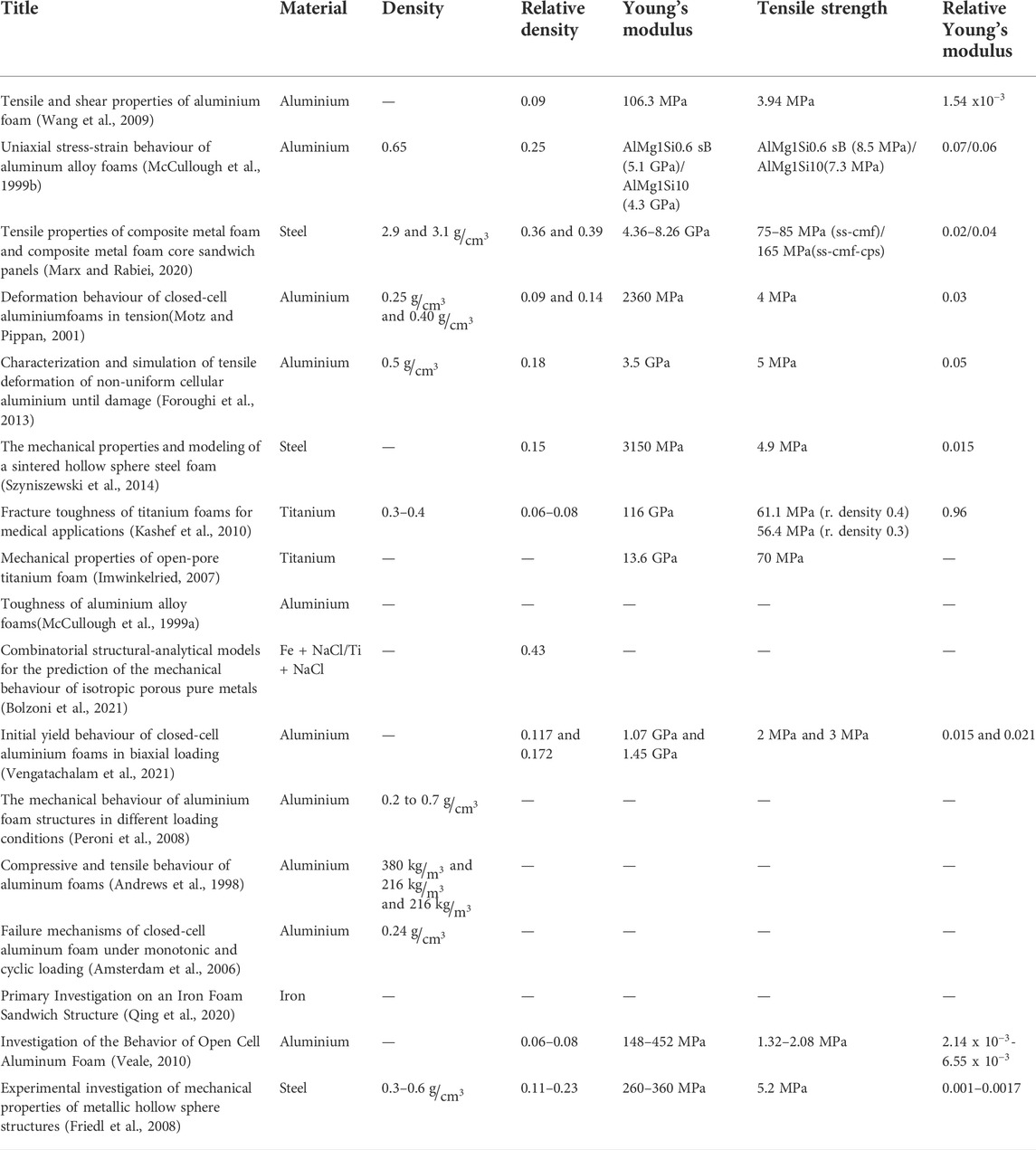
Table 2 presents key aspects of research work that investigates the mechanical properties of metal foams under tensile load, such as the base material, the type of foam, the pore size, specimen size, loading rate, and if a particular standard was followed. According to the literature, most works concentrate on aluminium alloy closed cell foams, and a small percentage investigate open or hollow spheres foam. Clearly, this space in the literature is not very contested, perhaps due to practical reasons, such as the applicability of open cell foams in structural applications or the more expensive production of hollow spheres, but this needs extra investigation. Furthermore, it is clear that there is no precise standard method for this test, unlike compression, and no correlation exists between the loading rate and the pore sizes.

TABLE 2

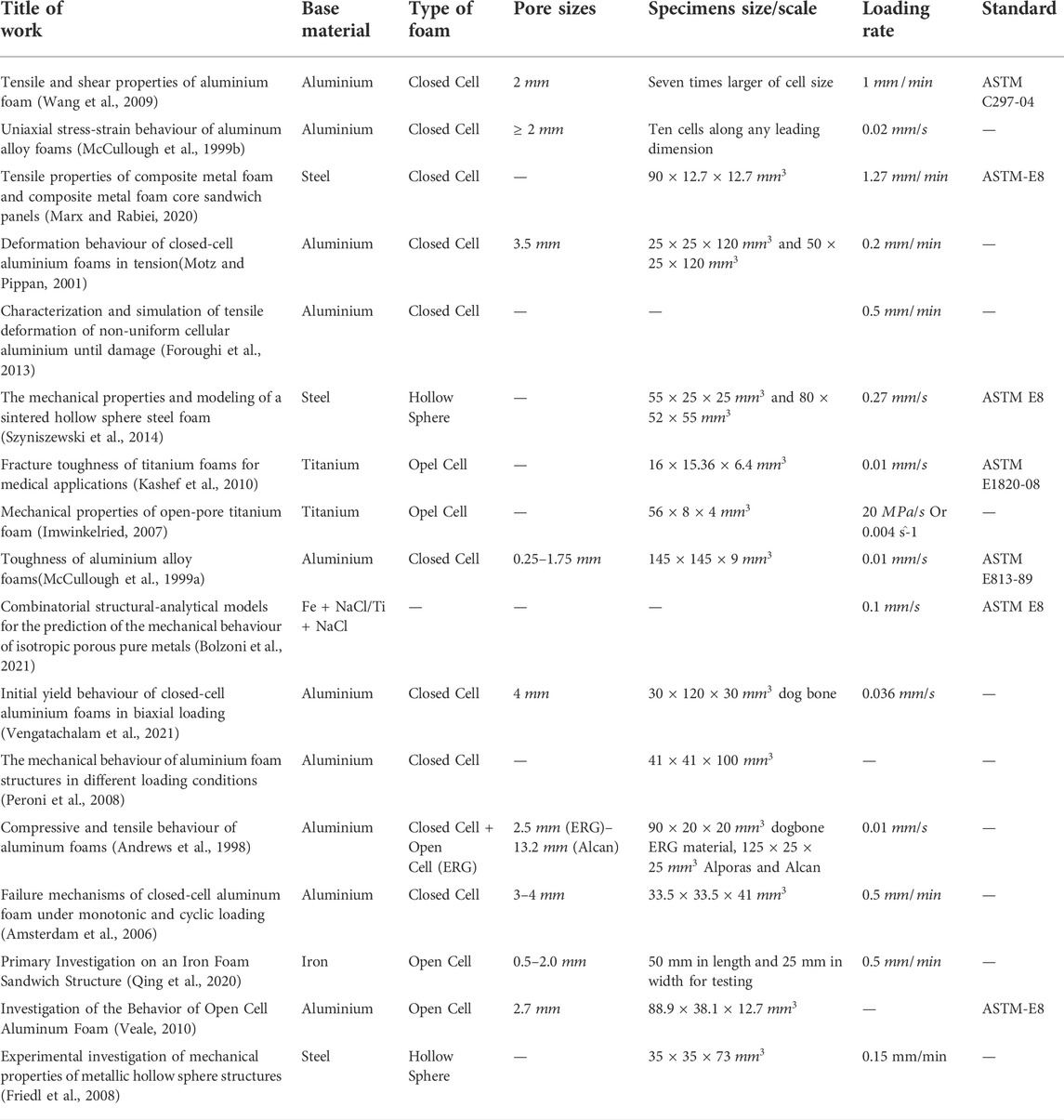
TABLE 2. Summary table of previous work and information about: type of foam, size of porous, specimens size/scale, loading rate, type of test, standart.

Aluminium

According to Table 2, aluminium is the most common material for metal foam construction. This can be attributed to its physical properties (such as melting point), which allow for relatively manageable heat treatment procedures for scaling up production of metal foams.

Andrews et al. (1998) point out lower than expected values for mechanical properties in closed-cell metal foams and conclude that improving their manufacturing process will improve the above values.

McCullough et al. (1999b) investigated close cell foam with the trade name Alulight. Their results show a different behaviour of foam under compression and tension. Under tensile load, the foam has semi-brittle behaviour, while the compression loading presents ductile behaviour. This type of foam has common properties with open-cell foams. In earlier research work (McCullough et al., 1999a), they studied crack propagation on the same material and highlighted the positive role of increased density in improving the plane strain fracture toughness and the unloading modulus.

Motz and Pippan (2001) confirm the different behaviour of tensile loading for the metal foam in comparison with the compression loading investigated closed-cell foam with two different densities ( 0.25 g/${cm}^3$ and 0.40 g/${cm}^3$). No deformation band was observed, except for the final failure.

Amsterdam et al. (2006) studied the spread of cracks in closed-cell foams under either monotonic or cyclic loading. Emphasis was placed on the microstructure of the foams, and the authors concluded that during uniaxial loading, the propagation of cracks occurs through the endodontic network of ${Al}_4$Ca while in the case of cyclic loading through the $Al$ dendrites.

Peroni et al. (2008) observed that the specimens showed significant non-linear behavior, even at low stress. This is explained due to the material non-homogeneity, thus weak points are created, which lead to plastic failure on low loads.

Wang et al. (2009) highlight the different behaviour, deformation, and fracture mechanics between tension and compression. Specimens did not show the deformation band except for the final failure. Also, their results for the loading and unloading modulus confirm the McCullough el. at (McCullough et al., 1999b) conclusions.

Vealy (2010) investigated specimens with different pores per inch (20 ppi and 40 ppi) and relative density of 6%–8% about the mechanical behaviour. He highlighted the significant difference between experimental results for elasticity modulus and theoretical predictions by Gibson and Ashby (1997). He explained the mentioned conclusion due to the difference in porosity and ligament geometry between porosities. Zimar et al. (2016) investigated the non-linear behaviour of metal foams under tensile loading using the finite element method and compared their simulation results with the experimental results by Vealy (2010). They found larger stress for the same strain in comparison with experimental results. Also, The Υoung’s modulus was higher than Gibson and Ashby’s theoretical values (1997).

Foroughi et al. (2013) investigated closed cell foam with the trade name Alulight. They exported models that allow FEM analysis to predict mechanical properties for cellular materials and hollow spheres’ structures or fiber architectures.

Marx and Rabiei (2020) investigated two specimens’ versions and pointed out the fracture areas that differ. To avoid the uniaxial loading due to the wrong position of specimens that were not centered, they used aluminium spacer on the grips for centering.

Vengatachalam et al. (2021) investigated closed-cell foam with the trade name Alporas with two different relative densities, 11.7%, and 17.2%, under other loading conditions. Significant differences were observed in the deformations of the specimens under tensile and compressive loads. They proposed an initial criterion for calculating the performance of closed-cell foams. This criterion is a performance criterion for closed-cell aluminum foams that sufficiently present the asymmetric nature of the yield surface with respect to the active voltage axis, as a parameter requires only uniaxial compressive strength.

Steel

One other common material for metal foam construction is steel (Salimon et al., 2005). Friedl et al. (2008) investigated the effect of density and structure of hollow sphere metal foams under tensile loading. They observed that the increase of density guides the more significant ultimate tensile strength of specimens.

Szyniszewski et al. (2014) investigated hollow sphere specimens that were characterized by small ductility. For the loading transfer to the specimen used, a steel plate into a notch in the specimen. The fracture is located between the connection zone of the spheres. The larger diameter spheres positively affect the total specimens’ strength, without changing their density.

Titanium

Titanium metal foam has many applications (Xue-Zheng, 2018).

Imwinkelried (2007) highlighted the better permeability of titanium foam compared with aluminum foam, making them suitable for medical applications. They also confirm the observations on compression and tensile loading in the research mentioned above. Kashef et al. (2010) observed that specimens with higher density show more considerable strength.

Other metals and alloys

Qing et al. (2020) investigated iron metal foam. They focused on achieving an effective bonded method between the iron foam and metal face. They used a bespoke construction consisting of a stainless-steel plate that came in contact with the specimen and connected by a steel rod with grips to perform the experiments.

Bolzoni et al. (2021) investigated $Fe+NaCl$ and $Ti+NaCl$ open and close cell foam. $Fe$ foam has better elastoplastic behaviour depending on $Ti,$ which exhibits pseudoplastic behaviour. According to the author’s conclusions, the empirical models cannot predict the behaviour of the general foam. On the other hand, structural-analytical models can give satisfactory results for specific mechanical properties, such as the measure of elasticity but a certain volume of pores. In summary, they developed new models for the efficient calculation of the mechanical properties of foams.

Table 3 includes summarized information for the physical properties of the foams, such as the density and relative density and the observed mechanical properties from the tests in the works reported in Table 2.

TABLE 3

TABLE 3. Mechanical Properties of foams.

It is noted that density increases lead to corresponding increases in Young’s modulus and tensile strength for the same type of material. Also, the connection bonds between the hollow spheres seems to be weaker than the connection bonds in foams made with classical methods.

Figures 5A–C, show the direct stress-strain curves presented in the above works.

FIGURE 5

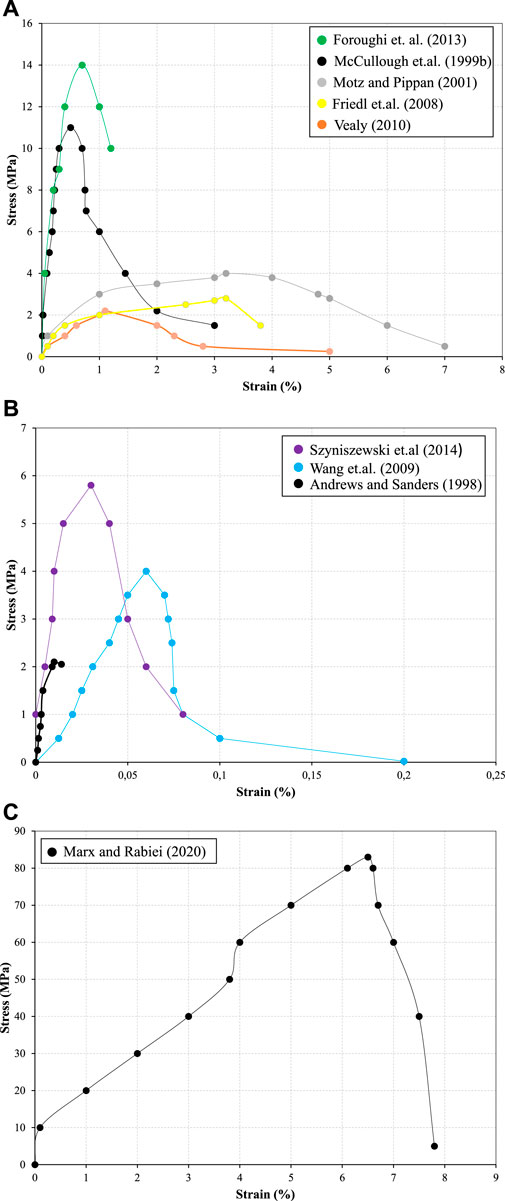
FIGURE 5. (A) and (B) Stress-Strain curves from the sources in Table 3. (C) Stress-Strain curve by Marx and Rabiei (2020) also presented in Table 3.

Figure 6 shows data for Relative Tensile Strength, $\raisebox{1ex}{${\sigma }^{*}$}\!\left/ \!\raisebox{-1ex}{${\sigma }_{ys}$}\right.$ , plotted against relative density, $\raisebox{1ex}{${\rho }^{*}$}\!\left/ \!\raisebox{-1ex}{${\rho }_s,$}\right.$ from the sources in Table 3. The solid blue, orange and grey curves represent the theoretical relationships for open cell, close cell, and hollow sphere metal foam, respectively. The above curves are described from the following mathematical relations:

$\raisebox{1ex}{${\sigma }^{*}$}\!\left/ \!\raisebox{-1ex}{${\sigma }_{ys}$}\right.=0.3{\left(\frac{{\rho }^{*}}{{\rho }_s}\right)}^{1.5}\left(opencell\right),$

$\raisebox{1ex}{${\sigma }^{*}$}\!\left/ \!\raisebox{-1ex}{${\sigma }_{ys}$}\right.=0.33{\left(\frac{{\rho }^{*}}{{\rho }_s}\right)}^2+0.44\left(\raisebox{1ex}{${\rho }^{*}$}\!\left/ \!\raisebox{-1ex}{${\rho }_s$}\right.\right)\left(closecell\right),$

FIGURE 6

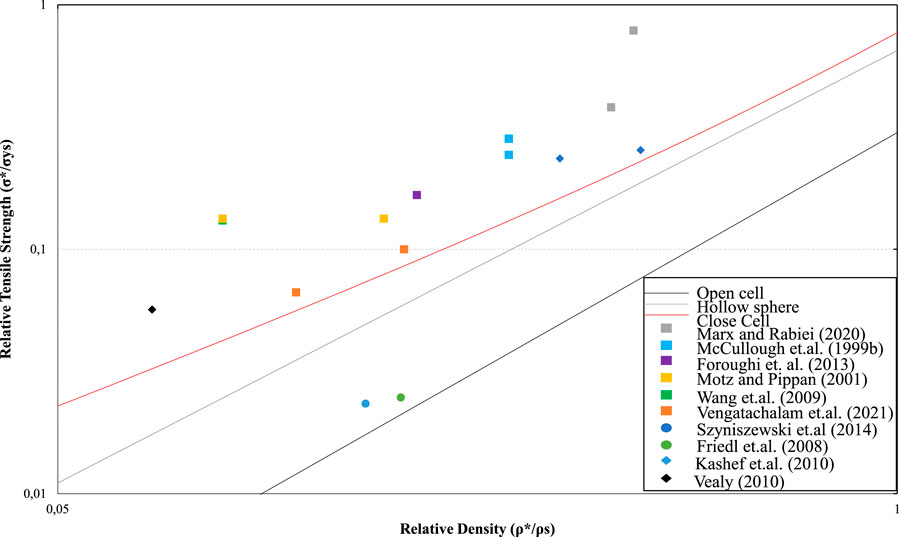
FIGURE 6. Values obtained from the aforementioned works for Relative Tensile Strength of foams against relative Density. Circles indicates hollow sphere foams, rhombuses indicate open-cell foams, and squares indicate closed cell foams. The scale in both axes is logarithmic.

$\raisebox{1ex}{${\sigma }^{*}$}\!\left/ \!\raisebox{-1ex}{${\sigma }_{ys}$}\right.=0.65{\left(\frac{{\rho }^{*}}{{\rho }_s}\right)}^{1.36}\left(hollowsphere\right)$ (Sanders and Gibson, 2003).

For the range of relative densities reported, the theoretical curves are generally conservative for relative strength. There is no real difference between the different types of metal porosity for the cases examined. Figure 6 shows the linearity between the values for open-cell foams and the important deduction from the theoretical line for this type of foam. The use of the same standard method (ASTM E8) in both works should be emphasized and can be taken as a possible reason for the deviation. For closed-cell foams, there is satisfactory comparison with the theoretical line. For the hollow sphere foams, the values are approximately the same, which can be inferred from the similar size/scale of specimens used in both works. There is also a smooth dispersion of values on both axes.

Figure 7 shows data relative to Young’s modulus of foams, $\raisebox{1ex}{${{\rm E}}^{*}$}\!\left/ \!\raisebox{-1ex}{${{\rm E}}_s$}\right.$ , plotted against relative density, $\raisebox{1ex}{${\rho }^{*}$}\!\left/ \!\raisebox{-1ex}{${\rho }_s$}\right.$. The solid blue curve represents the theory for open-cell foam. The solid orange and grey curves represent the theory for closed-cell foam with φ = 0.8 and φ = 0.6, respectively. The above lines are described from the following mathematical relation: $\raisebox{1ex}{$E^{*}$}\!\left/ \!\raisebox{-1ex}{$E_s$}\right.={\phi }^2{\left(\raisebox{1ex}{${\rho }^{*}$}\!\left/ \!\raisebox{-1ex}{${\rho }_s$}\right.\right)}^2+\left(1-\phi \right)\raisebox{1ex}{${\rho }^{*}$}\!\left/ \!\raisebox{-1ex}{${\rho }_s$}\right.$ , where φ = 1 for open-cell foam and φ = 0.6 or φ = 0.8 for close cell foam (Gibson and Ashby, 1997). The individual points are separate values for works in Table 3. It is clear that there is a deviation between the theoretical values and experimental ones. Martin (2021) highlights the significant difference between the theoretical estimation by Gibson and Ashby and experimental results. He also points out that some authors (Olurin et al., 2000; Kadkhodapour and Raeisi, 2014) consider the cause of this significant difference to be the defects that exist in the structures of metal foams, such as cavities and incorrect distribution of density, amongst others. There is a significant identification of all types of foam results with the theoretical line for open type foam, despite the fact that foams are closed cell or hollow spheres. It can be observed that the theoretical curves are relatively close to each other, but within what range of deviations from them can there be between them and the experimental values without worrying about the error in the specimens. In other words, what is the acceptable difference from the theoretical curves, for an experimental result to be valid. It should be emphasized that the significant difference that appears in the value that finds by Kashef et al. (2010) and in the theoretical curves can be explained by the size/scale of the specimens used by them.

FIGURE 7

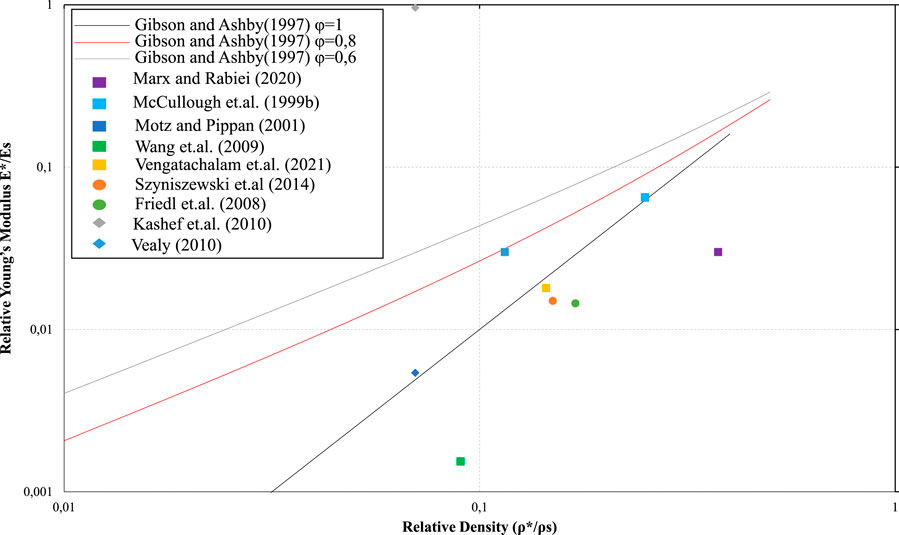
FIGURE 7. Comparison of theoretical values with the values obtained from the aforementioned works for Relative Young’s modulus of foams against relative density. Circles indicates hollow sphere foams, rhombuses indicate open-cell foams, and squares indicate closed cell foams. The scale in both axes is logarithmic.

Mechanical properties in shear

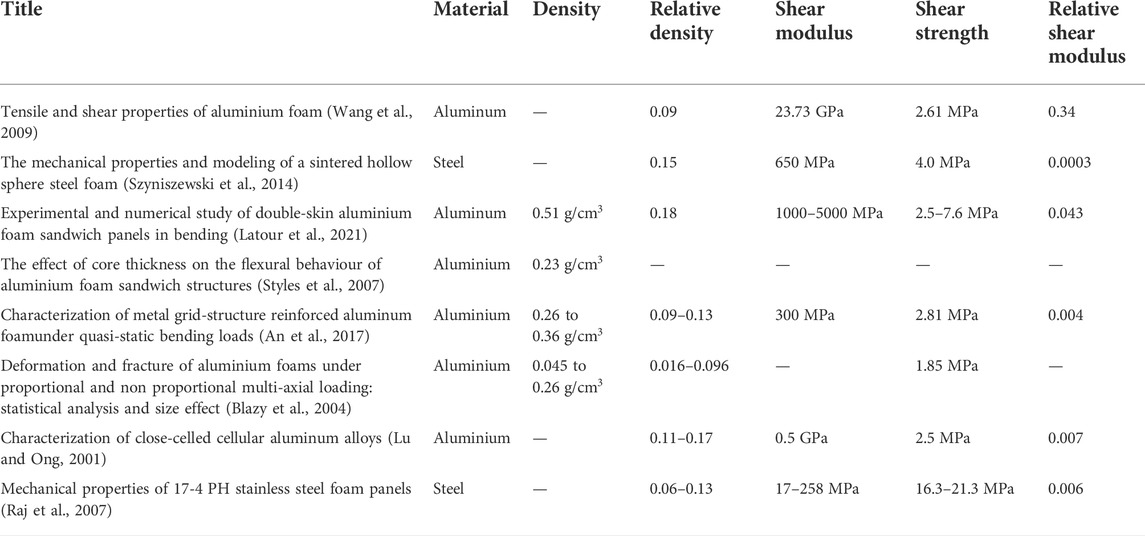
Metal foams as porous materials can take advantage of their low weight and can be used as core material in closed or sandwich structures (Golovin and Sinning, 2003). As core materials, they must exhibit shear rigidity and contribute to stress distribution in the specimens (Harte et al., 2000; Yao et al., 2019). Figure 8 shows the typical stress-strain curves for ductile materials in shear (Ishrat, 2013). The first part of the curve is the elastic region that is similar to tensile stress-strain curves. After the yield point shear stress, the plastic deformation of the specimen starts before the final fracture. Figure 9 shows the typical stress-strain curves for metal foams in shear (von Hagen and Bleck, 1998). Initially, the stress displacement curve is almost linearly elastic and then changes to plastic deformation. The maximum load is determined by the failure that is visible as a crack and determines the shear strength of the foam. Then the load decreases sharply. Table 4 shows research that studies the mechanical properties of metal foams under shear load.

FIGURE 8

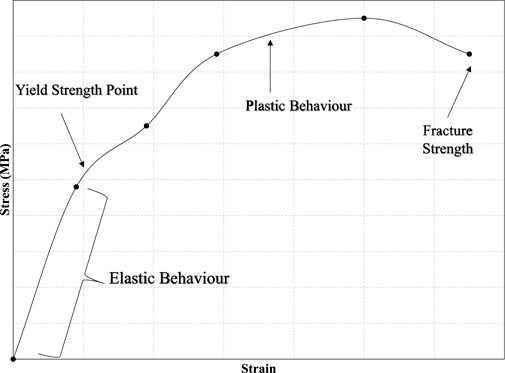
FIGURE 8. Shear Stress against shear strain (Ishrat, 2013).

FIGURE 9

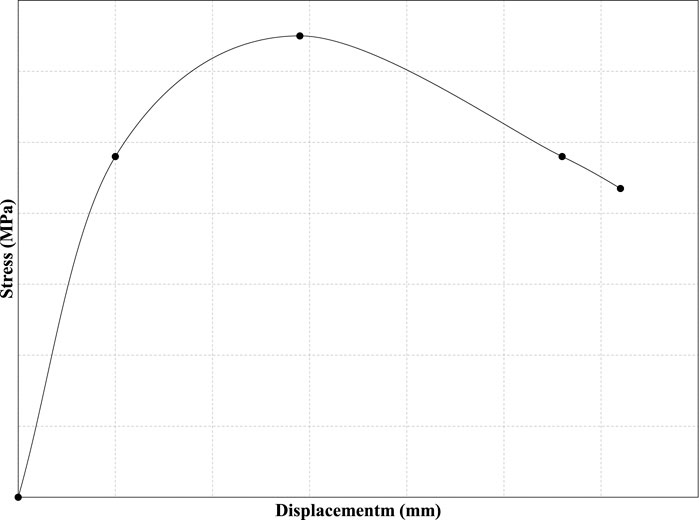
FIGURE 9. Stress-strain curves for the shear test for metal foams (von Hagen and Bleck, 1998).

TABLE 4

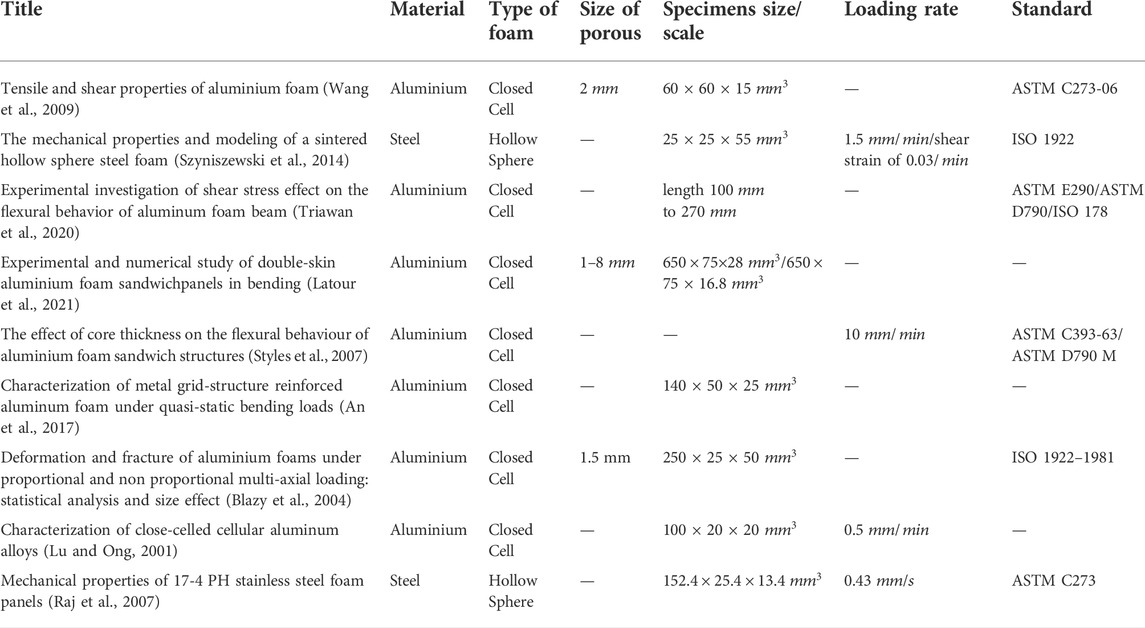
TABLE 4. Summary table of previous work and information about: type of foam, size of porous, specimens size/scale, loading rate, type of test, standard.

As in the case of tests under tension, no clear specific standard method was used in the works mentioned in Τable 4. The most prominent works for testing metal foams in shear, related to aluminium and steel as base materials.

Aluminium

Lu and Ong (2001) investigated the deformations mechanism of close cell foams. The specimens showed the expected results.

Blazy et al. (2004) used the longitudinal displacement of two stainless-steel plates to transfer the shear loading in the specimen.

Styles et al. (2007) studied the flexural behaviour of foam sandwich structures. They investigated the mechanical properties with four point bending tests. The stress-strain curve is under its standard form, as shown in Figure 2.

Wang et al. (2009) investigated the deformation mechanics of $Al$ close cell foam. Rigid plates were used to ensure the best bond between the specimens and the test machine grips. The resulting curve confirms the behaviours mentioned above for shear stress-strain.

An et al. (2017) investigated foam enhanced with metal grid structure under three-point bending loads. The enhanced specimens had better mechanical properties compared with the typical specimens.

Triawan et al. (2020) studied the flexure behaviour of close cell foam under shear stress. They selected a three-point bending configuration for the experimental tests with different lengths of sandwich beam specimens. Their results show a significant difference between the experimental and theoretical values (Timoshenko, 1921).

Latour et al. (2021) look into double-skin aluminum foam sandwich panels in bending. They used three types of glue to create the specimens and discovered through three-point testing that shear strength and modulus of specimens differ according to the kind of adhesive.

Steel

Raj et al. (2007) investigated the mechanical properties of 17-4 PH stainless steel foam panels. They point out that failures are evident either in the foam and sheet metal interface in poorly welded specimens or in the foam core in well-welded specimens and suggest the development of welding methods.

Szyniszewski et al. (2014) examined the mechanical properties of hollow sphere (HS) steel foam under shear stress. To stabilize specimens on the test machine, they tried to create flat surfaces, but limited quantities of epoxy were strong enough to hold the total specimen. For this reason, they reduced the specimens size comparison with the standard that they used. The stress-strain curves confirmed the expected behaviour.

Table 5 includes summarized information for the physical properties of the foams, such as the density and relative density and the observed mechanical properties from the tests in the works reported in Table 4.

TABLE 5

TABLE 5. Mechanical Properties of foam.

Table 5 shows that the type of foam impacts the specimens’ shear strength and moduli. In other words, the connection between the spheres is weaker in proportion to the contact created on foams made with classical methods.

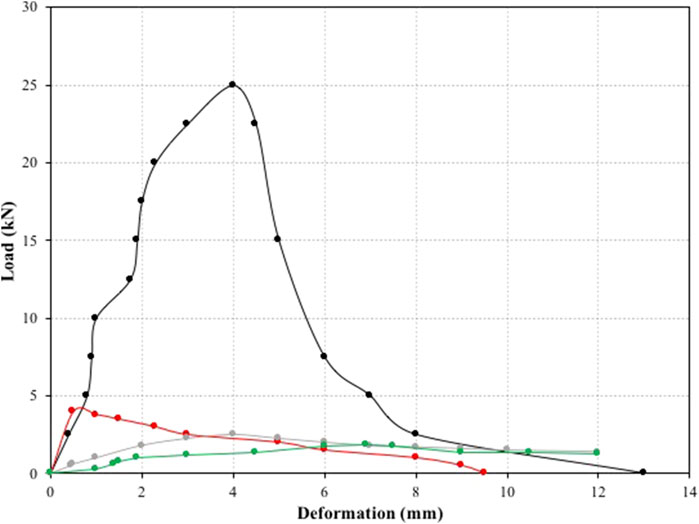
Figures 10, 11 show the shear stress-shear strain and load-deformation curves presented in the above works, respectively. All the data included in Figure 10 were gathered via shear tests. In Figure 11, all the data emerged from bending tests except from the black curve data (Wang et al., 2009) which was produced by shear test.

FIGURE 10

FIGURE 10. Stress-Strain curve from above mentioned works.

FIGURE 11

FIGURE 11. Load-Deformantion curve from above mentioned works.

Figure 12 show data for Relative Shear Strength, $\raisebox{1ex}{${\tau }^{*}$}\!\left/ \!\raisebox{-1ex}{${\sigma }_{ys}$}\right.$ , plotted against relative density, $\raisebox{1ex}{${\rho }^{*}$}\!\left/ \!\raisebox{-1ex}{${\rho }_s$}\right.$, from the above works. The above curves are described from the following mathematical relation:

$\raisebox{1ex}{${\tau }^{*}$}\!\left/ \!\raisebox{-1ex}{${\sigma }_{ys}$}\right.=0.21{\left(\frac{{\rho }^{*}}{{\rho }_s}\right)}^{1.5}\left(opencell\right),$

$\raisebox{1ex}{${\tau }^{*}$}\!\left/ \!\raisebox{-1ex}{${\sigma }_{ys}$}\right.=0.23(\frac{{\rho }^{*}}{{\rho }_s}{)}^2+0.3(\frac{{\rho }^{*}}{\rho })(closecell),$

FIGURE 12

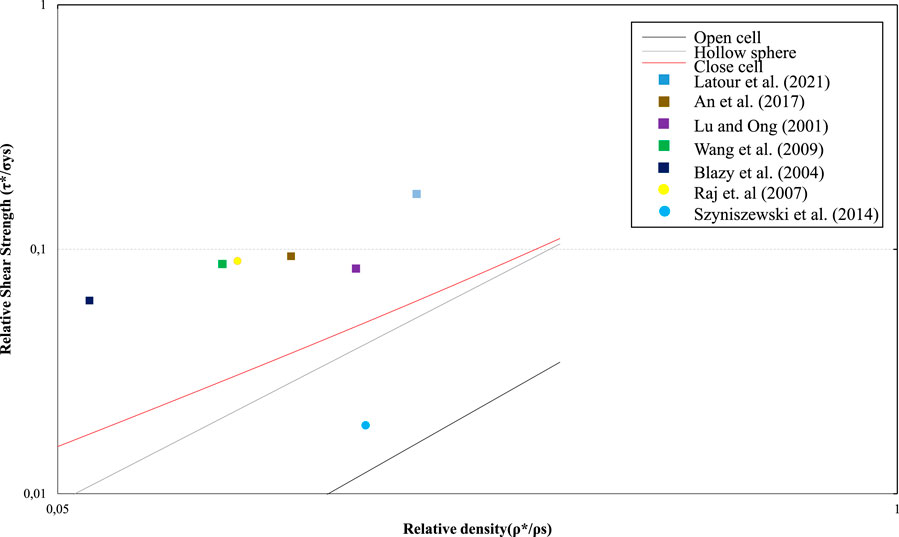
FIGURE 12. Values obtained from the aforementioned works for Relative Shear Strength of foams against Relative density. Circles indicates hollow sphere foams, rhombuses indicate open-cell foams, and squares indicate closed cell foams. The scale in both axes is logarithmic.

$\raisebox{1ex}{${\tau }^{*}$}\!\left/ \!\raisebox{-1ex}{${\sigma }_{ys}$}\right.=0.54{\left(\frac{{\rho }^{*}}{{\rho }_s}\right)}^{1.36}\left(hollowsphere\right)$ (Sanders and Gibson, 2003).

Figure 12 indicates the deviation between the theoretical curves and the experimental values. Linearity is observed between the values of the experimental specimens in the case of closed-cell foam. However, there is no match in the size of the specimens. Also, from Figure 12, it appears that no value is identical to the theoretical curves. Something like this is expected, but at what distance from the theoretical one can a value be accepted since these values have emerged from experimental tests based on different standards. There is also a relatively smooth dispersion of values on both axes with the exception of the value associated with Szyniszewski et al. (2014).

Figure 13 shows data for relative Shear modulus of foams, $\raisebox{1ex}{$G$}\!\left/ \!\raisebox{-1ex}{${{\rm E}}_s$}\right.$ , plotted against relative density, $\raisebox{1ex}{${\rho }^{*}$}\!\left/ \!\raisebox{-1ex}{${\rho }_s$}\right.$. The solid light blue curve represents the theory for open-cell foam. The solid dark blue and red curve represent the theory for closed-cell foam with φ = 0.8 and φ = 0.6, respectively. The above lines are described from the following mathematical relation:$\raisebox{1ex}{$G^{*}$}\!\left/ \!\raisebox{-1ex}{$E_s$}\right.=\raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$8$}\right.\left[{\phi }^2\left(\raisebox{1ex}{${\rho }^{*}$}\!\left/ \!\raisebox{-1ex}{${\rho }_s$}\right.\right)+\left(1-\phi \right)\raisebox{1ex}{${\rho }^{*}$}\!\left/ \!\raisebox{-1ex}{${\rho }_s$}\right.\right]$, where φ = 1 for open-cell foam and φ = 0.6 or φ = 0.8 for close cell foam (Gibson and Ashby, 1997). The experimental values are outside the expected limits of the theoretical values. Something expected based on Martin research (2021). Furthermore, the experimental values are all in a very small segment of relative density (0.09–0.18). Ιt is observed that the two works deviate significantly from the theoretical curves. There is also an identification of the value of two works related to closed type foam works with the theoretical open type foam curve. There are no data demonstrating that these projects fall into the category with φ = 0.6 or in the category with φ = 0.8, so that the extent of the deviations can be accurately determined.

FIGURE 13

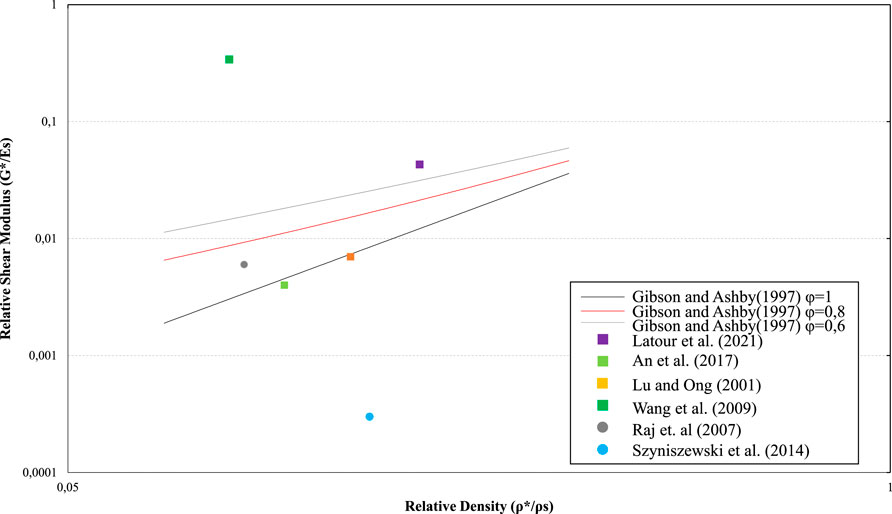
FIGURE 13. Comparison of theoretical values with the values obtained from the aforementioned works for Relative Shear Modulus of foams against Relative Density. Circles indicate hollow sphere foams and squares indicate closed cell foams. The scale in both axes is logarithmic.

Discussion

The current research work aims to collect different experimental studies on the mechanical properties of metal foams, particularly in tension and shear.

For metal foams and other porous materials under tension, one of the main deductions from Table 2 is that there is no connection between the cell size and the loading rate. Even though a significant number of the above works use ASTM E8, this is conducted broadly with diverging geometric specimen parameters and loading rates. ASTM E8 is a standard for metallic materials, so for this reason parameters pertinent to the cell size of the specimens were not considered. For confirmation of this, the conclusions of Figure 6 in the case of open-cell foam experiments can be considered, where the deviation between the theoretical curve and experimental results is highlighted, and the possible reasons for that. The general conclusion from Tables 2, 4 is that there is no single standard for this type of material. In the case of shear, no specific standard was followed in the works mentioned herein. Indeed, this fact is a reasonable basis for further investigation and development of specific techniques and methods for studying the mechanical properties of foams against the effect of shear loads. A specific standard for shear test, that can produce reproducible results can provide the industry with confidence for the uptake of the material from the industry.

According to Tables 2, 4, a small percentage of work that focused on the mechanical properties investigation of open cell foams appears. The open cell foam applications are found it multi areas (medical applications, Noise absorption etc.) (Quadbeck, 2016). What is quite interesting is that, while this type of foams could have applications in leading sectors of industry, currently it attracts such little interest. This may be occurring due to the adoption of standards that can contribute to their study in tensile and shear, or possibly the combination of technical and economic reasons compared to closed cell foams. A similar small number of works investigated hollow sphere foams. This may be connected to the complicated production process of this type of foam as well, which might be creating scaling challenges.

According to Table 3, as the relative density increases, it leads to more significant tensile strength. This connection between the relative density and strength does not follow through under shear loading, in any case, the number of relevant publications on this is very small, as in the case of shear, Table 5. For this reason, no clear deductions can be drawn, and more tests should be undertaken over a larger range of relative densities, as well as specimen dimensions.

Another feature that stands out from Figures 3, 5, 10 is that hollow sphere structures exhibit better behaviour under stress than the other two types of metal foams. This is confirmed by higher stability and resistance to deformation that showed on mentioned Figures.

Figures 6, 7, 12, 13 indicate that the theoretical limits are conservative and need to include more data from different relative densities. Also, in order to improve the results and increase the accuracy, the effect of the microstructure of the specimens on the determination of the limits, as mentioned above, should be investigated in future works. Possible changes in the mathematical formula should also be considered to consider the differences between the experimental results and the theoretical calculations made for ideal samples. The percentage differences experimental results may present compared to the theoretical values from the curves within which the former can be accepted should also be defined/clarified. In other words, the acceptance distance between a theoretical and an experimental curve must be defined, where within which the second can be accepted.

Conclusion

This article provides an overview of findings pertinent to key aspects of the mechanical behaviour of metal foams under two types of loading. It records essential mechanical parameters of metal foams such as Young’s modulus, tensile and shear strength, relative density, etc. Significant gaps were discovered in the experimental methodology, the theoretical calculation of mechanical properties, and the evaluation of mechanical properties in tension and shear. In shear there is a linear relationship between shear strength and relative density, something similar did not occur in tension. It was also observed that in works where the specimens have a similar size/dimensions and obviously the same type of foam had similar values for their mechanical properties. In tensile strength the relative tensile strength is maintained within a certain range despite the variation of the relative density which can be related to the base material that is the same in most experimental specimens.

When designing mechanical tests, careful selection should be made for their geometric features and the metal foam type of material. This is confirmed by the different characteristics of the specimens included in Tables 2–5, as well as the other materials that have been selected, which are also associated with the final use of the foam. For example, titanium is selected as a structural material in medical applications, while in heavier structures, aluminium and steel or their alloys could be used. In other words, the origin material of metal foams provides different foam properties connected with tensile or shear strength, Young’s modulus and Shear modulus.

The current work highlights the difference between the theoretical and experimental values for some of the main mechanical properties of metal foams. As a result, the connection between theoretical and experimental values, needs further investigation, more specifically regarding the mathematical relationship limits for calculating the mechanical properties of foams (Young’s modulus and Shear Modulus). One parameter that may be of interest in future research is the effect of microstructure on the determination of these limits.

Metal foams have many applications in the industry due to their physical and mechanical properties. More specifically, they can be used as core material in open or closed structures, due to their ability to distribute stress in the specimen under shear stress. Specifically as a core material in sandwich panels, it can be a promising solution for bridge decks (Tuwair et al., 2016; Saleem et al., 2021), or blast walls (Balázs et al., 2017) or other floating structures under hydrodynamic loading (Grabian et al., 2017), due to the potential benefits of mitigating buckling in compression or bending and dissipating energy in collision or under cycling loading.

This leads to the conclusion that it is helpful to have a specific methodology or standards for identifying the properties of these materials. This is not the case now, as the works summarized in the present study use different standards for specimen preparation and test protocols. Even in the case where a particular standard was used, its use was in broad terms without coherence to loading rates and specimen size. This may be a reason for the difference between the theoretical and experimental results presented in Figures 6, 7, 12, 13. The lack of a specific standard for tensile and shear tests may hamper further industry use of this type of material, thus a consistent experimental method/standard exclusively for these two types of loading is necessary and should be prioritized.

Author contributions

TK and SY shared equally the collection and processing of data as well as the critique and discussion of the findings.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alavi, R., Akbarzadeh, A. H., and Hermawan, H. (2021). Post-corrosion mechanical properties of absorbable open cell iron foams with hollow struts. J. Mech. Behav. Biomed. Mater. 117 (2020), 104413. doi:10.1016/j.jmbbm.2021.104413

PubMed Abstract | CrossRef Full Text | Google Scholar

Allioux, F. M., Merhebi, S., Tang, J., Idrus-Saidi, S. A., Abbasi, R., Saborio, M. G., et al. (2020). Catalytic metal foam by chemical melting and sintering of liquid metal nanoparticles. Adv. Funct. Mat. 30 (5), 1907879. doi:10.1002/ADFM.201907879

CrossRef Full Text | Google Scholar

Amsterdam, E., De Hosson, J. T. M., and Onck, P. R. (2006). Failure mechanisms of closed-cell aluminum foam under monotonic and cyclic loading. Acta Mater. 54 (17), 4465–4472. doi:10.1016/j.actamat.2006.05.033

CrossRef Full Text | Google Scholar

An, Y., Yang, S., Zhao, E., and Wang, Z. (2017). Characterization of metal grid-structure reinforced aluminum foam under quasi-static bending loads. Compos. Struct. 178, 288–296. doi:10.1016/J.COMPSTRUCT.2017.07.031

CrossRef Full Text | Google Scholar

Andrews, E., Sanders, W., and Gibson, L. J. (1998). Compressive and tensile behaviour of aluminum foams. Mater. Sci. Eng. A A270, 113–124. doi:10.1016/s0921-5093(99)00170-7

CrossRef Full Text | Google Scholar

Ashby, M. F., Evans, T., Fleck, N. A., Hutchinson, J. W., Wadley, H. N. G., Gibson, L. J., et al. (2000a). Metal foams: A design guide library of congress cataloguing-in-publication data. 1st edition. Amsterdam, Netherlands: Elsevier. Available at: http://www.bh.com (Accessed: September 3, 2021).

Google Scholar

Ashby, M. F., Evans, T., Fleck, N. A., Hutchinson, J. W., Wadley, H. N. G., Gibson, L. J., et al. (2000b). Metal foams: Α design. Oxford: UK: Butterworth Heinemann. Banhart. doi:10.1016/S0261-3069(01)00049-8

CrossRef Full Text | Google Scholar

ASTM E8 (2010). ASTM E8/E8M standard test methods for tension testing of metallic materials 1. West Conshohocken, Pennsylvania, United States: Annual Book of ASTM Standards 4 C, 1–27. doi:10.1520/E0008

CrossRef Full Text | Google Scholar

ASTM-C273-C273M-11 (2011). ‘ASTM-C273-C273M-11-Shear_properties_of_sandwich_core_materials.pdf’.

Balázs, D. A., Nyikes, Z., and Kovács, T. (2017). Building protection with composite materials application. Key Eng. Mat. 755, 286–291. doi:10.4028/WWW.SCIENTIFIC.NET/KEM.755.286

CrossRef Full Text | Google Scholar

Banhart, J. (2013). Light-metal foams - history of innovation and technological challenges. Adv. Eng. Mat. 15 (3), 82–111. doi:10.1002/adem.201200217

CrossRef Full Text | Google Scholar

Bastawros, A. F., Bart-Smith, H., and Evans, A. G. (2000). Experimental analysis of deformation mechanisms in a closed-cell aluminum alloy foam. J. Mech. Phys. Solids 48 (2), 301–322. doi:10.1016/S0022-5096(99)00035-6

CrossRef Full Text | Google Scholar

Bisht, A., Patel, V. K., and Gangil, B. (2019). Future of metal foam materials in automotive industry. in Automotive tribology, 51–63. doi:10.1007/978-981-15-0434-1_4

CrossRef Full Text | Google Scholar

Biswas, S. (2022). A low-cost non-conventional method for the determination of the Young modulus of the material of a cantilever. Phys. Educ. 57 (5), 055022. doi:10.1088/1361-6552/AC7D88

CrossRef Full Text | Google Scholar

Blazy, J. S., Marie-Louise, A., Forest, S., Chastel, Y., Pineau, A., Awade, A., et al. (2004). Deformation and fracture of aluminium foams under proportional and non proportional multi-axial loading: Statistical analysis and size effect. Int. J. Mech. Sci. 46 (2), 217–244. doi:10.1016/J.IJMECSCI.2004.03.005

CrossRef Full Text | Google Scholar

Bolzoni, L., Carson, J. K., and Yang, F. (2021). Combinatorial structural-analytical models for the prediction of the mechanical behaviour of isotropic porous pure metals. Acta Mater. 207, 116664. doi:10.1016/j.actamat.2021.116664

CrossRef Full Text | Google Scholar

Buonomo, B., Cascetta, F., di Pasqua, A., and Manca, O. (2022). ‘Performance parameters enhancement of a thermoelectric generator by metal foam in exhaust automotive lines. doi:10.2139/ssrn.4054207

CrossRef Full Text | Google Scholar

Carranza, I., Crocombe, A. D., Mohagheghian, I., Smith, P. A., Sordon, A., Meeks, G., et al. (2019). Characterising and modelling the mechanical behaviour of polymeric foams under complex loading. J. Mat. Sci. 54 (16), 11328–11344. doi:10.1007/s10853-019-03673-8

CrossRef Full Text | Google Scholar

Chen, C., Zhao, S., Tang, X., Yi, H., Gao, F., Yu, Q., et al. (2023). δ-MnO2 decorated layered double oxides in-situ grown on nickel foam towards electrothermal catalysis of n-heptane. J. Environ. Sci. 126, 308–320. doi:10.1016/J.JES.2022.03.017

CrossRef Full Text | Google Scholar

Chibani, A., Merouani, S., and Benmoussa, F. (2021). Computational analysis of the melting process of Phase change material-metal foam-based latent thermal energy storage unit: The heat exchanger configuration. J. Energy Storage 42, 103071. doi:10.1016/J.EST.2021.103071

CrossRef Full Text | Google Scholar

Davis, J. R. (2004). Tensile testing, Editors J. R. Davis, and D. Associates. 2nd edition (Materials Park, Ohio: ASM International). Available at: https://www.asminternational.org/search/-/journal_content/56/10192/05106G/PUBLICATION.

Google Scholar

Du, R., Jin, X., Hubner, R., Fan, X., Hu, Y., and Eychmuller, A. (2020). Engineering self-supported noble metal foams toward electrocatalysis and beyond. Adv. Energy Mat. 10 (11), 1901945. doi:10.1002/AENM.201901945

CrossRef Full Text | Google Scholar

Farhadi, S., Kafili, D., and Ziadloo, S. (2020). Review of aluminum foam applications in architecture. Eur. J. Eng. Sci. Technol. 3 (1), 62–70. doi:10.33422/EJEST.V3I1.162

CrossRef Full Text | Google Scholar

Foroughi, B., Degischer, H. P., and Kottar, A. (2013). Characterization and simulation of tensile deformation of non-uniform cellular aluminium until damage. Adv. Eng. Mat. 15 (4), 276–286. doi:10.1002/adem.201200163

CrossRef Full Text | Google Scholar

Friedl, O., Motz, C., Peterlik, H., Puchegger, S., Reger, N., and Pippan, R. (2008). Experimental investigation of mechanical properties of metallic hollow sphere structures. Metall. Materi. Trans. B 39 (1), 135–146. doi:10.1007/s11663-007-9098-2

CrossRef Full Text | Google Scholar

Galvagnini, F., Valentini, F., and Dorigato, A. (2022). Development of polymeric insulating foams for low-temperature thermal energy storage applications. J. Appl. Polym. Sci. 139 (25), e52397. doi:10.1002/APP.52397

CrossRef Full Text | Google Scholar

García-Moreno, F. (2016). Commercial applications of metal foams: Their properties and production. Materials 9 (2), 85–24. doi:10.3390/ma9020085

CrossRef Full Text | Google Scholar

Gibson, L. J., and Ashby, M. F. (1997). Cellular solids: Structure and properties. second edition. Cambridge, United Kingdom: Cambridge University Press. doi:10.1017/CBO9781139878326

CrossRef Full Text | Google Scholar

Golovin, I. S., and Sinning, H. R. (2003). Damping in some cellular metallic materials. J. Alloys Compd. 355 (1–2), 2–9. doi:10.1016/S0925-8388(03)00241-X

CrossRef Full Text | Google Scholar

Google Ngram Viewer (2022). Google Ngram viewer. Available at: https://books.google.com/ngrams/graph?content=metal+foam&year_start=1800&year_end=2019&corpus=26&smoothing=3&direct_url=t1%3B%2Cmetalfoam%3B%2Cc0#t1%3B%2Cmetalfoam%3B%2Cc0 (Accessed April 11, 2022).

Google Scholar

Grabian, J., Ślączka, A., Pawłowska, P., and Kostrzewa, W., (2017). The role of innovative composite materials in the safe and efficient operation of floating marine structures. Zesz. Nauk. Akad. Morskiej w Szczecinie 52 (124), 23–29. doi:10.17402/241

CrossRef Full Text | Google Scholar

Harte, A. M., Fleck, N. A., and Ashby, M. F. (2000). Sandwich panel design using aluminum alloy foam. Adv. Eng. Mat. 2 (4), 219–222. doi:10.1002/(sici)1527-2648(200004)2:4<219:aid-adem219>3.0.co;2-#

CrossRef Full Text | Google Scholar

Hibbeler, R. C., and Yap, K. B. (2018). Mechanics of materials. Editor K. B. Yap. 10th edition (London, United Kingdom: Pearson Education Limited). Available at: https://books.google.com/books/about/Mechanics_of_Materials.html?id=hCgrvgAACAAJ (Accessed August 31, 2022).

Google Scholar

Hu, Y., Zhuo, H., Chen, Z., Peng, X., Zhong, L., and Sun, R. (2021). Metal coordination assists fabrication of multifunctional aerogel. J. Mat. Sci. Technol. 71, 67–74. doi:10.1016/j.jmst.2020.09.007

CrossRef Full Text | Google Scholar

Huang, X., Chen, X., Li, A., Atinafu, D., Gao, H., Dong, W., et al. (2019). Shape-stabilized phase change materials based on porous supports for thermal energy storage applications. Chem. Eng. J. 356, 641–661. doi:10.1016/J.CEJ.2018.09.013

CrossRef Full Text | Google Scholar

Imwinkelried, T. (2007). Mechanical properties of open-pore titanium foam. J. Biomed. Mat. Res. A 81 (4), 964–970. doi:10.1002/jbm.a.31118

PubMed Abstract | CrossRef Full Text | Google Scholar

Iowa State University of Science and Technology (2020). Nondestructive evaluation physics: Materials. Available at: https://www.nde-ed.org/Physics/Materials/Mechanical/FatigueGrowthRate.xhtml (Accessed: June 23, 2021).

Google Scholar

Ishrat, A. K. (2013). Shear stress strain curve & modulus of rigidity (10.01.03.039). Available at: https://www.slideshare.net/pixyafsana/shear-stress-strain-curve-modulus-of-rigidity-100103039 (Accessed: 6 July 2021).

Google Scholar

Jin, I., Kenny, L. D., and Sang, H. (1990). United States patent-METHOD of producing lightweight foamed metal. US Patent, 96(19), 62–66.

Kadkhodapour, J., and Raeisi, S. (2014). Micro–macro investigation of deformation and failure in closed-cell aluminum foams. Comput. Mater. Sci. 83, 137–148. doi:10.1016/J.COMMATSCI.2013.10.017

CrossRef Full Text | Google Scholar

Kai Li, X. (2000). Fundamentals of fluid mechanics by joseph A. Schetz and allen E. Fuhs (eds.), John wiley & sons, New York, 1999, price £80.95. ISBN 0-471-34856-2, 935 pp. J. Newt. Fluid Mech. 91 (2–3), 297. doi:10.1016/S0377-0257(99)00088-9

CrossRef Full Text | Google Scholar

Kashef, S., Asgari, A., Hilditch, T. B., Yan, W., Goel, V. K., and Hodgson, P. D. (2010). Fracture toughness of titanium foams for medical applications. Mater. Sci. Eng. A 527 (29–30), 7689–7693. doi:10.1016/j.msea.2010.08.044

CrossRef Full Text | Google Scholar

Kulshreshtha, A., and Dhakad, S. K. (2020). Preparation of metal foam by different methods: A review. Mater. Today Proc. 26, 1784–1790. doi:10.1016/J.MATPR.2020.02.375

CrossRef Full Text | Google Scholar

Lafdi, K., Mesalhy, O., and Elgafy, A. (2008). Graphite foams infiltrated with phase change materials as alternative materials for space and terrestrial thermal energy storage applications. Carbon 46 (1), 159–168. doi:10.1016/J.CARBON.2007.11.003

CrossRef Full Text | Google Scholar

Latour, M., D’Aniello, M., Landolfo, R., and Rizzano, G. (2021). Experimental and numerical study of double-skin aluminium foam sandwich panels in bending. Thin-Walled Struct. 164, 107894. doi:10.1016/J.TWS.2021.107894

CrossRef Full Text | Google Scholar

Lei, J., Tian, Y., Zhou, D., Ye, W., Huang, Y., and Zhang, Y. (2021). Heat transfer enhancement in latent heat thermal energy storage using copper foams with varying porosity. Sol. Energy 221, 75–86. doi:10.1016/J.SOLENER.2021.04.013

CrossRef Full Text | Google Scholar

Liu, X., Zhao, D., Guan, D., Becker, S., Sun, D., and Sun, X. (2022). Development and progress in aeroacoustic noise reduction on turbofan aeroengines. Prog. Aerosp. Sci. 130, 100796. doi:10.1016/J.PAEROSCI.2021.100796

CrossRef Full Text | Google Scholar

Lu, T. J., and Ong, J. M. (2001). Characterization of close-celled cellular aluminum alloys. J. Mat. Sci. 36 (11), 2773–2786. doi:10.1023/A:1017977216346

CrossRef Full Text | Google Scholar

Madhavan, S., Singh, P., and Ekkad, S. (2019). Jet impingement heat transfer enhancement by packing high-porosity thin metal foams between jet exit plane and target surface. J. Therm. Sci. Eng. Appl. 11 (6). 1. doi:10.1115/1.4043470

CrossRef Full Text | Google Scholar

Mahadev, M. R., Sreenivasa, C. G., and Shivakumar, K. M. (2018). A review on prodution of aluminium metal foams. IOP Conf. Ser. Mat. Sci. Eng. 376 (1), 012081. doi:10.1088/1757-899X/376/1/012081

CrossRef Full Text | Google Scholar

Maimouni, I., Cejas, C. M., Cossy, J., Tabeling, P., and Russo, M. (2020). Microfluidics mediated production of foams for biomedical applications. Micromachines 11 (1), 83. doi:10.3390/MI11010083

CrossRef Full Text | Google Scholar

Martín, E. P. (2021). Microstructural parameters affecting the compressive response of closed-cell aluminum foams. Mech. Adv. Mater. Struct. 29 (18), 2639–2651. doi:10.1080/15376494.2021.1872747

CrossRef Full Text | Google Scholar

Marx, J., and Rabiei, A. (2020). Tensile properties of composite metal foam and composite metal foam core sandwich panels. Jnl. Sandw. Struct. Mater. 23, 3773–3793. doi:10.1177/1099636220942880

CrossRef Full Text | Google Scholar

McCullough, K. Y. G., Fleck, N. A., and Ashby, M. F. (1999a). Toughness of aluminium alloy foams. Acta Mater. 47 (8), 2331–2343. doi:10.1016/S1359-6454(99)00125-1

CrossRef Full Text | Google Scholar

McCullough, K. Y. G., Fleck, N. A., and Ashby, M. F. (1999b). Uniaxial stress–strain behaviour of aluminium alloy foams. Acta Mater. 47 (8), 2323–2330. doi:10.1016/S1359-6454(99)00128-7

CrossRef Full Text | Google Scholar

Mert, H. H., Kekevi̇, B., Mert, E. H., and Mert, M. S. (2022). Development of composite phase change materials based on n-tetradecane and β-myrcene based foams for cold thermal energy storage applications. Thermochim. Acta 707, 179116. doi:10.1016/J.TCA.2021.179116

CrossRef Full Text | Google Scholar

Miyoshi, T., Itoh, M., Akiyama, S., and Kitahara, A. (1998). Aluminum foam, “ALPORAS”: The production process, properties and applications. MRS Proc. 521, 133–137. doi:10.1557/PROC-521-133

CrossRef Full Text | Google Scholar

Motz, C., and Pippan, R. (2001). Deformation behaviour of closed-cell aluminium foams in tension. Acta Mater. 49 (13), 2463–2470. doi:10.1016/S1359-6454(01)00152-5

CrossRef Full Text | Google Scholar

Murugesan, G., and Mansuri, H. (2018). Experimental study of composite foam sandwich structures for aerospace applications. SSRG Int. J. Mech. Eng. (SSRG-IJME) 5, 17–19. doi:10.14445/23488360/IJME-V5I3P104

CrossRef Full Text | Google Scholar

Nisa, S. U., Pandey, S., and Pandey, P. (2022). A review of the compressive properties of closed-cell aluminum metal foams. Proc. Inst. Mech. Eng. E: J. Process Mech. Eng.. doi:10.1177/09544089221112291

CrossRef Full Text | Google Scholar

Olurin, O. B., Fleck, N. A., and Ashby, M. F. (2000). Deformation and fracture of aluminium foams. Mater. Sci. Eng. A 291 (1–2), 136–146. doi:10.1016/S0921-5093(00)00954-0

CrossRef Full Text | Google Scholar

Papadopoulos, D. P., Konstantinidis, I., Papanastasiou, N., Skolianos, S., Lefakis, H., and Tsipas, D. (2004). Mechanical properties of Al metal foams. Mater. Lett. 58 (21), 2574–2578. doi:10.1016/j.matlet.2004.03.004

CrossRef Full Text | Google Scholar

Parveez, B., Jamal, N. A., Anuar, H., Ahmad, Y., Aabid, A., and Baig, M. (2022). Microstructure and mechanical properties of metal foams fabricated via melt foaming and powder metallurgy technique: A review. Materials 15, 5302. doi:10.3390/MA15155302

PubMed Abstract | CrossRef Full Text | Google Scholar

Patel, P., Bhingole, P. P., and Makwana, D. (2018). Manufacturing, characterization and applications of lightweight metallic foams for structural applications: Review. Mater. Today Proc. 5 (9), 20391–20402. doi:10.1016/j.matpr.2018.06.414

CrossRef Full Text | Google Scholar

Peroni, L., Ã, M. A., and Peroni, M. (2008). The mechanical behaviour of aluminium foam structures in differentloading conditions. Int. J. Impact Eng. 35, 644–658. doi:10.1016/j.ijimpeng.2007.02.007

CrossRef Full Text | Google Scholar

Qing, H. B., Liu, P. S., and Xu, X. B. (2020). Primary investigation on an iron foam sandwich structure. Met. Mat. Int. 27, 610–617. doi:10.1007/s12540-020-00830-6

CrossRef Full Text | Google Scholar

Quadbeck, P. (2016). Open cell metal foams. Fraunhofer Inst. Manuf. Technol. Adv. Mater. IFAM, Branch lab Dresden, 4–5. Available at: http://www.ifam.fraunhofer.de/content/dam/ifam/en/documents/dd/Infoblätter/open_cell_metal_foams_fraunhofer_ifam_dresden.pdf.

Google Scholar

Raj, S. V., Ghosn, L., Lerch, B., Hebsur, M., Cosgriff, L., and Fedor, J. (2007). Mechanical properties of 17-4PH stainless steel foam panels. Mater. Sci. Eng. A 456 (1–2), 305–316. doi:10.1016/J.MSEA.2006.11.142

CrossRef Full Text | Google Scholar

Rajak, D. K., and Gupta, M. (2020). Introduction to metallic foams. Adv. Struct. Mater. 145, 1–20. doi:10.1007/978-981-15-9069-6_1

CrossRef Full Text | Google Scholar

Rodriguez-Contreras, A., Punset, M., Calero, J. A., Gil, F. J., Ruperez, E., and Manero, J. M. (2021). Powder metallurgy with space holder for porous titanium implants: A review. J. Mat. Sci. Technol. 76, 129–149. doi:10.1016/j.jmst.2020.11.005

CrossRef Full Text | Google Scholar

Sajid Hossain, M., and Shabani, B. (2015). Metal foams application to enhance cooling of open cathode polymer electrolyte membrane fuel cells. J. Power Sources 295, 275–291. doi:10.1016/j.jpowsour.2015.07.022

CrossRef Full Text | Google Scholar

Saleem, M. A., Zafar, M. N., and Xia, J. (2021). Recent developments in the prefabricated bridge deck systems. Case Stud. Constr. Mater. 15, e00750. doi:10.1016/J.CSCM.2021.E00750

CrossRef Full Text | Google Scholar

Salimon, A., Brechet, Y., Ashby, M. F., and Greer, A. L. (2005). Potential applications for steel and titanium metal foams. J. Mat. Sci. 40 (22), 5793–5799. doi:10.1007/s10853-005-4993-x

CrossRef Full Text | Google Scholar

Sanders, W. S., and Gibson, L. J. (2003). Mechanics of hollow sphere foams. Mater. Sci. Eng. A 347 (1–2), 70–85. doi:10.1016/S0921-5093(02)00583-X

CrossRef Full Text | Google Scholar

Singh, R., Lee, P. D., Dashwood, R. J., and Lindley, T. C. (2013). Titanium foams for biomedical applications: A review. Mater. Technol. 25 (3–4), 127–136. doi:10.1179/175355510X12744412709403

CrossRef Full Text | Google Scholar

Singh, S., and Bhatnagar, N. (2017). A survey of fabrication and application of metallic foams (1925–2017). J. Porous Mat. 25 (2), 537–554. doi:10.1007/S10934-017-0467-1

CrossRef Full Text | Google Scholar

Song, J., Hu, D., Luo, S., Liu, W., Wang, D., Sun, Q., et al. (2021). Energy-absorption behavior of metallic hollow sphere structures under impact loading. Eng. Struct. 226 (2020), 111350. doi:10.1016/j.engstruct.2020.111350

CrossRef Full Text | Google Scholar

Stone, M. H., Sanborn, K., O'Bryant, H. S., Hartman, M., Proulx, C., et al. (2003). Maximum strength-power-performance relationships in collegiate throwers. J. Strength Cond. Res. 17 (4), 739–745. doi:10.1519/1533-4287(2003)017<0739:msrict>2.0.co;2

PubMed Abstract | CrossRef Full Text | Google Scholar

Styles, M., Compston, P., and Kalyanasundaram, S. (2007). The effect of core thickness on the flexural behaviour of aluminium foam sandwich structures. Compos. Struct. 80 (4), 532–538. doi:10.1016/j.compstruct.2006.07.002

CrossRef Full Text | Google Scholar

Sun, G., Wang, Z., Yu, H., Gong, Z., and Li, Q. (2019). Experimental and numerical investigation into the crashworthiness of metal-foam-composite hybrid structures. Compos. Struct. 209, 535–547. doi:10.1016/J.COMPSTRUCT.2018.10.051

CrossRef Full Text | Google Scholar

Sunder Sharma, S., Yadav, S., Joshi, A., Goyal, A., and Khatri, R. (2022). Application of metallic foam in vehicle structure: A review. Mater. Today Proc. 63, 347–353. doi:10.1016/J.MATPR.2022.03.201

CrossRef Full Text | Google Scholar

Szyniszewski, S. T., Smith, B., Hajjar, J., Schafer, B., and Arwade, S. (2014). The mechanical properties and modeling of a sintered hollow sphere steel foam. Mat. Des. 54, 1083–1094. doi:10.1016/j.matdes.2013.08.045

CrossRef Full Text | Google Scholar

Timoshenko, S. P. (1921). LXVI. On the correction for shear of the differential equation for transverse vibrations of prismatic bars. Lond. Edinb. Dublin Philosophical Mag. J. Sci. 41 (245), 744–746. doi:10.1080/14786442108636264

CrossRef Full Text | Google Scholar

Tong, X., Shi, Z., Xu, L., Lin, J., Zhang, D., Wang, K., et al. (2020). Degradation behavior, cytotoxicity, hemolysis, and antibacterial properties of electro-deposited Zn–Cu metal foams as potential biodegradable bone implants. Acta Biomater. 102, 481–492. doi:10.1016/J.ACTBIO.2019.11.031

PubMed Abstract | CrossRef Full Text | Google Scholar

Triawan, F., Nakagawa, R., Inaba, K., Budiman, B. A., and Kishimoto, K. (2020). Experimental investigation of shear stress effect on the flexural behavior of aluminum foam beam. J. Mech. Sci. Technol. 34 (5), 1831–1836. doi:10.1007/s12206-020-0403-1

CrossRef Full Text | Google Scholar

Tuwair, H., Volz, J., ElGawady, M. A., Chandrashekhara, K., and Birman, V. (2016). Modeling and analysis of GFRP bridge deck panels filled with polyurethane foam. J. Bridge Eng. 21 (5), 04016012. doi:10.1061/(ASCE)BE.1943-5592.0000849

CrossRef Full Text | Google Scholar

Uy, B. (2021). Local and interaction buckling of composite construction members. Analysis Des. Plated Struct. Volume 1 Stab. 2022, 343–363. doi:10.1016/B978-0-12-823570-6.00017-3

CrossRef Full Text | Google Scholar

Veale, P. J. (2010). Investigation of the behavior of open cell aluminum foam. Available at: https://scholarworks.umass.edu/theses/443 (PhD thesis 1911 - February 2014. 443).

Google Scholar

Vengatachalam, B., Huang, R., Poh, L. H., Liu, Z., Qin, Q., and Swaddiwudhipong, S. (2021). Initial yield behaviour of closed-cell aluminium foams in biaxial loading. Int. J. Mech. Sci. 191, 106063. doi:10.1016/j.ijmecsci.2020.106063

CrossRef Full Text | Google Scholar

Völlmecke, C., Todt, M., and Stylionos, S. (2021). Buckling and postbuckling of architectured materials: A review of methods for lattice structures and metal foams. Compos. Adv. Mater. 30, 263498332110039. doi:10.1177/26349833211003904

CrossRef Full Text | Google Scholar

von Hagen, H., and Bleck, W. (1998). Compressive, tensile and shear testing of melt-foamed aluminium. MRS Proc. 521, 59. doi:10.1557/proc-521-59

CrossRef Full Text | Google Scholar

Wang, X. Z., Wu, L., and Wang, S. X., (2009). Tensile and shear properties of aluminium foam. Mater. Technol. 24 (3), 161–165. doi:10.1179/106678509X12475884746705

CrossRef Full Text | Google Scholar

Xue-Zheng, Y. (2018). Mechanical properties of titanium foams having disordered and ordered cell structures 不規則及び規則セル構造を有するポーラスチタンの機械 的特性 Yue xue-zheng department of aerospace engineering graduate school of system design tokyo metropolitan university january 2018.

Google Scholar

Yao, C., Hu, Z., Mo, F., and Wang, Y. (2019). Fabrication and fatigue behavior of aluminum foam sandwich panel via liquid diffusion welding method. Metals 9 (5), 582–611.

CrossRef Full Text | Google Scholar

Yiatros, S., Marangos, O., Votsis, R. A., and Brennan, F. P. (2018). Compressive properties of granular foams of adhesively bonded steel hollow sphere blocks. Mech. Res. Commun. 94, 13–20. doi:10.1016/j.mechrescom.2018.08.005

CrossRef Full Text | Google Scholar

Zhao, B., Gain, A. K., Ding, W., Zhang, L., Li, X., and Fu, Y. (2017). A review on metallic porous materials: pore formation, mechanical properties, and their applications. Int. J. Adv. Manuf. Technol. 95 (5), 2641–2659. doi:10.1007/S00170-017-1415-6

CrossRef Full Text | Google Scholar

Zhu, L., Li, N., and Childs, P. R. N. (2018). Light-weighting in aerospace component and system design. Propuls. Power Res. 7 (2), 103–119. doi:10.1016/J.JPPR.2018.04.001

CrossRef Full Text | Google Scholar

Zimar, A. M. Z., Nowsath, M. H., Muhammad, M.N., Herath, S. R., et al. (2016). “Non-linear behaviour of open-cell metal foam under tensile loading,” in Proceedings of the 2nd International Moratuwa Engineering Research Conference, MERCon 2016, Moratuwa, Sri Lanka, 05-06 Apr. 2016, 349–354. doi:10.1109/MERCON.2016.7480166

CrossRef Full Text | Google Scholar