- 1School of Civil Aviation, Northwestern Polytechnical University, Taicang, China
- 2Collaborative Innovation Center of NPU, Shanghai, China
- 3College of Sericulture, Textile and Biomass Sciences, Southwest University, Chongqing, China
- 4College of Aerospace Engineering, Chongqing University, Chongqing, China
In this work, a physics-based analytical model without any fitting parameters for fracture toughness depending on temperature was proposed. The quantitative relationship between fracture toughness, melting point, Young’s modulus, Poisson’s ratio, and temperature was established. Furthermore, the effect of notch root radius on fracture toughness was investigated, and then we developed a simple theoretical model to characterize the combined effect of temperature and notch root radius on the fracture toughness. Satisfactory agreement between the available experimental measurements and our model predictions was achieved. This study not only advances our in-depth understanding of the quantitative relationship between the temperature and fracture toughness but also provides a powerful and convenient tool to predict the temperature-dependent fracture toughness at different notch root radius.
1 Introduction
Fracture toughness (KIc), as a vital factor of materials, plays a crucial role in structure integrity assessment and damage tolerance design since it can determine whether a crack reaches an unstable state in a particular material (Mu et al., 2015; Jia et al., 2019). Currently, the demand of metallic materials in high-temperature applications becomes more and more intense, such as in nuclear power reactors and components in aerospace (Tong et al., 2014). The working temperature of metals is getting increasingly higher in service, and several studies have indicated that temperature has a significant influence on KIc (Wen et al., 2008; Byun et al., 2013; Chandra Rao et al., 2008). Meanwhile, several experimental studies proved that the notch root radius of a specimen also affected the value of fracture toughness (Fujita et al., 2007; Mourad et al., 2013; Vratnica et al., 2013). Therefore, investigating the influence of temperature and notch root radius on KIc is important and necessary for the design and application of materials working at high temperatures.
In recent years, a large number of valuable experimental studies have reported the KIc of metals at different temperatures (Wen et al., 2008; Byun et al., 2013; Chandra Rao et al., 2008), (Srinivas and Kamat, 2000; Harimon et al., 2017; Li et al., 2018; Jia et al., 2019; Pan et al., 2019; Li et al., 2020; Zhang et al., 2020). Wen et al. (2008) demonstrated that temperature has a complex effect on the fracture toughness of nickel-based, single-crystal superalloys and found that the fracture mode of the specimens transitioned from brittle to ductile as the temperature increased. Byun et al. (2013) reported the fracture toughness of HT9 steel from room temperature to 504°C. They found that it decreased with the temperature increasing for non-irradiated specimens. Srinivas and Kamat (2000) found that the fracture toughness of a dispersion-strengthened aluminum alloy was significantly affected by temperature and notch root radius, and it increased linearly with the square root of notch root radius beyond a critical value and decreased with increasing test temperature. Jia et al. (2019) investigated the impact of temperature on fracture toughness of Ti60 alloy and its fracture mechanism, and the result showed that the fracture toughness increased from room temperature to 400°C but decreased at 600°C due to the area of the crack tip around the plastic zone. The abovementioned experimental research provides a solid basis for understanding and revealing the effects of the relevant factors on the high-temperature fracture toughness of materials. However, a high temperature test for KIc lacks the standard unified method as yet, and the experimental values of KIc from different literatures are quite different. Moreover, measuring KIc is difficult and complex at high temperatures, which also causes considerable consumption of time and money (Li et al., 2018; Pan et al., 2019). Currently, it is difficult to provide a systematic knowledge of temperature’s influence on KIc only by experiments. Thus, establishing a theoretical model for uncovering the quantitative influence of temperature on KIc is urgently needed.
The existing temperature-dependent fracture toughness models mainly focus on empirical or semi-empirical models (Jia et al., 2019; Amar and Pineau, 1985; Margolin et al., 2003a; Margolin et al., 2003b; Shao et al., 2016), which lack a detailed physical mechanism. They all rely on large number of experimental data at different temperatures to fit the fitting parameters in models. Thus, the use of these models including fitting parameters that predict temperature-dependent KIc is inconvenient. In addition, Wallin (1984) put forward the Master Curve method (Wallin, 2010) to calculate temperature-dependent KIc of ferritic steel. Recently, Li et al. (2018) established a temperature-dependent fracture toughness model for superalloys, which developed the relationship between fracture toughness, Young’s modulus, and strain-hardening exponent at different temperatures. However, it depends on extensive experiments to determine the temperature-dependent strain-hardening exponent when KIc is predicted at high temperatures, which seriously weakens the predictability of their model.
In view of the current situation, the objective of the present work is to reveal and quantify the influence of temperature and notch root radius on KIc. To this end, we first proposed a concept called the maximum storage energy density associated with material failure and established a temperature-dependent fracture toughness model without any fitting parameters. A comparison was made between the model predictions and the available experimental measurements, which validated our model well. On the basis of the model, we further considered the effect of notch root radius on KIc and established a temperature- and notch root radius-dependent model, which offers a good approach to predict KIc at different temperatures and notch root radius. At the end, discussions and conclusions were obtained.
2 Temperature-dependent fracture toughness model
2.1 Derivation of the model
In this work, we consider the fracture process as a process of bond breaking in the fractured parts to create a new material surface. Volokh’s research (Volokh, 2007) demonstrated that there exists a maximum strain energy density related to material fracture. But, temperature’s influence was not included in his work. Based on thermodynamics theory, the internal energy of a particular system is composed of kinetic energy due to atomic motion in the system and potential energy between atoms (Zhang et al., 2017a; Deng et al., 2017). To investigate the quantitative influence of temperature on KIc, we assumed that there is a temperature-independent maximum storage energy density associated with material fracture (Li et al., 2010), which includes the critical strain energy density arising from externally applied stress and internal energy density. Moreover, it was assumed that the critical strain energy density and the system’s internal energy density have an equivalent relationship, based on their different contribution to material fracture. From the abovementioned discussion, the maximum storage energy density WTOTAL has the following form:
where T denotes the ambient temperature, WKc(T) is the critical strain energy density at temperature T, and Ep(T) and Ek(T), respectively, denote the potential energy density and kinetic energy density at temperature T. α is a hypothetical constant, which represents the ratio coefficient between the critical elastic energy density and internal energy density. Based on the classical fracture mechanics theory, the critical strain energy density for the plain strain WKc(T) under linearly elastic conditions can be expressed as
where WKc(T) is the temperature-dependent fracture toughness and v(T) and E(T) are the temperature-dependent Poisson’s ratio and Young’s modulus, respectively.
According to the thermodynamics theory, the kinetic energy density can be described as
where N denotes the number of atoms per unit volume and kB denotes the Boltzmann constant.
Moreover, the kinetic energy and potential energy in the material transforms periodically, and their mean value is equivalent (Zhang et al., 2017a). Thus, Ep(T) can be described as
Combining Eqs. 1–4, the maximum storage energy density for a particular material is obtained as
Substituting an arbitrary reference temperature T0 into Eq. 5, WTOTAL can also be expressed as
where KIc(T0) denotes the fracture toughness at T0 and v (T0) and E (T0), respectively, denote the Poisson’s ratio and Young’s modulus at T0.
At melting point Tm, the material loses its ability to carry any external stress, so
Substituting T=Tm and Eq. 7 into Eq. 5, we can obtain
Combining Eqs. 6, 8, we can deduce that
Substituting Eq. 9 into Eq. 5 yields
Finally, combining Eqs. 8–10, the temperature-dependent fracture toughness model is obtained:
The physics-based model without any fitting parameters reveals the inherent relationship between fracture toughness, melting point, Poisson’s ratio, Young’s modulus, and temperature. Considering that these material parameters in Eq. 11 can be obtained easily from the existing literatures or material handbooks, this model provides a convenient approach to predict KIc(T) at different temperatures. In particular, influence factors such as test approach and size and shape of specimen and microstructure, whose effect on KIc is complex and less sensitive to temperature, are considered by the KIc(T0) in the model.
2.2 Validation of the model
To validate our temperature-dependent fracture toughness model, the available experimental data of KIc(T) for GH4720Li alloy, GH4169 alloy, HT9 steel, sintered steel, and aluminum alloy were compared with those of our model predictions (Figures 1–4). All material parameters used in the calculations were obtained from the existing literatures. The reference temperature T0 in the model can be selected arbitrarily. For convenience, it was set at room temperature in this study. In addition, Poisson’s ratio was assumed to be a constant at different temperatures due to its weak temperature dependence (Li et al., 2016). For more details about the materials and experiment method, interested readers could refer to Refs. (Shan and Leng, 1999; Srinivas and Kamat, 2000; High Temperature Materials Session of China Metal Institute, 2012; Byun et al., 2013; Baek et al., 2014; Li et al., 2018).
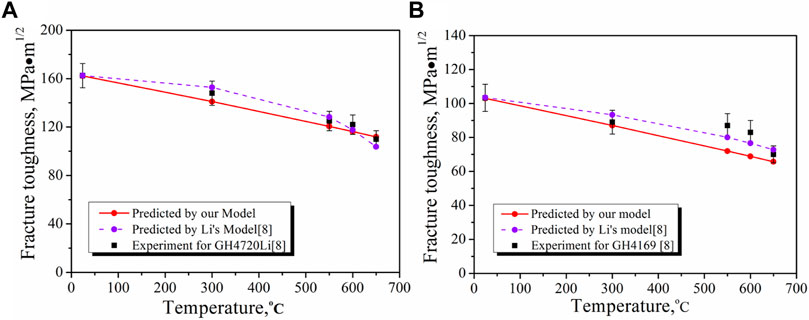
FIGURE 1. Temperature-dependent fracture toughness of (A) GH4720Li (Li et al., 2018) and (B) GH4169 (High Temperature Materials Session of China Metal Institute, 2012).
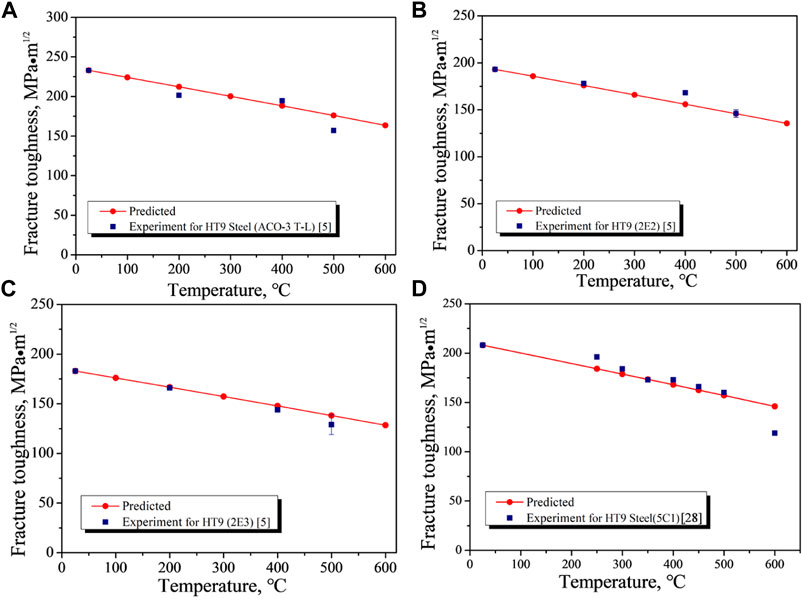
FIGURE 2. Temperature-dependent fracture toughness of HT9 Steel (Byun et al., 2013; Baek et al., 2014).
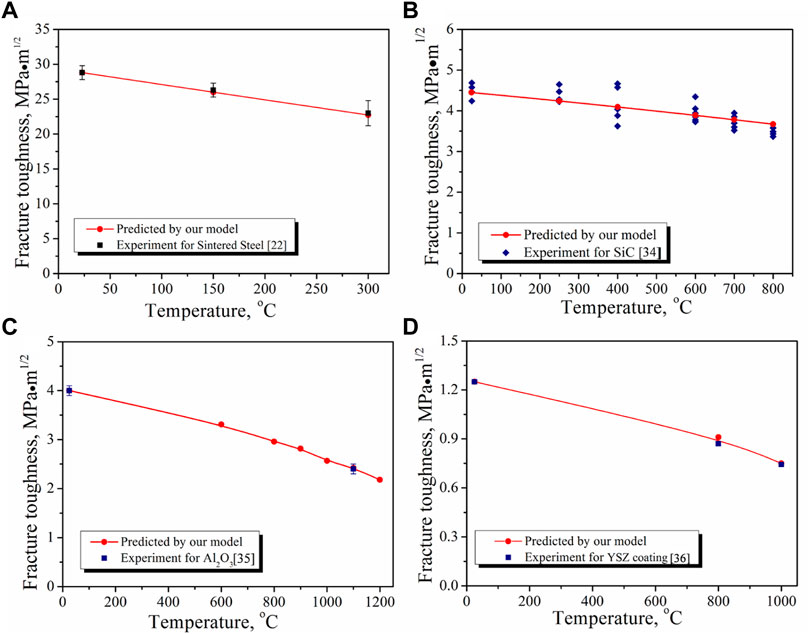
FIGURE 3. Temperature-dependent fracture toughness of (A) sintered steel (B) SiC (Xu et al., 1992). (C) Al2O3 (Sglavo et al., 1999) and (D) YSZ coating (Qu et al., 2018).
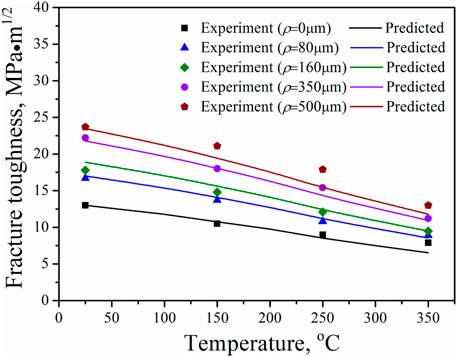
FIGURE 4. Temperature- and notch root radius-dependent fracture toughness of aluminum alloy (Srinivas and Kamat, 2000).
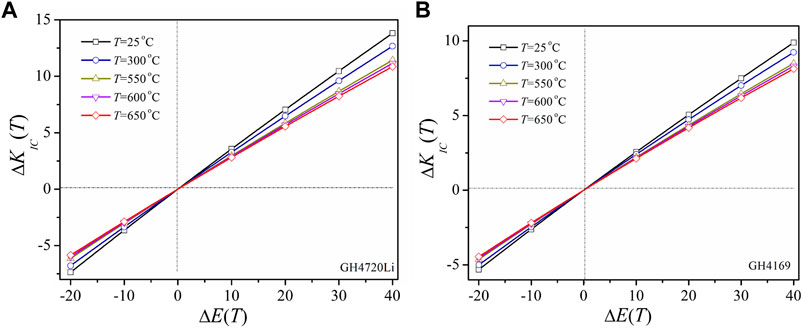
First, we used our model to predict the temperature-dependent KIc(T) of GH4720Li alloy. The material parameters in the calculation are given as follows: KIc(T0)=162.5
Figure 1B showed the comparison between the experimental data and theoretical prediction of KIc(T) for the GH4169 alloy. The needed material parameters are given as follows: KIc(T0)=103 MPa.m1/2,
Figure 2 displayed the comparison between the theoretical predictions and experimental measurement of four HT9 steel. The needed material parameters for HT9 steel are given as follows: E(T)=216.2–0.0692T (Shan and Leng, 1999), Tm=1480°C (Klug et al., 1996), and T0=25°C. The experimental value at room temperature was set as KIc(T0) for each HT9 steel. The predictions by our model achieved good consistency with the experimental results (Byun et al., 2013; Baek et al., 2014) (Figure 2). However, in Figure 2D, the model prediction is larger than the experimental data at 600°C, which is likely due to the interaction between gliding dislocations and light elements (Baek et al., 2014).
Then, we predicted the KIc(T) of sintered steel from room temperature to 300°C. The needed material parameters are given as follows: KIc(T0)=28.8 MPa.m1/2, E(T)=128.5–0.11T (Shan and Leng, 1999), Tm=1538°C (Shan and Leng, 1999), and T0=23°C. An excellent agreement was obtained between the experimental results (Shan and Leng, 1999) and our model predictions (Figure 3A).
In addition, the KIc(T) at high temperatures of some ceramic materials (SiC, Al2O3, and YSZ coating) was also predicted by our model. The relative material parameters are listed in Table 1. As can be seen from Figures 3B–D, our model predictions achieved satisfactory agreement with the corresponding experiment measurement (Xu et al., 1992; Sglavo et al., 1999; Qu et al., 2018).
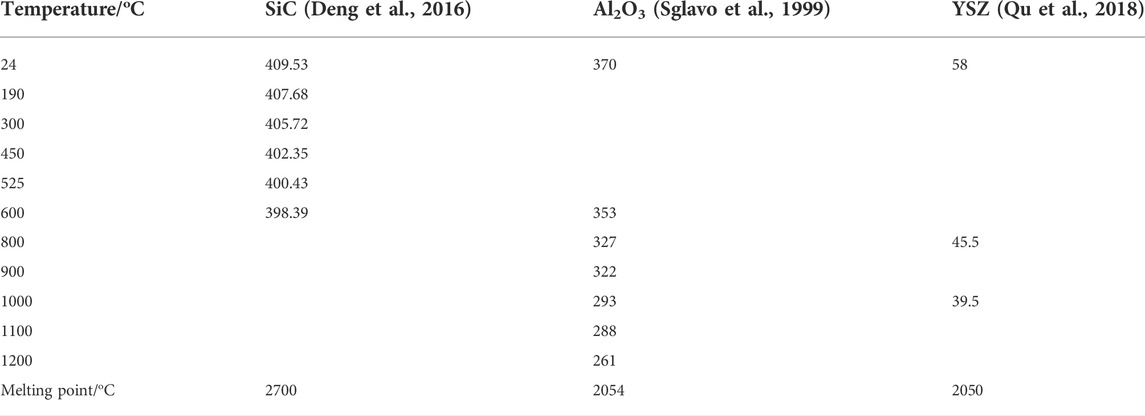
TABLE 1. Temperature-dependent Young’s modulus and melting point (Sglavo et al., 1999; Deng et al., 2016; Qu et al., 2018).
Based on the abovementioned results (Figures 1–3), it can be concluded that our temperature-dependent fracture toughness model (Eq. 11) can well-predict the KIc(T) at different temperatures. It is worth noting that the factors which have an effect on KIc and does not evolve with temperature are included in the KIc(T0). However, the factors with temperature evolution, which have influence on KIc(T), such as plastic deformation, phase transition, gliding dislocations, and microstructure evolution are not included in the current work, which will be considered in our next work.
3 Temperature- and notch root radius-dependent fracture toughness model
3.1 Derivation of the model
It is well-known that KIc is not only temperature-dependent but also has a strong dependence on notch root radius of test specimen (ρ). In general, when ρ is smaller than critical data ρ0, KIc is independent on ρ. When ρ is larger than ρ0, KIc increases linearly with ρ1/2, namely (Carolan et al., 2011),
where
where
3.2 Validation of the model
Srinivas and Kamat (2000) have reported the value of KIc(T,ρ) of aluminum alloy at different notch root radius (ρ) from room temperature to 350 °C. To validate our temperature- and notch root radius-dependent fracture toughness model, the KIc(T,ρ) of aluminum alloy at different notch root radius (from 0 to 500 μm) and different temperatures was predicted by Eq. 13. Based on the experimental data of KIc(T0) of aluminum alloy at room temperature (Srinivas and Kamat, 2000) and from Eq. 12, we can obtain the values of m and
Figure 4 presented the comparison between the experimental (Srinivas and Kamat, 2000) and theoretical predictions of aluminum alloy. In the calculation, Young’s modulus of aluminum alloy was obtained by the existing yield strength in the literature (Srinivas and Kamat, 2000), and the temperature-dependent yield strength model is established by Zhang et al. (2017a) due to lack of its values at elevated temperatures. Also Tm=660°C (Zedalis et al., 1989), T0=25°C, and d=2
4 Discussion
As discussed previously, high-temperature plastic deformation significantly affects the fracture toughness of materials when the temperature is higher than the brittle–ductile transition temperature. In this case, it is necessary to consider its effect when modeling. Thus, the temperature-dependent fracture toughness includes two parts above brittle–ductile transition temperature:
where K1(T) and K2(T) are the initial fracture toughness and its incremental value due to plastic deformation, respectively. K1(T) is expressed by Eq. 11. The next critical step is to give the formula of K2(T). Based on the yielding fracture mechanics (Egan, 1973; Larsson, 2011) and our previous work (Wang et al., 2019), the fracture toughness plasticity component (K2(T)) is inversely proportional to the yield strength (
As a result, K2(T) can be expressed as (Zhang et al., 2017b):
where T1 is the brittle–ductile transition temperature and K2 (T1) is the fracture toughness plasticity component at T1.
Then, the temperature-dependent fracture toughness model, considering the effect of plastic deformation at temperature higher than T1, is expressed as
Moreover, the proposed fracture toughness model indicates that Young’s modulus has a significant effect on the fracture toughness of materials. The influencing factor of fracture toughness was analyzed by the theoretical model, and the effect of Young’s modulus on the fracture toughness of GH4720Li and GH4169 in the temperature range of 25–650°C was analyzed, as shown in Figure 5. The sensitivity of fracture toughness to Young’s modulus decreases with increasing temperature, and Figure 5 also indicates that improving Young’s modulus is helpful in increasing the fracture toughness of alloys.
5 Conclusion
In summary, based on the equivalent relationship between the critical strain energy density associated with material fracture and the system’s internal energy density, we established a physics-based model without any fitting parameters for predicting the temperature-dependent fracture toughness. The quantitative relationship between fracture toughness, melting point, Young’s modulus, Poisson’s ratio, and temperature was uncovered. The comparisons were made between the available experimental results and the model predictions, which showed good agreement. Considering that the material parameters in the model can be obtained easily, the fracture toughness at high temperatures can be predicted conveniently, avoiding difficult and laborious high-temperature experiments. Moreover, by further considering the influence of notch root radius on fracture toughness, a theoretical model of fracture toughness dependent on temperature and notch root radius was developed. It was validated by comparison with experimental values at different notch root radius. This work provides a practical and convenient technical means for predicting the fracture toughness at different temperature and notch root radius.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material. Further inquiries can be directed to the corresponding authors.
Author contributions
YD: conceptualization, methodology, and writing—original draft. CZ: modeling, supervision, and validation. JS: formal analysis and visualization. WL: supervision and writing—review and editing.
Funding
This work was supported by the National Natural Science Foundation of China [grant numbers 12102354, 12002288, and 12002223]; the Shanghai Sailing Program [grant number 21YF1450900]; the Natural Science Basic Research Plan in Shaanxi Province of China [grant number 2021JQ-073]; and the Fundamental Research Funds for the Central Universities [grant number G2021KY05111].
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Reference
Amar, E., and Pineau, A. (1985). Interpretation of ductile fracture toughness temperature dependence of a low strength steel in terms of a local approach. Eng. Fract. Mech. 22, 1061–1071. doi:10.1016/0013-7944(85)90044-x
An, X. L., Zhang, B., Chu, C. L., Zhou, L., and Chu, P. K. (2019). Evolution of microstructures and properties of the GH4169 superalloy during short-term and high-temperature processing. Mater. Sci. Eng. A 744, 255–266. doi:10.1016/j.msea.2018.12.019
Baek, J. H., Byun, T. S., Maloy, S. A., and Toloczko, M. B. (2014). Investigation of temperature dependence of fracture toughness in high-dose HT9 steel using small-specimen reuse technique. J. Nucl. Mater. 444, 206–213. doi:10.1016/j.jnucmat.2013.09.029
Byun, T. S., Toloczko, M. B., Saleh, T. A., and Maloy, S. A. (2013). Irradiation dose and temperature dependence of fracture toughness in high dose HT9 steel from the fuel duct of FFTF. J. Nucl. Mater. 432, 1–8. doi:10.1016/j.jnucmat.2012.07.019
Chandra Rao, B. S. S., Srinivas, M., and Kamat, S. V. (2008). Effect of temperature on fracture toughness of timetal 834 titanium alloy under mode I and mixed mode I/III loading. Metall. Mat. Trans. A 39, 1340–1349. doi:10.1007/s11661-008-9516-3
Carolan, D., Alveen, P., Ivankovic´, A., and Murphy, N. (2011). Effect of notch root radius on fracture toughness of polycrystalline cubic boron nitride. Eng. Fract. Mech. 78, 2885–2895. doi:10.1016/j.engfracmech.2011.08.003
Deng, Y., Li, W. G., Shao, J. X., Zhang, X. H., Kou, H. B., Geng, P. J., et al. (2017). A novel theoretical model to predict the temperature-dependent fracture strength of ceramic materials. J. Eur. Ceram. Soc. 37, 5071–5077. doi:10.1016/j.jeurceramsoc.2017.06.044
Deng, Y., Li, W. G., Wang, R. Z., J Geng, P., and Ma, J. Z. (2016). The temperature-dependent fracture models for fiber-reinforced ceramic matrix composites. Compos. Struct. 140, 534–539. doi:10.1016/j.compstruct.2016.01.020
Egan, G. R. (1973). Compatibility of linear elastic (k1c) and general yielding (COD) fracture mechanics. Eng. Fract. Mech. 5 (1), 167–185. doi:10.1016/0013-7944(73)90014-3
Fujita, K., Okamoto, A., Nishiyama, N., Yokoyamad, Y., Kimurad, H., and Inoued, A. (2007). Effects of loading rates, notch root radius and specimen thickness on fracture toughness in bulk metallic glasses. J. Alloys Compd. 434–435, 22–27. doi:10.1016/j.jallcom.2006.08.328
High temperature materials session of China metal institute (2012). China superalloy handbook. Standards Press of China.
Harimon, M. A., Hidayati, N. A., Miyashita, Y., Otsuka, Y., Mutoh, Y., Yamamoto, S., et al. (2017). High temperature fracture toughness of TZM alloys with different kinds of grain boundary particles. Int. J. Refract. Met. Hard Mat. 66, 52–56. doi:10.1016/j.ijrmhm.2017.02.006
Jia, R., Zeng, W., He, S., Gao, X., and Xu, J. (2019). The analysis of fracture toughness and fracture mechanism of Ti60 alloy under different temperatures. J. Alloys Compd. 810, 151899. doi:10.1016/j.jallcom.2019.151899
Klug, R. C., Krauss, G., and Matlock, D. K. (1996). Recrystallization in oxide-dispersion strengthened mechanically alloyed sheet steel. Metall. Mat. Trans. A 27, 1945–1960. doi:10.1007/bf02651944
Larsson, L. H. (2011). Elastic-plastic fracture mechanics: Proceedings of the 4th advanced seminar on fracture mechanics. Ispra, Italy: Springer, Joint Research Centre.
Latella, B. A., and Humphries, S. R. (2004). Young’s modulus of a 2.25Cr–1Mo steel at elevated temperature. Screen. Mat. 51, 635–639. doi:10.1016/j.scriptamat.2004.06.028
Li, B.-S., Marrow, T. J., and Armstrong, D. E. J. (2020). Measuring the brittle-to-ductile transition temperature of tungsten–tantalum alloy using chevron-notched micro-cantilevers. Scr. Mater. 180, 77–82. doi:10.1016/j.scriptamat.2020.01.030
Li, P. Y., Cheng, L., Yan, X. J., Huang, D. W., Qin, X. Y., and Zhang, X. Y. (2018). A temperature-dependent model for predicting the fracture toughness of superalloys at elevated temperature. Theor. Appl. Fract. Mech. 93, 311–318. doi:10.1016/j.tafmec.2017.10.002
Li, W. G., Yang, F., and Fang, D. N. (2010). The temperature-dependent fracture strength model for ultra-high temperature ceramics. Acta Mech. Sin. 26, 235–239. doi:10.1007/s10409-009-0326-7
Li, W. G., Zhang, X. H., Kou, H. B., and WangFang, R. Z. D. N. (2016). Theoretical prediction of temperature dependent yield strength for metallic materials. Int. J. Mech. Sci. 105, 273–278. doi:10.1016/j.ijmecsci.2015.11.017
Margolin, B. Z., Gulenko, A. G., Nikolaev, V. A., and Ryadkov, L. N. (2003). A new engineering method for prediction of the fracture toughness temperature dependence for RPV steels. Int. J. Press. Vessels Pip. 80, 817–829. doi:10.1016/j.ijpvp.2003.12.005
Margolin, B. Z., Kostylev, V. I., and Minkin, A. I. (2003). The effect of ductile crack growth on the temperature dependence of cleavage fracture toughness for a RPV steel with various degrees of embrittlement. Int. J. Press. Vessels Pip. 80, 285–296. doi:10.1016/s0308-0161(03)00046-2
Mourad, A. I., E Domiaty, A., and Chao, Y. J. (2013). Fracture toughness prediction of low alloy steel as a function of specimen notch root radius and size constraints. Eng. Fract. Mech. 103, 79–93. doi:10.1016/j.engfracmech.2012.05.010
Mu, M. Y., Wang, G. Z., Xuan, F. Z., and Tu, S. T. (2015). Unified correlation of in-plane and out-of-plane constraints with cleavage fracture toughness. Theor. Appl. Fract. Mech. 80, 121–132. doi:10.1016/j.tafmec.2015.10.005
Pan, J. H., Chen, Z., and Hong, Z. Y. (2019). A novel method to estimate the fracture toughness of pressure vessel ferritic steels in the ductile to brittle transition region using finite element analysis and Master Curve method. Int. J. Press. Vessels Pip. 176, 103949. doi:10.1016/j.ijpvp.2019.103949
Qu, Z. L., Wei, K., He, Q., He, R. J., Pei, Y. M., Wang, S. X., et al. (2018). High temperature fracture toughness and residual stress in thermal barrier coatings evaluated by an in-situ indentation method. Ceram. Int. 44, 7926–7929. doi:10.1016/j.ceramint.2018.01.230
Sglavo, V. M., Trentini, E., and Boniecki, M. (1999). Fracture toughness of high-purity alumina at room and elevated temperature. J. Mat. Sci. Lett. 18, 1127–1130. doi:10.1023/a:1006696900177
Shan, Z., and Leng, Y. (1999). Fracture and fatigue behavior of sintered steel at elevated temperatures: Part I. Fracture toughness. Metall. Mat. Trans. A 30, 2885–2893. doi:10.1007/s11661-999-0126-5
Shao, H., Shan, D., Zhao, Y., Ge, P., and Zeng, W. (2016). Accordance between fracture toughness and strength difference in TC21 titanium alloy with equiaxed microstructure. Mater. Sci. Eng. A 664, 10–16. doi:10.1016/j.msea.2016.02.088
Srinivas, M., and Kamat, S. V. (2000). Influence of temperature and notch root radius on the fracture toughness of a dispersion-strengthening aluminium alloy. Fatigue. Fract. Eng. M. 23, 181–183. doi:10.1046/j.1460-2695.2000.00251.x
Tong, J. Y., Ding, X. F., Wang, M. L., Zheng, Y., Yagi, K., and Feng, Q. (2014). Evaluation of a serviced turbine blade made of GH4033 wrought superalloy. Mater. Sci. Eng. A 618, 605–613. doi:10.1016/j.msea.2014.09.025
Volokh, K. Y. (2007). Hyperelasticity with softening for modeling materials failure. J. Mech. Phys. Solids 55, 2237–2264. doi:10.1016/j.jmps.2007.02.012
Vratnica, M., Pluvinage, G., Jodin, P., Cvijovic´, Z., Rakin, M., Burzic´, Z., et al. (2013). Notch fracture toughness of high-strength Al alloys. Mat. Des. 44, 303–310. doi:10.1016/j.matdes.2012.07.031
Wallin, K. (2010). Structural integrity assessment aspects of the Master Curve methodology. Eng. Fract. Mech. 77, 285–292. doi:10.1016/j.engfracmech.2009.02.010
Wallin, K. (1984). The scatter in KIC results. Eng. Fract. Mech. 19, 1085–1093. doi:10.1016/0013-7944(84)90153-x
Wang, R. Z., Li, D. Y., Wang, X. R., and Li, W. G. (2019). Temperature dependent fracture toughness of the particulate-reinforced ultra-high-temperature-ceramics considering effects of change in critical flaw size and plastic power. Compos. Part B Eng. 158, 28–33. doi:10.1016/j.compositesb.2018.09.049
Wen, Z. X., Hou, N. X., Dou, Z. X., and Yue, Z. F. (2008). Fracture toughness analysis of anisotropic nickel-based single crystal superalloys at high temperature. J. Mat. Sci. 43, 5878–5883. doi:10.1007/s10853-008-2866-9
Xu, Y. L., Delale, F., and Liaw, B. M. (1992). Effect of temperature and fiber distribution on matrix cracking in ceramic matrix composites. Compos. Eng. 2, 67–79. doi:10.1016/0961-9526(92)90019-3
Zedalis, M. S., Gilman, P. S., Raybould, D., and Inc, A. S. (1989). Thermomechanical processing of rapidly solidified high temperature al-base alloys.
Zhang, P., Zeng, W., Zheng, Y., Xu, J., Liang, X., and Zhao, Y. (2020). Fracture toughness of Ti–22Al–25Nb alloy at room and high temperatures. Mater. Sci. Eng. A 796 (21), 140009. doi:10.1016/j.msea.2020.140009
Zhang, X. H., Li, W. G., Ma, J. Z., Geng, P. J., Shao, J. X., and Wu, X. Z. (2017). A novel temperature dependent yield strength model for metals considering precipitation strengthening and strain rate. Comput. Mater. Sci. 129, 147–155. doi:10.1016/j.commatsci.2016.12.005
Keywords: fracture toughness, temperature, model, notch root radius, metallic materials
Citation: Deng Y, Zhang C, Shao J and Li W (2022) Modeling the effect of temperature and notch root radius on fracture toughness. Front. Mater. 9:990314. doi: 10.3389/fmats.2022.990314
Received: 09 July 2022; Accepted: 11 August 2022;
Published: 09 September 2022.
Edited by:
Yan Gu, Qingdao University, ChinaReviewed by:
Huang Guizao, Southwest Jiaotong University, ChinaLingling Wang, Guizhou University, China
Copyright © 2022 Deng, Zhang, Shao and Li. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Chao Zhang, Y2hhb3poYW5nQG53cHUuZWR1LmNu; Weiguo Li, d2dsaUBjcXUuZWR1LmNu
 Yong Deng
Yong Deng Chao Zhang
Chao Zhang Jiaxing Shao3
Jiaxing Shao3