Modeling of extra strengthening in gradient nanotwinned metals based on molecular dynamics

Gradient nanotwinned metals exhibit extra strengthening and work hardening behaviors, which have enormous potential for engineering applications. In this study, molecular dynamics method is performed for analyzing the effects of nanotwinned structure gradient on uniaxial tensile loading behaviors of gradient nanotwinned metals. Results show that the elasticity, dislocation stored ability and dislocation evolution of the nanotwinned lamellar are affected by the surrounding nanotwinned structure. Moreover, we established a quantitative phenomenological plastic flow stress model for gradient nanotwin metals based on physical connotation, and discussed the effects of nanotwinned thickness and nanotwinned structure gradient on the strength. Particularly, the back stress associated with the nanotwinned structure gradient and the contribution of geometrically necessary dislocations to statistically stored dislocations is included in our model. The tensile response the theoretical model descripted is in good agreement with the experimental results. We hold the opinion that the promotion effect of geometrically necessary dislocations to statistically stored dislocations will not be manifested until the nanotwinned structure gradient reaches a critical value. This research provides guidance for the structural design of gradient nanotwinned metals.

Introduction

Making nanometals stronger and more malleable by adjusting their microstructures has been an enduring pursuit owing to their appealing potential in materials science and engineering (Li et al., 2020). Inspired by natural gradient structures such as human teeth and bamboo, the gradient nanomaterials are received a lot of attention (Lu and Lu, 2004). Due to the strain gradients inherent in gradient materials during deformation, gradient metals and gradient amorphous materials can be designed to exhibit a combination of high strength and high toughness (Fang et al., 2011; Tang et al., 2022). At the same time, the introduction of nanotwinned (NT) structure has been recognized as an effective strategy to obtain superior mechanical and physical properties (Lu et al., 2009). Numerous experimental, simulative and theoretical studies have shown that the spatial gradient distribution of twin boundaries (TBs) in metal materials has great potential to overcome the strength-ductility trade-off dilemma faced by conventional materials (Li et al., 2010; Chen et al., 2011; You et al., 2011). The union of gradient structures and TBs puts gradient nanotwinned (GNT) metals at the forefront of materials science.

Recently, some experimental results show that GNT metals have significant strength, superior to even the strongest compositions (Cheng et al., 2018; Zhu et al., 2019). When uniaxial loading parallel to the TBs is applied, bundles of concentrated dislocations (BCDs) form and interact to maintain the plastic deformation of the GNT metal (Cheng et al., 2018). The additional back stress generated by the NT thickness gradient are the main reason for the extra strength of GNT Cu (Cheng et al., 2022). A comprehensive understanding of the main strengthening mechanisms in GNT metals is essential to obtain the best mechanical properties of metals through microstructural design. Atomic simulation based on molecular dynamics (MD) method provides an intuitive mean of observing the kinetic behavior of metal deformation and defect evolution in GNT metals at the atomic level. Some researches based on MD simulation method have been reported. There is significant dislocation aggregation behavior in GNT metals, with the local dislocation density of BCDS being nearly 30% larger than the average dislocation density within grains (Cheng et al., 2018). The plastic deformation mechanism of GNT metals is influenced by the TB spacing, the gradient distribution of strain is induced by TB gradient distribution (Sun et al., 2019). Several theoretical models of NT and GNT Cu have also been proposed. For instance, Zhu et al. developed a theoretical model for NT structure depended on grain size and twin spacing (Zhu et al., 2011). Chen et al. descripted a constitutive model based on dislocation density of extra strengthening in GNT metals (Chen et al., 2021). Zhang et al. developed a gradient theory of plasticity by incorporating the strengthening effect of plastic strain gradients into the classical J2 flow theory (Zhang et al., 2020). Zhou et al. used gradient Eshelby force to explain the motion of twinning partial dislocations on TBs in the absence of any resolved shear stress and the detwinning behavior in GNT metals (Zhou et al., 2022). However, the results of extra back stress in the latest experiment does not be considered into the description of above GNT material models. Due to the novel extra back stress in GNT metals observed in experiment (Cheng et al., 2022), a practical constitutive model is urgent to be developed for reflecting the origin of extra strengthening in GNT metals.

To understand the extraordinary mechanical behaviors of GNT metals, the present work aims to develop a theoretical framework to quantify the extra strengthening inspired by the experimental observations (Cheng et al., 2022). Firstly, MD simulations of the tensile behavior parallel to the TBs of GNT copper materials were performed. The GNT structure has a significant effect on dislocation evolution in twin lamellar, based on MD results a phenomenological back stress model related to NT structure gradient is established. Furthermore, the evolution of dislocation density in the Kocks–Mecking (KM) model (Kocks and Mecking, 2003) is modified to consider the promotion effect of geometrically necessary dislocations (GNDs) generation on statistically stored dislocations (SSDs). Finally, a quantitative phenomenological model of GNT material tensile behavior is established, which is in good agreement with the experimental work (Cheng et al., 2018; Cheng et al., 2022). The important factors in GNT materials such as NT lamellar thickness and NT structure gradient are considered in the model. This study has guiding significance for the structural design of GNT high-performance metals.

Materials and methods

In order to explore the possible mechanism of extra strengthening of GNT copper, MD simulations of three-dimensional GNT copper sample stretching were performed to compare with homogeneous nanotwinned (HNT) copper. Atomsk (Hirel, 2015) modeling software was used to establish one HNT copper sample as control group and three GNT copper samples as experimental group. In this investigation, MD simulations were carried out on GNT copper uniaxial tensile behavior using the Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS) (Plimpton, 1995) and the interaction force was calculated by the embedded-atom-method (EAM) potentials function for Cu (Mishin et al., 2001). The total potential energy of crystal is expressed as:

$U={\displaystyle \sum _i{F}_i\left({\rho }_i\right)}+\frac{1}{2}{\displaystyle \sum _i{\displaystyle \sum _{j\ne i}{\mathit{\varphi }}_{ij}\left(r_{ij}\right)}}(1)$

where $F\left(\rho \right)$ is the energy to embed the atom in the area of electron density ${\rho }_i$; ${\varphi }_{ij}$ is the pairwise potential between two atoms; $r_{ij}$ is the distance between atoms $i$ an $j$. The stresses in different direction are calculated by the virial scheme, which is the average of all atomic stresses.

${\sigma }_i^{\xi \eta }=\frac{1}{{\mathrm{\Omega }}_i}\left\{-m_i{v}_i^{\xi }{v}_i^{\eta }+\frac{1}{2}{\displaystyle \sum _{j\ne i}\left[\frac{\mathit{\partial }\varphi }{\mathit{\partial }{r}_{ij}}+\left(\frac{\mathit{\partial }F}{\mathit{\partial }{\rho }_i}+\frac{\mathit{\partial }F}{\mathit{\partial }{\rho }_j}\right)\frac{\mathit{\partial }f}{\mathit{\partial }{r}_{ij}}\right]}\frac{r_{ij}^{\xi }{r}_{ij}^{\eta }}{r_{ij}}\right\}(2)$

where ${\sigma }_i^{\xi \eta }$ is the $\xi \eta$ component of the atomic stress tensor of atom $i$, ${\Omega }_i$ is the average volume of atom $i$, $v_i^{\xi }$ and $v_i^{\eta }$ are the velocity components in the $\xi$ and $\eta$ direction of atom $i$ respectively, $r_{ij}^{\xi }$ and $r_{ij}^{\eta }$ are the displacement components in the $\xi$ and $\eta$ directions of $r_{ij}$ respectively.

The atomic strain calculation in OVITO (Stukowski and Albe, 2010) visualization software is based on finite strain theory. Therefore, the Green-Lagrange strain tensor is used to measure strain as:

$\mathit{E}=\frac{1}{2}\left(\mathit{F}{\mathit{F}}^T-\mathit{I}\right)(3)$

where $\mathit{F}$ is the deformation gradient. Based on the symmetric strain tensor, the von Mises local shear invariant is calculated and this scalar quantities as particle properties named shear strain ($\gamma$):

$\gamma ={\left[{\mathit{E}}_{xy}^2+{\mathit{E}}_{xz}^2+{\mathit{E}}_{yz}^2+\frac{1}{6}\left({\left({\mathit{E}}_{xx}-{\mathit{E}}_{yy}\right)}^2+{\left({\mathit{E}}_{xx}-{\mathit{E}}_{zz}\right)}^2+{\left({\mathit{E}}_{yy}-{\mathit{E}}_{zz}\right)}^2\right)\right]}^{\frac{1}{2}}(4)$

Figure 1 shows one of the GNT samples studied in this paper. The microstructural characteristic and dislocation information were visualized with common neighbor analysis (CNA) method (Faken and Jónsson, 1994). Face-centered cubic (FCC) atoms are colored green, hexagonal close-packed (HCP) atoms at the TBs are marked in red, while disordered atoms of initial dislocation nucleation and the others on the surface are colored blue, as shown in Figure 1. The atoms in matrix arranged in perfect FCC crystal structures were with [$1\overline{1}0$] direction along the X-direction, [$11\overline{2}$] direction along the Y-direction and [$111$] direction along the Z-direction, respectively. The atoms in twin were arranged in extension twin orientation with the matrix. All the samples have a total of about 1.2 million atoms and three dimensions of 15.3 × 15.5 × 14.8 nm³. The 4.93 nm thick twin lamellas at the center of all samples are called inner cores, and the rest parts are called outer layers. The HNT copper sample is named NT-Cu0, the GNT copper sample with four 2.47 nm thick twin lamellas in outer layers is named NT-Cu1, the GNT copper sample with two 2.47 nm thick and four 1.23 nm thick twin lamellas in outer layers is named NT-Cu2, and the GNT copper sample with eight 1.23 nm thick twin lamellas in outer layers is named NT-Cu3.

FIGURE 1

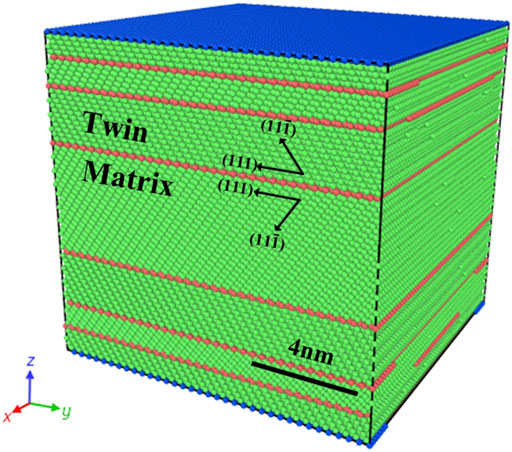
FIGURE 1. Illustration of the simulation sample. (HCP atoms are colored red. FCC atoms are colored green. The other atoms are colored blue).

The same relaxation and tension methods were adopted for the simulated samples. To be specific, the system was initially equilibrated for 100ps at 1K, followed by uniaxial tensile loading along the X axis to a total engineering strain of 20% at a constant strain rate of 2 × 10⁸ s⁻¹. It is worth to note that 20% engineering strain is equivalent to 18.2% true strain, and the term true strain will be used uniformly in this paper. Throughout the simulation, periodic boundary conditions were applied in X-direction and Y-direction, while non-periodic boundary condition was applied in Z-direction. Constant temperature was controlled by Nose-Hoover thermostat (Hoover, 1986) algorithm with a typical MD time step of 1 fs.

Theoretical model

In this research, the evolution of dislocation density in KM model is modified, and the promotion effect of GND generation on SSD is considered. Meanwhile, the saturated back stress model of GNT metals is modified to consider the influence of NT structure gradient on back stress. The relationship between flow stress and dislocation density is expressed as follows:

${\sigma }_f={\sigma }_0+M\alpha \mu b\sqrt{\rho }+{\sigma }_b(5)$

where $M$, $\alpha$, $\mu$, $\text{b}$, $\rho$ are Taylor factor, Taylor constant, shear modulus, magnitude of Burgers vector and dislocation density respectively; ${\sigma }_0$ is the resistance stress without constraint by TBs, which mainly derive from the lattice friction stress, The second term on the right side of Eq. 5 describes the Taylor relationship between the flow stress and dislocation density; the last term ${\sigma }_b$ denotes the back stress that induces kinematic hardening which will be discussed later.

The dislocations generated during the plastic deformation of GNT metals are divided into two parts: $\rho ={\rho }_{GND}+{\rho }_{SSD}$. Part of dislocations is GNDs stored to accommodate the deformation gradients and allow compatible deformation, the other part is SSDs accumulated in pure crystals during the plastic deformation process (Ashby, 1970). The GND density is expressed as follows:

${\rho }_{GND}=\frac{\eta }{b}(6)$

$\eta =\frac{\mathrm{\Delta }{\sigma }_y}{Eh}(7)$

where $\eta$, $\mathrm{\Delta }{\sigma }_y$, $E$, $h$ are plastic deform gradient, yield strength difference, elasticity modulus and material height.

When HNT metal is applied uniaxial tensile loading parallel to the TBs, it is assumed that the TBs are evenly distributed in NT metal, so each NT lamella is regarded as an ideal elastic-plastic material and yields simultaneously. On the basis of the confined layer slip (CLS) model the yield strength can be presented as follows (Misra et al., 2005; You et al., 2011):

${\sigma }_y\left(\mathit{\lambda }\right)={\sigma }_0+\beta \frac{\mu b}{\mathit{\lambda }}\ln \left(\frac{\alpha \mathit{\lambda }}{b}\right)(8)$

where $\alpha$ and $\beta$ are material constants. Using the parameters ${\sigma }_0=72\pm 50$ MPa, $\alpha =0.16\pm 0.02$ and $\beta =0.40\pm 0.06$.

Based on KM model (Kocks and Mecking, 2003), the relationship p between SSD storage rate and strain is expressed as follows:

$\frac{\mathit{\partial }{\rho }_{SSD}}{\partial {\mathit{\epsilon }}_p}=M\left(K_0+K_1\sqrt{{\rho }_{SSD}}-K_2{\rho }_{SSD}+K_3{\rho }_{GND}\right)(9)$

where $K_0=1/\left(b\cdot d_G\right)$; $K_1=\psi /b$; $K_2=k_{20}{\left({\dot{\epsilon }}_p/{\dot{\epsilon }}_0\right)}^{-1/n}$, $\psi$ is proportionality factor,

$k_{20}$ is a material parameter, ${\dot{\epsilon }}_0$ is the reference strain rate, n is inversely, $n$ is inversely proportional to temperature, and ${\epsilon }^P$ is the local plastic strain. The first and second terms on the right side of the equation are associated with the athermal storage of dislocations, the third term is related to the annihilation of dislocations during dynamic recovery, and the fourth term is connected with the promotion effect of GNDs on SSDs. The new parameter $K_3$ indicate that dislocation promotion effect has been added to the KM model. Experimental results (Cheng et al., 2018) show that BCDs existed in GNT copper during stretching, resulting in the local dislocation density much higher than average dislocation density. Previous studies (Ashby, 1970; Mughrabi, 2001a; Mughrabi, 2001b) have shown that the flow stress produced by dislocations with non-uniform distribution is lower than homogeneous distribution. Therefore, the calculated flow stress of Taylor relation in this study is slightly higher than the actual situation.

In this research, the back stress in NT metals is attributed to the interaction between dislocations and TBs. At small strains, the GNT metals firstly deform in the region with low strength, and the TBs act as barriers to dislocations in adjacent NT lamellas. Storage of dislocations at TBs results in hardening of the material causing back stress. Here, some hypotheses about the form of back stress are proposed based on the experimental phenomena. 1) There is a saturation value of dislocation number in NT lamellas during yield process. 2) The number of saturated dislocations is influenced by the thickness of adjacent lamellas and the local plastic strain gradient. 3) The back stress caused by dislocation accumulation at TBs exists for a long time. The back stress ${\sigma }_b$ and number of saturated dislocations $N_S$ are expressed as follows:

${\sigma }_b=\frac{M\mu b}{a_1\mathit{\lambda }}N(10)$

$N_S=\sqrt{1+a_2\eta }\cdot N_0(11)$

where $\lambda$, $N_0$, $a_1$, $a_2$ are NT lamellas thickness, the number of saturated dislocations per unit thickness in HNT metals, dimensionless constants and strain gradient coefficient. The number of dislocations stored at the TBs depends on the plastic strain which can be described as follows (Sinclair et al., 2006; Zhu et al., 2011):

$\frac{\mathit{\partial }N}{\mathit{\partial }{\epsilon }_P}=\frac{\xi }{b}\left(1-\frac{N}{N_S}\right)(12)$

where $\xi$ is the average distance between slip bands and is thought to be proportional with the grain size $\xi =\theta \cdot d_G$.

Since a GNT material is subjected to uniaxial uniform strain through its thickness in experiments (Cheng et al., 2018), the rule of mixture (ROM) of Voigt model can be employed to accurately determine the overall stress-strain response in the material (Clyne and Withers, 1993; Lu et al., 2022). Therefore, the tensile stress ${\sigma }_{GNT}$ in GNT material can be expressed as:

${\sigma }_{GNT}=\frac{{\displaystyle \sum _{i=1}^n{\sigma }_i{h}_i}}{h}(13)$

where $i$ denote the various components of GNT metals; ${\sigma }_i$, $h_i$ are the stress applied on component $i$ and thickness of the corresponding component, respectively.

Results and discussion

In this paper, MD simulations tensile behavior were performed HNT and GNT copper samples. By comparing the dislocation state of the samples at 10.14% true strain, as shown in Figure 2, the shear strain distribution in NT-Cu0 is uniform, while the shear strain in the other GNT samples mainly occurs in the inner cores. During the tensile preliminary stage, the inner cores of the samples yields first, and the outer layers of the GNT samples can withstand larger elastic strain than inner cores. In order to satisfy the deformation coordination between the NT lamellas, the GNDs is generated at inner cores of samples to provide plastic strain difference.

FIGURE 2

FIGURE 2. Shear strain cloud maps of samples with 10.14% tensile true strain.

As shown in Figure 3. Further observation of the dislocation state in samples shows that the NT structure gradient has a limited effect on the dislocation movement, and the inner cores of GNT sample yields later than that of the HNT samples. In other words, the GNT structure in the outer layers provides additional elastic strain for inner cores.

FIGURE 3

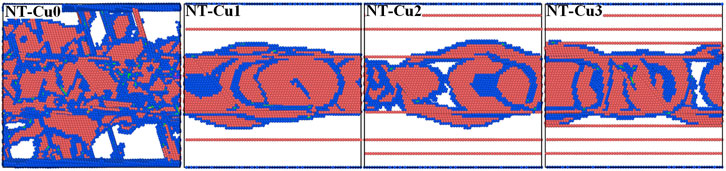
FIGURE 3. At 10.14% tensile true strain, pictures of dislocations for HNT and GNT samples (FCC atoms are hidden for a clear representation of dislocations).

Take NT-Cu1 for example, the tensile process of HNT and GNT was compared. As shown in Figure 4, NT-Cu0 yields at about 9.98% tensile strain, while NT-Cu1 yields at about 10.12% tensile strain. Primarily, dislocations in NT-Cu0 is emitted inwards from the material surface, and almost the same time dislocations begin to appear in inner cores. In general, the dislocation distribution in NT-Cu0 is relatively uniform, while part dislocations near outer surface, resulting in the dislocation density in outer layers is lower than that in inner cores. Dislocations in NT-Cu1, NT-Cu2 and NT-Cu3 start at the inner cores of samples and slip along the {111} plane inclined to the TBs. Taking NT-Cu1 for example, the GNT structure design can make the material yield in the inner cores but not in the outer layers. The dislocations generated in the inner cores provide work hardening capability for the material, which may be one of the reasons why the GNT material has higher yield strength than the uniform NT material. We hold the opinion that the hard phase in GNT metals provides additional elastic deformation capacity for the soft phase, and the soft phase provides additional work hardening for the hard phase.

FIGURE 4

FIGURE 4. The yield process of NT-Cu0 (A–D) and NT-Cu1 (E–H).

In the back stress model of Eqs 10, 11, based on the GNDs generated by NT structure of MD simulations result, we assume that the dislocation storage capacity of inner cores is related to the NT gradient and plastic strain gradient. However, due to the size and time scale of MD simulation, we were not able to obtain a quantitative description of this effect of NT structure, but obtained by fitting experimental data.

As shown in the Figure 5, the phenomenon of dislocations aggregation at the TBs occurred in all samples, which has been discussed in the existing studies (Dao et al., 2006). To further discuss the effect of outer layers GNT structure on dislocation evolution of inner cores, the dislocation density variation at the inner cores of samples. As shown in the Figure 6. The dislocation density in the inner cores of the samples quickly reaches a high level after yield. As the tensile continues, the dislocation density decreases about 20% and then fluctuates in a limited range. The dislocation density in the inner core of NT-Cu0 is about twice as much as that of NT-Cu1, NT-Cu2 and NT-Cu3. Since there are only two TBs in NT-Cu0, most dislocations are clustered near the inner core, causing the dislocation density in the inner core is higher than other samples, and the dislocation distribution is more heterogeneous. In our opinion, the GNT structure changes the dislocation distribution in NT metals, and more homogeneous dislocation distribution provides higher flow stress, which may be a source of additional plastic flow stress for GNT metals.

FIGURE 5

FIGURE 5. Images of the dislocations in samples with 18.2% tensile true strain (a/6<112> Shockley partial dislocations are colored in green, a/2<110> Perfect dislocations are marked in blue, a/6<110> Stair-rod dislocations are marked in pink and other dislocations are set in red).

FIGURE 6

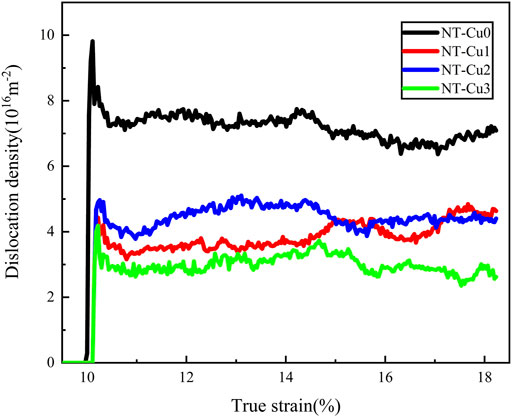
FIGURE 6. Variation of dislocation density with tensile true strain in the inner cores of samples (There is no dislocation in the inner cores, until tensile true strain researches about 10%).

The coherence of the TBs is reduced by the pile up of dislocations at TBs. As shown in Figure 7, the TBs in NT-Cu0 has damaged to some extent. Compared with NT-Cu1 and NT-Cu2, there is no GNT structure in the outer layers of NT-Cu0 to limit the inner dislocations escape to the samples surface. A large amount of dislocations slips outwards, leading to more adequate work hardening behavior did not occur in NT-Cu0. However, larger structure gradients are not always better. The NT lamellas with same 1.24 nm thickness were remained intact in NT-Cu2, but that were detwinned in NT-Cu3. In short, the NT structure gradient within a certain range is helpful to improve the strength and ductility of NT materials.

FIGURE 7

FIGURE 7. Images of the deformation structure in samples with 18.2% tensile true strain (The black boxes are typical areas of detwinning).

Based on the results and discussion of MD simulations above, a quantitative phenomenological model for GNT metals was established. In order to verify the correctness of the theoretical model, the back stress-true strain curve and tensile stress-true strain curve of the theoretical model and experimental (Cheng et al., 2018; Cheng et al., 2022) are compared. During the calculation of the theoretical model, the twin thickness and grain size are considered to vary continuously with sample thickness in GNT metals, whereas in HNT metals are considered to be constant, as shown in Figure 8. Relevant material parameters used for studying GNT copper tensile deformation are listed in Table 1. Material parameters were either fitted from experimental data or obtained from other literature (You et al., 2011; Zhu et al., 2011; Zhu et al., 2019; Chen et al., 2021).

FIGURE 8

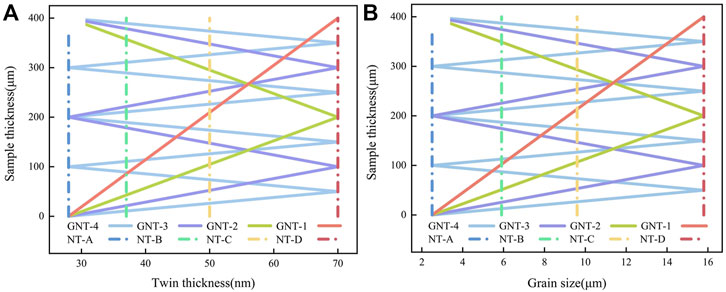
FIGURE 8. Material structure parameters used in theoretical model calculation. (A) The twin thickness used in theoretical model. (B) The grain size used in theoretical model.

TABLE 1

TABLE 1. Descriptions, symbols and magnitudes of different material parameters of the model.

Experimental data come from Ref. (Cheng et al., 2018; Cheng et al., 2022). As shown in Figure 9. Previous studies (Cheng et al., 2022) have shown that the extra strength of GNT metals is related to its higher back stress, the dependency between back stress and NT lamellas thickness can be demonstrated in our model. In order to show the effect of GNT structure on the back stress of NT metals, the parameters related to plastic strain gradient is introduced into our back stress model. It can be seen from Eqs 10, 11 that the decrease of NT lamellas thickness and the increase of NT structure gradient will promote the back stress of GNT material during tensile process. The MD simulations result shows that the dislocation evolution in NT lamellas is influenced by GNT structure. In this study, a phenomenological form of back stress model related to strain gradient is proposed. The rapid increase of back stress in the initial stage of deformation can be reflected in our back stress model. In other words, the main influencing factors of additional strength in GNT metals is included in the model. As characterized by the true stress-true strain curves, we can observe that the plastic stress becomes strain insensitive gradually. The direct cause to the insensitivity is that the back stress in the model gradually tends to saturation with the true strain. At this time, the hardening of the model is mainly derived from the dislocation evolution in the modified KM model.

FIGURE 9

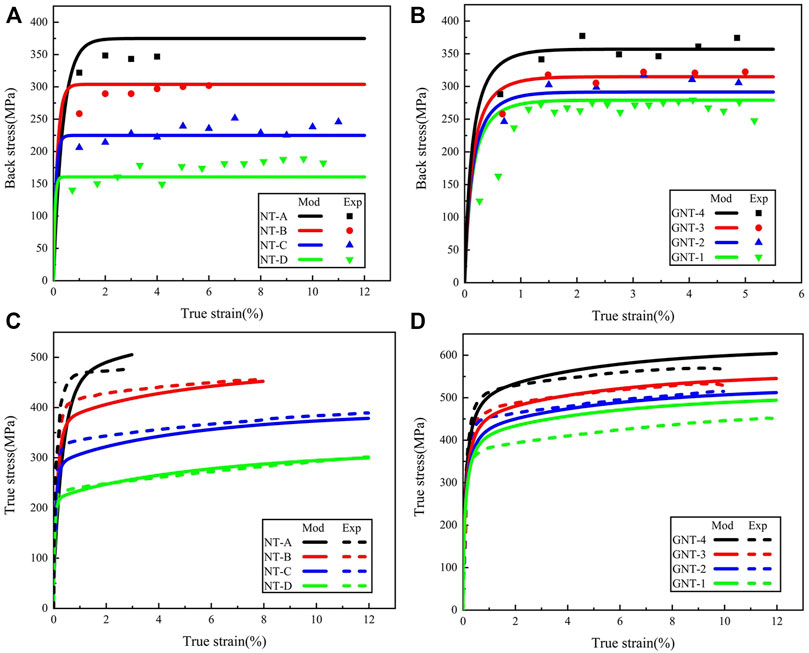
FIGURE 9. Mechanical properties of samples from modeling results and previous experiment. (A) Back stress-true strain curves of NT metals. (B) Back stress-true strain curves of GNT metals. (C) Tensile true stress-true strain curves of NT metals. (D) Tensile true stress-true strain curves of GNT metals.

The extra strengthening in GNT material is obvious, and some strength can even exceed the optimal component in the structure. This phenomenon is consistent with the previous experimental results (Cheng et al., 2018). The contribution of GND is very small compared with that of SSD in Taylor’s hardening law. The promotion of GND to SSD forms a unique BCD structure, and its influence on material hardening cannot be ignored. The GNDs density is much lower than SSDs density in GNT metals, and the contribution of GNDs to work hardening is mainly due to its promoting effect on SSDs rather than its effect on flow stress.

It is worth noting that the true stress of GNT-1 in Figure 9D obtained by the theoretical model is significantly higher than experimental value. We hold the opinion that the GNT structure plays a positive role in the improvement of GNT-1 back stress, but the promoting effect of GNDs on SSDs seems to be not obvious. We speculate that GNDs promoting effect on SSD seems to work only when the NT structure gradient reaches a certain value. The NT structure gradient of GNT-1 is too low to bring GNDs play the original hardening effect, which may be the reason why the GNT-1 strength calculated by our theoretical model is higher than the experimental value.

Conclusion

In this study, MD simulations are performed for analyzing the effects of NT structure gradient on uniaxial tensile loading behaviors of GNT metals. Results show that the elasticity, dislocation storage capacity and dislocation evolution of NT lamellas are affected by the GNT structure. On this basis, a back stress model related to the NT lamellas thickness and the plastic strain gradient is established. Moreover, a physically based theoretical framework is developed to describe the mechanical behaviors of GNT metals under uniaxial tensile. The back stress strengthening caused by GNT structure and the promotion effect of GNDs on SSDs that is the unique hardening effect of BCDs in GNT metals is considered in this model. This model can well describe the tensile stress response of HNT and GNT metals. Our study imply that NT lamellas thickness and NT structure gradient have a significant effect on the back stress of GNT metals. There will not be obvious promotion effect of GNDs on SSDs until the NT structure reaches a certain gradient. This work may provide necessary guides for the design and optimization of GNT metals.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

YY: Conceptualization, Methodology, Software, Investigation, Formal Analysis, Writing—Original Draft; XD: Data Curation, Writing—Original Draft; YY: Visualization, Investigation; ML: Resources, Supervision; SC: Software, Validation.

Funding

The work is supported by the Program for Innovative Research Team in China Earthquake Administration.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ashby, M. F. (1970). The deformation of plastically non-homogeneous materials. Philosophical Mag. A J. Theor. Exp. Appl. Phys. 21 (170), 399–424. doi:10.1080/14786437008238426

CrossRef Full Text | Google Scholar

Chen, W, Wan, P, Zhao, Q, and Zhou, H (2021). Constitutive description of extra strengthening in gradient nanotwinned metals. Nanomater. (Basel, Switz. 11 (9), 2375. doi:10.3390/nano11092375

CrossRef Full Text | Google Scholar

Chen, X. H., Lu, L., and Lu, K. (2011). Grain size dependence of tensile properties in ultrafine-grained Cu with nanoscale twins. Scr. Mater. 64 (4), 311–314. doi:10.1016/j.scriptamat.2010.10.015

CrossRef Full Text | Google Scholar

Cheng, Z., Zhou, H., Lu, Q., Gao, H., and Lu, L. (2018). Extra strengthening and work hardening in gradient nanotwinned metals. Science 362 (6414), eaau1925. doi:10.1126/science.aau1925

PubMed Abstract | CrossRef Full Text | Google Scholar

Cheng, Z, Bu, L, Zhang, Y, Wu, H. A, Zhu, T., Gao, H., et al. (2022). Unraveling the origin of extra strengthening in gradient nanotwinned metals. Proc. Natl. Acad. Sci. U. S. A. 119 (3), e2116808119. doi:10.1073/pnas.2116808119

PubMed Abstract | CrossRef Full Text | Google Scholar

Clyne, T., and Withers, P. (1993). An introduction to metal matrix composites (cambridge solid state science series). Cambridge: Cambridge University Press. doi:10.1017/CBO9780511623080

CrossRef Full Text | Google Scholar

Dao, M., Lu, L., Shen, Y. F., and Suresh, S. (2006). Strength, strain-rate sensitivity and ductility of copper with nanoscale twins. Acta Mater. 54 (20), 5421–5432. doi:10.1016/j.actamat.2006.06.062

CrossRef Full Text | Google Scholar

Faken, D., and Jónsson, H. (1994). Systematic analysis of local atomic structure combined with 3D computer graphics. Comput. Mat. Sci. 2, 279–286. doi:10.1016/0927-0256(94)90109-0

CrossRef Full Text | Google Scholar

Fang, T. H., Li, W. L., Tao, N. R., and Lu, K. (2011). Revealing extraordinary intrinsic tensile plasticity in gradient nano-grained copper. Sci. (New York, N.Y.) 331 (6024), 1587–1590. doi:10.1126/science.1200177

PubMed Abstract | CrossRef Full Text | Google Scholar

Hirel, P. (2015). Atomsk: A tool for manipulating and converting atomic data files. Comput. Phys. Commun. 197, 212–219. doi:10.1016/j.cpc.2015.07.012

CrossRef Full Text | Google Scholar

Hoover, W. G. (1986). Constant-pressure equations of motion. Phys. Rev. A 34, 2499–2500. doi:10.1103/physreva.34.2499

PubMed Abstract | CrossRef Full Text | Google Scholar

Kocks, U. F., and Mecking, H. (2003). Physics and phenomenology of strain hardening: the FCC case. Prog. Mater. Sci. 48 (3), 171–273. doi:10.1016/S0079-6425(02)00003-8

CrossRef Full Text | Google Scholar

Li, X., Lu, L., Li, J., Zhang, X., and Gao, H. (2020). Mechanical properties and deformation mechanisms of gradient nanostructured metals and alloys. Nat. Rev. Mat. 5 (9), 706–723. doi:10.1038/s41578-020-0212-2

CrossRef Full Text | Google Scholar

Li, X., Wei, Y., Lu, L., Lu, K., and Gao, H. (2010). Dislocation nucleation governed softening and maximum strength in nano-twinned metals. Nature 464 (7290), 877–880. doi:10.1038/nature08929

PubMed Abstract | CrossRef Full Text | Google Scholar

Lu, K., and Lu, J. (2004). Nanostructured surface layer on metallic materials induced by surface mechanical attrition treatment. Mater. Sci. Eng. A 375-377, 38–45. doi:10.1016/j.msea.2003.10.261

CrossRef Full Text | Google Scholar

Lu, K., Lu, L., and Suresh, S. (2009). Strengthening materials by engineering coherent internal boundaries at the nanoscale. Sci. (New York, N.Y.) 324 (5925), 349–352. doi:10.1126/science.1159610

PubMed Abstract | CrossRef Full Text | Google Scholar

Lu, S., Zhao, J., Huang, M., Li, Z., Kang, G., and Zhang, X. (2022). Multiscale discrete dislocation dynamics study of gradient nano-grained materials. Int. J. Plasticity 156, 103356. doi:10.1016/j.ijplas.2022.103356

CrossRef Full Text | Google Scholar

Mishin, Y., Mehl, M. J., Papaconstantopoulos, D. A., Voter, A. F., and Kress, J. D. (2001). Structural stability and lattice defects in copper: Ab initio, tight-binding, and embedded-atom calculations. Phys. Rev. B 63, 224106. doi:10.1103/PhysRevB.63.224106

CrossRef Full Text | Google Scholar

Misra, A., Hirth, J. P., and Hoagland, R. G. (2005). Length-scale-dependent deformation mechanisms in incoherent metallic multilayered composites. Acta Mater. 53 (18), 4817–4824. doi:10.1016/j.actamat.2005.06.025

CrossRef Full Text | Google Scholar

Mughrabi, H. (2001). The effect of geometrically necessary dislocations on the flow stress of deformed crystals containing a heterogeneous dislocation distribution. Mater. Sci. Eng. A 319-321, 139–143. doi:10.1016/S0921-5093(01)01003-6

CrossRef Full Text | Google Scholar

Mughrabi, H. (2001). On the role of strain gradients and long-range internal stresses in the composite model of crystal plasticity. Mater. Sci. Eng. A 317 (1-2), 171–180. doi:10.1016/S0921-5093(01)01173-X

CrossRef Full Text | Google Scholar

Plimpton, S. (1995). Fast parallel Algorithms for short-Range molecular dynamics. J. Comput. Phys. 117, 1–19. doi:10.1006/jcph.1995.1039

CrossRef Full Text | Google Scholar

Sinclair, C. W., Poole, W. J., and Bréchet, Y. (2006). A model for the grain size dependent work hardening of copper. Scr. Mater. 55 (8), 739–742. doi:10.1016/j.scriptamat.2006.05.018

CrossRef Full Text | Google Scholar

Stukowski, A., and Albe, K. (2010). Dislocation detection algorithm for atomistic simulations. Model. Simul. Mat. Sci. Eng. 18, 025016. doi:10.1088/0965-0393/18/2/025016

CrossRef Full Text | Google Scholar

Sun, J., Ye, H., Tao, J., Li, Q., Zhang, J., Shen, L., et al. (2019). Gradient structure regulated plastic deformation mechanisms in polycrystalline nanotwinned copper. J. Phys. D. Appl. Phys. 52 (36), 365304. doi:10.1088/1361-6463/ab29ca

CrossRef Full Text | Google Scholar

Tang, Y., Zhou, H., Lu, H., Wang, X., Cao, Q., Zhang, D., et al. (2022). Extra plasticity governed by shear band deflection in gradient metallic glasses. Nat. Commun. 13 (1), 2120. doi:10.1038/s41467-022-29821-4

PubMed Abstract | CrossRef Full Text | Google Scholar

You, Z. S., Lu, L., and Lu, K. (2011). Tensile behavior of columnar grained Cu with preferentially oriented nanoscale twins. Acta Mater. 59 (18), 6927–6937. doi:10.1016/j.actamat.2011.07.044

CrossRef Full Text | Google Scholar

Zhang, Y., Cheng, Z., Lu, L., and Zhu, T. (2020). Strain gradient plasticity in gradient structured metals. J. Mech. Phys. Solids 140, 103946. doi:10.1016/j.jmps.2020.103946

CrossRef Full Text | Google Scholar

Zhou, H., Zhu, P., Yang, W., and Gao, H. (2022). A gradient Eshelby force on twinning partial dislocations and associated detwinning mechanism in gradient nanotwinned metals. J. Mech. Phys. Solids 159, 104746. doi:10.1016/j.jmps.2021.104746

CrossRef Full Text | Google Scholar

Zhu, L., Wen, C., Gao, C., Guo, X., Chen, Z., and Lu, J. (2019). Static and dynamic mechanical behaviors of gradient-nanotwinned stainless steel with a composite structure: Experiments and modeling. Int. J. Plasticity 114, 272–288. doi:10.1016/j.ijplas.2018.11.005

CrossRef Full Text | Google Scholar

Zhu, L., Ruan, H., Li, X., Dao, M., Gao, H., and Lu, J. (2011). Modeling grain size dependent optimal twin spacing for achieving ultimate high strength and related high ductility in nanotwinned metals. Acta Mater. 59 (14), 5544–5557. doi:10.1016/j.actamat.2011.05.027

CrossRef Full Text | Google Scholar