Influence of Marangoni convection, solar radiation, and viscous dissipation on the bioconvection couple stress flow of the hybrid nanofluid over a shrinking surface

The heat transfer ratio plays an important role in the industrial and engineering sectors; in this model, the authors used the hybrid nanofluid because the heat transfer ratio of the hybrid nanofluid is more than that of the base fluid. The key objective of this research work is to boost up the heat transfer ratio, for example, not only the accomplishment of energy is enough but is also expected to regulate the feeding of energy, and this is possible only to approve the development of heat transmission liquids to the mechanism of the expenditures of energy and improvement. The current research study investigates the influence of Marangoni convection, solar radiation, and viscous dissipation on the bioconvection couple stress flow of the hybrid nanofluid over a shrinking surface. This type of flow has some important application in the industrial and engineering sectors for the purpose of cooling and heating effect. To transform the non-dimensionless form of the differential equation to the dimensionless form, the authors used the defined similarity transformation. The transformed dimensionless form of the differential equation is solved by the homotopic analysis method. The obtained important result is determined with the help of graphs which is obtained from velocity and temperature equations. The impression of different parameters such as couple stress parameter, Marangoni convection parameter, nanoparticle volume fraction, solar radiation parameter, magnetic field parameter, thermophoresis parameter, Eckert number, and Prandtl number is taken over graphs. The skin friction coefficient and Nusselt number are described in the form of tables.

Introduction

Nanotechnology has produced massive consciousness amongst the researchers due to its wide possibility of applications in different branches of science and technology. The important use of the research on nanotechnology is to boost the heat transfer ratio. To enhance the heat transfer ratio, different approaches are used for the regular fluid. Several researchers work on the combination of solid and liquid for the improvement of ratio. The importance of magneto-Marangoni convection due to the immoderate uses precisely, sprinkling of thin film flow, use in the important apparatus in atom, and helpful in making semiconductors, played a very enormous role in the process of welding and showed good performance in the crystal growth. Marangoni convection is also used in material science, varnish, and silicon melts and plays an important role in factories and industries. Moreover, to color the ground, the Marangoni phenomenon is commonly used. The pigment is hanged on the exterior surface of the essential medium like water or other thickness fluids in this procedure. Das et al. (2008) for the first time introduced the concept of nanofluids. Buongiorno (2006) studied the convective heat transport in nanofluids. Due to the important uses of nuclear reactors, plasma studies, wire drawing, hot rolling, and manufacturing of glass fiber, researchers take more interest in the flow of nanofluids over the extending surface and attended by Lorentz’s effect. Makinde and Aziz (2011) used a stretching surface to study the boundary-layer flow of a nanofluid. Rana and Bhargava (2012) used a non-linear stretching surface to study the flow and heat transfer of a nanofluid. Khan and Pop (2010) used a stretching surface to study boundary-layer flow of a nanofluid. Makinde et al. (2016) used a stretching surface to study the MHD flow of a variable viscosity nanofluid over a radially stretching convective surface with radiative heat. Besthapu et al. (2017) used a stretching surface to study the MHD flow of the nanofluid. Acharya et al. (2016) used a stretching surface to study ramification of variable thickness on MHD TiO₂ and Ag nanofluid. Acharya NDas and Prabir (2016) used two parallel plates to study squeezing flow of Cu–water and Cu–kerosene nanofluids. Das et al. (2016) used a shrinking sheet to study the onset of the nanofluid in the presence of a heat source/sink. Ishfaq et al. (2016) used a stretching surface to study the estimation of the boundary-layer flow of a nanofluid. Rana P Bhargava and Beg (2012) used a pour surface to study the mixed convective boundary-layer flow of a nanofluid numerically. The researchers take more interest in magneto-Marangoni convection which is produced due to the surface tension. The purpose behind this is some important applications such as, scattering of the thin liquid layer, atomic reactor, the processing of semiconductors, dynamic use in the welding process, crystal growth, material science, varnish, and silicon melt. The other important application of Marangoni convection is fine art mechanism, for instance, pigment on the ground. Pop Postelnicu (2001) studied the effect of Marangoni convection. Al-Mudhaf and Chamkha (2005) with the help of a porous medium investigated the Marangoni convection effect. Wang (2006) used a series solution method to study the influence of Marangoni convection. Chen (2007) discussed the inspiration of Marangoni convection. Magyari and Chamkha (2007) using the high magnitude of Re discussed the inspiration of Marangoni convection. Zheng et al. (Lin et al., 2013; Lin et al., 2014) studied the MHD Marangoni convection along with the thermal gradients. Aly and Ebaid (2016) used the Laplace transform to study the Marangoni flow over a permeable surface. Ellahi et al. (2016) used the ethylene glycol-based nanofluid to study the different shapes of nano-scale materials. Xu and Chen (Jiao et al., 2016) used permeable media to study Marangoni convection. Sheikholeslami and Chamkha (2017) studied the MHD Marangoni convection along with the two-phase nanoliquid hydrothermal model. The researchers take more interest in the novel kind of nanofluid known as the hybrid nanofluid due to a high heat transmission relation, which plays a significant role in the field of science and technology (Hussanan et al., 2019). They studied novel kind known as the hybrid nanofluid flow for some useful applications in manufacturing. (Eastman et al., 1996; Eastman et al., 1999; Moldoveanu et al., 2019; Kumar et al., 2020; Wakif et al., 2020). The thermal conductivity of EG (ethylene glycol) is little as compared to the other nanofluid. The required demand of the heat transfer ratio for current technologies and the wide requirement for thermal energy cannot be satisfied by the usually used fluids. The heat transfer ratio of the base fluid increases when the base liquids are mixed by the addition of minor shaped particles (Buongiorno et al., 2009). Thus, the increase in thermal possessions of usual fluids advanced strong interest of researchers to conduct more research. The overflowing literature on nanofluid and CNTs both (SWCNTs and MWCNTs) is studied by numerous researchers. Normally used in the energy sector and nanoscience (Kandasamy et al., 2016), copper oxide water was studied by Animasaun et al. (2019), carbon nanotube/water by Aman et al. (2017), heat transfer enrichment using the carbon nanotube by Raza et al. (2019), and the investigation of $F{e}_3{O}_4$ /water by Qasim et al. (Muhammad et al., 2020). The investigation of magnetite-ferrium oxide $F{e}_3{O}_4$ was discussed by Hussanan et al. (Qasim et al., 2014) and Al₂O₃/water by Sheikholeslami et al. (Hussanan et al., 2018). The study of the nanofluid flow over a stirring surface was conducted by Haq et al. (Sheikholeslami et al., 2017). Joseph, S. P et al. (Haq et al., 2017) discussed exact solutions for incompressible couple stress fluid flows. Baranovskii (Joseph, 2020) discussed exact solutions to the Navier–Stokes equations with couple stresses. Srinivas et al. (Baranovskii et al., 2021) discussed thermal analysis of a flow of immiscible couple stress fluids in a channel. Mishra, A., and Kumar (Gladys and Reddy, 2022) studied velocity and thermal slip effects on the MHD nanofluid flow past a stretching cylinder with viscous dissipation and Joule heating. Gladys, T., and Reddy (Rachid et al., 2021) studied the contributions of variable viscosity and thermal conductivity on the dynamics of the non-Newtonian nanofluid flow past an accelerating vertical plate. Rachid, H et al. (Mishra and Kumar, 2020b) studied entropy generation and mechanical efficiency in the laminar peristaltic flow through an elliptical duct. Mishra and Kumar (2019a) studied the thermal performance of the MHD nanofluid flow over a stretching sheet due to viscous dissipation, Joule heating, and thermal radiation. Mishra, A., and Kumar, M (Mishra et al., 2021) studied viscous dissipation and Joule heating influences past a stretching sheet in a porous medium with thermal radiation saturated by silver–water and copper–water nanofluids. Mishra and Kumar (2019b) studied the thermal performance of the Ag–water nanofluid flow over a curved surface due to chemical reaction using Buongiorno’s model. Mishra et al. (2020) studied the influence of viscous dissipation and heat generation/absorption on Ag–water nanofluid flow over a Riga plate with suction. Daniel et al. (2020a) studied the roles of nanoparticles and heat generation/absorption on the MHD flow of the Ag–H₂O nanofluid via porous stretching/shrinking convergent/divergent channel. Daniel et al. (2019a) studied the slip role for unsteady MHD mixed convection of the nanofluid over a stretching sheet with thermal radiation and electric field. Daniel and Daniel (2015) studied the stratified electro magneto hydrodynamic flow of the nanofluid supporting the convective role. Daniel et al. (2017a) studied the effects of buoyancy and thermal radiation on the MHD flow over a stretching porous sheet by the homotopy analysis method. Daniel et al. (2017b) studied entropy analysis in the electrical magneto hydrodynamic (MHD) flow of the nanofluid with effects of thermal radiation, viscous dissipation, and chemical reaction. Daniel (2016a) studied double stratification effects on the unsteady electrical MHD mixed convection flow of the nanofluid with viscous dissipation and Joule heating. Daniel et al. (2018a) studied the laminar convective boundary-layer slip flow over a flat plate by the homotopy analysis method. Daniel (2017) studied thermal stratification effects on the MHD radiative flow of the nanofluid over a nonlinear stretching sheet with variable thickness. Daniel et al. (2018b) studied MHD laminar flows and heat transfer adjacent to permeable stretching sheets with a partial slip condition. Daniel et al. (2018c) studied the effects of slip and convective conditions on the MHD flow of the nanofluid over a porous nonlinear stretching/shrinking sheet. Daniel et al. (2017c) studied the impact of thermal radiation on the electrical MHD flow of the nanofluid over a nonlinear stretching sheet with variable thickness. Daniel (2015) studied the numerical study of entropy analysis for the electrical unsteady natural magneto hydrodynamic flow of the nanofluid and heat transfer. Daniel (2016b) studied steady MHD laminar flows and heat transfer adjacent to porous stretching sheets by the HAM. Daniel et al. (2019b) studied the steady MHD boundary-layer slip flow and heat transfer of the nanofluid over a convectively heated non-linear permeable sheet. Daniel et al. (2018d) studied thermal radiation on the unsteady electrical MHD flow of the nanofluid over a stretching sheet with a chemical reaction. Daniel et al. (2017d) studied the slip effects on the electrical unsteady MHD natural convection flow of the nanofluid over a permeable shrinking sheet with thermal radiation. Daniel et al. (2020b) studied the entropy analysis of the unsteady magnetohydrodynamic nanofluid over a stretching sheet with electric field. Liao (2012) studied the hydromagnetic slip flow of the nanofluid with thermal stratification and convective heating. Garia et al. (2021) studied the hybrid nanofluid flow over two different geometries with the Cattaneo–Christov heat flux model and heat generation: a model with correlation coefficient and probable error. Yaseen et al. (2022a) studied the Cattaneo–Christov heat flux model in the Darcy–Forchheimer radiative flow of MoS₂–SiO₂/kerosene oil between two parallel rotating disks. Yaseen et al. (2022b) studied the hybrid nanofluid (MoS₂–SiO₂/water) flow with viscous dissipation and Ohmic heating on an irregular variably thick convex/concave‐shaped sheet in a porous medium. Yaseen (2021) studied an opposing flow of a MHD hybrid nanofluid flow past a permeable moving surface with a heat source/sink and thermal radiation. Gumber et al. (2022) studied the heat transfer in the micropolar hybrid nanofluid flow past a vertical plate in the presence of thermal radiation and suction/injection effects. This is one of the most serious issues nowadays, and most of the researchers are trying to study the advance resources to reestablish the energy and to regulate the feeding of heat transfer devices. All these resources are dependent on solids, gases, and liquids. To increase the thermal efficiency of common liquids, it is possible through the addition of small solid metal particles. There are many liquids with a low heat transfer rate which are used in different engineering sectors. These liquids are bio-liquid, polymeric solution, various oils, greases, water, toluene, refrigerants, and ethylene glycol. The important aim of this study is to deliver the idea to boost the heat transfer which is used in the new technology. In our study, the authors used different types of hybrid nanofluids for the improvement of the heat transfer ratio which play an important role. For example, not only the achievement of energy is enough but is also expected to adjust the consumption of energy, and this is possible only to approve the development of heat transmission liquids to the mechanism of the expenditures of energy and improvement. Most of the heat transmission is the demand of the industry and other related scientific fields. The flow problem analysis was conducted on the basis of converting non-linear partial differential equations to non-linear ordinary differential equations by similarity transformation. The model non-linear differential equations have been analyzed by an approximate analytical method. The impact of different developing results has been inspected with the help of figures and tables and the novelty of the present research article. For the first time, the impact of Marangoni convection, solar radiation, and viscous dissipation on the bioconvection couple stress flow of the hybrid nanofluid over a shrinking surface is studied analytically. The stability of both velocity and temperature equations is discussed in the form of tables and graphs, the comparison of the present research work is presented in the form of tables with the already published work, the defined model is discussed for the first time analytically on a shrieking surface, and the convergence control parameter is discussed in the table form for both velocity and temperature equations.

Mathematical formulation

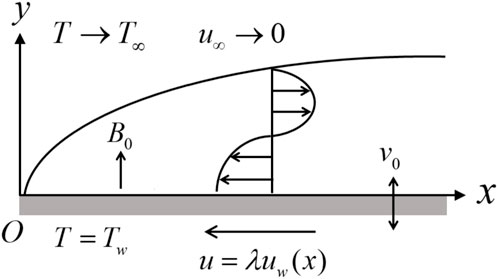
Consider a two-dimensional time-independent laminar incompressible flow of $T{e}_2{O}_3+MWCNTs+H_{2}O$ and $SWCNTs+H_{2}O$ hybrid nanofluids on a shrinking and stretching surface, where $\lambda <0and\lambda >0$ represent shrinking and stretching surface and $\lambda =0$ rigid surface, in which water is the base fluid. In this combination, $T{e}_2{O}_3+MWCNTs+H_{2}O$ represents the hybrid nanofluid, and $SWCNTs+H_{2}O$, represents the nanofluid. The coordinate axes are arranged as the x axis is along the surface and y axis is perpendicular to the surface. Under the aforementioned assumption, the governing equation for the given flow problem is settled as follows (Garia et al., 2021):

$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0,(1)$

${\rho }_{hnf}\left(u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}\right)={\mu }_{hnf}\frac{{\partial }^{2}u}{\partial y^2}-{\sigma }_{hnf}{B}_0^{2}u-\frac{ϵ{\mu }_{hnf}}{k_1}u-\frac{{\nu }_{hnf}}{{\rho }_{hnf}}\frac{{\partial }^{4}u}{\partial y^4},(2)$

$u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}=\alpha \frac{{\partial }^{2}T}{\partial y^2}+\frac{{\mu }_{hnf}}{{\left({\rho c}_p\right)}_{hnf}}{\left(\frac{\partial u}{\partial y}\right)}^2,(3)$

where $uandv$ represent velocity along x and y directions, respectively, $T$ represents the temperature, $\epsilon$ represents the porosity of the porous medium, $k_1$ represents the permeability of the porous medium, ${\sigma }_{hnf}$ represents the electrical conductivity, $\alpha$ represents the thermal diffusivity, $k_{hnf}$ is the thermal conductivity, $\tau$ represents the ratio of the effective heat capacity, ${\rho }_{hnf}$ represents the density of the hybrid nanofluid, and ${\mu }_{hnf}$ represents the viscosity of the hybrid nanofluid.

The boundary conditions for the given flow problem are as follows:

$\begin{array}{l}u=\lambda u_w\left(x\right),v=v_0,T=T_{w\left(x\right)}aty=0\\ u\to 0,v\to 0,T\to T_{\infty }asy\to \infty .\end{array}(4)$

From Eq. 4, we see that the velocity of the fluid and temperature changes along the x axis and above the x axis, the temperature of the surface remains constant, and the velocity of the fluid particles is zero; $v_w$ represents the suction injection velocity, and $T_{\infty }$ represents constant wall temperature.

To convert the non-dimensionless form of Eqs 2, 3, we introduced a dimensionless function of $fand\theta$, with the similarity variable $\eta$ as

$\eta =\frac{y}{x}R{a}_x^{\frac{1}{4}},\psi =\alpha R{a}_x^{\frac{1}{4}}f\left(\eta \right),\theta \left(\eta \right)=\frac{T-T_{\infty }}{T_w-T_{\infty }}.(5)$

In Eq. 5, $\psi \left(x,y\right)$ represents the stream function and is defined by $u=\frac{\partial \psi }{\partial y}andv=-\frac{\partial \psi }{\partial x}$. The stream function satisfied the equation identically, and Eq. 5 converts Eqs 2, 3 to the following form ((Srinivas and Ramana Murthy, 2016)):

$\begin{array}{l}\frac{{\left(1-{\varphi }_1-{\varphi }_2\right)}^{-2.5}}{\left(1-{\varphi }_1-{\varphi }_2\right)+{\varphi }_1\left(\frac{{\rho }_1}{{\rho }_f}\right)+{\varphi }_2\left(\frac{{\rho }_2}{{\rho }_f}\right)}{f}^{‴}+\frac{1}{4}{m}^{\ast }\left(3f{f}^{″}-2{f^{\prime }}^2\right)-\\ {\left(1-{\varphi }_1\right)}^{2.5}{\left(1-{\varphi }_2\right)}^{2.5}M{f}^{\prime }-K{f}^v=0,\end{array}(6)$

$\begin{array}{l}\frac{1}{\mathrm{Pr}}\frac{{\left(1-{\varphi }_1-{\varphi }_2\right)}^{-2.5}}{\left(1-{\varphi }_1-{\varphi }_2\right)+{\varphi }_1\left(\frac{{\rho }_1}{{\rho }_f}\right)+{\varphi }_2\left(\frac{{\rho }_2}{{\rho }_f}\right)}{\theta }^{″}+\\ \frac{3}{4}{\left(1-{\varphi }_1\right)}^{2.5}{\left(1-{\varphi }_2\right)}^{2.5}f{\theta }^{\prime }+EcNt{{\theta }^{\prime }}^2=0.\end{array}(7)$

The boundary conditions for the given flow problem are as follows:

$\begin{array}{l}f\left(0\right)=S,f^{\prime }\left(0\right)=\lambda ,f^{\prime }\left(\infty \right)=0,\\ \theta \left(0\right)=1,\theta \left(\infty \right)=0,\end{array}(8)$

where $\lambda <0and\lambda >0$ represent the shrinking and stretching surface and $\lambda =0$ represents the rigid surface. $Rb=\frac{{\gamma }^{\ast }\Delta n_w\Delta \rho }{{\rho }_{hnf}\left(1-{\phi }_{\infty }\right)\beta \Delta T_w}$ represents the bioconvection Rayleigh number, $Br=\frac{\left({\rho }_{hnf}-{\rho }_{nf\infty }\right)\Delta C_w}{{\rho }_{hnf}\left(1-{\varphi }_{\infty }\right)\beta \Delta T_w}$ represents the boundary ratio parameter, $\mathrm{E}\mathrm{c}=\frac{U_{\varpi }^2}{c_p\left(T_{\varpi }-T_0\right)}$ shows Eckert number, $N=\frac{4\sigma T_{\infty }^3}{\left(\rho c_p\right)k^{\ast }}$ shows the solar radiation parameter, $M=\frac{{\sigma }_{hnf}{B}_0^2}{{\rho }_{hnf}a}$ shows the magnetic parameter, $\mathrm{Pr}=\frac{{\nu }_{hnf}}{\alpha }$ shows Prandtl number, $N_t=\frac{\tau D_T\left(T_w-T_{\infty }\right)}{{\nu }_{hnf}{T}_{\infty }}$ shows the thermophoresis parameter, $m^{\ast }=\frac{a\gamma {\delta }_0{T}_{ref}}{{\upsilon }_{hnf}}$ shows the Marangoni convection parameter, $R$ shows the Reynold number, $K=\frac{va}{{\nu }_{hnf}^2}$ shows the couple stress parameter, and $C_T=\frac{T_{\infty }}{T_w-T_{\infty }}$ shows the temperature ration parameter.

The non-dimensionless forms of skin friction and Nusselt number are as follows:

$C_f=\frac{{\mu }_{hnf}{\left(\frac{\partial u}{\partial y}\right)}_{y=0}}{{\rho }_{hnf}{U}^2},Nu=\frac{1}{k_f\left(T_w-T_{\infty }\right)}{\left(k_{hnf}\frac{\partial T}{\partial y}\right)}_{y=0}.(9)$

Using Eq. 5 in Eq 9, we have the dimensionless forms of skin friction and Nusselt number.

$C_f\left(R{a}_x^{-\frac{1}{4}}{\mathrm{R}\mathrm{e}}_x\mathrm{Pr}\right)=\left(\frac{{\left(1-{\varphi }_1\right)}^{2.5}.{\left(1-{\varphi }_2\right)}^{-2.5}}{\left(1-{\varphi }_2\right)\left\{\left(\left(1-{\varphi }_1\right)+{\varphi }_1.\left(\frac{{\rho }_{s_1}}{{\rho }_f}\right)+{\varphi }_2.\left(\frac{{\rho }_{s_2}}{{\rho }_f}\right)\right)\right\}}\right)f^{″}\left(0\right),(10)$

$R{a}_x^{-\frac{1}{4}}Nu=-\left(1+\frac{4N}{3}\right)\frac{k_{hnf}}{k_f}{\theta }^{\prime }\left(0\right).(11)$

Solution by the HAM

To solve Eqs 6, 7 along with the boundary conditions (8), we apply the homotopy analysis method (HAM) with the following technique. The solutions having the auxiliary parameters $\mathrm{\hslash }$ adjust and control the convergence of the solutions.

The initial guesses are selected as follows:

$f_0\left(\eta \right)=\eta and{\theta }_0\left(\eta \right)=1.(12)$

The linear operators are taken as $L_f{\text{and}\mathrm{L}}_{\theta }$:

$L_f\left(f\right)=f^{‴}and{\mathrm{L}}_{\theta }\left(\theta \right)={\theta }^{″},(13)$

which have the following properties:

$L_f\left(c_1+c_2\eta +c_3{\eta }^2\right)=0and{\mathrm{L}}_{\theta }\left(c_4+c_5\eta \right)=0,(14)$

where $c_i\left(i=1-7\right)$ are the constants in a general solution.

The resultant non-linear operatives $N_{f}and{N}_{\theta }$ are given as follows:

$\begin{array}{l}{N}_f\left[f\left(\eta ;p\right)\right]=\frac{{\partial }^{3}f\left(\eta ;p\right)}{\partial {\eta }^3}+\frac{1}{4}{m}^{\ast }\left[3\frac{{\partial }^{2}f\left(\eta ;p\right)}{\partial {\eta }^2}\frac{{\partial }^{3}f\left(\eta ;p\right)}{\partial {\eta }^3}-{\left(\frac{\partial f\left(\eta ;p\right)}{\partial \eta }\right)}^2\right]\\ -M\frac{\partial f\left(\eta ;p\right)}{\partial \eta }-K\frac{{\partial }^{5}f\left(\eta ;p\right)}{\partial {\eta }^5}=0,\end{array}(15)$

$\begin{array}{l}{N}_{\theta }\left[f\left(\eta ;p\right),\theta \left(\eta ;p\right),\phi \left(\eta ;p\right)\right]=\frac{1}{\mathrm{Pr}}\frac{{\partial }^2\theta \left(\eta ;p\right)}{\partial {\eta }^2}-\\ \frac{3}{4}f\left(\eta ;p\right)\frac{\partial \theta \left(\eta ;p\right)}{\partial \eta }+EcNt{\left(\frac{\partial \theta \left(\eta ;p\right)}{\partial \eta }\right)}^2=0.\\ \end{array}(16)$

The basic idea of the HAM is described in Liao (2003), Liao (2004b), Liao (2010), and Acharya et al. (2017); the zero^th -order problems from Eqs 6, 7 are as follows:

$\left(1-p\right)L_f\left[f\left(\eta ;p\right)-f_0\left(\eta \right)\right]=p{\hslash }_f{N}_f\left[f\left(\eta ;p\right)\right],(17)$

$\left(1-p\right)L_{\theta }\left[\theta \left(\eta ;p\right)-{\theta }_0\left(\eta \right)\right]=p{\hslash }_{\theta }{N}_{\theta }\left[f\left(\eta ;p\right),\theta \left(\eta ;p\right),\phi \left(\eta ;p\right)\right].(18)$

The equivalent boundary conditions are as follows:

$\begin{array}{l}{f\left(\eta ;p\right)|}_{\eta =0}=0,{\frac{\partial f\left(\eta ;p\right)}{\partial \eta }|}_{\eta =0}=1,{\frac{{\partial }^{2}f\left(\eta ;p\right)}{\partial {\eta }^2}|}_{\eta =\beta }=0,\\ {\theta \left(\eta ;p\right)|}_{\eta =0}=1,{\frac{\partial \theta \left(\eta ;p\right)}{\partial \eta }|}_{\eta =\beta }=0,\end{array}(19)$

where $p\in \left[\mathrm{0,1}\right]$ is the imbedding parameter and ${\mathrm{\hslash }}_f\text{and}{\mathrm{\hslash }}_{\theta }$ are used to control the convergence of the solution. When $p=0\text{and}\mathrm{p}=1$, we have

$f\left(\eta ;1\right)=f\left(\eta \right)and\theta \left(\eta ;1\right)=\theta \left(\eta \right).(20)$

Expanding $f\left(\eta ;p\right)and\theta \left(\eta ;p\right)$ in Taylor’s series about $p=0$

$f\left(\eta ;p\right)=f_0\left(\eta \right)+{\displaystyle \sum }_{m=1}^{\infty }{f}_m\left(\eta \right)p^m,(21)$

$\begin{array}{l}\\ \theta \left(\eta ;p\right)={\theta }_0\left(\eta \right)+{\displaystyle \sum }_{m=1}^{\infty }{\theta }_m\left(\eta \right)p^m,\end{array}(22)$

where

$f_m\left(\eta \right)={\frac{1}{m!}\frac{\partial f\left(\eta ;p\right)}{\partial \eta }|}_{p=0}\text{and}{\theta }_m\left(\eta \right)={\frac{1}{m!}\frac{\partial \theta \left(\eta ;p\right)}{\partial \eta }|}_{p=0}.(23)$

The secondary constraints ${\mathrm{\hslash }}_f\text{and}{\mathrm{\hslash }}_{\theta }$ are chosen in such a way that series (22) converges at $p=1$; switching $p=1$ in (22), we obtain

$\begin{array}{l}f\left(\eta \right)=f_0\left(\eta \right)+{\displaystyle \sum }_{m=1}^{\infty }{f}_m\left(\eta \right),\\ \theta \left(\eta \right)={\theta }_0\left(\eta \right)+{\displaystyle \sum }_{m=1}^{\infty }{\theta }_m\left(\eta \right).\end{array}(24)$

The $m$ th-order problem satisfies the following:

$\begin{array}{l}{L}_f\left[f_m\left(\eta \right)-{\chi }_m{f}_{m-1}\left(\eta \right)\right]={\mathrm{\hslash }}_f{R}_m^f\left(\eta \right),\\ L_{\theta }\left[{\theta }_m\left(\eta \right)-{\chi }_m{\theta }_{m-1}\left(\eta \right)\right]={\mathrm{\hslash }}_{\theta }{R}_m^{\theta }\left(\eta \right).\\ \end{array}(25)$

The corresponding boundary conditions are

$\begin{array}{l}{f}_m\left(0\right)=S,f_m^{\prime }\left(0\right)=\lambda ,f_m^{\prime }\left(\infty \right)=0,\\ {\theta }_m\left(0\right)=1,{\theta }_m\left(\infty \right)=0.\end{array}(26)$

Here,

$R_m^f\left(\eta \right)=f_{m-1}^{‴}+\frac{1}{4}{m}^{\ast }{\displaystyle \sum }_{k=0}^{m-1}{f}_{m-1-k}^{″}-2{\left(f_{m-1-k}^{\prime }\right)}^2-M{\displaystyle \sum }_{k=0}^{m-1}{f}_{m-1-k}^{\prime }K{\displaystyle \sum }_{k=0}^{m-1}{f}_{m-1-k}^v=0,(27)$

$\begin{array}{l}{R}_m^{\theta }\left(\eta \right)=\frac{1}{\mathrm{Pr}}{\theta }_{m-1}^{″}+\frac{3}{4}{\displaystyle \sum }_{k=0}^{m-1}f{\theta }_{m-1-k}^{\prime }+EcNt{{\displaystyle \sum }_{k=0}^{m-1}\left({\theta }_{m-1-k}^{\prime }\right)}^2=0.\\ \end{array}(28)$

Stability analysis

The time-based stability of the multiple solutions as time changes is studied. This analysis was first presented by Merkin (1986) and then followed by Weidman et al. (2006). In order to achieve the solution time-based stability, the unsteady form of Eqs 2, 3 must be considered by suggesting the new dimensionless time variable equation one which will be unchanged. The unsteady forms of Eqs 2, 3 are

$\frac{\partial u}{\partial t}+\left(u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}\right)=\frac{1}{{\rho }_{hnf}}\left({\mu }_{hnf}\frac{{\partial }^{2}u}{\partial y^2}-{\sigma }_{hnf}{B}_0^{2}u-\frac{ϵ{\mu }_{hnf}}{K}u-{\nu }_{hnf}\frac{{\partial }^{4}u}{\partial y^4}\right),(29)$

$\frac{\partial T}{\partial t}+u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}=\alpha \frac{{\partial }^{2}T}{\partial y^2}+\frac{{\mu }_{hnf}}{{\left(\rho cp\right)}_{hnf}}{\left(\frac{\partial u}{\partial y}\right)}^2.(30)$

First, consider the new variables as follows:

$\eta =\frac{y}{x}R{a}_x^{\frac{1}{4}},\psi =\alpha R{a}_x^{\frac{1}{4}}f\left(\eta \right),\theta \left(\eta \right)=\frac{T-T_{\infty }}{T_w-T_{\infty }},\tau =at(31)$

Now, using Eq. 29 in Eqs 30, 31, the unsteady forms of Eqs 29, 30 become

$\begin{array}{l}\frac{{\left(1-{\varphi }_1-{\varphi }_2\right)}^{-2.5}}{\left(1-{\varphi }_1-{\varphi }_2\right)+{\varphi }_1\left(\frac{{\rho }_1}{{\rho }_f}\right)+{\varphi }_2\left(\frac{{\rho }_2}{{\rho }_f}\right)}\frac{{\partial }^{3}f}{\partial {\eta }^3}+\frac{1}{4}{m}^{\ast }\left(3f\frac{{\partial }^{2}f}{\partial {\eta }^2}-2{\left(\frac{\partial f}{\partial \eta }\right)}^2\right)-\\ {\left(1-{\varphi }_1\right)}^{2.5}{\left(1-{\varphi }_2\right)}^{2.5}M\frac{\partial f}{\partial \eta }-K\frac{{\partial }^{5}f}{\partial \eta 5}-\frac{{\partial }^{2}f}{\partial \eta \partial \tau }=0,\end{array}(32)$

$\begin{array}{l}\frac{1}{\mathrm{Pr}}\frac{{\left(1-{\varphi }_1-{\varphi }_2\right)}^{-2.5}}{\left(1-{\varphi }_1-{\varphi }_2\right)+{\varphi }_1\left(\frac{{\rho }_1}{{\rho }_f}\right)+{\varphi }_2\left(\frac{{\rho }_2}{{\rho }_f}\right)}\frac{{\partial }^2\theta }{\partial {\eta }^2}+\\ \frac{3}{4}{\left(1-{\varphi }_1\right)}^{2.5}{\left(1-{\varphi }_2\right)}^{2.5}f\frac{{\partial }^2\theta }{\partial {\eta }^2}+EcNt{\left(\frac{\partial \theta }{\partial \eta }\right)}^2-\frac{\partial \theta }{\partial \tau }=0.\end{array}(33)$

The unsteady boundary conditions are

$\begin{array}{l}f\left(0,\tau \right)=S,\frac{\partial f}{\partial \eta }\left(0,\tau \right)=\lambda ,\theta \left(0,\tau \right)=1,\\ \frac{\partial f}{\partial \eta }\left(\infty ,\tau \right)=0,\theta \left(\infty ,\tau \right)=0.\end{array}(34)$

Now, consider the following perturbation function (Harris et al., 2009):

$f\left(\eta ,\tau \right)=f_0\left(\eta \right)+e^{-\gamma \tau }F\left(\eta \right),\theta \left(\eta ,\tau \right)={\theta }_0\left(\eta \right)+e^{-\gamma \tau }G\left(\eta \right).(35)$

Equation 34 is used to apply a small disturbance $f=f_0\left(\eta \right)and\theta ={\theta }_0\left(\eta \right)$ of Eqs 6, 7. The functions $F\left(\eta \right)andG\left(\eta \right)$ in Eq. 33 are relatively small as compared with $f_0\left(\eta \right)and{\theta }_0\left(\eta \right)$. The sign (positive or negative) of the eigenvalue $\gamma$ determines the stability of the solution, now, using Equation 34 in Eqs 32–4, we have

$\frac{{\left(1-{\varphi }_1-{\varphi }_2\right)}^{-2.5}}{\left(1-{\varphi }_1-{\varphi }_2\right)+{\varphi }_1\left(\frac{{\rho }_1}{{\rho }_f}\right)+{\varphi }_2\left(\frac{{\rho }_2}{{\rho }_f}\right)}{F}^{‴}++\frac{1}{4}{m}^{\ast }\left(f_0{F}^{″}+f_0^{″}F-2f_0^{\prime }{F}^{\prime }\right)-{\left(1-{\varphi }_1\right)}^{2.5}{\left(1-{\varphi }_2\right)}^{2.5}M{F}^{\prime }-K{F}^V+\gamma F^{\prime }=0,(36)$

$\frac{1}{\mathit{Pr}}\frac{{\left(1-{\varphi }_1-{\varphi }_2\right)}^{-2.5}}{\left(1-{\varphi }_1-{\varphi }_2\right)+{\varphi }_1\left(\frac{{\rho }_1}{{\rho }_f}\right)+{\varphi }_2\left(\frac{{\rho }_2}{{\rho }_f}\right)}{G}^{″}-\frac{3}{4}{\left(1-{\varphi }_1\right)}^{2.5}{\left(1-{\varphi }_2\right)}^{2.5}\left[f_0{G}^{″}+F_0{\theta }_0^{″}\right]-2EcNt{\theta }_0^{\prime }{G}^{\prime }-\gamma G=0.(37)$

Subject to the boundary conditions

$\begin{array}{l}F\left(0\right)=0,F^{\prime }\left(0\right)=0,G\left(0\right)=0,\\ F^{\prime }\left(\infty \right)=0,G\left(\infty \right)=0.\end{array}(38)$

Without the loss of generality, we set $F^{″}\left(0\right)=1$ , (Mishra and Kumar, 2020a) to get the eigenvalue of Eqs 36, 37).

The solution will be stable if and only if the eigenvalue is positive, which shows the initial decay as time passes, and if the eigenvalue is negative at that point, the flow solution shows the initial growth of development, and the solution is said to be unstable as time passes.

Results and discussion

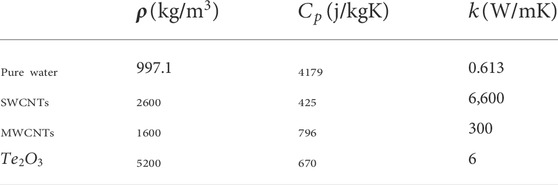
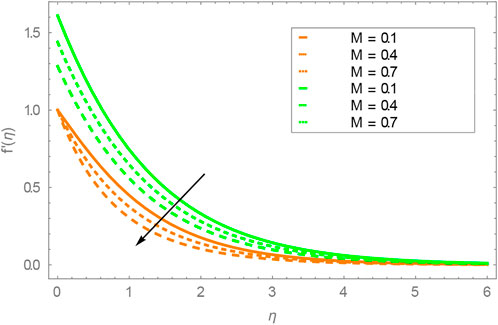
The important aim of this study is to deliver the idea of boost of the heat transfer, which is used in the new technology. In our study, we used different types of hybrid nanofluids for the improvement of the heat transfer ratio, which play an important role, for example, not only is the achievement of energy enough but is also expected to adjust the consumption of energy, and this is possible only to improve the development of heat transmission liquids to mechanism of the expenditures of energy and improvement. Most of the heat transmission is the demand of the industry and other related scientific fields. The second and important feature of this research is the enhancement of heat to reduce energy consumptions. The flow problem is conducted using a shrinking and stretching surface. The outputs of this study will be used to reduce energy consumption in industry and other engineering fields. In our research study, we used a new type of nanofluid known as the hybrid nanofluid for the enhancement of the heat transfer ratio because the heat transfer ratio of hybrid nanofluid is more than that of the base fluids. The hard elements dissolve in the base liquid, and after its constant diffusion, the hybrid nanofluid is produced. To transform the non-dimensionless form of the differential equation to the dimensionless form of the differential equation, the authors used the defined similarity transformation. The transformed dimensionless form of the differential equations is solved by the approximate analytical method. The total results obtained from the given flow problem are presented through figures. (Buongiorno, 2006; Khan and Pop, 2010; Makinde and Aziz, 2011; Rana and Bhargava, 2012; Acharya et al., 2016; Acharya N Das and Prabir, 2016; Makinde et al., 2016; Besthapu et al., 2017), the influence of different parameters on the velocity profile is presented in figures (Buongiorno, 2006; Khan and Pop, 2010; Makinde and Aziz, 2011; Rana and Bhargava, 2012; Makinde et al., 2016), and the influence of different parameters on the temperature profile is presented in figures (Acharya et al., 2016; Acharya NDas and Prabir, 2016; Besthapu et al., 2017). Table 1 shows the thermo-physical properties of water, $CNTs$, and $T{e}_2{O}_3$ nanoparticles, Tables 2, 3 show the convergence control parameter for both velocity and temperature for the defined flow problem, while Tables 4, 5 show the influence of different parameters on skin friction and Nusselt number, respectively.

TABLE 1

TABLE 1. Thermo-physical properties of water, $CNTs$, and $T{e}_2{O}_3$ nanoparticles.

TABLE 2

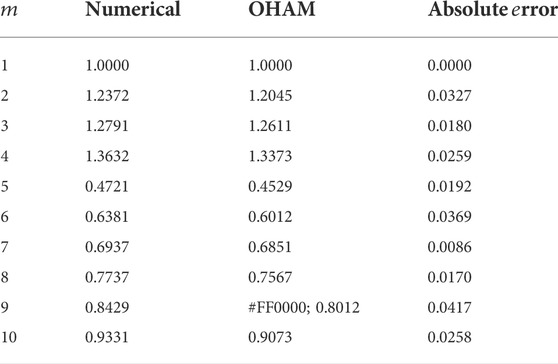
TABLE 2. Convergence of the defined problem for the velocity equation; from table 2, we noted that as we increase the number of iteration, the residual error decreases and strong convergence is obtained.

TABLE 3

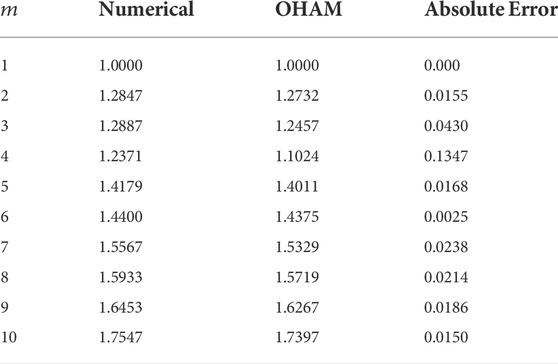
TABLE 3. Convergence of the defined problem for the temperature equation; from table 3, we see that as we increase the number of iteration, the residual error decreases and strong convergence is obtained.

TABLE 4

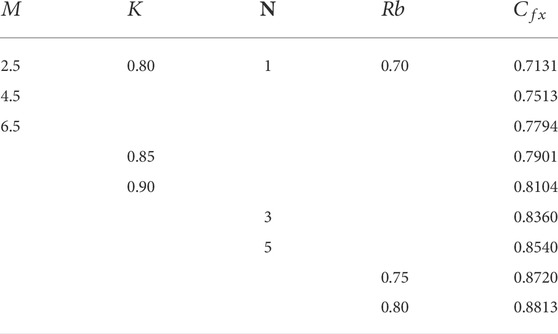
TABLE 4. Consequence of different parameters such as $M,K,N,Nb$ on skin friction, from table 4, we see that skin friction is the decreasing function of $M,K,N,Nb$. Physically, by increasing these parameters the surface friction forces increase due to the increase in skin friction, as shown in table 4.

TABLE 5

TABLE 5. Consequence of $\mathrm{Pr},N_t,Ec$ on Nusselt number; from table 5, we see that Nu is the growing function of $\mathrm{Pr},N_t,Ec$. Actually, by enhancing $\mathrm{Pr},N_t,Ec$, heat energy is stored in the system due to the frictional force, which increases the Nusselt number.

Table 6 shows the comparison of the present work with already published work for the velocity equation.

TABLE 6

TABLE 6. OHAM and numerical comparison for$f\left(\eta \right).$

Table 7 shows the comparison of the present work with already published work for the temperature equation.

TABLE 7

TABLE 7. OHAM and numerical comparison for $\theta \left(\eta \right)$.

There are two solutions in a certain range of parameters; an investigation of stability is conducted to find the most stable solution between them. To solve Eqs 24, 25 and the boundary conditions ((Liao, 1997)), the bvp4c solver in MATLAB software is used. This tool helps solve the equations numerically. Table 8 shows the certain values of $M$ and the smallest eigenvalue $\gamma$. From this table, it can be seen that the second solutions show negative values, while the first ones show positive values. At this point, it is clear that the second solution is not stable and is not possible in real life. On the other hand, the first solution is stable and is possible in real life (Liao, 2004a).

TABLE 8

TABLE 8. List of several values of the smallest eigenvalue $\gamma$ when${\varnothing }_1={\varnothing }_2=0.3,K=2.5,M=5.5,m^{*}=0.99.$

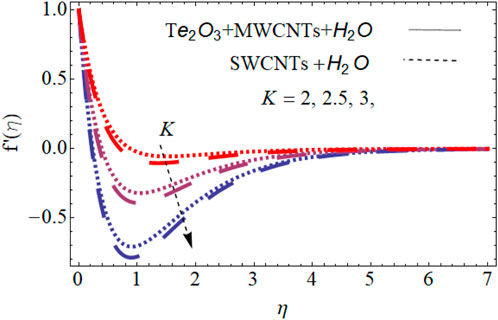
Figure 2 shows variation in $M$ (magnetic field parameter) on velocity distribution for both $T{e}_2{O}_3+MWCNTs+H_{2}O$ and $SWCNTs+H_{2}O$; from Figure 2, we observed that velocity is the declining function of $M$ or there is an inverse relation between the magnetic field parameter and the velocity distribution, that is, the growing magnitude of the magnetic field parameter decreases the velocity distribution. Physically, by increasing the magnetic field parameter, the resistive types of forces known as Lorentz forces are produced. The strength of such forces enhances with the rising strength of the magnetic field parameter $M$, which counteracts the motion of the fluid within the boundary layer and drops the thickness of boundary layer. Also, these forces create resistance to the flow of fluid particle moments, and as a result, the velocity field decreases, as shown in Figure 2; this type of flow is used for heating purpose in the industrial sector.

FIGURE 1

FIGURE 1. Geometry of the flow problem.

FIGURE 2

FIGURE 2. Inspiration of the magnetic field parameter on velocity profile.

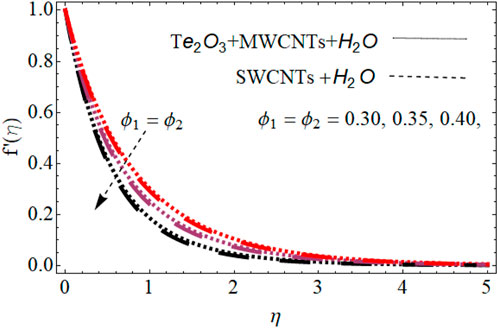
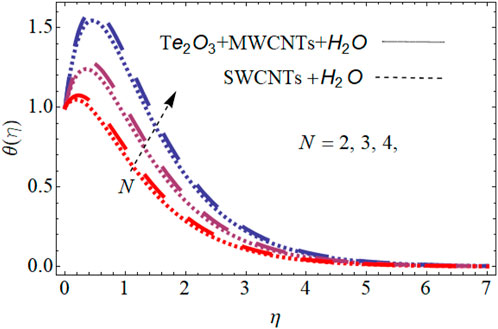
Figure 3 shows the variation in nanoparticle volume fraction ${\phi }_1={\phi }_2$ on the velocity profile for both $T{e}_2{O}_3+MWCNTs+H_{2}O$ and $SWCNTs+H_{2}O$; we noted from Figure 3 that velocity is the decreasing function of ${\varphi }_1={\varphi }_2$, or there is an inverse relation between the nanoparticle volume fraction ${\varphi }_1={\varphi }_2$ and the velocity distribution, that is, the increasing magnitude of nanoparticle volume fraction ${\varphi }_1={\varphi }_2$ decreases the velocity distribution. Physically, by increasing nanoparticle volume fraction, it produced viscous forces; these forces have direct relation to viscosity, so by increasing theses forces, it produced resistance to the flow of fluid particles, so as a result, the velocity of the fluids particles decreases, as shown in Figure 3; this type of flow is used for heating purpose in the industrial sector.

FIGURE 3

FIGURE 3. Inspiration of the nanoparticle volume fraction on the velocity profile.

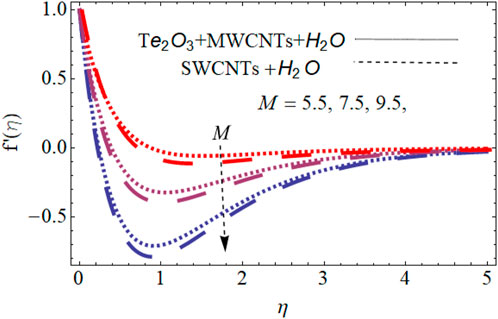
Figure 4 shows the variation in couple stress $K$ on velocity profile for both $T{e}_2{O}_3+MWCNTs+H_{2}O$ and $CNTs+H_{2}O$ , we noted from Figure 4, that velocity is the decreasing function of couple stress $K$ or there is an inverse relation between couple stress $K$ and velocity distribution, that is, the increasing magnitude of couple stress $K$ decreases the velocity distribution. Physically, by increasing couple stress $K$ produced viscous forces, these forces have a direct relation to viscosity, so by increasing theses forces produced resistance to the flow of fluids particles, so as a result the velocity of the fluids particles is decreasing as shown in Figure 4, this type of flow is used for hotness purpose in the industrial sector.

FIGURE 4

FIGURE 4. Inspiration of the couple stress parameter on the velocity profile.

Figure 5 shows the impact of the solar radiation parameter on velocity distribution for both $T{e}_2{O}_3+MWCNTs+H_{2}O$ and $SWCNTs+H_{2}O$; from Figure 5, we noted that the relation between solar radiation parameter and velocity distribution is directly related, or velocity is the increasing function of the fluid relaxation parameter. Physically, the solar radiation parameter has an inverse relation to viscosity, that is, by increasing the solar radiation parameter, the viscosity of fluid decreases and as a result, the fluid particles move easily and the velocity profile increases, or here, the thermal boundary layer converges faster than the momentum boundary layer; however, all the aforementioned effects on velocity and temperature profiles are prominent for small values of $R$ only, as shown in Figure 5.

FIGURE 5

FIGURE 5. Inspiration of the solar radiation parameter on the velocity profile.

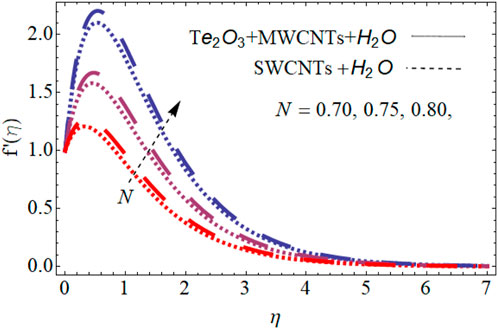
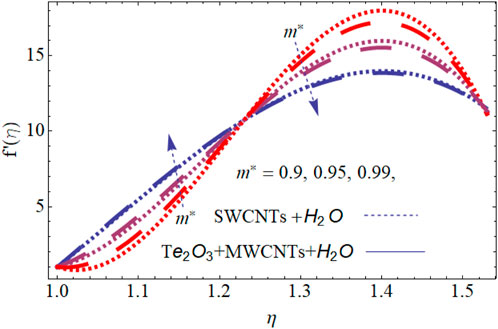
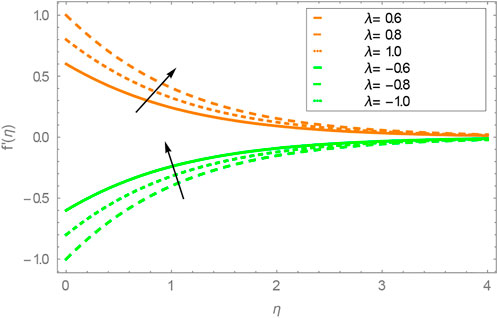
Figure 6 shows the variation in Marangoni convection $m^{*}$ on the velocity profile for both $T{e}_2{O}_3+MWCNTs+H_{2}O$ and $SWCNTs+H_{2}O$; as we know that Marangoni conviction is produced due to the change in the surface, so Marangoni convection have double effects on moments of the fluid particles; from Figure 6, we noted that Marangoni convection has dual consequence on the velocity distribution. First, the velocity profile boosts up due to Marangoni convection. This result is changed, and after some time, the velocity profile decreased, as shown in Figure 6. It is not necessary that initially the velocity will be increasing and then it will be decreasing; in some cases, initially, the velocity decreases and then it increases.

FIGURE 6

FIGURE 6. Inspiration of Marangoni convection on the velocity profile.

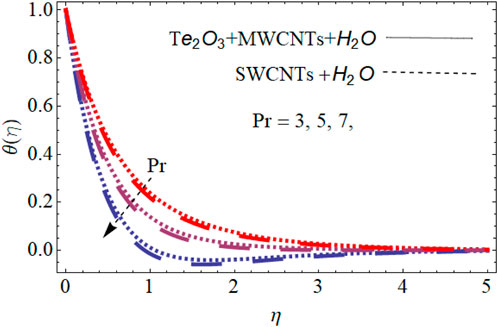
Figure 7 shows the relation between the solar radiation parameter and temperature profile for both $T{e}_2{O}_3+MWCNTs+H_{2}O$ and $SWCNTs+H_{2}O$; from Figure 7, we noted that temperature profile is the growing function solar radiation parameter, that is, by increasing the solar radiation parameter, the temperature field is increasing. The energy coming to the structural element will increase its temperature until heat losses are able to balance heat gain. Heat losses occur at the expense of emission, convective transport to the atmosphere, and transmission to adjacent areas, caused by heat conduction. The higher the temperature of the heated element in comparison to the surrounding objects, the more significant the heat losses. Therefore, by enhancing the relaxation parameter, heat energy is stored in the system, and hence, $\theta \left(\eta \right)$ enhances and the solar radiation parameter can be used as a heating agent.

FIGURE 7

FIGURE 7. Inspiration of the solar radiation parameter on the temperature profile.

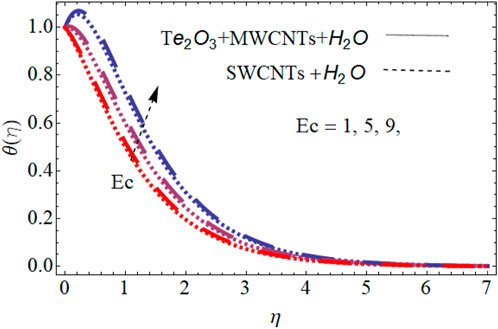
Figure 8 shows the relation between Eckert number and temperature profile for both $T{e}_2{O}_3+MWCNTs+H_{2}O$ and $SWCNTs+H_{2}O$; from Figure 8, we see that temperature profile is the increasing function of the Eckert number, that is, as we increase the Eckert number, the temperature field is increasing, as shown in Figure 8, physically by increasing the Eckert number. It will enhance the kinetic energy as the intermolecular collision is increasing, so the temperature profile is increasing, and the Eckert number can be used as a heating agent.

FIGURE 8

FIGURE 8. Inspiration of the thermophoresis parameter on the temperature profile.

Figure 9 shows schemed $\mathrm{Pr}$ for both $T{e}_2{O}_3+MWCNTs+H_{2}O$ and $SWCNTs+H_{2}O$. It is obvious that in Figure 9 temperature is the decreasing function $\mathrm{Pr}$, as shown in Figure 9; physically, the thickness of the momentum boundary layer will be larger than that of the thermal boundary layer, or that the viscous diffusion is larger than the thermal diffusion and therefore, the larger amount of Prandtl number reduces the thermal boundary layer, so by increasing $\mathrm{Pr}$, there is a decrease in the temperature field, and the Prandtl number can be used as a cooling agent.

FIGURE 9

FIGURE 9. Inspiration of Prandtl number on the temperature profile.

Figure 10 shows that the fluid velocity increases when the effect of the shrinking and shrinking parameters $\lambda$ is increased in the dual solutions; consequently, the momentum boundary layer thickness decreases. This contraction in the boundary layer thickness is caused by the introduction of tensile stress due to elasticity. The effect of magnetic parameter M, for dual solutions, is noticed in Figure 11. Furthermore, in the results, it is noticed that the first solution is stable, whereas the second solution is unstable.

FIGURE 10

FIGURE 10. Inspiration of shrinking and stretching parameters $\lambda$ on the velocity profile.

FIGURE 11

FIGURE 11. Inspiration of shrinking and stretching parameters $\lambda$ on the velocity profile.

Conclusion

This study investigates the influence of Marangoni convection, solar radiation, and viscous dissipation on the bioconvection couple stress flow of the hybrid nanofluid over a shrinking surface is investigated analytically. The novelty of current research is that for the first time, the influence of Marangoni convection, solar radiation, and viscous dissipation on the bioconvection couple stress flow of the hybrid nanofluid over a stretching surface is investigated analytically. To transform the non-dimensionless form of the DE (differential equation) to the dimensionless form of DE (differential equation), we used similarity transformation. The transformed dimensionless form of the DEs (differential equations) are solved by the approximate analytical method. In the future, we will face the problem to adjust the consumptions of energy; in our research article, we used a hybrid nanofluid which helped in the enhancement of the heat transfer ratio, which have some important applications, for example, not only the achievement of energy is enough but is also expected to adjust the consumptions of energy, and this is possible only to approve the development of heat transmission liquids to the mechanism of the expenditures of energy and improvement. Most of the heat transmission is the demand of the industry and other related scientific fields. Former to the application of nanotechnology, analysts and engineers have challenged such huge numbers of questions recognizing with heat transmission fluids. Still, with the development of nanometer-sized particles, and its uses in the heat transfer fluids have overall improved thermal conductivity. The development of heat transport via nanofluid has involved a number of scientists due to a lot of uses in various sectors such as distillation and separation of bio-molecules, biosensors, atomic system cooling, manufacture of glass fiber, thermal storing, in solar water boiler, in the field of defense, MRI, thermal absorption process, drug delivery, and transportation (thermal management od vehicle and cooling of engine). The impression of different parameters is taken by graphs for the velocity equation and the temperature equation. The key findings of the present research article are as follows:

1.Increasing the value of the solar radiation parameter increases the velocity field.

2.Increasing the value of the magnetic field parameter decreases the velocity field.

3.Increasing the value of nanoparticle volume fraction decreases the velocity field.

4.Increasing the value of the couple stress parameter decreases the velocity field.

5.Increasing the value of the Marangoni convection parameter doubles the effect in velocity field.

6.Increasing the value of the Prandtl number decreases the temperature field.

7.Increasing the value of the solar radiation parameter increases the temperature field.

8.Increasing the value of the Eckert number increases the temperature field.

Data availability statement

The original contributions presented in the study are included in the article/supplementary materials; further inquiries can be directed to the corresponding author.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

The authors will pay all the outstanding dues after the acceptance of this manuscript.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Acharya, N., Das, K., and Prabir, K. K. (2016). Ramification of variable thickness on MHD TiO2 and Ag nanofluid flow over a slendering stretching sheet using NDM. Eur. Phys. J. Plus 131, 303. doi:10.1140/epjp/i2016-16303-4

CrossRef Full Text | Google Scholar

Acharya, N., Das, K., and Prabir, K. K. (2016). Squeezing flow of Cu–Water and Cu–Kerosene nanofluid flow between two parallel plates. Alex Eng. J. 55, 1177–1186. doi:10.1016/j.aej.2016.03.039

CrossRef Full Text | Google Scholar

Acharya, N., Das, K., and Kundu, P. K. (2017). Cattaneo–christov intensity of magnetised upper-convected maxwell nanofluid flow over an inclined stretching sheet: A generalised fourier and fick's perspective. Int. J. Mech. Sci. 130, 167–173. doi:10.1016/j.ijmecsci.2017.05.043

CrossRef Full Text | Google Scholar

Al-Mudhaf, A., and Chamkha, A. J. (2005). Similarity solutions for MHD thermo-solutal Marangoni convection over a flat surface in the presence of heat generation or absorption effects. Heat. Mass Transf. 42, 112–121. doi:10.1007/s00231-004-0611-8

CrossRef Full Text | Google Scholar

Aly, E. H., and Ebaid, A. (2016). Exact analysis for the effect of heat transfer on MHD and radiation Marangoni boundary layer nanofluid flow past a surface embedded in a porous medium. J. Mol. Liq. 215, 625–639. doi:10.1016/j.molliq.2015.12.108

CrossRef Full Text | Google Scholar

Aman, S., Khan, I., Ismail, Z., Salleh, M. Z., and Al-Mdallal, Q. M. (2017). Heat transfer enhancement in free convection flow of CNTs Maxwell nanofluids with four different types of molecular liquids. Sci. Rep. 7 (2), 2445–45. doi:10.1038/s41598-017-01358-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Animasaun, I. L., Mahanthesh, B., Jagun, A. O., Bankole, T. D., Sivaraj, R., Shah, N. A., et al. (2019). Significance of Lorentz force and thermoelectric on the flow of 29 nm CuO–water nanofluid on an upper horizontal surface of a paraboloid of revolution. J. Heat. Transf. 141 (2), 384–402. Journal of Heat Transfer. doi:10.1115/1.4041971

CrossRef Full Text | Google Scholar

Baranovskii, E. S., Burmasheva, N. V., and Prosviryakov, E. Y. (2021). Exact solutions to the Navier–Stokes equations with couple stresses. Symmetry 13 (8), 1355. doi:10.3390/sym13081355

CrossRef Full Text | Google Scholar

Besthapu, P., Ul Haq, R., Bandari, S., and Al-Mdallal, M. Q. (2017). Mixed convection flow of thermally stratified MHD nanofluid over an exponentially stretching surface with viscous dissipation effect. J. Taiwan Inst. Chem. Eng. 71, 307–314. doi:10.1016/j.jtice.2016.12.034

CrossRef Full Text | Google Scholar

Buongiorno, J. (2006). Convective transport in nanofluids. J. Heat. Transf. 128, 240–250. doi:10.1115/1.2150834

CrossRef Full Text | Google Scholar

Buongiorno, J., Venerus, D. C., Prabhat, N., Mckrell, T., Townsend, J., Christianson, R., et al. (2009). A benchmark study on the thermal conductivity of nanofluids. J. Appl. Phys. 106 (9), 094312–312. doi:10.1063/1.3245330

CrossRef Full Text | Google Scholar

Chen, C. H. (2007). Marangoni effects on forced convection of power-law liquids in a thin film over a stretching surface. Phys. Lett. A 370, 51–57. doi:10.1016/j.physleta.2007.05.024

CrossRef Full Text | Google Scholar

Daniel, Y. S., Aziz, Z. A., Ismail, Z., Bahar, A., and Salah, F. (2020). Slip role for unsteady MHD mixed convection of nanofluid over stretching sheet with thermal radiation and electric field. Indian J. Phys. 94 (2), 195–207. doi:10.1007/s12648-019-01474-y

CrossRef Full Text | Google Scholar

Daniel, Y. S., Aziz, Z. A., Ismail, Z., Bahar, A., and Salah, F. (2019). Stratified electromagnetohydrodynamic flow of nanofluid supporting convective role. Korean J. Chem. Eng. 36 (7), 1021–1032. doi:10.1007/s11814-019-0247-5

CrossRef Full Text | Google Scholar

Daniel, Y. S., Aziz, Z. A., Ismail, Z., and Salah, F. (2017). Double stratification effects on unsteady electrical MHD mixed convection flow of nanofluid with viscous dissipation and Joule heating. J. Appl. Res. Technol. 15 (5), 464–476. doi:10.1016/j.jart.2017.05.007

CrossRef Full Text | Google Scholar

Daniel, Y. S., Aziz, Z. A., Ismail, Z., and Salah, F. (2018). Effects of slip and convective conditions on MHD flow of nanofluid over a porous nonlinear stretching/shrinking sheet. Aust. J. Mech. Eng. 16 (3), 1–17. doi:10.1080/14484846.2017.1358844

CrossRef Full Text | Google Scholar

Daniel, Y. S., Aziz, Z. A., Ismail, Z., and Salah, F. (2017). Entropy analysis in electrical magnetohydrodynamic (MHD) flow of nanofluid with effects of thermal radiation, viscous dissipation, and chemical reaction. Theor. Appl. Mech. Lett. 7 (4), 235–242. doi:10.1016/j.taml.2017.06.003

CrossRef Full Text | Google Scholar

Daniel, Y. S., Aziz, Z. A., Ismail, Z., and Salah, F. (2017). Entropy analysis of unsteady magnetohydrodynamic nanofluid over stretching sheet with electric field. Int. J. Multiscale Comput. Eng. 15 (6), 545–565. doi:10.1615/intjmultcompeng.2017021952

CrossRef Full Text | Google Scholar

Daniel, Y. S., Aziz, Z. A., Ismail, Z., and Salah, F. (2020). Hydromagnetic slip flow of nanofluid with thermal stratification and convective heating. Aust. J. Mech. Eng. 18 (2), 147–155. doi:10.1080/14484846.2018.1432330

CrossRef Full Text | Google Scholar

Daniel, Y. S., Aziz, Z. A., Ismail, Z., and Salah, F. (2018). Impact of thermal radiation on electrical MHD flow of nanofluid over nonlinear stretching sheet with variable thickness. Alexandria Eng. J. 57 (3), 2187–2197. doi:10.1016/j.aej.2017.07.007

CrossRef Full Text | Google Scholar

Daniel, Y. S., Aziz, Z. A., Ismail, Z., and Salah, F. (2017). Numerical study of Entropy analysis for electrical unsteady natural magnetohydrodynamic flow of nanofluid and heat transfer. Chin. J. Phys. 55 (5), 1821–1848. doi:10.1016/j.cjph.2017.08.009

CrossRef Full Text | Google Scholar

Daniel, Y. S., Aziz, Z. A., Ismail, Z., and Salah, F. (2018). Slip effects on electrical unsteady MHD natural convection flow of nanofluid over a permeable shrinking sheet with thermal radiation. Eng. Lett. 26 (1), 195–207. doi:10.1007/s12648-019-01474-y

CrossRef Full Text | Google Scholar

Daniel, Y. S., Aziz, Z. A., Ismail, Z., and Salah, F. (2019). Thermal radiation on unsteady electrical MHD flow of nanofluid over stretching sheet with chemical reaction. J. King Saud Univ. - Sci. 31 (4), 804–812. doi:10.1016/j.jksus.2017.10.002

CrossRef Full Text | Google Scholar

Daniel, Y. S., Aziz, Z. A., Ismail, Z., and Salah, F. (2018). Thermal stratification effects on MHD radiative flow of nanofluid over nonlinear stretching sheet with variable thickness. J. Comput. Des. Eng. 5 (2), 232–242. doi:10.1016/j.jcde.2017.09.001

CrossRef Full Text | Google Scholar

Daniel, Y. S., and Daniel, S. K. (2015). Effects of buoyancy and thermal radiation on MHD flow over a stretching porous sheet using homotopy analysis method. Alexandria Eng. J. 54 (3), 705–712. doi:10.1016/j.aej.2015.03.029

CrossRef Full Text | Google Scholar

Daniel, Y. S. (2016). Laminar convective boundary layer slip flow over a flat plate using homotopy analysis method. J. Inst. Eng. India. Ser. E 97 (2), 115–121. doi:10.1007/s40034-016-0084-6

CrossRef Full Text | Google Scholar

Daniel, Y. S. (2017). MHD laminar flows and heat transfer adjacent to permeable stretching sheets with partial slip condition. J. Adv. Mech. Eng. 4 (1), 1–15. doi:10.7726/jame.2017.1001

CrossRef Full Text | Google Scholar

Daniel, Y. S. (2016). Steady MHD boundary-layer slip flow and heat transfer of nanofluid over a convectively heated of a non-linear permeable sheet. J. Adv. Mech. Eng. 3 (1), 1–14. doi:10.7726/jame.2016.1001

CrossRef Full Text | Google Scholar

Daniel, Y. S. (2015). Steady MHD laminar flows and heat transfer adjacent to porous stretching sheets using HAM. Am. J. heat mass Transf. 2 (3), 146–159. doi:10.7726/ajhmt.2015.1010

CrossRef Full Text | Google Scholar

Das, K., Acharya, N., and Prabir, K. K. (2016). The onset of nanofluid flow past a convectively heated shrinking sheet in presence of heat source/sink: A lie group approach. Appl. Therm. Eng. 103, 38–46. doi:10.1016/j.applthermaleng.2016.03.112

CrossRef Full Text | Google Scholar

Das, S. K., Choi, S. U. S., Yu, W., and Pradeep, Y. (2008). Nanofluids: Science and technology. NJ: Wiley.

Google Scholar

Eastman, J. A., Cho, S. U. S., Li, S., Soyez, G., Thompson, L. J., and Dimelfi, R. J. (1999). Novel thermal properties of nanostructured materials. J. Metastable Nanocrystal Mater. 2, 629–634. doi:10.4028/www.scientific.net/msf.312-314.629

CrossRef Full Text | Google Scholar

Eastman, J. A., Choi, U. S., Li, S., Thompson, L. J., and Lee, S. (1996). Enhanced thermal conductivity through the development of nanofluids (No. ANL/MSD/CP-90462. IL (United States): Argonne National Lab. CONF-961202-94).

Google Scholar

Ellahi, R., Zeeshan, A., and Hassan, M. (2016). Particle shape effects on Marangoni convection boundary layer flow of a nanofluid. Int. J. Numer. Methods Heat. Fluid Flow. 26, 2160–2174. doi:10.1108/hff-11-2014-0348

CrossRef Full Text | Google Scholar

Garia, R., Rawat, S. K., Kumar, M., and Yaseen, M. (2021). Hybrid nanofluid flow over two different geometries with cattaneo–christov heat flux model and heat generation: A model with correlation coefficient and probable error. Chin. J. Phys. 74, 421–439. doi:10.1016/j.cjph.2021.10.030

CrossRef Full Text | Google Scholar

Gladys, T., and Reddy, G. R. (2022). Contributions of variable viscosity and thermal conductivity on the dynamics of non-Newtonian nanofluids flow past an accelerating vertical plate. Partial Differ. Equations Appl. Math. 5, 100264. doi:10.1016/j.padiff.2022.100264

CrossRef Full Text | Google Scholar

Gumber, P., Yaseen, M., Rawat, S. K., and Kumar, M. (2022). Heat transfer in micropolar hybrid nanofluid flow past a vertical plate in the presence of thermal radiation and suction/injection effects. Partial Differ. Equations Appl. Math. 5, 100240. doi:10.1016/j.padiff.2021.100240

CrossRef Full Text | Google Scholar

Haq, R. U., Rashid, I., and Khan, Z. H. (2017). Effects of aligned magnetic field and CNTs in two different base fluids over a moving slip surface. J. Mol. Liq. 24 (3), 682–688. doi:10.1016/j.molliq.2017.08.084

CrossRef Full Text | Google Scholar

Harris, S. D., Ingham, D. B., and Pop, I. (2009). Mixed convection boundary-layer flow near the stagnation point on a vertical surface in a porous medium: Brinkman model with slip. Transp. Porous Media 77, 267–285. [CrossRef]. doi:10.1007/s11242-008-9309-6

CrossRef Full Text | Google Scholar

Hussanan, A., Salleh, M. Z., Khan, I., and Chen, Z. M. (2019). Unsteady water functionalized oxide and non-oxide nanofluids flow over an infinite accelerated plate. Chin. J. Phys. 6 (2), 115–131. doi:10.1016/j.cjph.2019.09.020

CrossRef Full Text | Google Scholar

Hussanan, A., Salleh, M. Z., and Khan, I. (2018). Microstructure and inertial characteristics of a magnetite ferrofluid over a stretching/shrinking sheet using effective thermal conductivity model. J. Mol. Liq. 255, 64–75. doi:10.1016/j.molliq.2018.01.138

CrossRef Full Text | Google Scholar

Ishfaq, N., Khan, Z. H., Khan, W., and Culham, J. R. (2016). Estimation of boundary layer flow of a nanofluid past a stretching sheet: A revised model. J. Hydrodyn. 28, 596–602. doi:10.1016/s1001-6058(16)60663-7

CrossRef Full Text | Google Scholar

Jiao, C., Zheng, L., Lin, Y., Ma, L., and Chen, G. (2016). Marangoni abnormal convection heat transfer of power-law fluid driven by temperature gradient in porous medium with heat generation. Int. J. Heat. Mass Transf. 92, 700–707. doi:10.1016/j.ijheatmasstransfer.2015.09.017

CrossRef Full Text | Google Scholar

Joseph, S. P. (2020). Some exact solutions for incompressible couple stress fluid flows. Malaya J. Mat. S, 648–652. doi:10.26637/mjm0s20/0123

CrossRef Full Text | Google Scholar

Kandasamy, R., Mohamad, R., and Ismoen, M. (2016). Impact of chemical reaction on Cu, Al2O3 and SWCNTs–nanofluid flow under slip conditions. Eng. Sci. Technol. Int. J. 19 (2), 700–709. doi:10.1016/j.jestch.2015.11.011

CrossRef Full Text | Google Scholar

Khan, W. A., and Pop, I. (2010). Boundary-layer flow of a nanofluid past a stretching sheet. Int. J. Heat. Mass Transf. 53, 2477–2483. doi:10.1016/j.ijheatmasstransfer.2010.01.032

CrossRef Full Text | Google Scholar

Kumar, K. A., Sandeep, N., Sugunamma, V., and Animasaun, I. L. (2020). Effect of irregular heat source/sink on the radiative thin film flow of MHD hybrid ferrofluid. J. Therm. Anal. Calorim. 139 (3), 2145–2153. doi:10.1007/s10973-019-08628-4

CrossRef Full Text | Google Scholar

Liao, S. (2003). Beyond perturbation: Introduction to the homotopy analysis method. Boca Raton: Chapman & Hall/CRC.

Google Scholar

Liao, S. J. (1997). A kind of approximate solution technique which does not depend upon small parameters (II) – an application in fluid mechanics. Int. J. Non. Linear. Mech. 32, 815–822. doi:10.1016/s0020-7462(96)00101-1

CrossRef Full Text | Google Scholar

Liao, S. J. (2010). An optimal homotopy-analysis approach for strongly nonlinear differential equations. Commun. Nonlinear Sci. Numer. Simul. 15, 2003–2016. doi:10.1016/j.cnsns.2009.09.002

CrossRef Full Text | Google Scholar

Liao, S. J. (2012). Homotopy analysis method in nonlinear differential equations. Shanghai 200030China: Springer & Higher Education Press Heidelberg.

Google Scholar

Liao, S. J. (2004). On the homotopy analysis method for nonlinear problems. Appl. Math. Comput. 147, 499–513. doi:10.1016/s0096-3003(02)00790-7

CrossRef Full Text | Google Scholar

Liao, S. (2004). On the homotopy analysis method for nonlinear problems. Appl. Math. Comput. 147, 499–513. doi:10.1016/s0096-3003(02)00790-7

CrossRef Full Text | Google Scholar

Lin, Y., Zheng, L., and Zhang, X. (2013). Magneto-hydrodynamics thermo-capillaryMarangoni convection heat transfer of power-law fluids driven by temperature gradient. J. Heat. Transf. 135, 051702. doi:10.1115/1.4023394

CrossRef Full Text | Google Scholar

Lin, Y., Zheng, L., and Zhang, X. (2014). Radiation effects on Marangoni convectionflow and heat transfer in pseudo-plastic non-Newtonian nanofluids with variable thermal conductivity. Int. J. Heat. Mass Transf. 77, 708–716. doi:10.1016/j.ijheatmasstransfer.2014.06.028

CrossRef Full Text | Google Scholar

Magyari, E., and Chamkha, A. J. (2007). Exact analytical solutions for thermo-solutal Marangoni convection in the presence of heat and mass generation or consumption. Heat. Mass Transf. 43, 965–974. doi:10.1007/s00231-006-0171-1

CrossRef Full Text | Google Scholar

Makinde, O. D., and Aziz, A. (2011). Boundary layer flow of a nanofluid past a stretching sheet with a convective boundary condition. Int. J. Therm. Sci. 50, 1326–1332. doi:10.1016/j.ijthermalsci.2011.02.019

CrossRef Full Text | Google Scholar

Makinde, O. D., Mabood, F., Khan, W. A., and Tshehla, M. S. (2016). MHD flow of a variable viscosity nanofluid over a radially stretching convective surface with radiative heat. J. Mol. Liq. 219, 624–630. doi:10.1016/j.molliq.2016.03.078

CrossRef Full Text | Google Scholar

Merkin, J. H. (1986). On dual solutions occurring in mixed convection in a porous medium. J. Eng. Math. 20, 171–179. [CrossRef]. doi:10.1007/bf00042775

CrossRef Full Text | Google Scholar

Mishra, A., and Kumar, M. (2019). Influence of viscous dissipation and heat generation/absorption on Ag-water nanofluid flow over a Riga plate with suction. Inter. J. Fluid Mech. Res. 46 (2), 113–125. doi:10.1615/interjfluidmechres.2018025291

CrossRef Full Text | Google Scholar

Mishra, A., and Kumar, M. (2020). Thermal performance of MHD nanofluid flow over a stretching sheet due to viscous dissipation, Joule heating and thermal radiation. Int. J. Appl. Comput. Math. 6 (4), 1–17. doi:10.1007/s40819-020-00869-4

CrossRef Full Text | Google Scholar

Mishra, A., and Kumar, M. (2020). Velocity and thermal slip effects on MHD nanofluid flow past a stretching cylinder with viscous dissipation and Joule heating. SN Appl. Sci. 2 (8), 1–13. doi:10.1007/s42452-020-3156-7

CrossRef Full Text | Google Scholar

Mishra, A., and Kumar, M. (2019). Viscous dissipation and Joule heating influences past a stretching sheet in a porous medium with thermal radiation saturated by silver–water and copper–water nanofluids. Spec. Top. Rev. Porous Media. 10 (2), 171–186. doi:10.1615/specialtopicsrevporousmedia.2018026706

CrossRef Full Text | Google Scholar

Mishra, A., Kumar Pandey, A., and Kumar, M. (2021). Thermal performance of Ag–water nanofluid flow over a curved surface due to chemical reaction using Buongiorno's model. Heat. Transf. 50 (1), 257–278. doi:10.1002/htj.21875

CrossRef Full Text | Google Scholar

Mishra, A., Pandey, A. K., Chamkha, A. J., and Kumar, M. (2020). Roles of nanoparticles and heat generation/absorption on MHD flow of Ag–H2O nanofluid via porous stretching/shrinking convergent/divergent channel. J. Egypt. Math. Soc. 28 (1), 17–18. doi:10.1186/s42787-020-00079-3

CrossRef Full Text | Google Scholar

Moldoveanu, G. M., Minea, A. A., Huminic, G., and Huminic, A. (2019). Al2O3/TiO2 hybrid nanofluids thermal conductivity. J. Therm. Anal. Calorim. 13 (7), 583–592. doi:10.1007/s10973-018-7974-4

CrossRef Full Text | Google Scholar

Muhammad, T., Waqas, H., A Khan, S., Ellahi, R., and Sait, S. M. (2020). Significance of nonlinear thermal radiation in 3D eyring–powell nanofluid flow with arrhenius activation energy. J. Therm. Anal. Calorim. 10 (2), 929–944. doi:10.1007/s10973-020-09459-4

CrossRef Full Text | Google Scholar

PopPostelnicu, A. T. G. (2001). Thermo-solutal Marangoni forced convection boundarylayers. Meccanica 36, 555–571. doi:10.1023/A:1017431224943

CrossRef Full Text | Google Scholar

Qasim, M., Khan, Z. H., Khan, W. A., and Shah, I. A. (2014). MHD boundary layer slip flow and heat transfer of ferrofluid along a stretching cylinder with prescribed heat flux. PloS one 9 (1), e83930–930. doi:10.1371/journal.pone.0083930

PubMed Abstract | CrossRef Full Text | Google Scholar

Rachid, H., Ouazzani, M. T., and Lahlou, N. (2021). Entropy generation and mechanical efficiency in laminar peristaltic flow through an elliptical duct. Heat. Transf. 50 (8), 8525–8539. doi:10.1002/htj.22288

CrossRef Full Text | Google Scholar

Rana, P., Bhargava, R., and Beg, O. A. (2012). Numerical solution for mixed convection boundary layer flow of a nanofluid along an inclined plate embedded in a porous medium. Comput. Math. Appl. 64, 2816–2832. doi:10.1016/j.camwa.2012.04.014

CrossRef Full Text | Google Scholar

Rana, P., and Bhargava, R. (2012). Flow and heat transfer of a nanofluid over a nonlinearly stretch- ing sheet: A numerical study. Commun. Nonlinear Sci. Numer. Simul. 17, 212–226. doi:10.1016/j.cnsns.2011.05.009

CrossRef Full Text | Google Scholar

Raza, M., Ellahi, R., Sait, S., M Sarafraz, M., Shadloo, M. S., and Waheed, I. (2019). Enhancement of heat transfer in peristaltic flow in a permeable channel under induced magnetic field using different CNTs. J. Therm. Anal. Calorim. 3 (1), 1277–1291. doi:10.1007/s10973-019-09097-5

CrossRef Full Text | Google Scholar

Sheikholeslami, M., and Chamkha, A. J. (2017). Influence of Lorentz forces on nanofluid forced convection considering Marangoni convection. J. Mol. Liq. 225, 750–757. doi:10.1016/j.molliq.2016.11.001

CrossRef Full Text | Google Scholar

Sheikholeslami, M., Kataria, H. R., and Mittal, A. S. (2017). Radiation effects on heat transfer of three dimensional nanofluid flow considering thermal interfacial resistance and micro mixing in suspensions. Chin. J. Phys. 55 (6), 2254–2272. doi:10.1016/j.cjph.2017.09.010

CrossRef Full Text | Google Scholar

Srinivas, J., and Ramana Murthy, J. V. (2016). Thermal analysis of a flow of immiscible couple stress fluids in a channel. J. Appl. Mech. Tech. Phy. 57 (6), 997–1005. doi:10.1134/s0021894416060067

CrossRef Full Text | Google Scholar

Wakif, A., Chamkha, A., Thumma, T., Animasaun, I. L., and Sehaqui, R. (2020). Thermal radiation and surface roughness effects on the thermo-magneto-hydrodynamic stability of alumina–copper oxide hybrid nanofluids utilizing the generalized Buongiorno’s nanofluid model. J. Therm. Anal. Calorim. 2 (1), 1201–1220. doi:10.1007/s10973-020-09488-z

CrossRef Full Text | Google Scholar

Wang, C. Y. (2006). Liquid film sprayed on a stretching surface. Chem. Eng. Commun. 193, 869–878. doi:10.1080/00986440500267352

CrossRef Full Text | Google Scholar

Weidman, P. D., Kubitschek, D. G., and Davis, A. M. J. (2006). The effect of transpiration on self-similar boundary layer flow over moving surfaces. Int. J. Eng. Sci. 44, 730–737. [CrossRef]. doi:10.1016/j.ijengsci.2006.04.005

CrossRef Full Text | Google Scholar

Yaseen, A. (2021), Opposing flow of a MHD hybrid nanofluid flow past a permeable moving surface with heat source/sink and thermal radiation. Partial Differ. Equations Appl. Math. 4., 100168, doi:10.1016/j.padiff.2021.100168

CrossRef Full Text | Google Scholar

Yaseen, M., Rawat, S. K., and Kumar, M. (2022). Cattaneo–Christov heat flux model in Darcy–Forchheimer radiative flow of MoS2–SiO2/kerosene oil between two parallel rotating disks. J. Therm. Anal. Calorim., 1–23. doi:10.1007/s10973-022-11248-0

CrossRef Full Text | Google Scholar

Yaseen, M., Rawat, S. K., and Kumar, M. (2022). Hybrid nanofluid (MoS2–SiO2/water) flow with viscous dissipation and Ohmic heating on an irregular variably thick convex/concave‐shaped sheet in a porous medium. Heat. Trans. 51 (1), 789–817. doi:10.1002/htj.22330

CrossRef Full Text | Google Scholar

Nomenclature

Abbreviations

x, y Cartesian coordinates

u, v velocity components

U_w velocities of the stretching sheet

$K$ couple stress parameter

$T$ local temperature

$Nu$ local Nusselt number

$\mathrm{Pr}$ Prandtl number

$T_w$ surface temperature

$T_{\infty }$ ambient temperature

$C_f$ skin friction coefficient

$N$ radiation parameter

$\rho$ fluid density

${\varphi }_1={\varphi }_2$ nanoparticle volume fraction

$\theta$ dimensionless temperature

$\eta$ independent variable

$Ec$ Eckert number

$m^{*}$ Marangoni convection

$C_T$ temperature ratio parameter

$Rb$ bioconvection Rayleigh number

$Br$ boundary ratio parameter

$\lambda$ shrinking and stretching surface

$Nt$ thermophoresis parameter.