- 1School of Microelectronics and Materials Engineering, Guangxi University of Science and Technology, Liuzhou, China
- 2The State Key Laboratory of Millimeter Waves, School of Information Science and Engineering, Southeast University, Nanjing, China
In this paper 1-bit dual-polarized ultra-thin lens antennas are presented based on Huygens’ principle. The unit cell provides two-state transmission phase compensation for dual-polarized waves. By tuning state 0 away from resonance and state 1 near Huygens’ resonance, the 180° transmission phase difference between the two states is achieved. In the frequency range of 27.5–28.5 GHz, the transmission phase difference between the two states of the unit cell is 180° ± 20°, and the transmission amplitude is greater than −2 dB. Using the proposed unit cell, three ultrathin 1-bit Huygens’ metasurface antennas comprising 33 × 33 unit cells with single beams pointing separately at 0°, 15°, and 30° are designed, fabricated and measured. Simulated and measured results show that the proposed 1-bit transmitarray antenna can achieve single-beam patterns, which is useful for the development of reconfigurable transmission and digital metasurface antennas in the future.
Introduction
Over the past decades, metasurfaces have been gaining increasing attention for researchers. As a two-dimensional (2D) planar version of metamaterial, metasurfaces provides an easy way to manipulate electromagnetic (EM) waves by introducing an abrupt phase and amplitude discontinuity along the interface (Yu et al., 2011). A variety of metasurface-based functional devices are realized which can be found in several reviews (Chen et al., 2016; Ren et al., 2018; Chen et al., 2020; Hu et al., 2021). As a branch of metasurfaces, the concept of digital metasurfaces is first introduced by Cui et al. (2014). By encoding two units with opposite phase responses as “0” and “1” digital states, the EM parameter is briefly connected with the digital expression. As a result, the conventional metasurface pattern configuration is totally digitized as coding pattern, which can greatly simplify the design process and create more functionalities. Digital metasurfaces have been widely used for beam steering (Yin et al., 2021), scattering reduction (Wei et al., 2022), holographic imaging (Li et al., 2017), signal processing (Liu et al., 2016), magnetic near-field reconfiguration (Li et al., 2021) and wireless communications (Zhang et al., 2021).
Metasurfaces are usually classified into two types in reflective and transmissive modes. For a single-layer reflectarray, it is easy to simultaneously achieve high reflection and binary digital state of phase (Glybovski et al., 2016). In contrast, it is difficult for a single- or double-layer transmitarray (Abdelrahman et al., 2014). Therefore, the current digital metasurfaces are mostly based on reflective mode. Recently, as a typical transmissive metasurface, Huygens’ metasurfaces achieve a near-uniform transmission amplitude and a transmission phase shift over 360° by designing the balance between current and magnetic current on the surface (Pfeiffer and Grbic, 2013). Huygens’ metasurfaces thus exhibit the ultimate transmitted wave manipulation abilities such as beam splitting (Cai et al., 2017), wide-angle refraction (Chen et al., 2018), directional emission (Long et al., 2020; Guo et al., 2021), generation of airy beams (Hao et al., 2019; Xu et al., 2019), imaging holography (Wang et al., 2018; Wang et al., 2020) and parametric wave control (Liu et al., 2018). Moreover, Huygens’ metasurfaces exhibit their unique capabilities for lens antenna applications, such as improvement of the antenna efficiency (Epstein et al., 2016; Epstein and Eleftheriades, 2017) and reconfigurations of radiated EM waves (Chen et al., 2017).
In particular, Huygens’ metasurfaces can be used to simplify the structure complexity and reduce the assembly cost, which is crucial for antenna engineering. Recent investigations have shown that the Huygens’ metasurface can be realized on a single-layered dielectric substrate based on induced magnetism (Xue et al., 2019; Xue et al., 2020a; Xue et al., 2020b). Therefore, the high-efficiency planar lens based on Huygens’ metasurface can be achieved (Xue et al., 2020c; Lou et al., 2021). In this paper 1-bit dual-polarized ultra-thin lens antennas based on Huygens’ principle are proposed. Based on induced magnetism, the 1-bit dual-polarized Huygens’ metasurface can be realized by using one PCB substrate. The 1-bit Huygens’ lens antenna achieve the refraction functions of 0°, 15°, and 30° radiated beams for dual polarizations. The antennas have simple structure, small size, light weight, and low cost characteristics. We believe this has great significance for the future development of digitally reconfigurable lens antennas.
Theoretical analysis of the 1-bit Huygens’ units
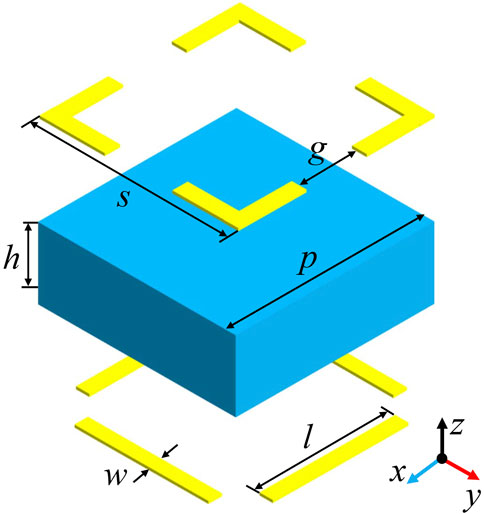
The 1-bit Huygens’ unit is shown in Figure 1. The unit consists of the top and bottom metallic patterns on one dielectric substrate. The dielectric substrate is Rogers RO4003C with dielectric constant εr = 3.55, loss tangent tanθ = 0.0027 and thickness h = 1.524 mm. The metallic patterns are made of 18 μm-thick copper. In the millimeter-wave frequency band, the copper cladding can be regarded as an ideal conductor with negligible ohmic losses. The upper and lower metallic patterns are the angular square ring and the metallic wires with symmetric geometry. The period of the unit is p = 5 mm, the sizes of the metallic patterns are s = 4.8 mm, and all the width of metallic wire is w = 0.2 mm. The different parameters g and l are used to characterize the “0” and “1” states, as shown in Table 1. Due to the symmetry, the EM responses of this unit cell is identical for both X and Y polarized EM wave and thus is dual-polarized. For convenience, we just analyze the frequency response for y-polarized incident EM wave. The frequency-domain solver in commercial software CST Microwave Studio is used to obtain the frequency response of the unit cell.
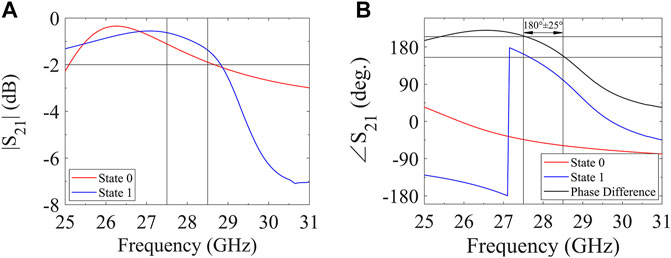
The simulated transmission amplitude is shown in Figure 2A. It can be seen that the transmission amplitudes of two units are greater than −2 dB when the frequency is lower than 28.5 GHz. A wideband transparent window is exhibited. On the one hand, for “0” state, the top and the bottom patterns are typical frequency-selective-surface (FSS) structures and their electric resonant frequencies are much lower than 28 GHz. As a result, the 28 GHz frequency for “0” state is in the non-resonant passband region. On the other hand, for “1” state, the top and the bottom patterns have similar electric resonant frequencies near 28 GHz but opposite current flow directions. Opposite current flows on both surfaces form a current loop which excites an orthogonal magnetic field. Such response is called induced magnetism (Epstein et al., 2016; Epstein and Eleftheriades, 2017). Finally, the balance between the intrinsic electric field and the induced magnetic field stimulate the Huygens’ resonance, opening a transparent window near the resonant frequency.
The simulated transmission phase spectrum are shown in Figure 2B. For “0” state, the transmission phase near 0° at 28 GHz. For “1” state, the transmission phase is near 180° due to Huygens’ resonance. They have opposite phase. The simulated results further show that the phase difference between two states satisfies the range of 180° ± 25° in the frequency region of 27.5–28.5 GHz. Therefore, these two units can be regarded as binary digital states for transmitted wave manipulation.
Design, simulation and measurement of 1-bit Huygens’ lens antenna
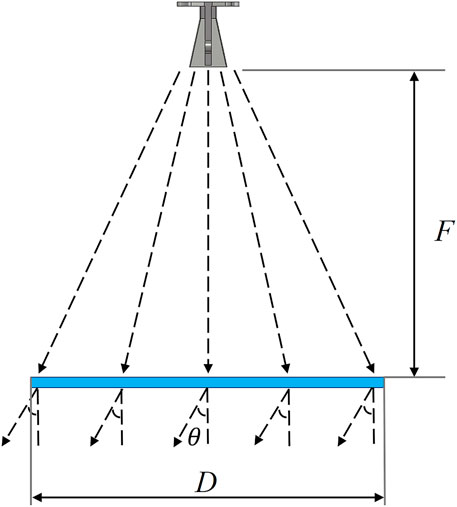
Using the proposed 1-bit Huygens’ units, the 1-bit dual-polarized Huygens’ lens antennas are designed. The center operating frequency of the lens antenna is 28 GHz. As shown in Figure 3, the lens antennas can convert spherical waves from horn feed to high-gain beams of directional radiation. The radiated EM waves include the normal direction radiation, the refraction angles of 15° and 30° along x axis, and the refraction angles of 15° and 30° along y axis, respectively. The sizes of Huygens’ lens are 33 × 33 unit cells. A LB-28-15-A standard gain horn antenna as a feed source illuminates the planar lens with the focusing length of F = 148 mm. The precise phase compensation on the transmissive surface satisfy the following expression
where Δφ(m, n) is the phase difference between the unit cell placed at the location of (m, n) on the surface and the unit cell at the origin (m = 0, n = 0), and θ is the azimuth angle. The unit can be digitized as “0” state when Δφ(m, n) is between 0° and 180°, and can be digitized as “1” state when Δφ(m, n) is between 180° and 360°, which is given by
Then the distribution status of all elements on the surface of the lens antenna can be obtained. Figures 4A–C show the unit state distribution for the radiated angles of 0°, 15°, and 30°, respectively. Figures 4D–F exhibits the corresponding distribution of parameter g, and Figures 4G–I exhibits the corresponding distribution of parameter l, respectively.
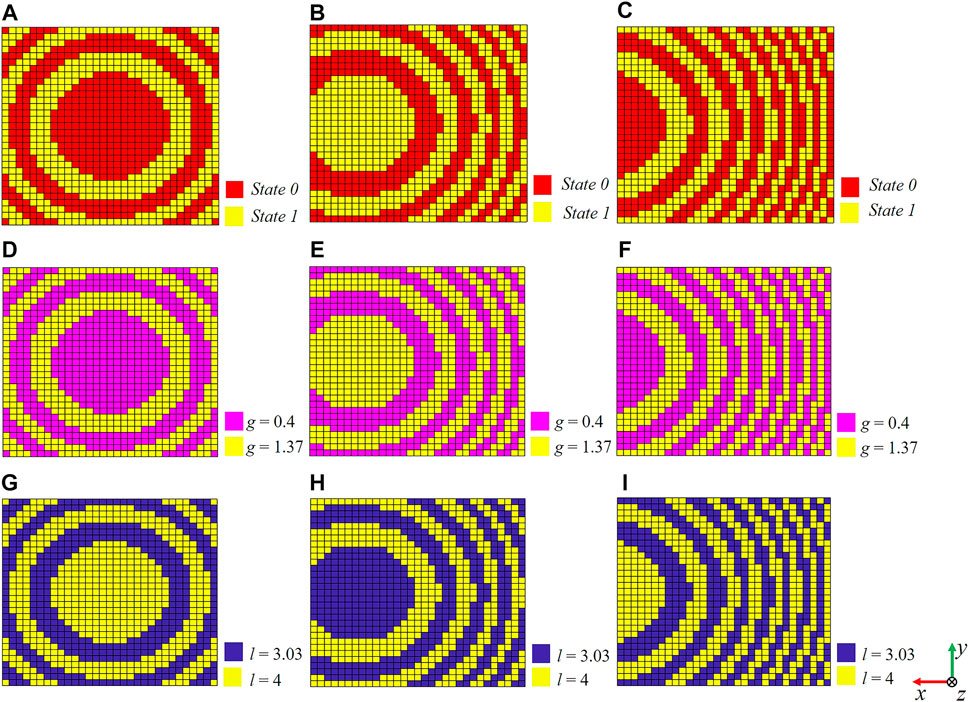
FIGURE 4. (A–C) are the unit state distribution diagrams for the radiated angles 0°, 15°, and 30° at 28 GHz, respectively (D–F) are the corresponding distribution of parameter g, and (G–I) are the corresponding distribution of parameter l, respectively.
The prototype of Huygens’ lens antenna is shown in Figure 5. To avoid any possible interference from the environment, all far-field measurements are carried out in a microwave anechoic chamber. Another horn antenna is used as a transmitter for far-field measurement which is connected to an Agilent E8363C analog signal generator. In order to determine the dual-polarized radiation properties, the simulation and measurement are carried out for the two cases where the horns are placed in the x and y directions, respectively. By assembling the antenna under test on the rotary platform, the forward radiated patterns can be obtained accordingly.
The simulated and measured far-field radiation patterns are shown in Figure 6. For x-polarization, as shown in Figure 6A, the simulated results show that refraction directions of radiated EM waves are 0°, 15°, and 30°, respectively, which is consistent with the design expectations. The half-power beam-width of the radiated beam are 3.9°, 4.1°, and 4.0° for E-plane, respectively. They have similar radiated properties. The peak gain of 0° refraction is 0.7 dB greater than that of 15° refraction and 2.23 dB stronger than that of 30° refraction, respectively. Moreover, the measured results show that refraction directions of radiated EM waves are 0°, 15°, and 30°, respectively, which is also consistent with the design expectations. The half-power beam-width of the radiated beam are 3.9°, 4.4°, and 4.2° for E-plane, respectively. They are consistent with the simulated results. For y-polarization, the simulated and measured results of Figure 6B is similar with those of Figure 6A. The half-power beam-width of the radiated beam of 0°, 15°, and 30° are 3.9°, 4.0°, and 4.1° for E-plane, respectively. The peak gain of 0° refraction is equal to that of 15° refraction and is 1.4 dB stronger than that of 30° refraction. Moreover, the measured results show that refraction directions of radiated EM waves are 0°, 15°, and 30°, respectively, which is also consistent with the design expectations. The half-power beam-width of the radiated beam are 3.9°, 4.1°, and 4.1° for E-plane, respectively. They are consistent with the simulated results. Moreover, the results show that half-power beam-width of the radiated beam are almost unchanged for different radiation angles, whether for x-polarization or y-polarization. In brief, the results of Figure 6 exhibit the dual-polarization property.
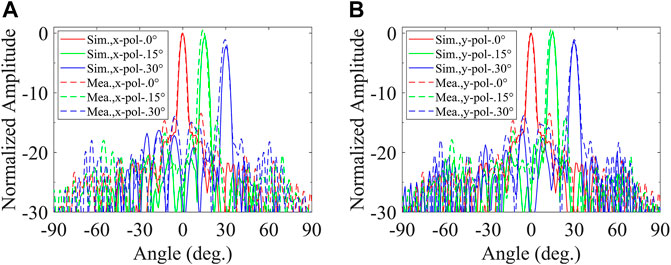
FIGURE 6. The E-plane far-field radiation pattern of 1-bit metasurfaces with the radiated angles of 0°, 15°, and 30° (A) for x polarization and (B) y polarization.
The gains spectrum is given in Figure 7. For x-polarization, the simulated maximum gain at 28 GHz is 27.22 dBi for 0°, 26.52 dBi for 15°, and 24.99 dBi for 30°, respectively. The results are about 4.00 dB weaker than the case of precise phase compensation. The measured results are consistent with the simulated results. For y-polarization, the simulated maximum gain at 28 GHz is 27.22 dBi for 0°, 27.32 dBi for 15°, and 25.82 dBi for 30°, respectively, and are about 4.00 dB weaker than the case of precise phase compensation. Furthermore, we note that, considering the radiation angle of 30°, the gain for the x-polarization case is significantly lower than that for the y-polarization case when the frequency is lower than 27.5 GHz. The reason is that the Huygens’ resonance is discussed just for the vertical radiation case. For the oblique radiation case, x- and y-polarizations cause different angular dispersions, which give rise to different changes of transmission amplitude and phase as the frequency is away from the designed frequency. Such difference leads to the phenomenon of very different gain in the case of x- and y-polarization when the frequency is away from the designed frequency. In addition, as seen from Figure 7, the 1-dB gain bandwidth is very wide, which shows good antenna radiation performance. The measured results are also consistent with the simulated results.
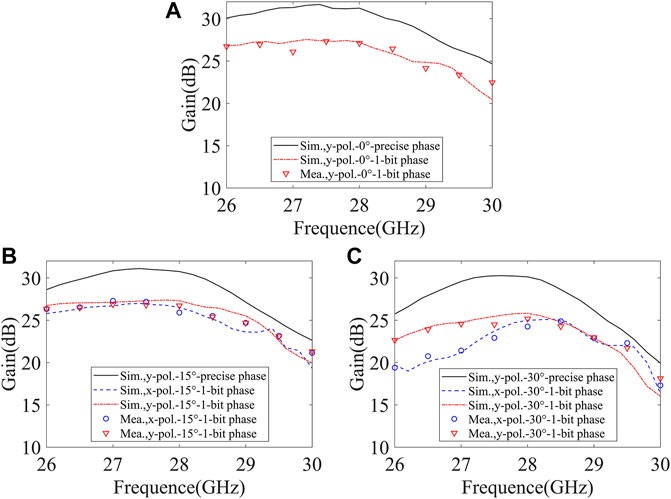
FIGURE 7. (A–C) The gain spectrum for refraction angles of (A) 0°, (B) 15°, and (C) 30°. All cases are compared to the exact phase compensation case.
Conclusion
In summary, we propose the configurations of 1-bit dual-polarized Huygens’ ultra-thin lens antenna. Two units with phase difference of 180° ± 25° are used for mimicking the “0” and “1” states. The metasurfaces designed with these two units achieve beam refraction at angles of 0°, 15°, and 30° for dual polarization. In addition, it is expected that the unit is available for circularly polarized transmitted wave manipulation by changing its structural symmetry. The Huygens’ lens antenna in this work have the advantages of low complexity, easy fabrication, and strong focusing ability, which is of great significance to the development of digital reconfigurable transmission array antennas in future.
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author contributions
CX and QH carried out the design, simulation of metasurfaces and drafted the manuscript. TL carried out the measurement of metasurfaces. All authors analyzed and discussed the results. The project was conceived and supervised by CX, TL, and XG.
Funding
This work was financially supported by the National Natural Science Foundation of China under Grant 62071133 and 62001102, and by the Key Program of Natural Science Foundation of Guangxi Province under Grant 2019GXNSFDA245011 and 2021GXNSFDA220003.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Abdelrahman, A. H., Elsherbeni, A. Z., and Yang, F. (2014). Transmission phase limit of multilayer frequency-selective surfaces for transmitarray designs. IEEE Trans. Antennas Propag. 62, 690–697. doi:10.1109/TAP.2013.2289313
Cai, T., Tang, S., Wang, G., Xu, H., Sun, S., He, Q., et al. (2017). High-performance bifunctional metasurfaces in transmission and reflection geometries. Adv. Opt. Mat. 5, 1600506. doi:10.1002/adom.201600506
Chen, H -T., Taylor, A. J., and Yu, N. (2016). A review of metasurfaces: Physics and applications. Rep. Prog. Phys. 79, 076401. doi:10.1088/0034-4885/79/7/076401
Chen, K., Feng, Y., Monticone, F., Zhao, J., Zhu, B., Jiang, T., et al. (2017). A reconfigurable active Huygens’ metalens. Adv. Mat. 29, 1606422. doi:10.1002/adma.201606422
Chen, M., Sánchez, E. A., Epstein, A., and Eleftheriades, G. V. (2018). Theory, design, and experimental verification of a reflectionless bianisotropic Huygens' metasurface for wide-angle refraction. Phys. Rev. B 97, 125433. doi:10.1103/PhysRevB.97.125433
Chen, S., Liu, W., Li, Z., Cheng, H., and Tian, J. (2020). Metasurface‐empowered optical multiplexing and multifunction. Adv. Mat. 32, 1805912. doi:10.1002/adma.201805912
Cui, T. J., Qi, M. Q., Wan, X., Zhao, J., and Cheng, Q. (2014). Coding metamaterials, digital metamaterials and programmable metamaterials. Light. Sci. Appl. 3, e218. doi:10.1038/lsa.2014.99
Epstein, A., and Eleftheriades, G. V. (2017). Arbitrary antenna arrays without feed networks based on cavity-excited omega-bianisotropic metasurfaces. IEEE Trans. Antennas Propag. 65, 1749–1756. doi:10.1109/TAP.2017.2670358
Epstein, A., Wong, J. P. S., and Eleftheriades, G. V. (2016). Cavity-excited Huygens’ metasurface antennas for near-unity aperture illumination efficiency from arbitrarily large apertures. Nat. Commun. 7, 10360. doi:10.1038/ncomms10360
Glybovski, S. B., Tretyakov, S. A., Belov, P. A., Kivshar, Y. S., and Simovski, C. R. (2016). Metasurfaces: From microwaves to visible. Phys. Rep. 634, 1–72. doi:10.1016/j.physrep.2016.04.004
Guo, Z. W., Long, Y., Jiang, H. T., Ren, J., and Chen, H. (2021). Anomalous unidirectional excitation of high-k hyperbolic modes using all-electric metasources. Adv. Photonics 3 (3), 036001. doi:10.1117/1.AP.3.3.036001
Hao, W. M., Deng, M., Chen, S. Q., and Chen, L. (2019). High-efficiency generation of airy beams with Huygens’ metasurface. Phys. Rev. Appl. 11, 054012. doi:10.1103/PhysRevApplied.11.054012
Hu, J., Bandyopadhyay, S., Liu, Y –H., and Shao, L -Y. (2021). A review on metasurface: From principle to smart metadevices. Front. Phys. 8, 586087. doi:10.3389/fphy.2020.586087
Li, G., Guo, Z. W., Ren, J., Sun, Y., Jiang, H. T., Li, Y. H., et al. (2021). Reconfigurable magnetic near-field distributions based on the coding metasurfaces in MHz band. Opt. Express 29 (9), 13908–13924. doi:10.1364/OE.424234
Li, L., Cui, T. J., Ji, W., Liu, S., Ding, J., Wan, X., et al. (2017). Electromagnetic reprogrammable coding-metasurface holograms. Nat. Commun. 8, 197. doi:10.1038/s41467-017-00164-9
Liu, M., Powell, D. A., Zarate, Y., and Shadrivov, I. V. (2018). Huygens’ metadevices for parametric waves. Phys. Rev. X X8, 031077. doi:10.1103/PhysRevX.8.031077
Liu, S., Cui, T. J., Zhang, L., Xu, Q., Wang, Q., Wan, X., et al. (2016). Convolution operations on coding metasurface to reach flexible and continuous controls of terahertz beams. Adv. Sci. 3, 1600156. doi:10.1002/advs.201600156
Long, Y., Ren, J., Guo, Z. W., Jiang, H. T., Wang, Y. Q., Sun, Y., et al. (2020). Designing all-electric subwavelength metasources for near-field photonic routings. Phys. Rev. Lett. 125 (15), 157401. doi:10.1103/PhysRevLett.125.157401
Lou, Q., Xue, C., and Chen, Z. N. (2021). High efficiency metalens antenna using Huygens’ metasurface with glide symmetric I-shape metal strips. IEEE Trans. Antennas Propag. 69, 7394–7403. doi:10.1109/TAP.2021.3083738
Pfeiffer, C., and Grbic, A. (2013). Metamaterial Huygens’ surfaces: Tailoring wave fronts with reflectionless sheets. Phys. Rev. Lett. 110, 197401. doi:10.1103/PhysRevLett.110.197401
Ren, X., Jha, P. K., Wang, Y., and Zhang, X. (2018). Nonconventional metasurfaces: From non-hermitian coupling, quantum interactions, to skin cloak. Nanophotonics 7, 1233–1243. doi:10.1515/nanoph-2018-0006
Wang, Z., Ding, X., Zhang, K., Ratni, B., Burokur, S. N., Gu, X., et al. (2018). Huygens metasurface holograms with the modulation of focal energy distribution. Adv. Opt. Mat. 6, 1800121. doi:10.1002/adom.201800121
Wang, Z., Liu, J., Ding, X., Zhao, W., Zhang, K., Li, H., et al. (2020). Three-dimensional microwave holography based on broadband Huygens' metasurface. Phys. Rev. Appl. 13, 014033. doi:10.1103/PhysRevApplied.13.014033
Wei, J., Qi, Y., Zhang, B., Ding, J., Liu, W., and Wang, X. (2022). Research on beam manipulate and RCS reduction based on terahertz ultra-wideband polarization conversion metasurface. Opt. Commun. 502, 127425. doi:10.1016/j.optcom.2021.127425
Xu, H -X., Hu, G., Han, L., Jiang, M., Huang, Y., Li, Y., et al. (2019). Chirality-assisted high-efficiency metasurfaces with independent control of phase, amplitude, and polarization. Adv. Opt. Mat. 7, 1801479. doi:10.1002/adom.201801479
Xue, C., Lou, Q., and Li, T. (2019). Ultra-compact, broadband Huygens’ metasurfaces based on induced magnetism. Appl. Phys. Express 12, 072005. doi:10.7567/1882-0786/ab266c
Xue, C., Lou, Q., and Chen, Z. N. (2020a). Broadband double-layered Huygens’ metasurface lens antenna for 5G millimeter-wave systems. IEEE Trans. Antennas Propag. 68, 1468–1476. doi:10.1109/TAP.2019.2943440
Xue, C., Sun, J., Niu, L., and Lou, Q. (2020b). Ultrathin dual-polarized Huygens’ metasurface: Design and application. Ann. Phys. Berl. 532, 2000151. doi:10.1002/andp.202000151
Xue, C., Chen, F., Pang, Z., and Lou, Q. (2020c). “An ultrathin and low-profile Huygens meta-lens antenna,” in 2020 IEEE 5th International Conference on Signal and Image Processing, Nanjing, China, 23-25 October 2020, 909–913. doi:10.1109/ICSIP49896.2020.9339362
Yin, J., Lou, Q., Wang, H., Chen, Z. N., and Hong, W. (2021). Broadband dual-polarized single-layer reflectarray antenna with independently controllable 1-bit dual beams. IEEE Trans. Antennas Propag. 69, 3294–3302. doi:10.1109/TAP.2020.3037686
Yu, N., Genevet, P., Kats, M. A., Aieta, F., Tetienne, J -P., Capasso, F., et al. (2011). Light propagation with phase discontinuities: Generalized laws of reflection and refraction. Science 334, 333–337. doi:10.1126/science.1210713
Keywords: Huygens’ metasurface, dual-polarization, 1-bit, lens antenna, induced magnetism
Citation: Xue C, He Q, Li T and Gao X (2022) 1-Bit dual-polarized ultrathin lens antennas based on Huygens’ metasurface. Front. Mater. 9:962798. doi: 10.3389/fmats.2022.962798
Received: 06 June 2022; Accepted: 25 July 2022;
Published: 26 August 2022.
Edited by:
Zhiwei Guo, Tongji University, ChinaCopyright © 2022 Xue, He, Li and Gao. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Teng Li, bGl0ZW5nQGllZWUub3Jn
 Chunhua Xue
Chunhua Xue Qingqi He
Qingqi He Teng Li2*
Teng Li2* Xi Gao
Xi Gao