
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Mater. , 12 October 2022
Sec. Smart Materials
Volume 9 - 2022 | https://doi.org/10.3389/fmats.2022.958813
This article is part of the Research Topic Innovators in Smart Materials View all 4 articles
A correction has been applied to this article in:
Corrigendum: Inversion of thermal properties of lunar soil from penetration heat of projectile using a 2D axisymmetric model and optimized PSO algorithm
 Fan Li1,2
Fan Li1,2 Honglang Li1
Honglang Li1 Zixiao Lu1*
Zixiao Lu1* Junhao Cao3
Junhao Cao3 Weiwei Zhang4*
Weiwei Zhang4* Junyue Tang4
Junyue Tang4 Yahui Tian5
Yahui Tian5 Cheng Chi4
Cheng Chi4 Shengyuan Jiang4
Shengyuan Jiang4The thermophysical parameters of lunar soil can be inferred from the temperature field during the invasion process of reconnaissance projectile. This paper adopts a two-dimensional axisymmetric model to reconstruct the projectile invasion process. An optimized particle swarm optimization method is then used to retrieve the thermophysical parameters of lunar soil. When the reconnaissance projectile penetrates the lunar interior, it rubs against the lunar soil and generates heat, which diffuses between the projectile body and the lunar soil. The sensors inside the reconnaissance projectile measure the temperature variation of the projectile body to inverse the thermophysical parameters. This paper carried out physical modeling of the penetration process of reconnaissance projectile. A two-dimensional axisymmetric simulation model is constructed for the physical process, and the adaptive inertial weight particle swarm algorithm is adopted. The inversion experiment of lunar soil thermophysical parameters based on the simulation model shows that the inversion error is less than 10%, which verifies the feasibility of this method.
An in-depth understanding of the lunar surface thermal environment is of great significance for further research on the origin of the Moon and the Solar System, deep lunar exploration, lunar base construction, and lunar resource development. The parameters describing the lunar thermal environment mainly include lunar soil temperature, solar radiation heat flow, and thermophysical parameters. According to the energy transfer method, the lunar soil thermophysical parameters are divided into radiation thermophysical parameters and conduction thermophysical parameters (Table 1). The radiation thermophysical parameters mainly include the lunar surface infrared emissivity, solar reflectance, and absorptivity. They determine the heat exchange between the lunar soil and space. The conduction thermophysical parameters mainly include the lunar soil density, heat capacity, thermal conductivity, and thermal diffusivity. They determine the flow state of heat in lunar soil (Kömle et al., 2011). The latter is the research object of this paper.
The measurement of lunar soil thermophysical parameters is mainly through three methods: remote sensing measurement, lunar soil sample detection, and in situ measurement. Remote sensing measurements generally only obtain lunar surface parameters. The properties of lunar soil samples may change during transportation. Compared with the first two methods, in situ measurement can obtain more reliable results. At present, the in situ measurement projects for the Moon mainly include the Apollo program in the United States and the Lunar-A program in Japan. In the Apollo program, astronauts conducted a series of in situ measurement experiments on the lunar surface. Among them, Apollo 15–17 were operated by astronauts with drilling tools, and probes were placed in the drilled deep holes to detect the thermophysical parameters of lunar soil (Langseth et al., 1972). The results show that the thermal conductivity of the regolith around the borehole ranges from 0.9 to 1.3*10−4W/(cm*K). This method is mainly imitated by the line heat source method in the laboratory to measure thermophysical soil parameters. However, the heat source does not meet the assumption of wireless long thin lines in in-situ measurement. So the measurement results have large errors. In addition, manual operations are required and the steps are complicated. In 2004, Japan’s Lunar A planned to carry three unmanned automatic penetrators, which could be used to detect the temperature gradient and thermal conductivity of lunar soil. The penetrators have sensors mounted on the interior and housing, with heaters mounted on the outer surface. By establishing a thermal mathematical model and by matching the mathematical model and the temperature curve obtained by the penetrators, the lunar soil thermophysical parameters can be inverted (Mizutani et al., 2003). The disadvantage of this approach is that many factors cannot be represented mathematically or it would be too complex (Hagermann et al., 2009). The project was eventually canceled due to its potential thruster failure.
There have been some attempts on the ground to measure soil thermophysical parameters in situ. Similar to the Lunar A, a cylindrical cone is generally used on the ground to penetrate deep into the soil, and a sensor is installed inside the cone. The heat generated by the friction between the cone and the soil is also used to cause the response of the sensor. The thermal properties of the soil are calculated accordingly. Akrouch et al. (2016) used a cone penetrometer equipped with a thermocouple to push into the soil and obtain the temperature change curve. They conducted 11 experiments at three different locations and fitted the empirical formula of parameters through the simulation model, which was consistent with the results obtained in the field experiment. However, this approach is somewhat contingent and dependent. PHILIP J. V Vardon et al. (2019) gave an analytical solution for thermal conductivity and volumetric heat capacity and compared it with the results of physical tests. The results show that the analytical solution can obtain accurate thermal conductivity. The analytical solution proposed by this method may vary with many conditions. It also ignores the coupling effects of soil thermal conductivity and heat capacity on the temperature profile. Mo et al. (2021) established a simplified one-dimensional model of the cone to simulate the field experiment. They used the particle swarm method to invert the thermophysical parameters based on the temperature curve. The particle swarm algorithm used in it avoids the shortcomings of the traditional grid parameter search, which requires a large amount of calculation, and the experiment shows good convergence characteristics and inversion results. However, the one-dimensional model only considers the heat diffusion of the cone in the radial direction. For the case where the length of the cone is not much larger than the radius of the cone, the heat diffusion in the axial direction needs to be considered. To sum up, the above methods generally have the problem of relying on experience, contingency, and model simplicity.
The particle swarm algorithm adopted by Mo et al. (2021) belongs to the swarm intelligence algorithm (Kennedy and Eberhart, 1995). This type of method simulates the foraging behavior of organisms and discards a large number of useless solutions compared to grid search. The particle swarm optimization algorithm finds the optimal solution of the function by simulating the predation behavior of birds. The algorithm defines potential solutions as particles, and each particle corresponds to a fitness value. Particles contain two attributes, speed, and position. The speed determines the particle’s position at the next moment, and it is dynamically adjusted according to the speed of itself and other particles so as to achieve optimization in the feasible region. The basic particle swarm optimization algorithm has the problems of slow convergence speed and local optimal solution, so this paper introduces adaptive inertia weight to optimize the basic particle swarm optimization algorithm. In terms of soil parameter inversion, genetic algorithm and simulated annealing algorithm are often used (Zhang et al., 2017) (Li et al., 2012) (Zhang et al., 2015). Therefore, this paper adopts an ordinary particle swarm optimization algorithm, genetic algorithm, and simulated annealing algorithm to invert lunar soil parameters, respectively. We compare the performance of the four algorithms at last.
For the problems of using cones to measure lunar soil and soil, this paper proposes a method to obtain lunar soil thermophysical parameters using reconnaissance projectile penetration heat. When the lander landed on the lunar surface with a reconnaissance projectile, it launched a reconnaissance projectile to the Moon during the landing process. The reconnaissance projectile entered the interior of the Moon, and the surface of the projectile rubbed against the lunar soil to generate heat. The temperature change curve of the surrounding medium is obtained by the sensor installed inside the projectile to invert the thermophysical parameters of lunar soil. Considering the axisymmetric structure of the projectile, the ratio of the projectile length to the radius length is small, and a two-dimensional axisymmetric model is constructed in this paper. We set temperature measurement points inside the missile model and obtain the temperature change curve. Based on the basic particle swarm optimization algorithm, the adaptive inertia weight technology is introduced to speed up the convergence speed of the algorithm and enhance the global search ability. In this paper, four temperature measurement points are set to obtain data, and the inversion results have small errors and good consistency, which verifies the feasibility of this approach. The advantages of the method proposed in this paper compared with the previous work are: 1) Compared with the mathematical model proposed by the Japanese Lunar-A plan, the analytical solution proposed by Vardon et al. (2019) and the one-dimensional axisymmetric model adopted by mo et al. (2021). The two-dimensional simulation model constructed in this paper is more able to restore the real environment and can consider more physical factors. For example, the diffusion of heat in the axial direction of the cone is considered; 2) Mo et al. adopted the basic particle swarm algorithm. Since it adopts a one-dimensional axisymmetric model, it is suitable for a small amount of calculation. In order to fit the two-dimensional axisymmetric model adopted in this paper, this paper introduces adaptive inertia weight technology to improve the basic particle swarm method, thereby improving its global search ability and convergence speed.
Temperature differences cause heat transfer. There are three main ways of heat transfer: heat conduction, heat convection, and heat radiation. The heat transfer process on the contact surface mainly involves heat conduction caused by microscopic particles’ thermal motion. This principle can be described by Fourier’s law:
Thermal convection occurs at the fluid or the contact surface between a fluid and an object. All surfaces with a temperature greater than 0 K have thermal radiation. In this paper, since there is no air flow on the lunar soil surface, thermal convection can be ignored. The heat of the projectile body mainly radiates through the upper end, which has a small area. Its thermal radiation power to the space compared to the heat exchange between the projectile and the lunar soil is much smaller. Therefore, the effect of thermal radiation can also be ignored.
In this paper, we consider that projectile falls in the permanently shadowed region of the Moon. The temperature of this place remains at 40 K all year round. This paper assumes that the material of the reconnaissance projectile is titanium alloy and selects values of the lunar soil parameters from previous studies (Langseth et al., 1976). Table 2 lists the parameters of the materials.
The velocity of the reconnaissance projectile is
Considering the trend of temperature field change, the main direction of heat, and actual detection, this paper divides the whole thermal diffusion process into three stages:
(1) Penetration stage. It starts from the contact of the reconnaissance projectile with the lunar soil to the end of the stationary reconnaissance projectile. At this stage, the friction between the surface of the projectile and the lunar soil generates heat. The external surface of the projectile is the heat source that transmits heat from the surface to the interior. The short infiltration time makes the heat concentrated on the surface of the projectile. The temperature far from the surface is lower, while the center temperature is unchanged.
(2) Detection stage. The detection stage refers to the period within one hour after the detection projectile stop. After the projectile is stationary, sensors work and collect temperature data. The heat conduction during this period will be the focus of this paper. The material used for the reconnaissance projectile is TC4 titanium alloy, whose thermal diffusivity is greater than that of the lunar soil. The main direction of heat transfer is from the exterior to the interior of the projectile at the early stage. Relatively little heat flows from the surface of the projectile into the surrounding soil. When the temperature of each point inside the projectile body is close, the heat diffuses from the projectile body to the soil.
(3) Stationary stage. It refers to the static time after the detection stage. At this stage, most of the penetration heat carried by the projectile body has already diffused into the lunar soil. The temperature difference in the whole system is tiny, and the heat flow is languid. Temperature sensors are difficult to detect significant temperature variation.
Due to the complexity of the projectile penetration process, including disturbance to the surrounding lunar soil and contact with the lunar soil, these environmental factors are difficult to quantify at present. Therefore, the simulation process is assumed as follows:
A. Ignoring the projectile’s damage to the lunar soil structure, including the impact on the physical and chemical parameters of the lunar soil.
B. Due to the fine particles of the lunar soil, it can be considered that the surface of the reconnaissance projectile in the exploration stage is in close contact with the lunar soil, and there is no contact thermal resistance on the interface.
C. It is assumed that the thermal conductivity and heat capacity of TC4 titanium alloy and lunar soil are temperature-independent constants, and the parameters used in the simulation are all data at room temperature.
D. It is assumed that the projectile body performs uniform deceleration in the penetration stage, and the heat generated by the penetration is evenly distributed on the external surface of the projectile.
E. Only the diffusion of heat between the missile body and the lunar soil is considered. Since the overall temperature of the system is very low. According to the simulation verification, the effect of void heat radiation of interspace can be ignored compared with heat conduction.
A numerical simulation model is established for the penetration process, and the shape and axial section of the projectile body is shown in Figure 1A. The projectile consists of a conehead and a hollow cylinder. The projectile penetrates the lunar soil. The overall model is shown in Figure 1B, and the two-dimensional axisymmetric model is adopted for simulation. The inside of the missile body is air, and the outer rectangular area is lunar soil. To accurately calculate heat diffusion inside the missile body, finer grids are used to divide the projectile and internal air. The physical field was set as solid heat transfer, and the contact surface between the projectile body and the lunar soil was set as the boundary heat source. The heating time lasted for 0.05s, the heating decreased linearly with time, and the initial power was 8.7*105 W.
The thermal diagram can reflect the distribution of heat in various model regions. Local regions are selected for magnification observation. The changes in the temperature field are observed at several moments (Figure 2). As can be seen from the figures, since the thermal conductivity of titanium alloy of missile body material is much higher than that of lunar soil, the heat generated by friction is mainly transferred from contact to the interior of the missile body, and part of the energy is transferred to the lunar soil, with a small range of disturbance to the temperature field of lunar soil. The heat was mainly transferred to the interior of the missile body. Later, the heat began to transfer to the interior of the lunar soil, and the overall heat of the system began to dissipate outward.
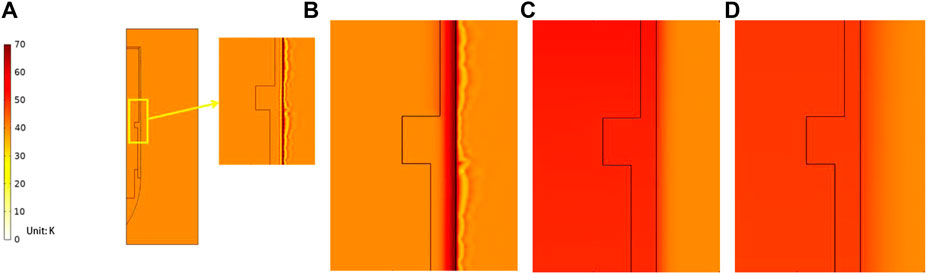
FIGURE 2. Thermal diffusion at different times (A) Observation location (B) t = 1 s (C) t = 600 s (D) t = 3600 s.
There are four sensors installed on the inner wall of the projectile to obtain temperature variation data. Figure 3 shows the positions for installing sensors. Wherein the distance between B1, B2, and B3 sensors is 10 cm apart, B2 is at the connection position of the projectile tip and the projectile body, and B1 is at the wall position at the bottom of the projectile tip. Temperature variation data of these four points were extracted from the simulation model. The results are shown in Figure 4. It can be seen from the figure that the temperature of the four sensors reached a peak in a short period and then gradually decreased. The distance between each sensor and the contact surface is different. The upper part of the elastic wall is thinner than the lower part, so more heat passes through the elastic wall, leading to a more significant temperature rise in the upper sensor. Temperature variation and heat diffusion in different periods are analyzed for the B4 sensor, and the results are shown in Figure 4. The temperature at the B4 position rises to maximum value before 10s and decreases from 10 to 3600s. The temperature variation of other sensors is similar.
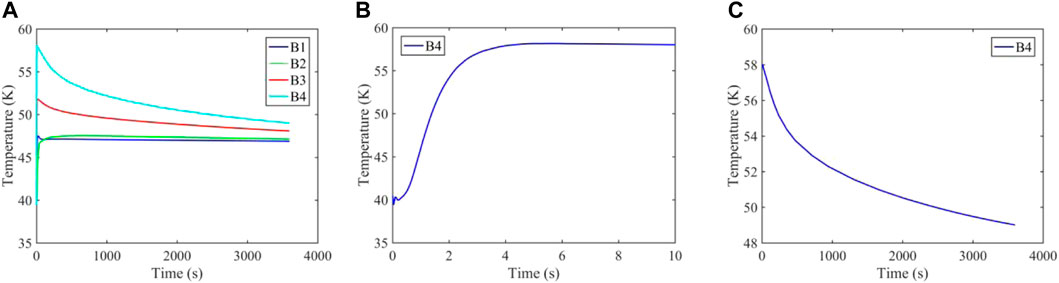
FIGURE 4. Temperature change curve of sensors. (A) Four sensors (B) Sensor B4, 0-10 s (C) Sensor B4, 10-3600 s.
In order to verify the feasibility of the inversion idea, it is necessary to analyze the sensitivity of the temperature curve to the change of thermophysical parameters, that is, to observe the influence of parameter change on the temperature curve. Assuming that the inversion error is ±10%, the thermal conductivity varies from 0.009 W/(m*K) to 0.011 W/(m*K), and the volume heat capacity varies from 1.026*106 J/(m3*K) to 1.254*106 J/(m3*K). The finite element method was used to scan the parameters at both ends. The temperature curve of the B4 sensor is extracted. The result is shown in Figure 5. The difference between the curves of
The particle swarm algorithm finds the optimal solution to the problem by simulating the motion of particles. Each particle updates its speed and next position according to its previous position and the best position of the group. The particle velocity iteration formula of the basic particle swarm algorithm is Eqs 5,6.
For the inversion problem, the thermophysical parameters
In basic particle swarm optimization, each particle has the same inertia weight and does not change with time. However, as the number of iterations increases, the global solution is closer to the optimal solution, the motion of each particle is also different, and the solution process is dynamic. The constant inertia weight obviously cannot meet the needs of the dynamic solution, so the dynamically changing adaptive weight is used and assigned to each particle. Therefore, this paper introduces an Optimized PSO which uses adaptive inertia weight technology.
Optimized PSO uses Eq. 8 to update inertia weights.
This paper set 100 for the number of populations and 50 for the maximum number of iterations. The extreme value of particle position
This paper compares Optimized PSO with ordinary particle swarm optimization, genetic algorithm, and simulated annealing algorithm and compares the iteration time, and inversion error of the four methods. These four algorithms all have similar parameters. The parameters that determine the performance of the algorithm are the number of populations, the maximum number of iterations, and the minimum fitness value. In order to facilitate the comparison of algorithms, this paper sets the population number of the four algorithms to 100, the maximum number of iterations to 50, and the minimum fitness to 0.001 K. This paper records the fitness iteration value, iteration time, and inversion error of the algorithms. The iterative curves of the four algorithms are shown in Figure 6, and the algorithm stops when the minimum fitness is reached. In this paper, iteration time and inversion error of thermal conductivity
From the perspective of fitness value, both Optimized PSO and SA algorithms can reach the minimum fitness value (i.e., 0.001 K) within the maximum number of iterations. This shows that these two algorithms have strong global search ability. Conversely, ordinary PSO and GA are prone to fall into local optimal solutions. From the perspective of running time, the Optimized PSO algorithm has fewer iterations than the ordinary PSO algorithm. Since the time consumed by each round of these two algorithms is similar, the time required for Optimized PSO to search for the optimal solution is shorter. GA and SA algorithms are prone to fall into local optimal solutions and require many iterations. At the same time, the genetic algorithm includes additional operations such as population crossover and mutation, which requires more time. The SA algorithm needs to search for new feasible solutions in each solution neighborhood and calculate the fitness value, so each round takes more time. In conclusion, Optimized PSO improves the global search ability of PSO and shortens the time required for algorithm convergence. At the same time, it also shows better performance than the commonly used GA and SA. From the inversion error and running time of the algorithm, the optimized particle swarm algorithm has similar average errors to other three algorithms. But it takes the least time among them.
This paper firstly analyzes the energy conversion process of the projectile penetrating the lunar soil. After the projectile came into contact with the lunar soil, it went through the stages of penetration, detection, and static in sequence. This paper qualitatively analyzes the heat diffusion process in the projectile and the surrounding lunar soil and provides a theoretical basis for building a simulation model. Due to the simplification of the process, complex factors such as the inclination angle of the projectile incident on the lunar soil and the deformation caused by the projectile force have not been considered, and further detailed analysis can be carried out in the future.
Based on the analysis of the projectile penetration process, this paper constructs a two-dimensional axisymmetric simulation model using the axisymmetric characteristics of the projectile. Compared with the one-dimensional model, this approach considers the heat dissipation in the axial direction of the projectile, so it is more in line with the actual situation. However, the contact between the projectile and the lunar soil surface is complicated, and its void size will affect heat diffusion when the soil particles are large. A more quantitative analysis of void size can be carried out subsequently through penetration experiments.
Finally, the particle swarm algorithm with adaptive inertia weight is used to invert the lunar soil parameters. This method improves the global search capability and iteration time of basic particle swarm optimization. At the same time, compared with GA and SA, the algorithms commonly used for soil parameter inversion show better performance.
For the problem of the inversion of lunar soil thermophysical parameters through projectile penetration, this paper combines theoretical analysis, model simulation and algorithm inversion methods. Firstly, we analyze the energy conversion and heat diffusion of projectile penetration. Secondly, we construct a two-dimensional axisymmetric model based on the physical process of the reconnaissance projectile penetrating into the lunar soil. The heat dissipation of the projectile in the axial direction is considered. Finally, the particle swarm algorithm with adaptive weight is used to search the lunar soil thermophysical parameters, which improves the convergence speed and global search ability of the algorithm. The average error of the inversion results is less than 10%. And it is compared with three other algorithms, which demonstrates the feasibility of the optimized algorithm. The scheme in this paper provides a new idea for the inversion of lunar soil thermophysical parameters. The simulation model has not yet quantified some complex environmental factors, such as the complex contact between the lunar soil and the surface of the projectile. The establishment of a physical model that is closer to the actual environment can be considered in the future. Optimization algorithms should also be further developed to speed up the inversion process. The rapid development of simulation technology and computer computing power will facilitate the inversion of soil parameters.
The data that support the findings of this study are available from the corresponding authors.
FL: constructing model and programming ZL, YT, and JC: Theoretical analysis and guidance Others: paper revision and suggestions.
This work is funded by Research and Development Program of China (Grant No. 2019YFB1405403), The Key Research Project of Guangdong Province (Grant No. 2020B0101040002), and Technology Nova Program of Beijing (Grant No. Z201100006820012).
The authors would also like to thank the two reviewers for their detailed and constructive comments and suggestions, which have helped to improve this study.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Akrouch, G. A., Briaud, J.-L., Sanchez, M., and Yilmaz, R. (2016). Thermal cone test to determine soil thermal properties. J. Geotechnical Geoenvironmental Eng. 142 (3). doi:10.1061/(asce)gt.1943-5606.0001353
Hagermann, A., Tanaka, S., and Saito, Y. (2009). “Thermal measurements on penetrators: Geometry, sensitivity and optimisation issues,” in Penetrometry in the solar system II. Editors G. n. Kargl, N. I. Kömle, A. J. Ball, and R. D. Lorenz (Vienna: Austrian Academy of Sciences Press), Vienna, Austria, 109–122.
Kennedy, J., and Eberhart, R. (1995). "Particle swarm optimization"in: Proceedings of ICNN'95 - International Conference on Neural Networks, Perth, Australia, 1942–1948.
Kömle, N. I., Hütter, E. S., Macher, W., Kaufmann, E., Kargl, G., Knollenberg, J., et al. (2011). In situ methods for measuring thermal properties and heat flux on planetary bodies. Planet. Space Sci. 59 (8), 639–660. doi:10.1016/j.pss.2011.03.004
Langseth, M., Clark, S. P., Chute, J., Keihm, S., and Wechsler, A. (1972). The Apollo 15 lunar heat-flow measurement. The moon 4, 390–410. doi:10.1007/BF00562006
Langseth, M. G., Keihm, S. J., and Peters, K. (1976). Revised lunar heat-flow values. Geochim. Cosmochim. Acta. l, 3143–3171.
Li, S.-j., Shao, L.-t., Wang, J.-z., and Liu, Y.-x. (2012). Inverse procedure for determining model parameter of soils using real-coded genetic algorithm. J. CENTRAL SOUTH Univ. 19 (6), 1764–1770. doi:10.1007/s11771-012-1203-2
Mizutani, H., Fujimura, A., Tanaka, S., Shiraishi, H., and Nakajima, T. (2003). LUNAR-A mission : Goals and status. Adv. Space Res. 31 (11), 2315–2321. doi:10.1016/S0273-1177(03)00542-8
Mo, P.-Q., Ma, D.-Y., Zhu, Q.-Y., and Hu, Y.-C. (2021). Interpretation of heating and cooling data from thermal cone penetration test using a 1D numerical model and a PSO algorithm. Comput. Geotechnics 130. doi:10.1016/j.compgeo.2020.103908
Vardon, P. J., Baltoukas, D., and Peuchen, J. (2019). Interpreting and validating the thermal cone penetration test (T-CPT). Geotechnique 69 (7), 580–592. doi:10.1680/jgeot.17.P.214
Zhang, C., Wang, D., Liu, Y., Sun, S., and Peng, D. (2015). Application of simulated annealing algorithm for determining parameters of rock-soil thermal properties. CIESC J. 66 (2), 545–552.
Keywords: inversion, thermophysical parameters, lunar soil, penetration, particle swarm optimization
Citation: Li F, Li H, Lu Z, Cao J, Zhang W, Tang J, Tian Y, Chi C and Jiang S (2022) Inversion of thermal properties of lunar soil from penetration heat of projectile using a 2D axisymmetric model and optimized PSO algorithm. Front. Mater. 9:958813. doi: 10.3389/fmats.2022.958813
Received: 01 June 2022; Accepted: 13 September 2022;
Published: 12 October 2022.
Edited by:
Jian Zhou, Hunan University, ChinaReviewed by:
Jianguo Yan, Wuhan University, ChinaCopyright © 2022 Li, Li, Lu, Cao, Zhang, Tang, Tian, Chi and Jiang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Zixiao Lu, bHV6eDIwMTlAbmFub2N0ci5jbg==; Weiwei Zhang, endlaWVyQGhpdC5lZHUuY24=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.