Modeling precipitation kinetics in multicomponent alloys during deformation

A new mean-field modeling tool is developed to correctly tackle the problem of precipitation during deformation. The model is an extension of a previously developed Langer–Schwartz–Kampmann–Wagner precipitation modeling approach for multicomponent alloys. The latter is now integrated together with Thermo-Calc software and with physically based equations describing the evolution of the dislocation density during hot-working. New equations for the nucleation barrier and the critical size have also been added to correctly simulate the early stages of precipitation. The model is applied to hot compression tests, for which experimental information was available. The model shows the importance of accounting for the overall precipitation kinetics, and not only for constant values of the precipitate volume fraction or size, to investigate the mechanical property evolution. This is due to a complex interplay between the defects and the precipitates’ evolution driven by a competition between thermodynamics and kinetics. Finally, it is highlighted how the strain rate used affects the final microstructure of the material.

1 Introduction

Precipitation is a very important phase transformation in metallurgy, leading to the decomposition of a supersaturated matrix into two or more phases. Through the generation and evolution of the precipitates, the mechanical properties can be tuned by adjusting the processing step. Indeed, depending on their nature, that is, composition, stoichiometry, and distribution, precipitates can also be detrimental. In any case, it is very important to be able to fully control the precipitation kinetics to achieve the desired mechanical properties as a result of certain precipitates and particle size distribution (PSD). To overcome a trial-and-error approach and to be able to predict the PSD of the precipitates formed, as a function of the thermal profile, many modeling approaches have been developed over the years. Depending on the length scale at which they operate, they give different types of information. In precipitation, it is very important to correctly describe the nucleation stage, as it defines the starting point and magnitude of the number of precipitates formed. For non-stoichiometric precipitates, the use of a non-constant interfacial energy is highly recommended to correctly track the composition evolution (Kozeschnik, 2008; Philippe and Blavette, 2011) that in turn affects the kinetics. Kinetic Monte Carlo (KMC) (Golubov et al., 1995) and cluster dynamics (CD) (Clouet et al., 2005) tools that operate at the atomistic scale are specifically appropriate to study the first stage, that is, nucleation, of the precipitation kinetics. However, the size of the investigated system is limited using KMC since a simulation box with only a certain number of atoms is used. In addition, the thermodynamic information stored in the databases cannot be directly used as input in KMC and CD because of its atomistic parameters that are needed. Phase field (PF) modeling (Steinbach, 2009), on the other hand, can be coupled with thermodynamic databases and is applicable to different system sizes depending on the mesh used for the simulation box. Nevertheless, the treatment of the interface requires system sizes consistent with the features in the system. Therefore, when dealing with nano-sized objects such as precipitates, the considered system becomes quite small. In addition, because PF deals with deterministic equations, the nucleation stage that is stochastic cannot be handled properly. The macroscopic level modeling tools can be semi-empirical laws or mean-field approaches such as those implemented in a Langer–Schwartz–Kampmann–Wagner (LSKW) framework (Langer and Schwartz, 1980; Wagner et al., 2001). The latter is the approach chosen in this work as it has the advantage to concomitantly include nucleation, growth, and coarsening. Furthermore, it can be easily coupled with thermodynamic and kinetic databases, implying the possibility to derive generic modeling tools very useful for integrated computational material engineering (ICME) (Olson, 1997). Since there is no limitation by any simulation box sizes, an unlimited number of precipitates can be simulated, as well as many different types of precipitates, which is not the case with the previously introduced methods. It is important to highlight that the accuracy of the thermodynamic and kinetic databases is decisive for correctly understanding the precipitation kinetics. Steels are quite well-described because they were the first alloys to be investigated in this regard. However, well-known LSKW tools such as TC-Prisma (Thermo-Calc, 2022) from Thermo-Calc software (Andersson et al., 2002), MatCalc (Svoboda et al., 2004), or Preciso (Perez et al., 2008) have not yet been developed to account for the effect of a thermomechanical treatment.

Deformation during the processing step introduces dislocations in the material that modify the diffusion behavior and the arrangement of grains, which can become favorable nucleation sites. It is well-known that the excess of vacancies that could be generated during a specific thermomechanical treatment increases diffusion, precipitation rates, segregation, and recrystallization (Militzer et al., 1994; Hutchinson et al., 2014; Robson, 2020). In steels, a comparison of as-cast, hot-worked, and cold-worked microstructures highlighted differences in both the size of the grains and of the carbides due to the dislocations affecting both precipitation and grain rearrangement kinetics (Farahat et al., 2008; Zhou et al., 2015). It is known that during hot-working, precipitation is favored through its occurrence in a heterogenous fashion on dislocations and, thus, the dislocation number density is a crucial parameter for correctly predicting the precipitation kinetics (Dutta et al., 2001). It is thus very important to understand and control the extent to which the deformation of a metallic material can increase the precipitation kinetics to set a proper time, temperature, and strain rates to design the best thermomechanical treatment.

Micromechanical models that are physically based and dedicated to flow stress calculations do exist in the literature. They include analytical expressions for the rate of dislocation generation as a function of the applied stress. Micromechanical models such as the one developed by Engberg and Lissel (2008) operate with equations that are dependent on the precipitate mean size and volume fraction. However, when this type of approach is not interactively combined with the actual precipitation kinetics, they cannot be fully realistic. Undeniably, assuming that the precipitates do not change in size or even do exist from the beginning during a treatment where an initial microstructure is experimentally observed to be homogeneous leads to wrong estimation of the dislocations elimination through glide. Even when the models are applied to very short deformation times, where the existing precipitates would not have time to evolve, it is needed to back calculate their mean size and volume fraction by comparing with experimental results of the flow stress (Safara et al., 2019). To move toward a fully generic tool, with the processing conditions as the only input in combination with thermodynamic and kinetic databases, here, we propose a new integrated model coupling the strength of a mean-field precipitation model with a micromechanical model describing the dislocation density evolution as a function of time. Although they are not exactly operating at the same time scale, the precipitation mean-field models and micromechanical models deal with the same macroscopic values such as, among others, dislocation density, precipitate volume fraction, and size. The main considerations that are made are the fact that precipitation takes place on dislocations once the material is deformed and diffusion is enhanced along these dislocations. A heterogeneous nucleation model is thus used.

In this study, we describe how a precipitation model and a micromechanical model can be coupled to efficiently simulate the effect of thermomechanical treatment on the precipitation kinetics. The model is applied to an experimental test carried out in a Gleeble system (Safara et al., 2019). The model is also used to investigate the effect of strain rate on the precipitation kinetics to highlight the great influence of deformation on precipitation and the importance to account for the entire precipitation sequence to predict correct microstructures.

2 Materials and methods

2.1 Material and thermomechanical treatment

In this work, we investigate the microstructural evolution of chromium steel subjected to a thermomechanical treatment simulating hot compression. The steel, with the composition given in Table 1, has previously been experimentally investigated by Safara et al. (2019) and Safara et al. (2020) by means of a Gleeble thermomechanical simulator, hardness measurements, scanning electron microscopy (SEM), and energy-dispersive spectroscopy (EDS). The non-isothermal thermomechanical treatment applied consists of cooling from the austenitization temperature, 1,250°C, with a rate of 5°C/s down to holding temperatures (900, 1,000, and 1,100°C). The material is maintained for 15 s at each temperature and deformed to reach a strain of 0.7 at different strain rates, 10s⁻¹ and 1s⁻¹. The total holding time is 300 s. The obtained microstructure consisted of a distribution of precipitates embedded in a martensitic matrix. The first work by Safara et al. (2019) included a plastic deformation of the material after 15 s holding exactly as in the Figure 1. The authors determined both the flow stress curve experimentally during this deformation and used a physically based model—consisting of a set of equations for the dislocations evolution, vacancies, recrystallization, and grain growth—to estimate the flow stress numerically. This model is dependent on the volume fraction of precipitates and their mean size. They were, thus, able to adjust these values in order to obtain a good agreement between the experimental measurement and the model predictions of the flow stress. Table 2 gives the evolution of the ratio between the volume fraction and mean size of precipitates, as estimated by Safara et al. (2019). In addition, in a second work, Safara et al. (2020) performed the Gleeble test on the same steel and with the same thermal profile but without plastic deformation. The holding at the holding temperature was stopped after 15 s in order to experimentally characterize the microstructure of the steel right before the deformation in comparison to their first work. Comparing theoretical calculations of the hardness involving the precipitate’s mean size and volume fraction with experimentally measured hardness values gave an estimation of the mean size and volume fraction of the precipitates in the steel. These values are given in Table 2 and used in this work to parametrize the simulations, especially the interfacial energy, even though it was considered that the precipitate’s mean size and volume fraction were not evolving during the deformation.

TABLE 1

TABLE 1. Nominal composition of the investigated material.

FIGURE 1

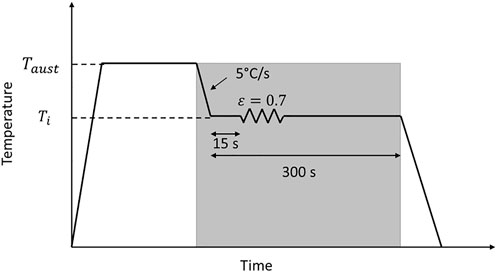
FIGURE 1. Schematic of the thermomechanical treatment applied. The grey shadowed area represents what is simulated with the modeling tool. $T_{aust}=\mathrm{1,250}°C$ and $T_i=900,\mathrm{1,000},\mathrm{a}\mathrm{n}\mathrm{d}\mathrm{1,100}°C.$

TABLE 2

TABLE 2. Ratio of the volume fraction of precipitates over the mean size of precipitates estimated from the experimental work of Safara et al. (2019) and obtained from this work with the integrated modeling tool.

2.2 Modeling approach

2.2.1 Governing equations

In this part, the generic framework is described for modeling the precipitation of $\beta$ particles in a supersaturated $\alpha$ matrix subjected to a strain rate $d\epsilon /dt$.

The nucleation stage is described by the classical nucleation theory. In this one-dimensional theory, the change in Gibbs energy, $∆G$, associated with the creation of a small nucleus in the supersaturated matrix, is expressed as a function of the size of this nucleus. For a spherical nucleus, with the radius $r$, it is written as follows:

$∆\mathit{G}=-\frac{\mathbf{4}}{\mathbf{3}}\mathit{\pi }{\mathit{r}}^{\mathbf{3}}∆{\mathit{G}}_{\mathit{m}}+\mathbf{4}\mathit{\pi }{\mathit{r}}^{\mathbf{2}}\mathit{\sigma }(1)$

${\frac{\mathit{\partial }∆\mathit{G}}{\mathit{\partial }\mathit{r}}|}_{\mathit{r}*}=\mathbf{0}(2)$

where $∆G_m$ is the driving force for precipitation and $\sigma$ is the interfacial energy. The first term in this equation is negative when the material is supersaturated. Hence, when the material decomposes into two phases with the equilibrium molar fractions, as predicted by the thermodynamic equilibrium, it leads to a decrease in the overall energy of the system. However, Eq. 1 also contains a penalty term, the second term, related to the creation of an interface between the matrix and the precipitates. The possibility to nucleate or not is thus dependent on the competition between the two terms. The maximum change in energy to overcome in order to nucleate is the well-known nucleation barrier ${∆G}^{*}$. The radius leading to this value of $∆G$ is the critical radius $r^{*}$. These two parameters are obtained solving the following equation:

In the case of spherical nuclei, one gets the following:

${\mathit{r}}^{*}=\frac{\mathbf{2}\mathit{\sigma }}{∆{\mathit{G}}_{\mathit{m}}},(3)$

${∆\mathit{G}}^{*}=\left(\mathbf{16}\mathit{\pi }{\mathit{\sigma }}^{\mathbf{3}}\right)/\left(\mathbf{3}{∆{\mathit{G}}_{\mathit{m}}}^{\mathbf{2}}\right).(4)$

The higher the nucleation barrier, the more difficult it is to nucleate. This is captured in the exponential dependency on the nucleation barrier of the expression of the number of precipitates created per unit time and per unit volume, that is, the nucleation rate, given by

$\frac{\mathit{d}{\mathit{N}}_{\mathit{v}}}{\mathit{d}\mathit{t}}=\mathit{n}\left(\mathbf{1}-\mathit{f}\right)\mathit{Z}{\mathit{\beta }}^{*}\mathbf{exp}\left(-\frac{{∆\mathit{G}}^{*}}{{\mathit{k}}_{\mathit{B}}\mathit{T}}\right)\mathbf{exp}\left(-\frac{\mathit{\tau }}{\mathit{t}}\right)(5)$

where $N_v$ is the number density of precipitates, $n$ is the number of nucleation sites, $f$ is the volume fraction of precipitates (equal to 0 initially), $T$ is the temperature, and $t$ is the time. $Z$ is the Zeldovich factor, given by

$\mathit{Z}=\frac{{\mathit{V}}_{\mathit{m}}\sqrt{\mathit{\sigma }}}{\mathbf{2}\mathit{\pi }{{\mathit{r}}^{*}}^{\mathbf{2}}\sqrt{{\mathit{k}}_{\mathit{B}}\mathit{T}}{\mathit{N}}_{\mathit{a}}}(6)$

where $V_m$ is the molar volume of the matrix phase and $N_a$ is the Avogadro number. ${\beta }^{*}$ is the atomic attachment rate, given by

${\mathit{\beta }}^{*}=\frac{{\mathit{k}}_{\mathit{B}}\mathit{T}{\mathit{V}}_{\mathit{m}}}{\mathbf{4}\mathit{\pi }{{\mathit{r}}^{*}}^{\mathbf{3}}{∆\overline{\mathbf{x}}}^{\mathbf{T}}{\mathbf{L}}^{-\mathbf{1}}∆\overline{\mathbf{x}}}(7)$

where $\mathbf{L}$ is the mobility matrix and $∆\overline{\mathbf{x}}$ is a vector consisting of the elements ${∆\overline{x}}_i={\overline{x}}_i^{\alpha }-{\overline{x}}_i^{\beta }$, the equilibrium tie-line, that is, the difference between equilibrium composition, of element $i$. $\tau$ is the incubation time, and is expressed as follows:

$\mathit{\tau }=\frac{\mathbf{2}}{\mathit{\pi }{\mathit{\beta }}^{*}{\mathit{Z}}^{\mathbf{2}}}.(8)$

Eq. 1 is a classical way to express the change in energy with nucleation. Nevertheless, it is possible to add other terms that will affect the energy balance. For instance, one could add the effect of an elastic misfit that produces an elastic field around the precipitates (Bonvalet et al., 2019). In the case of a deformed material, which is the context of this study, nucleation on dislocations can induce a decrease in the nucleation barrier. Indeed, nucleation on a dislocation leads to a larger decrease in the overall energy of the system compared to bulk nucleation through the elimination of a part of the dislocation that is replaced by the new nucleus. In that case, the Gibbs energy change can be rewritten as follows:

$∆\mathit{G}=-\frac{\mathbf{4}}{\mathbf{3}}\mathit{\pi }{\mathit{r}}^{\mathbf{3}}∆{\mathit{G}}_{\mathit{m}}+\mathbf{4}\mathit{\pi }{\mathit{r}}^{\mathbf{2}}\mathit{\sigma }-\mathbf{2}\mathit{r}{\mathit{E}}_{\mathit{d}\mathit{i}\mathit{s}\mathit{l}\mathit{o}}(9)$

where $E_{dislo}$ is the linear energy of an edge dislocation and can be rewritten as follows:

${\mathit{E}}_{\mathit{d}\mathit{i}\mathit{s}\mathit{l}\mathit{o}}=\mathit{\mu }{\mathit{b}}^{\mathbf{2}}\mathit{ln}\left(\mathit{R}/{\mathit{r}}_{\mathbf{0}}\right)/\left(\mathbf{4}\mathit{\pi }\left(\mathbf{1}-\mathit{\nu }\right)\right),(10)$

where $\mu =G_0\left[1+G_1\frac{T-300}{T_m}\right]$ is the shear modulus, where $G_0$ and $G_1$ are parameters to calculate it, $T_m$ is the melting temperature of the material; $b$ is the Burgers vector; $\mathit{\nu }$ is the Poisson ratio; $R$ is the extension of the stress field; and $r_0$ is the core radius of the dislocations (Hirth et al., 1983). In the context of Eq. 9, the nucleation barrier and the critical radius are also affected. They are computed numerically by solving Eq. 2.

When nucleation is treated in the classical way, that is, occurring in the bulk of a material, $n$ in Eq. 5 is calculated with respect to the volume density of atoms, thus with the molar volume. However, when nucleation is considered to take place on dislocations, the number of available nucleation sites is different and must be adjusted using the following relationship:

$\mathit{n}=\mathit{\rho }{\left(\frac{{\mathit{N}}_{\mathit{A}}}{{\mathit{V}}_{\mathit{m}}}\right)}^{\mathbf{1}/\mathbf{3}}(11)$

where $\rho$ is the dislocation density.

When the dislocations are generated during a previous processing step, it can be calculated or evaluated experimentally once and not changed in the course of the precipitation simulation. Yet, when one studies precipitation in the course of a thermomechanical treatment and submitted to a strain rate $\frac{d\epsilon }{dt}$, the number of dislocations comes to a dynamic value that changes with time. In this work, we, therefore, use the expression of the dislocation density evolution, as given by Engberg and Lissel (2008). The main equations of the set of equations are given, but for more information regarding their derivation refer to Safara et al. (2019), Safara et al. (2020), and Safara Nosar (2021). The dislocation density rate is then expressed as follows:

$\frac{\mathit{d}\mathit{\rho }}{\mathit{d}\mathit{t}}=\frac{\mathit{m}}{\mathit{b}{\mathit{L}}_{\mathit{d}}}\frac{\mathit{d}\mathit{\epsilon }}{\mathit{d}\mathit{t}}-{\mathit{M}}_{\mathit{m}}{\mathit{\rho }}^{\mathbf{2}}\left(\mathbf{1}-\frac{\mathbf{3}\mathit{f}}{\mathbf{4}{\mathit{r}}_{\mathit{m}}\sqrt{\mathit{\rho }}}\right)-\mathit{\Omega }\mathit{\rho }\frac{\mathit{d}\mathit{\epsilon }}{\mathit{d}\mathit{t}},(12)$

where $m$ is the Taylor factor, $M_m$ is the rate parameter of recovery, $r_m$ is the mean size of precipitates, $\Omega$ is a material parameter representing dynamic recovery and annihilation of dislocations, and $L_d$ is the dislocation mean free distance of slip, given by

$\frac{\mathbf{1}}{{\mathit{L}}_{\mathit{d}}}=\mathbf{4}\frac{\mathit{f}}{{\mathit{r}}_{\mathit{m}}}+\frac{\mathbf{1}}{\mathbf{2}\mathit{R}}+\sqrt{\mathit{\rho }},(13)$

where $R$ is the grain size.

In Eq. 12, the first term represents the generation of dislocations due to the strain rate, whereas the two last terms represent their elimination through glide and climb, respectively.

It is worth noting that Eq. 5, 12 are interdependent, as the number density of dislocations drives the nucleation rate and size distribution of the precipitate governs the density of dislocation evolution.

Finally, the growth rate of precipitates is calculated using the expression for diffusion-limited growth (Philippe and Voorhees, 2013). This expression is obtained considering the solute atoms diffusion flux coming from the matrix at the interface, between a precipitate of size r and the matrix, and considering local equilibrium at the interface and a low-supersaturation. The growth rate can be rewritten as follows:

$\frac{\mathit{d}\mathit{r}}{\mathit{d}\mathit{t}}=\frac{\mathbf{2}\mathit{\sigma }{\mathit{V}}_{\mathit{m}}}{\mathit{r}{∆\overline{\mathbf{x}}}^{\mathbf{T}}{\mathbf{L}}^{-\mathbf{1}}∆\overline{\mathbf{x}}}\left(\frac{\mathbf{1}}{{\mathit{r}}^{*}}-\frac{\mathbf{1}}{\mathit{r}}\right)(14)$

2.2.2 Implementation

The framework adopted in this work is the well-known LSKW type of implementation with a Lagrange-like approach (Perez et al., 2008). The time is discretized and, at every time step, a class of precipitates is created using Eq. 5. The class is then defined by a fixed number density of precipitates of the same size. The latter evolves as each class of precipitates can grow or shrink during every time step following Eq. 14. The time step must be carefully chosen because a too large time step would lead to non-physical results with classes that are too average. In addition, the time step that must be used for the computation of the dislocation density must be smaller than that for nucleation and growth of precipitates as the kinetics for the dislocation evolution is faster than that for nucleation and growth of the precipitates.

At every time step, once the particle size distribution of precipitates and number density of dislocations are updated, the matrix content is revised (Bonvalet et al., 2015) so that the thermodynamic state is updated and the correct driving force is used at the next time step.

The nucleation stage is stopped once the nucleation rate becomes insignificant. Nucleation is allowed to continue, while

$\frac{\mathit{d}{\mathit{N}}_{\mathit{v}}}{\mathit{d}\mathit{t}}>\mathbf{0.001}\times {\frac{\mathit{d}{\mathit{N}}_{\mathit{v}}}{\mathit{d}\mathit{t}}|}_{\mathit{max}}(15)$

where ${\frac{d{N}_v}{dt}|}_{\mathit{max}}$ is the maximum value reached since the beginning of the deformation. This criterion is set only from the deformation stage. Indeed, classically, at a constant temperature and with a continuous decrease of the number of nucleation sites, while the precipitates are created, the nucleation rate first increases as time approaches the incubation time and then starts to decrease once the creation of the precipitates has led to a depletion of the solute content in the matrix. However, when the temperature is not constant, which is the case at the beginning of the heat treatment, the nucleation rate is not monotonous because of the change in the driving force at every temperature increment. It would, thus, be difficult to differentiate a decrease of the rate due to a drop in the supersaturation from the one due to the change of temperature. In addition, deformation, which leads to an increase in the number of nucleation sites, might lead to a second increase in the nucleation rate, which is not the case for classical non-mechanical isothermal treatment.

Depending on whether the material is being deformed or not, the relevant nucleation barrier, that is, Eq. 3, is computed. Indeed, it is assumed that nucleation on dislocations takes place only once the material has been deformed. Previously, deformation of the precipitation is assumed to take place in the bulk. Nucleation could definitely also take place on dislocations simultaneously at this stage, but the dislocation number density is rather low, and it is thus assumed that nucleation is significant only in the bulk. Once the applied stress is stopped, nucleation, if still ongoing, can continue to take place on dislocations until their number densities reach critically low values, stated as 1x10¹² m⁻² in this work. This value is based on previous theoretical (Yoshie et al., 1996) and experimental work (Macchi et al., 2021).

Finally, since it is well-known that diffusion is enhanced by the presence of a high number of vacancies and dislocations leading to so-called pipe diffusion, the diffusion coefficients are increased by two orders of magnitude when deformation is taking place and when the number density of dislocations is higher than the previously introduced critical value. The diffusion coefficient is set to initial value once the dislocation density is back to its original value.

2.3 Parametrization

The developed model requires many input parameters, which can be divided into several classes depending on their kind. The parameters in Table 3 are intrinsic material properties and can be found in handbooks or derived from a thermodynamic database. The parameters related to the micromechanical model that are necessary in Eq. 12, are taken from Safara et al. (2019), Safara et al. (2020), and Safara Nosar (2021). The molar volume and lattice parameter are extracted from a thermodynamic database (TCFE12, 2022). In addition, the number of nucleation sites for bulk precipitation is simply the number of atoms per cubic meter that can be obtained from the molar volume as well. Finally, the interfacial energy was adjusted to reproduce experimental results. A discussion is given about this parameter later on. The modeling tool is coupled with Thermo-Calc using the TCFE12 database (TCFE12, 2022), MOBFE4 database (MOBFE4, 2022), and tc-python library to compute the driving force and the equilibrium composition as a function of the temperature and also to extract the mobility data that are necessary to run the simulations. They are all updated as a function of temperature in the course of the transformation.

TABLE 3

TABLE 3. Intrinsic properties and thermodynamics-related parameters.

3 Results and discussion

The modeling tool is applied to simulate precipitation of M₇C₃ carbides in an austenitic matrix with or without plastic deformation in multicomponent steel with the composition given in Table 1. Although the room temperature experimental microstructure consisted of carbides in a martensitic matrix (Safara et al., 2019), the matrix here is assumed to be austenitic since the quenching step is not included in this work. Nevertheless, the precipitation did take place in the austenitic matrix both experimentally and in the simulation, as the compression tests were performed above 900°C where the austenite is stable. The martensitic transformation that took place upon quenching did not affect the PSD, which was frozen in from the hot compression temperature.

3.1 Equilibrium thermodynamics results

Figure 2 presents the equilibrium property diagram of the molar fraction of phases as a function of temperature of the investigated steel as predicted by Thermo-Calc software and the TCFE12 database. At the austenitization temperature, 1,250°C, the matrix is fully austenitic and at the holding temperatures M₇C₃ is expected to precipitate. It is worth noting that although some sulfides were observed experimentally, they are not considered in this modeling work due to their low volume fraction. Table 2 gives the equilibrium volume fraction of M₇C₃ as a function of temperature. It is clear that when the kinetics is not accounted for, it is difficult to understand the obtained volume fraction that is lower than equilibrium.

FIGURE 2

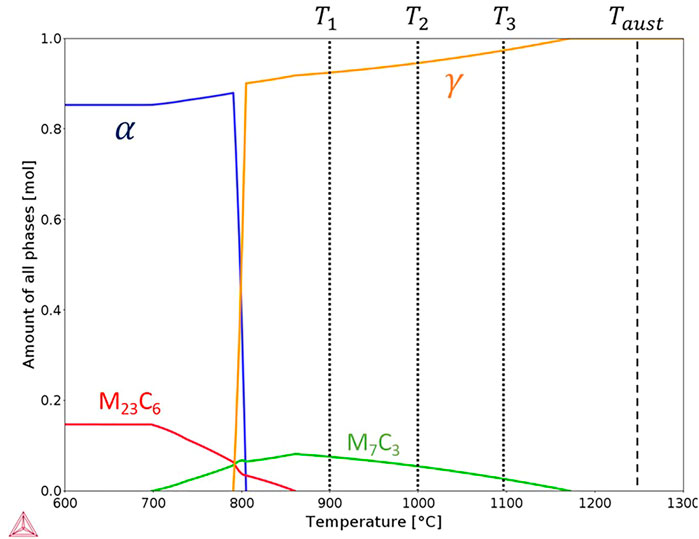
FIGURE 2. Equilibrium property diagram of Fe–C–Mn–Si–Cr computed with TCFE12. $T_{aust}$ is the austenitization temperature, and $T_i$ are the three holding temperatures.

3.2 Kinetics- and thermodynamics-based results

In order to understand the effect of deformation on the precipitation kinetics, the precipitation model presented in the previous section will be compared with a so-called classical precipitation treatment, in which nucleation takes place only in the bulk and where the dislocation density evolution is not accounted for. In the following, this model will be called “classical,” while the newly developed integrated and coupled model will be called “integrated” scheme.

In Figures 3A,B,C,D, the evolution of the M₇C₃ precipitate volume fraction, number density, mean size, and the evolution of the dislocations density, respectively, as a function of time for the three holding temperatures (900, 1,000, and 1,100°C) and for a strain rate of 10 s⁻¹ are presented. The strain rate was chosen as it was the strain rate applied in hot compression tests performed in the Gleeble thermomechanical simulator to back calculate the $f/r_m$ ratio by Safara et al. (2019). Despite that the experimental measurements were made after only 15 s of holding; we perform in this work simulation for 300 s holding in order to investigate the impact of deformation on the overall kinetics. For the treatment at 1,100°C, both the volume fraction and number density of precipitates do not appear in the graphs, since their values were too small for the used log scale.

FIGURE 3

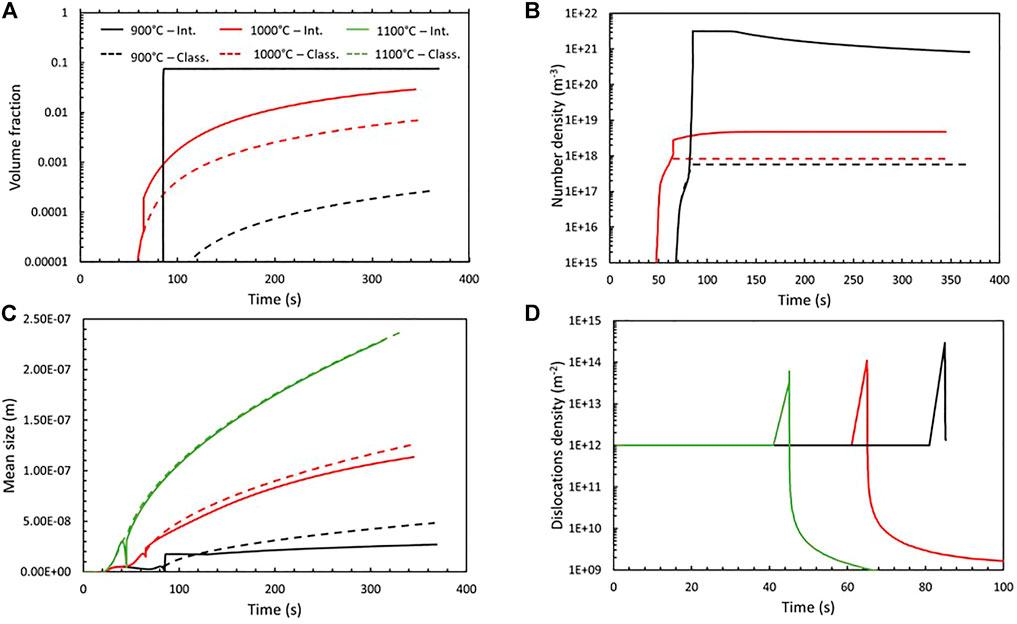
FIGURE 3. Evolution of volume fraction (A), number density (B), mean size (C) of M₇C₃ precipitates, and dislocation density (D) as a function of time for holding at 900°C (black), 1,000°C (red), and 1,100°C (green) using the integrated modeling tool (plain lines) and the classical precipitation model (dashed lines).

Deformation takes place after 45, 65, and 85 s for the holding temperatures 1,100, 1,000, and 900°C, respectively, due to different times to reach the holding temperatures upon cooling from the austenitization temperature. This explains the changes, at different times for the different holding temperatures, in the curves of the integrated scheme in Figure 3. The precipitate volume fraction, number density, and mean size (Figures 3A,B,C) for the classical implementation and the newly integrated scheme are overlapping, as they must at the beginning of the treatment before the deformation starts. Indeed, at this stage, nucleation, if happening, takes place classically. At the beginning of the simulation (from 1,250°C), there is no driving force for precipitation, and thus, there is no nucleation. When the temperature has decreased enough, nucleation starts to take place classically in the bulk, and the volume fraction, number density, and mean size start to increase. Once the stress is applied and dislocations are generated, a clear increase is observed in the volume fraction (Figure 3A) for the integrated scheme results, since nucleation increases due to the decrease in the nucleation barrier (Figure 4). At the same time, growth of the already created precipitates is enhanced by the diffusion increase due to the presence of the dislocations. The volume fraction increases to a greater extent for the lower temperature, that is, 900°C, despite the volume fraction being smaller than the one for the 1,000°C treatment right before the deformation of the material. It is worth highlighting that the compression has already stopped when the increase takes place, since at a strain rate equal to 10 s⁻¹, it only takes 0.07 s to deform the material. Nevertheless, until the dislocation density has reduced to its original value or until nucleation has stopped because the volume fraction is close to the equilibrium value, the dislocations assist nucleation and enhance diffusion. The competition between thermodynamics and kinetics can explain why at 1,000°C, the highest volume fraction is obtained right before deformation starts. At a higher temperature, diffusion is faster but the driving force for precipitation lower, compared to lower temperature, where the driving force is higher but diffusion is slower. The maximum volume fraction is thus obtained for the intermediate temperature of this study. Additionally, the lower the holding temperature, the longer the treatment time since for all tests the cooling rate is kept the same. This leads to more time for the intermediate temperature compared to the highest one for forming the first precipitates. All the curves are actually overlapping until the first deformation takes place at 45 s for the highest temperature.

FIGURE 4

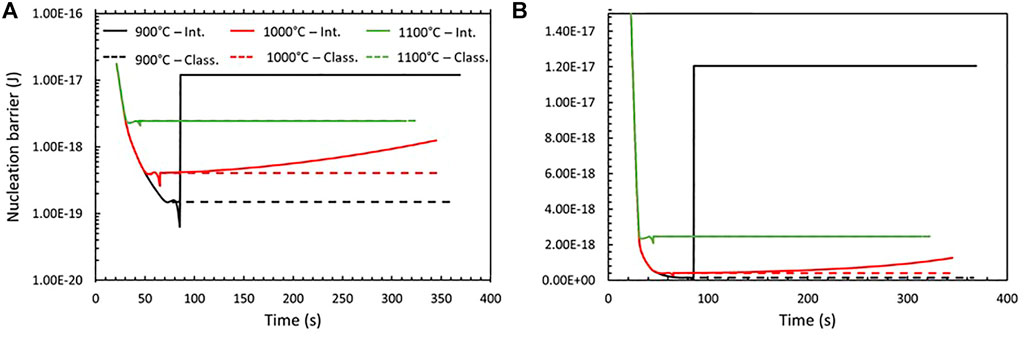
FIGURE 4. Evolution of the nucleation barrier as a function of time in log scale (A) and normal scale (B) for holding at 900°C (black), 1,000°C (red), and 1,100°C (green) using the integrated modeling tool (plain lines) and the classical precipitation model (dashed lines).

The number density of precipitates (Figure 3B) also exhibits a sharp increase right after deformation. The increase in the number density is higher for the lower temperature, 900°C, than for 1,000°C. This is due to the lower precipitate volume fraction (Figure 3A) compared to the one at 1,000°C when the deformation starts. Therefore, the matrix content at 900°C is still very close to the nominal composition, and the driving force for precipitation is, thus, very high and higher than that at 1,000°C. When nucleation becomes heterogeneous after the application of the stress, this results in a Lower heterogeneous nucleation barrier at 900°C than at 1,000°C (Figure 4) and thus in a higher nucleation rate and, therefore, in the creation of more precipitates. The number density of precipitates decreases for the treatment at 900°C after a while. This is due to coarsening. Indeed, this treatment is the only one for which the volume fraction has reached its equilibrium value. Therefore, to continue to decrease its overall energy, the material eliminates the smaller precipitates and lets the larger ones grow.

The evolution of the mean size is more exotic. This is first due to the fact that while the temperature decreases, the driving force increases and in turn the critical size decreases. It leads to the creation of smaller and smaller size classes of precipitates with time affecting the average size drastically. This decrease in the mean size is visible for the 900°C treatment. Once the holding temperature is reached, the mean size increases again since the newly created precipitates are not smaller than the average value.

The abrupt changes in the different precipitates characteristics are, of course, directly connected to the abrupt change in the dislocation density, as depicted in Figure 3D. The dislocation density for the treatment at 900°C is not presented after 90 s, but this is only due to a modeling aspect. Indeed, nucleation stops very rapidly for the 900°C treatment, since the volume fraction is rapidly approaching the equilibrium value; thus, the number density of dislocations is not computed anymore as it is not needed for calculating the growth and coarsening rates. The classical treatment of precipitation predicts final sizes that are larger than the prediction from the integrated scheme (Figure 3) for the 900 and 1,000°C. The trend as a function of temperature is the same for both schemes with lower temperatures giving rise to a smaller mean size. However, the volume fraction at the end of the treatment is larger in the integrated scheme for the lower temperature. This is not surprising in view of the thermodynamics predicting larger equilibrium volume fraction at the lower temperature and since the kinetics is enhanced with deformation. Finally, the impact of the deformation is more pronounced when the deformation takes place at an early stage of precipitation as at 900°C. Indeed, there are almost three orders of magnitude of difference in the final volume fraction obtained at 900°C between the classical treatment and the integrated scheme.

The ratio $f/r_m$ that have been back calculated by Safara et al. (2019) while calibrating their micromechanical model to flow stress measurements are 3.9 x 10⁻⁴, 2.7 x 10⁻⁴, and 5.2 x 10⁻⁵ nm⁻¹ at 900, 1,000, and 1,100°C, respectively (Table 2). It is important to note that these values give information about the ratio during deformation and not about the ratio at the end of the 300 s-long holding. Therefore, the values from the simulation using the integrated scheme to compare with are the ones obtained after 0.7 s of applied stress. They are 4.53 x 10⁻⁴, 6.58 x 10⁻⁶, and 0 nm⁻¹, respectively, (Table 2). Despite that, there is a qualitative agreement, with the highest ratio obtained for the 900°C treatment; the results do not agree quantitatively. Several reasons can be given to explain the mismatch:

1) First, as highlighted in the introduction, the back calculations performed by Safara et al. consider a constant value of the volume fraction of precipitates and the mean size during the overall deformation, which is not what the integrated scheme does.

2) Second, if the ratio is extracted from the simulations one second after the stress application is stopped, it becomes 4.2 x 10⁻³, 8.8 x 10⁻⁶, and 0 nm⁻¹ at 900, 1,000, and 1,100°C, respectively. This highlights the fast changes taking place in the microstructure and the potential uncertainty regarding the perfect timing for comparing experiments and simulations. Again, the highest ratio is obtained for the 900°C treatment.

3) The quantitative mismatch could also be affected by the high uncertainty of the interfacial energy used. Indeed, when using a value of the interfacial energy equal to 0.14 J m⁻², the ratio becomes 3.92 x 10⁻³, 1.38 x 10⁻³, and 0 nm⁻¹ for 900, 1,000, and 1,100°C, respectively.

4) Moreover, precipitation on subgrains and grain boundaries has not been taken into account in this study, which can affect the obtained quantities.

5) In addition, the micromechanical model also took recrystallization and recovery into account, which is not done here.

6) Finally, sulfides were observed experimentally, which could have acted as precursors for the carbides and, thus, enhanced the precipitation.

The volume fractions that have been back calculated from Safara et al. in their second work (Safara et al., 2020) while calibrating their hardness equation to their experimental measurements are 1.3%, 1.6%, and 0.3% at 900, 1,000, and 1,100°C, respectively. These values were obtained without any plastic deformation, but they were determined using the ratio $f/r_m$ obtained with plastic deformation. Safara et al. used these values as they assumed that deformation was too short to affect the precipitation kinetics. The integrated scheme predicts 0.0001%, 0.004%, and 0% right before deformation and 0.23%, 0.012%, and 0% right after deformation for 900, 1,000, and 1,100°C, respectively, when the interfacial energy is equal to 0.16 J m⁻². The values show that it is maybe too strong to assume that deformation cannot affect the PSD because of the short stress application time. Finally, when using an interfacial energy equal to 0.14 J m⁻², the obtained volume fractions at the end of the deformation are ∼2.1%, 4.1%, and 0%. The latter are in better agreement with the experimental back-calculated values, but the corresponding ratio $f/r_m$ obtained with this interfacial energy and that are given previously is too high. It is important to highlight that in that case, the deformation does not affect the precipitation kinetics integrated scheme results much when compared to the classical treatment results. This is because with such a value of the interfacial energy, the onset of precipitation is very rapid with or without dislocations. It shows that deformation would affect the precipitation kinetics more when the interfacial energy is larger, and thus, when it is more difficult to nucleate in the classical fashion.

The carbides are also supposed to be larger at higher holding temperatures according to Safara’s calculations after 15 s. This is also obtained with both the classical and integrated scheme, see Table 2 and Figure 3. In general, the predictions from the integrated scheme are giving larger precipitates with a lower volume fraction compared to the back-calculation from experiments.

In Figure 4, the evolution of the nucleation barrier as a function of time for the three holding temperatures using the new integrated scheme and the classical implementation is displayed. The curves are all overlapping at the beginning of the kinetics because they all follow the same temperature profile. They are decreasing with time because the lower the temperature, the higher the driving force as illustrated in the equilibrium property diagram (Figure 2). The highest holding temperature stops decreasing earliest and at the highest value of the nucleation barrier for the same reason. Once the stress is applied, the nucleation barrier drops for all treatments since the nucleation is favored as it eliminates part of the dislocations (Eq. 9). Therefore, despite that the number of nucleation sites for heterogenous precipitation on dislocations is significantly lower than the available bulk sites, it becomes much more favorable to nucleate on dislocations because it is thermodynamically easier. However, because of the high strain rate used in these tests (10 s⁻¹), the deformation time is very small and the nucleation barrier goes back to a higher value very rapidly. It is interesting to note that for 900°C, for which it has been shown (Figure 3) that the volume fraction of precipitates right after the deformation is the largest one, the nucleation barrier goes back to a further away value, that is, to a very high nucleation barrier, relative to its initial value before deformation, compared to the result at 1,000°C. This is of course because the supersaturation in the matrix has been more affected during the deformation and the elimination of the dislocations at 900°C. The nucleation barrier value for the 900°C treatment, in addition, reaches a constant value after deformation. This is because the concentration in the matrix has reached its equilibrium value and the material is undergoing coarsening during which the driving force is almost not evolving anymore, as is the nucleation barrier. For the 1,000°C treatment, the behavior is different with a nucleation barrier continuously increasing after the deformation. This is due to the evolution of the material toward the thermodynamic equilibrium. Finally for the 1,100°C treatment, the nucleation barrier is also constant after deformation, and this time, it is because the driving force is also constant since nothing is precipitating into the material. The difference in the nucleation barrier between the classical precipitation modeling tool and the integrated scheme is not negligible and impacts the continuation of the transformation, as shown in Figure 3. Indeed, the critical step during precipitation is usually nucleation and the help given by deformation, even though very short, allows to activate many nucleation sites becoming precipitates that will continue to grow during the rest of the thermal treatment. In addition, one can easily expect that the longer the deformation time, the more significant the impact.

Figure 5 presents the same type of results as the one presented in Figure 3, that is, volume fraction, number density and mean size of the precipitates, and dislocation density as a function of time for the holding temperature 1,000°C, but comparing two different strain rates, $d\epsilon /dt=$ 1 s⁻¹ and 10 s⁻¹. The deformation time is then extended to 0.7 s, and the overall precipitation kinetics is affected from 65 s, the time at which the deformation starts. With this longer deformation time, the volume fraction (Figure 5A) is increasing even faster. The maximum number density of dislocations generated is slightly higher for the largest strain rate, 10s⁻¹; despite that, the deformation time is 10 times shorter. In addition, while dislocations are generated, they are also eliminated, see Eq. 12. Yet, this higher number of dislocations is not positively correlated with the number density of precipitates as shown in Figure 5B. Indeed, for a lower strain rate, the maximum value of the number density of precipitates is higher than for the larger strain rate because the number density of dislocations stays higher for a longer time. The precipitates have had more time to nucleate and thus to be stabilized in view of the critical size for coarsening. Finally, Figure 5C shows that the precipitates are slightly bigger at the end of the treatment for the lower strain rate. This can be explained by a lower nucleation barrier after deformation for the lower strain rate, since the volume fraction of precipitates already reached its equilibrium value and thus, a larger value than for the larger strain rate.

FIGURE 5

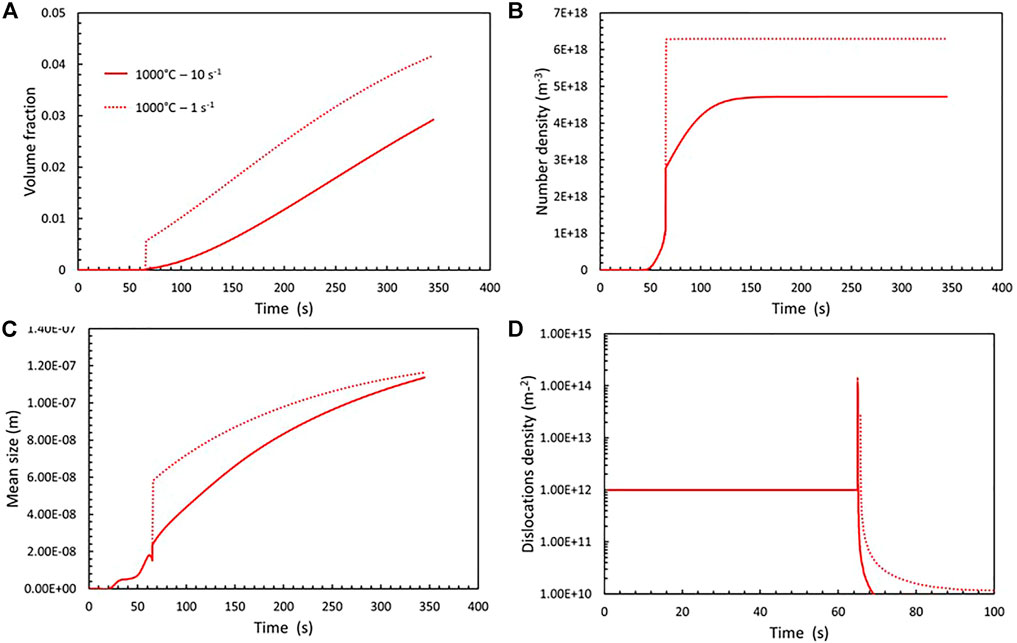
FIGURE 5. Evolution of volume fraction (A), number density (B), mean size (C) of M₇C₃ precipitates, and dislocation density (D) as a function time for two different strain rates: 10s⁻¹ (red curve) and 1s⁻¹ (dotted red curve) for a holding at 1,000°C.

3.3 Perspectives

This new integrated modeling tool allows to account for the dislocation density evolution as a function of time and shows a great impact on the overall kinetics of the generation of precipitates. However, it is well-known that nucleation can also occur at grain and subgrain boundaries (Militzer et al., 1994; Trillo and Murr, 1998), and it, thus, impacts the recrystallization process essentially through the pinning effect and that the precipitates can delay the onset of recrystallization (Robson, 2020). In Al alloys, the coupling between precipitation kinetics and plasticity has been intensively investigated (Deschamps et al., 2012; Genevois et al., 2006; Hutchinson et al., 2014). It has for instance been shown that precipitation can be initiated even at room temperature under cyclic loading; regardless of whether a heat treatment is applied during or after deformation, an effect on the precipitation kinetics can be observed especially for temperatures lower than 300°C. At higher temperatures, the morphology of the precipitate can be modified during the plastic deformation.

It is also well-known from experimental observations that larger precipitates than the ones observed in the matrix usually are obtained both at subgrains and grain boundaries (Kwon and DeArdo, 1991; Wang et al., 2018). However, in this work, we do not consider rearrangement of the subgrains taking place during recrystallization and recovery. The coupling with a model describing grain growth during these transformations would be very beneficial even for the micromechanical model as the pinning effect of precipitates on subgrains and grain boundaries is well-known to impede grain growth. It is also known that elastic stresses around a nucleus can affect the nucleation barrier (Bonvalet et al., 2019), which is not yet accounted for. Nevertheless, it is important to highlight that the subgrains formed during recovery and recrystallization are created due to a rearrangement of the dislocations, and the dislocations are already included in this work. From that perspective, precipitation on subgrain boundaries might not be that different as considered in this work. However, considering the fact that the precipitation is homogenous, there is no effect of the specific location within the material. The kinetic difference between nucleation where recovery is already going on or where the density of dislocations is still high is not accounted for. Even if, to the opinion of the authors, the impact on precipitation kinetics compared to classical bulk precipitation, especially its increasing rate, would still exist, the magnitude of this impact might be different from what is presented in this work. In any case, this study demonstrated the importance of accounting for the microstructural changes generated by a deformation in order to understand the precipitation.

The simulations were performed with two different values of the interfacial energy in order to highlight its strong impact on the proposed modeling tool. The high impact is not surprising as the nucleation barrier is proportional to the interfacial energy to the power of three. In addition, the critical size for nucleation and coarsening is also proportional to the interfacial energy. Therefore, all stages of the precipitation are affected by the interfacial energy, which is difficult to estimate properly. In theory, it is a function of the composition on both sides of the interface, temperature, and crystallographic structures. Density functional theory (Lu et al., 2013) can help to calculate the value, but it is computationally expensive to obtain values as a function of temperature, composition, and phases. Broken bounds models (Sonderegger and Kozeschnik, 2009) have also been developed and implemented in mean-field approaches to capture the dependency of the interfacial energy on temperature, composition, and present phases with input from thermodynamic databases. However, large uncertainties still exist because of the simplicity of the approach. It would be extremely valuable for the community if more generic and systematic tools would exist. In the meantime, models such as the one proposed in this study can be adjusted to experimental data in order to extract a valuable function for the interfacial energy, using so-called reverse modeling.

This integrated modeling tool could also be applied to more complex thermomechanical treatments with several deformation cycles, mimicking an industrial process and could be compared to experimental investigations. Nevertheless, in that case, it would also be interesting to treat the precipitation locally. Indeed, the distribution of both stress and heat can be inhomogeneous for larger steel parts affecting the overall precipitation kinetics. LSKW approaches have in the past been coupled with one-dimensional finite elements schemes to account for this non-homogeneous matrix phase (Bardel et al., 2016; Roussel et al., 2018). The same approach could be applied to deformed parts.

Finally, coupling this type of modeling tool with other phase transformation tools such as the austenitic transformation to ferrite or martensite during cooling would allow capturing the initiation and evolution of the microstructural changes of a complete thermomechanical treatment.

4 Conclusion

The use of LSKW approaches that naturally account for nucleation and are easily coupled with thermodynamic and kinetic databases is very relevant for developing modeling tools, accelerating the development of new materials. Nevertheless, these tools may suffer from their simple assumptions for some specific complex thermomechanical treatment. In this work, we propose an expansion of the usage of such a mean-field tool by combining it with physically based models simulating deformation.

The results of the modeling tool presented here highlight a complex interplay between the dislocations acting as nucleation sites and the evolution of precipitates. It is shown that the effect of deformation, even for a stress applied very shortly, is affecting the following transformation, through the transient reduction of the nucleation barrier. In addition, this effect is more important at very early stages of the precipitation when the microstructure is mostly still homogeneous. Indeed, in that case, the high driving force, combined with a reduced incubation time due to the enhanced diffusion and the reduction of the nucleation barrier, allows many small particles to nucleate in the material. The impact of deformation will, therefore, be strongly connected to the interfacial energy of the precipitates. Indeed, a low interfacial energy leads to easier nucleation in the classical fashion; therefore, the decrease of the nucleation barrier with the presence of dislocations is not more favorable.

The effect of the used strain rate is also shown to be very large. Deformation affects the precipitation kinetics, but to a larger or lesser extent depending on the used strain rate even for the same final strain. The obtained microstructures are in turn also very different. It therefore seems complicated without an appropriate integrated modeling tool, such as the one developed in this work, to correctly predict the particle size distribution at the end of a treatment, the microstructure, and thus the final properties.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

MR developed and implemented the modeling tool. MR and AB wrote together the article and analyzed the results of the modeling tool.

Funding

This work was performed in the FinBeam project, within the strategic innovation program Metallic Materials (Diarienummer 2018-02380), a joint initiative by Vinnova Formas and the Swedish Energy Agency.

Acknowledgments

The authors would like to acknowledge Göran Engberg, Dalarna Universitet, for the valuable discussion and explanation regarding his physically based micromechanical model.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Andersson, J.-O., Helander, T., Höglund, L., Shi, P., and Sundman, B. (2002). Thermo-Calc & DICTRA, computational tools for materials science. Calphad 26, 273–312. doi:10.1016/S0364-5916(02)00037-8

CrossRef Full Text | Google Scholar

Bardel, D., Fontaine, M., Chaise, T., Perez, M., Nelias, D., Bourlier, F., et al. (2016). Integrated modelling of a 6061-T6 weld joint: From microstructure to mechanical properties. Acta Mat. 117, 81–90. doi:10.1016/j.actamat.2016.06.017

CrossRef Full Text | Google Scholar

Bonvalet, M., Philippe, T., Sauvage, X., and Blavette, D. (2015). Modeling of precipitation kinetics in multicomponent systems: Application to model superalloys. Acta Mat. 100, 169–177. doi:10.1016/j.actamat.2015.08.041

CrossRef Full Text | Google Scholar

Bonvalet, M., Sauvage, X., and Blavette, D. (2019). Intragranular nucleation of tetrahedral precipitates and discontinuous precipitation in Cu-5wt%Ag. Acta Mat. 164, 454–463. doi:10.1016/j.actamat.2018.10.055

CrossRef Full Text | Google Scholar

Clouet, E., Barbu, A., Laé, L., and Martin, G. (2005). Precipitation kinetics of AlZr and AlSc in aluminum alloys modeled with cluster dynamics. Acta Mat. 53, 2313–2325. doi:10.1016/j.actamat.2005.01.038

CrossRef Full Text | Google Scholar

Deschamps, A., Fribourg, G., Bréchet, Y., Chemin, J. L., and Hutchinson, C. R. (2012). In situ evaluation of dynamic precipitation during plastic straining of an Al–Zn–Mg–Cu alloy. Acta Mat. 60, 1905–1916. doi:10.1016/j.actamat.2012.01.002

CrossRef Full Text | Google Scholar

Dutta, B., Palmiere, E. J., and Sellars, C. M. (2001). Modelling the kinetics of strain induced precipitation in Nb microalloyed steels. Acta Mat. 49, 785–794. doi:10.1016/S1359-6454(00)00389-X

CrossRef Full Text | Google Scholar

Engberg, G., and Lissel, L. (2008). A physically based microstructure model for predicting the microstructural evolution of a C-Mn steel during and after hot deformation. Steel Res. Int. 79, 47–58. doi:10.1002/srin.200806315

CrossRef Full Text | Google Scholar

Farahat, A. I. Z., El-Bitar, T., and El-Shenawy, E. (2008). Austenitic stainless steel bearing Nb compositional and plastic deformation effects. Mater. Sci. Eng. A 492, 161–167. doi:10.1016/j.msea.2008.04.027

CrossRef Full Text | Google Scholar

Genevois, C., Fabrègue, D., Deschamps, A., and Poole, W. J. (2006). On the coupling between precipitation and plastic deformation in relation with friction stir welding of AA2024 T3 aluminium alloy. Mater. Sci. Eng. A 441, 39–48. doi:10.1016/j.msea.2006.07.151

CrossRef Full Text | Google Scholar

Golubov, S. I., Osetsky, Yu.N., Serra, A., and Barashev, A. V. (1995). The evolution of copper precipitates in binary FeCu alloys during ageing and irradiation. J. Nucl. Mater. 226, 252–255. doi:10.1016/0022-3115(95)00088-7

CrossRef Full Text | Google Scholar

Hirth, J. P., Lothe, J., and Mura, T. (1983). Theory of dislocations (2nd ed.). J. Appl. Mech. 50, 476–477. doi:10.1115/1.3167075

CrossRef Full Text | Google Scholar

Hutchinson, C. R., de Geuser, F., Chen, Y., and Deschamps, A. (2014). Quantitative measurements of dynamic precipitation during fatigue of an Al–Zn–Mg–(Cu) alloy using small-angle X-ray scattering. Acta Mat. 74, 96–109. doi:10.1016/j.actamat.2014.04.027

CrossRef Full Text | Google Scholar

Kozeschnik, E. (2008). Thermodynamic prediction of the equilibrium chemical composition of critical nuclei: Bcc Cu precipitation in α-Fe. Scr. Mat. 59, 1018–1021. doi:10.1016/j.scriptamat.2008.07.008

CrossRef Full Text | Google Scholar

Kwon, O., and DeArdo, A. J. (1991). Interactions between recrystallization and precipitation in hot-deformed microalloyed steels. Acta Metallurgica Materialia 39, 529–538. doi:10.1016/0956-7151(91)90121-G

CrossRef Full Text | Google Scholar

Langer, J. S., and Schwartz, A. J. (1980). Kinetics of nucleation in near-critical fluids. Phys. Rev. A 21, 948–958. doi:10.1103/PhysRevA.21.948

CrossRef Full Text | Google Scholar

Lu, S., Hu, Q.-M., Punkkinen, M. P. J., Johansson, B., and Vitos, L. (2013). First-principles study of fcc-Ag/bcc-Fe interfaces. Phys. Rev. B 87, 224104. doi:10.1103/PhysRevB.87.224104

CrossRef Full Text | Google Scholar

Macchi, J., Gaudez, S., Geandier, G., Teixeira, J., Denis, S., Bonnet, F., et al. (2021). Dislocation densities in a low-carbon steel during martensite transformation determined by in situ high energy X-Ray diffraction. Mater. Sci. Eng. A 800, 140249. doi:10.1016/j.msea.2020.140249

CrossRef Full Text | Google Scholar

Militzer, M., Sun, W. P., and Jonas, J. J. (1994). Modelling the effect of deformation-induced vacancies on segregation and precipitation. Acta Metallurgica Materialia 42, 133–141. doi:10.1016/0956-7151(94)90056-6

CrossRef Full Text | Google Scholar

MOBFE4 (2022). Thermo-calc software MOBFE4 (01-04-2022.

Google Scholar

Olson, G. B. (1997). Computational design of hierarchically structured materials. Science 277, 1237–1242. doi:10.1126/science.277.5330.1237

CrossRef Full Text | Google Scholar

Perez, M., Dumont, M., and Acevedo-Reyes, D. (2008). Implementation of classical nucleation and growth theories for precipitation. Acta Mat. 56, 2119–2132. doi:10.1016/j.actamat.2007.12.050

CrossRef Full Text | Google Scholar

Philippe, T., and Blavette, D. (2011). Nucleation pathway in coherent precipitation. Philos. Mag. 91, 4606–4622. doi:10.1080/14786435.2011.616548

CrossRef Full Text | Google Scholar

Philippe, T., and Voorhees, P. W. (2013). Ostwald ripening in multicomponent alloys. Acta Mat. 61, 4237–4244. doi:10.1016/j.actamat.2013.03.049

CrossRef Full Text | Google Scholar

Robson, J. D. (2020). Deformation enhanced diffusion in aluminium alloys. Metall. Mat. Trans. A 51, 5401–5413. doi:10.1007/s11661-020-05960-5

CrossRef Full Text | Google Scholar

Roussel, M., Sauvage, X., Perez, M., Magné, D., Hauet, A., Steckmeyer, A., et al. (2018). Influence of solidification induced composition gradients on carbide precipitation in FeNiCr heat resistant steels. Materialia 4, 331–339. doi:10.1016/j.mtla.2018.10.010

CrossRef Full Text | Google Scholar

Safara, N., Engberg, G., and Ågren, J. (2019). Modeling microstructure evolution in a martensitic stainless steel subjected to hot working using a physically based model. Metall. Mat. Trans. A 50, 1480–1488. doi:10.1007/s11661-018-5073-6

CrossRef Full Text | Google Scholar

Safara, N., Golpayegani, A., Engberg, G., and Ågren, J. (2020). Study of the mean size and fraction of the second-phase particles in a 13% chromium steel at high temperature. Philos. Mag. 100, 217–233. doi:10.1080/14786435.2019.1674455

CrossRef Full Text | Google Scholar

Safara Nosar, N. (2021). Modeling the microstructure evolution during and after hot working in martensitic steel.

Google Scholar

Sonderegger, B., and Kozeschnik, E. (2009). Generalized nearest-neighbor broken-bond analysis of randomly oriented coherent interfaces in multicomponent fcc and bcc structures. Metall. Mat. Trans. A 40, 499–510. doi:10.1007/s11661-008-9752-6

CrossRef Full Text | Google Scholar

Steinbach, I. (2009). Phase-field models in materials science. Model. Simul. Mat. Sci. Eng. 17, 073001. doi:10.1088/0965-0393/17/7/073001

CrossRef Full Text | Google Scholar

Svoboda, J., Fischer, F. D., Fratzl, P., and Kozeschnik, E. (2004). Modelling of kinetics in multi-component multi-phase systems with spherical precipitates: I: Theory. Mater. Sci. Eng. A 385, 166–174. doi:10.1016/j.msea.2004.06.018

CrossRef Full Text | Google Scholar

TCFE12 (2022). Thermo-calc software TCFE12. accessed 01-04-2022).

Google Scholar

Thermo-Calc (2022). The precipitation module (TC-PRISMA) user guide 2022a.

Google Scholar

Trillo, E. A., and Murr, L. E. (1998). Effects of carbon content, deformation, and interfacial energetics on carbide precipitation and corrosion sensitization in 304 stainless steel. Acta Mat. 47, 235–245. doi:10.1016/S1359-6454(98)00322-X

CrossRef Full Text | Google Scholar

Wagner, R., Kampmann, R., and Voorhees, P. W. (2001). Phase transformations in materials. Mat. Sci. Technol. 5, 213. doi:10.1002/352760264X

CrossRef Full Text | Google Scholar

Wang, J., Hodgson, P. D., Bikmukhametov, I., Miller, M. K., and Timokhina, I. (2018). Effects of hot-deformation on grain boundary precipitation and segregation in Ti-Mo microalloyed steels. Mat. Des. 141, 48–56. doi:10.1016/j.matdes.2017.12.023

CrossRef Full Text | Google Scholar

Yoshie, A., Fujita, T., Fujioka, M., Okamoto, K., and Morikawa, H. (1996). Formulation of the decrease in dislocation density of deformed austenite due to static recovery and recrystallization. ISIJ Int. 36, 474–480. doi:10.2355/isijinternational.36.474

CrossRef Full Text | Google Scholar

Zhou, Y., Liu, Y., Zhou, X., Liu, C., Yu, L., Li, C., et al. (2015). Processing maps and microstructural evolution of the type 347H austenitic heat-resistant stainless steel. J. Mat. Res. 30, 2090–2100. doi:10.1557/jmr.2015.168

CrossRef Full Text | Google Scholar