First-Principles Study of Metal Impurities in Silicon Carbide: Structural, Magnetic, and Electronic Properties

The configurations of 10 types of metal-doped silicon carbide (SiC) systems were investigated by the first-principles calculations. The dopants include eight types of 3d-series transition metal atoms, one semi-metal Ge atom, and one other metal Al atom. For all the metal-doped SiC systems, the steadiest doping sites are fixed at the substituted Si site, while the Ti-SiC system exhibits the most potent binding activity. The properties of these new systems vary with the doping atoms. The SiC- and Al-SiC systems convert to magnetic metals. The Ti- and Ge-SiC systems remain non-magnetic semiconductors, while the V-, Cr-, Mn-, Fe-, Co-, and Zn-SiC systems turn into magnetic semiconductors with magnetic moments related to the valence electron number of dopants. Partial charge transfers from the metal atoms to the adjacent C atoms accompanied the change in the electron-emitting capacity of the new systems. The work function achieves the minimum of 3.439 eV in the Co-SiC system, just 71.6% of the original SiC system. Our analysis indicates that the potent binding energy of the Ti-SiC system is due to the complete bonding states between the transition metal Ti and the adjacent C atoms. The magnetism evolution in semiconducting metal-doped SiC is attributed to the occupation mode of the hybridization orbitals nearby the Fermi level, which are determined by the coupling of the 3d orbital of transition metal atoms and the defect states of the vacancy atoms. The adjustable magnetic and electronic properties of the metal-doped SiC systems provide a flexible method in designing more suitable SiC-based spintronics and field electron-emitting devices.

Introduction

Two-dimensional silicon carbide (2D SiC) has become the hot spot (Mélinon et al., 2007; Castelletto et al., 2014) of 2D materials (Li and Kaner, 2008; Luo et al., 2021; Cui et al., 2022) for the virtues, such as the high thermal capacity (Hsueh et al., 2011; Chowdhury et al., 2017) and the graphene-like planar structure (Eddy and Gaskill, 2009; Susi et al., 2017; Ferdous et al., 2019). The high thermal capability makes 2D SiC competent not only as high-power electronic and optoelectronic devices (Zhang and Cui, 2022a) but also in high-temperature circumstances and quantum information processing (Chabi and Kadel, 2020). The two-dimensional structure induces unique optical and electronic properties which are essential in optoelectronics (Stankovich et al., 2006; Bratschitsch, 2014; Sun et al., 2017a; Cui et al., 2021a; Sun et al., 2021), catalysis (Komsa et al., 2012; Ziletti et al., 2015), spintronic devices (Wang et al., 2018; Li et al., 2021), energy conversion (Pospischil et al., 2014; Cui et al., 2020a; Sun et al., 2020; Sun and Schwingenschlögl, 2020), and gas sensing (Lin et al., 2013; Kooti et al., 2019; Cui et al., 2020b). The success in the wet exfoliation of 2D SiC accelerates the further investigation of the SiC-based system (Chabi et al., 2021).

The previous studies on other 2D materials and dopants provide many predictive references (He et al., 2010; Tang et al., 2018; Cui et al., 2020b; Cui et al., 2021b). In non-metal doped SiC (NM-SiC), the sp² hybridization orbitals of NM atoms form more robust coupling interactions, inducing the magnetism of the systems (Bekaroglu et al., 2010). When the transition metal (TM) atom is doped in 2D material, the occupation mode of d hybridization orbitals of TM atoms determines the magnetism of the systems (Santos et al., 2010; He et al., 2014a; He et al., 2014b; Sun et al., 2017b; Yuan et al., 2020; Cui et al., 2021c). All these results indicate that the electronic and magnetic properties of 2D-SiC can be adjusted by the doping of atoms effectively. Although SiC systems have been studied while doping some TM and NM atoms, the discussion on the law of universality is relatively few, especially the effects of the valence electron number of the dopant on magnetism are seldom discussed (Luo et al., 2017; Luo and Shen, 2018; Wu et al., 2019). In this work, the configurations of 10 types of the metal-doped SiC systems were investigated. The doping atoms include not only eight 3d-series TM atoms but also one semi-metal atom and one other metal atom. The electronic and magnetic performances were investigated at the most stable structures systematically. The high stability in Ti-SiC was explained by the complete bonding states between the Ti atom and the neighboring C atoms because of the same valence electron number with the substituted Si atom. The magnetism evolution in transition metal-doped SiC was attributed to the occupation mode of hybridization orbitals nearby the Fermi level.

Computational Details

The first-principles theory calculations are based on the density functional theory and executed by the Vienna Ab initio simulation package (VASP) (Kresse and Furthmüller, 1996) and Perdew–Burke–Ernzerhof functions (PBE) (Perdew et al., 1996; Kresse and Joubert, 1999). Projector-augmented wave (PAW) schemes (Kresse and Joubert, 1999) are employed in the electron–ion interaction. To expand the Kohn–Sham orbitals, the cut-off energy for plane-waves basis is set to 550 eV. To minimize the interaction between the metal atoms, a 4 × 4×1 supercell with one vacancy atom is selected, corresponding to a 3.125% doping concentration. To eliminate the molecular interactions between layers, a vacuum layer of 15 Å height was constructed along the normal direction of the SiC plane. The first Brillouin zone was structured with a 3 × 3 × 1 k-point grid (Grimme et al., 2010). The final stable system is achieved until all the particles experience enough relaxation, the Hellmann–Feynman force on each atom is less than 0.01 eV/Å, and the total energy change is lower than 10^–5 eV/atom. The magnetic and electronic properties of the metal-doped SiC systems are explored in their steadiest configurations.

Results and Discussion

Our calculation shows that the pristine SiC exhibits a two-dimensional planar structure with a lattice parameter of 3.10 Å, as depicted in Figure 1. The 2D SiC system is a direct band semiconductor with a band gap 2.5 eV, whose band edge of the conduction band and the valence band are both located at the K point. These calculation results are similar to those of the other groups (Luo et al., 2017; Chabi et al., 2021), which demonstrates the correctness of our method.

FIGURE 1

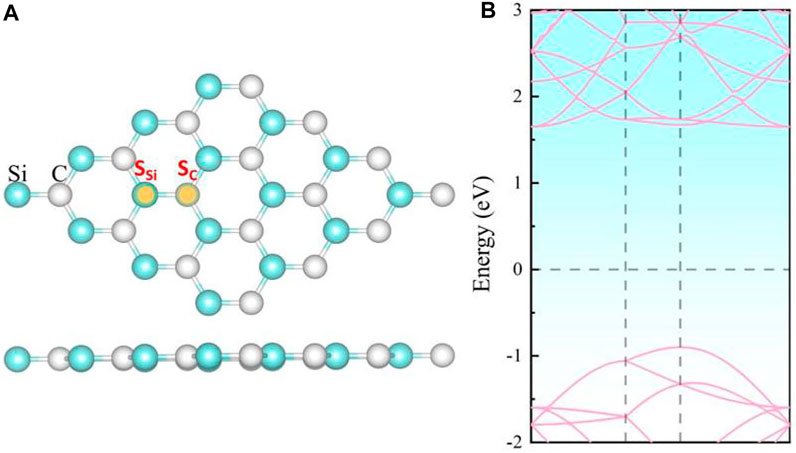
FIGURE 1. (A) Top and side views of the crystal structure and (B) the energy band structure of intrinsic 2D SiC.

The practical application of 2D materials is based on the structural stability, which is evaluated by the binding energy of the new system:

$E_{\text{b}}=E_{\text{metal}+\text{ SiC}}-\left(E_{\text{SiC}}+E_{\text{metal}}\right),(1)$

where E_b represents the binding energy of the metal-doped SiC system. E_metal+SiC, E_SiC, and E_metal denote the energies of the final metal-doped SiC, the original SiC with one vacancy, and the doping atom. Negative binding energy indicates that the metal-doped SiC system is more stable than the original SiC system with one vacancy. The most possible configuration corresponds to the structure with the largest binding energy.

In our work, the doping atoms include not only the eight 3d-series transition metal atoms but also one semi-metal Ge, and one other metal Al atom. The binding energies for metal-doped SiC system are investigated at the two possible symmetry sites, the Si-substituted site S_Si and the C-substituted site S_C, as depicted in Figure 1A. Our calculation shows that all the doping atoms exhibit more powerful bindings when doped at the site S_Si, and the systems with the maximum of binding energies are listed in Table 1. All these systems exhibit binding energies larger than 4.9 eV, indicating that these substitutional doping atoms are very favorable in thermodynamics for the original system with the vacancy atom. The semi-metal Ge and other metal Al atoms present weaker bindings with the SiC systems than the TM atoms do. The binding energy achieves the maximum of 18.625 eV in the Ti-SiC system, presenting a monotonous decrease with the increase in the atomic number from the 3d-series TM atom Ti to Co. The most robust binding in the Ti-SiC system is because the Ti atom substitutes the Si atom with the same number of valence electrons and reconstructs the complete bonding states with the adjacent C atoms. Potent coupling forms between the 3d hybridization orbital of Ti atoms and the neighboring defect states of C atoms. As the electron number of the dopant increases, the energy of the TM-SiC system decreases, and the coupling degree of the hybridization orbitals nearby the Fermi energy level reduces, diminishing the binding energy of the corresponding system, which agrees with the results in 4d TM atom-doped graphene (Santos et al., 2010). The larger binding energy of 12.411 eV in Ge-SiC is also attributed to the complete metal-carbon bonding states, while the less binding energy relative to Ti-SiC is due to the lower orbital hybridization degree in Ge-SiC.

TABLE 1

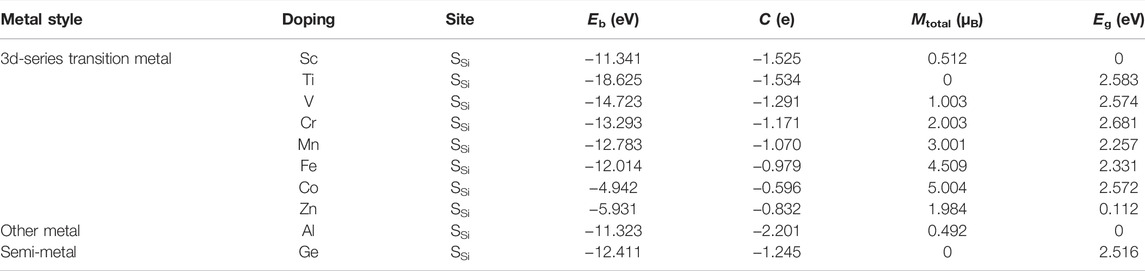
TABLE 1. Doping site, binding energy (E_b), charge transfer (C), magnetic moment (M_total), and bandgap (E_g) of the metal-doped SiC systems.

Figure 2 illustrates the energy band structures of the 10 metal-doped SiC systems. All these energy band structures are similar to those of the original SiC system, with several impurity energy levels appearing in the forbidden band. In the Al- and Sc-SiC systems, the spin-up and spin-down components of the SiC energy levels intersect with the Fermi level, and the corresponding Al- and Sc-SiC systems turn into the magnetic metals. Considering the energy levels intersected by the Fermi level are the hybridization result of the impurity levels and the vacancy states of C atoms, the Cr-, Fe- and Co-SiC systems remain the properties of semiconductors. The corresponding bandgaps are calibrated by the nearest electronic states above and below those impurity energy levels. The metal-doped SiC system exhibit an adjustable band gap: 2.583 eV (Ti), 2.574 eV (V), 2.681 eV (Cr), 2.257 eV (Mn), 2.331 eV (Fe), 2.572 eV (Co), 0.112 eV (Zn), and 2.516 eV (Ge), respectively. Among them, the Ge- and Ti-SiC systems are still non-magnetization for the consistency of the spin-up and the spin-down components of energy levels, while the other 3d-series transition metal-doped SiC systems exhibit the behaviors of magnetic semiconductors for the asymmetry in the spin-up and the spin-down components of energy levels, as shown in the V-, Cr-, Mn-, Fe-, Co-, and Zn-SiC systems.

FIGURE 2

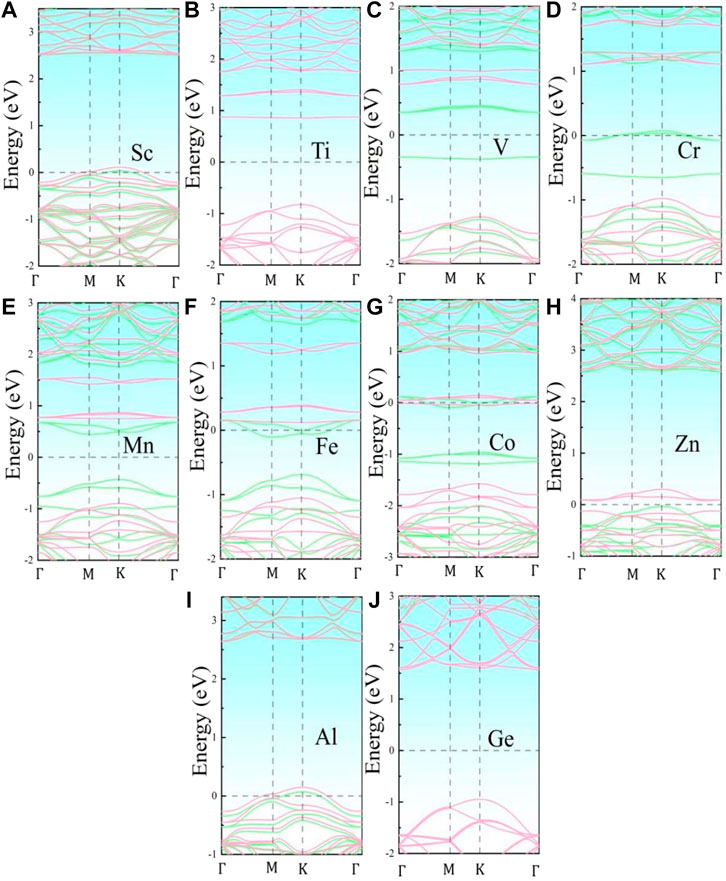
FIGURE 2. Band structures of the metal-doped SiC systems: (A) Sc-SiC, (B) Ti-SiC, (C) V-SiC, (D) Cr-SiC, (E) Mn-SiC, (F) Fe-SiC, (G) Co-SiC, (H) Zn-SiC, (I) Al-SiC, and (J) Ge-SiC. The green and the pink lines represent the spin-up and the spin-down component of the energy levels, respectively. The Fermi level is shifted to zero.

To estimate the magnetism of TM-SiC roughly, a hybridization orbital model of E.J.G. Santos (Santos et al., 2010; Sun et al., 2017b) was employed based on the energy band structure. Considering that the energy of 4s orbitals of metal atoms is much higher than the Fermi level, the contribution of 4s orbitals is neglected. When the 3d-series transition metal is doped in SiC, the 3d orbitals of TM atoms split into one A and two twofold-degenerate E levels, while the p orbitals of the vacancy C atom split and form two A and one twofold-degenerate E levels. Magnetic coupling occurs between the electron states of 3d TM atoms and the localized defect states of the C atom. Based on A or E irreducible representations, the coupling just occurs under the same irreducible representation. The corresponding band structures of TM-SiC are schemed in Figure 3, where the energy values are calibrated by the first-principles calculations and orbital theory. It can be seen that the energy of systems decreases with the valence electron number, accompanying the change in the energy variation between energy levels. Electrons occupy the energy levels from low-energy to high-energy gradually, while the hybridization orbitals are filled based on the Hund’s rule. When Ti atom is injected, the four valence electrons of the Ti atom form complete bonding states with the defect states of the C atoms, and the corresponding Ti-SiC exhibits no magnetism. With the increase in the valence electron number along the 3d Ti atom to Co atom, the electrons of TM atoms fill the hybridization orbital with the same spinned direction, and the magnetism moments increase with the valence electron number. When all the hybridization orbitals are occupied with the same spin-polarized charge, the system presents the largest magnetism, as depicted in Co-SiC. With the further increase in the valence electron number, the remaining electrons start to fill these hybridization orbitals with an opposite spinned direction, and the magnetism of system decreases, as shown in the Zn-SiC system. The occupation mode of the hybridization orbitals nearby the Fermi level determines the magnetism of the TM-SiC system. Based on this simple principle, the magnetism moments of the transition metal-doped SiC can be acquired roughly, about 0 μ_B (Ti), 1 μ_B (V), 2 μ_B (Cr), 3 μB (Mn), 4 μ_B (Fe), 5 μ_B (Co), and 2 μ_B (Zn).

FIGURE 3

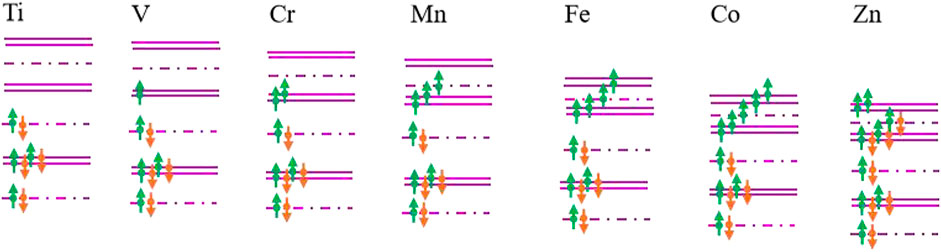
FIGURE 3. Evolution of the occupation mode of the hybridization orbitals nearby the Fermi level for the transition metal-doped SiC systems. The purple double lines represent the electronic states with E-symmetry, while the short line point represents the electronic states with A-symmetry. The green and the orange arrows denote the spin-up and the spin-down components, respectively. The distances between the lines reflect the energy variation between the energy levels.

The spin-polarized charge distributions near the metal atom are calculated, as illustrated in Figure 4. It can be seen that the three surrounding C atoms of the TM atom-doped SiC make equal contribution to the spin-polarized charge distribution. In the Sc- and Al-SiC systems, the spinned-polarized charge density exhibits a long-range distribution, even the atoms far away make a strong contribution, similar to the results shown in the GeC adsorbed by the F or Cl atom (Zhang and Cui, 2022b). However, Fe atom makes a decisive effect on the spin-polarized charge distributions of Fe-SiC, and the contributions of the adjacent C atoms are hard to be seen. In the V-, Cr-, Mn-, and Co-SiC systems, the TM atoms make more dominant effects than the adjacent C atoms. The magnetic moments of the metallic Sc- and Al-SiC systems are further calculated 0.512 μ_B (Sc) and 0.492 μ_B (Al), while the magnetic moments in semiconducting TM-SiC are 0 μ_B (Ti), 1.003 μ_B (V), 2.003 μ_B (Cr), 3.001 μ_B (Mn), 4.509 μ_B (Fe), 5.004 μ_B (Co), and 1.984 μ_B (Zn), respectively. Although there is a 0.5 μ_B variation in the Fe-SiC system, the magnetic moments of the other six TM-SiC systems are consistent with the forecasting results in Figure 3 as well, which demonstrates the validity of the hybridization orbital model.

FIGURE 4

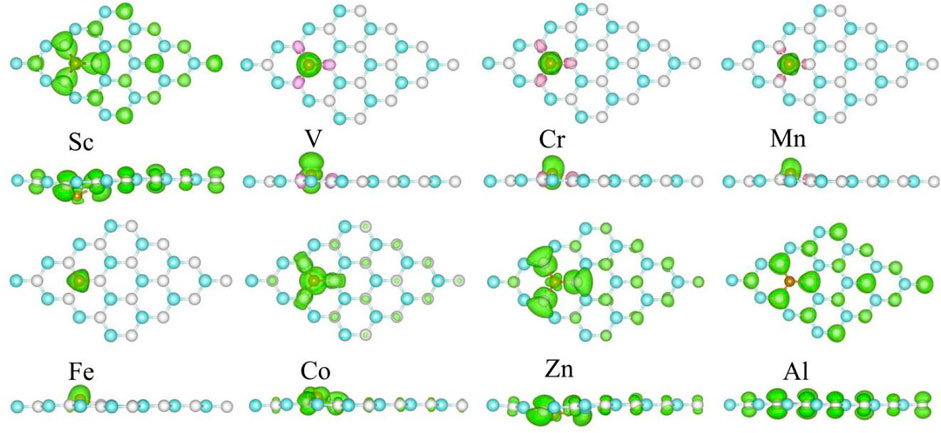
FIGURE 4. Spin-polarized charge density of the metal-doped SiC system. The green and the pink areas represent the spin-up and the spin-down regions, respectively. The isovalue is set to 0.001 e/ų.

To investigate the change in the electronic properties of metal-atom–doped SiC, the charge transfer between doping and the adjacent atoms is studied. The charge density difference (CDD) of metal-doped SiC is calculated by the Bader charges (Henkelman et al., 2006; Sanville et al., 2007),

$\mathrm{\Delta }\rho ={\rho }_{\text{Total}}-\left(\rho {}_{\text{SiC}}+{\rho }_{\mathrm{NM}}\right),(2)$

where ∆ρ is the difference in the charge density, ρ_Total, ρ_SiC, and ρ_NM represent the charge densities of the metal-doped SiC, the pristine SiC, and the metal atom, respectively.

The charge density difference of metal-doped SiC is illustrated in Figure 5. It can be seen that the metal atoms act as charge donors, transferring some charges to the adjacent C atoms. The charge transfers are F02D1⁻.525|e| (Sc), F02D1⁻.534|e| (Ti), F02D1⁻.291|e| (V), F02D1⁻.171|e| (Cr), F02D1⁻.070|e| (Mn), F02D0⁻.979|e| (Fe), F02D0⁻.596|e| (Co), F02D0⁻.832|e| (Zn), F02D2⁻.202|e| (Al), and F02D1⁻.245|e| (Ge), respectively. New metal-carbon bonds are formed to achieve the stability of the metal-doped SiC systems. The systems with semiconducting properties (the V-, Cr-, Mn-, Fe-, Co-, Zn, and Ge-SiC systems) exhibit relatively weak transfer charges than those with the metallic properties (the Sc- and Al-SiC systems). Among the semiconducting doped SiC systems, the most robust metal-carbon bonds are formed in the Ti-SiC system for the larger binding energy than the others, while Co-SiC exhibits weaker metal-carbon bonds for the smaller binding energy.

FIGURE 5

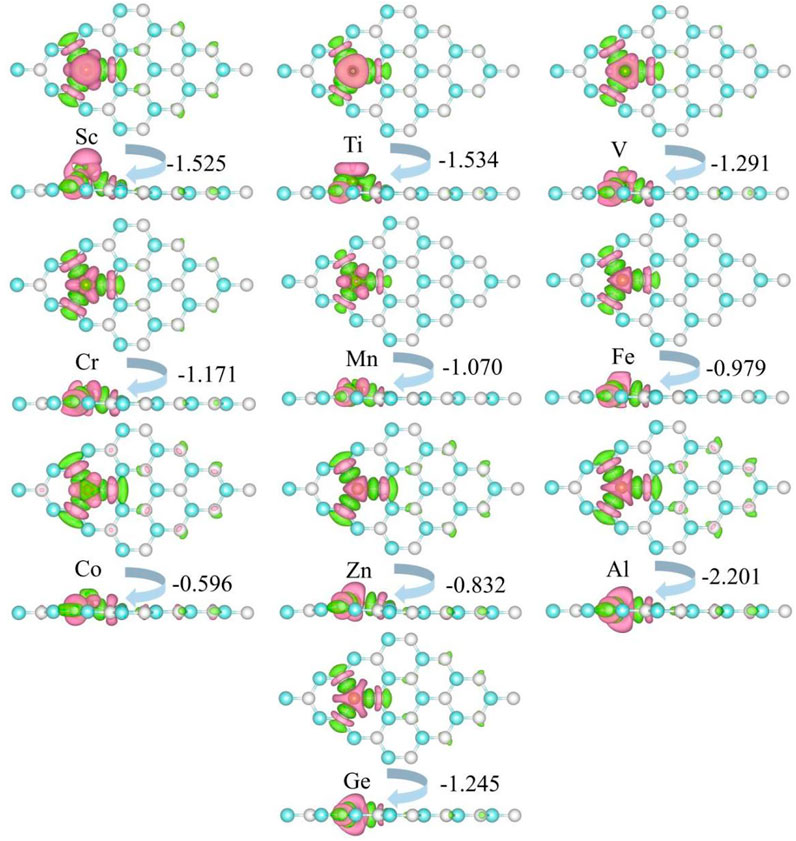
FIGURE 5. Charge density difference of the metal-doped SiC system. The green and the pink areas represent the loss and the obtained charge, respectively. The isovalue is set to 0.001 e/ų.

The formation of the new metal-carbon bonds induces the change in the system work function, leading to the variation in the electron-emitting capacity. A weak metal-carbon bond indicates a smaller work function and a stronger electron-emitting capacity. The work functions of the conventional 2D field electron emission devices are about several eV (Yu et al., 2009; Jiao et al., 2012; Cai et al., 2014; Soo et al., 2014), such as 4.50 eV (phosphorene), 4.60 eV (graphene), 4.90 eV (boron nitride), and 5.15 eV (MoS₂). In our work, the calculated work function of the pristine SiC is 4.80 eV, while the metal-doped SiC systems change from 3.439 to 5.158 eV, as depicted in Figure 6. Although the work function increases in the Al- and Zn-SiC systems, it decreases in the Sc-, Ti-,V-, Cr-, Mn-, Fe-, Co-, and Ge-SiC systems. The minimum work function of 3.439 eV is in the Co-SiC system, just 71.16% of the pristine SiC. The adjustment on the work function causing by metal dopants expands the application of the SiC-based system in the field emission devices.

FIGURE 6

FIGURE 6. Work function of the intrinsic SiC and metal-doped SiC systems.

Conclusion

We investigated the structural, electronic, and magnetic performances of 10 metal-doped SiC systems. The doping metal atoms include eight 3d-series transition metals, one semi-metal Ge, and one other metal Al atom. Our calculations indicate that the steadiest doping sites for all metal-doped SiC systems are located at the substituted Si site. Ti-SiC presents the most stable configuration for the largest binding energy. Although the Ti- and Ge-SiC systems remain nonmagnetic semiconductors, the Sc- and Al-SiC systems convert to magnetic metals, and the V-, Cr-, Mn-, Fe-, Co-, and Zn-SiC systems turn into magnetic semiconductors whose magnetic moments are related to the valence electron number of dopants. With the doping of the metal atoms, particle charge transfers from the metal atoms to the adjacent C atoms, causing the variation in the work function. Except for the increase in the Zn- and Al-SiC systems, the work function of the other metal-doped SiC systems decreases and achieves the minimum of 3.439 eV in the Co-SiC system, just 71.6% of the original SiC system. Our analysis indicates that the intense binding energy in the Ti-SiC system is due to the complete bonding states between the transition metal Ti and the adjacent C atoms. The magnetism in 3d TM-SiC is attributed to the occupation mode of the hybridization orbitals contributed by the coupling of 3d orbitals of the TM atom and the defect states of the vacancy. The adjustment on the electronic and magnetic performances by metal atoms extends the applications of SiC, especially in the design of field emission and spin electronic devices.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author Contributions

LZ: conceptualization, methodology, and validation. ZC: supervision, software, and writing—reviewing and editing.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We gratefully acknowledge the funding support from the National Natural Science Foundation of China 11904285.

References

Bekaroglu, E., Topsakal, M., Cahangirov, S., and Ciraci, S. (2010). First-principles Study of Defects and Adatoms in Silicon Carbide Honeycomb Structures. Phys. Rev. B, Condens. Matter Mat. Phys. 81, 1–9. doi:10.1103/physrevb.81.075433

CrossRef Full Text | Google Scholar

Bratschitsch, R. (2014). Monolayer Diodes Light up. Nat. Nanotech 9, 247–248. doi:10.1038/nnano.2014.66

PubMed Abstract | CrossRef Full Text | Google Scholar

Cai, Y., Zhang, G., and Zhang, Y.-W. (2014). Layer-dependent Band Alignment and Work Function of Few-Layer Phosphorene. Sci. Rep. 4, 6677. doi:10.1038/srep06677

PubMed Abstract | CrossRef Full Text | Google Scholar

Castelletto, S., Johnson, B. C., Ivády, V., Stavrias, N., Umeda, T., Gali, A., et al. (2014). A Silicon Carbide Room-Temperature Single-Photon Source. Nat. Mater 13, 151–156. doi:10.1038/nmat3806

PubMed Abstract | CrossRef Full Text | Google Scholar

Chabi, S., Guler, Z., Brearley, A. J., Benavidez, A. D., and Luk, T. S. (2021). The Creation of True Two-Dimensional Silicon Carbide. Nanomaterials 11, 1799. doi:10.3390/nano11071799

PubMed Abstract | CrossRef Full Text | Google Scholar

Chabi, S., and Kadel, K. (2020). Two-dimensional Silicon Carbide: Emerging Direct Band Gap Semiconductor. Nanomaterials 10, 2226. doi:10.3390/nano10112226

PubMed Abstract | CrossRef Full Text | Google Scholar

Chowdhury, C., Karmakar, S., and Datta, A. (2017). Monolayer Group IV-VI Monochalcogenides: Low-Dimensional Materials for Photocatalytic Water Splitting. J. Phys. Chem. C 121, 7615–7624. doi:10.1021/acs.jpcc.6b12080

CrossRef Full Text | Google Scholar

Cui, Z., Bai, K., Ding, Y., Wang, X., Li, E., Zheng, J., et al. (2020). Electronic and Optical Properties of Janus MoSSe and ZnO vdWs Heterostructures. Superlattices Microstruct. 140, 106445. doi:10.1016/j.spmi.2020.106445

CrossRef Full Text | Google Scholar

Cui, Z., Luo, Y., Yu, J., and Xu, Y. (2021). Tuning the Electronic Properties of MoSi₂N₄ by Molecular Doping: A First Principles Investigation. Phys. E Low-dimensional Syst. Nanostructures 134, 114873. doi:10.1016/j.physe.2021.114873

CrossRef Full Text | Google Scholar

Cui, Z., Lyu, N., Ding, Y., Bai, K., and Bai, K. F. (2021). Noncovalently Functionalization of Janus MoSSe Monolayer with Organic Molecules. Phys. E Low-dimensional Syst. Nanostructures 127, 114503. doi:10.1016/j.physe.2020.114503

CrossRef Full Text | Google Scholar

Cui, Z., Wang, M., Lyu, N., Zhang, S., Ding, Y., and Bai, K. (2021). Electronic, Magnetism and Optical Properties of Transition Metals Adsorbed Puckered Arsenene. Superlattices Microstruct. 152, 106852. doi:10.1016/j.spmi.2021.106852

CrossRef Full Text | Google Scholar

Cui, Z., Wang, X., Ding, Y., Li, E., Bai, K., Zheng, J., et al. (2020). Adsorption of CO, NH₃, NO, and NO₂ on Pristine and Defective g-GaN: Improved Gas Sensing and Functionalization. Appl. Surf. Sci. 530, 147275. doi:10.1016/j.apsusc.2020.147275

CrossRef Full Text | Google Scholar

Cui, Z., Zhang, S., Wang, L., and Yang, K. (2022). Optoelectronic and Magnetic Properties of Transition Metals Adsorbed Pd₂Se₃ Monolayer. Micro Nanostructures 167, 207260. doi:10.1016/j.micrna.2022.207260

CrossRef Full Text | Google Scholar

Eddy, C. R., and Gaskill, D. K. (2009). Silicon Carbide as a Platform for Power Electronics. Science 324, 1398–1400. doi:10.1126/science.1168704

PubMed Abstract | CrossRef Full Text | Google Scholar

Ferdous, N., Islam, M. S., Park, J., and Hashimoto, A. (2019). Tunable Electronic Properties in Stanene and Two Dimensional Silicon-Carbide Heterobilayer: A First Principles Investigation. AIP Adv. 9, 025120. doi:10.1063/1.5066029

CrossRef Full Text | Google Scholar

Grimme, S., Antony, J., Ehrlich, S., and Krieg, H. (2010). A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu. J. Chem. Phys. 132, 154104. doi:10.1063/1.3382344

PubMed Abstract | CrossRef Full Text | Google Scholar

He, J., Jiao, N., Zhang, C., Xiao, H., Chen, X., and Sun, L. (2014). Spin Switch of the Transition-Metal-Doped Boron Nitride Sheet through H/F Chemical Decoration. J. Phys. Chem. C 118, 8899–8906. doi:10.1021/jp410716q

CrossRef Full Text | Google Scholar

He, J., Wu, K., Sa, R., Li, Q., and Wei, Y. (2010). Magnetic Properties of Nonmetal Atoms Absorbed MoS₂ Monolayers. Appl. Phys. Lett. 96, 082504. doi:10.1063/1.3318254

CrossRef Full Text | Google Scholar

He, J., Zhou, P., Jiao, N., Ma, S. Y., Zhang, K. W., Wang, R. Z., et al. (2014). Magnetic Exchange Coupling and Anisotropy of 3d Transition Metal Nanowires on Graphyne. Sci. Rep. 4, 4014. doi:10.1038/srep04014

PubMed Abstract | CrossRef Full Text | Google Scholar

Henkelman, G., Arnaldsson, A., and Jónsson, H. (2006). A Fast and Robust Algorithm for Bader Decomposition of Charge Density. Comput. Mater. Sci. 36, 354–360. doi:10.1016/j.commatsci.2005.04.010

CrossRef Full Text | Google Scholar

Hsueh, H. C., Guo, G. Y., and Louie, S. G. (2011). Excitonic Effects in the Optical Properties of a SiC Sheet and Nanotubes. Phys. Rev. B 84, 085404. doi:10.1103/physrevb.84.085404

CrossRef Full Text | Google Scholar

Jiao, N., He, C., Zhang, C. X., Peng, X., Zhang, K. W., and Sun, L. Z. (2012). Modulation Effect of Hydrogen and Fluorine Decoration on the Surface Work Function of BN Sheets. AIP Adv. 2, 022125. doi:10.1063/1.4719097

CrossRef Full Text | Google Scholar

Komsa, H. P., Kotakoski, J., Kurasch, S., Lehtinen, O., Kaiser, U., and Krasheninnikov, A. V. (2012). Two-dimensional Transition Metal Dichalcogenides under Electron Irradiation: Defect Production and Doping. Phys. Rev. Lett. 109, 035503. doi:10.1103/PhysRevLett.109.035503

PubMed Abstract | CrossRef Full Text | Google Scholar

Kooti, M., Keshtkar, S., Askarieh, M., and Rashidi, A. (2019). Progress toward a Novel Methane Gas Sensor Based on SnO₂ Nanorods-Nanoporous Graphene Hybrid. Sensors Actuators B Chem. 281, 96–106. doi:10.1016/j.snb.2018.10.032

CrossRef Full Text | Google Scholar

Kresse, G., and Furthmüller, J. (1996). Efficient Iterative Schemes Forab Initiototal-Energy Calculations Using a Plane-Wave Basis Set. Phys. Rev. B 54, 11169–11186. doi:10.1103/physrevb.54.11169

CrossRef Full Text | Google Scholar

Kresse, G., and Joubert, D. (1999). From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method. Phys. Rev. B 59, 1758–1775. doi:10.1103/physrevb.59.1758

CrossRef Full Text | Google Scholar

Li, D., and Kaner, R. B. (2008). Graphene-based Materials. Science 320, 1170–1171. doi:10.1126/science.1158180

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, D., Li, S., Zhong, C., and He, J. (2021). Tuning Magnetism at the Two-Dimensional Limit: a Theoretical Perspective. Nanoscale 13, 19812–19827. doi:10.1039/d1nr06835k

PubMed Abstract | CrossRef Full Text | Google Scholar

Lin, X., Lin, S., Xu, Y., Hakro, A. A., Hasan, T., Zhang, B., et al. (2013). Ab Initio study of Electronic and Optical Behavior of Two-Dimensional Silicon Carbide. J. Mat. Chem. C 1, 2131–2135. doi:10.1039/c3tc00629h

CrossRef Full Text | Google Scholar

Luo, M., and Shen, Y. H. (2018). Magnetic Properties of SiC Monolayer with Different Nonmagnetic Metal Dopants. J. Supercond. Nov. Magn. 31, 3277–3282. doi:10.1007/s10948-018-4589-8

CrossRef Full Text | Google Scholar

Luo, M., Shen, Y. H., and Yin, T. L. (2017). Ab Initio study of Electronic and Magnetic Properties in TM-Doped 2D Silicon Carbide. Phys. E Low-dimensional Syst. Nanostructures 85, 280–284. doi:10.1016/j.physe.2016.08.028

CrossRef Full Text | Google Scholar

Luo, Y., Ren, C. D., Xu, Y. J., Yu, J., Wang, S., and Sun, M. L. (2021). A First Principles Investigation on the Structural, Mechanical, Electronic, and Catalytic Properties of Biphenylene. Sci. Rep. 11, 19008. doi:10.1038/s41598-021-98261-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Mélinon, P., Masenelli, B., Tournus, F., and Perez, A. (2007). Playing with Carbon and Silicon at the Nanoscale. Nat. Mat. 6, 479–490. doi:10.1103/PhysRevB.90.205421

CrossRef Full Text | Google Scholar

Perdew, J. P., Burke, K., and Ernzerhof, M. (1996). Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 77 (18), 3865–3868. doi:10.1103/physrevlett.77.3865

PubMed Abstract | CrossRef Full Text | Google Scholar

Pospischil, A., Furchi, M. M., and Mueller, T. (2014). Solar-energy Conversion and Light Emission in an Atomic Monolayer P-N Diode. Nat. Nanotech 9, 257–261. doi:10.1038/nnano.2014.14

PubMed Abstract | CrossRef Full Text | Google Scholar

Santos, E. J. G., Ayuela, A., and Sánchez-Portal, D. (2010). First-principles Study of Substitutional Metal Impurities in Graphene: Structural, Electronic and Magnetic Properties. New J. Phys. 12, 053012. doi:10.1088/1367-2630/12/5/053012

CrossRef Full Text | Google Scholar

Sanville, E., Kenny, S. D., Smith, R., and Henkelman, G. (2007). Improved Grid-Based Algorithm for Bader Charge Allocation. J. Comput. Chem. 28, 899–908. doi:10.1002/jcc.20575

PubMed Abstract | CrossRef Full Text | Google Scholar

Soo, H. C., Zhang, S. L., and Woo, C. Y. (2014). Layer-number-dependent Work Function of MoS₂ Nanoflakes. J. Kor. Phys. Soc. 64, 1550–1555.

Google Scholar

Stankovich, S., Dikin, D. A., Dommett, G. H. B., Kohlhaas, K. M., Zimney, E. J., Stach, E. A., et al. (2006). Graphene-based Composite Materials. Nature 442, 282–286. doi:10.1038/nature04969

PubMed Abstract | CrossRef Full Text | Google Scholar

Sun, M., Chou, J.-P., Ren, Q., Zhao, Y., Yu, J., and Tang, W. (2017). Tunable Schottky barrier in van der Waals heterostructures of graphene and g-GaN. Appl. Phys. Lett. 110, 173105. doi:10.1063/1.4982690

CrossRef Full Text | Google Scholar

Sun, M. L., and Schwingenschlögl, U. (2020). A Direct-Band-Gap Semiconductor Combining Auxeticity, Ferroelasticity, and Potential for High-Efficiency Solar Cells. Phys. Rev. Appl. 14, 044015. doi:10.1103/physrevapplied.14.044015

CrossRef Full Text | Google Scholar

Sun, M., Luo, Y., Yan, Y., and Schwingenschlögl, U. (2021). Ultrahigh Carrier Mobility in the Two-Dimensional Semiconductors B8Si4, B8Ge4, and B8Sn4. Chem. Mat. 33, 6475–6483. doi:10.1021/acs.chemmater.1c01824

CrossRef Full Text | Google Scholar

Sun, M., Ren, Q., Zhao, Y., Chou, J.-P., Yu, J., and Tang, W. (2017). Electronic and Magnetic Properties of 4d Series Transition Metal Substituted Graphene: a First-Principles Study. Carbon 120, 265–273. doi:10.1016/j.carbon.2017.04.060

CrossRef Full Text | Google Scholar

Sun, M., Yan, Y., and Schwingenschlögl, U. (2020). Beryllene: A Promising Anode Material for Na- and K-Ion Batteries with Ultrafast Charge/Discharge and High Specific Capacity. J. Phys. Chem. Lett. 11, 9051–9056. doi:10.1021/acs.jpclett.0c02426

PubMed Abstract | CrossRef Full Text | Google Scholar

Susi, T., Skákalová, V., Mittelberger, A., Kotrusz, P., Hulman, M., Pennycook, T. J., et al. (2017). Computational Insights and the Observation of SiC Nanograin Assembly: Towards 2D Silicon Carbide. Sci. Rep. 7, 4399. doi:10.1038/s41598-017-04683-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Tang, W., Sun, M., Yu, J., and Chou, J.-P. (2018). Magnetism in Non-metal Atoms Adsorbed Graphene-like Gallium Nitride Monolayers. Appl. Surf. Sci. 427, 609–612. doi:10.1016/j.apsusc.2017.08.210

CrossRef Full Text | Google Scholar

Wang, S., Ren, C., Tian, H., Yu, J., and Sun, M. (2018). MoS₂/ZnO van der Waals heterostructure as a high-efficiency water splitting photocatalyst: a first-principles study. Phys. Chem. Chem. Phys. 20, 13394–13399. doi:10.1039/c8cp00808f

PubMed Abstract | CrossRef Full Text | Google Scholar

Wu, C.-W., Huang, J.-H., and Yao, D.-X. (2019). Tunable Room-Temperature Ferromagnetism in the SiC Monolayer. J. Magnetism Magnetic Mater. 469, 306–314. doi:10.1016/j.jmmm.2018.08.054

CrossRef Full Text | Google Scholar

Yu, Y.-J., Zhao, Y., Ryu, S., Brus, L. E., Kim, K. S., and Kim, P. (2009). Tuning the Graphene Work Function by Electric Field Effect. Nano Lett. 9, 3430–3434. doi:10.1021/nl901572a

PubMed Abstract | CrossRef Full Text | Google Scholar

Yuan, J., Chen, Y., Xie, Y., Zhang, X., Rao, D., Guo, Y., et al. (2020). Squeezed Metallic Droplet with Tunable Kubo Gap and Charge Injection in Transition Metal Dichalcogenides. Proc. Natl. Acad. Sci. U.S.A. 117, 6362–6369. doi:10.1073/pnas.1920036117

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, L., and Cui, Z. (2022). Electronic, Magnetic, and Optical Performances of Non-metals Doped Silicon Carbide. Front. Chem. 10, 898174. doi:10.3389/fchem.2022.898174

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, L., and Cui, Z. (2022). Theoretical Study on Electronic, Magnetic and Optical Properties of Non-metal Atoms Adsorbed onto Germanium Carbide. Nanomaterials 12, 1712. doi:10.3390/nano12101712

PubMed Abstract | CrossRef Full Text | Google Scholar

Ziletti, A., Carvalho, A., Campbell, D. K., Coker, D. F., and Castro Neto, A. H. (2015). Oxygen Defects in Phosphorene. Phys. Rev. Lett. 114, 046801. doi:10.1103/PhysRevLett.114.046801

PubMed Abstract | CrossRef Full Text | Google Scholar