Visualization of the disordered structure of Fe-Ni Invar alloys by reverse monte carlo calculations

Reverse Monte Carlo (RMC) calculation was performed to visualize the atomic arrangement in a disordered Fe₅₅Ni₄₅ alloy, which is classified as an intermediate structure between the non-crystalline glass and crystalline structures. The optimized structure of the ferromagnetic phase at low pressures revealed that Fe and Ni atoms were displaced from a perfect fcc lattice to elongate the nearest neighboring Fe-Fe atomic pairs, therefore, Fe-Fe atomic pairs have longer bond length than Fe-Ni and Ni-Ni atomic pairs. Because the elongation becomes negligible during the pressure-induced destabilization of the ferromagnetic state, the elongation of Fe-Fe pairs is the atomic scale origin of the volume expansion due to a large magnetovolume effect. Compared with the atomic arrangement in the Fe₆₅Ni₃₅ Invar alloy, a relationship between Fe-Fe atomic pairs, the Invar effect and elastic anomalies in the compression curve is elucidated.

Introduction

The atomic arrangement in disordered alloys is classified as an intermediate structure between the non-crystalline glass and crystalline structures, because different metal atoms randomly occupy the lattice accompanied by small displacements from the periodic positions. Therefore, it has been difficult to investigate the atomic arrangement of disordered alloy. However, reverse Monte Carlo (RMC) calculation with complementary data sets of extended X-ray absorption fine structure (EXAFS) and X-ray diffraction (XRD) is a useful method to visualize the atomic arrangement in disordered alloys.

Ferromagnetic Fe-Ni disordered alloy is a suitable material to investigate the distortion of atomic arrangements by the magnetovolume effect (Yokoyama and Eguchi, 2011; Kousa et al., 2020; Yokoyama, 2021). The large magnetovolume effect of Fe-Ni alloys compresses the lattice with increasing temperature, which offsets normal thermal expansion and leads to the zero thermal expansion. This is known as the Invar effect. Disordered Fe₆₅Ni₃₅ is a well-known Invar alloy that exhibits zero thermal expansion in a wide temperature range up to the Curie temperature, T_C ≈ 505 K, at ambient pressure (Guillaume and Seances, 1897). We have previously examined the compressibility of Fe-Fe, Fe-Ni, and Ni-Ni atomic pairs in the Invar alloy using RMC calculations, revealing elongation of Fe-Fe atomic pairs compared with the other two atomic pairs (Ishimatsu et al., 2021). Because the elongation disappears with the pressure-induced transition to the paramagnetic phase, we concluded that the magnetovolume effect is due to the elongation of Fe-Fe atomic pairs.

To systematically discuss the relationship between Fe-Fe atomic pairs and the Invar effect, herein we performed a similar analysis on a Ni-rich alloy of Fe₅₅Ni₄₅, known as a pressure-induced Invar alloy, and compared the results with those of the Fe₆₅Ni₃₅ Invar alloy. Fe-Ni alloys recover normal thermal expansion with a slight increase in the Ni content from 35 at.%, but the pressure-induced Invar effect occurs at a characteristic pressure. According to a report by Dubrovinsky et al. (Dubrovinsky et al., 2001), Fe₅₅Ni₄₅ undergoes the pressure-induced Invar effect at $\approx 7.7$ GPa, although this alloy has a 7.5 times larger thermal expansion coefficient (α ≈ 9 × 10^–6/K) than the Invar alloy (α ≈ 1.19 × 10^–6/K) at ambient pressure (Hayase et al., 1973). Therefore, this study focuses on the atomic arrangement at the vicinity of the pressure-induced Invar effect of the Fe₅₅Ni₄₅ alloy. Consequently, our RMC calculation with complementary data sets of EXAFS and XRD demonstrate that the atomic arrangement in disordered Fe-Ni alloys is not completely random and that the Fe₅₅Ni₄₅ alloy also exhibit elongation of the Fe-Fe atomic pairs, depending on the magnetovolume effect under pressure.

Experimental procedures

Polycrystalline Fe₅₅Ni₄₅ non-Invar alloys were grained from ingots and pelletized for the EXAFS and XRD measurements. The pressure dependences of EXAFS and XRD were independently measured on beamline 39XU at SPring-8 (Kawamura et al., 2009) using a fresh (uncompressed) pellet. We utilized diamond anvil cells to apply pressure to the sample. The applied pressure was monitored using the conventional ruby fluorescence method. Nano-polycrystalline diamond anvils were utilized for the EXAFS measurement to prevent Bragg diffraction from the anvil crystals superimposed on the absorption profile (Irifune et al., 2003; Ishimatsu et al., 2012, 2016). A Fluorinert 70 + 77 solution was used as a pressure transmitting medium. All the measurements were performed at room temperature.

The software RMCProfile was used to carry out the RMC calculations (Krayzman et al., 2008). A cluster structure, which reproduces the experimental results of both EXAFS and XRD, was found by RMC calculation. By using conventional EXAFS analysis, element-dependent differences in the local structure have been reported (Yokoyama and Eguchi, 2011; Kousa et al., 2020; Yokoyama, 2021). However, it is typically difficult to distinguish the neighboring atoms to the X-ray absorbing atoms by conventional EXAFS analysis, because metal elements with close atomic numbers, such as Fe and Ni, give comparable scattering amplitudes of the photoelectrons. In contrast, the RMC calculation constructs and optimizes the best model of the atomic cluster that matches the experimental EXAFS profiles at multiple absorption edges via trial-and-error iterations. RMCProfile is suitable for this purpose, because it allows for the input of a dataset of EXAFS spectra at the Fe and Ni K-edges together with XRD patterns. A cluster of randomly distributed 2201 Fe and 1799 Ni atoms to a 10 × 10 × 10 fcc unit cell was used as the starting structure. In our calculation, atom swapping was not allowed. Therefore, long-range disorder was unchanged during the calculation. The minimum atomic separation was set to 1.8 Å. Each RMC calculation was performed for 720 min. Although the calculation time depends on the computer power, we judged that this time was sufficient to achieve convergence by monitoring the residual of the fitting. All single scattering paths calculated by the FEFF85L code were used in the EXAFS part of the RMC optimization. Furthermore, chainlike multiple scattering paths, which give significant intensities comparable to those of the single scattering paths, were also included in our model. The RMC calculation was performed three times, and the averaged result was used for the discussion.

Results and discussion

The calculated profiles are in good agreement with both EXAFS and XRD experimental data, as shown in Figure 1. The good reproducibility allows us to investigate how the distorted local structure coexists with the long-range periodicity in the calculated atomic cluster. The absolute values of Fourier transformed (FT) profiles (|FT [k²χ(k)]|) increase with increasing pressure at both the Fe and Ni K-edges, indicating that Debye-Waller factor decreases with the volume compression (Figures 1A, B). The prominent peak at radial distance R = 2.1–2.2 Å, which corresponds to the first nearest neighboring (1NN) 12 Fe/Ni atoms of the X-ray absorbing atom, shows significant enhancement of the peak intensity with increasing pressure. This trend was well reproduced by the RMC calculation in a wide range of R (up to 6 Å).

FIGURE 1

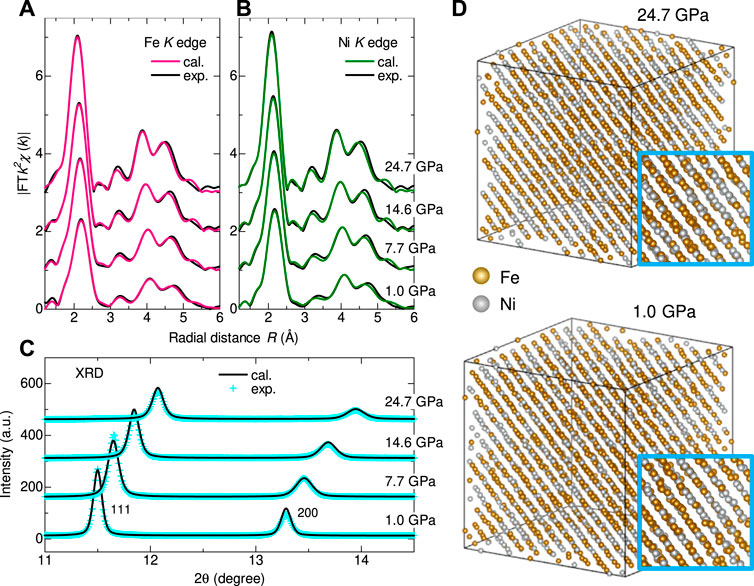
FIGURE 1. Comparison of the experimental profiles with fits by the RMC calculations. Absolute values of the |FT [k²χ(k)]| profiles of Fe₅₅Ni₄₅ non-Invar at (A) Fe K-edge and (B) Ni K-edges. (C) X-ray diffraction patterns at selected pressures. (D) Atomic arrangements of the Fe₅₅Ni₄₅ alloy obtained by the RMC calculation viewed from the $[11\bar{2}]$ direction. The insets show enlarged illustrations of the atomic clusters.

Experimental XRD patterns at selected pressures are compared with the calculated profiles in Figure 1C. The pressure dependence of the 111 and 200 Bragg peaks were chosen for our XRD measurements using a flat panel with a limited window size of 50 × 50 mm². The RMC calculations successfully reproduced the appearance of 111 and 200 Bragg peaks. As shown in Figure 1D, the calculated atomic cluster conserves the sequential stacking of the atomic planes, although the atoms are displaced from the ideal positions of the fcc lattice. Therefore, the RMC calculations found a structure, in which the local structure was largely distorted; however, the disordered atomic cluster maintained the long-range periodicity to satisfy the Bragg law owing to pseudo fcc symmetry.

Figure 2A shows the partial pair distribution functions g_ij(R), where i, j = Fe or Ni, in the range of R = 1.8 Å to 6 Å  corresponding to the histogram of the first to fifth nearest neighboring (1NN–5NN) Fe-Fe, Fe-Ni and Ni-Ni atomic pairs at selected pressures. The g_ij(R) function is normalized to approach unity with increasing R (Keen, 2001). In Figure 2A, the cross marks represent the lengths of atomic pairs expected from the lattice constant of a cluster with fcc symmetry, revealing small deviations. Moreover, the broad g_ij(R) profile around the expected peak positions indicates the displacements of Fe/Ni atoms from the fcc lattice positions.

FIGURE 2

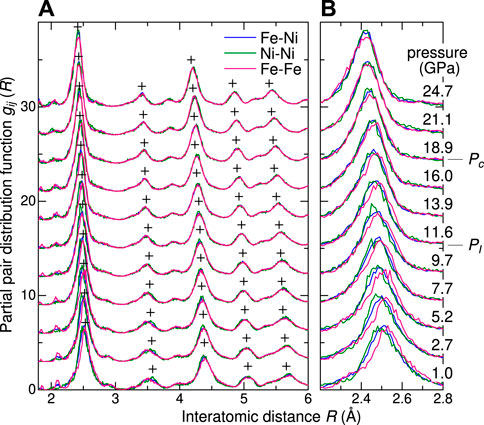
FIGURE 2. (A) Partial pair distribution functions g_ij(R), where i, j = Fe or Ni, for the Fe₅₅Ni₄₅ alloy at selected pressures. The cross marks indicate the lengths expected from the lattice constant of fcc structure. (B) Enlarged plot of g_ij(R) around the first nearest neighboring Fe-Fe and Fe-Ni and Ni-Ni atomic pairs.

A noted result of g_ij(R) is the elongation of 1NN Fe-Fe pairs in comparison with 1NN Fe-Ni and Ni-Ni pairs. To highlight the elongation, an enlarged plot of g_ij(R) profiles around the 1NN peak is shown in Figure 2B. Compared to the profiles of g_Fe-Ni(R) and g_Ni-Ni(R) at 1.0 GPa, the peak and whole profile of g_Fe-Fe(R) around the 1NN Fe-Fe pairs shift to the longer R direction. As the pressure increases, the shift of the g_Fe-Fe(R) gradually decreases, and the g_ij(R) profiles of Fe-Fe, Fe-Ni and Ni-Ni pairs are located at the same positions at pressures above 18.9 GPa. The elongation and pressure-induced shrinkage of the Fe-Fe pairs have also been observed in the g_ij(R) profiles of Invar alloys (Ishimatsu et al., 2021).

To investigate the elongation of the Fe-Fe atomic pairs quantitatively, average lengths of the 1NN atomic pairs, R_Fe-Fe, R_Fe-Ni, and R_Ni-Ni were evaluated. Gaussian fitting was performed within a range of 2.2 Å $\le R\le$ 2.8 Å, which encompasses the 1NN peaks in the asymmetric real space function. The fitted values of R_ij are plotted in Figure 3A as a function of pressure. We confirmed that a similar result was obtained by Gaussian fitting of the converted profile to the radial distribution function n_ij(R) (Keen, 2001). Figures 3A–C summarize the pressure dependences of R_ij, the integrated intensity of X-ray magnetic circular dichroism (XMCD), and the compression curve of Fe₅₅Ni₄₅ alloy. The compression curve was derived from the XRD patterns. Our previously reported results for the Fe₆₅Ni₃₅ alloy are shown in Figures 3D–F for comparison.

FIGURE 3

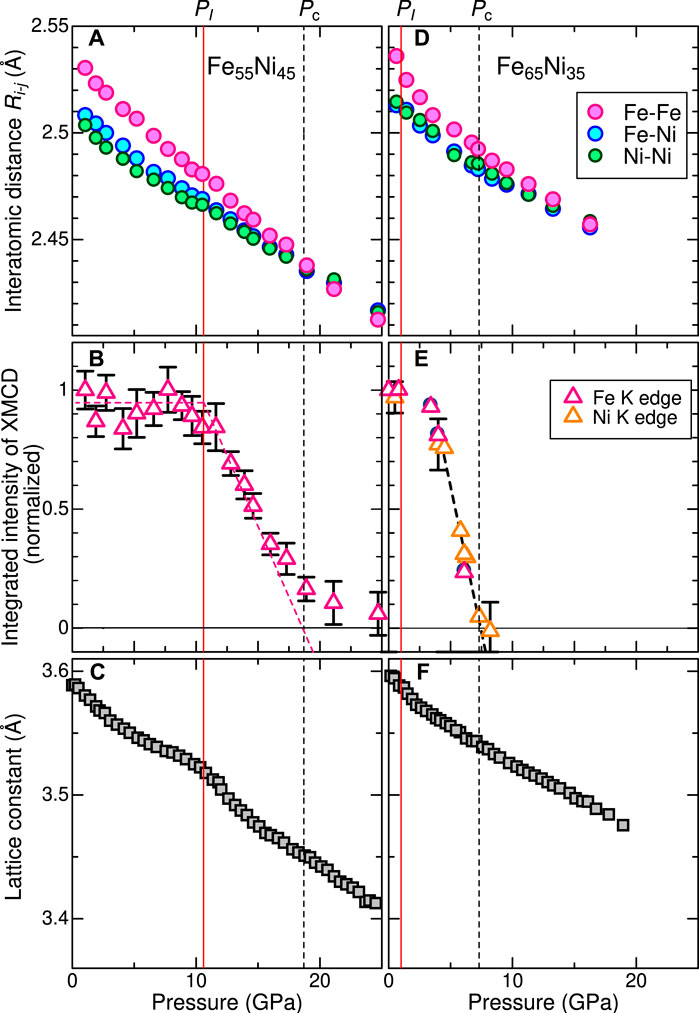
FIGURE 3. Comparison of the results between Fe₅₅Ni₄₅ non-Invar alloy and Fe₆₅Ni₃₅ Invar alloy as a function of pressure: (A, D) Average lengths of R_ij fitted within a range of 0.6 Å centered on the 1NN peaks of Fe-Fe, Fe-Ni, and Ni-Ni pairs. (B, E) Integrated intensity of X-ray magnetic circular dichroism (XMCD). (C, F) Compression curves determined by XRD. The vertical solid and dashed lines represent characteristic pressures P_I and P_c.

Figure 3A shows that R_Fe-Fe is longer than R_Fe-Ni and R_Ni-Ni in the low-pressure region. The evaluated bond lengths are 2.536, 2.513, and 2.515 Å for Fe-Fe, Fe-Ni, and Ni-Ni pairs, respectively, at 1.0 GPa. The magnitude of the elongation for the R_Fe-Fe is estimated to be approximately 0.021–0.023 Å, which is comparable to that of Invar alloy ($\approx 0.02$ Å).

The integrated XMCD at the K-edge corresponds to the 4p orbital moment (Igarashi and Hirai, 1994; Torchio et al., 2011). Because the 4p orbital moment is induced by the net magnetization, the integrated XMCD allows for the investigation of the pressure dependence of the magnetization. As shown in Figures 3B, E, both alloys undergo a phase transition from the ferromagnetic to the paramagnetic phase with increasing pressure. The vertical lines indicate the characteristic pressures labeled P_I and P_c, where the magnetization starts to decrease and becomes nearly zero, respectively. At pressures above P_c, the magnetic structure enters a paramagnetic phase. Fe₅₅Ni₄₅ alloy exhibits higher pressures (P_I ≈ 10.6 GPa and P_c ≈ 18.7 GPa) than the Fe₆₅Ni₃₅ alloy (P_I ≈ 1 GPa and P_c ≈ 7 GPa), indicating that the ferromagnetic order in Fe₅₅Ni₄₅ is more stable under pressure. This trend is consistent with the $\approx 215$ K higher T_C of Fe₅₅Ni₄₅ than that of Fe₆₅Ni₃₅ (Hayase et al., 1973). The softening behavior appears as a hump in the compression curves near the onset pressure P_I as shown in Figures 3C, F. According to previous reports (van Schilfgaarde et al., 1999; Dubrovinsky et al., 2001), the Invar effect occurs at pressures of the softening behavior and is accompanied by the destabilization of the ferromagnetic phase at P_I.

In Invar alloys, the destabilized ferromagnetic structure leads to a rapid shrinkage of R_Fe-Fe due to the pressure-induced loss of the magnetovolume effect above P_I ≈ 1 GPa. Similar elastic anomalies of softening and shrinkage of R_Fe-Fe have also been observed for Fe₅₅Ni₄₅. Fe₅₅Ni₄₅ is characterized by the wide pressure range of the pressure-independent ferromagnetic state below P_I. The broader pressure range of the stable ferromagnetic state enables us to understand the correlation between the magnetic instability, elongation of Fe-Fe atomic pairs and the softening behavior.

Interestingly, the elongation rate of R_Fe-Fe remains unchanged in the wide pressure region below P_I, and then a rapid contraction of the R_Fe-Fe occurs accompanied by the destabilization of the ferromagnetic state in a pressure range of P_I ≤ P ≤ P_c. As mentioned above, the maximum elongation of R_Fe-Fe is comparable to that exhibited by the Invar alloy. Thus, a large magnetovolume effect commonly works in the ferromagnetic phase of Fe-Ni alloys below P_I, and a similar interpretation of the elongation of R_Fe-Fe can be given to this alloy as well as Fe₆₅Ni₃₅ Invar alloy. Therefore, although we did not measure temperature dependences, we expect that Fe₅₅Ni₄₅ alloy exhibits a pressure-induced Invar effect at pressures near P_I, where a rapid contraction of R_Fe-Fe occurs. It is noted that the softening behavior of Fe₅₅Ni₄₅ is observed at a pressure that is $\approx 3$ GPa higher than that reported by Dubrovinsky et al. (Dubrovinsky et al., 2001), where they observed a small hump in the compression curve at P_I ≈ 7.5 GPa. This deviation is attributed to a different nonhydrostatic condition in the sample chamber that strongly depends on the pressure transmitting medium and sample shape. We also note that the lattice constant of the sample recovered the original value, as the pressure was released to ambient pressure. Therefore, it is confirmed that the plastic deformation was not introduced to the sample during the compression.

Finally, to confirm the validity of the element-dependent elongation, the expected value, ⟨R_ij⟩, was evaluated by using the equation:

$⟨R_{ij}⟩={\int }_{R_1}^{R_2}R\times 4\pi R^2{g}_{ij}\left(R\right){\rho }_{j}dR/{\int }_{R_1}^{R_2}4\pi R^2{g}_{ij}\left(R\right){\rho }_{j}dR,(1)$

where parameters R₁ and R₂ define the lower and upper limits of integration, respectively, and ρ_j is the number of j atoms in a unit volume. An advantage of the expected value is to minimize the effects from the asymmetric real space function. We used a wide integration range from R₁ = 1.8 Å to R₂ ≈ 3.1 Å  ensuring inclusion of all 12 Fe/Ni atoms in the first shell of the fcc lattice. This range is wide enough to avoid ambiguities due to the integration range. The obtained pressure dependence of ⟨R_ij⟩ is plotted in Figure 4. Although the elongation of the Fe-Fe bond is reproduced, it is a factor of one quarter smaller than the result of the Gaussian fit (Figure 3A). This is because the integration range includes not only main 1NN peak but also small humps and a moderate slope at both sides of the peak. However, we note that a similar trend is observed in the pressure dependence of the elongation: the elongation starts to decrease at pressures above P_I, and the lengths of three bond become comparable above P_c.

FIGURE 4

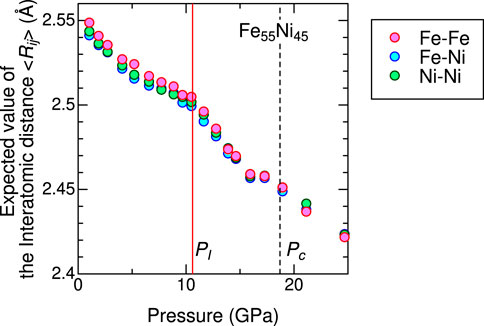
FIGURE 4. Pressure dependence of the expected values ⟨R_ij⟩ as the average length of 1NN bonds integrated within the entire first shell. Details are described in the text.

Concluding remarks

We successfully visualized the atomic arrangement of the disordered Fe₅₅Ni₄₅ alloy using the RMC calculation with the datasets of EXAFS and XRD measurements. The g_ij(R) profile was evaluated from the visualized atomic cluster, which showed that Fe and Ni atoms were displaced from a perfect fcc lattice, while the element-dependent distribution of the atomic bond length revealed an elongation of Fe-Fe pairs in the ferromagnetic phase at low pressures. Similar to the interpretation proposed for the Fe₆₅Ni₃₅ Invar alloy, the elongation of Fe-Fe pairs is the atomic scale origin of the volume expansion due to a large magnetovolume effect. The elongation becomes negligible upon the pressure-induced destabilization of the ferromagnetic state and softening behavior in the compression curve. Therefore, a strong correlation between the elongation of Fe-Fe atomic pairs, magnetization, and elastic anomalies has been clearly demonstrated. We note that the visualization procedure using RMC calculations can be employed to solve various problems of alloys such as the composition dependence of elastic anomalies, magnetism, and hydrogen embrittlement.

Data availability statement

All data supporting this study within the article are available from the corresponding author upon reasonable request.

Author contributions

NI, YK, and NKi designed the research and performed the RMC calculations; NI, NKa, MM. SK, and RN performed EXAFS and XRD measurements. TI and HS manufactured nano-diamond anvils; NI and YK wrote the paper. All other authors helped in writing the paper.

Funding

The studies presented herein were partially supported by a Grant-in-Aid for Scientific Research on Innovative Areas (Grant Number 15H05829), Grant-in-Aid for Transformative Research Areas (A) “Hyper-Ordered Structures Science” (Grant Numbers 20H05880 and 21H05567), and KAKENHI (Grant Numbers 17K05518 and 21H01043).

Acknowledgments

The X-ray absorption measurements were performed at SPring-8 with the approval of PRC-JASRI (Nos. 2017B1304, 2017B1974, 2018B1355, 2019A1530, and 2021A1434).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Dubrovinsky, L., Dubrovinskaia, N., Abrikosov, I. A., Vennström, M., Westman, F., Carlson, S., et al. (2001). Pressure-induced invar effect in fe-ni alloys. Phys. Rev. Lett. 86, 4851–4854. doi:10.1103/PhysRevLett.86.4851

PubMed Abstract | CrossRef Full Text | Google Scholar

Guillaume, C., and Seances, C. H. (1897). Acad. Sci. 125, 235.

Hayase, M., Shiga, M., and Nakamura, Y. (1973). Spontaneous volume magnetostriction and lattice constant of face-centered cubic fe-ni and ni-cu alloys. J. Phys. Soc. Jpn. 34, 925–933. doi:10.1143/JPSJ.34.925

CrossRef Full Text | Google Scholar

Igarashi, J.-i., and Hirai, K. (1994). Magnetic circular dichroism at the k edge of nickel and iron. Phys. Rev. B 50, 17820–17829. doi:10.1103/PhysRevB.50.17820

PubMed Abstract | CrossRef Full Text | Google Scholar

Irifune, T., Kurio, A., Sakamoto, S., Inoue, T., and Sumiya, H. (2003). Materials: Ultrahard polycrystalline diamond from graphite. Nature 421, 599–600. doi:10.1038/421599b

PubMed Abstract | CrossRef Full Text | Google Scholar

Ishimatsu, N., Iwasaki, S., Kousa, M., Kato, S., Nakajima, N., Kitamura, N., et al. (2021). Elongation of fe-fe atomic pairs in the invar alloy fe₆₅ni₃₅. Phys. Rev. B 103, L220102. doi:10.1103/PhysRevB.103.L220102

CrossRef Full Text | Google Scholar

Ishimatsu, N., Kawamura, N., Mizumaki, M., Maruyama, H., Sumiya, H., Irifune, T., et al. (2016). Applications of nano-polycrystalline diamond anvils to x-ray absorption spectroscopy under high pressure. High. Press. Res. 36, 381–390. doi:10.1080/08957959.2016.1205048

CrossRef Full Text | Google Scholar

Ishimatsu, N., Matsumoto, K., Maruyama, H., Kawamura, N., Mizumaki, M., Sumiya, H., et al. (2012). Glitch-free X-ray absorption spectrum under high pressure obtained using nano-polycrystalline diamond anvils. J. Synchrotron Radiat. 19, 768–772. doi:10.1107/S0909049512026088

PubMed Abstract | CrossRef Full Text | Google Scholar

Kawamura, N., Ishimatsu, N., and Maruyama, H. (2009). X-Ray magnetic spectroscopy at high pressure: Performance of SPring-8 BL39XU. J. Synchrotron Radiat. 16, 730–736. doi:10.1107/S0909049509034700

PubMed Abstract | CrossRef Full Text | Google Scholar

Keen, D. A. (2001). A comparison of various commonly used correlation functions for describing total scattering. J. Appl. Crystallogr. 34, 172–177. doi:10.1107/S0021889800019993

CrossRef Full Text | Google Scholar

Kousa, M., Iwasaki, S., Ishimatsu, N., Kawamura, N., Nomura, R., Kakizawa, S., et al. (2020). Element-selective elastic properties of fe65ni35 invar alloy and fe72pt28 alloy studied by extended x-ray absorption fine structure. High. Press. Res. 40, 130–139. doi:10.1080/08957959.2019.1702175

CrossRef Full Text | Google Scholar

Krayzman, V., Levin, I., and Tucker, M. G. (2008). Simultaneous reverse Monte Carlo refinements of local structures in perovskite solid solutions using EXAFS and the total scattering pair-distribution function. J. Appl. Crystallogr. 41, 705–714. doi:10.1107/S0021889808013277

CrossRef Full Text | Google Scholar

Torchio, R., Kvashnin, Y. O., Pascarelli, S., Mathon, O., Marini, C., Genovese, L., et al. (2011). X-ray magnetic circular dichroism measurements in ni up to 200 gpa: Resistant ferromagnetism. Phys. Rev. Lett. 107, 237202. doi:10.1103/PhysRevLett.107.237202

PubMed Abstract | CrossRef Full Text | Google Scholar

van Schilfgaarde, M., Abrikosov, I., and Johansson, B. (1999). Origin of the invar effect in iron–nickel alloys. Nature 400, 46–49. doi:10.1038/21848

CrossRef Full Text | Google Scholar

Yokoyama, T., and Eguchi, K. (2011). Anharmonicity and quantum effects in thermal expansion of an invar alloy. Phys. Rev. Lett. 107, 065901. doi:10.1103/PhysRevLett.107.065901

PubMed Abstract | CrossRef Full Text | Google Scholar

Yokoyama, T. (2021). Thermal expansion of feni invar and zinc-blende cdte from the view point of local structure. Microstructures 1, 2021003. doi:10.20517/microstructures.2021.001

CrossRef Full Text | Google Scholar