The Effective Diffusion Coefficient of Hydrogen in Tungsten: Effects of Microstructures From Phase-Field Simulations

1 Introduction

Due to the energy crisis caused by the exploitation of the limited fossil energy, nuclear fusion energy with many potential advantages such as abundant raw materials, pollution-free products, and high energy efficiency, has been constantly studied. The Tokamak, a magnetically confined fusion device, is considered to be the most likely future fusion device (Artsimovich, 1972). In the nuclear fusion reactor environment, tungsten (W) has been considered as one of the most promising candidate materials for plasma-facing materials (PFMs), owing to its advantages of high melting point, good thermal conductivities, as well as low sputtering rate (Bolt et al., 2004; Cottrell, 2004). However, PFMs will be irradiated by high energy neutron (14 MeV) in combination with the high temperature (300 < T < 2000 K) (Li et al., 2017), which will inevitably induce microstructure changes such as grain boundary migration (Stepper, 1972; Vaidya and Ehrlich, 1983; Mannheim et al., 2018), and second-phase formation (voids/dislocations caused by clustering of point defects (Hasegawa et al., 2014; Hu et al., 2016), precipitates formed by the precipitation of the transmutation elements (Hasegawa et al., 2016)), etc. Besides, hydrogen (H) and its isotope escaped from the plasma can penetrate through the W surfaces and diffuse inside the bulk under plasma irradiation (El-Kharbachi et al., 2014; Hodille et al., 2014; Grisolia et al., 2015). The interaction between H and the defect microstructures may result in a set of safety issues of W such as surface blistering (Zhou H. et al., 2019), embrittlement (Louthan et al., 1972), and cracking (Ueda et al., 2005), which can notably degrade the mechanical and thermal properties of W and thus reduce its service lifetime. In addition, H and its isotope are very expensive reactants, finding a way to recycle them can greatly reduce the cost. The diffusion process of H and its isotope in such complex microstructures is extremely important. Therefore, understanding the effect of the microstructure on the diffusion of H is critical to improving the irradiation properties and reducing the cost of fuels.

Recently, numerous simulations and experimental studies have been conducted on the H diffusion in the bulk (Frauenfelder, 1969; Heinola et al., 2010a; Yang and Oyeniyi., 2017) and on the surface of W (Heinola and Ahlgren, 2010b; Xue and Hassanein, 2014; Yang and Wirth, 2019), as well as the effect of irradiated defects such as vacancies (Eleveld and Veen, 1994; Liu et al., 2009; Johnson and Carter, 2010), dislocations (Taketomi et al., 2008; Kimizuka and Ogata, 2011; Wang et al., 2019), and grain boundaries (Oudriss et al., 2012; Yu et al., 2014; González et al., 2015; Fu et al., 2021) on the H diffusion. The thermal desorption experimental results show that the H diffusion is influenced by various factors such as defect type (Jin et al., 2017), distribution (Fujita et al., 2017), temperature (Rieth et al., 2019), and annealing time (Sakurada et al., 2017). In addition, it is found that the desorption temperature of H from vacancies or voids does not exceed 800 K (Eleveld and Veen, 1994), and from grain boundaries is about 400–500 K (Hodille et al., 2017). And the molecular dynamics studies indicate that the H diffusion largely depends on the type of grain boundaries, i.e., certain types of grain boundaries (e.g., ${\displaystyle \sum 5\left(310\right)\left[001\right]}$) can promote the H diffusion (Yu et al., 2014), while others (e.g., ${\displaystyle \sum 25\left(430\right)\left[100\right]}$) can inhibit it (Zhou X. et al., 2019) compared to it in the bulk. Vacancies always hinder the H diffusion in W, the diffusion coefficient of H can be reduced by two orders of magnitude in the single crystalline W when the mono-vacancy concentration is only 0.5% at 1800 K and this effect becomes more obvious with the increase of the vacancy concentration (Wang et al., 2019). Results also show that the materials with mono-vacancies have a stronger inhibition effect on H diffusion than that containing vacancy clusters with the same porosity, due to mono-vacancies can provide more H capture sites (Wang et al., 2019). Despite atomistic simulations can give the microscopic mechanism of H interacting with defects, they are hard to predict the effective diffusion coefficient at the microstructural scale due to the limited spatial and time scales. Several analytical models have been developed to estimate the effective diffusion coefficient of the diffusion component in microstructures (Maxwell, 1881; Hart, 1957; Bakker et al., 1995; Chen and Schuh, 2007; Moradi, 2015; Jiang et al., 2021). Maxwell-Garnett et al. (Maxwell, 1881; Moradi, 2015) developed a model to predict the effect of the volume fraction of the second phase on the effective diffusion coefficient in a two-phase system. Hashin-Shtrikman et al. developed a model (Chen and Schuh, 2007) to calculate the effective diffusion coefficient in isometric polycrystalline materials, etc. However, these analytical models have difficulties in giving the inhomogeneous concentration distribution of the diffusion component intuitively, and more importantly, they are far from enough to investigate the effect of the complex microstructural features (e.g., arrangement and morphology) on the effective diffusion coefficient of the diffusion component in materials.

In this work, we demonstrate an efficient numerical method to study the effect of the microstructure on the H effective diffusion coefficient in W at relevant high temperatures. Grain structures and irradiated voids are considered as the main defect microstructures generated by using phase-field simulations, although other defect microstructures such as dislocations, precipitates, and gas bubbles can also be easily incorporated in the model. A spectral iterative algorithm (Wang et al., 2016; Li et al., 2022) is used to solve the stationary diffusion equation based on the phase-field microstructures to obtain the effective diffusion coefficient. The current method is only applied at high temperature or there is no interaction between the diffusion component and microstructure, where H atoms can be eventually desorbed from grain boundaries and voids consisting with the thermal desorption experimental observations (Eleveld and Veen, 1994; Hodille et al., 2014). Using this method, the effects of grain boundaries, voids, and their synergistic effect on the effective diffusion coefficient of H are systematically investigated in W. Two sets of correlations that can be used to transfer the two-dimensional (2D) into three-dimensional (3D) effective diffusion coefficient are fitted based on our simulation results, which can be used to predict the effective diffusion coefficient of H in the porous polycrystalline W. We believe that this method provides a good reference for understanding the influence of the microstructure on the H diffusion in W, and offers an efficient way to study the effect of the complex microstructure on the effective diffusion coefficient in other similar systems.

2 Computational Details

2.1 Phase-Field Model of Microstructure Evolutions

Controlling the grain size is a common way to tune the thermal and mechanical properties of the polycrystalline W. Within the phase-field model, a set of continuous non-conservative phase variables ${\eta }_i$ (i = 1, … , n) are used to represent the different grain orientations, in which n is the total number of the grain orientations. Following the free energy of describing the grain growth developed by Chen et al. (Fan and Chen, 1997; Krill and Chen, 2002), the total free energy of the system can be written as,

$\begin{array}{c}{F}_{total}^{poly}={\displaystyle \int [m{f}_0\left({\eta }_1\left(\mathit{r}\right),{\eta }_2\left(\mathit{r}\right),\dots ,{\eta }_n\left(\mathit{r}\right)\right)+f_{grad}^{poly}({\eta }_1\left(\mathit{r}\right),{\eta }_2\left(\mathit{r}\right),\dots ,{\eta }_n\left(\mathit{r}\right))]dV}\end{array},(1)$

where $f_0$ is a local microstructural energy density, and $f_{grad}^{poly}$ is the gradient energy density contributed by the grain boundary. $\mathit{ r}=\left\{x,y,z\right\}$ is the spatial coordinate, m is a positive constant associated with the grain boundary width and energy, and V is the volume of the simulated system. Boldface characters (e.g., r) denote vectors in this work.

The local microstructural free energy density can be formulated as (Fan and Chen, 1997; Krill and Chen, 2002)

$\begin{array}{c}{f}_0\left({\eta }_1,{\eta }_2,\dots ,{\eta }_n\right)={\displaystyle \sum }_i^n[-\frac{1}{2}{\eta }_i^2+\frac{1}{4}{\eta }_i^4+\frac{1}{4}]+\gamma {\displaystyle \sum }_i^n{\eta }_i^2{\displaystyle \sum }_{j(j>i)}^n{\eta }_j^2\end{array},(2)$

where the first term describes a multi-well potential with a minimal value zero located at ${\eta }_i=1\text{ and} {\eta }_j=0,\left( j\ne i\right)$. The second term represents an energy penalty term among adjacent grains, and $\gamma$ is a positive constant that equals 1.5 (Moelans et al., 2008).

The gradient energy terms contributed by the grain boundaries are written as

$\begin{array}{c}{f}_{grad}^{poly}=\frac{k_{\eta }}{2}{\displaystyle \sum }_i{\left|\nabla {\eta }_i\right|}^2,\end{array}(3)$

where $k_{\eta }$ is the gradient coefficient.

The evolution of the grain parameters is controlled by the Allen-Cahn equation (Allen and Cahn, 1972; Allen and Cahn, 1973),

$\begin{array}{c}\frac{\partial {\eta }_i}{\partial t}=-L_{GB}\frac{\delta F_{total}^{poly}}{\delta {\eta }_i},i=\mathrm{1,2,3},\dots ,n,\end{array}(4)$

where $L_{GB}=L_0{e}^{-\frac{E_a}{k_{B}T}}$ is a temperature-dependent kinetic coefficient related to the migration of grain boundaries, $L_0$ is a constant, $E_a$ is the activation energy of the grain boundary migration, $k_B$ is the Boltzmann’s constant, and T is the annealing temperature. By solving the above equation, we can get the polycrystalline structure with designed grain size of W. We then fix the grain structure to further simulate the void formation in W by using a phase-field model.

A high density of point defects will be produced in W due to the high-energy neutron irradiation (Eleveld and Veen, 1994; Hasegawa et al., 2014; Hasegawa et al., 2016; Hu et al., 2016). Although the interstitial atoms and vacancies are always generated in pairs, we only consider the evolution of vacancies based on the fact that the diffusion coefficient of the interstitial atom is at least 10³ magnitudes larger than that of the vacancy in W at 300 < T < 2000 K (Hao et al., 2020). Therefore, the diffusion of vacancies is the rate-controlling process in the formation of voids and the interstitial atoms can be always considered at the equilibrium state. This scenario was also used in previous work to study the effect of the void evolution on effective thermal conductivities in W (Wang et al., 2018). And it will not affect our main conclusions since the objective of this work is to investigate the effects of the porosity and void size on the effective diffusion coefficient of H in W.

In the phase-field model, a conservative phase variable $C_v(r, t)$ is used to describe the vacancy concentration and a non-conservative phase variable $\phi (r, t)$ is used to distinguish the matrix phase and void phase. $\phi (r, t)$ equals 1.0 in the void phase and zero in the matrix phase, and continuously changes from 1.0 to zero across the void-matrix interface. Following the Kim-Kim-Suzuki (KKS) model (Kim et al., 1999; Kim, 2007), the free energy density employed for the void evolution is described as

$\begin{array}{c}{F}_{total}^{void}={\displaystyle \int [h\left(\phi \right)f^v+(1-h\left(\phi \right))f^m+wg\left(\phi \right)+f_{grad}^{void}\left(\phi \right)]dV}\end{array},(5)$

$\begin{array}{c}{f}^m=\frac{k_{B}T}{\Omega }\left(C_m^v\ln C_m^v/C_{eq}^v+\left(1-C_m^v\right)\ln (1-C_m^v))\right),\end{array}(6)$

$\begin{array}{c}{f}^v=\frac{k_{B}T}{\text{Ω}}{(C_v^v-1.0)}^2,\end{array}(7)$

where $f^m$ and $f^v$ is the free energy of the matrix and void phase, respectively. $\Omega =1.5\times {10}^{-29} {\text{m}}^3$ is the atomic volume of W. $C_m^v$ and $C_v^v$ is the vacancy concentration in the matrix and void phase, respectively, and $C_{eq}^v$ is the thermodynamic equilibrium concentration of the vacancy in the matrix phase. $h\left(\phi \right)={\phi }^3(6{\phi }^2-15\phi +10)$ is a monotonous interpolation function satisfying $h\left(0\right)=0\text{ and }h\left(1\right)=1$, $w$ is a constant, and $g\left(\phi \right)={\phi }^2\left(1-{\phi }^2\right)$ is a double-well potential function.

The gradient energy term contributed by the void-matrix interface is written as

$\begin{array}{c}{f}_{grad}^{void}=\frac{k_{\phi }}{2}\left|{\nabla }^2\phi \right|,\end{array}(8)$

where $k_{\phi }$ is the gradient coefficient.

The temporal and spatial evolution equations of the phase variable and concentration can be described by the Allen-Cahn (Allen and Cahn, 1972; Allen and Cahn, 1973) and Cahn-Hilliard equations (Cahn and Hilliard, 1958; Cahn and Hilliard, 1958) as

$\begin{array}{c}\frac{\partial \phi }{\partial t}=-L_v\frac{\delta F_{total}^{void}}{\delta \phi }+{\xi }_{\phi }\left(r,t\right)+P_v,\end{array}(9)$

$\begin{array}{c}\frac{\partial C_v}{\partial t}=\nabla .M_v\nabla \frac{\delta F_{total}^{void}}{\delta C_v}+{\xi }_{C_v}\left(r,t\right)+P_v-S\left(1-\text{Φ}\right)C_v,\end{array}(10)$

where $M_v=\frac{D_V\Omega }{k_{B}T}$ is the mobility of a vacancy, $D_V$ is the diffusion coefficient of a vacancy, and $L_v$ is the kinetic coefficient. $\xi \left(r,t\right)$ is a stochastic function. The last term in Eq. 10 represents the annihilation of vacancies by grain boundaries (Millett et al., 2009), and S is the interaction intensity set as 1.0 to meet the experimental observation of no cavity nucleation on grain boundaries (Klimenkov et al., 2016). The term $\text{Φ}={\eta }_i^2$ is employed to ensure that the interaction is only valid at grain boundaries instead of within grains (Chen and Yang 1994). $P_v$ is the source term of vacancies generated by cascade collisions caused by neutron irradiation, which can be described as (Millett et al., 2009),

$\begin{array}{c}{P}_v\left(\mathit{r},t\right)=\{\begin{array}{c}0\\ R_2{V}_G\end{array}\begin{array}{c}\phi \gg 0.8or{R}_1>P_{casc}\\ \phi <0.8\text{ and }{R}_1<P_{casc}\end{array},\end{array}(11)$

where $P_{casc}$ is the probability of cascade collisions at each grid point for each time step, which is related to the neutron irradiation, and $V_G$ is the maximum net increase in vacancy concentration from cascade events. $R_1$ and $R_2$ are random numbers between zero and 1.0.

According to the assumption of the KKS model that the total concentration is a mixture of two phases and the chemical potential is the same at every position in the system (Kim et al., 1999; Kim, 2007), the concentrations satisfy the following two equations,

$\begin{array}{c}{C}_v=h\left(\phi \right)C_v^v+(1-h\left(\phi \right))C_m^v,\end{array}(12)$

$\begin{array}{c}\frac{\partial f^v}{\partial C_v^v}=\frac{\partial f^m}{\partial C_m^v}.\end{array}(13)$

To sum up, the evolution Eqs. 9, 10 can be rewritten as

$\begin{array}{c}\frac{\partial {\phi }_i}{\partial t}=-L_v\left\{h^{\prime }\left(\phi \right)\left[\left(f^v-f^m\right)+\frac{\partial f^v}{\partial C_v^v}\left(C_m^v-C_v^v\right)\right]-k_{\phi }{\mathit{\nabla }}^2{\phi }_i+w{g}^{\prime }\left(\phi \right)\right\}+{\xi }_{\phi }\left(r,t\right),\end{array}(14)$

$\begin{array}{c}\frac{\partial C_v}{\partial t}=M_v{\nabla }^2\left(\frac{\partial f^v}{\partial C_v^v}\right)+{\xi }_{C_v}\left(r,t\right)-S\left(1-\text{Φ}\right)C_v,\end{array}(15)$

The semi-implicit FFTW numerical method is used to solve the Eqs. 4, 14, 15 (Chen and Shen, 1998). A Newton’s method is adopted to solve the nonlinear Eqs. 12, 13 for each time step.

2.2 Effective Diffusion Coefficient of H

Once we have the phase-field simulated grain structures and voids in W, we can investigate the effects of these microstructure evolutions on the effective diffusion coefficient of H. To do so, we solve the steady-state diffusion equation,

$\begin{array}{c}\frac{\partial }{\partial r_i}\left(D_{ij}\left(\mathit{r}\right)\frac{\partial C\left(\mathit{r}\right)}{\partial r_j}\right)=0,\end{array}(16)$

where $D_{ij}\left(\mathit{r}\right)$ is the microstructure-dependent diffusion coefficient tensor, which has different values in the bulk, grain boundary, and void in W and can be written as follows,

$\begin{array}{c}{D}_{ij}=\{\begin{array}{c}{D}_{ij}^m\\ \begin{array}{c}{D}_{ij}^{GB}\\ D_{ij}^{void}\end{array}\end{array}\begin{array}{c}\left(\eta >0.9 \text{and }\phi <0.5\right)\\ \left(\eta \le 0.9\right)\\ \left(\phi \ge 0.5\right)\end{array},\end{array}(17)$

where $D_{ij}^m$, $D_{ij}^{GB}$, and $D_{ij}^{void}$ is the H diffusion coefficient in the bulk, grain boundary, and void phase, respectively. In this inhomogeneous system, we can separate the diffusion coefficient into the homogeneous part $D_{ij}^0$ independent of the position and the inhomogeneous part $\text{Δ}{D}_{ij}\left(\mathit{r}\right)$ dependent on the position. Thus, the H diffusion coefficient $D_{ij}\left(\mathit{r}\right)$ can be written as

$\begin{array}{c}{D}_{ij}\left(\mathit{r}\right)=D_{ij}^0+\text{Δ}{D}_{ij}\left(\mathit{r}\right),\end{array}(18)$

Accordingly, the stationary distribution of the H concentration can be separated into linear and nonlinear parts, which corresponds to the homogeneous and inhomogeneous diffusion coefficient, respectively, i.e.,

$\begin{array}{c}C\left(\mathit{r}\right)=C^{linear}\left(\mathit{r}\right)+C^{non-linear}\left(\mathit{r}\right),\end{array}(19)$

where $C^{linear}\left(\mathit{r}\right)$ is the linear part of the concentrate, and $C^{non-linear}\left(\mathit{r}\right)$ is the nonlinear part that comes from the inhomogeneous distribution of the concentrate.

Based on the Fick’s first law, the flux of the H concentration along the j-direction is expressed as

$\begin{array}{c}{J}_i=-D_{ij}\left(\mathit{r}\right)\partial C/\partial r_j\end{array},(20)$

where $\partial C/\partial r_j$ is the gradient of the concentration along the j-direction.

Finally, the effective diffusion coefficient tensor $D_{ij}^{eff}$ of the system caused by the inhomogeneous microstructure can be determined by solving

$\begin{array}{c}{D}_{ij}^{eff}=-\langle J_i\rangle /\langle \partial C/\partial r_j\rangle ,\end{array}(21)$

where $J_i$ is the averaged flux along the i-direction, and $\partial C/\partial r_j$ represents the averaged concentration gradient along the j-direction.

To solve the steady-state diffusion equation shown in Eq. 16, a spectral iterative method is adopted, which has been used to solve the heat conduction equation in previous work (Wang et al., 2016; Li et al., 2022). In order to facilitate the reader’s understanding, we present the details of the solution process here. Firstly, combining the Eqs 18, 19, the Eq. 16 can be rewritten as,

$\begin{array}{c}\frac{\partial }{\partial r_i}\left[(D_{ij}^0+\text{Δ}{D}_{ij}\left(\mathit{r}\right))\left(\frac{\partial C^{linear}\left(\mathit{r}\right)}{\partial r_j}+\frac{\partial C^{non-linear}\left(\mathit{r}\right)}{\partial r_j}\right)\right]=0,\end{array}(22)$

Then rearranging the Eq. 22, we get

$\begin{array}{c}{D}_{ij}^0\frac{{\partial }^2{C}^{non-linear}\left(\mathit{r}\right)}{\partial r_i\partial r_j}=-\frac{\partial }{\partial r_i}\left[\text{Δ}{D}_{ij}\left(\mathit{r}\right)\left(\frac{\partial C^{linear}\left(\mathit{r}\right)}{\partial r_j}+\frac{\partial C^{non-linear}\left(\mathit{r}\right)}{\partial r_j}\right)\right].\end{array}(23)$

After that, by taking the Fourier transform on both sides of Eq. 23, we have,

$\begin{array}{c}-D_{ij}^0{\xi }_i{\xi }_j{C}^{non-linear}\left(\mathrm{\xi }\right)=-{\xi }_i{\left[\text{Δ}{D}_{ij}\left(r\right)\left(\frac{\partial C\left(r\right)}{\partial r_j}\right)\right]}_{\mathrm{\xi }},\end{array}(24)$

where $C^{non-linear}\left(\mathrm{\xi }\right)$ and ${\left[\text{Δ}{D}_{ij}\left(\mathit{r}\right)\left(\frac{\partial C\left(\mathit{r}\right)}{\partial r_j}\right)\right]}_{\mathrm{\xi }}$ is the Fourier transform of $C^{non-linear}\left(\mathit{r}\right)$ and $\text{Δ}{D}_{ij}\left(\mathit{r}\right)\left(\frac{\partial C\left(\mathit{r}\right)}{\partial r_j}\right)$, respectively.

Thus, we can get

$\begin{array}{c}{C}^{non-linear}\left(\mathrm{\xi }\right)= IG\left(\mathbf{\xi }\right){\xi }_i{\left[\text{Δ}{D}_{ij}\left(\mathit{r}\right)\left(\frac{\partial C\left(\mathit{r}\right)}{\partial r_j}\right)\right]}_{\mathrm{\xi }},\end{array}(25)$

where $G{\left(\mathrm{\xi }\right)}^{-1}$ = $k_{ij}^0{\xi }_i{\xi }_j$, and $I$ is the imaginary unit. At last, by taking the inverse Fourier transforms on both sides of Eq. 25, the nonlinear part concentration distribution can be written as,

$\begin{array}{c}{C}^{non-linear}\left(\mathit{r}\right)={\displaystyle \int \frac{d^3\xi }{{\left(2\pi \right)}^3}{C}^{non-linear}\left(\mathit{\xi }\right)e^{\mathit{I}\mathrm{\xi }\cdot \mathit{r}}}\end{array},(26)$

To sum up, the total concentration distribution $C\left(\mathit{r}\right)$ shown in Eq. 19 can be calculated as,

$\begin{array}{c}C\left(\mathit{r}\right)=C^{non-linear}\left(\mathit{r}\right)+{\displaystyle \int \frac{\partial C^{linear}\left(\mathit{r}\right)}{\partial r_j}d{r}_j}\end{array},(27)$

Once we have the total concentration $C\left(\mathit{r}\right)$, $\partial C/\partial r_j$ and the flux can be calculated based on Eq. 20. Thus, the effective diffusion coefficient $D_{ij}^{eff}$ can be obtained by using Eq. 21.

2.3 Simulation Details and Parameters

To simulate the grain growth and void microstructure evolutions, the phase-field Eqs. 4, 14, 15 are numerically solved with periodic boundary conditions. The time step for the grain growth is set at 2.4 s, and the grid spacing $\text{is }\text{Δ}\text{x}=\text{Δ}\text{y}=\text{Δ}\text{z}=1.0\text{ nm}$. A model sizes of 256.0 nm $\times$ 256.0 nm in 2D and 96.0 nm $\times$ 96.0 nm $\times$ 96.0 nm in 3D are used. According to Moelans et al. (Moelans et al., 2008), the gradient coefficient $k_{\eta }$ and potential height $m$ can be obtained by ${\sigma }_{gb}=\sqrt{2m{k}_{\eta }}/3$ and $l_{gb}=\sqrt{8k_{\eta }}/\sqrt{m}$ once the grain boundary energy ${\sigma }_{gb}$ and length $l_{gb}$ were given. In this work, ${\sigma }_{gb}=2.32 \text{J }{m}^{-2}$ is determined by averaging the grain boundary energies of 408 grain boundaries of W (Ratanaphan et al., 2017), and $l_{gb}$ is assumed to be 4.0 nm to ensure there are sufficient grid points across the diffused interface. The grain boundary migration energy $E_a$ is 0.6 eV based on the annealing experiment of the grain growth in W (Guo et al., 2018), and $L_0$ is 8.33 $\times {10}^{-6}{m}^3 {\text{J}}^{-1}{\text{ s}}^{-1}$ obtained by fitting the annealing experimental results of the grain growth (Guo et al., 2018; Li et al., 2022).

The input parameters for simulating the void evolutions under irradiation are set as follows. The sizes of the simulation domain are set as 256 $\text{Δ}\text{x}\times$ 256 $\text{Δ}\text{y}$ in 2D and 64 $\text{Δ}\text{x}\times 64\text{Δ}\text{y}\times$ 64 $\text{Δ}\text{z}$ in 3D. The time scale is set as ${10}^{-9}$ s. According to the previous work, the gradient coefficient $k_{\phi }$ and the potential height $w$ can be obtained by ${\sigma }_{void}=\frac{\sqrt{\omega k_{\eta }}}{3\sqrt{2}}$ and $l_{width}=2.2\sqrt{\frac{2k_{\eta }}{\omega }}$ (Aagesen et al., 2021), where the surface energy ${\sigma }_{void}$ is set as $1.0\text{ J} {\text{m}}^{-2}$ (Briant and Walter, 1988), and interface width $l_{width}=4.0 \text{nm}$. Following the Arrhenius formula, $D_V=D_0\times e^{\frac{E_a^v}{K_{B}T}}$, in which $D_0$ is the pre-exponential factor and $E_a^v$ is the activation energy of the vacancy diffusion. They are equal to $4.0\times {10}^{-6} {\text{m}}^2 {\text{s}}^{-1}$ and 1.8 eV based on the experimental measurements (Rasch and Schultz 1980).

The diffusion coefficients of H in the bulk, grain boundary, and void are required to calculate the effective diffusion coefficient of H in W. Previous atomistic simulations have listed the diffusion coefficient of H in the bulk is 5.13 $\times {10}^{-8} e^{0.21 \text{eV}/k_{B}T}{\text{ m}}^2 {\text{s}}^{-1}$ at the temperature range of 200–3000 K (Liu et al., 2014). The effect of the grain boundary on the H diffusion largely depends on the type of the grain boundary (Yu et al., 2014; Zhou et al., 2019B). Thus, we systematically study the effect of the grain boundary on the effective diffusion coefficient of H by using various diffusion coefficients. The diffusion coefficient of H in the void is set to be zero due to the strong inhibition of the vacancy/void on H diffusion (Wang et al., 2019). It should be noted that we assume our model is an ideal phase-field model with ignoring the effect of the faster diffusion of H along the inner surface of the irradiated voids on the effective diffusion coefficient to simplify the calculation. To ensure there is a flow of the H concentration along its diffusion direction, the concentrates on the two boundaries perpendicular to the H diffusion orientations are fixed at 0.4 and 0.1. These boundary values do not affect our main calculation results. The H concentration on other boundaries is fixed at 0.4.

3 Results and Discussions

We first use three simple structures having analytical solutions of the effective diffusion coefficient to validate our simulation code. We then quantitively calculate the effective diffusion coefficient of H in the polycrystalline and porous W. A correlation of converting the 2D effective diffusion coefficient into 3D in the porous polycrystalline W is fitted by using our simulation data, respectively. The effects of the grain morphology, porosity, and their synergistic effect on the effective diffusion coefficient of H are systematically investigated.

3.1 Simulation Code Validation

Three simple structures are used to fully validate our simulation code for calculating the effective diffusion coefficient of the diffusion component, including a two-phase structure consisting of two different arrangements of slabs (parallel and perpendicular to each other), a spherical structure embedded in a cubic box, and a 3D isometric crystalline structure. The calculated effective diffusion coefficients are compared with the analytical solutions to verify our simulation code.

3.1.1 Two Slab Structures for Validation

We first use a two-phase system with a simple slab structure to validate the code since it has an analytical solution. Two different configurations of the two-phase system are constructed. One is that these two slabs are parallel to each other (Figure 1A), while the other one is that they are perpendicular to each other (Figure 1B). For the first structure shown in Figure 1A, the effective diffusion coefficient along the X and Y direction can be described analytically as (Hart, 1957; Jiang et al., 2021)

$\begin{array}{c}{D}_x^{eff}=D_b+\frac{2w_{slab}}{L_x}(D_{slab}-D_b),\end{array}(28)$

$\begin{array}{c} D_y^{eff}=\frac{D_b{D}_{slab}}{\left(1-\frac{2w_{slab}}{L_x}\right)D_{slab}+\frac{2w_{slab}}{L_x}{D}_b},\end{array}(29)$

where $D_b \text{and} D_{slab}$ is the diffusion coefficient in the matrix and slab phase, respectively. $w_{slab}$ and $L_x$ is the width of the slab phase and the side length of the simulation domain.

FIGURE 1

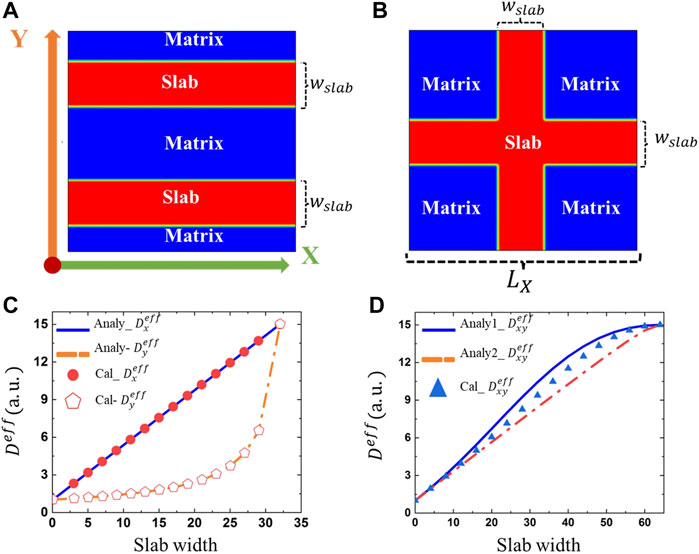
FIGURE 1. A two-phase system with a simple slab structure (A) parallel with each other, and (B) intersect with each other. (C) Comparison between the calculated and theoretical effective diffusion coefficients as a function of the slab width for structure (A), and (D) for structure (B). The diffusion coefficient in the matrix and slab phase is set as 15.0 and 1.0 in the same unit, respectively.

For the other configuration of the slab structure shown in Figure 1B, the effective diffusion coefficients along the X and Y direction are the same because of the symmetric structure. Two different solutions derived by Jiang et al. based on Eqs 28, 29 are respectively expressed as (Jiang et al., 2021)

$\begin{array}{c}{D}_1^{eff}=\left(1-\frac{w_{slab}}{L_x}\right)\left(\frac{D_b{D}_{slab}}{\left(1-\frac{w_{slab}}{L_x}\right)D_{slab}+\frac{w_{slab}}{L_x}{D}_{slab}}\right)+\frac{D_{slab}}{L_x}{D}_b,\end{array}(30)$

$\begin{array}{c}{D}_2^{eff}=D_{slab}{L}_x\frac{D_b{L}_x-D_b{w}_{slab}+D_{slab}{w}_{slab}}{D_b{L}_x{w}_{slab}-D_b{w}_{slab}^2+D_{slab}{L}_x^2-D_{slab}{L}_x{w}_{slab}+D_{slab}{w}_{slab}^2}\end{array}(31)$

It is believed that the true solution of this configuration should be somewhere in between these two solutions. We then calculate the effective diffusion coefficient in these two-phase structures by solving Eq. 16, where $D_b$ is set to 15.0 and $D_{slab}$ is set to 1.0. The simulation and analytical results as a function of the width of the slab phase are compared as shown in Figures 1C, D. Cal_$D_x^{eff}$ and Cal_$D_x^{eff}$ are numerical results. Analy_$D_x^{eff}$ and Analy_$D_y^{eff}$ represent the analytical results along the X and Y orientations based on Eqs 28, 29. From Figure 1C, it can be seen that the numerical and analytical solutions are almost identical for the first slab structure in Figure 1A. For the second configuration as shown in Figure 1B, our simulation results shown in Figure 1D are within those predicted by two different analytical formulas as expected. Thus, these results can preliminarily validate our simulation code.

3.1.2 Sphere Embedded in a Cubic Box for Validation

We then construct a spherical structure inside a cubic box as shown in Figure 2A, in which the purple part refers to the spherical phase and the blank part is the matrix phase. The effective diffusion coefficient can be expressed analytically by the Maxwell-Garnett model (Maxwell, 1881; Moradi, 2015),

$\begin{array}{c}{D}_{eff}=D_m\frac{2D_m+D_p+2f_p(D_p-D_m)}{2D_m+D_p-f_p(D_p-D_m)},\end{array}(32)$

where $D_p$ and $f_p$ is the diffusion coefficient in the spherical structure and the volume fraction of the spherical structure, respectively. We assume these two phases have different diffusion coefficients. We test two different cases to compare with the analytical solutions, one is the ratio $D_p/D_m$ greater than 1.0 and the other one is less than 1.0. In each case, three different ratios of the diffusion coefficient are selected. The calculated results as well as the analytical solutions of the effective diffusion coefficient as a function of the volume fraction of the sphere are shown in Figures 2B,C, in which the scatter points represent the simulation results and the curves represent the analytical results derived by the Maxwell-Garnett model (Maxwell, 1881; Moradi, 2015). It can be seen that our simulation results agree well with the analytical solutions, which further validate our simulation code.

FIGURE 2

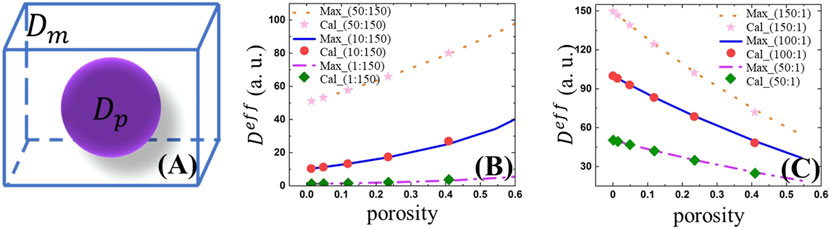
FIGURE 2. (A) A spherical phase is embedded in a cubic box. Comparison of simulated and analytical effective diffusion coefficients as a function of the volume fraction of the spherical phase for three different diffusion coefficient ratios (B) $D_p/D_m$ >1.0 and (C) $D_p/D_m$ <1.0. The scatter points represent the simulation results, and the curves represent the results calculated by the Maxwell-Garnett model (Maxwell, 1881; Moradi, 2015).

3.1.3 Isotropic Polycrystalline Structure for Validation

To further verify our code of solving the stationary diffusion equation with inhomogeneous diffusion coefficient distribution, we compare our results with the Hashin-Shtrikman (HS) model of a 3D isometric crystalline structure (Chen and Schuh, 2007). In the previous work, Hashin-Shtrikman derived an analytical solution that can be used to estimate the effective diffusion coefficient of H in isometric crystals as a function of the grain boundary density (Chen and Schuh, 2007),

$\begin{array}{c}{D}_{eff}=D_{GB}+\frac{f_m}{{(D_m-D_{GB})}^{-1}+1/3f_{GB}{D}_{GB}^{-1}},\end{array}(33)$

where $D_{eff},D_{GB}, \text{and }{D}_m$ is the effective diffusion coefficient, the diffusion coefficient in the grain boundary, and the diffusion coefficient in the matrix phase, respectively. $f_m$ and $f_{GB}$ is the volume fraction of the matrix phase and grain boundary, respectively.

We first generate a 3D isometric crystalline microstructure by using the phase-field simulation as shown in Figure 3A, where the yellow parts represent the bulk phase and the blue lines stand for grain boundaries. After that, we consider two different diffusion coefficient ratios between grain boundary and matrix phase for comparison, i.e., promoting the diffusion (5:1) and inhibiting diffusion (0.1:1). As shown in Figure 3B, the effective diffusion coefficients in three directions are all in good agreement with those predicted by the HS model, which further proves that our code is suitable for the calculation of the effective diffusion coefficients of the polycrystalline materials.

FIGURE 3

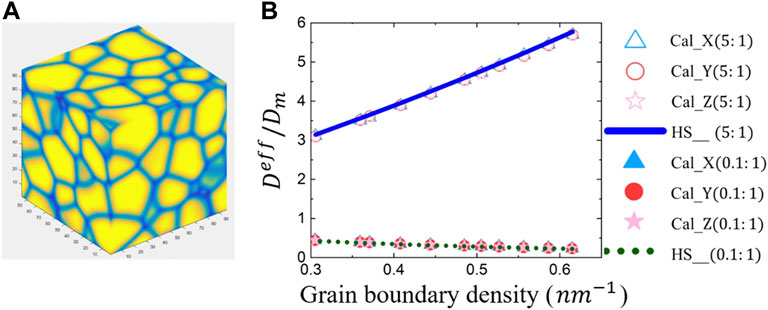
FIGURE 3. (A) The simulated isometric polycrystalline microstructure. Blue lines are grain boundaries and the yellow parts are grains. (B) Comparison between the simulated and analytical effective diffusion coefficients as a function of the grain boundary density alone three different directions with diffusion coefficient ratios of H in the grain boundary to that in matrix phase are 0.1:1.0 and 5.0:1.0.

Based on the above three testing examples, we validate our simulation code for calculating the effective diffusion coefficients in different structures.

3.2 Effective Diffusion Coefficient of H in Polycrystalline W

Based on our validated simulation code, we first study the effective diffusion coefficient of H in the polycrystalline W. The polycrystalline structures are generated using the phase-field model by solving Eqs 1–4. Three different polycrystalline structures including an isotropic grain structure and two columnar grain structures with different grain sizes are constructed as shown in Figures 4A–C. Then the effective diffusion coefficients of H in these three different polycrystalline structures can be obtained by solving Eq. 16.

FIGURE 4

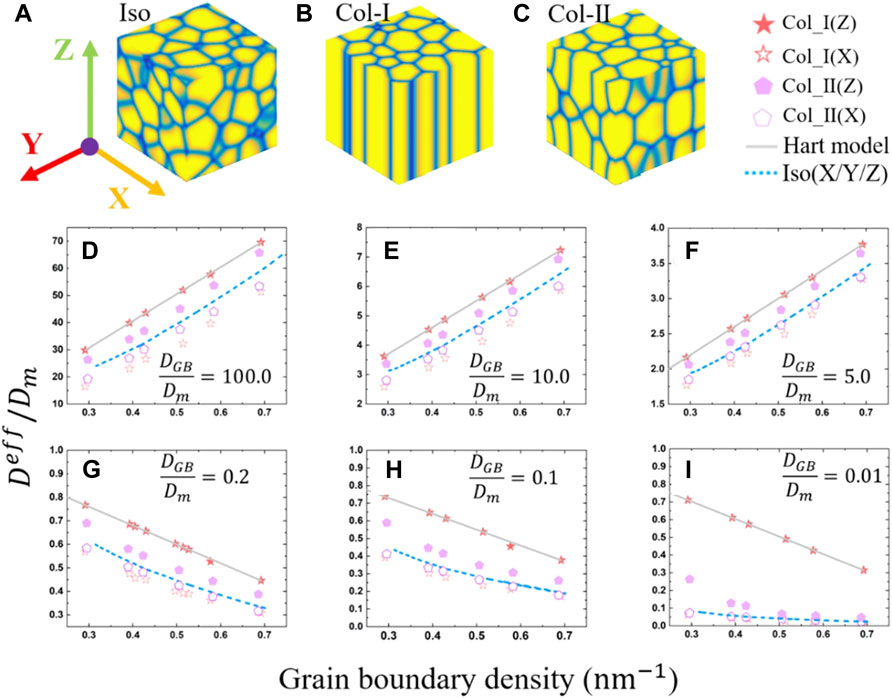
FIGURE 4. Polycrystalline structure of the (A) isometric crystal, (B) columnar-I crystal, and (C) columnar-II crystal. The calculated effective diffusion coefficients for three different polycrystalline structures with three diffusion coefficient ratios $D_{GB}/D_m$ of H are greater than 1.0 (D–F) and less than 1.0 (G–I). The solid and hollow scatter points represent the effective diffusion coefficient parallel and perpendicular to the direction of the elongated grains of the columnar crystals. The gray solid lines represent the predicted effective diffusion coefficient as a function of the grain boundary density along the elongated orientations of structure Col-I by Hart’s model and the blue dotted lines represent that predicted by the HS’s model for the isometric crystal.

The diffusion coefficient $D_{ij}$ of H in the grain boundaries and grains can be defined as

$\begin{array}{c}{D}_{ij}=\{\begin{array}{c}{D}_{GB}\\ D_m\end{array} \begin{array}{c}\left(\eta \le 0.9\right)\\ \left(\eta >0.9\right)\end{array}.\end{array}(34)$

According to previous atomic simulation results, the H diffusivity in the grain boundary can be either larger or smaller than that in the bulk, depending on the grain boundary type (Yu et al., 2014; Zhou et al., 2019B). To systematically investigate the effect of the grain boundary on the H diffusion in the polycrystalline W, six different ratios $D_{GB}/D_m$ of the H diffusion coefficient in grain boundaries with respect to that in grains are considered in this work, i.e., three with $D_{GB}/D_m>1.0$ and three with $D_{GB}/D_m$ <1.0 are selected for isometric and columnar grain structures.

Figure 4 shows the comparison of the numerically simulated and analytically calculated effective diffusion coefficients as a function of the grain boundary density in three polycrystalline structures. Figures 4D–F are for the case of $D_{GB}/D_m$ >1.0, while Figures 4G–I for the case of $D_{GB}/D_m$ <1.0. It can be seen that the effective diffusion coefficient increases with the increase of the grain boundary density when $D_{GB}/D_m$ is greater than 1.0, while it decreases with the increase of the grain boundary density when the ratio $D_{GB}/D_m$ is less than 1.0 as expected. Interestingly, the effective diffusion coefficient of H is greater in columnar crystals than that in isometric crystals along the Z direction, regardless of whether the H diffusivity in the grain boundary is larger or smaller than that in the bulk. And the effective diffusion coefficient of H in a simple columnar crystal containing parallel grain boundaries plotted in Figure 4B can be described by Hart’s model (Hart, 1957), as shown in Eq. 28. It can be seen that our calculation results agree well with those results predicted by Hart’s model. For the columnar-II crystal, the grains elongate along the Z-direction and grain boundaries have high density along this direction. The effective diffusion coefficient is believed to be larger than that for the isotropic crystal but smaller than that for the columnar-I crystal along the Z-direction. Both Hart’s model and HS’s model are hard to fit the simulation results in this case, which suggests that the numerical model without having the complex morphology of the microstructure can only predict the effective diffusion coefficient for simple grain structures.

2D simulations can save lots of computational resources compared to 3D simulations. We also calculate the effective diffusion coefficient of H in isometric structures in 2D. At the same grain boundary density, the effective diffusion coefficients in 2D are usually smaller than that in 3D. Next, we derive a correlation that transfers the 2D effective diffusion coefficient into 3D based on Bakker et al.‘s derivations, in which two formulas depending on the ratio of the diffusivity in the grain boundary and bulk that can transfer the 2D thermal conductivity into 3D were given (Bakker et al., 1995). When the H diffusion coefficient $D_{GB}$ in the grain boundary is greater than the H diffusion coefficient $D_m$ inside the grains, the correlation is given by

$\begin{array}{c}\frac{D_{3D}^{eff}-b}{D_{2D}^{eff}-b}=C_1+\frac{1}{\frac{D_{GB}}{D_m}+C_2}(D_{GB}>D_m),\end{array}(35)$

$\begin{array}{c}b=\frac{D_{GB}{D}_m}{f_{GB}{D}_m+D_{GB}-f_{GB}{D}_{GB}},\end{array}(36)$

where $D_{2D}^{eff}$ and $D_{3D}^{eff}$ is the effective diffusion coefficient of H in the 2D and 3D simulations, respectively. $C_1$ and $C_2$ are fitting constants. We calculate the effective diffusion coefficients in 2D and 3D in order to fit the constants $C_1$ and $C_2$. By using three sets of the calculated effective diffusion coefficient from both 2D and 3D simulations, the fitted constants $C_1$ and $C_2$ are determined to be 1.13 and 3.8, respectively. The effective diffusion coefficients and the fitted results using Eq. 35 are shown in Figure 5A–C, in which the purple dotted and pink solid lines represent the simulation results and fitted results by Eq. 35. It can be seen that the Eq. 35 can fit well with the simulated data in all three cases.

FIGURE 5

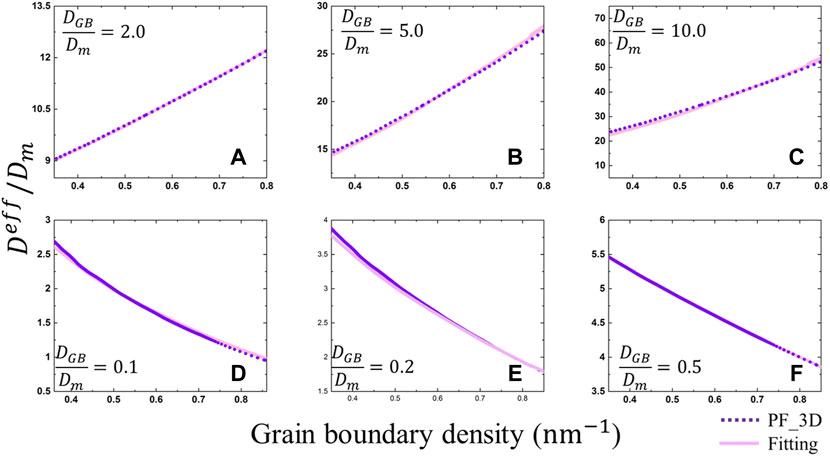
FIGURE 5. The comparison between the simulated and fitted effective diffusion coefficients of H in 3D polycrystalline W with three diffusion coefficient ratios D_GB/D_m of H are greater than 1.0 (A-C) and less than 1.0 (D-F). The fitted 3D data is calculated from the 2D results by using Eqs 30, 31. The purple dotted curves represent the simulated results and the pink solid curves represent the results predicted by the fitting formula.

For the H diffusion coefficient $D_{GB}$ smaller than the H diffusion coefficient $D_m$, a correlation for transferring the 2D effective diffusion coefficients of H into 3D is (Bakker et al., 1995),

$\begin{array}{c}\frac{1-\left(1-\frac{D_{GB}}{D_m}\right)f_{GB}-\frac{D_{2D}^{eff}}{D_m}}{1-\left(1-\frac{D_{GB}}{D_m}\right)f_{GB}-\frac{D_{3D}^{eff}}{D_m}}=C_3+\frac{1}{\frac{D_m}{D_{GB}}+C_4}(D_{GB}<D_m),\end{array}(37)$

where $D_{2D}^{eff}$ and $D_{3D}^{eff}$ is the effective diffusion coefficient in the 2D and 3D simulations, respectively. We use our simulated 2D and 3D effective diffusion coefficients to fit this correlation, and the fitted constants are determined as $C_3=1.07\text{ and} C_4=1.03$. The simulated and fitted effective diffusion coefficients of H in the 3D polycrystalline W are shown in Figures 5D–F, in which the purple dotted curves represent the simulated results and the pink solid curves represent the results predicted by the fitting formula Eq. 37. It can be seen that the fitting results are consistent with the simulation results for all three cases.

3.3 Effective Diffusion Coefficient of H in Porous Single Crystalline W

In addition to grain boundaries, irradiation-induced vacancies and their clusters can also affect the diffusion of H atoms (Wang et al., 2019). The porous structures formed by clustering of vacancies are generated by phase-field simulations through solving Eqs 5–15. Based on the phase-field simulated porous single crystalline W microstructures, we then study the effect of the porosity on the effective diffusion coefficient of H.

The diffusion tensor in the void and the matrix can be expressed as

$\begin{array}{c}{D}_{ij}=\{\begin{array}{c}{D}_{void}\\ D_m\end{array} \begin{array}{c}(\phi \ge 0.5)\\ (\phi <0.5)\end{array},\end{array}(38)$

where $D_{void}$ and $D_m$ represents the diffusion coefficient of H in the void and matrix phase, respectively. We assume that the diffusion coefficient $D_{void}$ is equal to zero based on the molecular dynamics results that the vacancy-type defects can greatly inhibit the H diffusion (Wang et al., 2019). Simulated and analytical effective diffusion coefficients as a function of the temperature and porosity in 2D and 3D porous W are plotted in Figures 6A, B. The colored scatter points represent the simulation results, and the solid black lines represent values of the effective diffusion coefficients predicted based on the Bakker’s model (Bakker et al., 1995), i.e., $D^{eff}=D_m{(1-p)}^{2.0}$ in 2D and $D^{eff}=D_m{(1-p)}^{1.5}$ in 3D. It can be seen that the effective diffusion coefficient significantly decreases with the increase of the porosity, and values $D^{eff}/D_m$ are basically consistent with those predicted by Bakker’s model, especially in the 3D simulations. Compared with the results of 2D and 3D simulation, it can be seen that the effective diffusion coefficient of 3D simulations is higher than that of the 2D simulations under the same annealing temperature and porosity. This is because the 3D diffusion flux has one more degree of freedom than that in the 2D simulations (Bakker et al., 1995). Interestingly, the higher the temperature, the greater value $D^{eff}/D_m$ is obtained at the same porosity. And the difference of $D^{eff}/D_m$ between the high and low temperature increases with the increase of the porosity, which is attributed to the rapid increase in size of the void at high temperature. With the increase of the temperature, larger voids are formed due to the faster diffusion of the vacancies, which is consistent with previous results (Li et al., 2011). This also shows the advantage of our model, which can take the spatial morphology of the voids into account rather than the volume fraction in the analytical model.

FIGURE 6

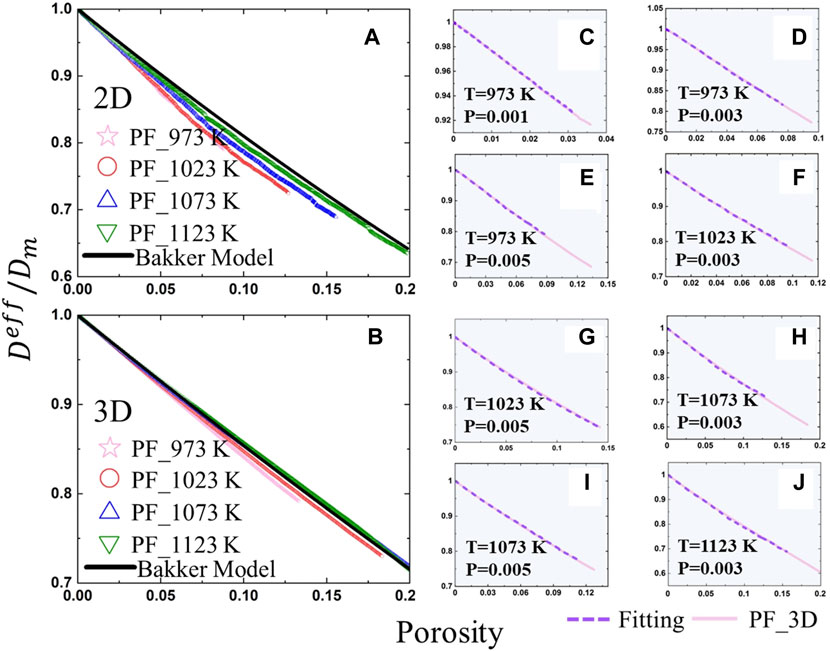
FIGURE 6. The simulated and analytical effective diffusion coefficients as a function of the porosity for four different temperatures in 2D (A) and 3D (B). (C)–(J) Comparison between the simulated and fitted effective diffusion coefficients of H in 3D porous W as a function of the temperature and porosity, in which the pink solid curves represent the simulation results and the purple dotted curves represent the results predicted by Eq. 39 based on 2D results.

Both the 2D and 3D effective diffusion coefficients of H as a function of the temperature and porosity in the porous single crystalline W are calculated. To obtain a general correlation that can transfer the 2D effective diffusion coefficient into the 3D in porous materials, we use the 2D and 3D calculated results to fit the parameter A by using the Eq. 39 proposed by Bakker et al. (Bakker et al., 1995),

$\begin{array}{c}\frac{1-p-\frac{D_{2D}^{eff}}{D_m}}{1-p-\frac{D_{3D}^{eff}}{D_m}}=A,\end{array}(39)$

where p, $D_{2D}^{eff}$, and $D_{3D}^{eff}$ is the porosity, the effective diffusion coefficient in 2D, and 3D, respectively. A is a fitting constant. The fitted effective diffusion coefficient of H as well as the simulated 3D data in the porous W are plotted in Figures 6C–J, in which the pink solid curves represent the simulation results and the purple dotted curves represent the results predicted by Eq. 39. And the fitted parameter A is determined to be 2.4. We can see that the fitted results agree well with the simulated effective diffusion coefficients. Therefore, this fitted correlation can be used to predict the 3D effective diffusion coefficient based on the 2D data to save computational resources.

3.4 Effective Diffusion Coefficient of H in Porous Polycrystalline W

We study the effective diffusion coefficient of H during the formation of voids in two different polycrystalline W as a function of the porosity. We take a particular temperature of 1073 K for an example. The polycrystalline microstructures are generated using phase-field simulations by solving Eqs 1–4. The nucleation and growth of voids are simulated by solving Eqs 5–15. It is simply assumed that the grain structures don’t evolve with the time during the formation of voids, and the same scenario was used in other relevant work (Wang et al., 2018). The simulated microstructures of the porous polycrystalline W at 0.001 s are shown in Figure 7C, where the solid lines represent the grain boundaries and the solid red round areas represent the voids. We assume the grain boundary is a perfect sink for vacancies, which is consistent with the experimental observations (Klimenkov et al., 2016).

FIGURE 7

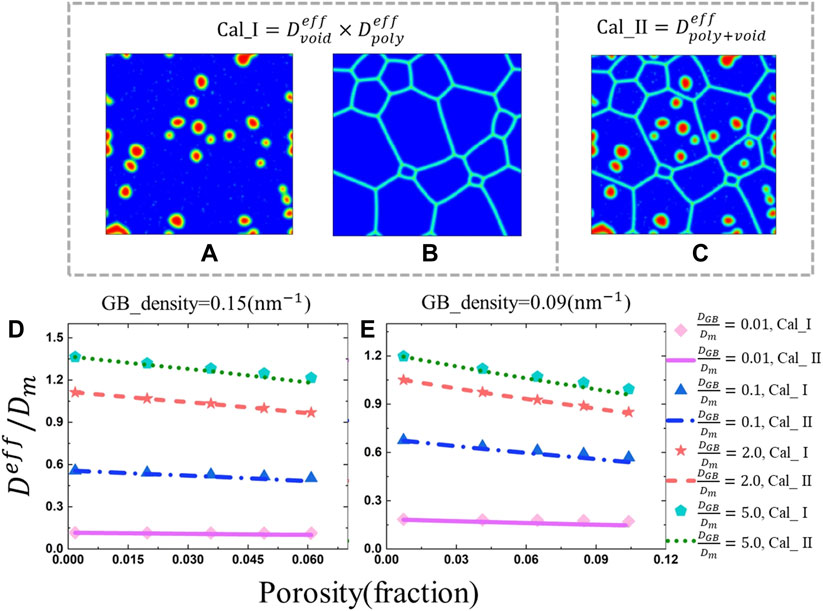
FIGURE 7. Microstructure used for the first method (A, B) and second method (C) for calculating the effective diffusion coefficient. Comparison of the value $D^{eff}/D_m$ calculated by two different methods as a function of the porosity under two different grain boundary densities of 0.15 nm⁻¹ (D) and 0.09 ${\text{nm}}^{-1}$ (E), in which the scatter points denote $D^{eff}/D_m$ obtained by the first method, and the curves represent that obtained by the second method.

The simulated microstructure is divided into three separate phases including the matrix, grain boundary, and void phases. We use two different methods to calculate the effective diffusion coefficient of H in this three-phase system. Firstly, we calculate the effective diffusion coefficient of H in the polycrystalline structure and porous structure separately as shown in Figures 7A,B. For the polycrystalline structure part, the solution process is the same as that in section 3.2, while for the effect of the porosity on the diffusion of H, the solution process is the same as that in section 3.3. The overall effective diffusion coefficient of H in the three-phase structure is assumed to be a product of the effective diffusion coefficient of the polycrystalline system $D_{poly}^{eff}$ and that of the porous system $D_{void}^{eff}$, which can be described as,

$\begin{array}{c}{D}^{eff}/D_m=(D_{void}^{eff}/D_m)\times (D_{poly}^{eff}/D_m).\end{array}(40)$

Secondly, the effective diffusion coefficients of H can be calculated directly from the three-phase structure by solving Eq. 16 as shown in Figure 7C. The diffusion coefficient in each phase can be described in section as Eq. 17.

Figures 7D, E show the effective diffusion coefficients as a function of the porosity for different diffusion coefficient ratios obtained by above two different means, in which the scatter points represent the results obtained by the first approach that are calculated by multiplying the results of two separate systems as shown in Eq. 40, and the curves represent the results derived from the second method that are directly calculated according to the three-phase system. Two different grain boundary densities of 0.15 nm⁻¹ and 0.09 nm⁻¹ are considered. Results show that the effective diffusion coefficient decreases with the increase of the porosity. In the case of $D_{GB}<D_m$, it also decreases with the increase of the grain boundary density, but it increases with the increase of the grain boundary density for the case of $D_{GB}>D_m$. More importantly, it can be seen that results obtained by these two different means agree well with each other, which verifies our above guess and also provides an important reference for estimating the effective diffusion coefficient of H in complex microstructures.

Based on the above 2D results, the effective diffusion coefficient of H in a 3D porous polycrystalline W can be predicted by using Eqs. 35, 37, 39. The predicted effective diffusion coefficients of H in the 3D porous polycrystalline W as a function of the porosity are shown in Figure 8. Results show that the effective diffusion coefficient decreases with the increase of the porosity, which has the same trend as that in 2D. The effective diffusion coefficient decreases with the increase of the grain boundary density for the case of $D_{GB}<D_m$, but it increases with the increase of the grain boundary density for the case of $D_{GB}>D_m$ in 3D microstructures. These results show that the grain size and grain morphology can largely affect the effective diffusion coefficient of H in W. However, by comparing the calculation results in 3D porous polycrystalline W with that in 2D plotted in Figures 7A, B, it is found that the effective diffusion coefficient of H in the 3D microstructure is always larger than that in 2D. This is reasonable because the effective diffusivities of H both in 3D polycrystalline or porous W are greater than that in their corresponding 2D microstructures.

FIGURE 8

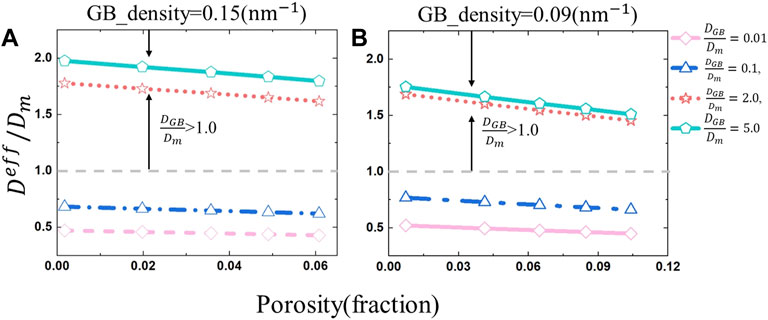
FIGURE 8. Predicted values of $D^{eff}/D_m$ for 3D porous polycrystalline W at 1073 K calculated by Eqs 35, 37, 39 based on 2D simulation results (as shown by the scatter data in Figures 7D, E) as a function of the porosity under two different grain boundary densities of 0.15 nm⁻¹ (A) and 0.09 nm⁻¹ (B).

4 Conclusion

We propose a numerical method to systemically study the effective diffusion coefficients of hydrogen (H) atoms in the porous polycrystalline tungsten (W). We assume the H atoms can be eventually desorbed from the grain boundaries and voids once they were trapped, which is based on thermal desorption experimental results (Eleveld and Veen, 1994; Hodille et al., 2017). The grain structure and irradiated voids are generated by using phase-field simulations. The effective diffusion coefficient in such an inhomogeneous system is obtained by solving the steady-state diffusion equation with a spectral iterative algorithm. The effects of the grain morphology, porosity, and their synergistic effect on the effective diffusion coefficient of H in W are systemically investigated. Our main research findings from the above simulations can be summarized as follows.

1) Using a spectral iterative algorithm, the calculated effective diffusion coefficients of three simple microstructures agree well with those predicted by previous analytical models, which fully validates our simulation code.

2) In the polycrystalline W, when the grain boundary density is a constant, the effective diffusion coefficient of H is always greater in columnar crystals than that in isometric crystals along the elongated grain direction, regardless of whether the diffusion coefficient in the grain boundary is larger or smaller than that in the bulk.

3) For the porous W, the effective diffusion coefficient of H significantly decreases with the increase of the porosity. When the porosity is a constant, our simulation results show that the effective diffusion coefficient increases with the increase of the average size of voids.

4) Based on our simulated effective diffusion coefficients in polycrystalline and porous W, two correlations that can transfer the two-dimensional (2D) effective diffusion coefficient into three-dimensional (3D) are fitted. Using these fitted correlations, we predict the effective diffusion coefficient of H in the 3D porous polycrystalline W based on 2D results, which can greatly save computational resources. It is found that the effective diffusion coefficient of H in a heterogeneous system is equal to the product of the effective diffusion coefficient of H in each phase.

The present study can help to better understand the influence of the grain boundary and void evolutions on the H diffusion in W. Other defect structures such as gas bubbles, dislocations, and precipitates influence the H diffusion can also be easily included in the model. It is also worthy to point out that the experimental observations can be used as input microstructures instead of the phase-field simulated microstructures to calculate the effective diffusion coefficient of H. We expect that our findings can provide some references on how to control the H and its isotope retention and for the design of W-based materials fusion devices in the future. The current method can also be used in other systems that the diffusion component is not trapped by the microstructures.

Data Availability Statement

The original contributions presented in this study are included in the article. The raw/processed data required to reproduce these findings cannot be shared at this time as the data also forms part of an ongoing study.

Author Contributions

BL performed the numerical simulations, produced the figures, conducted analysis, and wrote the draft of the manuscript. JH, BX, SJ, H-BZ, and LL made substantial contributions to the analysis of the simulation results. LL and G-HL proposed the idea, revised it critically for important intellectual content, and approved the final version to be published. All authors contributed to the article and approved the submitted version.

Funding

This research is supported by the National Natural Science Foundation of China with Grant Nos 12075021, 12075023, and 51720105006, and the National MCF Energy R&D Program of China with Grant No. 2018YFE0308103.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Aagesen, L. K., Biswas, S., Jiang, W., Andersson, D., Cooper, M. W. D., and Matthews, C. (2021). Phase-field Simulations of Fission Gas Bubbles in High Burnup UO2 during Steady-State and LOCA Transient Conditions. J. Nucl. Mater. 557, 153267. doi:10.1016/j.jnucmat.2021.153267

CrossRef Full Text | Google Scholar

Allen, S. M., and Cahn, J. W. (1973). A Correction to the Ground State of Fcc Binary Ordered Alloys with First and Second Neighbor Pairwise Interactions. Scr. Metall. 7, 1261–1264. doi:10.1016/0036-9748(73)90073-2

CrossRef Full Text | Google Scholar

Allen, S. M., and Cahn, J. W. (1972). Ground State Structures in Ordered Binary Alloys with Second Neighbor Interactions. Acta Metall. 20, 423–433. doi:10.1016/0001-6160(72)90037-5

CrossRef Full Text | Google Scholar

Artsimovich, L. A. (1972). Tokamak Devices. Nucl. Fusion 12, 215–252. doi:10.1088/0029-5515/12/2/012

CrossRef Full Text | Google Scholar

Bakker, K., Kwast, H., and Cordfunke, E. H. P. (1995). Determination of a Porosity Correction Factor for the Thermal Conductivity of Irradiated U02 Fuel by Means of the Finite Element Method. J. Nucl. Mater. 226, 128–143. doi:10.1016/0022-3115(95)00087-9

CrossRef Full Text | Google Scholar

Bolt, H., Barabash, V., Krauss, W., Linke, J., Neu, R., Suzuki, S., et al. (2004). Materials for the Plasma-Facing Components of Fusion Reactors. J. Nucl. Mater. 329-333, 66–73. doi:10.1016/j.jnucmat.2004.04.005

CrossRef Full Text | Google Scholar

Cahn, J. W., and Hilliard, J. E. (1958). Free Energy of a Nonuniform System. I. Interfacial Free Energy. J. Chem. Phys. 28, 258–267. doi:10.1063/1.1744102

CrossRef Full Text | Google Scholar

Cahn, J. W. (1961). On Spinodal Decomposition. Acta Metall. 9, 795–801. doi:10.1016/0001-6160(61)90182-1

CrossRef Full Text | Google Scholar

Chen, L.-Q., Yang, W., et al. (1994). Computer Simulation of the Domain Dynamics of a Quenched System with a Large Number of Nonconserved Order Parameters: The Grain-Growth Kinetics. Phys. Rev. B 50, 15752–15756. doi:10.1103/physrevb.50.15752

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, L. Q., and Shen, J. (1998). Applications of Semi-implicit Fourier-Spectral Method to Phase Field Equations. Comput. Phys. Commun. 108, 147–158. doi:10.1016/s0010-4655(97)00115-x

CrossRef Full Text | Google Scholar

Chen, Y., and Schuh, C. A. (2007). Geometric Considerations for Diffusion in Polycrystalline Solids. J. Appl. Phys. 101, 063524. doi:10.1063/1.2711820

CrossRef Full Text | Google Scholar

Cottrell, G. A. (2004). Sigma Phase Formation in Irradiated Tungsten, Tantalum and Molybdenum in a Fusion Power Plant. J. Nucl. Mat. 334, 66–68. doi:10.1016/j.jnucmat.2004.07.001

CrossRef Full Text | Google Scholar

El-Kharbachi, A., Chêne, J., Garcia-Argote, S., Marchetti, L., Martin, F., Miserque, F., et al. (2014). Tritium Absorption/desorption in ITER-like Tungsten Particles. Int. J. Hydrogen Energy 39, 10525–10536. doi:10.1016/j.ijhydene.2014.05.023

CrossRef Full Text | Google Scholar

Eleveld, H., and van Veen, A. (1994). Void Growth and Thermal Desorption of Deuterium from Voids in Tungsten. J. Nucl. Mater. 212-215, 1421–1425. doi:10.1016/0022-3115(94)91062-6

CrossRef Full Text | Google Scholar

Fan, D., and Chen, L.-Q. (1997). Computer Simulation of Grain Growth Using a Continuum Field Model. Acta Mater. 45, 611–622. doi:10.1016/s1359-6454(96)00200-5

CrossRef Full Text | Google Scholar

Frauenfelder, R. (1969). Solution and Diffusion of Hydrogen in Tungsten. J. Vac. Sci. Technol. 6, 388–397. doi:10.1116/1.1492699

CrossRef Full Text | Google Scholar

Fu, B., Qiu, M., Cui, J., Wang, J., and Hou, Q. (2021). Diffusion, Trapping, and Dissociation Behaviours of Helium at the Σ5 Grain Boundary in Tungsten: A Molecular Dynamics Study. J. Nucl. Mater. 543, 152599. doi:10.1016/j.jnucmat.2020.152599

CrossRef Full Text | Google Scholar

Fujita, H., Uemura, Y., Sakurada, S., Azuma, K., Zhou, Q., Toyama, T., et al. (2017). The Damage Depth Profile Effect on Hydrogen Isotope Retention Behavior in Heavy Ion Irradiated Tungsten. Fusion Eng. Des. 125, 468–472. doi:10.1016/j.fusengdes.2017.05.141

CrossRef Full Text | Google Scholar

González, C., Panizo-Laiz, M., Gordillo, N., et al. (2015). H Trapping and Mobility in Nanostructured Tungsten Grain Boundaries: a Combined Experimental and Theoretical Approach Nucl. Fusion 55, 113009. doi:10.1088/0029-5515/55/1/113009

CrossRef Full Text | Google Scholar

Grisolia, C., Hodille, E., Chene, J., Garcia-Argote, S., Pieters, G., El-Kharbachi, A., et al. (2015). Tritium Absorption and Desorption in ITER Relevant Materials: Comparative Study of Tungsten Dust and Massive Samples. J. Nucl. Mater. 463, 885–888. doi:10.1016/j.jnucmat.2014.10.089

CrossRef Full Text | Google Scholar

Guo, W., Cheng, L., De Temmerman, G., Yuan, Y., and Lu, G.-H. (2018). Retarded Recrystallization of Helium-Exposed Tungsten. Nucl. Fusion 58, 106011. doi:10.1088/1741-4326/aad2b0

CrossRef Full Text | Google Scholar

Hao, J., Jin, S., Lu, G.-H., and Xu, H. (2020). Migration Energy Barriers and Diffusion Anisotropy of Point Defects on Tungsten Surfaces. Comput. Mater. Sci. 184, 109893. doi:10.1016/j.commatsci.2020.109893

CrossRef Full Text | Google Scholar

Hart, E. W. (1957). On the Role of Dislocations in Bulk Diffusion. Acta Metall. 5, 597–605. doi:10.1016/0001-6160(57)90127-x

CrossRef Full Text | Google Scholar

Hasegawa, A., Fukuda, M., Nogami, S., and Yabuuchi, K. (2014). Neutron Irradiation Effects on Tungsten Materials. Fusion Eng. Des. 89, 1568–1572. doi:10.1016/j.fusengdes.2014.04.035

CrossRef Full Text | Google Scholar

Hasegawa, A., Fukuda, M., Yabuuchi, K., et al. (2016). Neutron Irradiation Effects on the Microstructural Development of Tungsten and Tungsten Alloys. J. Nucl. Mat. 471175-183. doi:10.1016/j.jnucmat.2015.10.047

CrossRef Full Text | Google Scholar

Heinola, K., and Ahlgren, T. (2010a). Diffusion of Hydrogen in Bcc Tungsten Studied with First Principle Calculations. J. Appl. Phys. 107, 113531. doi:10.1063/1.3386515

CrossRef Full Text | Google Scholar

Heinola, K., and Ahlgren, T. (2010b). First-principles Study of H on the Reconstructed W (100) Surface. Phys. Rev. B 81, 073409. doi:10.1103/physrevb.81.073409

CrossRef Full Text | Google Scholar

Hodille, E. A., Begrambekov, L. B., Pascal, J. Y., Saidi, O., Layet, J. M., Pégourié, B., et al. (2014). Hydrogen Trapping in Carbon Film: From Laboratories Studies to Tokamak Applications. Int. J. Hydrogen Energy 39, 20054–20061. doi:10.1016/j.ijhydene.2014.09.027

CrossRef Full Text | Google Scholar

Hodille, E. A., Ghiorghiu, F., Addab, Y., Založnik, A., Minissale, M., Piazza, Z., et al. (2017). Retention and Release of Hydrogen Isotopes in Tungsten Plasma-Facing Components: the Role of Grain Boundaries and the Native Oxide Layer from a Joint Experiment-Simulation Integrated Approach. Nucl. Fusion 57, 076019. doi:10.1088/1741-4326/aa6d24

CrossRef Full Text | Google Scholar

Hu, X., Koyanagi, T., Fukuda, M., Kumar, N. A. P. K., Snead, L. L., Wirth, B. D., et al. (2016). Irradiation Hardening of Pure Tungsten Exposed to Neutron Irradiation. J. Nucl. Mater. 480, 235–243. doi:10.1016/j.jnucmat.2016.08.024

CrossRef Full Text | Google Scholar

Jiang, C., Ke, J. H., Simon, P. C. A., et al. (2021). Atomistic and Mesoscale Simulations to Determine Effective Diffusion Coefficient of Fission Products in SiC. Idaho National Lab. (INL), Idaho Falls, ID (United States) https://www.osti.gov/servlets/purl/1825508.

Google Scholar

Jin, Y., Roh, K.-B., Sheen, M.-H., Kim, N.-K., Song, J., Kim, Y.-W., et al. (2017). Enhancement of Deuterium Retention in Damaged Tungsten by Plasma-Induced Defect Clustering. Nucl. Fusion 57, 126042. doi:10.1088/1741-4326/aa856c

CrossRef Full Text | Google Scholar

Johnson, D. F., and Carter, E. A. (2010). Hydrogen in Tungsten: Absorption, Diffusion, Vacancy Trapping, and Decohesion. J. Mat. Res. 25, 315–327. doi:10.1557/jmr.2010.0036

CrossRef Full Text | Google Scholar

Kim, S. G. (2007). A Phase-Field Model with Antitrapping Current for Multicomponent Alloys with Arbitrary Thermodynamic Properties. Acta Mater. 55, 4391–4399. doi:10.1016/j.actamat.2007.04.004

CrossRef Full Text | Google Scholar

Kim, S. G., Kim, W. T., and Suzuki, T. (1999). Phase-field Model for Binary Alloys. Phys. Rev. E 60, 7186–7197. doi:10.1103/physreve.60.7186

PubMed Abstract | CrossRef Full Text | Google Scholar

Kimizuka, H., and Ogata, S. (2011). Slow Diffusion of Hydrogen at a Screw Dislocation Core Inα-Iron. Phys. Rev. B 84, 024116. doi:10.1103/physrevb.84.024116

CrossRef Full Text | Google Scholar

Klimenkov, M., Jäntsch, U., Rieth, M., Schneider, H. C., Armstrong, D. E. J., Gibson, J., et al. (2016). Effect of Neutron Irradiation on the Microstructure of Tungsten. Nucl. Mater. Energy 9, 480–483. doi:10.1016/j.nme.2016.09.010

CrossRef Full Text | Google Scholar

Krill III, C. E., and Chen, L.-Q. (2002). Computer Simulation of 3-D Grain Growth Using a Phase-Field Model. Acta Mater. 50, 3059–3075. doi:10.1016/s1359-6454(02)00084-8

CrossRef Full Text | Google Scholar

L. Briant, C., and Walter, J. L. (1988). Void Growth in Tungsten Wire. Acta Metall. 36, 2503–2514. doi:10.1016/0001-6160(88)90196-4

CrossRef Full Text | Google Scholar

Li, B., Jin, S., Xue, B., Liang, L., and Lu, G.-H. (2022). Phase-field Microstructure-Based Effective Thermal Conductivity Calculations in Tungsten. Nucl. Fusion 62, 076041. doi:10.1088/1741-4326/ac6284

CrossRef Full Text | Google Scholar

Li, Y.-H., Zhou, H.-B., Jin, S., Zhang, Y., Deng, H., and Lu, G.-H. (2017). Behaviors of Transmutation Elements Re and Os and Their Effects on Energetics and Clustering of Vacancy and Self-Interstitial Atoms in W. Nucl. Fusion 57, 046006. doi:10.1088/1741-4326/aa5893

CrossRef Full Text | Google Scholar

Li, Y., Hu, S., Sun, X., Gao, F., Henager, C. H., and Khaleel, M. (2011). Phase-field Modeling of Void Evolution and Swelling in Materials under Irradiation. Sci. China Phys. Mech. Astron. 54, 856–865. doi:10.1007/s11433-011-4316-y

CrossRef Full Text | Google Scholar

Liu, Y.-L., Zhang, Y., Zhou, H.-B., Lu, G.-H., Liu, F., and Luo, G.-N. (2009). Vacancy Trapping Mechanism for Hydrogen Bubble Formation in Metal. Phys. Rev. B 79, 172103. doi:10.1103/physrevb.79.172103

CrossRef Full Text | Google Scholar

Liu, Y.-N., Wu, T., Yu, Y., Li, X.-C., Shu, X., and Lu, G.-H. (2014). Hydrogen Diffusion in Tungsten: A Molecular Dynamics Study. J. Nucl. Mater. 455, 676–680. doi:10.1016/j.jnucmat.2014.09.003

CrossRef Full Text | Google Scholar

Louthan, M. R., Caskey, G. R., Donovan, J. A., and Rawl, D. E. (1972). Hydrogen Embrittlement of Metals. Mater. Sci. Eng. 10, 357–368. doi:10.1016/0025-5416(72)90109-7

CrossRef Full Text | Google Scholar

Mannheim, A., Van Dommelen, J. A. W., and Geers, M. G. D. (2018). Modelling Recrystallization and Grain Growth of Tungsten Induced by Neutron Displacement Defects. Mech. Mater. 123, 43–58. doi:10.1016/j.mechmat.2018.04.008

CrossRef Full Text | Google Scholar

Maxwell, J. C. A. (1881). Treatise on Electricity and Magnetism: Pt. III. Magnetism. Pt. IV. Electromagnetism. Clarendon Press.

Google Scholar

Millett, P. C., Rokkam, S., El-Azab, A., Tonks, M., and Wolf, D. (2009). Void Nucleation and Growth in Irradiated Polycrystalline Metals: a Phase-Field Model. Model. Simul. Mat. Sci. Eng. 17, 064003. doi:10.1088/0965-0393/17/6/064003

CrossRef Full Text | Google Scholar

Moelans, N., Blanpain, B., and Wollants, P. (2008). Quantitative Analysis of Grain Boundary Properties in a Generalized Phase Field Model for Grain Growth in Anisotropic Systems. Phys. Rev. B 78, 024113. doi:10.1103/physrevb.78.024113

CrossRef Full Text | Google Scholar

Moradi, A. (2015). Maxwell-Garnett Effective Medium Theory: Quantum Nonlocal Effects. Phys. Plasmas 22, 042105. doi:10.1063/1.4917252

CrossRef Full Text | Google Scholar

Oudriss, A., Creus, J., Bouhattate, J., Conforto, E., Berziou, C., Savall, C., et al. (2012). Grain Size and Grain-Boundary Effects on Diffusion and Trapping of Hydrogen in Pure Nickel. Acta Mater. 60, 6814–6828. doi:10.1016/j.actamat.2012.09.004

CrossRef Full Text | Google Scholar

Rasch, K.-D., Siegel, R. W., and Schultz, H. (1980). Quenching and Recovery Investigations of Vacancies in Tungsten. Philos. Mag. A 41, 91–117. doi:10.1080/01418618008241833

CrossRef Full Text | Google Scholar

Ratanaphan, S., Boonkird, T., Sarochawikasit, R., Beladi, H., Barmak, K., and Rohrer, G. S. (2017). Atomistic Simulations of Grain Boundary Energies in Tungsten. Mater. Lett. 186, 116–118. doi:10.1016/j.matlet.2016.09.104

CrossRef Full Text | Google Scholar

Rieth, M., Doerner, R., Hasegawa, A., Ueda, Y., and Wirtz, M. (2019). Behavior of Tungsten under Irradiation and Plasma Interaction. J. Nucl. Mater. 519, 334–368. doi:10.1016/j.jnucmat.2019.03.035

CrossRef Full Text | Google Scholar

Sakurada, S., Uemura, Y., Fujita, H., Azuma, K., Toyama, T., Yoshida, N., et al. (2017). Impact of Annealing on Deuterium Retention Behavior in Damaged W. Fusion Sci. Technol. 72, 785–788. doi:10.1080/15361055.2017.1350480

CrossRef Full Text | Google Scholar

Stepper, H.-J. (1972). Recrystallization of α Particle Irradiated Tungsten. Mt 3, 2293–2294. doi:10.1007/bf02643247

CrossRef Full Text | Google Scholar

Taketomi, S., Matsumoto, R., and Miyazaki, N. (2008). Atomistic Study of Hydrogen Distribution and Diffusion Around a {112} Edge Dislocation in Alpha Iron. Acta Mater. 56, 3761–3769. doi:10.1016/j.actamat.2008.04.011

CrossRef Full Text | Google Scholar

Ueda, Y., Funabiki, T., Shimada, T., Fukumoto, K., Kurishita, H., and Nishikawa, M. (2005). Hydrogen Blister Formation and Cracking Behavior for Various Tungsten Materials. J. Nucl. Mater. 337-339, 1010–1014. doi:10.1016/j.jnucmat.2004.10.077

CrossRef Full Text | Google Scholar

Vaidya, W. V., and Ehrlich, K. (1983). Radiation-Induced Recrystallization, its Cause and Consequences in Heavy-Ion Irradiated 20% Cold-Drawn Steels of Type 1.4970. J. Nucl. Mat. 113, 149–162. doi:10.1016/0022-3115(83)90137-X

CrossRef Full Text | Google Scholar

Wang, H., Biswas, S., Han, Y., and Tomar, V. (2018). A Phase Field Modeling Based Study of Microstructure Evolution and its Influence on Thermal Conductivity in Polycrystalline Tungsten under Irradiation. Comput. Mater. Sci. 150, 169–179. doi:10.1016/j.commatsci.2018.03.070

CrossRef Full Text | Google Scholar

Wang, J.-J., Wang, Y., Ihlefeld, J. F., Hopkins, P. E., and Chen, L.-Q. (2016). Tunable Thermal Conductivity via Domain Structure Engineering in Ferroelectric Thin Films: A Phase-Field Simulation. Acta Mater. 111, 220–231. doi:10.1016/j.actamat.2016.03.069

CrossRef Full Text | Google Scholar

Wang, L. F., Shu, X., Lin, D. Y., et al. (2019). Molecular Dynamics Studies of Hydrogen Diffusion in Tungsten at Elevated Temperature: Concentration Dependence and Defect Effects. Int. J. Hydrogen Energy 45, 822–834. doi:10.1016/j.ijhydene.2019.10.151

CrossRef Full Text | Google Scholar

Xue, Y., and Hassanein, A. (2014). Kinetic Monte Carlo Simulation of Hydrogen Diffusion on Tungsten Reconstructed (0 0 1) Surface. Fusion Eng. Des. 89, 2545–2549. doi:10.1016/-j.fusengdes.2014.06.001

CrossRef Full Text | Google Scholar

Yang, L., and Wirth, B. D. (2019). First-principles Study of Hydrogen Diffusion and Self-Clustering below Tungsten Surfaces. J. Appl. Phys. 125, 1651051–2165105.14. doi:10.1063/1.5092595

CrossRef Full Text | Google Scholar

Yang, X., and Oyeniyi, W. O. (2017). Kinetic Monte Carlo Simulation of Hydrogen Diffusion in Tungsten. Fusion Eng. Des. 114, 113–117. doi:10.1016/j.fusengdes.2016.12.012

CrossRef Full Text | Google Scholar

Yu, Y., Shu, X., Liu, Y.-N., and Lu, G.-H. (2014). Molecular Dynamics Simulation of Hydrogen Dissolution and Diffusion in a Tungsten Grain Boundary. J. Nucl. Mater. 455, 91–95. doi:10.1016/j.jnucmat.2014.04.016

CrossRef Full Text | Google Scholar

Zhou, H., Yu, J., Chen, C., and Zhu, K. (2019a). Effect of Pre-damage Induced by Argon Ions on the Deuterium Blister Formation in Tungsten-Tantalum Alloys Exposed to Deuterium Plasma. Int. J. Hydrogen Energy 44, 23320–23329. doi:10.1016/j.ijhydene.2019.07.061

CrossRef Full Text | Google Scholar

Zhou, X., Mousseau, N., and Song, J. (2019b). Is Hydrogen Diffusion along Grain Boundaries Fast or Slow? Atomistic Origin and Mechanistic Modeling. Phys. Rev. Lett. 122, 215501. doi:10.1103/physrevlett.122.215501

PubMed Abstract | CrossRef Full Text | Google Scholar