- 1School of Mechanical, Electronic and Control Engineering, Beijing Jiaotong University, Beijing, China
- 2State Key Laboratory of Tribology, Tsinghua University, Beijing, China
In this article, a full-scale computational model for fluid–particle interaction under a magnetic field is developed. In this model, the fluid field is solved by the lattice Boltzmann method, and the hydrodynamic force acting on the particle is computed by the immersed boundary method . The numerical solutions of the magnetic field in the fluid–solid domain are achieved by the immersed interface method with a finite difference scheme, in which the normal and tangential jump conditions of the magnetic field intensity are applied to modify the standard finite difference scheme. The magnetic stress tensor along the fluid–particle interface can be calculated accurately. Unlike the widely used point–dipole model, the magnetic force acting on the particle is determined by the stress integration method. Numerical simulation of several numerical tests are carried out to validate the proposed model. The numerical results demonstrate the validity of the present model. Moreover, the magnetoviscous effect is studied by simulating the motion of elliptical particles under the uniform magnetic field in shear flow.
Introduction
Fluid–particle two-phase flows under a magnetic field can be usually found in nature and engineering applications, ranging from mineral screening (Ku et al., 2015), microfluidic control systems (Cao et al., 2014), magnetorheological fluid (Climent et al., 2004), and other chemical and biological applications. For the modeling of such flows, the two most important issues are to calculate the interaction forces between the particles and fluid/magnetic fields accurately and efficiently.
Fluid–particle interaction is one of the research hotspots in the computational fluid community. The existing models for fluid–particle interaction can fall into two categories: the Eulerian–Eulerian models and the Eulerian–Lagrangian models (Chiesa et al., 2005; Patel et al., 2017). The Eulerian–Eulerian models can capture the collective behavior of particles. However, it needs complex constitutive equations, and it is difficult to predict the details of the flow. Alternatively, the Eulerian–Lagrangian models easily obtain the detailed flowing behavior around the particles. The Eulerian–Lagrangian models can also be classified into two types: the point source model and the full-scale model (Luo et al., 2007; Hu et al., 2018). For the point source model, the empirical drag force formula is utilized to compute the fluid-particle interaction force. However, the point model i lacks enough accuracy for cases with dense or large-sized particles. For full-scale simulation, the fluid is governed by the Navier–Stokes equations, and the particle motion is solved by the Newtonian laws. The interaction force between the fluid and particle is determined by the no-slip condition. From this point of view, the full-scale model is most suitable for the study of flow mechanisms. Within the framework of full-scale models, the fixed mesh methods, which do not require time-consuming mesh generation, have received considerable attention in recent years. Unlike the body-fitted mesh methods, the governing equations of the fluid field are discretized on a fixed mesh, and the boundary is tracked by a set of Lagrangian points or captured by an implicit function. As a result, the computational efficiency is greatly improved. Kang et al. applied the distributed Lagrange multiplier/fictitious domain method to solve flows with suspended paramagnetic particles, in which the no-slip boundary condition on the particle boundary is implemented by Lagrange multipliers (Kang et al., 2008). Kang and Suh proposed the one-stage smoothed profile method for simulation of flows with suspended paramagnetic particles, in which the sigmoid function was used to construct body force by ensuring the rigidity of particles (Kang and Suh, 2011a). Kim and Park presented a level-set method for the analysis of magnetic particle dynamics on a fixed mesh (Kim and Park, 2010). Ke et al. introduced an IBM to simulate the behavior of magnetic particles in a fluid with an external magnetic field (Ke et al., 2017). These works show the effectiveness of fixed mesh methods in handling the fluid–particle interaction under a magnetic field.
In terms of calculation of magnetic force, the calculation models can also be divided into the point–dipole model and the force integration model. For example, Sand et al. developed a point–dipole model to simulate the magnetic particle suspension flow in which the single particle attraction force towards the magnetic pole was computed by a simple Kelvin force formula, and the interaction force between two nearby particles was computed by a magnetic dipole model (Sand et al., 2016). Like the point source model for fluid–particle interaction, the point–dipole model for particle–magnetic field interaction also suffers from inaccurate force estimation in nondilute flow or particle shape-dependent conditions. To this end, some work based on the force integration model has been done. In these models, the governing equation of the magnetic field in the multimedia zone was solved firstly. Then, the magnetic force acting on the particle can be obtained by integrating the force density. The magnetic force density can be calculated by the Helmholtz force density (Kang et al., 2008) or the virtual air gap scheme (Kang and Suh, 2011b). It should be pointed out that the fluid–particle interface is smeared out over several mesh cells in these above-the-force integration models. However, the magnetic stress force at the interface is treated as the continuous smoothed form, which will cause the loss of numerical accuracy.
In this paper, we develop a fully resolved simulation method for the fluid–particle interaction under a magnetic field. The LBM, which is a simple and efficient flow field solver, is adopted. The fluid–particle interaction is handled by the momentum-exchange-based IBM. More importantly, we give a Maxwell stress integration method to calculate the magnetic force based on the IIM with a finite difference scheme. According to the normal and tangential jump conditions of magnetic scalar potential along the medium interface, the discretized difference scheme is modified to ensure second-order accuracy. Then, the Maxwell stress tensor at the interface can be calculated accurately. The magnetic force acting on the particle can be obtained by integrating the magnetic stress force along the interface. Several numerical examples are simulated to validate the present IIM–IBM–LBM coupling model. The numerical results indicate that the present calculated stress force values agree well with the numerical results obtained by the body-fitted mesh. The circular particle sedimentation and motion of elliptical particles in shear flow under the magnetic field are also studied.
Mathematical Model and Numerical Method
In this study, LBM is used to simulate fluid flow, IBM is used to simulate the interaction between fluid and particles, and IIM is used to calculate magnetic field. In this section, we introduce the numerical implementation procedures of LBM, IBM, and IIM.
Lattice Boltzmann Model for Incompressible Fluid Flow
Using a standard uniform Cartesian grid with lattice space
where
where
where
The density and macrovelocity are written as
Immersed Boundary Method for the Fluid–Particle Interaction
The momentum exchange-based IBM proposed by Niu et al. (2006) is used to calculate the interaction force between fluid and solid particles. In Figure 1, the flow domain is covered with a uniform Cartesian grid, and the fluid–solid interface is divided into a series of Lagrange points
where
where
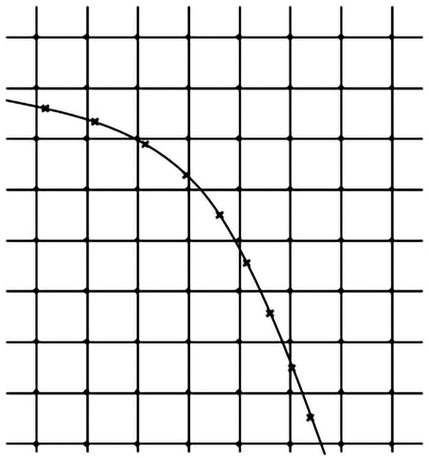
FIGURE 1. Configuration of the grids used in the IBM. Euler points (circles) represent the flow field and Lagrange points (crosses) represent the fluid–solid interface.
The calculation of the force density
Then, the new distribution function
where
Furthermore, we define
The hydrodynamic force
where
Immersed Interface Method for Magnetic Field Calculation
The magnetic field in the multimedia zone can be solved by the Maxwell equations with the interface conditions. As shown in Figure 2, we consider two types of methods to impose the magnetic field: one is the given external uniform magnetic field, and the other is the permanent magnetic field. The Maxwell equations without current are expressed as follows:
where
where
where
Due to the irrotationality condition of
The equations for solving the magnetic potential
The interface conditions for
In order to solve the magnetic field and compute magnetic force accurately, the IIM is used. The basic idea of IIM is to adopt the interface jump conditions to modify the finite difference scheme near the interface. As a result, second-order solutions can be achieved in the whole domain. A finite difference scheme for Poisson equation (Eq. 19) can be written as
for use at the point
The following formula is used to solve the magnetic field force.
The Maxwell stress tensor is
where
where
Here, we introduce a six-point interpolation method to calculate from the correct side of the interface. In Figure 3, for the point P on the interface, we find the nearest point
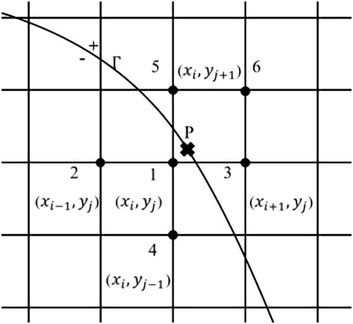
FIGURE 3. Selection of six points in the modified six-point method. Select the Euler point 1 closest to the Lagrange point (P), and the sixth point is the Euler point closest to the Lagrange point (P) except points 1 to 5.
Applying the Taylor expansion method for each point, we have
Ignoring the high order term
Particle Dynamics
In this study, the dynamics of particle adopts Newton’s equation of motion, and the equations controlling particle translation and rotation are as follows:
where
where
Then, the velocity
Numerical Results and Discussion
In this section, the present IIM–IBM–LBM model is used to simulate several problems with fluid–particle–magnetic interaction.
Numerical Method Validation
Particle Dynamics Verification of IB–LBM
In order to examine the accuracy of the present IB–LBM, the free settlement of a single particle is simulated, which has been used by some scholars as a benchmark problem (Glowinski et al., 2001; Hu et al., 2015). In Figure 4A, we use a fluid domain with a width of 2 cm and a height of 6 cm, where the fluid density is
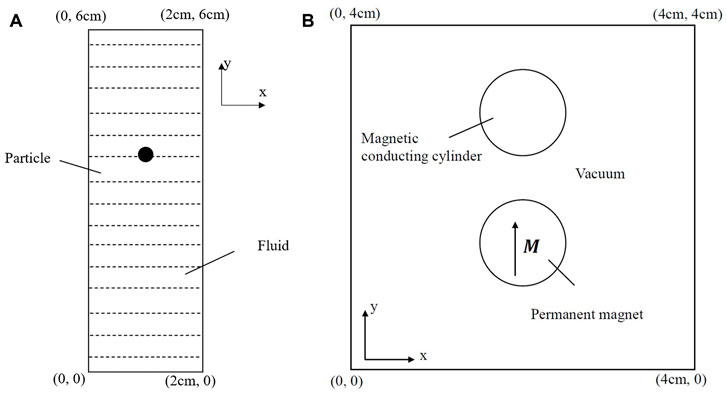
FIGURE 4. Model of free settlement of a single particle (A). Model of permanent magnet attracting magnetic conducting cylinder (B).
A
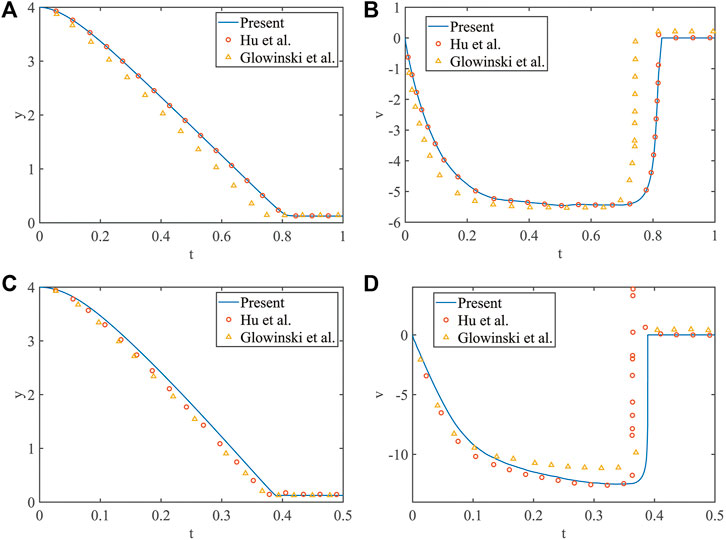
FIGURE 5. The position of the center of the particle for
Verification of Magnetic Field Calculation of IIM
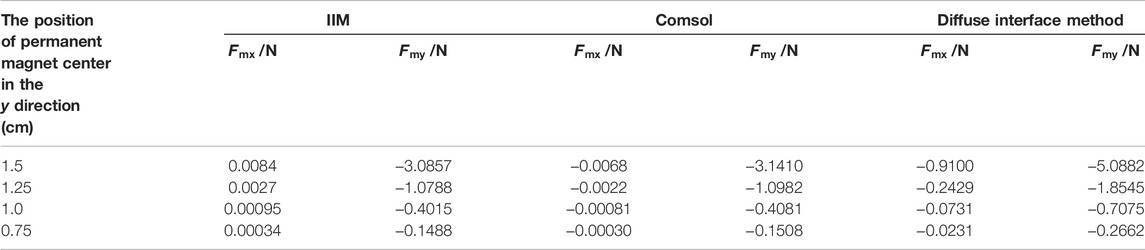
To test the accuracy of IIM in terms of calculation of magnetic field, the problem of a permanent magnet attracting a magnetic conducting cylinder is studied. The results obtained are compared with those calculated by COMSOL in which the body-fitted mesh is used. As shown in Figures 4A,B, a circular permanent magnet with remanence
This numerical simulation is carried out in a
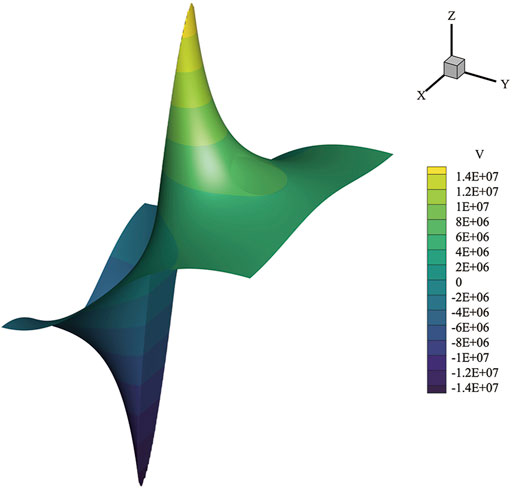
FIGURE 6. The magnetic potential
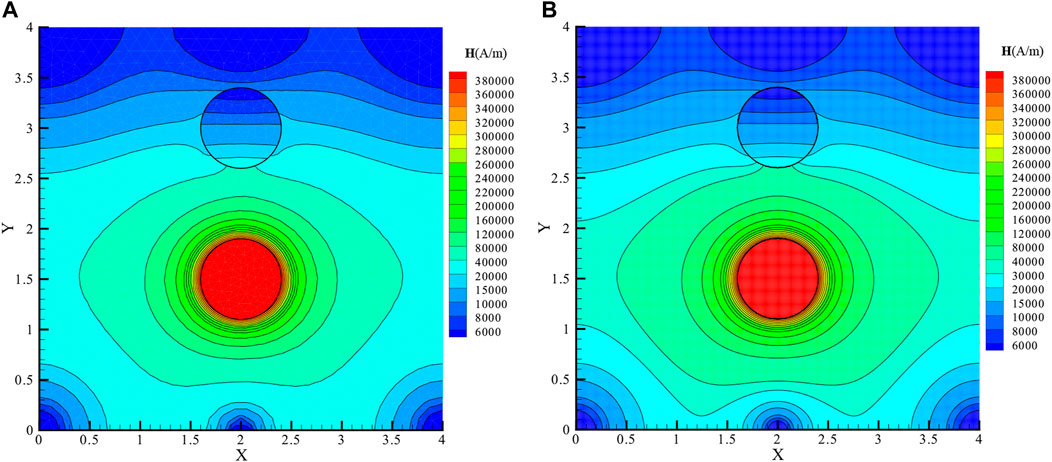
FIGURE 7. The permanent magnet attracts the magnetic field of the magnetic conducting cylinder model, which is calculated by COMSOL (A) and IIM (B).
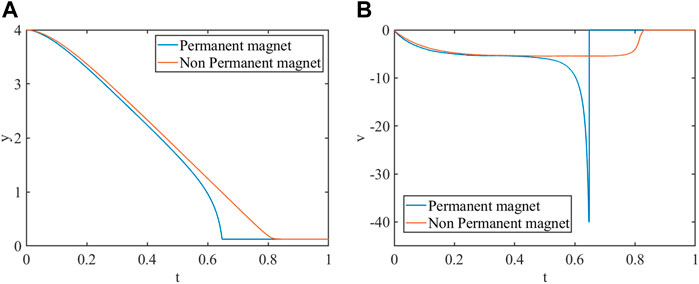
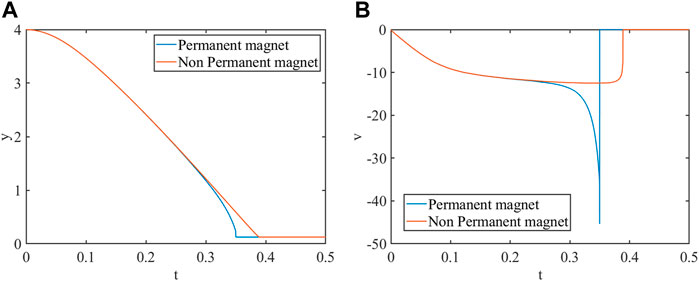
Particle Sedimentation Under Permanent Magnetic Field
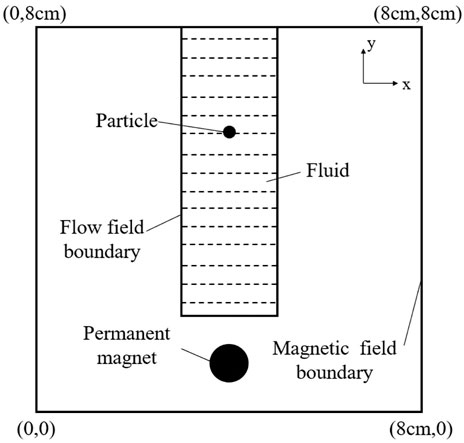
The diagram of particle sedimentation under a permanent magnetic field is shown in Figure 9. The computational domain for the magnetic field is 8 cm wide and 8 cm high. The computational domain for the flow field is 2 cm wide and 6 cm high. The circular particle with
A
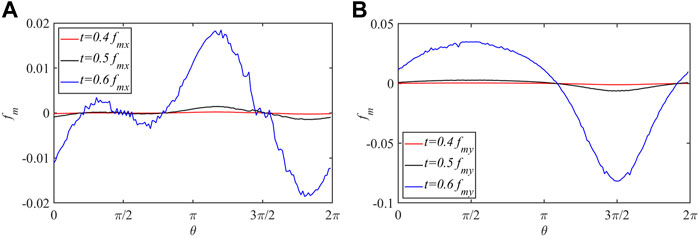
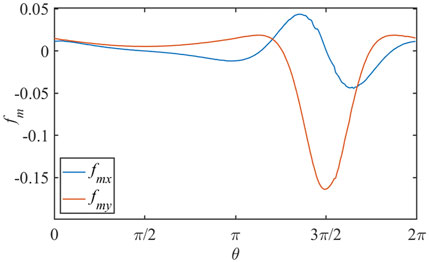
FIGURE 11. The magnetic stress
Shear Viscosity of Suspension Containing Elliptical Particles Under the Magnetic Field
It should be pointed out that the point–dipole model is suitable for spherical-like particles. We also consider an ellipsoidal particle immersed in the two-dimensional shear flows, as shown in Figure 13. In order to verify the reliability of the numerical method, we calculate an example of an elliptic particle rotating in a simple shear flow when Reynolds number
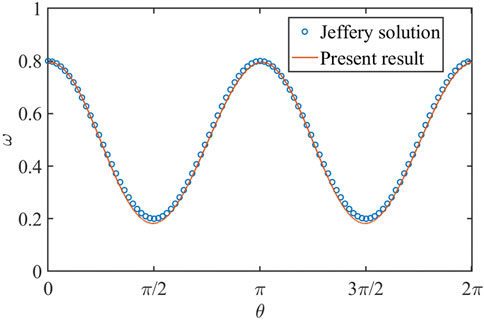
FIGURE 14. Comparison of Jeffery solution (Jeffery, 1922) and the present simulation result.
The relation between angular velocity
where the fluid shear rate
Then, we study the shear viscosity of suspension containing elliptical particles under the magnetic field. The computational domain is 2 cm long and 1 cm wide, in which the velocities of the upper and lower planes are
The shear stress at the fluid node is calculated as
To study the simple rheological properties of a suspension containing elliptical particles under the external magnetic field, the effective viscosity of the suspension is calculated:
where
A grid of
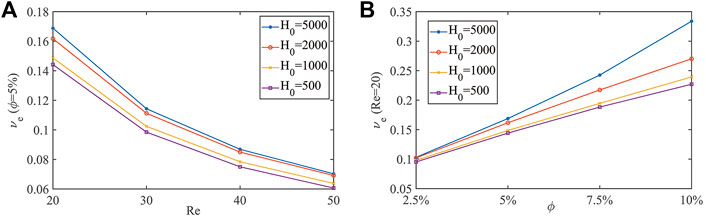
FIGURE 15. Variation of effective kinematic viscosity
Conclusion
The fluid–particle–magnetic interactions are modeled using the IIM–IBM–LBM coupling method. The fluid flow simulations are handled by the simple and efficient LBM. The particle motion and the hydrodynamics interaction between the particle and the flow field are computed by the momentum exchange-based IBM. Especially, we use the IIM to solve the magnetic field and calculate the magnetic force with the aid of the interface jump conditions. Unlike the point-source model or point dipole model, the hydrodynamics and magnetic forces acting on the particle are calculated using an integration method, in which the flow details and magnetic distribution around the particle are considered. Two numerical examples are simulated to verify the numerical accuracy of the present full-scale model. Moreover, particle sedimentation under a permanent magnetic field and shear viscosity of suspension containing elliptical particles under the magnetic field are also studied by the present model. The obtained results indicate that the present model has the potential to treat the complex fluid–particle–magnetic interactions.
Data Availability Statement
The original contributions presented in the study are included in the article/supplementary material; further inquiries can be directed to the corresponding author.
Author Contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Funding
This work was supported by the National Natural Science Foundation of China (grant nos. 12172039, 12102228, and 11802159) and Fundamental Research Funds for the Central Universities (grant no. 2020RC201).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Blūms, E., T͡Sebers, A. O., Cebers, A. O., and Maiorov, M. M. (1997). Magnetic Fluids. Berlin, Germany: Walter de Gruyter.
Cao, Q., Han, X., and Li, L. (2014). Configurations and Control of Magnetic Fields for Manipulating Magnetic Particles in Microfluidic Applications: Magnet Systems and Manipulation Mechanisms. Lab. Chip 14 (15), 2762–2777. doi:10.1039/c4lc00367e
Chen, S., and Doolen, G. D. (1998). Lattice Boltzmann Method for Fluid Flows. Annu. Rev. Fluid Mech. 30 (1), 329–364. doi:10.1146/annurev.fluid.30.1.329
Chiesa, M., Mathiesen, V., Melheim, J. A., and Halvorsen, B. (2005). Numerical Simulation of Particulate Flow by the Eulerian-Lagrangian and the Eulerian-Eulerian Approach with Application to a Fluidized Bed. Comput. Chem. Eng. 29 (2), 291–304. doi:10.1016/j.compchemeng.2004.09.002
Climent, E., Maxey, M. R., and Karniadakis, G. E. (2004). Dynamics of Self-Assembled Chaining in Magnetorheological Fluids. Langmuir 20 (2), 507–513. doi:10.1021/la035540z
Glowinski, R., Pan, T. W., Hesla, T. I., Joseph, D. D., and Périaux, J. (2001). A Fictitious Domain Approach to the Direct Numerical Simulation of Incompressible Viscous Flow Past Moving Rigid Bodies: Application to Particulate Flow. J. Comput. Phys. 169 (2), 363–426. doi:10.1006/jcph.2000.6542
Hu, Y., Li, D., Shu, S., and Niu, X. (2015). Modified Momentum Exchange Method for Fluid-Particle Interactions in the Lattice Boltzmann Method. Phys. Rev. E Stat. Nonlin Soft Matter Phys. 91 (3), 033301. doi:10.1103/PhysRevE.91.033301
Hu, Y., Li, D., Niu, X., and Shu, S. (2018). Fully Resolved Simulation of Particulate Flows with Heat Transfer by Smoothed Profile-Lattice Boltzmann Method. Int. J. Heat Mass Transf. 126, 1164–1167. doi:10.1016/j.ijheatmasstransfer.2018.05.137
Huang, H., Yang, X., Krafczyk, M., and Lu, X.-Y. (2012). Rotation of Spheroidal Particles in Couette Flows. J. Fluid Mech. 692, 369–394. doi:10.1017/jfm.2011.519
Jeffery, G. B. (1922). The Motion of Ellipsoidal Particles Immersed in a Viscous Fluid. Proc. R. Soc. Lond. Ser. A Contain. Pap. Math. Phys. Character 102 (715), 161–179. doi:10.1098/rspa.1922.0078
Kang, S., and Suh, Y. K. (2011). An Immersed-Boundary Finite-Volume Method for Direct Simulation of Flows with Suspended Paramagnetic Particles. Int. J. Numer. Meth. Fluids 67 (1), 58–73. doi:10.1002/fld.2336
Kang, S., and Suh, Y. K. (2011). Direct Simulation of Flows with Suspended Paramagnetic Particles Using One-Stage Smoothed Profile Method. J. Fluids Struct. 27 (2), 266–282. doi:10.1016/j.jfluidstructs.2010.11.002
Kang, T. G., Hulsen, M. A., den Toonder, J. M. J., Anderson, P. D., and Meijer, H. E. H. (2008). A Direct Simulation Method for Flows with Suspended Paramagnetic Particles. J. Comput. Phys. 227 (9), 4441–4458. doi:10.1016/j.jcp.2008.01.005
Ke, C.-H., Shu, S., Zhang, H., and Yuan, H.-Z. (2017). LBM-IBM-DEM Modelling of Magnetic Particles in a Fluid. Powder Technol. 314, 264–280. doi:10.1016/j.powtec.2016.08.008
Kim, Y. S., and Park, I. H. (2010). FE Analysis of Magnetic Particle Dynamics on Fixed Mesh with Level Set Function. IEEE Trans. Magn. 46 (8), 3225–3228. doi:10.1109/tmag.2010.2045747
Ku, J., Chen, H., He, K., and Yan, Q. (2015). Simulation and Observation of Magnetic Mineral Particles Aggregating into Chains in a Uniform Magnetic Field. Miner. Eng. 79, 10–16. doi:10.1016/j.mineng.2015.05.002
LeVeque, R. J., and Li, Z. (1994). The Immersed Interface Method for Elliptic Equations with Discontinuous Coefficients and Singular Sources. SIAM J. Numer. Anal. 31 (4), 1019–1044. doi:10.1137/0731054
Luo, K., Wang, Z., Fan, J., and Cen, K. (2007). Full-Scale Solutions to Particle-Laden Flows: Multidirect Forcing and Immersed Boundary Method. Phys. Rev. E Stat. Nonlin Soft Matter Phys. 76 (6), 066709. doi:10.1103/PhysRevE.76.066709
Niu, X. D., Shu, C., Chew, Y. T., and Peng, Y. (2006). A Momentum Exchange-Based Immersed Boundary-Lattice Boltzmann Method for Simulating Incompressible Viscous Flows. Phys. Lett. A 354 (3), 173–182. doi:10.1016/j.physleta.2006.01.060
Patel, R. G., Desjardins, O., Kong, B., Capecelatro, J., and Fox, R. O. (2017). Verification of Eulerian-Eulerian and Eulerian-Lagrangian Simulations for Turbulent Fluid-Particle Flows. AIChE J. 63 (12), 5396–5412. doi:10.1002/aic.15949
Peskin, C. S. (2002). The Immersed Boundary Method. Acta Numer. 11, 479–517. doi:10.1017/s0962492902000077
Keywords: full-scale simulation, fluid-particle interactions, magnetic field, immersed interface method, immersed boundary method, lattice Boltzmann method
Citation: Peng W, Hu Y, Li D and He Q (2022) Full-Scale Simulation of the Fluid–Particle Interaction Under Magnetic Field Based on IIM–IBM–LBM Coupling Method. Front. Mater. 9:932854. doi: 10.3389/fmats.2022.932854
Received: 30 April 2022; Accepted: 03 June 2022;
Published: 05 August 2022.
Edited by:
Xuan Shouhu, University of Science and Technology of China, ChinaReviewed by:
Huaxia Deng, University of Science and Technology of China, ChinaXufeng Dong, Dalian University of Technology, China
Copyright © 2022 Peng, Hu, Li and He. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yang Hu, eWFuZ2h1QGJqdHUuZWR1LmNu
 Wei Peng
Wei Peng Yang Hu1*
Yang Hu1* Decai Li
Decai Li Qiang He
Qiang He