Abstract
In this article, the phase stability, elastic properties, and electronic structure of the β-TiX (X = Nb, Ta) alloy body-centered cubic (bcc) structure were systematically studied with the aid of first-principles calculations. The results show that the phase stability and elastic properties of the β-TiX alloys are closely related to the contents of alloying element X. For β-TiX alloys, the contents of Nb and Ta that satisfy their mechanical stability are 10% and 13%, respectively; at room temperature, both β-TiNb and β-TiTa alloys can reach a thermodynamically stable state when the content of Nb or Ta is 25%. In terms of elastic properties, the content of alloying element X is positively correlated with the elastic constant, Young’s modulus, and shear modulus of the β-TiX alloys. The elastic modulus reaches its minimum when the X content is 25%, and the smallest direction of Young’s modulus appears in the <111> direction. The calculation results of the electronic structure show that the bonding strength between the Ti atom and X atom increases with the content of alloying element X, which leads to improvement of phase stability and elastic modulus.
1 Introduction
Since the 1990s, β-Ti alloys with body-centered cubic (bcc) structure have become the primary research focus of biomedical Ti alloys due to their lower elastic modulus, better biocompatibility, higher strength, and corrosion resistance (Rack and Qazi, 2006; Geetha et al., 2009). β-Ti alloys can be obtained by adding transition metal (TM) elements, which can reduce the relatively high stiffness (Jackson and Dring, 2013; Hao et al., 2018). The alloying is an important way to improve the mechanical properties of titanium alloy and enhance the stability of the phase. The stability, biocompatibility, and non-toxicity of alloying elements are important for the selection of β-type biomedical titanium alloying elements. Nb and Ta are commonly added to β-type biomedical titanium alloys. On the one hand, as strong β-phase stable elements, Nb and Ta can inhibit the formation of non-equilibrium phases such as α′, α′′, and ω phase and effectively reduce the modulus of titanium alloy (Lee et al., 2002; Zhou et al., 2004). On the other hand, Nb and Ta have good biocompatibility and less toxicity and are considered to be safe biomedical alloying elements (Zhang et al., 2010). Generally speaking, thermoelastic martensite β→α′′ transformation or thermal ω phase formation will proceed with low content of TM elements and poor phase stability (Formanoir et al., 2019; Kapoor et al., 2020). However, the elastic modulus of the bcc structure will be increased with the additional content of TM alloying elements (Banerjee and Williams, 2013; Huang et al., 2021). This contradiction is a problem that needs to be solved urgently.
Recently, with the rapid development of computer-aided material design, the first-principles methods based on density functional theory have been widely used to study the elastic properties, phase stability, and electronic structure of β-Ti alloys. The study by Yu et al. showed that the non-spherical distribution of electrons will lead to difficult plastic deformation of the alloy and high modulus. Koval et al., (2019) also analyzed the effect of electronic structure on the elastic properties of β-Ti alloys. Zhang et al., (2016) used the first-principles method to study the effect of alloying element content on the phase stability of binary titanium alloys. Moreno et al., (2017; Moreno et al., (2018) determined the most stable structure of Ti1-xNbx (x < 31.5%) alloy by using the energy minimization method and calculated its elastic constant by using the first-principles full potential supplemented plane wave. Jia et al., (2020) simulated the effect of doping trace transition metal elements on the stability of β-Ti alloys by density functional theory. However, the studies mentioned above ignored the effect of temperature on the thermodynamic stability of β-Ti alloys. In addition, the composition range of alloys adopted in those studies is too limited to carry out the alloy design. These shortcomings lead to lack of effective theoretical support for the composition design of β-Ti alloy, which is not conducive to further research.
Therefore, based on the first-principles method, this work researched the influence of Nb and Ta contents on the mechanical stability, thermodynamic stability, and elastic properties of β-TiX (X = Nb, Ta) alloys. The supercell method is used to approximate disordered solid solution properties. In this study, the calculation has been performed systematically from the perspective of the structure, formation enthalpy, Gibbs free energy, elastic constant, and electronic structure of β-TiX (X = Nb, Ta) alloys with different compositions. First, according to the Gibbs free energy, the alloy composition range satisfying the thermodynamic stability was determined. Second, based on the single-crystal elastic constants, Young’s modulus and shear modulus of the β-TiX (X = Nb, Ta) alloys were predicted and evaluated by the Hill arithmetic averaging method, and the elastic anisotropy was analyzed. Finally, in line with the electronic structure, the influence mechanism of alloying element content on the stability and elastic properties of β-TiX (X = Nb, Ta) alloys was expounded from the electronic level.
2 Computational Methodology
2.1 Computational Settings
In this research, density functional theory calculations were performed by means of the Vienna ab initio simulation package (VASP) (Kresse and Furthmüller, 1996a; b), which is based on the projected augmented wave (PAW) method (Blochl, 1994). The generalized gradient approximation parameterized by Perdew, Burke, and Ernzerhof (GGA-PBE) (Perdew et al., 1996) was used as the exchange–correlation function. The valence electron configurations of the PAW potentials were 3s23p63d24s2 for Ti, 4s24p64d45s1 for Nb, and 5s25p65d36s2 for Ta. The supercell method was used to calculate the total energy and the elastic moduli of the β-TiX (X = Nb, Ta) binary alloys with different compositions. A 2 × 2 × 2 supercell containing eight β-Ti bcc unit cells (space group Im3m) was constructed, and the number of Ti atoms is 16. The Ti atoms in the supercell were replaced at intervals of 2 by Nb or Ta atoms. The nominal molecular formula of β-TiX (X = Nb, Ta) alloys is Ti16-nXn (X = Nb, Ta; n = 0, 2, 4, 6, 8, 10, 12, 14, 16), as shown in Figure 1.
FIGURE 1
Models of β-TiX (X = Nb, Ta) alloys.
During the calculation, a plane-wave expansion of the wave functions with a cut-off energy of 500 eV, and the Brillouin Zone (BZ) was sampled with a Monkhorst-Pack k-point grid (Monkhorst and Pack, 1976). Then, a 10 × 10 × 10 k-point mesh was used for structure optimization. In calculations related to the density of states (DOS), the one-electron wave functions were expanded in a plane-wave basis set with an energy cut-off of 600 eV. For the usually sensitive calculations of the elastic tensor, the energy cut-off was increased to 700 eV. The energy convergence criterion of the electron step self-consistent cycle was 1.0 × 10–7 eV. The convergence criterion of the ion step is that the interatomic force was less than 0.01 eV/Å. Energy-volume fitting comprised the Birch–Murnaghan equation of state (Birch, 1947) so as to obtain the corresponding equilibrium volume of each component, and the calculations of the total energy were performed by using the tetrahedron method with Blöchel correction (Blöchl et al., 1994).
2.2 Calculation of Thermodynamic Stability
The formation enthalpy can be described as follows:where , , and represent the total energy of the system, the energy of a single Ti atom, and the energy of a single X atom, respectively and and correspond to the number of Ti atoms and X atoms in the system according to its subscript, respectively.
The Gibbs free energy can be expressed bywhere stands for the mixing entropy of the alloys, is the free energy of lattice vibration of the alloys, and represents the temperature. The mixing entropy of the alloys can be calculated bywhere is the atomic percentage of alloying element X (Nb, Ta) and is the Boltzmann constant. For stable structure alloys, the effect of lattice vibration on Gibbs free energy is generally much less than that of the mixing entropy (Benisek et al., 2014). Therefore, in this case, the influence of is ignored. Based on Eqs 1, 2, 3, the Gibbs free energy of the β-TiX (X = Nb, Ta) alloys can be obtained at a range of temperatures.
2.3 Calculation of the Elastic Properties
The elastic constant of the single crystal can be obtained by the relationship between stress and strain. Hooke’s law can be expressed as represents the 6 × 6 stiffness matrix. represents the stress tensor, and represents the strain tensor. Both and were given by the Viogt notation. The Viogt notation is a representation method that converts two indexes into one index: 11→1, 22→2, 33→3, 32 (23)→4, 13 (31)→5, and 12 (21)→6. Also, the strain tensor is defined as
The number of independent elastic constants is different if crystal structures vary. The higher the degree of symmetry of the crystal structure, the less the number of independent elastic constants will be. So, there are only three independent elements , , and which exist in β-TiX (X = Nb, Ta) alloys to account for cubic symmetry.
All the elastic constants of the crystal structure can be obtained by calculating the total energy change after elastic strain which can be expanded by the Taylor formula as (Giustino, 2014):where and represent the total energy of the system before and after strain, respectively, and represents the crystal volume before strain. Since the number of independent elastic constants in the bcc structure is three, the same amount of cubic crystal strains needs to be applied, as shown in Table 1. Each independent elastic constant is contained in the second-order coefficients of the Taylor expansion. Several strain values ( = −0.04, −0.02, 0, 0.02, 0.04) are selected to fit the total energy.
TABLE 1
| Applied Strain (unlisted eij = 0) | The energy of the cubic crystal subjected to the strain on the left column | ΔD/V0 |
|---|---|---|
| e 4 = e5 = e6 = δ | ||
| e 1 = e2 = δ | ||
| e 1 = e2 = e3 = δ |
Strains used to calculate the elastic constants of β-TiX (X = Nb, Ta) alloys.
In addition, since the independent elastic constants are included in the quadratic coefficient, the energy change after strain must be a positive value, which can determine whether the dynamics of the cubic crystal is stable:
The elastic constants of polycrystalline materials, such as bulk (B) modulus and Young’s (E) modulus, can be derived from the independent elastic constants calculated in the previous section. The maximum and minimum values of the elastic constants are given by the Voigt and Reuss averaging procedures, respectively, (Voigt, 1910; Reuss, 1929).
In order to reduce the deviation, the Hill arithmetic averaging is adopted in this work (Hill, 1952). The formula for calculating the bulk modulus of the bcc structure is the same under the three methods (Hill arithmetic average, Voigt, and Reuss averaging procedures):Also, the theoretical polycrystalline Young’s modulus and shear modulus can be obtained by the Hill average method as follows:where and are the Reuss and Voigt averages, respectively, which can be described in the following forms:
In addition, the effects of Nb or Ta content on the critical stress for the slips of <111> on {011}, {112}, or {123} planes were evaluated. The shear modulus along <111> on {011},{112}, or {123} of the bcc structure alloys is estimated based on the elastic constants by the following equation:
Then, the ideal shear strength can be expressed as
3 Results and Discussion
3.1 Lattice Constants
Calculating lattice constants can estimate the effectiveness of structural optimization. Figure 2 illustrates the curve of the lattice constant of the β-TiX (X = Nb, Ta) alloys with the content of alloy elements X. For comparison, lattice parameter data from several other experimental or simulated works (Ikehata et al., 2004; Kim et al., 2006; Wan et al., 2014) are also presented in Figure 2. Among them, the black marks represent related work on TiNb alloys, and the red marks represent related work on TiTa alloys. It can be clearly seen that the lattice constant of β-TiX (X = Nb, Ta) alloys increases linearly with the increase of the alloying element X content. With the increase of the alloying element Nb and Ta content, the lattice constants of β-TiNb and β-TiTa increased by about 1.7% and 2%, respectively. This is because the atomic radius of Nb and Ta are larger than that of Ti, and the atomic radius of Ta is slightly larger than that of Nb.
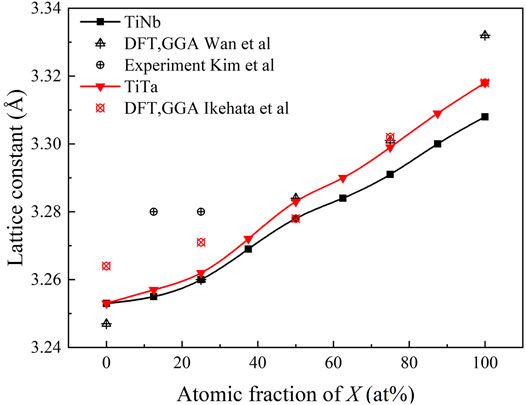
FIGURE 2
Lattice constants (Å) of β-TiX (X = Nb, Ta) alloys. (Wan et al., 2014) (Kim et al., 2006); (Ikehata et al., 2004)
3.2 Thermodynamic Stability
It is well known that the thermodynamic stability of materials can be determined by calculating the formation enthalpy and Gibbs free energy. Figure 3 shows the relationship between the formation enthalpy and the content of alloying elements. The formation enthalpies of β-TiX (X = Nb, Ta) alloys are greater than 0. Moreover, as the content of alloying elements increases, the formation enthalpies all show a downward trend. In addition, the formation enthalpy of the β-TiTa alloy is always higher than that of the β-TiNb alloy, which indicates that Nb can provide better β-phase stability than Ta as an alloying element.
FIGURE 3
Formation enthalpy of β-TiX (X = Nb, Ta) alloys.
The Gibbs free energy of the β-TiX (X = Nb, Ta) alloys is shown in Figure 4. If is less than zero, the alloy is thermodynamically stable at the corresponding temperature. It can be clearly seen that as the temperature increases, the Gibbs free energy of β-TiX (X = Nb, Ta) decreases. Also, the Gibbs free energy of β-TiNb is always lower than that of β-TiTa at the same composition and temperature, which also interprets that Nb provides stronger phase stability than Ta. Among other things, the Gibbs free energy of β-TiX (X = Nb, Ta) alloys almost always reaches its minimum value when the alloying element content is about 50% because the mixing entropy of the alloys has the maximum value when the composition is similar, whereas at the position of about 75% alloying element content, the Gibbs free energy curve of the β-TiTa alloy shows a peak. Therefore, in the range of 200–600 K, there are two troughs in the Gibbs free energy curve of the β-TiTa alloy, which is due to the amplitude modulation decomposition of the β-TiTa alloy in this temperature range. It should be pointed out that the dotted line in Figure 4 is at the position of . As a matter of fact, at room temperature (about 300 K), both β-TiNb and β-TiTa can reach a thermodynamically stable state when the alloying element content is more than 25%.
FIGURE 4
Gibbs free energies of (A)β-TiNb and (B)β-TiTa alloys.
3.3 Elastic Properties
3.1.1 Elastic Constants
The , , and of β-TiX (X = Nb, Ta) alloys change with alloying element content as shown in Figure 5. Both and increase with the increase of alloying element content. In the case of , the calculation results have different degrees of underestimation. This phenomenon also exists in other transition metal simulation calculations, and some reports have pointed out that it is caused by the existence of Van Hove singularity (Katahara et al., 1979; Koči et al., 2008; Nagasako et al., 2010). Moreover, the anomalies of have been captured experimentally at low temperatures in transition metals (Talmor et al., 1977; Walker, 1978; Walker and Bujard, 1980), which also indicates that the calculation results are reasonable.
FIGURE 5
Single-crystal constants of (A)β-TiNb and (B)β-TiTa alloys.
Both and are automatically met because is always positive. Hence, the mechanical stability of the alloys depends on . Figure 6 shows the change of the in the β-TiX (X = Nb, Ta) alloys. The value of increases with the increase of the alloying element's content, and the value of is 0 when Nb element content is 10% or Ta element content is 13%. In other words, the bcc structure β-TiX (X = Nb, Ta) alloys can satisfy the mechanical stability requirements when Nb content is greater than 10% in the β-TiNb alloy or Ta content is greater than 13% in the β-TiTa alloy.
FIGURE 6
Mechanical stability of β-TiX (X = Nb, Ta) alloys.
3.3.2 Young’s Modulus and Shear Modulus
The Young’s modulus of β-TiX (X = Nb, Ta) alloys is shown in Figure 7. For β-TiNb, Young’s modulus reaches the minimum value of 40.75 GPa when the Nb content is about 25%. Then, Young’s modulus increases with the increase of Nb content. But, Young’s modulus slightly decreases when the Nb content is about 75%. For β-TiTa, when the Ta content is 12.5% and 25%, Young’s modulus is basically equivalent. After that, Young’s modulus kept increasing monotonously. The mechanical stability of 12.5% Ta does not meet the requirements. Therefore, the minimum Young’s modulus of β-TiTa is obtained when the Ta content is 25%, and its value is 37.36 GPa.
FIGURE 7
Young’s moduli of (A)β-TiNb and (B)β-TiTa alloys.
The DFT method can also be used to calculate the anisotropy of Young’s modulus (Wróbel et al., 2012). It has been pointed out that the direction of low Young’s modulus is more conducive to the formation of texture and the nucleation of metastable martensite (Hanada et al., 2014; Guo et al., 2015; Hou et al., 2016). Therefore, the analysis of elastic anisotropy and the direction of the minimum value of Young’s modulus is helpful in further regulating the elastic properties of β-TiX (X = Nb, Ta) alloys. Figure 8 shows the distribution of Young’s modulus of β-TiX (X = Nb, Ta) alloys with 25%, 37.5%, and 50% alloying elements. The closer to the origin of the space coordinate system, the smaller Young’s modulus will be. Young’s modulus of Ti12Nb4 has a minimum value in the <100> direction in Figure 8A. In Figure 8C, the minimum value of Young’s modulus shifts from the <100> direction to the <111> direction. Also, Young’s modulus of Ti10Nb6 has a minimum value in the <111> direction in Figure 8B. Later, as the Nb content increases, the minimum value of Young’s modulus remains in the <111> direction. For β-TiTa alloy in Figures 8D–F, Young’s modulus of Ti12Ta4 has a minimum value in the <100> direction, but when the Ta element content reaches 37.5%, Young’s modulus in all directions is basically the same, and the subsequent change is small. Overall, as the atomic ratio of β-TiX (X = Nb, Ta) alloys gradually increases to 1, its elastic anisotropy gradually increases.
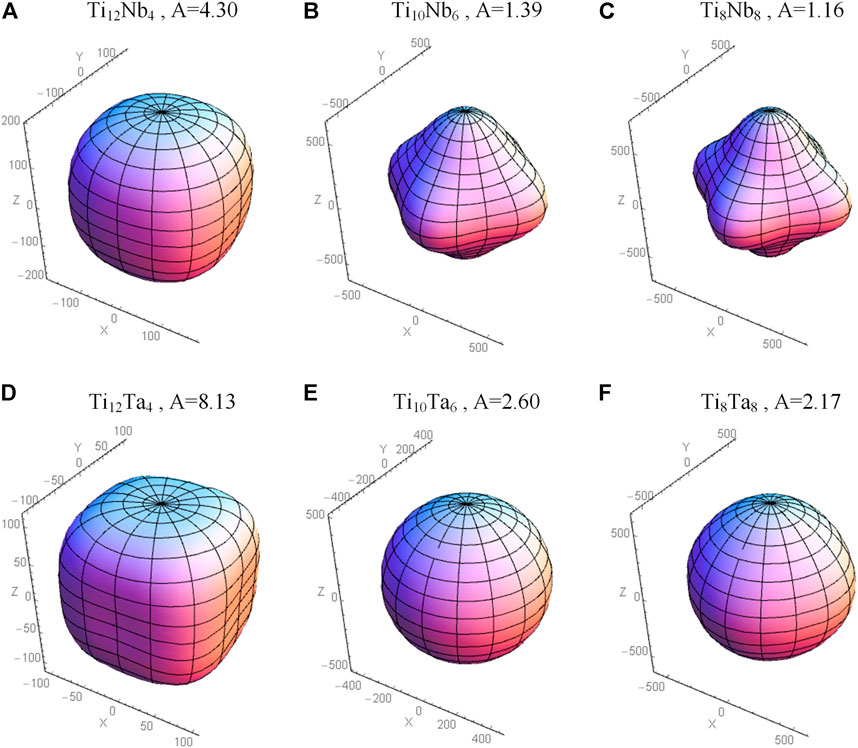
FIGURE 8
Young’s moduli of (A) Ti12Nb4, (B) Ti10Nb6, (C) Ti8Nb8, (D) Ti12Ta, (E) Ti10Ta, and (F) Ti8Ta8. (The Zener ratio is a measure of the elastic anisotropy.)
Figure 9 shows the shear moduli of β-TiX (X = Nb, Ta) alloys. With the increases in alloying element content, the value has increased to varying degrees. The value of β-TiTa basically keeps increasing linearly, while the growth of the value of β-TiNb gradually becomes slow. Moreover, Ta has a stronger influence on the shear modulus of β-TiX (X = Nb, Ta) alloys than Nb. The result shows that the higher the content of β-phase stabilizing elements in the titanium alloys, the higher the critical stress required for slip deformation.
FIGURE 9
Shear moduli of (A)β-TiNb and (B)β-TiTa alloys.
3.4 Electronic Structure
In this section, the total density of states (TDOS) and partial density of states (PDOS) of β-TiX (X = Nb, Ta) alloys are calculated to reveal the influence mechanism of alloying element X content on the phase stability and mechanical properties of β-TiX alloys, as shown in Figure 10. The dotted line in Figure 10 represents the position of the Fermi level, at x = 0. The left side of the Fermi level is the valence band and the right side is the conduction band. First, it can be seen that the TDOS near the Fermi level of both β-TiNb and β-TiTa alloys mainly originates from the contribution of Ti-d and X-d orbital electrons. This indicates that the phase stability and mechanical properties of the β phase of titanium alloy are closely related to the d-orbital electrons, which is consistent with the report of Kuroda et al., (1998). Second, the TDOS value corresponding to the position of the Fermi level is related to phase stability, and the lower the value is, the more stable the structure is (Guo and Wang, 2000). It can be seen from Figure 10 that as the content of alloy element X increases, the value corresponding to the position of the Fermi level on the TDOS image of β-TiX alloys gradually decreases. This indicates that the phase stability of β-TiX alloys is improved with the increase of the content of Nb and Ta elements, which can be attributed to the fact that alloying elements Nb and Ta can provide additional d-orbital electrons. In addition, dp valence state orbital hybridization of the alloying element X and Ti is found in the conduction band near the Fermi level. This hybridization phenomenon can increase the bonding strength, which is not only beneficial to improve the phase stability of β-TiX alloys but also to improve their tensile strength. The abovementioned points also explain why the elastic modulus of β-TiX alloys increases when the alloying element X content exceeds 25%.
FIGURE 10
TDOS and PDOS of (A)β-TiNb and (B)β-TiTa alloys.
To understand the bonding characteristic more intuitively and vividly, the three-dimensional difference charge densities map of β-TiX alloys is plotted by the VESTA package (Momma and Izumi, 2008) and shown in Figure 11. In each plot, the atomic positions of all alloying elements are the same as in the model in Figure 1. The yellow area represents the gain of electrons, while the blue area represents the loss of electrons. It can be seen from Figure 11 that the Ti atom in β-TiX alloys loses electrons and the alloying element X gains electrons. Also, there is almost no difference in charge density between Ti–Ti atomic pairs and X–X atomic pairs, showing typical metallic properties. When the content of alloying elements is low, as shown in Figures 11A,B,E,F, the charge density profile between Ti-X atoms is symmetrically distributed, which indicates the existence of weak metallic bonds between Ti-X atoms (Ouadah et al., 2020). As the content of alloying element X increases, the bonding electron density between Ti atoms and X atoms is obviously increased and forms the ring-type features, leading to an increase in bond strength and indicating an effective solid-solution strengthening the effect. When alloying element X content is 37.5%, as shown in Figures 11C,G, the distribution of electron cloud between solute atom X and solvent atom Ti is asymmetrical. The non-spherical distribution of electrons will act as a barrier to make deformation difficult and high modulus in the plastic deformation process of the material, while this is consistent with the research results of Yu et al., (2021). When the alloying element X content reaches 50%, as shown in Figures 11D,H, the Ti-X bond is strengthened by sharing electron pairs to form a covalent bond, and the bonding direction is obviously concentrated in the <111> direction. This result is consistent with that of the previous studies on thermodynamic stability and elastic anisotropy. Moreover, by comparing the difference charge density of β-TiNb and β-TiTa alloys with the same content of alloying elements, it can be seen that the bonding effect of β-TiNb alloys is better than that of β-TiTa alloys, which is consistent with the conclusion of formation enthalpy.
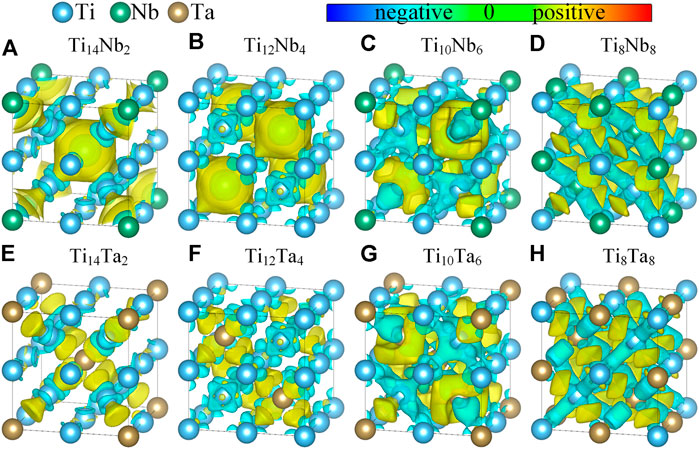
FIGURE 11
Difference charge densities of β-TiX (X = Nb, Ta) alloys. (A) Ti14Nb2; (B) Ti12Nb4; (C) Ti10Nb6; (D) Ti8Nb8; (E) Ti14Ta2; (F) Ti12Ta4; (G) Ti10Ta6; (H) Ti8Ta8. The value of all the isosurface level is 0.0051e/Å3.
4 Conclusion
This article presents an ab initio study of phase stability and elastic properties of
β-Ti
X(
X= Nb, Ta) alloys. The phase stability of the
β-Ti
X(
X= Nb, Ta) alloys was determined from two aspects of mechanical stability and thermodynamic stability. The elastic modulus was estimated by the Hill arithmetic averaging, and the elastic anisotropy was analyzed. Also, the influence mechanism of the content of alloying element
X(
X= Nb, Ta) on the phase stability and elastic properties of
β-Ti
X(
X= Nb, Ta) alloys was expounded from the electronic level. The conclusions of this study are as follows:
1) The mechanical stability of the β-TiX (X = Nb, Ta) alloys meets the requirements when the Nb element content is 10% in the β-TiNb alloy or when the Ta element content is 13% in the β-TiTa alloy.
2) The formation enthalpy of β-TiX (X = Nb, Ta) alloys decreases with the increase of alloying element Nb or Ta content. At room temperature (about 300 K), β-TiNb and β-TiTa alloys are thermodynamically stable when the content of alloying elements Nb or Ta is more than 25%.
3) The minimum Young’s modulus of β-TiX (X = Nb, Ta) alloys was obtained when the content of alloying elements is 25%. The minimum Young’s modulus of the β-TiNb alloy is 40.75 GPa and that of the β-TiTa alloy is 37.36 GPa.
4) As the alloy element's content increases, the minimum value of Young’s modulus of β-TiX (X = Nb, Ta) alloys shifts from the <100> direction to the <111> direction. Also, Young’s modulus anisotropy of the β-TiTa alloy is smaller than that of β-TiNb alloy.
5) Alloying element X (X = Nb, Ta) can provide additional d-orbital electrons, that is to say, the increase of alloying element X content will lead to the increase of valence electron concentration and bonding strength, thus improving the phase stability and elastic modulus of β-TiX (X = Nb, Ta) alloys.
In summary, the β-TiX (X = Nb, Ta) alloys with an alloying element content of 25% meet the requirements of mechanical stability and thermodynamic stability and have the lowest elastic modulus. The optimum content of β-TiNb and β-TiTa alloying elements determined in this work is 25%, and the corresponding elastic moduli under this composition are 40.75 and 37.36 GPa, respectively.
Statements
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding authors.
Author contributions
HSL, LJX, and WYX contributed to the conception and design of the study. HSL organized the database and performed the statistical analysis. HSL and WZM wrote the first draft of the manuscript. LJX, WYX, and YDY wrote sections of the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1
Banerjee D. Williams J. C. (2013). Perspectives on Titanium Science and Technology. Acta Mater.61 (3), 844–879. 10.1016/j.actamat.2012.10.043
2
Benisek A. Dachs E. Salihović M. Paunovic A. Maier M. E. (2014). The Vibrational and Configurational Entropy of α-brass. J. Chem. Thermodyn.71, 126–132. 10.1016/j.jct.2013.11.012
3
Birch F. (1947). Finite Elastic Strain of Cubic Crystals. Phys. Rev.71 (11), 809–824. 10.1103/PhysRev.71.809
4
Blöchl P. E. Jepsen O. Andersen O. K. (1994). Improved Tetrahedron Method for Brillouin-Zone Integrations. Phys. Rev. B49 (23), 16233. 10.1103/PhysRevB.49.16223
5
Blochl P. E. (1994). Projector Augmented-Wave Method. Phys. Rev. B50 (24), 17979. 10.1103/PhysRevB.50.17953
6
de Formanoir C. Martin G. Prima F. Allain S. Y. P. Dessolier T. Sun F. et al (2019). Micromechanical Behavior and Thermal Stability of a Dual-phase α+α' Titanium Alloy Produced by Additive Manufacturing. Acta Mater.162, 149–162. 10.1016/j.actamat.2018.09.050
7
Geetha M. Singh A. K. Asokamani R. Gogia A. K. (2009). Ti Based Biomaterials, the Ultimate Choice for Orthopaedic Implants – A Review. Prog. Mater. Sci.54 (3), 397–425. 10.1016/j.pmatsci.2008.06.004
8
Giustino F. (2014). Materials Modelling Using Density Functional Theory: Properties and Predictions. New York: Oxford University Press.
9
Guo G. Y. Wang H. H. (2000). Calculated Elastic Constants and Electronic and Magnetic Properties of Bcc, Fcc, and Hcp Cr Crystals and Thin Films. Phys. Rev. B62 (8), 5136–5143. 10.1103/PhysRevB.62.5136
10
Guo S. Meng Q. Zhao X. Wei Q. Xu H. (2015). Design and Fabrication of a Metastable β-type Titanium Alloy with Ultralow Elastic Modulus and High Strength. Sci. Rep.5 (1), 1–8. 10.1038/srep14688
11
Hanada S. Masahashi N. Jung T. K. Miyake M. Sato Y. S. Kokawa H. (2014). Effect of Swaging on Youngs Modulus of β Ti–33.6Nb–4Sn Alloy. J. Mech. Behav. Biomed. Mater.32, 310–320. 10.1016/j.jmbbm.2013.10.027
12
Hao Y. L. Gong D. L. Li T. Wang H. L. Cairney J. M. Wang Y. D. et al (2018). Continuous and Reversible Atomic Rearrangement in a Multifunctional Titanium Alloy. Materialia2, 1–8. 10.1016/j.mtla.2018.08.013
13
Hill R. (1952). The Elastic Behaviour of a Crystalline Aggregate. Proc. Phys. Soc. A65 (5), 349–354. 10.1088/0370-1298/65/5/307
14
Hou Y. P. Guo S. Qiao X. L. Tian T. Meng Q. K. Cheng X. N. et al (2016). Origin of Ultralow Young׳ S Modulus in a Metastable β-Type Ti–33Nb–4Sn Alloy. J. Mech. Behav. Biomed. Mater.59, 220–225. 10.1016/j.jmbbm.2015.12.037
15
Huang S. Zhao Q. Wu C. Lin C. Zhao Y. Jia W. et al (2021). Effects of β-Stabilizer Elements on Microstructure Formation and Mechanical Properties of Titanium Alloys. J. Alloys Compd.876, 160085. 10.1016/j.jallcom.2021.160085
16
Ikehata H. Nagasako N. Furuta T. Fukumoto A. Miwa K. Saito T. (2004). First-principles Calculations for Development of Low Elastic Modulus Ti Alloys. Phys. Rev. B70 (17), 174113. 10.1103/PhysRevB.70.174113
17
Jackson M. Dring K. (2013). A Review of Advances in Processing and Metallurgy of Titanium Alloys. Mater. Sci. Technol.22 (8), 881–887. 10.1179/174328406X111147
18
Jia S. Wang L. Zhang L. Wu K. Wu W. Gao Z. (2020). Structures and Properties of β-Titanium Doping Trace Transition Metal Elements: a Density Functional Theory Study. Russ. J. Phys. Chem.94 (10), 2055–2063. 10.1134/s0036024420100283
19
Kapoor K. Ravi P. Naragani D. Park J.-S. Almer J. D. J. Sangid M. D. (2020). Strain Rate Sensitivity, Microstructure Variations, and Stress-Assisted β→α′′ Phase Transformation Investigation on the Mechanical Behavior of Dual-phase Titanium Alloys. Mater. Charact.166, 110410. 10.1016/j.matchar.2020.110410
20
Katahara K. W. Manghnani M. H. Fisher E. S. (1979). Pressure Derivatives of the Elastic Moduli of BCC Ti-V-Cr, Nb-Mo and Ta-W Alloys. J. Phys. F. Metall. Phys.9 (5), 773–790. 10.1088/0305-4608/9/5/006
21
Kim H. Y. Ikehara Y. Kim J. I. Hosoda H. Miyazaki S. (2006). Martensitic Transformation, Shape Memory Effect and Superelasticity of Ti–Nb Binary Alloys. Acta Mater.54 (9), 2419–2429. 10.1016/j.actamat.2006.01.019
22
Koči L. Ma Y. Oganov A. R. Souvatzis P. Ahuja R. (2008). Elasticity of the Superconducting Metals V, Nb, Ta, Mo, and W at High Pressure. Phys. Rev. B77 (21), 214101. 10.1103/PhysRevB.77.214101
23
Koval N. E. Juaristi J. I. Díez Muiño R. Alducin M. (2019). Elastic Properties of the TiZrNbTaMo Multi-Principal Element Alloy Studied from First Principles. Intermetallics106, 130–140. 10.1016/j.intermet.2018.12.014
24
Kresse G. Furthmüller J. (1996a). Efficiency of Ab-Initio Total Energy Calculations for Metals and Semiconductors Using a Plane-Wave Basis Set. Comput. Mater. Sci.6 (1), 15–50. 10.1016/0927-0256(96)00008-0
25
Kresse G. Furthmüller J. (1996b). Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set. Phys. Rev. B54 (16), 11169–11186. 10.1103/PhysRevB.54.11169
26
Kuroda D. Niinomi M. Morinaga M. Kato Y. Yashiro T. (1998). Design and Mechanical Properties of New Type Titanium Alloys for Implant Materials. Mater. Sci. Eng. A243 (1-2), 244–249. 10.1016/S0921-5093(97)00808-3
27
Lee C. M. Ju C. P. Chern Lin J. H. (2002). Structure–property Relationship of Cast Ti–Nb Alloys. J. Oral Rehabil.29 (4), 314–322. 10.1046/j.1365-2842.2002.00825.x
28
Momma K. Izumi F. (2008). VESTA: a Three-Dimensional Visualization System for Electronic and Structural Analysis. J. Appl. Cryst.41 (3), 653–658. 10.1107/S0021889808012016
29
Monkhorst H. J. Pack J. D. (1976). Special Points for Brillouin-Zone Integrations. Phys. Rev. B13 (12), 5188–5192. 10.1103/PhysRevB.13.5188
30
Moreno J. Papageorgiou D. G. Evangelakis G. A. Lekka C. E. (2018). An ab initio Study of the Structural and Mechanical Alterations of Ti-Nb Alloys. J. Appl. Phys.124 (24), 245102. 10.1063/1.5025926
31
Moreno J. J. G. Bönisch M. Panagiotopoulo N. T. Calin M. Papageorgiou D. G. Gebert A. et al (2017). Ab-Initio and Experimental Study of Phase Stability of Ti-Nb Alloys. J. Alloys Compd.696, 481–489. 10.1016/j.jallcom.2016.11.231
32
Nagasako N. Jahnátek M. Asahi R. Hafner J. (2010). Anomalies in the Response of V, Nb, and Ta to Tensile and Shear Loading: Ab Initio Density Functional Theory Calculations. Phys. Rev. B81 (9), 094108. 10.1103/PhysRevB.81.094108
33
Ouadah O. Merad G. Saidi F. Mendi S. Dergal M. (2020). Influence of Alloying Transition Metals on Structural, Elastic, Electronic and Optical Behaviors of γ-TiAl Based Alloys: A Comparative DFT Study Combined with Data Mining Technique. Mater. Chem. Phys.242, 122455. 10.1016/j.matchemphys.2019.122455
34
Perdew J. P. Burke K. Ernzerhof M. (1996). Generalized Gradient Approximation Made Simple. Phys. Rev. Lett.77 (18), 3865–3868. 10.1103/PhysRevLett.77.3865
35
Rack H. J. Qazi J. I. (2006). Titanium Alloys for Biomedical Applications. Mater. Sci. Eng. C26 (8), 1269–1277. 10.1016/j.msec.2005.08.032
36
Reuss A. (1929). Berechung der Fliessgrenze von Mischkristallen auf grund der plastizitätsbedingung für einkristalle. Z. Angew. Math. Mech.9 (1), 49–58. 10.1002/zamm.19290090104
37
Talmor Y. Walker E. Steinemann S. (1977). Elastic Constants of Nionium up to the Melting Point. Solid State Commun.23 (9), 649–651. 10.1016/0038-1098(77)90541-5
38
Voigt W. (1910). Lehrbuch der kristallphysik:(mit ausschluss der kristalloptik). Ann Arbor: BG Teubner.
39
Walker E. (1978). Anomalous Temperature Behaviour of the Shear Elastic Constant C44 in Vanadium. Solid State Commun.28 (7), 587–589. 10.1016/0038-1098(78)90495-7
40
Walker E. Bujard P. (1980). Anomalous Temperature Behaviour of the Shear Elastic Constant C44 in Tantalum. Solid State Commun.34 (8), 691–693. 10.1016/0038-1098(80)90957-6
41
Wan X. Wu C. Tan C. Lin J. (2014). Structure Stability and Elastic Properties of β Type Ti-X (X=Nb, Mo) Alloys from First-Principles Calculations. Rare Metal Mater. Eng.43 (3), 553–558. 10.1016/S1875-5372(14)60075-8
42
Wróbel J. Hector L. G. Wolf W. Shang S. L. Liu Z. K. Kurzydłowski K. J. (2012). Thermodynamic and Mechanical Properties of Lanthanum–Magnesium Phases from Density Functional Theory. J. Alloys Compd.512 (1), 296–310. 10.1016/j.jallcom.2011.09.085
43
Yu W. Zhou Y. Chong X. Wei Y. Hu C. Zhang A. et al (2021). Investigation on Elastic Properties and Electronic Structure of Dilute Ir-Based Alloys by First-Principles Calculations. J. Alloys Compd.850, 156548. 10.1016/j.jallcom.2020.156548
44
Zhang M. H. Yu Z. T. Zhang D. Z. Jing W. S. (2010). Biocompatibility Evaluation of β-type Titanium Alloys. J. Clin. Rehabilitative Tissue Eng. Res.14 (42),7849–7853. 10.3969/j.issn.1673-8225.2010.42.014
45
Zhang S.-Z. Cui H. Li M.-M. Yu H. Vitos L. Yang R. et al (2016). First-principles Study of Phase Stability and Elastic Properties of Binary Ti-xTM (TM = V,Cr,Nb,Mo) and Ternary Ti-15TH-yAl Alloys. Mater. Des.110, 80–89. 10.1016/j.matdes.2016.07.120
46
Zhou Y. L. Niinomi M. Akahori T. (2004). Effects of Ta Content on Young's Modulus and Tensile Properties of Binary Ti–Ta Alloys for Biomedical Applications. Mater. Sci. Eng. A371 (1-2), 283–290. 10.1016/j.msea.2003.12.011
Summary
Keywords
β-Ti alloys, first-principles, phase stability, elastic properties, electronic structure
Citation
Shuluo H, Jiuxiao L, Yixue W, Dongye Y and Zhaomei W (2022) Study on Stability and Elastic Properties of β-TiX (X=Nb, Ta) Alloys From First-Principles Calculations. Front. Mater. 9:932007. doi: 10.3389/fmats.2022.932007
Received
29 April 2022
Accepted
30 May 2022
Published
22 July 2022
Volume
9 - 2022
Edited by
Daixiu Wei, Tohoku University, Japan
Reviewed by
Xiaojie Li, Taizhou University, China
Fuxing Yin, Hebei University of Technology, China
Updates
Copyright
© 2022 Shuluo, Jiuxiao, Yixue, Dongye and Zhaomei.
This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Li Jiuxiao, lijiuxiao@126.com; Wang Yixue, sunnywang2013@sina.com
This article was submitted to Biomaterials, a section of the journal Frontiers in Materials
Disclaimer
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.