Fussy Inverse Design of Metamaterial Absorbers Assisted by a Generative Adversarial Network

The increasing demands for metasurfaces have led researchers to seek effective inverse design methods, which are counting on the developments in the optimization theory and deep learning techniques. Early approaches of the inverse design based on deep learning established a unique mapping between the device’s geometry parameters and its designated EM characteristics. However, the generated solution based on the traditional inverse design method may not be applicable due to practical fabrication conditions. The designers sometimes want to choose the most practical one from multiple schemes which can all meet the requirements of the given EM indicators. A fuzzy inverse design method is quite in demand. In this study, we proposed a fuzzy inverse design method for metamaterial absorbers based on the generative adversarial network (GAN). As a data-driven method, self-built data sets are constructed and trained by the GAN, which contain the absorber’s design parameters and their corresponding spectral response. After the training process is finished, it can generate multiple possible schemes which can satisfy the customized absorptivity and frequency bands for absorbers. The parameters generated by this model include structure sizes and impedance values, which indicates that it has the ability to learn a variety of features. The effectiveness and robustness of the proposed method have been verified by several examples for the design of both narrowband and broadband metamaterial absorbers. Our work proves the feasibility of using deep learning methods to break the limits of one-to-one mapping for the traditional inverse design method. This method may have profound usage for more complex EM device design problems in the future.

1 Introduction

Metamaterials are artificial materials that have the robust ability to manipulate the intrinsic properties of EM waves, including frequency, polarization, and wavefront. The EM characteristics of metamaterials rely on the pattern and order of the meta-atom (Cui, 2017). In the past few decades, metamaterial-inspired devices, such as the frequency selective filter (Khan and Eibert, 2018; Zhang et al., 2021a), perfect absorber (Peng et al., 2019; Zhang et al., 2021b), holographic imaging (Tsai et al., 2013; Wan et al., 2017), and meta-lens (Pendry, 2000), have found variety of applicationsin academia and industries (Zhang et al., 2021c; Dong et al., 2022; Wang et al., 2022). Among these applications, metamaterial absorbers (MMA) have been realized in the spectrum ranging from microwave to optics. According to its performance, the MMAs can be classified as narrowband (Landy et al., 2008), multi-band (Yahiaoui et al., 2013; Cheng et al., 2017), and broadband types (Zhao and Cheng, 2016; Yahiaoui and Ouslimani, 2017; Beeharry et al., 2018). Different unit cell designs must guarantee perfect impedance matching at the interface between air and the metamaterial. In other words, the absorption property of the MMA counts on the geometric shape and material composition of the meta-atom.

With the help of commercial EM simulation software, researchers are able to design the meta-atom using brute force trial and error method (Arbabi et al., 2015; Jahani and Jacob, 2016) or intelligent algorithm. It is quite obvious that the brute force method is time consuming and inefficient. Thus, intelligent algorithms have been widely utilized in the customized design of metamaterials. Approaches to this problem can be divided into two categories: the first is to directly optimize the design parameters of the device with the optimization algorithm. The second is to use deep learning (DL) as an alternative to generate Maxwell’s equation solution (Khatib et al., 2021). A machine learning-based model can be used to guide the design progress. These optimization algorithms can be roughly divided into gradient-based algorithms (Molesky et al., 2018) and non-gradient-based algorithms.

The gradient-based optimization methods, such as the steepest gradient descent method and the quasi-Newtonian method, are very convenient when the optimization goal can be represented by specific mathematical analytic formula. Non–gradient-based methods, such as genetic algorithms (Chen et al., 2008) and particle swarm optimization algorithms (Liu et al., 2017), can find local optimal solutions quickly in a large search space. However, there are two drawbacks for these optimization algorithms. First, the global optimal solution may not exist for some optimization problems. Second, the generalization performance of the optimization procedure is weak. It is still a challenge to identify the optimal scheme under given objectives and constraints.

Recently, deep learning has accomplished remarkable achievements in computer vision, natural language processing, drug synthesis, and robot control (Deng and Yu, 2014; Hatcher and Yu, 2018). Merging AI (artificial intelligence) with the automatic design of metamaterial appeals to researchers (Qiu et al., 2019). The main models of deep learning are neural networks and various other variants (Chen and Lin, 2014). Because neural networks can approximate the nonlinear relationship between metamaterial geometry parameters and electromagnetic response, researchers anticipate that the deep neural network can learn the complex electromagnetic characteristics of metamaterial from trained data sets generated by numerical simulations (Liu et al., 2018; An et al., 2019b). In Itzik et al. (2018), researchers built a cascading neural network which accepts horizontal polarized spectrum, vertical polarized spectrum, and material properties as input for the design of plasmonic metamaterial. It shows that neural networks can solve the problem of multiple design indicators when performing inverse design. In An et al. (2019a), researchers constructed two deep neural networks that implement predictive and inverse design functions separately. The predictive model accepts the physical parameters as input and accurately predicts the real and imaginary parts of the structure’s S parameters. The inverse model accepts both the amplitude and phase as inputs and produces the meta-atoms’ parameters. Since the electromagnetic S parameters have complex form, neural networks can process both real and imaginary parts. In Sajedian et al. (2019), researchers utilized an interactive learning approach where an agent made up of two neural networks is trained to guide the model’s optimization at each step. This agent is continuously learning and approaching the goal. This method adopts a cumulative method of experience, which greatly reduces the search space. The aforementioned examples achieve the inverse design of metamaterials. Under a given design goal, these deep learning models can quickly obtain its solution. However, considering actual manufacturing, the AI-generated schemes may not be applicable or practical. In this case, the methods based on deep learning should provide the researchers with multiple choices. Researchers may select the appropriate design scheme, according to actual manufacturing criteria. Therefore, inverse design should be a process that can generate multiple design solutions on the basis of specific design indicators.

In this study, a fuzzy inverse design method based on the GAN (generative adversarial network) has been proposed for a metamaterial absorber design. This model accepts the starting frequency and bandwidth of the absorption band as input (in this study, we defined the absorption band with an absorptivity greater than 90%) and generates multiple schemes. Then, the designers can select the most suitable one among all the given solutions, according to practical needs. The numerical experimental results show that all the generated schemes are not in the training data set. They are also highly consistent with the design indicators. This method provides a feasible way to achieve multi-solutions in the inverse design of metamaterials. We believe that this method is more suitable for practical engineering applications. The arrangement of this study is as follows: the second part introduces the parameter definition of MMA and the pre-processing of the data set; the third part introduces our GAN model; and the fourth part analyzes the experimental results.

2 Schematic Representation of the MMA

In this study, we considered the inverse design process of a resistive-film based absorber as an example to illustrate the effectiveness of the proposed fussy design manner. Figure 1 exhibits the schematic representation of the proposed Jerusalem cross absorber. This MMA contains five layers. The middle substrate is composed of polymethacrylimide (PMI) foam, the top and bottom of which are covered with two layers of polyethylene terephthalate (PET) sheets. The relative dielectric constant of PET is 3.2, and the tangent of the loss angle is 0.003. The resistive film is deposited on the two outermost layers. The period p is set as a constant at 12mm. The thickness of the PET layer is confirmed at 0.175 mm. A complete set of design parameters includes five geometric parameters and one material parameter: the cross length L₁, the width W₁, the length L₂, the width W₂, the thickness of the substrate T_d,, and the surface impedance R of the resistive film on the top surface. The bottom layer is fixed at 10Ω/sq, which also performed parameter as the ground of the absorber.

We used full wave simulators to build the dataset with prior knowledge of the GAN model. The dataset is composed of spectrum response between 4 ∼20 GHz. The simulated S parameters are sampled at an interval of 0.5 GHz. The range of each design parameters is shown in Table 1.

FIGURE 1

FIGURE 1. Schematic diagram of the Jerusalem cross absorber.

TABLE 1

TABLE 1. Parameter distribution of absorbers.

The absorptivity is calculated using the formula A = 1 − |S₁₁|² − |S₂₁|². The design parameters and the corresponding absorption spectrum form a complete set. A total of 22,500 pairs are in the self-built dataset. When building the data set, we took full account of the spatial distribution characteristics of design parameters to ensure that the data set contains sufficiently diverse features. As a data-driven design method, it is necessary to eliminate the unreasonable distribution of data which may influence the experimental results. For design parameters, the distribution of size parameters and surface impedance is completely different. We took each parameter as a unique feature of the MMA. If the numerical difference between the different features is too large, it will interfere with the training progress. Therefore, preprocessing the data is mandatory before training the model. In order to achieve rapid convergence, we defined a parameter transformation to restrict the parameters’ value within the range -1 to 1. The maximum value of a certain feature is defined as F_max; the minimum is defined as F_min. The feature before transformation is defined as F, and the new feature is as f. The design parameters are transformed using the following formula:

$f=\left(\frac{F-F_{min}}{F_{max}-F_{min}}-0.5\right)\times 2.(1)$

The transformed features, regardless of the previous value range, will be restricted between -1 and 1 without affecting the probability distribution. The inverse transformation can be performed as follows:

$F=\frac{f+1}{2}\times \left(F_{max}-F_{min}\right)+F_{min}.(2)$

3 Methods

The GAN consists of two parts: the generator G and discriminator D (Mirza and Osindero, 2014). The whole design flow is shown in Figure 2, which is divided into two stages: training and design. In the training stage, the generator learns the physical characteristics of its potential distribution from the data, and the discriminator participates in the training of the generator. First, the spectrum response in the data set is extracted for data reduction processing. To expand the potential diversity, white noise is introduced and stitched with the reduced-dimensional spectrum as the input feature vector. Second, the input features are fed into the generator, and the generator is trained under the supervision of the discriminator. Third, the fake design schemes by the generator are put into the discriminator together with the real spectrum response in the data set. Finally, the discriminator learns to judge the authenticity of the metamaterial design parameters. These steps will be repeated throughout the model’s training process. The entire training process is illustrated in the blue area of Figure 2. After the training is completed, the design stage is performed, following the steps in the orange area of Figure 2. The inner parameters of the generator are fixed and remain unchanged. The generator takes the start/end frequency of the absorption band as input. It can directly generate several design schemes that meet the design requirements.

FIGURE 2

FIGURE 2. Schematic representation of the design flow.

Before training the GAN, it is necessary to process the data in conjunction with specific design tasks. For MMA design, researchers generally pay more attention to the frequency bands where the absorption efficiency is greater than 90%. The response of the non-absorption band is out of consideration since it is redundant information for neural network training. In the data preprocessing phase, the absorptivity greater than 0.9 is compulsively set to 1, while less than 0.9 is to 0. This step can effectively remove small features and facilitate the training of our model. In this way, the transformed spectrums are treated as labels, and the number of labels is greatly reduced. If the transformed data are leveraged to directly train the generator, this model cannot be converged. This is because the same label may map out a variety of physical parameters, which means the solutions are not unique. Thus, the tail of the input vector consists of spliced pieces of noise ranging from 0 to 1. Due to the disorder and diversity of noise, the diversity of input vectors will be greatly increased.

The generator and discriminator are composed of multi-layer perceptual neural networks. The generator contains eight layers, where the number of neurons in each layer is 50, 100, 100, 100, 100, 50, 10, and 6. The total neurons in the middle layers are activated by the LeakReLU function, as shown in Eq. 3. This activation function solves the problem of the vanishing gradient during the training progress compared with the sigmoid activation function. On the other hand, the LeakReLU function makes training progress more stable.

$LeakReLU\left(x\right)=\left\{\begin{array}{cc}x\hfill & \text{\hspace{0.17em}if\hspace{0.17em}}x\ge 0,\hfill \\ 0.2x\hfill & \text{\hspace{0.17em}if\hspace{0.17em}}x<0,\hfill \end{array}\right.(3)$

The discriminator consists of eight layers, and the neurons in each layer are 6, 20, 50, 50, 50, 20, 5, and 1. The hidden layers are also activated by the LeakReLU function, while the output is activated by the sigmoid function, as shown in Eq. 4. The sigmoid function forces the output to be compressed between 0 and 1, which represents the authenticity of the discriminator’s judgment.

$Sigmoid\left(x\right)=\frac{1}{1+e^{-x}}.(4)$

m is the batch size, which means the amount of data that are simultaneously fed into the model. Each hidden layer of the generator and discriminator is also connected to the batch normalization layer. As can be seen from Eq. 5, for the loss function of the discriminator, the discriminator will try to expand the positive judgment of the realsamples in the data set and improve the negative judgment of the fake schemes generated by the generator. From Eq. 6, the generator tries to make its generated numerical distribution close to the discriminatory boundary under the constraints of the discriminator. In the process of continuously optimizing the two models, the loss value of the discriminator will enter a dynamic equilibrium.

$\text{Loss}\left(\text{Dis}\right)=\frac{1}{m}\sum _{i=1}^m\left[\log \left(\text{Dis}\left(x_i\mid y_i\right)\right)+\log \left(1-\text{Dis}\left(\text{Gen}\left(z_i\mid y_i\right)\right)\right)\right],(5)$

$\text{Loss}\left(Gen\right)=\frac{1}{m}\sum _{i=1}^m\log \left(1-\text{Dis}\left(\text{Gen}\left(z_i\mid y_i\right)\right)\right).(6)$

In order to prevent direct divergence during GAN training, before training the generator, the discriminator needs to be trained first. A certain number of iterations of positive sample training for the discriminator are performed. This makes it possible for the discriminator to give a preliminary judgment on the generated data by the generator during the alternate training stage. In this manner, the whole training process is more stable. Once the model is built, the process of training the model transforms into an optimization process aimed at minimizing the loss function. The total problem becomes an optimization problem. With the help of optimization tools, adjusting the model parameters causes the values of loss function to drop in the direction of gradient decline, and finally the model parameters converge to the global optimal solution. SGD (stochastic gradient descent) is selected as the optimized method, and the learning rate is set to 0.00005. Excessive learning rates may cause models to diverge directly and crash. In the training process, after the generator is trained every five times, the generator is trained again. The entire flow is showed in Figure 3.

FIGURE 3

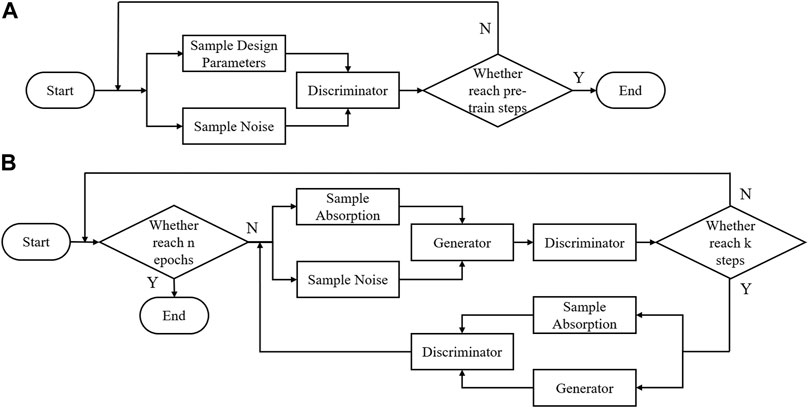
FIGURE 3. Schematic diagram of the entire training process. (A) indicates the pre-training progress. (B) represents the entire training progress.

4 Results and Discussion

After the model is trained completely, all the parameters in the GAN model are decided. First, we used this model to fulfill the design of narrowband absorbers. We separately chose 5 ∼9 GHz, 6 ∼14 GHz, 5.5 ∼12 GHz, and 9 ∼12 GHz as targets, which are fed into the generator along with different noise signals. For each target, the generator can generate several solutions, which do not appear in the training set. Some of these results do not differ much. Then we utilized full wave simulation to validate whether these solutions can meet the design targets. The simulated results are shown in Figure 4. Obviously, the absorption spectra generally satisfy the requirements. The design result is not unique under the same design indicator. In Figure 5, we tried to illustrate the difference between the solutions, which has an absorption band of 5.5 ∼12 GHz. None of the design schemes appeared in the training data set, which indicates that the GAN has learned to design absorbers from the data set. From the results, although the absorption spectrum in 5.5 ∼12 GHz is similar, some of the design parameters vary greatly, especially for surface impedance R and thickness T_d. This is reasonable since R depends on film impedance and T_d represents the thickness of the MMA, which are precisely the two most important parameters in metamaterial design. However, the width W₁ seems to make little difference. It is speculated that W₁ may have little effect on the absorption performance of the absorber. As a fuzzy design method, the purpose of designing a variety of design schemes according to the design indicators has been achieved, and these results prove the effectiveness of this design method.

FIGURE 4

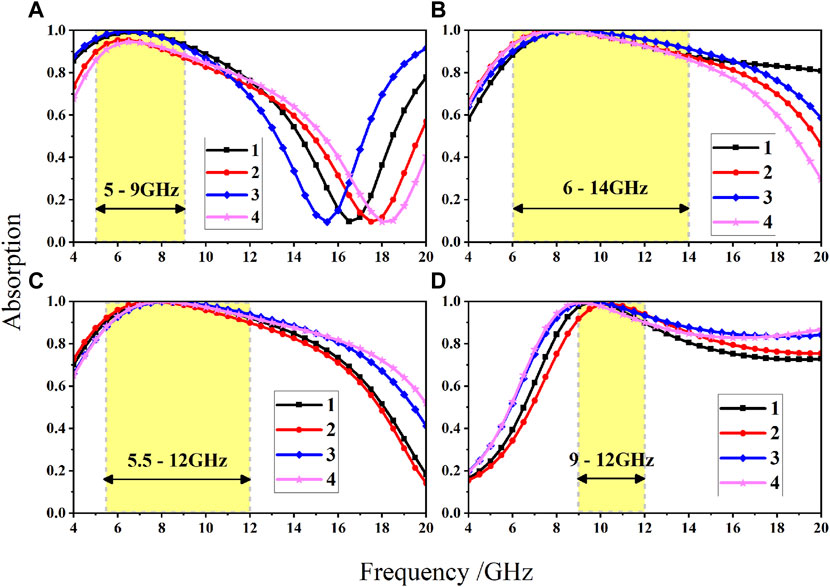
FIGURE 4. Schematic diagram of a narrowband customized design. (A) The simulated results of the designed absorber under 5∼9 GHz. (B) The simulated results of the designed absorber under 6∼14 GHz. (C) The simulated results of the designed absorber under 5.5∼12 GHz. (D) The simulated results of the designed absorber under 9∼12 GHz.

FIGURE 5

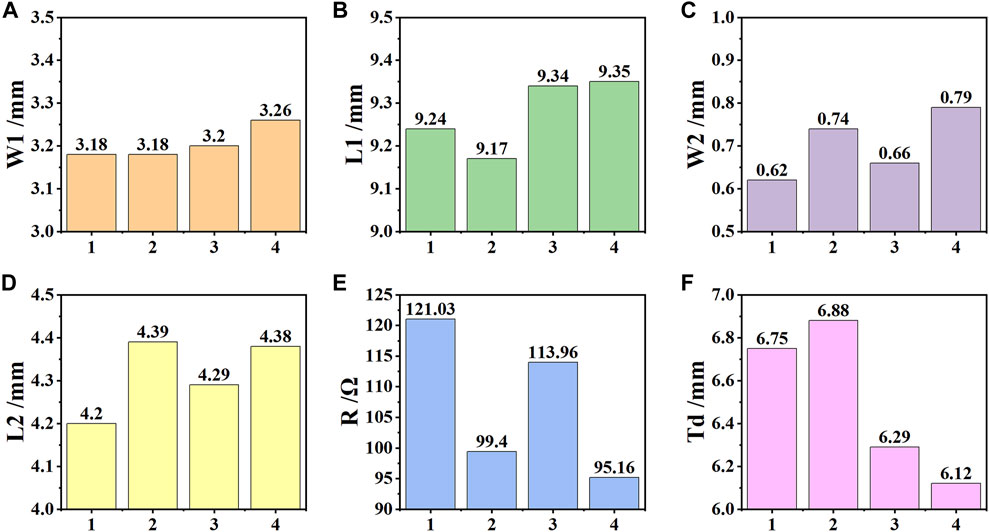
FIGURE 5. Schematic diagram of partial results at 5.5 ∼12 GHz. The horizontal axis represents the design scheme number, and the vertical axis is the specific parameters of each design scheme. (A) The designed results of W₁. (B) The designed results of L₁. (C) The designed results of W₂. (D) The designed results of L₂. (E) The designed results of R. (F) The designed results of T_d.

Second, this model is used for broadband absorber design. After the model training is finished, broadband design indicators combined with noises are fed into the generator. Since the absorption performance is restricted by the fixed pattern of the meta-atom, the fussy design method can be used to explore the ultimate capability of a designated pattern. Thus, although design indicators can be set arbitrarily, the generator does not necessarily generate a solution that fully meets the requirements. This also proves that it is not an easy task for broadband absorber design. However, we still need to find an ultra-broadband solution. We considered 8 ∼20 GHz as the input indicators, and the results of the design parameters are exhibited in Figure 6. From the results, W₁ and L₁ are not much different. W₁ basically tends to around 3.3mm, and the L₁ tends to around 9.6 mm. For broadband absorbers, not every design parameter varies greatly. L₂ and W₂ have certain differences. The surface impedance R and thickness T_d still vary greatly. For this type of absorber, thickness and surface impedance are often important physical parameters that have a great impact on the function. This is consistent with the resonance loss mechanism of the absorber.

FIGURE 6

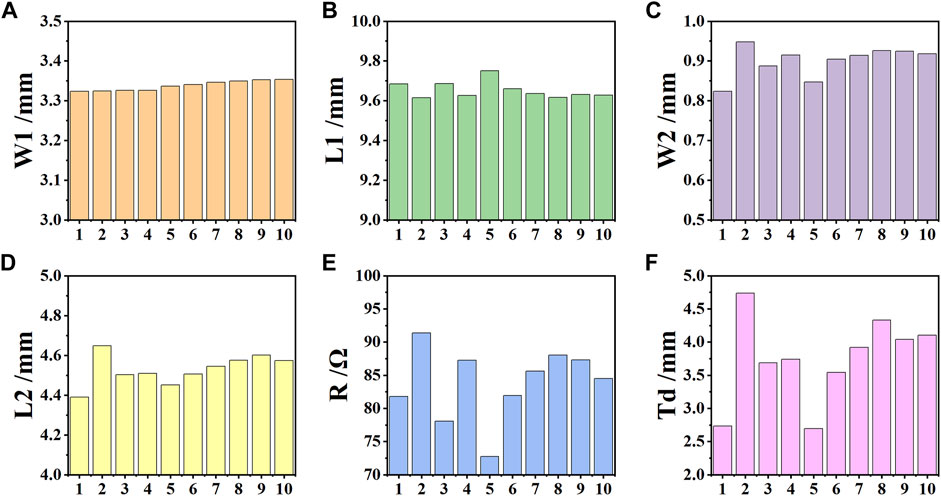
FIGURE 6. Schematic diagram of partial results under the 8 ∼20 GHz customized design. (A) The designed results of W₁. (B) The designed results of L₁. (C) The designed results of W₂. (D) The designed results of L₂. (E) The designed results of R. (F) The designed results of T_d.

From all the inverse design solutions, design parameters are generally distributed around W₁ = 3.3mm, L₁ = 9.6mm, W₂ = 0.85mm, L₂ = 4.3mm, r = 85Ω, and T_d = 4 mm. These parameter sets also never appear in the training data set, which proves that the GAN can effectively learn various features from the original data set. The electromagnetic simulation of this structure is performed again in the range of 1 ∼29 GHz using microwave studio software. Moreover, Figures 7A,B show the absorption properties of the designed structure under TE and TM polarization for different incident angles. Under TE polarization, the absorptivity decreases with the increase in the incident angle. When the incident angle is less than 40°, the absorptivity is still above 85%. Similarly, under TM polarization, the absorption bandwidth is small with the increase in the incident angle. When the incident angle is less than 40°, the absorptivity is still above 90%. Therefore, the designed absorber has good angular stability.

FIGURE 7

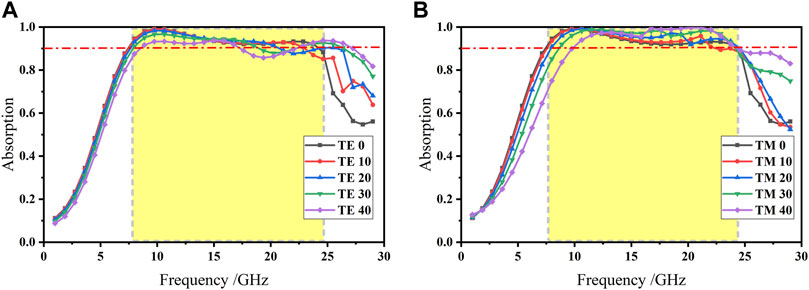
FIGURE 7. Schematic diagram of the absorption rate at 1 ∼29 GHz. (A) is under TE polarization at incident angles from 0 to 40. (B) is under TM polarization at incident angles from 0 to 40.

According to the absorption curves in Figure 7, it has two absorption peaks at 10 and 23 GHz. In order to better analyze its absorption mechanism, we observed the electric field distribution of the designed absorber. As shown in Figure 8A, the red area shows the strongest electric field strength, which indicates that resonance occurs mainly in the regions at both ends of the cross structure in the high-frequency range. As shown in Figure 8B, the red area shows that resonance occurs in the middle regions of the cross structure in the low-frequency range.

FIGURE 8

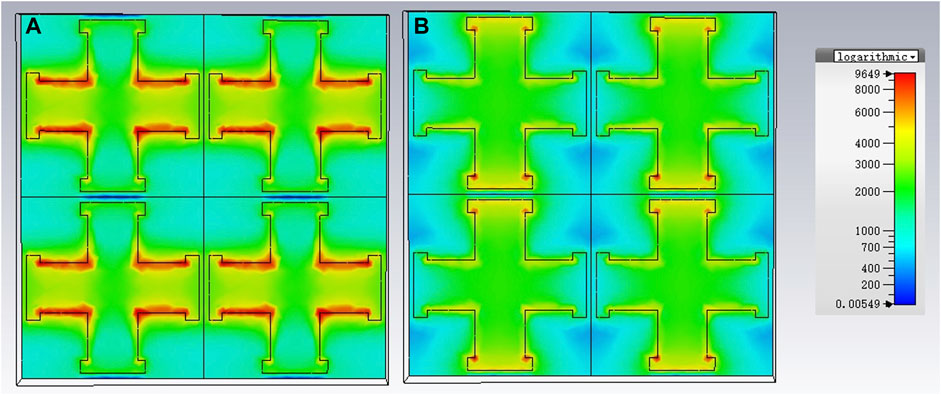
FIGURE 8. Schematic diagram of the electric field distribution on the surface under TE polarization. (A) Frequency at 23 GHz. (B) Frequency at 10 GHz.

5 Conclusion

In conclusion, a fussy design method is proposed for the inverse design of a metamaterial absorber based on a generative adversarial model. This method can be used to design narrowband and broadband absorbers, according to customized design indicators. It accepts the absorption bandwidth and noise signal as inputs and efficiently generates multiple design schemes as outputs. Researchers can choose a suitable design scheme based on actual needs. The leverage of noise parameters can effectively solve the problem of non-unique solutions in the inverse design progress of metamaterials. Moreover, the distribution of various design parameters generated by the GAN can also show the importance of each parameter on the performance of the device. Compared with ordinary neural networks that can only achieve one-to-one mapping, the GAN can achieve one-to-many mapping. Compared with the traditional optimization method, this model converges easily, and it is easy to find solutions that meet the requirements. From the experimental results, the GAN can effectively capture the characteristics of the absorption spectrum in the data set. In order to get a broadband design scheme, the GAN seems to combine different features to form a broadband absorption solution, which never appears in the data set. In our future work, we will focus on more polarization-sensitive devices and more complex structures of the unit cell. No longer limited to a single function, we will try to explore in the direction of multi-function–assisted active metasurfaces. We envisioned that this method can be applied to the design of digital programmable metasurfaces.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

HL and YT conceived and designed the experiments; JH designed the simulations; XS analyzed the data; WX contributed to the analysis tools; HL and RT revised the manuscript. All authors have read and agreed to the published version of the manuscript.

Funding

This research is funded by the Fundamental Research Funds for the Central University of China under Grant Nos. CCNU20GF004 and CCNU19TS073, the open fund of the Guangxi Key Laboratory of Wireless Wideband Communication and Signal Processing under the Grant No. GXKL06190202, the open fund of the China Ship Development and Design Centre under the Grant No. XM0120190196, the National Natural Science Foundation of China under the Grant No. 41974195, and the Hongque Innovation Center under grant HQ202104001.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

An, S., Fowler, C., Zheng, B., Shalaginov, M. Y., Tang, H., Li, H., et al. (2019b). A Novel Modeling Approach for All-Dielectric Metasurfaces Using Deep Neural Networks. ArXiv [Preprint]. Available at: https://arxiv.org/abs/1906.03387.

Google Scholar

An, S., Fowler, C., Zheng, B., Shalaginov, M. Y., Tang, H., Li, H., et al. (2019a). A Deep Learning Approach for Objective-Driven All-Dielectric Metasurface Design. ACS Photonics 6, 3196–3207. doi:10.1021/acsphotonics.9b00966

CrossRef Full Text | Google Scholar

Arbabi, A., Horie, Y., Bagheri, M., and Faraon, A. (2015). Dielectric Metasurfaces for Complete Control of Phase and Polarization with Subwavelength Spatial Resolution and High Transmission. Nat. Nanotech 10, 937–943. doi:10.1038/nnano.2015.186

CrossRef Full Text | Google Scholar

Beeharry, T., Yahiaoui, R., Selemani, K., and Ouslimani, H. H. (2018). A Co-polarization Broadband Radar Absorber for Rcs Reduction. Mater. (Basel) 11. doi:10.3390/ma11091668

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, P. Y., Chen, C. H., Wang, H., Tsai, J. H., and Ni, W. X. (2008). Synthesis Design of Artificial Magnetic Metamaterials Using a Genetic Algorithm. Opt. Express 16, 12806–12818. doi:10.1364/oe.16.012806

PubMed Abstract | CrossRef Full Text | Google Scholar

Cheng, Y., Cheng, Z., Mao, X., and Gong, R. (2017). Ultra-thin Multi-Band Polarization-Insensitive Microwave Metamaterial Absorber Based on Multiple-Order Responses Using a Single Resonator Structure. Materials 10, 1241. doi:10.3390/ma10111241

PubMed Abstract | CrossRef Full Text | Google Scholar

Cui, T. J. (2017). Microwave Metamaterials. Natl. Sci. Rev. 5, 134–136. doi:10.1093/nsr/nwx133

CrossRef Full Text | Google Scholar

Deng, L., and Yu, D. (2014). Deep Learning: Methods and Applications. FNT Signal Process. 7, 197–387. doi:10.1561/2000000039

CrossRef Full Text | Google Scholar

Dong, B., Zhang, C., Guo, G., Zhang, X., Wang, Y., Huang, L., et al. (2022). Bst-silicon Hybrid Terahertz Meta-Modulator for Dual-Stimuli-Triggered Opposite Transmission Amplitude Control. Nanophotonics 11, 1. doi:10.1515/nanoph-2022-0018

CrossRef Full Text | Google Scholar

Hatcher, W. G., and Yu, W. (2018). A Survey of Deep Learning: Platforms, Applications and Emerging Research Trends. IEEE Access 6, 24411–24432. doi:10.1109/access.2018.2830661

CrossRef Full Text | Google Scholar

Itzik, M., Michael, M., Achiya, N., Uri, A., Lior, W., and Haim, S. (2018). Plasmonic Nanostructure Design and Characterization via Deep Learning. Light Sci Appl. 7 (1), 60. doi:10.1038/s41377-018-0060-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Jahani, S., and Jacob, Z. (2016). All-dielectric Metamaterials. Nat. Nanotech 11, 23–36. doi:10.1038/nnano.2015.304

PubMed Abstract | CrossRef Full Text | Google Scholar

Khan, S., and Eibert, T. F. (2018). A Multifunctional Metamaterial-Based Dual-Band Isotropic Frequency-Selective Surface. IEEE Trans. Antennas Propagat. 66, 4042–4051. doi:10.1109/TAP.2018.2835667

CrossRef Full Text | Google Scholar

Khatib, O., Ren, S., Malof, J., and Padilla, W. J. (2021). Deep Learning the Electromagnetic Properties of Metamaterials-A Comprehensive Review. Adv. Funct. Mat. 31, 2101748. doi:10.1002/adfm.202101748

CrossRef Full Text | Google Scholar

Landy, N. I., Sajuyigbe, S., Mock, J. J., Smith, D. R., and Padilla, W. J. (2008). Perfect Metamaterial Absorber. Phys. Rev. Lett. 100, 207402. doi:10.1103/PhysRevLett.100.207402

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, D., Tan, Y., Khoram, E., and Yu, Z. (2018). Training Deep Neural Networks for the Inverse Design of Nanophotonic Structures. Acs Photonics 5, 1365–1369. doi:10.1021/acsphotonics.7b01377

CrossRef Full Text | Google Scholar

Liu, N., Sheng, X., Zhang, C., Fan, J., and Guo, D. (2017). Design of Fss Radome Using Binary Particle Swarm Algorithm Combined with Pixel-Overlap Technique. J. Electromagn. Waves Appl. 31, 522–531. doi:10.1080/09205071.2017.1294506

CrossRef Full Text | Google Scholar

Mirza, M., and Osindero, S. (2014). Conditional Generative Adversarial Nets. Comput. Sci. 2014, 2672–2680.

Google Scholar

Molesky, S., Lin, Z., Piggott, A. Y., Jin, W., Vucković, J., and Rodriguez, A. W. (2018). Inverse Design in Nanophotonics. Nat. Phot. 12, 659–670. doi:10.1038/s41566-018-0246-9

CrossRef Full Text | Google Scholar

Pendry, J. B. (2000). Negative Refraction Makes a Perfect Lens. Phys. Rev. Lett. 85, 3966–3969. doi:10.1103/PhysRevLett.85.3966

PubMed Abstract | CrossRef Full Text | Google Scholar

Peng, Y., Besteiro, L. V., Huang, Y., Jiang, W., Fu, L., Tan, H. H., et al. (2019). Broadband Metamaterial Absorbers. Adv. Opt. Mater. 7.

Google Scholar

Qiu, T., Shi, X., Wang, J., Li, Y., Qu, S., Cheng, Q., et al. (2019). Deep Learning: A Rapid and Efficient Route to Automatic Metasurface Design. Adv. Sci. 6, 1900128. doi:10.1002/advs.201900128

PubMed Abstract | CrossRef Full Text | Google Scholar

Sajedian, I., Lee, H., and Rho, J. (2019). Double-deep Q-Learning to Increase the Efficiency of Metasurface Holograms. Sci. Rep. 9, 10899. doi:10.1038/s41598-019-47154-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Tsai, Y.-J., Larouche, S., Tyler, T., Llopis, A., Royal, M., Jokerst, N. M., et al. (2013). Arbitrary Birefringent Metamaterials for Holographic Optics at λ = 155 μm. Opt. Express 21, 26620–26630. doi:10.1364/OE.21.026620

PubMed Abstract | CrossRef Full Text | Google Scholar

Wan, W., Gao, J., and Yang, X. (2017). Metasurface Holograms for Holographic Imaging. Adv. Opt. Mater. 5, 1700541. doi:10.1002/adom.201700541

CrossRef Full Text | Google Scholar

Wang, Y., Song, Y., Zhang, B., Chen, S., Chen, Q., and Zhang, C. (2022). A High-Efficiency and Reconfigurable Rectenna Array for Dynamic Output Dc Power Control. Front. Phys. 2022, 150. doi:10.3389/fphy.2022.866656

CrossRef Full Text | Google Scholar

Xue-Wen Chen, X.-W., and Xiaotong Lin, X. (2014). Big Data Deep Learning: Challenges and Perspectives. IEEE access 2, 514–525. doi:10.1109/access.2014.2325029

CrossRef Full Text | Google Scholar

Yahiaoui, R., Guillet, J. P., de Miollis, F., and Mounaix, P. (2013). Ultra-flexible Multiband Terahertz Metamaterial Absorber for Conformal Geometry Applications. Opt. Lett. 38, 4988–4990. doi:10.1364/ol.38.004988

PubMed Abstract | CrossRef Full Text | Google Scholar

Yahiaoui, R., and Ouslimani, H. H. (2017). Broadband Polarization-independent Wide-Angle and Reconfigurable Phase Transition Hybrid Metamaterial Absorber. J. Appl. Phys. 122, 093104. doi:10.1063/1.4989933

CrossRef Full Text | Google Scholar

Zhang, C., Long, C., Yin, S., Song, R. G., Zhang, B. H., Zhang, J. W., et al. (2021a). Graphene-based Anisotropic Polarization Meta-Filter. Mater. Des. 206, 109768. doi:10.1016/j.matdes.2021.109768

CrossRef Full Text | Google Scholar

Zhang, C., Yin, S., Long, C., Dong, B. W., He, D., and Cheng, Q. (2021b). Hybrid Metamaterial Absorber for Ultra-low and Dual-Broadband Absorption. Opt. Express 29, 14078–14086. doi:10.1364/oe.423245

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, C., Zhao, J., Zhang, B. H., Song, R. G., Wang, Y. C., He, D. P., et al. (2021c). Multilayered Graphene-Assisted Broadband Scattering Suppression through an Ultrathin and Ultralight Metasurface. ACS Appl. Mat. Interfaces 13, 7698–7704. doi:10.1021/acsami.0c20499

CrossRef Full Text | Google Scholar

Zhao, J., and Cheng, Y. (2016). Ultrabroadband Microwave Metamaterial Absorber Based on Electric Srr Loaded with Lumped Resistors. J. Elec Materi 45, 5033–5039. doi:10.1007/s11664-016-4693-0

CrossRef Full Text | Google Scholar