The Strain Rate Sensitivity of Heterogeneous Thin Film Metallic Glasses: Interplay Between Nanoscale Heterogeneity and Dynamic Plasticity

The dynamic mechanical properties of metallic glasses (MGs) are crucial to capturing the deformation signatures as well as for structural and functional applications. In this work, we investigate the influence of nanoscale structural heterogeneity of MGs on dynamic plasticity, focusing on the variation in strain rate sensitivity and the transition of deformation mechanisms, using a combined experimental and simulation approach. The Cu₅₀Zr₅₀ thin-film MGs with different nanoscale heterogeneities are synthesized using magnetron sputtering and further characterized using dynamic force microscopy and nanoindentation. All the films exhibit a strain rate hardening effect, but a transition in strain rate sensitivity as the indentation rate increases has been found in the MG with a higher heterogeneity. To understand the underlying mechanisms, mesoscale shear transformation zone dynamics simulations are performed on model Cu₅₀Zr₅₀ MGs. The simulation results are able to capture the experimental trend. Notably, the transition in strain rate sensitivity for a heterogenous MG stems from a change in deformation mechanisms: from structure-dictated strain localization at a lower strain rate to stress-dictated strain percolation into a shear band at a higher strain rate. The observed strain rate sensitivity and the corresponding mechanisms are summarized in a deformation mechanism map where nanoscale structural heterogeneity and strain rate are varied. We envision our study not only providing insights into the structure and property relationship of MGs on the nanoscale but also will facilitate the design of heterogeneous MGs for dynamic applications.

Introduction

Metallic glasses (MGs) exhibit remarkable mechanical properties of high strength, excellent hardness, large elastic strain limit, and high corrosion resistance (Wang et al., 2004; Greer et al., 2013) due to their disordered atomic structure (Schroers, 2013). These unique characteristics recognize MGs as a promising candidate for microelectromechanical system applications, including high-performance micro-actuators and structures (Wang et al., 2009; Van Toan et al., 2020). For such demanding applications, it is vital to characterize the dynamic mechanical properties of MGs and understand their deformation mechanisms at various strain rates. Unlike crystalline materials, the structures of defects that carry deformation are not well established in the MGs. However, the fundamental deformation process is identified to be thermally activated local atomic rearrangement that can produce shear strain, namely the shear transformation zones (STZs) (Argon, 1979; Fan et al., 2014; Ramachandramoorthy et al., 2019; Tian et al., 2020). During the deformation, a cluster of atoms rearranges locally and forms an STZ to accommodate shear strain based on the transition-state kinetic law (Schuh et al., 2004). Subsequent STZs will then form under the influence of the stress field, which becomes the nucleation sites for shear bands. With the increasing size of those nucleation sites, STZs rapidly grow into a shear band. After that, under the influence of accumulating plastic deformation, the fully developed shear band begins to propagate. Such shear banding behaviors are influenced by the strain rate. At a low strain rate, the STZs are developed into only one or a few shear bands. As the strain rate increases, more STZs will be activated to form nucleation sites for multiple shear bands when one shear band cannot accommodate increasing strain and relieve stress in the MG fast enough (Jiang and Atzmon, 2003; Schuh et al., 2004; Harris et al., 2016).

To quantify the dynamic plasticity, the strain rate sensitivity m is used, which measures the variation of hardness/yield stress as a function of the strain rate change. In the literature, the effect of strain rate on the strength of MGs has not been well established. Large variations in strain rate effects can be found with strain rate sensitivity m varying from positive (Ma et al., 2021) to zero (González et al., 2011) to negative (Trexler and Thadhani, 2010). For example, Ma et al. (2021), observed strain rate hardening with positive m between 0.014 and 0.04 for Cu₅₀Zr₅₀ films. González et al. (2011) reported Zr₆₅Cu₂₀Fe₅Al₁₀ MG showed no strain rate sensitivity upon compression test over the strain rates from 5 × 10⁻³ s⁻¹ to 5 × 10⁻² s⁻¹. Negative strain rate sensitivity for MGs is also reported as a result of increasing strain rate raises the degree of adiabatic heating that caused softening (Trexler and Thadhani, 2010). Such conflicting results suggest that many factors, such as chemical composition or thermo-mechanical processing history, could significantly influence the dynamic response of MGs. The main challenge that prevents the clarification of the strain rate sensitivity is to identify the structural features of MGs, and further, understand the relationship between the structural features and dynamic responses.

MGs have been unveiled to have nanoscale structural heterogeneities, owing to their complex atomic structures, which are highly correlated with their mechanical properties, plasticity, and glass dynamics (Cheng and Ma, 2011; Ding et al., 2014a; Ding et al., 2014b; Ding et al., 2021; Wang et al., 2018a; Zhu et al., 2018; Qiao et al., 2019; Wang et al., 2020; Nomoto et al., 2021). The inherent structural heterogeneity in the MGs originates from the wide distribution of atomic packing motifs within the short- and medium-range orders, leading to the formation of both loosely- and densely-packed regions at the nanoscale (Ding et al., 2014a; Ding et al., 2014b; Zhu et al., 2018). Using atomistic simulations, Ding et al. (2014a) have identified the geometrically unfavorable atomic clusters, which are soft spots where inelastic events prefer to be initiated during the deformation of MGs. Using advanced transmission electron microscopy, Im et al. (2018) provided precise details of the medium-range orders and structural heterogeneity in Zr₅₀Co₂₅Al₂₀ MGs, including size, volume fraction, and spatial distribution of various medium-range order types. Atomic force microscopy (AFM) has also been used as an efficient tool to characterize the nanoscale structural heterogeneity in amorphous solids (Zhu et al., 2018). Using the phase shift data of AFM, it is possible to calculate the distribution of energy dissipation on the glass surface, which is in accordance with the loosely- and densely-packed regions in the amorphous structure. Wang et al. (2018b) reported that the change in the chemical composition significantly affected the nanoscale structural heterogeneity, which was related to the variations of local atomic structures. Zhu et al. (2017), employed dynamic AFM analysis to characterize the mechanism of relaxation-to-rejuvenation transition in MGs (Zhu et al., 2018). Lu et al. (2016) indicated that the fluctuations of nanoscale heterogeneity on the surface corresponded with the reorientation and percolation of energy-dissipating zones with non-affine strain behavior. Some recent experimental and simulation works (Zhao et al., 2013; Zhao et al., 2014) have found that such nanoscale spatial heterogeneity of MGs can be quantitively related to their modulus, strength, and ductility, which may serve as a structural feature for MGs (Wang et al., 2018a; Zhu et al., 2018; Wei et al., 2019).

In this work, we are studying the influence of nanoscale heterogeneity on the dynamic plasticity of MGs, focusing on the variation in strain rate sensitivity and the transition of deformation mechanisms. Two Cu₅₀Zr₅₀ thin-film metallic glasses (TFMGs) with different levels of nanoscale heterogeneity have been synthesized using magnetron sputtering. The nanoscale heterogeneities are characterized using dynamic force microscopy (DFM), and nanoindentation is performed in the strain rate range of 0.01/s to 0.12/s. The strain rate sensitivity and activation volume are calculated for the dynamic signature of deformation mechanisms. Both samples exhibit positive strain rate sensitivity, and a transition of the sensitivity over the strain rate is noted in the co-sputtered TFMG that has higher heterogeneity. To understand the underlying mechanisms of such dynamic plasticity, mesoscale STZ dynamics simulations are performed in a model Cu₅₀Zr₅₀ MG with various degrees of nanoscale heterogeneity. Specifically, with medium heterogeneity, the STZs initiate in the local soft regions, and deformation is dictated by the heterogeneous structure. This results in a small activation volume and large strain rate sensitivity. A transition in strain rate sensitivity is identified in a high heterogeneity MG due to competition between structure-dictated strain localization and stress-dictated shear band percolation as a function of increasing strain rate. We conclude with a dynamic deformation mechanism map of MGs, where nanoscale heterogeneities and deformation strain rates are both taken into account.

Experiments

Thin-Film Metallic Glasses Synthesis and Nanoscale Heterogeneity Characterization

By using the direct current magnetron sputtering method with an ATC Orion-5 magnetron sputtering system (AJA International, United States), two Cu₅₀Zr₅₀ TFMGs are deposited on single-crystal silicon chips. As shown in Figure 1A, the first TFMG, ST-CuZr, is made by using a single Cu₅₀Zr₅₀ target; and the second TFMG, CS-CuZr, is made by using a Cu target and a Zr target. The structures of two samples are further examined and analyzed using X-ray diffraction [XRD, Philips X’Pert MPD X-ray diffractometer with Cu Kα (λ = 1.5405 Å)]. As shown in Figure 1B, the main XRD peak positions of both samples are at approximately 43 degrees and lack sharp crystalline peaks in the XRD spectra. Therefore, the states of both samples are confirmed to be amorphous (Gao and Jian, 2016).

FIGURE 1

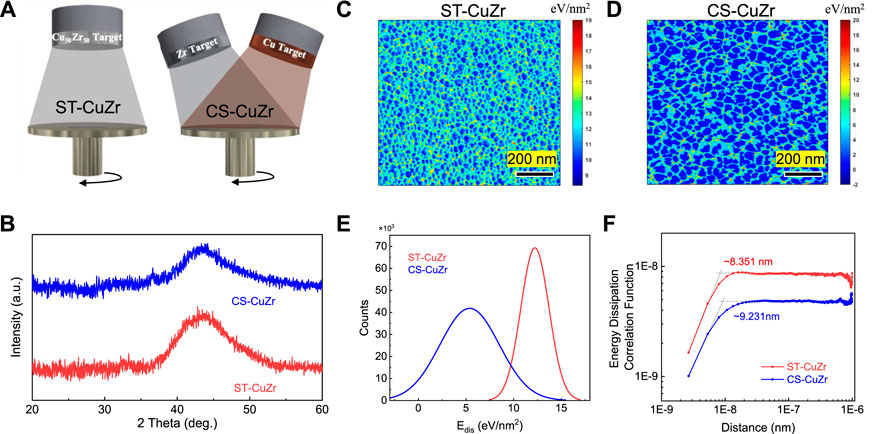
FIGURE 1. TFMGs prepared by magnetron sputtering which results in different nanoscale heterogeneities. (A) The schematic diagram of single-target (ST) sputtering vs. co-sputtering (CS) to synthesize Cu₅₀Zr₅₀ TFMGs, namely, ST-CuZr vs. CS-CuZr. (B) The X-ray diffraction spectra of ST-CuZr vs. CS-CuZr confirm the amorphous phase. Energy dissipation maps obtained from DFM measurements for ST-CuZr in (C) vs. CS-CuZr in (D). (E) The Gaussian distribution of energy dissipation of the two samples. (F) The spatial autocorrelation functions of energy dissipation of two samples, and the corresponding correlation lengths.

The nanoscale heterogeneity is characterized using an AFM (AFM, Park System XE-70) in DFM mode. The energy dissipation of ST-CuZr and CS-CuZr samples are calculated based on the phase shift of the viscoelastic responses upon tapping the AFM tip on the surface of TFMGs (Wang et al., 2018b; Liu et al., 2011). As shown in Figures 1C,D, the higher energy dissipation regions represent the loosely-packed liquid-like regions, whereas the lower energy dissipation regions reflect the densely-packed solid-like regions. The Gaussian distributions of energy dissipation for both samples are provided in Figure 1E. The standard deviation of the distribution of energy dissipation for ST-CuZr and CS-CuZr are 1.35 eV/nm² and 2.29 eV/nm², respectively. Furthermore, the spatial correlation length ξ is calculated based on the autocorrelation function of energy dissipation, as shown in Figure 1F, effectively reflecting the size of loosely-packed and densely-packed regions (Karabacak et al., 2001; Kawasaki et al., 2007; Liu et al., 2011; Wang et al., 2018b). The correlation lengths of ST-CuZr and CS-CuZr are ∼8.36 and ∼9.22 nm, respectively. When compared to ST-CuZr, CS-CuZr has a higher standard deviation and larger correlation length of the energy dissipation, indicating larger loosely-packed atomic regions and exhibiting a higher level of nanoscale heterogeneity.

Nanoindentation Test

To characterize the mechanical properties of the two TFMGs, nanoindentation tests are carried out. The modulus, E, and hardness, H, are measured using an Agilent Technologies Nano Indenter G200 equipped with Berkovich diamond indenter in the dynamic contact module (DCM) mode. The continuous stiffness measurement technique is used to indent both samples at five different strain rates, i.e., 0.01/s, 0.02/s, 0.03/s, 0.06/s, and 0.12/s.

Mesoscale STZ Dynamics Simulations

Simulation Framework

A STZ dynamics model is used to simulate STZ events, which are localized clusters of atoms that undergo a characteristic shear transformation to accommodate the external stimuli (e.g. stress, heat) during the MG deformation (Bulatov and Argon, 1994; Homer and Schuh, 2009; Homer et al., 2010). More specifically, the STZ dynamics model employs a coarse-graining technique by replacing the cluster of atoms that represent a potential STZ with features of a finite element mesh, as shown in Figure 2A, and thus each potential STZ has the ability to shear in the same manner as a cluster of atoms. Such coarse-graining enables the STZ dynamics model to more efficiently sample the larger system sizes. In addition, the STZ dynamics model considers the transient STZ activation as a transition state between the initial and final equilibrium configurations and uses the kinetic Monte Carlo algorithm to control the activation of STZs, thereby simulating longer system times more efficiently. Since being developed, the STZ dynamics model has successfully captured the general deformation behaviors of MGs and has been extended for various implementations (Li et al., 2014; Wang et al., 2015a; Hardin and Homer, 2015; Harris et al., 2016; Wang et al., 2018a). Notably, the activation rate for a potential STZ to shear in one direction is given by

${\dot{s}}_{STZ}=v_{STZ}exp\left(-\frac{\text{Δ}\text{F}\left(\text{μ}\right)-\text{τ}{\text{Ω}}_0{\text{γ}}_0/2}{kT}\right)(1)$

where ν_STZ is the attempt frequency and is on the order of the Debye frequency, Ω₀ is the activation volume of the STZ, is a characteristic shear strain increment upon STZ transition, and kT is the thermal energy of the system. According to Argon (Argon, 1979), ΔF is the activation energy barrier, which can be written as a function of local shear modulus μ (Wang et al., 2018a). The STZ dynamics simulation parameters are summarized in Table 1. The attempt frequency which is calculated based on Debye temperature, is about 1.02 × 10¹²/s and the entropic effect is ignored here. The STZ volume Ω₀ is from 2.7 to 4.0 nm³, corresponding to 40∼70 atoms, which is in the range commonly reported in the literature. The characteristic shear strain increment is taken to be 0.1, which is in line with Argon’s model (Argon, 1979) and atomistic simulations (Zink et al., 2006).

FIGURE 2

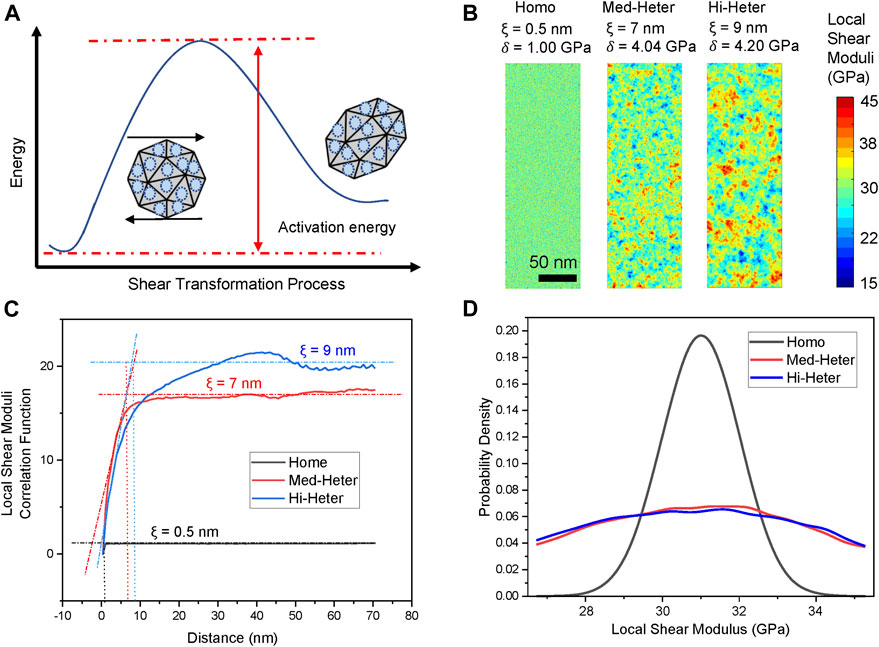
FIGURE 2. Mesoscale STZ dynamics model setup. (A) A coarse-grained STZ event and its transformation on the potential energy landscape from an unsheared to a sheared state. (B) The simulated samples with various nanoscale elastic heterogeneities are characterized by the correlation length ξ and the standard deviation δ of local shear moduli. (C) The spatial autocorrelation functions of local elastic moduli of three samples, and the corresponding correlation lengths. (D) The probability density distributions of local shear moduli of each sample.

TABLE 1

TABLE 1. List of simulation parameters.

Simulated Samples With Nanoscale Heterogeneity and Simulation Setups

The key material properties of the simulated samples are summarized in Table 2. The simulated samples are configured as Cu₅₀Zr₅₀ with an average shear modulus of 31 GPa and a Poisson’s ratio of 0.36. Three simulated samples with dimensions 300 nm by 100 nm are designed based on the nanoscale heterogeneity characteristics from the experimental results, as shown in Figure 2B. In Figures 2C,D, among all three simulated samples, the Homo sample is simulating a homogenous MG with spatial correlation length ξ = 0.5 nm and a standard deviation δ = 1 GPa of local shear moduli, and the Homo sample serves as a reference baseline. The Med-Heter sample is simulating ST-CuZr with ξ = 7 nm and δ = 4.04 GPa, whereas the Hi-Heter sample is simulating CS-CuZr with ξ = 9.0 nm and δ = 4.20 GPa. For Hi-Heter, its STZ activation volume is increased to 4 nm³ from the 2.7 nm³ of the other samples, as indicated by the experiments. All simulated samples are subjected to uniaxial tension at six different strain rates, i.e., 0.001/s, 0.005/s, 0.01/s, 0.02/s, 0.05/s, and 0.1/s at a temperature of 300 K.

TABLE 2

TABLE 2. List of material properties of the simulated samples.

Results

Nanoindentation Results of Thin-Film Metallic Glasses

The load-displacement curves at five different strain rates (i.e., 0.01/s, 0.02/s, 0.03/s, 0.06/s, and 0.12/s) of ST-CuZr and CS-CuZr are shown in Figures 3A,B, respectively. For ST-CuZr, as the strain rate increases, a larger load is required to reach the same depth. A strain rate hardening effect is observed. All the load-displacement curves are free of pop-ins, indicating that deformations are homogeneous, and no major shear band is formed during the indentation. For CS-CuZr, a strain rate hardening effect is still present, but a variation of strain rate sensitivity can be noticed. For instance, the load-displacement curves from 0.01/s to 0.03/s are more widely spaced when compared to the curves from 0.03/s to 0.12/s. Such changes in the load-displacement curves over the strain rates indicate a change in deformation mechanisms.

FIGURE 3

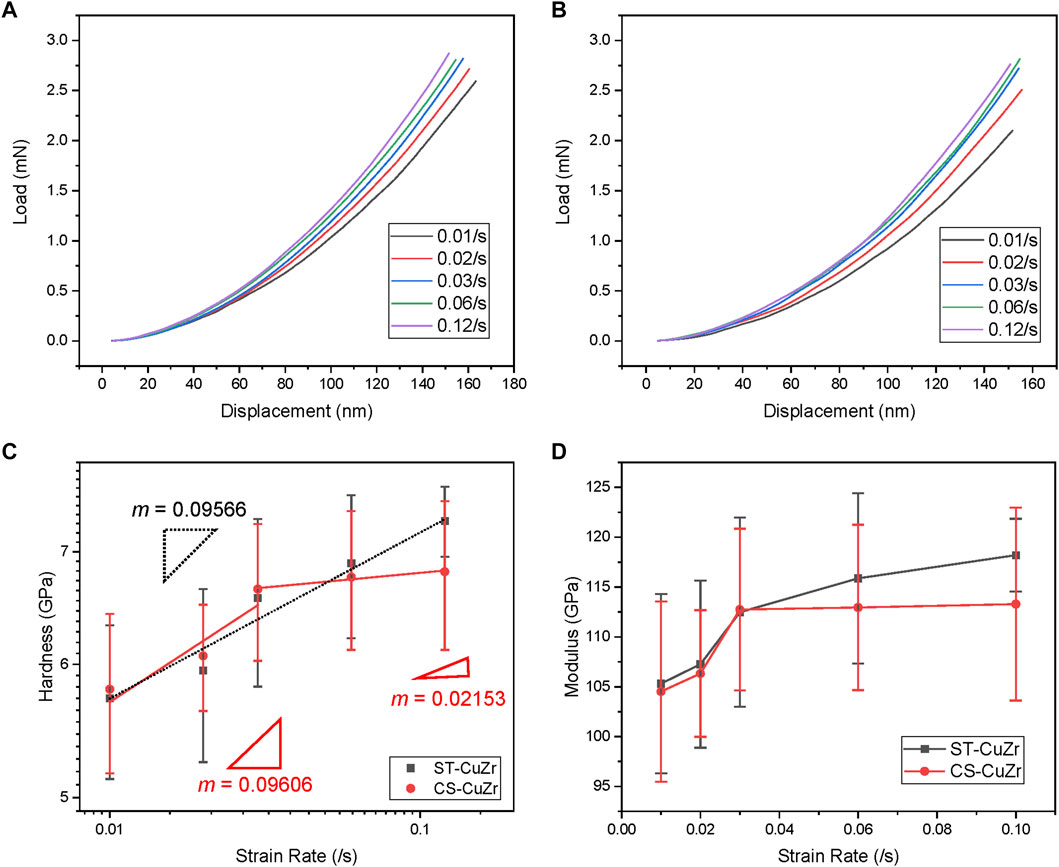
FIGURE 3. The nanoindentation results of TFMGs. Load-displacement curves of ST-CuZr in (A) vs. CS-CuZr in (B) at various strain rates. (C) Hardness vs. strain rate for ST-CuZr (in black) and CS-CuZr (in red), and the strain rate sensitivity m is derived from the slope and the error bars represent one standard deviation. (D) Modulus vs. strain rate of the two TFMGs, and the error bars represent one standard deviation.

The measured hardness vs. strain rate of the two TFMGs is presented in Figure 3C. As the strain rate increases from 0.01/s to 0.12/s, the hardness of ST-CuZr increases from 5.73 to 7.30 GPa; while the hardness of CS-CuZr increases from 5.80 to 6.81 GPa. Accordingly, the strain rate sensitivity m is calculated from the slope of the plot as follows:

$m=\frac{\partial logH}{\partial log\dot{\epsilon }}(2)$

where H and $\dot{\text{ε}}$ are the hardness and the corresponding strain rate, respectively. For ST-CuZr, m = 0.09566 over the strain rates between 0.01/s and 0.12/s. For CS-CuZr, m = 0.06738 on average, but a reduction of m is noted with the strain rate increases. For lower strain rates between 0.01/s and 0.03/s, m = 0.09606; whereas for higher strain rates between 0.03/s and 0.12/s, m = 0.02153. Such change in m signifies a transition of deformation mechanisms in CS-CuZr. Furthermore, the activation volume V* can be calculated based on m (Ma et al., 2019):

$V^{\ast }=\frac{kT}{m\left(\frac{H}{3\sqrt{3}}\right)}(3)$

where k is the Boltzmann constant and T is the temperature. The activation volume of ST-CuZr and CS-CuZr are 0.0321 and 0.0455 nm³, respectively. There is a 41.7% increase in V* in CS-CuZr compared to ST-CuZr. Using the cooperative shearing model (Johnson and Samwer, 2005; Pan et al., 2008), the volume of STZs can be estimated from the strain rate sensitivity m:

$\Omega =\frac{kT}{C^{\prime }mH}(4)$

where C′ = $\left(\frac{2G_0{\gamma }_c^2{R}_0\vartheta }{\sqrt{3}{\tau }_c}\right){\left(1-\frac{{\tau }_{CT}}{{\tau }_c}\right)}^{1/2}$ , τ_CT is the temperature-dependent threshold shear resistance. $R_0$ and $\vartheta$ are constants with values of 0.5 and 3, respectively. G₀ and τ_c are the isotropic shear modulus and the threshold shear resistance of the MG at 0 K, respectively. τ_c/G₀ ≈ 0.036 (Johnson and Samwer, 2005). The estimated STZ volume, therefore, is 1.2 and 1.7 nm³ of ST-CuZr and CS-CuZr, respectively. The CS-CuZr sample has a larger activation volume and a larger STZ volume than those of the ST-CuZr. This is consistent with the sample heterogeneity characterization using DFM, where CS-CuZr has a larger correlation length.

The variation of modulus with respect to the strain rate of the TFMGs is displayed in Figure 3D. As the strain rate increases from 0.01/s to 0.12/s, the modulus of ST-CuZr increases from 105 to 118 GPa; while the modulus of CS-CuZr increases from 105 to 113 GPa. The moduli of both samples slightly increase with respect to strain rates. For CS-CuZr, modulus remains constant as the strain rate goes past 0.03/s. The modulus variation of the ST-CuZr and CS-CuZr is in the range of reported values (Pang et al., 2012; Zeman et al., 2017). Using atomistic simulations, Wang et al. (2015b) showed that during elastic deformation, atoms conglomerate near pre-existing “sub-atomic cavities”, and the local atomic strain becomes more heterogeneous as the applied strain increases. When the strain rate increases, the conglomeration rate also increases, leading to a stiffer MG structure. This observation supports our experimental results from the load-displacement curves (i.e., a deformation mechanism change may be occurring at a strain rate of 0.03/s).

Simulated Stress-Strain Responses of Samples With Various Degrees of Nanoscale Heterogeneities

The representative simulated stress-strain responses of samples with different nanoscale heterogeneities at various strain rates from 0.001/s to 0.1/s are shown in Figure 4A, the corresponding local von Mises strain distributions at 0.02% plastic strain, the yielding point, for different samples are provided in Figures 4B–D. For the Homo sample, it yields at higher stresses when compared to the other heterogeneous samples. The stress-strain responses exhibit a noticeable stress overshoot at all the strain rates, along with an increase in yield stress of 20.67% from 0.001/s to 0.1/s. The stress overshoot is attributed to the formation of shear bands, as shown in Figure 4B. At a lower strain rate, only one major shear band forms with large strain localization, and as the strain rate increases, multiple shear bands appear. An increase in the strain rate leads to a diffuse flow, but all the shear bands form along the maximum shear stress direction (i.e., 45 degrees along the tensile direction).

FIGURE 4

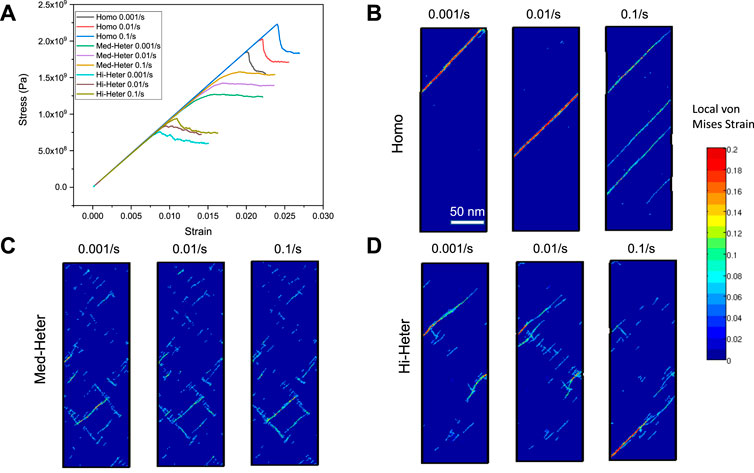
FIGURE 4. The STZ dynamics simulation results of samples with various degrees of nanoscale heterogeneities. (A) The representative stress-strain curves at 0.001/s, 0.01/s, and 0.1/s strain rates for the Homo, Med-Heter, and Hi-Heter samples. Local von Mises strain distribution at 0.02% plastic strain for Homo in (B), Med-Heter in (C) and Hi-Heter in (D) at various strain rates.

For the Med-Heter sample, the yielding occurs at intermediate stresses. It exhibits elastic-nearly perfect plastic flow at all strain rates studied here. The yield and flow stresses increase with increasing strain rate, and the change in yield stress is 24.03% from 0.001/s to 0.1/s. As shown in Figure 4C, the plastic flow is widely distributed in the sample, and no major shear band is formed at any strain rate. The STZs predominately initiate in local soft regions, and the deformation patterns remain unchanged for all the strain rates.

For the Hi-Heter sample, it yields at the lowest stress level. Notably, there is a transition in the stress-strain response from gradually strain softening to stress overshoot as the strain rate increases. From Figure 4A, at the lowest strain rate, 0.001/s, its stress-strain curve shows strain softening; while at 0.01/s, it exhibits steady plastic flow after yielding. When the strain rate reaches the highest value at 0.1/s, a stress overshoot emerges. Those transitions in the stress-strain responses are associated with the changes in the deformation patterns with respect to strain rate. In Figure 4D, the local von Mises strain distribution maps of the Hi-Heter sample show the local strain distribution is diffusing and then localized into the shear band as the strain rate increases. At 0.001/s, a noticeable shear band is formed in a larger soft region, which is slightly bent along with the soft region morphology. A few other strain localization regions are also observed in the smaller soft regions. At 0.01/s strain rate, strain localization is happening primarily in the smaller soft regions, alleviating strain concentration and diffusing plastic flow. However, when the strain rate increases to 0.1/s, the shear localization percolates into the hard regions, connecting several small strain localization paths, and forming a major shear band.

Strain Rate Sensitivity of the Simulated Samples With Different Heterogeneities

The strain rate sensitivity m and activation volume V* of each simulated sample calculated using Eqs 2, 3 are summarized in Figure 5. The simulated samples with a lower level of heterogeneity have a higher yield stress, which agrees with experimental observations. The strain rate sensitivity is 0.03994 and 0.04492 for the Homo and Med-Heter samples, respectively, both of which do not change with respect to strain rate. The Hi-Heter sample, as shown in Figure 5A, has two different m values, i.e., m₁ = 0.05362 at low strain rate vs. m₂ = 0.02949 at high strain rate, which agrees with the experimental results of CS-CuZr (Figure 3D). Figure 5B compiles the strain rate sensitivity m and the activation volume V* as a function of nanoscale heterogeneity measured by spatial correlation length. Accordingly, three regimes are noted. In Regime 1 at a lower heterogeneity, the deformation takes place by stress-dictated shear band formation. In Regime 2 at a higher heterogeneity, the deformation takes place by structure-dictated strain localization. An increase in strain rate sensitivity and reduction of activation volume is observed when compared to Regime 1. The plastic deformation is carried by STZ activations that are localized in the soft regions. In Regime 3, a transition in the deformation mechanism from structure-dictated to stress-dictated occurs as the strain rate increases. Consequently, the deformation patterns change from diffuse STZ activations to shear band percolations, resulting in an increase in activation volume and reduced strain rate sensitivity.

FIGURE 5

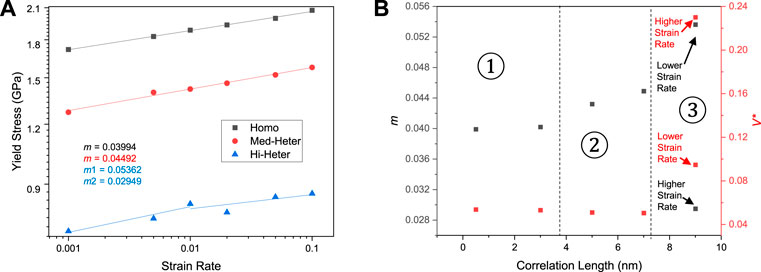
FIGURE 5. (A) Yield stress vs. strain rate for all the simulated samples, along with the calculated strain rate sensitivity m. For Hi-Heter sample with a correlation length of 9 nm, a change in strain rate sensitivity is found, m₁ = 0.05362 at low strain rates vs. m₂ = 0.02949 at high strain rates. (B) Strain rate sensitivity m and activation volume V* for samples with different degrees of nanoscale heterogeneities that measured by the spatial correlation length.

Discussion

The connection between the structures and properties of the MGs at the atomic level has been extensively studied in the past decade. It is found that there exists some correlation between loosely-packed atomic regions and the localized deformation events in the heterogeneous atomic packing configurations of MGs (Wang et al., 2018a; Li et al., 2019; Qiao et al., 2019). Those loosely-packed atomic regions that have relatively lower local shear moduli are considered the “fertile regions” that have a large propensity to undergo shear transformation (Hufnagel et al., 2016). As shown in Figure 6A, the activation of STZs in the simulated samples preferentially occurs in regions with relatively lower local shear moduli. The MG structure-property connection beyond the atomic length scale remains largely unexplored. The activation of STZs (and their development into shear bands) is related to nanoscale structural heterogeneity factors, such as the size and number of the soft (loosely-packed) regions, but is also influenced dynamically by the loading strain rate. Both structural heterogeneities at the nanoscale and the strain rate affect the deformation mechanisms and, as a result, the mechanical properties of the MG.

FIGURE 6

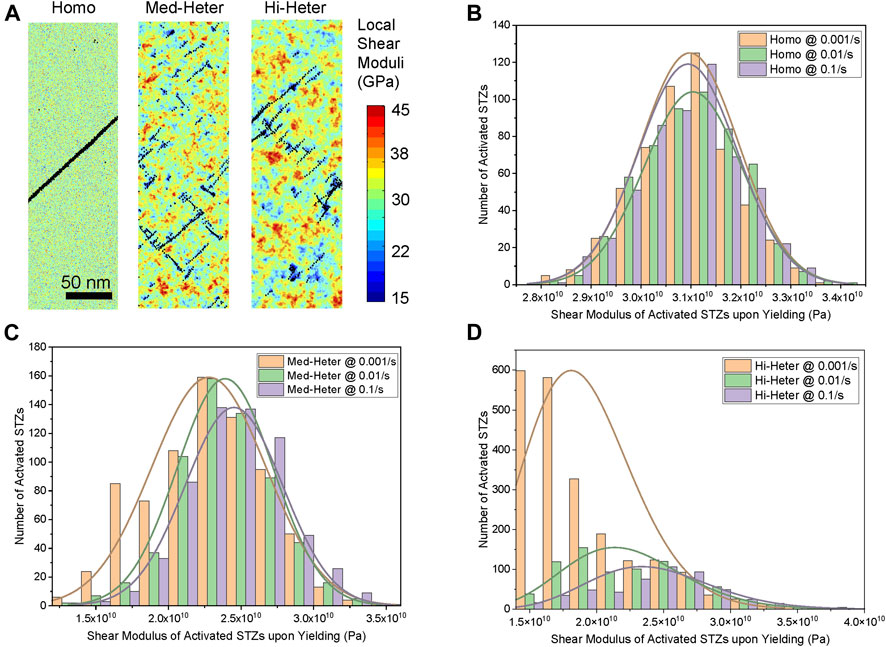
FIGURE 6. Correlation between STZ activations and the MG structural heterogeneity at the nanoscale. (A) The activated STZs upon yielding for three simulated samples at 0.01/s strain rate, overlapping on their local shear modulus distribution maps. The statistical distribution of local shear moduli of activated STZs from 0.001/s to 0.1/s for (B) the Homo sample (C) the Med-Heter sample and (D) the Hi-Heter sample.

At the low heterogeneity (i.e., the Homo sample), shown in Figure 7 as region ①, stress-dictated shear band nucleation and growth is the controlling mechanism. More specifically, the MG has a rather homogenous atomic packing motif (i.e., there are no loosely-packed regions that are larger than the size of an STZ across the MG). As shown in Figure 6B, the average local shear modulus of the activated STZs upon yielding of the Homo samples remains unchanged as the strain rate increases, and there is no clear shift in the distribution fitting either. As shown in Figure 4B, when shear bands start to form, they will follow the maximum shear stress direction to grow and propagate (Greer et al., 2013; Wang et al., 2018a; Yang et al., 2016). Consequently, only one or at most a few major shear bands will form and propagate rapidly, leading to the stress overshoot and brittle failure of the MG. At a low strain rate, one major shear band is formed to accommodate stress-dictated propagation as shown in Figure 7ⓐ. When the strain rate increases, the propagation of a major shear band is not fast enough to accommodate strain change; consequently, more bands are nucleated (Sun et al., 2012) as shown in Figure 7ⓑ. The rate-dependent observation is in line with the shear band dynamics and serrated flow reported in the literature (Xue et al., 2012; Harris et al., 2016). The yield stress of MG at this level of heterogeneity is slightly sensitive to strain rate, and the strain rate sensitivity m remains nearly unchanged until multiple shear bands are formed in the higher strain rates. When multiple shear bands are formed, the strain rate sensitivity m drops by less than 5%.

FIGURE 7

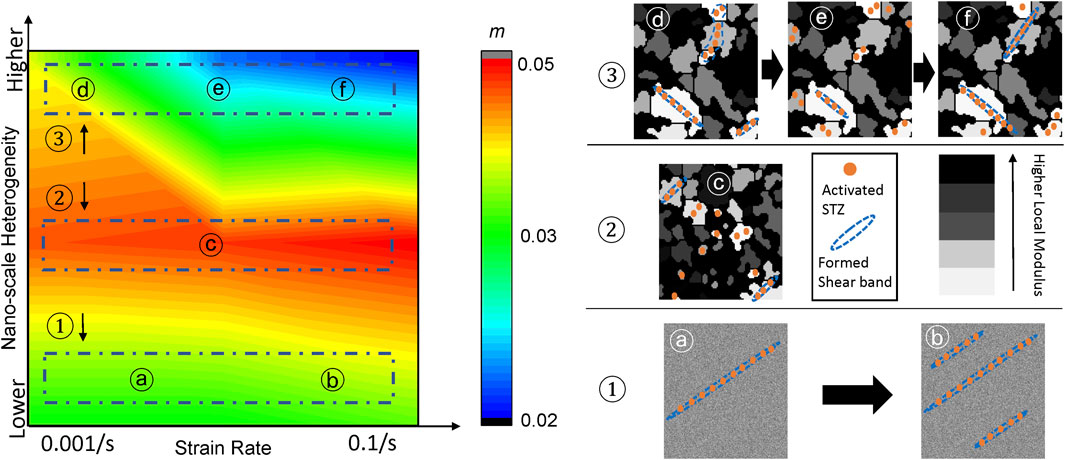
FIGURE 7. The deformation mechanisms along with strain rate sensitivity of the simulated MGs as a function of nanoscale heterogeneity and strain rate. MGs in Region 1 have low heterogeneity that undergo stress-dictated shear banding; MGs in Region 2 with medium heterogeneity undergo structure-dictated strain localization. MGs in Region 3 with high heterogeneity undergo structure-dictated strain localization to stress-dictated strain percolation.

At the medium heterogeneity (i.e., the Med-Heter sample), as shown in Figure 6C, the average local shear modulus of the activated STZs upon yielding of Med-Heter increases ∼5% as the strain rate increases from 0.001/s to 0.1/s. Correspondingly, the distribution fitting is also slightly shifting to the higher modulus direction with the increasing strain rate. Most of the activated STZs have a local shear modulus that is less than the average shear modulus of the entire sample, regardless of strain rate. This indicates there are enough preferred soft (loosely-packed) regions to accommodate STZ activations, and no less desired densely-packed regions get involved even at a higher strain rate. As shown in Figure 7 as region ②, the deformation mechanism becomes structure-dictated strain localization. In particular, the loosely-packed atomic regions become larger than an STZ size, and the STZs are preferably activated in those soft regions which are widely distributed across the MG (Ma et al., 2021; Wang et al., 2018a). As illustrated in Figure 7ⓒ, these soft regions, however, are not large enough to accommodate more than a few activated STZs, preventing the self-proliferation of STZs into shear bands. Instead of growing into the densely-packed (hard) region, more STZs will activate in other loosely-packed (soft) regions. Considering the large number and uniform distribution of soft regions at this medium heterogeneity level, the deformation of the MG becomes homogeneous. The deformation patterns remain unchanged with strain rate as shown in Figure 4C. No major shear band is formed. There are enough loosely-packed (soft) regions in the MG that can carry plastic deformation and these are rather uniformly distributed in the sample (Ma et al., 2021). As a result, the deformation mechanism is structure-dictated strain localization and remains unchanged over the variation of strain rate. The strain rate sensitivity m is high as the activation volume is small, which is localized within the soft regions and m remains unchanged as the strain rate increases. The deformation behavior of this case is similar to the ST-CuZr case.

At the high heterogeneity (i.e., the Hi-Heter sample), as shown in Figure 6D, the average local shear modulus of activated STZs upon yielding increases over 30% as the strain rate increases from 0.001/s to 0.1/s. The distribution fitting is shifting to the higher modulus direction significantly with the increasing strain rate. There is a lower percentage of activated STZs that have a local shear modulus close to or greater than the average shear modulus of the entire sample compared to simulated samples with lower heterogeneity, regardless of strain rate. This indicates that fewer densely-packed regions get involved, and this is due to soft regions being large enough to accommodate shear bands. Especially, at a lower strain rate (e.g, 0.001/s), the STZs are almost only activated in those soft regions, and shear bands are formed inside those very soft regions without the need to grow into harder regions. Consequently, most activated STZs at low strain rates have very low shear moduli. Moreover, in the experimental part of this study, a transition of the deformation mechanism occurs at a 0.03/s strain rate for the CS-CuZr sample, and a similar transition is also observed in this simulation case. As shown in Figure 7 as region ③, a transition of deformation mechanisms from structure-dictated strain localization to stress-dictated shear banding is observed as the strain rate increases. Specifically, some of the loosely-packed (soft) regions become large enough to accommodate multiple STZ activations, forming an incipient shear band. At a low strain rate, a few incipient shear bands are localized in the larger soft regions as shown in Figure 7ⓓ, and the incipient bands that follow the soft pattern do not percolate into the hard regions. As the strain rate increases, the growth rate of the incipient shear bands in the soft regions outpaces the applied deformation rate. More STZs are activated, and minor shear bands are formed in other relatively small soft regions. The deformation mechanism is primarily structure-dictated strain localization, as shown in Figure 7ⓔ. Due to the enlarged soft region size and formation of incipient shear bands, the strain rate sensitivity decreases, and activation volume increases compared to the Med-Heter sample. Furthermore, at a higher strain rate, stress is built up rapidly, allowing some incipient shear bands in the nearby soft regions to break through the surrounding densely-packed (hard) regions. The incipient bands are connected, forming a major shear band, thus resulting in a stress overshoot. Consequently, the deformation mechanism is gradually changed to stress-dictated shear banding, where longer major shear bands are formed, as shown in Figure 7ⓕ. The strain percolation in multiple soft regions to form a shear band increases the activation volume, resulting in a reduction of strain rate sensitivity m at a higher strain rate for the Hi-Heter sample.

Notably, the nanoscale heterogeneity in Figure 7 is controlled by two statistical factors, namely, the standard deviation and the spatial correlation length of the local shear modulus distribution in the simulated samples. Those two statistical factors further modulate the characteristics of loosely packed soft regions, including both their sizes and numbers, which serve as “fertile regions” for STZs. At low heterogeneity, the average soft region size is smaller or comparable to one STZ size. At medium heterogeneity, there are a sufficient amount of soft regions that are larger than one STZ, but not large enough to form a major shear band. Based on the simulation results, the diameter of those soft regions is in the range of 1∼8 times that of STZ. At high heterogeneity, the soft regions are much larger than an STZ, and some of them are large enough, typically having a diameter larger than that of eight STZs, to form a major shear band. It is noteworthy that such quantification of nanoscale heterogeneity and further the deformation mechanism map is based on the coarse-graining assumptions in the STZ dynamics model. The STZ size, activation energy, characteristic shear transition strain, and the nanoscale heterogeneity are assumed to remain unchanged during deformation. The influence of these assumptions on the large-scale deformation behaviors of MG and the interpretation of experimental observations requires further exploration. Recently, Liu and Fan have found that the activation barrier of STZs can be a function of external shear, creating an emergent low-barrier mode with highly tortuous pathways (Liu and Fan, 2021). Furthermore, the MG structure relaxation during thermally activated STZs could influence the nanoscale heterogeneity, leading to complex interplays between thermal activation and the applied strain rate (Bai and Fan, 2018). The incorporation of such physical insights into the STZ dynamics model will enable many more rich deformation phenomena to be captured, deserving research efforts shortly.

Conclusion

In this work, we investigate the strain rate effects on the deformation mechanisms and dynamic mechanical properties of heterogeneous TFMGs using a combined experimental and simulation approach. The CuZr TFMGs are fabricated using magnetron sputtering. The co-sputtered TFMG (i.e., CS-CuZr) exhibits larger nanoscale heterogeneity with the spatial correlation length in energy dissipation of 9.23 nm when compared to single-target TFMG (i.e., ST-CuZr) which has a correlation length of 8.35 nm. Upon nanoindentation tests with strain rates from 0.01/s to 0.12/s, ST-CuZr shows a larger strain rate sensitivity m = 0.096 than that of CS-CuZr with m = 0.067. More importantly, a transition in strain rate sensitivity from m = 0.09606 to m = 0.02153 has been captured in CS-CuZr as the strain rate increases. To understand the underlying mechanisms that give rise to the dynamic plasticity observed experimentally, mesoscale STZ dynamics simulations have been conducted with model MGs having different levels of nanoscale heterogeneities. The model sample with medium heterogeneity (Med-Heter) captures the mechanical responses of ST-CuZr, where the deformation is controlled by the structure-dictated STZ activation in the abundant, uniformly distributed soft regions. The plastic deformation is carried uniformly throughout the sample, and the deformation patterns remain unchanged with increasing strain rates. The activation volume is small and strain rate sensitivity is large due to the localized STZ activation in the small soft regions. The model sample with large nanoscale heterogeneity (Hi-Heter) reproduces the trend of CS-CuZr in dynamic plasticity. A transition in strain rate sensitivity results from a change in deformation mechanism from structure-dictated strain localization at a lower strain rate to stress-dictated strain percolation into a shear band at a higher strain rate. In addition, the simulated results of a homogeneous model sample show stress-dictated shear banding. A transition from shear band propagation to shear band nucleation is found as the strain rate increases, leading to the formation of multiple shear bands. A deformation mechanism map is created to summarize the observed strain rate sensitivity and the corresponding mechanisms with the consideration of both nanoscale structural heterogeneity and strain rate. We envision our study will provide insights into the nanoscale structure and property relationship of MGs and also facilitate the design of nanostructured MGs for dynamic applications.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

YG, XH, FY, and LL conceived and planned the experiments. XH prepared samples. YG and XH carried out the experiments. YG and LL planned and carried out the simulations. YG and LL contributed to the interpretation of the results and wrote the manuscript. All authors provided critical feedback and helped shape the research and manuscript.

Funding

This work is supported by the U.S. National Science Foundation (CMMI-1727875). LL acknowledges the additional financial support from the US National Science Foundation (CMMI-2132383).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Argon, A. S. (1979). Plastic Deformation in Metallic Glasses. Acta metall. 27 (1), 47–58. doi:10.1016/0001-6160(79)90055-5

CrossRef Full Text | Google Scholar

Bai, Z., and Fan, Y. (2018). Abnormal Strain Rate Sensitivity Driven by a Unit Dislocation-Obstacle Interaction in bcc Fe. Phys. Rev. Lett. 120 (12), 125504. doi:10.1103/PhysRevLett.120.125504

PubMed Abstract | CrossRef Full Text | Google Scholar

Bulatov, V. V., and Argon, A. S. (1994). A Stochastic Model for Continuum Elasto-Plastic Behavior. I. Numerical Approach and Strain Localization. Model. Simul. Mat. Sci. Eng. 2 (2), 167–184. doi:10.1088/0965-0393/2/2/001

CrossRef Full Text | Google Scholar

Cheng, Y. Q., and Ma, E. (2011). Atomic-level Structure and Structure-Property Relationship in Metallic Glasses. Prog. Mater. Sci. 56 (4), 379–473. doi:10.1016/j.pmatsci.2010.12.002

CrossRef Full Text | Google Scholar

Ding, J., Cheng, Y.-Q., and Ma, E. (2014). Full Icosahedra Dominate Local Order in Cu64Zr34 Metallic Glass and Supercooled Liquid. Acta mater. 69, 343–354. doi:10.1016/j.actamat.2014.02.005

CrossRef Full Text | Google Scholar

Ding, J., Patinet, S., Falk, M. L., Cheng, Y., and Ma, E. (2014). Soft Spots and Their Structural Signature in a Metallic Glass. Proc. Natl. Acad. Sci. U.S.A. 111 (39), 14052–14056. doi:10.1073/pnas.1412095111

PubMed Abstract | CrossRef Full Text | Google Scholar

Ding, J., Li, L., Wang, N., Tian, L., Asta, M., and Ritchie, R. O. (2021). Universal Nature of the Saddle States of Structural Excitations in Metallic Glasses. Materials Today Physics. 17, 100359. doi:10.1016/j.mtphys.2021.100359

CrossRef Full Text | Google Scholar

Fan, Y., Iwashita, T., and Egami, T. (2014). How Thermally Activated Deformation Starts in Metallic Glass. Nat. Commun. 5 (1), 5083–5087. doi:10.1038/ncomms6083

PubMed Abstract | CrossRef Full Text | Google Scholar

Gao, Q., and Jian, Z. (2016). Kinetics Study on Non-isothermal Crystallization of Cu50Zr50 Metallic Glass. Trans. Indian Inst. Met. 70 (7), 1879–1885. doi:10.1007/s12666-016-0992-7

CrossRef Full Text | Google Scholar

González, S., Xie, G., Louzguine-Luzgin, D., Perepezko, J., and Inoue, A. (2011). Deformation and Strain Rate Sensitivity of a Zr–Cu–Fe–Al Metallic Glass. Mater. Sci. Eng. A 528 (9), 3506–3512. doi:10.1016/j.msea.2011.01.049

CrossRef Full Text | Google Scholar

Greer, A. L., Cheng, Y. Q., and Ma, E. (2013). Shear Bands in Metallic Glasses. Mater. Sci. Eng. R Rep. 74 (4), 71–132. doi:10.1016/j.mser.2013.04.001

CrossRef Full Text | Google Scholar

Hardin, T. J., and Homer, E. R. (2015). Microstructural Factors of Strain Delocalization in Model Metallic Glass Matrix Composites. Acta Mater. 83, 203–215. doi:10.1016/j.actamat.2014.09.043

CrossRef Full Text | Google Scholar

Harris, M. B., Watts, L. S., and Homer, E. R. (2016). Competition between Shear Band Nucleation and Propagation across Rate-dependent Flow Transitions in a Model Metallic Glass. Acta Mater. 111, 273–282. doi:10.1016/j.actamat.2016.03.066

CrossRef Full Text | Google Scholar

Homer, E., Rodney, D., and Schuh, C. (2010). Kinetic Monte Carlo Study of Activated States and Correlated STZ Activity during the Deformation of an Amorphous Metal. Phys. Rev. B Condens. Matter Mater. Phys. 81 (064204), 1–11. doi:10.1103/physrevb.81.064204

CrossRef Full Text | Google Scholar

Homer, E. R., and Schuh, C. A. (2009). Mesoscale Modeling of Amorphous Metals by Shear Transformation Zone Dynamics. Acta Mater. 57 (9), 2823–2833. doi:10.1016/j.actamat.2009.02.035

CrossRef Full Text | Google Scholar

Hufnagel, T. C., Schuh, C. A., and Falk, M. L. (2016). Deformation of Metallic Glasses: Recent Developments in Theory, Simulations, and Experiments. Acta Mater. 109, 375–393. doi:10.1016/j.actamat.2016.01.049

CrossRef Full Text | Google Scholar

Im, S., Chen, Z., Johnson, J. M., Zhao, P., Yoo, G. H., Park, E. S., et al. (2018). Direct Determination of Structural Heterogeneity in Metallic Glasses Using Four-Dimensional Scanning Transmission Electron Microscopy. Ultramicroscopy 195, 189–193. doi:10.1016/j.ultramic.2018.09.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Jiang, W. H., and Atzmon, M. (2003). Rate Dependence of Serrated Flow in a Metallic Glass. J. Mat. Res. 18 (4), 755–757. doi:10.1557/jmr.2003.0103

CrossRef Full Text | Google Scholar

Johnson, W. L., and Samwer, K. (2005). A Universal Criterion for Plastic Yielding of Metallic Glasses with a(T/Tg)2/3Temperature Dependence. Phys. Rev. Lett. 95 (19), 195501. doi:10.1103/physrevlett.95.195501

PubMed Abstract | CrossRef Full Text | Google Scholar

Karabacak, T., Zhao, Y. P., Wang, G. C., and Lu, T. M. (2001). Growth-front Roughening in Amorphous Silicon Films by Sputtering. Phys. Rev. B 64 (8), 085323. doi:10.1103/physrevb.64.085323

CrossRef Full Text | Google Scholar

Kawasaki, T., Araki, T., and Tanaka, H. (2007). Correlation between Dynamic Heterogeneity and Medium-Range Order in Two-Dimensional Glass-Forming Liquids. Phys. Rev. Lett. 99 (21), 215701. doi:10.1103/physrevlett.99.215701

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, L., Wang, N., and Yan, F. (2014). Transient Response in Metallic Glass Deformation: a Study Based on Shear Transformation Zone Dynamics Simulations. Scr. Mater. 80, 25–28. doi:10.1016/j.scriptamat.2014.02.005

CrossRef Full Text | Google Scholar

Li, S., Huang, P., and Wang, F. (2019). Rejuvenation Saturation upon Cyclic Elastic Loading in Metallic Glass. Comput. Mater. Sci. 166, 318–325. doi:10.1016/j.commatsci.2019.05.007

CrossRef Full Text | Google Scholar

Bai, C., and Fan, Y. (2021). Emergent Fractal Energy Landscape as the Origin of Stress-Accelerated Dynamics in Amorphous Solids. Phys. Rev. Lett. 127 (21), 215502. doi:10.1103/PhysRevLett.127.215502

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, Y. H., Wang, D., Nakajima, K., Zhang, W., Hirata, A., Nishi, T., et al. (2011). Characterization of Nanoscale Mechanical Heterogeneity in a Metallic Glass by Dynamic Force Microscopy. Phys. Rev. Lett. 106 (12), 125504. doi:10.1103/physrevlett.106.125504

PubMed Abstract | CrossRef Full Text | Google Scholar

Lu, Y. M., Zeng, J. F., Wang, S., Sun, B. A., Wang, Q., Lu, J., et al. (2016). Structural Signature of Plasticity Unveiled by Nano-Scale Viscoelastic Contact in a Metallic Glass. Sci. Rep. 6 (1), 29357–29359. doi:10.1038/srep29357

PubMed Abstract | CrossRef Full Text | Google Scholar

Ma, C. F., Huang, P., and Wang, F. (2021). Enhanced Strain Rate Sensitivity in Thermal-Cycling-Rejuvenated Metallic Glasses. J. Alloys Compd. 861, 158632. doi:10.1016/j.jallcom.2021.158632

CrossRef Full Text | Google Scholar

Ma, Y., Huang, X., Song, Y., Hang, W., and Zhang, T. (2019). Room-temperature Creep Behavior and Activation Volume of Dislocation Nucleation in a LiTaO3 Single Crystal by Nanoindentation. Materials 12 (10), 1683. doi:10.3390/ma12101683

PubMed Abstract | CrossRef Full Text | Google Scholar

Nomoto, K., Ceguerra, A. V., Gammer, C., Li, B., Bilal, H., Hohenwarter, A., et al. (2021). Medium-range Order Dictates Local Hardness in Bulk Metallic Glasses. Mater. Today 44, 48–57. doi:10.1016/j.mattod.2020.10.032

CrossRef Full Text | Google Scholar

Pan, D., Inoue, A., Sakurai, T., and Chen, M. W. (2008). Experimental Characterization of Shear Transformation Zones for Plastic Flow of Bulk Metallic Glasses. Proc. Natl. Acad. Sci. U.S.A. 105 (39), 14769–14772. doi:10.1073/pnas.0806051105

PubMed Abstract | CrossRef Full Text | Google Scholar

Pang, J.-J., Tan, M.-J., Liew, K. M., and Shearwood, C. (2012). Nanoindentation Study of Size Effect and Loading Rate Effect on Mechanical Properties of a Thin Film Metallic Glass Cu49.3Zr50.7. Phys. B Condens. Matter 407 (3), 340–346. doi:10.1016/j.physb.2011.10.050

CrossRef Full Text | Google Scholar

Qiao, J. C., Wang, Q., Pelletier, J. M., Kato, H., Casalini, R., Crespo, D., et al. (2019). Structural Heterogeneities and Mechanical Behavior of Amorphous Alloys. Prog. Mater. Sci. 104, 250–329. doi:10.1016/j.pmatsci.2019.04.005

CrossRef Full Text | Google Scholar

Ramachandramoorthy, R., Schwiedrzik, J., Petho, L., Guerra-Nuñez, C., Frey, D., Breguet, J.-M., et al. (2019). Dynamic Plasticity and Failure of Microscale Glass: Rate-dependent Ductile-Brittle-Ductile Transition. Nano Lett. 19 (4), 2350–2359. doi:10.1021/acs.nanolett.8b05024

PubMed Abstract | CrossRef Full Text | Google Scholar

Schroers, J. (2013). Bulk Metallic Glasses. Phys. Today 66 (2), 32–37. doi:10.1063/pt.3.1885

CrossRef Full Text | Google Scholar

Schuh, C. A., Lund, A. C., and Nieh, T. G. (2004). New Regime of Homogeneous Flow in the Deformation Map of Metallic Glasses: Elevated Temperature Nanoindentation Experiments and Mechanistic Modeling. Acta Mater. 52 (20), 5879–5891. doi:10.1016/j.actamat.2004.09.005

CrossRef Full Text | Google Scholar

Sun, B. A., Pauly, S., Tan, J., Stoica, M., Wang, W. H., Kühn, U., et al. (2012). Serrated Flow and Stick-Slip Deformation Dynamics in the Presence of Shear-Band Interactions for a Zr-Based Metallic Glass. Acta Mater. 60 (10), 4160–4171. doi:10.1016/j.actamat.2012.04.013

CrossRef Full Text | Google Scholar

Tian, L., Fan, Y., Li, L., and Mousseau, N. (2020). Identifying Flow Defects in Amorphous Alloys Using Machine Learning Outlier Detection Methods. Scr. Mater. 186, 185–189. doi:10.1016/j.scriptamat.2020.05.038

CrossRef Full Text | Google Scholar

Trexler, M. M., and Thadhani, N. N. (2010). Mechanical Properties of Bulk Metallic Glasses. Prog. Mater. Sci. 55 (8), 759–839. doi:10.1016/j.pmatsci.2010.04.002

CrossRef Full Text | Google Scholar

Van Toan, N., Tuoi, T. T. K., Tsai, Y. C., Lin, Y. C., and Ono, T. (2020). Micro-fabricated Presure Sensor Using 50 Nm-Thick of Pd-Based Metallic Glass Freestanding Membrane. Sci. Rep. 10 (1), 10108–10109. doi:10.1038/s41598-020-67150-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, N., Ding, J., Yan, F., Asta, M., Ritchie, R. O., and Li, L. (2018). Spatial Correlation of Elastic Heterogeneity Tunes the Deformation Behavior of Metallic Glasses. npj Comput. Mater. 4 (1), 1–10. doi:10.1038/s41524-018-0077-8

CrossRef Full Text | Google Scholar

Wang, N., Ding, J., Luo, P., Liu, Y., Li, L., and Yan, F. (2018). Chemical Variation Induced Nanoscale Spatial Heterogeneity in Metallic Glasses. Mater. Res. Lett. 6 (12), 655–661. doi:10.1080/21663831.2018.1532465

CrossRef Full Text | Google Scholar

Wang, N., Yan, F., and Li, L. (2015). Mesoscopic Examination of Cyclic Hardening in Metallic Glass. J. Non-Crystalline Solids 428, 146–150. doi:10.1016/j.jnoncrysol.2015.08.007

CrossRef Full Text | Google Scholar

Wang, S., Sun, D., Hata, S., Sakurai, J., and Shimokohbe, A. (2009). Fabrication of Thin Film Metallic Glass (TFMG) Pipe for a Cylindrical Ultrasonic Linear Micro-actuator. Sensors Actuators A Phys. 153 (1), 120–126. doi:10.1016/j.sna.2009.04.029

CrossRef Full Text | Google Scholar

Wang, W-H., Dong, C., and Shek, C. (2004). Bulk Metallic Glasses. Mater. Sci. Eng. R Rep. 44 (2-3), 45–89. doi:10.1016/j.mser.2004.03.001

CrossRef Full Text | Google Scholar

Wang, W., Mraied, H., Diyatmika, W., Chu, J. P., Li, L., and Cai, W. (2020). Effects of Nanoscale Chemical Heterogeneity on the Wear, Corrosion, and Tribocorrosion Resistance of Zr-Based Thin Film Metallic Glasses. Surf. Coatings Technol. 402, 126324. doi:10.1016/j.surfcoat.2020.126324

CrossRef Full Text | Google Scholar

Wang, X. D., Aryal, S., Zhong, C., Ching, W. Y., Sheng, H. W., Zhang, H., et al. (2015). Atomic Picture of Elastic Deformation in a Metallic Glass. Sci. Rep. 5 (1), 9184–9186. doi:10.1038/srep09184

PubMed Abstract | CrossRef Full Text | Google Scholar

Wei, D., Yang, J., Jiang, M-Q., Wei, B-C., Wang, Y-J., and Dai, L-H. (2019). Revisiting the Structure–Property Relationship of Metallic Glasses: Common Spatial Correlation Revealed as a Hidden Rule. Phys. Rev. B 99 (1), 014115. doi:10.1103/physrevb.99.014115

CrossRef Full Text | Google Scholar

Xue, Y., Wang, L., Cheng, X., Wang, F., Cheng, H., Zhang, H., et al. (2012). Strain Rate Dependent Plastic Mutation in a Bulk Metallic Glass under Compression. Mater. Des. (1980-2015) 36, 284–288. doi:10.1016/j.matdes.2011.11.025

CrossRef Full Text | Google Scholar

Yang, G. N., Shao, Y., and Yao, K. F. (2016). The Shear Band Controlled Deformation in Metallic Glass: a Perspective from Fracture. Sci. Rep. 6 (1), 21852–21911. doi:10.1038/srep21852

PubMed Abstract | CrossRef Full Text | Google Scholar

Zeman, P., Zítek, M., Zuzjaková, Š., and Čerstvý, R. (2017). Amorphous Zr-Cu Thin-Film Alloys with Metallic Glass Behavior. J. Alloys Compd. 696, 1298–1306. doi:10.1016/j.jallcom.2016.12.098

CrossRef Full Text | Google Scholar

Zhao, P., Li, J., and Wang, Y. (2014). Extended Defects, Ideal Strength and Actual Strengths of Finite-Sized Metallic Glasses. Acta mater. 73, 149–166. doi:10.1016/j.actamat.2014.03.068

CrossRef Full Text | Google Scholar

Zhao, P., Li, J., and Wang, Y. (2013). Heterogeneously Randomized STZ Model of Metallic Glasses: Softening and Extreme Value Statistics during Deformation. Int. J. Plasticity 40, 1–22. doi:10.1016/j.ijplas.2012.06.007

CrossRef Full Text | Google Scholar

Zhu, F., Song, S., Reddy, K. M., Hirata, A., and Chen, M. (2018). Spatial Heterogeneity as the Structure Feature for Structure-Property Relationship of Metallic Glasses. Nat. Commun. 9 (1), 3965–3967. doi:10.1038/s41467-018-06476-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhu, F., Hirata, A., Liu, P., Song, S., Tian, Y., Han, J., et al. (2017). Correlation between Local Structure Order and Spatial Heterogeneity in a Metallic Glass. Phys. Rev. Lett. 119 (21), 215501. doi:10.1103/physrevlett.119.215501

PubMed Abstract | CrossRef Full Text | Google Scholar

Zink, M., Samwer, K., Johnson, W. L., and Mayr, S. G. (2006). Plastic Deformation of Metallic Glasses: Size of Shear Transformation Zones from Molecular Dynamics Simulations. Phys. Rev. B 73 (17), 172203. doi:10.1103/physrevb.73.172203

CrossRef Full Text | Google Scholar