A Qualitative Study of the Disorder Effect on the Phonon Transport in a Two-Dimensional Graphene/h-BN Heterostructure

Recently, massive efforts have been made to control phonon transport via introducing disorder. Meanwhile, materials informatics, an advanced material-discovery technology that combines data-driven search algorithms and material property simulations, has made significant progress and shown accurate prediction ability in studying the target properties of new materials. However, with the introduction of disorder, the design space of random structures is greatly expanded. Global optimization for the entire domain is nearly impossible with the current computer resource even when materials informatics reduces the design space to a few percent. Toward the goal of reducing design space, we investigate the effect of different types of disorders on phonon transport in two-dimensional graphene/hexagonal boron nitride heterostructure using non-equilibrium molecular dynamics simulation. The simulation results show that when the hexagonal boron nitride is distributed disorderly in the coherent phonon-dominated structure, that is, the structure with a period length of 1.23 nm, the thermal conductivity is significantly reduced due to the appearance of coherent phonon localization. By qualitatively analyzing different types of disorder, we found that the introduction of disordered structure in the cross direction with a larger shift distance can further reduce the thermal conductivity. Further physical mechanism analysis revealed that the structures with lower thermal conductivity were caused by weak propagation and strong localization of phonon. Our findings have implications for accelerating machine learning in the search for structures with the lowest thermal conductivity, and provide some guidance for the future synthesis of 2D heterostructures with unique thermal properties.

Introduction

With the development of low-dimensional materials and the increasing demand for microelectronic devices, effective management of nanoscale heat transport has gradually become an urgent problem to be solved. Traditionally, the thermal conductivity can manipulate by introducing additional defects (Chen et al., 2010; Hao et al., 2011; Zhang et al., 2011; Ding et al., 2015; Feng et al., 2015; Nai et al., 2015), impurities (Chen et al., 2009; Chen et al., 2012), nanoparticles (Maldovan, 2013; Wang et al., 2013; Lin et al., 2016; Mendoza and Chen, 2016; Lu et al., 2021), and ion-intercalation (Qian et al., 2016) into the pristine materials. Additionally, the underlying physical mechanism can be well explained by solving the Boltzmann transport equation (BTE), in which phonons are regarded as incoherent particles (particle nature of phonons).

Recently, periodic nanostructures (Hopkins et al., 2011; Zen et al., 2014; Alaie et al., 2015; Yang et al., 2015; Hu et al., 2016; Ma et al., 2016; Sledzinska et al., 2019; Vasileiadis et al., 2021; Nomura et al., 2022) constructed based on the phonon wave interference (wave nature of phonons), which can modify the phonon dispersion and further reduce the group velocity (Swinteck et al., 2013; Latour et al., 2014; Xiong et al., 2016; Ma et al., 2018), have attracted widespread attention from researchers. Subsequently, the researchers additionally introduced randomness into periodic nanostructures. The results showed that a certain degree of randomness could significantly suppress the thermal conductivity (Hu et al., 2018; Hu et al., 2019). However, the mentioned results above were obtained by calculating a limited number of random structures, mainly because it is impossible to perform global optimization with the current computer resource for all possible configurations (a vast design space).

However, material informatics (machine learning), which applies informatics principles to materials science and engineering to improve the understanding, use, selection, development, and discovery of materials, seems to have brought dawn to the solution of large-scale design space problems. Such as, in some recent studies, Wan et al. used a convolutional neural network method to effectively design the structure of porous with the lowest thermal conductivity (Wan et al., 2020). Wei et al. obtained the result that the thermal conductivity of disordered structures is unexpectedly more significant than that of the periodic system through the efficient genetic algorithm search (Wei et al., 2020). Hu et al. realized the ultimate impedance of coherent heat conduction in van der Waals graphene-MoS₂ heterostructures based on Bayesian optimization (Hu et al., 2021). Nevertheless, it is worth noting that the studies mentioned above were all performed in a relatively small design space, even if machine learning (Bayesian optimization) can reduce the number of calculations to a few percent (Ju et al., 2017; Hu et al., 2020). Therefore, to effectively broaden the application scope of machine learning and expand the design space, exploring the typical characteristics of target properties is becoming an urgent task and research hotspot.

In this work, we use non-equilibrium molecular dynamics (NEMD) simulations to investigate the effect of disorder on the phonon transport in a two-dimensional graphene/hexagonal boron nitride (G/h-BN) heterostructure. First, the signature for coherent phonon transport is observed in G/h-BN heterostructure by varying the period length. Furthermore, we introduce five types of disorders to identify the heterostructure’s common feature with low thermal conductivity. The underlying mechanism is further uncovered by performing wave packet simulation. The present findings help to reveal the underlying physical mechanism of phonon transport in two-dimensional heterostructures, and will be instructive for the future synthesis of heterostructures with unique thermal properties.

Simulation Method

In our simulations, the G/h-BN heterostructure (Figures 1D,E) is composed of the unit cells constructed by distributing h-BN periodically/disorderly into the pristine graphene (Figures 1A,B). Meanwhile, the edge of h-BN is guaranteed to be zigzag, mainly considering that different defect type have different effects on the thermal transport of graphene (Feng et al., 2015). The period length (L_p) and replacement ratio (Re_r) are used to characterize the unit cells. Figures 1A,B shows two representative unit cells with different L_p. The replacement ratio is N_B/N_G, where N_B and N_G are the numbers of atoms in h-BN and the total number of atoms in pristine graphene, respectively. Here, the replacement ratio fixes at 10%.

FIGURE 1

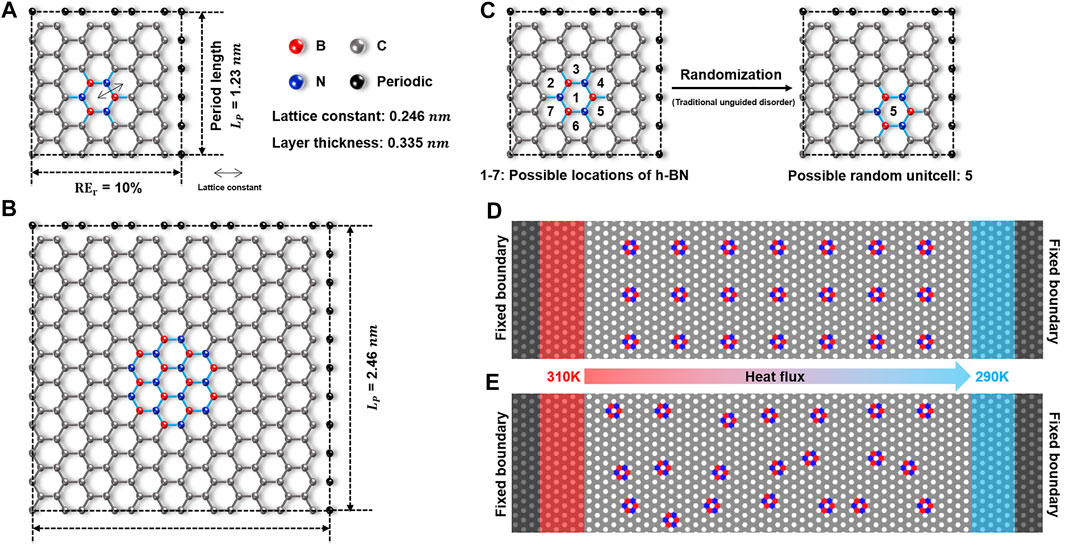
FIGURE 1. Schematic figures of G/h-BN lateral heterostructure. (A)–(B) Schematic diagrams of the unit cells with $L_p=1.23 nm$ and $2.46 nm$. The replacement rate is fixed at 10%. (C) Schematic diagram of the introduction of disorder. (D)–(E) Schematic diagram of periodic structure and TU-DS.

Our study’s NEMD simulations are implemented using the LAMMPS package (Plimpton, 1995). The optimized Tersoff potential function describes the covalent-bonds interaction in graphene and h-BN(Sevik et al., 2011; Kınacı et al., 2012). The time step is set as 0.5 fs The fixed and periodic boundary conductions are adopted along the length and width direction in our simulations, respectively. The width is fixed at 7.38 nm, which is enough to eliminate the numerical size effect caused by the periodic boundary condition (Hu et al., 2017). Two Langevin thermostats with temperatures of 310 and 290 K are applied at both ends of the simulation system (red and blue region in Figure 1D) to establish a temperature gradient. The system first runs 50 ps in the NPT ensemble and then relaxes for 2 ns in the NVE ensemble to reach the steady-state. The cumulative energy ΔE added/subtracted to the heat source/sink region and the temperature are recorded for another 5 ns. The energy change per unit time (ΔE/Δt) was obtained by linearly fitting the raw data of the accumulated energy ΔE, which was used to calculate the heat flux $\mathit{J}=\frac{\mathit{\Delta E}}{\mathit{\Delta t}\cdot \mathit{S}}$. Here S is the cross-sectional area of G/h-BN heterostructure. We use Fourier’s Law to calculate the thermal conductivity (κ), κ =—J/ $\nabla \mathit{T}$, where $\mathit{J}$ and $\nabla \mathit{T}$ are, respectively, the heat flux and the temperature gradient.

Results and Discussion

Thermal Conductivity of G/h-BN Heterostructure

We first study the effective thermal conductivity of G/h-BN heterostructure with different L_p in a finite-size system. Here, the system length fixes to 76.7 nm. Such treatments have been extensively employed in literature (Chang et al., 2008; Liu et al., 2014; Xu et al., 2014) when the thermal transport behavior is not necessarily diffusive. As shown in Figure 2, the thermal conductivity of the periodic structure first decreases and then increases as the increase of $L_p$. The competition mechanism between coherent and incoherent phonons in heat conduction leads to this nonlinear trend (Wu and Han, 2022). At smaller $L_p$, the heat transport mainly depends on coherent phonons. In contrast, the heat transport mainly contributes from the incoherent phonons at larger $L_p$. As $L_p$ increases, the transition from coherent phonon to incoherent phonon-dominated thermal transport is observed, and a similar trend was found in previous studies (Hu et al., 2018; Hu et al., 2019; Roy Chowdhury et al., 2020). The detailed discussion of the relevant physical mechanisms can be found in the Refs (Latour et al., 2014; Lee et al., 2017; Hu et al., 2018; Xie et al., 2018; Felix and Pereira, 2020). In addition, we further construct five traditional unguided disorder structures (TU-DS) by randomly introducing disorders at each $L_p$ to explore the disorder’s effect on thermal conductivity. Figure 1C shows the seven center positions of h-BN (denoted 1–7) that can be selected when constructing the TU-DS. The results show that different TU-DS heterostructures exhibit different thermal conductivities, which originate from different degrees of phonon localization caused by different disorders. In addition, introducing the disorder at smaller $L_p$ can greatly reduce the thermal conductivity (Figure 2). However, as $L_p$ increases, the effect of disorder on the thermal conductivity is becoming not apparent anymore. For instance, as shown in the inset, when $L_p=1.23 nm$, the thermal conductivity of the TU-DS heterostructures is reduced to 37% of the corresponding periodic structure. Inversely, when the disorder is introduced into the heterostructure with $L_p=$ $8.61 nm$, the thermal conductivity is reduced by only 5.4%. Therefore, to gain further insight into how disorder affects coherent phonon transport and thus reduces thermal conductivity, we performed a qualitative analysis of several different disorder types, with $L_p$ fixed $\text{ at }1.23 nm$ in the following simulations.

FIGURE 2

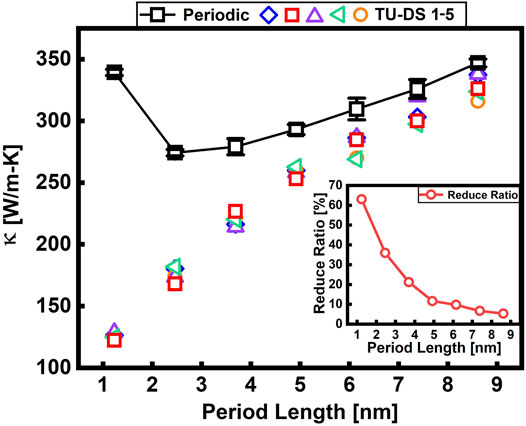
FIGURE 2. The effect of ${\mathit{L}}_{\mathit{p}}$ on the thermal conductivity of periodic structure and TU-DS at 300 K. The inset shows the relative difference between the thermal conductivity of the TU-DS and the corresponding periodic structure with different $L_p$. The relative difference is defined as $\left({\kappa }_{periodic}-{\kappa }_{TU-DS}\right)/{\kappa }_{periodic}\times 100\%$. The error bars are the standard deviations of five independent simulations with different initial conditions.

Qualitative Analysis of Disorder Effects

To classify different types of disorder, we first introduced a descriptor, shift distance (SD), to characterize the strength of the disorder. The SD is defined as the deviation length from the current h-BN center (dots of different colors in Figures 3A,C,E) to the original center (denoted as “O” in Figures 3A,C,E). For example, as shown in Figure 3A, the distance between the red point and the original center O is defined as $a$ (SD = $a$). In addition to SD, we further propose another descriptor, the direction of disorder, to complement the description of the disorder type. We randomly generated 20 disordered structures (changing the disorder direction and SD) for each specific disorder type in the following qualitative analysis simulations.

FIGURE 3

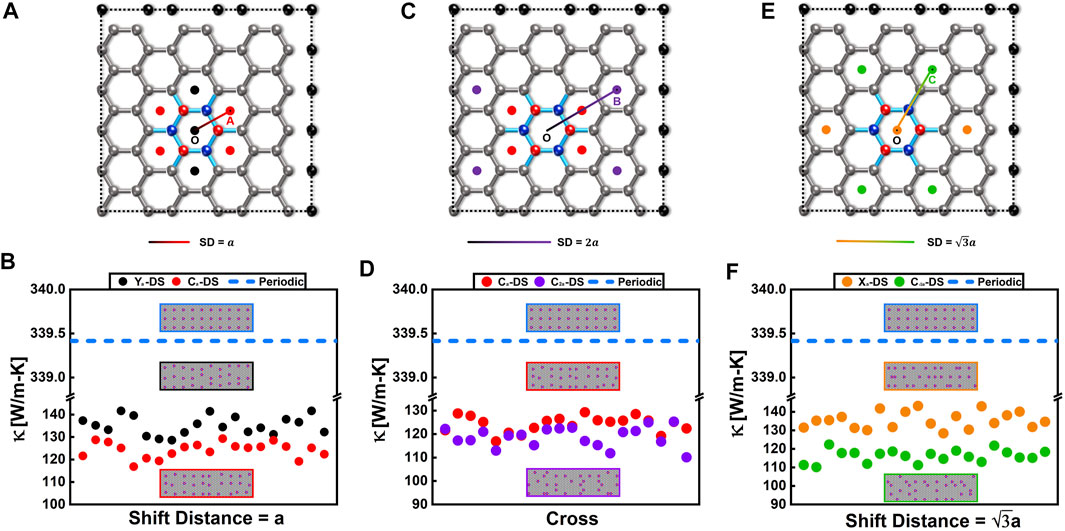
FIGURE 3. Qualitative analysis of the effect of disorder on thermal conductivity at 300 K (A)–(B) Schematic diagrams of $Y_a$-DS and $C_a$-DS and their corresponding thermal conductivity. (C)–(D) Schematic diagrams of $C_a$-DS and $C_{2a}$-DS and their corresponding thermal conductivity. (E)–(F) Schematic diagrams of $C_{\sqrt{3}a}$-DS and $X_{\sqrt{3}a}$-DS and their corresponding thermal conductivity.

We first construct the disordered structures by shifting the h-BN with fixed SD = $a$ in the y-direction ($Y_a$-DS) and cross direction ($C_a$-DS), respectively. The possible centers of the h-BN in $Y_a$-DS and $C_a$-DS are denoted as black and red dots, respectively. (Figure 3A). The corresponding thermal conductivity results (Figure 3B) show that the average thermal conductivity of $C_a$-DS ($124.77$ W/m-K) is lower than that of the $Y_a$-DS $(135.21$ W/m-K). It inspires us that the introduction of disorder in the cross-direction can more effectively hinder phonon transport, thereby further reducing the thermal conductivity of the heterostructures. Therefore, we fix the disorder direction as the cross-direction and increase the SD to $2a$ ($C_{2a}$-DS). The possible centers are denoted as purple points in Figure 3C. The thermal conductivity results show that the ${\overline{\kappa }}_{C_{2a}-DS}$ ($118.78$ W/m-K) are further reduced compared to the ${\overline{\kappa }}_{C_a-\text{DS}}$ (Figure 3D). This result suggests that the larger SD appears more promising to block phonon transport. Along this design route, we introduce two additional disorder types at x ($X_{\sqrt{3}a}$-DS) and cross-direction ($C_{\sqrt{3}a}$-DS) with a fixed SD = $\sqrt{3}a$. As we expected, the ${\overline{\kappa }}_{C_{\sqrt{3}a}-DS}$ ($116.16$ W/m-K) is significantly lower than the ${\overline{\kappa }}_{X_{\sqrt{3}a}-DS}$ ($135.46$ W/m-K), which again confirms that larger SD and introducing disorder at cross-direction can effectively reduce the thermal conductivity. In Figures 3B,D,F, we plot the horizontal dashed line to denote the thermal conductivity of the periodic structure (${\overline{\kappa }}_{periodic}=339.42$ W/m-K). Our qualitative analysis establishes a rationale between the disorder characteristics (direction and SD) and the thermal conductivity of heterostructure with different disorder types. It manifests that the heterostructure with a larger $\text{SD}$ and disorder in the cross-direction leads to a further reduction in thermal conductivity. Our study focuses on manipulating phonon thermal transport in heterostructures through different disorder types, which provides two characteristics for considering the introduction of the disorder in structural design, bringing new insights into further narrowing the design space.

Structural Analysis

To understand the underlying physical mechanism of the above results, we conducted phonon wave packet simulations in pristine graphene, periodic structure, TU-DS, and $C_{\sqrt{3}a}$-DS, which can directly record the wave characteristics of phonon transport behavior (phonon transmission and reflection) in the coordinate space. As shown in Figures 4A–D, we launched the same phonon wave packet from the pristine graphene side with a fixed frequency of 6.11 THz (Hu et al., 2019) and recorded its propagation along the length direction. The length ratio between the pristine graphene and the four targeted structures mentioned above is 1:1. Periodic boundary conditions are used for all directions. Before the wave packet simulation performing, each structure was relaxed with an NPT ensemble at 0 K. The initial wave packet was formed via linear combinations of normal vibration modes as follows:

${\mu }_{n,\alpha }=Re\left\{A{\epsilon }_{j\alpha ,\lambda }{e}^{i{\mathit{k}}_0\left(x_n-x_0\right)}{e}^{-{\left(x_n-x_0\right)}^2/{\eta }^2}\right\},(1)$

where ${\mu }_{n,\alpha }$ denotes $\alpha th$ displacement component of the $n$ th atom in the simulated structure. $A$ is the amplitude of the wave packet, $\eta$ is the spatial width of the wave packet, and ${\epsilon }_{j\alpha ,\lambda }$ represents the αth eigenvector component of the eigenmode λ for the jth atom in the pristine graphene. To initialize velocities, we added time dependence to Eq. 1 and differentiated it as

$v_{n,\alpha }=Re\left\{-i{\omega }_{\lambda }{\mu }_{n,\alpha }\right\}.(2)$

FIGURE 4

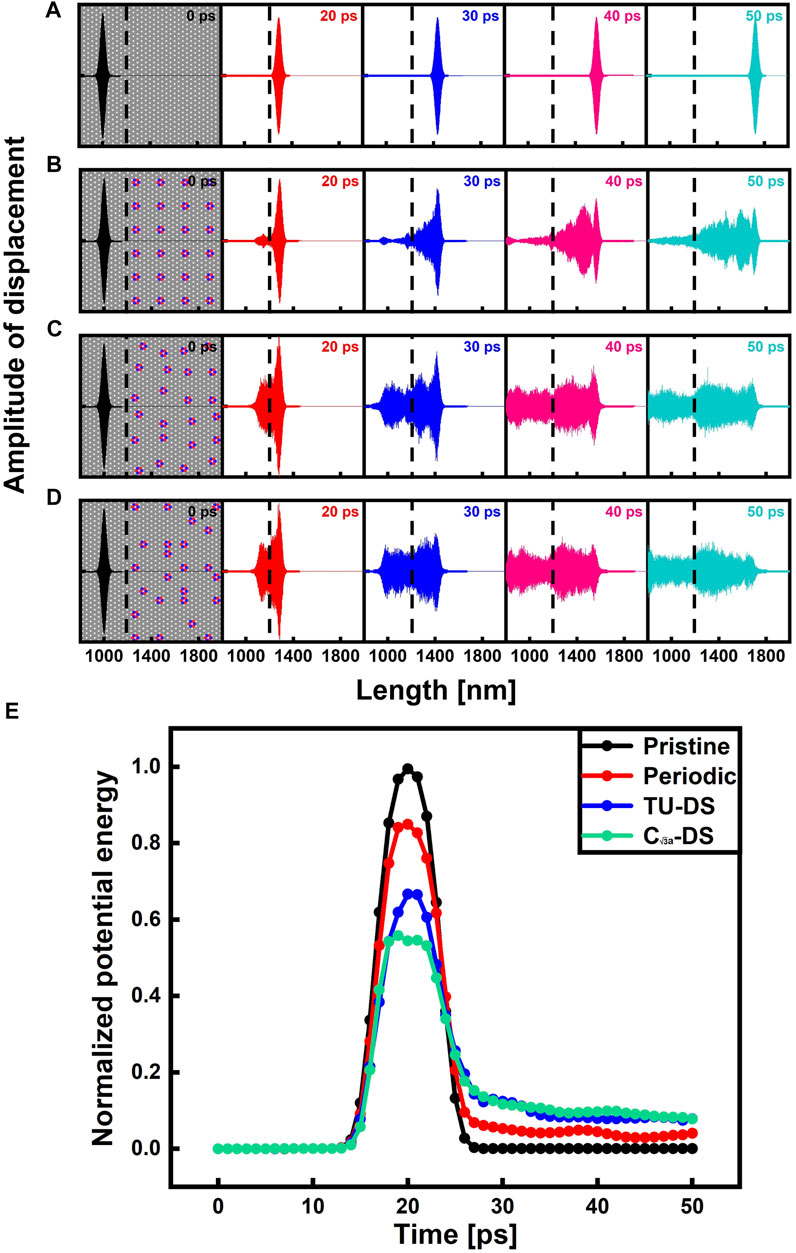
FIGURE 4. Phonon wave-packet simulations in different structures. Snapshots of displacement for a TA wave packet in (A) pristine graphene, (B) periodic structure, (C)TU-DS, and (D) $C_{\sqrt{3}a}$-DS, at 0 K. The black dashed line at 1,240 nm represents the position of the interface. (E) The kinetic energy in the region of 1,240 nm–1,340 nm in length versus time for pristine graphene, periodic structure, TU-DS, and $C_{\sqrt{3}a}$-DS.

We chose the transverse acoustic (TA) phonon mode of pristine graphene as the excited wave packet with the wavevector $\stackrel{\rightharpoonup }{k_0}=0.1\text{*}\stackrel{\rightharpoonup }{b_1}+0.1\text{*}\stackrel{\rightharpoonup }{b_2}$, where $\stackrel{\rightharpoonup }{b_1}$ and $\stackrel{\rightharpoonup }{b_2}$ are two reciprocal basis vectors of the graphene unit cell. $x_n$ is the coordinate of the $n$ th atom in the structure, and $x_0$ determines the center of the wave packet.

After the initial wave packet is excited, the wave packet continues to run for 50 ps at 0 K under the NVE system. We limited the wave packet simulation to 0 K, mainly because the anharmonic phonons-phonons interaction can be ignored at this temperature, which is beneficial for us to focus only on the wave nature of the phonon transport process. The method of introducing low-temperature conditions in the wave packet simulation has been widely used in previous research works (Wei et al., 2012; Chen et al., 2015; Zhang et al., 2017). Figures 4A–D show the wave packets propagation process in the pristine graphene, periodic structure, TU-DS, and $C_{\sqrt{3}a}$-DS, respectively. As expected, the phonon can be ballistically transported at a constant speed (group velocity) and maintain its shape in the pristine graphene since the anharmonic phonons-phonons interaction is negligible (Figure 4A).

As shown in Figure 4B, when the wave packet enters the periodic structure, the original wave is divided into a transmitted and a reflected wave after colliding with the interface. In addition, it is worth noting that most waves can transmit through the periodic structure and continue to propagate, exhibiting the wave propagation characteristics in the coordinate space. Interestingly, when the same wave packet enters the TU-DS (Figure 4C), the phonons in the reflected part increase significantly. Furthermore, the transmitted wave gradually dissipates during the propagation process in the TU-DS system, reflecting a solid signal that impedes the phonons’ transport. Moreover, as shown in Figure 4D, the wave packet shows a similar transport behavior when propagating in the $C_{\sqrt{3}a}$-DS, except that it exhibits a much stronger dissipation. The wave packet simulation results correspond to our thermal conductivity results above, that is, the $C_{\sqrt{3}a}$-DS has the smallest thermal conductivity. We show that the G/h-BN heterostructure relying on local-specific disorder can impede heat transport at the nanoscale through wave packet simulations.

To further quantify the difference, we also monitored the lattice vibrational kinetic energy of the target region near the interface (1,240–1340 nm) in the above four different structures, which can directly reveal the propagation capability and localization degree of phonons. As shown in Figure 4E, all the energy of the wave-packet can go into the target region in pristine graphene, and it then exits completely (energy decays to zero after 27 ps), reflecting the propagating nature of the phonon. In contrast, when the h-BN structures are introduced into pristine graphene to construct the heterostructures, less energy could enter the target region, and the entering energy decrease sequentially in the periodic, TU-DS, and $C_{\sqrt{3}a}$-DS heterostructure. This decreasing trend is consistent with the case of thermal conductivity. In addition, it is worth noting that the power in the target region cannot completely decay to zero within the same simulation time, which further confirms the localized nature of the phonon modes in these heterostructures. Moreover, in the $C_{\sqrt{3}a}$-DS, the most energy stays in the target region, reflecting the most substantial phonons localization. In the disordered G/h-BN heterostructures, the non-periodic distribution of the h-BN induces randomness and thus leads to the localization of the phonons. In most cases, localized strength is difficult to discern. However, we effectively identify the localization difference with the lattice vibrational kinetic energy method, which is a significant feature of this paper. It is worth noting that since the essence of thermal conductivity decrease is the localization of coherent phonons caused by disorder, this effect will not be limited to graphene system, but also applies to other 2D materials and thin films.

Conclusion

In summary, we have investigated the different types of the disorder effect on the thermal conductivity of the G/h-BN heterostructure via non-equilibrium molecular dynamics simulations The study found that when hexagonal boron nitrides are disorderly distributed in the cross–direction with a larger shift distance in graphene, the thermal conductivity could be reduced by 37%, which is much larger than the random disorder introduction. The wave packet simulation revealed that a larger shift distance in the cross-direction would induce a much more robust phonon localization. Moreover, our research proposes two useful descriptors (direction and shift distance) to effectively reduce the design space of the random structures and gives a more in-depth physical understanding of the disorder effect on phonon transport.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.

Author Contributions

WR, SH and CZ conceived the idea and supervised the entire project. YL performed the MD simulations, supported by SH. YL, WR, SH, and CZ analyzed the data and prepared the manuscript. All authors participated in the discussion.

Funding

This research was funded in parts by the National Natural Science Foundation of China (Grant Nos. 12105242, 12004242, 11864020, and 61904072), by Yunnan Fundamental Research Project (Grant Nos. 202001AU070047, 202201AT070161, 2019FI002, 202101AS070018, 202001AU070025, and 202101BE070001-049), and by Shanghai Rising-Star Program (No. 21QA1403300), the Yunnan Ten Thousand Talents Plan Young and Elite Talents Project, and the Yunnan Province Computational Physics and Applied Science and Technology Innovation Team.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alaie, S., Goettler, D. F., Su, M., Leseman, Z. C., Reinke, C. M., and El-Kady, I. (2015). Thermal Transport in Phononic Crystals and the Observation of Coherent Phonon Scattering at Room Temperature. Nat. Commun. 6, 7228. doi:10.1038/ncomms8228

PubMed Abstract | CrossRef Full Text | Google Scholar

Chang, C. W., Okawa, D., Garcia, H., Majumdar, A., and Zettl, A. (2008). Breakdown of Fourier's Law in Nanotube Thermal Conductors. Phys. Rev. Lett. 101, 075903. doi:10.1103/PhysRevLett.101.075903

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, J., Zhang, G., and Li, B. (2009). Tunable Thermal Conductivity of Si_1−xGe_x Nanowires. Appl. Phys. Lett. 95, 073117. doi:10.1063/1.3212737

CrossRef Full Text | Google Scholar

Chen, J., Zhang, G., and Li, B. (2010). Remarkable Reduction of Thermal Conductivity in Silicon Nanotubes. Nano Lett. 10, 3978–3983. doi:10.1021/nl101836z

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, S., Wu, Q., Mishra, C., Kang, J., Zhang, H., Cho, K., et al. (2012). Thermal Conductivity of Isotopically Modified Graphene. Nat. Mater 11, 203–207. doi:10.1038/nmat3207

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, J., Walther, J. H., and Koumoutsakos, P. (2015). Covalently Bonded Graphene-Carbon Nanotube Hybrid for High-Performance Thermal Interfaces. Adv. Funct. Mat. 25, 7539–7545. doi:10.1002/adfm.201501593

CrossRef Full Text | Google Scholar

Ding, Z., Pei, Q.-X., Jiang, J.-W., and Zhang, Y.-W. (2015). Manipulating the Thermal Conductivity of Monolayer MoS₂ via Lattice Defect and Strain Engineering. J. Phys. Chem. C 119, 16358–16365. doi:10.1021/acs.jpcc.5b03607

CrossRef Full Text | Google Scholar

Felix, I. M., and Pereira, L. F. C. (2020). Suppression of Coherent Thermal Transport in Quasiperiodic Graphene-hBN Superlattice Ribbons. Carbon 160, 335–341. doi:10.1016/j.carbon.2019.12.090

CrossRef Full Text | Google Scholar

Feng, T., Ruan, X., Ye, Z., and Cao, B. (2015). Spectral Phonon Mean Free Path and Thermal Conductivity Accumulation in Defected Graphene: The Effects of Defect Type and Concentration. Phys. Rev. B 91, 224301. doi:10.1103/physrevb.91.224301

CrossRef Full Text | Google Scholar

Hao, F., Fang, D., and Xu, Z. (2011). Mechanical and Thermal Transport Properties of Graphene with Defects. Appl. Phys. Lett. 99, 041901. doi:10.1063/1.3615290

CrossRef Full Text | Google Scholar

Hopkins, P. E., Reinke, C. M., Su, M. F., Olsson, R. H., Shaner, E. A., Leseman, Z. C., et al. (2011). Reduction in the Thermal Conductivity of Single Crystalline Silicon by Phononic Crystal Patterning. Nano Lett. 11, 107–112. doi:10.1021/nl102918q

PubMed Abstract | CrossRef Full Text | Google Scholar

Hu, S., An, M., Yang, N., and Li, B. (2016). Manipulating the Temperature Dependence of the Thermal Conductivity of Graphene Phononic Crystal. Nanotechnology 27, 265702. doi:10.1088/0957-4484/27/26/265702

PubMed Abstract | CrossRef Full Text | Google Scholar

Hu, S., Chen, J., Yang, N., and Li, B. (2017). Thermal Transport in Graphene with Defect and Doping: Phonon Modes Analysis. Carbon 116, 139–144. doi:10.1016/j.carbon.2017.01.089

CrossRef Full Text | Google Scholar

Hu, S., Zhang, Z., Jiang, P., Chen, J., Volz, S., Nomura, M., et al. (2018). Randomness-Induced Phonon Localization in Graphene Heat Conduction. J. Phys. Chem. Lett. 9, 3959–3968. doi:10.1021/acs.jpclett.8b01653

PubMed Abstract | CrossRef Full Text | Google Scholar

Hu, S., Zhang, Z., Jiang, P., Ren, W., Yu, C., Shiomi, J., et al. (2019). Disorder Limits the Coherent Phonon Transport in Two-Dimensional Phononic Crystal Structures. Nanoscale 11, 11839–11846. doi:10.1039/c9nr02548k

PubMed Abstract | CrossRef Full Text | Google Scholar

Hu, R., Iwamoto, S., Feng, L., Ju, S., Hu, S., Ohnishi, M., et al. (2020). Machine-Learning-Optimized Aperiodic Superlattice Minimizes Coherent Phonon Heat Conduction. Phys. Rev. X 10, 021050. doi:10.1103/physrevx.10.021050

CrossRef Full Text | Google Scholar

Hu, S., Ju, S., Shao, C., Guo, J., Xu, B., Ohnishi, M., et al. (2021). Ultimate impedance of coherent heat conduction in van der Waals graphene-MoS₂ heterostructures. Mater. Today Phys. 16, 100324. doi:10.1016/j.mtphys.2020.100324

CrossRef Full Text | Google Scholar

Ju, S., Shiga, T., Feng, L., Hou, Z., Tsuda, K., and Shiomi, J. (2017). Designing Nanostructures for Phonon Transport via Bayesian Optimization. Phys. Rev. X 7, 021024. doi:10.1103/physrevx.7.021024

CrossRef Full Text | Google Scholar

Kınacı, A., Haskins, J. B., Sevik, C., and Çağın, T. (2012). Thermal Conductivity of BN-C Nanostructures. Phys. Rev. B 86, 115410. doi:10.1103/physrevb.86.115410

CrossRef Full Text | Google Scholar

Latour, B., Volz, S., and Chalopin, Y. (2014). Microscopic Description of Thermal-Phonon Coherence: From Coherent Transport to Diffuse Interface Scattering in Superlattices. Phys. Rev. B 90, 014307. doi:10.1103/physrevb.90.014307

CrossRef Full Text | Google Scholar

Lee, J., Lee, W., Wehmeyer, G., Dhuey, S., Olynick, D. L., Cabrini, S., et al. (2017). Investigation of Phonon Coherence and Backscattering Using Silicon Nanomeshes. Nat. Commun. 8, 14054. doi:10.1038/ncomms14054

PubMed Abstract | CrossRef Full Text | Google Scholar

Lin, Z., Yin, A., Mao, J., Xia, Y., Kempf, N., He, Q., et al. (2016). Scalable Solution-Phase Epitaxial Growth of Symmetry-Mismatched Heterostructures on Two-Dimensional Crystal Soft Template. Sci. Adv. 2, 1600993. doi:10.1126/sciadv.1600993

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, S., Hänggi, P., Li, N., Ren, J., and Li, B. (2014). Anomalous Heat Diffusion. Phys. Rev. Lett. 112, 040601. doi:10.1103/PhysRevLett.112.040601

PubMed Abstract | CrossRef Full Text | Google Scholar

Lu, S., Ouyang, Y., Yu, C., Jiang, P., He, J., and Chen, J. (2021). Tunable Phononic Thermal Transport in Two-Dimensional C₆CaC₆ via Guest Atom Intercalation. J. Appl. Phys. 129, 225106. doi:10.1063/5.0051259

CrossRef Full Text | Google Scholar

Ma, D., Ding, H., Meng, H., Feng, L., Wu, Y., Shiomi, J., et al. (2016). Nano-Cross-Junction Effect on Phonon Transport in Silicon Nanowire Cages. Phys. Rev. B 94, 165434. doi:10.1103/physrevb.94.165434

CrossRef Full Text | Google Scholar

Ma, D., Wan, X., and Yang, N. (2018). Unexpected Thermal Conductivity Enhancement in Pillared Graphene Nanoribbon with Isotopic Resonance. Phys. Rev. B 98, 245420. doi:10.1103/physrevb.98.245420

CrossRef Full Text | Google Scholar

Maldovan, M. (2013). Narrow Low-Frequency Spectrum and Heat Management by Thermocrystals. Phys. Rev. Lett. 110, 025902. doi:10.1103/PhysRevLett.110.025902

PubMed Abstract | CrossRef Full Text | Google Scholar

Mendoza, J., and Chen, G. (2016). Anderson Localization of Thermal Phonons Leads to a Thermal Conductivity Maximum. Nano Lett. 16, 7616–7620. doi:10.1021/acs.nanolett.6b03550

PubMed Abstract | CrossRef Full Text | Google Scholar

Nai, C. T., Lu, J., Zhang, K., and Loh, K. P. (2015). Studying Edge Defects of Hexagonal Boron Nitride Using High-Resolution Electron Energy Loss Spectroscopy. J. Phys. Chem. Lett. 6, 4189–4193. doi:10.1021/acs.jpclett.5b01900

PubMed Abstract | CrossRef Full Text | Google Scholar

Nomura, M., Anufriev, R., Zhang, Z., Maire, J., Guo, Y., Yanagisawa, R., et al. (2022). Review of Thermal Transport in Phononic Crystals. Mater. Today Phys. 22, 100613. doi:10.1016/j.mtphys.2022.100613

CrossRef Full Text | Google Scholar

Plimpton, S. (1995). Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 117, 1–19. doi:10.1006/jcph.1995.1039

CrossRef Full Text | Google Scholar

Qian, X., Gu, X., Dresselhaus, M. S., and Yang, R. (2016). Anisotropic Tuning of Graphite Thermal Conductivity by Lithium Intercalation. J. Phys. Chem. Lett. 7, 4744–4750. doi:10.1021/acs.jpclett.6b02295

PubMed Abstract | CrossRef Full Text | Google Scholar

Roy Chowdhury, P., Reynolds, C., Garrett, A., Feng, T., Adiga, S. P., and Ruan, X. (2020). Machine Learning Maximized Anderson Localization of Phonons in Aperiodic Superlattices. Nano Energy 69, 104428. doi:10.1016/j.nanoen.2019.104428

CrossRef Full Text | Google Scholar

Sevik, C., Kinaci, A., Haskins, J. B., and Çağın, T. (2011). Characterization of Thermal Transport in Low-Dimensional Boron Nitride Nanostructures. Phys. Rev. B 84, 085409. doi:10.1103/physrevb.84.085409

CrossRef Full Text | Google Scholar

Sledzinska, M., Graczykowski, B., Maire, J., Chavez‐Angel, E., Sotomayor‐Torres, C. M., and Alzina, F. (2019). 2D Phononic Crystals: Progress and Prospects in Hypersound and Thermal Transport Engineering. Adv. Funct. Mat. 30, 1904434. doi:10.1002/adfm.201904434

CrossRef Full Text | Google Scholar

Swinteck, N. Z., Muralidharan, K., and Deymier, P. A. (2013). Phonon Scattering in One-Dimensional Anharmonic Crystals and Superlattices: Analytical and Numerical Study. J. Vib. Acoust. 135, 041016. doi:10.1115/1.4023824

CrossRef Full Text | Google Scholar

Vasileiadis, T., Varghese, J., Babacic, V., Gomis-Bresco, J., Navarro Urrios, D., and Graczykowski, B. (2021). Progress and Perspectives on Phononic Crystals. J. Appl. Phys. 129, 160901. doi:10.1063/5.0042337

CrossRef Full Text | Google Scholar

Wan, J., Jiang, J.-W., and Park, H. S. (2020). Machine Learning-Based Design of Porous Graphene with Low Thermal Conductivity. Carbon 157, 262–269. doi:10.1016/j.carbon.2019.10.037

CrossRef Full Text | Google Scholar

Wang, J., Zhu, L., Chen, J., Li, B., and Thong, J. T. L. (2013). Suppressing Thermal Conductivity of Suspended Tri-layer Graphene by Gold Deposition. Adv. Mat. 25, 6884–6888. doi:10.1002/adma.201303362

PubMed Abstract | CrossRef Full Text | Google Scholar

Wei, Z., Chen, Y., and Dames, C. (2012). Wave Packet Simulations of Phonon Boundary Scattering at Graphene Edges. J. Appl. Phys. 112, 024328. doi:10.1063/1.4740065

CrossRef Full Text | Google Scholar

Wei, H., Bao, H., and Ruan, X. (2020). Genetic Algorithm-Driven Discovery of Unexpected Thermal Conductivity Enhancement by Disorder. Nano Energy 71, 104619. doi:10.1016/j.nanoen.2020.104619

CrossRef Full Text | Google Scholar

Wu, X., and Han, Q. (2022). Transition from incoherent to coherent phonon thermal transport across graphene/h-BN van der Waals superlattices. Int. J. Heat Mass Transf. 184, 122390. doi:10.1016/j.ijheatmasstransfer.2021.122390

CrossRef Full Text | Google Scholar

Xie, G., Ding, D., and Zhang, G. (2018). Phonon Coherence and its Effect on Thermal Conductivity of Nanostructures. Adv. Phys. X 3, 721–755. doi:10.1080/23746149.2018.1480417

CrossRef Full Text | Google Scholar

Xiong, S., Sääskilahti, K., Kosevich, Y. A., Han, H., Donadio, D., and Volz, S. (2016). Blocking Phonon Transport by Structural Resonances in Alloy-Based Nanophononic Metamaterials Leads to Ultralow Thermal Conductivity. Phys. Rev. Lett. 117, 025503. doi:10.1103/PhysRevLett.117.025503

PubMed Abstract | CrossRef Full Text | Google Scholar

Xu, X., Pereira, L. F. C., Wang, Y., Wu, J., Zhang, K., Zhao, X., et al. (2014). Length-dependent Thermal Conductivity in Suspended Single-Layer Graphene. Nat. Commun. 5, 3689. doi:10.1038/ncomms4689

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, L., Chen, J., Yang, N., and Li, B. (2015). Significant Reduction of Graphene Thermal Conductivity by Phononic Crystal Structure. Int. J. Heat Mass Transf. 91, 428–432. doi:10.1016/j.ijheatmasstransfer.2015.07.111

CrossRef Full Text | Google Scholar

Zen, N., Puurtinen, T. A., Isotalo, T. J., Chaudhuri, S., and Maasilta, I. J. (2014). Engineering Thermal Conductance Using a Two-Dimensional Phononic Crystal. Nat. Commun. 5, 3435. doi:10.1038/ncomms4435

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, H., Lee, G., and Cho, K. (2011). Thermal Transport in Graphene and Effects of Vacancy Defects. Phys. Rev. B 84, 115460. doi:10.1103/physrevb.84.115460

CrossRef Full Text | Google Scholar

Zhang, H., Han, H., Xiong, S., Wang, H., Volz, S., and Ni, Y. (2017). Impeded Thermal Transport in Composition Graded SiGe Nanowires. Appl. Phys. Lett. 111, 121907. doi:10.1063/1.4998998

CrossRef Full Text | Google Scholar