
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Mater., 24 June 2022
Sec. Metamaterials
Volume 9 - 2022 | https://doi.org/10.3389/fmats.2022.909381
This article is part of the Research TopicEditors’ Showcase: MetamaterialsView all 5 articles
In momentum space, the nodal loop is regarded as a ring-shaped band degeneracy and is classified into type-I and type-II configurations depending on the positive/negative dispersions of the degenerating bands. Here, we experimentally observe a new class of nodal loop in the photonic band structure, employing an artificially designed bilayer metasurface. Such degeneracy, termed type-III nodal loop, is formed by the crossing between a resonant flat band and a positively dispersive band and is protected by mirror symmetry
Two-dimensional (2D) materials have opened new physics horizons in nanoscience studies, and the most known 2D matter is graphene that is a single atomic layer of honey-comb carbon lattice and has exhibited many unusual physics effects (Castro Neto et al., 2009). With the addition of one more carbon layer and the appearance of the inter-layer twisting degree of freedom, bilayer graphene is found to own exotic physical properties, such as flat band (FB) and strongly correlated phases (Suárez Morell et al., 2010; Bistritzer and MacDonald, 2011; Balents et al., 2020), and is also evoking intense attention to general van der Waals materials (Geim and Grigorieva, 2013; Basov et al., 2016). Analogous to graphene, the metasurface that is a single layer of artificially designed subwavelength electromagnetic (EM) scatters can be regarded as the 2D version of metamaterials in photonic studies and may manipulate the light propagation in a unique planar way (Yu et al., 2011; Holloway et al., 2012; Kildishev et al., 2013; Chen et al., 2016; Glybovski et al., 2016; Hu et al., 2020; Wang et al., 2020). Furthermore, with multi-layer structures, the extra symmetry and the degree of freedom may be engineered. It has been known that mirror symmetry along the stacking direction, e.g., z-direction, can play an important role in forming a nodal loop (NL) degeneracy in band theory (Feng et al., 2017; Gao et al., 2018; Yang et al., 2018; Wang et al., 2019a; Deng et al., 2019; Feng et al., 2019; You et al., 2019), where NLs are considered as a continuous set of degenerate nodes such as Dirac points (DPs) or Weyl points (WPs) in momentum space (k-space) (Pyrialakos et al., 2017; Wang et al., 2017; Armitage et al., 2018; Hu et al., 2018; Mann et al., 2018). In addition, a nodal line can be formed through cascading multilayers in three-dimensional (3D) periodic structures and featured an orientation along the z-direction (Qiu et al., 2019). Because of different dimensionalities, NLs may transform into DPs or WPs and further into gapped phase with symmetry-breaking mechanisms, featuring the topological phase transitions in the frequency–momentum space (Volovik, 2017). Investigating them and identifying the underlying symmetries have been one of the main topics in condensed matter systems and have been found to be associated with various interesting transport properties and quantum effects, such as quantum Hall effect and quantum spin Hall effect (Hasan and Kane, 2010; Qi and Zhang, 2011; Chiu et al., 2016).
In terms of the dispersion of degenerating bands, NL can be classified into type-I and type-II configurations with the former meaning the cross between positive and negative bands and the latter representing the cross between positive (negative) bands (Li et al., 2020). There is also a hybrid configuration, where the dispersion of at least one band is strongly momentum-dependent and changes the dispersion sign over the closed-loop in k-space (Li et al., 2020; Xiong et al., 2020). Such classifications are applicable likewise to both DPs and WPs and have been investigated extensively in 2D/3D photonics (Pyrialakos et al., 2017; Wang et al., 2017; Hu et al., 2018; Mann et al., 2018). Newly, the type-III configuration, which is termed for the cross between the flat band and the dispersive band, has been identified for nodal point degeneracy (Milićević et al., 2019). However, as far as NL degeneracy is concerned, the type-III configuration is just proposed theoretically in phonon context (Zheng et al., 2020) and is not experimentally observed in any wave system in either 2D or 3D cases yet.
In the study, we design and fabricate a bilayer metasurface that consists of two layers of fractal-shaped resonant metallic patterns located, respectively, at top and bottom surfaces. A photonic FB is developed due to local resonance supported by the fractal patterns. The FB is odd eigenmode under mirror symmetry
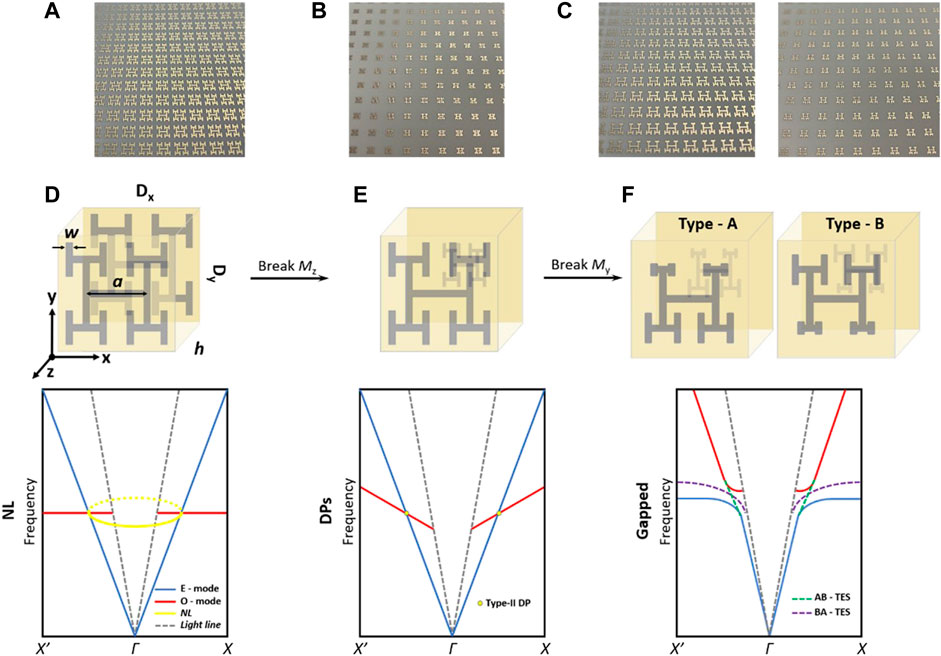
FIGURE 1. Photos and sketches illustrating how the symmetry breaking in the metasurface induces the photonic topological phase transition in the band structure. The metasurface is composed of double layers of H-shaped metallic patterns spaced by an insulating dielectric slab. Top panels: (A) photo of the top layer of metallic patterns, (B) photo of the bottom layer of metallic patterns with
The metallic elements in our design are based on the 2D H-shaped fractal pattern with a space-filling dimension of two at the limit of infinite scaling orders and have been shown to support significantly subwavelength EM resonance (Hou et al., 2004; Hou et al., 2008). The resonance is found to play an essential role in the formation of type-III NLs in k-space. The NL metasurface is a bilayer structure with the unit cell consisting of two identical metallic patterns located at opposite surfaces and arranged into a square lattice, seeing the top panel of Figures 1A,D. The fractal pattern in the unit cell has the following geometric parameters: The line length in the first scaling order (i.e., the central line) a = 2 mm, the scaling factor is 0.5, the linewidth w = 0.2 mm, the layer separation h = 0.762 mm, and the lattice constant along with two directions Dx = Dy = 4 mm (see Supplementary Material). Obviously, the metasurface is invariant under three mirror symmetry operations:
It is known that the photonic FB is readily achieved in localized resonance structures (Hou et al., 2008; Wang et al., 2019b), e.g., metamaterials, because of the strong localization of resonance modes from the point view of tight-binding band (see Supplementary Material). In our structure, the metallic patterns in each layer support a subwavelength dipole resonance, and the resonant mode in one pattern will couple to its in-plane neighbors (inter-cell coupling along the x- and y-directions) and its out-of-plane neighbor (intra-cell coupling along the z-direction) in nearest neighbor approximation. When the latter’s strength is much larger than the former’s strength under the tiny bilayer separation, h, the band due to resonant mode will be flat. The flatness of the band can be controlled by the parameter h (see Supplementary Material).
To confirm the existence of the type-III NL, we employ the numerical simulation software (CST Microwave Studio) to calculate the photonic energy bands as well as their eigenmodes. The calculated results along high symmetrical paths are plotted in Figure 2A, where a flat band (band 2, red line) is seen crossing with a dispersive band (band 1, blue line). The eigenmodes display that the two bands have different parity with respect to mirror symmetry
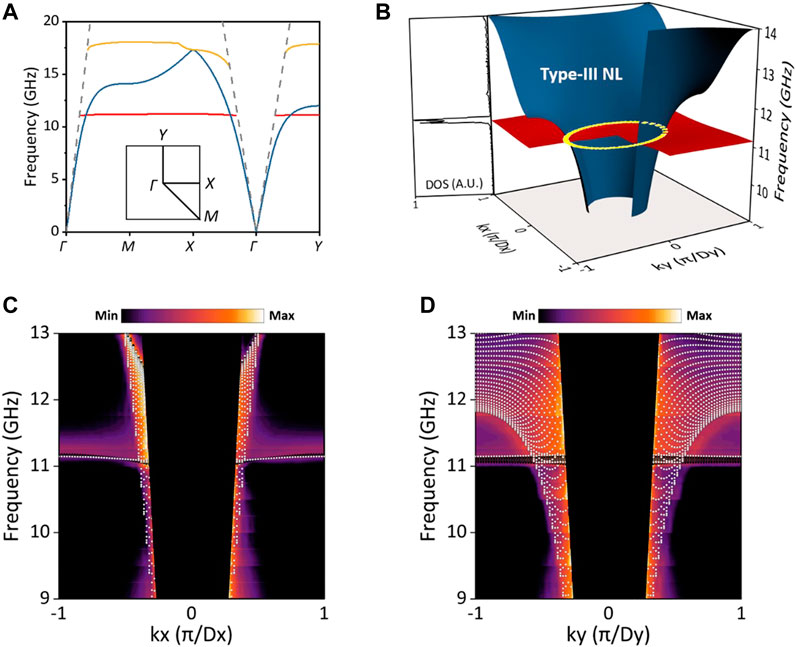
FIGURE 2. Type-III nodal loop in the
To experimentally observe the type-III Dirac NL degeneracy, the bilayer metasurface is fabricated by using a standard printed circuit board (Rogers 4350B). In order to ensure a high resolution in k-space, the whole sample includes the 100 × 100 unit cells and measures the overall size 400 × 400 mm2. The dielectric slab separating two layers of metallic patterns has the thickness of 0.762 mm and the relative permittivity of 3.5 at 10 GHz. In the experiment, a z-polarized electric dipole antenna is placed at the center of the lower surface of the sample and radiates the microwave, while a receiving dipole antenna probes the wave field on the upper surface through point-by-point scanning (the measuring area being 300 × 300 mm2 and resolution being 4 × 4 mm). The field data in real space are recorded using a microwave network analyzer (Agilent N5230C) and then are Fourier-transformed to obtain the energy band in momentum space (see Supplementary Material). As shown in Figures 2C,D, we plot the measured projected band structure along the kx and ky directions, respectively, in order to make the crossing of bands 1 and 2 more clear. (The flat band in single kx = 0 or ky = 0 cut is not as clear as the projected band diagram, possibly because the resonant field is concentrated in the dielectric slab for the O-mode.) At the same time, the simulated results are superposed as solid symbols and are seen in good agreement with measurement. The flat band is identified around 11.1 GHz, and the measured results display the slight broadening over frequency because of the finite size effect of the bilayer metasurface.
It is known that nodal point degeneracy can be obtained from higher-order degeneracy, e.g., nodal line, through breaking the symmetry (Yang et al., 2018). For our bilayer metasurface, the NL is protected by
In the experiment, we shrink the size of the lower metallic pattern to half of the upper one in the unit cell and fabricate a
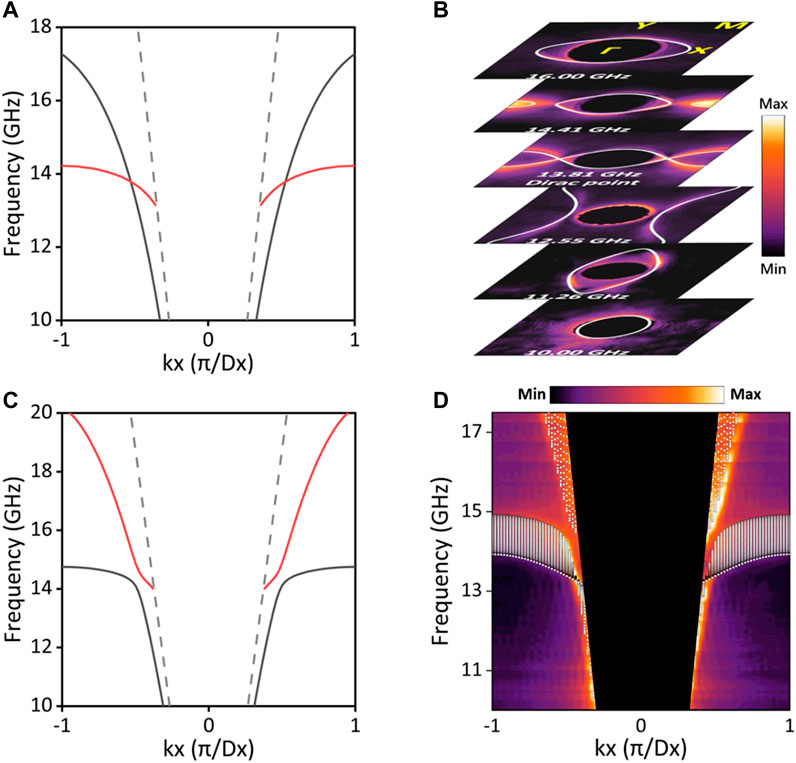
FIGURE 3. Band structures of the metasurfaces in different broken symmetry phases. (A) Calculated dispersion along the kx direction for the metasurface without
Because the DPs in the
For topological materials, the gapless edge state is found on the boundary separating different domains of the gapped system, i.e., domain wall. For our metasurface, such a domain wall is constructed by stacking two types of gapped patterns, type-A and type-B, along the y-direction and aligning the wall direction along the x-axis. We obtain the x-directed AB and BA domain walls depending on which domain is occupying the +y half-plane. That is, in the former (latter), domain A (B) is distributed in the -y half plane and domain B (A) is in the +y half plane. The experiment and calculation reveal the gapless edge states existing inside the gap, seeing Figures 4A–D. The electric field energy map and Poynting vector profiles for these two types of TESs are simulated and plotted in Figure 4E, where the opposite energy flux directions correspond to the opposite wavevectors and the evanescent nature of the field profile inside both domain interiors is justified by the decaying along the y-direction. Furthermore, the calculated photonic spin direction in the domain wall mode agrees with the spin-wavevector locking property (see Supplementary Material; Aiello et al., 2015; Bliokh et al., 2015).
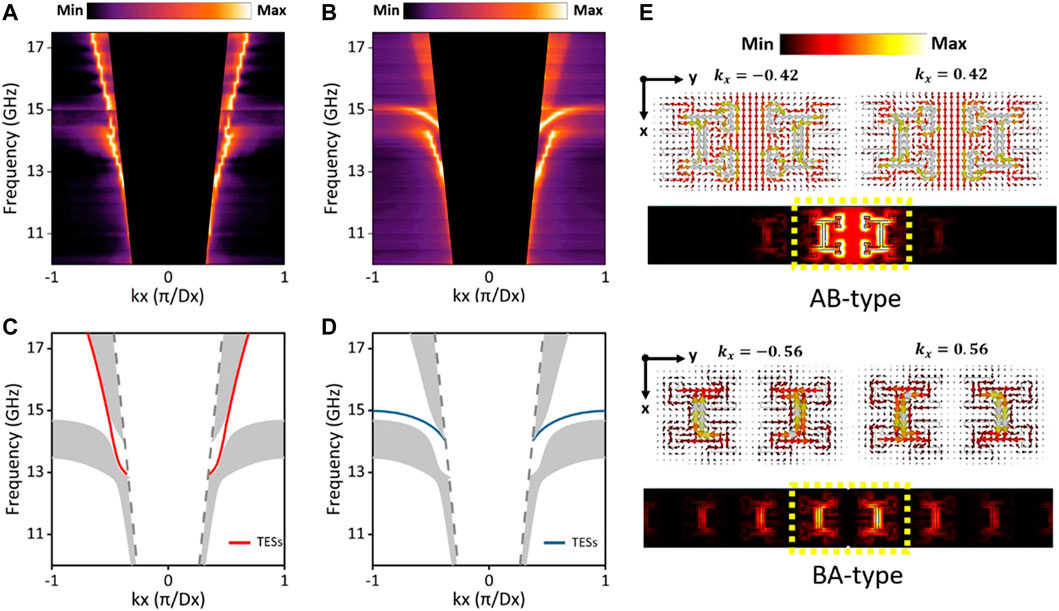
FIGURE 4. Observation of the topological edge states in the gapped phase. (A) and (B) Measured projected bands of AB-type and BA-type domain walls, respectively. The domain wall is constructed by staking different domains along the y-direction and making the wall along the x-direction. (C) and (D) Corresponding calculated results, in which the gray regions indicate the bulk states and the red and blue solid lines represent the topological edge states in the AB-type and BA-type domain walls, respectively. (E) Simulated Poynting vector (arrow maps on two domain elements nearest neighboring the wall, labeled by the dashed rectangular frame in color maps) and electric field energy (colormaps) for the edge states in the AB-type (upper panel) and BA-type (lower panel) domain walls. For the opposite propagation denoted by kx, the electric field energy has an identical distribution, and the Poynting vector has an oppositive orientation.
In summary, we realize the type-III NL degeneracy is protected by the mirror symmetry
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.
BH and CH conceived and supervised the research; HL performed the research; JHJ assisted in analyzing the data; JW and WW helped with the measurement; and BH, CH, and HL wrote the manuscript.
This work was supported by the Natural Science Foundation of China (NSFC) (Grant No. 12074279), the Major Program of Natural Science Research of Jiangsu Higher Education Institutions (Grant No. 18KJA140003), and the Priority Academic Program Development (PAPD) of Jiangsu Higher Education Institutions. The work by WW was supported partly by Hong Kong Areas of Excellence Scheme grant (AOE/P-02/12) and HK RGC 16204019.
Author CH is employed by Shenzhen Fantwave Tech, Co., Ltd.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
BH acknowledges the beneficial discussion with Shubo Wang.
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmats.2022.909381/full#supplementary-material
Aiello, A., Banzer, P., Neugebauer, M., and Leuchs, G. (2015). From Transverse Angular Momentum to Photonic Wheels. Nat. Phot. 9, 789–795. doi:10.1038/nphoton.2015.203
Armitage, N., Mele, E., and Vishwanath, A. (2018). Weyl and Dirac Semimetals in Three-Dimensional Solids. Rev. Mod. Phys. 90, 015001. doi:10.1103/revmodphys.90.015001
Balents, L., Dean, C. R., Efetov, D. K., and Young, A. F. (2020). Superconductivity and Strong Correlations in Moiré Flat Bands. Nat. Phys. 16, 725–733. doi:10.1038/s41567-020-0906-9
Basov, D. N., Fogler, M. M., and García de Abajo, F. J. (2016). Polaritons in van der Waals materials. Science 354, 6309. doi:10.1126/science.aag1992
Bistritzer, R., and MacDonald, A. H. (2011). Moiré Bands in Twisted Double-Layer Graphene. Proc. Natl. Acad. Sci. U.S.A. 108, 12233–12237. doi:10.1073/pnas.1108174108
Bliokh, K. Y., Smirnova, D., and Nori, F. (2015). Quantum Spin Hall Effect of Light. Science 348, 1448–1451. doi:10.1126/science.aaa9519
Castro Neto, A. H., Guinea, F., Peres, N. M. R., Novoselov, K. S., and Geim, A. K. (2009). The Electronic Properties of Graphene. Rev. Mod. Phys. 81, 109–162. doi:10.1103/revmodphys.81.109
Chen, H.-T., Taylor, A. J., and Yu, N. (2016). A Review of Metasurfaces: Physics and Applications. Rep. Prog. Phys. 79, 076401. doi:10.1088/0034-4885/79/7/076401
Chiu, C.-K., Teo, J. C., Schnyder, A. P., and Ryu, S. (2016). Classification of Topological Quantum Matter with Symmetries. Rev. Mod. Phys. 88, 035005. doi:10.1103/revmodphys.88.035005
Deng, W., Lu, J., Li, F., Huang, X., Yan, M., Ma, J., et al. (2019). Nodal Rings and Drumhead Surface States in Phononic Crystals. Nat. Commun. 10, 1769. doi:10.1038/s41467-019-09820-8
Feng, B., Fu, B., Kasamatsu, S., Ito, S., Cheng, P., Liu, C.-C., et al. (2017). Experimental Realization of Two-Dimensional Dirac Nodal Line Fermions in Monolayer Cu2Si. Nat. Commun. 8, 1007. doi:10.1038/s41467-017-01108-z
Feng, B., Zhang, R.-W., Feng, Y., Fu, B., Wu, S., Miyamoto, K., et al. (2019). Discovery of Weyl Nodal Lines in a Single-Layer Ferromagnet. Phys. Rev. Lett. 123, 116401. doi:10.1103/physrevlett.123.116401
Gao, W., Yang, B., Tremain, B., Liu, H., Guo, Q., Xia, L., et al. (2018). Experimental Observation of Photonic Nodal Line Degeneracies in Metacrystals. Nat. Commun. 9, 950. doi:10.1038/s41467-018-03407-5
Geim, A. K., and Grigorieva, I. V. (2013). Van der Waals heterostructures. Nature 499, 419–425. doi:10.1038/nature12385
Glybovski, S. B., Tretyakov, S. A., Belov, P. A., Kivshar, Y. S., and Simovski, C. R. (2016). Metasurfaces: From Microwaves to Visible. Phys. Rep. 634, 1–72. doi:10.1016/j.physrep.2016.04.004
Hasan, M. Z., and Kane, C. L. (2010). Colloquium: Topological Insulators. Rev. Mod. Phys. 82, 3045–3067. doi:10.1103/revmodphys.82.3045
Holloway, C. L., Kuester, E. F., Gordon, J. A., O'Hara, J., Booth, J., and Smith, D. R. (2012). An Overview of the Theory and Applications of Metasurfaces: The Two-Dimensional Equivalents of Metamaterials. IEEE Antennas Propag. Mag. 54, 10–35. doi:10.1109/map.2012.6230714
Hou, B., Xie, H., Wen, W., and Sheng, P. (2008). Three-dimensional Metallic Fractals and Their Photonic Crystal Characteristics. Phys. Rev. B 77, 125113. doi:10.1103/physrevb.77.125113
Hou, B., Xu, G., Wen, W., and Wong, G. K. L. (2004). Diffraction by an Optical Fractal Grating. Appl. Phys. Lett. 85, 6125–6127. doi:10.1063/1.1840112
Hu, C., Li, Z., Tong, R., Wu, X., Xia, Z., Wang, L., et al. (2018). Type-II Dirac Photons at Metasurfaces. Phys. Rev. Lett. 121, 24301. doi:10.1103/physrevlett.121.024301
Hu, G., Ou, Q., Si, G., Wu, Y., Wu, J., Dai, Z., et al. (2020). Topological Polaritons and Photonic Magic Angles in Twisted α-MoO3 Bilayers. Nature 582, 209–213. doi:10.1038/s41586-020-2359-9
Kildishev, A. V., Boltasseva, A., and Shalaev, V. M. (2013). Planar Photonics with Metasurfaces. Science 339, 1232009. doi:10.1126/science.1232009
Li, S., Yu, Z.-M., Yao, Y., and Yang, S. A. (2020). Type-II Topological Metals. Front. Phys. 15, 43201. doi:10.1007/s11467-020-0963-7
Mann, C.-R., Sturges, T. J., Weick, G., Barnes, W. L., and Mariani, E. (2018). Manipulating Type-I and Type-II Dirac Polaritons in Cavity-Embedded Honeycomb Metasurfaces. Nat. Commun. 9, 2194. doi:10.1038/s41467-018-03982-7
Milićević, M., Montambaux, G., Ozawa, T., Jamadi, O., Real, B., Sagnes, I., et al. (2019). Type-III and Tilted Dirac Cones Emerging from Flat Bands in Photonic Orbital Graphene. Phys. Rev. X 9, 031010.
Pyrialakos, G. G., Nye, N. S., Kantartzis, N. V., and Christodoulides, D. N. (2017). Emergence of Type-II Dirac Points in Graphynelike Photonic Lattices. Phys. Rev. Lett. 119, 113901. doi:10.1103/physrevlett.119.113901
Qi, X.-L., and Zhang, S.-C. (2011). Topological Insulators and Superconductors. Rev. Mod. Phys. 83, 1057–1110. doi:10.1103/revmodphys.83.1057
Qiu, H., Qiu, C., Yu, R., Xiao, M., He, H., Ye, L., et al. (2019). Straight Nodal Lines and Waterslide Surface States Observed in Acoustic Metacrystals. Phys. Rev. B 100, 041303. doi:10.1103/physrevb.100.041303
See Supplemental Materials for Sample Details, Microwave Measurements, Effect of the Slab Thickness, Parity of Eigenmodes of Two Bands Around the NL, edge states and spin-wavevector locking on domain walls, and tight-binding model.
Suárez Morell, E., Correa, J. D., Vargas, P., Pacheco, M., and Barticevic, Z. (2010). Flat Bands in Slightly Twisted Bilayer Graphene: Tight-Binding Calculations. Phys. Rev. B 82, 121407.
Volovik, G. E. (2017). Topological Lifshitz Transitions. Low. Temp. Phys. 43, 47–55. doi:10.1063/1.4974185
Wang, H.-X., Chen, Y., Hang, Z. H., Kee, H.-Y., and Jiang, J.-H. (2017). Type-II Dirac Photons. npj Quant. Mater 2, 54. doi:10.1038/s41535-017-0058-z
Wang, H., Yang, B., Xu, W., Fan, Y., Guo, Q., Zhu, Z., et al. (2019). Highly Degenerate Photonic Flat Bands Arising from Complete Graph Configurations. Phys. Rev. A 100, 043841. doi:10.1103/physreva.100.043841
Wang, S.-S., Yu, Z.-M., Liu, Y., Jiao, Y., Guan, S., Sheng, X.-L., et al. (2019). Two-dimensional Nodal-Loop Half-Metal in Monolayer MnN. Phys. Rev. M. 3, 084201. doi:10.1103/physrevmaterials.3.084201
Wang, W., Gao, W., Chen, X., Shi, F., Li, G., Dong, J., et al. (2020). Moiré Fringe Induced Gauge Field in Photonics. Phys. Rev. Lett. 125, 203901. doi:10.1103/physrevlett.125.203901
Xiong, Z., Zhang, R.-Y., Yu, R., Chan, C. T., and Chen, Y. (2020). Hidden-symmetry-enforced Nexus Points of Nodal Lines in Layer-Stacked Dielectric Photonic Crystals. Light Sci. Appl. 9, 176. doi:10.1038/s41377-020-00382-9
Yang, S.-Y., Yang, H., Derunova, E., Parkin, S. S. P., Yan, B., and Ali, M. N. (2018). Symmetry Demanded Topological Nodal-Line Materials. Adv. Phys. 3, 1. doi:10.1080/23746149.2017.1414631
You, J.-Y., Chen, C., Zhang, Z., Sheng, X.-L., Yang, S. A., and Su, G. (2019). Two-dimensional Weyl Half-Semimetal and Tunable Quantum Anomalous Hall Effect. Phys. Rev. B 100, 064408. doi:10.1103/physrevb.100.064408
Yu, N., Genevet, P., Kats, M. A., Aieta, F., Tetienne, J.-P., Capasso, F., et al. (2011). Light Propagation with Phase Discontinuities: Generalized Laws of Reflection and Refraction. Science 334, 333–337. doi:10.1126/science.1210713
Keywords: metamaterials, band structure, dispersion relations, phase transition, symmetry
Citation: Li H, Hu C, Jiang J-H, Wu J, Wen W and Hou B (2022) Photonic Type-III Nodal Loop and Topological Phase Transitions at Bilayer Metasurfaces. Front. Mater. 9:909381. doi: 10.3389/fmats.2022.909381
Received: 31 March 2022; Accepted: 19 April 2022;
Published: 24 June 2022.
Edited by:
Huanyang Chen, Xiamen University, ChinaCopyright © 2022 Li, Hu, Jiang, Wu, Wen and Hou. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Chuandeng Hu, Y2h1YWVAY29ubmVjdC51c3QuaGs=; Bo Hou, aG91Ym9Ac3VkYS5lZHUuY24=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.