- 1Physics Division, National Center for Theoretical Sciences, Hsinchu, Taiwan
- 2Institute of Physics, Academia Sinica, Taipei, Taiwan
With first-principles calculations we predict tunable topological phase transition in two-dimensional (2D) ternary transition metal halides α-TiXI (X = P and As) via strain engineering. Besides, changing the number of stacking layers or van der Waals interlayer spacing can also result in topological phase transition in few-layer TiXI. The on-site Coulomb U of Ti atoms is neither tunable nor empirical in this work. Instead, it is evaluated by the density functional perturbation theory and hence the results are more accurate. The tunable topological phase of 2D α-TiXI via strain engineering makes them promising in spintronics devices that exploit quantum spin Hall effect. Furthermore, the topological edge states of the single-layer TiAsI exhibit interesting feature. They do not cross at the time-reversal invariant momenta (TRIM) where the band inversion occurs. Instead, they extend over the whole one-dimensional Brillouin zone and cross at the other TRIM. While all requirements of Z2 topological phase are fulfilled, it is rare especially for those with direct gap. The linear bulk bands around and at Γ point may be the reason for the unusual crossing.
Introduction
The search for new functional materials has been one of the main research fields in materials science. Among various types of materials, two-dimensional (2D) materials have attracted much attention and been successfully applied to various fields of application such as electronics, opto-electronics, spintronics, etc. One of the intriguing parts of 2D materials is that some unusual physical properties may occur when the dimension is reduced. In addition, tunable properties of 2D materials are also essential for the applications. For example, the physical properties of 2D materials can be tuned via strain engineering or by changing the number of stacking layers, and/or van der Waals interlayer spacing (for multi-layers). Many 2D materials, such as graphene (Geim and Novoselov, 2007; Castro Neto et al., 2009; Allen et al., 2010), transition metal dichalcogenides (Mak et al., 2010; Radisavljevic et al., 2011; Gutiéerrez et al., 2012; Wang et al., 2012), metal-organic frameworks (Janiak, 2003; Férey, 2008; Long and Yaghi, 2009; Zhou and Kitagawa, 2014; Mezenov et al., 2019) etc., have been widely used in device applications. Therefore, it is of great importance and interest to continue the search for new functional 2D materials in both fundamental science and applications.
In recent years, ternary transition metal halides have been intensively studied for their interesting semiconducting properties (Yun and Lee, 2017; Liang et al., 2018; Liu et al., 2020; Shi et al., 2022). More importantly, ternary transition metal halides can be easily exfoliated into single or few layers due to the van der Waals stacking. Therefore, ternary transition metal halides are regarded to be promising in device applications owing to their potential for next-generation semiconductors. Besides, some metallic ternary transition metal halides are found to be superconductors (Yamanaka, 2010; Schurz et al., 2011). Among various interesting physical properties that ternary transition metal halides may exhibit, attention has recently been paid to the topological phases. Topological phases have been intensively studied in the past decade for their exotic features and potential for applications such as spintronics. The topological insulators (TIs) (Murakami et al., 2004; Kane and Mele, 2005; Bernevig et al., 2006; Fu et al., 2007; König et al., 2007), characterized by Z2 invariant, are the one that has been studied extensively and intensively among all topological phases. It requires strong spin-orbit coupling (SOC) to induce the band inversion, so materials with heavier atoms are more likely to exhibit nontrivial Z2 invariant. For nontrivial TIs, there exist topological edge states (the so-called bulk-edge correspondence) that are robust against perturbations preserving the protecting time-reversal symmetry. Recently, it has been predicted that single-layer α-TiNI is a 2D topological insulator (Wang et al., 2016), while α-TiNBr and α-TiNCl are topologically trivial due to the weaker SOC strength. The proposed topological phase is claimed to be robust against external strain and persists up to the room temperature due to the relatively large band gap ( ∼ 50 meV).
In this work, we demonstrate by first-principles calculations that 2D α-TiXI (X = P and As) undergoes topological phase transition by applying external strain, changing the van der Waals (vdW) interlayer spacing, or increasing the number of stacking layers. Despite that the strain-free single-layer α-TiXI (α will be omitted in the following for brevity) is topologically trivial, it is easy to drive the topological phase transition via strain engineering. It is thus more promising because the tunable topological phase may serve as a switch in devices to turn on and off the topological edge currents. Unusual topological edge states, which will be discussed later, are also found in single-layer TiAsI, making them an interesting family of materials.
Computational Methods
The ab initio density functional theory (DFT) calculations of electronic structures, phonons, and molecular dynamics (MD) are performed using Quantum Espresso (QE) code (Baroni et al., 2001; Giannozze et al., 2009). Ultrasoft PBE functionals (Perdew et al., 1996) are used to deal with the exchange-correlation effects. Energy cut-off for plane-wave expansion is chosen to be 60 Ry and a 16 × 16×1 k-mesh and a 6 × 6×1 q-mesh are used to sample the Brillouin zone in electronic and phonon calculations, respectively. Since both TiPI and TiAsI are predicted to be metallic using PBE functionals, HSE functionals (Heyd et al., 2003; Heyd et al., 2004) may not be the most adequate method for band correction (Heyd, 2004; Krukau et al., 2006; Paier et al., 2006). As a result, the DFT + U method is adopted here to improve the computed band structure. The on-site Coulomb repulsion U = 4.3 eV of Ti atoms in both TiPI and TiAsI is obtained via the density functional perturbation theory (Timrov et al., 2018; Ricca et al., 2019; Ricca et al., 2020) implemented in QE and is used in all calculations in this work. For MD simulations, the Verlet algorithm is adopted for the ion dynamics and the time step is 3 femto-seconds. Velocity rescaling is used to control the ionic temperature at 300 K. The Grimme-D2 method (Grimme, 2004) is adopted to correct the vdW interactions in few-layer and bulk TiXI. The SOC is considered in all calculations, except the phonon calculations. Vacuum space larger than 15 Å is used in all calculations to avoid artificial interactions along the c-direction between TiXI layers. Semi-infinite slab model based on Green’s functions (Sancho et al., 1984; Sancho et al., 1985) is used to calculate the edge band structures. The inter- and intra-layer couplings are computed using Wannier orbitals obtained from Wannier90 code (Mostofi et al., 2014).
Results and Discussion
The crystal structure of the single-layer TiXI is shown in Figure 1. The relaxed structural parameters of TiPI are a = 3.79 Å and b = 5.02 Å. The Ti-P and Ti-I bond lengths are 2.53 Å and 2.87 Å, respectively. Ti-P-Ti bond angle (along b-axis) is 166.9◦, indicating slight buckling of the Ti-P plane. For TiAsI, the relaxed structural parameters are a = 3.87 Å and b = 5.24 Å. The Ti-As and Ti-I bond lengths are 2.64 Å and 2.87 Å, respectively. Ti-As-Ti bond angle (along b-axis) is 165.9◦. The dynamical and thermal stability is confirmed by the phonon spectra and MD simulations shown in Figure 2 for both TiPI and TiAsI. For multi-layer TiXI, the relaxed vdW interlayer spacing of TiPI and TiAsI are about 2.65 Å and 2.55 Å, respectively. We note that the b-axis of both TiPI and TiAsI is much longer than that of TiNI whose b = 3.97 Å. In addition to the larger atomic radius of P and As, it is speculated that the contributing orbitals of the occupied states near Fermi level play an essential role. In TiNI, the occupied states near Fermi level are mainly comprised of I-px orbital. On the contrary, in both TiPI and TiAsI the P-py orbital is pushed up to be the highest valence band and thus affects the structure along b-axis.
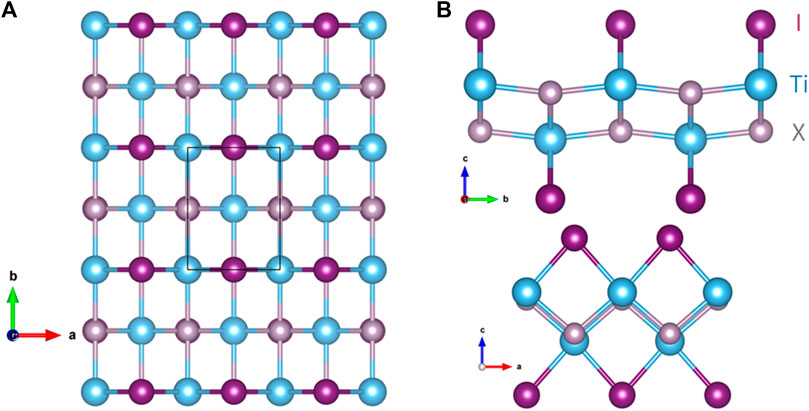
FIGURE 1. The (A) top view, (B) side view of the crystal structure of single-layer TiXI. The black box in (A) denotes the unit cell. The upper and lower panels in (B) represent the view along the short axis (a-axis) and the long axis (b-axis), respectively. The blue, grey, and purple spheres denote the Ti, X, and I atoms, respectively.
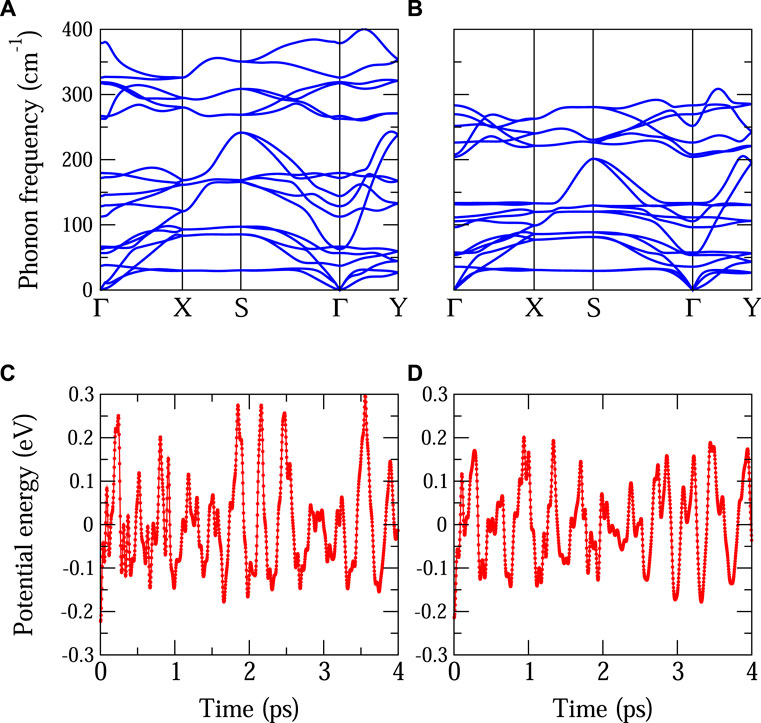
FIGURE 2. (A,B) The phonon spectra of strain-free single-layer TiPI and TiAsI. The absence of imaginary phonons indicates the dynamical stability of both TiPI and TiAsI. (C,D) The MD simulations of TiPI and TiAsI at 300 K supporting the thermal stability of both TiPI and TiAsI. The average potential energy is chosen to be zero.
For TiPI, the band structure, as is shown in Figure 3A, reveals that strain-free single-layer TiPI is a small-gap semiconductor with a direct band gap ∼ 0.21 eV at Γ. The valence band maximum (VBM) and conduction band minimum (CBM) are mainly comprised of P-py and Ti-
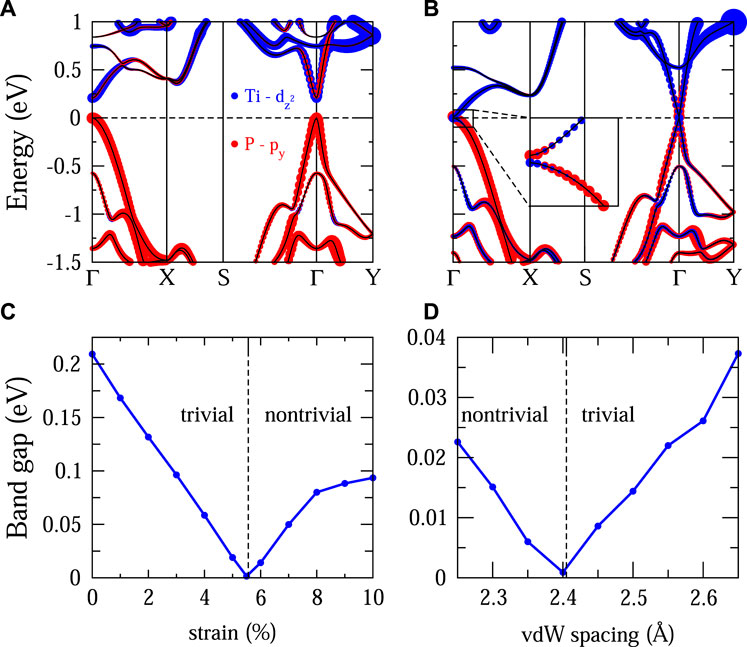
FIGURE 3. (A,B) The band structure of strain-free single-layer TiPI and 6% uniaxial strained single-layer TiPI, respectively. The inset in (B) shows the band inversion around Γ. The color representation is shown in (A) for both cases. (C) The magnitude of band gap of single-layer TiPI versus strain. (D) The magnitude of band gap of bilayer TiPI versus the vdW spacing.
In a similar fashion, topological phase transition may also occur when the Ti-
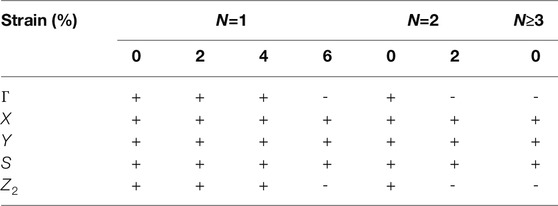
TABLE 1. The computed parities of N-layer TiPI at TRIM under strain. The more precise critical strain can be found in the main text. The relaxed vdW interlayer spacing is adopted in this table. Bulk (N → ∞) is also considered.
For single-layer TiAsI, the direct band gap is even smaller (∼0.07 eV) as displayed in Figure 4A. Despite the trivial phase, it is close to the topological phase transition point. As shown in Figure 4B, only 2% strain can induce band inversion and make TiAsI topological. For bilayer and thicker TiAsI, they are Z2 nontrivial without strain. The reason why it is easier to tune TiAsI into topological phase is because of the heavier As atoms as compared with the P atoms. The stronger SOC of heavy atoms is beneficial for the Z2 topological phase. However, substituting the heavier Sb for As incurs dynamical instability (imaginary phonon modes) in single-layer TiSbI. Therefore, only TiPI and TiAsI are discussed in this work.
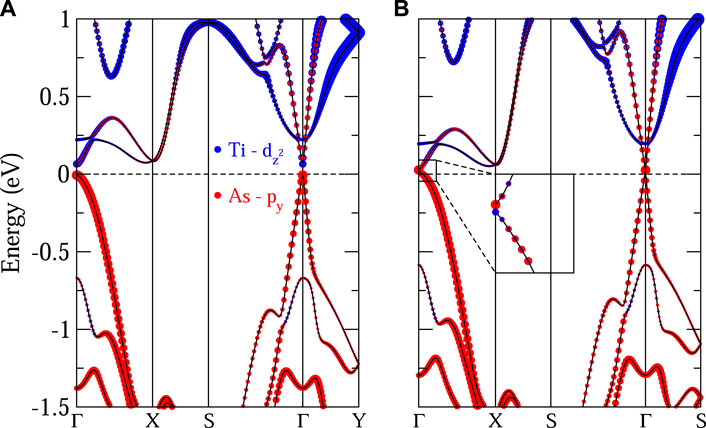
FIGURE 4. The band structure of single-layer TiAsI: (A) strain-free and (B) 2% strain. The color representation of the orbital decomposition is remarked in (A) for both cases. The inset in (B) shows the band inversion of the nontrivial phase.
Because of the presence of inversion symmetry in TiXI, the Z2 topological invariants can be computed from the parities at the time-reversal invariant momenta (TRIM). As inferred from the band structures shown in Figures 3, 4, the parity change, resulted from the band inversion, only takes place at the Γ point. The topological phase of TiXI is confirmed by the Z2 invariant listed in Table 1. The gap closing and re-opening shown in Figures 3C,D also indicates the occurrence of topological phase transition under uniaxial strain and compression of the vdW interlayer spacing (for bilayer TiPI).
The topological feature of the nontrivial phase, i.e., the topological edge states, is revealed in Figure 5. It can be seen that the in-gap topological edge states exist and cross at the TRIM. Interestingly, the topological edge states of the single-layer TiAsI do not cross at Γ where the band inversion occurs. Rather, they extend over the Brillouin zone and cross at the other TRIM, the Y point (0.0, π/b, 0.0). While all requirements of the Z2 topological phase are fulfilled, it is rare in TIs with direct gap: most of the Z2 topological edge or surface states exist around the band inversion region in reciprocal space and cross at the TRIM where the band inversion occurs. Some exceptions can be found in Z2 topological metals such as PbTaSe2 (Chen et al., 2016; Guan et al., 2016) where the band inversion results from the SOC-induced gap opening when two bands cross at the low-symmetry points without symmetry protection. It is speculated that the band dispersion aournd Γ may be the reason for the unusual crossing. By comparing Figures 5A,B, it can be found that the band dispersion around Γ in TiPI is flattened, yielding a region for the band crossing. For TiAsI, however, the two bulk bands where the topological edge states come from remain (nearly) linear even at Γ. Because the topological edge states tend to come out of the bulk bands along the tangential direction, the linearity of the bulk bands to Γ makes the topological edge states difficult to cross here. As a result, they find an alternative way to fulfill the topological requirement that two topological edge states have to cross at the TRIM.
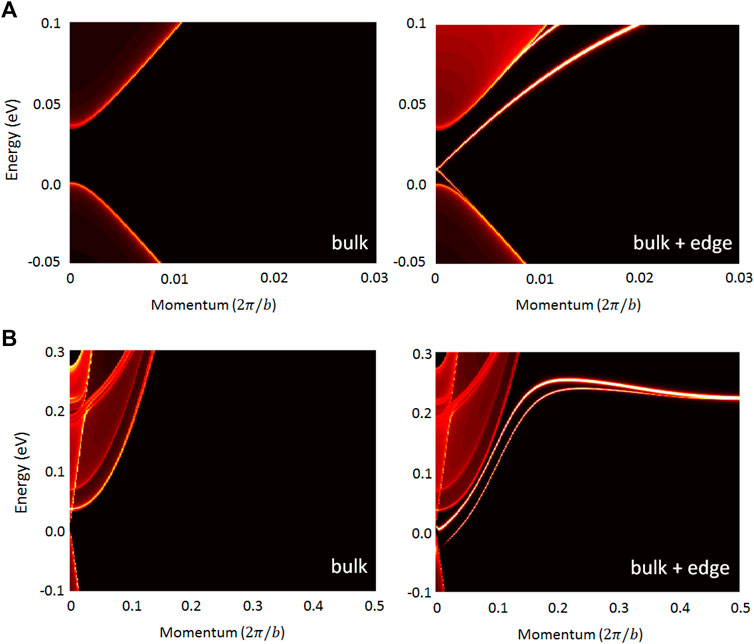
FIGURE 5. The edge band structures along y-direction of single-layer (A) TiPI with 7% strain and (B) TiAsI with 2% strain. The left (right) panel displays the bulk (bulk plus edge) components of the band structure. The topological edge states of TiPI cross at Γ while those of TiAsI cross at Y.
Before closing, we would like to discuss the accuracy of using the DFPT-obtained value of U in determining the band gap of TiXI, which is essential for the study of Z2 topological phase. By comparing our results of monolayer TiNI whose U is also determined to be
Summary
Using first-principles calculations, the electronic and topological properties of TiPI and TiAsI are investigated. The on-site Couloumb U of Ti atoms is computed via the density functional perturbation theory, rather than determined by empirical choice or by fitting of a given physical property such as band gap. Few-layer strain-free TiPI (trilayer or thicker) and TiAsI are found to be topological nontrivial. For strain-free single-layer TiXI and bilayer TiPI, on the other hand, they are trivial band insulators. However, topological phase transition can take place via strain engineering. The vdW interlayer spacing of the bilayer TiPI can also be tuned to reach the topologically nontrivial phase. The tunable topological phase transition raises the applicability of TiXI because of the potential for acting as a switch to turn on and off the topologically protected edge currents. Our work demonstrates that the ternary transition metal halides are a promising family of materials due to their possible applications.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author Contributions
P-JC conceived the project, did the calculations, analyzed the data, and wrote the manuscript.
Conflict of Interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The reviewer CK declared a shared affiliation, with no collaboration, with one of the authors, PC, to the handling editor at the time of the review.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Allen, M. J., Tung, V. C., and Kaner, R. B. (2010). Honeycomb Carbon: A Review of Graphene. Chem. Rev. 110, 132–145. doi:10.1021/cr900070d
Baroni, S., de Gironcoli, S., Dal Corso, A., and Giannozzi, P. (2001). Phonons and Related Crystal Properties from Density-Functional Perturbation Theory. Rev. Mod. Phys. 73, 515–562. doi:10.1103/revmodphys.73.515
Bernevig, B. A., Hughes, T. L., and Zhang, S.-C. (2006). Quantum Spin Hall Effect and Topological Phase Transition in HgTe Quantum Wells. Science 314, 1757–1761. doi:10.1126/science.1133734
Castro Neto, A. H., Guinea, F., Peres, N. M. R., Novoselov, K. S., and Geim, A. K. (2009). The Electronic Properties of Graphene. Rev. Mod. Phys. 81, 109–162. doi:10.1103/revmodphys.81.109
Chen, P.-J., Chang, T.-R., and Jeng, H.-T. (2016). Ab Initiostudy of the PbTaSe2-Related Superconducting Topological Metals. Phys. Rev. B 94, 165148. doi:10.1103/physrevb.94.165148
Férey, G. (2008). Hybrid Porous Solids: Past, Present, Future. Chem. Soc. Rev. 37, 191–214. doi:10.1039/b618320b
Fu, L., Kane, C. L., and Mele, E. J. (2007). Topological Insulators in Three Dimensions. Phys. Rev. Lett. 98, 106803. doi:10.1103/physrevlett.98.106803
Geim, A. K., and Novoselov, K. S. (2007). The Rise of Graphene. Nat. Mater. 6, 183–191. doi:10.1038/nmat1849
Giannozze, P., Baroni, S., Bonini, N., Calandra, M., Car, R., Cavazzoni, C., et al. (2009). QUANTUM ESPRESSO: A Modular and Open-Source Software Project for Quantum Simulations of Materials. J. Phys. Condens. Matter 21, 395502. doi:10.1088/0953-8984/21/39/395502
Grimme, S. (2004). Accurate Description of van der Waals Complexes by Density Functional Theory Including Empirical Corrections. J. Comput. Chem. 25, 1463–1473. doi:10.1002/jcc.20078
Guan, S.-Y., Chen, P.-J., Chu, M.-W., Sankar, R., Chou, F., Jeng, H.-T., et al. (2016). Sci. Adv. 2, e1600894. doi:10.1126/sciadv.1600894
Gutiéerrez, H. R., Perea-López, N., Elías, A. L., Berkdemir, A., Wang, B., Lv, R., et al. (2012). Nano Lett. 13, 3447.
Heyd, J. (2004). “Rice University Electronic Theses and Dissertations,”. PhD thesis (Houston, TX, USA: Rice University).
Heyd, J., Scuseria, G. E., and Ernzerhof, M. (2004). Efficient Hybrid Density Functional Calculations in Solids: Assessment of the Heyd-Scuseria-Ernzerhof Screened Coulomb Hybrid Functional. J. Chem. Phys. 121, 1187–1192. doi:10.1063/1.1760074
Heyd, J., Scuseria, G. E., and Ernzerhof, M. (2003). Hybrid Functionals Based on a Screened Coulomb Potential. J. Chem. Phys. 118, 8207–8215. doi:10.1063/1.1564060
Kane, C. L., and Mele, E. J. (2005). Z2Topological Order and the Quantum Spin Hall Effect. Phys. Rev. Lett. 95, 146802. doi:10.1103/physrevlett.95.146802
König, M., Wiedmann, S., Brüne, C., Roth, A., Buhmann, H., Molenkamp, L. W., et al. (2007). Quantum Spin Hall Insulator State in HgTe Quantum Wells. Science 318, 766. doi:10.1126/science.1148047
Krukau, A. V., Vydrov, O. A., Izmaylov, A. F., and Scuseria, G. E. (2006). Influence of the Exchange Screening Parameter on the Performance of Screened Hybrid Functionals. J. Chem. Phys. 125, 224106. doi:10.1063/1.2404663
Liang, Y., Dai, Y., Ma, Y., Ju, L., Wei, W., and Huang, B. (2018). Novel Titanium Nitride Halide TiNX (X = F, Cl, Br) Monolayers: Potential Materials for Highly Efficient Excitonic Solar Cells. J. Mat. Chem. A 6, 2073–2080. doi:10.1039/c7ta09662c
Liu, X., An, X., Xu, B., Xia, Q., Lu, G., Yu, G., et al. (2020). Ab Initio Prediction of Thermoelectric Properties of Monolayer ZrNCl and HfNCl. J. Solid State Chem. 290, 121500. doi:10.1016/j.jssc.2020.121500
Long, J. R., and Yaghi, O. M. (2009). The Pervasive Chemistry of Metal-Organic Frameworks. Chem. Soc. Rev. 38, 1213. doi:10.1039/b903811f
Mak, K. F., Lee, C., Hone, J., Shan, J., and Heinz, T. F. (2010). Atomically ThinMoS2: A New Direct-Gap Semiconductor. Phys. Rev. Lett. 105, 136805. doi:10.1103/physrevlett.105.136805
Marrazzo, A., Gibertini, M., Campi, D., Mounet, N., and Marzari, N. (2019). Relative Abundance of Z2 Topological Order in Exfoliable Two-Dimensional Insulators. Nano Lett. 19, 8431–8440. doi:10.1021/acs.nanolett.9b02689
Mezenov, Y. A., Krasilin, A. A., Dzyuba, V. P., Nominé, A., and Milichko, V. A. (2019). Metal-Organic Frameworks in Modern Physics: Highlights and Perspectives. Adv. Sci. 6, 1900506. doi:10.1002/advs.201900506
Mostofi, A. A., Yates, J. R., Pizzi, G., Lee, Y.-S., Souza, I., Vanderbilt, D., et al. (2014). An Updated Version of Wannier90: A Tool for Obtaining Maximally-Localised Wannier Functions. Comput. Phys. Commun. 185, 2309–2310. doi:10.1016/j.cpc.2014.05.003
Murakami, S., Nagaosa, N., and Zhang, S.-C. (2004). Spin-Hall Insulator. Phys. Rev. Lett. 93, 156804. doi:10.1103/physrevlett.93.156804
Paier, J., Marsman, M., Hummer, K., Kresse, G., Gerber, I. C., and Ángyán, J. G. (2006). Screened Hybrid Density Functionals Applied to Solids. J. Chem. Phys. 124, 154709. doi:10.1063/1.2187006
Perdew, J. P., Burke, K., and Ernzerhof, M. (1996). Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 77, 3865–3868. doi:10.1103/physrevlett.77.3865
Radisavljevic, B., Radenovic, A., Brivio, J., Giacometti, V., and Kis, A. (2011). Single-Layer MoS2 Transistors. Nat. Nanotech. 6, 147–150. doi:10.1038/nnano.2010.279
Ricca, C., Timrov, I., Cococcioni, M., Marzari, N., and Aschauer, U. (2020). Self-Consistent DFT +U +V Study of Oxygen Vacancies in SrTiO3. Phys. Rev. Res. 2, 023313. doi:10.1103/physrevresearch.2.023313
Ricca, C., Timrov, I., Cococcioni, M., Marzari, N., and Aschauer, U. (2019). Self-Consistent Site-Dependent DFT+U Study of Stoichiometric and Defective SrMnO3. Phys. Rev. B 99, 094102. doi:10.1103/physrevb.99.094102
Sancho, M. P. L., Sancho, J. M. L., and Rubio, J. (1984). Quick Iterative Scheme for the Calculation of Transfer Matrices: Application to Mo (100). J. Phys. F. Metall. Phys. 14, 1205–1215. doi:10.1088/0305-4608/14/5/016
Sancho, M. P. L., Sancho, J. M. L., Sancho, J. M. L., and Rubio, J. (1985). Highly Convergent Schemes for the Calculation of Bulk and Surface Green Functions. J. Phys. F. Metall. Phys. 15, 851–858. doi:10.1088/0305-4608/15/4/009
Schurz, C. M., Shlyk, L., Schleid, T., and Niewa, R. (2011). Superconducting Nitride Halides MNX (M = Ti, Zr, Hf; X = Cl, Br, I). Z. Krist. 226, 395. doi:10.1524/zkri.2011.1350
Shi, W., Ge, N., Wang, X., and Wang, Z. (2022). Thermoelectric Performance of ZrNX (X = Cl, Br and I) Monolayers. Phys. Chem. Chem. Phys. 24, 560–567. doi:10.1039/d1cp01928g
Timrov, I., Marzari, N., and Cococcioni, M. (2018). Hubbard Parameters from Density-Functional Perturbation Theory. Phys. Rev. B 98, 085127. doi:10.1103/physrevb.98.085127
Wang, A., Wang, Z., Du, A., and Zhao, M. (2016). Band Inversion and Topological Aspects in a TiNI Monolayer. Phys. Chem. Chem. Phys. 18, 22154–22159. doi:10.1039/c6cp02617f
Wang, Q. H., Kalantar-Zadeh, K., Kis, A., Coleman, J. N., and Strano, M. S. (2012). Electronics and Optoelectronics of Two-Dimensional Transition Metal Dichalcogenides. Nat. Nanotech. 7, 699–712. doi:10.1038/nnano.2012.193
Yamanaka, S. (2010). Intercalation and Superconductivity in Ternary Layer Structured Metal Nitride Halides (MNX: M = Ti, Zr, Hf; X = Cl, Br, I). J. Mat. Chem. 20, 2922. doi:10.1039/b922149b
Yun, W. S., and Lee, J. D. (2017). Two-Dimensional Semiconductors ZrNCl and HfNCl: Stability, Electric Transport, and Thermoelectric Properties. Sci. Rep. 7, 17330. doi:10.1038/s41598-017-17590-w
Keywords: topological insulator, topological phase transition, first-principles calculations, two-dimensional semiconductor, strain engineering
Citation: Chen P-J (2022) Tunable Topological Phase Transition in Two-Dimensional Ternary Transition Metal Halides TiXI (X = P and As). Front. Mater. 9:909344. doi: 10.3389/fmats.2022.909344
Received: 31 March 2022; Accepted: 13 June 2022;
Published: 22 July 2022.
Edited by:
Ryan Requist, Hebrew University of Jerusalem, IsraelReviewed by:
Chunmei Zhang, Northwest University, ChinaChao-Cheng Kaun, Academia Sinica, Taiwan
Minglei Sun, King Abdullah University of Science and Technology, Saudi Arabia
Copyright © 2022 Chen. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Peng-Jen Chen, cGpjaGVuMTAxNUBnbWFpbC5jb20=
 Peng-Jen Chen
Peng-Jen Chen