Grain Size and Heterophase Effects on Mechanical Properties of Mg-Cu Nanoglasses

Tailoring heterogeneities in amorphous alloys is a promising strategy for promoting the strength-ductility synergy. Here, molecular dynamics simulations are performed to investigate the effects of grains size and heterogeneous chemical composition on the mechanical properties of Mg-Cu nanoglasses (NGs). The reduced grain size in single-phase NGs improves the plasticity but at the expense of strength. In addition, the mechanical properties of dual-phase NGs composed of two chemical compositions depend critically upon the fraction of softer phase. In particular, the plasticity is improved for the low fraction of the softer phase, but is deteriorated for the high fraction of the softer phase, which is in striking contrast to the observations of the plasticity improvement reported in the traditional nanostructured metals/alloys. This is because that heterogeneities at the glass-glass interfaces intentionally introduce more stress concentration sites which are easier to accelerate the shear band formation. For an appropriate fraction of heterogeneous composition, a balance among strength and plasticity can be realized, which is useful for the design of novel NGs with high strength and superior ductility.

Introduction

Metallic glass (MG) is a unique type of glassy alloy obtained by melting multi-component metallic alloys and then cooling it at a high rate (Klement et al., 1960). MGs possess some outstanding properties such as high strength and high elastic limit compared to their crystalline counterparts due to the intrinsic amorphous structures (Cyrot-Lackmann, 1980; Boudreaux and Frost, 1981; Greer, 1995; Zhang et al., 2004). Although MGs are considered to be one of the structural materials with great potential of engineering applications (Ashby and Greer, 2006; Shan et al., 2008; Cheng et al., 2009a; Chen et al., 2011; Liu et al., 2011), they suffer from certain challenging issues, especially the lack of macroscopic tensile plasticity at room temperature due to the fact that the plastic deformation of MGs under tensile loading is concentrated in a narrow shear band (SB) region (Zhang et al., 2003; Greer et al., 2013).

Nanoglass (NG) is a new type of structural material which was first proposed by Herbert Gleiter (Gleiter, 2008). It is composed of nanometer-sized glassy grain and a large number of glass-glass interfaces (GGIs) with high free volume and low density relative to the glassy grains, which hence has the potential to tune the macroscopical plastic behavior (Şopu et al., 2011; Fang et al., 2012). Previous work in the past decade has shown that the plasticity of NGs is effectively improved compared with MGs, due to the introduced GGIs which can induce multiple SBs formation (Adibi et al., 2013; Wang et al., 2015; Wang et al., 2016; Brink and Albe, 2018). However, improved plasticity in NGs is at the expense of strength, which is a common dilemma in nanostructured materials (Şopu et al., 2011; Adibi et al., 2013; Wang et al., 2015; Ivanisenko et al., 2018).

One of the common methods to promote the strength-ductility synergy is to tailor heterogeneities such as the introduction of secondary phases in form of nanoprecipitates (Hofmann et al., 2008; Greer et al., 2013). For example, by adding a small amount of Nb to Zr-Cu-Ni-Al MG matrix, the formation of dual-phase MGs results in the improved plasticity without sacrificing strength (Chen and Todd, 2015). Inspired by this observation, a great deal of research has been dedicated to the preparation of heterogeneous nanostructured MGs (Pan et al., 2009; Kuan et al., 2010; Kim et al., 2013; Sha et al., 2015; Yao and Jin, 2015; Sha et al., 2017; Liu et al., 2018; Sun et al., 2018; Wu et al., 2020). In addition, Jian et al. have demonstrated that it is an effective way to balance strength and plasticity by controlling the heterogeneous structure, through the investigation of the mechanical behaviors of crystalline/amorphous nanocomposites (Jian et al., 2016; Jian et al., 2018a, 2018b). Therefore, it is of both great scientific and technological significance to provide an atomic-scale understanding of the deformation and failure mechanism of NGs with heterogeneous chemical compositions.

To this end, we perform molecular dynamics (MD) simulations on the NGs composed of heterogeneous chemical compositions, with focus on the effects of grain size and heterogeneous composition. Here, we choose Mg₃₃Cu₆₇ and Mg₈₅Cu₁₅ NGs due to their large differences in shear modulus. Our results reveal that, as the grain size decreases from 15 to 5 nm, the plasticity of single-phase Mg₃₃Cu₆₇ and Mg₈₅Cu₁₅ NGs are improved, accompanied by a decrease in strength, while a transition from catastrophic fracture to super-plasticity occurs. On the other hand, by introducing softer Mg₈₅Cu₁₅ NGs into the Mg₃₃Cu₆₇ NGs, the strength of dual-phase NGs decreases, while the plasticity improves at first and then deteriorates with the increase of the fraction of softer Mg₈₅Cu₁₅ NGs. Our results show that the mechanical properties of dual-phase NGs can be tuned by controlling the content ratio of soft to hard phase, providing an effective design approach for NGs architectures.

Methodology

MD simulations are performed using the Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS) (Plimpton, 1995). The atomic interactions are described by using an embedded atom model (EAM) potential fitted to Mg-Cu alloys (Ding et al., 2012). The system pressure and temperature are controlled by a Parrinello-Rahman barostat (Parrinello and Rahman, 1982) and a Nose-Hoover thermostat (Nosé, 1984), respectively. An integration time step of 2 fs is used in all simulations. Mg₃₃Cu₆₇ and Mg₈₅Cu₁₅ NG samples containing ∼2.0 million atoms are prepared in a slab with dimensions of 6.1 (x) × 48.8 (y) × 97.6 (z) nm³. In constructing the NG samples, a small MG cube with a side length of 6.1 nm is first equilibrated at 2000 K for 2 ns with periodic boundary conditions (PBCs) along all three dimensions, and then cooled to 50 K at a quenching rate of 10¹⁰ K/s under the condition of zero external pressure (Ding et al., 2012; Sha et al., 2014). The large MG samples are constructed by replications of the small cubes, then annealed at a temperature near the glass transition temperature ($T_g$) for 0.5 ns. Note that the value of T_g is 650 K for Mg₃₃Cu₆₇ MGs and 450 K for Mg₈₅Cu₁₅ MGs. The $T_g$ value is estimated by monitoring the kink point of the volume-temperature curve for the glassy and liquid states.

The NG samples are generated by using the Poisson-Voronoi tessellation method implemented in the Atomsk code (Hirel, 2015) and the MG structure as a source of material for the glassy grains. By setting the number of grains to change the grain size (d) in the sample, columnar glassy grains with average d of 5, 10, and 15 nm are prepared to study the grain size effect. For dual-phase NGs, the d is fixed at 10 nm, and some Mg₃₃Cu₆₇ grains are randomly replaced by Mg₈₅Cu₁₅ grains, as shown in Figure 1. There is a total of 50 grains. And the dual-phase NGs with replaced 15, 25, and 35 grains are used to investigate the effect of heterogeneous composition, and are hereafter referred to as NGI, NGII, and NGIII, respectively. In the work of Adjaoud and Albe (2018), spherical grains were equilibrated in the liquid state (above $T_g$) and then quenched to the glassy state to mimic the inert gas condensation, followed by the application of an external hydrostatic pressure at 50 K for consolidation. Due to the surface segregation effects, the glassy spheres consist of core and shell regions with different compositions. Besides, in the work of Sopu and Albe (2015), columnar grains were equilibrated at an external hydrostatic pressure at 50 K. It is speculated that the annealing process is influenced by the shape of grains. In our work, all NG samples are subjected to an external hydrostatic pressure of 1 GPa at 50 K, in order to relax the interfacial atomic structure and eliminate voids.

FIGURE 1

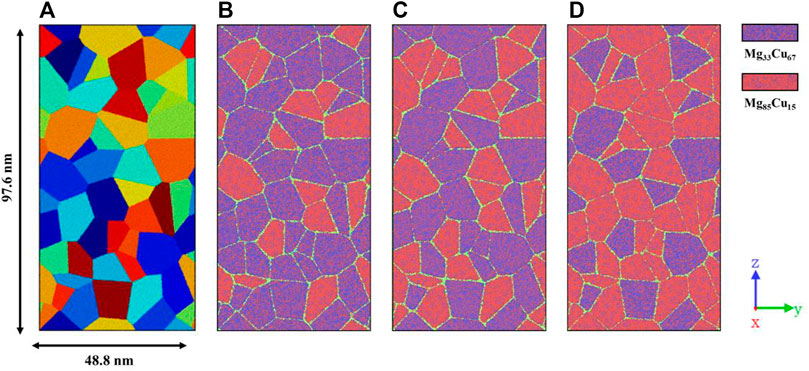
FIGURE 1. (A) Atomic configuration of single-phase NG sample with d = 10 nm. Grains are shown in different colors to highlight the architectures. (B–D) Atomic configurations of dual-phase NGs composed of Mg₃₃Cu₆₇ grains and Mg₈₅Cu₁₅ grains, i.e., NGI, NGII, and NGIII, respectively.

For uniaxial tensile tests, the MD simulations are carried out in isothermal-isobaric (NPT) ensembles at 50 K and zero pressure. A constant tensile strain rate of 1 × 10⁸ s⁻¹ along the z-direction is applied (Cao et al., 2009). PBCs are applied in all three dimensions directions to eliminate the surface effects (Şopu et al., 2011; Albe et al., 2013). The stress is calculated from the normal tensor component of the virial stress along the loading direction (Cao and Wei, 2007). The generation and evolution of local inelastic deformations are analyzed by calculating the atomic local von Mises shear strain ${\eta }^{Mises}$ (Shimizu et al., 2007). OVITO is used to visualize the atomic configuration (Stukowski, 2009).

Results and Discussion

Single-Phase NGs

We first investigate the effect of grain size d of the single-phase Mg₃₃Cu₆₇ and Mg₈₅Cu₁₅ NGs. Figures 2A,B depict the tensile engineering stress-strain curves for Mg₃₃Cu₆₇ and Mg₈₅Cu₁₅ NGs with different d values in comparison with the MG specimen. For MGs, the peak stress for Mg₃₃Cu₆₇ MG is 3.3 GPa, which is higher than 1.4 GPa for Mg₈₅Cu₁₅ MG. In addition, a colossal drop in the stress is observed, corresponding to a rapid localization of the plastic strain into the SB region. For NGs, the peak stresses are lower than those of the MGs and decrease with grain size. For a fixed grain size, the peak stress of Mg₃₃Cu₆₇ NG is higher compared to the Mg₈₅Cu₁₅ NG. In other words, Mg₈₅Cu₁₅ NG is softer than Mg₃₃Cu₆₇ NG.

FIGURE 2

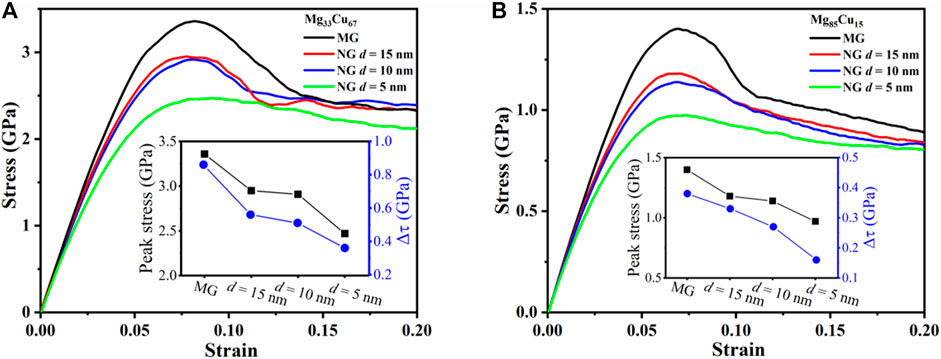
FIGURE 2. Engineering tensile stress-strain curves for (A) Mg₃₃Cu₆₇ and (B) Mg₈₅Cu₁₅ NGs with d = 15, 10, and 5 nm. MG counterparts are also plotted for comparison. The inset shows the peak stress and $\Delta \text{τ }$ for MGs and NGs as a function of grain size.

The stress drop is defined as $\Delta \tau ={\tau }_{peak}-{\tau }_{flow}$, where ${\tau }_{peak}$ and ${\tau }_{flow}$ are defined as the peak stress and the flow stress after the first stress drop, respectively. In the work of Cheng et al., they defined these two characteristic stresses (Cheng et al., 2008). The ${\tau }_{peak}$ reflects the stress resisting the initial flow, and the ${\tau }_{flow}$ means the shear resistance when the system enters a steady flow state. The difference, $\Delta \tau ={\tau }_{peak}-{\tau }_{flow}$, indicates the contrast in strength of the glass structure between the two states, and may reflect the propensity for strain localization. A larger $\Delta \tau$ indicates the severe strain localization. For NGs with d = 10 and 15 nm, the stress drop is also exhibited, but is less abrupt compared to the MG counterparts. However, when d is reduced to 5 nm, the stress drop is even less obvious and a stable plastic flow up to large strains with no sign of localization is observed. In our work, the PBC is imposed. The SB is formed at first, followed by a stable SB sliding process. The stress-strain curve will enter a balance region without any signal of fracture. Without PBC, the SB will slide along a shear plane until fracture due to the existence of the surface, while the stress will drop to zero gradually. The stress-strain response implies a grain size-dependent transition from brittle to ductile with decreasing grain size.

To understand the mechanism underlying the above-mentioned failure transition, we probe the atomic deformation processes by examining the local atomic shear strain ${\eta }^{Mises}$ for each atom (Shimizu et al., 2007). The regions with large ${\eta }^{Mises}$ implies that they have undergone large localized shear strain and host a high density of shear transformation zones (STZs) (Cao et al., 2009). Figure 3 shows the deformation processes for Mg₃₃Cu₆₇ and Mg₈₅Cu₁₅ NGs with different d values. It can be seen that the initial activated STZs are primarily located in the softer GGIs due to the higher free volume at the GGIs (Ritter et al., 2011; Nandam et al., 2017). Compared with the grains which provide the high shear resistance, GGIs are characterized by a defective short-range order and an excess free volume (Şopu et al., 2009; Ritter et al., 2011). In addition, the GGIs possess a reduced density relative to the density of glassy grains. Due to the microstructure of NGs, high strength and high plasticity may be imparted from nano-sized glassy grains and GGIs, respectively. For NGs with d = 10 and 15 nm, multiple SBs initiate and decorate the GGIs as the tensile loading is further increased. However, for NG with d = 5 nm, the scenario changes dramatically. STZs become widespread from the GGIs to the entire sample as the loading increases. In contrast to the NGs with d = 10 and 15 nm, homogeneous plastic flow without the SB formation is observed for NG with d = 5 nm. It should be emphasized that although STZs initially decorate the GGI and then become widespread with increasing strain in all cases, the spatial distribution of STZs will lead to the different failure mechanism. The increased fraction of GGIs leads to the more homogeneous distribution of STZs in the deformation process and the less local stress state change by the STZs activation, and then the NGs with the small grain size have less opportunity to have a localized deformation, which will grow to SB.

FIGURE 3

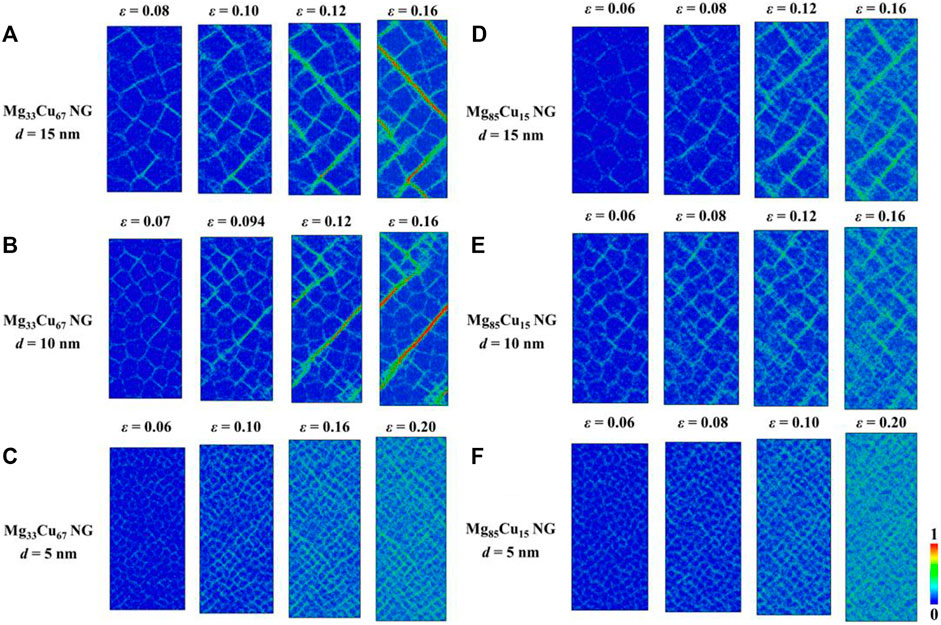
FIGURE 3. Sequence of snapshots capturing the atomic deformation processes for (A–C) Mg₃₃Cu₆₇ NGs with d = 15, 10, and 5 nm, respectively, and (D–F) Mg₈₅Cu₁₅ NGs with d = 15, 10, and 5 nm, respectively. The colors indicate the atomic shear strain.

To further quantify the fraction of the atoms involved in the plastic deformation during the tensile loading, the fraction of atoms with relatively high ${\eta }^{Mises}$ is calculated. Figures 4A,B show the fraction of atoms with ${\eta }^{Mises}\ge 0.2$ during deformation for NGs with different d values in comparison with the MG specimens. Compared to the MG specimens, the NGs have a higher fraction of atoms undergoing plastic shear strain due to the existence of GGIs. The decrease in d leads to an increase in the fraction of GGIs. Especially, the fraction of atoms with high ${\eta }^{Mises}$ for NG with d = 5 nm is close to 60%, implying that a considerable portion of the material experiences structural changes that promote the homogeneous plastic flow. In addition to counting the atomic ratio of ${\eta }^{Mises}\ge 0.2$ during the loading tests, we calculate the strain localization parameter defined in the work of Cheng et al. (2009b), $\psi ={\left[{\displaystyle {\sum }_{i=1}^N{\left({\eta }_i^{Mises}-{\eta }_{ave}^{Mises}\right)}^2}/N\right]}^{1/2}$, to quantitatively explain the degree of strain localization. A larger $\psi$ value indicates a more localized deformation mode. As shown in Figures 4C,D, the $\psi$ values of NGs are larger than that of MG when the strain is less than 0.12, because more localized deformation in NGs is activated at the GGIs before initial yielding. Inversely, the $\psi$ value of MG increases sharply when the strain is larger than 0.12. And for NG with d = 5 nm, the $\psi$ value is smallest, indicating that the deformation is more homogeneous. Furthermore, for single-phase NG, the ψ value depends on the grain size. When the strain is less than 0.08, it can be seen that the $\psi$ value increases as the grain size decreases, which is attributed to the effect of the fraction of GGIs.

FIGURE 4

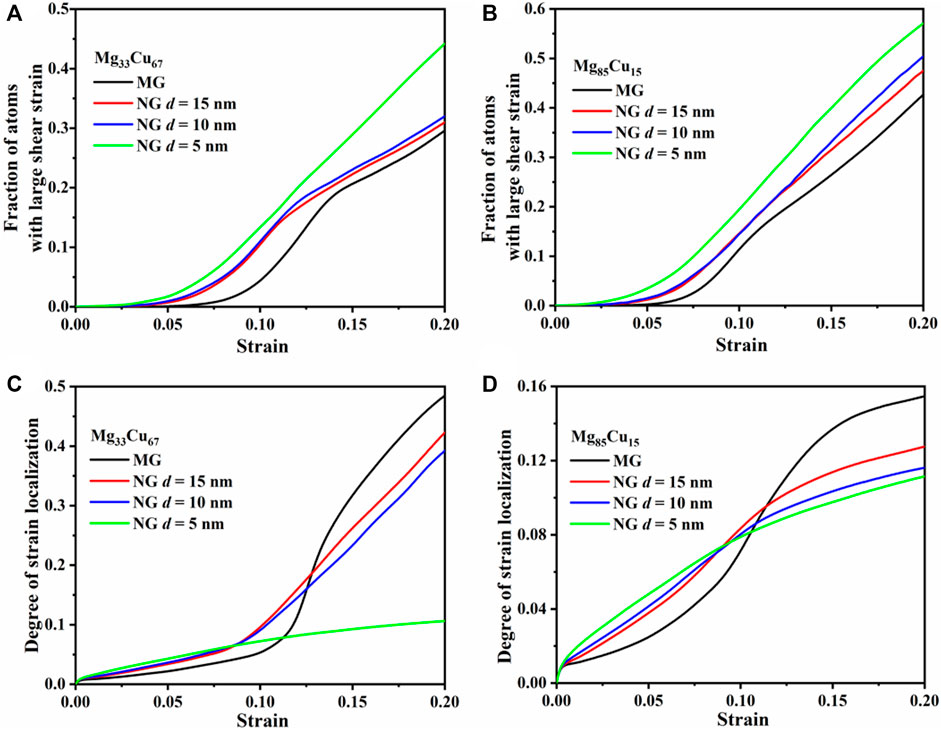
FIGURE 4. (A,B) The fraction of atoms with large ${\eta }^{Mises}\ge 0.2$, and (C,D) the strain localization parameter values during deformation for Mg₃₃Cu₆₇ and Mg₈₅Cu₁₅ NGs with d = 15, 10, and 5 nm. The trends in the MG counterparts are also plotted for comparison.

Dual-Phase NGs

Figure 5A depicts the tensile engineering stress-strain curves for NGI, NGII, NGIII, together with single-phase NGs for comparison. Two features, i.e., the peak stress and the stress drop $\Delta \tau$ from the stress-strain curves are taken into account. As expected, the peak stress decreases with increasing fractions of softer Mg₈₅Cu₁₅ nanograins, as shown in Figure 5B. Figure 5C shows the trend of $\Delta \text{τ}$ value. A high value of $\Delta \text{τ}$ indicates a high propensity for strain localization, and hence suggests less plasticity. For NGI samples with low fraction of softer Mg₈₅Cu₁₅ nanograins, a perfect plastic flow stage without any stress drop beyond the peak stress exhibits. However, the stress drop increases for NGIII with high fraction of softer Mg₈₅Cu₁₅ nanograins. This observation is in contrast to the observations of the plasticity improvement reported in the traditional nanostructured metals/alloys (Li et al., 2020). In our work, the dual-phase NGs with low fraction of softer second phase exhibit the enhanced combinations of strength and high plasticity.

FIGURE 5

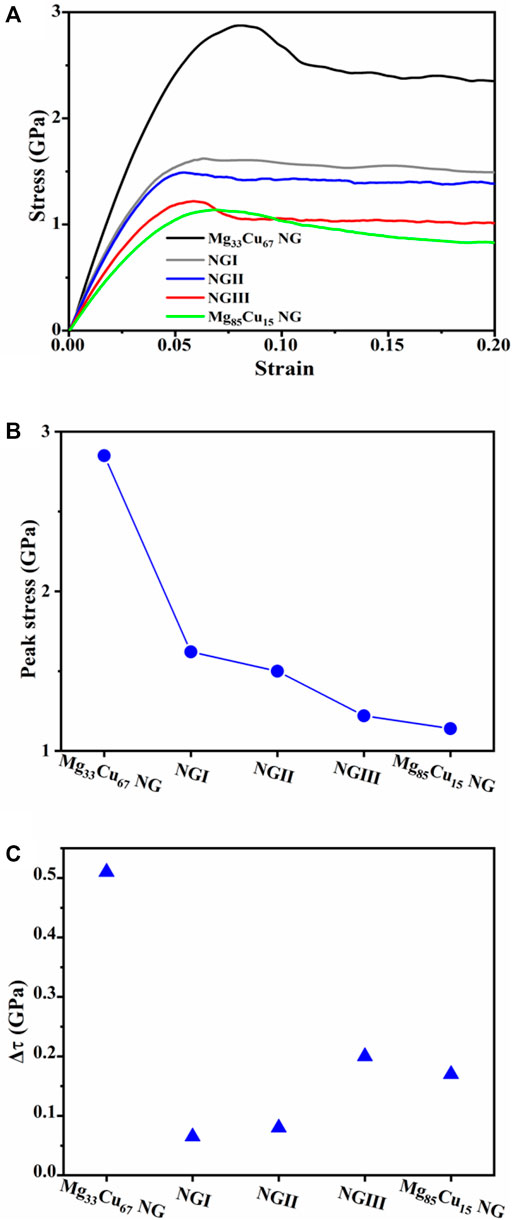
FIGURE 5. (A) Engineering tensile stress-strain curves, (B) peak stress, and (C) $\Delta \text{τ}$ for NGI, NGII, NGIII, together with single-phase NGs for comparison.

To unravel the conflict, a sequence of snapshots capturing the atomic deformation processes for NGI, NGII, and NGIII is shown in Figures 6A–C, respectively. For NGI, the plastic deformation takes place at the softer regions, including the GGIs and the Mg₈₅Cu₁₅ nanograins. Upon further tensile loading, the STZs are constrained in the softer Mg₈₅Cu₁₅ grains, and the development of a mature SB is possibly blocked by the harder Mg₃₃Cu₆₇ grains. In contrast to NGI, the network of STZs grows into a mature SB for NGII when the fraction ratio of soft to hard phase exceed 1.0 (i.e., NGIII), a mature predominant SB develops. This is because that more free volume at the softer Mg₈₅Cu₁₅/Mg₈₅Cu₁₅ interfaces introduces more stress concentration sites, and void nucleation at these GGIs can develop into cracks and propagate along interfaces, as shown in Figure 6C. Our simulation results thus highlight that the more addition of the softer second phase in MGs deteriorates the overall plasticity.

FIGURE 6

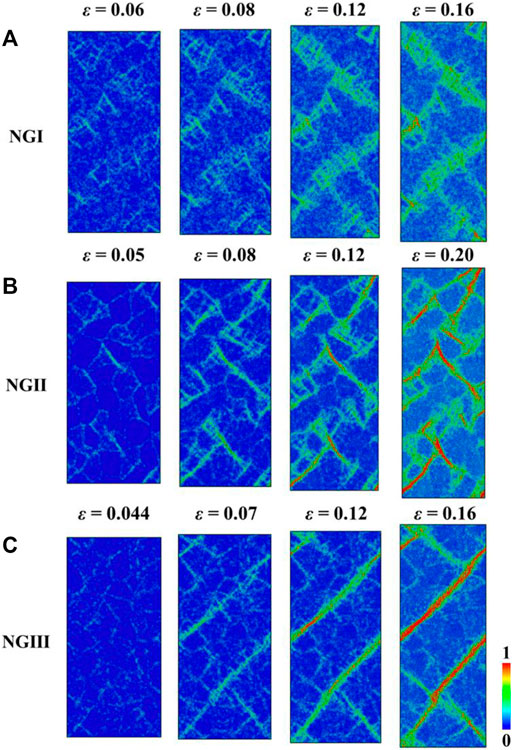
FIGURE 6. (A–C) Sequence of snapshots capturing the atomic deformation processes for NGI, NGII, and NGIII, respectively. The colors indicate the atomic shear strain.

To better understand the failure transition mechanism in dual-phase NGs with different grain ratios, five identical grains are selected and we compare the evolution of the local structure during deformation, as shown in Figure 7. It is found that the vast majority of STZs initially decorate the GGIs among grains with different compositions, referred to as soft-hard GGIs hereafter. For NGI with few soft phases, the STZs are difficult to propagate, because the soft Mg₈₅Cu₁₅ grains are completely surrounded by the hard Mg₃₃Cu₆₇ grains. In comparison with NGI, the incorporation of more soft phases in NGII increases the opportunity of the STZs to penetrate or propagate. For NGIII with overwhelming soft phases, it is intriguing to observe the rapid propagation of the STZs initiated at the soft-hard GGIs, and the other STZs do not participate in the development of the mature SB.

FIGURE 7

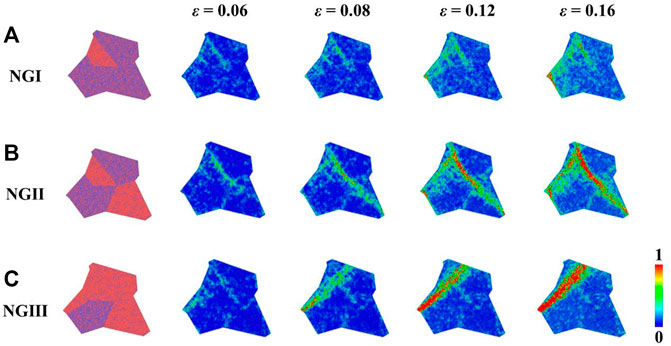
FIGURE 7. (A–C) Deformation snapshots of the selected grains capturing the atomic deformation processes for NGI, NGII, and NGIII, respectively. The colors indicate the atomic shear strain.

Figure 8A shows the fraction of atoms with ${\eta }^{Mises}\ge 0.2$ during deformation for NGI, NGII, and NGIII. It is noted that, after the addition of soft phase, the dual-phase NGs have a higher fraction of atoms undergoing plastic shear strain compared to the single-phase NGs when the strain is less than 0.12. When the strain is larger than 12%, the largest proportion of atoms with high ${\eta }^{Mises}$ in Mg₈₅Cu₁₅ NG indicates that Mg₈₅Cu₁₅ NG has the best plasticity. This is because Mg₈₅Cu₁₅ NG is the softest one with the smallest shear modulus in all samples. It is noteworthy that the fraction of atoms with high ${\eta }^{Mises}$ decreases as the content of the second softer phase increases, which is consistent with the above observation on the plasticity. Figure 8B shows the strain localization parameters during deformation for NGI, NGII and NGIII. With the increase of the content of the second soft phase, the $\psi$ value increases close to that of hard Mg₃₃Cu₆₇ NG, indicating that the plasticity becomes deteriorated, which is consistent with our above-mentioned results.

FIGURE 8

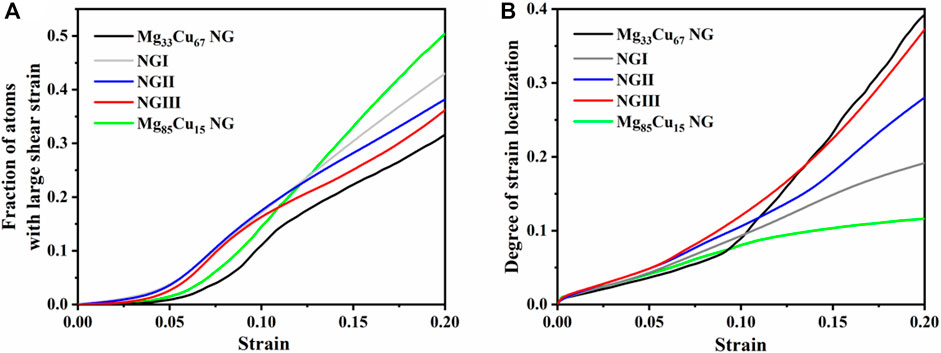
FIGURE 8. (A) The fraction of atoms with large ${\eta }^{Mises}\ge 0.2$, and (B) the strain localization parameter values during deformation for NGI, NGII, and NGIII. The trends in the single-phase NGs are also plotted for comparison.

Conclusion

In summary, atomistic simulations are performed on the single-phase NGs and dual-phase NGs, aiming at the effects of grain size and heterogeneous composition on the mechanical properties. Compared to MGs, single-phase NGs show decreased strength but improved plasticity. The failure mode switches from localized shear banding to homogeneous plastic deformation with decreasing grain size. The existence of GGIs is the main reason for the strength reduction and the plasticity enhancement. For dual-phase NGs, by adding the appropriate content of the softer second phase, the plasticity is improved. Another key finding is that for dual-phase NGs with the content ratio of soft to hard phase larger than 1.0, the plasticity is deteriorated, which is quite different from the improvement in plasticity reported in the traditional nanostructured metals/alloys. The physical origin of this conflict is attributed to the increased free volume or voids at the softer GGIs accelerate the SB formation. The present work provides an in-depth understanding of the mechanical properties and deformation mechanism of dual-phase NGs with heterogeneous chemical compositions.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

YC ran the simulations, performed the analysis, and wrote the first draft of the manuscript; JD and ZDS supervised the work and reviewed and edited the manuscript.

Funding

The authors would like to acknowledge financial support from the National Natural Science Foundation of China (NSFC) through Grant Nos. 11790293 and 11972278. Z-DS is also grateful for the support from the Science and Technology Developing Project of Shaanxi (No. 2019JC-03). JD acknowledges support from National Natural Science Foundation of China (12004294), National Youth Talents Program and the HPC platform of Xian Jiaotong University.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Adibi, S., Sha, Z.-D., Branicio, P. S., Joshi, S. P., Liu, Z.-S., and Zhang, Y.-W. (2013). A Transition from Localized Shear Banding to Homogeneous Superplastic Flow in Nanoglass. Appl. Phys. Lett. 103, 211905. doi:10.1063/1.4833018

CrossRef Full Text | Google Scholar

Adjaoud, O., and Albe, K. (2018). Microstructure Formation of Metallic Nanoglasses: Insights from Molecular Dynamics Simulations. Acta Mater. 145, 322–330. doi:10.1016/j.actamat.2017.12.014

CrossRef Full Text | Google Scholar

Albe, K., Ritter, Y., and Şopu, D. (2013). Enhancing the Plasticity of Metallic Glasses: Shear Band Formation, Nanocomposites and Nanoglasses Investigated by Molecular Dynamics Simulations. Mech. Mater. 67, 94–103. doi:10.1016/j.mechmat.2013.06.004

CrossRef Full Text | Google Scholar

Ashby, M., and Greer, A. (2006). Metallic Glasses as Structural Materials. Scr. Mater. 54, 321–326. doi:10.1016/j.scriptamat.2005.09.051

CrossRef Full Text | Google Scholar

Boudreaux, D. S., and Frost, H. J. (1981). Short-range Order in Theoretical Models of Binary Metallic Glass Alloys. Phys. Rev. B 23, 1506–1516. doi:10.1103/PhysRevB.23.1506

CrossRef Full Text | Google Scholar

Brink, T., and Albe, K. (2018). From Metallic Glasses to Nanocrystals: Molecular Dynamics Simulations on the Crossover from Glass-like to Grain-Boundary-Mediated Deformation Behaviour. Acta Mater. 156, 205–214. doi:10.1016/j.actamat.2018.06.036

CrossRef Full Text | Google Scholar

Cao, A. J., Cheng, Y. Q., and Ma, E. (2009). Structural Processes that Initiate Shear Localization in Metallic Glass. Acta Mater. 57, 5146–5155. doi:10.1016/j.actamat.2009.07.016

CrossRef Full Text | Google Scholar

Cao, A., and Wei, Y. (2007). Atomistic Simulations of Crack Nucleation and Intergranular Fracture in Bulk Nanocrystalline Nickel. Phys. Rev. B 76, 024113. doi:10.1103/PhysRevB.76.024113

CrossRef Full Text | Google Scholar

Chen, C. Q., Pei, Y. T., Kuzmin, O., Zhang, Z. F., Ma, E., and De Hosson, J. T. M. (2011). Intrinsic Size Effects in the Mechanical Response of Taper-free Nanopillars of Metallic Glass. Phys. Rev. B 83, 180201. doi:10.1103/PhysRevB.83.180201

CrossRef Full Text | Google Scholar

Chen, S. S., and Todd, I. (2015). Enhanced Plasticity in the Zr-Cu-Ni-Al-Nb Alloy System by In-Situ Formation of Two Glassy Phases. J. Alloys Compd. 646, 973–977. doi:10.1016/j.jallcom.2015.05.140

CrossRef Full Text | Google Scholar

Cheng, Y. Q., Cao, A. J., and Ma, E. (2009b). Correlation between the Elastic Modulus and the Intrinsic Plastic Behavior of Metallic Glasses: The Roles of Atomic Configuration and Alloy Composition. Acta Mater. 57, 3253–3267. doi:10.1016/j.actamat.2009.03.027

CrossRef Full Text | Google Scholar

Cheng, Y. Q., Cao, A. J., Sheng, H. W., and Ma, E. (2008). Local Order Influences Initiation of Plastic Flow in Metallic Glass: Effects of Alloy Composition and Sample Cooling History. Acta Mater. 56, 5263–5275. doi:10.1016/j.actamat.2008.07.011

CrossRef Full Text | Google Scholar

Cheng, Y. Q., Han, Z., Li, Y., and Ma, E. (2009a). Cold versus Hot Shear Banding in Bulk Metallic Glass. Phys. Rev. B 80, 134115. doi:10.1103/PhysRevB.80.134115

CrossRef Full Text | Google Scholar

Cyrot-Lackmann, F. (1980). Elastic Properties of a Metallic Glass Relative to the Crystal. Phys. Rev. B 22, 2744–2748. doi:10.1103/PhysRevB.22.2744

CrossRef Full Text | Google Scholar

Ding, J., Cheng, Y.-Q., Sheng, H., and Ma, E. (2012). Short-range Structural Signature of Excess Specific Heat and Fragility of Metallic-Glass-Forming Supercooled Liquids. Phys. Rev. B 85, 060201. doi:10.1103/PhysRevB.85.060201

CrossRef Full Text | Google Scholar

Fang, J. X., Vainio, U., Puff, W., Würschum, R., Wang, X. L., Wang, D., et al. (2012). Atomic Structure and Structural Stability of Sc75Fe25 Nanoglasses. Nano Lett. 12, 458–463. doi:10.1021/nl2038216

PubMed Abstract | CrossRef Full Text | Google Scholar

Gleiter, H. (2008). Our Thoughts Are Ours, Their Ends None of Our Own: Are There Ways to Synthesize Materials beyond the Limitations of Today? Acta Mater. 56, 5875–5893. doi:10.1016/j.actamat.2008.08.028

CrossRef Full Text | Google Scholar

Greer, A. L., Cheng, Y. Q., and Ma, E. (2013). Shear Bands in Metallic Glasses. Mater. Sci. Eng. R Rep. 74, 71–132. doi:10.1016/j.mser.2013.04.001

CrossRef Full Text | Google Scholar

Greer, A. L. (1995). Metallic Glasses. Science 267, 1947–1953. doi:10.1126/science.267.5206.1947

PubMed Abstract | CrossRef Full Text | Google Scholar

Hirel, P. (2015). Atomsk: A Tool for Manipulating and Converting Atomic Data Files. Comput. Phys. Commun. 197, 212–219. doi:10.1016/j.cpc.2015.07.012

CrossRef Full Text | Google Scholar

Hofmann, D. C., Suh, J.-Y., Wiest, A., Duan, G., Lind, M.-L., Demetriou, M. D., et al. (2008). Designing Metallic Glass Matrix Composites with High Toughness and Tensile Ductility. Nature 451, 1085–1089. doi:10.1038/nature06598

PubMed Abstract | CrossRef Full Text | Google Scholar

Ivanisenko, Y., Kübel, C., Nandam, S. H., Wang, C., Mu, X., Adjaoud, O., et al. (2018). Structure and Properties of Nanoglasses. Adv. Eng. Mat. 20, 1800404. doi:10.1002/adem.201800404

CrossRef Full Text | Google Scholar

Jian, W. R., Wang, L., Li, B., Yao, X. H., and Luo, S. N. (2016). Improved Ductility of Cu64Zr36metallic glass/Cu Nanocomposites via Phase and Grain Boundaries. Nanotechnology 27, 175701. doi:10.1088/0957-4484/27/17/175701

PubMed Abstract | CrossRef Full Text | Google Scholar

Jian, W. R., Wang, L., Yao, X. H., and Luo, S. N. (2018a). Balancing Strength, Hardness and Ductility of Cu64Zr36 Nanoglasses via Embedded Nanocrystals. Nanotechnology 29, 025701. doi:10.1088/1361-6528/aa994f

PubMed Abstract | CrossRef Full Text | Google Scholar

Jian, W. R., Wang, L., Yao, X. H., and Luo, S. N. (2018b). Tensile and Nanoindentation Deformation of Amorphous/crystalline Nanolaminates: Effects of Layer Thickness and Interface Type. Comput. Mater. Sci. 154, 225–233. doi:10.1016/j.commatsci.2018.07.054

CrossRef Full Text | Google Scholar

Kim, D. H., Kim, W. T., Park, E. S., Mattern, N., and Eckert, J. (2013). Phase Separation in Metallic Glasses. Prog. Mater. Sci. 58, 1103–1172. doi:10.1016/j.pmatsci.2013.04.002

CrossRef Full Text | Google Scholar

Klement, W., Willens, R. H., and Duwez, P. (1960). Non-crystalline Structure in Solidified Gold-Silicon Alloys. Nature 187, 869–870. doi:10.1038/187869b0

CrossRef Full Text | Google Scholar

Kuan, S. Y., Chou, H. S., Liu, M. C., Du, X. H., and Huang, J. C. (2010). Micromechanical Response for the Amorphous/amorphous Nanolaminates. Intermetallics 18, 2453–2457. doi:10.1016/j.intermet.2010.09.001

CrossRef Full Text | Google Scholar

Li, J., Lu, W., Chen, S., and Liu, C. (2020). Revealing Extra Strengthening and Strain Hardening in Heterogeneous Two-phase Nanostructures. Int. J. Plasticity 126, 102626. doi:10.1016/j.ijplas.2019.11.005

CrossRef Full Text | Google Scholar

Liu, A. C. Y., Paganin, D. M., Bourgeois, L., Nakashima, P. N. H., Ott, R. T., and Kramer, M. J. (2011). Quantitative Microscopic Measurement of Void Distribution in Shear Bands in Zr66.7Cu33.3metallic Glass. Phys. Rev. B 84, 094201. doi:10.1103/PhysRevB.84.094201

CrossRef Full Text | Google Scholar

Liu, W.-H., Sun, B. A., Gleiter, H., Lan, S., Tong, Y., Wang, X.-L., et al. (2018). Nanoscale Structural Evolution and Anomalous Mechanical Response of Nanoglasses by Cryogenic Thermal Cycling. ₹ Lett. 18, 4188–4194. doi:10.1021/acs.nanolett.8b01007

PubMed Abstract | CrossRef Full Text | Google Scholar

Nandam, S. H., Ivanisenko, Y., Schwaiger, R., Śniadecki, Z., Mu, X., Wang, D., et al. (2017). Cu-Zr Nanoglasses: Atomic Structure, Thermal Stability and Indentation Properties. Acta Mater. 136, 181–189. doi:10.1016/j.actamat.2017.07.001

CrossRef Full Text | Google Scholar

Nosé, S. (1984). A Molecular Dynamics Method for Simulations in the Canonical Ensemble. Mol. Phys. 52, 255–268. doi:10.1080/00268978400101201

CrossRef Full Text | Google Scholar

Pan, J., Liu, L., and Chan, K. C. (2009). Enhanced Plasticity by Phase Separation in CuZrAl Bulk Metallic Glass with Micro-addition of Fe. Scr. Mater. 60, 822–825. doi:10.1016/j.scriptamat.2009.01.032

CrossRef Full Text | Google Scholar

Parrinello, M., and Rahman, A. (1982). Strain Fluctuations and Elastic Constants. J. Chem. Phys. 76, 2662–2666. doi:10.1063/1.443248

CrossRef Full Text | Google Scholar

Plimpton, S. (1995). Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 117, 1–19. doi:10.1006/jcph.1995.1039

CrossRef Full Text | Google Scholar

Ritter, Y., Şopu, D., Gleiter, H., and Albe, K. (2011). Structure, Stability and Mechanical Properties of Internal Interfaces in Cu64Zr36 Nanoglasses Studied by MD Simulations. Acta Mater. 59, 6588–6593. doi:10.1016/j.actamat.2011.07.013

CrossRef Full Text | Google Scholar

Sha, Z.-D., Branicio, P. S., Lee, H. P., and Tay, T. E. (2017). Strong and Ductile Nanolaminate Composites Combining Metallic Glasses and Nanoglasses. Int. J. Plasticity 90, 231–241. doi:10.1016/j.ijplas.2017.01.010

CrossRef Full Text | Google Scholar

Sha, Z. D., Branicio, P. S., Pei, Q. X., Liu, Z. S., Lee, H. P., Tay, T. E., et al. (2015). Strong and Superplastic Nanoglass. Nanoscale 7, 17404–17409. doi:10.1039/C5NR04740D

PubMed Abstract | CrossRef Full Text | Google Scholar

Sha, Z. D., He, L. C., Pei, Q. X., Pan, H., Liu, Z. S., Zhang, Y. W., et al. (2014). On the Notch Sensitivity of CuZr Nanoglass. J. Appl. Phys. 115, 163507. doi:10.1063/1.4873238

CrossRef Full Text | Google Scholar

Shan, Z. W., Li, J., Cheng, Y. Q., Minor, A. M., Syed Asif, S. A., Warren, O. L., et al. (2008). Plastic Flow and Failure Resistance of Metallic Glass: Insight Fromin Situcompression of Nanopillars. Phys. Rev. B 77, 155419. doi:10.1103/PhysRevB.77.155419

CrossRef Full Text | Google Scholar

Shimizu, F., Ogata, S., and Li, J. (2007). Theory of Shear Banding in Metallic Glasses and Molecular Dynamics Calculations. Mat. Trans. 48, 2923–2927. doi:10.2320/matertrans.MJ200769

CrossRef Full Text | Google Scholar

Şopu, D., and Albe, K. (2015). Influence of Grain Size and Composition, Topology and Excess Free Volume on the Deformation Behavior of Cu-Zr Nanoglasses. Beilstein J. Nanotechnol. 6, 537–545. doi:10.3762/bjnano.6.56

PubMed Abstract | CrossRef Full Text | Google Scholar

Şopu, D., Albe, K., Ritter, Y., and Gleiter, H. (2009). From Nanoglasses to Bulk Massive Glasses. Appl. Phys. Lett. 94, 191911. doi:10.1063/1.3130209

CrossRef Full Text | Google Scholar

Şopu, D., Ritter, Y., Gleiter, H., and Albe, K. (2011). Deformation Behavior of Bulk and Nanostructured Metallic Glasses Studied via Molecular Dynamics Simulations. Phys. Rev. B 83, 100202. doi:10.1103/PhysRevB.83.100202

CrossRef Full Text | Google Scholar

Stukowski, A. (2009). Visualization and Analysis of Atomistic Simulation Data with OVITO-The Open Visualization Tool. Model. Simul. Mat. Sci. Eng. 18, 015012. doi:10.1088/0965-0393/18/1/015012

CrossRef Full Text | Google Scholar

Sun, M., Rauf, A., Zhang, Y., Sha, G., Peng, G., Yu, Z., et al. (2018). Enhanced Inter-diffusion of Immiscible Elements Fe/Cu at the Interface of FeZr/CuZr Amorphous Multilayers. Mater. Res. Lett. 6, 55–60. doi:10.1080/21663831.2017.1389773

CrossRef Full Text | Google Scholar

Wang, X., Jiang, F., Hahn, H., Li, J., Gleiter, H., Sun, J., et al. (2016). Sample Size Effects on Strength and Deformation Mechanism of Sc75Fe25 Nanoglass and Metallic Glass. Scr. Mater. 116, 95–99. doi:10.1016/j.scriptamat.2016.01.036

CrossRef Full Text | Google Scholar

Wang, X. L., Jiang, F., Hahn, H., Li, J., Gleiter, H., Sun, J., et al. (2015). Plasticity of a Scandium-Based Nanoglass. Scr. Mater. 98, 40–43. doi:10.1016/j.scriptamat.2014.11.010

CrossRef Full Text | Google Scholar

Wu, G., Zhang, J., Liu, C., Wang, Q., and Lu, J. (2020). Ductility of an Ultrastrong Glass-Crystal Nano-dual-phase Alloy in Sub-micron. Scr. Mater. 183, 17–21. doi:10.1016/j.scriptamat.2020.03.002

CrossRef Full Text | Google Scholar

Yao, L., and Jin, Z.-H. (2015). Stagnation Accommodated Global Plasticity in Nanoglass Composites. Scr. Mater. 106, 46–51. doi:10.1016/j.scriptamat.2015.05.002

CrossRef Full Text | Google Scholar

Zhang, B., Wang, R. J., Zhao, D. Q., Pan, M. X., and Wang, W. H. (2004). Properties ofCe-Based Bulk Metallic Glass-Forming Alloys. Phys. Rev. B 70, 224208. doi:10.1103/PhysRevB.70.224208

CrossRef Full Text | Google Scholar

Zhang, Z. F., Eckert, J., and Schultz, L. (2003). Difference in Compressive and Tensile Fracture Mechanisms of Zr59Cu20Al10Ni8Ti3 Bulk Metallic Glass. Acta Mater. 51, 1167–1179. doi:10.1016/S1359-6454(02)00521-9

CrossRef Full Text | Google Scholar