Understanding of Wood Anomalies in Metallic Gratings From Phase Gradient Metasurfaces

Phase-gradient metasurfaces (PGMs) have provided unprecedented opportunities for manipulating light. Here, we reexamine ordinary and well-studied subwavelength metallic gratings (OMGs) from the concept of PGMs to provide more insight into their diffraction properties. We will show that due to the existence of gauge invariance in PGMs, i.e., the diffraction law of PGMs is independent of the choice of initial value of abrupt phase shift that induces the phase gradient, the well-studied OMGs can be regarded as a PGM strictly, with its diffraction properties can be fully predicted by generalized diffraction law with phase gradient. In particular, the generalized diffraction law reveals that the phase gradient plays a significant role in the famous effect of Wood’s anomalies and Rayleigh’s conjecture.

1 Introduction

In recent years, Phase-gradient metasurfaces (PGMs) have been reported as a way to manipulate electromagnetic (EM) wave propagation, leading to numerous effects or applications (Yu et al., 2011; Kildishev et al., 2013; Xu et al., 2016; Sun et al., 2019). These include efficient focusing (Arbabi et al., 2017), ultrathin cloaking (Ni et al., 2015), photonic spin Hall effects (Yin et al., 2013), metalenses (Chen et al., 2012; Wang et al., 2018), wavefront control (Xie et al., 2014; Ra’di et al., 2017; Fu et al., 2019a), and others (Sun et al., 2012; Li et al., 2015; Tymchenko et al., 2015; Khorasaninejad et al., 2016; Hu et al., 2019). PGMs are periodic arrays of a carefully designed supercell with m unit cells (m is an integer) that discretely introduce a covering 2π abrupt phase shift (APS) $\varphi \left(x\right)$ along the surface (PGM condition), yielding a phase gradient $\nabla \varphi \left(x\right)$ that is physically equivalent to the wave vector, where the abrupt phase shift is the phase retardation when the incident light enters the groove. This phase gradient modifies Snell’s law, one of the fundamental laws of optics, leading to a generalized reflection/refraction law (Yu et al., 2011). Because the phase gradient of PGMs is independent of the initial choice value of APS (Aieta et al., 2015; Wang et al., 2018), the initial value of APS is not unique and can be arbitrary, which predicts the existence of gauge invariance in PGMs. Such gauge invariance provides insight to revisit the ordinary metallic grating (OMG) (Born and Wolf, 1999) that is well studied in plasmonics.

Wood anomalies are well-known effects in the optics community. They were first discovered by Wood in 1902 in experiments on reflection-type OMG (Wood, 1902) and have been investigated and attracted much attention from scientists for more than a century (Rayleigh, 1907; Fano, 1941; Hessel and Oliner, 1965; Maradudin et al., 2016). They have obvious sudden and intense variations in the reflectance/transmittance of various diffracted orders in certain narrow frequency bands or alternatively in a certain narrow range of incident angles for a fixed operating frequency (Maradudin et al., 2016). They are termed anomalies, as ordinary grating theory cannot explain them well. Various efforts (Rayleigh, 1907; Fano, 1941; Hessel and Oliner, 1965) have been made over the years to understand Wood’s anomalies. For instance, Ugo Fano attributed them to the excitations of surface plasmons in periodically corrugated metal interfaces (Fano, 1941). Rayleigh proposed a well-known interpretation based on his conjecture that these anomalies occur at the wavelength at which a diffracted order appears or disappears at a grazing angle (Rayleigh, 1907). Specifically, for the nth diffracted order, the anomaly occurs at the wavelength (Rayleigh, 1907; Maradudin et al., 2016),

$\lambda =\left(\pm 1-sin{\theta }_{in}\right)p/n,(1)$

where p is the period of grating, ${\theta }_{in}$ is the angle of incidence, and n is an integer. The Eq. 1 is a special case of the well-known grating equation $\lambda =\left(sin{\theta }_t-sin{\theta }_{in}\right)p/n$ with $sin{\theta }_t=\pm 1$, where θ_t is the diffraction angle of nth order. The Rayleigh conjecture shows that for a given grating with period p and incident angle ${\theta }_{in}$, the diffraction efficiency changes dramatically at wavelength $\lambda$ in the scattering spectrum, and diffracted waves arise and propagate tangentially to the surface of the grating, leading to the passing-off of a spectrum of higher order (Rayleigh, 1907). The Rayleigh conjecture was considered a valuable tool for the prediction of Wood’s anomalies; therefore, these anomalies are also termed Wood-Rayleigh (WR) anomalies. These anomalies are successful in many cases, but the physical reason for the conjecture is still unclear. In particular, there is a lack of reasonable explanation of why the passing-off of the order n should occur, i.e., the term $sin{\theta }_t=\pm 1$ in Eq. 1.

In this work, we start from the gauge invariance of PGMs, revisit the widely studied OMG from the concept of PGMs and present insight into Rayleigh’s conjecture. We will show that ordinary grating theory cannot accurately describe OMG diffractions. In contrast, only the diffraction law including the phase gradient can be used to fully determine their diffraction features. In this diffraction law, the diffraction order of n = 1 is the lowest order, while the 0th order is a higher diffraction order and is difficult to couple. This result completely contrasts with the ordinary understanding of the diffraction law and fully explains the conjecture of WR anomalies, as shown in Eq. 1. More importantly, we also show that WR anomalies can be seen in any OMG, but the physical mechanism can be understood more deeply and clearly by the gauge invariance in a PGM system. Our findings provide a way to study the physics in OMGs from the concept of PGMs, bridging the gap of two fields of optical metasurfaces and plasmonics.

2 Model and Theory

A typical reflection-type PGM with m = 2 is shown in Figure 1A, a textured metallic grating made of a periodic repeated supercell with a period of p. Each supercell contains two unit cells of different grooves. The width of each unit cell is $\text{Λ}=p/2$, the width of both grooves is w, and their depths are h₁ and h₂, respectively. To discuss the essential mechanism, the metal is assumed to be a perfect electric conductor (PEC). Similar results can be found if the PEC is replaced with real metals (see Supplementary Appendix SA). Consider a TM (i.e., only magnetic field along the y-direction) polarized EM wave obliquely incident from the air onto this PGM, with an incident angle of ${\theta }_{in}$. When light enters the jth (j = 1, 2) groove and travels along with it, the reflected wave will experience phase retardation ${\phi }_j=2\beta h_j$, where $\beta$ is the wave vector of an EM wave in the grooves. As mentioned above, the concept of PGM requires a full 2π phase shift in a supercell, which shows a phase difference of $\text{Δ}\phi =2\pi /m$ between two adjacent unit cells. In this case, m = 2 leads to $\text{Δ}\phi ={\phi }_2-{\phi }_1=\pi$, which can be achieved by adjusting the groove depth (Ra’di and Alu ̀, 2018; Cao et al., 2019). Physically, the diffraction properties of the designed PGM are governed by (Fu et al., 2019b):

$k_{0}sin{\theta }_r=k_{0}sin{\theta }_{in}+\kappa +vG,(2)$

where v is an integer, G = 2π/p is the reciprocal vector, and $\kappa =\frac{\text{Δ}\phi }{\text{Δ}x}=2\pi /p$ is the phase gradient. They share the same value but with different physical meanings: $\kappa$ is caused by the phase shifts along the interface, and G is caused by the periodicity of grating (Xu et al., 2015). Moreover, the diffraction of PGM can be re-expressed as

$k_{0}sin{\theta }_{r,n}=k_{0}sin{\theta }_{in}+nG,(3)$

where $n=1+v$ is the diffraction order. Note that Eq. 2 is very similar in formula to ordinary grating diffraction equation but quite different in physics because the phase gradient makes the lowest order corresponding to v = 0.

FIGURE 1

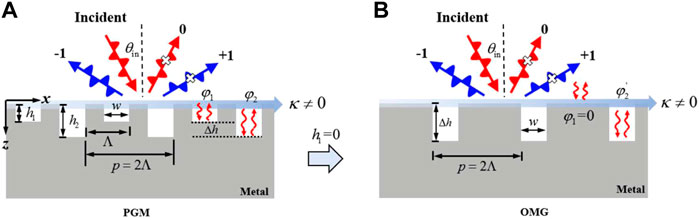
FIGURE 1. (A) Schematic diagram of reflection-type phase-gradient metagrating (PGM) in air, where one period is composed of two air grooves with depths h₁ and h₂. A TM wave incident to the PGM with an incident angle ${\theta }_{in}$, and the supercell with period p contains two unit cells with identical width $\text{Λ}$. The width of groove in each unit cell is w. (B) For h₁ = 0 in (A), the PGM becomes an ordinary metallic grating (OMG).

In fact, the initial value of APS is not unique for the design of PGMs. If we take the following transformation,

${\varphi }^{\prime }\left(x\right)\to \varphi \left(x\right)+{\text{Φ}}_0,(4)$

where ${\text{Φ}}_0$ is a constant, then $\nabla {\varphi }^{\text{'}}\left(x\right)=\nabla \varphi \left(x\right)$. This implies that when the APS of all spatial positions increases by the same value, the behaviors of PGMs and the associated diffraction law of Eq. 2 are completely unchanged. The reason behind this is the constant phase gradient of PGMs. This is a global gauge invariance of PGMs, which is similar to the electric potential of an electrostatic field, requiring the choice of zero point.

With this global gauge invariance in PGMs, we choose ${\phi }_1=0$ in PGM, as shown in Figure 1A, where h₁ = 0. Then, the PGM becomes an OMG, as seen from Figure 1B, and both cases should share the same diffraction law of Eq. 2. It should be emphasized that OMG is generally considered to be a simple periodic grating with no phase gradient. However, based on this global canonical invariance, it can be equivalent to a PGM of m = 2, whose two unit cells are grooves and metal blocks. In this way, the generalized diffraction law in the designed PGM can give more profound physics to the diffraction properties of OMG than that from ordinary diffraction theory. Ordinary diffraction theory describes the lowest diffraction order of n = 0, and it is preferred to be coupled and diffracted in the process of grating diffraction. From the view of PGMs, however, the lowest diffraction order of the OMG is not n = 0, but n = 1 corresponding to v = 0 in Eq. 2, which is preferred to be diffracted. More importantly, Eq. 2 indicates that n = 0 is a higher diffraction order and more difficult to couple than n = 1 (Fu et al., 2019b).

To further reveal the diffraction features, theoretical analyses were performed for the designed PGM and OMG. The total magnetic field in the air region ($z\le 0$) can be expressed as the sum of the incident and reflected fields $H_{y,1}={\displaystyle \sum }_n[{\delta }_{n,0}\exp \left(i{k}_{z,n}z\right)+r_n\text{exp}(-i{k}_{z,n}z)]\text{exp}\left(i{\alpha }_{n}x\right)$, where ${\delta }_{n,0}$ is the Kronecker delta function, $k_{z,n}=\sqrt{k_0^2-{\alpha }_n^2}$ is the z-component of the wave vector of the nth-order diffracted wave, ${\alpha }_n=k_{0}sin{\theta }_{in}+nG$ is the wave vector along the x-direction, and r_n is the reflection coefficient of the nth diffraction order. In this work, for illustrations, we take three cases of $\kappa =k_0$, $\kappa =1.5k_0$ and $\kappa =2k_0$ for discussion, corresponding to groove widths of ${\lambda }_0/2$, ${\lambda }_0/3$, and ${\lambda }_0/4$, respectively. These grooves have a cutoff wavelength ${\lambda }_{cutoff}=2w$ for the higher-order waveguide modes. Due to the subwavelength grooves and ${\lambda }_0\ge {\lambda }_{cutoff}$, we simply assume that only a fundamental mode exists inside the grooves with propagating wave vector $\beta =k_0$. In this way, the magnetic field inside the jth groove ($0\le z\le h_j$) is given by $H_{y,2,j}={\alpha }_j\exp \left(i{k}_{0}z\right)+b_j\exp \left(-i{k}_{0}z\right)$, where ${\alpha }_j$ and $b_j$ are the amplitude coefficients of the forward and backward waves. In addition, the corresponding electric fields of each region can be analytically obtained by solving Maxwell’s equations. By applying the continuous boundary conditions of electric and magnetic fields at z = 0 and z = h_j, we obtain the following equations:

${\displaystyle \sum _n{g}_n\left({\delta }_{n,0}+r_n\right)\exp \left(i{\alpha }_n{x}_j\right)=a_j+b_j},(5)$

$\sqrt{1-{\left({\alpha }_n/k_0\right)}^2}\left[{\delta }_{n,0}-r_n\right]={\displaystyle \sum _j\left(a_j-b_j\right)f{g}_n\text{exp}\left(-i{\alpha }_n{x}_j\right),}(6)$

where $b_j=a_{j}exp\left(2i{k}_0{h}_j\right)$ and x_j are coordinates of the jth groove, f = w/p is the filling factor, and $g_n=sinc({\alpha }_{n}w/2)$. By solving Eqs 5, 6, we can obtain all order reflection coefficients $r_n$, where reflectivity is $R_n={\left|r_n\right|}^2$.

3 Results and Discussions

To clearly illustrate our idea, we first consider a PGM with $p={\lambda }_0$ that corresponds to $\kappa =k_0$. The geometric parameters are $h_1=0$, $\Delta h=h_2=\frac{{\lambda }_0}{4}$ and $w=\frac{p}{2}$. The designed PGM is an OMG with a filling ratio of $f=0.5$, where WR anomalies can be observed in the spectra (see Supplementary Appendix SB). Because they are equivalent, the diffractions in OMG can be governed by Eq. 2, i.e.,

$sin{\theta }_{r,n}=sin{\theta }_{\mathrm{i}\mathrm{n}}+1+v.(7)$

In Eq. 7, the order $v=0$ is the lowest diffraction order, which corresponds to n = 1 and defines a critical incident angle of ${\theta }_{in}=0$ for the emergence of higher-order diffractions. For ${\theta }_{in}<0$, $v=0$, then $\sin {\theta }_{r,1}=\sin {\theta }_{in}+1$. When ${\theta }_{in}>0$, higher-order diffraction with $v\ne 0$ occurs. Therefore, according to Eqs 2, 7), the wave vector of the nth reflected wave in x and z direction are k_x = $k_{0}sin{\theta }_{in}+nG$ and k_z = $k_{0}cos{\theta }_{in}$, respectively. The iso-frequency contours of both incident light and the diffracted light of all possible channels are shown in Figure 2A. When ${\theta }_{in}>0$, higher orders such as $v=-1$ and −2 are obtained that correspond to n = 0 and n = −1, respectively. Considering the case of these two high diffraction orders, ordinary diffraction theory describes that $v=-1$ (n = 0) can be preferably coupled to $v=-2$ (n = −1). However, this is not possible due to phase gradient. In fact, the higher order of diffraction follows a rule of L = m + n (Fu et al., 2019b), which indicates that the higher the diffraction order is, the higher the coupling and diffraction. This statement strongly contrasts with ordinary diffraction theory, which reveals that the lower the diffraction order is, the higher the coupling priority. Therefore, in the current case, the -1st order is preferred to be coupled compared to the 0th order. These results are further validated and confirmed by the diffraction efficiency of each order. Figure 2B displays the relationship between the reflectivity of the 0th, 1st, and -1st diffraction orders and the incident angle. In this plot, solid lines represent the analytical results, while the circles depict the simulated results obtained from COMSOL Multiphysics. The analytical results agree well with the simulated results. In particular, when ${\theta }_{in}={30}^{\circ }$, the reflection is mainly dominated by the -1st order rather than the 0th order. The field pattern of incidence ${\theta }_{in}={30}^{\circ }$ is shown in Figure 2C, which clearly describes the retroreflection (Fu et al., 2019a) at ${\theta }_r=-{30}^{\circ }$ corresponding to n = −1.

FIGURE 2

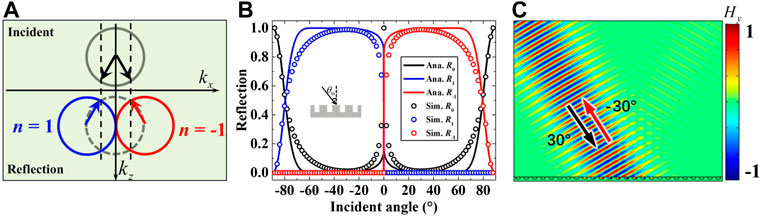
FIGURE 2. The case of $\kappa =k_0$. The relevant parameters are $p={\lambda }_0$, $\Delta h=\frac{{\lambda }_0}{4}$, and $w=\frac{p}{2}$. (A) The iso-frequency contours for wave diffraction in PGM. The gray circle is for the incident wave, with the black arrows indicating the incident direction. The blue circle, gray dashed circle, and red circle represent reflected waves of diffraction orders of n = 1, 0, and -1, respectively. The directions of the 1st- and -1st-order reflected waves are denoted by blue and red arrows, respectively. (B) The relationship between reflectivity and incident angle of all diffraction orders. Solid lines and hollow circles represent analytical and simulated results, respectively. (C) Magnetic field distribution for a nearly perfect retroreflection. The incident angle is 30°, and the reflection angle is −30°.

Similar results are obtained for other phase gradients, i.e., $\kappa =1.5k_0$. Figure 3A shows the corresponding iso-frequency contours, where the two lowest diffraction orders n = 1 (blue circle) and n = −1 (red circle) are separated. In this case, the period is $p=\frac{2{\lambda }_0}{3}$, which indicates the abrupt change in diffraction efficiency (i.e., WR anomaly) occurring at ${\theta }_{in}=30°$, predicted by Eq. 1. This transition angle can be clearly seen from the calculated diffraction efficiency of each order, as shown in Figure 3B. As the incident angle increases from zero and when it crosses ${\theta }_{in}=30°$ (or ${\theta }_{in}=-30°$), the dominant diffraction order instantaneously changes from the 0th order to the -1st order (or the 1st order), although the 0th order channel is still open. Nearly perfect retroreflection occurs when ${\theta }_{in}={48.6}^{\circ }$ (see Figure 3C), where the efficiencies of the n = 1 and 0 orders are 92% and 8%, respectively. Moreover, when $\kappa \ge 2k_0$ ($p\le \frac{{\lambda }_0}{2}$), only the 0th diffraction order channel is open for the incident wave, with the 1st and -1st orders that go out of the range of $\left(-k_0,k_0\right)$. In this case, the PGM is similar to a perfect mirror, with $R_0=1$ for all incidences (see Supplementary Appendix SC). Therefore, no WR anomalies are observed. These results are also consistent with the prediction of Eq. 1.

FIGURE 3

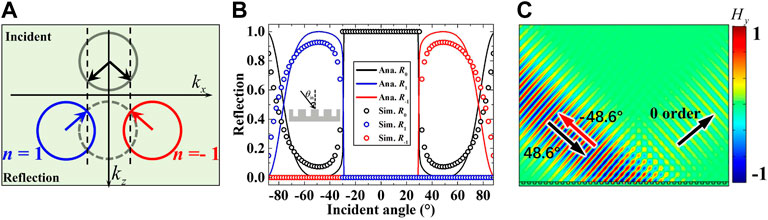
FIGURE 3. The case of $\kappa =1.5k_0$. The relevant parameters are $p=\frac{2{\lambda }_0}{3}$, $\Delta h=\frac{{\lambda }_0}{4}$, and $w=\frac{p}{2}$. (A) The iso-frequency contours for wave diffraction in PGM. (B) The relationship between reflectivity of orders of n = -1, 0, 1, and the incident angle. (C) Magnetic field distribution for nearly perfect retroreflection. The incident angle is 48.6°. The -1st order is dominant in the reflected wave.

It is believed that WR anomalies can be predicted for any groove depth, but their intensities are closely related to the depth of the grooves. Here, we find that when the APS along the interface covers full $2\pi$, i.e., it satisfies the condition of PGMs, the intensity of WR anomalies becomes strongest. To illustrate this point, Figure 4 shows the diffraction efficiency (i.e., reflection) of the -1st (Figure 4A) and 0th (Figure 4B) orders as a function of the incident angle and the groove depth for $\kappa =1.5k_0$. Here, only $R_{-1}$ and $R_0$ are shown, as the diffraction efficiencies of other orders are zero for $\Delta h\in \left[0, {\lambda }_0\right]$ and ${\theta }_{in}\in \left[0, 90°\right]$. By observing the groove depth with expected phase gradient, whose $\Delta h=0.25{\lambda }_0$ and $0.75{\lambda }_0$ (see dashed lines in Figure 4A), we can find the diffraction efficiency of n = −1 is strongest due to phase gradient $\Delta \phi$ is equal to the expected value of π. For other depths that deviate from these ideal values, $\Delta \phi$ differs from the ideal value of $\pi$, leading to imperfect APS along the interface. However, due to the tolerance in designing PGM (Cao et al., 2021), Eq. 2 still holds when the depth deviation is not very large. In contrast, the 0th-order efficiency is constant for all incident angles when $\Delta h=0.5{\lambda }_0$ (see the dashed line in Figure 4B). No WR anomalies can be observed even if the condition of Eq. 1 is satisfied. Therefore, we conclude that the WR anomalies are related to the phase gradient.

FIGURE 4

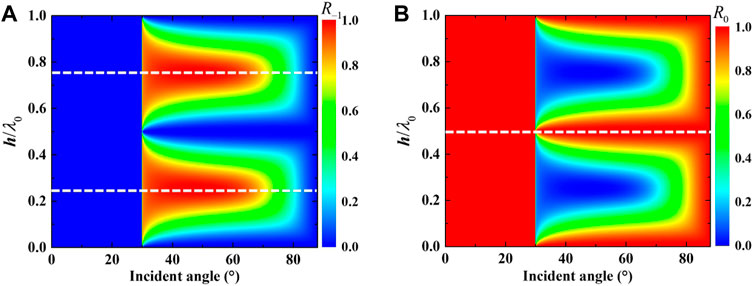
FIGURE 4. Analytical reflectivity as a function of ${\theta }_{in}$ and h for $\kappa =1.5k_0$. (A) Reflectivity of the -1st order. And the grooves depth at $\Delta h=0.25{\lambda }_0$ and $\Delta h=0.75{\lambda }_0$ (the dashed lines) conform to the phase gradient of ideal value $\Delta \phi$ = π, diffraction of the -1st order is dominant for ${\theta }_{in}\in \left[30°, 70°\right]$. The abrupt change in diffraction efficiency at ${\theta }_{in}=30°$ corresponds to WR anomalies. (B) Reflectivity of the 0th order. When $\Delta h=0.5{\lambda }_0$ (the dashed line), the diffraction efficiency of the 0th order is almost unity.

This physics provides us with guidance to design a high-efficiency retroflector (i.e., ${\theta }_r=-{\theta }_{in}$) using OMG through the -lst diffraction channel by adjusting the depth of the groove. The retroflection angle is determined by the period of p for a working wavelength, which is given by ${\theta }_{rtreo}=\arcsin \left({\lambda }_0/2p\right)$ based on Eq. 3. For $\kappa =k_0$ and $\kappa =1.5k_0$, retroflection occurs at ${\theta }_{rtreo}=30°$ and ${\theta }_{rtreo}=48.6°$, respectively. Figure 5 shows the retroreflected efficiency as a function of the depth of grooves in both cases, where Figure 5A is for $\kappa =k_0$ with other parameters that are the same as those in Figure 2, and Figure 5B is for $\kappa =1.5k_0$ with other parameters that are the same as those in Figure 3. As shown in Figure 5, the retroflection efficiency (i.e., the -1st diffraction efficiency) changes periodically with $\Delta h$. When $\Delta h=0.25{\lambda }_0$ or $\Delta h=0.75{\lambda }_0$, the retroflection efficiency is maximum and almost reaches 100%. Obviously, this outcome is due to the phase gradient. At $\Delta h=0.25{\lambda }_0$ or $\Delta h=0.75{\lambda }_0$, the APS is perfectly introduced, leading to a well-defined phase gradient, which makes the -1st diffraction the lowest order. This result is consistent with above discussions.

FIGURE 5

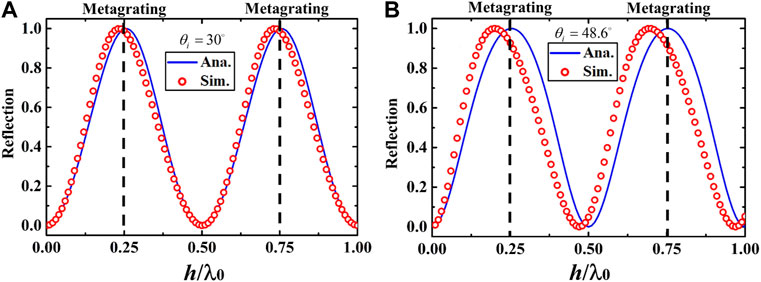
FIGURE 5. Retroreflection efficiency as a function of the groove depth of OMG. (A) is for $p={\lambda }_0$ and $\kappa =k_0$ with a retroreflected angle of 30°. (B) shows $p=\frac{2{\lambda }_0}{3}$ and $\kappa =1.5k_0$ with a retroreflected angle of 48.6°. The blue solid line and red circles represent analytical and simulated results, respectively. In both cases, the two dashed lines indicate the depths of $\Delta h=0.25{\lambda }_0$ and $\Delta h=0.75{\lambda }_0$, at which the APS is met. Then, the OMG can be treated as a PGM with m = 2.

4 Conclusion

In summary, we have demonstrated that the well-studied reflected-type OMGs can be regarded as a PGM with m = 2 due to the existence of gauge invariance in PGMs, with their diffraction properties that can be explained more deeply by the generalized grating diffraction equation derived from PGMs than the ordinary grating diffraction equation. In particular, such a generalized diffraction equation provides insight into Wood-Rayleigh (WR) anomalies, revealing that the phase gradient contributes to the physics of the Rayleigh conjecture. The gauge invariance and our results build a bridge between the fields of metasurfaces and plasmonics, enabling many potential applications of retroreflection, sensors, and wavefront control.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

JQ and QZ equal contribution including design, research, and simulation. YC and YX contributed by coming up with design ideas and theoretical research.

Funding

This work was supported by the National Natural Science Foundation of China (Grant Nos. 11974010 and 12104331), the project funded by the China Postdoctoral Science Foundation (Grant No. 2020M681701), the Postdoctoral Science Foundation of Jiangsu Province (Grant No. 2021K276B) and the Priority Academic Program Development (PAPD) of Jiangsu Higher Education Institutions.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

YX thanks the support from the Key Lab of Modern Optical Technologies of Education Ministry of China, Soochow University. QZ thanks the Postgraduate Research & Practice Innovation Program of Jiangsu Province (No. KYCX21_2936) for this work.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmats.2022.901794/full#supplementary-material

References

Aieta, F., Kats, M. A., Genevet, P., and Capasso, F. (2015). Multiwavelength Achromatic Metasurfaces by Dispersive Phase Compensation. Science 347, 1342–1345. doi:10.1126/science.aaa2494

PubMed Abstract | CrossRef Full Text | Google Scholar

Arbabi, A., Arbabi, E., Horie, Y., Kamali, S. M., and Faraon, A. (2017). Planar Metasurface Retroreflector. Nat. Phot. 11, 415–420. doi:10.1038/nphoton.2017.96

CrossRef Full Text | Google Scholar

Born, M., and Wolf, E. (1999). Principles of Optics: Electromagnetic Theory of Propagation, Interference, and Diffraction of Light. Cambridge, UK: Cambridge University Press.

Google Scholar

Cao, Y., Fu, Y., Zhou, Q., Ou, X., Gao, L., Chen, H., et al. (2019). Mechanism behind Angularly Asymmetric Diffraction in Phase-Gradient Metasurfaces. Phys. Rev. Appl. 12, 024006. doi:10.1103/physrevapplied.12.024006

CrossRef Full Text | Google Scholar

Cao, Y., Fu, Y., Jiang, J.-H., Gao, L., and Xu, Y. (2021). Scattering of Light with Orbital Angular Momentum from a Metallic Meta-Cylinder with Engineered Topological Charge. ACS Photonics 8, 2027–2032. doi:10.1021/acsphotonics.1c00077

CrossRef Full Text | Google Scholar

Chen, X., Huang, L., Mühlenbernd, H., Li, G., Bai, B., Tan, Q., et al. (2012). Dual-polarity Plasmonic Metalens for Visible Light. Nat. Commun. 3, 1198. doi:10.1038/ncomms2207

PubMed Abstract | CrossRef Full Text | Google Scholar

Fano, U. (1941). The Theory of Anomalous Diffraction Gratings and of Quasi-Stationary Waves on Metallic Surfaces (Sommerfeld’s Waves). J. Opt. Soc. Am. 31, 213–222. doi:10.1364/josa.31.000213

CrossRef Full Text | Google Scholar

Fu, Y., Cao, Y., and Xu, Y. (2019). Multifunctional Reflection in Acoustic Metagratings with Simplified Design. Appl. Phys. Lett. 114, 053502. doi:10.1063/1.5083081

CrossRef Full Text | Google Scholar

Fu, Y., Shen, C., Cao, Y., Gao, L., Chen, H., Chan, C. T., et al. (2019). Reversal of Transmission and Reflection Based on Acoustic Metagratings with Integer Parity Design. Nat. Commun. 10, 2326. doi:10.1038/s41467-019-10377-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Hessel, A., and Oliner, A. A. (1965). A New Theory of Wood's Anomalies on Optical Gratings. Appl. Opt. 4, 1275–1297. doi:10.1364/ao.4.001275

CrossRef Full Text | Google Scholar

Hu, G., Hong, X., Wang, K., Wu, J., Xu, H.-X., Zhao, W., et al. (2019). Coherent Steering of Nonlinear Chiral Valley Photons with a Synthetic Au-WS2 Metasurface. Nat. Photonics 13, 467–472. doi:10.1038/s41566-019-0399-1

CrossRef Full Text | Google Scholar

Khorasaninejad, M., Chen, W. T., Devlin, R. C., Oh, J., Zhu, A. Y., and Capasso, F. (2016). Metalenses at Visible Wavelengths: Diffraction Limited Focusing and Subwavelength Resolution Imaging. Science 352, 1190–1194. doi:10.1126/science.aaf6644

PubMed Abstract | CrossRef Full Text | Google Scholar

Kildishev, A. V., Boltasseva, A., and Shalaev, V. M. (2013). Planar Photonics with Metasurfaces. Science 339, 1232009. doi:10.1126/science.1232009

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, G., Chen, S., Pholchai, N., Reineke, B., Wong, P. W. H., Pun, E. Y. B., et al. (2015). Continuous Control of the Nonlinearity Phase for Harmonic Generations. Nat. Mater. 14, 607–612. doi:10.1038/nmat4267

PubMed Abstract | CrossRef Full Text | Google Scholar

Maradudin, A. A., Simonsen, I., Polanco, J., and Fitzgerald, R. M. (2016). Rayleigh and Wood Anomalies in the Diffraction of Light from a Perfectly Conducting Reflection Grating. J. Opt. 18, 024004. doi:10.1088/2040-8978/18/2/024004

CrossRef Full Text | Google Scholar

Ni, X., Wong, Z. J., Mrejen, M., Wang, Y., and Zhang, X. (2015). An Ultrathin Invisibility Skin Cloak for Visible Light. Science 349, 1310–1314. doi:10.1126/science.aac9411

PubMed Abstract | CrossRef Full Text | Google Scholar

Ra’di, Y., and Alù, A. (2018). Reconfigurable Metagratings. ACS Photonics 5, 1779–1785. doi:10.1021/acsphotonics.7b01528

CrossRef Full Text | Google Scholar

Ra’di, Y., Sounas, D. L., and Alù, A. (2017). Metagratings: beyond the Limits of Graded Metasurfaces for Wave Front Control. Phys. Rev. Lett. 119, 067404. doi:10.1103/physrevlett.119.067404

PubMed Abstract | CrossRef Full Text | Google Scholar

Rayleigh, L. (1907). On the Dynamical Theory of Gratings. Proc. R. Soc. Lond. A 79, 399–416.

Google Scholar

Sun, S., He, Q., Xiao, S., Xu, Q., Li, X., and Zhou, L. (2012). Gradient-index Meta-Surfaces as a Bridge Linking Propagating Waves and Surface Waves. Nat. Mater. 11, 426–431. doi:10.1038/nmat3292

PubMed Abstract | CrossRef Full Text | Google Scholar

Sun, S., He, Q., Hao, J., Xiao, S., and Zhou, L. (2019). Electromagnetic Metasurfaces: Physics and Applications. Adv. Opt. Phot. 11, 380–479. doi:10.1364/aop.11.000380

CrossRef Full Text | Google Scholar

Tymchenko, M., Gomez-Diaz, J. S., Lee, J., Nookala, N., Belkin, M. A., and Alù, A. (2015). Gradient Nonlinear Pancharatnam-Berry Metasurfaces. Phys. Rev. Lett. 115, 207403. doi:10.1103/physrevlett.115.207403

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, S., Wu, P. C., Su, V. –C., Lai, Y. –C., Chen, M. –K., Kuo, H. Y., et al. (2018). A Broadband Achromatic Metalens in the Visible. Nat. Nanotech. 13, 227–232. doi:10.1038/s41565-017-0052-4

CrossRef Full Text | Google Scholar

Wood, R. W. (1902). XLII. On a Remarkable Case of Uneven Distribution of Light in a Diffraction Grating Spectrum. Lond. Edinb. Dublin Philos. Mag. J. Sci. 4, 396–402. doi:10.1080/14786440209462857

CrossRef Full Text | Google Scholar

Xie, Y., Wang, W., Chen, H., Konneker, A., Popa, B.-I., and Cummer, S. A. (2014). Wavefront Modulation and Subwavelength Diffractive Acoustics with an Acoustic Metasurface. Nat. Commun. 5, 5553. doi:10.1038/ncomms6553

PubMed Abstract | CrossRef Full Text | Google Scholar

Xu, Y., Fu, Y., and Chen, H. (2015). Steering Light by a Sub-Wavelength Metallic Grating from Transformation Optics. Sci. Rep. 5, 12219. doi:10.1038/srep12219

PubMed Abstract | CrossRef Full Text | Google Scholar

Xu, Y., Fu, Y., and Chen, H. (2016). Planar Gradient Metamaterials. Nat. Rev. Mater. 1, 16067. doi:10.1038/natrevmats.2016.67

CrossRef Full Text | Google Scholar

Yin, X., Ye, Z., Rho, J., Wang, Y., and Zhang, X. (2013). Photonic Spin Hall Effect at Metasurfaces. Science 339, 1405–1407. doi:10.1126/science.1231758

PubMed Abstract | CrossRef Full Text | Google Scholar

Yu, N., Genevet, P., Kats, M. A., Aieta, F., Tetienne, J.-P., Capasso, F., et al. (2011). Light Propagation with Phase Discontinuities: Generalized Laws of Reflection and Refraction. Science 334, 333–337. doi:10.1126/science.1210713

PubMed Abstract | CrossRef Full Text | Google Scholar