Broadband and Dual-Polarized Terahertz Wave Anomalous Refraction Based on a Huygens’ Metasurface

Terahertz wavefront manipulation is one of the key terahertz technologies. While few of the research works on terahertz wavefront manipulation has broadband and dual-polarized responses. Here a broadband dual-polarized Huygens’ metasurface is proposed to realize high efficient terahertz wave anomalous refraction. By constructing simultaneous electric and magnetic responses in a bi-layer metasurface to produce Huygens’ resonance, broadband and large phase changes for dual-polarized terahertz wave are achieved. A phase change over 300° with transmission magnitude beyond 0.75 is realized between 0.4 THz and 1 THz. An array made of the metasurface with phase gradient is designed to achieve a 14.0° anomalous refraction for two orthogonal linear polarized waves at 0.93 THz. The structure consists of only two metal layers, providing a simple and high-efficiency design scheme for achieving efficient dual-polarized terahertz wavefront manipulation.

Introduction

Terahertz wave is a kind of electromagnetic wave which refers to the electromagnetic radiation wave whose frequency is between 0.1 THz and 10 THz. It has the characteristics of strong penetration, low ionizing radiation, good orientation and so on, making it play a huge role in medical, non-destructive detection, high-speed mobile communication and other fields (He et al., 2020). Metasurface is an artificial composite made of periodic or aperiodic arrangement of subwavelength structural units. Phase, polarization and amplitude of terahertz wave can be modulated effectively by employing its strong internal electromagnetic response (Gao et al., 2007; Yang et al., 2010; Liu et al., 2019; Xia et al., 2019; Karimi Habil and Roshan Entezar, 2020; Li et al., 2020; Wang et al., 2020; Wu et al., 2020; Zhu et al., 2020; Li et al., 2021). By designing the phase gradient between adjacent units based on the generalized Snell’s law, it can manipulate the wavefront of terahertz wave flexibly (Zhang et al., 2013; Shi et al., 2014; Qian et al., 2019). Owing to the advantages of low profile, mature production process and low cost, metasurfaces are widely used in terahertz modulation technology (Chen et al., 2018; Shi et al., 2018; Kappa et al., 2019; Hu et al., 2021).

Large phase modulation is required to achieve the efficient wavefront and polarization modulation of transmitted terahertz waves (Ryan et al., 2010; Li et al., 2013; Liu et al., 2016; Ren et al., 2019; Zang et al., 2020; Xu et al., 2022). In 2021, W. Yu’s team designed a reflective terahertz wave polarization converter using a metal-medium-metal structure, achieving a 75% linear polarization conversion at 0.5 THz. The polarization conversion efficiency between 0.35 and 0.65 THz exceeded 50% (Wang and Li, 2021), showing a broadband response. A bi-layer metallic metasurface capable of independently controlling the polarization and phase distribution of the terahertz beam was also proposed by H. Zhou et al. The metasurface consists of two layers of metal arrays separated by a quartz substrate, with one layer determine polarization and the other changes phase (Zhou et al., 2021). In 2019, R. Zhao’s team utilized a double-layer Huygens’ metasurface, achieving a phase shift over 360° for single-polarization (Zhao et al., 2019). J. Long’s team proposed a metasurface embedded in a phase transition material vanadium dioxide to achieve terahertz phase shifts. By changing the applied temperature, the vanadium dioxide conductivity can be altered, leading to a transmission phase change of the terahertz waves. Its maximum phase shift reached 355.37° at frequency 0.736 THz and exceeds 350° between 0.731 and 0.752 THz (Long and Li, 2021).

The above research work proposes many feasible schemes in terms of bandwidth and transmission magnitude. However, most of them are only work for single-polarization while few of them can function for dual-polarization. This paper propose a double-polarized and broadband terahertz phase modulator. The phase modulator achieves a large phase variation by constructing a Huygens’ resonance in a metasurface while maintaining impedance matching in a broadband. Since the designed structure has symmetric characteristics, two orthogonal linear polarized waves can achieve equal phase change modulation. On the basis of this unit structure, this paper also designed a one dimensional array with phase gradient. It can achieve efficient anomalous refraction of dual-polarized waves. This work provides a feasible scheme for the efficient wavefront modulation for dual-polarization in terahertz band, which can promote the application of metasurfaces in terahertz technology.

Unit Design and Simulation

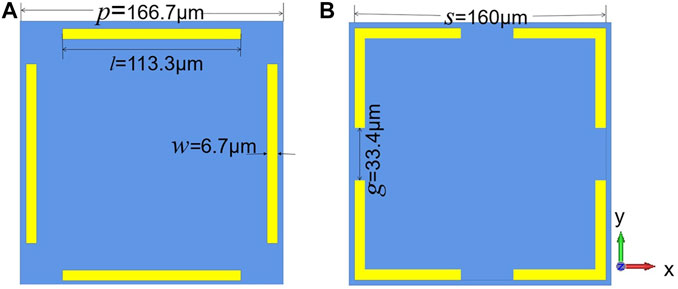
A bi-layer symmetric Huygens’ metasurface is designed in this paper as shown in Figure 1. From the Huygens’ basic principle, a wire excited by a parallel polarized incident wave can form an induced current on the metasurface. And a couple of wires can form an equivalent induced magnetic current. The metasurface consists of two metal layers, separated by a dielectric substrate called Benzocyclobutene (BCB) which has a permittivity of $\mathrm{\epsilon }$ = 2.67 and a loss tangent of 0.012 (Zhao et al., 2019). The front metal layer consists of four metal wires (the thickness of the metal wires is 0.02 $\mu m$), located at the four sides of the surface. The back metal layer is a strip ring with four gaps at each side. On the other hand, the strip ring consists of four L-shaped wires. The two arms of the L-shaped metal rings are equal and distributed at the four corners. Yellow parts in Figure 1 indicated gold. The remaining parameters are set as follows: the cell period of the Huygens’ metasurface is p = 166.7 $\mu m$. The thickness of the substrate is h = 50.8 $\mu m$, the length of the ring is s = 160 $\mu m$ and the gap length is g = 33.4 $\mu m$. On the front layer, the wire length is l = 113.3 $\mu m$. The width of all wires is w = 6.7 $\mu m$.

FIGURE 1

FIGURE 1. Schematic diagram of the front (A) and back (B) layers of the unit.

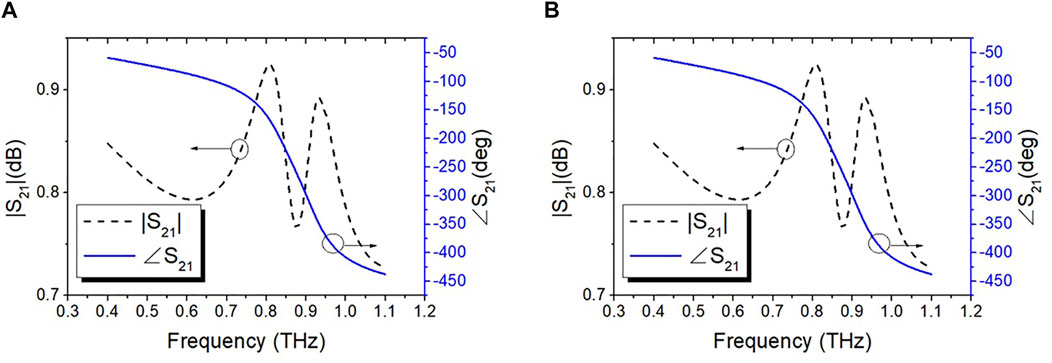
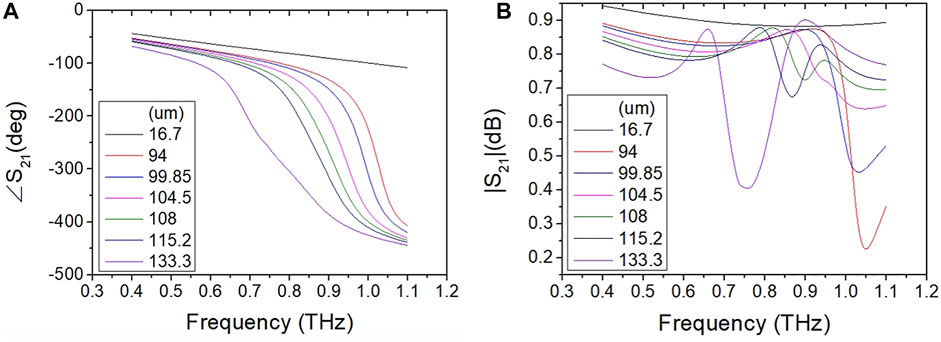
The above unit is modeled and simulated in the commercial full-wave simulation software CST. Boundary conditions in the x and y directions are all set as unit cell to simulate the periodic metasurface, while boundary condition in the z-direction is set as open. Simulation results were obtained by using the Floquet mode excitation. The transmission properties of the simulated model under TE/TM modes are shown in Figure 2. It can be seen that the unit structure implementation achieves a phase change over 300° in the 0.4-1 THz range and the transmission remains above 0.75, showing broadband and large phase change.

FIGURE 2

FIGURE 2. Magnitude and phase of S₂₁ under TM (A) and TE (B) mode.

For Huygens’ metasurfaces, surface electric conductance $Y_{es}$ and surface magnetic impedance $Z_{ms}$ are taken to characterize electromagnetic response and describe the discontinuities of the tangential electric field and magnetic field components respectively. Normally, $Y_{es}$ and $Z_{ms}$ are in tensor forms, depending on the polarization of the incident wave. An arbitrary electromagnetic wave can be represented as a superposition of two orthogonal components. For a unit with a symmetric structure, it has the same response to the two orthogonal polarized waves.

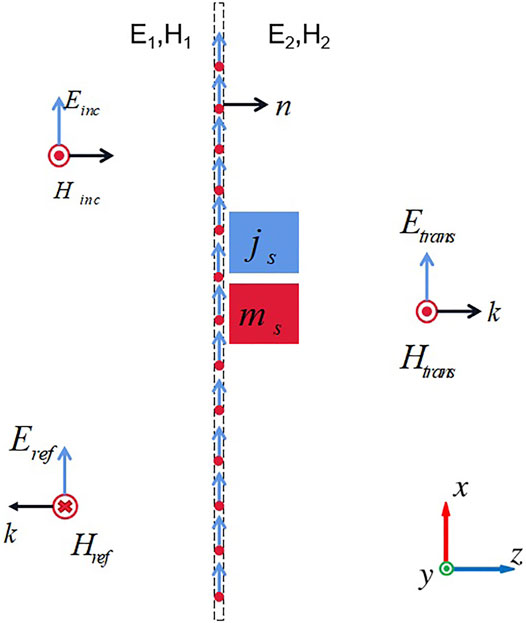
The directions of the electric fields are always consistent with the x-axis, as shown in Figure 3. Suppose the wave is incident on the left side of the metasurface, and the incident field excites Huygens’ source on the metasurface:

$\begin{array}{l}\frac{1}{2}\left(\stackrel{\rightharpoonup }{E_2^{+}}+\stackrel{\rightharpoonup }{E_1^{-}}\right)=Z_{se}.\left[\stackrel{\rightharpoonup }{n}\mathrm{\times }\left(\stackrel{\rightharpoonup }{H_2^{+}}-\stackrel{\rightharpoonup }{H_1^{-}}\right)\right],\\ \frac{1}{2}\left(\stackrel{\rightharpoonup }{H_2^{+}}+\stackrel{\rightharpoonup }{H_1^{-}}\right)=Y_{ms}.\left[-\stackrel{\rightharpoonup }{n}\mathrm{\times }\left(\stackrel{\rightharpoonup }{E_2^{+}}-\stackrel{\rightharpoonup }{E_1^{-}}\right)\right]\end{array}(1)$

where $\stackrel{\rightharpoonup }{E_1^{-}}$, $\stackrel{\rightharpoonup }{E_2^{+}}$, $\stackrel{\rightharpoonup }{H_1^{-}}$, and $\stackrel{\rightharpoonup }{H_2^{+}}$ represent the total fields of electric field E₁, magnetic field H₁, electric field E₂, and magnetic field H₂ at the two sides of metasurface shown in Figure 3 respectively, and $\stackrel{\rightharpoonup }{\text{n}}$ is the normal unit vector of the surface. The tangential total electric field on both sides can be expressed as:

$\begin{array}{l}{E}_1=E_{inc}+E_{ref},\\ H_1=H_{inc}-H_{ref},\\ E_2=E_{trans},\\ H_2=H_{trans}.\end{array}(2)$

FIGURE 3

FIGURE 3. Physical configuration of a Huygens’ metasurface.

By combining Eqs. 1, 2, the following formulas are obtained:

$\begin{array}{l}\frac{1}{2}\left(E_{trans}+E_{inc}+E_{ref}\right)=-Z_{se}.\left[H_{trans}-\left(H_{inc}-H_{ref}\right)\right],\\ \frac{1}{2}\left(H_{trans}+H_{inc}-H_{ref}\right)=-Y_{sm}.\left[E_{trans}-\left(E_{inc}+E_{ref}\right)\right].\end{array}(3)$

By introducing the wave impedance of free space $\eta =\sqrt{\mu /\mathrm{\epsilon }}$, Eq 3 can be rewritten as follows:

$\begin{array}{l}\frac{Y_{se}^e}{2}=\frac{E_{inc}-E_{trans}-E_{ref}}{E_{inc}+E_{trans}+E_{ref}},\\ \frac{Z_{sm}^e}{2}=\frac{E_{inc}-E_{trans}+E_{ref}}{E_{inc}+E_{trans}-E_{ref}}.\end{array}(4)$

Through Eq 4, the normalized surface electric admittance and the normalized surface magnetic impedance Y and Z have the following relation with the transmission coefficient T and reflection coefficient R:

$Y=Y_{es}\mathrm{\eta }=\frac{2\left(1-T-R\right)}{\left(1+T+R\right)}(5)$

$Z=Z_{ms}\mathrm{\eta }=\frac{2\left(1-T+R\right)}{\left(1+T-R\right)}(6)$

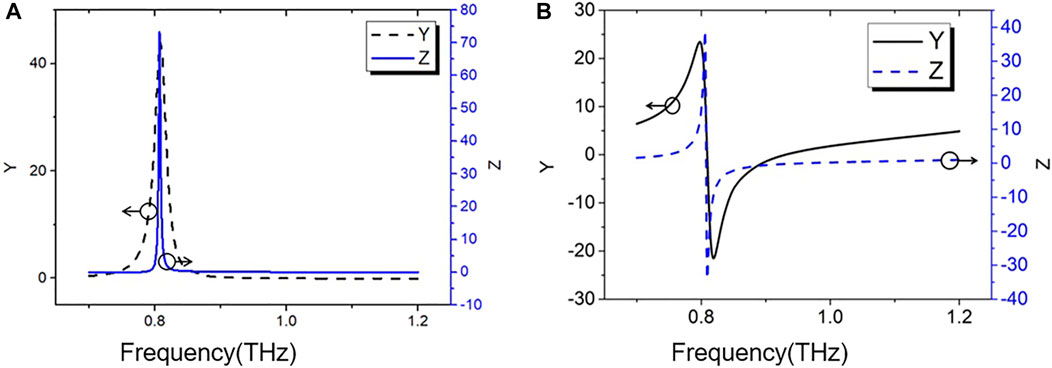
According to Ref (Xue et al., 2019), when the normalized surface conductance and surface magnet impedance are equal and are a pure imaginary number, the Huygens’ resonance can be excited to achieve impedance matching, yielding a transmission amplitude close to 1. The Y and Z parameters of the proposed metasurfaces are extracted with the simulated transmission and reflection coefficients, shown in Figure 4. When the normalized surface electric conductance and surface magnetic impedance are equal and pure imaginary, it can be seen that there is a Huygens’ resonance at 0.819 THz.

FIGURE 4

FIGURE 4. real part (A) and imaginary part (B) of Y and Z of the metasurface.

To further illustrate how the designed structure achieves the Huygens’ resonance, the current and electric field distribution for the two polarization at 0.819 THz have been analyzed. The current distributions are shown in Figure 5. For TM mode, a strong induced current appears along the front and back metal wires, oscillating along the x-axis, as shown in Figure 5A. On the contrary, current on the left and right metal wires are very small. On the backside of the metasurface, which is the back metal layer composed of four L-shaped metal wires, the induced current distribution is shown in Figure 5B. The induced current is formed on both the front and back sides. Compare Figures 5A, B, one can find that the currents on the front and back layers along the upper side metal wires are in opposite directions, forming an equivalent transverse magnetic dipole. For TE mode, strong induction current is aroused along the left and right metal wires on the front layer, as shown in Figure 5C. The induction current along the top and bottom metal wires is very weak. On the backside of the metasurface, the induced current distribution is shown in Figure 5D. The induced currents on the front and back layers are in the opposite direction along the y-axis, forming an equivalent transverse magnetic dipole.

FIGURE 5

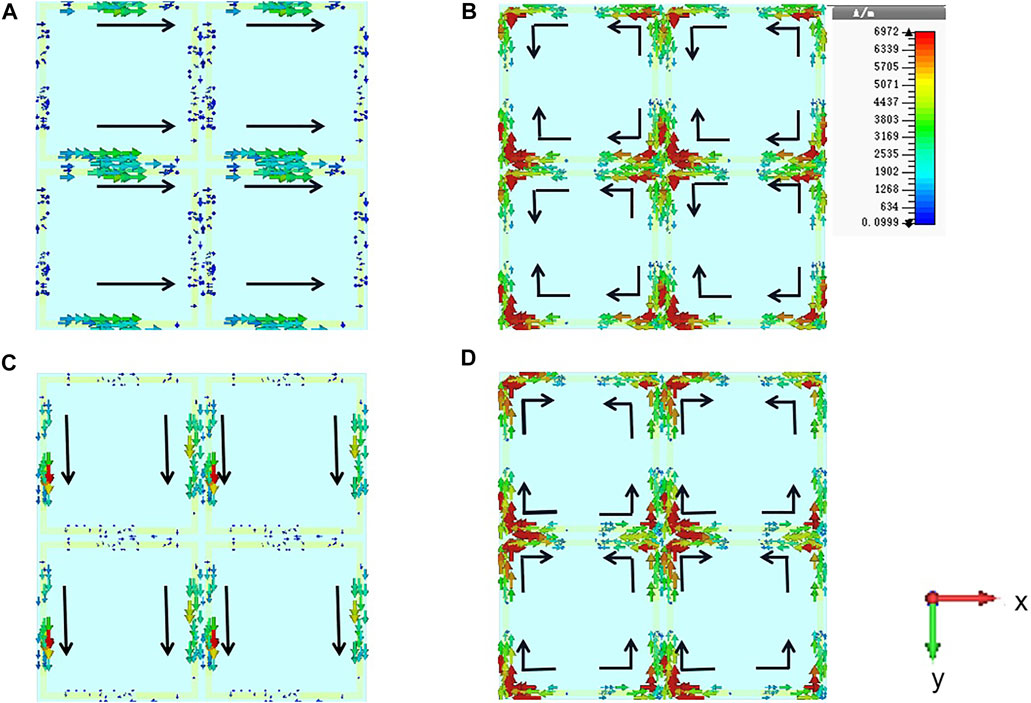
FIGURE 5. Current distribution of the metasurface at 0.819 THz. Current distribution excited by TM mode on the front (A) and back (B) layers. Current distribution excited by TE mode on the front (C) and back (D) layers.

Similar conclusions can be obtained by analyzing the electric field distribution on the metasurface, as shown in Figure 6. It can be seen that for TM mode, the electric field on the front layer is mainly localized at the upper and lower metal wires, as shown in Figure 6A. The electric field on the back layer of the metasurface is mainly localized around the ends of the L-shaped wires, as shown in Figure 6B. The electric field distribution on the front layer for TE mode is similar to the one for TM mode but rotated by 90° due to the symmetric property of the metasurface. The electric field on the front layer is mainly distributed at the left and right metal wires, as shown in Figure 6C. The electric field on the back layer is mainly distributed at the ends of the four L-shaped metal wires just like the one in the TM mode case, as shown in Figure 6D.

FIGURE 6

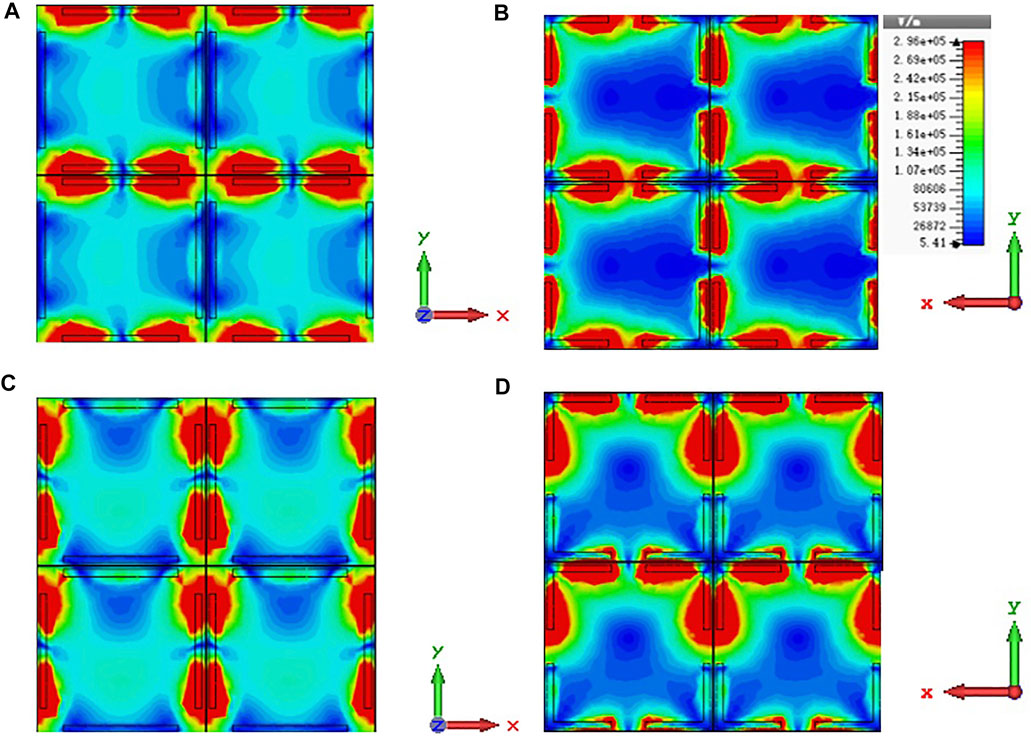
FIGURE 6. Distribution of electric field at 0.819 THz. Electric field distribution excited by TM mode on the front (A) and back (B) layer. Electric field distribution excited by TE mode on the front (C) and back (D) layer.

Huygens’ Metasurface Array

Applying the unit of the Huygens’ metasurface, a one-dimensional array with phase gradient in space is constructed. The transmission phase of each unit varies along with the array, making the array capable of achieving high efficient anomalous refraction for dual-polarized terahertz waves. The electromagnetic response of the Huygens’ metasurface depends on its geometric parameters, thus the required phase distribution can be obtained by adjusting the corresponding geometric parameters. When metal size l is swept while keeping l + g = 146.7 $\mu m$. Results are shown in Figure 7. By analyzing the magnitude and phase of the transmission coefficient, proper geometric parameters can be chosen for the phase distribution. One can find that the transmission coefficient varies with the change of l. The metasurface has a high transmittance which fluctuates in the range of 0.82–0.93 when varying l. Due to the Huygens’ resonance, the phase also increases rapidly with increasing l.A phase gradient of 45° between adjacent cells was selected for demonstration. While at the 0.819 THz frequency, the phase of S₂₁ is very sensitive to l. Small l changes will cause large phase change, which asks for a high accuracy for l to conduct accurate refraction and is not feasible in experiments. Therefore, we chose to construct the array at 0.93 THz.

FIGURE 7

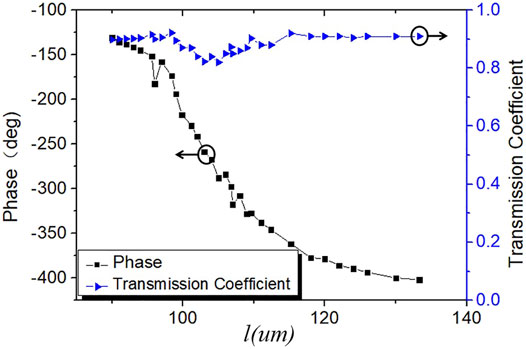
FIGURE 7. The amplitude and phase of the transmission coefficient of the Huygens’ metastructure at 0.93 TH vary with increasing l.

The abnormal refractive angle is usually calculated with the following expression:

${\theta }_0=\arcsin \left(\frac{\mathrm{\lambda }}{D}\frac{\theta }{2\pi }\right)(7)$

where $\lambda$ refers to the wavelength of the electromagnetic field, D refers to the length of the super array unit, $\theta$ refers to the total phase change along with the array. Since the change amount of the transmission phase at 0.93 THz is larger than 360° with varying l, other refraction angles can be obtained by changing $\theta$. Here the parameters in this work are: $\lambda$ = 323 $\mu m$, D = 7 *p = 1166.9 $\mu m$. For delection angle 13.7°, according to Eq 7, an array made of seven metasurface units is modeled with their l was chosen as $\left(\mu m\right)$:16.7, 94, 99.85, 104.5, 108, 115.2 and 133.3 respectively. The transmission performance is shown in Table 1. It shows that the transmission coefficients of the seven units at 0.93 THz are all greater than 0.82, ensuring high transmittance for the abnormal refraction.

TABLE 1

TABLE 1. List of the related information of each unit of the array at 0.93 THz.

An array made of the seven selected units is modeled in CST as shown in Figure 8. The l-parameter of the seven units increases successively from left to right according to Table 1.

FIGURE 8

FIGURE 8. Schematic diagram of the front surface (above) and back surface (below) of the array.

The transmission coefficient modulus and phases of the 7 cell structures were obtained by simulating the 7 cells, one can find that, the magnitude of S₂₁ of all seven units is larger than 0.7 between 0.83 THz and 0.97THz, with phase difference varying from 249 to 320°. Hence, it can be concluded from Figure 9 that the structure can achieve a large phase offset at a wide bandwidth.

FIGURE 9

FIGURE 9. Phases (A) and magnitude (B) of the transmission coefficients of the 7 cell structures.

To further illustrate the abnormal refraction capability of the Huygens’ metasurface array, simulations are performed with 16 Floquet modes. In order to obtain ab intuitive illustration of Huygens’ metasurface, air layers of several wavelengths in thickness are added on both sides of the metasurface. As shown in Figure 10, the terahertz wave at 0.93 THz is incident normally to the Huygens’ metasurface, while the outgoing wave is deflected at an angle of 14.0°, with an error of 2.2% compared with the proposed angle, showing a high consistent with the theory. From Figure 10, one can find that the wavefront for the TE and TM modes are slightly different, mainly due to the fact that the phase gradient is only in x-axis while it is periodic along the y-axis.

FIGURE 10

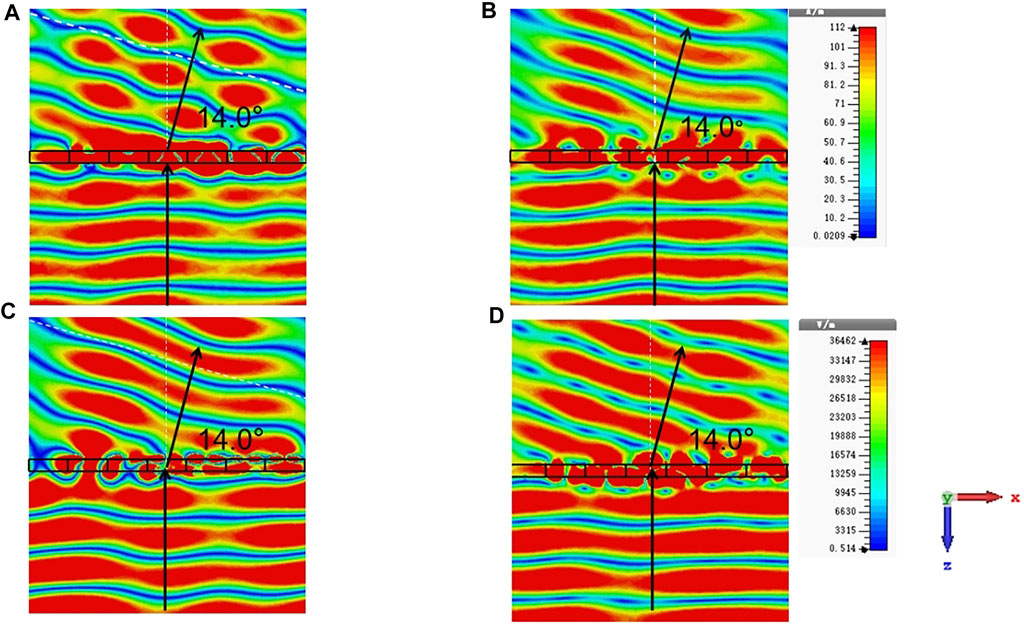
FIGURE 10. Magnetic field distribution for TM (A) and TE (B) modes when a plane waves at 0.93 THz is incident normally to the metasurface; Electric field distribution for TM (C) and TE (D) modes when a plane waves at 0.93 THz is incident normally to the metasurface.

Conclusion

In this paper, a broadband and dual-polarized terahertz phase modulator based on a bi-layer Huygens’ metasurface is designed. By introducing a transverse magnetic dipole into metasurface, a Huygens’ resonance is formed, enabling large phase changes while maintaining impedance matching. The incident wave phase of 0.93 THz is modulated over 300°, while the magnitude of the transmission coefficient can be maintained above 0.82. An array made of this bi-layer Huygens’ metasurface with phase gradient distribution is designed to realize abnormal refraction at 0.93 THz. Due to the symmetric characteristics of the designed structure, both waves in TE and TM modes can excite Huygens’ resonance in its structure, thus the Huygens’ metasurface has broadband and dual-polarized response, which provides a reliable design scheme for dual-polarized terahertz wave manipulation.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.

Author Contributions

JR and CX put forward the initial idea and supervised the project. JR and MX performed the theoretical calculations and wrote the manuscript. DW and XZ helped with the theoretical analyses. All authors fully contribute to the research.

Funding

This work was supported by the Science and Technology Research Program of Chongqing Municipal Education Commission of China (KJQN201900602; KJQN202000648; KJQN201900615); Natural Science Foundation of Chongqing, China (cstc2020jcyj-msxm0605; cstc2019jcyj-msxmX0639); National Natural Science Foundation of China under (62071133); partially by the Key Program of Natural Science Foundation of Guangxi Province (2019GXNSFDA245011).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Chen, Z., Chen, X., Tao, L., Chen, K., Long, M., Liu, X., et al. (2018). Graphene Controlled brewster Angle Device for Ultra Broadband Terahertz Modulation. Nat. Commun. 9, 4909. doi:10.1038/s41467-018-07367-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Gao, Q., Yan, D. B., Yuan, N. C., and Fu, Y. Q. (2007). Dualband and Dual-Polarized Frequency Selective Surfaces. J. Electron. Inf. Technol. 29 (2), 506–508.

Google Scholar

He, J., Dong, T., Chi, B., and Zhang, Y. (2020). Metasurfaces for Terahertz Wavefront Modulation: a Review. J. Infrared Milli Terahz Waves 41 (6), 607–631. doi:10.1007/s10762-020-00677-3

CrossRef Full Text | Google Scholar

Hu, J., Bandyopadhyay, S., Liu, Y. H., and Shao, L. Y. (2021). A Review on Metasurface: from Principle to Smart Metadevices. Front. Phys. 29. doi:10.3389/fphy.2020.586087

CrossRef Full Text | Google Scholar

Kappa, J., Sokoluk, D., Klingel, S., Shemelya, C., Oesterschulze, E., and Rahm, M. (2019). Terahertz Spatial Light Modulator with More Than 1 THz Working Range. Proc. SPIE 2019, 11124. doi:10.1117/12.2529205

CrossRef Full Text | Google Scholar

Karimi Habil, M., and Roshan Entezar, S. (2020). Polarization Conversion and Phase Modulation of Terahertz Electromagnetic Waves via Graphene-Dielectric Structure. Physica Scripta 95 (1), 015503.

CrossRef Full Text | Google Scholar

Li, G.-Q., Shi, H.-Y., Liu, K., Li, B.-L., Yi, J.-J., Zhang, A.-X., et al. (2021). Multi-beam Multi-Mode Vortex Beams Generation Based on Metasurface in Terahertz Band. Acta Phys. Sin. 70 (18), 188701. doi:10.7498/aps.70.20210897

CrossRef Full Text | Google Scholar

Li, J., Ning, T., Zhang, M., Li, I. L., Su, H., and Liang, H. (2020). Realization of Terahertz Wavefront Manipulation Using Transmission-type Dielectric Metasurfaces. Front. Phys. 8, 349. doi:10.3389/fphy.2020.00349

CrossRef Full Text | Google Scholar

Li, W., Wang, L. X., Li, M., and Zhu, N. H. (2013). Single Phase Modulator for Binary Phase-Coded Microwave Signals Generation. IEEE Photon. Technol. Lett. 25, 19. doi:10.1109/lpt.2013.2278277

CrossRef Full Text | Google Scholar

Liu, S., Chen, H., and Cui, T. J. (2016). A Broadband Terahertz Absorber Using Multi-Layer Stacked Bars. Appl. Phys. Lett. 106 (15), 151601. doi:10.1063/1.4918289

CrossRef Full Text | Google Scholar

Liu, T., Cao, X. Y., Lan, J. X., and Cong, L. L. (2019). Design of Wideband Metasurface Antenna Array with Low Scattering Characteristics. J. Electron. Inf. Technol. 41 (9), 2096–2102.

Google Scholar

Long, J., and Li, J.-S. (2021). Terahertz Phase Shifter Based on Phase Change Material-Metasurface Composite Structure. Acta Phys. Sin. 70 (7), 074201. doi:10.7498/aps.70.20201495

CrossRef Full Text | Google Scholar

Qian, J., Wang, Y., Yuan, S. Q., Sun, H. X., and Liu, X. J. (2019). Reflected Acoustic Wavefront Manipulation by an Ultrathin Metasurface Based on Three-Dimensional Generalized Snell’s Law. Appl. Phys. Express 12 (9), 094001. doi:10.7567/1882-0786/ab3492

CrossRef Full Text | Google Scholar

Ren, T., Zhang, M., Wang, C., Shao, L., Reimer, C., Zhang, Y., et al. (2019). An Integrated Low-Voltage Broadband Lithium Niobate Phase Modulator. IEEE Photon. Technol. Lett. 31, 11. doi:10.1109/lpt.2019.2911876

CrossRef Full Text | Google Scholar

Ryan, C. G. M., Chaharmir, M. R., Shaker, J., Bray, J. R., Antar, Y. M. M., and Ittipiboon, A. (2010). A Wideband Transmitarray Using Dual-Resonant Double Square Rings. IEEE Trans. Antennas Propagat. 58 (5), 1486–1493. doi:10.1109/tap.2010.2044356

CrossRef Full Text | Google Scholar

Shi, J., Fang, X., Rogers, E. T. F., Plum, E., MacDonald, K. F., and Zheludev, N. I. (2014). Coherent Control of Snell's Law at Metasurfaces. Opt. Express 22 (17), 21051–21060. doi:10.1364/oe.22.021051

PubMed Abstract | CrossRef Full Text | Google Scholar

Shi, Z.-W., Cao, X.-X., Wen, Q.-Y., Wen, T.-L., Yang, Q.-H., Chen, Z., et al. (2018). Terahertz Modulators Based on Silicon Nanotip Array. Adv. Opt. Mater. 6 (2), 1700620. doi:10.1002/adom.201700620

CrossRef Full Text | Google Scholar

Wang, Y., and Li, Z. H. (2021). Terahertz Linear Polarization Converter Based on Electromagnetic Metasurface. J. Terahertz Sci. Electron. Inf. Technol. 19 (5), 815–818.

Google Scholar

Wang, Z. X., Wu, J. W., Wang, X., Wu, L. W., Xiao, Q., Cheng, Q., et al. (2020). Broadband and Ultrathin Huygens’ Metasurface with High Transmittance. J. Phys. D: Appl. Phys. 124585, R1.

Google Scholar

Wu, L., Fu, Y., Xu, N., Sheng, Q., Zhang, X., Yang, Y., et al. (2020). Observation of Phase Transitions of Ba0.6Sr0.4TiO3-Silicon Hybrid Metamaterial by THz Spectra. ACS Appl. Electron. Mater. 2 (8), 2449–2453. doi:10.1021/acsaelm.0c00390

CrossRef Full Text | Google Scholar

Xia, L., Zou, Y., Zhang, M., Yan, W., Dang, S., Li, S., et al. (2019). Multi-mode Graphene Based Terahertz Amplitude Modulation Enhanced by Hollow Cross H-Structured Metasurface. Phys. Scr. 94 (12), 125701. doi:10.1088/1402-4896/ab1bfe

CrossRef Full Text | Google Scholar

Xu, G., Gao, L., Chen, Y., Ding, Y., Wang, J., Fang, Y., et al. (2022). Broadband Polarization Manipulation Based on W-Shaped Metasurface. Front. Mater. 9, 850020. doi:10.3389/fmats.2022.850020

CrossRef Full Text | Google Scholar

Xue, C., Lou, Q., and Li, T. (2019). Ultra-compact, Broadband Huygens' Metasurfaces Based on Induced Magnetism. Appl. Phys. Express 12, 072005. doi:10.7567/1882-0786/ab266c

CrossRef Full Text | Google Scholar

Yang, C.-f., Huang, M., Yang, J.-j., Yin, J.-g., and Peng, J.-h. (2010). Design of the N-Sided Regular Polygonal Electromagnetic Wave Concentrator Using Metamaterials. J. Electron. Inf. Technol. 32 (10), 2485–2489. doi:10.3724/sp.j.1146.2009.01027

CrossRef Full Text | Google Scholar

Zang, T., Chen, Y., Ding, Y., Sun, Y., and Wu, Q. (2020). Broadband Electromagnetically Induced Transparency in Metamaterials Based on Hybridization Bandgap. AIP Adv. 10, 115002. doi:10.1063/5.0022254

CrossRef Full Text | Google Scholar

Zhang, J., Mei, Z. L., Zhang, W. R., Yang, F., and Cui, T. J. (2013). An Ultrathin Directional Carpet Cloak Based on Generalized Snell's Law. Appl. Phys. Lett. 103 (15), 151115. doi:10.1063/1.4824898

CrossRef Full Text | Google Scholar

Zhao, R., Zhu, Z., Dong, G., Lv, T., Li, Y., Guan, C., et al. (2019). High-efficiency Huygens' Metasurface for Terahertz Wave Manipulation. Opt. Lett. 44, 3482–3485. doi:10.1364/OL.44.003482

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhou, H., Cheng, J., Fan, F., Wang, X., and Chang, S. (2021). Ultrathin Freestanding Terahertz Vector Beam Generators with Free Phase Modulation. Opt. Express 29 (18), 1384–1395. doi:10.1364/OE.413119

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhu, H., Li, J., Du, L., Huang, W., Liu, J., Zhou, J., et al. (2020). A Phase Transition Oxide/Graphene Interface for Incident‐Angle‐Agile, Ultrabroadband, and Deep THz Modulation. Adv. Mater. Inter. 7 (24), 2001297. doi:10.1002/admi.202001297

CrossRef Full Text | Google Scholar